Experimental assessment of a 3-D plenoptic endoscopic imaging system

Abstract

An endoscopic imaging system using a plenoptic technique to reconstruct 3-D information is demonstrated and analyzed in this Letter. The proposed setup integrates a clinical surgical endoscope with a plenoptic camera to achieve a depth accuracy error of about 1 mm and a precision error of about 2 mm, within a 25 mm × 25 mm field of view, operating at 11 frames per second.

Endoscopic imaging provides visualization in minimally invasive surgery and helps reduce the trauma associated with open procedures^[1]. Recent advances in 3-D peripheral reconstruction for endoscopy allow for better tissue assessment and objective risk evaluation by surgeons, and help enhance autonomous control in robotic surgery^[2–4]. These advances have enabled real-time surface reconstruction during surgery, and include stereoscopy, time-of-flight (ToF), structured illumination, and plenoptic imaging. To achieve realistic 3-D surface reconstructions of a surgical site in aminimally invasive surgical setting, a 3-D endoscopic system should provide high precision and accuracy within the desired field of view (FOV), and a frame rate adequate for observation and navigation by surgeons.

Stereoscopy uses a passive wide-field illumination and acquires two images of an object from two viewing angles to reconstruct depth information via disparity searching. The depth resolution ranges from 0.05 to 0.6 mm^[5,6], which can be achieved with enhanced searching algorithms^[7–9]. However, this requires sufficient spatial offset between the two views to achieve a high depth resolution.

ToF techniques measure the differences in phase and intensity of time or frequency modulated laser pulses. Depth information can hence be reconstructed with low computational cost based on the active light modulation information. However, depth resolution based on ToF is relatively poor from 0.89 to 4 mm^[10,11]. In addition, this technique often suffers from systemic errors in camera temperature tolerance and varying exposure time. Other impact factors include biological optical properties from studied samples such as absorption and scattering coefficients that can change with respect to the incoming light source and ray angle^[12].

The structured illumination technique is classical in 3-D reconstruction, with its principle based either on disparity searching, similar to the stereoscopy technique^[13], or on the reconstructed phase information^[14,15] from multiple artificial light patterns on the sample. Structured illumination can achieve a very high depth resolution, up to 0.05 mm^[16], and has been employed in several medical applications^[17–20]. However, it requires an active pattern projector for light modulation that cycles between different pattern illuminations, leading to complications in camera calibration and necessitating a high-power light source^[21].

In addition to the three techniques described above, plenoptic imaging is a fairly new 3-D reconstruction technique in the biomedical field. The technique involves a microlens array (MLA) integrated onto an imaging sensor, such that each point of the object can be viewed and imaged at different angles via adjacent microlenses. The depth information can be deduced similarly to the stereoscopy approach. However, in stereoscopy, the two imagers should maintain a set angle of separation to obtain two distinct views of the object while ensuring the desired depth accuracy^[22–24]. A stereoscope utilizes triangulation in which the two imagers maintain a set angle relative the object for correspondence searching. As an extension of the stereoscope, a plenoptic imager utilizes only one sensor with multiple micro lenses to create a higher number of viewing positions, and thus improve the correspondence searching performance. Moreover, a plenoptic camera offers the reduction of systematic calibration due to the known separation between each microlens (i.e., known distance between microsensors). In addition, plenoptic imaging also creates the expansion of parallax computation in both horizontal and vertical directions compared to one dimension in a stereoscope. Currently, plenoptic imaging is widely accepted in industry for multifocus imaging^[25,26]; however, plenoptic imaging in medicine is limited with a current depth precision of 1 mm^[27,28] in wide-field imaging. To adapt this technique to an endoscopic setting for minimally invasive surgery, we propose a plenoptic endoscopy design that consists of a clinical surgical endoscope, a plenoptic camera, and a relay optical system. The proposed setup compensates for the aperture mismatch between the endoscope and the MLA fabricated on the plenoptic camera.

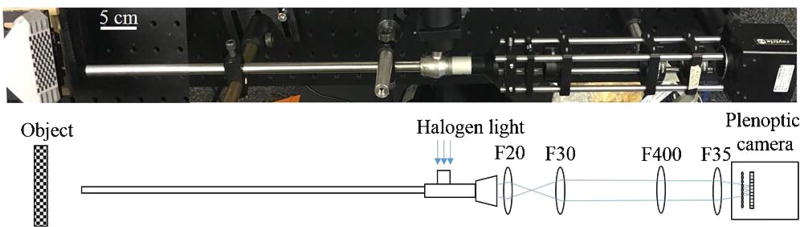
The endoscopic setup described in Fig. 1 employs a 0° surgical borescope with a scope housing diameter of 10 mm (Stryker, San Jose, California, USA) for both illumination and imaging. The light from a halogen bulb is coupled into the light pipe of the borescope to illuminate the surgical site and the image is coupled back to the plenoptic camera via the same borescope and a relay lens system. The plenoptic camera used is commercially available with a predefined MLA setting (Raytrix R5, Kiel, Germany). The relay lens system comprises four biconvex lenses with various focal lengths (Thorlabs, New Jersey, USA) to achieve the desired microlens image on the plenoptic camera. In particular, a 20 mm focal length biconvex lens (LA1859, Thorlabs, New Jersey, USA) is used to form an image with output light rays from the borescope eyepiece. This image is then expanded via three biconvex lenses with focal lengths of 30 mm (LA1805, Thorlabs, New Jersey, USA), 400 mm (LA1172, Thorlabs, New Jersey, USA), and 35 mm (LA1027, Thorlabs, New Jersey, USA) to form the microlens images with an aperture matching the aperture of the fabricated microlens. Beam expansion could be achieved with fewer lenses; however, the combination of F30 and F400 lenses is used to fine tune the image and to provide flexibility for beam delineation. A scale bar of 5 cm length is added in the system schematic for optical alignment reference. The imaging system is operated at 11 frames per second with CUDA GeForce GTX 690 on a Dell Precision T7600 workstation for image reconstruction.

Fig. 1.

Schematic of the endoscopic setup with the plenoptic camera and relay lens system.

In the plenoptic imaging setting, a main lens produces an image from a real object; this image then acts as the object for the MLA. Through the MLA, the incident light cone is split into multiple subimages collected by the sensor. Based on these collected microlens images, depth calculation is defined by the relation between the calculated virtual depth and the metric transformation relation^[29,30].

Depth calculation of a plenoptic setup relates to stereoscopy technology, where the MLA performs as a micro camera array that generates multiple views of a small portion of the object, which is also the image generated by the main lens. First, a correspondence search is established with each pixel location from one micro sensor correlated with the other pixel location from the adjacent micro sensor using the sum of the absolute difference method over a group of pixel points along the epipolar lines. The method searches for corresponding pixels between the two adjacent micro images by minimizing the absolute difference between the pixel values within a window size,

$$\sum _{i=1}^m\sum _{j=1}^n|I_1(i,j)-I_2(i+x,j+y)|,$$ (1)

where (i, j) is the pixel index of adjacent micro images I₁ and I₂, m and n are the pixel numbers along horizontal and vertical axes, and x and y represent the disparity along the two directions, respectively.

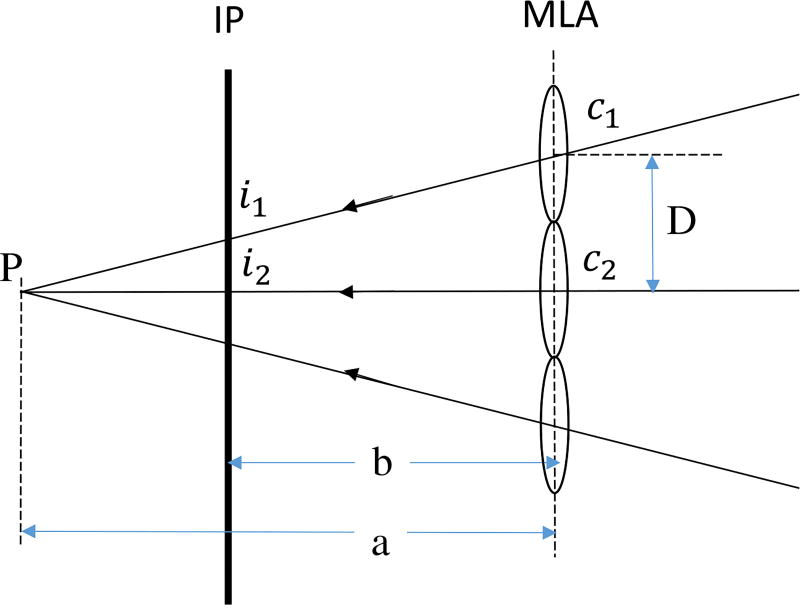
Once the correlated pixels of these micro images are determined, the intersection point of projected rays through these pixels into the virtual 3-D space determines the virtual depth of the object. This virtual depth is related to the distance between the observed object and the camera. An example depicted in Fig. 2 calculates the virtual depth υ_p to explain this calculation^[30],

$${\upsilon }_P=\frac{a}{b}=\frac{D}{D-(i_1-i_2)},$$ (2)

where a is the distance between MLA to the virtual parallax point, and b is the distance between the sensor and the MLA. D is the baseline distance between two microlenses with centers c₁ and c₂; i₁ and i₂ are the image pixels of the same object point projected by the two micro lenses.

Fig. 2.

Triangulation principle for virtual depth estimation. IP: Image plane.

From the virtual depth information, metric distance b_L of the virtual depth is computed as

$$b_L=h+{\upsilon }_{P}b,$$ (3)

where h is the distance between the main lens and the MLA.

As the optical property of the endoscope is proprietary, the overall system magnification is unknown theoretically; however, we determine the system magnification empirically using a known measurement height standard. Therefore, the scaled object height is determined using this magnification.

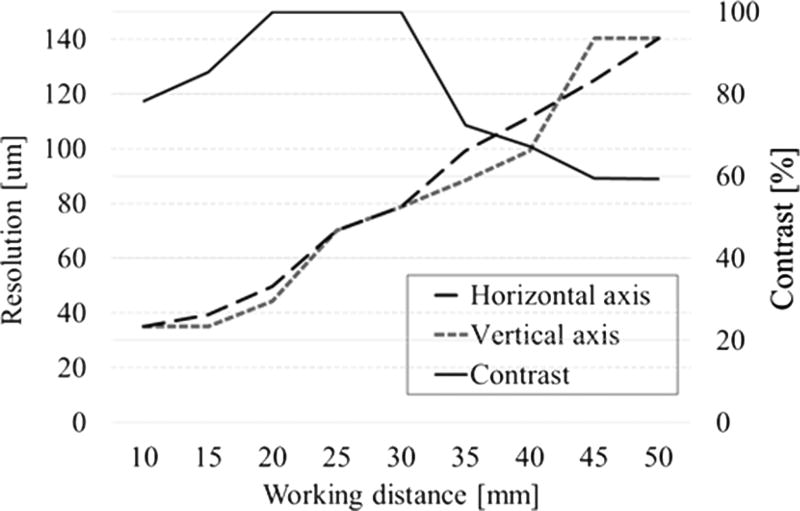
To evaluate the system performance, we calculate the depth of field (DOF) via the resolution and contrast measurement within a range of working distances. The resolution is the smallest resolvable width of a horizontal or vertical line on a USAF test target 1951 (R3L3S1 P, Thorlabs, New Jersey, USA). The standard target is moved away from the distal end of the borescope without refocusing, with an equal step size of 5 mm and increasing the located distance from 10 to 50 mm. In addition, a contrast change with the set working distance was also recorded. The resolution and DOF plot in Fig. 3 shows that the best contrast occurs at 20 to 30 mm away from the borescope. At this distance, the resolution is recorded to be within 50 to 80 µm, which is sufficient for imaging biological samples such as intestinal organs in anastomosis surgery.

Fig. 3.

Resolution and contrast measurements.

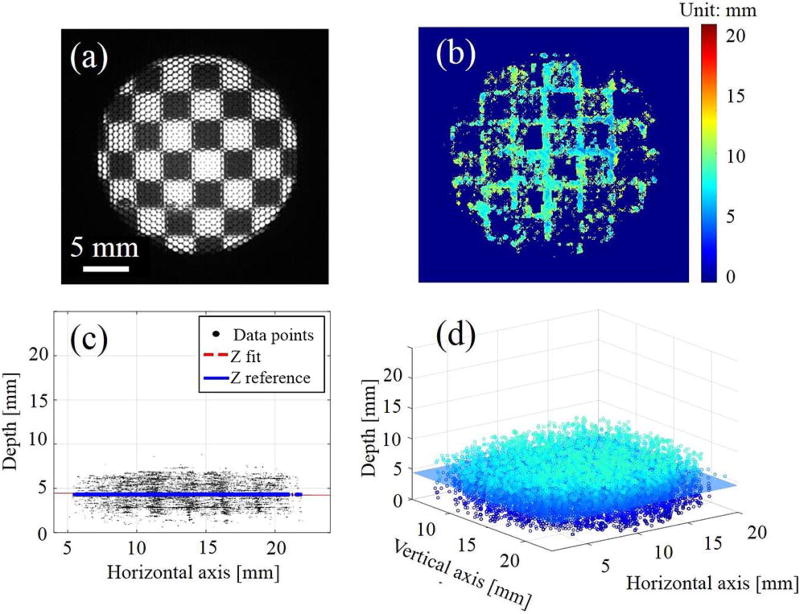
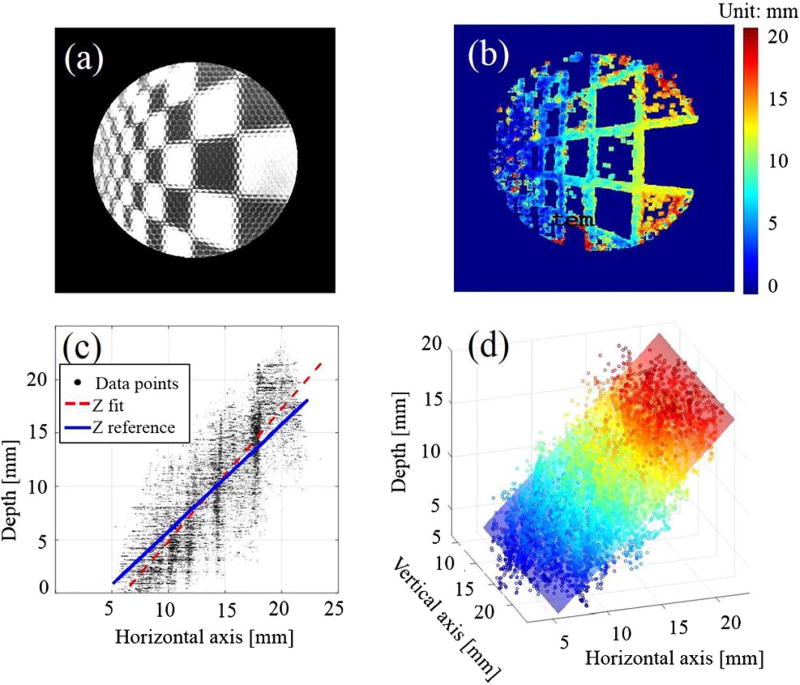
To further validate the system’s accuracy and precision, we used a checkerboard pattern with a known square size of 3.5 mm on a DOF target serving as the height standard (DOF 5–15, Edmund Optics, Barrington, New Jersey). The target is aligned at 0° and 45° and 20 mm away from the distal end plane of the borescope, as indicated in Figs. 4(a) and 5(a). The accuracy error is characterized by the mean distance and standard deviation between the fitted plane and the reference plane modeled at 0° and 45°, while the precision error is defined by the variation (mean distance and standard deviation) of the collected data points from the fitted planes [see Figs. 4(c) 4(d), 5(c), and 5(d)].

Fig. 4.

(a) Microlens image of the checker board at 0° with (b) its depth map and (c, d) point cloud data at different views.

Fig. 5.

Microlens image of the checker board at 45° with (b) its depth map and (c, d) point cloud data at different views.

Due to the triangulation, the depth reconstruction is only possible when sufficient object features and local contrast are achieved, such as at the edges and corners of the checkerboard, as observed in Figs. 4 and 5. As the angle deviates from 0° to 45°, the depth map and point cloud accumulations illustrate the change presented in the corresponding colormap. The calculated accuracy and precision are displayed in Table 1, with an average maximum accuracy and precision error of about 1–2 mm and a FOV of 25 mm × 25 mm. Depending on the object of interest, a required FOV, resolution, and depth precision is demanded accordingly. For a minimally-invasive surgical endoscope especially for anastomosis surgery, a FOV of 25 mm × 25 mm × 25 mm with a spatial resolution of about 200 µm and a depth precision of about 1 mm are sufficient for 3-D image guided anastomosis^[4].

Table 1.

Reconstruction Accuracy and Precision at Two Planar Angle Deviations at 0° and 45° (Unit: mm)

		0°	45°
Accuracy	Mean	0.085	0.818
	Standard deviation	0.032	0.440
	Maximum	0.103	1.439
Precision	Mean	1.141	2.367
	Standard deviation	0.721	1.800
	Maximum	3.863	11.658

A finer grid pattern for testing the system’s accuracy and precision in Figs. 4 and 5 can improve the 3-D reconstruction due to the increase in data points. However, in medical applications imaging targets often lack dense features. We thus believe that a sparsely distributed checkerboard provides a more realistic test pattern. We also believe that a custom-developed light-field endoscopic camera with a custom MLA will further improve the precision and accuracy in the future.

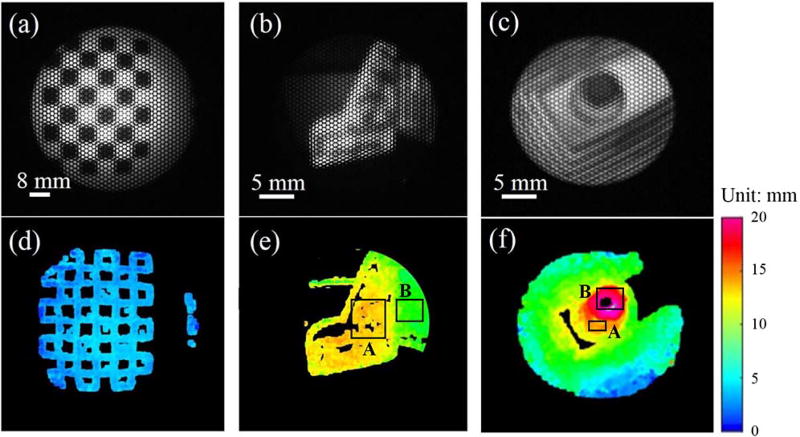
Other complicated 3-D-printed objects of polydimethylsiloxane material with defined structures and known dimensions were further used to examine the system spatial reconstruction. The result indicates the distinct curvature and heights of the objects with the displayed depth colormap (see Fig. 6). In particular, an average reconstructed height from the L-shape base A to the lower base B of the second object [Figs. 6(b) and 6(e)] is 5.5 mm compared to the physical height of 6.64 mm, leading to an error of 1.14 mm. Another height error for the third 3-Dprinted object in Figs. 6(c) and 6(f) was also recorded to be 0.75 mm from the base A to the podium base B. A biological sample of a fowl ventricular specimen was harvested for 3-D measurement (Fig. 7). The specimen’s structural features are contained; however, circular patterns between the microlenses were also detected. This can be explained by the unresolved depth information between the microlens’ edges.

Fig. 6.

(a–c) Microlens image of a plane and inhomogeneous objects and (d–f) its reconstructed depth maps.

Fig. 7.

(a) Microlens image of a fowl ventricular specimen and (b–d) its 3-D reconstructions at multiple angles.

Due to the nature of the plenoptic technique for searching for the disparity between adjacent microlens images, the reconstruction algorithm depends strongly on the inherent features of the tested samples. In other words, featureless or homogeneous regions of the object create outliers or missing depth information, thus data interpolation is essential. To compensate for this limitation, a projector can be used to actively illuminate known features onto the object and an efficient illumination setting can be used to resolve the finer details of the object as well as to avoid reflectance saturation. Nonexistent data points have no effect on the accuracy and precision. The depth estimation depends on detectable features that could be maximized by using active illumination. There are a few advantages of plenoptic endoscopy with active illumination over normal structured illumination. The first is that the plenoptic approach allows the user to observe the scene from a variety of angles in both horizontal and vertical directions due to the MLA arrangement. The second is that the entire scene can be brought into focus provided that it is within the FOV. Lastly, the structure of the illumination needs not be known beforehand, and is not a source of error. Typical structured light approaches rely on a precisely known projection pattern, whereas the plenoptic approach seeks only high contrast features, which can be provided in a myriad of ways.

In conclusion, a 3-D endoscopic system using a plenoptic imaging technique is demonstrated with reconstructed dimensions of both planar and complex samples. We are currently working with the research and development team at the Raytrix Company to further improve the design of MLA that will benefit from such endoscopic 3-D vision for minimally invasive surgery. The improvement involves the f-matching performance of aperture size between the MLA and the optics of the commercial surgical borescope, while maintaining an adequate frame rate for surgical guidance purpose (10 frames per second). Moreover, other optical analysis techniques, such as multispectral imaging or laser speckle contrast, can be registered onto the 3-D rendering to provide the dynamic properties of the studied tissue in minimally invasive surgery.