Abstract
θ-Defensins are mammalian cyclic peptides that have antimicrobial activity and show potential as stable scaffolds for peptide-based drug design. The cyclic cystine ladder structural motif of θ-defensins has been characterized using NMR spectroscopy and is important for their structure and stability. However, the effect of the pronounced elongated topology of θ-defensins on their molecular motion is not yet understood. Studies of molecular motion by NMR relaxation measurements have been facilitated by the recent development of a semirecombinant method for producing cyclic peptides that allows for isotopic labeling. Here we have undertaken a multifield 15N NMR relaxation analysis of the anti-HIV θ-defensin, HTD-2, and interpreted the experimental data using various models of overall and internal molecular motion. We found that it was necessary to apply a model that includes internal motion to account for the variations in the experimental T1 and NOE data at different backbone amide sites in the peptide. Although an isotropic model with internal motion was the simplest model that provided a satisfactory fit with the experimental data, we cannot exclude the possibility that overall motion is anisotropic, especially considering the strikingly elongated topology of θ-defensins. The presence of flexible side chains, self-association, interactions with solvent, and internal motions are all potential contributors to the observed relaxation data. Internal motion consistent with the constraints imposed by the cyclic cystine ladder was observed in that the order parameters, S2, show that residues in the turns are more flexible than those in the β-sheet. This study provides insights into the dynamics of θ-defensins and information that might be useful in their application as scaffolds in drug design.
Keywords: NMR relaxation, protein dynamics, theta-defensins
Graphical Abstract
INTRODUCTION
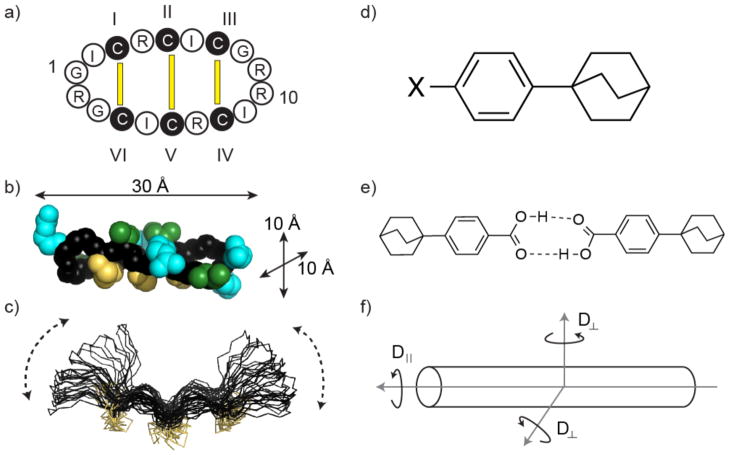
θ-Defensins(1) are ribosomally synthesized cyclic peptides that are part of the innate immune systems of old world primate species.(2) They are biosynthesized by the double head-to-tail ligation of two nine-residue “demidefensins” to form an 18-residue-backbone cyclic peptide. There is interest in developing θ-defensins as antimicrobial agents because they have antibacterial and antiviral activity, including activity against HIV and antibiotic-resistant pathogens.(3) Furthermore, θ-defensins have shown potential as scaffolds for peptide drug design.(4) θ-Defensins comprise a cyclic peptide backbone cross-braced by three disulfide bonds (Figure 1) in a structural motif that is known as the cyclic cystine ladder.(2) The I–VI, II–V, and III–IV disulfide connectivity of the cyclic cystine ladder results in θ-defensins having an elongated topology (Figure 1) with a length of ~30 Å and cross-sectional dimensions of ~10 × 10 Å2. This geometry suggests that θ-defensins might have highly anisotropic overall motion in solution, approximating that of an axially symmetric cylinder. Such geometry might also be expected to promote enhanced internal flexibility of the turns at the molecular extremities.
Figure 1.
θ-Defensins and phenylbicyclo[2.2.2]octanes have similar elongated topologies. (a) The cyclic peptide backbone of HTD-2 (retrocyclin-2) is cross-braced by three parallel disulfide bonds forming a cyclic cystine ladder (yellow bars). Amino acids are represented by their one-letter codes, with residues 1 and 10 numbered. Cystine residues are shown as filled black circles and the I–VI, II–V, and III–IV connectivity of the cyclic cystine ladder is indicated. (b) Solution structure of HTD-2 (PDB code: 2LZI)(6) in space-filling representation showing the molecular dimensions. The backbone is shown in black with disulfide bonds in yellow, arginine side-chains in cyan, and isoleucine side-chains in green. (c) NMR structure ensemble of RTD-1 (PDB code: 1HVZ)(7) showing a previously proposed “butterfly”-type motion of the backbone (dotted lines). The structure is shown in line representation with disulfide bonds in yellow. (d) Para-substituted phenylbicyclo[2.2.2]octanes have similar length to cross-section ratio to θ-defensins. The size and polarity of the substituent X affects the molecular dynamics. (e) Carboxyl-substituted phenylbicyclo[2.2.2]octanes dimerize in chloroform solution,(5) effectively doubling the length of the molecule. (f) Axially symmetric anisotropic motion. The diffusion tensors perpendicular (D⊥) to the principal axis are assumed to be equal. Rotation parallel to the principal axis is faster than rotation perpendicular to it.
Axially symmetric anisotropic motion has been well characterized by NMR spectroscopy for a series of substituted phenylbicyclo[2.2.2]octanes (Figure 1).(5) These elongated organic molecules are much smaller than θ-defensins but have a similar length to cross-section ratio of ~3:1, and the two classes of molecules might be expected to have similar extents of overall anisotropic motion. In a series of para-substituted phenylbicyclo[2.2.2]octanes, the ratios of the diffusion coefficients parallel (D||) and perpendicular (D⊥) to the symmetry axis (Dratio = D||/D⊥) ranging from ~3 to 12, i.e., indeed indicative of highly anisotropic overall motion. Whereas small nonpolar substituents resulted in a Dratio of ~3, bulky or polar substituents restricted rotation perpendicular to the symmetry axis, increasing the Dratio. In the most extreme case of anisotropic motion, substitution with a carboxyl group caused dimerization in chloroform solution, effectively doubling the length to cross-section ratio of the molecule (Figure 1).(5)
NMR spectroscopy has been used to study the structures of θ-defensins and their self-association in solution(6, 8) and is also well suited to characterizing the molecular dynamics of these elongated peptide structures. NMR relaxation measurements contain information about the motions of molecules because the nuclear spin relaxation is mediated by fluctuating local magnetic fields, caused by overall and internal molecular motion.(9) In the initial structural study on RTD-1, the observation of some broadened peaks led to the suggestion that the molecule is flexible in solution, undergoing a “butterfly”-type motion (Figure 1c).(7) However, later structures of RTD-1 and other θ-defensins suggested a more rigid backbone(6) based on minimal disorder in the ensemble of NMR structures. We focused here on NMR relaxation measurements as these provide direct insights into local motions at defined atomic sites in molecules. As shown in recent examples,(10–12) such NMR relaxation data can facilitate an understanding of molecular binding properties and mechanisms of action.
Molecular dynamics studies of proteins by NMR typically focus on the relaxation of 13C or 15N nuclei in the peptide backbone, as they are the most informative for understanding backbone dynamics. Isotopically labeled proteins greatly increase the sensitivity of the relaxation measurements and are easily accessible if the protein is produced recombinantly. However, small cyclic peptides such as θ-defensins are usually synthesized chemically, which makes isotope labeling immensely expensive. Recombinant synthesis of θ-defensins is challenging because their biosynthetic mechanism is not well understood.(2) However, recent developments in recombinant production using modified protein splicing and cell-free ribosomal synthesis have allowed for the cost-effective production of isotopically labeled θ-defensins for NMR applications.(13, 14) In the protein-splicing method, a precursor peptide is produced recombinantly. The sequence includes a C-terminal modified protein-splicing unit or intein and an N-terminal TEV (Tobacco Etch Virus) protease recognition sequence that are used to cyclize the peptide in vitro (or in vivo) using an intramolecular form of native chemical ligation between an N-terminal Cys and a C-terminal α-thioester.(15, 16)
In this study we took advantage of developments in the recombinant expression of θ-defensins(14) and NMR spectroscopic techniques(17) to investigate the overall and internal motions of the elongated peptide θ-defensin HTD-2. This peptide is also known as retrocyclin-2 and is a dimer of two demidefensins that differ by only one residue from one another and thus has a high degree of symmetry.(18) The demidefensins are encoded in the human genome; however, the mature peptide is not expressed because a stop codon in the signal sequence of each demidefensin prevents translation. HTD-2 has potent anti-HIV activity and so, ironically, its lack of expression in humans fails to produce a natural HIV defense that might have been present in ancestral species.(19) Nevertheless, an exogenous synthetic version is being investigated as a topical microbicide.(20) To understand the molecular dynamics of HTD-2, the fit of the NMR relaxation data to isotropic and anisotropic models of overall motion, with and without internal motions, was determined, giving insights into the effects of peptide topology on molecular motion.
EXPERIMENTAL
Peptide recombinant production and purification
The 15N-labeled HTD-2 used for NMR relaxation analysis was produced semirecombinantly using the modified protein splicing method as previously described.(14, 21) Briefly, synthetic DNA encoding the HTD-2-intein defensin precursor with an N-terminal TEV (Tobacco Etch Virus) protease recognition sequence (Supporting Information Table S1) was generated and cloned into plasmid pTXB1 using the NdeI and SapI restriction sites as previously described.(16) The ligated plasmid pTXB1-TEV-HTD2-GyrA was transformed into DH5α cells and screened as described above. The DNA sequence of the plasmid was confirmed by sequencing. This plasmid was transformed into competent BL21(DE3) cells for protein expression. Transformed cells were grown in 2 L of M9 minimal medium containing 0.1% 15NH4Cl as the nitrogen source and ampicillin (100 μg/mL) to an OD at 600 nm of ~0.6 at 37 °C and expression was induced by the addition of isopropyl-β-d-thiogalactopyranoside (IPTG) to a final concentration of 0.3 mM at 30 °C for 4 h. The cells were lysed and the intein fusion protein was purified on chitin beads as previously described.(16) Cyclization and folding of HTD-2 was performed in a one-pot reaction by incubating the TEV-HTD-2-intein precursor immobilized on chitin beads in freshly degassed TEV protease reaction buffer (100 mM Na2HPO4, 0.5 mM EDTA, pH 7.2) containing 100 mM reduced glutathione and 0.5 mg/mL TEV protease at room temperature for 3 days. Folded HTD-2 was purified by C18-RP-HPLC, providing ~200 μg of 15N-labeled HTD-2 per liter of bacterial culture. Peptide purity was checked by analytical C18-RP-HPLC and EM/MS (Expected mass: 2050.6 Da, observed mass: 2049.4 ± 0.2 Da) (Supporting Information, Figure S1).
NMR relaxation theory
The NMR parameters T1, T2, and NOE contain information about molecular motion because the relaxation of magnetically active nuclei is mediated by fluctuating local magnetic fields, which are caused by overall and internal molecular motions.(9) For 15N nuclei in small proteins, the main mechanisms of relaxation influenced by molecular motion are dipole–dipole interactions with directly bonded protons and chemical shift anisotropy.(22) The observed relaxation data T1 (=1/R1), T2 (=1/R2), and NOE are related by equations (1), (2), and (3) to the spectral density function, J(ω).(23, 24)
| (1) |
| (2) |
| (3) |
Here μ0 is the permeability of a vacuum, γN and γH are the gyromagnetic ratios for 15N and 1H, respectively, h is Planck’s constant, rNH is the N–H internuclear distance (1.02 Å), ωN and ωH are the Larmour frequencies of 15N and 1H, respectively, Rex is the chemical exchange contribution, and c = ωNΔσ/√3, where Δσ is the chemical shift anisotropy for 15N nuclei.(24) The spectral density function, J(ω), describes the energy available for transitions at different frequencies and is dependent on the amplitudes and frequencies of overall and internal motions. Mathematical models of molecular motion have been developed that define J(ω) in terms of motional parameters. Fitting the relaxation data calculated using these models to the experimental data is used to select an appropriate model and evaluate the associated motional parameters. In the “model-free” approach,(25, 26) overall molecular tumbling is quantified by the overall correlation time, τo, and the amplitude and rate of internal motions on the picosecond–nanosecond time scale are quantified by the generalized order parameter, S2, and the internal correlation time, τi, respectively.
Four motional models were selected to fit with the experimental relaxation data for HTD-2. In the isotropic rigid model (Iso rigid, eq. 4), the molecule is assumed to tumble isotropically as a sphere with a single overall correlation time, τo, and T1 and NOE are accordingly the same for all sites in the molecule. In the isotropic model with internal motion (Iso + int, eq. 5), the amplitudes of the internal motions are described by the order parameter, S2, and their rates by an internal correlation time, τi. In the axial rigid model (Ax rigid, eq. 6), motion is axially symmetric and the spectral density function is dependent on the diffusion tensors parallel (D||) and perpendicular (D⊥) to the principal axis and the angle, θ, between the bond vector and the principal axis. In the axial model with internal motion (Ax + int, eq. 7), the spectral density function depends on the axial parameters, D||, D⊥, and θ and the internal motion parameters S2 and τi.
| (4) |
| (5) |
Where
| (6) |
Where
| (7) |
Where
The apparent overall correlation time for the axial rigid model is defined(27) as:
| (8) |
NMR spectroscopy
The peptide sample for NMR analysis was prepared in 90% H2O/10% D2O at ~0.3 mM and pH 3.4. NMR spectra were recorded on Bruker Avance-500, 600, or 900 MHz spectrometers at 298 K. Spectra were processed with TopSpin (Bruker) using a zero scaling factor, phased, and calibrated and then assigned with CCPNMR software.(28) Chemical shifts in the 1H dimension were referenced to internal 4,4-dimethyl-4-silapentane-1-sulfate (DSS) and 15N dimensions were indirectly referenced to DSS.(29) Assignment of the 15N chemical shifts was achieved using a 15N HSQC-TOCSY spectrum.
T1 (spin–lattice) 15N relaxation times were measured using the Bruker pulse program hsqct1etf3gpsi. NMR spectra were acquired with a spectral width of 14.9 (500 MHz) or 16.0 (600 MHz) ppm over 2048 complex points in the 1H dimension and 35 ppm over 128 complex points in the 15N dimension with 128 transients. A recycle delay of 5 s (>5 × T1) was included and 11–14 relaxation delays in the range 0.01 to 10 s were used for each T1 determination. Experiments were carried out in triplicate, with a different order of relaxation delays used in each experiment. Peak heights (measured in CCPNMR) were fitted using a two-parameter fit exponential equation to determine T1 values for the backbone NH of each residue except for Cys3 and Cys12, which were overlapped with Ile6 and Ile15. Errors were calculated as the standard deviation of the three calculated T1 values.
Measurements of 15N NOEs were made by determining the ratio of peak intensities from 2D 1H–15N correlation spectra via double inept transfer using sensitivity improvement with decoupling during acquisition, using Bruker pulse program hsqcnoef3gpsi with a recycle delay of 5 s ((7.4–9.6) × T1 at 500 MHz, (7.2–8.8) × T1 at 600 MHz, and (7.0–8.9) × T1 at 900 MHz). A relaxation delay of ~10 × T1 has been recommended for heteronuclear NOE measurements;(30) however, in a trial, we found that there was no difference between NOEs measured using a relaxation delay of 5 s (~8 × T1) and 10 s (~16 × T1). NOE on and NOE off spectra were acquired in an interleaved fashion with 32 scans being obtained in each cycle and then split prior to Fourier transform with a zero scaling factor. The two spectra were phased identically and the intensities of the respective peaks were measured using CCPNMR software.(28) Experiments were carried out in triplicate on three different days and errors were calculated as the standard deviation over the three NOE experiments.
Relaxation analysis
The T1 and NOE relaxation data were fitted to models described in the “model-free” approach(25) (eqs 4–7) using the “solver” function in Microsoft Excel (data presented in Table 1) and the program Modelfree 4.15(24, 31) (data presented in Supporting Information Table S4). Although T2 data are often included in dynamics studies,(27) we did not attempt T2 measurements in this study due to instrument limitations and chose instead to measure T1 and NOE data at three field strengths, which provides six data points per residue, and therefore should be adequate for fitting the selected models of motion. The errors in the fitted values were estimated by fitting to simulated data generated using a Monte Carlo algorithm. The mean and standard deviation of the fitted values from the Excel spreadsheet and Modelfree are shown in Supporting Information Tables S5 and S6, respectively. The amide bond length was fixed at 1.02 Å and a 15N chemical shift anisotropy value of −160 ppm was used in the calculations.(24, 32) For fitting of the axial rigid model, the average structure of HTD-2 (PDB ID: 2LZI) was aligned with the principal axis of the molecule along the z-axis and θ was calculated as the angle of each N–H vector with the z-axis. A predicted Dratio of 2.44 and D|| of 2.5 × 108 s−1, both obtained using Hydronmr,(33) were used for computing the axial rigid model. Hydronmr(29) also provided an estimate of the overall rotational correlation time (τ0 = 1.09 ns). In the optimization of the fit of the model with the experimental data, the fit of the NOE values was given a 50% weighting compared to the T1 values to take into account the higher uncertainty in the experimental NOE measurements.(34) The fits were compared using the weighted average of the sum of the squared errors.
Table 1.
Experimental and fitted NMR relaxation data for HTD-2.
| Residue | Dataa | 500 | 600 | 900 | 500 | 600 | 900 | θ (deg) | τi (ps) | S2 | RMSDb |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Gly | Exp | 0.57 | 0.65 | 0.71 | −0.26 | 0.03 | 0.57 | 111 | |||
| IsoRigidc | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.33 | ||||
| Ax Rigidd | 0.46 | 0.48 | 0.47 | −0.39 | −0.04 | 0.52 | 111 | 0.33 | |||
| Iso + Inte | 0.63 | 0.65 | 0.63 | −0.29 | 0.05 | 0.57 | 2 | 0.71 | 0.10 | ||
| 2 Ile | Exp | 0.57 | 0.60 | 0.61 | −0.36 | 0.05 | 0.60 | 80 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.23 | ||||
| Ax Rigid | 0.47 | 0.49 | 0.48 | −0.47 | −0.10 | 0.49 | 80 | 0.25 | |||
| Iso + Int | 0.59 | 0.60 | 0.59 | −0.30 | 0.05 | 0.56 | 3 | 0.76 | 0.06 | ||
| 3 Cysf | Exp | −0.23 | 0.07 | 0.58 | 91 | ||||||
| IsoRigid | −0.36 | 0.00 | 0.55 | 0.11 | |||||||
| Ax Rigid | −0.49 | −0.11 | 0.48 | 91 | 0.24 | ||||||
| Iso + Int | −0.30 | 0.05 | 0.56 | 25 | 0.93 | 0.05 | |||||
| 4 Arg | Exp | 0.59 | 0.58 | 0.57 | −0.47 | 0.04 | 0.63 | 82 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.22 | ||||
| Ax Rigid | 0.47 | 0.49 | 0.48 | −0.48 | −0.10 | 0.49 | 82 | 0.22 | |||
| Iso + Int | 0.58 | 0.59 | 0.58 | −0.32 | 0.02 | 0.52 | 18 | 0.77 | 0.13 | ||
| 5 Cys | Exp | 0.56 | 0.60 | 0.63 | 0.39 | 0.06 | 0.67 | 79 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.25 | ||||
| Ax Rigid | 0.47 | 0.49 | 0.48 | −0.46 | 0.09 | 0.49 | 79 | 0.27 | |||
| Iso + Int | 0.59 | 0.60 | 0.58 | −0.28 | 0.06 | 0.57 | 1 | 0.77 | 0.11 | ||
| 6 Ile | Exp | 0.54 | 0.56 | 0.56 | −0.38 | 0.13 | 0.65 | 67 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.20 | ||||
| Ax Rigid | 0.46 | 0.47 | 0.47 | −0.38 | −0.02 | 0.53 | 67 | 0.21 | |||
| Iso + Int | 0.55 | 0.56 | 0.55 | −0.28 | 0.06 | 0.58 | 0 | 0.82 | 0.10 | ||
| 7 Cys | Exp | 0.53 | 0.57 | 0.57 | −0.35 | 0.12 | 0.61 | 86 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.19 | ||||
| Ax Rigid | 0.48 | 0.49 | 0.48 | −0.49 | −0.11 | 0.48 | 86 | 0.25 | |||
| Iso + Int | 0.55 | 0.56 | 0.55 | −0.28 | 0.06 | 0.58 | 0 | 0.82 | 0.08 | ||
| 8 Gly | Exp | 0.55 | 0.57 | 0.63 | −0.30 | 0.09 | 0.62 | 87 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.23 | ||||
| Ax Rigid | 0.48 | 0.49 | 0.48 | −0.49 | −0.11 | 0.48 | 87 | 0.29 | |||
| Iso + Int | 0.58 | 0.59 | 0.58 | −0.28 | 0.06 | 0.57 | 1 | 0.78 | 0.08 | ||
| 9 Arg | Exp | 0.61 | 0.65 | 0.64 | −0.31 | 0.08 | 0.56 | 85 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.30 | ||||
| Ax Rigid | 0.48 | 0.49 | 0.48 | −0.48 | −0.11 | 0.48 | 85 | 0.33 | |||
| Iso + Int | 0.63 | 0.64 | 0.62 | −0.29 | 0.06 | 0.57 | 2 | 0.72 | 0.04 | ||
| 10 Argg | Exp | 0.67 | 0.69 | −0.29 | −0.04 | 0.47 | 76 | ||||
| IsoRigid | 0.46 | 0.47 | −0.36 | 0.00 | 0.55 | 0.31 | |||||
| Ax Rigid | 0.47 | 0.48 | −0.45 | −0.08 | 0.50 | 76 | 0.31 | ||||
| Iso + Int | 0.67 | 0.68 | −0.35 | −0.02 | 0.49 | 18 | 0.66 | 0.05 | |||
| 11 Ile | Exp | 0.62 | 0.64 | 0.64 | −0.28 | −0.07 | 0.56 | 117 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.31 | ||||
| Ax Rigid | 0.46 | 0.47 | 0.46 | −0.34 | 0.00 | 0.54 | 117 | 0.31 | |||
| Iso + Int | 0.63 | 0.64 | 0.63 | −0.32 | 0.02 | 0.53 | 12 | 0.71 | 0.07 | ||
| 12 Cysf | Exp | −0.21 | 0.09 | 0.51 | 89 | ||||||
| IsoRigid | −0.36 | 0.00 | 0.55 | 0.13 | |||||||
| Ax Rigid | −0.49 | −0.11 | 0.48 | 89 | 0.25 | ||||||
| Iso + Int | −0.29 | 0.05 | 0.57 | 24 | 0.96 | 0.08 | |||||
| 13 Arg | Exp | 0.58 | 0.57 | 0.60 | −0.38 | 0.04 | 0.59 | 91 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.21 | ||||
| Ax Rigid | 0.48 | 0.49 | 0.48 | −0.49 | −0.11 | 0.48 | 91 | 0.23 | |||
| Iso + Int | 0.57 | 0.59 | 0.57 | −0.29 | 0.05 | 0.57 | 12 | 0.78 | 0.07 | ||
| 14 Cys | Exp | 0.56 | 0.59 | 0.59 | −0.39 | 0.06 | 0.65 | 101 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.22 | ||||
| Ax Rigid | 0.47 | 0.49 | 0.48 | −0.46 | −0.09 | 0.49 | 101 | 0.24 | |||
| Iso + Int | 0.59 | 0.60 | 0.58 | −0.29 | 0.05 | 0.57 | 4 | 0.77 | 0.09 | ||
| 15 Ile | Exp | 0.54 | 0.55 | 0.58 | −0.38 | 0.13 | 0.64 | 114 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.20 | ||||
| Ax Rigid | 0.46 | 0.47 | 0.47 | −0.37 | −0.01 | 0.53 | 114 | 0.20 | |||
| Iso + Int | 0.55 | 0.56 | 0.55 | −0.28 | 0.06 | 0.58 | 0 | 0.82 | 0.10 | ||
| 16 Cys | Exp | 0.52 | 0.58 | 0.59 | −0.25 | 0.07 | 0.62 | 98 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.21 | ||||
| Ax Rigid | 0.47 | 0.49 | 0.48 | −0.47 | −0.10 | 0.49 | 98 | 0.27 | |||
| Iso + Int | 0.56 | 0.57 | 0.56 | −0.28 | 0.06 | 0.58 | 0 | 0.81 | 0.06 | ||
| 17 Gly | Exp | 0.61 | 0.58 | 0.61 | −0.32 | 0.08 | 0.65 | 94 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.25 | ||||
| Ax Rigid | 0.48 | 0.49 | 0.48 | −0.49 | −0.11 | 0.48 | 94 | 0.30 | |||
| Iso + Int | 0.59 | 0.61 | 0.59 | −0.28 | 0.06 | 0.58 | 0 | 0.76 | 0.07 | ||
| 18 Arg | Exp | 0.60 | 0.68 | 0.71 | −0.25 | 0.04 | 0.44 | 127 | |||
| IsoRigid | 0.46 | 0.47 | 0.46 | −0.36 | 0.00 | 0.55 | 0.37 | ||||
| Ax Rigid | 0.44 | 0.45 | 0.45 | −0.22 | 0.10 | 0.58 | 127 | 0.40 | |||
| Iso + Int | 0.67 | 0.68 | 0.66 | −0.32 | 0.02 | 0.53 | 10 | 0.67 | 0.11 | ||
| RMSDh | IsoRigid | 0.47 | 0.55 | 0.63 | 0.23 | 0.23 | 0.22 | ||||
| Ax Rigid | 0.46 | 0.53 | 0.58 | 0.44 | 0.47 | 0.35 | |||||
| Iso + Int | 0.12 | 0.05 | 0.13 | 0.23 | 0.11 | 0.18 |
Abbreviations used: Exp, experimental data; Iso Rigid, isotropic rigid; Ax Rigid, axial rigid; Iso + Int, isotropic with internal motion.
RMSD is the root mean square deviation between the experimental and fitted (calc) T1 and NOE values. The NOE deviations were weighted by 50% because of their intrinsically higher errors compared to the T1 values.
For isotropic rigid motion, the overall correlation time, τ0 = 1.04 ns.
For axial rigid motion, the overall correlation time, τ0 = 1.09 ns and the Dratio = 2.44.
For isotropic with internal motion, the overall correlation time, τ0 = 1.09 ns.
The 15N HSQC peaks for Cys3 and Cys12 were overlapped with those of Ile6 and Ile15 and a satisfactory exponential fit could not be obtained to determine T1.
Broadening of the Arg10 NH peak resulted in a poor exponential fit so Arg10 T1 was excluded from the analysis.
RMSD is the root-mean-square deviation between the experimental and fitted T1 and NOE values calculated over all the residues at each field strength.
RESULTS AND DISCUSSION
Synthesis of 15N-labeled HTD-2 was achieved using the modified protein-splicing method.(14) Cyclization was carried out in vitro and proceeded smoothly, as for RTD-1,(14) and the peptide was further purified by HPLC (Supporting Information, Figure S1). The total yield of pure cyclic peptide was ~400 μg, which provided a sufficient quantity for NMR relaxation experiments.
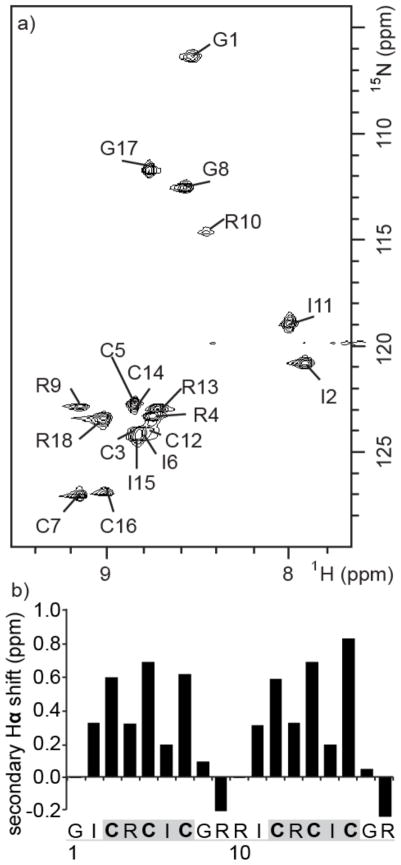
A three-dimensional 15N-HSQC-TOCSY spectrum was used to assign the 15N chemical shifts of HTD-2 (Figure 2a). The sequence comprises two nine-residue “demidefensins”, which differ by only one residue (GICRCICGR and RICRCICGR). This degeneracy results in significant spectral overlap and a three-dimensional spectrum was needed to assign the chemical shifts unambiguously. Secondary Hα chemical shifts were calculated as the difference between the measured Hα shift of each residue and its respective random coil shift (Figure 2b(35) and Supporting Information Figure S2).(36) The sign of the secondary shifts is consistent with the β-strand (positive secondary shifts) and turn (negative secondary shifts) structure of HTD-2. The magnitudes of the secondary shifts suggest that the peptide is highly structured in the β-sheet region,(35) but less well structured in the turns. Interestingly, the secondary shifts corresponding to the β-sheet regions show a two-residue periodicity; specifically, residues 3, 5, 7 and 12, 14, 16 have much higher secondary shifts compared with other residues within the β-sheets. This pattern has been predicted for β-sheets by Ösapay and Case(37) and has been interpreted in terms of solvent exposure.(38) In the θ-defensins that have been structurally characterized the two turns are of type β1′, a turn type in which a glycine residue is usually found in the i+2 position.(6) This preference for glycine in the i+2 position provides an explanation for the broadening of the Arg10 NH peak (Figure 2a) compared to that of Gly1. Peak broadening is a potential indicator of slow conformational exchange, consistent with the Arg-containing turn being less defined or stable than the Gly-containing turn.
Figure 2.
NMR data for HTD-2. (a) Assigned 15N HSQC spectrum of 15N-labeled HTD-2. (b) Secondary Hα chemical shifts of HTD-2. The secondary Hα shift is the difference between the measured chemical shift and the random coil shift.(35) Cysteine residues are shown in bold, β-sheet regions are highlighted in gray, and loops are underlined in gray in the peptide sequence.
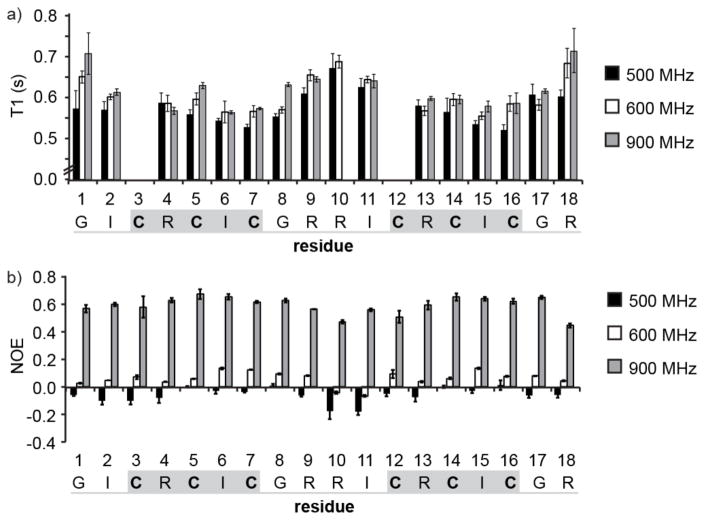
Spin–lattice (T1) relaxation times and NOEs were measured at 500, 600, and 900 MHz for each of the backbone amides in HTD-2 (Figure 3a and Supporting Information Table S2). The T1 relaxation times for residues in the turn regions (residues 8, 9, 10, 11 and 17, 18, 1, 2) are generally larger than those of the residues in the β-sheet region and smaller NOEs are observed for the turn residues than for the β-sheet (Figure 3b and Supporting Information Table S3). Parameters describing the molecular dynamics of HTD-2 were determined by fitting models of molecular motion to the observed T1 and NOE data. The spectral density equations used to describe the models were those developed in the “model-free” approach of Lipari and Szabo,(25) as implemented in Modelfree 4.15.(24, 31) The experimental and fitted data are shown in Table 1.
Figure 3.
Experimental relaxation data for amide nitrogen nuclei in 15N-labeled HTD-2. (a) Variation of T1 relaxation times along the peptide chain, measured at 500, 600, and 900 MHz. T1 relaxation data for Cys3 and Cys12 could not be determined accurately because of overlap of the peaks with Ile6 and Ile15, and so data for these residues were excluded from the analysis. The mean value of three replicate T1 experiments is shown and the error bars represent the standard deviation. (b) Variation in NOE along the peptide chain measured at 500, 600, and 900 MHz. The mean value of three replicate NOE experiments is shown and error bars represent the standard deviation. Cysteine residues are shown in bold, β-sheet regions are highlighted with a gray box, and the turns are underlined in gray.
The simplest motional model used was that of a rigid isotropic rotor in which the motion is described by a single overall correlation time, τ0. As seen in Table 1, this model was unable to fit the general trends in the T1 and NOE data seen at each site in the molecule simultaneously; specifically, the increase in T1 with increasing magnetic field strength is not reproduced well by this model. The average RMSD over all the residues was 0.24 ± 0.07 and the differences between observed and calculated T1 were all >10%, and thus outside the range of experimental error. We therefore concluded that an isotropic rigid model is insufficient to describe the motion of HTD-2 and that additional parameters (i.e., reflecting anisotropic overall motion and/or internal motion) are needed to fit the observed relaxation data. Nevertheless, as a rough estimate, the best fit overall correlation time, τ0 = 1.04 ns is consistent with the molecular weight of HTD-2(22) and in excellent agreement with the overall correlation time (τ0 = 1.09 ns) predicted by Hydronmr.(29)
In principle, a molecule with an elongated topology such as that of HTD-2 would be predicted to have axially symmetric anisotropic motion. The axial rigid model describes the motion of an axially symmetric molecule in terms of an overall correlation time, τ0, and the ratio of the diffusion tensors parallel (D||) and perpendicular (D⊥) to the symmetry axis of the molecule (Dratio = D||/D⊥). Using this model and a Dratio of 2.44 predicted by Hydronmr,(29) we calculated T1s and NOEs at the three field strengths. However, examination of Table 1 shows that, as with the rigid isotropic model, this model was unable to provide a satisfactory fit to the experimental data. The average RMSD over all the residues was 0.28 ± 0.07 and the differences between observed and calculated T1 were almost all (i.e., 46 of 47 data points) >10%.
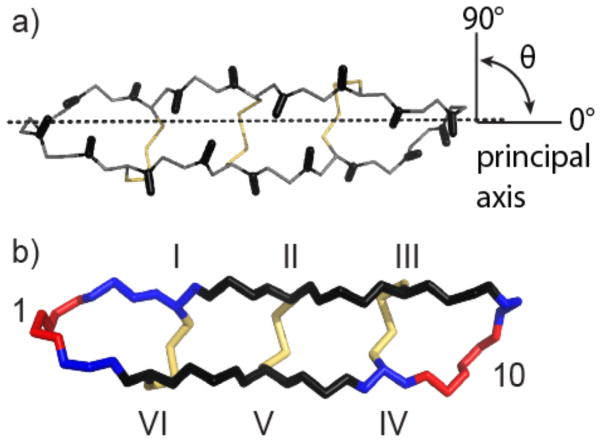
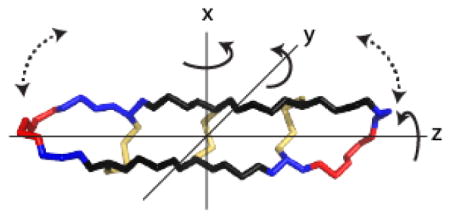
In the rigid anisotropic model, the spectral density depends on the diffusion tensors parallel and perpendicular to the principal axis of the molecule and specifically on the angle (θ) that the N–H vector of each residue makes with the principal axis (Figure 4a). In HTD-2, most of the N–H vectors are approximately perpendicular to the principal axis (75–105°), as shown in Figure 4a, so intrinsically even in the presence of anisotropic motion a high degree of variation in relaxation parameters at different sites would not be expected.
Figure 4.
Anisotropic and internal motion of HTD-2. (a) The backbone and disulfide bonds of HTD-2 (PDB code: 2LZI) are shown with the principal axis of the molecule aligned along the z-axis (dotted line). The angles (θ) that the N–H bond vectors (shown as black sticks) make with the z-axis are mostly ~90°. Backbone atoms are shown as gray lines and disulfide bonds are shown in yellow. (b) Backbone atoms of HTD-2 colored according to the S2 parameter as calculated for isotropic diffusion with internal motion: S2 < 0.76, red; 0.76 < S2 < 0.81, blue; S2 > 0.81, dark blue. Disulfide bonds are shown in yellow. Residues 1 and 10 and the disulfide connectivities are labeled.
As neither a rigid isotropic nor anisotropic model was able to satisfactorily fit the NMR relaxation data, we concluded that a rigid model is unable to describe the dynamics of HTD-2 and proceeded to models that included parameters describing internal motions. The simplest of these models is an isotropic model with internal motion. In addition to the overall correlation time of the molecule, τ0, the amplitude of motion of each residue is described by its order parameter, S2, and the rate of motion of each residue is described by its internal correlation time, τi. As shown in Table 1, this model was able to adequately fit the experimental data in both the magnitude and trends of the T1 and NOE data and the predicted overall correlation time was τ0 = 1.09 ns. The average RMSD over all the residues was 0.11 ± 0.06 and all calculated T1 values (except for three) were within 10% of the experimental value. Furthermore, the calculated data fitted the experimentally observed trend of increasing T1 with increasing field strength. The majority of the NOEs were within ±0.1 of the experimental value and the largest NOE deviation was 0.11 for Arg4 at 900 MHz. The isotropic model with internal motion therefore provided a satisfactory fit, considering the experimental error of the measurements.
Although the isotropic model with internal motion fitted the experimental data, for completeness we also tested an anisotropic model with internal motion. This did not produce any further improvement in the fit (Supporting Information, Table S4). The anisotropic model with internal motion describes molecular dynamics in terms of the overall correlation time, τ0, and the ratio of the diffusion tensors (Dratio = D||/D⊥) for the molecule, as well as the order parameter, S2, and internal correlation time, τi, for each residue. Using the anisotropic model with internal motion and a predicted Dratio = 2.44, we calculated data for the T1s and NOEs. Although no further improvement in the fit was gained over the isotropic model, we cannot exclude the possibility that the overall motion is anisotropic. Although the isotropic model with internal motion is the simplest model that fits the NMR relaxation data, there is very little difference between the theoretical T1 and NOE values calculated for the isotropic model with internal motion and the anisotropic model with internal motion.
The ability of the isotropic model with internal motion to fit the experimental data more closely than the anisotropic rigid model suggests that factors in addition to the backbone topology have a role in the molecular dynamics. This highlights several differences between small organic molecules, such as the phenylbicyclo[2.2.2]octanes,(5) and peptides or proteins. One property that could increase the isotropy of HTD-2 is self-association in solution. θ-Defensins have been shown to self-associate at millimolar concentrations and a side-to-side alignment of three peptide units has been proposed.(8) However, based on NMR diffusion measurements,(6) HTD-2 is not expected to self-associate at the concentration used for the NMR relaxation measurements. The excellent agreement between the overall correlation time predicted by Hydronmr(33) and that obtained by fitting our relaxation data provides confirmation that HTD-2 is monomeric under the experimental conditions used. Another difference between small organic molecules and peptides is the flexibility and orientation of the side chains. Whereas in small organic molecules there are few rotatable bonds and the positions of substituents are well-defined, peptides have various side chains that could significantly alter the shape from the topology suggested by the backbone alone. A further difference between peptides and small molecules is that the surfaces of peptides are usually covered with polar functional groups that can interact with aqueous solvent. For example, the five charged arginine residues in HTD-2 might attract a large solvent sphere, resulting in a decrease in anisotropy. Although hydrophobic molecules such as the substituted phenylbicyclo[2.2.2]ocanes would also attract a shell of nonpolar solvent, the interactions would be far weaker than those between a peptide and a polar solvent.
The need to invoke internal motion to fit the relaxation data suggests that parts of HTD-2 are more flexible than others, as supported by the observed variation in the S2 parameter between the residues. Figure 4b shows the structure of HTD-2 with each residue shaded according to the magnitude of its S2 parameter, determined using the isotropic diffusion model with internal motion. Whereas the residues comprising the β-sheet (residues 4, 5, 6, 7, 13, 14, 15, and 16) have S2 ≥ 0.77, the residues in the turns (residues 10, 11, 18, and 1) have S2 ≤ 0.71, suggesting that they are more flexible. Cross-bracing of the β-sheet by the disulfide bonds and the network of cross-strand hydrogen bonds accounts for the lower flexibility of the β-sheet compared to the turns. Overall, the order parameters of HTD-2 are in agreement with those reported for two other cyclic disulfide-rich peptides: MCoTI-I and MCoTI-II. Specifically, HTD-2 has S2 values of 0.67–0.96, similar to ranges of 0.76–0.94 and 0.72–0.91 for MCoTI-I(39) and MCoTI-II,(10) respectively. The proposed “butterfly”-type motion of the θ-defensin structure cannot be verified by the differences in the S2 parameter between the β-strand and turn regions because flexibility described by the S2 parameter is on the picosecond–nanosecond time scale, whereas a “butterfly”-type bending would occur on the millisecond time scale.
Knowledge of the relative flexibility of different parts of a peptide can guide their application as stable scaffolds for peptide drugs. Furthermore, motion in solution might affect the approach or binding of a peptide to its receptor. Both the cyclic cystine ladder and the cyclic cystine knot have been demonstrated to be stable and versatile scaffolds and the disulfide bonds cross-bracing the θ-defensin structure are important for their stability to proteases in serum.(4, 40) In the case of the cyclic cystine ladder of θ-defensins, the proteolytic stability of the cyclic cystine ladder is combined with the greater flexibility of the turn regions, which could allow a flexible-fit interaction with a target protein. In the case of the cyclic cystine knot proteins, for example, MCoTI-I and MCoTI-II, variations in the flexibility of the binding site have been reported between bound and free forms.(10, 39, 41)
A small amount of conformational flexibility can be an advantage in binding to protein targets. In a recent example, inclusion of the integrin-binding Arg-Gly-Asp epitope in the loops of RTD-1 results in a different integrin selectivity profile to the more highly constrained cilengitide peptide.(4) It is not yet understood whether flexibility of θ-defensins has a role in their mechanism of action; however, θ-defensin analogues lacking one or more of the disulfide bonds in the cyclic cystine ladder have the same membrane-binding and antibacterial activities as the native peptide.(42)
CONCLUSIONS
Despite the elongated topology of HTD-2, we found that simply invoking an anisotropic model of overall motion for a rigid molecule was insufficient to fit the observed NMR relaxation data; a contribution from internal motion was necessary to fit the variations in T1 and NOE observed. Although we cannot exclude the possibility that the overall motion is anisotropic, an isotropic model with internal motion provides an acceptable fit of the experimental NMR relaxation data. The order parameters, S2, are consistent with the constraints imposed by the cyclic cystine ladder in that the residues in the loop regions are more flexible than those in the β-strands. These differences in flexibility could be exploited in the design of peptide therapeutics based on the θ-defensin scaffold and the motional parameters provide further characterization of the θ-defensin structure.
Supplementary Material
Acknowledgments
Work in our laboratory on cyclic peptides is funded by the Australian Research Council (grant ID LP110200213). Work on intein biotechnological applications and cyclic proteins at the Camarero laboratory is supported by National Institutes of Health Research Grant R01-GM090323 (JAC). D.J.C. is a NHMRC Professorial Fellow (grant ID APP1026501). K.J.R. is an ARC Future Fellow (grant ID FT130100890). A.C.C. was supported by University of Queensland International PhD scholarship. We thank Dr. Peta Harvey for technical assistance with NMR spectroscopy.
ABBREVIATIONS
- HIV
human immunodeficiency virus
- HSQC
heteronuclear single quantum coherence
- HTD-2
human θ-defensin-2
- IPTG
isopropyl β-D-1-thiogalactopyranoside
- MCoTI-II
Momordica cochinchinensis trypsin inhibitor-II
- NOE
nuclear Overhauser enhancement
- NMR
nuclear magnetic resonance
- RP-HPLC
reverse-phase high performance liquid chromatography
- TOCSY
total correlation spectroscopy
Footnotes
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Supporting Information. Results of the NMR relaxation analyses carried out using the program ModelFree are supplied as Supporting Information. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Tang YQ, Yuan J, Ösapay G, Ösapay K, Tran D, Miller CJ, Ouellette AJ, Selsted ME. A Cyclic Antimicrobial Peptide Produced in Primate Leukocytes by the Ligation of Two Truncated α-Defensins. Science. 1999;286:498–502. doi: 10.1126/science.286.5439.498. [DOI] [PubMed] [Google Scholar]
- 2.Conibear AC, Craik DJ. The Chemistry and Biology of Theta Defensins. Angew Chem, Int Ed. 2014;53:10612–10623. doi: 10.1002/anie.201402167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lehrer RI, Cole AM, Selsted ME. Θ-Defensins: Cyclic Peptides with Endless Potential. J Biol Chem. 2012;287:27014–27019. doi: 10.1074/jbc.R112.346098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Conibear AC, Bochen A, Rosengren KJ, Stupar P, Wang C, Kessler H, Craik DJ. The Cyclic Cystine Ladder of Theta-Defensins as a Stable, Bi-Functional Scaffold: A Proof-of-Concept Study Using the Integrin-Binding RGD Motif. ChemBioChem. 2014;15:451–459. doi: 10.1002/cbic.201300568. [DOI] [PubMed] [Google Scholar]
- 5.Craik DJ, Adcock W, Levy GC. 13C NMR Spin Relaxation Studies of Molecular Dynamics of Substituted Phenylbicyclo[2.2.2]Octanes. Magn Reson Chem. 1986;24:783–791. [Google Scholar]
- 6.Conibear AC, Rosengren KJ, Harvey PJ, Craik DJ. Structural Characterization of the Cyclic Cystine Ladder Motif of Theta-Defensins. Biochemistry. 2012;51:9718–9726. doi: 10.1021/bi301363a. [DOI] [PubMed] [Google Scholar]
- 7.Trabi M, Schirra HJ, Craik DJ. Three-Dimensional Structure of RTD-1, a Cyclic Antimicrobial Defensin from Rhesus Macaque Leukocytes. Biochemistry. 2001;40:4211–4221. doi: 10.1021/bi002028t. [DOI] [PubMed] [Google Scholar]
- 8.Daly NL, Chen YK, Rosengren KJ, Marx UC, Phillips ML, Waring AJ, Wang W, Lehrer RI, Craik DJ. Retrocyclin-2: Structural Analysis of a Potent Anti-HIV Θ-Defensin. Biochemistry. 2007;46:9920–9928. doi: 10.1021/bi700720e. [DOI] [PubMed] [Google Scholar]
- 9.Craik DJ, Kumar A, Levy GC. Moldyn - a Generalized Program for the Evaluation of Molecular-Dynamics Models Using Nuclear Magnetic-Resonance Spin-Relaxation Data. J Chem Inf Comput Sci. 1983;23:30–38. [Google Scholar]
- 10.Daly NL, Thorstholm L, Greenwood KP, King GJ, Rosengren KJ, Heras B, Martin JL, Craik DJ. Structural Insights into the Role of the Cyclic Backbone in a Squash Trypsin Inhibitor. J Biol Chem. 2013;288:36141–36148. doi: 10.1074/jbc.M113.528240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hemmi H, Kuno A, Hirabayashi J. NMR Structure and Dynamics of the C-Terminal Domain of R-Type Lectin from the Earthworm Lumbricus Terrestris. FEBS J. 2013;280:70–82. doi: 10.1111/febs.12050. [DOI] [PubMed] [Google Scholar]
- 12.Takahashi D, Hiromasa Y, Kim Y, Anbanandam A, Yao X, Chang KO, Prakash O. Structural and Dynamics Characterization of Norovirus Protease. Protein Sci. 2013;22:347–357. doi: 10.1002/pro.2215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kawakami T, Ohta A, Ohuchi M, Ashigai H, Murakami H, Suga H. Diverse Backbone-Cyclized Peptides Via Codon Reprogramming. Nat Chem Biol. 2009;5:888–890. doi: 10.1038/nchembio.259. [DOI] [PubMed] [Google Scholar]
- 14.Gould A, Li YL, Majumder S, Garcia AE, Carlsson P, Shekhtman A, Camarero JA. Recombinant Production of Rhesus Theta-Defensin-1 (RTD-1) Using a Bacterial Expression System. Mol Biosyst. 2012;8:1359–1365. doi: 10.1039/c2mb05451e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dawson PE, Muir TW, Clark-Lewis I, Kent SB. Synthesis of Proteins by Native Chemical Ligation. Science. 1994;266:776–779. doi: 10.1126/science.7973629. [DOI] [PubMed] [Google Scholar]
- 16.Kimura RH, Tran AT, Camarero JA. Biosynthesis of the Cyclotide Kalata B1 by Using Protein Splicing. Angew Chem, Int Ed. 2006;45:973–976. doi: 10.1002/anie.200503882. [DOI] [PubMed] [Google Scholar]
- 17.Ishima R, Torchia DA. Protein Dynamics from NMR. Nat Struct Biol. 2000;7:740–743. doi: 10.1038/78963. [DOI] [PubMed] [Google Scholar]
- 18.Cole AM, Hong T, Boo LM, Nguyen T, Zhao C, Bristol G, Zack JA, Waring AJ, Yang OO, Lehrer RI. Retrocyclin: A Primate Peptide That Protects Cells from Infection by T- and M-Tropic Strains of HIV-1. Proc Natl Acad Sci U S A. 2002;99:1813–1818. doi: 10.1073/pnas.052706399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cole AM, Wang W, Waring AJ, Lehrer RI. Retrocyclins: Using Past as Prologue. Curr Protein Pept Sci. 2004;5:373–381. doi: 10.2174/1389203043379657. [DOI] [PubMed] [Google Scholar]
- 20.Penberthy WT, Chari S, Cole AL, Cole AM. Retrocyclins and Their Activity against HIV-1. Cell Mol Life Sci. 2011;68:2231–2242. doi: 10.1007/s00018-011-0715-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ji Y, Majumder S, Millard M, Borra R, Bi T, Elnagar AY, Neamati N, Shekhtman A, Camarero JA. In Vivo Activation of the p53 Tumor Suppressor Pathway by an Engineered Cyclotide. J Am Chem Soc. 2013;135:11623–11633. doi: 10.1021/ja405108p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Levy GC, Lichter RL. Nitrogen-15 Nuclear Magnetic Resonance Spectroscopy. John Wiley & Sons; New York: 1979. [Google Scholar]
- 23.Doddrell D, Glushko V, Allerhand A. Theory of Nuclear Overhauser Enhancement and 13C–1H Dipolar Relaxation in Proton Decoupled Carbon 13 NMR Spectra of Macromolecules. J Chem Phys. 1972;56:3683–3689. [Google Scholar]
- 24.Mandel AM, Akke M, Palmer AG., 3rd Backbone Dynamics of Escherichia Coli Ribonuclease Hi: Correlations with Structure and Function in an Active Enzyme. J Mol Biol. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
- 25.Lipari G, Szabo A. Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 1. Theory and Range of Validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- 26.Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. Deviations from the Simple Two-Parameter Model-Free Approach to the Interpretation of Nitrogen-15 Nuclear Magnetic Relaxation of Proteins. J Am Chem Soc. 1990;112:4989–4991. [Google Scholar]
- 27.Tjandra N, Wingfield P, Stahl S, Bax A. Anisotropic Rotational Diffusion of Perdeuterated HIV Protease from 15N NMR Relaxation Measurements at Two Magnetic Fields. J Biomol NMR. 1996;8:273–284. doi: 10.1007/BF00410326. [DOI] [PubMed] [Google Scholar]
- 28.Vranken WF, Boucher W, Stevens TJ, Fogh RH, Pajon A, Llinas P, Ulrich EL, Markley JL, Ionides J, Laue ED. The CCPN Data Model for NMR Spectroscopy: Development of a Software Pipeline. Proteins. 2005;59:687–696. doi: 10.1002/prot.20449. [DOI] [PubMed] [Google Scholar]
- 29.Wishart DS, Bigam CG, Yao J, Abildgaard F, Dyson HJ, Oldfield E, Markley JL, Sykes BD. 1H, 13C and 15N Chemical Shift Referencing in Biomolecular NMR. J Biomol NMR. 1995;6:135–140. doi: 10.1007/BF00211777. [DOI] [PubMed] [Google Scholar]
- 30.Craik DJ, Levy GC, Lombardo A. Carbon-13 and Nitrogen-15 Nuclear Magnetic Resonance of Polycyclic Polyamines. A Study of Solution Nitrogen-Hydrogen Hydrogen Bonding and Protonation. J Phys Chem. 1982;86:3893–3900. [Google Scholar]
- 31.Palmer AG, Rance M, Wright PE. Intramolecular Motions of a Zinc Finger DNA-Binding Domain from Xfin Characterized by Proton-Detected Natural Abundance Carbon-13 Heteronuclear NMR Spectroscopy. J Am Chem Soc. 1991;113:4371–4380. [Google Scholar]
- 32.Hiyama Y, Niu CH, Silverton JV, Bavoso A, Torchia DA. Determination of 15N Chemical Shift Tensor Via 15N-2H Dipolar Coupling in Boc-Glycylglycyl[15N Glycine]Benzyl Ester. J Am Chem Soc. 1988;110:2378–2383. [Google Scholar]
- 33.Ortega A, Garcia de la Torre J. Efficient, Accurate Calculation of Rotational Diffusion and NMR Relaxation of Globular Proteins from Atomic-Level Structures and Approximate Hydrodynamic Calculations. J Am Chem Soc. 2005;127:12764–12765. doi: 10.1021/ja053080l. [DOI] [PubMed] [Google Scholar]
- 34.Jarvis JA, Craik DJ. C-13 Nmr Relaxation Studies of Molecular-Motion in Peptide-Fragments from Human Transthyretin. J Magn Reson B. 1995;107:95–106. doi: 10.1006/jmrb.1995.1065. [DOI] [PubMed] [Google Scholar]
- 35.Wishart DS, Bigam CG, Holm A, Hodges RS, Sykes BD. 1H, 13C and 15N Random Coil NMR Chemical Shifts of the Common Amino Acids. I. Investigations of Nearest-Neighbor Effects. J Biomol NMR. 1995;5:67–81. doi: 10.1007/BF00227471. [DOI] [PubMed] [Google Scholar]
- 36.Andersen NH, Neidigh JW, Harris SM, Lee GM, Liu Z, Tong H. Extracting Information from the Temperature Gradients of Polypeptide NH Chemical Shifts. 1. The Importance of Conformational Averaging. J Am Chem Soc. 1997;119:8547–8561. [Google Scholar]
- 37.Osapay K, Case DA. Analysis of Proton Chemical Shifts in Regular Secondary Structure of Proteins. J Biomol NMR. 1994;4:215–230. doi: 10.1007/BF00175249. [DOI] [PubMed] [Google Scholar]
- 38.Avbelj F, Kocjan D, Baldwin RL. Protein Chemical Shifts Arising from Alpha-Helices and Beta-Sheets Depend on Solvent Exposure. Proc Natl Acad Sci U S A. 2004;101:17394–17397. doi: 10.1073/pnas.0407969101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Puttamadappa SS, Jagadish K, Shekhtman A, Camarero JA. Backbone Dynamics of Cyclotide Mcoti-I Free and Complexed with Trypsin. Angew Chem, Int Ed Engl. 2010;49:7030–7034. doi: 10.1002/anie.201002906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Craik DJ, Cemazar M, Daly NL. The Cyclotides and Related Macrocyclic Peptides as Scaffolds in Drug Design. Curr Opin Drug Discovery. 2006;9:251–260. [PubMed] [Google Scholar]
- 41.Puttamadappa SS, Jagadish K, Shekhtman A, Camarero JA. Corrigendum: Backbone Dynamics of Cyclotide MCoTI-I Free and Complexed with Trypsin. Angew Chem, Int Ed. 2011;50:6948–6949. doi: 10.1002/anie.201002906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Conibear AC, Rosengren KJ, Daly NL, Henriques ST, Craik DJ. The Cyclic Cystine Ladder in Theta-Defensins Is Important for Structure and Stability, but Not Antibacterial Activity. J Biol Chem. 2013;288:10830–10840. doi: 10.1074/jbc.M113.451047. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.