Memory and cognitive control circuits in mathematical cognition and learning

Abstract

Numerical cognition relies on interactions within and between multiple functional brain systems, including those subserving quantity processing, working memory, declarative memory, and cognitive control. This chapter describes recent advances in our understanding of memory and control circuits in mathematical cognition and learning. The working memory system involves multiple parietal–frontal circuits which create short-term representations that allow manipulation of discrete quantities over several seconds. In contrast, hippocampal–frontal circuits underlying the declarative memory system play an important role in formation of associative memories and binding of new and old information, leading to the formation of long-term memories that allow generalization beyond individual problem attributes. The flow of information across these systems is regulated by flexible cognitive control systems which facilitate the integration and manipulation of quantity and mnemonic information. The implications of recent research for formulating a more comprehensive systems neuroscience view of the neural basis of mathematical learning and knowledge acquisition in both children and adults are discussed.

1 INTRODUCTION

Knowledge of numerical magnitude and manipulations of symbolic and nonsymbolic quantity (number sense) are critical building blocks from which all mathematical knowledge is constructed. These basic building blocks rely on visual and auditory association cortices which help decode the visual form and phonological features of numerical stimuli, and the parietal attention system (Dehaene et al., 2003) which helps to build semantic representations of quantity (Ansari, 2008) from visuo-spatial primitives including object identification, spatial attention, eye gaze, and pointing (Simon et al., 2002). With increased proficiency, these functions are sub-served by a “core” visuospatial number system anchored in the fusiform gyrus (FG) and intraparietal sulcus (IPS).

The IPS subdivision of the posterior parietal cortex has been the focus of most neurobiological research on mathematical cognition and learning (Ansari, 2008; Butterworth, 1999; Dehaene et al., 2003). The IPS and FG form core building blocks from which number form and quantity representations are constructed in the brain (Ansari, 2008). But these regions do not function in isolation. They receive input from multiple brain regions and send outputs to several others. Furthermore, the development of core systems is supported by its engagement with multiple brain systems. Recent research is beginning to emphasize a multisystem approach (Arsalidou and Taylor, 2011; Fias et al., 2013; Qin et al., 2014). Multiple distributed neural processes involved in number form, magnitude and quantity representations, working memory, and declarative memory have been identified as being important for numerical problem solving and mathematical learning (Fig. 1). This chapter synthesizes emerging findings on multiple memory and cognitive control systems which play a critical, but heretofore underappreciated, role in mathematical cognition in adults, as well as in scaffolding children’s mathematics learning and skill development.

FIG. 1.

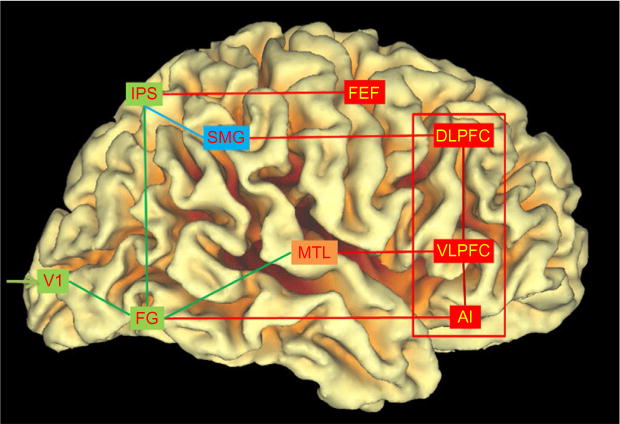
Schematic diagram of memory and control circuits. The fusiform gyrus (FG) in inferior temporal cortex decodes number form and together with the intraparietal sulcus (IPS) in the parietal cortex which helps builds visuospatial representations of numerical quantity (shown in green, light gray in the print version, boxes and links). Distinct parietal–frontal circuits differentially link the IPS and supramarginal gyrus (SMG) with the frontal eye field (FEF) and dorsolateral prefrontal cortex (DLPFC), respectively. These circuits facilitate visuospatial working memory for objects in space and create a hierarchy of short-term representations that allow manipulation of multiple discrete quantities over several seconds. The declarative memory system anchored in the medial temporal cortex (MTL)—the hippocampus, specifically, plays an important role in long-term memory formation and generalization beyond individual problem attributes. Finally, prefrontal control circuits (shown in red, dark gray in the print version) anchored in the anterior insula (AI), ventrolateral prefrontal cortex (VLPFC), and DLPFC serve as flexible hubs for integrating information across attentional and memory systems, thereby facilitating goal-directed problem solving and decision making.

We focus on two memory systems—working memory and declarative memory— that play distinct roles in mathematical cognition and learning. The working memory system anchored in parietal–frontal circuits creates short-term representations that allow manipulation of multiple discrete quantities over several seconds. In contrast, declarative memory systems anchored in hippocampal–frontal circuits play an important role in formation of associative memories and binding of new and old information, contributing to long-term memory and generalization beyond individual problem attributes. Both these processes require flexible integration of functional circuits anchored in prefrontal cognitive control systems. We describe cognitive control systems which guide allocation of attention resources and retrieval of facts from memory in the service of goal-directed numerical problem solving.

The roles of the two memory systems are greatly amplified during key developmental stages of learning, and their involvement in mathematical cognition and learning is best studied in the context of cognitive development. There is now growing evidence to suggest that functional circuits engaged by children are not the same as those engaged by adults who have evolved multiple strategies for learning and cognitive skill acquisition. Studies comparing children with adults are therefore likely to be insensitive to major changes that occur during specific stages of development. A number of scaffolding systems are likely to be engaged during development, and new studies are beginning to investigate the role of parietal–frontal and hippocampal–frontal circuits that might otherwise be missed in studies involving adults. The precise nature of this engagement is a function of developmental stage, domain knowledge, problem complexity, and individual proficiency in use of efficient problem-solving strategies. Accordingly, this review has a strong focus on both typical and atypical neurodevelopmental processes associated with the two memory systems and their associated prefrontal cognitive control systems.

The next sections are organized as follows. In Section 2, we first consider the relation between core systems and working memory and describe multiple parietal–frontal working memory circuits anchored in different subdivisions of the posterior parietal cortex, with a specific focus on functional circuits associated with the IPS and supramarginal gyrus. The role of parietal–frontal working memory circuits in the typical and atypical development of mathematical cognition is then discussed. In Section 3, we turn to the declarative memory system highlighting key hippocampal–prefrontal circuits. Emerging findings on the role of the hippocampal memory system in mathematical learning and development are then described. In Section 4, we consider how distinct prefrontal cortex (PFC) control systems facilitate mathematical cognition and learning. Section 5 summarizes the main points of this review. This chapter builds on related topical reviews (Menon, 2015, 2016) and attempts an integrative view of distinct, but overlapping, memory and cognitive control circuits involved in mathematical cognition and learning.

2 PARIETAL–FRONTAL WORKING MEMORY SYSTEMS

2.1 CORE AND NONCORE PARIETAL SYSTEMS OVERLAP IN THE IPS

Parietal–frontal circuits play a prominent role in mathematical cognition. Functional neuroimaging research has revealed significant overlap in multiple parietal and prefrontal cortical regions involved in working memory and numerical problem solving (Arsalidou and Taylor, 2011; Metcalfe et al., 2013; Rottschy et al., 2012). Common patterns of coactivation have most prominently been detected in the IPS, supramarginal gyrus, premotor cortex, and ventral and dorsal aspects of the lateral PFC.

A critical locus of intersection between “core” number system and “noncore” working memory systems is the IPS, a region important for representing and manipulating numerical quantity. It is now well known that “core” IPS regions implicated in quantity and numerosity judgement are also involved in a broader class of cognitive functions, including sequential ordering and manipulation of working memory contents for nonnumerical stimuli, as shown in several elegant studies by Fias and colleagues (Van Opstal et al., 2009). Furthermore, these IPS regions are also integral to short-term visual WM for object locations in space over a period lasting 1–2 s (Luck and Vogel, 2013). Thus, multiple lines of evidence suggest that parietal systems for numerical quantity processing and working memory show a prominent overlap in the parietal cortex. The crucial point these examples illustrate is that the distinction between “core” quantity and “noncore” working memory systems is not functionally segregated and that they draw on similar mechanisms for dynamic manipulation of representations over a timescale of several seconds.

2.2 MULTIPLE PARIETAL–FRONTAL WORKING MEMORY CIRCUITS

Analysis of intrinsic functional circuits associated with the posterior parietal cortex hints at multiple parietal–frontal working memory-related circuits involved in mathematical cognition. The three distinct subdivisions of the inferior parietal cortex, the IPS, supramarginal gyrus, and angular gyrus are associated with distinct but overlapping parietal–frontal circuits (Fig. 2). These circuits contribute to different aspects of mathematical cognition and learning by virtue of their differential large-scale functional organization. The IPS is part of an intrinsically connected parietal–frontal system that includes the frontal eye fields, supplementary motor area, anterior insula, and ventrolateral PFC (Corbetta and Shulman, 2002; Corbetta et al., 2008; Menon and Uddin, 2010; Supekar and Menon, 2012; Uddin et al., 2010a). A key distinguishing feature of the IPS is its connectivity with the frontal eye field: the IPS is more strongly connected with this region than the supramarginal gyrus (Uddin et al., 2010a). In contrast, the supramarginal gyrus is more tightly linked to the dorsolateral PFC, together with which it forms the canonical parietal–frontal central executive network (Bressler and Menon, 2010). The IPS also shows a distinct pattern of connectivity from the adjoining angular gyrus. The angular gyrus is strongly connected with ventromedial PFC and posterior cingulate regions, comprising the default mode network (Greicius et al., 2003, 2004; Raichle et al., 2001), a system with no direct involvement in working memory. Thus, the IPS and supramarginal gyrus form distinct parietal–frontal working memory-related circuits.

FIG. 2.

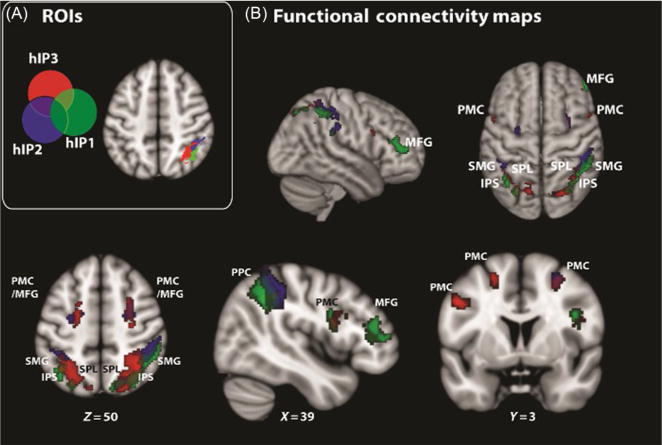
Parietal–frontal circuits associated with the IPS. Parietal–frontal circuits identified using intrinsic functional connectivity analysis of the intraparietal sulcus (IPS), a “core” region involved in basic magnitude judgment and arithmetic. (A) IPS region of interests (ROIs) derived from cytoarchitectonic maps for the three subdivisions of the IPS: hIP2 is the lateral and anterior subdivision of the IPS (blue, dark gray in the print version); hIP1 is the subdivision located posterior to hIP2 (green, gray in the print version); and hIP3 is the posterior subdivision of the IPS (red, light gray in the print version). (B) Functional connectivity maps associated with hIP1, hIP2, and hIP3. The color (different gray shades in the print version) code represents voxels correlated with each source ROI. The IPS has significant connectivity with distributed frontal (MFG and PMC) and parietal (SMG and SPL) cortical regions in both hemispheres. Additional functional circuits associated with the ventral-occipital temporal cortex are not shown. hIP, human intraparietal; MFG, middle frontal gyrus; PMC, premotor cortex; SMG, supramarginal gyrus; SPL, superior parietal lobule.

Adapted from Uddin, L.Q., Supekar, K., Amin, H., Rykhlevskaia, E., Nguyen, D.A., Greicius, M.D., Menon, V., 2010a. Dissociable connectivity within human angular gyrus and intraparietal sulcus: evidence from functional and structural connectivity. Cereb. Cortex 20, 2636–2646.

It should be noted that the IPS itself is not a homogeneous structure. Cytoarchitectonic maps obtained from postmortem brains suggest that the human IPS has a more finely grained parcellation than previously suggested by the classical Brodmann map (Caspers et al., 2008). While all three subdivisions identified to date have strong links to the frontal eye field, their large-scale connectivity patterns can also be dissociated. The anterior-most IPS subdivisions (hIP2 and hIP1) are linked with ventral premotor cortex, anterior insula, and dorsolateral PFC, while the posterior-most IPS subdivision (hIP3) has higher connectivity with extrastriate visual areas (Fig. 2). This functional connectivity profile suggests a strong coupling between the anterior IPS and PFC control regions. In sharp contrast, the posterior IPS region shows strong coupling with posterior occipital regions. Thus, connectivity analyses of networks associated with the IPS suggest a general principle of organization whereby posterior IPS regions that are closely linked to the visual system translate stimuli into motor action through anterior IPS connections with the PFC.

A key point suggested by extant findings is that IPS and supramarginal gyrus involved in mathematical cognition form overlapping but segregated working memory circuits. Precisely how these circuits work to serve the dual purpose of segregation and integration of core and noncore parietal systems involved in mathematical cognition and learning is less clear. A crucial hint comes from their distinct functional roles. Unlike the IPS, the supramarginal gyrus is not critically involved in quantity judgement per se, but it is strongly engaged during numerical problem-solving tasks that require active storage and manipulation of the contents of working memory. It is likely that the supramarginal gyrus provides a more general mechanism for manipulating the contents of working memory in a more flexible and context-dependent manner over an extended period of time, thus freeing up “core” IPS resources necessary for quantity processing.

2.3 PARIETAL–FRONTAL WORKING MEMORY SYSTEMS IN MATHEMATICAL COGNITION AND ITS DEVELOPMENT

The particular emphasis on parietal–frontal working memory systems in mathematical cognition is most prominent in developmental studies. This has origins in children’s immature problem-solving abilities which require them to break down numerical problems into more basic components. The use of such strategies requires greater reliance on working memory systems for problem solving in children. For example, children rely more on counting strategies during simple arithmetic problem solving and need to access multiple working memory components including short-term storage, rule-based manipulation, and updating of the stored contents. With increased proficiency and a shift to fact retrieval strategies, there is less demand and need for working memory resources (Bailey et al., 2012; Geary et al., 2007a). Consistent with this view, neuroimaging studies in typical and atypical development have provided strong evidence for coactivation of parietal and prefrontal regions that overlap with parietal–frontal circuits highlighted in the previous section.

The involvement of working memory in mathematical cognition had initially been surmised based on overlapping responses in parietal and PFC in the two domains (Cantlon et al., 2009; Grabner et al., 2009; Ischebeck et al., 2007; Rivera et al., 2005). Studies of typical development provided initial evidence for the changing role of working memory with age. For example, Rivera and colleagues found that relative to adults, children tend to engage the posterior parietal cortex less, and the PFC more, when solving arithmetic problems, likely reflecting the increased role of visuospatial processing and the concurrent decrease in demands on cognitive control. Other studies have more directly addressed the link between working memory abilities and numerical problem-solving skills. Dumontheil and Klingberg (2012) found that IPS activity during a visuospatial working memory task predicted arithmetic performance 2 years later in a sample of 6–16-year-old children and adolescents. This finding further reinforced the role of parietal–frontal working memory systems in mathematical cognition and pointed to the overlap between core and noncore functional systems in the IPS.

More detailed analyses of the neural correlates of individual components of working memory have provided evidence for the fractionation of neurofunctional systems associated with distinct working memory components during numerical problem solving (Arsalidou and Taylor, 2011; Metcalfe et al., 2013; Rottschy et al., 2012). Analysis of the relation between the central executive, phonological and visuospatial components of working memory, and brain activation during an arithmetic verification task in a large group of 7–9-year-old children revealed that visuospatial working memory is a strong predictor of mathematical ability in children in this age group and is associated with increased problem complexity-related responses in left dorsolateral and right ventrolateral PFC as well as in the bilateral IPS and supramarginal gyrus. Metcalfe and colleagues also found that visuospatial working memory and the central executive component were associated with largely distinct patterns of brain responses during arithmetic problem solving, and overlap was only observed in the ventral aspects of the left supramarginal gyrus, suggesting that this region is an important locus for the integration of information in working memory during numerical problem solving in children (Ansari, 2008; Dehaene et al., 2003; Kawashima et al., 2004; Kucian et al., 2008; Menon et al., 2000; Rivera et al., 2005; Rosenberg-Lee et al., 2014).

Finally, analysis of intrinsic functional connectivity suggests that a network of prefrontal cortical areas supports the longitudinal development of numerical abilities. Intrinsic functional connectivity between the IPS and dorsolateral and ventrolateral PFC predicted longitudinal gains in numerical problem-solving abilities over a 6-year period in children (Evans et al., 2015). These findings further confirm the pivotal role of overlapping parietal–frontal circuits in children’s mathematical skill development.

2.4 PARIETAL–FRONTAL IMPAIRMENTS IN CHILDREN WITH MATHEMATICAL DISABILITIES

Although mathematical disability (MD) was initially conceptualized as a disorder of a single brain region characterized by a localized deficit in the IPS (Cohen Kadosh et al., 2007; Isaacs et al., 2001; Price et al., 2007), more recently, prominent neurocognitive models of MD have posited that the disorder stems from more extensive functional aberrations in a distributed network of brain areas encompassing not only posterior parietal, but also prefrontal, as well as ventral temporal–occipital cortices that are known to serve multiple cognitive functions necessary for successful numerical problem solving. Studies have variably reported aberrant responses in the IPS, supramarginal gyrus, and multiple prefrontal cortical areas implicated in working memory (Butterworth et al., 2011; Davis et al., 2009; Iuculano et al., 2015; Kaufmann et al., 2009a; Kucian and von Aster, 2015; Kucian et al., 2006, 2011; Menon, 2014; Price et al., 2007; Rosenberg-Lee et al., 2014).

Behavioral studies have shown that disruptions to working memory are a prominent factor contributing to persistent deficits in arithmetic problem solving in children with MD (Geary et al., 2007b). Evidence to date suggests that visuospatial working memory is a specific source of vulnerability in symbolic numerical calculation deficits and thus needs to be seriously considered as a key component in neurobiological and developmental models of typical and atypical mathematical skill acquisition (Ashkenazi et al., 2013). Rotzer et al. (2009) found that compared to typically developing children, children with low math abilities had lower visuospatial abilities and lower activity levels in the right anterior IPS, ventrolateral PFC, and insular cortex during a visuospatial working memory task. In a different vein, Ashkenazi et al. (2013) identified impaired working memory components in children with MD and then examined their role in modulating brain responses to numerical problem solving. Children with MD had specific deficits in visuospatial working memory in addition to deficits in arithmetic task performance, even though they were matched on IQ and verbal abilities to their typically developing peers. Crucially, activations in IPS, and dorsolateral and ventrolateral PFC are positively correlated with visuospatial working memory ability in typically developing children, but no such relation was seen in children with MD. This result suggests that children with MD fail to appropriately exploit parietal–frontal working memory resources during problem solving.

2.5 HYPERACTIVE PARIETAL–FRONTAL WORKING MEMORY CIRCUITS IN CHILDREN WITH MD

While previous studies have focused on regional profiles of deficits, understanding cognitive deficits requires knowledge not only about aberrations in localized patterns of brain responses but also distributed functional circuits that might be impaired or organized in unusual ways (Uddin et al., 2010b). This is particularly true for numerical problem solving which typically requires the coordinated interaction of multiple brain regions (Rosenberg-Lee et al., 2011; Varma and Schwartz, 2008). A few recent studies have begun to probe parietal–frontal circuits in children with MD.

Analysis of both task and task-free data suggests that parietal–frontal working memory circuits are impaired in children with MD. Surprisingly, contrary to what might be predicted, relative to typically developing children, children with MD show hyperconnectivity of the IPS, rather than reduced connectivity, with several cortical areas (Rosenberg-Lee et al., 2014). Hyperconnectivity of the IPS with multiple regions in lateral PFC and parietal regions is most prominent in affected children. These regions include the bilateral ventrolateral and dorsolateral PFC and the supramarginal gyrus. This pattern of hyperconnectivity was observed during both a simpler addition task and a more cognitively challenging subtraction task (Fig. 3). Thus, children with MD engage multiple parietal–frontal working memory circuits differently from their typically developing peers—they require greater engagement of these circuits despite lower performance levels. The greater engagement of these circuits may arise from the activation of problem-irrelevant information that in turn disrupts problem solving. This view is consistent with behavioral studies that show the intrusion of problem-irrelevant information into working memory when children with MD attempt to retrieve arithmetic answers from long-term memory (Barrouillet et al., 1997; Geary et al., 2000, 2012). Further studies are needed to disentangle intrusive vs compensatory effects in this complex pattern of hyperconnectivity in parietal–frontal working memory circuits.

FIG. 3.

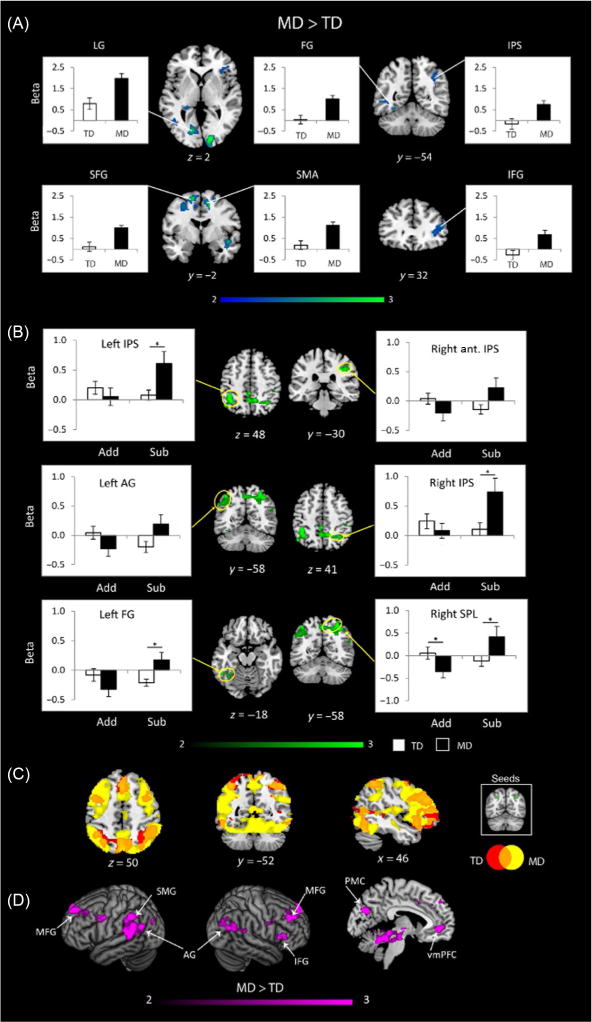
Aberrant parietal–frontal response and hyperconnectivity in children with mathematical disability. (A) Brain areas that showed significant main effect of group during problem solving involving addition and subtraction operations in children with mathematical disability (MD), compared to TD children. Signal levels demonstrate that, when activations are compared to a low-level passive fixation condition, arithmetic processing is associated with hyperactivation in the MD group in multiple brain areas including: left lingual gyrus (LG), left fusiform gyrus (FG), right intraparietal sulcus (IPS), right anterior insula, superior frontal gyrus (SFG) bilaterally, and right supplementary motor area (SMA), and right inferior frontal gyrus (IFG). (B) Brain areas that showed a significant group (MD, TD) × operation (addition, subtraction) interaction. Compared to TD children, children with MD showed hyperactivation in several posterior brain regions for subtraction (Sub), compared to addition (Add). These regions included bilateral posterior IPS, right anterior IPS, right superior parietal lobe (SPL), left angular gyrus (AG), and left FG. (C) Effective connectivity of the IPS during arithmetic problem solving in the MD (shown in yellow, white in the print version) and TD (shown in red, dark gray in the print version) groups. Note the more extensive connectivity in the MD group. Main effect of group is shown. (D) Brain regions that showed greater IPS connectivity in the MD group included multiple frontal, parietal and occipital regions: bilateral angular gyrus (AG), left supramarginal gyrus (SMG), right middle frontal gyrus (MFG), right inferior frontal gyrus (IFG), posteromedial cortex (PMC), and ventral medial prefrontal cortex (vmPFC).

Adapted from Rosenberg-lee, M., Ashkenazi, S., Chen, T., Young, C.B., Geary, D.C., Menon, V., 2014. Brain hyper-connectivity and operation-specific deficits during arithmetic problem solving in children with developmental dyscalculia. Dev. Sci. 18, 351–372.

Notably, this pattern of hyperconnectivity is also manifest in intrinsic functional circuits (Fig. 4). Compared to their typically developing peers, children with MD show aberrant IPS connectivity with multiple prefrontal and parietal regions (Jolles et al., 2016). Specifically, children with MD show greater functional connectivity between left and right IPS, as well as between IPS and dorsolateral and ventrolateral PFC. It is plausible that intrinsic hyperconnectivity in these parietal–frontal circuits in children with MD may underlie the increased activation and connectivity of these regions reported in several studies of numerical problem solving (Iuculano et al., 2015; Kaufmann et al., 2009a,b, 2011; Rosenberg-Lee et al., 2014). Interestingly, however, not all studies have found greater parietal–frontal activation in children with MD, but discrepancies between studies may be explained by the type of baseline conditions used. Specifically, it has been suggested that MD is characterized by reduced modulation of brain responses with increasing task complexity, rather than reduced activation per se (Ashkenazi et al., 2012). For example, children with MD show reduced activation in parietal–frontal regions for small vs large distances in number comparison tasks (Mussolin et al., 2010; Price et al., 2007; but see Kucian, 2011), and for complex vs simple problems in arithmetic tasks (Ashkenazi et al., 2012). Finally, aberrant connectivity within these parietal–frontal areas in children with MD is consistent with deficits in spatial attention that have been reported in domains outside mathematical problem solving (Ashkenazi and Henik, 2010; Szucs et al., 2013).

FIG. 4.

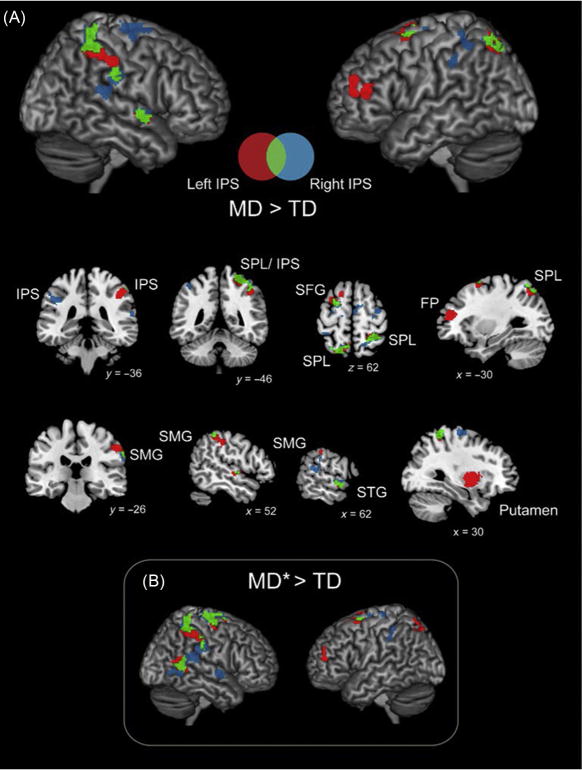
Parietal hyperconnectivity in children with MD. Brain areas that showed greater IPS connectivity in children with MD compared to typically developing (TD) children. (A) Children with MD showed hyperconnectivity between bilateral IPS and multiple dorsal frontal and parietal cortical regions, between bilateral IPS and right hemisphere SMG and STG, and between left IPS and right putamen. (B) Results were almost identical when examining a subset of 14 MD children who scored at or below 85 on the numerical operations subtest of the WIAT-II (MD*). Greater connectivity for MD>TD in red (dark gray in the print version) (left IPS), blue (gray in the print version) (right IPS), and green (light gray in the print version) (both left and right IPS). Coordinates are in MNI space. FP, frontal pole; IPS, intraparietal sulcus; SFG, superior frontal gyrus; SMG, supramarginal gyrus; SPL, superior parietal lobe; STG, superior temporal gyrus.

Adapted from Jolles, D., Ashkenazi, S., Kochalka, J., Evans, T., Richardson, J., Rosenberg-lee, M., Zhao, H., Supekar, K., Chen, T., Menon, V., 2016. Parietal hyper-connectivity, aberrant brain organization, and circuitbased biomarkers in children with mathematical disabilities. Dev. Sci.

An important question for future research is how aberrant parietal circuits impact the ability to modulate parietal–frontal responses in a context-specific manner and how this in turn influences skill development and learning.

3 HIPPOCAMPAL–FRONTAL DECLARATIVE MEMORY SYSTEM

3.1 THE MEDIAL TEMPORAL LOBE: A SYSTEM FOR ASSOCIATIVE LEARNING

Over the past few years, evidence has been accumulating for the differential involvement of the declarative memory system in mathematical learning, especially during key stages of skill acquisition in children (Qin et al., 2014). The importance of the medial temporal lobe, particularly its hippocampal subdivision, in learning and memory for events in space and time is well known (Davachi, 2006; Davachi et al., 2003; Diana et al., 2007; Eichenbaum et al., 2007; Tulving, 1983). Theories of memory consolidation posit that the hippocampus plays an important role in the early stages of learning and retrieval, but its involvement decreases over time with concomitant increase in reliance on neocortical memory systems (Eichenbaum et al., 2007). This might explain why despite its critical role in learning and memory formation, hippocampal contributions to mathematics learning and cognitive development more broadly have received little attention until recently.

3.2 HIPPOCAMPAL–FRONTAL CORTEX CIRCUITS

The hippocampus forms the structural core of the declarative memory system. Research over the past two decades has clarified the specific roles of its functional subdivisions in different aspects of encoding and retrieval of novel information (Kumaran et al., 2009; Schacter et al., 1998, 2007; Tulving, 1983, 2002). The hippocampus and its associated functional circuits play an important role in memory encoding and retrieval in both children and adults (Ghetti et al., 2010; Menon et al., 2005; Ofen et al., 2007). The hippocampus is thought to contribute to declarative memory through binding inputs from multiple cortical areas (Davachi, 2006; Eichenbaum, 2004; Eichenbaum et al., 2007), while its functional interactions with the PFC are thought to facilitate memory formation and retrieval through cognitive control processes acting on the contents of memory (Qin et al., 2007, 2009, 2011a,b). Declarative memory relies on the coordinated interactions of distributed brain areas, most prominently, the hippocampus and the PFC (Diekelmann et al., 2009; Frankland and Bontempi, 2005; McGaugh, 2000; Norman and O’Reilly, 2003; Qin et al., 2011a; Simons and Spiers, 2003). These studies suggest that newly acquired memories are strongly dependent on the hippocampus and its interactions with the PFC, and become increasingly independent of the hippocampus and MTL over time.

3.3 HIPPOCAMPAL–PREFRONTAL COACTIVATION IN CHILDREN’S MATHEMATICAL SKILL DEVELOPMENT

The first evidence for the differential engagement of the hippocampal memory system in arithmetic skill acquisition came from a cross-sectional study in children, adolescents, and adults who ranged in age from 8 to 19 (Rivera et al., 2005). Importantly, children exhibited significantly greater engagement of multiple medial temporal lobe regions including the hippocampus. Similarly, De Smedt et al. (2011) found greater hippocampal response in children compared to adults when solving addition problems; hippocampal activation was not detected for subtraction problems which are less well rehearsed and more difficult to memorize because subtraction problems are not commutative. These findings highlight the dynamic role of the hippocampus in the maturation of memory-based problem-solving strategies and its greater engagement in childhood followed by decreased involvement in adolescence and adulthood (Fig. 5).

FIG. 5.

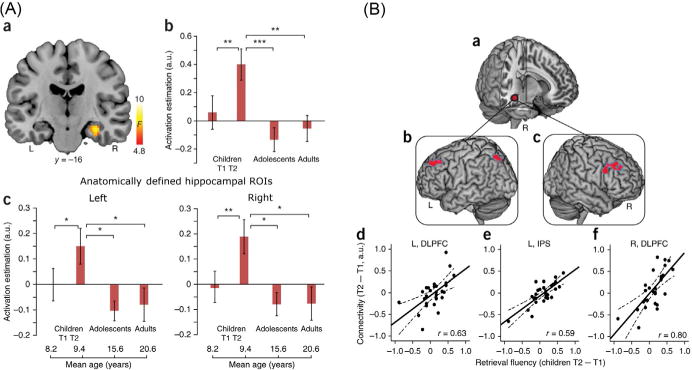
Longitudinal developmental changes in medial temporal lobe engagement and connectivity. (A) Longitudinal changes in hippocampal engagement during childhood, and further development through adolescence into adulthood. (a) Right hippocampus response showing main effect of group across children (at Time 1 and Time 2), adolescents, and adults. (b) Bar graphs depict developmental changes in the functionally defined hippocampus cluster. (c) Bar graphs show developmental changes in engagement of anatomically defined left and right hippocampal regions of interest. (B) Longitudinal changes in hippocampal–neocortical functional circuits in relation to individual improvements in children’s use of memory-based problem-solving strategies. (a) Right hippocampus seed region used in effective connectivity (ie, psychophysiological interaction) analysis. (b, c) Left and right dorsolateral prefrontal cortex (DLPFC) and the left intraparietal sulcus (IPS) regions that showed increased effective connectivity with the hippocampus, as a function of longitudinal improvements in retrieval fluency from Time 1 to Time 2. (d–f) Scatter plots depict the relation between longitudinal changes in retrieval fluency (x-axes) and changes in effective connectivity strength from Time 1 to Time 2 (y-axes).

Adapted from Qin, S., Cho, S., Chen, T., Rosenberg-Lee, M., Geary, D.C., Menon, V., 2014. Hippocampalneocortical functional reorganization underlies children’s cognitive development. Nat. Neurosci. 17, 1263–1269.

As noted earlier, children’s gains in problem-solving skills during the elementary school years are characterized by the gradual replacement of inefficient procedural strategies with direct retrieval of domain-relevant facts (Cho et al., 2011; Geary, 2011; Geary and Brown, 1991; Geary and Hoard, 2003). Cho et al. (2012) examined neurodevelopmental changes related to increased use of retrieval strategies and found that higher retrieval fluency was associated with greater response in multiple brain regions, including the hippocampus and parahippocampal gyrus subdivisions of the medial temporal lobe. Thus, children’s use of retrieval strategies, far from being idiosyncratic, is in fact associated with a predictable profile of hippocampal responses. A related study found that retrieval and counting strategies were associated with different activation patterns in hippocampal regions important for memory encoding and retrieval, including bilateral hippocampus and parahippocampal gyrus (Cho et al., 2011, 2012). The existence of decodable fine-scale pattern differences in fMRI signals suggests not only that the hippocampus is differentially engaged in relation to retrieval but also that the underlying neural resources are accessed and used differently in each strategy.

Qin and colleagues further investigated the transition from procedure-based to memory-based problem-solving strategies using longitudinal fMRI data from 7- to 9-year-old children (Qin et al., 2014). Children’s transition from counting to memory-based retrieval strategies over a 1.2-year interval was mediated by increased hippocampal activation and decreased parietal–frontal engagement. Following an initial increase in hippocampal engagement during middle childhood, this hippocampal dependency decreased during adolescence and adulthood despite further improvements in memory-based problem solving. This pattern of initial increase and subsequent decrease in activation provides novel support for models of long-term memory consolidation which posit that the hippocampus plays a time-limited role in the early phase of knowledge acquisition (McClelland et al., 1995; Tse et al., 2007). Consistent with this pattern of developmental change, previous studies in adults have reported no reliable hippocampal engagement during arithmetic tasks. Thus, the hippocampal system is critical to children’s early learning of arithmetic facts (Cho et al., 2011, 2012; De Smedt et al., 2011), while retrieval is largely dependent on the neocortex in adults (Dehaene et al., 2003; Menon, 2014).

3.4 HIPPOCAMPAL–FRONTAL CIRCUITS IN CHILDREN’S MATHEMATICAL SKILL DEVELOPMENT AND LEARNING

Dynamic coordination between the hippocampus and PFC plays an important role in memory formation (Norman and O’Reilly, 2003; Qin et al., 2011a; Simons and Spiers, 2003), and connectivity analyses are beginning to shed light on how the hippocampus and PFC interact to support memory formation for arithmetic facts. Analysis of task-related hippocampus connectivity has identified distributed functional circuits associated with retrieval fluency. In particular, right hippocampal connectivity with bilateral ventrolateral and dorsolateral PFC is strongly correlated with retrieval fluency (Cho et al., 2012). Analysis of longitudinal data has further clarified the relation between hippocampal–prefrontal circuits and individual differences in children’s mathematical skill development. In particular, the shift from counting to memory-based retrieval strategy and increased hippocampal activation is accompanied by decreased parietal–frontal engagement. Longitudinal improvements in retrieval fluency are best predicted by increased functional connectivity in hippocampal–neocortical circuits (Qin et al., 2014). Increased hippocampal functional coupling with prefrontal and parietal cortices is positively correlated with individual gains in memory-based strategy use. Finally, in a tutoring study designed to facilitate rapid retrieval, hippocampal–PFC functional circuits predicted performance gains over an 8-week interval (Fig. 6). Children who exhibited higher intrinsic functional connectivity in these circuits prior to tutoring showed the greatest performance improvement in math problem solving (Supekar et al., 2013). Hippocampal– neocortical circuit reorganization therefore plays an important role in children’s shift from effortful counting to more efficient memory-based problem solving.

FIG. 6.

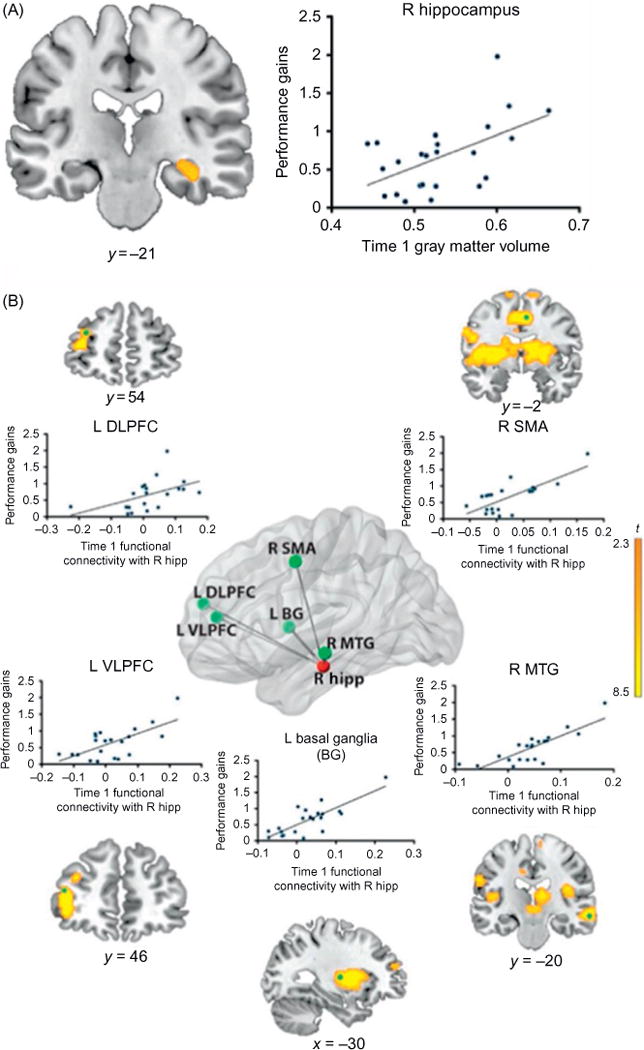
Medial temporal lobe structure and connectivity predict children’s math learning. (A) Gray matter volume in hippocampus correlates with improvement in arithmetic performance in response to 8 weeks of one-to-one math tutoring. (B) Intrinsic functional connectivity of the hippocampus correlates with improvement in arithmetic performance in response to 8 weeks of one-to-one math tutoring. Performance gains were predicted by hippocampal connectivity with the left dorsolateral prefrontal cortex (L DLPFC), left ventrolateral prefrontal cortex (L VLPFC), right supplementary motor area (R SMA), left basal ganglia (L BG), and right middle temporal gyrus (R MTG). Composite 3D view of connectivity network is shown in the central panel with the right hippocampus seed ROI highlighted in red (gray in the print version) and voxels showing peak connectivity with the hippocampus highlighted in green (light gray in the print version). Surrounding panels show brain areas correlated with performance gains with tutoring. Scatter plots in each panel are based on voxels showing peak connectivity.

Adapted from Supekar, K., Swigart, A.G., Tenison, C., Jolles, D.D., Rosenberg-Lee, M., Fuchs, L., Menon, V., 2013. Neural predictors of individual differences in response to math tutoring in primary-grade school children. Proc. Natl. Acad. Sci. U.S.A. 110, 8230–8235.

4 COGNITIVE CONTROL SYSTEMS IN MATHEMATICAL COGNITION

4.1 FLEXIBLE HUBS FOR COGNITIVE CONTROL

Prefrontal control processes are important for virtually every complex cognitive task, including mathematical cognition. The role of both working memory and declarative memory systems in mathematical cognition must therefore be considered in the context of cognitive control processes that support flexible problem solving and learning. Prefrontal control processes serve several functions in numerical cognition including maintenance of attention on goal-relevant numerical representations, manipulation of information in working memory, inhibition of irrelevant information, and implementation of task-relevant activations. Implementation of such control relies on dynamic functional interactions between multiple frontal regions (Cai et al., 2014, 2016; Cole et al., 2013; Ham et al., 2013; Seeley et al., 2007; Sridharan et al., 2008), and recent research has begun to elucidate the role of parietal–frontal and hippocampal–frontal circuits in different aspects of cognitive control during mathematical cognition.

4.2 DYNAMIC PARIETAL–FRONTAL CONTROL SIGNALS

As noted in Section 2, a common recurring theme in numerical problem solving is the coengagement of parietal and prefrontal regions associated with working memory. Children as young as 7 show reliable, and consistent, patterns of brain activity during arithmetic problem solving in multiple PFC regions (Houde et al., 2010). Commonly activated PFC regions include the anterior insula, and ventrolateral and dorsolateral PFC (Fig. 1). It should be noted that these regions are also implicated in a wide range of cognitive control tasks in adults as well as children (Cole et al., 2013; Cai et al., 2014, 2016; Ham et al., 2013; Seeley et al., 2007; Sridharan et al., 2008; Ordaz et al., 2013).This profile of anatomical overlap suggests a common mechanism by which maturation of basic cognitive control can influence skill development across multiple cognitive domains.

Efficient control requires the concerted coordination between multiple brain regions, and there is growing evidence to suggest that this is implemented via dedicated neurocognitive networks. Two-key networks play a fundamental role in cognitive control processes in the human brain: the insula–cingulate salience network, which includes the anterior insula and anterior cingulate cortex, and the dorsal parietal–frontal working memory network, which includes the ventrolateral and dorsolateral PFC and supramarginal gyrus. Supekar and Menon (2012) examined functional connectivity and dynamic causal interactions between the major nodes of these networks to investigate the maturation of control processes underlying numerical problem-solving skills in 7–9-year-old children, relative to adults. They found that, by age 9, the anterior insula node of the salience network is a major causal hub initiating control signals during problem solving (Fig. 7). The anterior insula, part of a larger network of regions previously shown to be important for salience processing and generating influential control signals, showed weaker influence over the ventrolateral and dorsolateral PFC and anterior cingulate cortex in children compared to adults. Despite higher levels of PFC activation in children, the strength of their causal modulatory influences to the parietal cortex was significantly weaker relative to adults.

FIG. 7.

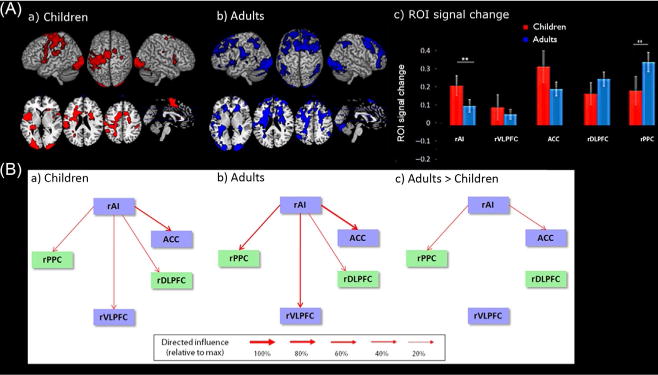
Developmental changes in causal network interactions during arithmetic problem solving. (A) Activation of the salience and parietal–frontal central executive networks in (a) children and (b) adults. (c) Task-related signal change in ROIs within the nodes of the two networks. Compared to adults, children showed stronger activation in the right anterior insula (AI) and weaker activation in the right posterior parietal cortex (PPC) (**p<0.01, FDR corrected). (B) Dynamic causal analysis of the five-key nodes of the salience network (blue, gray in the print version, rectangles), and parietal–frontal network (green, light gray in the print version, rectangles) in (a) children and (b) adults. (c) Weaker causal interactions in children, compared to adults. VLPFC, ventrolateral prefrontal cortex; DLPFC, dorsolateral prefrontal cortex; ACC, anterior cingulate cortex.

Adapted from Supekar, K., Menon, V., 2012. Developmental maturation of dynamic causal control signals in higher-order cognition: a neurocognitive network model. PLoS Comput. Biol. 8, e1002374.

Notably, weaker PFC control signals were associated with lower levels of arithmetic performance, and network interactions better predicted reaction time in both children and adults. In children, the strength of casual signals from the anterior insula to supramarginal gyrus and ventrolateral PFC predicted reaction times, while the strength of anterior insula to supramarginal gyrus, ventrolateral PFC, and anterior cingulate cortex predicted reaction times in adults. Reaction times were better predicted in adults, compared to children. It is noteworthy that even though a different set of links predicted reaction times in both groups, the anterior insula to supramarginal gyrus link was common in both. Similar results were observed when accuracy instead of reaction time was used as the performance measure. Thus, multiple PFC control signals contribute to efficient problem-solving skills in adults and weak signaling mechanisms contribute to lower levels of performance in children.

4.3 DYNAMIC HIPPOCAMPAL–FRONTAL CONTROL SIGNALS

As described in Section 3, both the ventrolateral and dorsolateral PFC are associated with increased use of memory-based strategies in children (Cho et al., 2012). The ventrolateral PFC is known to play a prominent role in cognitive control over memory retrieval processes both in adults (Badre and Wagner, 2007; Koechlin et al., 2003; Miller, 2000) and in children (Adleman et al., 2002; Bunge and Wright, 2007; Houde et al., 2010; Kwon et al., 2002). These control processes are thought to be important for accurate retrieval of relevant facts and inhibition of irrelevant information (Destefano and Lefevre, 2004; Kaufmann, 2002; Kaufmann et al., 2004; Logie et al., 1994).

Dynamic causal modeling of fMRI data has provided further insights into the temporal profile of interactions between the hippocampus and PFC regions involved in mediating retrieval fluency. Causal analysis has revealed strong bidirectional interactions between the hippocampus and both the left ventrolateral and dorsolateral PFC (Fig. 8). Crucially, causal influences from the left ventrolateral PFC to the hippocampus act as the main “top-down” component, while causal influences from the hippocampus to the left dorsolateral PFC serve as the main “bottom-up” component of this retrieval network. While still preliminary, these analyses highlight the differential contribution of hippocampal–prefrontal circuits to the early development of retrieval fluency in arithmetic problem solving and provide a novel framework for studying dynamic developmental processes involving the hippocampus and PFC that accompany the maturation of cognitive skills. Further research is needed to investigate how these processes contribute to concomitant improvements in cognitive control over retrieval, including successful inhibition of irrelevant information, such as incorrect answers, intermediate steps, and operand intrusions (Barrouillet and Lepine, 2005; Passolunghi and Siegel, 2004).

FIG. 8.

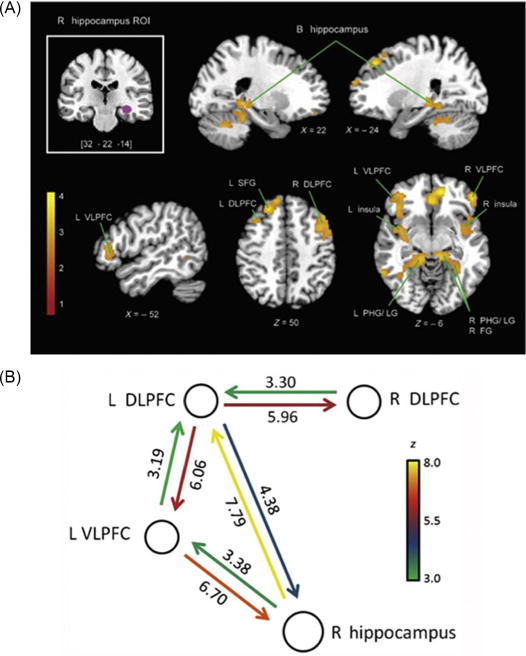
Hippocampal–prefrontal cortex circuits in children’s fact retrieval. (A) Functional connectivity of right hippocampus (top-left inset), showing greater effective connectivity during addition problem solving when compared with a control task. Greater connectivity was observed in the bilateral hippocampus, bilateral VLPFC, bilateral DLPFC, left SFG, bilateral insula, bilateral LG, bilateral PHG, and right FG. (B) Dynamic causal interactions in the hippocampal–prefrontal retrieval network. Analysis of causal interactions between left VLPFC, left and right DLPFC, and right hippocampus. Both the left VLPFC and the left DLPFC showed highly significant direct causal influences with the right hippocampus. Causal links depicted were all significant using p<0.01, after Bonferroni correction. VLPFC, ventrolateral prefrontal cortex; DLPFC, dorsolateral prefrontal cortex; SFG, superior frontal gyrus; PHG, parahippocampal gyrus; LG, lingual gyrus; FG, fusiform gyrus.

Adapted from Cho, S., Ryali, S., Geary, D.C., Menon, V., 2011. How does a child solve 7+8? Decoding brain activity patterns associated with counting and retrieval strategies. Dev. Sci. 14, 989–1001.

5 SUMMARY AND CONCLUSIONS

Multiple lines of evidence affirm that numerical cognition relies on interactions within and between multiple functional brain circuits, including those underlying numerical quantity representations (FG–IPS), working memory (IPS–SMG–ventrolateral and dorsolateral PFC), declarative memory (hippocampus–ventrolateral and dorsolateral PFC), and cognitive control (anterior insula–ventrolateral and dorsolateral PFC) (Fig. 1). We have highlighted the role of distinct memory and cognitive control systems that play distinct roles in mathematical cognition and learning.

We have reviewed evidence that the parietal–frontal working memory system is engaged during a wide range of numerical problem-solving tasks. Multiple working memory circuits anchored in different subdivisions of the inferior parietal cortex help create short-term representations that support the manipulation of multiple discrete quantities over several seconds. The IPS and supramarginal gyrus are associated with differential patterns of connectivity with the frontal eye field and ventrolateral and dorsolateral PFC. Findings to date suggest that the IPS plays an essential role not only in quantity representations but also in maintaining quantity-related information in short-term working memory. Rule-based and context-specific manipulation of these representations in working memory is in turn supported by multiple prefrontal cortical areas—here the supramarginal gyrus emerges as a key locus for integrating frontal control systems with quantity representations supported by the IPS.

The hippocampal–frontal declarative memory system has an entirely different role in mathematical cognition and learning. This system plays a critical, but time limited, role in the early phase of knowledge acquisition, and this hippocampal dependence is reduced following reconfiguration of neocortical connections and stabilization of newly acquired knowledge. Hippocampal–neocortical reorganization facilitates fluent retrieval and long-term neocortical memory consolidation in children, eventually resulting in retrieval processes that are independent of the hippocampus (Qin et al., 2014).

The working memory and declarative memory systems intersect most prominently in the ventrolateral and dorsolateral PFC, which together with the anterior insula likely serve as flexible hubs for integrating information across attentional and memory systems. As reviewed in Section 4, weak control signals from these PFC regions negatively impact the ability to maintain task-relevant representations needed for achieving mature levels of performance. Better understanding of control processes mediated by these PFC regions is essential for a more mechanistic characterization of mathematical cognition, skill development, and learning.

A challenging question for future research is to understand how the distinct functional circuits highlighted in this review interact dynamically to support different aspects of mathematical cognition and learning and how they change with different stages of development. Addressing this question will require developing appropriate computational models of dynamic causal interactions between brain regions, analyzing different stages of information processing, and utilizing more appropriate experimental designs that involve the controlled manipulation of symbolic and nonsymbolic quantity representations in posterior brain regions including the FG and IPS.