Statistical Significance Versus Clinical Importance of Observed Effect Sizes: What Do P Values and Confidence Intervals Really Represent?

Abstract

Effect size measures are used to quantify treatment effects or associations between variables. Such measures, of which >70 have been described in the literature, include unstandardized and standardized differences in means, risk differences, risk ratios, odds ratios, or correlations. While null hypothesis significance testing is the predominant approach to statistical inference on effect sizes, results of such tests are often misinterpreted, provide no information on the magnitude of the estimate, and tell us nothing about the clinically importance of an effect. Hence, researchers should not merely focus on statistical significance but should also report the observed effect size. However, all samples are to some degree affected by randomness, such that there is a certain uncertainty on how well the observed effect size represents the actual magnitude and direction of the effect in the population. Therefore, point estimates of effect sizes should be accompanied by the entire range of plausible values to quantify this uncertainty. This facilitates assessment of how large or small the observed effect could actually be in the population of interest, and hence how clinically important it could be. This tutorial reviews different effect size measures and describes how confidence intervals can be used to address not only the statistical significance but also the clinical significance of the observed effect or association. Moreover, we discuss what P values actually represent, and how they provide supplemental information about the significant versus nonsignificant dichotomy. This tutorial intentionally focuses on an intuitive explanation of concepts and interpretation of results, rather than on the underlying mathematical theory or concepts.

Medical researchers commonly report the effects of a treatment or describe relationships between variables. Treatment effects or associations can be quantified using measures like mean differences, risk ratios, or correlations. Null hypothesis (Ho) significance tests (eg, t tests or χ² tests) are commonly used to determine the “statistical significance” of the observed effect, usually defined by a P value of <.05. However, P values are often misinterpreted and provide no information on the magnitude or importance of the effect.^1–3 Hence, rather than merely focusing on statistical significance, researchers should provide plausible estimates about the magnitude of the effect in the population from which the data were sampled.^4,5

Previous statistical tutorials in this series initially discussed P values, confidence intervals (CIs), and effect size.^6–8 The aim of the present basic statistical tutorial is to discuss in greater detail how a treatment effect or association can be quantified using the effect size, and how a CI can help to assess the statistical but especially also the clinical significance of the observed effect. Moreover, we discuss what P values actually represent and how they should be interpreted.

We will recurrently use a study by Frey et al,⁹ which analyzed perioperative temperature management in 79 patients undergoing open colon surgery, to illustrate these concepts. These study patients were randomly assigned to standard temperature management, or standard management in combination with insufflation of warm, humidified carbon dioxide into the wound cavity. While these authors report several outcomes, we specifically focus here on the difference in core temperature at the end of surgery.

EFFECT SIZE

Effect size describes the magnitude of the quantitative relationship between one variable (eg, a variable that defines a treatment group) and another variable (eg, a specific outcome).^4,5,10–12 Note that while the term “effect” implies a causal relationship, calculation of an effect size does not imply or require causality, and the reported effect size provides no information on whether there is actually a direct effect of 1 variable on another.^4,5

Bias is especially possible in observational studies, yet is potentially present in all study designs. It can distort the relationship between variables, such that the estimated effect size does not necessarily reflect the actual, true effect in the population. Different types of study design, implications of bias and confounding, as well as the distinction between association and causation have previously been reviewed in this current series of statistical tutorials.^13–15

Types of Effect Size Measures

Effect sizes can be classified into 2 categories: (1) effect sizes that describe differences between groups and (2) effect sizes that describe the strength of an association.^10,16

The difference between groups is often reported as the difference in means when the outcome variable is continuous. In the study by Frey et al,⁹ the core temperature at the end of surgery was 36.9°C in the intervention group and 36.3°C in the control group. The difference in mean temperature of 0.6°C was the observed point estimate of the magnitude of the treatment effect in the overall population of patients from which the sample was taken.⁶ We will discuss CIs below as a type of interval estimate of the observed effect size.

Raw differences in means can be easily interpreted when meaningful units of measurement (eg, temperature in °C) are used. However, when the measurement scale does not have an intrinsic meaning (eg, a patient satisfaction score from 0 to 100), standardized differences are more informative.¹⁶ Such effect size measures are usually scaled to the standard deviation (SD), such that a standardized difference of 0.5 equates to 0.5 SDs. These measures (eg, Cohen’s d, Glass’ Δ) mainly differ by the type of SD that is used for scaling (eg, pooled SD, control group SD).¹¹

When the outcome variable is categorical, comparisons between the groups can be based on the proportion of group members being classified in an outcome category. Frey et al⁹ compared the percentage of patients being hypothermic (core temperature <36.5°C) at the end of surgery. In the control group, 24 of 39 (62%) of patients were hypothermic, whereas in the intervention group, 8 of 40 (20%) of patients were hypothermic. The authors report the difference in percentages (42%), but differences in proportions are also commonly reported. Because the proportion can be viewed as a risk of belonging to a certain outcome group, this effect size is often referred to as the risk difference.¹⁷ Alternatively, the ratio of the risks can be reported, which is termed the risk ratio or relative risk. In the example by Frey et al,⁹ a relative risk of 0.62/0.20 = 3.1 means that the risk of being hypothermic is 3.1 times greater in the control group. A related effect size is the odds ratio. We refer the reader to a previous tutorial on risks, odds, and their ratios.¹⁸

Among the effect sizes that address the association between variables, Pearson correlation coefficient is probably the most common. It describes the strength of a linear relationship between 2 continuous, normally distributed variables.¹⁹ Other measures such as Spearman’s ρ or Cramer’s V are used to assess associations between nonnormal continuous, rank-ordered or nominal data.¹² Correlation will be addressed in more detail in a subsequent tutorial in this series.

PART 1 FROM SAMPLE TO POPULATION: P VALUES

As in most studies, Frey et al⁹ used a sample from a population to make inferences or draw conclusions about the entire population. We are less concerned about the temperatures in the study sample of 79 patients, but far more so whether the study intervention is generally useful for temperature management during open colon surgery.

Any sample is inevitably affected to some extent by randomness, and even if there was absolutely no effect of the treatment, we would still likely—in fact certainly, if the measurements are precise enough—observe some difference between the groups. However, what would be the probability of observing an effect as large as or maybe even larger than the one observed in the sample, if there was actually no true effect in the population? The P value addresses this question.

P values are calculated in the context of null hypothesis significance testing. The null hypothesis (Ho) usually states that there is no effect (eg, the difference in the means between groups is 0), while the alternative hypothesis (Ha) states that there is some effect and difference.²⁰ Hypothesis testing aims to reach a dichotomous decision as to whether or not the null hypothesis can be rejected in favor of the alternative hypothesis. Null hypothesis significance testing, including type I and type II errors, as well as α and β levels, was previously reviewed in Anesthesia & Analgesia.⁸ Here, we focus on the interpretation of the P value itself.

The P value is the probability to observe a result at least as extreme as the one that was observed, under the assumption that the null hypothesis was actually true.^1,2,21 Frey et al⁹ report a P value of <.001 for the difference in temperature between the groups. This means that the probability of observing a difference of 0.6°C or more is <0.1% if there was actually no true difference between the groups (with the same sample size, data variability, and lack of bias). Hence, such a small P value suggests that the observed data are quite incompatible with the null hypothesis of no group difference.

Researchers commonly reject the null hypothesis (Ho) in favor of the alternative hypothesis (Ha) when the P value is below some threshold (traditionally 0.05). Such a result is termed “statistically significant,” but it should be noted that this threshold is arbitrary and there is no clear dividing line between a probable and an improbable result. Moreover, a simple dichotomy (significant versus nonsignificant) ignores the fact that a lower P value provides more convincing evidence against the null hypothesis.²² We therefore advocate that the P value can be used not only as a dichotomous decision instrument with some arbitrary threshold but also as an indicator of the strength of the evidence against the null hypothesis.

P values are commonly misinterpreted.^1–3,23 The P value is calculated assuming that the null hypothesis is true, and it is therefore not the probability that the null hypothesis is true. Another misconception is that a nonsignificant result demonstrates that there is no effect. A nonsignificant result simply indicates that there is no sufficient evidence against the null hypothesis. This must not be misinterpreted as proof that the null hypothesis is true. Importantly, P values also do not convey any information about the effect size or the clinical importance of the observed effect. The following section describes how this information gap can be addressed with CIs.

We finally emphasize that P values are used in the context of hypothesis testing, and it makes no sense to report P values when no hypothesis is being tested. A classic example of a misuse is the baseline comparison of study groups in a randomized controlled trial. With adequate randomization, participants in study groups are sampled from the same population, and irrespective of the P value, any differences between the groups at baseline are due to chance.²⁴ Nonetheless, baseline imbalances can affect the results and should be considered, but again, irrespective of the P value.²⁴ Therefore, the instructions for author of several journals, including Anesthesia & Analgesia, request reporting standardized differences instead of P values for baseline comparisons in a randomized controlled trial.²⁵

PART 2 FROM SAMPLE TO POPULATION: CIs

Frey et al⁹ observed a difference in temperature of 0.6°C between their sampled study groups. However, this provides only limited information on how large the actual effect in the population might be. In this context, a CI provides a range of plausible values for the estimate. Actually, a CI can not only be calculated for an effect size (eg, mean difference, risk ratio, or odds ratio) but also for a wide range of estimates of population parameters, including means and proportions.

Formally, a CI is an interval that contains the true population parameter in a fixed percentage of samples with repeated sampling.²⁶ The fixed percentage is termed the confidence level, which is often (though again arbitrarily) chosen as 95%. This indicates that when samples are repeatedly taken over and over again from the same population, and if we would calculate the 95% CI for each sample, about 95% of them will contain the true population parameter (Figure 1).

Figure 1.

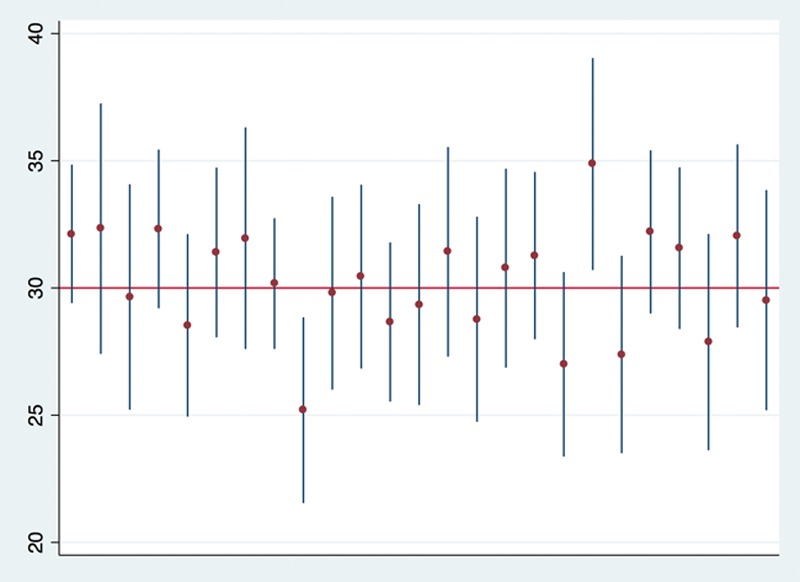
Ninety-five percent confidence intervals (vertical lines) and means (dots) calculated from a simulation of 25 samples (sample size of 30 each) drawn from a normally distributed population with a mean of 30 and a standard deviation of 10. One could think of this as a population of patients with a mean age of 30 y and a standard deviation of 10 y, from which we sample n = 30 patients to estimate the mean age in the population, and we repeat this experiment 25 times. Note that 23 of the confidence intervals (23/25 = 92%) cover the “true” population mean of 30. If we (infinitely) keep repeating this simulation, we would expect that 95% of the confidence intervals contain the true population parameter value.

A common misinterpretation is that there is a 95% probability that a given 95% CI contains the true population parameter.²⁷ The parameter is a fixed albeit unknown value. The 95% CI either contains the parameter or does not, and the probability is either 100% or 0%. This becomes clear when looking at an example with actual numbers. In Figure 1, the first 95% CI ranges from 29.4 to 34.8. While the true population parameter is usually unknown, we know that it is 30 in this simulated example. Now, it does not make any sense to say that the probability is 95% that 30 falls within the range between 29.4 and 34.8. While in this particular case we definitely know that the CI contains the true population parameter value, there is no way to know whether any CI estimated from a sample contains the parameter.

Given this limitation, some authors argue against the usefulness of CIs.²⁷ However, as the vast majority of the estimated 95% CIs will contain the unknown population parameter, it is plausible to believe that a particular 95% CI contains the true value of interest. Accordingly, the CI is often interpreted as the best estimate from a study of the range of plausible values of the parameter, and narrower CIs (with the same confidence level) are considered to indicate a higher precision of the estimate.^28,29

Note that the width of a CI is inversely related to sample size,³⁰ such that studies with a large number of subjects usually (but not always, as the width of the CI also depends on the variability of the data) provide more precise estimates than smaller sample studies. The choice of the confidence level also affects the width, as the CI widens when the confidence level increases.³⁰ This means that a 99% CI provides a higher confidence of including the true parameter value (ie, contains it more often) than a 95% or 90% CI, however, at the “cost” of a wider total range of values.

Applying CIs to effect sizes provides a range of plausible values of the effect size in the population. Note that there is a close relationship between CIs and significance testing.²⁸ If the 95% CI of the effect size contains the value that indicates “no effect” (eg, the null value of 0 for a difference, or 1 for a risk ratio or odds ratio), this means that the data are compatible with no effect, corresponding to a nonsignificant result with a 0.05 significance cut-point level. In the study by Frey et al,⁹ the 95% CI of the difference in core temperature was 0.4°C–0.8°C. Because this interval does not contain 0, the result is statistically significant at the 0.05 significance level. However, is this finding also clinically significant?

This question cannot be exclusively answered by statistics, but it instead needs to be addressed by clinical judgment. The data are compatible with an actual difference of as little as 0.4°C, and we are not sure whether this is important.

Researchers need to define and to support what they consider a minimal clinically important effect, and journal editors, reviewers, and readers need to assess whether this seems reasonable. Note that an important effect does not necessarily have to be large. For example, a small effect on mortality can make a huge difference not only for individual patients but also for society if a large percentage of patients is affected by the condition.

Whenever the confidence limits contain a clinically important effect, a clinically significant effect cannot be ruled out irrespective of the statistical significance. Vice versa, a CI that does not contain an important effect questions the clinical significance, even if the result is statistically significant. Figure 2 provides several examples from hypothetical studies, in which the CIs allow for a more detailed interpretation of the results than significance tests.

Figure 2.

Five examples (A–E) of 95% CIs (vertical lines) of the difference between mean SBP from 5 hypothetical studies in which SBP is compared between 2 groups. Note that in examples A–C, the 95% CI does not include 0 (horizontal solid line), indicating a significant difference at a 0.05 significance level, whereas D–E correspond to a nonsignificant result. For the sake of the example, we consider a difference of >5 mm Hg between the groups as clinically relevant (horizontal dashed lines at +5 and −5 mm Hg). Example A: the entire 95% CI covers a clinically relevant range, suggesting that the observed difference between the groups is not only statistically significant but also clinically important. Example B: although the result is statistically significant, the clinical relevance remains unclear. The result is compatible with a clinically nonimportant difference of only 2 mm Hg, but it is also compatible with a true difference as high as 15 mm Hg. Example C: the entire 95% CI includes a range that is clinically unimportant. Although there is a statistically significant effect, the clinical relevance of the finding appears to be limited. Example D: although the result is nonsignificant (95% CI spans 0), the data are also compatible with a clinically relevant difference in either direction. Hence, the result is inconclusive and should not be interpreted as demonstrating no effect. Example E: the narrow 95% CI around 0 does not include any clinically important values. In this specific example, there appears to be no clinically relevant effect. CI indicates confidence interval; SBP, systolic blood pressure.

PART 3 FROM SAMPLE TO POPULATION: OTHER CONSIDERATIONS

For CIs and P values to be valid, it is crucial that they have been calculated by appropriate methods, as different statistical models have different underlying assumptions, for example, concerning the distribution and independence of data. Even if the analysis methods are appropriate, real-world data seldom perfectly meet all assumptions, and real-world P values and CIs are therefore not exactly what that they claim to be.

We mentioned earlier that bias can substantially distort effect sizes, and it is crucial to consider sources of potential bias in the interpretation of study results. As all bias can hardly ever be excluded, and as statistics never provide definitive answers, we suggest interpreting research results carefully, rather than viewing them as conclusive evidence.

SUMMARY

Like previous tutorials in this series in Anesthesia & Analgesia, this one intentionally focuses on an intuitive explanation of concepts and interpretation of results rather than on the underlying mathematical theory or concepts. Effect sizes describe the magnitude of a quantitative relationship between variables. CIs and P values show 2 sides of the same coin. A CI provides a range of plausible values of the effect size estimate. While a CI can be used to determine whether a finding is statistically significant or not, it is especially useful for determining clinical significance (or relevance). The P value provides additional information on the statistically significant versus not significant dichotomy, and it can be viewed as a measure of the strength of evidence against the null hypothesis. Sources of bias should be considered when determining whether the observed treatment effects are actually present in the population of interest.

DISCLOSURES

Name: Patrick Schober, MD, PhD, MMedStat.

Contribution: This author helped write and revise the manuscript.

Name: Sebastiaan M. Bossers, MD, MSc.

Contribution: This author helped write and revise the manuscript.

Name: Lothar A. Schwarte, MD, PhD, MBA.

Contribution: This author helped write and revise the manuscript.

This manuscript was handled by: Thomas R. Vetter, MD, MPH.

Acting EIC on final acceptance: Thomas R. Vetter, MD, MPH.