Polarizable Empirical Force Field for Halogen-containing Compounds Based on the Classical Drude Oscillator

Abstract

The quality of the force field is crucial to ensure the accuracy of simulations used in molecular modeling, including computer-aided drug design (CADD). To perform more accurate modeling and simulations of halogenated molecules, in this study the polarizable force field based on the classical Drude oscillator model was extended to both aliphatic and aromatic systems using halogenated ethane and benzene model compounds, for the halogens F, Cl, Br or I. The force field parameters were optimized targeting quantum mechanical dipole moments, water interactions, and molecular polarizabilities as well as experimental observables, including enthalpies of vaporization, molecular volumes, hydration free energies, and dielectric constants. The developed halogenated polarizable force field is capable of reproducing QM relative energies and geometries of both halogen bonds and halogen-hydrogen bond donor interactions at an unprecedented level due to the inclusion of a virtual particle and anisotropic atomic polarizability on the halogen and, notably, the inclusion of Lennard-Jones parameters on the halogen Drude particle. The model was validated based on its ability to accurately reproduce pure solvent properties for halogenated naphthalenes and alkanes, including species analogous to those used as refrigerants. Accordingly, it is anticipated that the model will be applicable for the study of halogenated derivatives in CADD as well as in other chemical and biophysical studies.

Table of Contents

1. Introduction

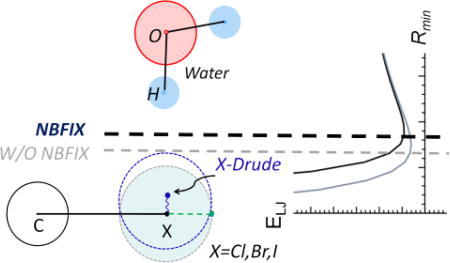
Halogenated molecules are used in a wide range of functions ranging from industrial uses, such as refrigerants,¹ to biological roles, including therapeutic agents.^2,3 To understand the properties of halogens that make them of such diverse use as well as the rational design of novel halogenated species, molecular dynamics (MD) simulations have been shown to be of great utility.^4–7 To assure the accuracy of MD simulations, a high quality force field is essential.⁸ Nowadays, a number of force fields for organic compounds, such as GAFF (Generalized Amber Force Field),⁹ OPLS (Optimized Potentials for Liquid Simulations),^10,11 or CGenFF (CHARMM General Force Field),^12–16 among others, have been developed. In these force fields the partial atomic charges are fixed, treating the induced polarization in a mean-field average way; however, in practice the electron density is not static and should be able to adjust in response to the local electric field, such that the electronic polarizability may be underestimated in the condense phase by using fixed charge models.¹⁷ Accordingly, to improve the accuracy of molecular simulations, efforts have been ongoing to incorporate the explicit treatment of electronic polarizability into the force field.^18–20 Towards this end, the classical Drude oscillator model has been successfully used to describe water,^21,22 a range of small molecules,^{23,24,24–27} proteins,²⁸ DNA^29,30 and selected lipids.^31,32 To explicitly treat the inducible polarization on molecules, electronic polarizability is introduced by using a charge-carrying auxiliary ‘‘Drude’’ particle linked to each non-hydrogen atom via a harmonic bond (Figure 1).²⁰ In this study, the polarizability will be treated via the classical Drude oscillator model.²⁰ From this model, the atomic polarizability, α_A, of a given atom (A) is defined based on the charge on the Drude particle (q_DA) and the force constant (k_D) of the harmonic spring between the Drude particle and parent atom nucleus according to Eq. 1, where k_D is assigned to be 500 kcal/mol/Ų and fixed for all the atoms.³³

$${\mathrm{\alpha }}_A=\frac{{q_{\mathit{\text{DA}}}}^2}{k_D}$$ Eq. 1

The charge on the atomic core (or nucleus), q_A, will be q - q_DA, where the q is the partial atomic charge on atom A. From this description, polarization is determined by a pair of point charges (q_A and q_DA) separated by a variable displacement, d, between the Drude particle and the atomic core, which is able to adjust in response to the electric field, E, according to the Eq. 2:

$$\mathbf{d}=\frac{q_{\mathit{\text{DA}}}\mathit{E}}{k_D}$$ Eq. 2

The induced atomic dipole, μ, is calculated as:

$$\mathbf{\mu }=\frac{{q_{\mathit{\text{DA}}}}^2\mathit{E}}{k_D}$$ Eq. 3

To provide better treatment of molecular polarizabilities in the energy calculation, the induced dipole–dipole interactions for atoms within three bonds (e.g. 1–2 or 1–3 atom pairs) are explicitly treated with those electrostatic interactions screened by a Thole-like screening function S_ij (Eq. 4).³⁴ This is different from the additive force fields where the nonbonded interactions between 1–2 and 1–3 atom pairs are excluded.

$$S_{\mathit{\text{ij}}}({\mathrm{r}}_{\text{ij}})=1-\left[\right(1+\frac{({\mathrm{t}}_{\mathrm{i}}+{\mathrm{t}}_{\mathrm{j}}){\mathrm{r}}_{\text{ij}}}{2{({\mathrm{\alpha }}_{\mathrm{i}}{\mathrm{\alpha }}_{\mathrm{j}})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}\left)\right]\mathrm{ exp }\left[\frac{-({\mathrm{t}}_{\mathrm{i}}+{\mathrm{t}}_{\mathrm{j}}){\mathrm{r}}_{\text{ij}}}{{({\mathrm{\alpha }}_{\mathrm{i}}{\mathrm{\alpha }}_{\mathrm{j}})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}\right]$$ Eq. 4

In equation 4, r_ij is the distance between atoms i and j, α_i and α_j are respective atomic polarizabilities according to Eq. 1, t_i and t_j are the respective atomistic Thole screening factors that dictate the degree of scaling. While parameters for halogenated methanes based on polarizable models have been developed,^35,36 a comprehensive set of parameters for halogenated molecules based on ethane and benzene systems is still not available.

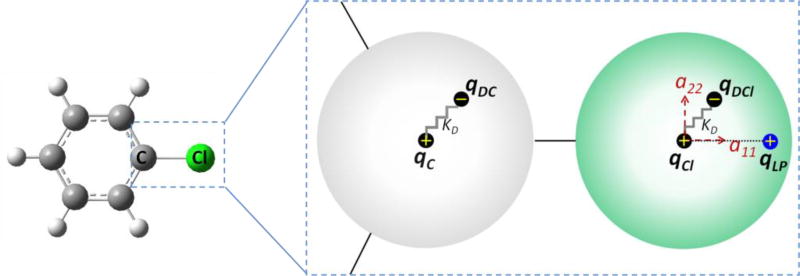
Figure 1.

Schematic of the Drude oscillator model for chlorobenzene. The addition of Drude oscillators to carbon (C) and chlorine (Cl) atoms via harmonic springs with a force constant, k_D, and the subsequent distribution of charge between the atoms (q_C and q_Cl) and their respective Drude oscillators (q_DC and q_DCl) are presented. A virtual particle to mimic the σ-hole on the chlorine atom is labeled “LP” with the charge, q_LP. The anisotropic polarization tensor components on the chlorine are labeled as a₁₁ and a₂₂. The other tensor component is orthogonal to a₁₁ and a₂₂ and is not shown.

Traditionally, halogens were considered to be hydrophobic;³⁷ however, halogens were more recently recognized to serve as hydrogen bond acceptors (HBA)^37–41 and as halogen bond (XB) donors,^37,42,43 both of which have been reported to contribute to ligand-protein interactions experimentally.^3,44–48 The dual roles of halogens result from their anisotropic electron distribution when the halogen is covalently bonded to a carbon atom (C). The p_z-orbital of halogens is shifted to participate in the formation of the C-X covalent bond, resulting in an electron diminished region on the outer side of the halogen linear to the C-X bond, yielding a slightly positive potential known as a σ-hole.^37,49,50 The presence of the σ-hole allows halogens to favorably interact with a nucleophilic atom when aligned along the C-X bond to form the well-known halogen bond (XB).^37,42,43,51 In contrast, the valence electrons on the perpendicular p_x and p_y atomic orbitals of halogens remain occupied, and thus the electron distribution around the periphery of the halogen in the region perpendicular to the C-X covalent bond is larger than that linear to the C-X bond.⁵² The presence of the electronegative potential perpendicular to the C-X bond allows halogens to interact with electrophilic atoms, such as a hydrogen bond donor.³⁷ Meanwhile, the van der Waals (vdW) surface of the halogen becomes asymmetric due to the shift of the electron density, resulting in a shorter vdW surface on the halogen linear to the C-X covalent bond.⁵³ This allows the electropositive σ-hole to have relatively shorter interaction distances with nucleophilic atoms, while the perpendicular peripheral region of halogens participate in a relatively longer distance when interacting with an electrophilic atom.⁵³

Force fields for halogens traditionally assigned a partial negative charge to the atom with a relatively large favorable dispersion contribution.⁵⁴ Due to the discovery of the σ-hole, recent halogen force fields have been extended, including the use of a virtual particle carrying a positive charge, to mimic the σ-hole on the halogen, thereby effectively modeling the halogen bond (XB).^13,55,56 While representing an improvement for XB interactions, such models do not accurately model the anisotropic nature of the vdW surface of the halogens, a problem that was effectively treated in the context of an additive force field by using a Lennard-Jones (LJ) function that included an angular dependence,⁵³ allowing for a flattening of the halogens along the σ-bond and a larger radii perpendicular to the C-X bond. However, all of these models have not explicitly addressed their ability to treat halogens interacting with hydrogen bond donors (termed X-HBD interactions), a role that has been less discussed in the literature.^{38,40,41,57,58} Work in our laboratory has investigated the X-HBD interactions using quantum mechanical (QM) calculations in conjunction with bioinformatics analysis and shown them to be the most favorable in the region perpendicular to C-X covalent bonds, consistent with the electron distribution around halogens, with these interactions being more favorable than halogen bonds and of similar strength as canonical hydrogen bonds.⁵⁹

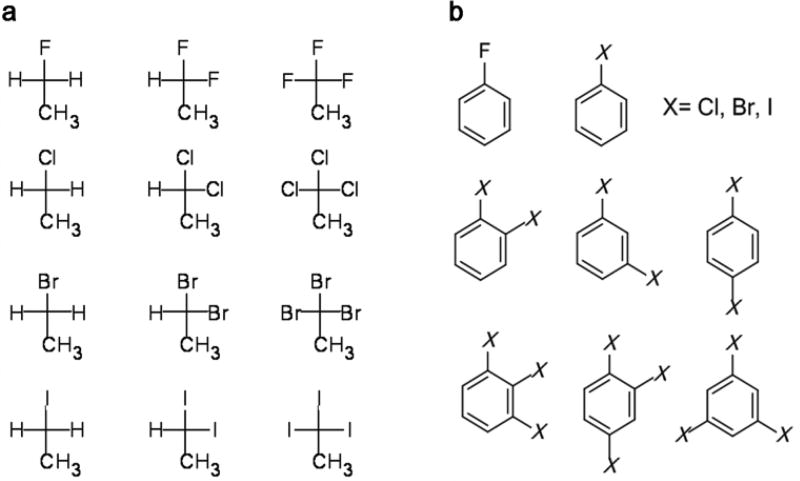
In this study, polarizable force field parameters were developed and validated for organohalogens based on the classical Drude oscillator model²⁰ for a series of halogenated molecules, including both aliphatic and aromatic systems, such as ethyl-X or phenyl-X, respectively, with X being F, Cl, Br, or I (Figure 2). The force field parameters were fitted to QM data, including dipole moments, molecular polarizabilities, and interactions with water, as well as experimental observables, including enthalpies of vaporization, molecular volumes, hydration free energies, and dielectric constants. The anisotropic charge distribution and shape of the halogens were reproduced by inclusion of a virtual particle along the C-X covalent bond and applying LJ parameters to the halogen Drude particle, resulting in better modeling of interaction energy and distance profiles when the halogens act as both halogen bond donors and hydrogen bond acceptors. The developed parameters were further validated on 20 halogenated aromatic and aliphatic derivatives, showing the model to be predictive of experimental pure solvent properties. Accordingly, the resulting polarizable force field will be applicable to CADD involving halogenated derivatives as well as modeling and simulation studies of halogens in a range of chemical systems.

Figure 2.

Structures of target-set of halogenated molecules under parametrization. a. Halogenated ethanes. b. Halogenated benzenes. See Table S1 for molecule names and abbreviations.

2. Computational Methods

The halogenated molecules under parametrization included halogenated ethane and benzene analogs (Figure 2). Parametrization of the Drude halogen force field required target data obtained from quantum mechanical (QM) calculations using the programs Gaussian03,⁶⁰ PSI4,⁶¹ and NWCHEM⁶² and experimental observables. Molecular mechanical (MM) and molecular dynamics (MD) calculations were performed using the programs CHARMM^63–65 and NAMD.⁶⁶

2.1 Quantum mechanical calculations

QM geometry optimizations were performed at the MP2 level of theory with the aug-cc-pVDZ basis set⁶⁷ for fluorinated and chlorinated species and with the aug-cc-pVDZ-PP basis set^68,69 for brominated and iodinated species. The QM vibrational spectra were calculated following QM geometry optimizations from the same model chemistry, with the resulting frequencies scaled by 0.959⁷⁰ for use as target values. Dihedral angle potential energy scans (PES) were initiated on the QM optimized geometries with the same model chemistry with only the targeted dihedral constrained while the remaining degrees of freedom were allowed to relax. Single point calculations were performed on the optimized geometries to obtain the final QM energies, molecular dipole moments and molecular polarizabilities for use as target data, where the MP2/cc-pVQZ model chemistry⁶⁷ was used for fluoro- and chloro-substituted analogs, and MP2/sdb-cc-pVQZ⁷¹ model chemistry was used for bromo- and iodo-analogs. The aforementioned QM calculations were performed using Gaussian03.⁶⁰

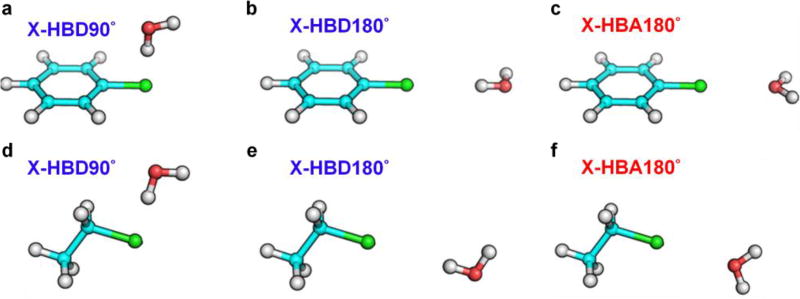
Single-point interaction energies for fluorinated, chlorinated and brominated analogs with water were obtained at the RIMP2 level of theory with the cc-pVQZ basis set⁶⁷ using PSI4.⁶¹ For iodinated analogs, single-point interaction energies were calculated with the sdb-cc-pVQZ basis set⁷¹ at the MP2 level of theory using NWCHEM.⁶² In the interaction energy calculations, the basis set superposition error (BSSE) was corrected using the counterpoise method,⁷² and the intramolecular geometries of the halogenated molecules were kept in their gas phase optimized geometries and water was maintained rigid in the SWM4 geometry.²¹ In calculating the QM interaction energies, when the halogen acts as a hydrogen bond acceptor, the hydrogen atom of water was directed toward the halogen in the perpendicular or linear orientation and served as a hydrogen bond donor (Figure 3a–b and 3d–e). When the halogen participates in a halogen bond interacting with water as a hydrogen bond acceptor, the acceptor atom was directed toward the halogen along the C-X direction (Figure 3c and 3f). The interaction energy profiles were calculated by varying the distance between the halogen and the interacting atom from 1.5 to 5.0 Å in intervals of 0.1 Å.

Figure 3.

Water interaction orientations for halogenated benzenes in a, b, and c, and halogenated ethanes in d, e, and f, where water acts as hydrogen bond donors (HBD) in perpendicular and linear orientations (HBD90° and HBD180°) as well as acts as a hydrogen bond acceptor (HBA) in linear orientations (HBA180°). Halogen atom is colored in green, hydrogen in white, carbon in cyan, and oxygen in red.

Single-point interaction energies between chlorobenzene or chloroethane and the rare gases Ne and He were performed at the MP3/6-311++G(3d,3p) model chemistry.^73,74 The interaction energy profile were calculated by varying the distance between the chlorine and the rare gas atom from 1.5 to 5.0 Å in intervals of 0.1 Å with chlorobenzene/chloroethane kept in their MP2/aug-cc-pVDZ⁶⁷ optimized geometry.

2.2 Molecular mechanical calculations

The program CHARMM^63–65 was used to obtain gas phase properties, including molecular dipole moments and polarizabilities, internal geometries, vibrational spectra, dihedral PES, as well as interaction energies with water. Vibrational frequencies were obtained as presented by Pulay et al.⁷⁵ using the Molvib module in CHARMM. The PES were obtained using the QM optimized geometries followed by minimizing the whole molecule with steepest-descent (SD) and adapted-basis Newton-Raphson (ABNR) method while keeping the dihedral of interest at the target values using a harmonic restraint of 10⁴ kcal/mol/radian. In calculating interaction energies, the monomers of two interacting molecules were computed by varying the distance between the halogen and the interacting atom from 1.5 to 5.0 Å in intervals of 0.1 Å. The monomer geometries were from SWM4 (for water)²¹ or the QM optimized geometries (for halogenated molecules), followed by relaxation of the Drude particles with steepest-descent (SD) method while other atoms were kept restrained using a harmonic force constant of 10⁶ kcal/mol/Å. Interaction energies were then calculated as the total energy of the complex at each distance minus the sum of the energies of the isolated monomers in which the Drude particles had been optimized, analogous to that done in the QM interaction energy calculations. Empirical dipole moments were calculated using CHARMM^63–65 with molecular polarizabilities obtained by applying electric fields in the x, y and z directions and calculating the change in the dipole moment.

Molecular dynamics (MD) simulations were performed to compute the enthalpies of vaporization (ΔH_vap), molecular volumes (V_m), static dielectric constants (ε) as well as hydration free energies (ΔG_hydr) as previous work described.^27,76 MD simulations were performed using the Velocity Verlet integrator with integration of the Drude particles performed using an extended Lagrangian.²⁰ A 0.5 fs time step was used for equilibrations and a 1 fs time step was used for production runs. Particle-Mesh Ewald (PME) was used to treat electrostatic interactions using a real-space cutoff of 12 Å, a kappa value of 0.34 and a 6-order spline.^77,78 LJ interactions were truncated via a switching function from 10 to 12 Å.⁷⁹ SHAKE was used to fix bonds involving hydrogen atoms.⁸⁰ Enthalpies of vaporization (ΔH_vap) were computed through Eq. 5, where the average per-molecule energy (U_liquid) in the condensed phase and the average gas-phase energy (U_gas) were derived from pure liquid and gas phase simulations. Each pure liquid simulation system consisted of a cubic unit cell of 216 molecules, for which the average per-molecule energy (U_liquid) in the condensed phase was obtained from a 10 ns simulation. The average gas-phase energy (U_gas) was obtained by performing a 50 ps equilibration followed by a 150 ps production simulation individually on each of the molecules from the pure liquid system from which the average U_gas was obtained. Molecular volume, V_m, was computed through Eq. 6, which was the average volume, 〈V〉, of the cubic unit cell obtained from the pure liquid simulation.

$$\mathrm{\Delta }{\mathrm{H}}_{\text{vap}}=-\frac{\langle {\mathrm{U}}_{\text{liquid}}\rangle }{\mathrm{n}}+\langle {\mathrm{U}}_{\text{gas}}\rangle +\text{RT},$$ Eq. 5

$${\mathrm{V}}_{\mathrm{m}}=-\frac{\langle \mathrm{V}\rangle }{\mathrm{n}},\mathrm{n}:\text{number of molecules}.$$ Eq. 6

Static dielectric constants (ε) were also computed from the pure liquid simulations. The static dielectric constant ε was calculated from the dipole moment fluctuations of the entire simulation system using Eq. 7:

$$\epsilon ={\mathrm{\epsilon }}_{\infty }+\frac{4\mathrm{\pi }}{3\langle \mathrm{V}\rangle {\mathrm{K}}_{\mathrm{B}}\mathrm{T}}(\langle {\mathrm{M}}^2\rangle -{\langle \mathrm{M}\rangle }^2).$$ Eq 7

where M is the total dipole moment of the cubic simulation system, 〈V〉 is the average volume of the cubic unit cell, and ε_∞ is the high-frequency optical dielectric constant which was estimated from the Clausius-Mossotti equation.⁸¹ The dipole moment fluctuations and volume were obtained from three independent 20 ns simulations. Tests using longer simulations (e.g. 30 ns) yielded a difference of only 0.02 for the chlorobenzene dielectric constant.

Hydration free energies (ΔG_hydr) were obtained as a difference between the free energy change upon annihilation of the solute in water (ΔG_wat) and in vacuum (ΔG_vac), with the free energy changes ΔG_wat and ΔG_vac computed through free energy perturbation (FEP).⁸² Following the previously reported protocol^83,84 that has been used in a number of studies,^35,85–89 the free energy is decomposed into nonpolar and electrostatic components. The nonpolar component is further decomposed into dispersion and repulsion parts using the method of Weeks, Chandler and Andersen (WCA).⁹⁰ Thus, three coupling parameters, s, ξ and λ were used. The repulsive contribution was controlled with staging parameter, s, varying according to 0.0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0. The dispersion contribution was calculated with a coupling parameter ξ, varying linearly from 0 to 1 in increments of 0.1. All the charges of the solute were set to 0 when calculating the nonpolar contributions. The electrostatic contribution was also controlled linearly with a coupling parameter λ varying from 0 to 1 in increments of 0.1. The states with λ=0 and λ=1 correspond to the fully discharged and charged solute, respectively. A 100 ps equilibration and a 1 ns production simulation were performed for each lambda window. Averages reported were obtained from the production phase, where the electrostatic contributions were determined by thermodynamic integration (TI)⁹¹ while the nonpolar contributions were determined by the weighted histogram analysis method (WHAM).⁹² The free energy change was calculated as a sum of the electrostatic, dispersive, and repulsive contributions. A long-range correction (LRC)⁹³ was included in the hydration free energy calculation ΔG_hydr, where the LRC was calculated by taking the difference in the LJ solvent-solute interaction energies using cutoff schemes of 12 and 50 Å.

2.3 Validation in halogenated derivatives

The resulting parameters were applied to 20 halogenated derivatives not included in the training set shown in Figure 2. The validation was carried out by calculating the pure solvent properties (i.e. ΔV_m and ΔH_vap) of the compounds. The procedure to run the simulations was essentially the same as described above except that the neat liquid simulations were performed with NAMD⁶⁶ with the dual Langevin thermostat integrator.⁹⁴ A 20 ps⁻¹ damping coefficient was applied to the Drude oscillators and a 5 ps⁻¹ damping coefficient for the real atoms. The pressure was set at 1 atm using Langevin piston pressure control with a piston oscillation period of 200 fs and a relaxation time of 100 fs.

3. Results and Discussion

3.1 Overview of parametrization process

Initial parameters were based on the halogen parameters in the additive CHARMM General Force Field (Table S8).¹³ For the halogenated benzene analogs, the electrostatic parameters on atoms which are beyond the C(H)-X atoms, where X is F, Cl, Br, and I, were transferred directly from the Drude benzene (BENZ) model⁹⁵ in order to have better transferability when extending the halogenated analogs to other aromatic systems. To model the electrostatic properties of the halogens, a virtual particle that models a σ-hole was attached to the halogen along the C-X bond axis, when X = Cl, Br, or I, at a fixed distance and carries a small positive charge (Figure 1). The virtual particle was built through the lone pair facility in CHARMM and the use of lone pairs is included in the Drude implementations in NAMD⁶⁶, GROMACS⁹⁶ and OpenMM (Huang, Lemkul and MacKerell, Work in Progress). The σ-hole particle was not added to fluorinated species as the sigma hole effect is not significant.⁹⁷

Parametrization included optimizing the electrostatic, internal or bonded, and Lennard-Jones (LJ) parameters. Electrostatic parameters being optimized include the atomic polarizabilities (alpha, α, in Eq. 1), anisotropic polarization tensors on the halogens, the Thole screening factors (t, in Eq. 4), partial atomic charges, and the charge of the σ-hole particle and its distance to the halogen (Figure 1). Note that the α value of the polarizable atoms dictates the charge on the Drude particle (Eq. 1) and adjustment of the Thole screening factors (Eq. 4) optimizes the induced dipole-induced dipole interactions on 1–2 and 1–3 atom pairs. Optimization of these values together with the other electrostatic parameters initially targeted the molecular dipole moments and molecular polarizabilities (Eq. 3). In the initial stage of the optimization, Monte Carlo simulated annealing⁹⁸ was used to target QM dipole moments and molecular polarizabilities. Manual adjustment of the electrostatic parameters was performed for the final refinement. LJ parameters were optimized based on pure solvent properties, for which the LJ intermolecular energies make a significant contribution,⁹⁹ and intermolecular QM interactions of the halogenated compounds with water. Once the electrostatics parameters were initially optimized, the internal parameters were adjusted to reproduce QM geometries and vibrational spectra. The bonded parameters well reproduce QM geometries and vibrational spectra as shown in Tables S2 to S7 of the supporting information. LJ parameters of fluorine, chlorine, bromine, and iodine were then optimized by targeting experimental pure liquid properties, including enthalpies of vaporization (∆H_vap) and molecular volumes (V_m), and hydration free energies (ΔG_hydr). The need for scaling of the atomic polarizabilities was evaluated through experimental dielectric constants as previously discussed.^100,101 Additional fine tuning of the electrostatic parameters and the addition of atom pair-specific LJ term (termed NBFIX in the program CHARMM^63–65) to treat the interactions with water and hydration free energies was then performed. NBFIX parameters will override the standard Lorentz-Berthelot combining rules,¹⁰² such that the LJ parameters between an atom pair are specified explicitly. The final nonbond parameters are summarized in Table S8 and presented in detail in Table S11 of the supporting information.

3.2 Molecular dipole moments and polarizabilities

Final electrostatic parameters were determined to balance reproduction of target QM molecular dipole moments, polarizabilities and the water interaction energies (see below). Scaling factors for molecular polarizabilities ranging from 0.6 to 1.0 have been applied in the Drude force field to better reproduce pure solvent dielectric constants.³³ In the present case the gas phase molecular polarizabilities obtained directly from the MP2/cc-pVQZ model chemistry⁶⁷ were used as target data similar to the Drude polarizable alkane model.²⁶ Computed gas phase molecular dipole moments and polarizabilities from the parametrized halogenated molecules along with the target QM values are summarized in Table 1. Overall, the gas phase molecular dipole moments and polarizabilities, including the molecular polarizability tensor components (Table S9 of the supporting information), were close to their QM computed values, indicating the polarizable model to be capable of capturing the polarization response. Importantly, the resulting polarizable halogen model sufficiently reproduces condensed phase experimental dielectric constants, as presented below.

Table 1.

Dipole moments and molecular polarizabilities computed from the optimized halogen model (Drude) compared to the target QM data. Dipoles and molecular polarizabilities were computed based on MP2/cc-pVQZ//MP2/aug-cc-pVDZ model chemistry⁶⁷ for fluoro- and chloro- analogs, and MP2/sdb-cc-pVQZ//MP2/aug-cc-pVDZ-PP model chemistry⁷¹ for bromo- and iodo- analogs.

		Dipole moment (D)		Molecular polarizability
X	Molecule	QM	Drude	QM	Drude
F	FETH	2.02	1.97	4.14	4.15
	DFET	2.36	2.26	4.17	4.16
	TFET	2.43	2.30	4.21	4.19
Cl	CLET	2.13	2.06	5.86	5.74
	DCLE	2.09	2.00	7.67	7.69
	TCLE	1.81	1.82	9.51	9.53
Br	BRET	2.00	1.95	6.77	6.78
	DBRE	1.84	1.91	9.50	9.52
	TBRE	1.52	1.50	12.24	12.27
I	IETH	1.92	1.90	8.23	8.24
	DIET	1.60	1.46	12.59	12.62
	TIET	1.22	1.27	17.01	17.00
F	FLUB	1.63	1.55	9.92	10.14
Cl	CHLB	1.77	1.74	11.97	11.99
	12DCB	2.51	2.52	13.93	13.98
	13DCB	1.65	1.71	14.12	14.15
	14DCB	0.00	0.00	14.16	14.18
	123TCB	2.52	2.40	15.97	16.02
	124TCB	1.26	1.21	16.20	16.24
	135TCB	0.00	0.00	16.35	16.41
Br	BROB	1.64	1.61	12.92	12.96
	12DBB	2.19	2.02	15.76	15.79
	13DBB	1.50	1.35	16.09	16.34
	14DBB	0.00	0.00	16.16	16.27
	123TBB	2.08	1.84	18.74	18.84
	124TBB	1.05	0.96	19.11	19.18
	135TBB	0.00	0.00	19.38	19.40
I	IODB	1.59	1.56	14.60	14.51
	12DIB	1.97	1.94	19.02	18.98
	13DIB	1.39	1.30	19.60	19.63
	14DIB	0.00	0.00	19.77	19.80
	123TIB	1.71	1.57	23.75	23.43
	124TIB	0.87	0.85	24.40	23.04
	135TIB	0.00	0.00	24.86	24.81

3.3 Molecular volumes and enthalpies of vaporization

The development of a halogenated polarizable force field requires parametrizing the LJ parameters of the new atom types associated with each halogen. Once preliminary electrostatics parameters of halogenated analogs were obtained, the LJ parameters for these new atom types were optimized by adjusting the well depths, ε, and the radii/2, R_min/2, to reproduce experimental pure solvent properties, including molecular volumes (V_m) and enthalpies of vaporization (∆H_vap). LJ parameters were explicitly optimized for the benzene versus ethane-based model compounds. However, for each type of halogen on benzene or ethane the atom type was constrained to be identical for all the benzene or ethane halogenated species, with exceptions noted below, to facilitate transferability to similar halogenated substituents as well as reduce the quantity of atom types in the force field. For example, in chlorinated benzene analogs, the LJ parameter of the chlorine on CHLB is used throughout multi-chlorinated benzene analogs. Similarly, the same LJ parameters are used for the mono and disubstituted ethanes, though unique parameters were used for the trifluoro- and trichloroethane species. Though such a strategy potentially limits the quality of individual pure solvent properties, the final LJ parameters achieved a compromise yielding overall acceptable agreement.

Computed and experimental ∆H_vap, and V_m values for all the model compounds are summarized in Tables 2, 3, 4 and 5. Overall, the level of agreement between the polarizable model and the experimental observables is quite acceptable. The LJ parameters for halogenated molecules yield predictions of V_m within 3% of the experimental values for all but two compound and with ∆H_vap the agreement is within 3% for the majority of compounds, although there are exceptions for some molecules with both overestimated and underestimated calculated results obtained. In general, the developed polarizable model for the halogenated benzenes is improved over the additive halogen force field,¹³ with smaller percentage difference from the target experimental data for both ∆H_vap and V_m in the present study. In the additive force field, ∆H_vap differences for halogenated benzenes of up to ±20% from the experimental values were obtained.¹³ Given the similarity of internal parameters between these two force fields, the inclusion of the polarization response in the polarizable model reflects an improved treatment of nonbonded terms, yielding a better agreement of these pure solvent properties among the halogenated ethanes and benzene analogs.

Table 2.

Molecular volumes (V_m, ų), enthalpies of vaporization (ΔH_vap, kcal/mol), and hydration free energies (ΔG_hydr, kcal/mol) for chlorinated molecules from the Drude halogen force field (Drude) and experimental data (Exp) with percentage difference of V_m and ΔH_vap (%Diff_vm and %Diff_hval), and difference of ΔG_hydr (Diff_ΔG). Averages and standard error of the mean (SE)^* are based on three independent simulations.

		Vm	%Diffvm	ΔHvap	%Diffhval	ΔGhydr	DiffΔG
CLET	Exp	115.95		5.89		−0.63
	Drude	116.85 ± 0.05	0.78	5.96 ± 0.01	1.19	−0.46 ± 0.01	0.17
DCLE	Exp	140.73		7.38		−0.84
	Drude	140.44 ± 0.01	−0.21	7.61 ± 0.00	3.12	−1.06 ± 0.04	−0.22
TCLE	Exp	165.44		7.78		−0.19
	Drude	165.02 ± 0.05	−0.25	7.54 ± 0.01	−3.08	−0.13 ± 0.05	0.06
CHLB	Exp	169.00		9.81		−1.12
	Drude	168.57 ± 0.04	−0.25	10.09 ± 0.00	2.85	−1.10 ± 0.03	0.02
12DCB	Exp	186.90		12.25		−1.36
	Drude	187.07 ±0.01	0.09	12.74 ± 0.00	4.00	−1.86 ± 0.12	−0.50
13DCB	Exp	189.40		12.89		−0.98
	Drude	190.40 ±0.07	0.53	12.04 ± 0.00	−6.59	−1.20 ± 0.02	−0.22
14DCB	Exp	195.60		11.10		−1.01
	Drude	195.12 ±0.02	−0.25	11.42 ± 0.00	2.88	−1.25 ± 0.13	−0.24
123TCB	Exp	207.32		13.68		−1.24
	Drude	210.82 ±0.04	1.69	13.98 ± 0.01	2.19	−1.10 ± 0.09	0.14
124TCB	Exp	207.31		13.28		−1.12
	Drude	212.74 ±0.03	2.62	13.51 ± 0.00	1.73	−0.73 ± 0.06	0.39
135TCB	Exp	206.90		14.11		−0.78
	Drude	210.90 ±0.03	1.93	14.04 ± 0.01	−0.50	−0.83 ± 0.02	−0.05

Properties were obtained at the same temperature as the experimental conditions: CLET 273 K,¹⁰³ DCLE 298 K,¹⁰⁴ TCLE 293 K¹⁰³, CHLB 298 K,¹⁰³ 12DCB 293 K,¹⁰³ 13DCB 293 K,¹⁰³ 14DCB 328 K,¹⁰³ 123TCB 298 K,¹⁰³ 124TCB 293 K,¹⁰⁵ 135TCB 293 K¹⁰⁶ for obtaining molecular volumes; CLET 285.3 K,¹⁰³ DCLE 298 K,¹⁰⁷ TCLE 298 K¹⁰⁷, CHLB 298 K,¹⁰⁷ 12DCB 293 K,¹⁰⁷ 13DCB 298 K,¹⁰⁷ 14DCB 328 K,¹⁰⁷ 123TCB 298 K,¹⁰⁷ 124TCB 298 K,¹⁰⁷ 135TCB 298 K¹⁰⁷, for obtaining enthalpies of vaporization. Hydration free energies were all obtained at 298.15 K.^108,109

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

Table 3.

Molecular volumes (V_m, ų), enthalpies of vaporization (ΔH_vap, kcal/mol), and hydration free energies (ΔG_hydr, kcal/mol) for brominated molecules from the Drude halogen force field (Drude) and experimental data (Exp) with percentage difference of V_m and ΔH_vap (%Diff_vm and %Diff_hval), and difference of ΔG_hydr (Diff_ΔG). Averages and standard error of the mean (SE)^* are based on three independent simulations.

		Vm	%Diffvm	ΔHvap	%Diffhval	ΔGhydr	DiffΔG
BRET	Exp	123.90		6.46		−0.74
	Drude	123.37 ± 0.04	−0.43	6.38 ± 0.00	−1.24	−0.72 ± 0.08	0.02
DBRE	Exp	151.77		9.46		NA
	Drude	147.83 ± 0.04	−2.60	8.90 ± 0.00	−5.92
TBRE	Exp	169.47		9.60
	Drude	172.30 ± 0.00	1.67	9.86 ± 0.00	2.71
BROB	Exp	174.40		10.72		−1.46
	Drude	173.68 ± 0.08	−0.41	10.71 ± 0.00	−0.09	−1.33 ± 0.03	0.13
12DBB	Exp	200.34		11.99		NA
	Drude	202.43 ±1.37	1.04	12.12 ± 0.01	1.08
13DBB	Exp	200.65		11.56
	Drude	200.69 ± 0.08	0.02	12.04 ± 0.00	4.15
14DBB	Exp	212.79		11.94		−2.30
	Drude	199.41 ± 0.07	−6.29	12.86 ±0.00	7.71	−2.72 ± 0.03	−0.42
123TBB	Exp	222.30		NA		NA
	Drude	226.35 ± 0.03	1.82
124TBB	Exp	222.30
	Drude	227.59 ± 0.04	2.38
135TBB	Exp	222.30
	Drude	227.65 ± 0.06	2.41

Properties were obtained at the same temperature as the experimental conditions: BRET 293 K,¹⁰³ DBRE 293 K,¹⁰³ TBRE 298 K¹¹⁰, BROB 293 K,¹⁰³ 12DBB 293 K,¹⁰³ 13DBB 298 K,¹⁰³ 14DBB 298 K,¹⁰³ 123TBB 293 K,¹⁰³ 124TBB 298 K,¹¹⁰ 135TBB 298 K¹¹⁰ for obtaining molecular volume; BRET 311.5 K,¹⁰³ DBRE 316 K,¹¹¹ TBRE 458.72 K¹¹⁰, BROB 298 K,¹⁰⁷ 12DBB 403 K,¹¹¹ 13DBB 432K,¹¹¹ 14DBB 388 K,¹¹¹ 123TBB 546.15 K,¹¹⁰ 124TBB 548.15 K,¹¹⁰ 135TBB 544.15 K¹¹⁰ for obtaining enthalpy of vaporization. Hydration free energies were all obtained at 298.15 K.^108,109

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

Table 4.

Molecular volumes (V_m, ų), enthalpies of vaporization (ΔH_vap, kcal/mol), and hydration free energy (ΔG_hydr, kcal/mol) for iodinated molecules from the Drude halogen force field (Drude) and experimental data (Exp) with percentage difference of V_m and ΔH_vap (%Diff_vm and %Diff_hval), and difference of ΔG_hydr (Diff_ΔG). Averages and standard error of the mean (SE)^* are based on three independent simulations.

		Vm	%Diffvm	ΔHvap	%Diffhval	ΔGhydr	DiffΔG
IETH	Exp	133.80		7.58		−0.74
	Drude	133.69 ± 0.02	−0.08	7.45 ± 0.00	−1.72	−0.77 ± 0.02	−0.03
DIET	Exp	167.80		9.30		NA
	Drude	172.26 ± 0.05	2.66	10.35 ± 0.01	11.29	---
TIET	Exp	207.81		10.41		NA
	Drude	206.20 ± 0.11	−0.77	11.25 ± 0.00	8.07	---
IODB	Exp	187.43		11.69		−1.74
	Drude	184.25 ± 0.00	−1.70	11.94 ± 0.00	2.14	−2.24 ± 0.03	−0.50
12DIB	Exp	219.00		12.40		NA
	Drude	218.31 ± 0.05	−0.32	12.38 ± 0.00	−0.16
13DIB	Exp	221.79		11.91
	Drude	229.95 ± 0.14	3.68	11.03 ± 0.01	−7.39
14DIB	Exp	221.88		11.91
	Drude	220.37 ± 0.05	−0.68	12.59 ± 0.00	5.71
123TIB	Exp	258.50
	Drude	261.88 ± 0.00	1.31

Properties were obtained at the same temperature as the experimental conditions: IETH 293 K,¹⁰³ DIET 298 K,¹¹⁰ TIET 298 K,¹¹⁰ IODB 293 K,¹⁰⁷ 12DIB 293 K,¹⁰³ 13DIB 298 K,¹⁰³ 14DIB 298 K,¹⁰³ and 123TIB 298 K¹⁰³ for obtaining molecular volume; IETH 298 K,¹⁰⁷ DIET 298 K,¹⁰⁷ TIET 493.81 K,¹¹⁰ IODB 298 K,¹⁰⁷ 12DIB 580.15 K,¹¹¹ 13DIB 558.20 K,¹¹¹ and 14DIB 558.20 K¹¹¹ for obtaining enthalpy of vaporization. Hydration free energies were all obtained at 298.15 K.^108,109 The compounds 124TIB and 135TIB were not studied due to a lack of experimental data.

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

Table 5.

Molecular volumes (V_m, ų), enthalpies of vaporization (ΔH_vap, kcal/mol), and hydration free energy (ΔG_hydr, kcal/mol) for fluorinated molecules from the Drude halogen force field (Drude) and experimental data (Exp) with percentage difference of V_mand ΔH_vap(%Diff_vm and %Diff_hval), and difference of ΔG_hydr (Diff_ΔG). Averages and standard error of the mean (SE)^* are based on three independent simulations.

		Vm	Diffvm%	ΔHvap	Diffhval%	ΔGhydr	DiffΔG
FETH	Exp	97.61112		4.95		NA
	Drude	99.26 ± 0.04	1.69	5.28 ±0.01	6.67	---
DFET	Exp	107.50113		5.57113		−0.11
	Drude	108.13 ± 0.06	0.59	5.72 ±0.00	2.69	−0.14 ± 0.07	−0.03
TFET	Exp	121.37114		4.48114		NA
	Drude	123.19 ± 0.04	1.50	4.58±0.00	2.23	---
FLUB	Exp	156.07		8.30		−0.80
	Drude	158.79 ± 0.06	1.74	8.37±0.00	0.84	−0.80 ± 0.02	0.00

Properties were obtained at the same temperature as the experimental conditions: FETH 236 K,¹¹² DFET 243.8 K,¹¹⁵ TFET 230 K,¹¹⁴ FLUB 298 K for obtaining molecular volume; FETH 236 K, DFET 243.8 K,¹¹⁶ TFET 230 K,¹¹⁴ FLUB 298K for obtaining enthalpy of vaporization. Hydration free energies were all obtained at 298.15 K.^108,109

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

3.4 Dielectric constants

An additional property of the pure solvents that was included as target data was the dielectric constant. An important feature of the polarizable model is the proper treatment of the dielectric constant, a property that was also used to determine the scaling of the polarizabilities. Such scaling is related to how the gas-phase polarizabilities are not directly appropriate for the condensed phase, as previously discussed.^{18,21,117–119} Dielectric constants for both the polarizable and additive halogen models as well as the experimental data are presented in Table 6. The developed halogen parameters yield an average percent difference of only −1% of the experiment results, representing a significant improvement over the additive halogen model. In addition, the additive halogen model systematically underestimates the dielectric constant with an average percent difference of −33% with respect to the experimental results. This improvement of the dielectric constants from the polarizable model is attributed to the explicit treatment of polarizability as previously discussed^21,26,33

Table 6.

Dielectric constants of halogenated molecules obtained from experiment (Exp), the optimized polarizable force field (Drude), additive force field (CGenFF) with percentage difference of the experimental values (%Diff_Drude and %Diff_CGenFF). Properties were obtained at the same temperature (T/K) as the experimental conditions. Averages and standard error of the mean (SE)^* are based on three independent simulations.

Mol.	T/K	Exp.	Drude	%DiffDrude.	CGenFF	%DiffCGenFF.
CLET	293	9.45103	10.24±0.06	8%	8.92±0.15	−6%
DCLE	298	10.10103	9.46±0.06	−6%	8.46±0.13	−16%
TCLE	293	7.243103	6.63±0.05	−8%	5.68±0.09	−22%
BRET	298	9.01103	9.07±0.14	1%	9.29±0.00	3%
IETH	293	7.82103	7.97±0.11	2%	NA	NA
FLUB	298	5.42120	5.24±0.09	−3%	4.27±0.06	−21%
CHLB	293	5.69103	5.69±0.05	0%	2.77±0.04	−51%
12DCB	293	10.12103	9.96±0.06	−2%	5.01±0.05	−50%
13DCB	293	5.02103	5.58±0.03	11%	3.15±0.03	−37%
14DCB	328	2.39103	2.40±0.00	0%	1.01±0.00	−58%
BROB	293	5.45103	5.19±0.02	−5%	2.86±0.04	−48%
12DBB	293	7.86103	6.33±0.10	−19%	5.51±0.11	−30%
13DBB	293	4.81103	4.41±0.03	−8%	3.38±0.01	−30%
14DBB	368	2.57103	2.56±0.00	−1%	1.03±0.00	−60%
IODB	293	4.59103	4.74±0.00	3%	3.15±0.05	−31%
12DIB	323	5.41103	6.05±0.02	12%	5.81±0.13	7%
13DIB	323	4.11103	3.94±0.04	−4%	3.45±0.03	−16%
14DIB	393	2.88103	2.76±0.00	−4%	1.02±0.00	−65%
Average%				−1%		−33%

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

3.5 Interaction energies with water

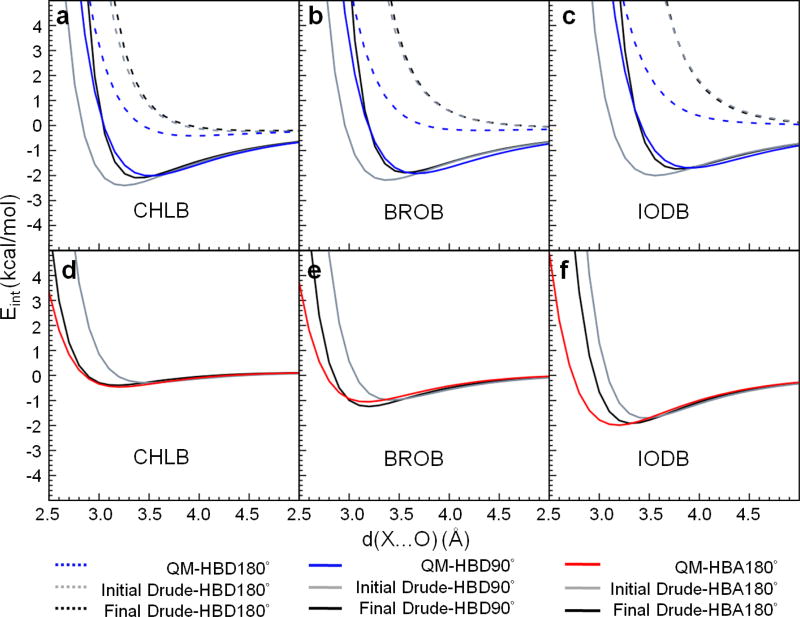
Electrostatic parameter optimization also included the reproduction of QM interactions with water, which was anticipated to provide better hydration free energies. Our recent study shows that halogens not only contribute to halogen bonds where the halogen is chlorine, bromine, and iodine (X-HBA interactions), they also act as hydrogen bond acceptors (HBA) to interact favorably with hydrogen bond donors (HBD), referred to as X-HBD interactions.⁵⁹ Thus, for chlorinated, brominated, and iodinated molecules, reproducing both X-HBD and X-HBA water interactions is crucial to obtain a more physical model. Accordingly, parametrization emphasized both QM perpendicular X-HBD (X-HBD90°) and linear X-HBD/X-HBA (X-HBA180° and X-HBD180°) water interactions (Figure 4). The perpendicular X-HBA (X-HBA90°) interactions were not used as target data as they are unfavorable.⁵⁹ Initially, the water interaction energies computed from the initial parameters based on pure solvent properties alone displayed poor agreement with the QM target data (Figure 4, Initial Drude). The X-HBD90° interaction energies between the halogens and water are too favorable with shorter interaction distances compared to the QM values, whereas the X-HBA180° interaction energies are less favorable with longer interaction distances compared to the QM values. These results imply that the halogens require a larger effective radius to yield a better agreement with the X-HBD90° water interactions while simultaneously having smaller radius to better reproduce the X-HBA180° water interactions, a scenario that cannot be addressed on the basis of the LJ parameters of the halogens alone. To more closely investigate this phenomenon, QM interactions with rare gases (He and Ne) were performed in different orientations to further understand the vdW shape of the halogens. Results show the minimum interaction energies to occur at distances around 0.3–0.5 Å shorter when He/Ne is approaching halogen along the C-X orientation (Supplementary Figure S1) versus the perpendicular orientation. This difference indicates that the asymmetric shape of the halogens is largely dominated by the vdW surface.

Figure 4.

Water interaction energy surfaces from the QM and Drude models with chlorobenzene (CHLB), bromobenzene (BROB), and iodobenzene (IODB) with water acting as hydrogen bond donors HBD90° (solid line) and HBD180° (dashed line) in a, b, and c, and hydrogen bond acceptors (HBA180°) in d, e, and f, respectively. QM results are labeled in blue and red, initial Drude force field without NBFIX parameters (Initial Drude) in gray, and final Drude force field with NBFIX parameters (Final Drude) in black. X is Cl, Br, or I. O is oxygen of water.

To more accurately account for the asymmetry in the vdW surface of the halogens, using LJ parameters on the halogen is obviously not adequate. To overcome this, we considered the use of LJ parameters on the X-Drude particle that would specifically interact with the hydrogen of water or other hydrogen bond donor using the NBFIX approach.¹³ This was rationalized by considering that when water, or any hydrogen bond donor interacts with the halogen, the negatively charged X-Drude particle shifts towards the hydrogen bond donor, such that the appropriate LJ parameters on the X-Drude particle would lead to repulsive interactions. In contrast, when a hydrogen bond acceptor approaches the halogen, as occurs in a halogen bond, the X-Drude particle will be displaced away from the negatively charged acceptor atom, thereby minimizing repulsive interactions between the hydrogen bond acceptor and the X-Drude particle. In addition, NBFIX between the halogens themselves and the water oxygen were included to better reproduce halogen bond interaction with water and the hydration free energies (see below). In combination with the standard LJ parameters on the halogen, this leads to the halogen effectively becoming asymmetric with respect to its vdW surface. Illustration of the utility of the approach is shown in Figure 4 where QM CHLB/BROB/IODB-water interaction energy surfaces are shown for the Drude model both with and without the X-Drude-H_water and X-O_water NBFIX terms. Without the NBFIX terms, there is a systematic trend for the HBD90° interaction to be substantially too short while the HBA180° halogen bond interaction is too long. This trend is more observable from CHLB, BROB to IODB. The inclusion of the X-Drude-H_water LJ NBFIX parameter with water allows for a significant improvement in the balance of these interaction orientations. The HBD180° interactions, which are weak or unfavorable, are poorly treated both with and without the NBFIX parameters. The final computed interaction energy surface using the combined NBFIX parameters are shown for the other halogenated molecules in supplementary Figures S2–S4. The ability of the final Drude model that includes the X-Drude/X and water NBFIX parameters to reproduce the QM data is evident for all the model compounds, though the balance with the ethane-based species is degraded slightly as compared to the halogenated aromatics. A summary of the differences between QM and Drude water minimum interaction energies and distances is shown in Table 7, which is based on all the individual water-model compound minimum interaction energies and distances presented in Table S10 of the supporting information. Water interaction energies computed using the NBFIX parameters (Final_Drude) yield average distances (AVG), averaged unsigned errors (AUE), and root-mean-square differences (RMSD) that are generally smaller than those in the absence of the NBFIX parameters (Initial_Drude). While the AVG minimum interaction distances from HBD180° was a little bit larger, overall, the interaction distances, particularly for the HBD90° and HBA180° interactions were improved using the NBFIX parameters.

Table 7.

Average differences (AVG), absolute unsigned error (AUE), and root-mean-square differences (RMSD) of the computed water minimum interaction energies (kcal/mol) and distances (Å) compared to their QM values for all the training set compounds (Table 1). Individual interaction results are shown in Table S1.

	Minimum interaction energies						Minimum interaction distances
Orientations	Initial_Drude			Final_Drude			Initial_Drude			Final_Drude
	AVG	AUE	RMSD	AVG	AUE	RMSD	AVG	AUE	RMSD	AVG	AUE	RMSD
HBD90°	−0.27	0.29	0.38	−0.02	0.18	0.21	−0.3	0.3	0.3	−0.1	0.1	0.1
HBD180°	−0.10	0.23	0.38	0.06	0.12	0.13	0.3	0.5	0.9	0.4	0.5	0.9
HBA180°	0.23	0.23	0.26	−0.02	0.12	0.15	0.4	0.4	0.5	0.2	0.2	0.5
All	−0.07	0.26	0.35	0.01	0.14	0.17	0.1	0.4	0.7	0.2	0.3	0.6

For fluorinated molecules, only the X-HBD90° and X-HBD180° water interactions were evaluated as F acts only as a hydrogen bond acceptor due to the σ-hole not being significant, which results in unfavorable X-HBA180° interactions.⁵⁹ The water interaction energy surfaces were again not optimal without the use of NBFIX parameters (Supplementary Figure S5). Addition of NBFIX parameters between fluorine and the water oxygen for all the fluorinated molecules lead to better agreement with the target QM-water interactions. For fluorinated benzene, an additional X-Drude NBFIX parameter between the fluorine-Drude and water hydrogen was also applied in order to better balance the X-HBD90° and X-HBD180° water interactions. The final computed interaction energies of the fluorinated molecules with water using NBFIX parameters are shown in Supplementary Figure S6, and the minima water interaction energies and distances are shown in Table S10.

3.6 Hydration free energies

The hydration free energies (∆G_hydr) of halogenated molecules were obtained with the use of NBFIX parameters with water as described above. Slight adjustments of NBFIX parameters initially determined targeting the QM X-HBD90° and X-HBA180° water interactions were required to obtain the final NBFIX parameters that better reproduce the experimental ∆G_hydr data. Computed ∆G_hydr for respective halogenated molecules are included in Tables 2–5. The overall agreement between experimental and computed values is quite acceptable, indicating the final NBFIX parameters are satisfactory for predicting ∆G_hydr and describing hydration. Notably, the computed ∆G_hydr for chlorobenzene analogs represent an improvement over those computed from the additive halogen model,¹³ where the average and RMS differences were −0.15 and 0.33, respectively, (see Table 5 of reference¹³ with relative free energies offset by the calculated benzene hydration free energy of −1.12 kcal/mol) versus values of −0.07 and 0.28, respectively, for the Drude model. These improvements of ∆G_hydr may be attributed to the ability of the Drude model to satisfactorily treat both the X-HBD90° and X-HBA180° water interactions due to the use of NBFIX terms between X-Drude and water hydrogen and between X and water oxygen along with the explicit treatment of electronic polarizability, resulting in adequately describing both halogen bond and X-HBD interactions and thus better reproducing ∆G_hydr. Overall, the use of NBFIX parameters combined with the explicit treatment of electronic polarizability yielded substantial improvements for the water-model compound interaction energy surfaces and the hydration free energies over all the halogenated molecules while allowing for the quality of the pure solvent properties to be maintained.

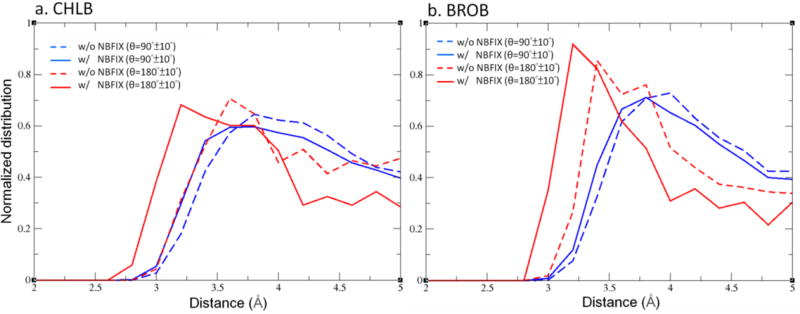
To better understand the impact of the use of NBFIX on the halogen-water interactions in aqueous solution, including the use of LJ parameters on the Cl, Br and I Drude particles, radial distribution functions (RDF) were calculated in the absence and presence of the NBFIX terms from 5 ns MD simulations of chlorobenzene and bromobenzene in aqueous solution. Shown in Figure 5 are the RDFs between the Cl or Br atoms and water oxygens for the C-X…O_w angle ranges of 90±10° and 180±10°. As is evident, the halogen bond interaction distances (i.e. 180±10° RDF) are significantly shorter due to the use of NBFIX, showing the model to yield the expected behavior in the condensed phase. However, with the perpendicular halogen-hydrogen bond donor interactions (i.e. 90±10° RDF), the RDF shifts slightly inward. As this behavior was somewhat unexpected additional RDF analysis was undertaken in which the 90±10° RDFs were partitioned based on the linearity of the X…H_w-O_w hydrogen bond (Figure S7 of the supporting information). This analysis revealed the X…O_w RDF to be shifted to longer distances in the presence of NBFIX with a linear X…H_w-O_w hydrogen bond, as expected, while shifts towards slightly shorter distances occur as the X…H_w-O_w angle decreased to 90°. Additional QM water-halogen interaction energy analysis was consistent with this behavior (Figure S8 of the supporting information). Notably, the addition of the NBFIX terms improved the agreement of the Drude model with the QM 90° X…H_w-O_w interaction energy surfaces, further indicating the robustness of the NBFIX approach and its ability to more accurately model the asymmetry of the halogen atom in the studied species.

Figure 5.

Water radial distribution functions around a. chlorobenzene (CHLB) and b. bromobenzene (BROB) when the C-Cl/Br…O angles are within 90° ± 10° or 180° ± 10°, where O is the oxygen of the water. Results are obtained from 5 ns aqueous MD simulations.

3.7 Validation of the resulting parameters using pure solvent properties

The resulting halogen force field was validated on a set of halogen derivatives based on its ability to reproduce experimental pure solvent properties (i.e. V_m and ΔH_vap). Halogen derivatives selected include chlorofluorocarbons (CFCs), multi-halogenated ethanes, and halogenated aromatic systems, such as pyridine, indole and naphthalene along with multi-halogenated benzenes. For halogenated aromatic systems, the electrostatic parameters on the halogen atom and the lone pair (i.e. charge, alpha, Thole screening factor and anisotropic polarizability on the halogen, and lone pair charge and its distance to the halogen) as well as LJ parameters were transferred from the corresponding halogenated benzenes. For example, the electrostatic parameters of chlorine in 1-chloronaphthalene will be the same as those of chlorine in chlorobenzene. This is to ensure the features of the halogen from the developed Drude model exist in the halogenated analogs in the validation sets. Initially in these analogs, electrostatic parameters of atoms which are beyond the C(H)-X atoms, where X is F, Cl, Br, and I, were directly transferred from the Drude parameters for naphthalene (NAFT, in Table S12, derived from the benzene (BENZ) model⁹⁵), pyridine, indole,²⁴ and benzene.⁹⁵ However, the charges on the carbon (C2) connected to the halogen within two bonds (X-C1-C2) needed to be adjusted to maintain the total charge of the analogs neutral. For multi-halogenated ethanes, when the carbon is substituted with one halogen (e.g. 1-chloro-2-fluoroethane), then the electrostatic and LJ parameters of the halogen will be derived directly from the halogen in the respective mono-halogenated ethane (i.e. FETH, CLET, or BRET). If the carbon is substituted with two halogens (e.g. 1-bromo-1-chloroethane), then the electrostatic and LJ parameters of the individual halogens will be derived from those in di-halogenated ethane (i.e. DFET, DCLE, or DBRE). If the carbon is substituted with three halogens (e.g. 1,1-dichloro-1-fluoroethane), then the electrostatic and LJ parameters of the individual halogens will be transferred from those in tri-halogenated ethane (i.e. TFET, TCLE, or TBRE). This approach is used by assuming that the magnitude of the σ-hole on the halogens will be impacted by the additional halogens connected to the carbon, which will enhance the σ-hole effect.³⁷ Similarly, the charge on the carbons in the multi-halogenated ethanes was adjusted to maintain the total charge of the molecule neutral. Internal parameters were transferred from the halogenated benzene or ethanes. All the parameters for the validation set are presented in Table S12.

The results are summarized for all the studied compounds in Table 8. The predicted V_m values are quite good for the majority of the validation set with the percent differences all within 3% from the experimental values. Most of the predicted ΔH_vap are close to the experimental values with percent differences less than 5%, while only a few molecules (i.e. 1-bromo-1-chloroethane, and 1,2-dichloro-1,1,2-trifluoro-ethane) show differences greater than 10%. These larger deviations are not unexpected and were considered acceptable as the ΔH_vap values obtained for multi-substituted halogenated ethanes model compounds in the training set (Tables 2– 5) already show slightly larger differences. Overall, the predicted values from the validation set are in good accordance with experimental results, which suggests that the parameters developed on halogenated benzenes and ethanes model compounds are transferrable to a wider range of halogenated molecules.

Table 8.

Validation set molecular volumes (V_m, ų) and enthalpies of vaporization (ΔH_vap, kcal/mol) from the Drude halogen force field (Drude) and experimental data (Exp) with percentage difference of V_m and ΔH_vap (%Diff_vm and %Diff_hval). Temperatures (T, K) were set to values used in the respective experimental studies. Averages and standard error of the mean (SE)^* are based on three independent simulations.

Molecule		Vm	T	%Diffvm	ΔHvap	T	%Diffhval
1-chloronaphthalene	Exp	227.30103			14.01107
	Drude	230.78 ± 0.01	298	1.53	13.86 ± 0.01	373	−1.07
2-chloronaphthalene	Exp	237.35103			13.98107
	Drude	238.94 ± 0.03	344	0.67	14.19 ± 0.01	373	1.5
1-bromonaphthalene	Exp	232.57103			15.27107
	Drude	234.95 ± 0.04	293	1.02	15.84 ± 0.00	298	3.73
2-bromonaphthalene	Exp	232.25121			15.80107
	Drude	232.58 ± 0.07	298a	0.14	16.02 ± 0.00	298	1.39
1-iodonaphthalene	Exp	242.61103			17.30107
	Drude	243.97 ± 0.07	298	0.56	17.27 ± 0.00	298	−0.17
2-iodonaphthalene	Exp	258.53103			16.67122
	Drude	257.95 ± 0.01	372	−0.22	17.39 ± 0.02	298	4.32
3-chloropyridine	Exp	157.91123			11.45107
	Drude	152.70 ± 0.01	298	−3.30	11.20 ± 0.00	298	−2.18
3-bromopyridine	Exp	159.49103			12.45107
	Drude	154.84 ± 0.01	273	−2.92	12.13 ± 0.00	298	−2.57
4-chloroindole	Exp	199.96124			12.21124
	Drude	200.63 ± 0.20	293	0.34	12.81 ± 0.01	298	4.91
1-chloro-4-fluorobenzene	Exp	176.82125			10.23126
	Drude	180.32 ± 0.02	298	1.98	10.42 ± 0.00	298	1.86
1-chloro-3-fluorobenzene	Exp	177.55103			10.28126
	Drude	180.05 ± 0.02	298	1.41	10.92 ± 0.00	298	6.23
1-bromo-4-fluorobenzene	Exp	194.50127			10.52126
	Drude	193.75 ± 0.05	341	−0.39	11.03 ± 0.00	298	4.85
1-chloro-2-fluoroethane	Exp	116.63103			7.67107
	Drude	120.37 ± 0.02	293	3.21	7.59 ± 0.00	303	−1.04
1-chloro-2-bromooethane	Exp	136.93103			9.11107
	Drude	140.56 ± 0.03	293	2.65	9.23 ± 0.01	298	1.32
1-bromo-1-chloroethane	Exp	142.86103			11.16107
	Drude	142.32 ± 0.02	293	−0.38	9.88 ± 0.00	252	−11.47
1,1,2-trichloro-1,2,2-trifluoroethane	Exp	199.07103			6.36107
	Drude	203.80 ± 0.04	298	2.38	6.26 ± 0.00	328	−1.57
1,2-dichloro-1,1,2,2-tetrafluoroethane	Exp	195.07103			5.54107
	Drude	198.56 ± 0.11	298	1.79	5.44 ± 0.00	298	−1.81
2,2-dichloro-1,1,1-trifluoroethane	Exp	173.48103			6.86128
	Drude	171.36 ± 0.03	298	−1.22	7.37 ± 0.00	298	7.43
1,2-dichloro-1,1,2-trifluoro-ethane	Exp	169.30103			6.41107
	Drude	172.77 ± 0.04	298	2.05	7.10 ± 0.01	298	10.76
1,1-dichloro-1-fluoroethane	Exp	155.36103			6.86107
	Drude	156.04 ± 0.04	283	0.44	6.40 ± 0.01	265	−6.71

^aTemperature assumed to be 298 K

^* $\text{SE}=\mathrm{\sigma }/\sqrt{\mathrm{n}}$, where σ is the standard deviation and n equals 3.

4. Conclusion

A polarizable force field for halogen-containing compounds is presented, which explicitly includes electronic polarization based on the classical Drude oscillator model. The resulting force field is able to reproduce QM molecular dipole moments and polarizabilities, as well as experimental enthalpies of vaporization, molecular volumes, hydration free energies, and dielectric constants. An important feature of halogens is that they act as both hydrogen bond donors and acceptors requiring accurate reproduction of halogen bond and X-HBD interactions during parametrization. To achieve this, LJ parameters were included on the halogen Drude particle-donor hydrogen pairs along with the use of anisotropic polarizabilities on the halogen atoms. This strategy results in a good agreement with QM water interaction energy surfaces and experimental ΔG_hydr data. Comparison of the present model with the additive halogen model in CGenFF shows the level of agreement of the polarizable halogen models with both QM and experimental data to be significantly better. This level of improvement demonstrates that explicit inclusion of electronic polarization combined with the use of pair-specific LJ parameters⁸⁴ and LJ parameters on the halogen Drude particles, thereby including a steric component in the polarization response,¹²⁹ significantly contributes to the accuracy of modeling condense phase properties, including dielectric constants.

While our laboratory focuses on biomolecular systems, the potential of using the developed halogen parameters in crystal engineering should be noted. Halogens have long been recognized to form favorable short contacts (X⋯X) in crystal structures since the 1950s.³⁷ Two geometric varieties observed in the crystals have been classified based on the contacts angle between intramolecular halogen atoms (X⋯X): Type I (symmetrical interactions) and Type II (bent interactions) contacts. Type I contacts are not halogen bonds, according to the IUPAC definition, as they are geometry-based contacts due to close-packing requirements, whereas Type II contacts have been recognized as halogen bonds.^37,130,131 From this perspective, the present parameters may possibly be limited to describing the X⋯X contacts exist in Type I geometries in the field of crystal engineering. However, the Drude model presented in this study certainly has the potential to be used in the study of Type II contacts though specific optimization of the parameters for dihalogens, such as Cl₂, Br₂ or I₂, would be required.

As a final point, the developed halogen force field has been specifically designed for organic molecules having the halogenated aliphatic or aromatic moieties. In practice, these developed halogen parameters could be transferred to the halogenated aliphatic or aromatic moieties of molecules (or ligands) in combination of the previously developed Drude small molecule parameters.^{23,24,24–27} To improve the utility of the presented parameters in biological systems, ongoing efforts are extending the developed halogen force field targeting interactions with protein model compounds to improve ligand-protein interactions and further evaluating for their ability to reproduce protein-ligand binding geometries in crystal structures (Lin and MacKerell, Work in progress). Accordingly, the presented polarizable model for halogenated species provides a building block towards a more accurate computational representation of molecules that will be applicable for in silico studies of halogen-containing molecules in biophysical studies, including computer-aided drug design.