The Advantages of Viscous Dissipation Rate over Simplified Power Loss as a Fontan Hemodynamic Metric

Abstract

Flow efficiency through the Fontan connection is an important factor related to patient outcomes. It can be quantified using either a simplified power loss or a viscous dissipation rate metric. Though practically equivalent in simplified Fontan circulation models, these metrics are not identical. Investigation is needed to evaluate the advantages and disadvantages of these metrics for their use in in vivo or more physiologically-accurate Fontan modeling. Thus, simplified power loss and viscous dissipation rate are compared theoretically, computationally, and statistically in this study. Theoretical analysis was employed to assess the assumptions made for each metric and its clinical calculability. Computational simulations were then performed to obtain these two metrics. The results showed that apparent simplified power loss was always greater than the viscous dissipation rate for each patient. This discrepancy can be attributed to the assumptions derived in theoretical analysis. Their effects were also deliberately quantified in this study.

Furthermore, statistical analysis was conducted to assess the correlation between the two metrics. Viscous dissipation rate and its indexed quantity show significant, strong, linear correlation to simplified power loss and its indexed quantity (p < 0.001, r > 0.99) under certain assumptions. In conclusion, viscous dissipation rate was found to be more advantageous than simplified power loss as a hemodynamic metric because of its lack of limiting assumptions and calculability in the clinic. Moreover, in addition to providing a time-averaged bulk measurement like simplified power loss, viscous dissipation rate has spatial distribution contours and time-resolved values that may provide additional clinical insight. Finally, viscous dissipation rate could maintain the relationship between Fontan connection flow efficiency and patient outcomes found in previous studies. Consequently, future Fontan hemodynamic studies should calculate both simplified power loss and viscous dissipation rate to maintain ties to previous studies, but also provide the most accurate measure of flow efficiency. Additional attention should be paid to the assumptions required for each metric.

INTRODUCTION

Fontan connection power loss is a hemodynamic metric used to quantify fluid flow efficiency through a palliative surgery for single ventricle congenital heart disease patients. Fluid flow efficiency through the Fontan connection is important because the Fontan circulation functions on a single ventricle, leaving the pulmonary circulation without ventricular support. Lack of pulmonary ventricular support increases the importance of fluid flow efficiency from the systemic venous return through the Fontan connection, and into the single atrium. Decreased Fontan flow efficiency decreases single ventricle filling¹⁴ and patient exercise performance^17,34, negatively impacting the entire circulation.

The importance of flow efficiency through the Fontan connection, and the studies conducted to understand it, has created different efficiency-related hemodynamic metrics. One of the first studies analyzing Fontan connection flow efficiency was by Low, et al²⁰. This study introduced a total energy loss coefficient to quantify Fontan connection flow efficiency. The current power loss metric was first computed by Dubini, et al, though it was termed the “hydraulic dissipated power”⁸. Dubini’s power loss employed a simplified control volume energy analysis easily calculated by measuring only inlet and outlet volumetric flow rate, cross sectional area, and static pressure. This simplified power loss is the power loss metric that remains in the literature today, gaining recent popularity because of its relationship to patient outcomes^13,17,34. The realization that flow efficiency losses through the Fontan connection are almost entirely due to mechanical energy converted to heat led to the introduction of viscous dissipation rate as a Fontan connection hemodynamic metric^6,15,21,26.

Unfortunately, simplified power loss and viscous dissipation rate are not equivalent quantities^11,21. Though practically equivalent for some Fontan hemodynamic studies that assume simplified physiological models^5,9,18,34, we will show the inequality of the two metrics in this study.

The purpose of this study is to compare simplified power loss and viscous dissipation rate as hemodynamic metrics, and show the benefits of using viscous dissipation rate for future Fontan studies. Any hemodynamic metric fit for future, more physiologically-accurate Fontan studies must fulfill three requirements: (1) accurately describe Fontan physiological flow efficiency; (2) be easily calculable from clinical measurements; and (3) maintain the relationship between Fontan connection flow efficiency and patient outcomes from previous studies. These criteria were selected to focus the hemodynamic metric on clinical utilization.

This study hypothesizes that viscous dissipation rate fulfills all three requirements as a Fontan hemodynamic metric and is fit for future studies, and that viscous dissipation rate has advantages over simplified power loss as a hemodynamic efficiency metric. This hypothesis is tested using theoretical, computational, and statistical methods.

MATERIALS AND METHODS

Theoretical Methods

Theoretical methods were used to derive simplified power loss and viscous dissipation rate. Simplified power loss was derived using a control volume energy conservation analysis. Viscous dissipation rate was derived from a differential volume energy conservation analysis. The simplified power loss derivation identifies assumptions separating it from true power loss and viscous dissipation rate values (which are equal). The individual terms required to calculate viscous dissipation rate were considered for clinical calculability against known clinical measurement devices.

Patient Information

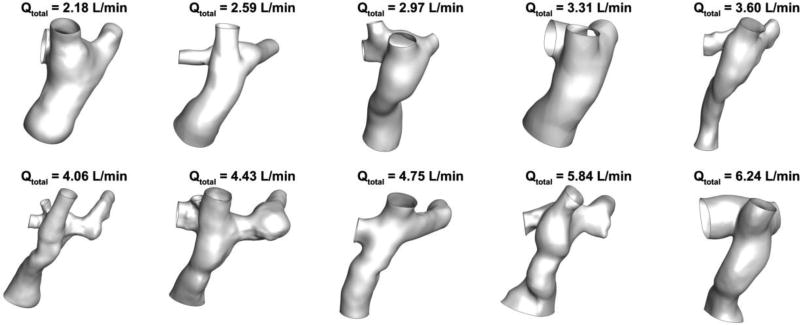
Computational fluid dynamics (CFD) and statistical analyses were conducted on a patient cohort (n=10) extracted from the Georgia Tech Cardiovascular Fluid Mechanics Fontan Database. The ten patients selected for this study were sampled to evenly span the range of total mean inflow (cardiac output) values found in the database. A large range of total inflows was desired because total inflow is associated with total energy at the Fontan connection inlets, and, therefore, different amounts of potential energy loss. The minimum and maximum total time-averaged volumetric inflow rate (Q) for the simulations was 2.18 L/min and 6.30 L/min, respectively. Figure 1 shows the Fontan connection anatomies used for the CFD analysis ordered by increasing total mean inflow rate.

Figure 1.

Ten patient-specific 3D anatomy models used for CFD analysis. The inferior vena cava (IVC) and superior vena cava (SVC) inflows are located at the bottom and top of each anatomy, respectively. The left pulmonary artery (LPA) outlet is toward the right side and the right pulmonary artery (RPA) and right upper pulmonary artery (RUPA) outlets are toward the left side of each model shown.

CFD Model Solution

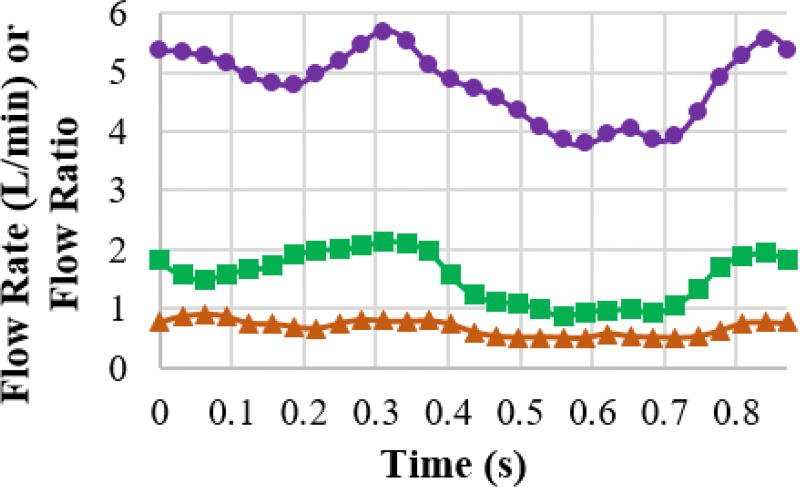
Unsteady simulations were employed using ANSYS Fluent 17.0 (ANSYS, Inc., Canonsburg, PA) to acquire simplified power loss and viscous dissipation rate values. The simulation domain and boundary conditions were defined according to magnetic resonance imaging data, further detailed by Wei et al³². The Fourier transform in MATLAB (The MathWorks, Inc., Natick, MA) was used to convert time-varying clinical measured flow rates to the frequency domain. User-defined functions were utilized to apply reverse Fourier transform to reconstruct the time-varying flow rate at the inlets and time-varying flow ratio at the outlets. This procedure ensured better flow periodicity between cycles than directly applying clinical measurements at the boundaries. Figure 2 shows a good agreement (R² > 0.999) between simulated flow and clinical measurements.

Figure 2.

The comparison of the flow rate and flow ratio between clinical measurement (markers) and the corresponding values from simulation (corresponding solid lines) for a representative case. Purple circular marker: IVC flow rate; Green rectangular marker: SVC flow rate; Orange triangular marker: flow ratio of LPA over RPA.

The coupled flow model was employed to solve the continuity and momentum equations simultaneously. Temporal and spatial discretizations employed second-order schemes; the momentum equation employed a third order scheme. The warped-face gradient correction was enabled to improve gradient calculation accuracy. Flow extensions equal to 10 times the vessel diameter were added to all inlets and outlets. Time step size was set at 0.001 seconds to ensure the Flow Courant number was ~ 0.1. Convergence criteria for continuity and momentum were set to 10⁻⁴. The vessel walls were assumed as rigid, and the fluid was assumed to be Newtonian with density equal to 1060 kg-m⁻³ and dynamic viscosity equal to 3.4×10⁻³ Pa-s.

Mesh Generation

The simulation was conducted on polyhedral meshes made in ANSYS Fluent 17.0 (ANSYS, Inc., Canonsburg, PA), converted from an unstructured tetrahedral mesh generated in ANSYS Workbench Meshing (ANSYS, Inc., Canonsburg, PA). A mesh independence study indicated that the adequate mesh has an edge size equal to D_avg/50, where D_avg is the average diameter of all TCPC inlets and outlets. Relevant results are discussed in Results section below. Moreover, boundary layer zones were created to improve numerical accuracy near the walls. A prismatic boundary mesh was generated by using the smooth transition approach with 10 layers and a geometric growth ratio of 1.05.

Hemodynamic Metrics

The CFD simulations resulted in time-resolved velocity vector and pressure scalar fields from which 4 metrics were calculated: simplified power loss (Ė_sim), indexed simplified power loss⁷ (iĖ_sim), viscous dissipation rate (Φ), and indexed viscous dissipation rate (iΦ). The indexed versions of the simplified power loss and viscous dissipation rate values were added, as indexed simplified power loss is correlated to Fontan patient exercise capacity¹⁷, and employed in multiple other studies^23,24,27. Equations (1), (2), (3), and (4) define each of these metrics, respectively:

$${\dot{E}}_{\mathit{\text{sim}}}=\sum _{\mathit{\text{inlets}}}(p+\frac{1}{2}\rho {\left[\frac{Q}{A}\right]}^2)Q-\sum _{\mathit{\text{outlets}}}(p+\frac{1}{2}\rho {\left[\frac{Q}{A}\right]}^2)Q$$ (1)

$$i{\dot{E}}_{\mathit{\text{sim}}}=\frac{{\dot{E}}_{\mathit{\text{sim}}}·{\mathit{\text{BSA}}}^2}{\rho Q^3}$$ (2)

$$\Phi =\mu {\int }_{V}2[{\left(\frac{\partial u_x}{\partial x}\right)}^2+{\left(\frac{\partial u_y}{\partial y}\right)}^2+{\left(\frac{\partial u_z}{\partial z}\right)}^2]+{(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x})}^2+{(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y})}^2+{(\frac{\partial u_z}{\partial x}+\frac{\partial u_x}{\partial z})}^2\mathit{\text{dV}}$$ (3)

$$i\Phi =\frac{\Phi ·{\mathit{\text{BSA}}}^2}{\rho Q^3}$$ (4)

where p is the fluid static pressure, ρ is the fluid density, A is the inlet or outlet cross-sectional area, BSA is the patient-specific body surface area, u is the directional velocity component (either x, y, or z direction), μ is the fluid dynamic viscosity, and V is the Fontan connection volume. The single value reported for statistical analysis was the time-averaged value of each metric.

Statistical Analysis

The statistical analyses comparing the simplified power loss and viscous dissipation rate metrics were performed using IBM SPSS Statistics (IBM, Inc., Aramark, NY). The metrics were first analyzed for normality using the Shapiro-Wilk test. Depending on normality results, bivariate correlations were analyzed using either Spearmen’s or Pearson’s correlation test. P < 0.05 was considered a statistically significant correlation.

RESULTS

Control Volume Energy Conservation

The simplified power loss term, Ė_sim, comes from a control volume energy conservation analysis of the TCPC with several assumptions. True power loss, Ė_loss, is derived first to highlight the assumptions made to arrive at Ė_sim. The derivation that follows closely aligns with Munson, Young, and Okiishi²².

The first law of thermodynamics for a system states that the time rate of increase of the total stored energy of the system is equal to the sum of the net time rate of energy addition by heat transfer into the system and the net time rate of energy addition by work transfer into the system. This is represented symbolically in Equation (5):

$$\frac{\partial }{\partial t}{\int }_V\rho \mathit{\text{e dV}}+{\int }_{\mathit{\text{CS}}}\rho e\stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\mathit{\text{ dA}}={\stackrel{·}{Q}}_{\mathit{\text{in}}}+{\stackrel{·}{W}}_{\mathit{\text{in}}}$$ (5)

where e is the intensive total energy, U⃑ is the fluid velocity vector, n⃑ is a unit vector normal (outward) to the control surface (cs), Q̇_in is the extensive heat rate added to the control volume, and Ẇ_in is the extensive work rate added to the control volume. The intensive total energy, e, is related to the intensive internal energy, û, the intensive kinetic energy, U²/2, and the intensive potential energy, gz, by Equation (6):

$$e=\hat{u}+\mathit{\text{gz}}+\frac{U^2}{2}$$ (6)

The work term, Ẇ_in, is broken into several forms of work by Equation (7):

$${\dot{W}}_{\mathit{\text{in}}}={\dot{W}}_{\mathit{\text{in}},\mathit{\text{shaft}}}+{\dot{W}}_{\mathit{\text{in}},\mathit{\text{press}}}+{\dot{W}}_{\mathit{\text{in}},\mathit{\text{viscous}}}$$ (7)

where Ẇ_in,shaft is the net shaft work rate into the system (i.e. via turbine), Ẇ_in,press is the net pressure work into the system acting on all the control surfaces, and Ẇ_in,viscous is the net viscous work rate into the system due to stress tangential to the control surfaces. Both Ẇ_in,press and Ẇ_in,viscous definitions are provided in Equation (8) and Equation (9), respectively:

$${\dot{W}}_{\mathit{\text{in}},\mathit{\text{press}}}=-{\int }_{\mathit{\text{CS}}}p(\stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n})\mathit{\text{ dA}}$$ (8)

$${\dot{W}}_{\mathit{\text{in}},\mathit{\text{viscous}}}={\int }_{\mathit{\text{CS}}}\stackrel{\rightharpoonup }{\tau }·\stackrel{\rightharpoonup }{U}\mathit{\text{ dA}}$$ (9)

where p is the hydrostatic fluid pressure and τ⃑ is the shear stress vector on the control surface.

Substituting Equations (6), (7), (8), and (9) into (5) results in Equation (10):

$$\frac{\partial }{\partial t}{\int }_V\rho (\hat{u}+\mathit{\text{gz}}+\frac{U^2}{2})\mathit{\text{ dV}}+{\int }_{\mathit{\text{CS}}}(\hat{u}+\mathit{\text{gz}}+\frac{U^2}{2})\rho \stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\mathit{\text{ dA}}={\dot{Q}}_{\mathit{\text{in}}}+{\int }_{\mathit{\text{CS}}}\stackrel{\rightharpoonup }{\tau }·\stackrel{\rightharpoonup }{U}\mathit{\text{ dA}}-{\int }_{\mathit{\text{CS}}}p(\stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n})\mathit{\text{ dA}}+{\dot{W}}_{\mathit{\text{in}},\mathit{\text{shaft}}}$$ (10)

The true power (energy rate) lost (Ė_loss) during the TCPC flow process is equal to the sum of the time rate of internal energy change and the heat rate out of the control volume. Isolating these terms on the left-hand side of the energy balance results in Equation (11):

$${\dot{E}}_{\mathit{\text{loss}}}={\dot{W}}_{\mathit{\text{in}},\mathit{\text{shaft}}}+{\int }_{\mathit{\text{CS}}}\stackrel{\rightharpoonup }{\tau }·\stackrel{\rightharpoonup }{U}\mathit{\text{ dA}}-{\int }_{\mathit{\text{CS}}}(\mathit{\text{gz}}+\frac{U^2}{2}+\frac{P}{\rho })\rho \stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\mathit{\text{ dA}}-\frac{\partial }{\partial t}{\int }_V\rho (\mathit{\text{gz}}+\frac{U^2}{2})\mathit{\text{ dV}}$$ (11)

Equation (11) is the most general form of power loss, and is applicable to all Newtonian fluids. To calculate simplified power loss, Ė_sim, 5 assumptions are first applied to the general power loss equation (Equation (11)):

1. No shaft work is present in the system:

   $${\dot{W}}_{\mathit{\text{in}},\mathit{\text{shaft}}}=0$$
2. No viscous work is present on the system control surface:

   $${\dot{W}}_{\tau }={\int }_{\mathit{\text{CS}}}\stackrel{\rightharpoonup }{\tau }·\stackrel{\rightharpoonup }{U}\mathit{\text{ dA}}\to 0$$
3. The control volume does not change in time:

   $${\dot{W}}_q=\frac{\partial }{\partial t}{\int }_V\rho (\mathit{\text{gz}}+\frac{U^2}{2})\mathit{\text{ dV}}\to 0$$

   It is worth noticing that Ẇ_q also involves the effect of time-derivative of dynamic pressure, which will be discussed later. Nevertheless, the time-averaged effect of dynamic pressure should be negligible because of conservation of mass.

4. There is no change in elevation between control surfaces:

   $${\int }_{\mathit{\text{CS}}}(\mathit{\text{gz}}+\frac{U^2}{2}+\frac{P}{\rho })\rho \stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\mathit{\text{ dA}}={\int }_{\mathit{\text{CS}}}(\frac{U^2}{2}+\frac{P}{\rho })\rho \stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\mathit{\text{ dA}}$$
5. The normal velocity profile at the control surfaces is constant

   $${\stackrel{\rightharpoonup }{U}}_n=\stackrel{\rightharpoonup }{U}·\stackrel{\rightharpoonup }{n}\to \frac{Q}{A}$$

Applying all of these assumptions to Equation (11) results in the simplified power loss most prevalent in the Fontan hemodynamic literature, as shown in Equation (1).

Differential Energy Conservation

The viscous dissipation rate metric comes from a differential energy conservation analysis. The first law of thermodynamics, restated for convenience, is that the time rate of increase of the total stored energy of the system is equal to the sum of the net time rate of energy addition by heat transfer into the system and the net time rate of energy addition by work transfer into the system. The differential work rate transferred into the system is broken into work done by pressure forces normal to the surface (Equation (12)), work done by shear forces tangential to the surface (Equation(13)) and body forces (Equation (14)).

$$d{\dot{w}}_p=\nabla ·(-p\underset{¯}{I}·\stackrel{\rightharpoonup }{U})\mathit{\text{ dV}}$$ (12)

$$d{\dot{w}}_s=\nabla ·(\underset{¯}{\tau }·\stackrel{\rightharpoonup }{U})\mathit{\text{ dV}}$$ (13)

$$d{\dot{w}}_b=\rho \stackrel{\rightharpoonup }{f}·\stackrel{\rightharpoonup }{U}\mathit{\text{ dV}}$$ (14)

where p is the static pressure, I̲ is the identity tensor, U⃑ is the velocity vecotry, τ̲ is the symmetric shear stress tensor, and f⃑ is a body force (gravity) per unit mass.

The differential heat rate transferred into the system is broken into volumetric heating (Equation (15)) and thermal conduction heating (Equation (16)) components.

$$d{\dot{Q}}_v=\rho {\dot{q}}_v\mathit{\text{ dV}}$$ (15)

$$d{\dot{Q}}_c=-(\nabla ·{\dot{q}}_c)\mathit{\text{dV}}$$ (16)

where q̇_v is a term representing heat added to the entire volume per unit mass (i.e. due to radiation or a chemical reaction), and q̇_c is the conductive heat vector.

The differential total energy rate increase of the system is defined in Equation (17).

$$d\dot{e}=\rho \frac{D}{\mathit{\text{Dt}}}(\hat{u}+\frac{U^2}{2})\mathit{\text{ dV}}$$ (17)

where ė is the total energy rate, û is the intensive internal energy, and U²/2 is the intensive kinetic energy. The potential energy contribution for this analysis is considered as part of the body forces term (Equation (14)).

Constructing Equations (12) through (14) to meet the first law of thermodynamics results in Equation (18):

$$\rho \frac{D}{\mathit{\text{Dt}}}(\hat{u}+\frac{U^2}{2})=\rho {\dot{q}}_v-(\nabla ·{\dot{q}}_c)-\nabla ·(p\underset{¯}{I}·\stackrel{\rightharpoonup }{U})+\nabla ·(\underset{¯}{\tau }·\stackrel{\rightharpoonup }{U})+\rho \stackrel{\rightharpoonup }{f}·\stackrel{\rightharpoonup }{U}$$ (18)

Similar to the control volume analysis, the sum of the change in internal energy and the heat rate leaving the system are equal to the power lost. These terms are isolated on the left-hand side of Equation (18) by subtracting the differential kinetic energy rate (Equation (19)) from both sides.

$$\rho \frac{D}{\mathit{\text{Dt}}}\left(\frac{U^2}{2}\right)=-\stackrel{\rightharpoonup }{U}·\nabla p+\stackrel{\rightharpoonup }{U}·(\nabla ·\underset{¯}{\tau })+\rho \stackrel{\rightharpoonup }{f}·\stackrel{\rightharpoonup }{U}$$ (19)

Equation (20) results, and defines the differential power lost in the Fontan connection.

$${\dot{e}}_{\mathit{\text{loss}}}=-p(\nabla ·\stackrel{\rightharpoonup }{U})+\underset{¯}{\tau }:\nabla \stackrel{\rightharpoonup }{U}$$ (20)

Assuming the fluid in question is Newtonian allows for a relationship between the shear stress vector and the velocity, which can then be substituted into Equation (20).

$${\dot{e}}_{\mathit{\text{loss}}}=-p(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})+\mu [2{\left(\frac{\partial u_x}{\partial x}\right)}^2+2{\left(\frac{\partial u_y}{\partial y}\right)}^2+2{\left(\frac{\partial u_z}{\partial z}\right)}^2+{(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x})}^2+{(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x})}^2+{(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y})}^2]-\frac{2}{3}\mu {(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})}^2$$ (21)

Equation (21) is simplified by assuming incompressible flow, which leaves Equation (22):

$$\mathit{\text{VDR}}=\mu [2{\left(\frac{\partial u_x}{\partial x}\right)}^2+2{\left(\frac{\partial u_y}{\partial y}\right)}^2+2{\left(\frac{\partial u_z}{\partial z}\right)}^2+{(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x})}^2+{(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x})}^2+{(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y})}^2]$$ (22)

A differential analysis is evaluated over a differential volume, so in order to truly equate viscous dissipation rate to the general power loss from the control volume analysis, Φ, (including equating their units of measure) the differential viscous dissipation rate must be integrated over the entire domain volume. The final relationship is found in Equation (23).

$$\Phi =\mu {\int }_V[2{\left(\frac{\partial u_x}{\partial x}\right)}^2+2{\left(\frac{\partial u_y}{\partial y}\right)}^2+2{\left(\frac{\partial u_z}{\partial z}\right)}^2+{(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x})}^2+{(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x})}^2+{(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y})}^2]\mathit{\text{ dV}}$$ (23)

Mesh-independence Study

The mesh-independence study was conducted based on the case with the highest flow rate (model #10). The study started with a D_avg/20 edge size, which was used in previous studies³¹. Every refinement reduced the edge size by 20%, resulting in ~50% reduction in mesh cell volume. Consequently, edge sizes were 1/20, 1/25, 1/31.25, 1/40, 1/50, and 1/62.5 of D_avg. It was found that the D_avg/20 mesh produced mesh-independent power loss as its resultant value has less than 2% discrepancy compared to the D_avg/25 mesh. However, the D_avg/50 mesh was needed for the calculated viscous dissipation rate to show less than a 5% discrepancy between the further refined mesh (D_avg/62.5). Therefore, the D_avg/50 mesh was chosen for all simulations, resulting in about 5 million polyhedral cells per mesh. The estimated numerical errors were 0.1% and 5% for power loss and viscous dissipation rate, respectively.

Viscous Dissipation Rate and Power Loss Comparison

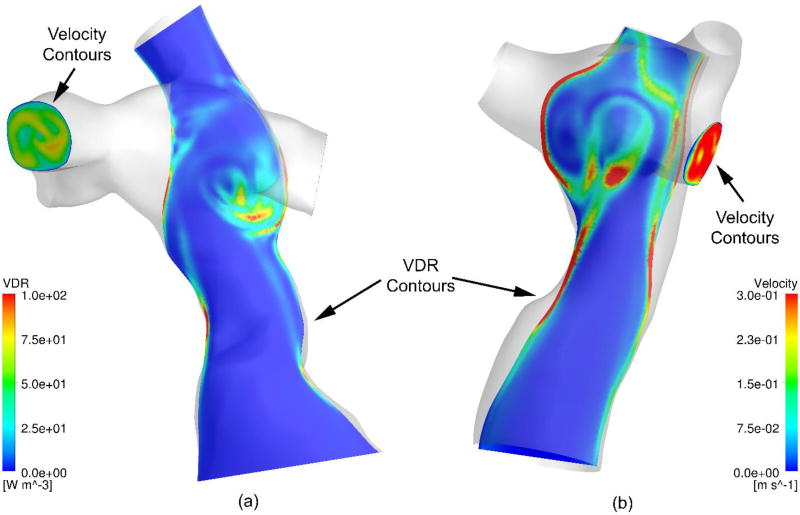
The results of the CFD simulations were time-resolved three-dimensional velocity fields and pressure values for each of the 10 patient-specific models. Figure 3 shows viscous dissipation rate contours on a coronal slice and outlet velocity contours for two different models.

Figure 3.

Coronal slices of viscous dissipation rate (VDR) contours and colored vectors representing velocity values.

Similar results exist for all 10 patient-specific geometries. Each result shows increased viscous dissipation rate values near the wall and stagnation points, and non-uniform velocity profiles at the outlets. The time-averaged values of the viscous dissipation rate and power loss terms from the 10 patient-specific CFD simulations are summarized in Table 1. Table 1 also quantifies the effect of three out of five assumptions made by the simplified power loss and viscous dissipation rate in comparison to the true power loss metric. The effect of the remaining two assumptions will be elaborated in the discussion section.

Table 1.

Time-averaged viscous dissipation rate, power loss, and analyses of assumptions 2,3, and 5 (see appendix for more details).

	Ėsim (mW)*1	Ėsim ∩ U⃑n (mW)*2	Ẇτ(μW)*3	Ẇq(μW)*4	Ėloss(mW)*5	Φ(mW)*6	ΔĖsimǂ1	Δ(Ėsim ∩ U⃑n)ǂ2	ΔẆτǂ3	ΔẆqǂ4	ΔΦǂ5
AVG§	3.9	3.3	2.8	4.98	3.33	3.22	−17.70%	−17.70%	0.1%	0.1%	2.7%
SD§§	3.2	2.9	1.45	7.68	2.92	2.79	9.00%	8.80%	0.1%	0.3%	1.3%
§AVG				average value
§§SD				standard deviation
*1Ėsim				simplified power loss
*2Ėsim ⋂ U⃑n				power loss with correctly calculated velocity profile (U⃑n)
*3Ẇτ = ∫CS τ⃑ · U⃑ dA				viscous work present on the control surface
*4 ${\dot{W}}_q=\frac{\partial }{\partial t}{\int }_V\rho \left(\frac{U^2}{2}\right)\mathit{\text{ dV}}$				effect of time-derivatives of dynamic pressure and volume
*5Ėloss = (Ėsim ⋂ U⃑n) + Ẇτ − Ẇq				true power loss
*6Φ				viscous dissipation rate
ǂ1ΔĖsim = (Ėloss−Ėsim)/Ėloss				discrepancy between simplified and true power losses
ǂ2Δ(Ėsim ⋂ U⃑n) = 1 ∸ Esim/(Ėsim ⋂ U⃑n)				percentage discrepancy between power loss obtained using an accurate spatial velocity profile (assumption #5) and true power loss.
ǂ3 ΔẆτ = Ẇτ/Ėloss				effect of viscous work on the control surface, assumption #2
ǂ4ΔẆq = Ẇq/Ėloss				effect of control volume and dynamic pressure, assumption #3
ǂ5ΔΦ = (Ėloss − Φ)/Ėloss				discrepancy between viscous dissipation rate and true power loss

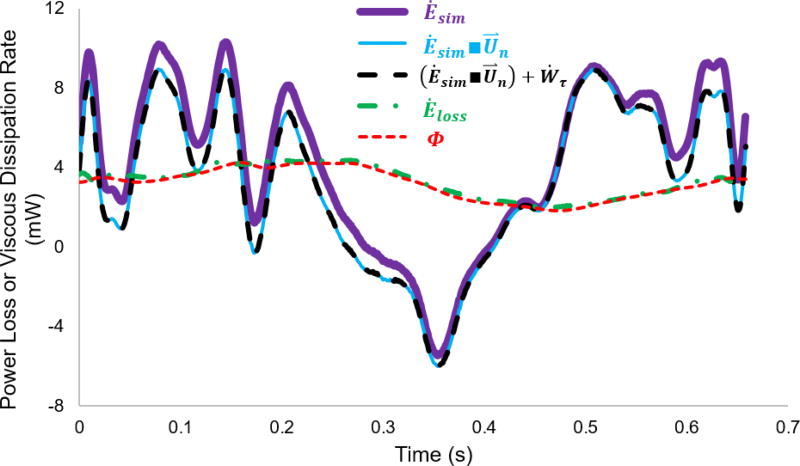
Figure 4 depicts the time-resolved difference between viscous dissipation rate and different forms of power loss as shown in Table 1. The instantaneous Ė_loss looks identical to instantaneous viscous dissipation rate, and the time-resolved effect of viscous work on the control surface (assumption 2) is minimal. Additionally, the time-resolved discrepancy between Ė_sim and Ė_sim∩U⃑_n are on the same order of the time-averaged discrepancy between them. However, the instantaneous difference between Ė_sim∩U⃑_n and Ė_loss are remarkable, while the time-averaged difference between them are very small (combined effect of ΔẆ_τ and ΔẆ_q, less than 0.1 ± 0.3% as shown in Table 1).

Figure 4.

Time-resolved differences between different forms of power loss and viscous dissipation rate over a cardiac cycle for model #8. Ė_sim: simplified power loss; Ė_sim■U⃑_n: power loss with correctly calculated velocity profile (U⃑_n); (Ė_sim■U⃑_n) + Ẇ_τ: true power loss without the effect of time-derivatives of dynamic pressure and control volume; Ė_loss: true power loss; Φ: viscous dissipation rate.

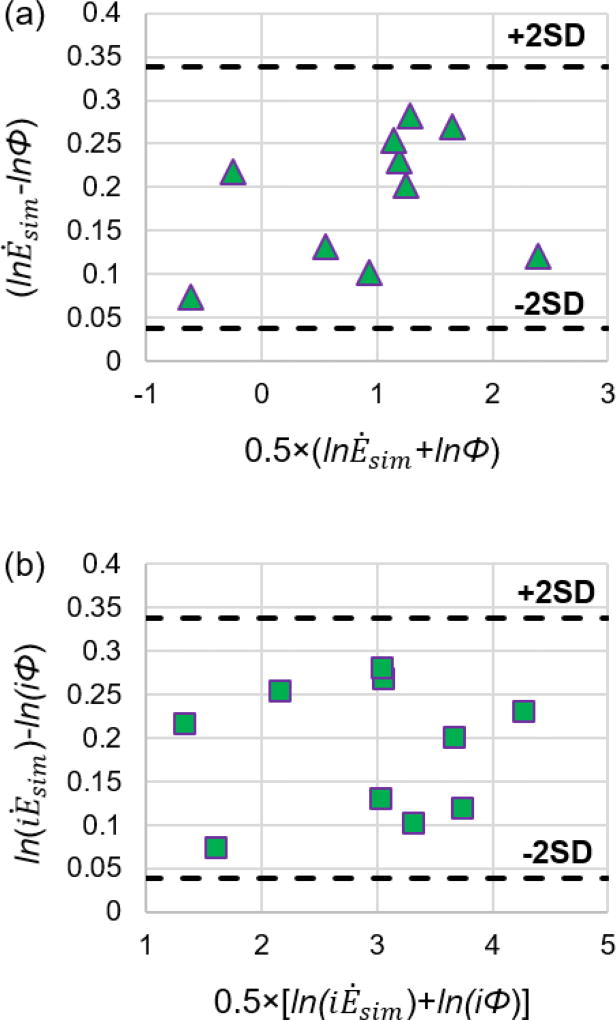
Both the comparison between Φ and Ė_sim, and the comparison between iΦ and iĖ_sim showed statistically significant relationships. Bland-Altman plots² are illustrated in Figure 5. The 95% limits of agreement are indicated by the 2SD lines. Ė_sim and iĖ_sim are generally higher than Φ and iΦ, respectively, as indicated by the positive average differences,

Figure 5.

Bland-Altman plots for (a) simplified power loss and viscous dissipation rate values and (b) indexed simplified power loss and indexed viscous dissipation rate values resulting from the CFD simulation. Ė_sim: simplified power loss; Φ: viscous dissipation rate;. iĖ_loss: indexed simplified power loss; iΦ: indexed viscous dissipation rate.

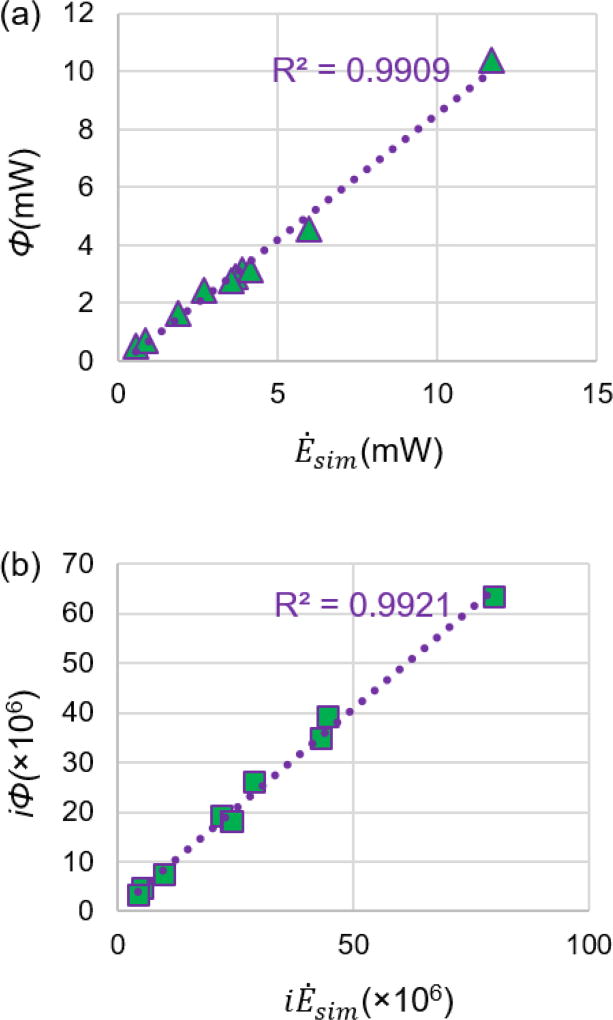
Moreover, neither Ė_sim, nor Φ, were found to be normal distributions, according to the Shapiro-Wilk test, so a Spearman’s correlation test was performed to compare these two metrics. The Spearman’s correlation test found that Ė_sim is significantly (R² = 0.992, p < 0.001) correlated with Φ, as shown in Figure 6. Both iĖ_sim, and iΦ, were normally distributed according to a Shapiro-Wilk test, so a Pearson’s correlation test was performed to determine their relationship. Similar to the non-indexed terms, a very strong (r = 0.991) statistically significant (p < 0.001) correlation was found between iĖ_sim and iΦ, as shown in Figure 6.

Figure 6.

Scatter plot comparing (a) simplified power loss and viscous dissipation rate values and (b) indexed simplified power loss and indexed viscous dissipation rate values resulting from the CFD simulation. The purple-dotted line stands for the linear curve-fitting line. Ė_sim: simplified power loss; Φ: viscous dissipation rate;. iĖ_sim: indexed simplified power loss; iΦ: indexed viscous dissipation rate.

DISCUSSION

This study shows advantages of viscous dissipation rate over simplified power loss as a Fontan connection hemodynamic metric. The focus, in particular, is on future Fontan in vitro and in silico studies with increased physiological modelling accuracy, or in vivo studies directly measuring true physiology.

The derivation of simplified power loss from true power loss via a control volume analysis highlighted the use of five assumptions. Of these five assumptions, two may be valid for physiologically accurate studies. Assuming no shaft work is present in the system (assumption 1) is always valid, unless the control volume included a mechanical energy source (i.e. a ventricular assist device). Assuming no change in elevation between the control surfaces (assumption 4) is also valid because most clinical measurements are made while the Fontan patient is in the supine position. The three remaining assumptions may not be completely valid in physiological settings.

First, involving properly measured velocity profiles (assumption 5) is important for all previous and future in vitro, in silico, and in vivo studies. Figure 2 showed two examples that can easily refute the validity of assumption 5. Table 1 quantitatively demonstrated that the effect of a constant velocity profile at the control surfaces, Δ(Ė_sim ∩ U⃑_n) = −17.7±8.8%, is the major contribution to the discrepancy between the simplified power loss and the true power loss, ΔĖ_sim= −17.7±9.0%. Highlighting the lack of proper velocity treatment for the simplified power loss calculation is not new. Grigioni et al. noted it as a critical issue when studying flow through the Fontan connection¹¹. However, this study did not identify all of the other assumptions made to arrive at a simplified power loss calculation, neither did they systematically quantify the effect of these assumptions.

Second, accounting for control volume changes in time (assumption 3) is important for in vivo studies, and is becoming important for in vitro and in silico studies as researchers add flexible Fontan models to experiments^25,30 and fluid-structure interaction models to computations¹⁹. Even with an unchanged control volume, the comparison between (Ė_sim ∩ U⃑n) + Ẇ_τ and Ė_loss in Figure 4 illustrates that Ẇ_q (assumption 3) plays a very important role to time-resolved discrepancies between the simplified power loss and viscous dissipation rate. Assumption 3 involves the time-derivative of the velocity field. The integration of the time-derivative over a cardiac cycle is negligible according to Table 1 (ΔĖ_τ = 0.1±0.1%), but its instantaneous values could be very large as the flow in the Fontan connection may be very unsteady.

Third, the presence of viscous work on control surfaces (assumption 2) is dependent on control volume selection and velocity measurement location. In addition, the velocity profile at the outlet control surfaces is rarely known prior to any (in vitro, in silico, or in vivo) Fontan hemodynamic study. Unless the inflow and outflow control surfaces are everywhere orthogonal to the velocity field, viscous work on the control surfaces may exist but could be neglected, ΔĖ_q = 0.1±0.3% as demonstrated in Table 1.

The results of the differential energy conservation derivation showed the assumptions made to arrive at the viscous dissipation rate metric. The viscous dissipation rate metric assumes that the fluid is Newtonian and that flow is incompressible. Incompressibility is commonly held for blood for cardiovascular systems. The Newtonian assumption is valid as long as flow within the Fontan connection exceeds a shear rate of 50/s^3,10. Even with a non-Newtonian effect, one can easily use non-Newtonian models to adjust Equation (23), e.g. Cheng et al.⁴.

Utilizing all of the results, one can compare simplified power loss and viscous dissipation rate according to the three requirements outlined for a future Fontan hemodynamic efficiency metric. The first requirement states that the metric must describe Fontan flow efficiency accurately while maintaining physical meaning. The derivation of both simplified power loss and viscous dissipation shows that simplified power loss assumes more potentially invalid conditions. Additionally, simplified power loss is only capable of representing time-averaged hemodynamics in the Fontan connection while the viscous dissipation rate is useful for both the time-resolved and time-averaged analyses. The time-resolved values may assist studies investigating Fontan hemodynamics under free-breathing or exercise conditions because of the significant hemodynamic variation between cardiac cycles under these conditions³³. The second requirement states that the metric should be easily calculable from clinical measurement devices. Simplified power loss, again, is the less ideal solution, as it requires invasive catheterization measurements to obtain static pressure data. Viscous dissipation rate requires a time-resolved three dimensional velocity field – data achievable via 4D MRI technology¹². It is also worth noticing that power loss is only a bulk measurement, while the viscous dissipation rate also provides distribution contours, like in Figure 2. The distribution contours help visualize energetic differences between patients and identify regions of high viscous dissipation rate. This information can be used for making better clinical strategies. The final requirement is that the Fontan hemodynamic efficiency metric of the future maintain the relationship between Fontan connection flow efficiency and patient outcomes from previous studies. Simplified power loss was the metric used for studies relating to patient outcomes, so it automatically fulfills this final requirement^14,17,34. In addition, the Bland-Altman plots in Figure 5 show the viscous dissipation rate is statistically equivalent to the simplified power loss. Strong correlations were also observed between viscous dissipation rate and simplified power loss for the CFD simulation results. The CFD methods employed are similar to those used in previous studies relating Fontan flow efficiency to patient outcomes, so this study concludes that viscous dissipation rate fulfills the final requirement as well. Ultimately, viscous dissipation rate fulfills all three requirements while simplified power loss only completely fulfills one. This shows the advantages of viscous dissipation rate over simplified power loss as a Fontan hemodynamic metric.

Nonetheless, a much higher resolution velocity field is required to obtain viscous dissipation rate in comparison to power loss. Therefore, the ability of the viscous dissipation rate metric to be entirely calculable in the clinic is dependent on 4D MRI technology. Work by Cibis et al explored the effects of 4D MRI spatial resolution on viscous dissipation rate calculations. Cibis’ study concluded that a CFD-based (high resolution) viscous dissipation rate was significantly greater than those based on a down-sampled CFD mesh, a down-sampled CFD mesh with simulated random noise, and a 4D MRI flow measurement. The study by Cibis showed lower viscous dissipation rate values for coarser resolution data fields across all patients. So, even though 4D MRI has a lower viscous dissipation rate value due to inadequate spatial resolution, comparisons between patients should still be valid. Nevertheless, advanced post-processing techniques are in development to improve the accuracy of MRI-derived hemodynamic metrics by merging CFD and MRI¹. However, the study by Cibis et al. calculated viscous dissipation rate values on grids as fine as 0.1 mm, but never showed the minimum grid size at which changes in viscous dissipation rate no longer occurred. Determining this sort of resolution requirement to achieve accurate viscous dissipation rate measurements should be the subject of future research. Additionally, the noise in 4D MRI may be amplified by the calculation of velocity derivatives needed to obtain the viscous dissipation rate^6,29. Future post-processing techniques shall also minimize the effect of the 4D MRI noise or quantify the budget of uncertainty for the impact of the noise on hemodynamic metrics, especially those derived from velocity derivatives. After all, 4D MRI technology must be thoroughly validated before clinical use for in vivo evaluation.

Closer examination of the CFD simulation methods show why the statistical correlation between the simplified power loss and viscous dissipation rate terms was so strong. The CFD simulations were conducted for patient-specific, rigid-walled Fontan connections under pulsatile flow conditions. This pre-established assumption drew the simplified power loss values closer to the viscous dissipation rate values, and undoubtedly played a role in the correlation strength and statistical significance. For example, with the vessel wall deformation, assumption 3 may not only influence the time-resolved discrepancy between simplified power loss and viscous dissipation rate but also affect the time-averaged one. However, examining the statistical relationship under the rigid wall assumption is permissible for the current study because similar pre-established assumptions were widely employed in previous studies that related simplified power loss to Fontan outcomes^17,28,34. The strength and significance of the relationship between simplified power loss and viscous dissipation rate are expected to decrease under more physiologically accurate conditions, i.e. the introduction of flexible vessel wall. Hence, viscous dissipation rate would be better than simplified power loss at representing true physical meaning under such conditions.

Moreover, the CFD simulations did not include any additional forms of work within the control volume (Ẇ_in,shaft), nor did they consider gravity effect. It is hypothesized that the presence of gravity would affect both simplified power loss and viscous dissipation rate in the same way. Therefore, even though gravity effect will affect the absolute values, any change in the relationship between these two metrics could be negligible.

Additionally, the CFD simulations used the Newtonian fluid, thereby ignoring the non-Newtonian effect. A non-Newtonian important factor (I_L = μ_eff/μ, where μ_eff is the effective viscosity) was introduced to determine the non-Newtonian effect, and the cut-off value was suggested to be 1.75¹⁶. In order to estimate μ_eff, this study plugged the shear rate from the simulation to a Carreau model which curve-fitted experimental data from Cheng et al⁴. One case, in this study, exhibited an I_L slightly above the cut-off line, i.e. 1.78. For this case, the differences between the Newtonian and non-Newtonian results were considered negligible for two reasons. Firstly, the non-Newtonian simulation indicates that both simplified power loss and viscous dissipation rate were increased by 4% compared to the Newtonian simulation. This marginally affected the difference between simplified power loss and viscous dissipation rate (18.3% with Newtonian properties vs. 19.0% with non-Newtonian properties). Secondly, including the non-Newtonian value for this patient produced the same statistical results in Bland-Altman plots and bivariate correlations. Therefore, to maintain consistency across patients for the sake of this study, the Newtonian results were used for this patient. This decision had no effect on our results.

Furthermore, energy equation was not involved in simulations of all patients. The effect of including energy equation was examined for the case with the maximum volumetric inflow rate. The simulation with the conservation of energy (converged to 10⁻⁷) resulted in less than 0.2% discrepancy in comparison with the simulation not including the energy equation. Therefore, it is reasonable to exclude the computation of conservation of energy for saving computational time because the impact is negligible.

Finally, the selection of 10 patient-specific cases that cover the full range of possible cardiac outputs is not the only way the cohort could have been determined. Similar CFD Fontan studies have selected cohorts according to Fontan connection type or Fontan connection anatomy characteristics while maintaining similar flow rates. However, it is worth noting that Fontan type and anatomy could affect power loss and viscous dissipation values differently. For example, the geometry would have impact on the normal velocity profile involved in assumption 5. Therefore, different type of Fontan anatomy could change the value of the discrepancy between simplified power loss and viscous dissipation rate but may not change the fact that assumption 5 dominates this discrepancy.

Overall, this study highlighted advantages of viscous dissipation rate over simplified power loss as a Fontan hemodynamic metric. Future studies of Fontan connection hemodynamics should include both simplified power loss and viscous dissipation rate metrics, with special attention paid to viscous dissipation rate’s relationship to patient outcomes for more complex and physiologically accurate studies.

APPENDIX

Table II.

Details for Table 1: Time-averaged viscous dissipation rate, power loss, and analyses of assumptions 2,3, and 5

Model	1	2	3	4	5	6	7	8	9	10	AVG§	SD§§
Ėsim (mW)*1	0.56	1.87	2.68	3.88	3.69	5.97	4.16	3.56	0.87	11.7	3.89	3.19
Ėsim ∩ U⃑n(mW)*2	0.52	1.67	2.53	3.28	3.05	4.65	3.24	2.84	0.71	10.9	3.34	2.93
Ẇτ(μW)*3	1.47	3.34	2.11	1.67	1.33	5.95	4.07	3.04	2.08	3.7	2.88	1.45
Ẇq(μW)*4	−1.58	2.36	−1.09	2.29	1.72	10.03	1.16	22.9	0.39	11.6	4.98	7.68
Ėloss(mW)*5	0.52	1.67	2.53	3.28	3.05	4.65	3.24	2.82	0.71	10.9	3.33	2.92
Φ(mW)*6	0.52	1.64	2.42	3.17	2.93	4.56	3.14	2.76	0.7	10.4	3.22	2.79
ΔĖsim ǂ1	−7%	−12%	−6%	−18%	−21%	−28%	−28%	−26%	−22%	−8%	−17.7%	9.0%
Δ(Ėsim ∩ U⃑n) ǂ2	−8%	−12%	−6%	−19%	−21%	−28%	−28%	−25%	−23%	−8%	−17.7%	8.8%
ΔẆτ ǂ3	0.3%	0.2%	0.1%	0.1%	0.0%	0.1%	0.1%	0.1%	0.3%	0.0%	0.1%	0.1%
ΔẆq ǂ4	−0.3%	0.1%	0.0%	0.1%	0.1%	0.2%	0.0%	0.8%	0.1%	0.1%	0.1%	0.3%
ΔΦ ǂ5	0.6%	1.9%	4.5%	3.3%	3.9%	1.8%	3.2%	2.1%	1.6%	4.5%	2.7%	1.3%
§Avg = average value			§§SD = standard deviation
*1Ėsim			simplified power loss
*2Ėsim ∩ U⃑n			power loss with correctly calculated velocity profile (U⃑n)
*3Ẇτ = ∫CS τ⃑ · U⃑ dA			viscous work present on the control surface
*4 ${\dot{W}}_q=\frac{\partial }{\partial t}{\int }_V\rho \left(\frac{U^2}{2}\right)\mathit{\text{ dV}}$			effect of time-derivatives of dynamic pressure and volume
*5Ėloss = (Ėsim ∩ U⃑n) + Ẇτ − Ẇq			true power loss
*6Φ			viscous dissipation rate
ǂ1ΔĖsim = (Ėloss − Ėsim)/Ėloss			discrepancy between simplified and true power losses
ǂ2Δ(Ėsim ∩ U⃑n) = 1 ∸ Ėsim/(Ėsim ∩ U⃑n)			time-averaged percentage discrepancy between power loss obtained using an accurate spatial velocity profile (assumption #5) and true power loss.
ǂ3 ΔẆτ = Ẇτ/Ėloss			time-averaged effect of viscous work on the control surface, assumption #2
ǂ4 ΔẆq = Ẇq/Ėloss			time-averaged effect of control volume and dynamic pressure, assumption #3
ǂ5ΔΦ = (Ėloss − Φ)/Ėloss			time-averaged discrepancy between viscous dissipation rate and true power loss