Assessment of the Combination of Temperature and Relative Humidity on Kidney Stone Presentations

Abstract

Temperature and relative humidity have opposing effects on evaporative water loss, the likely mediator of the temperature-dependence of nephrolithiasis. However, prior studies considered only dry-bulb temperatures when estimating the temperature-dependence of nephrolithiasis.

We used distributed lag non-linear models and repeated 10-fold cross-validation to determine the daily temperature metric and corresponding adjustment for relative humidity that most accurately predicted kidney stone presentations during hot and cold periods in South Carolina from 1997–2015. We examined three metrics for wet-bulb temperatures and heat index, both of which measure the combination of temperature and humidity, and for dry-bulb temperatures: (1) daytime mean temperature; (2) 24-hour mean temperature; and (3) most extreme 24-hour temperature. For models using dry-bulb temperatures, we considered four treatments of relative humidity.

Among 188,531 patients who presented with kidney stones, 24-hour wet bulb temperature best predicted kidney stone presentation during summer. Mean cross-validated residuals were generally lower in summer for wet-bulb temperatures and heat index than the corresponding dry-bulb temperature metric, regardless of type of adjustment for relative humidity. Those dry-bulb models that additionally adjusted for relative humidity had higher mean residuals than other temperature metrics. The relative risk of kidney stone presentations at the 99^th percentile of each temperature metric compared to the respective median temperature in summer months differed by temperature metric and relative humidity adjustment, and ranged from an excess risk of 8% to 14%. All metrics performed similarly in winter.

The combination of temperature and relative humidity determine the risk of kidney stone presentations, particularly during periods of high heat and humidity. These results suggest that metrics that measure moist heat stress should be used to estimate the temperature-dependence of kidney stone presentations, but that the particular metric is relatively unimportant.

1. Introduction

Nephrolithiasis (kidney stone disease), which affects 9% of the population in the United States and is estimated to cost $10 billion per year, is punctuated by acute, painful presentations caused by growth and detachment of stones from the renal papillae (Litwin and Saigal, 2012; Scales et al., 2012). Although the cause of kidney stone detachment is unknown, prior epidemiologic studies reported that high and low daily temperatures are associated with an increased risk of kidney stone presentations. The increase in kidney stone presentations following hot and cold days is likely mediated by increased evaporative water loss through sweating, and respiration (Masterson et al., 2013; Parks et al., 2003). The resultant low urine volume increases urinary supersaturation of calcium, oxalate, and phosphate, which leads to stone growth in susceptible patients. During the hours to days during which the risk of kidney stone presentations increase following hot and cold days (Tasian et al., 2014), evaporative water loss is determined by the difference in water vapor concentration between the body surface and ambient air (Withers and Cooper, 2014). Evaporative water loss increases exponentially as temperature increases and is inversely related to relative humidity. Metrics that measure the complex thermodynamic relationship between temperature and humidity, such as wet-bulb temperatures and heat index, may be considered a proxy for the combined effect of temperature and humidity on human physiology (Sherwood and Huber, 2010). However, prior studies considered only dry-bulb temperatures when estimating the temperature-dependence of nephrolithiasis. Whether the combined effect of temperature and relative humidity better predicts kidney stone presentations, and other temperature-dependent health outcomes, such as mortality, is unclear (Gasparrini et al., 2010; Gronlund et al., 2014; Hondula and Barnett, 2014; Oudin Astrom et al., 2016; Zheng et al., 2016). Although prior studies have reported that no one temperature metric best predicts mortality (Barnett et al., 2010), the association between temperature extremes and kidney stone presentations is likely mediated by a single process that is dependent on both temperature and relative humidity (evaporative water loss), whereas there are many potential causal pathways for temperature and mortality.

Identifying the temperature metric(s) that best predict kidney stone presentations will help identify the temperatures and times during which vulnerable populations are at greatest risk. This knowledge would also have implications for improving projections of the effect of climate change on nephrolithiasis, which have thus far only used dry-bulb temperatures (Brikowski et al., 2008). In this study, we used a time series design with distributed lag non-linear models (DLNMs) and repeated 10-fold cross-validation to estimate the differences between predicted and observed kidney stone presentations for different daily temperature metrics and adjustment for relative humidity during hot and cold periods in South Carolina from 1997 to 2015. We identified the daily temperature metrics that most accurately predicted kidney stone presentations.

2. Methods

2.1 Study Setting

We conducted this study using South Carolina Medical Encounter Data and Financial Reports. We included all patients aged 20 to 65 years who lived in South Carolina and presented to hospitals in South Carolina with kidney stones from January 1, 1997 to September 30, 2015. These age limits reflect the group of patients with the highest incidence of nephrolithiasis, ensuring sufficient power for the analyses, and limited potential imprecision that could be introduced by including patients at the extremes of life, who are more vulnerable to temperature extremes. We chose South Carolina because of its hot summers and cool winters and high prevalence of kidney stones, (Soucie et al., 1994) and because it is the largest of a few states with an all-payer claims database that captures all points of care where patients with symptomatic kidney stones present.

By law, South Carolina Medical Encounter Data records all Emergency Department visits, surgeries, and hospital admissions for South Carolina’s population, including those who are uninsured or have governmental insurance. Data are sent by all healthcare facilities in the state on a monthly basis. By law, all data must be 99.9 percent accurate (valid codes) and 99.5 percent complete. Routine audits are performed to ensure compliance and accuracy (Council, 2014). The database contains individual patient-level data using encounter-level data elements, including unique patient identifiers, ZIP code of patient’s mailing address, dates of services, and payer classification. We previously used this dataset to describe temporal trends in the incidence of nephrolithiasis (Tasian et al., 2016).

2.2 Outcome

The primary outcome was the daily count of kidney stone presentations in South Carolina. A kidney stone presentation was defined as emergency department, inpatient, or surgical care associated with primary international classification of diseases, 9^th revision codes for nephrolithiasis (592.0, 592.1, 592.9, 274.11). These criteria capture clinically important acute stone events because of the painful nature of stone episodes that require emergency evaluation, hospital admission, and/or surgery (Bush et al., 2010; Ghani et al., 2014). The first qualifying claim defined the date of presentation. Kidney stone presentations among unique individuals were limited to the earliest occurrence.

2.3 Exposures

We defined three distinct daily temperature metrics for wet-bulb temperatures, heat index, and dry-bulb temperatures: (1) daytime mean temperature (average temperature between the hours of 7am and 8pm); (2) 24-hour mean temperature (average temperature in a 24-hour period); and (3) most extreme temperature (maximum temperature in a 24-hour period during summer and minimum temperature in a 24-hour period during winter). This process resulted in nine distinct daily temperatures for each summer day of the study period and six distinct daily temperatures for each winter day of the study period since heat index only applies to temperatures above 26.7 °C. Average daily relative humidity was also determined.

These temperature metrics were derived by first obtaining hourly dry-bulb temperatures, relative humidity, and surface pressure from the NASA Land Data Assimilation Systems at the ZIP-code level from 1997 to 2015.(Mitchell et al., 2004) Land Data Assimilation Systems is a spatial grid of weather data measured at 2 meters above ground throughout North America with a resolution of 1/8 of a degree. These data are interpolated from real-time weather data and hydrology models (Cosgrove et al., 2003). Hourly wet-bulb temperatures were then estimated using the Davies-Jones pseudoadiabitic algorithm (Davies-Jones, 2008) as implemented in HumanIndexMod and heat index was calculated as described previously (Buzan et al., 2015). Heat index was converted to Celsius for internal consistency. All hourly weather metrics were then defined at the state-level by averaging ZIP-code level data, and the aforementioned daily temperature metrics were derived. Data were aggregated at the state-level into daily counts of kidney stone presentations, daily temperature metrics, and average daily relative humidity. The study period was stratified by summer and winter periods.

2.4 Statistical analysis

We applied a two-step procedure to determine the daily temperature metric that best predicted kidney stone presentations in South Carolina.

2.4.1. Estimation of the association between daily temperature metrics and kidney stone presentation

We first performed a time series study using distributed lag nonlinear models (DLNMs) (Gasparrini et al., 2010) to estimate the association between the different daily temperature metrics and kidney stone presentations separately during summer (June, July, August) and winter (December, January, February). DLNMs are a flexible family of models that simultaneously describe the association between time varying exposures and discrete outcomes, and the lag between the exposure and outcome (Gasparrini et al., 2010; Gronlund et al., 2014; Hondula and Barnett, 2014; Lubczynska et al., 2015; Oudin Astrom et al., 2016; Zheng et al., 2016). We built Poisson regression models for the daily number of kidney stone presentations, allowing for over-dispersion (Quasi-Poisson) as follows:

$$\begin{gathered} Y_t~\mathit{Quasi}-\mathit{Poisson}(\mu ) \\ log(\mu )=\alpha +\beta T_{t,l}+ns(t,32), \end{gathered}$$

where t represents the day of observation, Y_t the kidney stone count on day t, T_t,l the cross-basis matrix of daily temperature and lag and ns(t, 32) a natural spline with 32 degrees of freedom. For models using dry-bulb temperatures, we considered four treatments of humidity: no adjustment, linear adjustment, a natural spline term with 2 degrees of freedom for daily relative humidity on day t, and a natural spline term with 32 degrees of freedom for daily relative humidity on day t. We thus considered five different models to be applied to each of 3 different dry-bulb temperature metrics for a total of fifteen models per season. Consistent with the DLNM procedure, the association between temperature and kidney stone presentations was assessed through the cross-basis matrix of daily temperature (T_t,l). We used natural cubic splines to smooth the temperature-kidney stone presentation and lag-kidney stone presentation relationships. We used a maximum lag of 10 days based on our previous study that demonstrated the greatest risk of presentations occurred within 10 days of temperature exposure (Tasian et al., 2014). Separate DLNM models were built for each temperature metric. Since we did not know the optimal number of degrees of freedom for these relationships, we evaluated between one and four knots placed at equal intervals over the ranges of both temperature and lag days, with the latter natural-log transformed to increase sensitivity to shorter lags. This resulted in assessing the fit of 16 DLNMs for temperature metric in each season. The final model for each temperature metric was that which minimize the quasi-Akaike information criterion (quasi-AIC) (Gasparrini et al., 2010). The cumulative exposure-response and lag-response between temperature and kidney stone presentations over 10 days were estimated for each model using the median temperature for summer and winter as the referent value. The models were fitted using the dlnm package within R version 3.2.2 (Gasparini and Armstrong, 2011).

2.4.2. Determination of differences between predicted and observed kidney stone presentations

We determined the accuracy of each daily temperature metric to predict kidney stone presentations in each season using repeated 10-fold cross-validation (Han and Kamber, 2006). Cross-validation splits the sample into training and validation sets, where the model is built on the training set and evaluated using the validation set. Following the procedure outlined in Barnett et al., every day in the study period was randomly assigned a number between one and ten (Barnett et al., 2010). For each season and model, the quasi-Poisson regression model was run ten times, each time leaving out one of the ten groups. The squared Pearson residuals were obtained by comparing the predicted counts of kidney stone cases for the omitted days and the observed values to obtain the residuals using the equation:

$$r_{c,d}=\frac{{(Y_d-\widehat{{\mu }_d})}^2}{\widehat{{\mu }_d}},d\in D_c,c=1,\dots ,10,$$

where $\widehat{{\mu }_d}$ and Y_d are the predicted and observed number of kidney stone cases on day d, respectively, and D_c is the set of days left-out for cross-validation c. We then took the mean of the daily squared residuals to obtain the average for each excluded set:

$$\overline{r_c}=\sum _{d\in D_c}\frac{r_{c,d}}{N_c},$$

where N_c is the number of days left-out in cross-validation c, and smaller mean residual values indicate a better predictive model. This cross-validation procedure was performed separately for each season and repeated 50 times, each time using a different random sampling pattern.

We used a Bayesian model to summarize the mean residuals including separate intercepts for each model and cross-validation:

$$\begin{gathered} \overline{r_{a,c}}~N({\mu }_{a,c},{\sigma }^2),a=1,\dots ,15,c=1,\dots ,500, \\ {\mu }_{a,c}=\delta +{\gamma }_a+{\lambda }_c, \end{gathered}$$

where $\overline{r_{a,c}}$ is the observed mean for model a and cross-validation c, σ² is the estimated variance of the cross-validated residuals, δ is the overall intercept, γ_a is the mean for model a, and λc is the mean for cross-validation c. We placed uninformative priors on each of the regression parameters (Normal distributions with mean 0 and variance 1000). The Bayesian model was re-run using a Gamma prior distribution and the results were unchanged. We compared the performance of each of the models by plotting the estimated mean residual ( $\widehat{\delta }+\widehat{{\gamma }_a}$) and its 95% credible interval. The models were fitted using the inla package within R version 3.2.2.(Rue et al., 2009)

3. Results

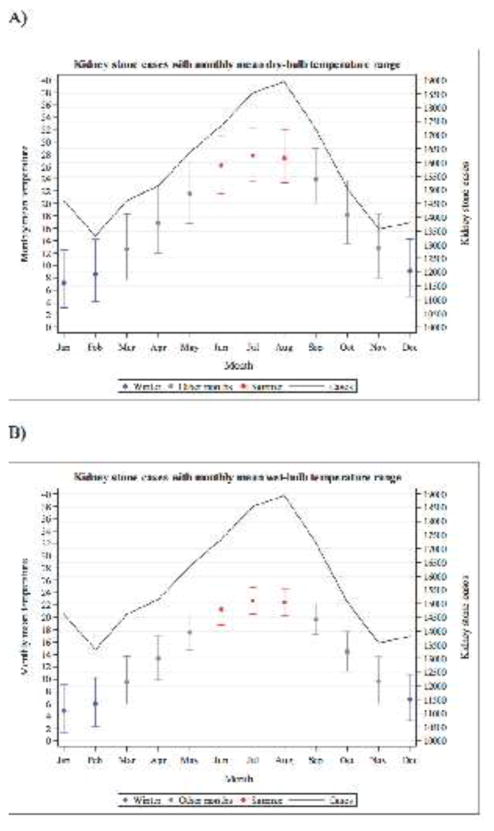
Among 188,531 adult patients who presented with kidney stones between 1997 and 2015 (Table 1), there was a bimodal increase in the frequency of kidney stone presentations per year (Figure 1). The greatest frequency of kidney stone presentations occurred in summer months. A smaller increase in the frequency of stone presentations was observed in winter months.

Table 1.

Characteristics of patients who presented with kidney stones and the population of South Carolina.

Characteristics		Cohort (n=188,531)	Census 2010 (n=4,625,364)
Male (%)		114,100 (60.5)	2,250,101 (48.6)
Urban (%)		143,201(76.0)	3,067,809 (66.3)
Race/Ethnicity (%)	White	159,468(84.6)	2,962,740 (64.1)
	African-American	23,391(12.4)	1,279,998 (27.7)
	Asian	673 (0.4)	58,307 (1.3)
	Native American	265 (0.1)	18,727 (0.4)
	Other	4,734 (2.5)	69,910 (1.5)
Age group (%)	<10 y/o	n/a	598,150 (12.9)
	10–14 y/o	n/a	297,286 (6.4)
	15–19 y/o	n/a	328,989 (7.1)
	20–24 y/o	12,089 (6.4)	332,494 (7.2)
	25–34 y/o	33,486 (17.8)	592,056 (12.8)
	35–44 y/o	39,181 (20.8)	601,292 (13.0)
	45–64 y/o	68,354 (36.3)	1,243,223 (27.0)
	>=65 y/o	27,414 (14.5)	631,874 (13.6)
Insurance (%)	Public	49,852 (26.4)
	Private	107,231(56.9)
	Self-pay	30,470 (16.2)
	No insurance	978 ( 0.5)

Figure 1.

Monthly mean temperature and frequency of kidney stone presentations in South Carolina from 1997 to 2015.

The limits of the temperature ranges for A) dry-bulb and B) wet-bulb temperatures are the averages of the monthly maximum and minimum temperature across the study period.

Table 2 reports the correlations among the daily weather metrics for summer and winter. In summer months, there were strong positive correlations (≥ 0.9) across the 3 wet-bulb temperature metrics, 3 heat index metrics, and the 3 dry-bulb temperature metrics, respectively. In general, there were relatively strong positive correlations (0.7–0.9) between the dry-bulb temperatures and moist temperature metrics (wet-bulb temperature and heat index). The exception was dry maximum daily temperatures, which had only moderate positive correlation with any wet-bulb temperature metric (0.5–0.7). Relative humidity was weakly correlated with wet-bulb temperature metrics and moderately negatively correlated with dry-bulb temperature and heat index metrics. In winter, there were strong positive correlations between all temperature measures. Relative humidity was only moderately correlated with any of the temperature measures.

Table 2.

Pearson correlation coefficients between daily temperature metrics and mean relative humidity in South Carolina.

Summer
	Wet daytime	Wet 24-hour	Wet maximum	Dry daytime	Dry 24-hour	Dry maximum	HI daytime	HI 24-hour	HI maximum	Rel. Humidity
Wet daytime	1	0.996	0.941	0.784	0.763	0.481	0.805	0.8	0.685	0.199
Wet 24-hour	0.996	1	0.95	0.777	0.761	0.47	0.804	0.803	0.677	0.207
Wet maximum	0.941	0.95	1	0.866	0.859	0.661	0.881	0.883	0.827	−0.012
Dry daytime	0.784	0.777	0.866	1	0.996	0.893	0.952	0.953	0.92	−0.447
Dry 24-hour	0.763	0.761	0.859	0.996	1	0.9	0.947	0.955	0.916	−0.474
Dry maximum	0.481	0.47	0.661	0.893	0.9	1	0.814	0.818	0.94	−0.718
HI daytime	0.805	0.804	0.881	0.952	0.947	0.814	1	0.996	0.903	−0.346
HI 24-hour	0.8	0.803	0.883	0.953	0.955	0.818	0.996	1	0.9	−0.36
HI maximum	0.685	0.677	0.827	0.92	0.916	0.94	0.903	0.9	1	−0.466
Rel. Humidity	0.199	0.207	−0.012	−0.447	−0.474	−0.718	−0.346	−0.36	−0.466	1

Winter
	Wet daytime	Wet 24-hour	Wet min	Dry daytime	Dry 24-hour	Dry min	Rel. Humidity
Wet daytime	1	0.995	0.982	0.990	0.982	0.980	0.652
Wet 24-hour	0.995	1	0.982	0.989	0.990	0.982	0.642
Wet minimum	0.982	0.982	1	0.966	0.963	0.990	0.673
Dry daytime	0.990	0.989	0.966	1	0.995	0.974	0.545
Dry 24-hour	0.982	0.990	0.963	0.995	1	0.972	0.530
Dry minimum	0.980	0.982	0.990	0.974	0.972	1	0.621
Rel. Humidity	0.652	0.642	0.673	0.545	0.530	0.621	1

In the first stage of the modeling framework where DLNMs were used to estimate the exposure-lag-response relationship for each temperature metric, a relatively small number of knots was selected in each dimension. The majority of models had the lowest quasi-AIC for 1 or 2 temperature knots and 1 or 2 lag knots for summer months (Table in Supplemental Material). In the winter months, all models used 1 knot for temperature and 1 or 2 knots for lag. The few knots selected across temperature metrics indicate that the exposure-lag-response relationship for daily temperature and kidney stone presentations is relatively simple. The models with maximum daily dry-bulb temperatures without adjustment for humidity and daytime mean dry-bulb temperatures without adjustment for humidity had the lowest quasi-AIC for summer and winter months, respectively.

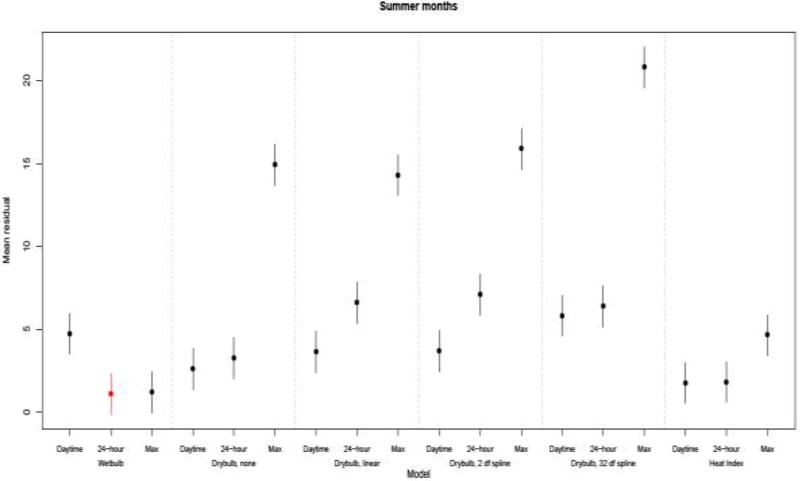
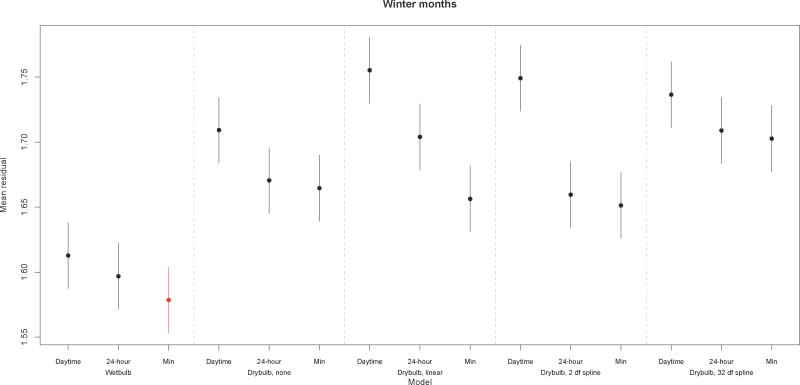
In summer months, there were differences in the mean cross-validated residuals (difference between predicted and observed kidney stone presentations) between wet-bulb temperature models, heat index models, and dry-bulb temperature models, with wet-bulb temperature and heat index models generally having lower residuals than dry-bulb temperature models (Figure 2). These lower cross-validated residuals indicated that moist temperature metrics (wet-bulb temperature and heat index) predicted kidney stone presentations with greater accuracy than dry-bulb temperatures in summer, regardless of the type of adjustment for humidity. The smallest cross-validated residuals were estimated for 24-hour mean wet-bulb temperatures. The differences in cross-validated residuals were minimal among the wet-bulb temperature and heat index metrics and greater among the dry-bulb temperature metrics. Those dry-bulb models that additionally adjusted for relative humidity had higher mean residuals than other temperature metrics In winter months, there were very little differences in the mean cross-validated residuals between wet-bulb temperature models and dry-bulb temperature models. The smallest cross-validated residuals were estimated for daily minimum wet-bulb temperatures.

Figure 2.

Mean cross-validated residuals for the 18 models predicting kidney stone presentations using different temperature metrics and adjustments for humidity.

Red highlights the minimum mean residual. Bars denote the 95% credible intervals.

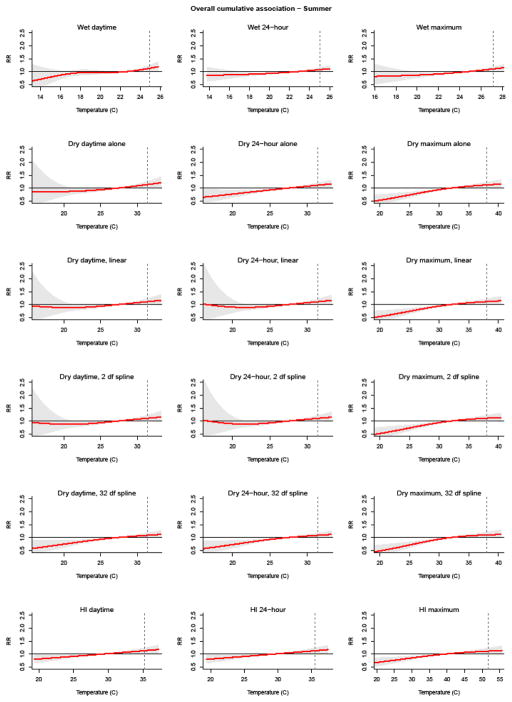
In summer months, an increased risk of kidney stone presentations was observed at high temperatures for each temperature metric compared to the respective median temperature in the summer period. The relative risk of kidney stone presentations at the 99^th percentile of each temperature metric compared to the respective median temperature in summer months differed by temperature metric and humidity adjustment, and ranged from an excess risk of 8% to 14% (Table 3). In winter months, there were no statistically significant changes in the risk of kidney stone presentations at the extremes of each temperature metric compared to the respective median temperatures for the winter period (Table 3). All temperature metrics produced similar shaped exposure-response relationships (Figure 3). The risk of stone presentations increased as temperatures increased and the highest risk for kidney stone presentations generally occurred the same day as the temperature exposure, with diminution of the risk over subsequent days (Figure in Supplemental Material).

Table 3.

Cumulative relative risk and 95% confidence intervals (CI) of kidney stone presentations associated with extremes of daily temperatures and varying adjustments for relative humidity.

	Summerc		Winterc
	P99 Temp (°C)	RR (95% CI)	P1 Temp (°C)	RR (95% CI)
Wet daytime	24.9	1.13 (1.03, 1.25)	−5.8	1.09 (0.95, 1.25)
Wet 24-hour	25.1	1.08 (1.01, 1.16)	−5.5	1.09 (0.95, 1.25)
Wet max/min	27.1	1.11 (1.04, 1.19)	−8.9	1.08 (0.96, 1.23)
Heat Index daytime	35.3	1.14 (10.4, 1.25)	--	--
Heat Index 24-hour	35.5	1.13 (1.03, 1.24)	--	--
Heat Index max	51.6	1.12 (1.01, 1.23)	--	--
Dry daytime†	31.4	1.14 (1.04, 1.26)	−3.7	1.11 (0.97, 1.27)
Dry 24-hour†	31.5	1.12 (1.04, 1.20)	−3.4	1.10 (0.97, 1.26)
Dry max/min†	38.1	1.13 (1.04, 1.23)	−7.5	1.11 (0.97, 1.27)
Dry daytime, linear††	31.4	1.12 (1.01, 1.23)	−3.7	1.11 (0.97, 1.27)
Dry 24-hour, linear††	31.5	1.12 (1.02, 1.22)	−3.4	1.10 (0.96, 1.26)
Dry max/min, linear††	38.1	1.12 (1.02, 1.23)	−7.5	1.11 (0.96, 1.27)
Dry daytime, 2 df spline*	31.4	1.11 (1.01, 1.23)	−3.7	1.11 (0.97, 1.27)
Dry 24-hour, 2 df spline*	31.5	1.11 (1.01, 1.22)	−3.4	1.10 (0.97, 1.26)
Dry max/min, 2 df spline*	38.1	1.12 (1.02, 1.22)	−7.5	1.10 (0.96, 1.27)
Dry daytime, 32 df spline**	31.4	1.09 (1.01, 1.18)	−3.7	1.10 (0.96, 1.26)
Dry 24-hour, 32 df spline**	31.5	1.09 (1.02, 1.18)	−3.4	1.10 (0.96, 1.26)
Dry max/min, 32 df spline**	38.1	1.11 (1.01, 1.22)	−7.5	1.11 (0.96, 1.27)

95% CIs: 95% confidence intervals

^a99^th percentile of summer months

^b1^st percentile of winter months

^cReferent temperature is the 50th percentile for both summer and winter months.

^†models did not adjust for relative humidity

^††models included a linear adjustment for relative humidity

^*models additionally adjusted for relative humidity as a natural spline with 2 degrees of freedom

^**: models additionally adjusted for relative humidity as a natural spline with 32 degrees of freedom

Figure 3.

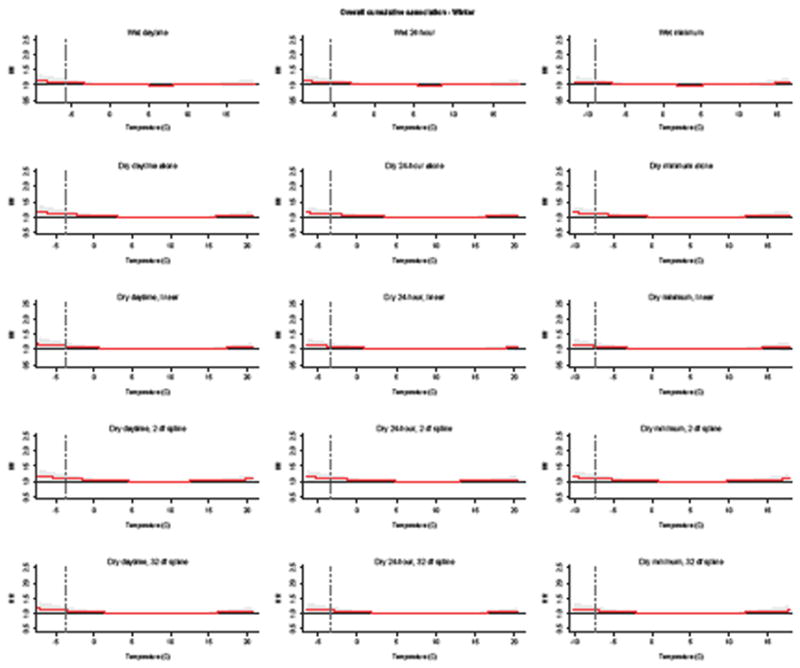
Cumulative relative risk of kidney stone presentations associated with different temperature metrics and humidity adjustment, relative to the 50th percentile for each season.

The number and placement of spline knots were selected using quasi-AIC for each model in A) summer and B) winter. Shaded areas denote the 95% confidence intervals. Vertical dashed line:1st and 99th percentile of each temperature metric in winter and summer periods, respectively.

4. Discussion

In this study, we implemented a two-step procedure to identify the most appropriate temperature metric (among wet-bulb temperatures, heat index, and dry-bulb temperatures with multiple types of adjustments for relative humidity) for predicting kidney stone presentations in South Carolina over a period of 19 years. We first used DLNMs to model the exposure-lag-outcome relationship for alternative daily temperature definitions and then used repeated 10-fold cross-validation to measure the accuracy of each temperature metric to predict the outcome within the dimensions of the exposure and lag. We used quasi-AIC to select the optimal number of knots in the dimensions of temperature and lag for each exposure metric included in the cross-validation to allow each temperature metric to perform at its peak when determining its capacity to predict kidney stone presentations.

Our results demonstrated that moist temperature metrics (wet-bulb temperatures and heat index) were better at predicting kidney stone presentations than dry-bulb temperature metrics, particularly in summer, regardless of type of adjustment for relative humidity. During summer, 24-hour mean wet-bulb temperature was the best predictor of kidney stone presentations. However, the differences in performance among daily wet-bulb temperature metrics, daily heat index metrics, and daytime mean and 24-hour mean dry-bulb temperatures without adjusting for relative humidity were generally small, and the estimated relative risk and confidence intervals for these metrics were generally similar. During winter, daily minimum wet-bulb temperature was the best predictor of kidney stone presentations, though all metrics performed quite similarly.

The better predictive ability estimated for moist temperature metrics suggest that there is a complex interaction between temperature and humidity in determining the risk of kidney stone presentations, and that this relationship is particularly important during periods of high heat. Moreover, when comparing the three dry-bulb models additionally adjusting for humidity in either season, the mean cross-validated residuals became larger as the complexity of the adjustment for relative humidity increased regardless of the dry-bulb temperature metric used. This result is likely an indication that additionally adjusting for humidity in dry-bulb models may be introducing unnecessary noise into the models.

These findings have implications for how best to model humidity in studies of the temperature-dependence of health outcomes that require adjustment for humidity for biological reasons. The issue of temperature and relative humidity is important because of the contributions that temperature and humidity have on heat intensity in urban areas, where 50% of the world’s populations live (Grimm et al., 2008; Zhao et al., 2014). The effect of temperature and humidity on human health, including kidney stone disease, will become more important given the projected increase of global average temperatures by 1 to 4°C during the 21^st century and the expected emergence of heat waves in major cities within the next 50 years (Meinshausen et al., 2011; Mora et al., 2013; Solomon et al., 2007). Considering that wet-bulb temperatures and heat index eliminate the need to model humidity separately, our results suggest that metrics that measure moist temperature stress should be used to estimate the temperature-dependence of kidney stone presentations, but that the particular metric is relatively unimportant. However, there are many metrics that measure moist heat, and the choice of which metric to use depends on the research question and local conditions. In this study, we assessed wet-bulb temperature and heat index, because they can be projected more accurately than other metrics of moist heat stress, such as wet-bulb globe temperatures (Fischer and Knutti, 2013). However, this study was not a comprehensive assessment of all temperature metrics, and it is possible that other temperature metrics that also measure the combination of temperature and humidity may perform similarly (or better) than wet-bulb temperature and/or heat index.

It is likely that temperature is the driving factor in kidney stone presentations given its known exponential relationship with evaporative water loss. However, failing to account for relative humidity (or accounting for it by adjusting for relative humidity in models that include dry-bulb temperature) does not accurately represent the relationship between temperature and kidney stone presentations. During hot, humid South Carolina summers, it is likely that the exponential effect of high temperatures on evaporative water loss overcomes the mitigating effect of high relative humidity, and results in increased kidney stone presentations. This tension between temperature and humidity also exists during cold periods and low relative humidity, but is likely not clinically important. Dry-bulb temperatures do not capture the tension between temperature and relative humidity, which likely contributes to the poorer capacity of these metrics to predict kidney stone presentations, even when adjusting for daily relative humidity. Future research that determines the relative contributions of temperature and relative humidity on kidney stone growth and detachment across the scale of each metric would provide further insight into the causal mechanisms for these associations and the precise relationship between temperature, relative humidity, and kidney stone presentations.

Our findings have implications for improving the accuracy of the risk of nephrolithiasis associated with temperature extremes. These results also raise questions about the inferences drawn from prior studies of the association between temperature and nephrolithiasis, including the 1.6 to 2.2 million new cases of nephrolithiasis that prior studies estimated would result from increases in mean annual dry-bulb temperatures by 2050 (Brikowski et al., 2008). Additionally, the differences in the predictive accuracy for kidney stone presentations between moist temperature metrics and dry-bulb temperatures suggest that the temperature metric that best predicts other health outcomes should be determined prior to defining the precise exposure-response relationship. Such comparisons are important because the magnitude of the association between temperature and a particular health outcome depends on the temperature metric used to model the relationship (Adam-Poupart et al., 2014; Kent et al., 2014; Rodopoulou et al., 2015; Wallace et al., 2005). Using an inappropriate temperature metric may lead to inaccurate estimations of the effect of temperature on human health. These inaccuracies could cause inappropriately premature or dangerously late activation of heat warning systems, thereby decreasing the effectiveness of such public health interventions (Ebi et al., 2004; Rogers et al., 2010). Identifying appropriate temperature metrics will increase the precision of estimates and improve their public health applications.

We acknowledge several limitations of this study. First, misclassification of temperature exposure is possible. As in other ecological studies of the temperature-dependence of health outcomes, we do not know which individuals had access to resources that lessen the effect of heat and cold. However, any misclassification of exposure should be non-differential across the temperature metrics included in our analysis. Second, while we explored different numbers and placements of knots in the natural splines, we did not explore different basis functions. There are many choices of smoothing functions for DLNMs, and there is no consensus in the literature as to what model selection criteria should be used to choose between alternatives (Gasparrini et al., 2010). In this study, we applied the accepted approach of selecting the number of knots for exposure and lag by identifying the model with the lowest quasi-AIC. Given the complex nature of the DLNMs to simultaneously describe the shape of the exposure-response relationship and its associated lag effects, future studies are needed to identify optimal model selection criteria for DLNMs. Third, the question remains of how best to model humidity with respect to lagged effects. The lag for humidity and kidney stone presentation may differ from the temperature-kidney stone relationship, but use of a single metric like wet-bulb temperature or heat idex does not allow for these potential differences. This issue is most relevant for periods of high heat considering that differences were not observed during winter months, where all models performed similarly, and the risk surfaces appear quite flat. Fourth, we assumed that the effect of combination of temperature and humidity on kidney stone presentations was similar across biologically relevant variables, such as age and sex, and across patients with different stone types. Future studies that determine whether such characteristics modify the temperature dependence of kidney stone presentations would complement these results. Finally, these results may not be generalizable to other areas with different climates. South Carolina has a humid subtropical climate with hot, humid summers and mild winters. It is possible that the predictive accuracy of wet-bulb temperatures, heat index, and dry-bulb temperatures would be different in areas that have more temperate, less humid climates. We recommend that future studies define the best temperature metric for kidney stone presentations and other health outcomes in areas with different geography or climates.

5. Conclusions

Our results show that moist heat stress metrics were better at predicting kidney stone presentations in summer than dry-bulb temperature metrics, regardless of type of adjustment for relative humidity. The differences in predictive accuracy among different moist and dry temperature metrics were minimal during winter. These results suggest that metrics that measure moist heat stress should be used to estimate the temperature-dependence of kidney stone presentations, but that the particular metric is relatively unimportant.

Highlights.

• Temperature and relative humidity have opposing effects on evaporative water loss

• Wet-bulb temperatures best predicted kidney stone presentations

• Differences in predictive capacity of temperature metrics were greatest in summer