Methods for Meta-analysis of Multiple Traits using GWAS Summary Statistics

Summary

Genome-wide association studies (GWAS) for complex diseases have focused primarily on single trait analyses for disease status and disease-related quantitative traits. For example, GWAS on risk factors for coronary artery disease analyze genetic associations of plasma lipids such as total cholesterol, LDL-cholesterol, HDL-cholesterol, and triglycerides separately. However, traits are often correlated and a joint analysis may yield increased statistical power for association over multiple univariate analyses. Recently several multivariate methods have been proposed which require individual-level data. Here, we develop metaUSAT, a novel unified association test of a single genetic variant with multiple traits that uses only summary statistics from existing GWAS. While the existing methods either perform well when most correlated traits are affected by the genetic variant in the same direction or are powerful when only a few of the correlated traits are associated, metaUSAT is designed to be robust to the association structure of correlated traits. metaUSAT does not require individual-level data and can test genetic associations of categorical and/or continuous traits. One can also use metaUSAT to analyze a single trait over multiple studies, appropriately accounting for overlapping samples, if any. metaUSAT provides an approximate asymptotic p-value for association and is computationally efficient for implementation at a genome-wide level. Simulation experiments show that metaUSAT maintains proper type-I error at low error levels. It has similar and sometimes greater power to detect association across a wide array of scenarios compared to existing methods, which are usually powerful for some specific association scenarios only. When applied to plasma lipids summary data from the METSIM and the T2D-GENES studies, metaUSAT detected genome-wide significant loci beyond the ones identified by univariate analyses. Evidence from larger studies suggest that the variants additionally detected by our test are, indeed, associated with lipid levels in humans. In summary, metaUSAT can provide novel insights into the genetic architecture of a common disease or traits.

Introduction

Meta-analysis of multiple independent studies is routinely performed to test genetic association of traits by aggregating information on a large number of individuals. Individual data are often not available due to restrictions on data sharing, and hence analysis using summary statistics proves useful. Combining association results from multiple samples of individuals increases statistical power to detect subtle genetic effects. For example, Willer et al. (2013) meta-analyzed lipid traits from 188, 577 individuals in 60 studies and detected 62 genome-wide significant loci that were not previously associated with lipid levels in humans.

While statistical approaches for analysis of individual-level data have moved from the single-trait-single-marker paradigm (e.g., Kang et al., 2010) to multiple markers (e.g., Wu et al., 2011; Ray et al., 2015), multiple traits (e.g., Ferreira and Purcell, 2009; Ray et al., 2016), and multiple markers and traits (e.g., Basu et al., 2013; Wu and Pankow, 2016), standard approaches for meta-analysis have focused on the analysis of a single trait and a single marker. Many complex-disease-related traits are correlated. Joint analysis of traits borrows information across all traits and may increase power to detect genetic associations by increasing effective sample size (Diggle et al., 2002). For individual-level data, many articles have developed and advocated statistical methods for jointly analyzing correlated traits (see Zhou and Stephens, 2014; Majumdar et al., 2015; Ray and Basu, 2017). Porter and O’Reilly (2017) performed a comprehensive comparison of some of these multi-trait methods.

It is only recently that joint meta-analysis of multiple traits using summary statistics has received attention. Stephens (2013) proposed a unified framework for multiple-traits-single-marker analysis using Bayesian model comparison and model averaging for multivariate regression. This framework allows for approximate testing and explaining genetic associations by using summary statistics. Zhu et al. (2015) proposed a general framework for integrating association evidence using GWAS summary statistics. Their framework can accommodate statistics of multiple continuous or categorical traits, correlated or independent, from a single study or multiple studies. Zhu et al. proposed two tests: S_Hom (which assumes equal genetic effect across all traits and studies) and S_Het (which allows for trait heterogeneity). Kim et al. (2015) proposed an adaptive sum of powered score (aSPU) test, which lacks a closed form null distribution and depends on Monte Carlo simulations to evaluate p-values. Cichonska et al. (2016) proposed metaCCA that tests association of multiple traits with multiple markers using canonical correlation analysis (CCA) (Ferreira and Purcell, 2009) framework.

Here, we propose the novel multivariate meta-analysis approach metaUSAT, a unified score based association test for the meta-analysis of multiple traits with a single marker using GWAS summary statistics. Current multivariate meta-analysis methods are powerful under certain association patterns (such as sparsity of signals, or homogeneity of signals), and there is a need for a robust association test. metaUSAT is based on the theoretical and empirical findings of Ray et al. (2016) regarding complimentary power performances of CCA/MANOVA (multivariate analysis of variance) and sum of squared score (SSU) tests (Pan, 2009) for individual-level data. Ray et al. (2016) demonstrated that MANOVA may lose significant power when the genetic marker is associated with all the traits, and any test statistic, such as SSU, that does not include the trait correlation structure can be more powerful in such a situation. On the other hand, MANOVA is usually more powerful than other tests when a subset of the correlated traits is associated. The true underlying association scenario (which varies from one genetic marker to another) is not known, and a fixed choice of association test may not be powerful enough. metaUSAT seeks to maximize power by adaptively combining the MANOVA and the SSU tests based solely on the univariate summary statistics. Although both metaMANOVA (the MANOVA test based on summary statistics) and the SSU tests are chi-squared distributed, metaUSAT does not have a closed form null distribution. However, it does not require compute intensive permutations to evaluate p-values; instead, we calculate an approximate p-value using a fast one-dimensional numerical integral. metaUSAT retains the flavor of Zhu et al.’s statistics by accommodating summary statistics for continuous and/or binary traits, correlated and/or independent, from one or more studies, which may include overlapping samples. Using metaUSAT, one may perform meta-analysis of a single trait over multiple studies, or multiple traits over one or more studies.

Material & Methods

Model and Notation

Consider a single GWAS with data on n individuals, genotyped on p genetic variants, and measured for K traits. Let Y_k be the n × 1 vector of values for the k-th trait and Y be the n × K matrix of all traits for all individuals. For a given SNP, let X_i = 0,1 or 2 be the number of copies of minor alleles for individual i andX be the n×1 vector of genotypes for all individuals. For simplicity, we assume there is no other covariate (note that this assumption can be relaxed easily). For the time being, we are interested in testing association between the SNP and the K correlated traits from a single study.

The usual approach is to test for association of each trait separately and report the summary statistics and the p-values for each trait based on the marginal/univariate model

$${\mathit{Y}}_k={\mathit{\alpha }}_k+{\beta }_k\mathit{X}+{\mathit{\epsilon }}_k,{\mathit{\epsilon }}_k~N_n(\mathbf{0},{\sigma }_k^2{\mathit{I}}_n)\text{for}\text{all}k=1,2,\dots ,K$$ (Equation 1)

for continuous traits, or marginal model

$$\text{logit}\left(P({\mathit{Y}}_k=1\mid \mathit{X})\right)={\mathit{\alpha }}_k+{\beta }_k\mathit{X}\text{for}\text{all}k=1,2,\dots ,K$$ (Equation 2)

for binary traits. For the k-th trait, β_k is the genetic effect and our null hypothesis is H_0,k : β_k = 0. The Wald test statistic for H_0,k is Z_k = β̂_k/ se( β̂_k), where β̂_k is the maximum likelihood estimate (MLE) of β_k and se( β̂_k) is its standard error. Under H_0,k, Z_k has an asymptotic N(0, 1) distribution. However, for k-th and l-th traits, Z_k and Z_l are not independently distributed if the trait correlation is non-zero. In fact, one can show that corr(Z_k, Z_l) ≈ corr(Y_k, Y_l) when the variability in the estimators of β_k and β_l are ignored (Zhu et al., 2015; Kim et al., 2015).

To test the global null hypothesis of no association with any trait H₀ : β₁ = ... = β_K = 0, one can use the summary statistics Z = (Z₁, ...,Z_K)′. Under H₀, Z has an asymptotic multivariate normal distribution with mean 0 and covariance matrix R, where R is the K × K correlation matrix of the original traits. Details on estimating R are provided in a later subsection.

Existing Methods

Here we describe how summary statistics of the K traits for a given SNP can be used to test H₀. Later, we describe how these methods can be used to conduct meta-analysis using summary statistics from multiple GWAS.

minP

The minimum p-value (minP) approach selects the most significant result among the K single trait association tests using the test statistic

$$T_{\text{minP}}=\underset{1\le k\le K}{max}\mid Z_k\mid$$ (Equation 3)

Its asymptotic p-value accounting for correlated Z statistics (Conneely and Boehnke, 2007) is given by

$$p_{\text{minP}}=1-\mathrm{P}\left(max\{\mid Z_1\mid ,\dots ,\mid Z_K\mid \}<t_{\text{minP}}\right)=1-{\int }_{-t_{\text{minP}}}^{t_{\text{minP}}}\dots {\int }_{-t_{\text{minP}}}^{t_{\text{minP}}}{f}_Z(.)d{z}_1\dots d{z}_K$$

where f_Z(.) is the multivariate N_K(0, R̂) density of Z, R̂ is the estimate of R and t_minP is the observed minP statistic. Computation of p_minP requires numerical integration, which can be implemented in R using pmvnorm() in the mvtnorm package (Genz et al., 2016).

metaMANOVA

An alternative is to carry out a joint analysis of all the Z statistics using a test similar to the multivariate score:

$$T_{\text{metaMANOVA}}={\mathit{Z}}^{\prime }{\widehat{\mathit{R}}}^{-1}\mathit{Z}\underset{H_0}{\overset{a}{\sim }}{\chi }_K^2$$ (Equation 4)

We will call this test metaMANOVA because of its similarity to MANOVA statistic in the context of testing multiple trait association with a SNP using individual-level data (Ray et al., 2016). Although multiple authors (Bolormaa et al., 2014; Pausch et al., 2016; He et al., 2016) employed this approach, metaMANOVA’s type I error and power have not been explored previously for stringent significance levels.

S_Hom and S_Het

Zhu et al. (2015) proposed a meta-analysis test S_Hom (similar to O’Brien (1984)’s test for individual-level data):

$$S_{\mathit{Hom}}={\left({\mathbf{1}}^{\prime }{(\widehat{\mathit{R}}\mathit{W})}^{-1}\mathit{Z}\right)}^{\prime }{\left({\mathbf{1}}^{\prime }{(\mathit{W}\widehat{\mathit{R}}\mathit{W})}^{-1}\mathbf{1}\right)}^{-1}\left({\mathbf{1}}^{\prime }{(\widehat{\mathit{R}}\mathit{W})}^{-1}\mathit{Z}\right)\underset{H_0}{\overset{a}{\sim }}{\chi }_1^2$$ (Equation 5)

where W is a diagonal matrix of weights for the Z-statistics. Zhu et al. (2015) took sample sizes for the weights. S_Hom achieves maximum power when the genetic effects for all traits are equal and in the same direction. Zhu et al. proposed a second statistic S_τ, which seeks to include only Z statistics corresponding to traits with non-zero genetic effects: $S_{\tau }={\left({\mathbf{1}}_{\tau }^{\prime }{({\widehat{\mathit{R}}}_{\tau }{\mathit{W}}_{\tau })}^{-1}{\mathit{Z}}_{\tau }\right)}^{\prime }{\left({\mathbf{1}}_{\tau }^{\prime }{({\mathit{W}}_{\tau }{\widehat{\mathit{R}}}_{\tau }{\mathit{W}}_{\tau })}^{-1}{\mathbf{1}}_{\tau }\right)}^{-1}\left({\mathbf{1}}_{\tau }^{\prime }{({\widehat{\mathit{R}}}_{\tau }{\mathit{W}}_{\tau })}^{-1}{\mathit{Z}}_{\tau }\right)$, where, for a given τ > 0, Z_τ is the sub-vector of Z satisfying |Z_k| > τ and the sub-matrices W_τ, R̂_τ, 1_τ are defined similarly. For large enough τ, it is possible to have all |Z_k| < τ. In this scenario, set S_τ = 0. Zhu et al. define the test statistic

$$S_{\mathit{Het}}=\underset{\tau >0}{max}{S}_{\tau }$$ (Equation 6)

The null distribution for S_Het can be approximated by a gamma distribution and p-value estimated using simulations in Zhu et al.’s R program CPASSOC.

aSPU and SSU

Kim et al. (2015) defined the Sum of Powered Score (SPU) test as $\mathit{SPU}(\gamma )={\sum }_{k=1}^K{Z}_k^{\gamma }$, where γ is a positive integer. They constructed multiple SPU(γ) tests, with γ values 1, 2, ...,8 or ∞, that put more weight on traits with larger Z statistics as γ increases. Kim et al. showed that SPU(1) = S_Hom. SPU(2), also known as the Sum of Squared Score (SSU) statistic, is approximately distributed as $a{\chi }_d^2+b$ under H₀, where a, b, d can be estimated from R̂ (Pan, 2009). The aSPU test adaptively selects the SPU test with minimum p-value. The SPU(γ) statistics for γ > 2, and hence the aSPU statistic, do not have closed form null distributions and require Monte Carlo simulations to estimate p-values.

Proposed Method: metaUSAT

In the presence of individual-level data, Ray et al. (2016) proposed a unified score-based association test (USAT) to analyze association of multiple traits with a single SNP. USAT seeks to maximize power by adaptively combining SSU (well suited to scenarios when most or all traits have non-zero genetic affects) and MANOVA (well-suited to most scenarios unless most or all traits are associated). Here, we propose metaUSAT, a meta-analysis version of USAT, that can be calculated using univariate summary statistics. We consider the weighted statistic T_ω = ωT_metaMANOVA + (1 − ω)T_SSU, ω ∈ [0, 1], where T_SSU = Z′Z is the SSU test statistic. Since T_metaMANOVA and T_SSU have asymptotic chi-square distributions under H₀, for a given weight ω, T_ω is approximately distributed as a linear combination of (potentially dependent) chi-squared variables. The p-value p_ω of T_ω can be calculated using many algorithms (e.g., Davies, 1980; Liu et al., 2009). We define metaUSAT as the weighted combination with the most significant p-value:

$$T_{\text{metaUSAT}}=\underset{\omega \in [0,1]}{min}{p}_{\omega }$$ (Equation 7)

We consider a grid of 11 equi-spaced values of ω from 0 to 1, and approximate the corresponding p-value using a fast one-dimensional numerical integral (see Supplementary S1).

Estimation of R and its Effect on metaUSAT

To estimate the trait correlation matrix R, we use the Z-statistics of the SNPs which are not associated with any of the K traits (i.e., SNPs with p-values greater than a pre-defined significance threshold, say 10⁻⁵, for any trait). Zhu et al. (2015) showed that under the null hypothesis of no association, the correlation matrix of the univariate summary statistics (obtained by calculating the sample correlation matrix R̂ of the Z’s over a large number of null SNPs) is the same as the trait correlation matrix. This result holds even in the presence of covariates in Equation 1 or Equation 2 (Liu and Lin, 2017).

It is noteworthy that the performance of metaUSAT and the other afore-mentioned summary statistic based tests depends on the estimation of R. In a GWAS, we expect most SNPs to be not associated with any trait, and these null SNPs can be conveniently used to estimate R. However, as pointed out by one reviewer, recent evidence from heavily studied complex traits such as height and schizophrenia seems to suggest that these traits are highly polygenic. Consequently, a large portion of the genome in linkage disequilibrium (LD) with the causal variants is also associated with the traits. For the joint analysis of such highly polygenic complex traits using summary statistics, the relation corr(Z_k, Z_l) ≈ corr(Y_k, Y_l) may not be valid and the estimate of R will be affected. The extent to which this misspecified R affects the validity of the tests depends on the strength of association (of the non-null SNPs used to estimate R) as well as on the structure of the test statistic. Our simulation experiments (see Supplementary S4) show that if non-null SNPs with low to moderate strengths of association are used to estimate R, the type I error estimates for metaUSAT and minP are largely unaffected while S_Hom, S_Het and metaMANOVA may be heavily affected. It seems to us that test statistics that directly incorporate R (e.g., metaMANOVA) are heavily affected by its misspecification while test statistics incorporating R indirectly only through its null distribution (e.g., minP) are mostly unaffected. The validity of metaUSAT (a data-adaptive minimum p-value approach) is largely unaffected by misspecified estimate of R arising due to polygenicity of traits. It is important to mention that our conclusion is based on a limited simulation experiment. It is beyond the scope of this paper to explore this aspect in more detail.

Extension to Meta-analysis of Multiple GWAS

Consider summary statistics Z_jk for association with a given SNP for trait k (k = 1, 2, ...,K) from study j (j = 1, 2, ..., J). Some or all J studies may or may not have overlapping samples. Let Z_j be the vector of K summary statistics for study j, Z be the JK×1 vector of summary statistics from all traits across all studies, and β be the corresponding JK×1 vector of effect sizes. We wish to test H₀ : β = 0 against the two-sided alternative that at least one of the traits has non-zero genetic effect in at least one of the studies.

For k-th and l-th traits from two studies j and j′, Lin and Sullivan (2009) showed that $\text{corr}(Z_{jk},Z_{j^{\prime }l})\approx \frac{n_{j{j}^{\prime },kl}}{\sqrt{n_{jk}{n}_{j^{\prime }l}}}\text{corr}(Y_{jk},Y_{j^{\prime }l})$, where n_jj′,kl is the number of overlapping samples, and n_jk & n_j′l are the sample sizes in the two studies. When the studies are independent (n_jj′,kl = 0), summary statistics from the two studies are uncorrelated.

For the perfect overlap scenario (n_jj′,kl = n_jk = n_j′l), the correlation of summary statistics is approximately same as the correlation of the traits (same as that of a single study with multiple traits). We estimate the JK × JK correlation matrix R from the JK Z-statistics for the SNPs that do not exceed a pre-defined significance threshold (say, p-value = 10⁻⁵) for any trait. The formulation of the Z statistic and the estimation of its correlation in this fashion addresses cryptic relatedness arising from overlapping samples in the studies (Zhu et al., 2015; Kim et al., 2015). Once Z and R are defined, we can use any of the existing methods and metaUSAT.

When meta-analyzing across studies, different studies may have varying sample sizes. Since sample sizes may vary widely across traits and/or studies, we suggest weighting the univariate summary statistics by the corresponding sample sizes. If n_jk is the sample size for trait k in study j, we use weighted statistics $\sqrt{n_{jk}}{Z}_{jk}$ to put more weights on statistics coming from larger studies. Note that this weighting scheme is incorporated in S_Hom (Equation 5) and S_Het (Equation 6) statistics.

Simulation Experiments

We conduct simulation experiments to assess type I error and compare power of metaUSAT and the existing methods. For type I error simulations, we consider significance levels α = 10⁻², 10⁻³, . . . , 10⁻⁶, 5 × 10⁻⁷. For power simulations, we report empirical powers, based on corrected critical values, at level α = 10⁻⁴. All analyses used the estimated R based on summary statistics across null replicates.

Simulation 1: A single study

We generated single study of n = 1, 000 unrelated individuals, each measured for K = 5 or 10 traits and a bi-allelic SNP X with MAF 0.1 at Hardy-Weinberg equilibrium. For each individual, we simulate K phenotypes using a multivariate normal linear model: Y _K×1 = β₀1_K×1+Xβ_K×1+ε_K×1 where β₀ = 1 and the error ε is simulated from N_K(0, σ²R(ρ)). We took R(ρ) as an exchangeable correlation matrix with pair-wise correlation ρ ∈ {0.2, 0.4, 0.6}. For type I error simulations, the genetic effects β are 0 for all K traits. For power simulations, we choose the genetic effect β_k for an associated trait so that the SNP explains 0.5% of the trait variance (k = 1, 2, ...,K). This, alongwith the MAF of the SNP, determines the genetic effect sizes (see Basu et al., 2013, ‘Simulations’). We took positive direction of the effect size for all associated traits. The total variance of an associated trait is fixed at 10, which ensures that the variance due to SNP is 0.05 while the residual variance is σ² = 9.95. We wish to test H₀ : β = 0.

Based on 10⁸ null datasets, we estimate type I error of S_Hom, S_Het, minP, metaMANOVA and metaUSAT as the proportion of null datasets that give p-value ≤α. Our literature search did not yield any article where type I errors of all these summary-statistic-based multivariate methods are studied at a level as low as 5×10⁻⁷. We do not consider aSPU for type I error analysis because it requires Monte Carlo simulations, making calculations for 10⁸ datasets computationally undesirable. For comparing statistical powers of all methods (including aSPU), we simulate 10⁴ non-null datasets assuming 20% to 100% of the traits are positively associated with the SNP. To avoid clutter, we are not including SSU (a special case of aSPU) in any of these comparisons.

Simulation 2: Two independent studies

We consider two independent studies of 1, 000 independent individuals, each with measurements on a single SNP with MAF 0.1 and 4 traits inspired by the METSIM lipids data on total cholesterol (TC), high-density lipoprotein (HDL), low-density lipoprotein (LDL) and triglycerides (TG). We use the trait correlation matrix R_metsim (Figure S1(a)) to simulate the 4 traits using the model described in Simulation 1. We consider 5 association scenarios: (i) only TC is associated, (ii) TC and LDL are associated, (iii) TC, LDL and TG are associated, (iv) all 4 traits are associated, and (v) none of the traits is associated. As before, the SNP explains 0.5% of the trait variance when associated. We assume TC, LDL and TG have negative genetic effects while HDL has positive effect when associated. We simulate two study types: “homogeneous” and “heterogeneous”. For “homogeneous” studies, the association pattern of the traits is same across both studies. For “heterogeneous” studies, we assume association scenarios (i)-(iv) in the first study while the traits are not associated (scenario (v)) in the second study. Figure S1(c) shows the estimated correlation matrix. For type I error analysis, we assume scenario (v) for both studies and simulate 10⁷ null datasets.

Simulation 3: Two studies with overlapping samples

We keep everything the same as in Simulation 2 except that the two studies now have 200 overlapping individuals. For “homogeneous” studies, we assume the association pattern is same across the two studies. For “heterogeneous” studies, excluding the overlap, we assume the association scenarios (i)-(iv) in one study while the traits are not associated (scenario (v)) in the other study. For individuals common to both studies, we assume scenario (v). Figure S1(d) shows the estimated correlation matrix, which is similar to the correlation structure of lipid traits from the METSIM and T2D-GENES studies (Figure S1(b)).

Application to Lipids Data

METSIM Study

The METSIM Study is a single-site, longitudinal study of 10, 197 men (aged 45 − 73 years) randomly selected from the population of Kuopio, Finland (Stančáková et al., 2009). Participants were genotyped with the Illumina OmniExpress GWAS chip and the Illumina exome chip. Here we focus on the association statistics of four lipid traits from the first visit: TC, HDL, LDL, TG. Before obtaining the summary statistics, individuals on lipid-lowering medication are removed and TG is log-transformed. The traits are, then, regressed on age and age², and residuals are inverse-normalized. We focus on 622, 950 autosomal SNPs with MAF ≥ 1%. We used kinship matrix in the mixed model framework of EMMAX (Kang et al., 2010) to account for within-ancestry population structure and relatedness.

T2D-GENES Study

The T2D-GENES consortium carried out exome sequencing on 6, 504 T2D cases and 6, 436 controls from five ancestry groups (Fuchsberger et al., 2016). Here, we consider the 4, 541 individuals of European origin, 983 of which are part of the METSIM study sample. As before, we focus on the four lipid traits. Exclusions, transformations and analysis parallel those for the METSIM lipid traits. Here, we also adjusted sex as a covariate.

Results

Simulation 1: A single study

The type I error estimates of metaUSAT and other methods are presented in Table 1. Regardless of the number of traits and the strength of trait correlations, all methods control type I error for moderate levels (α ≥ 10⁻⁴). For more stringent levels, we observe slightly inflated type I errors for all methods except S_Hom. The inflation seems to increase with increase in number of traits. We note that type I error of metaUSAT is worst at α = 5×10⁻⁷; in what follows we correct for this by computing power using empirical threshold. The empirical threshold is based on 10⁵ null replicates.

Table 1.

Simulation 1: Type I error estimates at various levels α. This table lists the type I error estimates divided by the significance level α and the corresponding 100(1 − α)% confidence intervals in brackets. The ideal point estimate for any cell is 1. Estimates are based on 10⁸ null datasets, each with K traits, 1 SNP and sample size 1, 000.

Level α	Method	K = 5			K = 10
		ρ= 0.2	ρ = 0.4	ρ = 0.6	ρ = 0.2	ρ = 0.4	ρ = 0.6
10−2	SHom	0.95 [0.95, 0.95]	1.00 [1.00, 1.00]	1.03 [1.03, 1.03]	1.00 [1.00, 1.00]	1.07 [1.07, 1.07]	1.01 [1.01, 1.01]
	SHet	1.05 [1.05, 1.05]	1.05 [1.04, 1.05]	0.98 [0.98, 0.98]	1.01 [1.01, 1.01]	1.06 [1.06, 1.06]	1.02 [1.01, 1.02]
	minP	1.03 [1.03, 1.03]	1.03 [1.03, 1.03]	1.02 [1.02, 1.02]	1.04 [1.04, 1.04]	1.03 [1.03, 1.03]	1.03 [1.03, 1.03]
	metaMANOVA	1.05 [1.05, 1.05]	1.05 [1.04, 1.05]	0.98 [0.98, 0.98]	1.04 [1.04, 1.04]	0.97 [0.97, 0.97]	1.06 [1.06, 1.06]
	metaUSAT	0.82 [0.82, 0.82]	0.92 [0.92, 0.92]	0.93 [0.93, 0.93]	0.93 [0.93, 0.93]	1.01 [1.01, 1.01]	1.06 [1.06, 1.06]
10−3	SHom	0.93 [0.93, 0.93]	1.00 [1.00, 1.00]	1.03 [1.03, 1.03]	1.00 [1.00, 1.00]	1.11 [1.11, 1.12]	1.02 [1.02, 1.03]
	SHet	1.11 [1.10, 1.11]	1.12 [1.11, 1.12]	1.02 [1.02, 1.02]	1.01 [1.01, 1.02]	1.10 [1.09, 1.10]	1.02 [1.02, 1.03]
	minP	1.05 [1.05, 1.06]	1.05 [1.05, 1.06]	1.05 [1.05, 1.06]	1.07 [1.07, 1.08]	1.06 [1.06, 1.06]	1.07 [1.07, 1.07]
	metaMANOVA	1.09 [1.09, 1.10]	1.08 [1.08, 1.08]	0.99 [0.99, 1.00]	1.08 [1.07, 1.08]	0.98 [0.98, 0.98]	1.11 [1.11, 1.12]
	metaUSAT	0.90 [0.90, 0.90]	1.00 [1.00, 1.00]	1.02 [1.01, 1.02]	1.05 [1.05, 1.05]	1.13 [1.12, 1.13]	1.19 [1.18, 1.19]
10−4	SHom	0.90 [0.89, 0.91]	1.00 [1.00, 1.00]	1.09 [1.08, 1.10]	1.01 [1.00, 1.02]	1.17 [1.16, 1.18]	1.04 [1.03, 1.05]
	SHet	1.18 [1.17, 1.19]	1.22 [1.21, 1.23]	1.09 [1.08, 1.10]	1.04 [1.03, 1.05]	1.14 [1.13, 1.15]	1.05 [1.04, 1.06]
	minP	1.10 [1.09, 1.11]	1.10 [1.09, 1.11]	1.13 [1.12, 1.14]	1.13 [1.12, 1.14]	1.11 [1.10, 1.12]	1.13 [1.12, 1.14]
	metaMANOVA	1.14 [1.13, 1.15]	1.13 [1.12, 1.14]	1.03 [1.02, 1.04]	1.11 [1.10, 1.12]	0.99 [0.98, 1.00]	1.17 [1.16, 1.18]
	metaUSAT	1.21 [1.20, 1.22]	1.29 [1.28, 1.30]	1.18 [1.17, 1.19]	1.59 [1.58, 1.61]	1.49 [1.48, 1.51]	1.39 [1.38, 1.40]
10−5	SHom	0.88 [0.85, 0.91]	1.00 [0.97, 1.03]	1.12 [1.09, 1.15]	1.07 [1.03, 1.10]	1.28 [1.25, 1.32]	1.11 [1.08, 1.14]
	SHet	1.31 [1.27, 1.34]	1.36 [1.32, 1.40]	1.17 [1.14, 1.21]	1.12 [1.09, 1.16]	1.27 [1.23, 1.31]	1.12 [1.09, 1.16]
	minP	1.14 [1.10, 1.17]	1.16 [1.12, 1.19]	1.30 [1.27, 1.34]	1.23 [1.20, 1.27]	1.13 [1.09, 1.16]	1.25 [1.21, 1.28]
	metaMANOVA	1.17 [1.14, 1.20]	1.16 [1.12, 1.19]	1.03 [1.00, 1.06]	1.19 [1.16, 1.23]	1.03 [1.00, 1.06]	1.31 [1.27, 1.34]
	metaUSAT	1.38 [1.35, 1.42]	1.45 [1.41, 1.49]	1.28 [1.25, 1.45]	1.92 [1.88, 1.97]	1.74 [1.70, 1.79]	1.58 [1.54, 1.62]
10−6	SHom	0.80 [0.71, 0.89]	0.92 [0.82, 1.02]	1.11 [1.00, 1.22]	1.12 [1.01, 1.23]	1.49 [1.37, 1.61]	1.26 [1.15, 1.38]
	SHet	1.44 [1.32, 1.56]	1.43 [1.31, 1.55]	1.26 [1.15, 1.37]	1.21 [1.10, 1.32]	1.47 [1.35, 1.59]	1.26 [1.15, 1.38]
	minP	1.31 [1.20, 1.42]	1.27 [1.16, 1.38]	1.64 [1.51, 1.77]	1.30 [1.19, 1.41]	1.16 [1.05, 1.27]	1.45 [1.33, 1.57]
	metaMANOVA	1.19 [1.08, 1.30]	1.10 [0.99, 1.21]	1.00 [0.90, 1.10]	1.32 [1.21, 1.43]	1.23 [1.12, 1.34]	1.54 [1.42, 1.66]
	metaUSAT	1.46 [1.34, 1.58]	1.48 [1.36, 1.60]	1.33 [1.22, 1.45]	2.38 [2.23, 2.53]	2.21 [2.06, 2.36]	2.08 [1.94, 2.22]
5 × 10−7	SHom	0.72 [0.60, 0.84]	0.82 [0.69, 0.95]	1.00 [0.86, 1.14]	1.20 [1.05, 1.35]	1.50 [1.33, 1.67]	1.25 [1.09, 1.41]
	SHet	1.30 [1.14, 1.46]	1.42 [1.25, 1.59]	1.32 [1.16, 1.48]	1.30 [1.14, 1.46]	1.38 [1.21, 1.55]	1.17 [1.02, 1.32]
	minP	1.46 [1.29, 1.63]	1.30 [1.14, 1.46]	1.90 [1.71, 2.10]	1.42 [1.25, 1.59]	1.08 [0.93, 1.23]	1.64 [1.46, 1.82]
	metaMANOVA	1.20 [1.05, 1.36]	1.25 [1.09, 1.41]	1.15 [1.00, 1.30]	1.32 [1.16, 1.48]	1.20 [1.05, 1.35]	1.62 [1.44, 1.80]
	metaUSAT	1.54 [1.36, 1.72]	1.74 [1.55, 1.92]	1.54 [1.36, 1.71]	2.52 [2.30, 2.74]	2.42 [2.20, 2.64]	2.18 [1.97, 2.39]

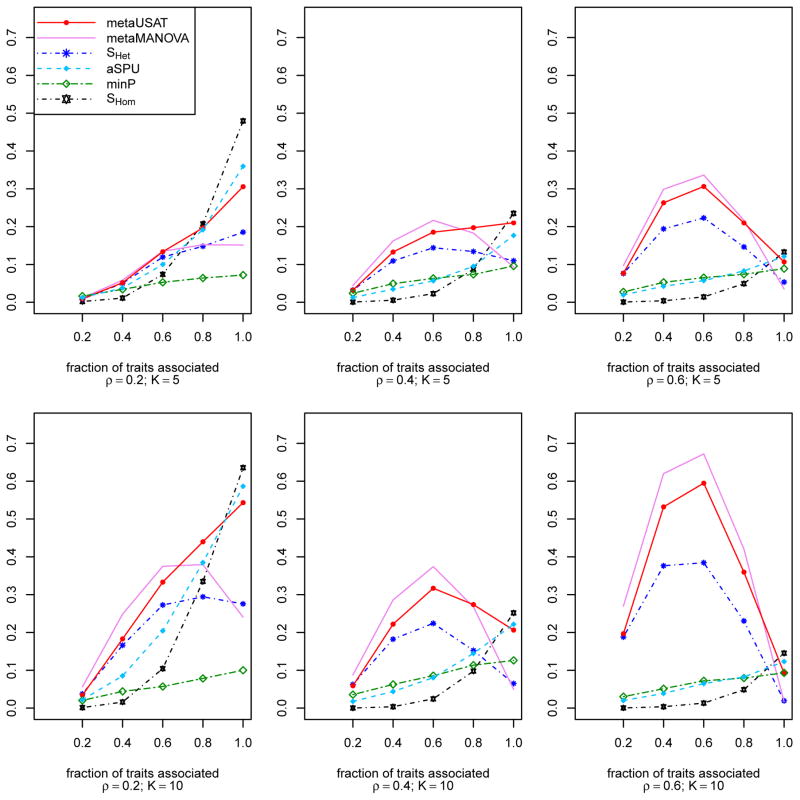
Figure 1 summarizes the empirical powers (based on corrected critical values) of all methods. We observe that as correlation becomes stronger and the number of associated traits increase, S_Hom, minP and aSPU lose power in most association scenarios. S_Het is dominated by metaMANOVA, which is usually most powerful. However, metaMANOVA loses power considerably as the proportion of associated traits increases. This phenomenon of metaMANOVA’s power loss is the same as what Ray et al. (2016) observed for MANOVA (for analyzing individual-level data) and provided an explanation for. When most or all of the traits are associated, aSPU and S_Hom are quite powerful. Irrespective of the number of associated traits and the strength of correlation, metaUSAT, being data-adaptive, has near optimal power to detect association at all scenarios. Results for marker with MAF 0.5 (not shown) are qualitatively similar. Apart from exchangeable correlation, we also consider an AR1(ρ) correlation structure (auto-regressive correlation matrix of order 1 with parameter ρ) and, as before, we find metaUSAT’s power to be robust across association scenarios (Figure S2).

Figure 1.

Simulation 1: Empirical power curves (based on corrected critical values) of S_Hom, S_Het, metaMANOVA, metaUSAT, minP and aSPU at significance level α = 10⁻⁴. Power estimates are based on 10⁴ datasets with 1, 000 unrelated samples. Each sample has K = 5 or 10 traits with pairwise trait correlations ρ = 0.2, 0.4 or 0.6.

Simulation 2: Two independent studies

The estimated correlation matrix, based on 5, 000 null summary statistics, is given in Figure S1(c). Figures S1(a) and S1(c) show that trait correlations can be approximated by the correlations of summary statistics. Type I error estimates (Table S1) indicate all methods control type I error for low error levels. Table 2 suggests S_Het, metaMANOVA, and metaUSAT are usually most powerful. metaMANOVA and metaUSAT have similar powers. S_Hom and minP are least powerful in most cases. aSPU is least powerful when a small proportion of traits is associated. Results for MAF 0.5 (not shown) are qualitatively similar. We also conducted this power comparison for binary traits and found metaUSAT to be robust across association scenarios (Table S4).

Table 2.

Simulation 2: Comparison of empirical powers (based on corrected critical values) for two independent studies at level α = 10⁻⁴. Power is estimated based on 10⁴ non-null datasets. For a given association scenario, the method with highest power is bold-faced and the method with lowest power is italicized.

Study type	No. of traits associated	Meta-analysis method
		SHom	SHet	minP	aSPU	metaMANOVA	metaUSAT
	1	0.999	0.923	0.034	0.009	1.000	1.000
Homogeneous	2	0.000	0.111	0.046	0.082	0.151	0.133
	3	0.306	0.254	0.078	0.364	0.250	0.285
	4	0.009	0.725	0.100	0.387	0.665	0.632
	1	0.357	0.661	0.019	0.004	0.995	0.992
Heterogeneous	2	0.000	0.016	0.024	0.019	0.023	0.020
	3	0.017	0.036	0.035	0.044	0.038	0.045
	4	0.001	0.194	0.050	0.068	0.159	0.141

Simulation 3: Two studies with overlapping samples

Type I error estimates (Table S2) are as expected from the earlier type I error analyses. Empirical powers (Table 3) of the methods in the presence of overlapping samples are similar to the simulation without shared individuals (Table 2). We observed similar conclusions when this power comparison is conducted for binary traits (Table S5).

Table 3.

Simulation 3: Comparison of empirical powers (based on corrected critical values) for two studies with overlapping samples at level α = 10⁻⁴. Power is estimated based on 10⁴ non-null datasets. For a given association scenario, the method with highest power is bold-faced and the method with lowest power is italicized.

Study type	No. of traits associated	Meta-analysis method
		SHom	SHet	minP	aSPU	metaMANOVA	metaUSAT
	1	0.984	0.852	0.034	0.018	1.000	1.000
Homogeneous	2	0.000	0.048	0.051	0.099	0.083	0.093
	3	0.244	0.127	0.077	0.300	0.146	0.216
	4	0.005	0.485	0.103	0.435	0.456	0.472
	1	0.101	0.495	0.006	0.001	0.865	0.807
Heterogeneous	2	0.000	0.004	0.009	0.006	0.007	0.006
	3	0.007	0.009	0.011	0.012	0.012	0.012
	4	0.001	0.038	0.018	0.026	0.041	0.034

METSIM Study: Joint analysis of lipid traits

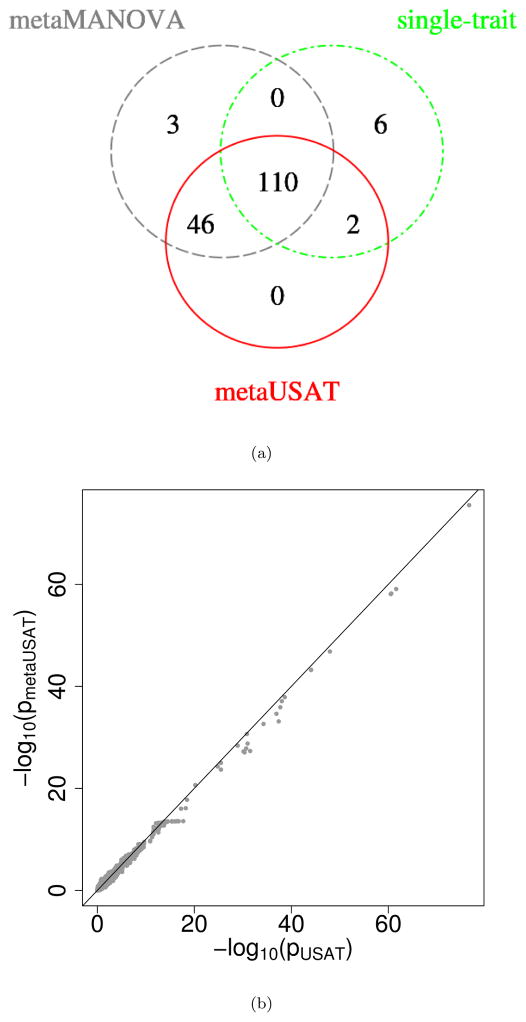
Single-trait analysis identified 118 associated variants at the 4-trait Bonferroni corrected threshold of 1.25×10⁻⁸ (Figure 2(a)). metaMANOVA and metaUSAT respectively identified 159 and 158 associated variants at threshold 5 × 10⁻⁸. To identify independent association signals, we grouped significant variants (with pairwise distance < 500 kb) into loci using LD r² > 0.1. Both metaMANOVA and metaUSAT identified 28 such independent loci, 27 of which (except rs3093032, a 3′-UTR variant in ICAM1 gene) are known to be associated with lipids from published literature (Table S6). Additionally, we jointly analyzed individual-level data on these lipid traits using USAT. Figure 2(b) shows concordance of p-values based on individual-level data and p-values based on summary statistics.

Figure 2.

METSIM Study: (a) Venn Diagram of the number of SNPs (and not independent loci) found significant by each of metaUSAT, metaMANOVA and single-trait analyses. A total of 622, 950 SNPs (MAF ≥ 1%) are tested. For the single-trait analysis, a variant is declared as significant if its p-value for at least one trait is < 1.25×10⁻⁸ (4-trait Bonferroni corrected GWAS threshold). It should be noted that most of these significant SNPs are in LD. (b) metaUSAT p-values (joint analysis based on summary data) plotted against USAT p-values (joint analysis based on individual-level data).

METSIM + T2D-GENES Studies: Meta-analysis of a single trait from studies with overlapping samples

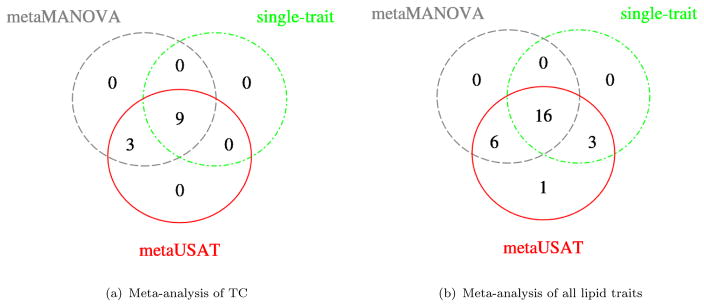
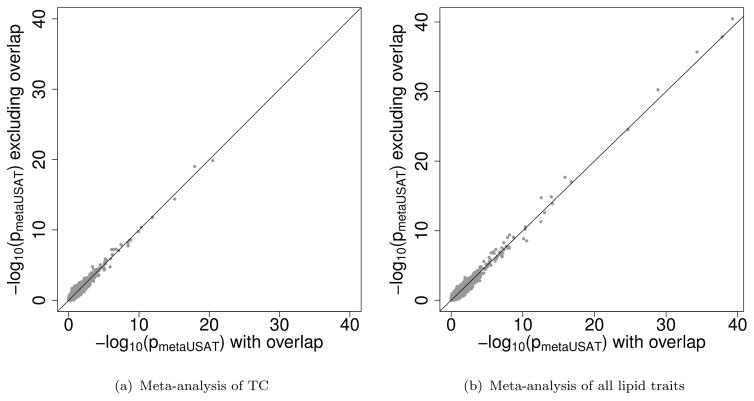
We tested genetic associations of TC with 31, 897 variants (MAF ≥ 1%) using summary statistics from METSIM and T2D-GENES studies. metaUSAT, metaMANOVA and single-trait analyses respectively found 12, 12 and 9 SNPs as significant (Figure 3(a)). Published literature indicate that signals identified by metaUSAT (or metaMANOVA) are known to be associated with cholesterol levels (Table S7). Figure 4(a) plots the metaUSAT p-values when overlap is present against metaUSAT p-values when the overlapping individuals are excluded from the METSIM sample. Concordance of the p-values suggest metaUSAT appropriately accounted for overlapping samples.

Figure 3.

METSIM+T2D-GENES Studies: Venn Diagram of the number of SNPs (and not independent loci) found significant by each of metaUSAT, metaMANOVA and single-trait analyses. A total of 31, 897 SNPs (MAF ≥ 1%) are tested. For the single-trait analysis, a variant is declared as significant if its p-value for at least one trait is < 1.25×10⁻⁸ (4-trait Bonferroni corrected GWAS threshold). It should be noted that most of these significant SNPs are in LD.

Figure 4.

METSIM+T2D-GENES Studies: metaUSAT p-values, with the overlapping individuals in the two studies, are plotted on the x-axis, while metaUSAT p-values after removing the overlap from METSIM are plotted on the y-axis.

METSIM + T2D-GENES Studies: Joint meta-analysis of lipid traits from studies with overlapping samples

metaUSAT, metaMANOVA and single-trait analysis respectively found 26, 22 and 19 SNPs as significant (Figure 3(b)). metaMANOVA and metaUSAT detected more signals by borrowing information from correlated traits across studies. All of the signals found by both metaMANOVA and metaUSAT are known to be associated with lipid levels in humans from previous studies (Table S8). All the SNPs detected by metaMANOVA and by independent analysis of each trait were identified by metaUSAT. Further, metaUSAT exclusively reports 4 significant SNPs (of which 3 are independent) that metaMANOVA fails to find (Table 4). For these SNPs, we also report the empirical p-values (calculated using 8.5 × 10⁹ Monte Carlo simulations) to ensure these are not false associations detected as a result of slightly inflated type I error of metaUSAT at stringent error levels. Details of this empirical p-value calculation of metaUSAT are provided in Supplementary S2. Finally, in Figure 4(b), we again observe concordance of metaUSAT p-values with and without shared individuals.

Table 4.

T2D-GENES + METSIM Studies: Meta-analysis of all 4 lipid traits. This table lists the SNPs exclusively detected by metaUSAT only. Only the independent SNPs (pairwise distance > 500 kb and r² < 0.1) are listed. We also report the empirical p-values of metaUSAT based on 8.5 × 10⁹ Monte Carlo simulations. P-values exceeding the genome-wide threshold of 5 × 10⁻⁸ have been bold-faced. The known association results are based on previously reported GWAS associations within 500 kb of and r² > 0.7 with any of our SNPs from the NHGRI GWAS catalog (Welter et al., 2014) and our in-house GWAS catalog.

rsID	chr	position	p-value		empirical p-value metaUSAT	Known association result
			meta-USAT	meta-MANOVA
rs2483205	1	55518316	2.5 × 10−8	1.1 × 10−7	3.2 × 10−8	Lipids, Lipoprotein fractions1
rs1367117†	2	21263900	1.5 × 10−9	2.3 × 10−7	2.8 × 10−9	Lipids, Lipoprotein fractions2
rs2304130	19	19789528	1.5 × 10−9	1.8 × 10−6	3.3 × 10−9	Lipids, Lipoprotein fractions, T2D3

¹near many known GWAS hits for lipids (Surakka et al., 2015), lipoprotein fractions (Kettunen et al., 2012), cardiovascular endpoints (Kathiresan et al., 2009).

^†Illumina OmniExpress Exome Chip ID is exm176096.

²known GWAS hit for lipids (Teslovich et al., 2010; Willer et al., 2013; Surakka et al., 2015)

³known GWAS hit for lipids (Kristiansson et al., 2012; Willer et al., 2013)

Discussion

MostGWAS have focused on testing genetic association to single traits. Several recent articles have advocated the joint analysis of multiple traits for improving statistical power to detect associated genetic variants. In this article, we propose a new method for multivariate meta-analysis, metaUSAT, an extension of our multivariate association test USAT (Ray et al., 2016). For a given genetic variant, metaUSAT tests the association of multiple traits from a single/multiple studies using univariate summary statistics. Importantly, it bypasses the need for individual-level data, which is often unavailable or difficult to obtain.

Our simulation experiments and real data analyses establish that metaUSAT is often more powerful than any of the existing tests for multivariate meta-analysis. It can be especially advantageous in detecting highly pleiotropic variants that simultaneously influence multiple traits. Apart from proposing new method metaUSAT, we also study power and type I error performances of metaMANOVA and other summary-statistic-based multi-trait methods at stringent error levels. metaUSAT and metaMANOVA can accurately control type I error for moderate α levels, but produce slightly inflated type I error rates at very small α levels (like the other methods). We found that metaMANOVA has a serious drawback: it may fail to detect association when most or all traits are associated (this behavior explored by Ray et al. (2016) in detail). The joint analysis of all lipid traits using METSIM and T2D-GENES studies further confirmed this. The power of metaMANOVA (and other multivariate tests) depends on a complex interplay of the number of truly associated traits, their correlation structure and the directions of the signals. The underlying association scenario changes from one variant to another, and is not known a priori for any real dataset. There is no uniformly most powerful multivariate test, and a particular choice of association test may not be powerful enough to detect true signals. metaUSAT, being data-adaptive in nature, is less affected by the true (unknown) association scenario, and proves to be a robust yet computationally efficient choice for investigators.

The assumption of equal genetic effects across traits and across studies is hardly tenable, making S_Hom unlikely to be powerful, especially when there is a moderate to large number of traits. aSPU relies on compute intensive p-value calculation approach, which is not feasible when analyzing large GWAS data. S_Het is usually dominated by metaMANOVA. On the other hand, metaUSAT is at least as powerful as metaMANOVA and a fast p-value calculation approach makes it suitable for testing genetic associations across multiple traits from multiple large-scale genome wide studies. Power of metaUSAT is robust to the proportion of associated traits. To alleviate any concern of inflated association signals of metaUSAT at stringent levels, we can calculate empirical metaUSAT p-values (as described in Supplementary S2). This need not be done for all variants; instead we can focus only on the handful of variants that have metaUSAT p-values just crossing the chosen threshold.

metaUSAT can be used in a few different ways. We can test association of one or more traits from a single or multiple studies, which may or may not be independent. metaUSAT does not assume homogeneity of trait effects across studies. If the studies are nearly independent and the trait effects are believed to be homogeneous across studies, we can use meta-analyzed summary statistics for each trait (e.g., Z-statistic output from METAL (Willer et al., 2010)) to perform joint meta-analysis of multiple traits. metaUSAT, also, does not require the independence of samples. When samples are related (e.g., in family-based GWAS), metaUSAT can use summary statistics from EMMAX (or other univariate mixed model framework) to appropriately test for genetic associations.

A potentially important contribution of metaUSAT can be in the emerging field of phenome wide association studies (PheWAS) based on epidemiological cohorts. PheWAS systematically analyzes the impact of a genetic variant on a wide variety of human traits. Restrictions on data sharing necessitate use of meta-analysis for PheWAS (Bush et al., 2016). In this age of using publicly available data for increasing power and decreasing sequencing costs, overlapping samples may be a concern when it comes to meta-analysis. Furthermore, current single-trait meta-analysis approach for PheWAS is burdened by multiple comparison testing both at the variant level and at the trait level (Hebbring, 2014). We recommend using metaUSAT to overcome these challenges.