What is rheology?

Abstract

The topic of the 2017 Cambridge Ophthalmology Symposium was ‘Go with the flow: rheology, fluid flow and the eye’. This paper is based on the opening presentation that was aimed to introduce key concepts within the topic of rheology to ophthalmologists and other scientists unfamiliar with the field. Examples are drawn from applications related to the eye.

Introduction

Rheology is the science of deformation of material. The name was coined by Eugene Bingham, who founded the Society of Rheology in the USA, and its root lies in the Greek word for flow. It includes the theory ‘underlying’ the deformation and the practice of measurement. Spell checking tools often try to change the term to ‘theology’: those working in the field describe themselves as rheologists.

Many physiological materials and fluids exhibit complicated rheology. Within the eye, examples include the vitreous humour, the liquid in the tear film, and the blood in capillaries. This article is not a detailed account: rather, the article is written as a primer, leaving out quantitative detail but indicating where mathematical considerations must be considered. There are several good textbooks on rheology.

Rheology is concerned with the question ‘How does a material respond to a force?’. The basic equation in words is

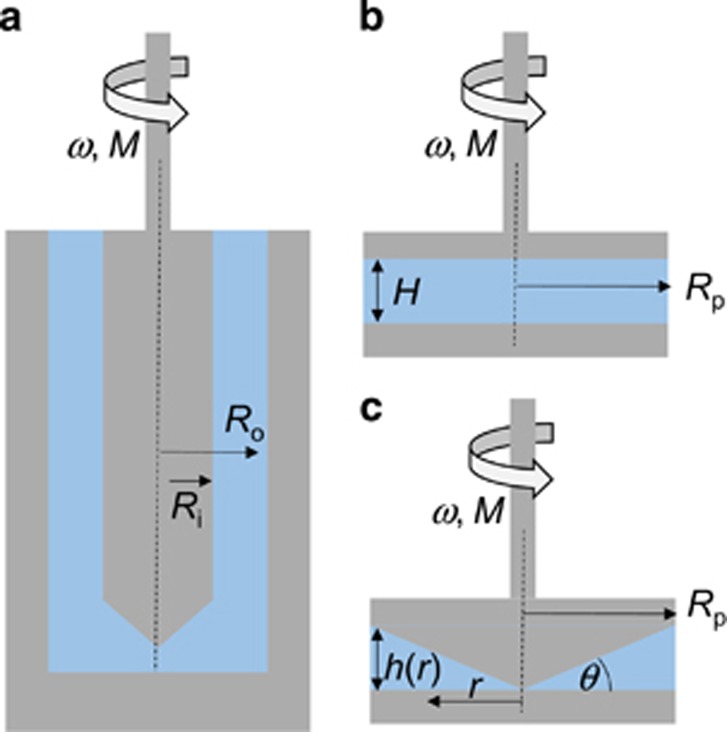
Physical scientists refer to forces acting on materials in terms of stresses, or force per unit area. The response is either quantified in terms of the amount of deformation, i.e. strain, or the rate of deformation, usually referred to as a strain rate. There are two different types of strain, which are illustrated in Figure 1. Shear strains are associated with change of shape, and are encountered in flows along tubes (e.g., arteries) as layers of material slide past one another. Figure 1a shows the velocity profile in the gap between two plates where one plate is moved relative to the other. An initially rectangular element becomes a parallelogram, with the change in shape expressed in terms of an angle, γ. If the material is flowing, the velocity gradient can be related to the shear strain rate. Normal strains, in contrast, are associated with a change in size such as that created by extension in Figure 1b. The normal strain ε is given by ε=ln[L/L_o]. Note that strains have sign: shrinkage, where L<L_o, is associated with a negative value of ε.

Figure 1.

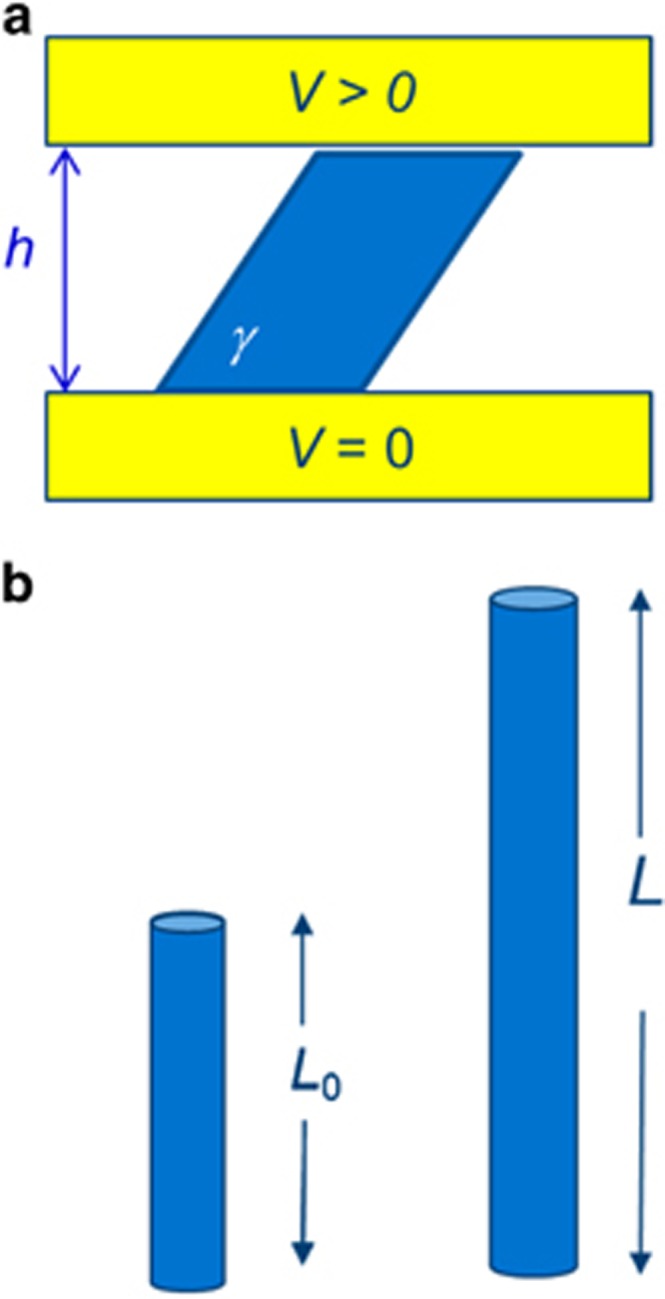
Deformation caused by (a) pure shear and (b) pure extension. In (a) h is the height of the gap between two plates. The top plate moves at velocity V. An initially rectangular sample changes shape to one characterised by angle γ. In (b) a rod is stretched from length L_o to L.

Just as strains have sign, it is important to note that forces (and stresses) have direction. This is best illustrated by the cube in Figure 2. Consider face A: a force acting on this face can have a component acting into, or away from, the face—this a normal force and gives rise to the normal stress on the face. There can also be components acting on the face tangentially, in effect sliding forces: these cause shearing so are labelled shear stresses. Since there are three faces perpendicular to each other on the box, there are nine components which define the stress state. It turns out that there are only six independent components, and their value depends on the orientation of the box. While forces can be thought in terms of vectors, the stress acting on a fluid is a tensor quantity and this gives rise to the more complex mathematics found in the literature. The term ‘pressure’ refers to the arithmetic average of the three normal stresses and in simple fluids these are equal. The units of stress and pressure are Newtons per square metre (N/m²), or Pascals (written Pa).

Figure 2.

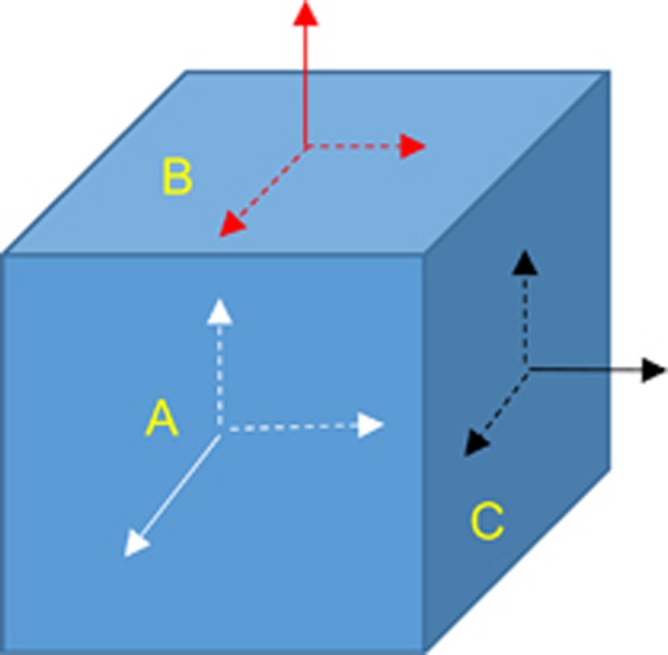
Components of stress acting on the three faces of a cuboidal element. Solid lines indicate a force acting normal to face A, B, or C. Dashed lines indicate forces acting along the face, generating shear.

The following manipulation gives a useful result:

Pressure is thus a measure of the energy content per unit volume of fluid.

Viscous or elastic?

Two of the key concepts in rheology were developed by scientists who also made significant contributions to optics: Isaac Newton and Robert Hooke. (Hooke and Newton lived in England in the 17th century. Newton (a Cambridge man) poked things in his eye as he developed theory of optics. Hooke (an Oxford man) discovered cells and published the first book on microscopy. They did not get on.) Newton considered the flow of liquids along pipes and determined that the shear stress, τ, in the fluid associated with fluid sliding past itself was proportional to the shear rate. In Figure 1a, the top plate moves at velocity V and the lower plate is fixed: the shear rate in this case is V/h. Writing Newton’s law as an Equation,

where η is the measure of the resistance of the fluid: it is the apparent viscosity. If η is independent of shear rate, the fluid is termed Newtonian and η is constant: it is often then called the dynamic viscosity (or simply viscosity), written as μ. Water is Newtonian, with a viscosity at 20 °C of 1 mPa s (in SI units: 1 centipoise (cP) in the cgs system). Blood is a suspension of different types of deformable cells and η depends on the local shear rate: it is non-Newtonian.

There is also the kinematic viscosity, with units of m²/s (SI) or Stokes (cgs). This quantity, often written ν, arises from the equations of motion governing fluid flow: ν=viscosity÷density. For water at 20 °C ν=10⁻⁶ m²/s.

Poiseuille presented the first expression linking the pressure drop along a tube to the flow rate at steady state. If the flow rate is Q m³/s and the tube is cylindrical, with radius R, the average velocity U=Q/πR². The shear rate is proportional to U/R so for a Newtonian fluid, the shear stress that the flow imposes on the wall is given by

The pressure drop, ΔP, is proportional to L/R, where L is the length of the tube, giving the familiar result

The factor of 8/π comes from the detailed working. The pressure drop is very sensitive to the narrowness of the tube, which is why dilated capillaries (larger R) can cause problems with blood distribution. The shear rate is also sensitive to R, so more information is required to calculate the relationship for a non-Newtonian fluid. In the case of blood flow through capillaries, the system is more complex as the size of the cells approaches R (see later).

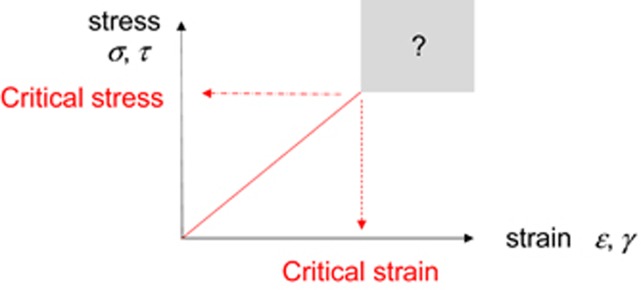
Hooke considered the initial, reversible deformation of solids, where the material deforms linearly until it reaches some critical strain or stress (Figure 3). The governing relationship for an elastic material is

Figure 3.

Behaviour of a Hookean elastic material: the deformation is linear up to the elastic limit associated with either a critical stress or a critical strain.

where E and G are the Young’s modulus and shear modulus, respectively. What happens when the critical measure is exceeded depends on the nature of the material.

Elastic materials respond instantaneously to a deformation, whereas the response of a viscous fluid is related to the rate at which it is deformed. Many non-Newtonian fluids are viscoelastic, exhibiting a combination of instant (elastic: τ∝Gγ) and delayed (viscous: τ∝ηdγ/dt, where t is time) responses. Viscoelasticity arises from interactions between components in the fluid, such as polymer chains, particles (cells), and droplets (or bubbles). Viscoelasticity is often studied by subjecting the material to a sinusoidal deformation with a small amplitude at a given frequency. At larger amplitudes the response is not linear. The elastic response will be in phase with the driving force or strain, and is quantified in terms of the elastic modulus, labelled G′. The viscous response lags the driving force and is quantified in terms of the viscous modulus, G″. Hint: the number of primes equals the number of letters ‘s’ in the label; elastic or viscous. The relationship between G′ and G″ is often expressed in terms of a phase angle δ, with δ=0 indicating a purely elastic response and δ=π/2 a viscous one.

The timescale of the response can vary from milliseconds to many seconds, and the response of a viscoelastic fluid at any particular time is then dictated by its history: such fluids have memory.

Example: food spreads

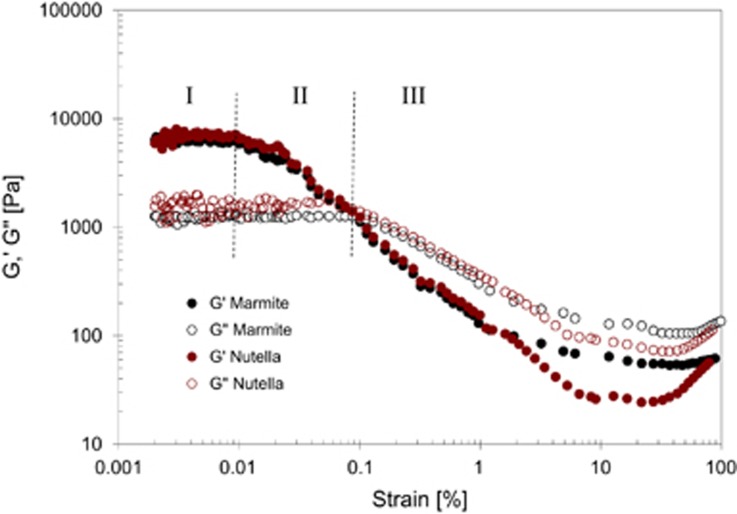
Figure 4 shows two examples of oscillatory testing of UK food spreads using a parallel plate device. The material is subject to a strain which varies sinusoidally with time at a frequency of 1 Hz: the amplitude of the strain is increased steadily and the torque exerted by the material on the moving plate measured and converted to a shear stress. The values of G′ and G″ are then calculated. Three regions of behaviour are evident. At low strain (region I), both moduli are independent of strain: this is the linearly elastic region. Here, G′ is an order of magnitude greater than G″—the material response is primarily elastic. In region II, G′ decreases with increasing strain. In region III, G″>G′ so the viscous response dominates: the material has moved from exhibiting solid-like behaviour to fluid-like behaviour. At 0.1% strain, G″≈G′ and this is some critical strain or stress, τ_c (some workers would call this a yield stress. Others will argue that it’s not). We can estimate the magnitude of τ_c from τ_c=G′γ=1000 × 0.001=1 Pa.

Figure 4.

Response of Marmite^® (black) and Nutella^® (brown) spreads to oscillatory shear testing in parallel plate geometry at 1 Hz and 20 °C. Vertical dashed lines indicate boundaries of regions I–III. Solid symbols–G′ open symbols–G″. Data collected by Dr D Torres Pérez.

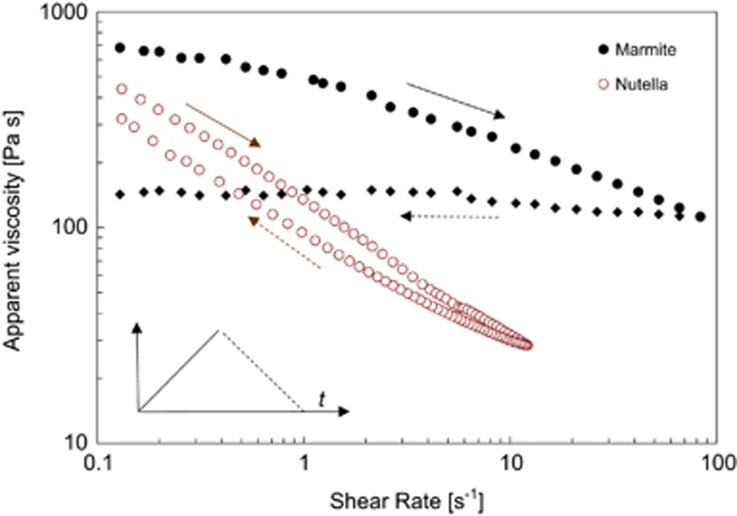
Figure 4 suggests that the two spread products are very similar, but those familiar with Nutella^® and Marmite^® will know that these two materials flow differently. Both materials are non-Newtonian and the apparent viscosity will depend on the shear rate: to compare the spreads we need to know the shear rate imposed by the blade when spreading. Experience (let us say that a slice of bread is approximately 10 cm wide and it takes 5 s to spread: V=0.1/5 m/s) suggests that V~0.02 m/s and h~1 mm, so the shear rate is about 20/s. The data for steady shear testing in Figure 5 show that the apparent viscosity of Marmite^® is noticeably larger than Nutella^® under spreading conditions. For both materials, the apparent viscosity decreases with increasing shear rate: they are termed shear-thinning, reflecting a disruption of interactions with the fluid as it is sheared. Many complex fluids are shear-thinning: some, like corn starch suspensions, are shear-thickening and η increases with shear rate.

Figure 5.

Effect of shear rate on apparent viscosity of Marmite^® (solid symbols) and Nutella^® (open symbols) in steady shear testing. Cartoon shows shear rate ramp: solid arrows—increasing shear rate; dashed arrows—decreasing shear rate. Parallel plates, 20 °C. Data collected by Dr D Torres Pérez.

The selection of correct time scales (the units of shear rate are s⁻¹, so shear rates are reciprocal time scales) and shear rates is important in making rheological measurements. Figure 5 shows that measurements made at an unrepresentative shear rate will yield incorrect results. Consider the tear film created by the blink of the eyelid. The eyelid travels back and forward about 15 mm in about 150 ms, so V~0.1 m/s: taking a tear film thickness as approximately 3 μm gives a shear rate associated with formation of the tear film is around 33 000/s. This is a high shear rate and making measurements in this region may require specialist devices. The other time scale to consider is the relaxation time, which can be related to the period between blinks (about 5 s), which will determine how long the fluid has to recover between shearing episodes.

This aspect of recovery of interactions is also evident in Figure 5, where data are presented for the shear rate being ramped up to the maximum value then ramped down again. The apparent viscosity of Nutella^® is lower on the return leg, a feature known as thixotropy, associated with the fluid requiring time to recover from the deformation. Marmite^® exhibits unusual behaviour, in that the apparent viscosity is almost constant on the return leg. It effectively remembers how fast it has been sheared.

Non-Newtonian behaviour arises from interactions between the components in a fluid. Marmite^® contains many dissolved protein fragments: many biological fluids are polymer solutions and the vitreous humour (VH) is an aqueous suspension of collagen fibrils. Silva et al¹ studied the rheology of rabbit VH using techniques similar to those in Figures 4 and 5 and showed that VH exists as a liquid or gel phase, both of which are viscoelastic.

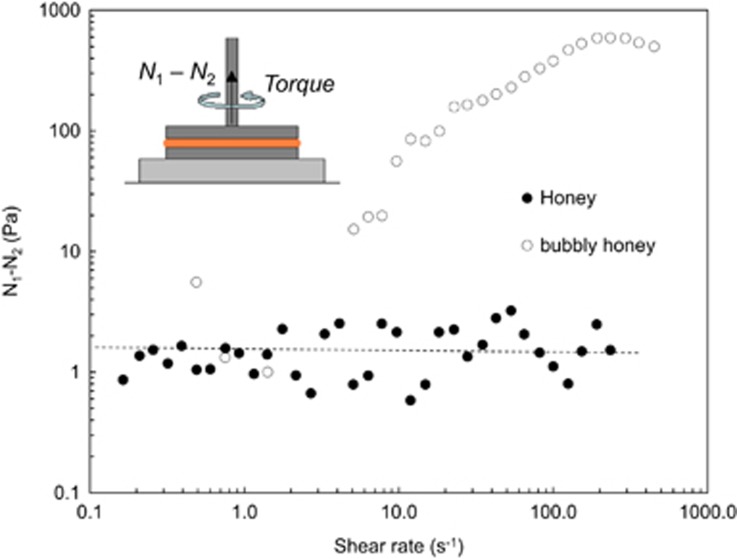
Nutella^® is a dense suspension, and the shear-thinning arises from interactions between the particles. Cells or bubbles, as micro-scale features, can cause a number of different interactions. Figure 6 shows an example of a strongly elastic response generated by shearing a bubbly liquid: the stirrer moves in one direction but the fluid responds by generating a force in a different direction, causing the batter to climb up the rod. The cartoon in Figure 7 shows a sample being rotated in a parallel plate test. The upthrust generated is expressed as a difference in the normal stresses, N₁–N₂. The data in Figure 7 show that bubble-free honey gives a constant, small N₁–N₂: adding bubbles gives a large upthrust. Flow of such a material along a tube can generate large normal stresses on the tube walls.

Figure 6.

Elastic response generated by shearing a bubbly liquid (cake batter): the rod rotates in the liquid and it responds by climbing the rod. Image provided by Dr A Chesterton.

Figure 7.

Normal force difference generated by addition of bubbles of air to honey. Solid symbols—honey: open symbols—bubbly honey, bubble volume fraction ranging from 0.13 to 0.27. Reproduced with permission.

There are a number of other types of non-Newtonian behaviour. Viscoplastic fluids are ones which do not flow until a critical stress is reached. A Bingham fluid is the simplest type of viscoplastic fluid. Below the critical stress—often referred to as a yield stress—the material exhibits solid-like behaviour such as elasticity and creep. Above the critical stress, the fluid flows and the apparent viscosity depends on the shear rate. Viscoplastic fluids are always shear-thinning but not all shear-thinning fluids are viscoplastic. Everyday examples include toothpaste and hair gel. Tomato ketchup is often described as viscoplastic, but it is arguably more complex again. Measuring the critical (or yield) stress can be challenging: the value estimated is often determined by the measurement method.

Rheometrical measurements

There are a wide range of techniques and devices available to make measurements under shearing conditions. Figure 8 shows some of the widely used configurations. Most impose a known shear stress (or torque) on the sample and measure the deformation generated, or measure the shear stress required to achieve a given shear rate. Extensional measurements are more difficult to make, particularly if the deformation is to be free from shear contributions. One way to do this is by filament stretching, where a sample is drawn apart between two plates and surface tension or the motion of the plates causes the sample to become thinner. Advances in imaging technology mean that these portable versions of these devices can be constructed at reasonable cost.²

Figure 8.

Examples of geometries used make shear rheology measurements (a) Couette (concentric cylinders); (b) parallel discs; (c) cone and plate. M is the torque required to move the top plate or central cylinder at rotational velocity ω.

Care needs to be taken in making rheometrical measurements, as the behaviour of a non-Newtonian sample can be influenced by how it was loaded into the device. Care also needs to be taken in interpreting the measurements, particularly with suspensions which may be subject to the phenomenon of wall slip. A solid wall, i.e. the surface of the measurement tool, can dictate the structure in a suspension at the wall to differ from the bulk material: particles can become ordered by the presence of the wall, or tend to move away from it. This will change the local apparent viscosity and the material can appear to ‘slip’ at the wall. It is therefore very important to know if this happens in the tests. This is checked by using surfaces with different roughness, imaging or different sample heights.

In thin ducts the ordering imposed by each wall spans the whole duct and it is then unwise to consider the rheology of the fluid as a continuum property. With blood flow through capillaries, as the flow is then determined by the passage of individual blood cells or groups thereof, which have dimensions similar to the duct.³ Blood flow in capillaries involves three deformable materials: the blood serum, the blood cells, and the walls.

Another type of boundary which requires great care is vapour–liquid interfaces, such as the surface of a tear film. Surface-active components (surfactants) accumulate at such interfaces and their presence there determines the surface tension. Differences in surfactant concentration across the interface will promote flow, known as the Marangoni effect, and the flow and rheology are then coupled. The meibum present in the human lipid layer gives rise to complex surface tension behaviour⁴ which determines tear film dynamics: this is the field of surface rheology and its description lies beyond the scope of this introductory article.

Concluding remarks

Rheology is the science of measurement of deformation. Virtually all materials deform in response to an imposed stress (‘everything breaks if you hit it hard enough’) and the materials present in the eye range from liquid-like to soft-solid behaviour. The rheology of the fluid or tissue is determined by its structure across several length scales, from the molecular to the dimensions of the duct or space. Rheometry allows one to probe the nature of the material and thus either understand how it flows, or why it does not flow as normal. Physiological differences can result in the absence (or excess) of components that promote non-Newtonian behaviour, or modify Newtonian behaviour, and well-designed rheometrical tests can quantify these.

It is important to define the characteristic timescale, mode, and extent of deformation involved in the flow of interest as these determine the type of device that should be used for testing. Rheometry is a practical subject and care needs to be taken in conducting measurements. Similar care is required in the interpretation of rheometrical measurements. In this regard, there is some overlap with ‘theology’ as it may require some faith that the model being discussed applies to the case under study.