Spatially-explicit model for assessing wild dog control strategies in Western Australia

Abstract

Large predators can significantly impact livestock industries. In Australia, wild dogs (Canis lupus familiaris, Canis lupus dingo, and hybrids) cause economic losses of more than AUD$40M annually. Landscape-scale exclusion fencing coupled with lethal techniques is a widely practiced control method. In Western Australia, the State Barrier Fence encompasses approximately 260,000km² of predominantly agricultural land, but its effectiveness in preventing wild dogs from entering the agricultural region is difficult to evaluate.

We conducted a management strategy evaluation (MSE) based on spatially-explicit population models to forecast the effects of upgrades to the Western Australian State Barrier Fence and several control scenarios varying in intensity and spatial extent on wild dog populations in southwest Western Australia.

The model results indicate that populations of wild dogs on both sides of the State Barrier Fence are self-sustaining and current control practices are not sufficient to effectively reduce their abundance in the agricultural region. Only when a combination of control techniques is applied on a large scale, intensively and continuously are wild dog numbers effectively controlled. This study identifies the requirement for addressing extant populations of predators within fenced areas to meet the objective of preventing wild dog expansion. This objective is only achieved when control is applied to the whole area where wild dogs are currently present within the fence plus an additional buffer of ~20 km. Our modelling focused on the use of baiting, trapping and shooting; however, we acknowledge that additional tools may also be applied. Finally, we recommend that a cost-benefit analysis be performed to evaluate the economic viability of an integrated control strategy.

Introduction

With the global expansion of production landscapes, areas of native habitat are diminishing (Foley et al. 2005), often forcing wildlife and livestock to co-exist, compete for resources, and increasing the frequency of their interactions. Significant human-wildlife conflicts and economic challenges can result when predators impact production systems, as occurs through predation on livestock by wolves and bears in North America and Europe, by felids in Asia and South America, and a range of species in Africa (Treves & Karanth 2003; Inskip & Zimmermann 2009; Treves, Wallace & White 2009).

In Australia, wild dogs, defined as dingoes (Canis lupus dingo), free-living domestic dogs (Canis lupus familiaris), and their hybrids, are important predators of livestock and can have significant economic impacts. These impacts result from direct predation, stock harassment, and the transmission of disease (Fleming et al. 2014). In Australia, total economic surplus losses due to wild dogs are estimated at AUD$21.9M to sheep industries and AUD$26.7M to the cattle industry (Gong et al. 2009). More recent estimates put yearly losses to the Western Australia (WA) sheep industry at $14M, and to the WA rangeland goat industry at $11M (Bell 2015). Small stock (sheep and goats) are so vulnerable to predation by wild dogs that it is generally considered that sheep enterprises and wild dogs cannot coexist (Thomson 1984; Newsome 2001; Fleming et al. 2014).

The primary mechanisms for the control of wild dogs in Australia are lethal means including trapping, shooting, and poison baiting (Fleming et al. 2014). In some areas, such as the southwest of Western Australia, these control strategies are augmented with landscape-scale fences. Landscape-scale fences separating high-value agricultural areas from predators have been used for over a century in Australia (Caughley et al. 1980; Newsome et al. 2001), and are being used increasingly in predator control programs (Binks, Kancans & Stenekes 2015).

The State Barrier Fence (SBF) runs 1190 km in a northwest-southeast direction and broadly separates a higher rainfall agricultural region suited to high-value stock and cropping from semi-arid to arid rangelands (Fig. 1). Originally designed to prevent the spread of European rabbits (Oryctolagus cuniculus) from the rangelands into the agricultural region, the SBF has also reduced the impacts of larger vertebrates, such as emus (Aves: Dromaius novaehollandiae) and wild dogs, in the agricultural region (Crawford 1967; Broomhall 1991; Ritchie 1997). However, in the last decade, wild dog impacts have increased at the interface of the agricultural region and the rangelands (DAFWA unpublished data). Wild dog control is becoming a priority for landholder biosecurity groups at the periphery of the agricultural region, and in 2014 the entire SBF was upgraded, at significant cost, to meet wild dog exclusion standards by adding a lap-wire protruding from the fence at 45 degrees to prevent tunnelling. The upgraded fence’s impacts on wild dog abundance and distribution have not been investigated, making it difficult to gauge its cost-effectiveness. The extent to which additional complementary predator controls will be required to protect livestock in the agricultural region has also not been examined.

Figure 1.

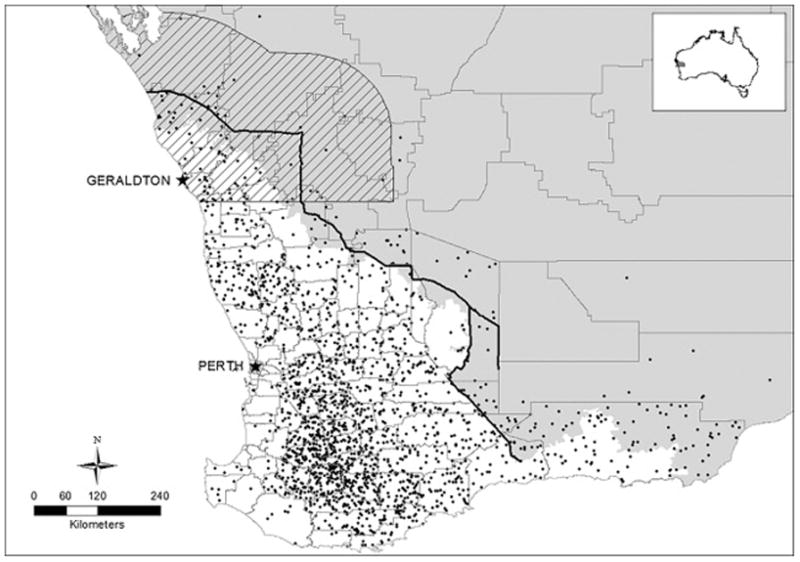
Study Area. Grey area indicates rangelands region, white indicates agricultural region. The State Barrier Fence is the heavy dark line and the study area is indicated by grey hatching. Each dot indicates 7000 sheep within marked local government area (Source ABS 2011).

Population modelling has been recommended to explore the relative effectiveness of different management options (Starfield 1997; Morris & Doak 2002; Campbell et al. 2015). This approach offers the advantage of identifying targets and timeframes for monitoring programs (Himes Boor 2014). Here we use spatially-explicit demographic models to evaluate whether current or foreseeable management practises, along with the SBF, are adequate to keep the agricultural region effectively wild dog free. Scenarios were developed for different levels of baiting, trapping, and shooting, as well as fence permeability. We then performed a Management Strategy Evaluation (MSE) based on the examination of wild dog demographic trajectories and social structure in both the agricultural region and the rangelands.

Methods

We developed spatially explicit, individual-based models for predicting abundance and distribution of wild dogs (see Supplementary material S1) using the HexSim 3.2.8 computer program (Schumaker 2015). We initially developed a baseline scenario in which no predator control measures were implemented (Fig. 2). We subsequently used modifications of this baseline model to forecast demographic and genetic changes, over a 30 year time span period, resulting from a number of simulated management scenarios (Table 1). We employed sensitivity analysis to evaluate the consequences of uncertainty in parameters whose values were estimated from sparse or unpublished data.

Figure 2.

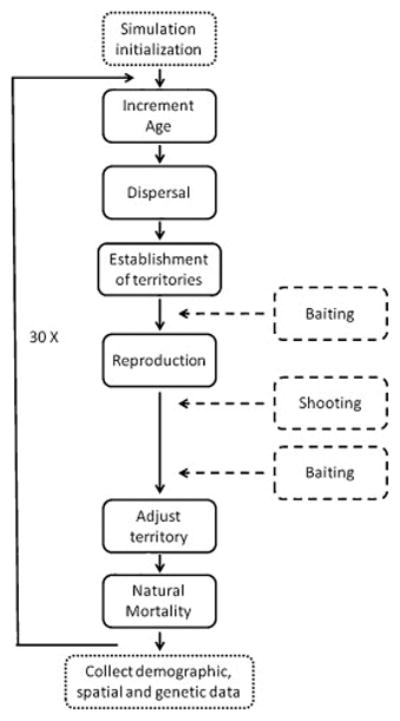
Flowchart summarising implementation of one time step (i.e. one year) of the dingo models in HexSim (Schumaker 2015). The baseline model is represented by solid lines and the additional events included in the management scenarios are represented with dashed lines.

Table 1.

Summary of spatially explicit, individual-based scenarios developed in HexSim (Schumaker 2015) to simulate dingo demographic and genetic dynamics over a 30 year time span.

Scenario	Description
DingoBase	Baseline model with no control or SBF implemented. Initial distribution of individuals is limited to currently known distribution.
DingoBase_PreEmpty50	As DingoBase, but the competition parameter is set to 50% to conduct a sensitivity analysis on this parameter.
DingoBase_STSurv	As DingoBase but with wider range of survival rates (see text for details) to conduct a sensitivity analysis on these parameters.
DingoBase_Bait_Shoot10	As DingoBase with non-baiting lethal control (with a 10% mortality) and baiting implemented.
DingoBase_Bait_Shoot05	As DingoBase with non-baiting lethal control (with a 5% mortality) and baiting implemented.
DingoBase_Bait_Shoot05_Ag_low	As DingoBase_Bait_Shoot05 with a regular baiting at medium intensity in selected properties (10%) in the agricultural region.
DingoBase_Bait_Shoot05_Ag_hi	As DingoBase_Bait_Shoot05 with a regular baiting at medium intensity in 22% properties in the agricultural region.
DingoBase_Shoot10	As DingoBase with non-baiting lethal control (with a 10% mortality) implemented.
DingoBase_Shoot05	As DingoBase with non-baiting lethal control (with a 5% mortality) implemented.
DingoBaseSBF	As DingoBase with a fully dog proof fence (i.e. 0% permeability).
DingoBaseSBF_Bait_Shoot10	As DingoBaseSBF with non-baiting lethal control (with a 10% mortality) and baiting implemented.
DingoBaseSBF_Bait_Shoot05	As DingoBaseSBF with non-baiting lethal control (with a 5% mortality) and baiting implemented.
DingoBaseSBF_Bait_Shoot05_Ag_low	As DingoBaseSBF_Bait_Shoot05 with a regular baiting at medium intensity in selected properties (10%) in the agricultural region.
DingoBaseSBF_Bait_Shoot05_Ag_hi	As DingoBaseSBF_Bait_Shoot05 with a regular baiting at medium intensity in 22% properties in the agricultural region.
DingoBaseSBF_Strat_Bait_Shoot05	As DingoBaseSBF_Bait_Shoot05 with baiting at high intensity in the agriculture region where wild dogs are present plus an additional buffer of ~20 km.
DingoBaseSBF_Strat_Bait_Shoot05	As DingoBaseSBF_Bait_Shoot10 with baiting at high intensity in the agriculture region where wild dogs are present plus an additional buffer of ~20 km.
DingoBaseSBF_Shoot10	As DingoBaseSBF with non-baiting lethal control (with a 10% mortality) implemented.
DingoBaseSBF_Shoot05	As DingoBaseSBF with non-baiting lethal control (with a 5% mortality) implemented.
DingoBaseSBF02	As DingoBaseSBF with fence permeability of 2%.
DingoBaseSBF02_Bait_Shoot10	As DingoBaseSBF02 with non-baiting lethal control (with a 10% mortality) and baiting implemented.
DingoBaseSBF02_Bait_Shoot05	As DingoBaseSBF02 with non -baiting lethal control (with a 5% mortality) and baiting implemented.
DingoBaseSBF02_Bait_Shoot05_Ag_low	As DingoBaseSBF02_Bait_Shoot05 with a regular baiting at medium intensity in selected properties (10%) in the agricultural region.
DingoBaseSBF02_Bait_Shoot05_Ag_hi	As DingoBaseSBF02_Bait_Shoot05 with a regular baiting at medium intensity in 22% properties in the agricultural region.
DingoBaseSBF02_Shoot10	As DingoBaseSBF02 with non-baiting lethal control (with a 10% mortality) implemented.
DingoBaseSBF02_Shoot05	As DingoBaseSBF02 with non-baiting lethal control (with a 5% mortality) implemented.
DingoBaseSBF05	As DingoBaseSBF with fence permeability of 5%.
DingoBaseSBF05_Bait_Shoot10	As DingoBaseSBF05 with non-baiting lethal control (with a 10% mortality) and baiting implemented.
DingoBaseSBF05_Bait_Shoot05	As DingoBaseSBF05 with non-baiting lethal control (with a 5% mortality) and baiting implemented.
DingoBaseSBF05_Bait_Shoot05_Ag_low	As DingoBaseSBF05_Bait_Shoot05 with a regular baiting at medium intensity in selected properties (10%) in the agricultural region.
DingoBaseSBF05_Bait_Shoot05_Ag_hi	As DingoBaseSBF05_Bait_Shoot05 with a regular baiting at medium intensity in 22% properties in the agricultural region.
DingoBaseSBF05_Shoot10	As DingoBaseSBF05 with non-baiting lethal control (with a 10% mortality) implemented.
DingoBaseSBF05_Shoot05	As DingoBaseSBF05 with non-baiting lethal control (with a 5% mortality) implemented.

Study Area

The SBF runs along the interface of the rangelands and the agricultural region of WA. The simulation study area incorporates 150 km on each side of the northern third of the SBF (Fig. 1). The area on the eastern side of the fence includes livestock grazing properties, protected areas and government-owned land and is, from now on, referred to as the ‘rangelands’. This area comprises occasional low-relief ranges (to 300m) separated by stony slopes and alluvial plains upslope of salt lakes. Sandy soils on sand-plains and granitic country predominate in this region (Payne et al. 1998).

Within the study area, the western side of the SBF has experienced increased wild dog impacts in recent years (DAFWA unpublished data). Approximately half of this area is cleared agricultural land used predominantly for crop production and small stock enterprises, plus a number of small towns and the city of Geraldton (population size: approx. 36,000). Although this area includes ‘rangelands’ for simplicity we refer to it as the ‘agricultural region’.

Baseline model

The study area (~118,300 km²) was mapped as a raster image comprised of square pixels of 1.3 km on each side. Pixel values were used to represent resource availability (a unitless parameter), which was determined by the minimum straight-line distance to fresh watercourses. A maximum resource value of 100 was assigned to pixels falling within the first 500 m from watercourses, and resource values declined as distance to fresh water increased, reaching a lower bound of 60 outside urban areas. Urban areas themselves were assigned a resource score of 20.

HexSim was then used to convert this raster map into a vector array of space-filling hexagonal cells, each of 1122.4 hectares and a width of 3.6 km (measured between parallel sides). The hexagons were assigned scores equal to the area-weighted mean of the pixel resource availability values falling within their bounds.

Wild dogs are known to be present in the rangelands, but are limited to, approximately, the first 40 km to the west of the SBF (DAFWA Unpublished data). Simulations were initialised with 10,000 individuals randomly distributed in the rangelands and within an area of between 15–60 km from the SBF, within the agricultural region. This would generate an initial density of approximately 10 animals per 100 km² as reported in the literature (Thomson, Rose & Kok 1992a).

Simulation parameters were drawn from published research on biology and ecology of dingo populations in the WA northern rangelands (see below for details). We assumed that domestic dogs and hybrids could be simulated using the same model parameters as dingoes (Claridge et al. 2014).

Dingoes are social animals that live in packs, and we used a maximum pack size of 13 (Thomson, Rose & Kok 1992a). The maximum pack size parameter limited the joining of packs by lone individuals, and forced juveniles to disperse if pack size exceeded 13 after breeding. Each pack establishes a territory, with the maximum allowed territory size being 113 km² (Thomson, Rose & Kok 1992a), from which pack members obtain their required resources. Pack territories are not overlapping, while individual’s home ranges are (Thomson, Rose & Kok 1992a). Following Heinrichs’ (2010) approach, we assumed that the smallest observed pack territory (i.e. 44.5 km² or 3.97 hexagons) (Thomson, Rose & Kok 1992a) could occur only in the best quality habitats (score 100), thus we required territories to contain a minimum cumulative resource availability score of 397. Individual resource targets (the amount dingoes would consume if resources were unconstrained) was set to 40 for adults and juveniles, and 5 for yearlings. This indirectly imposed a maximum density of approximately 22 animals per 100 km² (Thomson, Rose & Kok 1992a). During the simulations, a resource acquisition category (low, medium, high) was assigned to each individual based on the percentage of the resource target they were able to obtain.

Each pack was assigned an alpha male and an alpha female, and these individuals accounted for the majority of reproduction. In the event that one of these dominant individuals died, alpha status was assigned to another adult member of the pack at random. In roughly 20% of packs, a second female was allowed to successfully reproduce with the alpha-male as well (Thomson, Rose & Kok 1992a). Litter size was drawn from a normal distribution with of mean 5.2 and standard deviation 1.2.

Individuals that could not join or establish a pack were classified as loners (Thomson, Rose & Kok 1992a). Simulated loners were not allowed to reproduce (by definition, a pair that share a territory would constitute a pack). However, loners and packs may compete for the same resources. Data was not available in the literature to estimate the degree of competition between pack members and loners and we set the competition parameter (defined in HexSim as ‘pre-emption’) to an arbitrary 10%. That is, loners were allowed exclusive access to no more than 10% of the resources available in hexagons they shared with a pack. Given the uncertainty of this parameter, we included it in the sensitivity analysis and increased it to 50%, which we considered a very high value.

Simulated wild dogs were assigned to age classes including juveniles (<12 months), yearlings (13–24 months) and adults (>25 months). Pack size was maintained through density-dependent emigration, triggered when membership exceeded 13 (see above), or when an individual’s resources fell below 80% of its target value. Dispersal priority was stratified by age and resources, with non-alpha adults being the first to disperse, followed by yearlings. Pack members’ access to the resources available within a territory was stage-stratified, with the alpha male’s needs being met first, then the alpha female and juveniles, and finally any non-alpha adults and yearlings. Juveniles were assigned the same resource priority as the alpha female because they derived their resources from the alpha female.

Individuals from a pack dispersed for distances drawn from a lognormal distribution with mean=50.1 km and sd=40.3 km (Thomson, Rose & Kok 1992b). Dispersal distances exceeding 184 km (Thomson, Rose & Kok 1992b) were rejected and replaced with another random draw from the distribution. Loner dispersal distances were drawn from a uniform distribution bound between 11.4 and 42.8 km (Thomson, Rose & Kok 1992b), until they joined or establish a pack. After dispersal, animals explored the landscape in the attempt to establish a home range that met their resource requirements. Maximum allowed home range size was approximately 134 km² for adult males, 78 km² for other pack members that had dispersed, and 258 km² for loners (Thomson 1992).

Survival rates were stratified by both age and resource class, and were modified further to simulate environmental stochasticity. Age-class specific survival rates from Thomson et al (1992a) were assigned to individuals falling in the medium resource category. To include environmental stochasticity in the model, a collection of five values defined as the upper and lower 95% confidence interval (CIs) from Thomson et al (1992a), the mean, and the two mid points between the mean and the CIs were provided and randomly selected (with replacement) each simulated year. These values were then halved or increased by 50% for the low and high resource class, respectively. Given the lack of data available linking mortality rates to resource intake, we performed a sensitivity analysis in which low and high resource individuals’ survival rates were set to zero and 20% of the value for medium-resource individuals, respectively.

We were also interested in evaluating the genetic dynamics associated with possible changes in wild dog demography. Specifically, we wanted to explore whether estimates of genetic differentiation between regions could be used to evaluate the level of demographic separation the SBF imposed on wild dog populations. To this end, we initialised the simulations with the allele frequencies from 34 microsatellite loci obtained from the same study area (Stephens et al. 2015) and monitored the genetic distance between the wild dog population on the east and west of the SBF over time. Identical initial allele frequencies were used on both side of the SBF.

Management scenarios

The SBF was modelled as having four different levels of permeability: 100% (no fence), 5%, 2% and 0%. This range of permeability values reflects the actual uncertainty about wild dogs’ ability to penetrate the barrier. The simulated fence did not impart any mortality: individuals were either deflected by it, or they passed through it.

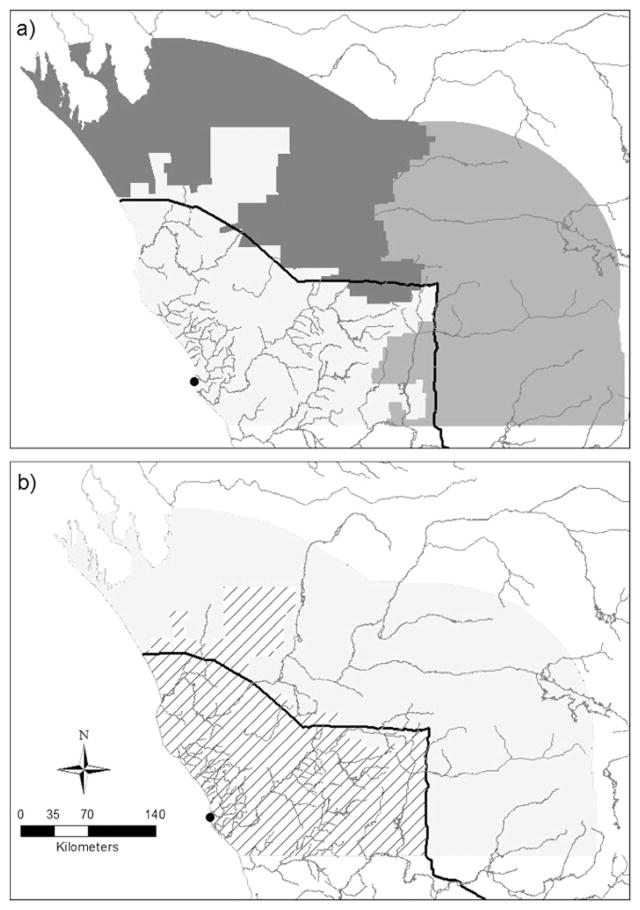
Wild dogs are controlled in the study area using a combination of baiting, trapping and shooting. We simulated three different baiting regimes (low, medium, and high intensity; Fig. 3) based on analysis of Western Australia Department of Agriculture and Food (DAFWA) landholder permits for the use of poison for wild dog control and expert opinions of DAFWA staff and local licenced pest management technicians. Most of the agricultural region is subjected to a low intensity baiting, characterised by occasional deployment of baits after the wild dog breeding season. We modelled low intensity baiting by applying additional mortality (details below) in two randomly selected years within each five year interval. We simulated medium intensity baiting as being conducted yearly, in the southeast of the rangelands, both pre- and post-breeding. High intensity baiting was modelled in the northeast of the study area, with one pre- and two post-breeding baiting rounds being conducted each year. All simulated wild dogs were associated to one of the three baiting regimes based on the location of their home range. Because baiting is usually used in association with another control method, no scenarios were developed where baiting occurs without shooting and trapping (scenarios with suffix “Bait_shoot” in Table 1). However, within the scenario there might be farms that conduct ground baiting but do not carry out shooting and trapping (i.e. not all control techniques may be applied concurrently in all properties, Fig. 3).

Figure 3.

a) Baiting regimes in study area, b) Non-baiting lethal control regimes in study area. Dark grey indicates high effort, intermediate grey indicates medium effort, light grey indicates low effort and hatching indicates very low effort. The city of Geraldton is marked as a black dot.

We further investigated the potential consequences of two plausible alternative baiting regimes that might realistically be implemented in the agricultural region. In the first (scenarios with suffix “Ag_low” in Table 1), all landholders within the agricultural region having current wild dog baiting permits, which accounts for 10% of the total agricultural properties within the study area – equivalent to 25% of landholders with registered stock brands – would shift to a medium level of control. The second scenario (scenarios with suffix “Ag_hi” in Table 1) supposes that 22% of properties west of the fence will implement a medium level of control (55% of properties with registered stock brands). This 22% figure represents the highest actual density of landholders holding baiting permits within any local government shire in the agricultural region (DAFWA unpublished data) and it includes all the properties with current baiting permits, all pastoral properties and a random selection of additional properties. In both alternative control strategies, shooting and trapping were assumed to also be imposed at all locations were baiting was applied. We considered the first of these scenarios as a plausible, modest response to wild dog impacts by affected producers in the agricultural region, while the second is a plausible, but more pronounced response.

Based on our results (see below), a final ‘strategic’ high-intensity simulated wild dog control assumed that baiting, trapping, and shooting would be imposed upon the entire area where wild dogs are currently found in the agricultural region, plus an additional buffer of approximately 20km. in this scenario, simulations were conducted in the presence of a completely impermeable fence (i.e. no passage of dogs across the fence), which would prevent re-invasion, in conjunction with a high baiting intensity within the controlled area in the agricultural region and the two levels of additional mortality due to trapping and shooting: 5% and 10% (scenarios with suffix “Strat_Bait_Shoot”, see below for details on how shooting and trapping was modelled).

The mean baiting rate (per baiting session) in the study area was calculated to be 2.99 baits/km based on the number of baits apportioned to properties at bi-annual bait preparations (Meekathara Rangeland Biosecurity Association unpublished data 2009–2015). We conservatively estimated the mortality caused by a baiting event by considering the lowest reported baiting mortality (25%), from the lowest baiting rate (8.4 km⁻¹) of collared dingoes from Thomson (1986) and Thomson et al (1992a), and calculated the mortality that would be observed using 2.99 baits/km assuming a linear relationship (i.e. 0.25: 8.4 × 2.99 ≈ 0.1). Fluctuations in baiting efficiency were simulated by arbitrarily applying a standard deviation of 20% as we do not have enough data to estimate this parameter more accurately. This stochasticity was implemented in the models with an approach similar to that used to model stochasticity in natural mortality: five values were drawn from the normal distribution parameterised with the mean mortality rate obtained from the fitted exponential function and the 20% standard deviation. In each year, one of these values is randomly selected and applied after taking into account natural mortality (i.e. removing the proportion of animals that would have already died of natural causes).

An analogous approach was used to model additional mortality caused by shooting and trapping, with the exception that a fixed value, rather than several values extracted from a normal distribution, was used to simulate the combined effect of these non-baiting control methods. This is because we only had very limited data on mortality associated with shooting and trapping. Based on Thomson et al (1992a), we estimated that up to a 10% of additional mortality can be due to non-baiting control methods, therefore we used two values, 5 and 10% (scenarios with suffix “Shoot05” and “Shoot10”, respectively, in Table 1), to evaluate what the consequences on the wild dog demography were if a level of control that would cause such additional mortality is regularly applied in the study area. The study area was divided in two regions of control (Fig. 3, panel B), based on expert opinion of DAFWA staff and licenced pest management technicians. Additional mortality was applied based on the animal’s home range.

Statistical analysis

We ran 200 replicates for each scenario and collated each scenario’s results. Data handling for preparation of statistical analysis, calculations of descriptive statistics, statistical comparisons between scenarios and data plotting was carried out with the R package HexSimR (https://github.com/carlopacioni/HexSimR) in R 3.2.2 (R Development Core Team 2015). HexSimR performs pairwise comparisons between scenarios using the Strictly Standardised Mean Difference (SSMD, Zhang 2007), which is a convenient statistic in this context because its significance is not influenced by sample size (which is large in our case).

Several demographic and genetic parameters were collected (S2 for a complete list), for each section of the study area (i.e. rangelands and agricultural region), each simulated year, after the breeding season. We then compared mean values at year five and 30.

We calculated the mean individual dispersal distance (stratified by gender and loner vs. pack member), mean pack size, mean number of packs, mean resources obtained by packs and mean territory size using only ten replicates. We found that 10 of 200 replicates were sufficient for this analysis because these statistics are derived from each pack’ data. With a total mean population size larger than 10,000 individuals, even with only ten replicates, these statistics were calculated with more than 300,000 data points.

Because wild dog distribution in the agricultural region is limited to within a 40 km wide strip against the SBF, we also monitored the progress of the western front of the wild dog distribution by selecting a linear array of patches (each of four hexagons, 14.4 km in length, around 4490 ha) and then determining the occupancy of these patches (by at least one animal) during the simulations using the function ‘invasion.front’ in HexSimR.

Genetic distance between animals on each side of the SBF was calculated for each replicate and then averaged within each scenario. HexSimR quantifies genetic distance using the Jost’s D (Jost 2008) as implemented in the R package mmod (Winter 2012) after having converted the HexSim generated genepop (Rousset 2008) input file into a ‘genind’ object with the R package adegenet (Jombart 2008).

Results

Sensitivity analysis

We explored the sensitivity of our model to the competition parameter to evaluate possible demographic and ecological changes associated with this parameter (Fig. S1). Increasing the competition parameter did impact the demographic and social structure of wild dog populations in the study area (Table S1). When the competition parameter was increased to 50%, the mean population size was significantly lower (p≤0.0001). A larger proportion of individuals in each population were loners (p<0.0001), and a slightly male-biased sex ratio emerged (mean 1.1, p≤0.033, Table S1). These differences were also reflected in the spatial use of the resources. Simulated wild dog packs were on average smaller (p<0.0001), with significantly more resources (p=0.006) and territory were marginally smaller (p=0.034).

Sensitivity analysis using less optimistic survival rates generated significantly smaller mean population sizes only at year 5 (p =0.034, Table S1) in the agricultural region.

Fence permeability and the role of wild dog control

No statistical differences in demographic projections were found when the same lethal control regime was applied with different levels of SBF permeability. Due to the presence of wild dogs in the agricultural region, the SBF on its own, irrespective of the level of permeability applied, did not prevent wild dog populations within the agricultural region from reaching carrying capacity in the explored timeframe (30 years). Further, expansion of wild dog distribution into agricultural areas followed similar temporal patterns of approximately 17.3 km/year (SD=27.2) regardless of the permeability of the SBF.

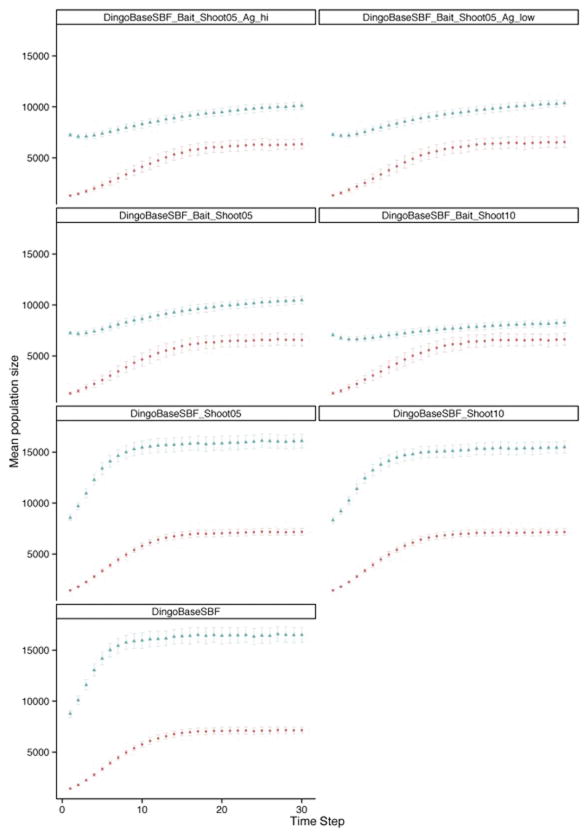
Within each fence-permeability scenario, wild dog abundance was consistently lowest in scenarios with highest co-ordinated baiting and non-baiting lethal control regimes in the rangelands (Fig. 4), with a density ranging between 7 and 11 individuals per 100 km² at year 30 as opposed to 15–18 individuals per 100 km² in absence of control.

Figure 4.

Plot of wild dog demographic projections in the rangelands (blue) and the agricultural region (red) over 30 simulated years. As projections between different levels of State Barrier Fence (SBF) permeability were similar, plots are limited to the scenarios with an impermeable SBF. See Table 1 for scenario abbreviations.

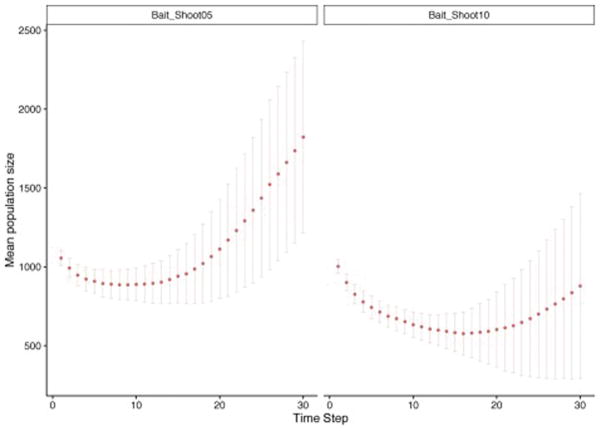
When baiting was applied at low intensity in the agricultural region (scenarios with suffix “Bait_shoot” in Table 1), but without the SBF, wild dogs were significantly less abundant in this region at year five of the simulations (approximately 7.5 individuals per 100 km² rather than 9.5–10), but this was not sustained until year 30 (Table S2). Similarly, the two additional scenarios where a higher level of control was modelled in the agricultural region (scenarios with suffix “Ag_low” and “Ag_hi” in Table 1) predicted a significantly lower population size only in year five (Table S2). Only when the control was strategically applied across the whole area where wild dogs were present in the agricultural region (scenarios with suffix “Strat_Bait_Shoot” in Table 1), was their abundance significantly reduced for the 30 simulated years (approximately 2.5 and 2.5–5 individuals per 100 km² in year 5 and 30, respectively). Such a level of control effectively prevented the wild dog population from growing for most of the simulated 30 years, with the higher mortality from non-baiting lethal control resulting in a more marked control in wild dog abundance (Fig. 5).

Figure 5.

Plot of wild dog demographic projections in the agricultural region over 30 simulated years. Control was implemented strategically to include the whole area where wild dogs are currently present plus an additional buffer of ~20 km. Simulations were conducted in the presence of an impermeable SBF and implementing a high baiting intensity and two levels of additional mortality due to trapping and shooting: 5% (on the left) and 10% (on the right).

In the absence of baiting, non-baiting lethal control did not reduce wild dog abundance, except at year five when it was modelled to cause a 10% additional mortality (Table S2).

No specific age and sex differences on either side of the fence were found. Population declines described above were typically a result of a global reduction in abundances. The exception to this was the reduction at year 30 in Bait_Shoot_10 which was male-biased, probably due to a greater propensity for males to be excluded from packs and therefore to become resource-deficient. When control was carried out, the proportion of individuals that were loners was reduced (Table S2). Typically, when no control was applied, the proportion of loners averaged 18% (SD=1.1%, range=16.8–19.2%). In comparison, when extensive control was in place it was reduced to as low as 8% (SD=0.5%, range= 6.9%–8.9%. Table S2 and Fig. S2). The extent of the reductions seemed inversely proportional to the level of control measures implemented. The mean number of pack members (pre-dispersal) was significantly smaller when coordinated non-baiting lethal control was carried out (Table S3), while the total number of packs was not altered. Accordingly, the territory size also tended to be smaller (Table S3).

After 30 years, the genetic distance between the wild dogs on the east and west of the fence was small and not significantly different from the baseline model with no fence (Fig. S4), reflecting the relative large population size of each population, which was not anticipated, and consequent limited genetic drift.

Discussion

Here, we developed models to simulate wild dog population dynamics and used them to determine the effect of different levels of permeability of the SBF and the degree of wild dog control within the agricultural region that would be required to prevent increases in wild dog abundance.

Fence permeability and the role of complementary control

The main premise for the upgrades to the SBF is that the primary driver for increased wild dog abundance in the agricultural region is immigration from the rangelands. However, our primary finding is that the presence of an extant population of wild dogs in the agricultural region meant that there were no significant differences in demographic projections across different levels of fence permeability for the same level of control. That is, invasion from the rangelands is not the only pathway to lead to increases in wild dog abundance and distribution in the agricultural region. Indeed, invasion from the rangelands would appear to have only a minimal role compared to the growth rate that the population in the agricultural region has in the presence of a fully dog-proof fence.

The control of the wild dog population in the agricultural region is a key element for the livestock industry to prevent further increase in wild dog numbers. However, based on the results we obtained, we conclude that to prevent increases of wild dog population in the agricultural region, it may be necessary to have a very high participation rate in wild dog control across the agricultural region. In fact, only when applying combined control, with baiting, shooting and trapping, that strategically encompassed the whole area in the agricultural region where wild dogs are present plus an additional buffer of ~20 km, wild dog population growth was effectively prevented for most of the simulated 30 years (on average, there was a reduction in the population size of approximately 75–80%, and up to 88% when trapping and shooting was applied with a 10% additional mortality). Overall, our results are in agreement with several empirical studies in other areas where intensive and coordinated control effort were recommended to achieve substantial reduction in wild dog populations (Allen & Fleming 2004; Allen 2015).

On the other hand, the modelled control participation rates of 10 and 22% within the agricultural region were insufficient to prevent further increase of wild dog distribution and abundance within the agricultural region. Indeed, simulations with what was already considered a somewhat optimistic level of participation in wild dog control in the agricultural region (22% of properties) only resulted in a short-term (around 30%) reduction in wild dog abundance.

These 22% of properties were selected partially at random and so they do not address responses to wild dog presence per se. Additionally, the simulated scenarios reflect a static management response to a population of wild dogs which changes in density and distribution over time. It was therefore expected that a more targeted response to wild dog presence would have had a more marked effect on wild dog distribution and abundance.

Our simulations demonstrate that substantially reducing and maintaining low wild dog numbers would entail a high level of participation in the agricultural region, which would require participation by a large number of cropping enterprises that do not benefit directly from baiting. Reducing the abundance of wild dogs in the agricultural region should be more achievable than controlling them within the rangelands because wild dog density and distribution is currently more limited in this area. However, our simulations considered a closed and limited area, whereas the agricultural region extends approximately 780 km further south to the study area and wild dogs, although in very limited numbers, have been detected within this region. Moreover, a reduction in wild dog numbers does not guarantee that there will be no livestock losses. While there are still benefits for the livestock industries when there is only a partial control of wild dogs (Binks, Kancans & Stenekes 2015), it is likely that the relationship between wild dog density and impacts is not linear (Fleming et al. 2014). Thomson (1986) indicates that prevention of losses for sheep is only achieved when there is 100% removal of resident wild dogs and reinvasion is prevented. Although limited to cattle enterprises, it has also been suggested that incomplete eradication of wild dogs may cause an increase of livestock losses owning to the social structure changes and hunting techniques (Allen 2015).

We acknowledge that the level of mortality that we applied as result of baiting is a conservative value and further research to more precisely estimate this parameter will improve the model prediction accuracy. However, if the aim is to maintain low wild dog numbers, there is a clear need for wild dog management to be undertaken cross-tenure, to include not only livestock producers but also crop producers and protected areas. Considering that shooting and trapping did not effectively reduce wild dog abundance when applied without poison baiting, effective management of wild dogs in the agricultural region would require a large proportion of landholders to participate in baiting (at least at ‘medium intensity’, based on the results obtained in simulations of the rangelands), irrespective of enterprise choice, which may be challenging. Further, because of the likely need for sustained high-intensity and spatially extensive control with the uncertainty of financial returns when partial removal is achieved, there may be a need to consider additional approaches to the protection of small stock industries from wild dog impacts in the agricultural region. Our modelling focused on the use of baiting, trapping and shooting; however additional tools may be applied to reduce wild dog impacts and population changes. Specifically the use of Canid Pest Ejectors is one tool that could assist as demonstrated for other canids (Fleming et al. 2006; Hooke, Allen & Leung 2006). Non-lethal methods such as property and cluster fencing (boundary fencing of a number of adjacent properties) (Allen & West 2013) and the use of guardian animals (van Bommel & Johnson 2012) may also be complimentary methods for reducing wild dog impacts. To this end, trials with alternative techniques should also be promoted in this area to optimise control methods that maximise the benefit-cost ratio. It should be noted that we deliberately did not include any indirect effects on farming due to wild dog presence (e.g. potential for kangaroo control (Letnic & Crowther 2013; Prowse et al. 2015) or transmission of diseases (King et al. 2011)) nor considered wild dogs’ potential additional ecological roles in our analysis because, to our knowledge, there are not sufficient data to adequately model such aspects in a temperate, Mediterranean climate such as that of the southwest of Western Australia and such effects are beyond the scope of this paper. However, we recognise that wild dog abundance is not the only element determining their impact. We also acknowledge that we did not assess the economic viability of an integrated control strategy and recommend that this should be addressed via economic modelling to inform the industry on the cost-benefit ratio before such a large investment is carried out.

Effects of control on social structure

Our modelling suggests that wild dog control causes a shift in the social structure with the proportion of loners in the population being inversely proportional to the persecution effort. This is likely related to behavioural differences between loners and pack members. The former have a tendency to explore larger areas, increasing their likelihood of encountering baits or being trapped/shot. These results reflect a similar pattern in baiting trials in north-western Australia (Thomson 1986), but diverge from Allen (2015) who found a disproportionate effect of baiting on juvenile animals, and social changes resulting from recolonisation of baited areas by yearling animals. We recognise that this is an area in need of further empirical investigation.

Sensitivity analysis

We carried out a sensitivity analysis for the competition and survival rate parameters to assess their effects on the simulations.

Increasing the competition parameter increased the proportion of loners in the population, as they were able to acquire more resources when this parameter was increased. However, because loners do not contribute to reproduction, this caused the overall population growth rate to fall, reducing the population size at 30 years. While we do not have sufficient field data to accurately determine the level of competition between loners and pack members, we maintained the selected baseline value of 10% for the competition parameter because it resulted in a social structure that approximates published data; that is, ~10–15% of individuals are loners (Thomson, Rose & Kok 1992a).

Modifying the survival rates had a significant effect only on the initial growth of the population in the agricultural region. In the baseline and management scenarios, we used relatively wide survival intervals and allowed the models to fluctuate between these intervals to simulate stochasticity. While the data we used were the best available to us, it is possible that our models are overestimating the population size of wild dogs, especially when the populations are small, if their survival is actually lower than we modelled, or if environmental changes compromise wild dog survival.

We inspected a number of secondary predictions to further establish that the models were adequately parameterised. For example, descriptive statistics of the baseline scenario were in line with general expectations from field data: the mean number of pack members was between 10 and 15; the mean territory size was around 80 km²; the mean distance covered by loners was about 17 km and around 23 km by members of a pack that dispersed (Thomson 1992; Thomson, Rose & Kok 1992b). Moreover, the growth rate and progress of the western front of the wild dog distribution were both in line with intervals considered realistic for the species (Prowse et al. 2013; Smith 2015).

Conclusions

This study is an example of how population modelling can be used to evaluate management options for wildlife populations, and has the benefit of quantifying possible outcomes resulting from the implementation of wildlife management actions and, as a result, the definition of management targets.

Our analysis identified that the SBF and current control practices are not sufficient to reduce the abundance of wild dogs in the agricultural region because: 1) a self-sustaining wild dog population is already extant in this region; and 2) existing control in the agricultural region does not impose sufficient mortality to effectively reduce abundance.

In order to maintain the agricultural region effectively dog free, control effort in this region needs to exceed the current effort, and be sustained across the whole area where wild dogs are currently distributed plus an additional buffer of 20 km. This presents a challenge because of the spatial extent of the control required and because it would require participation in the control operations of, not only livestock producers, but also other agricultural and non-agricultural enterprises.

We would like to thank J. Miller, C. Robins and G. McDonald (DAFWA) to provide expert opinion on baiting programs, M. Stadler (DAFWA) for information on fence management and K. Rose (DAFWA) for clarification and expert opinion on dingo ecology. We are also grateful to R. Jacob (DAFWA) for feedback on sheep industry and S. Campbell (DAFWA) for comments on early draft of this manuscript. This project was funded by the Royalties for Regions. The information in this document has been funded in part by the U.S. Environmental Protection Agency. It has been subjected to review by the National Health and Environmental Effects Research Laboratory’s Western Ecology Division and approved for publication. Approval does not signify that the contents reflect the views of the Agency, nor does mention of trade names or commercial products constitute endorsement or recommendation for use.

Supplementary Material

Sup 1

Table S1. Summary statistics – mean (standard deviation) – of simulated demographic parameters in scenarios conducted for sensitivity testing and p-values of their comparison with the baseline model.

Table S2. Summary statistics – mean (standard deviation) – of simulated demographic parameters and p-values of their comparisons with the baseline model (with the same level of SBF permeability).

Table S3. Summary statistics – mean (standard deviation) – of simulated spatial ecological parameters in scenarios and p-values of their comparison with the baseline mode (with the same level of SBF permeability).

Figure S1. Plot of wild dog demographic projections in the rangelands (blue) and the agricultural region (red) over 30 simulated years for sensitivity test scenarios. See Table S1 for scenario description.

Figure S2. Plot of proportion of individuals that are loners (i.e. no pack members) in the rangelands (blue) and agricultural region (red) over 30 simulated years of wild dog populations. As projections between different level of SBF permeability were similar, plots are limited to the scenarios with a fully dog proof fence. See Table S1 for scenario abbreviations.

Figure S3. Mean Genetic distance (± SD) at year 30 between wild dog populations in the agriculture region and rangelands measured using Jost’s D (Jost 2008). See Table S1 for scenario description.