Hydrodynamic mobility of confined polymeric particles, vesicles, and cancer cells in a square microchannel

Abstract

The transport of deformable objects, including polymer particles, vesicles, and cells, has been a subject of interest for several decades where the majority of experimental and theoretical studies have been focused on circular tubes. Due to advances in microfluidics, there is a need to study the transport of individual deformable particles in rectangular microchannels where corner flows can be important. In this study, we report measurements of hydrodynamic mobility of confined polymeric particles, vesicles, and cancer cells in a linear microchannel with a square cross-section. Our operating conditions are such that the mobility is measured as a function of geometric confinement over the range 0.3 < λ < 1.5 and at specified particle Reynolds numbers that are within 0.1 < Re_p < 2.5. The experimental mobility data of each of these systems is compared with the circular-tube theory of Hestroni, Haber, and Wacholder [J. Fluid Mech. 41, 689–705 (1970)] with modifications made for a square cross-section. For polymeric particles, we find that the mobility data agrees well over a large confinement range with the theory but under predicts for vesicles. The mobility of vesicles is higher in a square channel than in a circular tube, and does not depend significantly on membrane mechanical properties. The mobility of cancer cells is in good agreement with the theory up to λ ≈ 0.8, after which it deviates. Comparison of the mobility data of the three systems reveals that cancer cells have higher mobility than rigid particles but lower than vesicles, suggesting that the cell membrane frictional properties are in between a solid-like interface and a fluid bilayer. We explain further the differences in the mobility of the three systems by considering their shape deformation and surface flow on the interface. The results of this study may find potential applications in drug delivery and biomedical diagnostics.

I. INTRODUCTION

Understanding the transport of deformable particles, such as vesicles and cells, in moderately or tightly confined conduits is of practical interest in applications ranging from blood rheology^1,2 to drug delivery^3,4 to biomedical diagnostics.^5–7 A key parameter of interest in these studies is the hydrodynamic mobility of the deformable particle, β, which is defined as the ratio of the particle velocity (U) to the surrounding mean fluid velocity (V). This mobility is expected to be a function of the particle confinement, λ, defined as the ratio of the particle diameter (a) to the hydraulic diameter of the conduit (D), particle location in the conduit, mechanical properties as well as flow-based dimensionless parameters such as capillary number (Ca) and Reynolds number (Re).

Early studies of theory and measurement of particle mobility have focused on cylindrical geometries. Experimental measurements of particle mobility in cylindrical conduits have been reported with drops,^8–10 vesicles,¹¹ and red blood cells (RBCs).^12,13 Ho and Leal⁸ (λ = 0.72–1.10, Ca = 0.08–0.18) measured the mobility of neutrally buoyant drops in a Newtonian fluid and a viscoelastic fluid for inner to outer fluid viscosity ratios, K = 0.2–2.0. They found that the mobility monotonically decreased as a function of confinement for 0.72 < λ < 0.9. For highly confined drops (λ > 0.95), the mobility decreased with increasing viscosity ratio for a given capillary number and increased with increasing capillary number for a given viscosity ratio.¹⁰ Olbricht and Leal⁹ measured the mobility of buoyant drops, of diameters comparable to the tube diameter, and found that as the density difference between the drop fluid and outer fluid increased, the drop velocity decreased and the droplets experienced larger deformation.

There have been parallel efforts to develop theories for predicting the mobility of deformable particles,^14–17 as well as solid particles,^18–21 in cylindrical tubes. Hetsroni et al.²² (henceforth referred to as HHW) derived an analytical model using the method of reflections to determine the settling velocity of a spherical droplet under Stokes flow in a cylindrical tube. Hyman and Skalak¹⁵ considered a train of equally spaced axisymmetric spherical inertia-less droplets as a model for the flow of blood cells in capillaries. They used the stream function approach and adapted the general solution of Wang and Skalak²¹ for a train of elastic particles. Martinez and Udell¹⁶ conducted a numerical analysis study using the boundary integral method to derive the velocity of droplets of sizes comparable to the tube diameter. The mobility calculated from the HHW²² model was shown to be in good agreement with the experimental data reported by Belloul et al.²³ in cylindrical tubes at a lower confinement regime, λ < 0.7. For larger drops (0.7 < λ < 1.1), numerical simulations by Martinez and Udell¹⁶ showed that they could match the experimental results of Ho and Leal.⁸

With respect to the motion of vesicles in tubes, Vitkova et al.¹¹ measured the hydrodynamic mobility and deformation of vesicles in the confinement range of 0.25 < λ < 1.1 and compared the data with the HHW²² model, assuming the drop viscosity as infinite, i.e., they invoked the rigid sphere approximation. Reasonably good agreement was found with the HHW²² model, prompting them to suggest that there is no momentum transfer across the bilayer for motion of vesicle in tubes. Bruinsma²⁴ applied the lubrication theory to describe long and closely fitting vesicle motion in tubes and discussed the rheological regimes. More recently, Barakat and Shaqfeh²⁵ developed a singular perturbation theory for the motion of an inertia-less vesicle in a tube and found good agreement with the mobility data of Vitkova et al.¹¹

The motion of red blood cells (RBCs) in cylindrical tubes has been extensively studied^{12,13,26–32} in the context of blood rheology, but the number of mobility measurements are much less. Albrecht et al.¹³ measured the mobility (they referred it as overvelocity) of RBCs in a glass capillary at different hematocrits (0.1–0.6) and varying capillary diameter (3.3 to 11 μm). They compared the mobility of RBCs with the mobility of model particles measured in a circular tube by Lee and Fung³¹ and Sutera et al.³³ They found that RBCs have higher mobility than the model particles. Halpern and Secomb³² and Secomb et al.²⁷ also studied the mobility of RBCs in a circular tube through numerical analysis. We did not find any studies related to the measurement of mobility of cancer cells in tubes.

With advances in microfluidics, there is currently significant interest in studying the transport of particles in rectangular microchannels.^34,35 In contrast to the numerous investigations in the tubes discussed above, relatively few studies exist on studying particle mobility in microchannels. Mietke et al.³⁶ experimentally measured the velocity of rigid polystyrene (PS) beads in a square channel (Re ≈ 0.1, λ = 0.55–1) and good agreement was found with the analytical results obtained from the stream-function approach. With respect to cancer cells, there are several studies^37–41 that measured their passage time or velocity in rectangular or square microchannel at λ > 1, but attempts to determine mobility were not pursued.

It is clear from our survey of literature that there are several gaps in the experimental measurement of mobility of deformable particles and cells in microchannels. First, mobility data on vesicles and cancer cells in microchannel flow do not exist. Second, there has not been a systematic comparison of the mobility of polymeric particles, vesicles, and cells. Such a comparative investigation might allow insights drawn from understanding the mobility of simpler model systems to interpret data from cells that are more complex.

To address these gaps, we focused on the measurement of the mobility of vesicles and tumor cells in a microchannel with a square cross-section, supplemented by studies with rigid and elastic spheres. Our measurement regime for particle confinement is 0.3 < λ < 1.5, and the flow conditions are such that particle Reynolds numbers are 0.1 < Re_p < 2.5. Similar to Vitkova et al.,¹¹ we compare the results of our data with the HHW model. Our results show that simple modifications of the HHW model for cylindrical conduits can successfully capture the mobility of rigid and elastic spheres, even when λ → 1. For vesicles and cells, we find that the mobility of cancer cells is larger than that of rigid/elastic spheres but lower than vesicles. We explain our results by considering shape deformation and surface mobility at the interface in the three systems.

II. MATERIALS AND METHODS

A. Samples

1. Polymeric particles

Polystyrene beads (Polyscience Inc., USA) and polydimethylsiloxane (PDMS, Dow Corning) particles⁴¹ were used as a model for rigid and elastic spherical particles, respectively. The PDMS particles were synthesized using a 30:1 ratio of base to curing agent. 1 ml of the PDMS mixture was added to 10 ml of 3 wt. % Tween 20. The particle emulsion was created by mixing the solution for 2 min with a vortex mixer and curing it overnight at 70 °C. The particle solution was then filtered with a 30 μm filter (CellTrics, Germany) to obtain particles with a maximum diameter of 30 μm. Two different suspending phases were used: deionized (DI) water and 11 wt. % polyethylene glycol (PEG20000, Fluka Analytical) in phosphate buffered saline (PBS) with viscosities μ₀ = 1 and 10 mPa s, respectively. The particle solutions were prepared to a final concentration of 5 × 10⁵ particles/ml using the manufacturer reported particle diameter of 15.13 μm ± 6% and a concentration of 1 wt. % solid beads in water.

2. Vesicles

Giant unilamellar vesicles (GUVs) were prepared using standard electroformation protocols.⁴² The lipids used were 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1-stearoyl-2-oleoyl-sn-glycero-3-phospho-choline (SOPC). They were diluted with chloroform to achieve a concentration of 1 mg/ml. Vesicles were formed using 2 lipid solutions: DOPC and a 1:1 molar ratio of SOPC and cholesterol (here onwards referred to as SOPC:Chol). An electroformation chamber was created using two indium tin oxide glass slides (15–25 Ω/sq) and a 1 mm thick PDMS spacer. A thin film was created in the chamber by dispensing 10 μl of 1 mg/ml lipid solution onto one of the glass slides and then drying it in a vacuum desiccator for 30 min. In the closed chamber, the lipids were hydrated with a 0.11 M sucrose solution. The chamber was then connected to a waveform generator and AC voltage was applied at 2.6 V and 10 Hz for 3 h and then 4.4 V and 4 Hz for 45 min. After formation, the vesicle solution was diluted with 0.12 M glucose. The lipids were purchased from Avanti Polar Lipids and the remaining materials from Sigma Aldrich.

The membrane properties of these two vesicle systems are listed in Table I, which were obtained from the literature,^43–45 with vesicles made from SOPC:Chol having higher values of bending modulus (κ_b), stretching elasticity (K_s), and lysis tension (σ_c) than DOPC vesicles. Two dimensionless parameters that dictate the influence of thermal fluctuations in the lipid bilayer on the vesicle shape are excess area, Δ, and reduced volume, ν. Here, $\Delta =\frac{S}{4\pi R^2}-1$, where S is the measured surface area of the vesicle and R is the radius of a sphere with the same measured volume of the vesicle. The reduced volume is the ratio of the actual volume of the vesicle to the volume of a sphere with the same surface area, which can be shown to be related to Δ, as $\nu ={\left(1+\Delta \right)}^{-3/2}.$

TABLE I.

Membrane properties of the vesicles used in the study. The data was obtained from Refs. 43–45.

Parameter	DOPC	SOPC:Chol
Bending modulus, κb (J)	1.08 × 10−19	2.46 × 10−19
Stretching elasticity, Ks (mN/m)	310	1985
Lysis tension, σc (mN/m)	9.92	25.805

Garbin and coworkers⁴⁶ measured the excess area of these two systems. They measured the surface area and volume of the vesicles by flowing them in cylindrical capillaries and operating at conditions such that the vesicle membrane is flat and ironing out the thermal fluctuations but it is not stretched. These operating conditions correspond to Ca_b = μ₀VR²/κ_b > 1 and Ca_Κ = μ₀V/K_s < 10⁻³, where Ca_b and Ca_Κ are the two capillary numbers based on bending modulus and stretching elasticity, respectively. For the lipid systems used in this study, they measured average excess area values of 0.13 and 0.17 for DOPC and SOPC:Chol, respectively.⁴⁶ From these Δ values, we calculated the mean values for ν which are 0.83 and 0.79 for DOPC and SOPC:Chol, respectively. Note that ν = 1 corresponds to a fully inflated spherical vesicle.

3. Cancer cells

In this study, breast cancer cell lines MCF7 and MDA-MB231 and lung cancer cell lines H1437 and H1299 were used. MCF7 was obtained from Dr. Lauren Gollahon (TTU, Department of Biological Sciences), MDA-MB231 was purchased from ATCC (ATCC^® HTB-26™), and H1437 and H1299 were obtained from Dr. Sam Hanash (MD Anderson Cancer Center, The University of Texas). MCF7 and MDA-MB231 were cultured in Dulbecco's modified eagle medium (DMEM) supplemented with 10% fetal bovine serum (FBS), 1% Penicillin/Streptomycin (Gibco 15140-148), and 1% sodium pyruvate (Gibco). H1299 and H1437 were cultured in RPMI 1640 containing 10% FBS and 1% Penicillin/Streptomycin. All cells were cultured in an incubator at 37 °C in a 5% CO₂ environment. Confluent cells were harvested for the experiment using Trypsin/EDTA (0.25%, Gibco). All the experiments were completed within 30 min of being harvested. Trypan blue, at a final concentration of 10% v/v, was added to the suspending phase to identify dead cells entering into the channel and to have better contrast between cells and the surrounding fluid phase. The cell concentration used in the mobility experiments was 5–6 × 10⁵ cells/ml.

B. Microfluidic channel fabrication

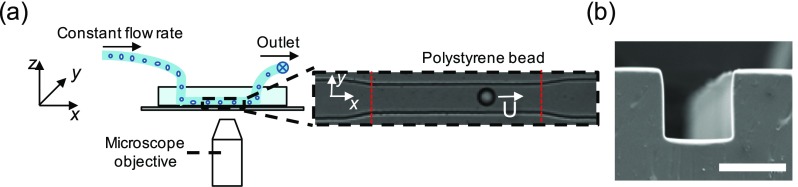
Linear microchannels of length 150 μm and a square cross-section (measured width is 25 ± 0.4 and height is 25.3 ± 0.4 μm), as shown in Figs. 1(a) and 1(b), were fabricated using standard soft lithography techniques.⁴⁷ The PDMS replicas was cut, peeled, and 1 mm holes were created using biopsy punchers (Miltex, Japan) for connecting the tubing. They were subsequently cleaned using isopropanol and bonded to cover glass (No. 2, Fisher Scientific) using corona treatment⁴⁸ for 2 min (BD-20AC Laboratory corona treater, Electro-technic products). After bonding, the devices were heated at 70 °C for 4 min to have a permanent seal. The channels were filled with 4 wt. % bovine serum albumin (BSA, Sigma Aldrich) in phosphate-buffered saline solution (Gibco) for at least 1 h at 37 °C to reduce non-specific adhesion of cells to the walls. The sealed devices were used within two days of bonding.

FIG. 1.

High throughput particle mobility measurements in microchannels. (a) Schematic of the experimental setup showing the microfluidic device, microscope objective, and the particle flow path through the microchannel. The inset shows the bright field image of the tapered entrance and the straight channel with a polystyrene bead traveling at a velocity U. The dashed vertical lines in red indicate the linear section of the microfluidic geometry. The straight channel has a height, width, and length of 25 ± 0.4, 25.3 ± 0.4, and 150 μm, respectively. (b) Scanning electron micrograph image showing the square channel cross-section. The scale bar is 25 μm.

C. Experimental protocol

The experimental setup for mobility measurement consisted of a microfluidic device, a syringe pump, and a microscope connected with a high-speed camera. A simplified schematic of the experimental setup is shown in Fig. 1(a). A syringe pump (PHD 2000, Harvard Apparatus, Massachusetts, USA) was used to drive fluid from a 100 μl Hamilton gastight syringe to the microfluidic device through a 0.02″ inner diameter Tygon tubing (Cole Parmer) and a 20-gauge hollow blunt pin (Instech, USA). A constant flow rate of 100 μl/h was used for the particle experiments and 50 μl/h was used for the vesicle and cell experiments.

Bright-field imaging was used to record particle and cell passage through the test section of the channel using a combination of an inverted microscope (Nikon eclipse TiU) and high-speed CMOS camera (Phantom v710 12-bit, Vision Research). The region of interest (ROI) included the area of test section and three channel widths before and after the test section. The ROI was recorded with a reduced resolution of 448 × 80 pixels at a frame rate of 2000 fps using 30× magnification. The microscope objective was focused approximately on the midplane of the linear channel. The effective pixel size for this optical setup is 0.64 μm and the depth of focus is ∼2.5 μm. Implementation of Köhler illumination combined with a high-power halogen bulb enabled us to use 1 μs exposure time to record blur-free motion of cells traveling at typically ∼3.0 cm/s. The image based auto trigger (IBAT) feature of the Phantom v710 camera was used to save only those frames when a cell or particle passes through the test section, which reduces the number of images that need to be analyzed drastically (about 15–20 frames per particle or cell). Imaging of vesicles was performed in the phase contrast mode on an inverted microscope (IX71, Olympus Inc.) connected with a CMOS camera (Phantom v310 12-bit, Vision Research). A frame rate of 5000 fps was used to record images at 32× magnification and 50 μs of exposure time. The effective pixel size for this optical setup is 0.625 μm.

D. Image processing

A custom written MATLAB routine was used for automated image processing and data analysis of particles and cells. For vesicle experiments, analysis was performed manually using the ImageJ software (NIH) due to the low contrast between the vesicles and the surrounding fluid. For automated analysis, images were segmented using different filters to enhance contrast, subtract background, and identify the presence of an object, in this case, a particle or a cell. After segmentation, each object was given an identification (ID) number when it appears in the ROI for the first time. The object's projected area (from top view), centroid location, perimeter, and frame number were recorded against that ID number for all the frames that the object takes to pass through the ROI. The object diameter was calculated from the cross-sectional area assuming that the cross-sectional area represents the maximum cross-section of a sphere (max error in size measurement <3%). MATLAB's built in function “regionprops” in the image processing toolbox was used to obtain the area, perimeter, and centroid location from the segmented image.

Image frames where multiple particles or cells occupied the ROI were discounted since it is possible that their mobility is affected due to hydrodynamic interactions. The degree to which the object was off-centered (in xy- plane) in the channel was measured from the y-coordinate of the centroid and the mobility data was discarded if the centroid deviated by more than 2.0% from the center. We also measured the shape deformation of each particle inside the test section of the channel and only picked the particles which are spherical in shape using a threshold deformation index value (discussed in Sec. IV A).

E. Flow conditions

Table II reports the particle-based Reynolds number and capillary numbers corresponding to the flow conditions used in this study. The particle-based Re⁴⁹ is defined as Re_p = ρ₀V_maxa²/μ₀D, where ρ₀ is the density of the suspending fluid and V_max is the maximum fluid velocity in the channel. Because of the polydispersity present in the systems being studied, here, we use the mean particle diameter a to calculate Re_p which ranged from 0.09 to 2.47. This range indicates that particles, vesicles, and cells all exhibited finite inertia while passing through the microchannel. For PS and PDMS particles, the capillary number is defined as, Ca = μ₀V/aG′, where G' is the elastic modulus of the particle [30:1 PDMS G′ = 95 kPa;⁴¹ PS G′ = 3.25 GPa (Ref. 50)] For the PS and PDMS particles, Ca ≪ 1, suggesting that the particles did not deform while flowing through the test channel. For cells, the capillary number is defined as Ca = μ₀V/γ, where γ is the membrane tension of the cell [0.01–1 mN/m (Refs. 51 and 52)]. The Ca values ranged from 0.017–2, suggesting that the cells did not deform significantly in the microchannel during flow.

TABLE II.

Experimental parameters and regime of operation for mobility measurement.

	Samples	Rep	Ca	Cab	CaK
Rigid particles	PSa	0.920	1.63 × 10−9	…	…
	PSb	0.092	1.63 × 10−8	…	…
	PDMSa	1.333	5.59 × 10−5	…	…
	PDMSb	0.133	5.59 × 10−4	…	…
Vesicles	DOPC	2.471	…	3.6 × 104	1.1 × 10−4
	SOPC: Chol	2.471	…	2.1 × 104	1.5 × 10−5
Cells	MCF7	0.863	0.02–2.0	…	…
	MB231	0.863	0.02–2.0	…	…
	H1299	1.029	0.017–1.7	…	…
	H1437	1.029	0.017–1.7	…	…

^aμ₀ = 1 mPa s.

^bμ₀ = 10 mPa s.

III. THEORETICAL MODEL FOR PARTICLE MOBILITY

In this study, we compare the measured mobility of particles, vesicles, and cells with predictions from the HHW model. HHW derived the settling velocity of a drop or bubble in a cylindrical tube under Stokes flow conditions using the method of reflections

$$\mathrm{U}=\frac{2\left({\rho }_i-{\rho }_0\right)\mathrm{g}{\left(\frac{a}{2}\right)}^2}{9{\mu }_0}\hspace{0.17em}\frac{1+\mathrm{K}}{\frac{2}{3}+K}\hspace{0.17em}\left[1-\frac{2+3K}{3\left(1+K\right)}\left(\lambda \right)\mathrm{f}\left(\frac{b}{R}\right)\right]+{\mathrm{V}}_{max}\hspace{0.17em}\left[1-{\left(\frac{b}{R}\right)}^2-\left(\hspace{0.17em}\frac{2K}{3K+2}\right)\hspace{0.17em}{\lambda }^2\right]+\hspace{0.17em}\mathrm{O}\hspace{0.17em}\left({\lambda }^3\right),$$ (1)

where ${\mathit{\rho }}_{\mathit{i}}$ and ${\mathit{\rho }}_{\mathit{e}}$ are the density of the drop and external fluid, respectively. The function $\mathrm{f}\left(\frac{\mathit{b}}{\mathit{R}}\right)$ is called the eccentricity function and the value of this function is determined in Happel and Brenner (1965, p. 309).⁶³

Here, we chose the HHW model to compare with our experimental data for several reasons. First, unlike HHW, other studies such as those of Hyman and Skalak,¹⁵ Martinez and Udell,¹⁶ and Wang and Skalak²¹ requires numerical analysis to predict mobility. Moreover, the analyses by Martinez and Udell¹⁶ and Wang and Skalak²¹ show that their computed hydrodynamic mobility of droplets in circular tubes is in good agreement with the small deformation model of HHW. Second, Murata¹⁹ derived a mobility model for an incompressible, neutrally buoyant, spherical, homogeneous, elastic particle in circular tube under Stokes flow condition, and the HHW result matches that of Murata, when the condition for an elastic particle, K → ∞, is imposed in the HHW solution. Third, Belloul et al.²³ showed that the HHW result agrees reasonably well with their measured droplet mobility in cylindrical tubes for λ < 0.7.

To apply the HHW model to our data from square microchannels, we modified Eq. (1) in the following ways: (I) we estimated the effect of gravitational settling of our buoyant solid particles which have a 5% density difference on their mobility and found it to be negligible, <0.0001%. Therefore, we simplified the model by removing the first term and assuming the mobility of the solid objects is equal to that of a neutrally buoyant object. (II) In a circular tube, the ratio of max-to-mean fluid velocity for Poiseuille flow is 2, whereas in a square microchannel it is 2.096.⁵³ It should be noted that the change in the prefactor only accounts for the change in the cross-section area of the channel and does not take into account the gutter flows that form when confined objects flow in microchannels (III). Lastly, we replaced the tube diameter with the hydraulic diameter of the square channel. With these adjustments, Eq. (1) becomes

$$\beta =2.096\hspace{0.17em}\left[1-{\left(\frac{b}{R_h}\right)}^2-\left(\hspace{0.17em}\frac{2K}{3K+2}\right)\hspace{0.17em}{\lambda }^2\right]+\hspace{0.17em}\mathrm{O}\hspace{0.17em}\left({\lambda }^3\right).$$ (2)

For a solid particle, we set K → ∞, and obtain

$$\beta =2.096\hspace{0.17em}\left[1-{\left(\frac{b}{{\mathrm{R}}_h}\right)}^2-\frac{2}{3}\hspace{0.17em}{\lambda }^2\right]+\hspace{0.17em}\mathrm{O}\hspace{0.17em}\left({\lambda }^3\right).$$ (3)

In this study, Eqs. (2) and (3) were used to compare the mobility of rigid spheres, elastic particles, vesicles, and cells.

IV. RESULTS

A. Quantification of particle mobility in channel flow

As discussed in Sec. I, the hydrodynamic mobility of a particle is defined as the ratio of the particle's steady velocity to the mean velocity of the surrounding fluid. In this section, we discuss three important factors that can affect the determination of the particle mobility: (i) the three-dimensional position of the particle in the square conduit, (ii) the slight non-spherical shape of the particle, and (iii) the region in the linear channel where the particle achieves steady velocity.

The three-dimensional location of a particle in the square conduit can influence its mobility with particles close to the wall moving less than those in the center. In our experiment, we are only able to determine the centroid of the particle in the x-y plane [see Fig. 1(a)] and do not have any control over the z-location of the particle. All the mobility data shown corresponds to the particle centroid (in the x-y plane) being within 1% of the conduit axis. Therefore, most of the uncertainty in determining mobility at a given particle confinement is due to variability in the z-position.

We also considered the influence of the particle shape on its mobility since both cells and vesicles can be non-spherical prior to entering the linear channel or undergo deformation in the channel and become non-spherical. In addition, it is important to consider shape effects, since the HHW model is applicable only for spherical objects. To characterize the object's shape and only consider for mobility analysis of those particles (and vesicles and cells) that are spherical in shape prior to entering the linear channel, we defined a deformation index, DI, as⁵⁴

$$\mathit{D}\mathit{I}=\mathrm{1}-\frac{\mathrm{2}\sqrt{\mathit{\pi }\mathit{A}}}{\mathit{p}}$$ (4)

In Eq. (4), A is the projected area of the object as seen in the microscope image and p is its perimeter. If the object is completely circular in the two-dimensional view, the DI will be zero, which implies a perfect circle. As the object deviates from a perfect circle, the DI will increase accordingly. We measured particle DI prior to entering the linear channel, where the instantaneous velocity starts to increase (referred to as Initial DI).

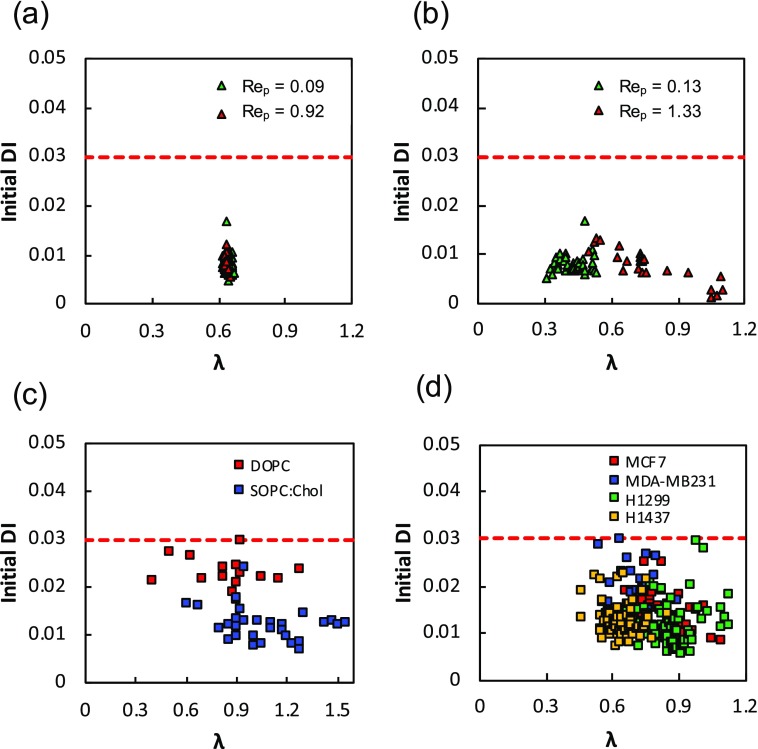
Figure 2 shows the Initial DI for the all the systems studied as a function of confinement, where we have only plotted those data points where DI < 0.03. We note that some vesicles and cancer cells were found to have DI > 0.03 which were not included in the mobility analysis. The Initial DIs of rigid PS particles were found to be very small, indicating that as expected, these particles enter the channel as spheres. There is some scatter in the DI data even for rigid spherical PS beads. This might be because of variation in the pixel intensity near the edge of the particle due to its rotation in flow or possible variation in the z-location of particles. Based on these polystyrene bead results, we use 0.03 as a cut-off value of Initial DI, to assess whether the PDMS particles, vesicles, and cells entering the channel are spherical. We analyzed only those vesicles and cancer cells having an initial DI ≤ 0.03 [Figs. 2(c) and 2(d)]. Since we measured the initial DI for all the systems before entering into the constricted channel where all the deformable objects are unconfined, we do not see any effect of confinement on the initial DI.

FIG. 2.

Deformation index of polymeric particles, vesicles, and cancer cells. The deformation index is plotted as a function of confinement for (a) polystrene beads, (b) PDMS particles, (c) vesicles, and (d) cancer cells. The red dashed lines represent DI = 0.03.

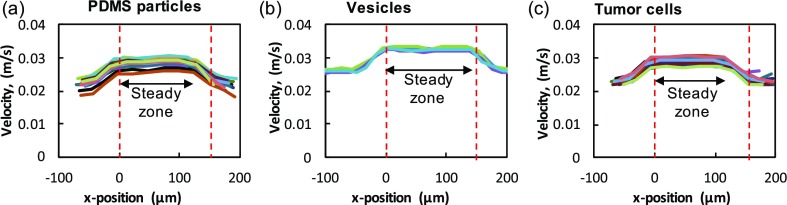
Finally, the region in the linear channel where the particle achieves steady velocity needs to be identified for accurate measurement of mobility. To determine this steady zone, we determined the instantaneous particle velocity as it travels in the microfluidic geometry. Figure 3 shows the instantaneous velocities for (a) PDMS particles, (b) vesicles, and (c) cells. In all cases, we find that as the particles enter the tapered entrance into the linear channel, their velocities begin to increase and reach a maximum at the beginning of the linear channel. To identify the region in the linear channel where the particle velocity is steady, we chose particles in the confinement range of 0.75 ≤ λ ≤ 0.80 and computed their velocity profiles as shown in Fig. 1(c). We find that the velocities remain steady for at least for the first ∼90% of the channel length before beginning to decrease as they exit into the larger exit channel. We compute the mean of the instantaneous velocities in this steady region and take it as U for mobility calculation. We find the maximum variation in particle velocity measurement in this region is <1%.

FIG. 3.

Velocity of the particles in the channel. The instantaneous velocity of (a) PDMS particles, (b) vesicles, and (c) tumor (MCF7) cells along the x-position of the channel length. For all three systems, the velocity is plotted for the confinement range of 0.75 < λ < 0.80. The region between the dashed vertical lines in red indicates the linear portion of the microfluidic geometry.

B. Mobility of polymeric particles

In this section, we present the mobility of (i) rigid polystyrene particles and (ii) elastic PDMS particles and compare them with the HHW model, Eq. (3), to determine if the data is in good agreement with the model and over what confinement range the model is applicable.

1. Rigid PS spheres

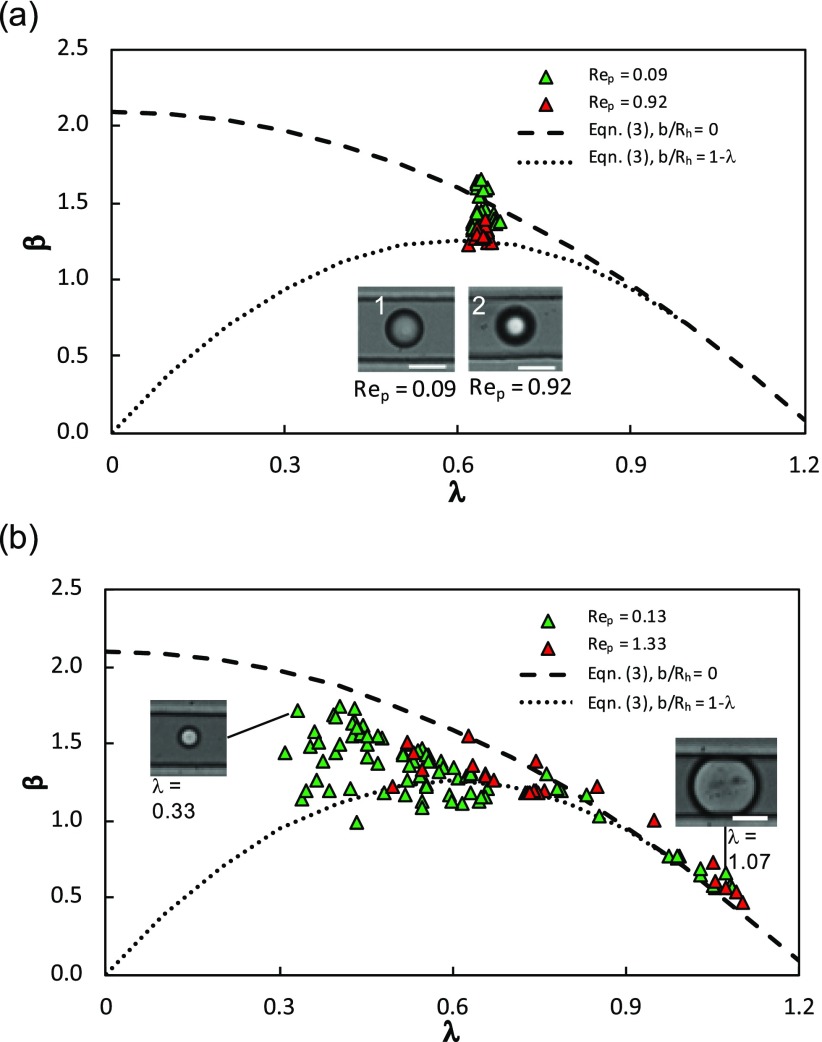
Figure 4(a) shows the hydrodynamic mobility of monodisperse rigid PS particles as a function of confinement at two values of Re_p corresponding to the two different suspending fluid viscosities. To compare this data with the HHW model, we plot Eq. (3) for the case where the particles are on the centerline, i.e., b/R_h = 0, and the case where the particles are touching the channel walls, i.e., b/R_h is maximum. Note that for a given λ, the maximum possible b/R_h is 1 − λ. The reason we plotted these two curves in Fig. 4(a) is that we filtered our data to only include those particles whose centroid was within 1% of the centerline. Here, the scatter could arise due to particles having different z-locations; nevertheless, we find that majority of the data points for the rigid spheres lie within these two bounds calculated from the HHW model.

FIG. 4.

Mobility of rigid and elastic particles. The mobility of (a) PS beads and (b) PDMS particles is plotted as a function of confinement. The red and green triangles represent continuous phase viscosities corresponding to Re_p = 0.92 and Re_p = 0.09 for PS beads and Re_p = 1.33 and Re_p = 0.13 for the PDMS particle, respectively. Two mobility model curves using Eq. (3) are shown where the dashed line represents a particle in the center of the channel (b/R_h = 0) and a particle with the maximum off-centeredness (b/R_h = 1 − λ). The inset in (a) shows a particle in focus that is in the center of the channel (1) and a particle out of focus that is at the roof of the channel (2). The insets in (b) show experimental images of the PDMS particles at different confinements. The scale bar in all the images is 15 μm.

An interesting observation from Fig. 4(a) is that particles at Re_p = 0.92 seem to have lower mobility than particles with Re_p = 0.09. This could be because the particle inertia at Re_p = 0.92 is about ten times more than that at Re_p = 0.09; the particles at Re_p = 0.92 might therefore be subjected to a higher inertial lift force making them to move away from the centerline and reducing their mobility. To provide evidence that the lower mobility is due to particles moving closer to the wall, in the inset of Fig. 4(a), we show representative images of particles with Re_p = 0.92 and 0.09. Indeed, we observe that at Re_p = 0.92, the particle appears defocused indicating it is away from the focal plane and therefore located closer to the channel wall. The two extreme bounds of the HHW model capture somewhat the migration effects due to the inertial lift of the particles.

2. Elastic PDMS particles

Due to the monodispersity of the PS particles, we were able to determine their mobility at a unique value of confinement λ ≈ 0.65. To evaluate how the mobility of solid particles changes over a wide confinement range, we measured the mobility of polydisperse elastic PDMS particles. In Fig. 4(b), as expected, we find that the mobility of the PDMS particles decreases with increase in confinement since larger particles occlude more of the conduit space. When comparing the mobility data with the HHW model across the entire confinement range, 0.3 ≤ λ ≤ 1.1, we find reasonably good agreement. Interestingly, the HHW model is able to predict the mobility up to λ = 1.1, where PDMS particles are slightly deformed and touching the walls [see the inset in Fig. 4(b)]. This is in contrast to the case of confined droplet motion in cylindrical tubes, where the HHW model could not predict the mobility of droplets with λ ≥ 0.7 because of drop deformation.^8,23 Another noteworthy observation is that for particles with confinements of λ = 0.40–0.65, we find that some of the data points have mobility less than the lower bound from the HHW model. It is possible that at these low confinements and near-wall condition, the simple modification of the HHW model, Eq. (3), is not sufficient because the hydrodynamics is more similar to the motion of a small particle near a planar wall rather than a large off-centered particle in a square duct.

C. Mobility of vesicles

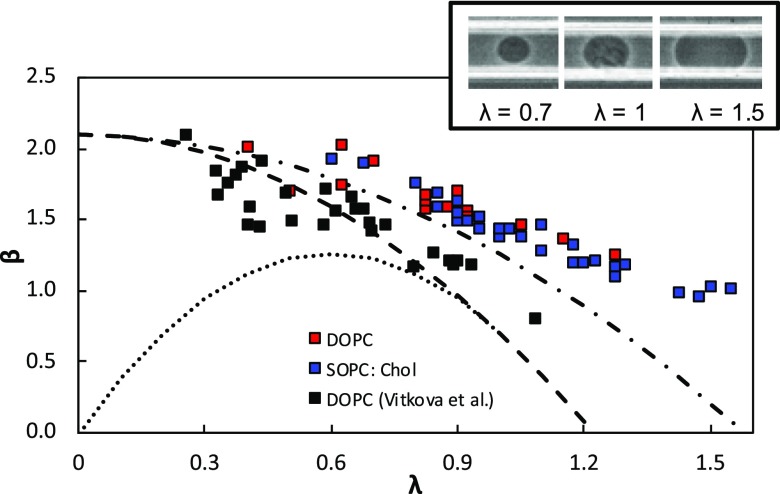
In this section, we report the mobility of vesicles formed from two different lipid systems and compare them to the HHW model and data from Vitkova et al.¹¹ In Fig. 5, we plot the mobility of the DOPC and SOPC:Chol vesicles as a function of confinement by considering only those vesicles with initial DI < 0.03. Similar to the polymeric particles, we observed that the vesicle mobility decreased as the confinement increased. Also, even though the mechanical properties of SOPC:Chol were different from that of DOPC (see Table I), there was not a significant difference in their mobility.

FIG. 5.

Mobility of vesicles verses confinement. DOPC and SOPC:Chol vesicles are the red squares and blue squares, respectively. Vitkova et al. data is plotted on top of our experimental data (black square). The dashed line is Eq. (3) with b/Rh = 0 and the dotted line is also Eq. (3) with b/R_h = 1 − λ for a given λ. The dot and dash line is Eq. (2) with K = 1. The inset shows experimental images of SOPC:Chol vesicles at different confinements.

In Fig. 5, we also compare our mobility data with that from the study of Vitkova et al.¹¹ for DOPC vesicles in a circular tube. We find that the vesicle mobility in square channels is higher than that in tubes. Interestingly, the data of Vitkova et al. is in good agreement with the HHW model for a solid particle, i.e., K → ∞. However, in our square channels, the vesicle mobility is higher than the predictions from the HHW model. Vitkova et al. explain that the good agreement comes from the absence of flow on the vesicle surface due to axisymmetry in the exterior fluid flow. Since the square channel has only a planar symmetry, there could be flow on the vesicle surface. To test this hypothesis, we plot the HHW model for droplets with K = 1, the case where the interface is completely mobile. We observe a good agreement between our vesicle data and the droplet model suggesting that the vesicle surface might be mobile.

D. Mobility of cancer cells

Next, we measured the mobility of four different cancer cell lines to assess how different is their mobility compared to rigid particles and vesicles. This comparison between model systems and cells is essential to interpret the mobility data of cancer cells, and understand the differences in the response of cell and vesicle membrane to hydrodynamic stresses. We considered two breast cancer cell lines, MCF7 and MDA-MB231, with the MCF7 being weakly metastatic and MDA-MB231 being highly metastatic.⁵⁵ We also considered two lung adenocarcinoma cell lines, H1299 and H1437, which have features of mesenchymal and epithelial cells, respectively.⁵⁶ During metastasis, epithelial cells lose their adherent junctions and switch to a mesenchymal phenotype allowing them to migrate and invade.^57,58 Selecting these different cell lines also allowed us to examine whether hydrodynamic mobility could be used to elicit differences between cancer cell lines.

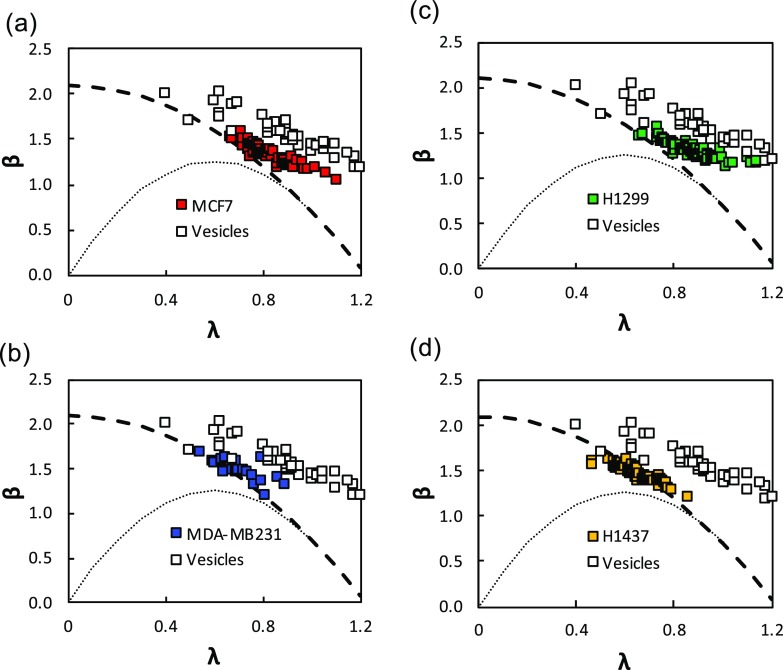
Figures 6(a)–6(d) show the mobility results of breast and lung cancer cell lines. Here, we have also plotted our vesicle mobility data along with predictions from the HHW model for cases when b/R_h = 0 and b/R_h = 1 − λ. Similar to polymeric particles and vesicles, we observe that mobility of cancer cells decreases with increasing confinement. The mobility data for all cancer cells is in good agreement with the HHW model up to λ ≈ 0.8. Interestingly, we find that tumor cells have higher mobility than rigid particles but lower than vesicles, suggesting that the membrane frictional properties are in between a solid-like interface and a fluid bilayer.

FIG. 6.

Mobility of cancer cells. Mobility versus confinement plot of breast cancer cell line (a) MCF7, (b) MDA-MB231 and lung adenocarcinoma cell line (c) H1299, and (d) H1437. Mobility of vesicles is plotted as white squares for comparison with cells. Also plotted is Eq. (3) for two conditions of b/R_h = 0 (dashed line) and b/R_h = 1 − λ (dotted line).

Differentiating the cancer cell lines based on mobility was difficult because the mean cell size was not the same in all cell lines. As shown in Figs. 6(a) and 6(b), the confinement for MCF7 and H1299 cells spanned up to λ ≈ 1.1, whereas for MDA-MB231 and H1437, it was limited to λ ≈ 0.8. By comparing the mobility data for λ ≤ 0.8, we observe there are no significant differences in the four cell lines. Here, we have used a single microchannel (of cross-sectional area 25 × 25 μm²), however, conducting more studies in microchannels of additional cross-sectional areas can produce a wider range of confinement allowing cancer cells of different metastatic capacity to be distinguished based on hydrodynamic mobility.

V. DISCUSSION

Here, we presented the measurements of mobility for three different systems, namely polymeric particles, vesicles, and cells in a square conduit. In all cases, we reported the mobility only for those objects that were spherical prior to entering the linear channel. Then, we compared the experimental measurements with the mobility theory for particle motion in a circular tube with modifications made for the square channel. Our key results are: (i) the mobilities of rigid and elastic particles are well predicted by the modified HHW model, even at higher confinements (0.7 < λ < 1), (ii) vesicles move faster in a square channel than in a circular tube and their mechanical properties did not significantly affect their mobility for the conditions studied here, and (iii) cancer cells have mobility that is lower than vesicles but higher than solid particles. In this section, we discuss the mechanisms that could lead to differences in mobility between the three systems studied.

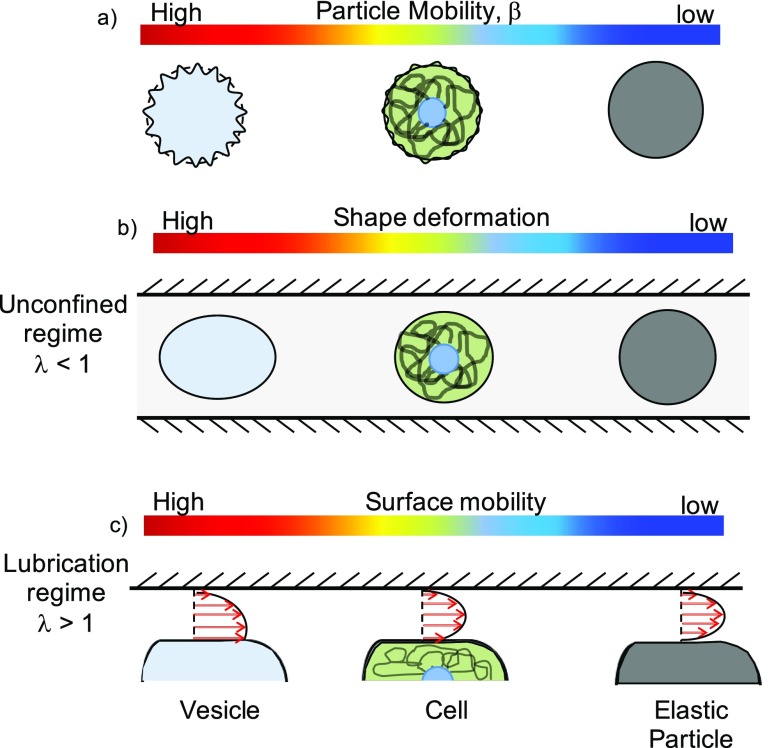
In Fig. 7(a), we show the three systems with a color bar indicating the mobility from high to low. When they are unconfined (λ < 1) as shown in Fig. 7(b), vesicles can deform under shear flow, with their deformation being more than cells and rigid particles. This is consistent with the images shown in the inset of Fig. 5, where a vesicle with λ = 0.7 appears deformed, i.e., the major axis is 5% larger than the minor axis. We did not observe any strong effect of the mechanical properties on the vesicle mobility since our operating regime is such that the bending fluctuations are ironed out (Ca_b ≫ 1). Although, we could not control the reduced volume in our experiments, we expect that the vesicles with a lower reduced volume will have a higher mobility.²⁵ In contrast, cells can deform, but much less because their membrane is bound to the cytoskeleton. These deformations effectively reduce their confinement and therefore produce higher hydrodynamic mobility.

FIG. 7.

Possible mechanisms to explain the differences in the mobility of vesicles, cells, and solid particles. Variation in (a) particle mobility, (b) shape deformation, and (c) surface mobility in the three particle systems studied. The color bar ranges from high (red) to low (blue).

Under conditions of stronger confinement i.e., λ > 1, the vesicles and cells can conformally fit to the square cross-section producing thin lubricating films and corner flows. We observe that in this lubricated regime as well, vesicle mobility is higher than the mobility of cells and solid elastic particles. A possible explanation for the higher mobility of vesicles is that their surface is mobile due to the swirling exterior fluid flow created by the presence of corners in a square duct. This surface mobility can admit non-zero velocity gradients on the membrane causing surface flow [see Fig. 7(c)]. In a circular tube, flow around a vesicle in the annulus is axisymmetric that does not permit surface flow on the vesicle membrane.¹¹ In contrast, motion of a vesicle in a square duct can generate surface flows creating effectively, a slip-like interface and therefore permitting the vesicle to move faster. Indeed, when we assume a fully mobile interface for the vesicle and fit the HHW model for a droplet, the vesicle mobility data is in good agreement with the theory (see Fig. 5). Furthermore, a recent study shows the presence of surface flows on a vesicle anchored to a solid surface and subjected to simple shear flow in a microfluidic device.⁵⁹

With regards to cells, their surface mobility might be less than vesicles due to the presence of membrane inclusions such as proteins. The fluidity in the plasma membrane of cells is well established⁶⁰ and has been linked to invasion⁶¹ and drug resistance⁶² in cancer cells. In our study, we did not find significant differences in the mobility of breast and lung cancer cells for λ < 0.8, suggesting that in this regime, the frictional properties of the membranes in all the cell lines are similar. More studies need to be pursued over a broader range of confinement to establish the validity of hydrodynamic mobility as a marker for distinguishing cancer cell lines.

VI. CONCLUSIONS

In this study, we presented the mobility results for solid particles, vesicles, and tumor cells. For polymeric particles, we found a good agreement between our experimental data and the modified analytical model of HHW. Interestingly, we discovered that the mobility of cells and vesicles was greater than those of the solid particles. In addition, we found that vesicle mobility is higher in a square channel than in a circular tube. We explained our observations by considering differences in shape deformation and surface mobility of the three systems studied. In the future, more studies are warranted to confirm the presence of surface flow during vesicle motion in channel flows. The experimental results of mobility reported in this study will perhaps motivate new theoretical and numerical simulations on the motion of deformable particles in microchannel flows.