Comparisons of energy cost and economical walking speed at various gradients in healthy, active younger and older adults

Abstract

Background/Objective

Oxygen consumption during walking per unit distance (C_w; mL/kg/m) is known to be greater for older adults than younger adults, although its underlying process is controversial.

Methods

We measured the C_w values at six gait speeds from 30 m/min to 105 m/min on level ground and gradient slopes (±5%) in healthy younger and older male adults. A quadratic approximation was applied for a relationship between C_w and gait speeds (v; m/min). It gives a U-shaped C_w–v relationship, which includes a particular gait speed minimizing the C_w, the so-called economical speed (ES). The age-related difference of the C_w–v relationship was assessed by comparisons of ES and/or C_w.

Results

A significantly greater C_w at 30 m/min and slower ES were found for older adults at the downhill gradient, suggesting that a combination of leftward and upward shifts of the C_w–v relationship was found at that gradient. Only a slower ES was found for older adults at the uphill gradient, suggesting that a leftward shift was found for older adults at that gradient. Neither a significant leftward nor an upward shift was found at the level gradient. Leg length significantly correlated to the ES for younger adults at the level and downhill gradients, while such a significant relationship was observed only at the level gradient for older adults. The maximal quadriceps muscle strength significantly correlated to the ES for older adults at all gradients, but not for younger adults.

Conclusion

The age-related alteration of the C_w–v relationship depends on the gradient, and its related factors were different between age groups.

Introduction

It is well known that there is a U-shaped relationship between oxygen consumption during walking per unit distance (C_w; mL/kg/m) and gait speeds (v; m/min).¹ This indicates that there is a particular gait speed minimizing the C_w in each individual, and it has been called economical speed (ES)2, 3, 4, 5, 6 or optimal speed.7, 8, 9, 10

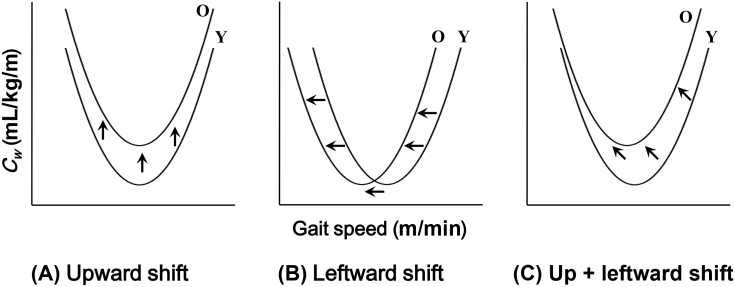
An age-related increase in the C_w values was found for healthy older adults,¹¹ and it was explained by a difference in the muscle strength in association with gait instability. This can be described as an upward shift of the C_w–gait speeds (v) relationship (Figure 1A). Such an age-related increase in the C_w values has also been reported by other studies, whereas mechanisms underlying the phenomenon have been controversial. Some related studies reported that several potential factors, including, but not limited to, training status,12, 13 aerobic fitness levels,¹⁴ differences in individual-limb mechanical work,15, 16 and leg-muscle activity patterns,15, 17, 18 are comprehensively related to the phenomenon. Given the results of these previous studies, no single factor alone can fully explain the age-related increase in the C_w values for older adults.

Figure 1.

Schematic illustration of (A) upward shift, (B) leftward shift, and (C) combination of upward and leftward shifts of the C_w–gait speed (v) relationship. Y and O represent younger and older adults, respectively. Arrows mean potential shifting directions. C_w–v = oxygen consumption during walking per unit distance and gait speeds.

An age-related increase in the C_w values for older adults will relate to a slower ES. However, such an increased C_w does not always result in a slower ES if the C_w–v relationship shifted only upward, as shown in Figure 1A. It is worth noting that most of the previous studies, except for Hortobágyi et al,¹⁸ tested only at the level gradient. Indeed, the C_w values increased steeply at faster walking speeds for older adults at the level gradient.11, 16 These previous results suggest that the physical characteristics, particularly in muscle strength, would relate to an alteration of the C_w–v relationship by aging, and it will result not only in a leftward shift (Figure 1B), but also in a combination of upward and leftward shifts of the C_w–v relationship (Figure 1C) at the gradient environments. However, as far as we know, no information has been available with regard to the ES in healthy older adults at the gradient environments. We further questioned whether the C_w–v relationship actually showed to be greater for healthy, older active manual workers than younger adults. We hypothesized that the age-related increase in the C_w values for older adults would result in an upward shift, or a combination of leftward and upward shifts of the C_w–v relationship at each gradient. The purpose of the present study was to investigate whether the C_w–v relationship could be affected by either aging or other factors, such as physical characteristics and environmental factors.

Methods

Participants

To eliminate the effects of different leg lengths on the C_w–v relationship, eight younger and eight older healthy male adults with equivalent body heights were recruited (Table 1). All older adults were nonretired full-time manual workers. After an explanation of all procedures, possible risks, and benefits of participation, written informed consent was obtained from each participant. This study conformed to the Declaration of Helsinki, and an ethical committee established in Kyushu Sangyo University approved the purpose and all procedures of this study (H240324).

Table 1.

Physical characteristics and muscle strength in two groups.

	Younger (n = 8)	Older (n = 8)
Age (y)	22.5 ± 0.6	64.8 ± 1.2*
Height (cm)	172.4 ± 1.9	170.2 ± 2.8
BM (kg)	63.4 ± 2.2	62.9 ± 2.4
Leg length (cm)	91.1 ± 1.3	87.7 ± 1.1
Ratio of length to height (%)	52.8 ± 0.4	51.6 ± 0.6
Muscle strength per BM	0.99 ± 0.05	0.72 ± 0.03*

Values are presented as mean ± standard error of the mean (S.E.M.).

*A significant difference (p < 0.05).

BM = body mass.

Exercise protocols and measurements

All experiments were carried out on a motor-driven treadmill of 4.0 m in length and 2.0 m in width (Biomill 1300; S&ME, Tokyo, Japan). Under all experimental conditions, each participant walked on the same treadmill with a freely chosen step frequency at each gait speed and gradient. The participants wore underwear, shirts, socks, shorts, and lightweight training shoes.¹⁹ To become accustomed to normal treadmill walking while wearing a gas-collection mask, each participant walked at least three preliminary practices (15-minute duration) on the same treadmill at several gait speeds and gradients. As a result, all participants were fully familiarized with walking on the treadmill.

The gait speeds were set at 30 m/min, 45 m/min, 60 m/min, 75 m/min, 90 m/min, and 105 m/min, and the treadmill gradient was set at 0% (level), −5% (downhill), and +5% (uphill) based on a recent work.⁶ The total number of trials performed by each participant was 18 (3 gradients × 6 speeds), and all participants were tested, at most, six gait speeds/d, each of which lasted for 4 minutes. The pulmonary oxygen uptake ($\dot{V}{\text{O}}_2$; mL/kg/min) and heart rate (HR) were measured throughout the study. All participants performed a series of walking trials, which were separated by a resting period of sitting in a chair for 4–5 minutes until the HR recovered to the baseline level. The order of the gradient trials was randomized.

The ventilation and gas-exchange variables were measured using an online computerized breath-by-breath method (Vmax; SensorMedics, CareFusion Corp., Yorba Linda, CA, USA). The inspired- and expired-gas volumes were measured using a hot-wire respiratory-flow system. Flow signals were electrically integrated for the duration of each breath to calculate minute ventilation. The expired fractions of O₂ and CO₂ were analyzed using a zirconium solid-electrolyte oxygen analyzer and an infrared carbon-dioxide analyzer, respectively. The standard known gases (O₂ 16.0%, CO₂ 4.0%, and N₂ 80.0%) and room air were used for the calibration of the gas analyzer. The HR was recorded using an electrocardiogram monitor, which was attached to the gas-analyzer system.

The leg length, defined as the length from the trochanter major to the ground, was measured in both legs for each participant using a steel tape measure. The individual leg length was defined as the average length of both legs. The leg-muscle strength (quadriceps muscles) was measured using a concentric-only knee-extension machine (Cybex VR2-1411 leg extension; Cybex International, Inc., Medway, MA, USA). The participants sat on an adjustable chair attached to the machine, and they were stabilized with straps across the shoulders, waist, and thighs throughout the test to prevent additional body movements. All participants crossed their arms across their chest to eliminate additional body twists using a handrail of the knee-extension machine. The participants were instructed to lift the load through the range of motion. After a warm-up, a maximal muscle-strength test using both legs was started. The maximal quadriceps muscle strength (MQMS; kg) was determined using increments of 10 kg until 60–80% of the perceived maximum. Then, the load was gradually increased by 1–5 kg weights until lift fail, in which the participant was not able to maintain proper form, or to completely lift the weight. Each trial was conducted with an enough-rest interval period in order to eliminate individual muscle fatigue and/or pain. The final acceptable lift with the highest possible load was determined as the individual MQMS.²⁰ The individual MQMS was expressed as the ratio of the individual body mass (BM)—MQMS/BM.

Determination of ES

A single sample with an average final 1-minute $\dot{V}{\text{O}}_2$ value (mL/kg/min) at each gait speed was calculated to obtain the oxygen consumption during walking per unit distance (C_w; mL/kg/m).⁶ Each particular C_w was determined by the ratio of the steady-state $\dot{V}{\text{O}}_2$ to the gait speed (v; m/min):

$$C_w=\dot{V}{\text{O}}_2/v$$ (1)

The relationship between gait speed and C_w can be well approximated using a quadratic equation.5, 6, 9, 19, 21 The C_w–v relationship can be mathematically described by the following equation:

$$C_w\left(v\right)=\text{a}{v}^2+\text{b}v+\text{c}$$ (2)

where the constants a, b, and c are determined by the least-square regressions with the actually observed C_w values at each gait speed. A differential function of the original quadratic equation (2) of each individual can be described as follows:

$$C_w^{\prime }\left(v\right)=2\text{a}v+\text{b}$$ (3)

Then, the individual ES was determined at the gait speed when $C_w^{\prime }\left(v\right)$ equals zero, that is, the individual ES can be observed using the following equation:

$$\text{ES}=-\text{b}/2\text{a}$$ (4)

A subtraction of standing or sitting $\dot{V}{\text{O}}_2$ from the gross (absolute) $\dot{V}{\text{O}}_2$ for calculating the ES has been argued.21, 22 Wall-Scheffler and Myers²¹ emphasized that numerous studies have found that people preferred walking speeds at or near the speed associated with their ES calculated by the gross $\dot{V}{\text{O}}_2$.23, 24, 25 The ES calculated from the gross $\dot{V}{\text{O}}_2$ was equivalent to a gait speed, at which the maximal transfer occurred between kinetic gravitational potential energy in adults and children.⁸ Indeed, other related studies did not subtract sitting or standing $\dot{V}{\text{O}}_2$ when calculating the individual ES3, 4, 8, 9, 10, 21, 24 or C_w values.²⁶ Thus, we used gross $\dot{V}{\text{O}}_2$ for calculating the ES or each C_w value for the purpose of this study. A comparison of the ES between age groups was used to examine whether the C_w–v relationship shifted leftward.

Comparison of C_w between age groups

The C_w values obtained from six gait speeds at each gradient were further averaged to determine a percent difference of the C_w–v relationship between age groups. We also compared the C_w values at each gradient between age groups to examine whether the C_w–v relationship shifted upward for older adults.

Statistics

All data are presented as mean ± standard error of the mean (S.E.M.), because the S.E.M. has been known to present a within-participant deviation,²⁷ which is substantially related to the “true” mean value. The C_w values obtained from six gait speeds tested were averaged in each age group to show a percent difference of the C_w values at each gradient between age groups, meaning that a statistical comparison could not be performed in those comparisons. A regression analysis using a quadratic equation was performed on the C_w–v relationship obtained from each gradient.3, 5, 6, 9, 19, 21 An unpaired t test was conducted for a comparison of the physical characteristics and muscle strength between age groups. A three-way repeated-measures analysis of variance (ANOVA) within participants was used to compare the C_w (age × speed × gradient) using online software ANOVA 4. A two-way repeated-measures ANOVA within participants was also conducted for a comparison of the ES (age × gradient). If a significant F value was obtained, Ryan's²⁸ multiple comparison as a post hoc test was applied to the appropriate data set to establish the significant mean differences. Ryan's²⁸ post hoc test is practical for human experiments, because it can be used regardless of sample size. Its statistical power for detecting statistical significance is equivalent to one of the most popular post hoc tests, Tukey's multiple comparison,²⁸ which is known as one of the most powerful post hoc tests.²⁹ Pearson's correlation coefficient was used to evaluate the relationship between ES and influencing factors, such as leg length and muscle strength. The statistical significance was set at p = 0.05 probability level.

Results

Physical characteristics and muscle strength

No significant differences were found for body height, BM, leg length, or the ratio of leg length to body height between age groups (Table 1). The MQMS/BM ratio was significantly lower for older adults (Table 1).

Comparison of C_w between age groups

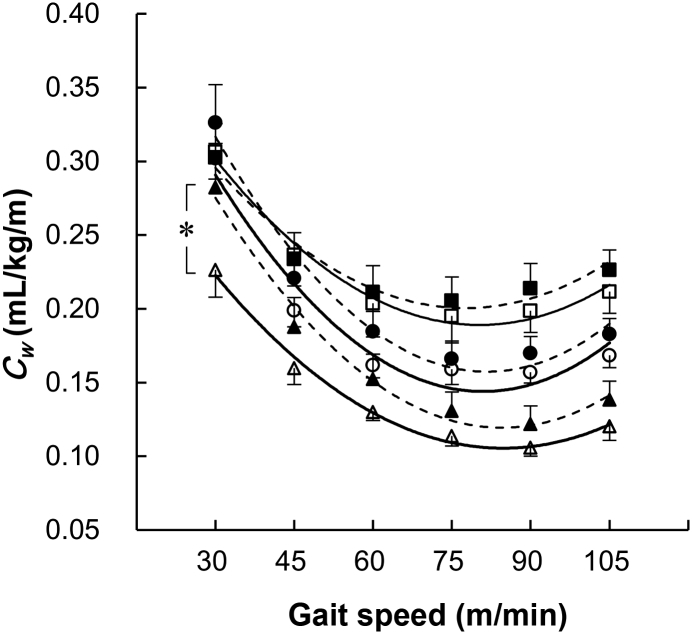
The averaged C_w values obtained from six gait speeds at each gradient were 9.0% greater at the level, +18.3% at the downhill, and +3.1% at the uphill gradient for older adults than for younger adults, although the two-way ANOVA failed to reveal the significant differences at each gradient between groups (Table 2). Figure 2 shows the quadratic relationships between C_w and gait speeds for the examined conditions. The C_w–v relationship showed a clear U-shape over the range of gait speeds tested, and the regression analysis showed that there was a strong correlation between gait speeds and C_w values for younger adults (r = 0.944–0.990) and older adults (r = 0.964–0.996). A significantly greater C_w value was obtained at 30 m/min at the downhill gradient for older adults (Figure 2). However, there were no significant differences in the C_w values at the level and uphill gradients at any gait speeds (Figure 2).

Table 2.

Comparisons of averaged oxygen consumption (C_w) and ES obtained at each gradient between younger and older adults.

	Averaged Cw (mL/kg/m)		Difference (%)	ES (m/min)		Difference (%)
	Younger	Older		Younger	Older
Level	0.190 ± 0.009a	0.201 ± 0.015	+9.0	81.8 ± 1.3a	77.6 ± 1.3a	−5.1
Downhill	0.139 ± 0.009a,b	0.170 ± 0.017a,b	+18.3	88.2 ± 2.0a,b,c	79.7 ± 1.4a,b	−9.6
Uphill	0.225 ± 0.020	0.232 ± 0.017	+3.1	78.2 ± 1.6c	71.8 ± 0.9	−8.2

Values are presented as mean ± S.E.M.

ES = economical speed.

^aSignificant differences versus uphill gradient within the same age group. The averaged C_w is “uphill > level > downhill” and the ES is “downhill > level > uphill” in both age groups. Signs (+/–) indicate the difference between younger and older groups: “+” is “older > younger,” and “–” is “younger > older,” respectively.

^bSignificant differences versus level gradient within the same age group.

^cSignificant differences between younger and older.

Figure 2.

Oxygen consumption of walking (C_w) in younger and older adults at each gradient. ○: level in younger adults; ●: level in older adults; △: downhill in younger adults; ▲: downhill in older adults; □: uphill in younger adults; and ■: uphill in older adults. * p < 0.05 between younger and older adults at a gait speed of 30 m/min at the downhill gradient. Values are mean ± standard error of the mean.

Comparison of ES

A comparison of the ES observed at each gradient is shown in Table 2. The ES seemed to be slower, but not significantly, for older adults than for younger adults at the level gradient (p = 0.058). By contrast, the ES observed at the downhill gradient was significantly slower for older adults (p < 0.001). The ES at the uphill gradient was also significantly slower for older adults (p = 0.006).

ES and physical characteristics

Table 3 summarizes the correlation coefficients between leg length and ES at each gradient. There was a significant positive relationship between leg length and ES at the level and downhill gradients for younger adults, while such a significant relationship was found only at the level gradient for older adults. Table 2 also shows that there was a significant relationship between MQMS/BM and ES only for older adults at all gradients; however, such a significant relationship was not observed for younger adults at any gradients.

Table 3.

Correlation coefficient between measured ES and leg length or muscle strength.

	Measured ES
	Younger			Older
	Level	Downhill	Uphill	Level	Downhill	Uphill
Leg length	r = 0.714	r = 0.729	r = 0.593	r = 0.777	r = 0.693	r = 0.506
	p < 0.05	p < 0.05	n.s.	p < 0.05	n.s.	n.s.
Muscle strength per BM	r = 0.595	r = 0.305	r = 0.470	r = 0.732	r = 0.719	r = 0.753
	n.s.	n.s.	n.s.	p < 0.05	p < 0.05	p < 0.05

Bold and italic r values show a significant relationship (p < 0.05).

BM = body mass; ES = economical speed; n.s. = nonsignificant relationship.

Discussion

Upward and leftward shifts of the C_w–v relationship

A significantly greater averaged C_w value obtained from six gait speeds for older adults was supported by a previous study.¹⁸ A greater C_w value was also found for older adults at 30 m/min at the downhill gradient (Figure 2). These results indicate that our hypothesis for the upward shift of the C_w–v relationship for older adults was partly supported. A significantly slower ES for older adults was found at the downhill and uphill gradients, but not at the level gradient (Table 2), indicating that the C_w–v relationship showed a leftward shift at the downhill and uphill gradients for older adults. In this matter of slower ES for older adults, our hypothesis for the leftward shift of the C_w–v relationship was supported at these sloped gradients.

Some considerations are further necessary with regard to the leftward shift alone of the C_w–v relationship (Figure 1B), because such a leftward shift alone results in a decrease in the C_w values particularly at slower gait speeds. This is a contradiction of our proposed shifting model of the C_w–v relationship due to aging. As shown in Figure 2, our data show a trend for a steeper increase in the C_w–v relationship for older adults at the uphill gradient, particularly at faster gait speeds, which is supported by other previous studies.3, 6 A striking finding of the present study was that a significantly slower ES was not found for older adults only at the level gradient (p = 0.058, Table 2). Another remarkable finding was that a significantly greater C_w value was found for older adults only at 30 m/min at the downhill gradient, meaning that any particular C_w values were not significantly greater for older adults at the level and uphill gradients (Figure 2). A sample size of this study was equivalent to that of some previous studies.11, 14, 16 The statistical power of the post hoc test used in this study has been reported to be strong enough to detect statistical differences.28, 29 The differences between gross and net C_w could partly explain such nonsignificant differences in the C_w values at the level and uphill gradients. If the resting $\dot{V}{\text{O}}_2$ is subtracted from the gross (absolute) $\dot{V}{\text{O}}_2$ for calculating the net C_w, then such net C_w values are likely to lead to significant differences, particularly at slower gait speeds. This is because the fraction of the resting $\dot{V}{\text{O}}_2$ amounted to approximately 60% of the gross $\dot{V}{\text{O}}_2$ at slower gait speeds.²² These facts indicate that a nonsignificant difference of the average ES at the level gradient and C_w values at the level and uphill gradients should not be due to effects of sample size and/or statistical power.

The individual ES depends on the leg length.⁶ The leg length was not significantly different between age groups (Table 1), although the average ESs obtained at the downhill and uphill gradients were significantly slower for older adults (Table 2). Our present study focused on nonretired full-time manual workers, who were approximately 10 years younger than those in previous studies.13, 15, 16, 18 No single factor alone may fully explain the age-related increase in the C_w; however, as shown in our study, healthy older manual workers did not always show greater C_w values compared with those of younger adults. A combined effect of a 5.4% slower ES (as a leftward shift) and a 9.0% greater C_w value obtained from six gait speeds (as an upward shift) in association with a 27.3% lesser muscle strength comprehensively influenced the C_w–v relationship for older adults at the level gradient.

What determines individual ES?

Leg-muscle strength declines with aging.11, 30 The preferred and/or self-selected gait speed slows with aging.11, 31 Changes in physiological functions with aging, such as decreasing aerobic capacity and increasing difficulty for common daily activities, are associated with an elevated energy cost of walking.³² These previous findings could relate to the individual ES for older adults. In line with the results of a previous study,¹¹ the older adults exhibited 27.3% lesser MQMS/BM compared with younger adults (Table 1), even though they were habitually working as manual workers. It was interesting to note that a long-term training-based increase in the muscle strength of the quadriceps muscles for older adults did not conduct any alterations in the individual C_w values at any gait speeds.¹³ These previous and our present findings suggest that the muscular work strategy during walking at different gradient environments would be different between age groups. Indeed, older adults performed more positive work of the trailing leg using muscles crossing the hip during double-support phase at the level and steeper uphill gradients (+15.8%).³³ During the single-support phase, they did more positive work of the supporting leg than younger adults using muscles crossing the knee at the level and steeper uphill gradients (+10.5% and +15.8%).³⁴ These findings indicate that older adults were more dependent on the positive work of the quadriceps muscles during walking.

Table 2 summarizes the correlation coefficients for the relationships between the ES and leg length or MQMS/BM. The ES was significantly related to leg length for younger adults at the level and downhill gradients, but not at the uphill gradient. For older adults, the ES was significantly related to leg length only at the level gradient. It was worth noting that a significant relationship was found between the ES and MQMS/BM for older adults at all gradients, whereas this was not found at any gradients for younger adults (Table 3). These results indicate that leg length explained the individual ES for younger adults, while muscle strength in association with leg length explained the individual ES for older adults. Recent studies showed that the gait pattern for older people was characterized by a greater and/or longer coactivation of the agonists and their antagonists in the lower leg extremities during one gait cycle.15, 17, 18 This could result in a greater C_w–v relationship and slower ES for older adults in a negative manner, although antagonist coactivation presumably increases joint stiffness, and it may thereby improve joint stability in a positive manner. These considerations were supported by the fact that the MQMS/BM was significantly correlated to the individual ES only for older adults (Table 3).

Conclusion

The results of the present study suggest that the C_w–v relationship exhibited a combination of upward and leftward shifts for older adults at the downhill gradient. Only a leftward shift of the C_w–v relationship was found at the uphill gradient, being explained by a steeper increase in the C_w–v relationship particularly at faster gait speeds. Neither a significant leftward nor an upward shift was found at the level gradient. The leg length significantly correlated to the ES for younger adults at the level and downhill gradients, while such a significant relationship was observed only at the level gradient for older adults (Table 2). The quadriceps muscle strength significantly correlated to the ES for older adults at all gradients, but not for younger adults (Table 3). These comprehensive results indicate that the age-related alteration of the C_w–v relationship depends on the gradient, and its related factors are different between age groups.

Conflicts of interest

The authors declare no conflicts of interest.