A Powerful Approach to Estimating Annotation-Stratified Genetic Covariance via GWAS Summary Statistics

Abstract

Despite the success of large-scale genome-wide association studies (GWASs) on complex traits, our understanding of their genetic architecture is far from complete. Jointly modeling multiple traits’ genetic profiles has provided insights into the shared genetic basis of many complex traits. However, large-scale inference sets a high bar for both statistical power and biological interpretability. Here we introduce a principled framework to estimate annotation-stratified genetic covariance between traits using GWAS summary statistics. Through theoretical and numerical analyses, we demonstrate that our method provides accurate covariance estimates, thereby enabling researchers to dissect both the shared and distinct genetic architecture across traits to better understand their etiologies. Among 50 complex traits with publicly accessible GWAS summary statistics (N_total$\approx$ 4.5 million), we identified more than 170 pairs with statistically significant genetic covariance. In particular, we found strong genetic covariance between late-onset Alzheimer disease (LOAD) and amyotrophic lateral sclerosis (ALS), two major neurodegenerative diseases, in single-nucleotide polymorphisms (SNPs) with high minor allele frequencies and in SNPs located in the predicted functional genome. Joint analysis of LOAD, ALS, and other traits highlights LOAD’s correlation with cognitive traits and hints at an autoimmune component for ALS.

Introduction

Genome-wide association studies (GWASs) have been a success in the past 12 years. Despite a simple study design, GWASs have identified tens of thousands of robust associations for a variety of human complex diseases and traits. Based on the GWAS paradigm, linear mixed models, in conjunction with the restricted maximum likelihood (REML) algorithm, have provided great insights into the polygenic genetic architecture of complex traits.^{1, 2, 3} The cross-trait extension of linear mixed model has further revealed the shared etiology of many different traits.⁴ Compared to traditional, family-based approaches, these methods do not require all the traits to be measured on the same cohort and therefore make it possible to study a spectrum of human complex traits using independent samples from existing GWASs.^{5, 6} Recently, Bulik-Sullivan et al. developed cross-trait LDSC, a computationally efficient method that utilizes GWAS summary statistics to estimate genetic correlation between complex traits.⁷ LDSC is a major advance. As summary statistics from consortium-based GWASs become increasingly accessible,⁸ it provides great opportunities for systematically documenting the shared genetic basis of a large number of diseases and traits.^{9, 10} However, large-scale inference sets a high bar for both estimation accuracy and statistical power. Furthermore, existing methods do not allow explicit modeling of functional genome annotations. As shown in later sections, the estimated genetic correlations in many cases are neither statistically significant nor easy to interpret.

To address these challenges, there is a pressing need for a statistical framework that provides more accurate covariance and correlation estimates and allows integration of biologically meaningful functional genome annotations. The method of moments has recently been shown to outperform LDSC in single-trait heritability estimation.¹¹ Integrative analysis of GWAS summary statistics and context-specific functional annotations has provided novel insights into complex disease etiology through a variety of applications.^{12, 13, 14} In this paper, we introduce GNOVA (genetic covariance analyzer), a principled framework to estimate annotation-stratified genetic covariance using GWAS summary statistics. Through extensive numerical simulations, integrative analysis of 50 complex traits, and an in-depth case study on late-onset Alzheimer disease (LOAD [MIM: 104300]) and amyotrophic lateral sclerosis (ALS [MIM: 105400]), we demonstrate that GNOVA provides accurate covariance estimates and powerful statistical inference that are robust to linkage disequilibrium (LD) and sample overlap. Furthermore, we show that annotation-stratified analysis enhances the interpretability of genetic covariance and provides novel insights into the shared genetic basis of complex traits.

Material and Methods

Statistical Model

Here we outline the genetic covariance estimation framework. The complete derivation, detailed justification for all approximations, and theoretical proofs are presented in Appendix A. In short, the genetic covariance that we aim to estimate is the covariance between the genetic effects of a group of single nucleotide polymorphisms (SNPs) on two complex traits. When functional genome annotations are present, we allow such covariance to vary in different annotation categories. Specifically, we define K functional annotations S₁, S₂, ..., S_K (e.g., protein-coding genes and non-coding regions), whose union covers the entire genome; assume two studies share the same list of m SNPs; and assume two standardized traits y₁ and y₂ follow the linear models below:

$$y_1=\sum _{i=1}^K{X}_i{\beta }_i+\mathit{ϵ}$$

$$y_2=\sum _{i=1}^K{Z}_i{\gamma }_i+\delta ,$$

where X_i and Z_i denote the standardized genotype matrices defined through annotation S_i. Random effects terms β_i and γ_i denote the corresponding genetic effects for each annotation category. SNPs’ genetic effects on two traits follow an annotation-dependent covariance structure:

$$\mathbb{E}\left({\beta }_i\right)=\mathbb{E}\left({\gamma }_i\right)=0,i=1,\dots ,K$$

$$Cov\left({\beta }_i,{\gamma }_i\right)=\mathbb{E}\left({\gamma }_i{\beta }_i^T\right)=\frac{{\rho }_i}{m_i}I,i=1,\dots ,K$$

where m_i and ρ_i denote the total number of SNPs and the total genetic covariance in annotation category S_i, respectively. Random variables $\mathit{ϵ}$ and δ denote the non-genetic effects. Of note, this notation implicitly assumes the genetic covariance to follow an additive structure in regions where functional annotations overlap.

In practice, two different GWASs often share a subset of samples. Without loss of generality, we assume N₁ and N₂ to be the sample sizes of two studies and the first N_s samples in each study are shared. To account for the non-genetic correlation introduced by sample overlapping, we allow random error terms $\mathit{ϵ}$ and δ to be correlated:

$$Cov\left({\mathit{ϵ}}_i,{\delta }_j\right)=\mathbb{E}\left({\mathit{ϵ}}_i{\delta }_j\right)=\{\begin{array}{c}{\rho }_e,1\le i=j\le N_s\\ 0,otherwise\end{array}.$$

We note that our model does not require any additional assumption on the heritability structure of either trait.

Estimation of Covariance Parameters via the Method of Moments

To estimate genetic covariance parameters (i.e., ${\rho }_i,i=1,\dots ,K$), we developed an analysis framework based on the method of moments. First, we derive equations that relate the population moments to the parameters of interest. For an arbitrary N₁ × N₂ matrix A, we study the expectation of $y_1^{T}A{y}_2$. It can be shown that

$$\mathbb{E}\left(y_1^{T}A{y}_2\right)=\sum _{i=1}^K\frac{{\rho }_i}{m_i}tr\left(A{Z}_i{X}_i^T\right)+{\rho }_e\left(\sum _{t=1}^{N_s}{A}_{tt}\right).$$

Here, quantity A_tt denotes the t^th diagonal element of matrix A. Since there are K+1 parameters in total in the model (K genetic covariance parameters and ρ_e), we build a linear system of K+1 equations by plugging in K+1 different matrices A₁,...,A_K+1 into the equation above. Further, we approximate $\mathbb{E}\left(y_1^T{A}_j{y}_2\right)$ using the sample moments, i.e., the observed value $y_1^T{A}_j{y}_2$, and get the following equation:

$$y_1^T{A}_j{y}_2=\sum _{i=1}^K\frac{{\rho }_i}{m_i}tr\left(A_j{Z}_i{X}_i^T\right)+{\rho }_e\sum _{t=1}^{N_s}{\left(A_j\right)}_{tt},j=1,\dots ,K+1.$$

Solving this linear system of K+1 equations would get us the method of moments estimators for genetic covariance.

Choices of Matrix A

The method of moments estimation procedure described above works for arbitrary A matrices. However, it is critical and non-trivial to choose A in practice. Since individual-level genotype and phenotype data from consortium-based GWASs are in many cases difficult to access, it is of practical interest to estimate genetic covariance based on summary statistics only. To achieve this goal, we define the first K matrices as:

$${\tilde{A}}_j=\frac{X_j{Z}_j^T}{m_j},j=1,\dots ,K.$$

Plugging in these matrices, the first K equations become:

$$\frac{1}{m_j}{\left(X_j^T{y}_1\right)}^T{Z}_j^T{y}_2=\sum _{i=1}^K\frac{{\rho }_i}{m_i{m}_j}tr\left(Z_j^T{Z}_i{X}_i^T{X}_j\right)+\frac{{\rho }_e}{m_j}\sum _{t=1}^{N_s}{\left(X_j{X}_j^T\right)}_{tt},j=1,\dots ,K.$$

The equality is based on the property of trace and the fact that first N_s samples are shared between two studies. These equations can be further approximated by (Appendix A):

$$\frac{1}{m_j\sqrt{N_1{N}_2}}{\left(z_1\right)}_j^T{\left(z_2\right)}_j=\sum _{i=1}^K\frac{{\rho }_i}{m_i{m}_j}\sum _{l=1}^{m_i}\sum _{l^{\prime }=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2+\frac{N_s{\rho }_e}{N_1{N}_2},j=1,\dots ,K.$$

Here, $r_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2$ denotes the LD between the l^th SNP from category S_i and the $\left(l^{\prime }\right)$^th SNP from category S_j; z₁ and z₂ denote the z-scores of SNP-level associations from two GWASs; and ${\left(z_1\right)}_j$ and ${\left(z_2\right)}_j$ represent subsets of z-scores corresponding to the SNPs in annotation category S_j. LD can be estimated using an external reference panel. However, if samples in two studies have different ancestries, $X_i^T{X}_j$ and $Z_j^T{Z}_i$ need to be estimated separately using two reference panels. When such reference panels do not exist, individual-level genotype data for a subset of study samples may be needed.

Next, we study the (K+1)^th equation. We define:

$${\tilde{A}}_{K+1}={\left(\begin{array}{cc}{I}_{N_s\times N_s}& 0\\ 0& 0\end{array}\right)}_{N_1\times N_2}.$$

Divide N₁N₂ on both sides of the (K+1)^th equation, and we get:

$$\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t=\frac{N_s}{N_1{N}_2}\sum _{i=1}^K{\rho }_i+\frac{N_s}{N_1{N}_2}{\rho }_e.$$

Since ρ₁, …, ρ_Κ are the parameters of interest, we subtract the (K+1)^th equation from the first K equations and remove ρ_Κ+1 from the linear system. We denote the remaining K equations in matrix form:

$$\begin{array}{l}\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\end{array}\right)=\\ \left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2-\frac{N_s}{N_1{N}_2}& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2-\frac{N_s}{N_1{N}_2}\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2-\frac{N_s}{N_1{N}_2}& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2-\frac{N_s}{N_1{N}_2}\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).\end{array}$$

When the sample sizes of both GWASs are large and the sample overlap between two studies is moderate, the K equations can be approximated by:

$$\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).$$

We define

$$v={\left(\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1,\dots ,\frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\right)}^T$$

$$M=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right).$$

Then, the point estimate of covariance parameters can be denoted as

$$\hat{\rho }=M^{-1}v.$$

Importantly, M can be estimated using a reference panel (e.g., 1000 Genomes Project¹⁵) and v is based only on GWAS summary statistics. Of note, the same estimation framework can be directly applied to ascertained case-control studies as well (Appendix A).

Special Cases

Two Independent GWASs

If samples from two GWASs do not overlap, then the non-genetic effects $\mathit{ϵ}$ and δ are independent and only K equations are needed for estimating covariance parameters. We still define ${\tilde{A}}_j=\left(X_j{Z}_j^T\right)/m_j$ for j = 1,…,K. That gives us the same covariance estimator:

$$\hat{\rho }=M^{-1}v.$$

No Annotation Stratification

If no functional annotation is present, it can be shown that

$$\hat{\rho }=\frac{\overline{z_1{z}_2}}{\overline{r^2}\sqrt{N_1{N}_2}}.$$

Here, $\overline{z_1{z}_2}$ is the average product of z-scores from two GWASs; $\overline{r^2}$ is the average LD across all SNP pairs in the study. Under the non-stratified scenario, this estimator can be seen as a two-trait extension of the heritability estimator proposed in Bulik-Sullivan.¹⁶

Two GWASs with Substantial Sample Overlap

If the two GWASs have substantial sample overlap, some approximations we have applied in previous sections would fail (Appendix A). The problem gets down to solving the following equations:

$$\left(\begin{array}{c}\frac{1}{m_{1}N}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N^2}\sum _{t=1}^N{\left(y_1\right)}_t{\left(y_2\right)}_t\\ ⋮\\ \frac{1}{m_{K}N}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N^2}\sum _{t=1}^N{\left(y_1\right)}_t{\left(y_2\right)}_t\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).$$

Therefore,

$$\hat{\rho }=M^{-1}\left(\begin{array}{c}\frac{1}{m_{1}N}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N}{\hat{\rho }}_{pheno}\\ ⋮\\ \frac{1}{m_{K}N}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N}{\hat{\rho }}_{pheno}\end{array}\right)=M^{-1}\left(v-\frac{{\hat{\rho }}_{pheno}}{N}\mathbf{1}\right)$$

where the phenotypic correlation ${\hat{\rho }}_{pheno}$ can be either acquired from the literature or estimated using computational methods^{7, 17, 18} (Appendix A).

Remarks on Overlapping Functional Annotations

When functional annotations overlap, the covariance parameter ρ is not the real quantity of interest. Instead, the total covariance in each annotation category is more biologically meaningful and can be estimated using the weighted estimator

$${\hat{\rho }}^W=W\hat{\rho }$$

where W is a K × K matrix with element

$$W_{ij}=\frac{m_{j\cap i}}{m_j},1\le i,j\le K.$$

Here, $m_{j\cap i}$ denotes the number of SNPs in region $S_i\cap S_j$.

Theoretical Properties

In this section, we establish the statistical optimality of our estimator by showing that it is “almost” the unbiased estimator with minimum variance. Here we state all the propositions (see Appendix A for detailed proofs). Assume y₁ and y₂ follow a multivariate normal distribution:

$$\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\sim MVN\left(0,\left(\begin{array}{cc}{H}_1& \text{Θ}\\ {\text{Θ}}^T& H_2\end{array}\right)\right).$$

We begin with calculating the variance of the quadratic form-like quantity $y_1^{T}A{y}_2$.

Proposition 1. Let A be an N₁ × N₂ matrix. Then $Var\left(y_1^{T}A{y}_2\right)=tr\left(A^T{H}_{1}A{H}_2\right)+tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$.

It can be shown that the second part, i.e., $tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$, is very small compared to the first term $tr\left(A^T{H}_{1}A{H}_2\right)$ in real GWAS data (Appendix A):

$$tr\left(A^T{H}_{1}A{H}_2\right)\gg tr\left(A^T\text{Θ}{A}^T\text{Θ}\right).$$

With this in mind, the following claim is approximately true:

$$Var\left(y_1^{T}A{y}_2\right)\approx tr\left(A^T{H}_{1}A{H}_2\right).$$

Next, we define a matrix $A_{\ast }$ and show that $A_{\ast }$ minimizes tr(A^TH₁AH₂) under some conditions. Based on the argument above, $A_{\ast }$ “almost” minimizes $Var\left(y_1^{T}A{y}_2\right)$ too.

Proposition 2. Assume two GWASs do not share samples. We define the following quantities.

• (i)Let $p={\left(p_1,\dots p_K\right)}^T$ be an arbitrarily given K-dimensional vector;
• (ii)Let S be a K × K symmetric matrix with element $S_{l{l}^{\prime }}=tr\left(H_1^{-1}{X}_{l^{\prime }}{Z}_{l^{\prime }}^T{H}_2^{-1}{Z}_l{X}_l^T\right)/m_l{m}_{l^{\prime }}$ for $1\le l,l^{\prime }\le K$;
• (iii)Let $\lambda ={\left({\lambda }_1,\dots {\lambda }_K\right)}^T$ be a vector such that $S\lambda =p$;
• (iv)Define $A_{\ast }=\sum _{j=1}^K\frac{{\lambda }_j}{m_j}{H}_1^{-1}{X}_j{Z}_j^T{H}_2^{-1}.$

Then, we have:

• (1)$\mathbb{E}\left(y_1^T{A}_{\ast }{y}_2\right)=\sum _{t=1}^K{p}_t{\rho }_t$;
• (2)Let $A$ be a matrix such that $\mathbb{E}\left(y_1^{T}A{y}_2\right)={\sum }_{t=1}^K{p}_t{\rho }_t$. Then, $tr\left(A^T{H}_{1}A{H}_2\right)\ge tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right)$.

Proposition 2 tells us that given arbitrary p = (p₁,…p_K)^T, if $\exists \lambda ={\left({\lambda }_1,\dots {\lambda }_K\right)}^T$ such that Sλ = p, then $y_1^T{A}_{\ast }{y}_2$ is an unbiased estimator for ${\sum }_{t=1}^K{p}_t{\rho }_t$. Furthermore, among all unbiased estimators with the form $y_1^{T}A{y}_2$, $y_1^T{A}_{\ast }{y}_2$ has the minimum value of $tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right)$, hence “almost” the minimum variance $Var\left(y_1^T{A}_{\ast }{y}_2\right)$. Interestingly, by carefully choosing p and λ, we can let $A_{\ast }$ equal the $\tilde{A}$ matrix we have been using throughout the paper. Therefore, we have the following corollary.

Corollary 1. We assume:

• (i)Two GWASs do not overlap;
• (ii)The samples in each study are completely independent;
• (iii)True LD in both studies (i.e., Z^TZ and X^TX) is known.

Consider all matrices A that suffice

$$tr\left(AZ{X}^T\right)=\frac{tr\left(Z^{T}Z{X}^{T}X\right)}{m}.$$

We define

$${\hat{\rho }}_A=m\left(y_1^{T}A{y}_2\right)/tr\left(AZ{X}^T\right).$$

Then, ${\hat{\rho }}_{\tilde{A}}$ with $\tilde{A}=\left(X{Z}^T\right)/m$ has the lowest variance.

Similarly, we could extend these results to annotation-stratified scenarios (Appendix A). These results show that although we initially defined ${\tilde{A}}_j$ for the purpose of simplifying calculation, the derived covariance estimator actually enjoys some good theoretical properties.

Variance Estimation via Block-wise Jackknife

Following previous work,⁷ we apply a block-wise jackknife approach to estimate the variance. We divide the genome into b (e.g., b = 200) blocks B₁, …, B_b. Let

$$v_i^{\left(t\right)}=\frac{{\left(z_1\right)}_i^T{\left(z_2\right)}_i-{\left(z_1\right)}_{S_i\cap B_t}^T{\left(z_2\right)}_{S_i\cap B_t}}{\left(m_i-m_{S_i\cap B_t}\right)\sqrt{N_1{N}_2}},1\le i\le Kand1\le t\le b.$$

Here, subscript $S_i\cap B_t$ indicates the subset of SNPs in both functional annotation S_i and block B_t. Then, Cov(v) is estimated as:

$${\left(\widehat{Cov}\left(v\right)\right)}_{ij}=\frac{b-1}{b}\sum _{t=1}^b\left(v_i^{\left(t\right)}-\frac{1}{b}\sum _{s=1}^b{v}_i^{\left(s\right)}\right)\left(v_j^{\left(t\right)}-\frac{1}{b}\sum _{s=1}^b{v}_j^{\left(s\right)}\right).$$

Therefore, we get

$$\widehat{Cov}\left(\hat{\rho }\right)=M^{-1}\widehat{Cov}\left(v\right)M^{-1}.$$

If annotations overlap,

$$\widehat{Cov}\left({\hat{\rho }}^W\right)=W{M}^{-1}\widehat{Cov}\left(v\right)M^{-1}{W}^T.$$

Finally, the test statistic for each covariance parameter is

$$z-scor{e}_i=\frac{{\hat{\rho }}_i}{\sqrt{{\left(\widehat{Cov}\left(\hat{\rho }\right)\right)}_{ii}}},1\le i\le K.$$

When annotations overlap,

$$z-scor{e}_i^W=\frac{{\hat{\rho }}_i^W}{\sqrt{{\left(\widehat{Cov}\left({\hat{\rho }}^W\right)\right)}_{ii}}},1\le i\le K.$$

Genetic Correlation

We provide genetic correlation estimates for non-stratified analysis:

$$cor=\frac{\hat{\rho }}{\sqrt{{\hat{h}}_1^2{\hat{h}}_2^2}}.$$

We use the estimator proposed in Bulik-Sullivan¹⁶ to estimate heritability for each trait:

$${\hat{h}}_t^2=\frac{\frac{1}{m}{\left(z_t\right)}^T\left(z_t\right)-1}{\frac{N_t}{m^2}\sum _{l=1}^m\sum _{l^{\prime }=1}^m{r}_{l{l}^{\prime }}^2},t=\mathrm{1,2.}$$

When functional annotations are present, the true heritability in each annotation category may be small. Although methods for estimating annotation-stratified heritability have been proposed,^{11, 12} they may provide unstable, sometimes even negative, heritability estimates, especially when a number of annotation categories are related to the repressed genome. When true heritability is low, variability in the denominator will have great impact on genetic correlation estimates. Therefore, we use genetic covariance as a more robust metric when performing annotation-stratified analysis.

Simulation Settings

We simulated quantitative traits using real genotype data from the WTCCC1 cohort. We removed individuals with genetic relatedness coefficient greater than 0.05 and filtered SNPs with missing rate above 1% and/or MAF lower than 5% in samples with European ancestry from the 1000 Genomes Project.¹⁵ In addition, we removed all the strand-ambiguous SNPs. After quality control, 15,918 samples and 254,221 SNPs remained in the dataset. Each simulation setting was repeated 100 times.

Setting 1

We equally divided 15,918 samples into two sub-cohorts. We simulated two traits using genetic effects sampled from an infinitesimal model.

$$\left(\begin{array}{c}\beta \\ \gamma \end{array}\right)\sim MVN\left(0,\frac{1}{254221}\left(\begin{array}{cc}{h}_1^{2}I& \rho I\\ \rho I& h_2^{2}I\end{array}\right)\right)$$

Heritability for both traits was set as 0.5. We set the genetic covariance to be 0, 0.05, 0.1, 0.15, 0.2, and 0.25.

Setting 2

Instead of fixing the heritability, we assumed only that the heritability for both traits was equal. Genetic correlation was fixed as 0.2. We set the genetic covariance to be 0.05, 0.1, 0.15, and 0.2 and chose heritability value accordingly.

Setting 3

We simulated two traits on the same sub-cohort of 7,959 samples. Heritability was fixed as 0.5 for both traits. We set the genetic covariance to be 0, 0.05, 0.1, 0.15, 0.2, and 0.25. Sample overlap correction was applied to estimate genetic covariance.

Setting 4

We randomly partitioned the genome into two annotation categories of the same size. We set the heritability for both traits to be 0.5, and the heritability structure does not depend on functional annotations. Genetic covariance in the first annotation was set to be 0, 0.05, 0.1, 0.15, and 0.2. Genetic effects for two traits are not correlated in the second annotation category.

Setting 5

We randomly partitioned the genome into three categories of the same size. Define annotation-1 to be the union of the first and the second categories, and let annotation-2 be the union of the second and the third categories. We set the heritability for both traits to be 0.5, and the heritability structure does not depend on functional annotations. Genetic covariance parameter for annotation-1 (i.e., ρ₁) is set to be 0.1. We set ρ₂ to be −0.2, −0.1, 0, and 0.1. The genetic covariance in regions where two annotations overlap follows an additive structure. For example, when ρ₁ = 0.1 and ρ₂ = 0.2, the total covariance in annotation-1 is

$${\rho }_1+\frac{{\rho }_2}{2}=0.$$

Similarly, the total covariance in annotation-2 is

$$\frac{{\rho }_1}{2}+{\rho }_2=-\mathrm{0.15.}$$

GWAS Data Analysis

Details of 48 GWASs and the URLs for summary statistics files are summarized in Table S1. For each summary statistics dataset, we applied the same quality-control steps described in Bulik-Sullivan et al.⁷ using the munge_sumstats.py script in LDSC. In addition, we removed all the strand-ambiguous SNPs from each dataset. For each pair of complex traits, we took the overlapped SNPs between two summary statistics files, matched the effect alleles, and removed SNPs with MAF below 5% in the 1000 Genomes Project phase III samples with European ancestry. SNPs on sex chromosomes were also removed from the analysis. We then applied the GNOVA framework to the remaining SNPs to estimate genetic covariance. Sample overlap correction was applied when two GWASs have a large sample overlap. When calculating genetic correlation between ALS and other traits, we used previously reported 0.085 as the heritability of ALS due to negative heritability estimates.¹⁹

Annotation Data

GenoCanyon and GenoSkyline functional annotations, as previously reported,^{14, 20, 21} integrate various types of transcriptomic and epigenomic data from ENCODE²² and Roadmap Epigenomics Project²³ to predict functional DNA regions in the human genome. GenoCanyon utilizes an unsupervised learning framework to identify non-tissue-specific functional regions. GenoSkyline and GenoSkyline-Plus further extended this framework to identify tissue- and cell type-specific functionality in the human genome. We applied GenoSkyline-Plus annotations for seven broadly defined tissue categories (i.e., brain, cardiovascular, epithelium, gastrointestinal, immune, muscle, and other) to stratify genetic covariance by tissue type. When integrating these annotations in GNOVA, we also included the whole genome as an annotation category to guarantee that the union of all annotations covers the genome. The whole genome was not added as an additional annotation track in analyses or simulations when the functional annotations covered all SNPs in the dataset. The MAF quartiles were calculated using the genotype data of phase III samples with European ancestry from the 1000 Genomes Project after filtering SNPs with MAF below 5%.

LD Score Regression Implementation

We implemented cross-trait LD score regression using the LDSC software package. For the purpose of fair comparison, we ran LD score regression on all SNPs in the dataset in the simulation studies. When analyzing real GWAS data, we followed the protocol suggested in Bulik-Sullivan et al.⁷ and used HAPMAP3 SNPs. LD scores were estimated using phase I samples with European ancestry in the 1000 Genomes Project.

Ethical Statement

Procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation. Proper informed consent was obtained when needed.

Results

Simulations

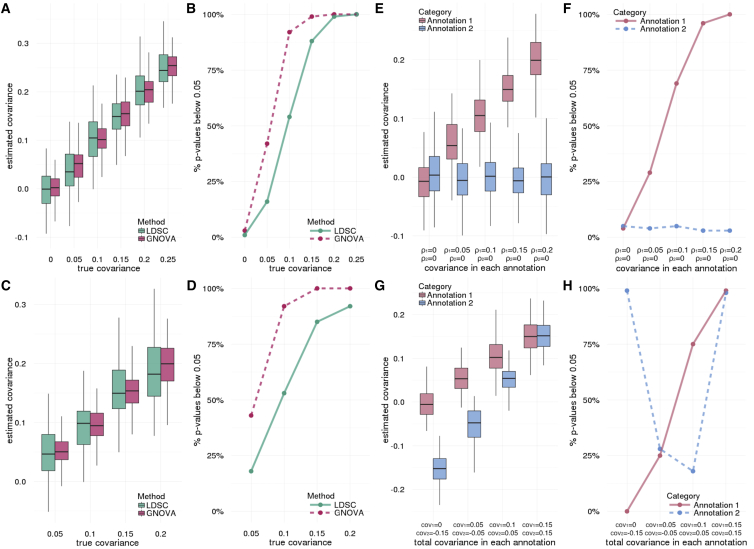
We simulated two traits using genotype data from the Wellcome Trust Case Control Consortium (WTCCC) while assuming a correlated genetic covariance structure. Detailed simulation settings are described in the Material and Methods. Since LDSC cannot estimate annotation-stratified genetic covariance, we compared GNOVA and LDSC using data simulated from a non-stratified, infinitesimal genetic covariance structure (Figures 1A–1D). Both methods provided unbiased covariance estimates, but GNOVA estimator had consistently lower variance across all simulation settings. The same pattern could be observed for genetic correlation estimates (Figure S1). Neither method showed inflated type I error when the true covariance is 0. When comparing the frequencies of rejecting the null hypothesis, GNOVA is nearly twice as powerful as LDSC when the true genetic covariance is below 0.1. To evaluate GNOVA’s robustness against sample overlap, we simulated two traits using genotype data of the same cohort. After applying sample overlap correction, GNOVA still outperformed LDSC, showing higher estimation accuracy and statistical power (Figure S2).

Figure 1.

Evaluation of Covariance Estimation and Statistical Power through Simulations

Detailed simulation settings are described in the Material and Methods.

(A–D) Compare GNOVA and LDSC using traits simulated from a non-stratified covariance structure. We first fixed heritability for both traits but set genetic correlation to different values. The covariance estimates are shown in (A). (B) shows the statistical power. Next, we fixed genetic correlation but chose different values for heritability and covariance. Covariance estimates and statistical power are shown in (C) and (D), respectively.

(E–H) Estimate annotation-stratified genetic covariance. In (E) and (F), we simulated data using two non-overlapping functional annotations. Results in (G) and (H) are based on two overlapping annotations. The true covariance values are labeled under each setting. Type I error was not inflated when the true covariance was zero.

Next, we investigated GNOVA’s capability to estimate annotation-stratified genetic covariance. We randomly partitioned the genome into two non-overlapping annotation categories and simulated two traits using annotation-dependent genetic covariance (Material and Methods). GNOVA provided unbiased estimates for the genetic covariance in each category across all settings (Figures 1E and 1F). Of note, type I error was well controlled in the annotation category without genetic covariance even when the true covariance in the other annotation category was non-zero, suggesting GNOVA’s robustness under the influence of LD. Furthermore, when functional annotations overlapped, our method still provided accurate covariance estimates and powerful inference (Figures 1G and 1H).

Estimation of Pairwise Genetic Correlation for 48 Human Complex Traits

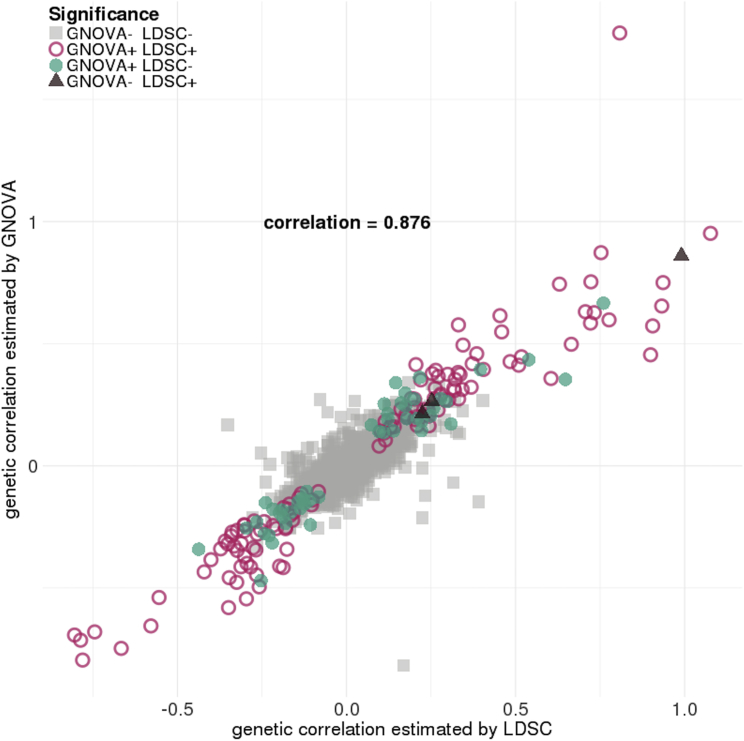
We applied GNOVA to estimate genetic correlations for 48 complex traits using publicly available GWAS summary statistics (N_total $\approx$ 4.5 million). Trait acronyms and other details of all GWASs are summarized in Table S1. Out of 1,128 pairs of traits in total, we identified 176 pairs with statistically significant genetic correlation after Bonferroni correction (Table S2 and Figure S3). We also applied LDSC to the same datasets and identified only 127 significant pairs (Table S3 and Figure S4). A total of 52 significantly correlated trait pairs were uniquely identified by GNOVA while only 3 trait pairs were uniquely identified using LDSC. Overall, the genetic correlations estimated using GNOVA and LDSC are concordant (Figure 2). Consistent with our simulation results, GNOVA is more powerful when genetic correlation is moderate.

Figure 2.

Comparison of Genetic Correlations Estimated via GNOVA and LDSC

Each point represents a pair of traits. Overall, genetic correlation estimates are concordant between GNOVA and LDSC, but GNOVA is more powerful when genetic correlation is moderate. Color and shape of each data point represent the significance status given by GNOVA and LDSC. Trait pairs that involve gout were removed from this figure because LDSC estimated its heritability to be negative and could not properly output p values.

To evaluate model validity, we examined correlations between several traits that are closely related either physiologically or epidemiologically (Table S4). As expected, femoral and lumbar bone mineral density (FNBMD and LSBMD) and depressive symptoms (DEP) and major depressive disorder (MDD [MIM: 608516]) showed strong positive genetic correlations. We also observed negative correlations between subjective well-being (SWB) and neuropsychiatric disorders such as schizophrenia (MIM: 181500), anxiety (MIM: 607834), two depression traits (DEP and MDD), and neuroticism.

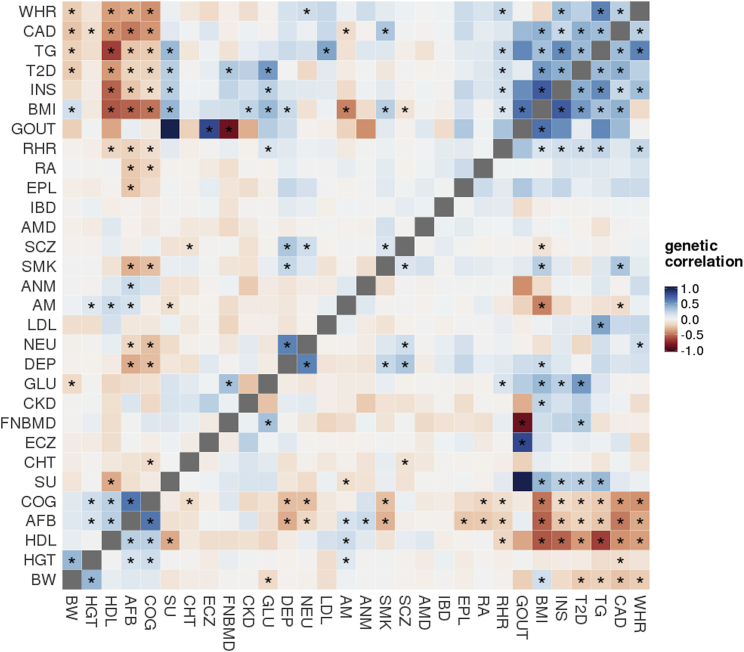
We further examined pairwise correlations between 48 traits (Figures 3 and S3). Following hierarchical clustering, broad patterns suggesting disease relatedness emerged. These results are well documented in the literature: neuropsychiatric conditions, metabolic diseases, and gastrointestinal inflammatory disorders clustered together with positive correlations within each individual cluster. We replicated several previous genetic correlation findings,⁷ including significant correlations of adult height (HGT) with coronary artery disease (CAD [MIM: 608320]) and age at menarche (AM), and of years of education (EDU) with CAD, bipolar disorder (BIP), body-mass index (BMI), triglycerides, and smoking status (SMK). Furthermore, two previous results that passed multiple correction testing at only 1% FDR passed Bonferroni correction in our analysis; namely, we observed a statistically significant negative correlation between AM and CAD and a positive correlation between autism (ASD [MIM: 209850]) and EDU.

Figure 3.

Estimated Genetic Correlations of 435 Pairs of Traits from 30 GWASs

To visualize a large number of pairwise correlations more efficiently, we excluded closely related traits and studies with smaller sample sizes (N < 30,000) in this figure. Asterisks highlight significant genetic correlations after Bonferroni correction for all 1,128 pairs (p < 4.4 × 10⁻⁵). The complete heatmap matrix is presented in Figure S3. The order of traits was determined by hierarchical clustering.

We also identified a number of genetic correlations that are consistent with the genetic relationships reported in the previous literature. For example, previous genetic correlation analyses identified a negative correlation between anorexia nervosa (AN [MIM: 606788]) and obesity, a result we also observed.⁷ In addition, we found negative correlations of AN with glucose and triglyceride levels, as well as a positive correlation with high-density lipoprotein (HDL). These results provide further support for existing hypotheses proposing an underlying neural, rather than metabolic, etiology for metabolic syndrome.^{12, 21, 24} We see an unsurprising positive correlation between glucose and insulin levels, which is consistent with our understanding of diabetes.²⁵ Positive correlations between multiple sclerosis (MS [MIM: 126200]) and Crohn disease (CD) and more generally, inflammatory bowel disease (IBD [MIM: 266600]), agree with existing reports of shared susceptibility for these diseases.^{26, 27, 28} We demonstrate a positive correlation between asthma (MIM: 600807) and eczema (MIM: 603165), which share numerous loci identified in previous GWASs.²⁹ We also reproduced recent findings linking bone mineral density with metabolic dysfunction with positive correlations between FNBMD and both glucose and type II diabetes (T2D [MIM: 125853]).³⁰ Interestingly, however, we did not see significant correlations of bone mineral density with cardiovascular diseases. Among neuropsychiatric disorders, we identified positive correlations between BIP and both depression and neuroticism. Associations between neuroticism and depression are well documented. Neuroticism is highly comorbid with MDD,^{31, 32} and our findings are consistent with previously observed genetic pleiotropy among neuroticism, MDD, BIP, and schizophrenia.^{33, 34}

Especially notable are findings that suggest a genetic basis for associations between traits regarding which the literature is either equivocal or absent, and which provide useful information to guide further study. For example, we observed correlations of serum urate (SU) with AM (−0.12), T2D (0.275), and triglycerides (0.38), and we consistently observed associations of SU and markers of metabolic syndrome. In the literature, the genetic architecture of this association has not been extensively studied.³⁵ Alleles in IRF8 (MIM: 601565), a regulatory factor of type I interferons, are associated with MS and systemic lupus erythematosus (SLE [MIM: 152700]), but with opposite effect; high type I IFN titers are thought to be causal in SLE but are lower in MS relative to healthy controls.³⁶ In this analysis, however, we found a positive correlation between MS and SLE. We also draw attention to the significant negative correlation between MS and ASD. This replicates a previous genetic association between MS and ASD, with more recent evidence suggesting shared biomedical markers, such as increase in concentrations of tumor necrosis factor-alpha (TNF-α) in serum in ASD and in cerebrospinal fluid in MS.^{37, 38} However, previous treatment of MS with anti-TNF-α led to an increase in the number of demyelinating lesions and a significantly higher relapse rate.³⁹ Furthermore, we observed a positive genetic correlation between ulcerative colitis (UC) and primary billary cirrhosis (PBC [MIM: 109720]). CD, also an IBD and thus closely related, has been reported to share susceptibility genes with PBC including TNFSF15 (MIM: 604052), ICOSLG (MIM: 605717), and CXCR5 (MIM: 601613).⁴⁰ Here we show that ulcerative colitis may also be genetically related to PBC.

Stratification of Genetic Covariance by Functional Annotation

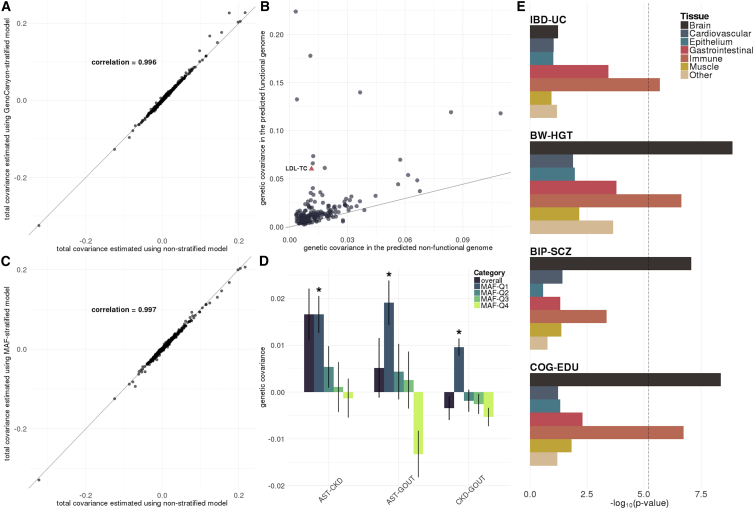
In this section, we apply functional annotations to further dissect the shared genetic architecture of 48 complex traits. We have previously developed GenoCanyon, a statistical framework to predict functional DNA elements in the human genome through integration of annotation data.²⁰ We partitioned the genome into two non-overlapping categories (i.e., functional and non-functional) based on GenoCanyon scores (Material and Methods) and estimated genetic covariance within the functional and the non-functional genome for each pair of traits (Table S5). The total genetic covariance estimated using the stratified model is highly concordant with covariance estimated using the non-stratified model (Figure 4A). However, genetic covariance is enriched in the predicted functional genome for most traits (Figure 4B). Based on this approach, we identified one more pair of correlated traits, i.e., low-density lipoprotein (LDL) and total cholesterol (TC), whose genetic covariance largely concentrated in the predicted functional genome and achieved significance (ρ_func = 0.060; p = 1.0 × 10⁻⁶) while the overall covariance did not (ρ_overall = 0.062; p = 7.7 × 10⁻⁵).

Figure 4.

Annotation-Stratified Covariance Analysis

(A) Stratify genetic covariance by genome functionality predicted by GenoCanyon. Total genetic covariance estimates were highly concordant between stratified and non-stratified models.

(B) For significantly correlated pairs of traits based on the non-stratified model, we compared genetic covariance in the functional and the non-functional genome. Solid line marks the expected value based on annotation’s size. Trait pair LDL-TC is also plotted.

(C) Stratify genetic covariance by MAF quartile. We compared the genetic covariance estimated by MAF-stratified and non-stratified models.

(D) Six pairs of traits that are uniquely correlated in the lowest MAF quartile. Intervals show the standard error of covariance estimates. Asterisks indicate p values below 4.4 × 10⁻⁵.

(E) Stratify genetic covariance by tissue type. Each bar denotes the log-transformed p value. Dashed line highlights the Bonferroni-corrected significance level 0.05/(7 × 1128) = 6.3 × 10⁻⁶.

Next, we partitioned genetic covariance based on quartiles of SNPs’ minor allele frequencies (MAFs) in subjects with European ancestry from the 1000 Genomes Project (Material and Methods; Table S6). Similar to the previous analysis, we identified high concordance between the total covariance estimated using MAF-stratified model and the covariance estimates based on non-stratified model (Figure 4C). Overall, the estimated genetic covariance in four MAF quartiles was comparable (Figure S5). However, we identified three pairs of traits that are uniquely correlated in the lowest MAF quartile (Figure 4D), namely asthma with chronic kidney disease (CKD; p = 1.8 × 10⁻⁵), gout (MIM: 138900) with CKD (p = 4.2 × 10⁻⁸), and asthma with gout (p = 4.4 × 10⁻⁵). For several trait pairs, covariance in the lowest MAF quartile showed reversed direction compared to other quartiles. Covariance between CKD and gout even showed reversed direction compared to the estimated total covariance, highlighting the distinction in how common and less common variants are involved in the shared genetic architecture between these traits. Our findings also hint at the possible selection pressure on DNA variations contributing to metabolic traits including CKD and gout, as well as immune diseases including asthma.

Finally, we studied tissue specificity of genetic covariance through integration of GenoSkyline-Plus annotations (Material and Methods). GenoSkyline-Plus integrates multiple epigenomic and transcriptomic annotations from the Roadmap Epigenomics Project to identify tissue- and cell type-specific functional regions in the human genome.¹⁴ We utilized seven broadly defined tissue and cell types (i.e., brain, cardiovascular, epithelium, gastrointestinal, immune, muscle, and other) to stratify genetic covariance for 1,128 pairs of traits (Table S7). Six tests from four pairs of traits passed Bonferroni correction, i.e., p < 0.05/(1,128 × 7) = 6.3 × 10⁻⁶ (Figures 4E and S6). As expected, UC, as an IBD, was significantly and positively correlated with IBD in immune-related functional genome (p = 2.0 × 10⁻⁶), and two psychiatric diseases, BIP and schizophrenia, were specifically correlated in the genome predicted to be functional in brain (p = 8.7 × 10⁻⁸). In addition, we identified cognitive function (COG) and EDU, and birth weight (BW) and HGT to be significantly correlated in both brain- and immune-related functional genome. Of note, since the sizes of functional annotations are linked to statistical power, p values here should not be interpreted as reflecting the importance of each tissue. Some tissues may be critically involved in the etiology of analyzed traits even if they may have p values that are not statistically significant. For example, IBD and UC were substantially correlated in the gastrointestinal tract (p = 3.7 × 10⁻⁴). Many of these tests may become significant in the near future as GWASs with larger sample sizes are published.

Dissection of Shared and Distinct Genetic Architecture between LOAD and ALS

LOAD and ALS are neurodegenerative diseases. Despite success of large-scale GWASs,^{19, 41} our understanding of their genetic architecture is still far from complete. We applied GNOVA to dissect the genetic covariance between LOAD and ALS using publicly available GWAS summary statistics (N_LOAD = 54,162; N_ALS = 36,052; Table S8).

We identified positive and significant genetic correlation between LOAD and ALS (correlation = 0.175, p = 2.0 × 10⁻⁴). LDSC provided similar estimates but failed to achieve significance (Table 1). 82.6% of the total genetic covariance between LOAD and ALS is concentrated in 33% of the genome predicted to be functional by GenoCanyon (p = 8.2 × 10⁻⁵). Furthermore, MAF-stratified analysis showed that 54.6% of the covariance could be explained by the SNPs in the highest MAF quartile (p = 0.005). In fact, genetic covariance is lower with lower MAF, and covariance in the lowest MAF quartile is nearly negligible. This is surprising considering that the heritability of ALS is enriched in variants with lower MAF.¹⁹ We also performed tissue-stratified analysis using GenoSkyline-Plus annotations (Table S9). No tissue passed the significance threshold after multiple testing correction, but covariance is more concentrated in immune, brain, and cardiovascular functional genome, and showed nominal significance in the immune annotation track (p = 0.014). Whether this will lead to a potential neuroinflammation pathway shared between LOAD and ALS remains to be studied in the future using larger datasets.

Table 1.

Dissection of Genetic Covariance between LOAD and ALS

Annotation	Category	Covariance	p Value
Non-stratified	GNOVA	0.016 (0.004)	∗2.0 × 10−4
	LDSC	0.012 (0.007)	0.075a
GenoCanyon	functional	0.016 (0.004)	∗8.2 × 10−5
	non-functional	0.003 (0.004)	0.377
MAF	Q1	−0.001 (0.003)	0.842
	Q2	0.003 (0.004)	0.361
	Q3	0.004 (0.004)	0.327
	Q4	0.008 (0.003)	∗0.005

Numbers in parentheses indicate standard errors. Significant p values after adjusting for multiple testing within each section are indicated by an asterisk (^∗).

^ap value in LDSC was calculated from genetic correlation instead of genetic covariance.

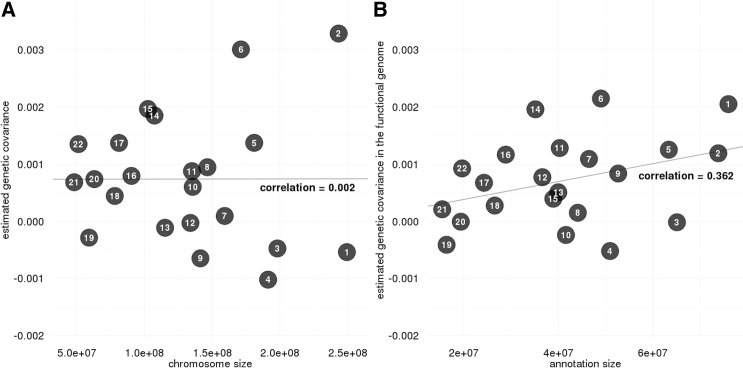
Next, we stratified genetic covariance between LOAD and ALS by chromosome. Somewhat surprisingly, we did not observe a linear relationship between per-chromosome genetic covariance and chromosome size (Figure 5A) given that the overall genetic covariance is positive and significant. Since we have observed the concentration of genetic covariance in the functional genome, we further partitioned each chromosome by genome functionality. We identified a clear and positive linear relationship between genetic covariance in the functional genome and the size of predicted functional DNA on each chromosome (Figure 5B). The correlation between per-chromosome genetic covariance in the non-functional genome and the size of non-functional chromosome is negative and significantly smaller than the corresponding quantity in the functional genome (Figure S7; p = 0.044; tested using Fisher transformation). Our findings suggest a polygenic covariance architecture between LOAD and ALS and highlight the importance of stratifying genetic covariance by functional annotation.

Figure 5.

Stratification of Genetic Covariance between LOAD and ALS by Chromosome

(A) Comparisons of the estimated per-chromosome genetic covariance with chromosome size.

(B) Comparisons of the estimated genetic covariance in the predicted functional genome on each chromosome with size of the functional genome.

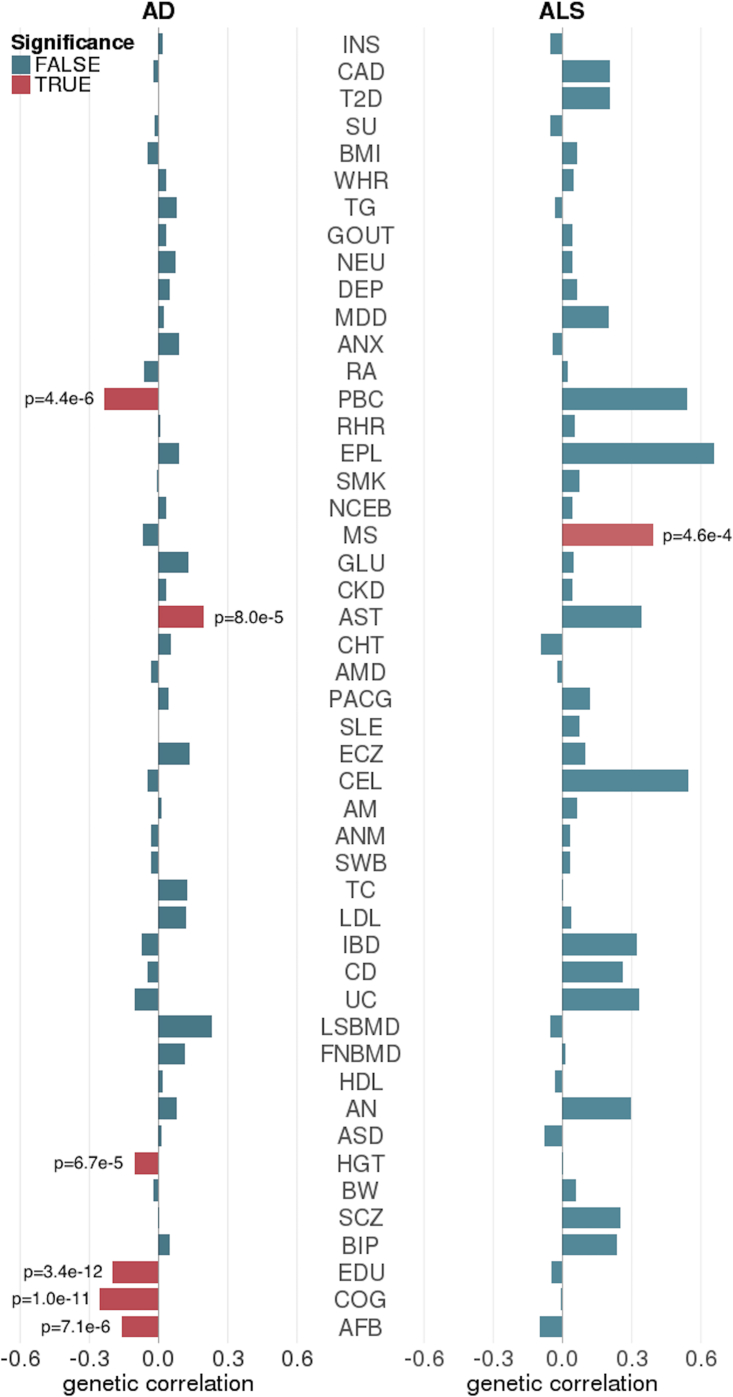
Finally, we jointly analyzed LOAD, ALS, and 48 other complex traits (Table S10). Interestingly, LOAD and ALS showed distinct patterns of genetic correlations with other complex traits (Figure 6). We identified negative and significant correlations between LOAD and cognitive traits including COG and EDU. HGT and age at first birth (AFB), two traits related to hormonal regulation as well as socio-economic status, were also significantly and negatively correlated with LOAD. Consistent with previous reports, we did not identify substantial correlation between LOAD and other neurological and/or psychiatric diseases.^{7, 9} We identified negative correlations between LOAD and gastrointestinal inflammatory diseases including a significant correlation with PBC. Asthma and eczema were both positively correlated with LOAD, suggesting a complex genetic relationship between LOAD and different immune-related diseases. Although some of these traits had the same correlation direction with ALS, none of them were significant. Instead, ALS was significantly and positively correlated with MS, a neurological disease with a well-established immune component.⁴² ALS was also positively correlated with several other immune-related diseases including celiac disease (CEL [MIM: 212750]), asthma, PBC, and IBD (including CD and UC), though none of these were statistically significant. The nominal correlations between ALS and neurological and psychiatric diseases including epilepsy, schizophrenia, BIP, AN, and MDD also remain to be validated in the future using studies with larger sample sizes.

Figure 6.

Genetic Correlations between LOAD, ALS, and 48 Complex Traits

Significant pairs with p < 0.05/(48 × 2) = 5.2 × 10⁻⁴ are highlighted in red.

Discussion

Although our understanding of complex disease etiology is still far from complete, we have gained valuable knowledge about the genetic architecture of numerous complex traits from large-scale association studies, partly due to advances in statistical genetics. First, a large proportion of trait heritability can be explained by SNPs that do not pass the Bonferroni-corrected significance threshold.¹ Therefore, it is often helpful to utilize genome-wide data instead of focusing only on significant SNPs in post-GWAS analyses. Second, sample size is critical for many statistical genetics applications. However, individual-level genotype and phenotype data from consortium-based GWASs are not always easily accessible due to policy and privacy concerns. Thanks to the great efforts from large international collaborations such as the Psychiatric Genomics Consortium in promoting open science and data sharing, it has become a tradition for GWAS consortia to share summary statistics to the broader scientific community. Therefore, it is of practical interest to use GWAS summary statistics as the input of downstream analytical methods.⁸ Finally, integration of high-throughput transcriptomic and epigenomic annotation data has been shown to improve statistical power as well as interpretability in many recent complex trait studies.^{12, 13, 14} As large consortia such as ENCODE²² and Roadmap Epigenomics Project²³ continue to expand, integrative approaches based on functional genome annotations will become an even greater success. In this paper, we developed a novel method to estimate and partition genetic covariance between complex traits. Our method enjoys all the aforementioned advantages. It requires only genome-wide summary statistics and a reference panel as input and allows stratification of genetic covariance by functional genome annotation, which provides novel insights into the shared genetic basis between complex traits and, in some cases, improves the statistical power.

Numerous studies have hinted at a shared genetic basis among neurodegenerative diseases.^{43, 44} Due to the convenience and efficiency of LDSC and the wide accessibility of GWAS summary statistics, several attempts have been made to estimate genetic correlation between neurodegenerative diseases.^{9, 45} To date, these efforts have not been as successful as similar studies on psychiatric diseases and immune-related traits. One reason is that existing methods may not be statistically powerful enough to identify moderate genetic correlation using GWASs with limited sample sizes. In addition, the shared genetics among neurodegenerative diseases may not fit the global, infinitesimal covariance structure that most existing tools are based on. In this study, we applied GNOVA to dissect the genetic covariance between LOAD and ALS, two major neurodegenerative diseases, using summary statistics from the largest available GWASs. Our findings suggest that covariance between LOAD and ALS is concentrated in the predicted functional genome and in very common SNPs. Moreover, after applying functional annotations to stratify the genome, estimated per-chromosome genetic covariance is proportional to chromosome size, suggesting a shared polygenetic architecture between LOAD and ALS and also demonstrating the importance of incorporating predicted genetic activity with GenoCanyon. In addition, joint analysis with 50 complex traits also revealed distinctive genetic covariance profiles for LOAD and ALS. LOAD is negatively correlated with multiple traits related to cognitive function and hormonal regulation, while ALS is positively correlated with MS and a few other immune-related traits. Our findings provided novel insights into the shared and distinct genetic architecture between LOAD and ALS and also further demonstrated the benefits of incorporating functional genome annotations into genetic covariance analysis.

Also of note are findings involving serum urate. SU was positively correlated with gout but also with a few metabolic traits. Gout is an arthritic inflammatory process caused by deposition of uric acid crystals in joints, and the role of hyperuricemia in gout is well established. More recently, a role for hyperuricemia in the pathophysiology of metabolic syndrome and CKD has been suggested.⁴⁶ While associations between hyperuricemia and cardiovascular disease are well described,⁴⁷ multiple hypotheses exist regarding details of its involvement.⁴⁸ For example, hyperuricemia may lead to inflammation in the kidney through vascular smooth muscle proliferation, inducing hypertension via pre-glomerular vascular changes.⁴⁹ It has also been shown to induce oxidative stress in various settings; in adipocytes and islet cells, this may be involved in development of diabetes, and it may also result in impaired endothelin function and activation of the renin-angiotensin-aldosterone system, leading to hypertension.^{50, 51, 52, 53} Despite this evidence, genetic investigations have not identified a strong relationship between hyperuricemia and metabolic syndrome. Polymorphism in gene SLC22A12 (MIM: 607096) was associated with hyperuricemia but not with metabolic syndrome.⁵⁴ Mendelian randomization studies showed an association between uric acid and gout but did not find an association with T2D or cardiovascular risk factors such as hypertension, glucose, or CAD.^{55, 56} Our results suggest that GNOVA successfully isolated a signal of biological and clinical significance that provides important impetus for further inquiry in the etiology of metabolic syndrome.

Dissecting relationships among complex traits is a major goal in human genetics research. Genetic covariance is a useful metric to quantify such relationships, but it has its limitations. First, genetic covariance implicitly imposes a strong assumption on the shared genetic basis between complex traits. Not only may the same set of genetic components affect multiple traits, but their effect sizes on both traits are also assumed to be proportional. In the future, it is of interest to extend our method to estimate more generalized metrics, e.g., consistency in effect directions. Second, genetic covariance analysis does not highlight specific DNA segments with pleiotropic effects. Several SNP-based methods have been developed to identify pleiotropic associations using GWAS summary statistics.^{57, 58} However, due to the large number of SNPs in the genome, statistical power is a critical issue and large-scale inference remains challenging. In addition, we have demonstrated that integrating functional annotations into genetic covariance analysis could reveal subtle structures in shared genetics between complex traits, but interpretation of genetic covariance remains a challenge. Pickrell et al. recently proposed an approach to distinguishing causal relationships among traits from pleiotropic effects via independent biological pathways.⁵⁹ Han et al. developed a method to distinguish pleiotropy from phenotypic heterogeneity.⁶⁰ Although many questions remain unanswered, these recent studies have broadened our view on interpreting complex genetic relationships between human traits. Further, statistical power in genetic covariance analysis will be reduced if the shared genetic components have discordant effect directions on different traits. This problem can be partly addressed by the aforementioned SNP-based methods. Recently, Shi et al. developed a method to estimate local heritability and genetic correlation.^{61, 62} This approach provides an alternative methodological option for analyzing genetic effects at specific loci. Finally, we note that common SNPs in GWASs do not fully explain phenotypic similarity. For example, the estimated genetic covariance among lipid traits explains only 10%–15% of their phenotypic covariance available on LD Hub.¹⁰ Other factors such as rare variants, copy-number variations, and environmental factors may have substantial contributions to the phenotypic covariance among complex traits. Dissection of these complex relationships will be an interesting topic to pursue in the future. Our method, in conjunction with many other tools, provides the most complete picture to date about shared genetics between complex phenotypes.

In summary, we developed GNOVA, a novel statistical framework to perform powerful, annotation-stratified genetic covariance analysis using GWAS summary statistics. Through theoretical proof, we have established GNOVA’s statistical optimality within the framework of method of moments. Compared to LD score regression, GNOVA provides more accurate genetic covariance estimates and powerful statistical inference. Its unique feature of performing annotation-stratified analysis also adds depth to existing analysis strategies. Using GNOVA, we were able to expand the discovery of genetic covariance among a spectrum of common diseases and complex traits. Our findings shed light onto the shared and distinct genetic architecture of complex traits. As the sample sizes in genetic association studies continue to grow, our method has the potential to continue identifying shared genetic components and providing novel insights into the etiology of complex diseases.

Published: December 7, 2017

Appendix A

Model Details

We begin with introducing a general scenario. Assume two standardized traits y₁ and y₂ follow a linear model:

$$y_1=X\beta +\mathit{ϵ}$$

$$y_2=Z\gamma +\delta .$$

Matrices X and Z denote the standardized genotype information for two GWASs. To simplify the algebra, we assume both the genotypes (X and Z) and phenotypes (y₁ and y₂) are standardized. We define K possibly overlapping functional annotations S₁, S₂, …, S_K. All together, these annotations cover the entire genome. We assume two studies share the same list of m SNPs. Vectors $\beta$ and $\gamma$ are random effect terms that quantify the genetic effects on traits y₁ and y₂, respectively. Variables $\mathit{ϵ}$ and $\delta$ denote the non-genetic effects. Genetic and non-genetic effects on the same trait are assumed to be independent. A SNP’s genetic effects on two different traits can be correlated. The genetic covariance depends on functional annotations and follows an additive structure in regions where functional annotations overlap. Specifically, we have

$$\mathbb{E}\left({\beta }_{SN{P}_j}\right)=\mathbb{E}\left({\gamma }_{SN{P}_j}\right)=0and\mathbb{E}\left({\gamma }_{SN{P}_j}{\beta }_{SN{P}_j}\right)=\sum _{c:j\in S_c}\frac{{\rho }_c}{m_c},j=1,\dots ,m$$

$$\mathbb{E}\left({\gamma }_{SN{P}_i}{\beta }_{SN{P}_j}\right)=0,i\ne j,$$

where m_c denotes the total number of SNPs in annotation S_c. Notation $j\in S_c$ indicates that the j^th SNP is located in functional annotation S_c. If we use X_i and Z_i to denote the genotype matrices within annotation S_i (some SNPs may be counted multiple times if the functional annotations overlap) and use ${\beta }_i$ and ${\gamma }_i$ to denote the corresponding genetic effects, the model can be equivalently re-written as follows:

$$y_1=\sum _{i=1}^K{X}_i{\beta }_i+\mathit{ϵ}$$

$$y_2=\sum _{i=1}^K{Z}_i{\gamma }_i+\delta$$

$$\mathbb{E}\left({\gamma }_i{\beta }_i^T\right)=\frac{{\rho }_i}{m_i}I,i=1,\dots ,K.$$

In practice, two different GWASs often share a subset of samples. Without loss of generality, we assume N₁ and N₂ to be the sample sizes of two studies and the first N_S samples in each study are shared. Therefore, the first N_S rows of matrices X_i and Z_i (i = 1, …, K) are identical. To account for the non-genetic correlation introduced by sample overlapping, we allow random error terms $\mathit{ϵ}$ and $\delta$ to be correlated.

$$\mathbb{E}\left({\mathit{ϵ}}_i{\delta }_j\right)=\{\begin{array}{c}{\rho }_e,1\le i=j\le N_s\\ 0,otherwise\end{array}$$

To summarize, this framework explicitly models the annotation-stratified genetic covariance in the genome. It also allows functional annotations to overlap, which is important when applied to real-world annotation data. Furthermore, we take the sample overlap between different GWASs into account. Finally, our model does not require any additional assumption on the heritability structure. In following sections, we discuss how to estimate covariance parameters ρ₁, …, ρ_K.

Estimate Covariance Parameters

First, for an arbitrary N₁ × N₂ matrix A, we study the expectation of $y_1^{T}A{y}_2$.

$$\begin{array}{c}\mathbb{E}\left(y_1^{T}A{y}_2\right)=\mathbb{E}\left(\left(\sum _{i=1}^K{\beta }_i^T{X}_i^T+{\mathit{ϵ}}^T\right)A\left(\sum _{i=1}^K{Z}_i{\gamma }_i+\delta \right)\right)\\ =tr\left(\mathbb{E}\left(\left(\sum _{i=1}^K{\beta }_i^T{X}_i^T+{\mathit{ϵ}}^T\right)A\left(\sum _{i=1}^K{Z}_i{\gamma }_i+\delta \right)\right)\right)\\ =tr\left(\mathbb{E}\left(\sum _{i=1}^K{\beta }_i^T{X}_i^{T}A{Z}_i{\gamma }_i\right)+\mathbb{E}\left({\mathit{ϵ}}^{T}A\delta \right)\right)\\ =\mathbb{E}\left(tr\left(\sum _{i=1}^K{\beta }_i^T{X}_i^{T}A{Z}_i{\gamma }_i\right)+tr\left({\mathit{ϵ}}^{T}A\delta \right)\right)\\ =\mathbb{E}\left(\sum _{i=1}^{K}tr\left(A{Z}_i{\gamma }_i{\beta }_i^T{X}_i^T\right)\right)+\mathbb{E}\left(tr\left(A\delta {\mathit{ϵ}}^T\right)\right)\\ =\sum _{i=1}^{K}tr\left(A{Z}_i\mathbb{E}\left({\gamma }_i{\beta }_i^T\right)X_i^T\right)+tr\left(A\mathbb{E}\left(\delta {\mathit{ϵ}}^T\right)\right)\\ =\sum _{i=1}^K\frac{{\rho }_i}{m_i}tr\left(A{Z}_i{X}_i^T\right)+{\rho }_e\left(\sum _{t=1}^{N_s}{A}_{tt}\right)\end{array}$$

Here, quantity A_tt denotes the t^th diagonal element of matrix A. To estimate the covariance parameters, we plug in K+1 different matrices $A_1$,...,$A_{K+1}$ into the equation above. Next, we apply method of moments to approximate $\mathbb{E}\left(y_1^T{\tilde{A}}_j{y}_2\right)$ using the observed value $y_1^T{\tilde{A}}_j{y}_2$. After these steps, we get the following equations:

$$y_1^T{A}_j{y}_2=\sum _{i=1}^K\frac{{\rho }_i}{m_i}tr\left(A_j{Z}_i{X}_i^T\right)+{\rho }_e\sum _{t=1}^{N_s}{\left(A_j\right)}_{tt},j=1,\dots ,K+1.$$

Solving this linear system of K+1 equations would get us a set of point estimates ${\hat{\rho }}_1,\dots ,{\hat{\rho }}_K$ for covariance parameters. We discuss the details in the following section.

Choose Matrix A

The estimation approach described the previous section works for an arbitrary set of A matrices. So how do we properly choose them in practice? We begin with solving a practical issue. Processing large-scale GWASs requires a substantial amount of resource for both computation and data storage. Moreover, individual-level genotype and phenotype data from consortium-based GWASs are often non-accessible due to policy concerns. However, sharing the summary statistics has become a common practice in the field of complex disease genetics. Summary data for many GWASs are openly accessible online. Therefore, it is of practical interest to estimate genetic covariance based on summary statistics only. To achieve this goal, we define the first K matrices as:

$${\tilde{A}}_j=\frac{X_j{Z}_j^T}{m_j},j=1,\dots ,K.$$

Plugging in these matrices, the first K equations become:

$$\frac{1}{m_j}{\left(X_j^T{y}_1\right)}^T{Z}_j^T{y}_2=\sum _{i=1}^K\frac{{\rho }_i}{m_i{m}_j}tr\left(X_j{Z}_j^T{Z}_i{X}_i^T\right)+\frac{{\rho }_e}{m_j}\sum _{t=1}^{N_s}{\left(X_j{Z}_j^T\right)}_{tt}=\sum _{i=1}^K\frac{{\rho }_i}{m_i{m}_j}tr\left(Z_j^T{Z}_i{X}_i^T{X}_j\right)+\frac{{\rho }_e}{m_j}\sum _{t=1}^{N_s}{\left(X_j{X}_j^T\right)}_{tt},j=1,\dots ,K.$$

The second equality is based on the property of trace and the fact that first N_S samples are shared between two studies. To calculate all the terms in these equations, we note that

$$\sum _{t=1}^{N_s}{\left(X_j{X}_j^T\right)}_{tt}=\sum _{t=1}^{N_s}\sum _{l=1}^{m_j}{\left(X_j\right)}_{tl}=\sum _{l=1}^{m_j}\sum _{t=1}^{N_s}{\left(X_j\right)}_{tl}\approx \sum _{l=1}^{m_j}{N}_s=m_j{N}_s.$$

Here, we used approximation $\left({\sum }_{t=1}^{N_s}{\left(X_j\right)}_{tl}\right)/N_s\approx 1$. This is because genotype data are standardized and the shared sub-cohort is a subset of all individuals. In practice, if two GWASs share samples, the shared sample size is usually greater than several hundred, which is sufficient to make this approximation reasonable.

$$\frac{1}{m_i{m}_j}tr\left(Z_j^T{Z}_i{X}_i^T{X}_j\right)=\frac{N_1{N}_2}{m_i{m}_j}tr\left(\left(\frac{Z_j^T{Z}_i}{N_2}\right)\left(\frac{X_i^T{X}_j}{N_1}\right)\right)\approx \frac{N_1{N}_2}{m_i{m}_j}tr\left(D_{ij}^T{D}_{ij}\right)=\frac{N_1{N}_2}{m_i{m}_j}\sum _{l=1}^{m_i}\sum _{l^{\prime }=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2.$$

We approximate the sample linkage disequilibrium (LD) matrices from both studies, i.e., $\left(Z_i^T{Z}_j\right)/N_2$ and $\left(X_i^T{X}_j\right)/N_1$, using the population LD matrix D_ij. In practice, we estimate LD using a reference panel, e.g., samples from the 1000 Genomes Project with European ancestry. In the formula, $r_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2$ denotes the LD between the $l$^th SNP from category S_i and the (l′)^th SNP from category S_j.

$${\left(X_j^T{y}_1\right)}^T{Z}_j^T{y}_2=\sqrt{N_1{N}_2}{\left(\frac{1}{\sqrt{N_1}}{X}_j^T{y}_1\right)}^T\left(\frac{1}{\sqrt{N_2}}{Z}_j^T{y}_2\right)=\sqrt{N_1{N}_2}{\left(z_1\right)}_j^T{\left(z_2\right)}_j$$

Here, z₁ and z₂ denote the z-scores of SNP-level associations from two GWASs; ${\left(z_1\right)}_j$ and ${\left(z_2\right)}_j$ represent z-scores corresponding to the SNPs in annotation category S_j.

We plug in these quantities and divide N₁N₂ on both sides of the K equations, then we get:

$$\frac{1}{m_j\sqrt{N_1{N}_2}}{\left(z_1\right)}_j^T{\left(z_2\right)}_j=\sum _{i=1}^K\frac{{\rho }_i}{m_i{m}_j}\sum _{l=1}^{m_i}\sum _{l^{\prime }=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2+\frac{N_s{\rho }_e}{N_1{N}_2},j=1,\dots ,K.$$

Next, we study the (K+1)^th equation. We define:

$${\tilde{A}}_{K+1}={\left(\begin{array}{cc}{I}_{N_s\times N_s}& 0\\ 0& 0\end{array}\right)}_{N_1\times N_2}.$$

We make the following observations.

$$y_1^T{\tilde{A}}_{K+1}{y}_2=\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t$$

$$\frac{1}{m_i}tr\left({\tilde{A}}_{K+1}{Z}_i{X}_i^T\right)=\frac{1}{m_i}\sum _{t=1}^{N_s}{\left(Z_i{X}_i^T\right)}_{tt}=\frac{1}{m_i}\sum _{t=1}^{N_s}{\left(X_i{X}_i^T\right)}_{tt}\approx \frac{1}{m_i}{m}_i{N}_s=N_s$$

Again, the approximation is based on the facts that the genotype data are standardized, the first N_S rows of matrices X_i and Z_i are identical, and the shared sub-cohort is a subset of the complete study with sufficient sample size.

$$\sum _{t=1}^{N_s}{\left({\tilde{A}}_{K+1}\right)}_{tt}=\sum _{t=1}^{N_s}1=N_s$$

Plugging in these quantities and dividing N₁N₂ on both sides of the (K+1)^th equation, we get:

$$\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t=\frac{N_s}{N_1{N}_2}\sum _{i=1}^K{\rho }_i+\frac{N_s}{N_1{N}_2}{\rho }_e.$$

We denote all K+1 equations in matrix form:

$$\begin{array}{l}\left(\begin{array}{c}\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\end{array}\\ \frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\end{array}\right)=\\ \left(\begin{array}{cccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2& \frac{N_s}{N_1{N}_2}\\ ⋮& \ddots & ⋮& ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2& \frac{N_s}{N_1{N}_2}\\ \frac{N_s}{N_1{N}_2}& \cdots & \frac{N_s}{N_1{N}_2}& \frac{N_s}{N_1{N}_2}\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\\ {\rho }_{K+1}\end{array}\right).\end{array}$$

Since ρ₁, …, ρ_K are the parameters of interest, we subtract the (K+1)^th equation from the first K equations and remove ρ_K+1 from the linear system:

$$\begin{array}{l}\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\end{array}\right)=\\ \left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2-\frac{N_s}{N_1{N}_2}& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2-\frac{N_s}{N_1{N}_2}\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2-\frac{N_s}{N_1{N}_2}& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2-\frac{N_s}{N_1{N}_2}\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right)\end{array}$$

When the sample sizes of both GWASs are large and the sample overlap between two studies is moderate, then N_S / (N₁N₂) is a small quantity. We use the approximation $N_s/\left(N_1{N}_2\right)\approx 0$. Similarly, we have:

$$\frac{1}{N_1{N}_2}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t=\frac{N_s}{N_1{N}_2}\left(\frac{1}{N_s}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)\approx 0.$$

Here, $\left({\sum }_{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)/N_s$ is the phenotypic correlation between two traits among the shared N_S samples and is bounded by 1. Therefore the approximation is reasonable. Additional justification on these approximations will be given in the next section.

In summary, the K equations can be approximated by:

$$\begin{array}{l}\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\end{array}\right)=\\ \left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).\end{array}$$

We denote

$$v={\left(\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1,\dots ,\frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\right)}^T$$

$$M=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right).$$

Then, the point estimate of covariance parameters can be denoted as

$$\hat{\rho }=M^{-1}v.$$

Importantly, we emphasize that M can be estimated using a reference panel and v is based only on GWAS summary data. No individual-level genotype or phenotype information from the original GWASs is needed in this framework. Finally, we note that in some rare cases (e.g., very similar annotations are used simultaneously in the analysis), matrix M may not be invertible. In that case, we can acquire the genetic covariance estimator through the following minimization problem.

$$\hat{\rho }=\underset{\rho }{\min }{\Vert M\rho -v\Vert }_2^2$$

Remarks on Approximation

Several approximations are critical in the estimation framework described above. In this section, we discuss why these approximations are reasonable.

Approximation 1.

$$\frac{1}{N_s}\sum _{t=1}^{N_s}{\left(X_j\right)}_{tl}\approx 1$$

This approximation is based on law of large numbers and two assumptions. (1) The genotype matrix is standardized. (2) If two GWASs share samples, the shared sample size N_S needs to be sufficiently large. The first assumption is commonly seen in complex trait genetic models. It is actually not a required condition, but it simplifies the algebra. The second assumption is also most likely going to hold in practice. If two GWASs have a sample overlap, it is often because one or more cohorts were used in both studies. A cohort like this usually has a sample size that ranges from several hundred to a few thousand, which is sufficiently large for the law of large numbers to hold.

Approximation 2.

$$\frac{1}{m_i{m}_j}\sum _{l=1}^{m_i}\sum _{l^{\prime }=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2-\frac{N_s}{N_1{N}_2}\approx \frac{1}{m_i{m}_j}\sum _{l=1}^{m_i}\sum _{l^{\prime }=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2$$

Since the first term $\left({\sum }_{l=1}^{m_i}{\sum }_{l^{\text{'}}=1}^{m_j}{r}_{l^{\left(i\right)}{l}^{\prime \left(j\right)}}^2\right)/m_i{m}_j$ does not depend on GWAS sample size, this approximation holds when N₁ and N₂ are large and the shared sample size N_S is moderate. Notably, this condition does not contradict with the condition in approximation 1. In approximation 1, we require the value of N_S to exceed several hundred so that the law of large numbers could hold. Here, we require the ratio between N_S and the actual GWAS sample size to be small. Since large-scale GWAS meta-analyses published in recent years often have sample sizes on the scale of 10⁴ or 10⁵, this approximation is reasonable. Of note, the term N_S / N₁N₂ is introduced when we remove parameter ${\rho }_{K+1}$ from the linear system by subtracting the (K+1)^th equation from the first K equations. If the true value of ${\rho }_{K+1}$, i.e., the non-genetic covariance introduced by sample overlap, is in fact very small compared with the genetic covariance, then this approximation can be omitted. Finally, we note that even if the two GWASs are performed on the identical cohort (i.e., complete sample overlap), then N_S / N₁N₂ = 1/N is still a small quantity as long as the sample size N is big.

Approximation 3.

$$\frac{1}{\sqrt{N_1{N}_2}}\left(\frac{1}{m_j}{\left(z_1\right)}_j^T{\left(z_2\right)}_j\right)-\frac{N_s}{N_1{N}_2}\left(\frac{1}{N_s}\sum _{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)\approx \frac{1}{\sqrt{N_1{N}_2}}\left(\frac{1}{m_j}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\right)$$

The z-scores in GWASs usually do not deviate much from the standard normal distribution. Therefore ${\left(z_1\right)}_j^T{\left(z_2\right)}_j/m_j$ is close to the true correlation between z₁ and z₂. Similarly, since we assume the phenotypes are standardized, $\left({\sum }_{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)/N_s$ is the phenotypic correlation between two traits among the shared N_S samples. Therefore, as long as

$$\frac{N_s}{N_1{N}_2}\ll \frac{1}{\sqrt{N_1{N}_2}}$$

or equivalently,

$$\frac{N_s}{\sqrt{N_1{N}_2}}\ll 1,$$

then it is reasonable to omit the term $\left({\sum }_{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)/N_1{N}_2$. Therefore, similar to the condition in approximation 2, if the GWAS sample sizes N₁ and N₂ are large and the shared sample size N_S is moderate, then approximation 3 holds. However, we note that if there is a substantial overlap between two studies (e.g., when analyzing two traits measured on the same cohort), then $N_s/\sqrt{N_1{N}_2}\approx 1$ and we can no longer omit the term $\left({\sum }_{t=1}^{N_s}{\left(y_1\right)}_t{\left(y_2\right)}_t\right)/N_1{N}_2$ from the equation.

Special Cases

(1) Two Independent GWASs

If samples from two GWASs do not overlap, then the non-genetic effects $\mathit{ϵ}$ and $\delta$ are independent and ρ_e = 0. So only K equations are needed for estimating covariance estimators. We still define ${\tilde{A}}_j=\left(X_j{Z}_j^T\right)/m_j$ for j = 1,…,K. That gives us:

$$\begin{array}{l}\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\end{array}\right)=\\ \left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).\end{array}$$

Therefore, none of the approximations discussed in the previous section is needed in this simple scenario. The covariance estimator remains the same:

$$\hat{\rho }=M^{-1}v.$$

(2) No Annotation Stratification

If we do not stratify covariance by functional annotation, then $\hat{\rho }$ is just a one-dimensional estimator for the overall genetic covariance.

$$\hat{\rho }=v/M=\left(\frac{1}{m\sqrt{N_1{N}_2}}{\left(z_1\right)}^T\left(z_2\right)\right)/\left(\frac{1}{m^2}\sum _{l=1}^m\sum _{l^{\prime }=1}^m{r}_{l{l}^{\prime }}^2\right)=\frac{\overline{z_1{z}_2}}{\overline{r^2}\sqrt{N_1{N}_2}}$$

Here, $\overline{z_1{z}_2}$ is the average product of z-scores from two GWASs; $\overline{r^2}$ is the average LD across all SNP pairs in the study, or equivalently, the average LD score across all SNPs in the study. Interestingly, this estimator can be seen as a two-trait extension of the heritability estimator proposed by Bulik-Sullivan.¹⁶

(3) Two Different Traits Measured on the Same Cohort

If the samples completely overlap between two GWASs (i.e., N₁ = N₂ = N_S = N), as we discussed in the previous section, approximations 1 and 2 still hold as long as the sample size is large but approximation 3 would fail. Therefore, after subtracting the (K+1)^th equation from the first K equations and removing parameter ${\rho }_{K+1}$, we get:

$$\left(\begin{array}{c}\frac{1}{m_{1}N}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N^2}\sum _{t=1}^N{\left(y_1\right)}_t{\left(y_2\right)}_t\\ ⋮\\ \frac{1}{m_{K}N}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N^2}\sum _{t=1}^N{\left(y_1\right)}_t{\left(y_2\right)}_t\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ ⋮\\ {\rho }_K\end{array}\right).$$

In practice, since we do not assume access to the individual-level phenotype data, an estimate of phenotypic correlation ${\hat{\rho }}_{pheno}$ needs to be acquired elsewhere (since we assumed phenotypes to be standardized, this is equivalent to phenotypic covariance). Then, we could get the covariance estimate under sample overlap correction:

$$\hat{\rho }=M^{-1}\left(\begin{array}{c}\frac{1}{m_{1}N}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\frac{1}{N}{\hat{\rho }}_{pheno}\\ ⋮\\ \frac{1}{m_{K}N}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\frac{1}{N}{\hat{\rho }}_{pheno}\end{array}\right)=M^{-1}\left(v-\frac{{\hat{\rho }}_{pheno}}{N}\mathbf{1}\right).$$

For some traits, ${\hat{\rho }}_{pheno}$ may have been reported in the literature. Otherwise, we need to estimate ${\hat{\rho }}_{pheno}$ using GWAS summary statistics. Bulik-Sullivan et al. showed the following LD score regression equation without annotation structure in the genome:⁷

$$\mathbb{E}\left({\left(z_1\right)}_j{\left(z_2\right)}_j\right)=\frac{\sqrt{N_1{N}_2}\rho }{m}\sum _{i=1}^m{r}_{ij}^2+\frac{N_s{\rho }_{pheno}}{\sqrt{N_1{N}_2}}.$$

In this special case when two traits are measured on the same cohort, the formula becomes

$$\mathbb{E}\left({\left(z_1\right)}_j{\left(z_2\right)}_j\right)=\frac{N\rho }{m}\sum _{i=1}^m{r}_{ij}^2+{\rho }_{pheno}.$$

Therefore, we could apply LD score regression and use the estimated intercept as ${\hat{\rho }}_{pheno}$.

(4) Binary Traits

In this section, we investigate whether we could analyze ascertained case-control studies using our framework. It has been previously shown that the following formula holds under the liability threshold model:⁷

$$\mathbb{E}\left(\frac{1}{\sqrt{N_1{N}_2}}{\left(z_1\right)}_{SN{P}_j}{\left(z_2\right)}_{SN{P}_j}\right)=\frac{{\rho }_{obs}}{m}\sum _{i=1}^m{r}_{ij}^2+\sqrt{P_1\left(1-P_1\right)P_2\left(1-P_2\right)}\left(\frac{N^{cas,cas}}{N_1^{cas}{N}_2^{cas}}+\frac{N^{con,con}}{N_1^{con}{N}_2^{con}}-\frac{N^{cas,con}}{N_1^{cas}{N}_2^{con}}-\frac{N^{con,cas}}{N_1^{con}{N}_2^{cas}}\right),$$

where ρ_obs denotes the covariance on the observed scale, N^a,b denotes the number of samples with phenotype a in study 1 and phenotype b in study 2, $N_i^a$ denotes the total number of samples with phenotype a in study i, and P_i denotes the sample prevalence of trait y_i. Using the same approximation we used in method of moments,

$$\mathbb{E}\left(\frac{1}{\sqrt{N_1{N}_2}}{\left(z_1\right)}_{SN{P}_j}{\left(z_2\right)}_{SN{P}_j}\right)\approx \frac{1}{\sqrt{N_1{N}_2}}{\left(z_1\right)}_{SN{P}_j}{\left(z_2\right)}_{SN{P}_j},$$

it is straightforward to extend it to the following matrix form that allows annotation stratification:

$$\left(\begin{array}{c}\frac{1}{m_1\sqrt{N_1{N}_2}}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\eta \\ ⋮\\ \frac{1}{m_K\sqrt{N_1{N}_2}}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\eta \end{array}\right)=\left(\begin{array}{ccc}\frac{1}{m_1{m}_1}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(1\right)}{l}^{\prime \left(1\right)}}^2& \cdots & \frac{1}{m_K{m}_1}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_1}{r}_{l^{\left(K\right)}{l}^{\prime \left(1\right)}}^2\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1{m}_K}\sum _{l=1}^{m_1}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(1\right)}{l}^{\prime \left(K\right)}}^2& \cdots & \frac{1}{m_K{m}_K}\sum _{l=1}^{m_K}\sum _{l^{\prime }=1}^{m_K}{r}_{l^{\left(K\right)}{l}^{\prime \left(K\right)}}^2\end{array}\right)\left(\begin{array}{c}{\rho }_{obs,1}\\ ⋮\\ {\rho }_{obs,K}\end{array}\right),$$

where

$$\eta =\sqrt{P_1\left(1-P_1\right)P_2\left(1-P_2\right)}\left(\frac{N^{cas,cas}}{N_1^{cas}{N}_2^{cas}}+\frac{N^{con,con}}{N_1^{con}{N}_2^{con}}-\frac{N^{cas,con}}{N_1^{cas}{N}_2^{con}}-\frac{N^{con,cas}}{N_1^{con}{N}_2^{cas}}\right).$$

We note that $\eta =0$ when two GWASs do not share any sample. In that case, covariance estimator remains the same:

$$\hat{\rho }=M^{-1}v.$$

We just need to interpret it as the covariance on the observed scale.

When two studies have a substantial sample overlap, $\eta$ cannot be ignored in the equations and therefore needs to be estimated. Notably, $\sqrt{N_1{N}_2}\eta$ is in fact the intercept term in cross-trait LD score regression. Therefore, similar to the previous scenario in this section, we could estimate $\hat{\eta }$ by running LD score regression first and then plug it in the equations to calculate the covariance estimate:

$$\hat{\rho }=M^{-1}\left(\begin{array}{c}\frac{1}{m_{1}N}{\left(z_1\right)}_1^T{\left(z_2\right)}_1-\hat{\eta }\\ ⋮\\ \frac{1}{m_{K}N}{\left(z_1\right)}_K^T{\left(z_2\right)}_K-\hat{\eta }\end{array}\right)=M^{-1}\left(v-\hat{\eta }\mathbf{1}\right).$$

Finally, we note that the argument can be extended to estimate the covariance between a continuous trait and a binary trait. However, the estimated genetic covariance will be on the half-observed scale.⁷

Remarks on Overlapping Functional Annotations

We have discussed parameter estimation in previous sections. Our framework allows functional annotations to overlap, which is an important feature in real data analysis. However, when functional annotations overlap, the covariance parameter ρ is not the real quantity of interest. Instead, the total covariance in each annotation category is more meaningful biologically. For instance, the total covariance in functional annotation S₁ is

$$covariance\left(S_1\right)=\sum _{i=1}^K{\rho }_i\frac{m_{i\cap 1}}{m_i},$$

where $m_{i\cap 1}$ denotes the number of SNPs in region $S_1\cap S_i$. Of note, this quantity equals to ρ₁ when S₁ does not overlap with any other functional annotation. Therefore, we use the weighted estimator ${\hat{\rho }}^W$ to estimate the total covariance in each category when functional annotations overlap:

$${\hat{\rho }}^W=W\hat{\rho }.$$

Here, W is a K × K matrix with element

$$W_{ij}=\frac{m_{j\cap i}}{m_j},1\le i,j\le K.$$

Theoretical Properties of Covariance Estimator and Some Numerical Justifications

As discussed in previous sections, matrices ${\tilde{A}}_j$ have two major properties under the ideal case where two GWASs do not share samples.

• (1)Vector $v={\left(y_1^T{\tilde{A}}_1{y}_2,\dots ,y_1^T{\tilde{A}}_K{y}_2\right)}^T/N_1{N}_2$ can be directly calculated using GWAS summary statistics.
• (2)$\mathbb{E}\left(y_1^T{\tilde{A}}_j{y}_2\right)={\sum }_{i=1}^{K}tr\left({\tilde{A}}_j{Z}_i{X}_i^T\right){\rho }_i/m_i$, where terms $tr\left({\tilde{A}}_j{Z}_i{X}_i^T\right)$ only depends on LD and therefore can be estimated using a reference panel.

In this section, we investigate whether changing A could get us another covariance estimator, ${\hat{\rho }}_A$, that is even better than $\hat{\rho }$, which is based on ${\tilde{A}}_j$. We show that under reasonable conditions, all estimators in our framework are unbiased but $\hat{\rho }=M^{-1}v$ “almost” has the minimal variance. The proof is an extension of the MINQUE theory developed in Rao et al.⁶³

To prove the theoretical properties, we need an additional assumption on the distribution of y₁ and y₂. We assume that y₁ and y₂ are marginally standardized and follow a multivariate normal distribution:

$$\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\sim MVN\left(0,\left(\begin{array}{cc}{H}_1& \text{Θ}\\ {\text{Θ}}^T& H_2\end{array}\right)\right).$$

H₁ and H₂ denote the variance-covariance matrices of two traits; $\text{Θ}$ denotes the covariance elements between two traits. Based on the model we have described throughout the paper:

$$\text{Θ}=\mathbb{E}\left(y_1{y}_2^T\right)=\sum _{i=1}^K\frac{{\rho }_i}{m_i}{X}_i{Z}_i^T.$$

We begin with calculating the variance of the quadratic form-like quantity $y_1^{T}A{y}_2$.

Proposition 1. Let A be a N₁ × N₂ matrix. Then $Var\left(y_1^{T}A{y}_2\right)=tr\left(A^T{H}_{1}A{H}_2\right)+tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$.

Proof:

We note that

$$\mathbb{E}\left(y_1|y_2\right)=\text{Θ}{H}_2^{-1}{y}_2$$

$$Var\left(y_1|y_2\right)=H_1-\text{Θ}{H}_2^{-1}{\text{Θ}}^T.$$

Therefore,

$$Var\left(y_1^{T}A{y}_2\right)={\mathbb{E}}_2\left(Va{r}_{1|2}\left(y_1^{T}A{y}_2\right)\right)+Va{r}_2\left({\mathbb{E}}_{1|2}\left(y_1^{T}A{y}_2\right)\right)={\mathbb{E}}_2\left(Va{r}_{1|2}\left(y_2^T{A}^T{y}_1\right)\right)+Va{r}_2\left({\mathbb{E}}_{1|2}\left(y_2^T{A}^T{y}_1\right)\right)={\mathbb{E}}_2\left(y_2^T{A}^T\left(H_1-\text{Θ}{H}_2^{-1}{\text{Θ}}^T\right)A{y}_2\right)+Va{r}_2\left(y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2\right)=tr\left(A^T\left(H_1-\text{Θ}{H}_2^{-1}{\text{Θ}}^T\right)A{H}_2\right)+Va{r}_2\left(y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2\right)=tr\left(A^T{H}_{1}A{H}_2\right)-tr\left(A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2\right)+Va{r}_2\left(y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2\right).$$

Since

$$y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2=y_2^T{H}_2^{-1}{\text{Θ}}^{T}A{y}_2,$$

we have

$$y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2=\frac{1}{2}\left(y_2^T{A}^T\Theta H_2^{-1}{y}_2+y_2^T{H}_2^{-1}{\Theta }^{T}A{y}_2\right)=\frac{1}{2}{\text{y}}_2^{\text{T}}\left({\text{A}}^{\text{T}}\text{Θ}{H}_2^{-1}+H_2^{-1}{\text{Θ}}^{T}A\right)y_2.$$

Matrix $A^T\text{Θ}{H}_2^{-1}+H_2^{-1}{\text{Θ}}^{T}A$ is symmetric; therefore $y_2^T\left(A^T\text{Θ}{H}_2^{-1}+H_2^{-1}{\text{Θ}}^{T}A\right)y_2$ is a quadratic form. This gives us

$$Var\left(y_2^T{A}^T\text{Θ}{H}_2^{-1}{y}_2\right)=\frac{1}{4}\times 2tr\left(\left(A^T\text{Θ}{H}_2^{-1}+H_2^{-1}{\text{Θ}}^{T}A\right)H_2\left(A^T\text{Θ}{H}_2^{-1}+H_2^{-1}{\text{Θ}}^{T}A\right)H_2\right)=\frac{1}{2}tr\left(A^T\text{Θ}{A}^T\text{Θ}+A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2+H_2^{-1}{\text{Θ}}^{T}A{H}_2{A}^T\text{Θ}+H_2^{-1}{\text{Θ}}^{T}A{\text{Θ}}^{T}A{H}_2\right)=\frac{1}{2}\left(2tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)+2tr\left(A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2\right)\right)=tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)+tr\left(A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2\right).$$

Therefore,

$$Var\left(y_1^{T}A{y}_2\right)=tr\left(A^T{H}_{1}A{H}_2\right)-tr\left(A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2\right)+tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)+tr\left(A^T\text{Θ}{H}_2^{-1}{\text{Θ}}^{T}A{H}_2\right)=tr\left(A^T{H}_{1}A{H}_2\right)+tr\left(A^T\text{Θ}{A}^T\text{Θ}\right).$$

Notably, if y₁ = y₂ and A is symmetric, then this result becomes the well-known variance formula for quadratic forms.

$$Var\left(y_1^{T}A{y}_1\right)=2tr\left(A{H}_{1}A{H}_1\right)$$

Proposition 1 tells us that the variance of $y_1^{T}A{y}_2$ contains two parts. Later we will show that the second part, i.e., $tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$, is very small compared to the first term, $tr\left(A^T{H}_{1}A{H}_2\right)$, when analyzing real GWAS data. This is because the individuals in GWASs are almost independent samples and the elements of matrix $\text{Θ}$ are small. On the contrary, we assume the data to be standardized, so the diagonal elements of matrices H₁ and H₂ are always 1. This leads to

$$tr\left(A^T{H}_{1}A{H}_2\right)\gg tr\left(A^T\Theta A^T\Theta \right).$$

With this in mind, the following claim is approximately true.

$$Var\left(y_1^{T}A{y}_2\right)\approx tr\left(A^T{H}_{1}A{H}_2\right)$$

In the next proposition, we define a N₁ × N₂ matrix $A_{\ast }$ and show that $A_{\ast }$ minimizes $tr\left(A^T{H}_{1}A{H}_2\right)$ under some conditions. Based on the argument above, $A_{\ast }$ “almost” minimizes $Var\left(y_1^{T}A{y}_2\right)$ too.

Proposition 2. Assume two GWASs do not share samples. We define the following quantities.

• (i)Let $p={\left(p_1,\dots p_K\right)}^T$ be an arbitrarily given K-dimensional vector;
• (ii)Let $S$ be a $K\times K$ symmetric matrix with element $S_{l{l}^{\prime }}=tr\left(H_1^{-1}{X}_{l^{\prime }}{Z}_{l^{\prime }}^T{H}_2^{-1}{Z}_l{X}_l^T\right)/m_l{m}_{l^{\prime }}$ for $1\le l,l^{\prime }\le K$;
• (iii)Let $\lambda ={\left({\lambda }_1,\dots {\lambda }_K\right)}^T$ be a vector such that $S\lambda =p$;
• (iv)Define $A_{\ast }={\sum }_{j=1}^K\left({\lambda }_j/m_j\right)H_1^{-1}{X}_j{Z}_j^T{H}_2^{-1}$.

Then, we have:

• (1)$\mathbb{E}\left(y_1^T{A}_{\ast }{y}_2\right)={\sum }_{t=1}^K{p}_t{\rho }_t$;
• (2)Let A be a matrix such that $\mathbb{E}\left(y_1^{T}A{y}_2\right)={\sum }_{t=1}^K{p}_t{\rho }_t$. Then, $tr\left(A^T{H}_{1}A{H}_2\right)\ge tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right)$.

Proof:

(1)

Note that

$$\mathbb{E}\left(y_1^T{A}_{\ast }{y}_2\right)=\sum _{t=1}^K\frac{tr\left(A_{\ast }{Z}_t{X}_t^T\right){\rho }_t}{m_t}.$$

Therefore, it is equivalent to show

$$\frac{tr\left(A_{\ast }{Z}_t{X}_t^T\right)}{m_t}=p_t,1\le t\le K.$$

In fact,

$$\frac{1}{m_t}tr\left(A_{\ast }{Z}_t{X}_t^T\right)=\sum _{j=1}^K\frac{{\lambda }_j}{m_j{m}_t}tr\left(H_1^{-1}{X}_j{Z}_j^T{H}_2^{-1}{Z}_t{X}_t^T\right)=\sum _{i=1}^K{\lambda }_j{S}_{tj}=p_t.$$

(2)

Let $B=A-A_{\ast }$, then

$$tr\left(A^T{H}_{1}A{H}_2\right)=tr\left({\left(A_{\ast }+B\right)}^T{H}_1\left(A_{\ast }+B\right)H_2\right)=tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right)+tr\left(A_{\ast }^T{H}_{1}B{H}_2\right)+tr\left(B^T{H}_1{A}_{\ast }{H}_2\right)+tr\left(B^T{H}_{1}B{H}_2\right).$$

First, we show that $tr\left(A_{\ast }^T{H}_{1}B{H}_2\right)=tr\left(B^T{H}_1{A}_{\ast }{H}_2\right)=0$.

$$tr\left(A_{\ast }^T{H}_{1}B{H}_2\right)=tr\left(H_2^T{B}^T{H}_1^T{A}_{\ast }\right)=tr\left(H_2{B}^T{H}_1{A}_{\ast }\right)=tr\left(B^T{H}_1{A}_{\ast }{H}_2\right)=tr\left(B^T{H}_1\sum _{j=1}^K{\lambda }_j{H}_1^{-1}{\tilde{A}}_j{H}_2^{-1}{H}_2\right)=\sum _{j=1}^K{\lambda }_{j}tr\left(B^T{H}_1{H}_1^{-1}{\tilde{A}}_j{H}_2^{-1}{H}_2\right)=\sum _{j=1}^K{\lambda }_{j}tr\left(B^T{\tilde{A}}_j\right)$$

In the first part of this proof, we have shown that

$$\frac{tr\left(A_{\ast }{Z}_j{X}_j^T\right)}{m_j}=p_j,1\le j\le K.$$

Since

$$\mathbb{E}\left(y_1^{T}A{y}_2\right)=\sum _{t=1}^K{p}_t{\rho }_t$$

or equivalently,

$$p_j=\frac{tr\left(A{Z}_j{X}_j^T\right)}{m_j}=tr\left(\left(A_{\ast }+B\right){\tilde{A}}_j^T\right),1\le j\le K.$$

Therefore,

$$tr\left(B^T{\tilde{A}}_j\right)=tr\left(B{\tilde{A}}_j^T\right)=0,1\le j\le K.$$

This gives us

$$tr\left(A_{\ast }^T{H}_{1}B{H}_2\right)=tr\left(B^T{H}_1{A}_{\ast }{H}_2\right)=0.$$

Thus, all that remains is to show that $tr\left(B^T{H}_{1}B{H}_2\right)\ge 0$. Since H₁ and H₂ are positive definite, $\exists D_1$, $D_2$ such that $H_1=D_1^T{D}_1$ and $H_2=D_2^T{D}_2$. Then,

$$tr\left(B^T{H}_{1}B{H}_2\right)=tr\left(B^T{D}_1^T{D}_{1}B{D}_2^T{D}_2\right)=tr\left(D_{1}B{D}_2^T{D}_2{B}^T{D}_1^T\right)=tr\left(D_{1}B{D}_2^T{\left(D_{1}B{D}_2^T\right)}^T\right)\ge 0.$$

Hence,

$$tr\left(A^T{H}_{1}A{H}_2\right)\ge tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right).$$

Proposition 2 tells us that given arbitrary $p={\left(p_1,\dots p_K\right)}^T$, if $\exists \lambda ={\left({\lambda }_1,\dots {\lambda }_K\right)}^T$ such that $S\lambda =p$, then $y_1^T{A}_{\ast }{y}_2$ is an unbiased estimator for ${\sum }_{t=1}^K{p}_t{\rho }_t$. Furthermore, among all unbiased estimators with the form $y_1^{T}A{y}_2$, $y_1^T{A}_{\ast }{y}_2$ has the minimum value of $tr\left(A_{\ast }^T{H}_1{A}_{\ast }{H}_2\right)$, hence “almost” the minimum variance $Var\left(y_1^T{A}_{\ast }{y}_2\right)$.

Corollary 1. (without annotation stratification) We assume:

• (i)Samples from two GWASs do not overlap;
• (ii)The samples in each study are completely independent;
• (iii)True LD in both studies (i.e., $Z^{T}Z$ and $X^{T}X$) is known.

Consider all matrices A that suffice

$$tr\left(AZ{X}^T\right)=\frac{tr\left(Z^{T}Z{X}^{T}X\right)}{m}.$$

We define

$${\hat{\rho }}_A=m\left(y_1^{T}A{y}_2\right)/tr\left(AZ{X}^T\right).$$

Then, ${\hat{\rho }}_{\tilde{A}}$ with $\tilde{A}=\left(X{Z}^T\right)/m$ has the lowest variance.

Proof:

Let A be a matrix that suffices $tr\left(AZ{X}^T\right)=tr\left(Z^{T}Z{X}^{T}X\right)/m$. The goal is to show that

$$Var\left({\hat{\rho }}_A\right)\ge Var\left({\hat{\rho }}_{\tilde{A}}\right)$$

Since the samples in each GWAS are completely independent, we have:

$$H_1=I_{N_1\times N_1}$$

$$H_2=I_{N_2\times N_2}$$

Therefore,

$$S=\frac{1}{m^2}tr\left(H_1^{-1}X{Z}^T{H}_2^{-1}Z{X}^T\right)=\frac{1}{m^2}tr\left(Z^{T}Z{X}^{T}X\right).$$

Let $p=S$ and $\lambda =1$. Then, by definition we have

$$A_{\ast }=\frac{H_1^{-1}X{Z}^T{H}_2^{-1}}{m}=\frac{X{Z}^T}{m}=\tilde{A}.$$

Since we have

$$\frac{1}{m}tr\left(AZ{X}^T\right)=\frac{1}{m^2}tr\left(Z^{T}Z{X}^{T}X\right)=p,$$

by proposition 2, we know that

$$Var\left(y_1^{T}A{y}_2\right)\ge Var\left(y_1^T\tilde{A}{y}_2\right).$$

Therefore,

$$Var\left({\hat{\rho }}_A\right)=Var\left(\frac{y_1^{T}A{y}_2}{\frac{1}{m^2}tr\left(Z^{T}Z{X}^{T}X\right)}\right)={\left(\frac{m^2}{tr\left(Z^{T}Z{X}^{T}X\right)}\right)}^{2}Var\left(y_1^{T}A{y}_2\right)\ge {\left(\frac{m^2}{tr\left(Z^{T}Z{X}^{T}X\right)}\right)}^{2}Var\left(y_1^T\tilde{A}{y}_2\right)=Var\left({\hat{\rho }}_{\tilde{A}}\right).$$

Of note, ${\hat{\rho }}_{\tilde{A}}$ is identical to the non-annotation-stratified covariance estimator we developed in previous sections (see section Special Cases). Although we initially defined $\tilde{A}=\left(X{Z}^T\right)/m$ for the purpose of simplifying calculation, corollary 1 tells us that $\tilde{A}$ actually enjoys some good theoretical properties. As we have emphasized before, matrix $\tilde{A}$ could greatly simplify the estimation procedure because (1) $y_1^T\tilde{A}{y}_2$ can be calculated from GWAS summary statistics and (2) $tr\left(\tilde{A}Z{X}^T\right)=tr\left(Z^{T}Z{X}^{T}X\right)/m$ depends only on LD. In corollary 1 we showed that if we want to keep the convenient property $tr\left(AZ{X}^T\right)=tr\left(Z^{T}Z{X}^{T}X\right)/m$, then it is impossible to improve the variance of estimator $\hat{\rho }$ by choosing another matrix $A$. We note, however, additional variability may be introduced when we estimate LD using a reference panel in practice.

Similarly, we have a corollary for annotation-stratified covariance estimator.

Corollary 2. (with annotation stratification) We assume:

• (i)Samples from two GWASs do not overlap;
• (ii)The samples in each study are completely independent;
• (iii)The two LD matrices are known and identical (i.e., $X^{T}X/N_1=Z^{T}Z/N_2$);
• (iv)SNPs in different functional annotations are not in LD.

Consider all matrix sets $A_j$ $\left(1\le j\le K\right)$ that suffice

$$tr\left(A_j{Z}_j{X}_j^T\right)=\frac{tr\left(Z_j^T{Z}_j{X}_j^T{X}_j\right)}{m_j},1\le j\le K.$$

We define

$${\hat{\rho }}_A={\left(\begin{array}{ccc}\frac{1}{m_1}tr\left({\tilde{A}}_1{Z}_1{X}_1^T\right)& \cdots & \frac{1}{m_K}tr\left({\tilde{A}}_1{Z}_K{X}_K^T\right)\\ ⋮& \ddots & ⋮\\ \frac{1}{m_1}tr\left({\tilde{A}}_K{Z}_1{X}_1^T\right)& \cdots & \frac{1}{m_K}tr\left({\tilde{A}}_K{Z}_K{X}_K^T\right)\end{array}\right)}^{-1}\left(\begin{array}{c}{y}_1^T{\tilde{A}}_1{y}_2\\ ⋮\\ y_1^T{\tilde{A}}_K{y}_2\end{array}\right).$$

Then, ${\hat{\rho }}_{\tilde{A}}$ with ${\tilde{A}}_j=\left(X_j{Z}_j^T\right)/m_j$ $\left(1\le j\le K\right)$ has the lowest variance.

Proof:

Since the samples in each GWAS are completely independent, we have:

$$H_1=I_{N_1\times N_1}$$

$$H_2=I_{N_2\times N_2}$$

Therefore,

$$S_{l{l}^{\prime }}=\frac{1}{m_l{m}_{l^{\prime }}}tr\left(H_1^{-1}{X}_{l^{\prime }}{Z}_{l^{\prime }}^T{H}_2^{-1}{Z}_l{X}_l^T\right)=\frac{1}{m_l{m}_{l^{\prime }}}tr\left(X_{l^{\prime }}{Z}_{l^{\prime }}^T{Z}_l{X}_l^T\right).$$

Given integer $c$ such that $1\le c\le K$, let $p^{\left(c\right)}={\left(p_1,\dots p_K\right)}^T$ where

$$p_i=\frac{1}{m_c{m}_i}tr\left(X_c{Z}_c^T{Z}_i{X}_i^T\right),1\le i\le K$$

and ${\lambda }^{\left(c\right)}={\left({\lambda }_1,\dots {\lambda }_K\right)}^T$ where

$${\lambda }_i=\{\begin{array}{c}1,i=c\\ 0,i\ne c\end{array}.$$

Then, by definition we have

$$A_{\ast }=\sum _{j=1}^K\frac{{\lambda }_j}{m_j}{H}_1^{-1}{X}_j{Z}_j^T{H}_2^{-1}=\frac{X_c{Z}_c^T}{m_c}={\tilde{A}}_c.$$

By condition (iii), it is straightforward to check

$$p^{\left(c\right)}=S{\lambda }^{\left(c\right)}.$$

Therefore, by proposition 2 we know that

$$Var\left(y_1^T{A}_c{y}_2\right)\ge Var\left(y_1^T{A}_{\ast }{y}_2\right)=Var\left(y_1^T{\tilde{A}}_c{y}_2\right).$$

Since c is arbitrary, we have

$$Var\left(y_1^T{A}_c{y}_2\right)\ge Var\left(y_1^T{\tilde{A}}_c{y}_2\right),1\le c\le K.$$

Finally, since SNPs in different functional annotations are not in LD,

$$\frac{1}{m_j}tr\left({\tilde{A}}_i{Z}_j{X}_j^T\right)=\frac{1}{m_i{m}_j}tr\left(Z_i^T{Z}_j{X}_j^T{X}_i\right)=0,\forall i\ne j.$$

Therefore, the variance of the c^th estimated covariance component:

$$Var\left({\left({\hat{\rho }}_A\right)}_c\right)=Var\left(\frac{y_1^T{A}_c{y}_2}{\frac{1}{m_c^2}tr\left(Z_c^T{Z}_c{X}_c^T{X}_c\right)}\right)={\left(\frac{m_c^2}{tr\left(Z_c^T{Z}_c{X}_c^T{X}_c\right)}\right)}^{2}Var\left(y_1^T{A}_c{y}_2\right)\ge {\left(\frac{m_c^2}{tr\left(Z_c^T{Z}_c{X}_c^T{X}_c\right)}\right)}^{2}Var\left(y_1^T{\tilde{A}}_c{y}_2\right)=Var\left({\left({\hat{\rho }}_{\tilde{A}}\right)}_c\right),1\le c\le K.$$

It is straightforward to check that ${\hat{\rho }}_{\tilde{A}}$ is identical to the annotation-stratified covariance estimator we developed in previous sections. In corollary 2, we showed that under some reasonable conditions, the annotation-stratified covariance estimator also has the minimal variance property. However, since we assumed linkage equilibrium for SNPs in different functional annotations, this result does not apply to overlapping annotations.

In this section, we have shown some theoretical properties of our covariance estimator. However, the claim

$$tr\left(A^T{H}_{1}A{H}_2\right)\gg tr\left(A^T\Theta A^T\Theta \right)$$

is critical in our argument. Moreover, each proposition and corollary has its assumptions, which may or may not hold in practice. Therefore, we provide numerical justifications to our claims.

Numerical Study 1. Compare $tr\left(A^T{H}_{1}A{H}_2\right)$ and $tr\left(A^T\Theta A^T\Theta \right)$

Simulation workflow:

Step 1. We simulate a $500\times 500$ matrix $A$ whose elements are independently sampled from standard normal distribution $N\left(\mathrm{0,1}\right)$.

Step 2. We simulate the $\mathrm{1,000}\times \mathrm{1,000}$ matrix

$$\mathbb{E}\left(\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\left(\begin{array}{cc}{y}_1^T& y_2^T\end{array}\right)\right)=\left(\begin{array}{cc}{H}_1& \Theta \\ {\Theta }^T& H_2\end{array}\right)$$

by fixing the diagonal elements to be 1 and sampling the non-diagonal elements from uniform distribution $Unif\left(0,0.05\right)$. Sample pairs with a genetic relatedness coefficient greater than 0.05 are often removed from GWAS analysis. Therefore, the matrix we simulate here closely mimics the phenotypic covariance matrices we see in real studies.

Step 3. We sample 10,000 independent vectors from the distribution

$$\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)\sim MVN\left(0,\left(\begin{array}{cc}{H}_1& \Theta \\ {\Theta }^T& H_2\end{array}\right)\right).$$

Step 4. We calculate and record $tr\left(A^T{H}_{1}A{H}_2\right)$, $tr\left(A^T\Theta A^T\Theta \right)$, and the sample variance of $y_1^{T}A{y}_2$.

Step 5. Repeat steps 1–4 100 times.

From the simulations, we can see that $tr\left(A^T{H}_{1}A{H}_2\right)$ closely approximates the sample variance of $y_1^{T}A{y}_2$, while $tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$ is a negligible term (Figure S9). The median log fold, i.e., ${\text{log}}_{10}\left(\left|tr\left(A^T{H}_{1}A{H}_2\right)/tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)\right|\right)$, is 3.12. Therefore, $tr\left(A^T{H}_{1}A{H}_2\right)$ is on average around 1,300 times greater than $tr\left(A^T\text{Θ}{A}^T\text{Θ}\right)$ in our simulation, which is consistent with our claim.

Numerical Study 2. Compare $Var\left(y_1^{T}A{y}_2\right)$ and $Var\left(y_1^T\tilde{A}{y}_2\right)$

Simulation workflow:

Step 1. Randomly divide 15,918 samples from the Wellcome Trust Case Control Consortium (WTCCC) dataset into two subgroups (each with 7,959 samples and m = 254,221 SNPs after quality control). We simulate 100 independent sets of continuous traits y₁ and y₂ using real genotype data from WTCCC and the following covariance structure on heritability and genetic covariance:

$$\left(\begin{array}{c}\beta \\ \gamma \end{array}\right)\sim MVN\left(0,\frac{1}{m}\left(\begin{array}{cc}\frac{1}{2}I& \frac{1}{10}I\\ \frac{1}{10}I& \frac{1}{2}I\end{array}\right)\right).$$

Step 2. We simulate a 7,959 × 7,959 matrix A whose elements are independently sampled from standard normal distribution N(0,1). We also simulate a matrix A′ of the same size by permuting elements of $\tilde{A}$. Then we rescale matrices A and A′ so that

$$\mathbb{E}\left(y_1^{T}A{y}_2\right)=\mathbb{E}\left(y_1^T{A}^{\prime }{y}_2\right)=\mathbb{E}\left(y_1^T\tilde{A}{y}_2\right)$$

or equivalently,

$$tr\left(AZ{X}^T\right)=tr\left(A^{\prime }Z{X}^T\right)=tr\left(\tilde{A}Z{X}^T\right).$$

This makes all three matrices comparable.

Step 3. Calculate $y_1^{T}A{y}_2$ and $y_1^T{A}^{\prime }{y}_2$ for all 100 independent sets. Record the sample variance for each quantity.

Step 4. Repeat steps 2–3 100 times and get a distribution for $\widehat{Var}\left(y_1^{T}A{y}_2\right)$ and $\widehat{Var}\left(y_1^T{A}^{\prime }{y}_2\right)$. Compare them with the sample variance of $y_1^T\tilde{A}{y}_2$.

The results are consistent with our previous conclusions. Both $\widehat{Var}\left(y_1^{T}A{y}_2\right)$ and $\widehat{Var}\left(y_1^T{A}^{\prime }{y}_2\right)$ are consistently and substantially greater than $\widehat{Var}\left(y_1^T\tilde{A}{y}_2\right)$. In fact, the variances are not on the same scale. Median $\widehat{Var}\left(y_1^{T}A{y}_2\right)$ is 8.4 × 10⁷ times greater than $\widehat{Var}\left(y_1^T\tilde{A}{y}_2\right)$ and median $\widehat{Var}\left(y_1^T{A}^{\prime }{y}_2\right)$ is also 2.5 × 10⁷ times greater (Figure S10). These results suggest that matrix $\tilde{A}$ indeed enjoys the minimal variance property when applied to real genetic data.

Estimate Variance via Block-wise Jackknife

In the previous section, we showed that if two traits follow multivariate normal distributions, then $Var\left(y_1^T{\tilde{A}}_j{y}_2\right)=2tr\left({\tilde{A}}_j^T{H}_1{\tilde{A}}_j{H}_2\right)$. In fact, we could get similar results for covariance, too.

$$Cov\left(y_1^T{\tilde{A}}_i{y}_2,y_1^T{\tilde{A}}_j{y}_2\right)=2tr\left({\tilde{A}}_i^T{H}_1{\tilde{A}}_j{H}_2\right)$$

Therefore, the variance-covariance matrix of $\hat{\rho }$ can be calculated accordingly:

$$Cov\left(\hat{\rho }\right)=Cov\left(M^{-1}v\right)=Cov\left(\frac{1}{N_1{N}_2}{M}^{-1}\left(\begin{array}{c}{y}_1^T{\tilde{A}}_1{y}_2\\ ⋮\\ y_1^T{\tilde{A}}_K{y}_2\end{array}\right)\right)=\frac{2}{{\left(N_1{N}_2\right)}^2}{M}^{-1}\left(\begin{array}{ccc}tr\left({\tilde{A}}_1^T{H}_1{\tilde{A}}_1{H}_2\right)& \cdots & tr\left({\tilde{A}}_K^T{H}_1{\tilde{A}}_1{H}_2\right)\\ ⋮& \ddots & ⋮\\ tr\left({\tilde{A}}_1^T{H}_1{\tilde{A}}_K{H}_2\right)& \cdots & tr\left({\tilde{A}}_K^T{H}_1{\tilde{A}}_K{H}_2\right)\end{array}\right)M^{-1}.$$

However, it is difficult to calculate $tr\left({\tilde{A}}_i^T{H}_1{\tilde{A}}_j{H}_2\right)$. Estimating H₁ and H₂ would involve additional assumptions on the heritability structure. Even if we could accurately estimate H₁ and H₂, $tr\left({\tilde{A}}_i^T{H}_1{\tilde{A}}_j{H}_2\right)$ cannot be calculated using standard GWAS summary statistics. Therefore, following Bulik-Sullivan et al.,⁷ we apply a block-wise jackknife approach to estimate the variance.

First, we estimate the variance-covariance matrix of

$$v=\frac{1}{\sqrt{N_1{N}_2}}\left(\begin{array}{c}\frac{1}{m_1}{\left(z_1\right)}_1^T{\left(z_2\right)}_1\\ ⋮\\ \frac{1}{m_K}{\left(z_1\right)}_K^T{\left(z_2\right)}_K\end{array}\right).$$

We divide the genome into b (e.g., b = 200) blocks B₁, …, B_b. Let

$$v_i^{\left(t\right)}=\frac{{\left(z_1\right)}_i^T{\left(z_2\right)}_i-{\left(z_1\right)}_{S_i\cap B_t}^T{\left(z_2\right)}_{S_i\cap B_t}}{\left(m_i-m_{S_i\cap B_t}\right)\sqrt{N_1{N}_2}},1\le i\le Kand1\le t\le b.$$

Here, subscript $S_i\cap B_t$ indicates the subset of SNPs in both functional annotation S_i and block B_t. Therefore, $v_i^{\left(t\right)}$ is the re-calculated v_i after removing all SNPs in block B_t from the analysis. Then, Cov(v) is estimated as:

$${\left(\widehat{Cov}\left(v\right)\right)}_{ij}=\frac{b-1}{b}\sum _{t=1}^b\left(v_i^{\left(t\right)}-\frac{1}{b}\sum _{s=1}^b{v}_i^{\left(s\right)}\right)\left(v_j^{\left(t\right)}-\frac{1}{b}\sum _{s=1}^b{v}_j^{\left(s\right)}\right).$$

Therefore, we get

$$\widehat{Cov}\left(\hat{\rho }\right)=M^{-1}\widehat{Cov}\left(v\right)M^{-1}.$$

If annotations overlap,

$$\widehat{Cov}\left({\hat{\rho }}^W\right)=W{M}^{-1}\widehat{Cov}\left(v\right)M^{-1}{W}^T.$$

Finally, the test statistic for each covariance parameter is

$$z-scor{e}_i=\frac{{\hat{\rho }}_i}{\sqrt{{\left(\widehat{Cov}\left(\hat{\rho }\right)\right)}_{ii}}},1\le i\le K.$$

When annotations overlap,

$$z-scor{e}_i^W=\frac{{\hat{\rho }}_i^W}{\sqrt{{\left(\widehat{Cov}\left({\hat{\rho }}^W\right)\right)}_{ii}}},1\le i\le K.$$

Genetic Correlation

In non-stratified analysis, we could provide the genetic correlation estimate as follows:

$$cor=\frac{\hat{\rho }}{\sqrt{{\hat{h}}_1^2{\hat{h}}_2^2}}.$$

We use the estimator proposed in Bulik-Sullivan¹⁶ to estimate heritability for each trait.

$${\hat{h}}_t^2=\frac{\frac{1}{m}{\left(z_t\right)}^T\left(z_t\right)-1}{\frac{N}{m^2}\sum _{l=1}^m\sum _{l^{\prime }=1}^m{r}_{l{l}^{\prime }}^2}=\frac{\overline{{\chi }_t^2}-1}{N\overline{r^2}},t=\mathrm{1,2}$$

Compared to genetic covariance, genetic correlation is a more interpretable metric. It is also robust against certain systematic bias that exists in both genetic covariance and heritability (e.g., genomic control correction). However, statistical inference based on genetic covariance is equivalent to that based on genetic correlation. Estimating heritability requires additional model assumptions on the heritability structure and introduces additional variability into the estimation framework. Therefore, although we report the point estimate for genetic correlation, the statistical inference in our method is completely based on genetic covariance only.

In annotation-stratified analysis, the heritability in each annotation category may be small. This is especially true when applying annotations related to the repressed genome. Although methods for estimating annotation-stratified heritability have been proposed,¹¹, ¹² they may provide unstable, sometimes even negative, heritability estimates. Therefore, we focus on genetic covariance only when performing annotation-stratified analysis.

Web Resources

• GNOVA, https://github.com/xtonyjiang/GNOVA

• LD Hub, http://ldsc.broadinstitute.org/ldhub/

• LDSC, https://github.com/bulik/ldsc/

• OMIM, http://www.omim.org/