On the absence of a correlation between population size and ‘toolkit size' in ethnographic hunter–gatherers

Abstract

In apparent contradiction to the theoretically predicted effect of population size on the quality/quantity of material culture, statistical analyses on ethnographic hunter–gatherers have shown an absence of correlation between population size and toolkit size. This has sparked a heated, if sometimes tangential, debate as to the usefulness of the theoretical models and as to what modes of cultural transmission humans are capable of and hunter–gatherers rely on. I review the directly relevant theoretical literature and argue that much of the confusion is caused by a mismatch between the theoretical variable and the empirical observable. I then confirm that a model incorporating the appropriate variable does predict a positive association between population size and toolkit size for random oblique, vertical, best-of-K, conformist, anticonformist, success bias and one-to-many cultural transmission, with the caveat that for all populations sampled, the population size has remained constant and toolkit size has reached the equilibrium for this population size. Finally, I suggest three theoretical scenarios, two of them involving variable population size, that would attenuate or eliminate this association and hence help to explain the empirical absence of correlation.

This article is part of the theme issue ‘Bridging cultural gaps: interdisciplinary studies in human cultural evolution'.

1. Introduction

Collard and his colleagues have shown, in a series of papers beginning with Collard et al. [1], that population size and ‘toolkit size’ (see below) in ethnographic hunter–gatherers are neither totally nor partially correlated (the actual statistical analyses used multiple regression; see also [2,3]). Based partly on this finding, Collard et al. [4] and Vaesen et al. [5] criticize the theoretical models of Henrich [6] and Powell et al. [7], which they aver do not ‘really' predict such a correlation. A major bone of contention is whether the modes of cultural transmission (social learning) assumed by Henrich [6] and Powell et al. [7] in their models are empirically justifiable [8,9]. The modes of cultural transmission that humans are capable of and hunter–gatherers rely on are important issues in themselves [8,10]), but, as I will show, irrelevant to the immediate question.

I agree with Collard et al. [4] and Vaesen et al. [5] that the models of Henrich [6] and Powell et al. [7] are not pertinent to the question of whether population size and toolkit size are correlated. However, my reasons are entirely different—these models were not intended to address this question—and I believe their criticisms are misplaced. The first, technical and less important, reason is that these models do not possess equilibria. The second, more substantive, reason is that the variable interpreted as representing toolkit size in these models does not correspond to how toolkit size is recorded in the ethnographic literature, i.e. the observable.

My purpose in writing this paper is limited. I will argue that when more appropriate theoretical models with more relevant variables are invoked, a correlation between population size and toolkit size is predicted regardless of the mode of cultural transmission. But how can this be reconciled with the fact that such a correlation is not observed in ethnographic hunter–gatherers [1–3,11,12]? I discuss three possible theoretical scenarios that would attenuate or eliminate the predicted correlation: saturation of toolkit size [13], population growth and decline [14], and bistability [15]. If these scenarios are accepted, then theory and observation can be reconciled.

2. Henrich model

I will begin with a brief description of the basic model proposed by Henrich [6], pp. 200–204) and explain why its predictions are not pertinent to the question at hand. The Powell et al. [7] model and other extensions of the basic Henrich [6] model, which share the same limitations, will not be discussed.

The underlying variable is the ‘skill', z, of an individual belonging to a population of constant finite size N. When attempting to fit this model to the ethnographic data on toolkit size, the most natural interpretation of this variable may be that individuals with larger values of z manufacture a greater variety of tools. Other interpretations (e.g. ‘cultural complexity') are possible in other contexts [4,5].

Generations are discrete with overlap only insofar as oblique social learning occurs. Each naive newborn of the offspring generation identifies the maximally skilled individual of the parental generation and attempts to imitate his/her skill, z_max. However, social learning is noisy and biased so that the skill acquired by the imitator deviates probabilistically from the skill of the exemplar and is, on average, lower. Nevertheless, and importantly, the skill acquired by the imitator may exceed that of the exemplar. More specifically, it is assumed that the skill acquired by each imitator follows a Gumbel distribution with mode 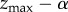and dispersion parameter β (α > 0, β > 0).

Now let be the population mean skill of the N individuals. Rigorously speaking, it is the expected value of the population mean. Given the interpretation of z above, it may be natural to regard as in some way representing the average number of different tools attributable to an individual. Using subscript t to denote the value of in that generation, Henrich [6] showed that

2.1

where 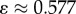is Euler's constant. Hence,

2.2

where 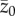is the initial value of 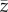(see also [16]).

Clearly, equation (2.1) entails that 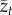either keeps on increasing or decreasing with time, depending on whether the right-hand side, 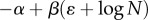, is positive or negative. Hence, there is no equilibrium that is determined by the population size, N. More significantly, when we attempt to apply equation (2.2) to a sample of populations, the relation between 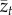and N will be confounded by the effects of the two other variables 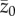and t, which are unknowns that may differ among the populations (I assume throughout this paper, except in the last paragraph of the discussion, that the model parameters—in this case α and β—are the same in all populations.). This is the technical reason noted in the introduction as to why the Henrich [6] model is not pertinent. The other, more important, reason is discussed in the next section.

A slight modification to this model produces an equilibrium. From equation (2.1) or equation (2.2), we see that parameter α measures the decay per generation in the population mean skill due to the infidelity of social learning. Mesoudi [17] assumed that errors in social learning by the offspring generation would be proportional to the population mean skill in the parental generation and replaced α by 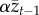in equation (2.1) to obtain

2.3

Then, on setting 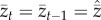(a super-hat here and elsewhere indicates that the variable is evaluated at equilibrium), the population mean skill at equilibrium is

2.4

Clearly, equation (2.4) predicts a (nonlinear) correlation between N and 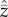, with the caveat that, for all populations sampled, N has remained constant and 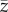has reached, or is close to, the equilibrium for this value of N.

3. The nature of the observable

The ethnographic data on toolkit size in the earlier studies [1–3,11] were taken entirely or mostly from Oswalt [18]. Toolkit refers to ‘subsistants’ (food-getting tools) and ‘technounits’ (component parts of such tools) as defined by Oswalt [18], who unfortunately does not explain how the data cited in his book were obtained. Moreover, the original references are, as far as I can tell, not available online.

Quantification of ethnographic data appears to be based on a ‘qualitative assessment of the ethnographic literature' ([19]; also [20]). More explicitly, quantitative data on toolkit size are ‘assembled [as] a list of all technologies mentioned' ([21] supplement). Tools are apparently not identified as belonging to individual members of the population, and hence it is not known how many different tools the average individual has. Thus, I assume in what follows that the toolkit size of a target population refers to the number of different subsistants or technounits of which at least one specimen exists in that population, as reported by an informant or observed by the investigator.

The variable that is most relevant, if this is the case, is S of Strimling et al. ([22], their equation (2.3)), ρ_P of Lehmann et al. ([23], their eq. 2.5), C_pop of Fogarty et al. ([13], see below) and possibly x of Ghirlanda & Enquist [24]. However, it is not 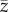of Henrich [6], because 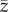is most naturally interpreted as an average over the number of different tools per individual.

4. The 0,1 vector model of cultural evolution

This model was first proposed by Strimling et al. [22] and is an adaptation to cultural evolution of the neutral infinite sites Moran model of population genetics [25–29]. Here, I present an outline of this model as modified and generalized by Fogarty et al. [13,14] to modes of cultural transmission other than random oblique (see below), and including some results newly obtained here.

Assume a finite population of fixed size N in which a potentially infinite number of cultural traits may occur. In the context of this paper, a cultural trait is the knowhow to manufacture a particular tool. The underlying variable is C_ij, which equals 1 if the ith individual possesses the jth cultural trait, and 0 if he/she does not (i = 1,2, … ,N; j = 1,2, …). Hence, the state of an individual can be represented by a vector of 1s and 0s, and of the population by a matrix formed by aligning N such vectors; C_ij is the ijth element of this matrix.

The cultural dynamics are defined by four events occurring during one time step. For a population of fixed size N, one generation (life expectancy at birth) comprises N time steps. Let us refer to the N individuals alive at the beginning of a time step as adults. Then, the four events are: (i) innovation by all N adults, (ii) birth of one naive individual (temporarily increasing the population size to N + 1), (iii) social learning by the newborn from a subset of the N adults (the exemplars), and (iv) death of a random adult who is replaced by the newborn (bringing the population size back to N).

Innovations have not been seen before (i.e. result is an entirely new cultural trait) and occur at the rate μ per adult per generation, or μ/N per adult per time step (μ > 0). This assumption differs from most previous models in which only the one newborn was allowed to innovate [22,23].

In terms of the underlying C_ij, the number of cultural traits possessed by the ith individual can be written as 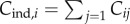(the upper bound of the summation may be infinite). Hence, the number of cultural traits possessed by the average individual is

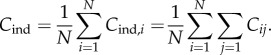4.1

The expected value of this variable, which we write as 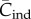, is a close analogue of the population mean skill, 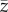, of the Henrich [6] model.

Next, define 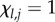if 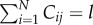, and 0 otherwise, where l ≤ l ≤ N. That is, 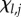counts the jth cultural trait if it is possessed by exactly l individuals in the population. Then, the number of different cultural traits possessed by exactly l individuals is

4.2

Strimling et al. [22] refer to this variable, P_l, as the number of cultural traits of ‘popularity' l.

In terms of the P_ls, we can write the number of distinct cultural traits in the population (i.e. possessed by at least one individual) as

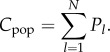4.3

If we focus on material culture and assume that the possession of a cultural trait by an individual entails the manufacture of the corresponding subsistant or technounit, then C_pop is the variable that most closely approximates the observable. However, what is really needed is a theory in terms of artefacts rather than the individuals that make them, i.e. a theory that allows for possible production bias.

We can also express C_ind in terms of the P_l's. Note that 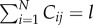if and only if the jth cultural trait has popularity l, and that there are P_l cultural traits of popularity l. Hence,

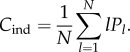4.4

Clearly, C_ind ≤ C_pop with equality if and only if P_l = 0 for 1 ≤ l ≤ N − 1.

For each variable, we indicate the expected value with a bar, the value at the end of a time step with a prime, and the equilibrium value with a caret.

5. Recursions and equilibrium for the expected values of the popularities

We make two crucial independence assumptions. First, there is no association among the cultural traits carried by an individual; for example, the possession of one cultural trait does not predict possession of another cultural trait (analogous to the assumption of ‘linkage equilibrium' in genetics). Second, the cultural traits carried by an exemplar, or exemplars, are transmitted independently of each other to the newborn (analogous to ‘free recombination'). Not all modes of cultural transmission can be accommodated within this analytical framework, in which case individual-based simulations prove useful. We also assume that there is no natural selection (see below).

The two independence assumptions in the 0,1 vector model are admittedly very strong. A general theory to deal with associations, either positive or negative, among cultural traits has not yet been formulated. Nevertheless, for the infinite sites model of population genetics, the spectrum 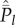is identical whether the sites are independent or completely linked—compare equations A 4 and A 5 of the appendix with equation 9.24 of Ewens [28]—and I expect this property will carry over, at least partially, to the current 0,1 vector model. A start on this problem has been made by Strimling et al. [22], who show that with random oblique transmission (see below) the spectra for mutually exclusive traits show the same dependencies on population size as for independent traits.

Denote the expected values of P_l by 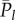(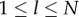). Using an asterisk to distinguish the values after innovation, we have

5.1

Equation (5.1) formalizes our assumption that all innovations are novel, i.e. are cultural traits of popularity 1. For each cultural trait of expected popularity l after innovation, let b_l be the (binomial) probability that the newborn acquires that cultural trait, and let d_l be the (binomial) probability that death then strikes an adult possessing that cultural trait. Then, at the end of the time step, we have

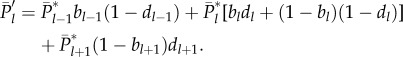5.2

The derivation of equation (5.2) is explained in Fogarty et al. [13,14]. Intuitively, the meaning of the recursion equation (5.2) is clear, if we disregard the possibility that each 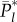is not necessarily an integer. For example, the first term on the right-hand side means that, of the cultural traits of popularity l − 1 among the adults immediately after innovation, a fraction b_l−1 are acquired by the newborn and a fraction 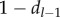are not lost by the death of an adult. Hence, this term represents the expected number of cultural traits of popularity l − 1 just after innovation that have popularity l at the end of the time step. Note in applying equation (5.2) that b₀ = 0 and .

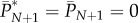At equilibrium, setting 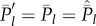, we obtain

5.3a

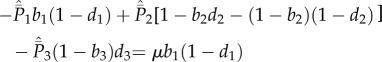5.3b

and

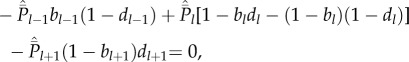5.3c

for .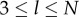

Equation (5.3) can be solved (see appendix) to yield

5.4a

and

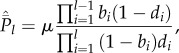5.4b

for .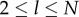

Then, noting equations (4.3) and (4.4), the expected values of C_pop and C_ind at equilibrium are

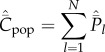5.5

and

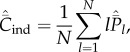5.6

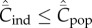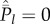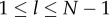respectively. Clearly, with equality if and only if for and 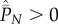, which is precluded if equation (5.4) holds.

6. Special case of random oblique transmission

Next, we consider explicit values of b_i and d_i. Our assumption of no selection implies d_i = i/N. The value of b_i depends on the mode of cultural transmission. For random oblique transmission (a mode of cultural transmission in which the newborn chooses a random adult to imitate),

6.1

where β (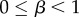) is the fidelity of cultural transmission (Under the assumptions of this model, vertical transmission cannot be distinguished from random oblique transmission.). Equation (5.4) reduces to

6.2a

and

6.2b

for 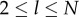. Equation (6.2) is identical to equation (2.2) of Strimling et al. [22], if we take into account that their model is formulated in terms of a death–birth chain rather than as in our case a birth–death chain, and that they evaluate the popularities just after innovation.

For random oblique transmission, it can be shown by a direct argument (see [22]) that the recursion in 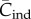satisfies

6.3

Hence, at equilibrium,

6.4

Equation (6.4) entails that 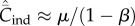when N is not too small, in which case 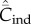does not depend on N (see below). This result is consistent with the statement in Collard et al. [4] that ‘under unbiased transmission, the association … fails to hold.' However, as noted above 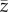and hence 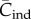is not the appropriate variable to represent toolkit size.

7. Biased transmission

Aoki et al. [30] define two other modes of cultural transmission, best-of-K and conformist, for which the expected values of the popularities at equilibrium can be obtained within the current framework. In best-of-K transmission, which assumes a preference for having each cultural trait as opposed to not having it, the newborn samples K adults (the exemplars) at random without replacement, and each cultural trait is independently acquired with probability β provided at least one of these K exemplars possesses it. Hence,

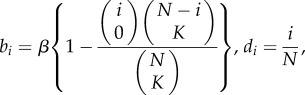7.1

where 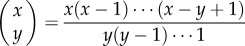and b_i = β for i > N −K [13]. Parameter K is analogous to the number of ‘cultural parents' in Enquist et al. [31].

Conformist transmission can be modelled in various ways [32–36]. Here, we adopt a model in which each newborn samples K adults at random without replacement, and each cultural trait is independently acquired with a probability that depends on the fraction of these K exemplars that possesses that cultural trait [30]. Specifically, set

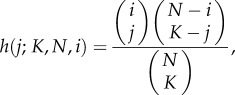7.2

where h(j; K, N, i) = 0 if j < 0, j > i, j > K, or j < K − (N − i). Equation (7.2) is the hypergeometric distribution giving the probability that a cultural trait of popularity i is represented exactly j times among the K exemplars. Then

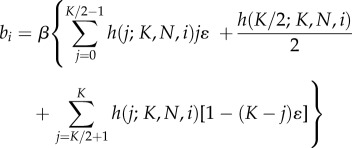7.3a

if K ≥ 2 is even, and

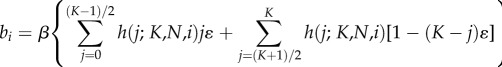7.3b

if K ≥ 3 is odd, and where ɛ < 1/K. Since ɛ < 1/K, the newborn will be less likely than by random copying to acquire a minority (less than frequency 1/2) cultural trait and more likely to acquire a majority (greater than frequency 1/2) cultural trait. Smaller values of ɛ entail stronger frequency-dependence and hence stronger conformity.

Similarly, anticonformist transmission can be modelled by setting 1/K < ɛ < 2/(K − 2) when K ≥ 4 is even, or 1/K < ɛ < 2/(K − 1) when K ≥ 3 is odd.

Equation (7.1), or equation (7.3) with (7.2), can be substituted into equation (5.4) to obtain the expected popularities at equilibrium for best-of-K, or conformist/anti-conformist transmission, respectively.

8. Positive correlation betwee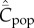n and N

Figure 1 shows how 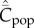increases with the population size, N, for these four modes of cultural transmission (random oblique, best-of-K, conformist, anticonformist). The scale on the vertical axis is not critical to the argument. Importantly, it is assumed that N has remained constant and that 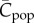has reached, or is close to, the equilibrium for this value of N. In particular, we see, contra Collard et al. [4] and Vaesen et al. [5], that an approximately linear monotone increasing relation is predicted even with random oblique (also vertical) and conformist transmission.

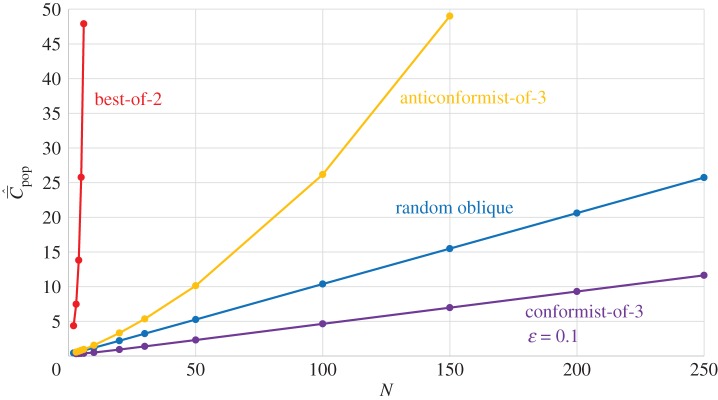
Figure 1.

Dependence of 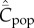on N, with random oblique (blue), best-of-2 (red), conformist-of-3 (purple) and anticonformist-of-3 (yellow) transmission. In the case of best-of-2, values of 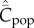for N > 10 are not shown. Parameter values are β = 0.9, μ = 0.04; ɛ = 0.1 for conformist and ɛ = 0.4 for anticonformist.

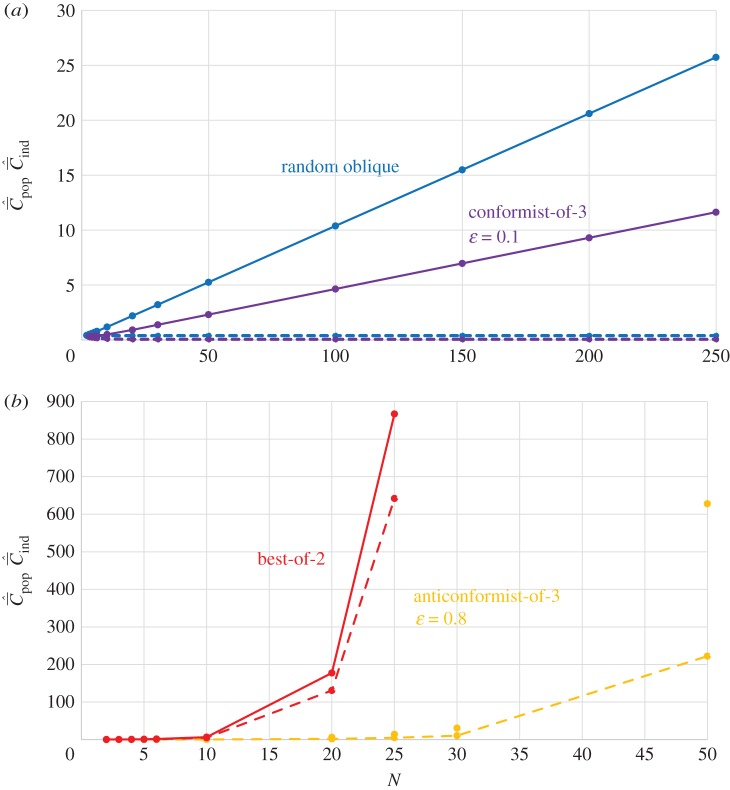
Figure 2a shows for random oblique and conformist transmission that 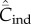and 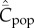depend on N in entirely different ways. Specifically, 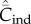with random oblique transmission (see equation (6.4)) or with conformist transmission rapidly converge to a constant value. Clearly, the theoretical predictions differ markedly with the choice of variable. Figure 2b shows on the other hand that, with best-of-K and anticonformist transmission, both 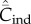and 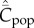are monotone increasing in N.

Figure 2.

Dependence of 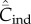(broken lines) and 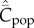(solid lines) on N. (a) Random oblique (blue) and conformist-of-3 (purple) transmission. 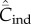is essentially independent of N. For the parameter values, β = 0.9, μ = 0.04, assumed here, asymptotes to 0.4 with random oblique transmission (see equation (6.4)) and converges to 0.055 with conformist-of-3 transmission. (b) Best-of-2 (red) and anticonformist-of-3 (yellow) transmission. 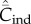Both and 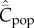are monotone increasing in N. Parameter values are β = 0.8, μ = 0.01; ɛ = 0.8 for anticonformist.

Fogarty et al. [13,14] also conducted individual-based simulations of the 0,1 vector model for random oblique, best-of-2, success bias, and one-to-many (but not conformist or anticonformist) transmission. In these simulations, the possible number of cultural traits was assumed to be finite, and a less restrictive model of innovation was also considered. Success bias, as defined by these authors, entails that the newborn samples K adults and chooses one adult possessing the greatest number of cultural traits as his/her exemplar. It most closely resembles the mode of cultural transmission assumed by Henrich [6] if we set K = N (see also [16]). One-to-many transmission entails that one adult has a special status and continues to be imitated by all newborns until his/her death. In all cases examined, 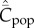showed an increase with N.

For random oblique and best-of-2 transmission, where the simulation results could be compared to the analytical predictions (equation (6.2), and equation (5.4) with equation (7.1), respectively), it was found that the former underestimated the latter at large values of N, especially when β and/or μ were also large. That is, a saturation effect was observed when an upper limit, M, was set on the possible number of cultural traits (figure 3). Incidentally, Fogarty et al. [13] observed a large difference in 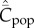between best-of-K and random oblique transmission when K = 2, but a relatively small effect of increasing K further. (This property is shared by the model of Enquist et al. [31], as can be seen from their figure 5).

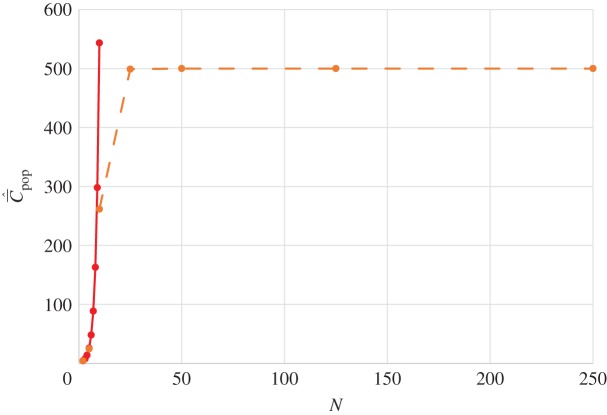
Figure 3.

Dependence of 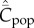on N for best-of-2. Analytical values (red), simulation values (orange). Parameter values are β = 0.9, μ = 0.04.

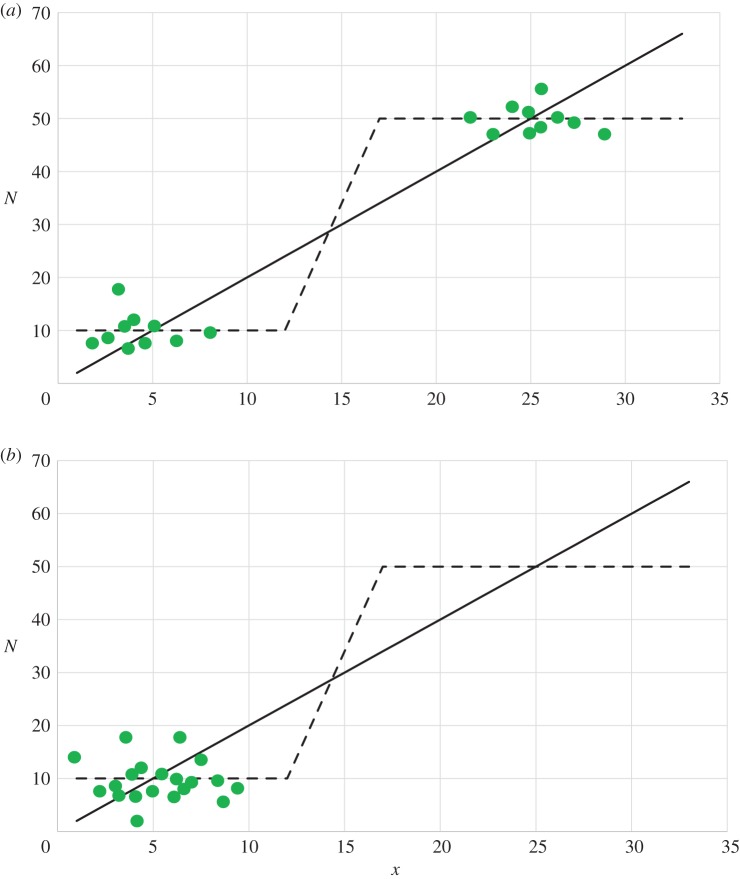
Figure 5.

Space of the variables x and N with the null clines equation (11.4a) and (11.4b) depicted by solid and broken lines, respectively. Of the three intersections of these null clines, the two on the outside are locally stable ‘attracting' equilibria. Each green dot represents a hypothetical sampled population. (a) Sampled populations are distributed around both locally stable equilibria; correlation is observed. (b) Sampled populations are randomly distributed around just one of the locally stable equilibria; correlation is not observed.

9. Three situations where the predicted correlation would be attenuated or eliminated

Given that C_pop is the appropriate theoretical variable that most closely approximates the observable, and a correlation is predicted between 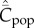and population size, N, for all modes of cultural transmission examined above, why have the empirical studies on toolkit size yielded negative results? I suggest three possibilities. The first is the saturation effect observed in the individual-based simulations noted in the last section. Figure 3 shows for best-of-2 transmission how 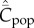may rapidly asymptote to the upper limit of the possible number of cultural traits (M = 500 in this example) as N increases. Clearly, for fixed N greater than about 25 in this example, a correlation is not predicted between population size and toolkit size. This saturation effect is not as pronounced for random oblique transmission [13].

The remaining two possibilities are discussed separately in the following two sections.

10. Population growth and decline driven by exogenous factors

The recursions equation (5.2) in the expected popularities can be generalized to deal with population growth and decline driven by exogenous factors [14]. For a growing population, each time step comprises innovation by all adults (equation (5.1)) followed by either a birth–death event (population size does not change) or a birth-only event (population size increases by one individual). For the former event equation (5.2) applies, and for the latter,

10.1

because d_l = 0. Fogarty et al. [14] show that if a birth-only event occurs every S time steps, then the growth rate per generation of the population is r = 1/S. For a declining population, the recursion for a death-only event,

10.2

replaces equation (10.1) for the birth-only event.

The effect of population growth and decline on the expected number of different cultural traits in the population, 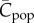, can be investigated by numerical iteration of equations (5.1), (5.2), (10.1) and (10.2). Figure 4 illustrates a case where a periodic solution is observed. Clearly, two different values of 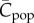are predicted for each (intermediate) value of N, depending on whether the population is in the growth phase or decline phase. Specifically, a relatively large population in the growth phase (e.g. N = 300) may be associated with a smaller value of 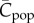(≈ 1000) than a smaller population in the decline phase (e.g. N = 200 with 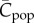≈ 2000).

Figure 4.

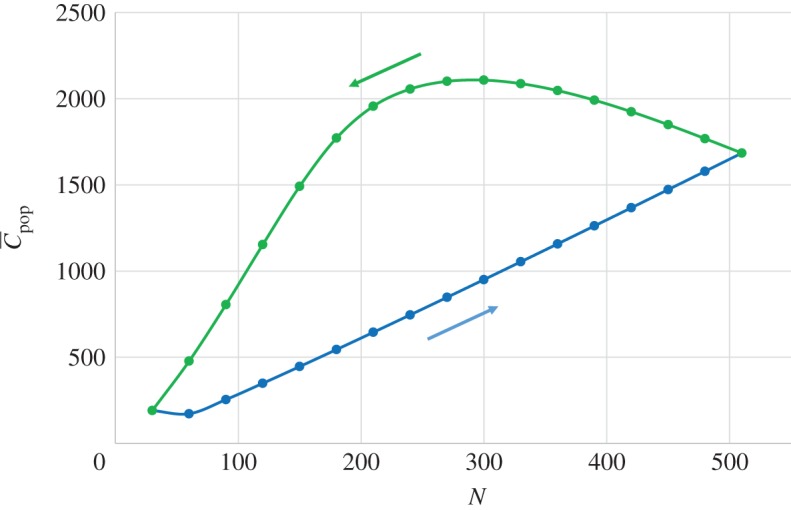
Dependence of 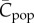on N during the growth (blue) and decline (green) phases of a periodic equilibrium. Best-of-2, with parameter values β = 0.7, μ = 1, S = 5.

11. Feedback between population size and ‘amount of culture'

Ghirlanda & Enquist [24] have defined a variable, x, which they call the ‘amount of culture' and assume satisfies the continuous-time deterministic dynamic

11.1

where, as before, N is the population size. Parameter γ is the rate of decay per unit time of the amount of culture due to the infidelity of social learning. Parameter δ is the rate of innovation per individual per unit time, and hence the second term on the right-hand side of equation (11.1) represents the total input of innovations per unit time.

In contrast with equation (2.3) for the Henrich [6] model as modified by Mesoudi [17] or equations (5.1) and (5.2) for the 0,1 vector model, equation (11.1) is not derived from mechanistic assumptions (realistic or not) on the behaviour of individuals. It is a ‘conceptual' model, which has a broad if nonspecific applicability. Clearly, variable x represents a population property; equation (11.1) is similar in form to equation (2.3), but variable x would seem to have a meaning more analogous to .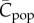

In the preceding theoretical analyses, population size N was either fixed or assumed to change independently of culture. Here, we combine equation (11.1) with a dynamic for N that depends reciprocally on the amount of culture. Specifically, we set

11.2

where the carrying capacity is assumed to be given by the following monotone non-decreasing ‘ramp' function of the amount of culture [37],

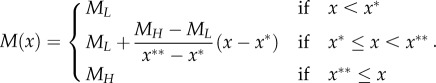11.3

The equilibria of the coupled system of equation (11.1), (11.2) and (11.3) are obtained on setting dx/dt = 0 and dN/dt = 0 simultaneously. In addition to the extinction equilibrium, 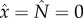, which is unstable, the intersection(s) of the two null clines,

11.4a

and

11.4b

yield equilibria.

Figure 5 shows the space of the variables x and N with null clines that, in this case, intersect three times. Of the three equilibria, the two on the outside are each locally stable and the one in the middle is unstable (bistability). The state of a population—its x and N values—can be represented by a point on this space. It is likely to coincide with or lie close to one of the two locally stable equilibria, because a locally stable equilibrium acts as an attractor.

Consider now a sample of more than one population for which estimates of population size and toolkit size are available. We can plot the state of each sampled population as a point on figure 5 (green dots), equating these estimates with the variables N and x, respectively. Then, two possible outcomes can be envisaged. First, some of the points may be distributed around one of the locally stable equilibria and the remainder around the other (figure 5a). Second, all of the points may be distributed around just one of the locally stable equilibria (figure 5b). In the first case, we should observe a correlation between population size and toolkit size, as empirical studies have shown to be the case for food producers [12,21]. In the second case, we do not expect to observe a correlation if the points are randomly distributed around the one equilibrium, which is perhaps the situation with the ethnographic hunter–gatherer data [15].

12. Discussion

The 0,1 vector model is the most general model of cultural evolution currently available [13,14,22,23,30]. It has also found use in empirical studies as a convenient way of summarizing data [19,38–40]. Any attempt to articulate theoretical and empirical studies must choose the variable(s) of the former and the observable(s) of the latter so that they agree. With regard to the empirical studies on toolkit size [1–3,11,41], I have argued that the variable C_pop, not C_ind, of the 0,1 vector model is most suitable. The variable 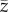of the Henrich [6] model is analogous to 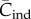, and hence Collard et al. [4] and Vaesen et al. [5] would seem to have criticized the wrong model for the wrong reasons. However, I repeat that what is really needed is a theory in terms of artefacts rather than the individuals that make them.

Focusing on the variable C_pop, I have shown that when the population size, N, is constant, the expected value of this variable at equilibrium, 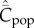, is predicted to correlate with N for the seven modes of cultural transmission examined or mentioned in this paper: random oblique, vertical, best-of-K, conformist, anticonformist, success bias and one-to-many. I have also suggested two theoretical scenarios based on the 0,1 vector model (sections 8 and 9) and one scenario based on a model of feedback between population size and amount of culture (section 10), which can explain the empirical absence of correlation.

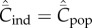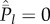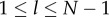It is of course possible that C_ind = C_pop. I noted above that the expected equilibrium values of these variables are equal, i.e. , if and only if for and 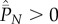. This is the situation in which each extant cultural trait is shared by all individuals in the population. I also noted that this special case is inconsistent with the positive solution of 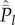(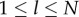) given by equation (5.4). This entails that 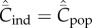cannot hold for random oblique, vertical, best-of-K, conformist, or anticonformist transmission.

I have omitted considerations of natural selection in this paper. Individual-level selection can be incorporated into the Henrich [6] model and the 0,1 vector model. For example, we could add directional selection, in which the viability of the ith individual is assumed to depend positively on the number of cultural traits he/she carries, 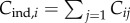. Preliminary individual-based simulation results for random oblique transmission indicate that the values of 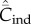and 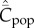are both displaced upward, relative to the case of no natural selection, but that for both variables the dependence on N remains qualitatively unchanged.

The model of feedback between population size and amount of culture is different. Here, the variable x represents a population property, and equation (11.1) cannot be modified to include individual-level selection. On the other hand, it is implicit in this model that group-level selection is acting, because a larger population size, N, is associated with more culture, x (equations (11.2), (11.3)). Gilpin et al. [37] have extended this model to deal with interspecific competition.

To return to the main argument, Collard et al. [1] have shown that ‘risk of resource failure' is a good predictor of toolkit size among ethnographic hunter–gatherers (see also [3]. Equations (5.4) and (5.5) may be relevant in this connection. These equations show that 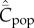increases linearly with the innovation rate, μ. Hence, if such risk stimulates innovation—i.e. if there is any truth in the commonplace, ‘necessity is the mother of invention'—then theory and observation would seem to be in agreement.

Appendix A

Note first that equation (5.3c) when spelled out comprises N − 2 lines. Adding equations (5.3a), (5.3b) and all N − 2 lines of equation (5.3c), we find that the terms in 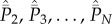cancel, yielding equation (5.4a) for 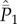. Next, adding equation (5.3b) and all N − 2 lines of equation (5.3c), we find that the terms in 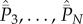cancel. Then, 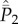can be expressed in terms of 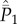as

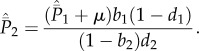A 1

Similarly, adding the 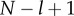lines of equation (5.3c) from the lth (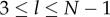) to the last, we obtain

A 2

and the last line of equation (5.3c) reduces to

A 3

because d_N = N/N = 1. Putting equations (5.4a), A 1, A 2 and A 3 together yields equation (5.4b).

With random oblique transmission of fidelity β = 1, the 0,1 vector model of cultural evolution reduces to the Moran model for a haploid genetic population. Direct substitution into equations (5.3a), (5.3b) and (5.3c) shows that the equilibrium expected popularities are

A 4

and

A 5

for 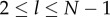. On the other hand, we have from the last line of equation (5.3c),

A 6

Hence, after has reached its equilibrium value of 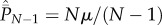, we see that 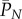will increase arithmetically at rate μ/N per time step, or μ per generation, which is the substitution rate. Equations A 4 and A 5 agree with equation 9.24 in Ewens [28] if we substitute the diploid number of genes 2N for N and take into account that 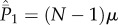is evaluated before innovation.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

This work was supported in part by Monbukagakusho grant 16H06412 to Joe Yuichiro Wakano.