Measures of clustering and heterogeneity in multilevel Poisson regression analyses of rates/count data

Abstract

Multilevel data occur frequently in many research areas like health services research and epidemiology. A suitable way to analyze such data is through the use of multilevel regression models. These models incorporate cluster‐specific random effects that allow one to partition the total variation in the outcome into between‐cluster variation and between‐individual variation. The magnitude of the effect of clustering provides a measure of the general contextual effect. When outcomes are binary or time‐to‐event in nature, the general contextual effect can be quantified by measures of heterogeneity like the median odds ratio or the median hazard ratio, respectively, which can be calculated from a multilevel regression model. Outcomes that are integer counts denoting the number of times that an event occurred are common in epidemiological and medical research. The median (incidence) rate ratio in multilevel Poisson regression for counts that corresponds to the median odds ratio or median hazard ratio for binary or time‐to‐event outcomes respectively is relatively unknown and is rarely used. The median rate ratio is the median relative change in the rate of the occurrence of the event when comparing identical subjects from 2 randomly selected different clusters that are ordered by rate. We also describe how the variance partition coefficient, which denotes the proportion of the variation in the outcome that is attributable to between‐cluster differences, can be computed with count outcomes. We illustrate the application and interpretation of these measures in a case study analyzing the rate of hospital readmission in patients discharged from hospital with a diagnosis of heart failure.

1. INTRODUCTION

Data with a multilevel nature occur frequently in public health, health services research, behavioral research, and in epidemiology. Examples include patients nested within hospitals, residents clustered within geographic regions, and employees nested within companies. The existence of multilevel information is relevant in the practice of epidemiology for both formal statistical and substantive epidemiological reasons. Analysts are increasingly aware that multilevel regression models are a suitable way to analyze clustered data.1, 2 A consequence of clustering of the subjects within clusters or higher‐level units (eg, hospitals) is that subjects from the same cluster may have outcomes that are more similar than will subjects from different clusters. Multilevel regression models incorporate cluster‐specific random effects that account for the dependency of the data by partitioning the total individual variance into variation due to the cluster and the individual‐level variation that remains.3

From an epidemiological perspective, knowing the share of the total individual variation in the outcome that is attributable to the cluster level or the “variance partition coefficient” (VPC) is useful information. The higher the VPC, the more relevant the context appears to be for understanding individual health or disease outcomes.3, 4 The VPC informs on the existence of a general contextual effect (GCE), which is called “general” because it reflects the influence of the cluster context as a whole, without specifying any contextual characteristic other than the very boundaries that delimit the cluster.5

The VPC is easy to calculate and interpret in multilevel linear regression models with continuous outcomes.6 In the case of discrete responses, the calculation and interpretation of the VPC is more complicated since, amongst other issues, the individual and cluster components of variance are modeled on different scales (the discrete response scale and the linear predictor scale, respectively). Furthermore, the components of variance depend on the covariates, so there is typically no unique VPC for models with discrete outcomes. Several alternative approaches for computing the VPC have been proposed when analyzing discrete outcomes. These include using a normal response approximation, the simulation method, Taylor series linearization, and the latent response method.3, 7

Another useful characteristic for epidemiological interpretation is the intraclass correlation (coefficient) (ICC), which is the correlation between 2 subjects within the same cluster. For nonnormal models the ICC also depends on the covariate values of the 2 subjects considered, but when these are the same, the ICC in a 2‐level model coincides with the VPC.

To avoid the interpretative technicalities of the VPC, Larsen et al introduced the concept of the median odds ratio (MOR) that can be used in the interpretation of the GCE when fitting a random effects logistic regression model.8, 9 The MOR indicates the median value of the odds ratios obtained when comparing the odds of the occurrence of the outcome in an individual from a randomly selected cluster with another individual with identical covariate values but randomly selected from a different cluster when the clusters are ordered by risk. In other words, to calculate the MOR, we should first measure the odds of the occurrence of the outcome for all randomly taken pairs of individuals from different clusters and, thereafter, compute the odds ratio for each pair of individuals having the individual from the cluster with the higher odds in the numerator and the individual from the cluster with the lower odds in the denominator. This would produce a distribution of odds ratios that are always equal to or higher than 1. The MOR is the median of this distribution of odds ratios.10 An advantage to the MOR is that it permits the analyst to present the between‐cluster variation as a measure of association (ie, an odds ratio) and thereby allows the comparison of the GCE with the fixed effects of the covariates in the model. More recently, the concept of the MOR has been extended to the analysis of survival or time‐to‐event outcomes, with the median hazard ratio (MHR) serving as a measure of the GCE.11, 12, 13 The MHR has an interpretation similar to the MOR, with the exception that the hazard ratio replaces the odds ratio.

While measures of variance and the GCE have been well described for settings in which the outcome is continuous, binary, or time‐to‐event in nature, there is a paucity of information as to how to assess these quantities when outcomes are counts. This is despite the fact that count outcomes are common in epidemiological and medical research. Common examples include the number of hospitalizations or physician consultations during an observation period, the number of infections or injuries, and the number of days in hospital.

Having an explicitly expository focus, the objective to the current paper was two‐fold. First, to describe the median rate ratio (MRR) to researchers in epidemiology and biostatistics. Second, to demonstrate how the VPC can be calculated for count outcomes. We will illustrate the utility of these 2 measures for assessing the magnitude of the general impact of the hospital context (ie, GCEs) on the number of hospital readmissions in patients discharged from hospital with a diagnosis of congestive heart failure (CHF). The paper is structured as follows. In Section 2, we describe methods for evaluating the VPC and for estimating the MRR when using a multilevel Poisson regression model for count outcomes. In Section 3, we provide a case study in which we illustrate the utility of these metrics for assessing the magnitude of the general contextual (ie, hospital) effects when analyzing hospital readmissions data. Finally, in Section 4, we summarize our findings.

2. MEASURES OF VARIANCE AND OF THE GCE IN MULTILEVEL POISSON REGRESSION

In this section, we describe the multilevel Poisson regression model. We then describe 2 different methods by which the VPC can be estimated for count outcomes when fitting multilevel Poisson regression models. We also describe the concept of the median (incident) rate ratio (MRR) and describe a formula for its evaluation.

2.1. The multilevel Poisson regression model

When the outcome is a count denoting the number of times that an event occurred (eg, number of hospital admissions or physicians consultations), a Poisson regression model can be used to relate the mean number of events to a set of explanatory variables using a logarithmic link function. The conventional Poisson regression model can be formulated as

$$\begin{array}{l}log\left({\lambda }_i\right)={\mathbf{\beta X}}_i\\ Y_i~\text{Poisson}\left({\lambda }_i\right),\end{array}$$ (1)

where X_i denotes a p × 1 column matrix of covariates measured on the ith subject, Y_i denotes the count outcome measured on the ith subject, and β denotes a 1 × p row matrix of regression coefficients. The parameter λ_i denotes the expected or mean number of events for the ith subject given their set of observed covariates. The model can be modified to include an offset term defined as the natural logarithm of the exposure, where the exposure could denote the time (ie, number of days) during which each subject is observed and therefore at risk for the occurrence of events (see later empirical example). The modification to include an offset term is

$$\begin{array}{l}log\left({\lambda }_i\right)={\mathbf{\beta X}}_i+log\left(T_i\right)\\ Y_i~\text{Poisson}\left({\lambda }_i\right),\end{array}$$ (2)

where T_i denotes the exposure. Below, we shall often incorporate the offset into X_i, since it may simply be viewed as an additional covariate whose regression coefficient is constrained to be equal to one.

The above formulation of the Poisson regression model assumes that the analyst is using individual subject‐level data. In other words, there is one record for each subject. For each record, we have the vector of covariates and the count outcome for the subject associated with that record. In many settings, the Poisson regression model is used with aggregated data. For example, the responses may be neighborhood‐level disease counts, in which case, the exposure would be the population at risk in each neighborhood. Alternatively, a given record may denote the aggregate data for all subjects with a given covariate pattern (we refer to all subjects with a given covariate pattern as a stratum). For instance, the record may contain the number of events observed amongst all females aged 55–64 years. In this case, the offset variable could be the number of subjects in the given stratum or the amount of person‐time contributed by subjects in the given stratum.

The exponentiated regression coefficients arising from the fitted model are interpreted as rate ratios. They denote the relative change in the mean number of events that would be expected to occur for a one‐unit increase in the relevant covariate. When an offset variable is included to denote the size of the population at risk, then the exponentiated regression coefficients denote the relative change in the rate of the events (ie, number of events per standardized population size). Frequently, when the outcome is an event that occurs at most once for each subject (eg, death or disease incidence) and an offset is included in the model, the exponentiated regression coefficient is referred to as the incidence rate ratio.

When subjects are nested or clustered in higher‐level units, the conventional Poisson regression model can be modified through the inclusion of cluster‐specific random effects to account for within‐cluster correlation in the outcome. The simplest modification is that of the random intercept regression model in which the intercept is allowed to vary randomly across clusters:

$$\begin{array}{l}log\left({\lambda }_{\mathit{ij}}\right)={\mathbf{\beta X}}_{\mathit{ij}}+{\alpha }_j\\ Y_{\mathit{ij}}~\text{Poisson}\left({\lambda }_{\mathit{ij}}\right),\end{array}$$ (3)

where α_j~N(0, σ²) for the K clusters, j = 1, …, K. The model with an offset variable can be modified similarly. Throughout the manuscript, we consider the values of the predictors and offsets to be fixed. Note that the inclusion of random effects means that the marginal distribution of Y_ij (averaged over α_j but given X_ij) is not a Poisson distribution. Equation (3) should be interpreted to mean that Y_ij follows a Poisson distribution conditional on the covariates and the cluster‐specific random effect (this is a similar interpretation as of a logistic model with random effects). The level 1 variance is the within‐cluster variance, thus conditional on the cluster random effects in the model.

2.2. VPC and ICC

The VPC denotes the proportion of the (unexplained) variation in the outcome that is due to between‐cluster variation. In other words, the VPC denotes the proportion of variation that is beyond that explained by the fixed predictors that is due to between‐cluster variation. As such, the VPC ranges from 0 to 1. A VPC of zero indicates that all of the variation in the outcome is due to within‐cluster‐between‐subject variability. In this case, the correlation in outcomes between 2 randomly selected subjects from the same cluster will be zero and therefore, equal to the correlation in outcomes between 2 randomly selected subjects from different clusters. At the other extreme, a VPC of one indicates that all of the variation in the outcome is due to between‐cluster variability and that all subjects within the same cluster display the same outcome. In this section, we describe 2 different methods for computing the VPC: exact calculation and a simulation‐based approach. When outcomes are binary or ordinal, an approach based on assuming an underlying latent continuous response can be used.1, 3 However, there is no latent response formulation for Poisson models, and so this approach is not a possibility here. Goldstein et al explored a model linearization approach.3 However, Stryhn et al found that this method performed poorly with count outcomes.14 Accordingly, we do not consider the count version of this approach in the current study.

2.2.1. Exact calculation

Given the random effects Poisson regression model described in Equation (2) or (3), Stryhn et al, in the proceedings of a symposium on veterinary epidemiology and economics, provided an exact calculation for the VPC and the ICC14:

$$\mathrm{VPC}=\mathrm{ICC}=\frac{exp\left(2\mathbf{\beta X}+2{\sigma }^2\right)-exp\left(2\mathbf{\beta X}+{\sigma }^2\right)}{exp\left(2\mathbf{\beta X}+2{\sigma }^2\right)-exp\left(2\mathbf{\beta X}+{\sigma }^2\right)+exp\left(\mathbf{\beta X}+{\sigma }^2/2\right)}.$$ (4)

As the proof of this calculation has not been presented in the peer‐reviewed literature, we include details of its derivation in Appendix A of this paper. Note that this quantity is simply the ratio between the cluster‐level variance and the total variance, as in a linear multilevel model. Using this exact calculation, the VPC can be expressed directly as a function of the linear predictor and the variance of the random effects. Note that in this expression, the offset variable, if present, has been incorporated into the linear predictor. Note that in contrast to the VPC in 2‐level random‐intercept models for continuous responses, the VPC is a function of not only the variance of the random effects but also the linear predictor. The VPC will therefore take different values for each covariate pattern. In the following, we will, for simplicity, refer to the VPC only, although all statements related to the above calculations are equally valid for the ICC (under the assumption that the 2 individuals being randomly compared have the same covariate and offset values).

2.2.2. Simulation‐based estimation

Goldstein et al described a simulation‐based approach to estimating the VPC when using a multilevel logistic regression model.3 This algorithm can be easily modified for use with Poisson regression. To do so, one first fits the multilevel Poisson model (Equation (3) above) and estimates the distribution of the cluster‐specific random effects. The algorithm then proceeds as follows:

1. Simulate a large number of cluster‐level random effects from the random effects distribution that was obtained from fitting the multilevel Poisson regression model: ${\alpha }_k~N\left(0,{\widehat{\sigma }}^2\right)$, for k = 1, …, M.

2. For a specific covariate pattern (and offset if present), use each of the simulated random effects drawn in step 1 to compute the predicted means using the regression coefficients from the fitted multilevel Poisson regression model: ${\widehat{Y}}_k=exp\left(\widehat{\mathbf{\beta }}\mathbf{X}+{\alpha }_k\right)$. For each of these computed count outcomes, compute the level 1 variance: $v_k={\widehat{Y}}_k$ (by the equality of the mean and variance in the Poisson distribution).

3. The VPC is then evaluated as $\frac{\mathrm{Var}\left({\widehat{Y}}_k\right)}{\mathrm{Var}\left({\widehat{Y}}_k\right)+\frac{1}{M}\sum _{k=1}^M{v}_k}$.

In the case study below, we used the above algorithm with M = 100 000 iterations. Note that the above algorithm provides an estimate of the VPC for a specific covariate pattern and size of the offset variable. As previously discussed, the above algorithm equally provides an estimate of the ICC.

2.3. The median (incidence) rate ratio

Given the random effects Poisson regression model described in Equation (3), Rabe‐Hesketh and Skrondal state that the median incidence rate ratio can be evaluated as15

$${\mathrm{IRR}}_{\text{median}}=exp\left(\sqrt{2{\sigma }^2}{\Phi }^{-1}\left(0.75\right)\right),$$ (5)

where Φ⁻¹ denotes the inverse of the standard normal cumulative distribution function. This statistic measures the median relative change in the rate of the occurrence of the event when comparing identical subjects from 2 randomly selected different clusters that are ordered by rate. While Rabe‐Hesketh and Skrondal use the term median incidence rate ratio, we will use the more general term median rate ratio (MRR). The primary reason for this is that an investigator may not be interested in a single incident event (eg, death or incidence of a specific disease). Instead, the investigator may be interested in the number of events that occurred when multiple events can occur per subject (eg, number of hospitalizations or episodes of unemployment). However, identical methods can be used regardless of whether the nature of the outcome is a single nonrecurring event or whether it is an event that can occur multiple times. As the definition of the median incidence rate ratio is a function of the variance of the random effects distribution, the same formula can be used regardless of whether one is examining incident events (eg, deaths or disease incidence) or the count of the number of events that an individual has experienced (eg, number of hospitalizations).

The corresponding measure of heterogeneity when outcomes are binary is the MOR,8, 9, 10 while the MHR can be used with survival outcomes.11, 12, 13 When using a logistic regression model with normally distributed random effects or a Cox model with normally distributed random effects, the MOR and the MHR can be evaluated using Equation (5). In other words, for the MRR, the MOR, and for the MHR when using a Cox model with normal random effects, the corresponding measure of heterogeneity is the same function of the variance of the random effects. This arises from the fact that when the random effects follow a normal distribution, then the distribution of ∣α_j' − α_j∣ follows a half‐normal distribution with variance equal to 2σ². The median of this half‐normal distribution is given by $\sqrt{2{\sigma }^2}{\Phi }^{-1}\left(0.75\right)$. As the measures of association for all 3 models are produced by exponentiating the regression coefficients and all 3 models incorporate normally distributed random effects, the formulas for estimating the MOR, the MHR, and the MRR are identical.

3. CASE STUDY

We provide a case study to illustrate application of the VPC and the MRR for evaluating the hospital GCE on the number of hospital readmissions subsequent to discharge from hospital with a diagnosis of CHF.

3.1. Data

The case study used patients from the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) study, which was an initiative to improve the quality of care for patients with cardiovascular disease in Ontario.16 The current study included 7162 patients discharged alive from hospital with a diagnosis of CHF between April 2004 and March 2005. These data have a multilevel structure, with patients nested within hospitals. The study sample consisted of 7162 patients treated at 96 hospitals. The number of patients per hospital ranged from 2 to 258, with a median of 74 (25th and 75th percentiles: 33 and 108, respectively). Due to the study inclusion and exclusion criteria, no patient had more than one hospital discharge during the 1‐year time frame of the study. We use the term index hospitalization to refer to the hospital admission that resulted in the patient being included in the EFFECT study.

The sample of patients discharged alive was linked to the Canadian Institute for Health Information Discharge Abstract Database (CIHI‐DAD) using unique encoded patient identifiers. The CIHI‐DAD contains records of all in‐patient hospitalizations in the province of Ontario. The CIHI‐DAD was used to determine the number of hospital admissions in the year subsequent to discharge from the index EFFECT hospitalization. The sample was also linked to the Registered Patients Database (RPDB), which contains basic demographic data on all residents of Ontario. In particular, it contains the date of death of all residents who have died since 1992. Using the RPDB, we were able to identify those subjects who died within 1 year of hospital discharge.

For each patient, the duration of time for which the patient was at risk of hospital readmission was the equal to the number of days between discharge from the index EFFECT hospitalization and the date of death. For those subjects who did not die during the first year subsequent to discharge, the duration of at‐risk time was set equal to 365 (26.4% of patients had less than 365 days of at‐risk time).

3.2. Study outcome

The outcome for the case study was the number of hospital admissions in the 1 year after discharge from the index EFFECT hospitalization. The median number of hospital readmissions was 1, while the 75th percentile was 2, and the maximum number of readmissions was 14.

3.3. Predictor variables

The EFFECT‐HF mortality prediction models estimate the probability of death within 30 days and 1 year of hospitalization for CHF.17 The model for predicting 1‐year mortality uses 11 variables: age, systolic blood pressure on admission, respiratory rate on admission, low sodium serum concentration (<136 mEq/L), low serum hemoglobin (<10.0 g/dL), serum urea nitrogen, presence of cerebrovascular disease, presence of dementia, chronic obstructive pulmonary disease (COPD), hepatic cirrhosis, and cancer. While this model was developed for predicting mortality in patients hospitalized with heart failure, we use it in this case study for illustrative purposes, acknowledging that it was not developed for the purposes of modeling the number of hospital readmissions. In the current case study, each of the 4 continuous covariates (age, systolic blood pressure, respiratory rate, and serum urea nitrogen) were standardized to have mean zero and unit variance (this was achieved by subtracting the sample mean from each subject's value of that covariate and then dividing the resultant quantity by the standard deviation of that covariate).

3.4. Statistical analyses

We fit 2 different multilevel Poisson regression models. First, we fit the null model, which included only hospital‐specific random effects:

$$log\left({\lambda }_{\mathit{ij}}\right)={\beta }_0+{\alpha }_j+log\left(T_{\mathit{ij}}\right).$$ (6)

T_ij denotes the exposure for the ith patient in the jth hospital and was set equal to the at‐risk time defined above. This model did not contain any patient characteristics and so the purpose of this analysis is to quantify the variation in the outcome and the proportion of this variation that is due to between‐hospital differences before accounting for any patient characteristics.

Second, we fit a multilevel Poisson regression model that comprised the 11 variables in the EFFECT‐HF mortality prediction model and the hospital‐specific random effects:

$$log\left({\lambda }_{\mathit{ij}}\right)={\mathbf{\beta X}}_{\mathit{ij}}+{\alpha }_j+log\left(T_{\mathit{ij}}\right),$$ (7)

where the vector X_ij denotes the vector of patient‐level characteristics (including an intercept term) and β denotes the vector of associated regression coefficients. In each of these 2 models, we assumed that the distribution of the random effects was normal: α_j~N(0, σ²).

For each of the 2 models, we computed the VPC using both the exact calculation and Goldstein's simulation‐based approach that were described in Section 2. When using the simulation‐based approach, we used 100 000 simulations to estimate the VPC. We computed the VPC for typical covariate patterns and values of the offset variable. In our sample, the 10th and 90th percentiles of the distribution of the at‐risk time were 74 and 365 days, respectively. For each selected covariate pattern, we evaluated the VPC at all values of the offset variable ranging from 74 to 365 days, in increments of 1 day. We also computed the MRR using the method described in Section 2. One could also determine the mean or median offset over all subjects in the sample and compute a sample‐specific “typical” VPC at the value of the mean or median offset (in our study sample, the mean and median offsets were 304 and 365, respectively). A caveat to this approach is that the mean offset may not correspond to a meaningful value (in our case, referring to subjects who had 304 days of at‐risk time subsequent to hospital discharge). We would suggest that examining the VPC across a range of offsets allows for a greater examination of the variation in the VPC across different values of the offset and allows for estimation of the VPC at different meaningful values (eg, those who remained alive for 1 year postdischarge).

Unless otherwise noted, all statistical analyses were conducted using R, version18 3.1.2. The multilevel Poisson regression model was fit using the glmer function in the lme4 package (version 1.1‐7). R and Stata code for conducting these analyses are provided in Appendices B and C.

3.5. Results

The median age of patients in the study sample was 78 years. The distribution of each of the 11 covariates in the regression model is summarized in Table 1.

Table 1.

Distribution of baseline covariates in the study sample

Variable	Median (IQR) or Percent With Condition
Continuous covariates
Age (years)	70 (70‐84)
Systolic blood pressure (mmHg)	145 (125‐168)
Respiratory rate (breaths per minute)	24 (20‐28)
Serum urea nitrogen (mmol/L)	8.2 (6.1‐11.7)
Binary covariates
Low sodium serum concentration (<136 mEq/L)	20.9%
Low serum hemoglobin (<10.0 g/dL)	12.8%
Cancer	11.3%
Chronic obstructive pulmonary disease (COPD)	27.1%
Cerebrovascular disease	17.9%
Hepatic cirrhosis	0.7%
Dementia	9.3%

Continuous covariates are summarized using the median (25th–75th percentiles), while binary covariates are summarized using the percentage of subjects in whom the condition is present. The sample consists of 7162 patients treated at 96 hospitals.

When fitting the null multilevel Poisson regression model, the estimated mean intercept was −5.60, while the variance of the hospital‐specific random effects was estimated to be 0.0226. The MRR was 1.15. The linear predictor was equal to the mean intercept (−5.60) plus the logarithm of the at‐risk time. The values of the VPC obtained using exact calculations and the simulation‐based approach are shown in Figure 1 for the different values of the at‐risk time. The VPC ranged from 0.006 when the at‐risk time was 74 day to 0.030 when the at‐risk time was 365 days. There was very good agreement between the 2 approaches across the range of number of at‐risk days. Amongst subjects who survived for 1‐year postdischarge from the index EFFECT hospitalization (73.6% of patients), 3.0% of the variation in the number of readmissions was due to systematic differences between hospitals, while the remaining 97.0% was due to within‐hospital between‐patient differences.

Figure 1.

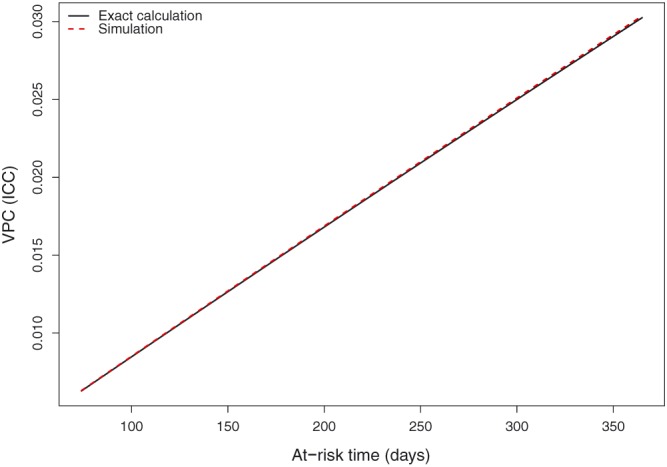
Variance partition coefficient (VPC) (intraclass correlation coefficient [ICC]) for null multilevel Poisson model [Colour figure can be viewed at wileyonlinelibrary.com]

Estimated rate ratios and associated 95% confidence intervals obtained from the multilevel Poisson regression model consisting of 11 patient characteristics are reported in Table 2. Seven of the 11 patient characteristics were significantly associated with the rate of hospitalization (P < .01). Four variables (age, presence of cerebrovascular disease, presence of dementia, and hepatic cirrhosis) were not significantly associated with the rate of hospitalization (P > .49). Note that the rate ratios for the 4 continuous covariates denote the relative change in the rate of hospital admission associated with a one standard deviation change in the covariate.

Table 2.

Rate ratios and 95% confidence intervals for the multilevel Poisson regression model

Variable	Rate Ratio	95% Confidence Interval	P Value
Fixed intercept
−5.69 (−5.74, −5.64)
Fixed effects (rate ratios)
Age	0.999	(0.976, 1.023)	P = .9506
Systolic blood pressure	0.912	(0.891, 0.933)	P < .0001
Respiratory rate	1.036	(1.013, 1.059)	P = .0021
Low sodium serum concentration (< 136 mEq/L)	1.098	(1.04, 1.159)	P = .0008
Low serum hemoglobin (< 10.0 g/dL)	1.151	(1.079, 1.227)	P < .0001
Serum urea nitrogen	1.167	(1.141, 1.194)	P < .0001
Cancer	1.239	(1.16, 1.324)	P < .0001
Chronic obstructive pulmonary disease (COPD)	1.109	(1.056, 1.165)	P < .0001
Cerebrovascular disease	1.021	(0.963, 1.082)	P = .4923
Hepatic cirrhosis	1.065	(0.827, 1.37)	P = .6262
Dementia	1.005	(0.924, 1.093)	P = .9047
Variance of random effect	0.0222

The rate ratios for the 4 continuous variables denote the relative change in the rate of the outcome associated with a one‐standard deviation change in the covariate. Age was standardized by centering at the mean age (76.4 years) and dividing by the standard deviation (11.6). For systolic blood pressure, the corresponding numbers were 147.0 and 29.2, respectively. For respiratory rate, the corresponding numbers were 24.9 and 6.1, respectively. For serum urea nitrogen, the corresponding numbers were 9.4 and 4.6, respectively. The sample consists of 7162 patients treated at 96 hospitals.

The relationship between VPC and the number of at‐risk days are described in Figure 2 for 4 different patient profiles. We considered four different patient profiles: (i—top left panel) a patient whose 4 continuous covariates were set to the cohort average and whose 5 binary covariates were set to absent (or zero). We refer to this patient profile as a reference patient; (ii—top right panel) a patient who was 20 years older than average, but who was similar to the reference patient in all other aspects; (iii—bottom left panel) a patient who was 10 years older than average and who had COPD, but who was similar to the reference patient in all other aspects; (iv—bottom right panel) a patient who was 20 years older than average and who had cancer, but who was similar to the reference patient in all other aspects. For each of these four patient profiles, the simulation‐based approach resulted in an estimate of the VPC that was very close to that provided by the exact calculation across the entire spectrum of at‐risk days. When the number of at‐risk days was equal to 365 (ie, amongst patients who survived for the entire year postdischarge), the VPC was approximately equal to 0.025 across the 4 patient profiles. Thus, amongst these patients, approximately 2.5% of the unexplained variation in the mean number of hospital readmissions was due to systematic differences between hospitals, while the remaining 97.5% was due to unmeasured patient characteristics.

Figure 2.

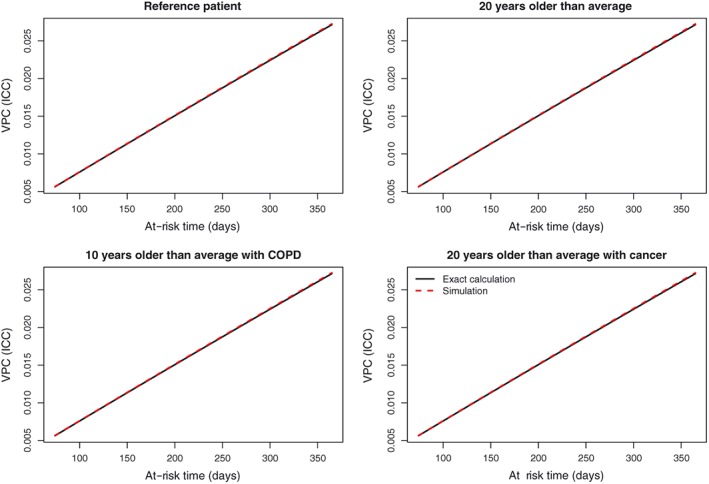
Variance partition coefficient (VPC) (intraclass correlation coefficient [ICC]) for multilevel Poisson model with patient characteristics [Colour figure can be viewed at wileyonlinelibrary.com]

To examine the dependency of the VPC on the linear predictor for a fixed exposure (at‐risk time = 365 days), we computed the VPC using exact calculations for all 7157 unique covariate patterns observed in the study sample. The VPC ranged from 0.019 to 0.074. The median was 0.029, while the 25th and 75th percentiles were 0.025 and 0.034, respectively. Thus, across the observed range of patient profiles, we saw moderate variation in the VPC. However, half of the observed VPCs lay in a relatively narrow interval.

To examine further the dependency of the VPC on the linear predictor for a fixed exposure (at‐risk time = 365 days), we computed the VPC using exact calculations for 80 000 hypothetical covariate patterns. For each of the four continuous covariates, we considered values that were 2 standard deviations above and below the mean, one standard deviation above and below the mean, and the mean value. For the 7 binary covariates, we considered both the presence and absence of the characteristic. This resulted in 80 000 unique covariate patterns (=5⁴ × 2⁷). Across the 80 000 covariate patterns, the VPC ranged from 0.015 to 0.085. The median was 0.037, while the 25th and 75th percentiles were 0.030 and 0.045, respectively. Thus, across a wide range of patient profiles, we saw moderate variation in the VPC. However, half of the estimated VPCs lay in a relatively narrow interval.

The MRR for the multilevel Poisson regression model with 11 patient characteristics was 1.153. Thus, if one were to repeatedly sample at random 2 subjects with the same covariates from different hospitals, then in half such comparisons, the rate ratio comparing the rate of hospital readmission between the subject at the hospital with the higher rate of hospitalizations and the subject at the hospital with the lower rate of hospitalizations (differences in rates are entirely quantified by the cluster‐specific random effects) is at least 1.153.

One can better understand the magnitude of between‐hospital variation in rates of readmission by comparing the MRR with the rate ratios for the patient‐level characteristics. The MRR was 1.153 (the reciprocal of this MRR is 1/1.153 = 0.867). Nine of the 11 patient‐level characteristics had a rate ratio that lay between 0.867 and 1.153. Two of the patient characteristics (urea nitrogen and cancer) had rate ratios that exceeded 1.153 (1.167 and 1.239, respectively). Thus, the median effect of clustering on the rate of hospital readmission was greater than the effect of nine of the 11 patient characteristics. Note that this is dependent on how the rate ratio is defined for the four continuous covariates. In the current analyses, these are the effects for a one standard deviation change in the continuous predictor (but other changes could be considered).

For the multilevel Poisson model with patient characteristics, the estimated variance of the distribution of the random effects was 0.022. One can use a likelihood ratio test to compare the full approximate likelihood of the fitted multilevel Poisson regression model with that of a conventional Poisson model that does not include any random effects. Such a test is provided by the mepoisson function in Stata (version 13.1, College Station, TX). The chi‐squared statistic associated with the likelihood ratio test was 72.77 (1 df), while the associated P value was less than .0001. Thus, even after adjustment for patient characteristics, we would reject the null hypothesis of no between‐hospital variation in the rate of hospital readmission (P < .001). This analysis was conducted using the mepoisson function in Stata as the likelihood ratio test is not formally provided in the glmer function of the lme4 package of R (however, one could extract the deviance of the fitted model and manually compare it with the deviance of the conventional Poisson model without random effects).

4. DISCUSSION

The objective of the current paper was to describe to researchers in epidemiology and medical research measures of variance and heterogeneity for use with multilevel Poisson regression models for count outcomes. The MRR allows one to quantify the magnitude of the GCEs (ie, the effect of clustering) on the rate of the occurrence of the outcome on the rate ratio scale. Furthermore, it also permits a comparison of the magnitude of this GCE with that of model covariates. The VPC permits the analyst to quantify the proportion of the variation in outcomes that is due to systematic differences between clusters.

In our case study, we used the MRR to quantify the magnitude of the effect of clustering within hospitals, that is, the “general contextual effect” on the rate of hospital admission subsequent to hospital discharge for CHF. We found that the MRR for a Poisson model that contained 11 patient characteristics was 1.15, indicating that, for 50% of possible pair‐wise comparisons, the rate of readmission for a reference patient was no more than 15% greater when comparing a hospital with higher readmission rates to a hospital with lower readmission rates. Furthermore, the MRR, which measures the median effect of clustering on the rate ratio scale, was larger in magnitude than the rate ratios for nine of the 11 patient characteristics. This suggests that, compared to the effect of patient characteristics, clustering exerted only a moderate effect on the rate of hospital readmission. Reporting the MRR complements the reporting of the variance of the random effects distribution. The MRR provides a characterization of the magnitude of the effect of clustering that would not have been possible had we simply reported the variances of the random effects distributions.

The MOR was introduced by Larsen et al8 in 2000. However, it began to be used more frequently only once it was introduced to the epidemiological literature9 in 2005. The MHR was empirically applied in 2007 to examine geographic variation in ischemic heart disease mortality in Sweden.19 Its formal derivation and interpretation was first published by Lanke in 2010 as a short appendix written in Historical Methods11, 12 to quantify the impact of the family‐specific frailty in southern Sweden during the period11 1766 to 1895. However, it was only introduced to the biostatistical and biomedical researchers in 2017.13 While the MRR was presented very briefly in a book published by Stata Press on multilevel analysis using Stata,15 our hope is that the current publication will increase its use in the medical and epidemiological literature.

The VPC can be calculated simply when outcomes are continuous: it is just the ratio of the cluster‐specific variance to the total individual variance (ie, the sum of the between and within cluster variance).1 When outcomes are binary, a variety of methods are available.3 Amongst these different methods, the latent variable approach appears to be the most commonly used. The latent variable approach assumes that underlying the observed binary outcome is an unobserved (latent) continuous version of that outcome.1 However, no such latent variable approach exists for count outcomes. Instead, when analyzing count outcomes, one can use either the exact calculation provided by Stryhn et al or use a simulation‐based approach based upon that described by Goldstein el al.3, 14 The VPC in each approach depends on the linear predictor. However, in Poisson regression, unlike with logistic regression, there is a potentially hidden variable in the linear predictor: the offset. Thus, while the use of the simulation‐based approach for binary outcomes can result in a different value of the VPC for each covariate pattern, the use of the simulation (and exact) approach with count outcomes can result in a different value of the VPC for each covariate pattern and each potential value of the offset variable (see Figures 1 and 2). In our case study, we found that for a given value of the at‐risk time, the value of the VPC did not differ meaningfully across 4 patient profiles. However, within a given patient profile, the VPC varied meaningfully across the different durations of at‐risk time. When the duration of at‐risk time was low, the VPC was very low. However, when the duration of at‐risk time was 365 (ie, in patients who survived the whole year subsequent to discharge from the index CHF hospitalization), the VPC was approximately 0.025, indicating that 2.5% of the variation in the number of hospital readmissions was due to systematic between‐hospital differences. The formula for the exact calculation of the VPC shows that this observation was to be expected, as a larger offset always results in an increase in the VPC. The analyses in our case study included an offset variable due to the relatively large number of deaths during the first year posthospital discharge with a diagnosis of CHF (26.4% of patients). However, in many settings, the use of an offset variable would not be necessary. The strong effect of the duration of the at‐risk period on the value of the VPC may limit its utility in some settings. Alternatively, the effect of the duration of the at‐risk time on the VPC can provide meaningful information on hospital comparisons. For instance, the increasing VPC with increasing duration of at‐risk time suggests that differences in the between‐hospital number of hospital readmissions increases as the at‐risk time increases. This suggests that differences in hospital outcomes are amplified as the duration of at‐risk time increases.

Given the very close agreement between the simulation‐based approach and the exact calculations, we would argue that, when using a multilevel Poisson regression model with random intercepts, there is no need to use the simulation‐based approach and that the exact calculations be used.

We derived an exact calculation for the VPC (or ICC) in the case of the random intercept Poisson multilevel model. However, the methodology can be extended easily to the random slopes Poisson multilevel model, as outlined in Appendix A.

In conclusion, the MRR allows one to determine the median relative change in the rate of occurrence of the outcome between a subject in a cluster with a higher rate of the outcome and an identical subject in a cluster with a lower rate of the outcome. Such a measure permits for an intuitive description of the magnitude of the impact of clustering within hospitals or GCEs when analyzing clustered count data. The MRR can be used in conjunction with the VPC which quantifies the proportion of variation in the outcome that is due to systematic between‐cluster differences. Together, the MRR and the VPC permit investigators to quantify variation and heterogeneity in count outcomes across clusters.

APPENDIX A. VARIANCE PARTITION AND INTRACLASS CORRELATION IN A MULTILEVEL POISSON REGRESSION MODEL

A.1.

Formulae for the mean, variance, and covariance in a Poisson‐Gaussian mixed model are derived in McCulloch et al. ³ , ⁷ , ²⁰ Here, we give a stand‐alone version of the derivation and state the connection to the VPC and ICC. Our calculations will use the well‐known integration formula (eg, Spiegel ^21(p98) ),

$$\underset{-\infty }{\overset{\infty }{\int }}{e}^{-\left({\mathit{ax}}^2+2\mathit{bx}+c\right)}\mathit{dx}=\sqrt{\frac{\pi }{a}}{e}^{\left(b^2-\mathit{ac}\right)/a},$$ (A.1)

for a > 0 and arbitrary real‐valued b and c. For σ > 0 and u ~ N(0,1), it therefore holds that

$$\mathrm{E}\left[e^{\mathit{\sigma u}}\right]=\underset{-\infty }{\overset{\infty }{\int }}{e}^{\mathit{\sigma u}}\left(\frac{1}{\sqrt{2\pi }}{e}^{-u^2/2}\right)\mathit{du}=e^{{\sigma }^2/2},$$ (A.2)

using Equation (A.1) with a = 1/2 and b = − σ/2; this is the moment‐generating function of a Gaussian variable. In the 2‐level Poisson multilevel model with normally distributed random effects, Formula 3 in the paper, we omit the indices where not needed, and denote by b = βX (or b = βX + log(T) with an offset) the linear predictor for a scalar observation Y, and write α ≡ σu. Then we have

$$\begin{array}{l}\mathrm{E}\left[Y\right]=\mathrm{E}\left[\mathrm{E}\left[Y|u\right]\right]=\mathrm{E}\left[e^{b+\mathit{\sigma u}}\right]=e^{b+{\sigma }^2/2},\\ \mathrm{Var}\left[Y\right]=\mathrm{Var}\left[\mathrm{E}\left[Y|u\right]\right]+\mathrm{E}\left[\mathrm{Var}\left[Y|u\right]\right]\\ =\mathrm{E}\left[{\left(\mathrm{E}\left[Y|u\right]\right)}^2\right]-{\left(\mathrm{E}\left[\mathrm{E}\left[Y|u\right]\right]\right)}^2+\mathrm{E}\left[\mathrm{E}\left[Y|u\right]\right]\\ =\mathrm{E}\left[e^{2b+2\mathit{\sigma u}}\right]-{\left(\mathrm{E}\left[Y\right]\right)}^2+\mathrm{E}\left[Y\right]\\ =e^{2b+2{\sigma }^2}-e^{2b+{\sigma }^2}+e^{b+{\sigma }^2/2},\end{array}$$ (A.3)

using the formulae for mean and variance of the Poisson distribution as well as Equation (A.2) for the last step in both the mean and variance calculations.

The calculation shows that in the resulting Equation (A.3), the last term should be understood as the lowest level (ie, within‐cluster) variance, whereas the 2 first terms together comprise the upper (cluster‐) level variance. For an alternative interpretation, we show below by similar calculations that the first 2 terms together also equal the covariance between 2 observations from the same cluster that have the same linear predictor b. Therefore, the VPC and the ICC for 2 such observations coincide and take the form, upon inserting b = βX,

$$\mathrm{VPC}=\mathrm{ICC}=\frac{e^{2\mathit{\beta X}+2{\sigma }^2}-e^{2\mathit{\beta X}+{\sigma }^2}}{e^{2\mathit{\beta X}+2{\sigma }^2}-e^{2\mathit{\beta X}+{\sigma }^2}+e^{\mathit{\beta X}+{\sigma }^2/2}},$$ (A.4)

as stated in Equation (4) in the paper.

Next, we calculate for 2 observations, say Y ₁ and Y ₂, from the same cluster with linear predictors b₁ and b₂,

$$\begin{array}{l}\mathrm{Cov}\left[Y_1,Y_2\right]=\mathrm{E}\left[Y_1{Y}_2\right]-\mathrm{E}\left[Y_1\right]\mathrm{E}\left[Y_2\right]=\mathrm{E}\left[\mathrm{E}\left[Y_1{Y}_2|u\right]\right]-\mathrm{E}\left[Y_1\right]\mathrm{E}\left[Y_2\right]\\ =\mathrm{E}\left[\mathrm{E}\left[Y_1|u\right]\mathrm{E}\left[Y_2|u\right]\right]-\mathrm{E}\left[Y_1\right]\mathrm{E}\left[Y_2\right]\\ =\mathrm{E}\left[e^{b_1+\mathit{\sigma u}}{e}^{b_2+\mathit{\sigma u}}\right]-\mathrm{E}\left[Y_1\right]\mathrm{E}\left[Y_2\right]\\ =e^{b_1+b_2+2{\sigma }^2}-e^{b_1+b_2+{\sigma }^2},\end{array}$$

which for b₁ = b₂ corresponds to the first 2 terms in Equation (A.3).

We finally outline how these calculations can be extended to a Poisson random slopes model. The method of calculating the mean and variance in A.3 still applies when the conditional linear predictor involves not only the term σu for the random intercept, but also similar random term(s) for random slope(s). With an assumed multivariate Gaussian distribution for all cluster‐level random terms, the linear combination of these in the linear predictor will be univariate Gaussian, and hence, after some algebraic manipulation, Equation (A.2) will once more yield expressions for the resulting means (expectations) over the random effects.

APPENDIX B. R CODE FOR THE CASE STUDY ANALYSES WITH THE FULLY ADJUSTED REGRESSION MODEL

B.1.

APPENDIX C. STATA CODE FOR FITTING THE MULTILEVEL POISSON REGRESSION MODEL

C.1.

Austin PC, Stryhn H, Leckie G, Merlo J. Measures of clustering and heterogeneity in multilevel Poisson regression analyses of rates/count data. Statistics in Medicine. 2018;37:572–589. https://doi.org/10.1002/sim.7532