In Silico Analysis of the Regulation of the Photosynthetic Electron Transport Chain in C3 Plants^,

A model-based analysis of photosynthetic electron transport chain identifies several mechanisms by which photosynthetic metabolic hubs may be coordinated under a range of environmental conditions.

Abstract

We present a new simulation model of the reactions in the photosynthetic electron transport chain of C3 species. We show that including recent insights about the regulation of the thylakoid proton motive force, ATP/NADPH balancing mechanisms (cyclic and noncyclic alternative electron transport), and regulation of Rubisco activity leads to emergent behaviors that may affect the operation and regulation of photosynthesis under different dynamic environmental conditions. The model was parameterized with experimental results in the literature, with a focus on Arabidopsis (Arabidopsis thaliana). A dataset was constructed from multiple sources, including measurements of steady-state and dynamic gas exchange, chlorophyll fluorescence, and absorbance spectroscopy under different light intensities and CO₂, to test predictions of the model under different experimental conditions. Simulations suggested that there are strong interactions between cyclic and noncyclic alternative electron transport and that an excess capacity for alternative electron transport is required to ensure adequate redox state and lumen pH. Furthermore, the model predicted that, under specific conditions, reduction of ferredoxin by plastoquinol is possible after a rapid increase in light intensity. Further analysis also revealed that the relationship between ATP synthesis and proton motive force was highly regulated by the concentrations of ATP, ADP, and inorganic phosphate, and this facilitated an increase in nonphotochemical quenching and proton motive force under conditions where metabolism was limiting, such as low CO₂, high light intensity, or combined high CO₂ and high light intensity. The model may be used as an in silico platform for future research on the regulation of photosynthetic electron transport.

Plants face highly variable environmental conditions, with fluctuations of light intensity, temperature, humidity, and CO₂ that occur over a wide range of time scales, from seconds to seasons. Imbalances between the rate of light capture and CO₂ assimilation can lead to an excess of energy in the system. Under such conditions, photosynthesis faces three main challenges:

1. To dissipate the excess of energy that could otherwise result in the production of reactive oxygen species (Foyer et al., 2011);

2. To couple the production and demand of ATP and NADPH in chloroplasts under a fluctuating environment (Noctor and Foyer, 2000);

3. To maintain an adequate redox state (Allen, 2004) of the photosynthetic electron transport chain (PETC).

In this study, we use the term regulation to indicate those mechanisms that allow photosynthesis to achieve these goals. These goals must be met simultaneously, and several mechanisms have been identified as contributing (Kramer et al., 2004), including:

1. Nonphotochemical quenching (NPQ) of excess energy absorbed by photosynthetic pigments;

2. Cyclic electron transport (CET) around PSI, including NADPH dehydrogenase (NDH) and ferredoxin-plastoquinone reductase (FQR);

3. Reduction of alternative electron acceptors including the water-water cycle (WWC), reduction of oxaloacetate by malate dehydrogenase (MDH) coupled to export of malate to the cytosol, and reduction (NiR) coupled to assimilation of . We group these reactions under the expression “alternative noncyclic electron transport” (ANCET);

4. Regulation of the proton motive force (pmf) via changes in ATP synthase (ATPase) activity and transthylakoid ion transport.

The study of NPQ in leaves makes use of measurements of chlorophyll fluorescence yield and lifetime (Nilkens et al., 2010; Dall’Osto et al., 2014; Sylak-Glassman et al., 2016). In plants, under many physiological conditions, NPQ is associated with the build-up of protonated PsbS (PsbS⁺) and zeaxanthin (ZX), as regulated by lumen pH (Zaks et al., 2013; Horton, 2014), a process denoted as qE. Accumulation of lutein has also been associated with NPQ (Matsubara et al., 2005). The exact relationship between lumen pH and NPQ is not fully understood yet, although several approaches have been used to estimate it (Takizawa et al., 2007; Johnson, 2011; Zaks et al., 2013).

Although several experimental techniques are available to study CET and ANCET (Bloom et al., 2002; Munekage et al., 2002; Driever and Baker, 2011; Walker et al., 2014; Strand et al., 2016), little is known about the interactions among the different mechanisms involved. Similarly, recent technological developments (Sacksteder et al., 2000, 2001) have led to a better understanding of the regulation of ATPase (Kanazawa and Kramer, 2002), the partitioning of pmf into ΔΨ and ΔpH (Cruz et al., 2001; Takizawa et al., 2007), and the range of lumen pH that is physiologically feasible (Kramer et al., 1999), but the interactions among the reactions that determine pmf have not been fully elucidated (Strand and Kramer, 2014).

The complex interactions among the various photosynthetic processes in vivo are difficult to disentangle from experimental studies of components in isolation (Keurentjes et al., 2011). One powerful approach is to develop computational models to explore the holistic behavior of the biological network (Kitano, 2002). Although many computational models of PETC in C3 plants have been published in recent years (Riznichenko et al., 2009; Ebenhöh et al., 2011; Zaks et al., 2012; Tikhonov and Vershubskii, 2014; Matuszyńska et al., 2016), they have been predominantly focused on specific mechanisms rather than on the interactions among mechanisms. For example, several models developed to study NPQ (Ebenhöh et al., 2011; Zaks et al., 2012; Matuszyńska et al., 2016) simplify the transport of electrons from PSII to NADPH and do not include any description of the metabolism that consumes ATP and NADPH. Such simplifications prevent the study of the complex interactions that characterize the behavior of the system under natural conditions, such as the effect that changes in Rubisco activity would have on NPQ (Carmo-Silva and Salvucci, 2013; Kaiser et al., 2016). More comprehensive models have been published recently (Laisk et al., 2009; Zhu et al., 2013), but they still miss some of the mechanisms of interest in the regulation of PETC, such as NiR (Bloom et al., 2002) or NDH (Strand et al., 2017). Furthermore, the testing of these models with experimental data has been limited to a narrow range of experimental conditions and measurement techniques, and thus it is not known to what extent their simulations are physiologically reasonable.

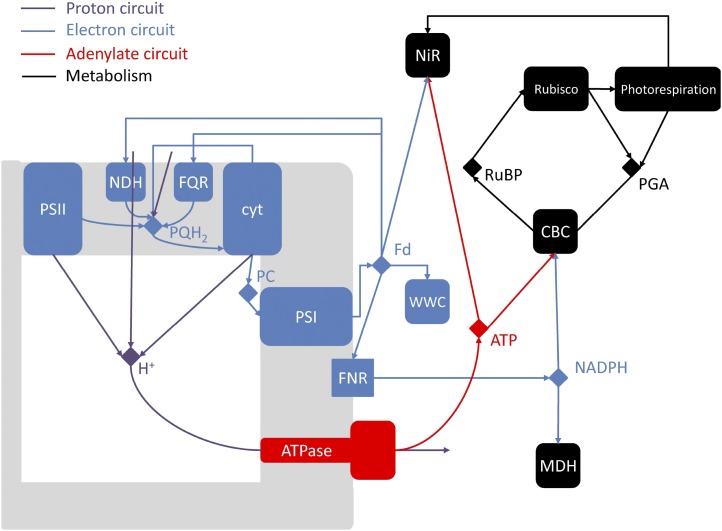
In this study, a mechanistic model of PETC is presented with the aim of analyzing, in silico, the role of the different mechanisms involved in the regulation of PETC under steady-state and fluctuating environmental conditions. All relevant process at the chloroplast and leaf level are taken into account (Fig. 1), with an emphasis on PETC. To ensure that the simulations represent physiologically reasonable conditions, the model is tested with published experimental data gathered on Arabidopsis (Arabidopsis thaliana), including steady-state and dynamic measurements of leaf gas exchange, modulated chlorophyll fluorescence, and absorbance changes at different wavelengths that probed the activities of PSI, pmf, and its components.

Figure 1.

Schematic diagram of the model of the photosynthetic electron transport chain coupled to the stromal metabolism. NDH and FQR are the cyclic pathways regulated by the NDH and PGRL1 protein complexes. NiR represents all reactions within the chloroplast responsible for reduction of 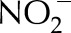and assimilation of 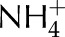. CBC stands for the reactions involved in the conversion of PGA into RuBP and photorespiration represents the reactions involved in the conversion of phosphoglycolate into PGA coupled to the release of CO₂ and 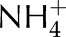from the mitochondria.

RESULTS AND DISCUSSION

Testing the Model with Experimental Data

The ability of the model to reproduce known patterns in the regulation of PETC was tested with published measurements, focusing on experimental results for Arabidopsis grown under similar growth conditions (20–23°C, 100–170 µmol m⁻¹ s⁻¹, ambient CO₂, 60–75% relative humidity). The following types of measurements were used to test the model: (1) pulse amplitude modulated chlorophyll fluorescence to test simulations of PSII quantum yield (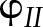) and NPQ; (2) absorbance changes at 820 nm due to the redox state of P700 (Harbinson et al., 1989; Harbinson and Hedley, 1989) to test simulations of the quantum yield of PSI (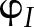) and electron transport between PSII and PSI; (3) electrochromic shift of pigment A₅₂₀ (Cruz et al., 2001) to test simulations of pmf and its components; and (4) net CO₂ assimilation (An), to test simulations of the Calvin cycle and CO₂ diffusion.

Pulse Amplitude Modulated Fluorescence

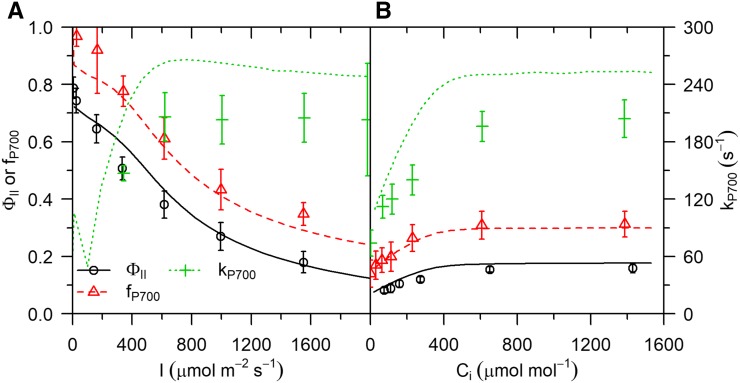
Simulations of the steady-state response of 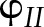to CO₂ and light intensity were tested with the measurements by Hald et al. (2008) on Arabidopsis Col-0 using a white light source. In the measurements and simulations, 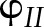was calculated as (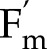− F)/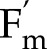, where 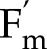is the maximum fluorescence yield achieved during a rectangular flash of 8,000 μmol m⁻² s⁻¹, and F is the fluorescence yield before the flash. The light intensity and CO₂ during the CO₂ and light response curves were 1,500 μmol m⁻² s⁻¹ and 2,000 μmol mol⁻¹, respectively. The model captured correctly (Fig. 2) the decrease of 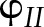with light intensity, and its increase with CO₂, with root mean square errors normalized by measured means (nRMSE) of 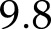%, and %, respectively.

Figure 2.

Measured (symbols) and simulated (lines) steady-state operational efficiency of PSII (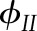 = ( 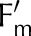− F)/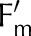), fraction of reduced P₇₀₀ (f_P700) and rate constant of 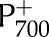reduction in the darkness (k_P700) as a function of light intensity (A) and CO₂ (B). Measurements from Hald et al. (2008) on Arabidopsis Col−0. The light intensity and CO₂ in the CO₂ and light response curves were 1,500 μmol m⁻² s⁻¹ and 2,000 μmol mol⁻¹, respectively. Error bars represent 95% confidence intervals.

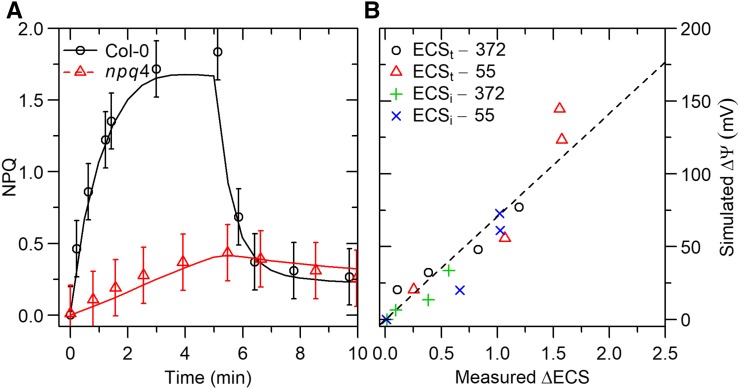
Simulations of NPQ induction and relaxation were tested with measurements by Nilkens et al. (2010) on Arabidopsis Col-0 and its associated npq4 mutant that lacks PsbS. In the measurements and simulations, NPQ was calculated as F_m/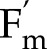– 1, where F_m is the dark-adapted maximum fluorescence yield. The model fitted the data accurately (nRMSE = 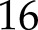%), including the lower NPQ and slower kinetics introduced by the mutation (Fig. 3A).

Figure 3.

A, Measured (symbols) and simulated (lines) NPQ (i.e. F_m ⁄ 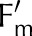− 1) on Arabidopsis Col−0 and the npq4 mutant during a transition from darkness to 900 μmol m⁻² s⁻¹ for 5 min, followed by a return to darkness. Measurements by Nilkens et al. (2010). Error bars represent 95% confidence intervals. B, Simulated changes in transthylakoid voltage (ΔΨ) versus measured changes in ECS for different light intensities (from darkness to 800 μmol m⁻² s⁻¹) and two air CO₂ mole fractions (372 and 55 μmol mol⁻¹).

Electrochromic Shift (ECS)

Simulations of changes in ΔΨ during dark intervals were tested with measurements of total ECS (ECS_t) and inverse ECS (ECS_i) as a function of CO₂ and light intensity on Arabidopsis Col-0 (using a red light source) by Takizawa et al. (2007). In the measurements, ECS_t = ECS_l − ECS_m and ECS_i = ECS_d − ECS_m, where ECS_l, ECS_d, and ECS_m are the steady-state ECS in the light and darkness, and the minimum ECS in darkness, respectively (Takizawa et al., 2007). In the simulations, the same parameters were calculated from simulations of ΔΨ during dark intervals (Supplemental Fig. S1), such that simulated ECS_t and ECS_i had units of voltage (mV). This relies on the assumption that the ECS signal is proportional to ΔΨ (Cruz et al., 2001).

The model predicted well the effect of CO₂ and light intensity on ECS_t and ECS_i (Fig. 3B) for a wide range of light intensities (0–800 μmol m⁻² s⁻¹) at ambient and low CO₂. The simulated values were linearly related to observations, with a nonsignificant intercept, a slope of 71 mV/ECS-unit, and nRMSE = 30%. In addition, the model predicted that ECS_t was linearly related to pmf (nRMSE = 1.6%, R² = 1) and ECS_i was linearly related to ΔpH (nRMSE = 4.7%, R² = 1), in agreement with the analysis by Cruz et al. (2001).

P700 Redox State

Simulations of the effect of CO₂ and white light intensity on the redox state of P700 and the rate constant of 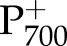reduction during a dark interval (k_P700) were tested with measurements by Hald et al. (2008) on Arabidopsis Col-0. The measurements used changes in A₈₂₀ with respect to dark-adapted conditions as a proxy for the fraction of P700 that was reduced (f_P700). In the simulation, f_P700 can be calculated directly from the model output, but to be comparable with the measurement, relative changes with respect to darkness were reported, such that simulated f_P700 becomes 1 in the darkness (the absolute value was 0.95). In both measurements and simulations, the rate constant of reduction was calculated by fitting an exponential decay to time series of f_P700 during a dark interval. The light intensity and CO₂ during the CO₂ and light response curves were 1,500 μmol m⁻² s⁻¹ and 2000 μmol mol⁻¹, respectively.

The model captured correctly (Fig. 2) the decrease of f_P700 with light intensity (nRMSE = 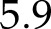%) and the increase with CO₂ (nRMSE = 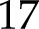%). In the absence of acceptor-side kinetic limitations, f_P700 is an estimate of 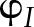(Harbinson and Hedley, 1989). In the simulations, the higher values of f_P700 compared to 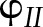were explained by (1) cyclic electron transport around PSI and (2) a higher excitation of chlorophyll pigments associated with PSII (i.e. 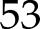% of excitations were associated with PSII).

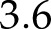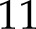The relative effects of light intensity and CO₂ on k_P700 were reproduced adequately (Fig. 2) by the model (nRMSE = % and %, respectively), although simulations tended to overestimate observations (on average by 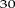%). k_P700 is associated with the rate constant of PQH₂ oxidation by cyt b₆f (Harbinson et al., 1989), and better agreement between simulations and data could be obtained by reducing either the rate constant of PQH₂ oxidation by cyt b₆f or the amount of cyt b₆f by 30% (results not shown). However, this also resulted in an underestimation of NPQ (because the equilibrium point was obtained at a higher lumen pH) and CO₂ assimilation (see below). This analysis suggests that this parameterization of the model may not be optimal and that further improvement is possible. However, an exhaustive search of parameter space to find optimal combinations is beyond the scope of this study. In addition, we cannot exclude the possibility of inconsistencies or lack of comparability across datasets, since they were obtained from different experiments.

Net CO₂ Assimilation

Simulations of the steady-state responses of An to CO₂ and light intensity, and dynamic responses of An to increases and decreases in light intensity were tested with measurements reported by Kaiser et al. (2016). The measurements were taken on 15 replicates Arabidopsis Col-0 using a LED light source (10% blue, 90% red). Except for the CO₂ response curve, all measurements were performed with CO₂ and O₂ mole fractions of 400 μmol mol⁻¹ and 210 mmol mol⁻¹, respectively. In the CO₂ response curve, light intensity was 1000 μmol m⁻² s⁻¹. Dynamic responses to changes in light intensity were always measured after the fluxes were in steady-state. These conditions were emulated in all simulations.

The model successfully reproduced the steady-state response of An to light intensity (Supplemental Fig. S2), with a nRMSE = 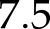%, a light-saturated An of 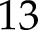μmol m⁻² s⁻¹ and a low light quantum yield of 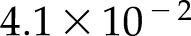mol mol⁻¹. Similarly, the steady-state response of An to CO₂ was also reproduced accurately (Supplemental Fig. S2), with a nRMSE = 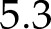% and CO₂ and light- and CO₂-saturated An of 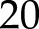μmol m⁻² s⁻¹.

Four light transients were chosen from the measurements by Kaiser et al. (2016), with initial and final light intensities (in μmol m⁻² s⁻¹) being 0 1000, 70 800, 800 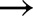130 and 600 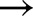200 (Supplemental Fig. S3). Simulated and measured relative An (normalized by initial and final steady-states for each transient) were compared, with nRMSE ranging from % to 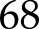% (RMSE varied between and 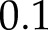). The model captured accurately the main patterns in the measurements, including the faster photosynthetic induction from low light intensity compared to darkness and the transient reduction of An below final steady-state levels after a decrease in light intensity (Supplemental Fig. S3).

Analysis in Silico

The tests presented in the previous section indicate that the model simulations are physiologically reasonable. To gain insight into how the different mechanisms interact in the regulation of PETC, a series of simulations are analyzed in detail. Steady-state responses to light and CO₂ were simulated (Figs. 4 and 5, respectively), with an air CO₂ mole fraction and light intensity of 400 μmol mol⁻¹ and 1,000 μmol m⁻² s⁻¹, respectively. In both simulations, the O₂ mole fraction was 210 mmol mol⁻¹ and the simulated light source was 10% blue, 90% red. Two photosynthetic induction curves at 1,000 μmol m⁻² s⁻¹ (on a background light intensity of 50 μmol m⁻² s⁻¹ to which the virtual leaf was previously adapted) with constant air CO₂ of 400 μmol mol⁻¹ and 100 μmol mol⁻¹, respectively, were simulated (Fig. 6; Supplemental Fig.e S4, respectively). The rest of simulated environmental conditions for the induction curves were as in the simulated steady-state response curves.

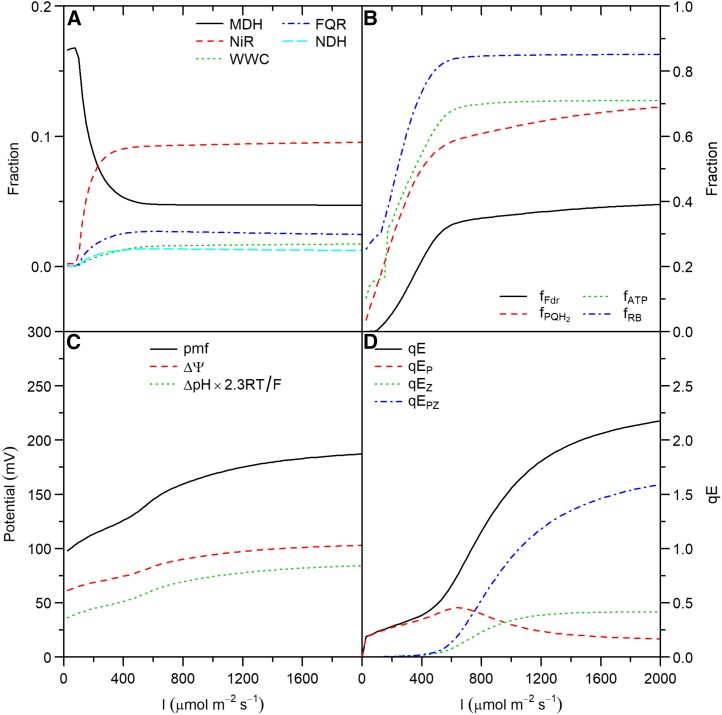
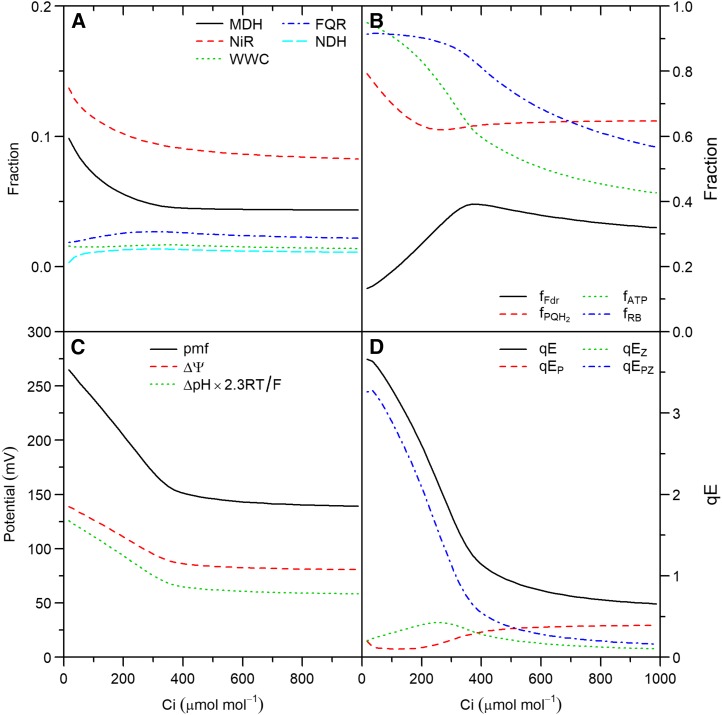
Figure 4.

Steady-state simulations of a virtual leaf as a function of light intensity. A, Fraction of electron flux through PSI allocated to MDH, NiR, WWC, FQR, and NDH. B, Fractions of the pool of ferredoxin and PQ/PQH₂ pair that are reduced (f_Fdr and f_PQH2), of Rubisco that is active (f_RB), and of adenylates as ATP (f_ATP). C, pmf, transthylakoid voltage (ΔΨ), and potential associated with transthylakoid ΔpH (ΔpH × 2.3RT/F). D, qE and its components due to independent effects of protonated PsbS (qE_p), zeaxanthin (qE_Z) and the interaction between the two (qE_PZ).

Figure 5.

Steady-state simulations of a virtual leaf as a function of intercellular CO₂ mole fraction (Ci). Symbols and panels as in Figure 4.

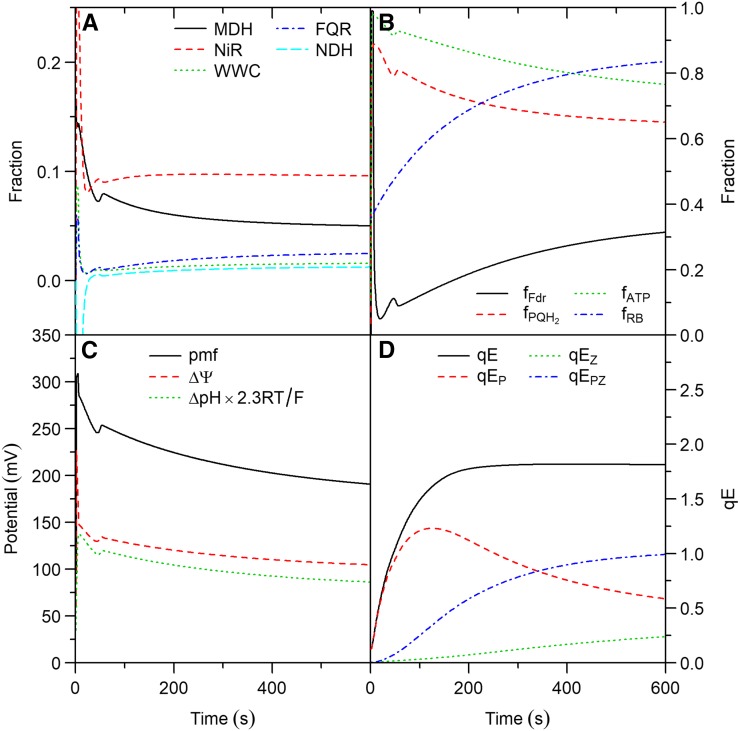
Figure 6.

Simulated photosynthetic induction from 25 to 1,000 μmol m⁻² s⁻¹ of light intensity for a virtual leaf. Air CO₂ mole fraction was constant at 400 μmol mol⁻¹. The system starts in steady-state and light intensity changes at the beginning of simulation. Symbols and panels as in Figure 4.

Cyclic and Noncyclic Electron Transport Are Complementary and Contribute to Balancing the Redox State of the Photosynthetic Electron Transport Chain

The fraction of electrons through PSI (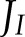) allocated to ANCET did not vary much with light intensity, but decreased with CO₂ (Figs. 4A and 5A) with a total range of variation between 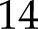% and 25%. WWC consumed a small fraction of these electrons, as most were allocated to NiR and MDH. The fraction of 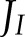allocated to cyclic electron transport (CET) was small (always ≤ 4%), increasing with light intensity, decreasing with CO₂, and being always higher for FQR than for NDH. At low light, MDH became more important than NiR. The reason is that the electron flux through MDH depends on the NADP⁺/NADPH pool, which the model predicted to be more reduced at low light than the pool of ferredoxin that controls the electron flux through NiR (Fig. 4B). The decrease of the fractions allocated to ANCET and CET with CO₂ paralleled the decrease in the ratio between ATP and NADPH consumption as the oxygenation/carboxylation ratio was reduced.

Under ambient CO₂, the fraction of 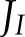allocated to ANCET and CET was significantly higher during the first two minutes of induction (Fig. 6A), and this affected all forms of alternative electron transport. Throughout induction, NiR and MDH remained the most important forms of alternative electron transport and the contributions of CET and WWC were small. Decreasing CO₂ (Supplemental Fig. S4A) resulted in similar patterns, although the period during which ANCET and CET were up-regulated was prolonged and the maximum fractions of 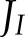allocated to ANCET and CET increased. These results suggest that alternative electron transport is particularly important in regulating the electron transport chain under fluctuating light conditions.

The strong difference between CET and ANCET can be explained by the lower maximum capacity of CET compared to ANCET (see Supplemental Table S1) but also by a more reduced state of the PQ/PQH₂ pair relative to Fd at all light intensities (Fig. 4B) and CO₂ (Fig. 5B). These redox states meant that, on average, FQR and NDH were only operating at 14% of their maximum capacity, whereas the WWC, NiR, and MDH operated, on average, at 28%, 34%, and 29% of their maximum capacity, respectively. This indicates that the contribution of each form of alternative electron transport does not depend only on its maximum capacity, but also on the redox states of electron donors and acceptors and the affinities of the protein complexes involved in the reactions with respect to these substrates.

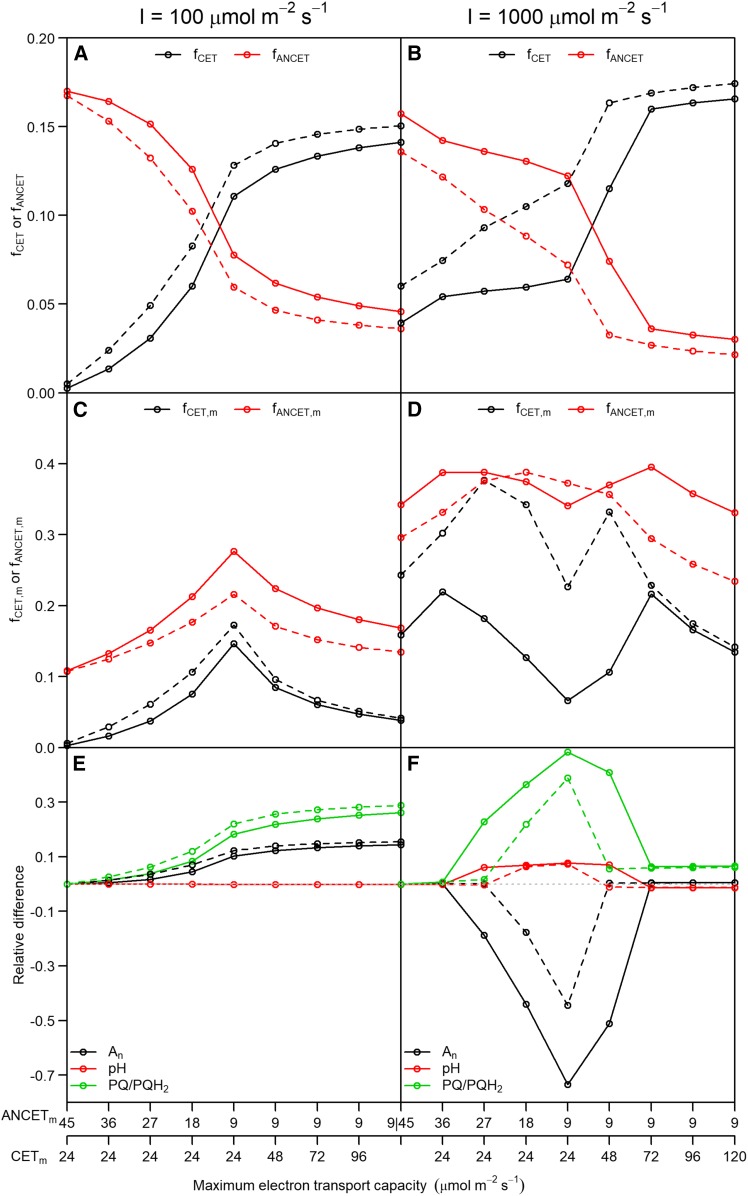
Given the lack of sufficient quantitative knowledge on the electron transport capacities of the different routes of alternative electron transport, a sensitivity analysis was performed by varying the total maximum capacity for electron transport of CET (CET_m) and ANCET (ANCET_m), at low (100 μmol m⁻² s⁻¹) and high (1,000 μmol m⁻² s⁻¹) light intensities (Fig. 7). The analysis revealed that, as ANCET_m (CET_m) decreased (increased), a significantly higher fraction of 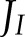was allocated to CET at both low and high light intensities (Fig. 7, A and B). However, the efficiency of CET was always lower than for ANCET (Fig. 7, C and D), meaning that a higher excess capacity was required for the same actual electron flux. Throughout all simulations, more than 60% of ANCET_m and CET_m remained unused, even when they were reduced 5-fold. This apparent inefficiency can be explained by a relatively strongly oxidized pool of Fd (Figs. 4 and 5), which always remained more oxidized than the PQH₂/PQ pool.

Figure 7.

The simulated fraction of electron flux through PSI (J_I) allocated to cyclic electron transport (f_CET = CET/J_I) and to alternative noncyclic electron transport (f_ANCET = ANCET/J_I) (A and B); the ratio between actual and maximum cyclic electron transport (f_CET,m = CET/CET_m) and between actual and maximum alternative noncyclic electron transprot (f_ANCET,m = ANCET/ANCET_m) (C and D); and the relative changes in net CO₂ assimilation (A_n), lumen pH (pH) and redox state of the plastoquinone/ol pool (PQ/PQH₂) (E and F), as a function of maximum cyclic and alternative noncyclic electron transport (CET_m and ANCET_m, respectively), at low (A, C, E) and high (B, D, F) light intensity. Simulations were performed with either the original (Supplemental Table S1) half-saturation constants for FQR and NDH (solid lines) or after reducing these constants by a factor of 2 (dashed lines). The leftmost values for each panel correspond to the original values of CET_m and ANCET_m (Supplemental Table S1) used in the rest of the study. The ratios of maximum capacities for electron transport of FQR and NDH, and of WWC, MDH and NiR were maintained across the different values of CET_m and ANCET_m, respectively.

At low light intensity, a higher rate of CO₂ assimilation was achieved when the fraction of 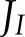allocated to CET increased, in parallel with an increase in the PQH₂/PQ ratio, whereas lumen pH did not change (Fig. 7E). This suggests that, under low light conditions, CET may play an important role in redox poising, i.e. preventing PETC from being over-oxidized, and thus ensuring sufficient electron flux through cyt b₆f. In addition, at low light intensity, the excess capacity for alternative electron transport is such that even with a 5-fold reduction of ANCET_m, more than 70% of this capacity is not being used (Fig. 7C), despite 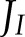being 3.6 times higher than ANCET_m. However, the maximum fraction of 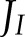that can go into ANCET or CET is limited by the ratio at which ATP and NADPH is consumed by the Calvin cycle and photorespiration.

At high light intensity, the same reduction in ANCET_m resulted in a 70% decrease in An and an overreduction of the PQH₂/PQ pool (Fig. 7F). This overreduction was associated to an increase in lumen pH, which decreased pmf to 104 mV (around the ATPase activation threshold), reducing NPQ from 2 to 0.5, and the ATP/ADP ratio from 2.4 to 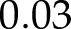. Therefore, CO₂ assimilation became limited by ATP synthesis and Rubisco activity was strongly down-regulated. On the other hand, provided that the sum of CET_m and ANCET_m were sufficiently large, the values of An, lumen pH, PQH₂/PQ, ATP/ADP, NPQ, and pmf achieved at high light intensity were the same or similar (≤ 5% variation) regardless of whether CET or ANCET were the dominant form.

Little is known about the affinity of NDH and the protein complexes involved in FQR for Fd and PQH₂, so the sensitivity analysis was repeated by reducing the half-saturation constants assumed for FQR and NDH (Supplemental Table S1) by a factor of two. The overall result was an increase in the fraction of 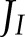allocated to CET, with larger effects at high light intensity compared to low light intensity. This could be explained by the fact that the maximum sensitivity to substrate concentration happens when such concentrations are in the order of the half-saturation constants, which is not the case at low light intensities. This analysis also illustrates the strong interaction between CET and ANCET: a modification in the kinetic properties of FQR or NDH will affect, indirectly, the activity of WWC, NiR and MDH, through changes in the redox state of Fd.

It is not possible to validate these simulations of CET and ANCET until a detailed profile of electron transport capacities of these reactions in vivo becomes available. However, these simulations reveal that, at high light intensity, an excess capacity for alternative electron transport (or a high affinity for substrates) may be required to prevent overreduction of the PQH₂/PQ pool due to insufficient pmf to drive ATP synthesis and pH to induce NPQ. On the other hand, an excess of ANCET capacity at low light intensity would be suboptimal as PETC would become overoxidized, decreasing the electron flux through cyt b₆f. Finally, the simulations highlight that lumen pH is not solely dependent on CET or ANCET as it is constrained by the pH sensitivity of qE, cyt b₆f, and APTase activity. Thus, changes in the amount or composition of CET and ANCET may not actually affect steady-state lumen pH, depending on the adjustments in the rest of the system.

The Electron Flux through NDH May Be Reversed When Metabolism Is Strongly Limiting

The simulated induction curves (Supplemental Fig. S4; Fig. 6) revealed that the flux of electrons through NDH could reverse its normal direction (i.e. reduction of PQ) under conditions where metabolism strongly limited linear electron transport. This means that PQH₂ was being used to reduce oxidized Fd, bypassing the normal route via PSI. Hence, this form of electron transport may be denoted as “pseudolinear electron transport” (PLET). PLET is possible because the equilibrium of the reaction catalyzed by NDH is sensitive to pmf, given that its electron transport activity is coupled to transthylakoid H⁺ transport (Strand et al., 2017). However, such reversal is only possible at high pmf and relatively high PQH₂/Fd ratios, as determined by its thermodynamic properties (see Supplementary Text for details). While pmf generally tends to increase whenever the capacity of metabolism to consume ATP is restricted, achieving a high PQH₂/Fd ratio under such conditions requires high ANCET, since NADPH consumption by the Calvin cycle will also be restricted. Indeed, reversal of NDH operation during the simulations always coincided with strong up-regulation of MDH and NiR (see Supplemental Fig. S4; Fig. 6) and the maximum flux occurred in the induction curve at low CO₂, with a value of 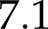μmol m⁻² s⁻¹ (i.e. 88% of the maximum electron flux assumed for NDH). However, such a high flux was only sustained for a few seconds.

PLET may have a photoprotective effect, by dissipating excess of energy under strong stromal metabolic restrictions (i.e. behaving as a “safety valve”), which could result in more oxidized Q_A. To test this effect, the simulation of photosynthetic induction at low CO₂ was repeated assuming absence of NDH. This resulted in an increase of reduced Q_A of up to 6% (on average 2%), during the first minute of induction, without any significant effect on CO₂ assimilation (i.e. relative changes below 0.01%). Despite the short duration of this effect, PLET may still play a role in photoprotection of leaves exposed to fluctuating light conditions, as most sunflecks within a canopy are known to last < 10 s (Smith and Berry, 2013).

PLET may also affect the redox state of ferredoxin. Indeed, in the simulations, the increased reduction of ferredoxin allowed for the increase in alternative electron sinks. A higher reduction of ferredoxin could also result in a higher activity of the Calvin cycle as many of the enzymes involved are redox regulated through the ferredoxin/thioredoxin system (Schürmann, 2003). However, the large differences in midpoint redox potentials between ferredoxin and these enzymes (Schürmann, 2003) suggest that the ferredoxin/thioredoxin system may act as a dark/light switch rather than a mechanism for the fine tuning of enzyme activity in the Calvin cycle.

qE Does Not follow First-Order Kinetics and Is Strongly Regulated by Light and CO₂

qE increased with light intensity (Fig. 4D) and decreased with CO₂ (Fig. 5D) due to changes in PsbS⁺ and ZX. These changes were driven by lumen pH that decreased with light intensity (Fig. 4C) and increased with CO₂ (Fig. 5C), with a range of values from 7.8 (in darkness) to 6.4 (high light intensity and ambient CO₂) to 5.8 (high light intensity and low CO₂), in agreement with the “moderate lumen pH” theory (Kramer et al., 1999). On the other hand, the pH of the stroma was highly buffered and varied between 7.8 and 8.0, partly due to the higher volume of the stroma relative to the lumen. The contribution of PsbS⁺ to qE at high lumen pH (pH > 6.8) was more important than the contribution of ZX, while the opposite became true at lower values (pH < 6.8). Although our model assumes a direct effect of PsbS⁺ (in the absence of ZX) and a direct effect of ZX (in the absence of PsbS⁺) on qE, most of the variation with CO₂ and light intensity was attributed to the combined effect of both factors. This is in agreement with previous models of qE (Takizawa et al., 2007; Zaks et al., 2012) that only accounted for the combined effect of PsbS and ZX. This also explains why qE increased in a sigmoidal fashion with light intensity (Fig. 4D).

However, the kinetics of qE cannot be explained by accounting only for the combined effect (Fig. 6D), as the build-up of ZX is much slower than the dynamics of PsbS protonation. Indeed, the evolution of qE during the first 10 min of simulation could not be described by a single rate constant (i.e. did not follow first-order kinetics). Although such kinetics are often explained as a sum of exponentials (Nilkens et al., 2010; Dall’Osto et al., 2014), a decomposition of qE into its components indicates that the direct contribution of PsbS⁺ to qE had an “overshooting” behavior, whereas the contribution of ZX increased in a sigmoidal fashion (Fig. 6D). Furthermore, the model predicts that, under conditions where the direct PsbS⁺ component dominates (e.g. low light intensity), qE would display an overshooting behavior. Such behavior has been observed experimentally (Armbruster et al., 2014; Kaiser et al., 2017) and cannot be explained by a sum of exponentials.

The Role of the ADP/ATP Ratio in the Regulation of Rubisco and Electron Transport Chain

Unlike pmf, the simulated H⁺ flux (v_H) coupled to ATP production increased with both light intensity and CO₂, as required by increasing rates of CO₂ assimilation. Thus, whereas v_H increased with pmf in a characteristic sigmoidal fashion when light intensity was varied (Supplemental Fig. S5A), v_H decreased and pmf increased as CO₂ was decreased (Supplemental Fig. S5B). This behavior was possible due to changes in the ATP/ADP ratio (Figs. 4B and 5B) that modulated the response of ATP synthesis to pmf. Thus, if the ATP/ADP ratio increases or remains constant, while v_H increases (i.e. when light intensity increases), pmf has to increase to sustain the required levels of v_H. However, when the ATP/ADP ratio decreases as v_H increases (i.e. when CO₂ decreases), the pmf may remain constant or decrease. An alternative way to analyze this relationship is to examine changes in the v_H/pmf ratio (known as ATPase conductance), as proposed by Kanazawa and Kramer (2002). In the simulations, this ratio decreased with light intensity (Supplemental Fig. S5A), in the range where ATP/ADP remained constant, coinciding with a strong increase in pmf and qE (Fig. 4). On the other hand, v_H/pmf increased with CO₂, in parallel to the decrease in ATP/ADP, qE, and pmf (Fig. 5). Similar patterns were observed by Kanazawa and Kramer (2002) using the rate constant of ECS decay in the darkness as an estimate of v_H/pmf. During induction, the ADP/ATP ratio remained low (Fig. 6B), which ensured a high pmf, a fast increase in qE, and a high Rubisco activase (Rca) activity that maximized the rate of Rubisco activation.

The effect that the ATP/ADP ratio can have on ATP synthesis is dual: (1) an effect on the free energy of the reaction, and (2) an effect on the kinetics of the reaction through changes in substrate binding and product release. Whereas the first effect would not explain the required large changes in pmf (Kanazawa and Kramer, 2002), the kinetic effect can be important if (1) the pool of adenylates is sufficiently small (in our simulations, 1 mm) and (2) the effects of pmf and product inhibition on the affinity of ATPase for its substrates is considered (Pänke and Rumberg, 1996). Parallel measurements of ECS and the adenylate pool in the stroma are lacking and thus it is not possible to verify whether such metabolic regulation is possible in vivo. However, the model suggests that changes in the ATP/ADP ratio are constrained by necessary changes in Rubisco activity (Figs. 4B and 5B). That is, adequate coupling of the Calvin cycle and PETC requires modulation of the activity of Rubisco, which is dependent on the ADP/ATP ratio through regulation of Rca activity (Zhang and Portis, 1999). Indeed, suppressing the effect of ADP/ATP on Rca through genetic manipulation results in lack of regulation of Rubisco activity (Carmo-Silva and Salvucci, 2013). As Rubisco activity is known to increase with light intensity and to decrease with CO₂ (von Caemmerer and Edmondson, 1986; Sassenrath-Cole et al., 1994), which the model predicted correctly (Figs. 4B and 5B), the ADP/ATP ratio should change accordingly. These results suggest that the ATP/ADP ratio may play a major role in coordinating the regulation of Rubisco activity and PETC as a function of CO₂ and light intensity, both under steady-state and dynamic conditions.

The Role of Inorganic Phosphate in the Regulation of the Electron Transport Chain

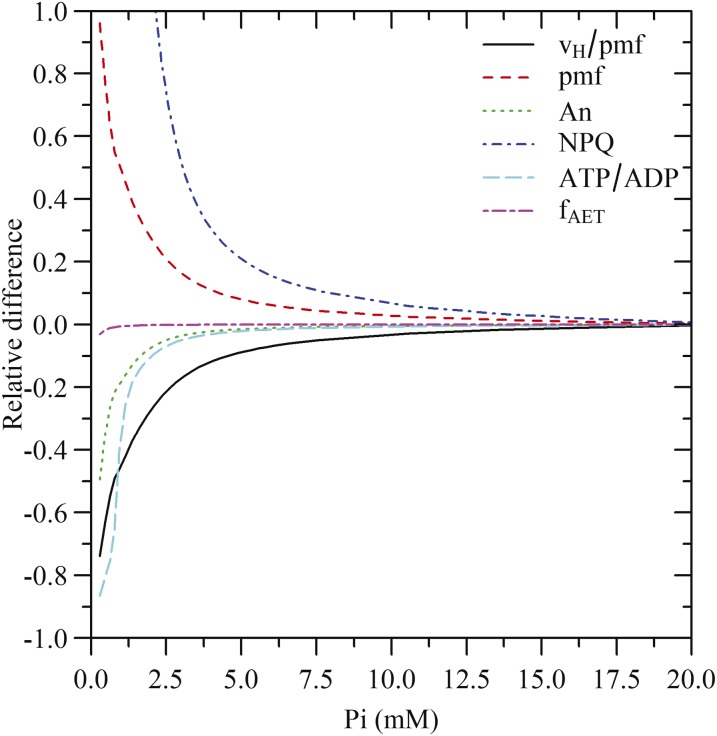
To explore the role of inorganic phosphate in the stroma (Pi) on the regulation of the electron transport chain, a series of simulations were performed. Different Pi levels were achieved by adjusting the total phosphate in the stroma and running the simulation until a steady-state was reached, under light and CO₂ saturating conditions. Then, the relative effect of Pi in different outputs of the model was analyzed (Fig. 8).

Figure 8.

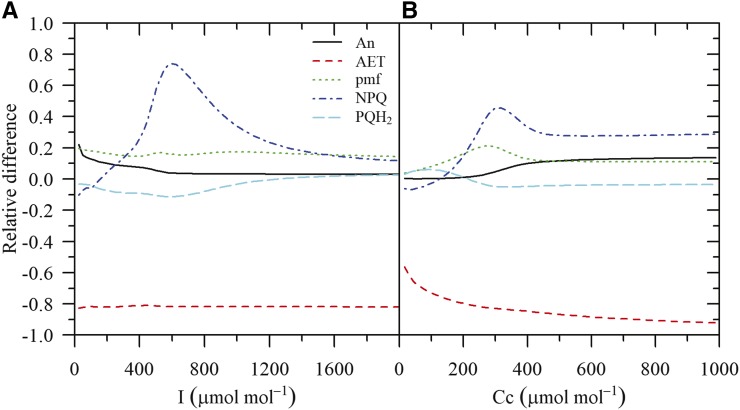
Simulated relative differences in the ratio between H⁺ flux through ATP synthase and proton motive (v_H/pmf), pmf, steady-state CO₂ assimilation (An), NPQ, ATP/ADP, and the total fraction of electron flux through PSI allocated to all forms of alternative electron transport (f_AET) as a function of free stroma Pi at saturating light intensity (1,000 μmol m⁻² s⁻¹) and CO₂ (2,000 μmol mol⁻¹). Relative differences for NPQ are truncated at a value of 1, but the maximum relative difference was 5.3 (for Pi = 0.28 mm).

As Pi decreased, the ATPase conductance decreased, which resulted in an increase of pmf and NPQ (Fig. 8). The increase in pmf was not associated with increased alternative electron transport, as the fraction of electrons allocated to these pathways remained constant. These results are in agreement with the experiment by Takizawa et al. (2008) where leaf discs were infiltrated with Man to sequester phosphate.

Changes in the regulation of electron transport chain could be observed with Pi concentrations as high as 10 mm. Estimations from experimental data indicated that Pi is expected to remain < 10 mm (Hampp et al., 1982; Sharkey and Vanderveer, 1989; Siebke et al., 1990), though the uncertainty on these estimations was not reported by the authors, even though assumptions on chloroplast volume or total chloroplast phosphate content were often required. This means that Pi could also contribute to the regulation of ATPase conductance, pmf, and NPQ at a wide range of light intensities and CO₂ levels, even when Pi does limit CO₂ assimilation. As with the ATP/ADP ratio, Pi can have both a thermodynamic and a kinetic effect on ATP synthesis, but the half-saturation of ATP synthesis with respect to Pi is an order of magnitude greater than for ADP (Pänke and Rumberg, 1996).

At a Pi concentration of 4 mm, pmf increased by 10% with respect to saturating Pi, whereas NPQ increased by 50%. These values were sufficiently high that linear electron transport started to decrease, resulting in a decrease of ATP synthesis and CO₂ assimilation. This also resulted in a decrease of the ATP/ADP ratio, but it did not offset the effects of low Pi and further reductions in Pi became increasingly limiting. Under conditions of Pi starvation (Pi = 0.28 mM), the model suggested that ATPase conductance can decrease by more than 50%, which led to a doubling of pmf and a 5-fold increase in NPQ with respect to saturating Pi. However, even though the Pi concentration was five times lower than the half-saturation of ATPase with respect to Pi (Pänke and Rumberg, 1996), CO₂ assimilation only decreased by 50%. Interestingly, even under these extreme conditions, RuBP levels remained saturating and the decrease in CO₂ assimilation was achieved via down-regulation of Rubisco activity.

These results indicate that Pi can have a dual role in the regulation of the electron transport chain, depending on the range of concentrations. Below 4 mm, decreases in Pi allow concerted down-regulation of ATP synthesis and Rubisco activity and are expected to occur under conditions where Suc and starch synthesis are limiting (e.g. high CO₂ and light intensity). Above 4 mm, changes in Pi allow adjustments of pmf and NPQ without affecting the rates of CO₂ assimilation or ATP synthesis. The latter role is not possible for adenylates as changes in the ATP/ADP ratio would result in changes in Rubisco activity and, since RuBP levels are saturating under most steady-state conditions (Sharkey, 1989), this would inevitably lead to changes in CO₂ assimilation. Although changes in Pi would lead to changes in triose phosphate export and starch synthesis and therefore may also be considered to be constrained, adjustments on the cytosolic side (for the former) and PGA concentration (for the latter) may allow a higher flexibility in the regulation of Pi than for adenylates.

The Impact of Uncertainties on the H⁺/ATP Ratio of ATP Synthase

According to the cooperative-binding theory for ATP synthase (Boyer, 1993), the number of H⁺ ions required to synthesize one molecule of ATP is equal to the ratio between the number of subunits in the c-ring of the F₀ component of ATPase (i.e. the rotor component embedded in the thylakoid membrane) and the number of catalytic sites that engage in ATP synthesis. Several independent studies on the crystal structure of photosynthetic ATPase from spinach (Spinacia oleracea) have identified these numbers to be 14 and 3, respectively (Seelert et al., 2000; Varco-Merth et al., 2008; Vollmar et al., 2009). That is the reason why, for the simulations discussed in the above, the H⁺/ATP ratio was assumed to be 14/3.

This ratio can also be estimated from the Gibbs free energy of ATP synthesis, if the proton motive force is known. Turina et al. (2003), Steigmiller et al. (2008) and Petersen et al. (2012) estimated the H⁺/ATP ratio for the photosynthetic ATPase of spinach using a biochemical equilibrium approach and both obtained a value of 4 or close to 4. Using a biochemical kinetic approach, Berry and Rumberg (1996) also concluded that the most likely value for this ratio in spinach was 4. Such mismatch between structure-based and biochemistry-based estimations of the H⁺/ATP has also been reported for the mitochondrial ATPase of Escherichia coli (Steigmiller et al., 2008) and Saccharomyces cerevisae (Petersen et al., 2012). However, the reason for the mismatch between the two methods is yet unknown.

To evaluate the effect of the H⁺/ATP ratio, the simulations of steady-state responses to light and CO₂ were repeated assuming a ratio of 4. Some of the thermodynamic and kinetic parameters of ATPase also had to be modified, as their original calculation relied on the value of the H⁺/ATP ratio (see Supplemental Text for details).

The most immediate effect was a strong reduction in the electron fluxes associated to CET and ANCET (Fig. 9). This is to be expected as, with a lower H⁺/ATP ratio, the same ATP/NADPH consumption can be met with a lower H⁺/e⁻ ratio, hence the need to decrease all forms of alternative electron transport. These results are similar to previous stoichiometric analyses (Yin et al., 2006). However, further changes were observed. Firstly, the rates of CO₂ assimilation also increased (Fig. 9), especially under conditions when ATP synthesis is expected to limit photosynthesis (low light and/or high CO₂) with relative increases of up to 20%. This effect reflects the fact that decreasing the H⁺/ATP ratio increases the overall energy efficiency of the electron transport chain to synthesize ATP.

Figure 9.

Simulated relative differences in steady-state CO₂ assimilation (An), total alternative electron transport (AET = CET + ANCET), pmf, NPQ, and concentration of plastoquinol (PQH₂) when the H⁺/ATP ratio of ATP synthase was reduced from 14/3 to 12/3, as a function of light intensity (A) and CO₂ (B).

Secondly, decreasing the H⁺/ATP ratio also affected ATPase conductance (Supplemental Fig. S5), because of the changes in the thermodynamics and kinetics of ATPase. The net result was an increase of the pmf required for a particular H⁺ flux, as well as an increase in the activation threshold of ATPase (Supplemental Fig. S5). This generated an increase in pmf across different light intensities and CO₂ (between 10% and 20% relative increase; Fig. 9) and a decrease in lumen pH (up to 0.37 pH units). This resulted in a strong increase in NPQ (up to 70% at light intensities close to saturation) and a slightly more oxidized plastoquinol pool.

These simulations indicate that the H⁺/ATP ratio has a strong effect on the requirements for alternative electron transport (CET and ANCET), the H⁺ budget of the lumen, photoprotection of PSII and the energy efficiency of the electron transport chain. Furthermore, these results indicate that lowering the H⁺/ATP ratio could result in significant increases in photosynthesis at low light intensities, while increasing photoprotection at higher light intensities. In this context, it is worth highlighting that the H⁺/ATP ratio of ATPase across different species varies in a wide range, from 2.7 to 5.0 (Pogoryelov et al., 2012). Therefore, reductions in the H⁺/ATP ratio may be considered as a potential strategy for improving photosynthesis.

CONCLUSIONS

The model can reproduce satisfactorily different aspects of steady-state and dynamic photosynthesis in vivo across a wide range of CO₂ and light intensities, which indicates that the simulations of the model are physiologically reasonable, at least for the case of Arabidopsis (other species may behave differently).

The model predicts that cyclic and noncyclic alternative electron transport are complementary, especially at high light intensities, and that they can play a role in regulating the redox states of the electron transport chain. The model simulations also show that, under certain conditions, reduction of Fd by PQH₂ is possible via NDH and this electron flux can have a photoprotective effect under fluctuating light conditions by acting as a “safety valve.” Metabolic regulation of ATP synthesis by changes in ADP/ATP allows coordinating the regulation of Rubisco, NPQ, and electron transport, across a wide range of CO₂ levels and light intensities. Similarly, regulation by changes in phosphate allows down-regulating the electron transport chain when consumption of triose phosphate is limiting. In addition, nonlimiting phosphate levels can have a strong control over NPQ and proton motive force. Finally, the different kinetics of the xanthophyll cycle and PsbS protonation results in qE following complex kinetics that cannot be summarized into a single or sum of exponential transients.

Further research is required to extend the model's coverage of metabolic regulatory processes, including (1) the interactions among the different ion transporters in the thylakoid membrane that affects the partitioning of proton motive force into its pH and voltage components, and (2) the regulation of inorganic phosphate in the stroma through the exchange of triose phosphates with the cytosol and phosphate release in the stroma by starch synthesis and photorespiration.

MATERIALS AND METHODS

Model Description

The model simulates dynamically the reactions associated with PETC and CO₂ assimilation (Fig. 1) by means of ordinary differential equations. Below, the main assumptions and general structure of the model are described in sufficient detail as required to interpret the results of this study. In the interest of reproducibility and transparency, all the equations, assumptions and parameters of the model are described in full detail in the Supplementary Text.

The model captures in detail the kinetics of the main protein complexes of PETC, including PSII, cytochrome b₆f complex (cyt b₆f), PSI, and ATPase, along with electron carriers, including plastoquinone/ol (PQ/PQH₂), plastocyanin (PC) and ferredoxin (Fd). Each protein complex is modeled using a master equation, similarly to previous models of PETC (Xin et al., 2013; Rubin and Riznichenko, 2014). The state of a protein complex is determined by the redox states of the components that form the protein complex. Let P be the vector containing all possible states of a protein complex, the rate of change of P is given by the following master equation:

(51)

where A is a matrix of kinetic expressions (or rate constants). Thus, applying the master equation to simulate the kinetics of electron transport within a protein complex implies: (1) constructing P from the combination of redox states of the components, (2) defining which transitions are feasible, and (3) choosing adequate kinetics for each transition.

PSII is modeled considering the oxygen evolving complex (Kok et al., 1970), the two electron-gate model of Q_B reduction by Q_A (Velthuys and Amesz, 1974), reversibility of charge separation and energy transfer to the reaction center (Holzwarth et al., 2006), and partial connectivity of the antenna and light harvesting complexes (Lavergne and Trissl, 1995). The equilibrium coefficients of the redox reactions within PSII are adjusted by ΔΨ, using the electrogenicities from Belyaeva et al. (Belyaeva et al., 2008). The model takes into account the spectral composition of the light source by including the leaf absorptance spectrum as well as the relative efficiency of different wavelengths in driving photosynthesis (McCree, 1972).

Energy-dependent nonphotochemical quenching (qE) is calculated as a function of PsbS⁺ and ZX based on previous models (Takizawa et al., 2007; Matuszyńska et al., 2016) and by assuming that PsbS and ZX may contribute to qE in the absence of each other. The xanthophyll cycle, including regulation of violaxanthin de-epoxidase by lumen pH is included. Because of the importance of chloroplast movement in Arabidopsis (Kasahara et al., 2002; Dall’Osto et al., 2014), this process is also included, with expressions calibrated to published experiments (Davis and Hangarter, 2012; Łabuz et al., 2015), as described in the Supplementary Text.

The model assumes a bifurcated reaction for the oxidation of PQH₂ at the oxidase site of cyt b₆f (Kramer and Crofts, 1993), such that the Q cycle is always engaged (Sacksteder et al., 2000). The master equation used to simulate cyt b₆f is a simplified version of the model by Schumaker et al. (Schumaker and Kramer, 2011), assuming that the high and low potential chains are in quasi-steady state, and including the effect of lumen pH on PQH₂ oxidation (Takizawa et al., 2007).

The model of PSI assumes that the reactions between the primary electron acceptor (A₀) and Fd are in quasi-steady state, while the rest of redox reactions within PSI are modeled explicitly. Antenna complexes of different PSI units are assumed to be fully connected (Lavergne and Trissl, 1995), and energy transfer to the reaction center is assumed irreversible with a quantum yield of 1, which is an adequate assumption given the high quantum efficiency of PSI (Croce and van Amerongen, 2013).

The equations describing ATPase are based on the model by Pänke and Rumberg (1996), modified to use a H⁺:ATP ratio of 14/3 (Seelert et al., 2000) and regulation of ATPase activity via reduction of the γ-subunit (Kramer and Crofts, 1989). The components of pmf in the lumen and stroma are simulated explicitly, taking into account the buffering of pH and counterion transport (Cruz et al., 2001).

Several alternative electron transport pathways are included in the model (Fig. 1). NDH and FQR are modeled taking into account the effect of pmf on NDH (Strand et al., 2017) and the redox regulation of FQR (Strand et al., 2016). WWC and NiR are simulated by constructing rate equations based on published kinetics, whereas MDH and export of malate are modeled as proposed by Fridlyand et al. (Fridlyand et al., 1998).

The Calvin cycle is simplified into two steps: the conversion of ribulose-1,5-bisphosphate (RuBP) into phosphoglycerate (PGA) by Rubisco, and the regeneration of RuBP from PGA (which includes PGA reduction and triose phosphate utilization for Suc and starch synthesis). The kinetic model of Rubisco by Farquhar (1979) was extended by a model of Rca that takes into account the effect of ADP/ATP and thioredoxin on Rca activity (Zhang and Portis, 1999) and the relationships between Rca and Rubisco activity as proposed by Mott and Woodrow (2000). The regeneration of RuBP from PGA is described by a pseudo-reaction that consumes ATP and NADPH in the correct stoichiometry depending on the ratio between carboxylation and oxygenation (Farquhar et al., 1980). It also takes into account the consumption of triose phosphates by Suc and starch synthesis, and the regulation of enzyme activity by light intensity through the thioredoxin system (Sassenrath-Cole et al., 1994).

The scaling of fluxes to the leaf-level is achieved with a “big chloroplast” approach (Farquhar, 1989). CO₂ diffusion is implemented as a dynamic version of conductance-based models (Vialet-Chabrand et al., 2013; Berghuijs et al., 2015), including conductances for the stomatal pores (Vialet-Chabrand et al., 2013), cell wall, and chloroplast (Berghuijs et al., 2015).

Simulations and Data Analysis

Dataset from literature were obtained by digitizing the original figures (including error bars) using WebPlotDigitizer by Ankit Rohatgi. The model was implemented in the C++ programming language, whereas all data analysis, setup of simulations, and figures were performed with the R programming language. Simulations were obtained by using the CVODE algorithm within the Sundials numerical library, with relative accuracy in the output of ≤ 10⁻⁶.

This article was written in R Markdown, following the principles of reproducible research. The files required to reproduce all the results presented in this article can be downloaded from https://github.com/AleMorales/RegulationETC or obtained from the corresponding author upon request.

Supplemental Data

The following supplemental materials are available.

• Supplemental Text. Detailed description of all equations in the model and its parameterization from literature.

• Supplemental Figures. List of supplemental figures including additional outputs of simulations (Supplemental Fig. S1–S5) and schematic diagrams of components of the model (Supplemental Figure S6–S10).

• Supplemental Tables. List of supplemental tables include parameters of the model with values (Supplemental Table S1), state variables of the model with default values (Supplemental Table S2), and transition rules with associated kinetics (Supplemental Table S3) as described in the Supplemental Text.