Distribution of cardiac sodium channels in clusters potentiates ephaptic interactions in the intercalated disc

Abstract

Key points

• It has been proposed that ephaptic conduction, relying on interactions between the sodium (Na⁺) current and the extracellular potential in intercalated discs, might contribute to cardiac conduction when gap junctional coupling is reduced, but this mechanism is still controversial.

• In intercalated discs, Na⁺ channels form clusters near gap junction plaques, but the functional significance of these clusters has never been evaluated.

• In HEK cells expressing cardiac Na⁺ channels, we show that restricting the extracellular space modulates the Na⁺ current, as predicted by corresponding simulations accounting for ephaptic effects.

• In a high‐resolution model of the intercalated disc, clusters of Na⁺ channels that face each other across the intercellular cleft facilitate ephaptic impulse transmission when gap junctional coupling is reduced.

• Thus, our simulations reveal a functional role for the clustering of Na⁺ channels in intercalated discs, and suggest that rearrangement of these clusters in disease may influence cardiac conduction.

Abstract

It has been proposed that ephaptic interactions in intercalated discs, mediated by extracellular potentials, contribute to cardiac impulse propagation when gap junctional coupling is reduced. However, experiments demonstrating ephaptic effects on the cardiac Na⁺ current (I _Na) are scarce. Furthermore, Na⁺ channels form clusters around gap junction plaques, but the electrophysiological significance of these clusters has never been investigated. In patch clamp experiments with HEK cells stably expressing human Na_v1.5 channels, we examined how restricting the extracellular space modulates I _Na elicited by an activation protocol. In parallel, we developed a high‐resolution computer model of the intercalated disc to investigate how the distribution of Na⁺ channels influences ephaptic interactions. Approaching the HEK cells to a non‐conducting obstacle always increased peak I _Na at step potentials near the threshold of I _Na activation and decreased peak I _Na at step potentials far above threshold (7 cells, P = 0.0156, Wilcoxon signed rank test). These effects were consistent with corresponding control simulations with a uniform Na⁺ channel distribution. In the intercalated disc computer model, redistributing the Na⁺ channels into a central cluster of the disc potentiated ephaptic effects. Moreover, ephaptic impulse transmission from one cell to another was facilitated by clusters of Na⁺ channels facing each other across the intercellular cleft when gap junctional coupling was reduced. In conclusion, our proof‐of‐principle experiments demonstrate that confining the extracellular space modulates cardiac I _Na, and our simulations reveal the functional role of the aggregation of Na⁺ channels in the perinexus. These findings highlight novel concepts in the physiology of cardiac excitation.

Key points

• It has been proposed that ephaptic conduction, relying on interactions between the sodium (Na⁺) current and the extracellular potential in intercalated discs, might contribute to cardiac conduction when gap junctional coupling is reduced, but this mechanism is still controversial.

• In intercalated discs, Na⁺ channels form clusters near gap junction plaques, but the functional significance of these clusters has never been evaluated.

• In HEK cells expressing cardiac Na⁺ channels, we show that restricting the extracellular space modulates the Na⁺ current, as predicted by corresponding simulations accounting for ephaptic effects.

• In a high‐resolution model of the intercalated disc, clusters of Na⁺ channels that face each other across the intercellular cleft facilitate ephaptic impulse transmission when gap junctional coupling is reduced.

• Thus, our simulations reveal a functional role for the clustering of Na⁺ channels in intercalated discs, and suggest that rearrangement of these clusters in disease may influence cardiac conduction.

Introduction

Action potential (AP) propagation is essential for the proper function of the heart. Disturbances of cardiac AP propagation (slow conduction, conduction block) can lead to arrhythmias (Kléber & Rudy, 2004). It is widely accepted that cardiac APs are propagated via depolarizing electrotonic current flow through gap junctions (Weidmann, 1970; Kléber & Rudy, 2004). Under physiological conditions, the Na⁺ current (I _Na), which is mainly carried by voltage‐gated Na_v1.5 channels, underlies the rapid upstroke of the cardiac AP. This current provides the charge necessary to depolarize downstream tissue (Kléber & Rudy, 2004). I _Na and the level of gap junctional coupling are thus the principal determinants of cardiac conduction (Shaw & Rudy, 1997; Kléber & Rudy, 2004).

Gap junction channels are expressed at high density in intercalated discs, thereby ensuring rapid conduction along myocardial fibres (Dolber et al. 1992). Intriguingly, Na⁺ channels are also expressed at high density in intercalated discs (Cohen, 1996; Maier et al. 2002; Lin et al. 2011; Shy et al. 2013; Leo‐Macias et al. 2016), where, according to most recent estimations, about 50% of Na⁺ channels are located (Lin et al. 2011; Shy et al. 2013; Leo‐Macias et al. 2016). A high density of Na⁺ channels was also observed at intercellular contacts in cardiomyocyte cultures (Kucera et al. 2002).

This high density of Na⁺ channels in intercalated discs suggests the involvement an alternate conduction mechanism, called ‘ephaptic coupling’ (Lin & Keener, 2010), ‘electric field mechanism’ (Sperelakis & Mann, 1977; Sperelakis, 2002), or ‘ephaptic conduction’ (Mori et al. 2008). Ephaptic coupling relies on the large number of Na⁺ channels in the membranes enclosing the intercellular cleft of the intercalated disc. According to this mechanism, upon activation of the Na⁺ channels in the membrane on one side of the intercalated disc, a large current flows radially through the large resistance of the narrow extracellular space, which causes a substantial negative extracellular potential (V _e) within the cleft (according to Ohm's law). This negative V _e then translates into membrane depolarization on the other side of the cleft, which contributes to the activation of Na⁺ channels and thus to cardiac conduction (Veeraraghavan et al. 2014), in conjunction or interaction with the classical mechanism based on electrotonic current flow through gap junctions (Weidmann, 1970).

It was recently reported that, in intercalated discs, Na⁺ channels are localized in the vicinity of gap junction plaques (Rhett & Gourdie, 2012; Rhett et al. 2013; Veeraraghavan et al. 2014). This finding has led to the concept of ‘perinexus’, the region surrounding the gap junction plaque (nexus) where connexin 43 hemichannels (the principal gap junction channel‐forming protein in ventricular myocardium) and Na⁺ channels interact with structural and regulatory proteins, highlighting a potential role of the perinexus in cardiac electrical function (Rhett & Gourdie, 2012; Rhett et al. 2013; Vermij et al. 2017). Clusters of Na⁺ channels in intercalated discs were also reported in further morphological studies (Leo‐Macias et al. 2016).

The ephaptic coupling mechanism is still controversial, even decades after it was first proposed. This controversy is certainly related to the fact that a direct experimental characterization of this mechanism is extremely difficult. As a result, a clear direct experimental proof at the cellular level is still absent. Therefore, ephaptic conduction has essentially been studied in mathematical models (Sperelakis & Mann, 1977; Kucera et al. 2002; Mori et al. 2008; Lin & Keener 2010; Tsumoto et al. 2011; Wei et al. 2016). These studies have shown that ephaptic coupling can indeed contribute to action potential propagation when the level of gap junctional coupling is reduced or even absent. These mathematical models also explain a certain number of paradoxical effects of Na⁺ channel blockers, gap junction uncouplers and changes in extracellular Na⁺ and K⁺ concentrations on conduction velocity and anisotropy ratio in optical mapping studies of whole hearts (George et al. 2015; Veeraraghavan et al. 2015). These effects cannot be explained by gap junctional coupling alone, thus providing support for the involvement of ephaptic coupling. Moreover, in connexin 43 knockout cardiac tissue, conduction slowing was smaller than expected from theories and models based on electrotonic gap junctional coupling (Gutstein et al. 2001; Beauchamp et al. 2004; van Rijen et al. 2004), again indirectly suggesting that ephaptic coupling is involved in conduction. However, these modelling studies assumed a uniform distribution of Na⁺ channels at intercellular junctions. The electrophysiological significance of the reported Na⁺ channel clustering was never examined.

In this work, our first aim was to provide experimental evidence at the cellular level that ephaptic effects modulate I _Na via V _e when the extracellular space is restricted by bringing the cell in proximity to a non‐conductive obstacle. In HEK cells expressing human Na_v1.5 channels, we show that restricting the extracellular space near the cell modulates I _Na. The modulation of I _Na was consistent with computer simulations using a new high‐resolution model of excitable membranes facing a narrow extracellular cleft that we developed using the finite element method. Using this model, our second aim was to evaluate the effects of Na⁺ channel distribution on ephaptic interactions. We found that aggregating Na⁺ channels potentiates ephaptic interactions and action potential transmission from one cell to the other, in particular when clusters of Na⁺ channels face each other across the intercellular cleft. These effects are due to complex spatiotemporal interactions between I _Na and V _e, which were revealed by using our high‐resolution modelling studies.

Methods

Patch clamp experiments

Human embryonic kidney 293 (HEK293) cells stably expressing wild‐type human cardiac Na_v1.5 channels were prepared and cultured at a low seeding density as described previously (Dhar Malhotra et al. 2001). Previous work indicates that these cells endogenously express Na_v1.5 β‐subunits (Dhar Malhotra et al. 2001; Valdivia et al. 2010). The Na⁺ current (I _Na) was recorded using the patch clamp technique in the whole‐cell configuration at room temperature (22°C) with glass pipettes of 1.9–2.6 MΩ resistance using a standard amplifier (Axopatch200B, Molecular Devices Corp., Sunnyvale CA, USA). Experiments were controlled using the pClamp10 software (Molecular Devices Corp., Sunnyvale CA, USA). Pipette capacitance and series resistance were compensated to 80–85 %. The Na⁺ current was low‐pass filtered (cut‐off frequency: 4 kHz) and recorded digitally at a sampling rate of 20 kHz. Residual capacitive transients and time‐independent leak currents were subtracted using a P/4 protocol. The cells were bathed in a medium containing (mm): NaCl 10, N‐methyl‐d‐glutamine chloride 80, CaCl₂ 2, MgCl₂ 1.2, CsCl 5, HEPES 10, and glucose 5, adjusted to a pH of 7.40 using 3 m CsOH. The pipettes were filled with an intracellular solution composed of (mm): Na₂‐ATP 5, caesium aspartate 70, CsCl 60, EGTA 11, HEPES 10, CaCl₂ 1, and MgCl₂ 1, adjusted to a pH of 7.20 using HCl. The amplifier head stage was mounted on a high‐precision motorized micromanipulator (MP‐225, Sutter Instruments, Novato, CA, USA). The liquid junction potential (estimated to be 21.5 mV) was not compensated.

A steady‐state activation protocol was used to examine peak I _Na and to establish steady‐state activation current–voltage relationships. It consisted of 25‐ms‐long voltage steps from −90 to +70 mV in increments of 5 mV, separated by 3 s intervals at the holding potential of −90 mV. A set of raw currents with and without processing using the P/4 protocol is illustrated in Fig. A1 (Appendix) for one representative cell that was detached from the growth substrate as described below.

Restricting the extracellular space

Every cell was first subjected to a steady‐state activation (current–voltage, I–V) protocol. The cell was then detached from the growth substrate without losing the gigaohm seal by gently moving the pipette horizontally using the motorized micromanipulator. The steady‐state activation protocol was repeated with the cell in a spherical shape. Subsequently, to restrict the extracellular space near a region of the cell membrane, the cell was approached slowly towards a non‐conducting obstacle consisting of a molten glass pipette tip with a spherical shape with a radius of approximately 100 μm. The cell was moved under visual control using phase‐contrast microscopy and video monitoring in a focal plane perpendicular to the glass obstacle and passing through the cell. Close physical contact of the cell with the obstacle was confirmed by a slight deformation of the cell. The steady‐state activation protocol was then repeated. Finally, the cell was moved away from the obstacle (>10 μm), and the steady‐state activation protocol was repeated one last time.

Data analysis

The currents were analysed using the Clampfit software (Molecular Devices Corp.) and custom‐written programs in MATLAB (MathWorks, Natick, MA, USA). The currents were normalized by cell capacitance and filtered using a 5‐sample moving average filter. Then, peak currents were fitted to a Boltzmann function, f(V _m) = 1/(1+exp((V _m − V _1/2)/K))), where f is the normalized current or conductance, V _m is the membrane potential, V _1/2 is the voltage at which half of the available channels are activated, and K is the slope factor.

Computer model

Mathematical model of excitable membranes with a restricted extracellular space

The interactions between I _Na and the extracellular potential (V _e) were investigated using high‐resolution two‐dimensional models of membranes adjacent to a narrow extracellular space. Two situations were assessed. In the first situation, we modelled one cell membrane facing a non‐conductive obstacle, separated by a narrow cleft. This corresponds to the experiments described above. In the second situation, we modelled two cell membranes separated by a narrow intercellular cleft. This situation corresponds to the membranes of two longitudinally abutting cardiomyocytes joined by an intercalated disc.

For the first situation, charge conservation in the membrane‐cleft system was described by:

$$-\nabla (w{\sigma }_{\mathrm{e}}\nabla V_{\mathrm{e}})=i_{\mathrm{ion}}+c\frac{\partial V_{\mathrm{m}}}{\partial t},$$ (1)

where w is the cleft width, σ_e is the extracellular conductivity tensor, i _ion is the ion current density through the membrane, c is the specific membrane capacitance (1 μF cm⁻²) and V _m is the transmembrane potential (V _m = V _i – V _e). The lefthand side of eqn (1) represents a Laplacian term in the two dimensions of the membrane. Because cleft width is considerably smaller than the spatial extent of the membrane, it was assumed that V _e gradients perpendicular to the membrane are negligible. The extracellular space was considered isotropic and σ_e was set to a scalar value of 6.667 mS cm⁻¹ (resistivity: 150 Ω cm).

For the second situation, charge conservation was described by:

$$-\nabla (w{\sigma }_{\mathrm{e}}\nabla V_{\mathrm{e}})=i_{\mathrm{ion},1}+c\frac{\partial V_{\mathrm{m},1}}{\partial t}+i_{\mathrm{ion},2}+c\frac{\partial V_{\mathrm{m},2}}{\partial t},$$ (2)

where i _ion,1 and i _ion,2 are the ion current densities through the two membranes, and V _m,1 and V _m,2 are the respective transmembrane potentials.

In intercalated disc clefts, wall effects and the presence of cell adhesion molecules such as N‐cadherin and nectins (Satomi‐Kobayashi et al. 2009) will decrease the mobility of ions, their effective diffusion coefficients, and therefore σ_e. However, diffusion coefficients or σ_e in narrow intercellular clefts and their dependence on cleft width are, to our knowledge, quantitatively unknown. In the lefthand sides of eqns (1) and (2), σ_e and w are linked by the product wσ_e. Therefore, decreasing σ_e by a given factor is equivalent to decreasing w by the same factor. Using this principle, all simulation results can be extrapolated to different values of σ_e.

The ionic current density was formulated as:

$$i_{\mathrm{ion}}=i_{\mathrm{Na}}+i_{\mathrm{K}},$$ (3)

where i _Na is the Na⁺ current density and i _K represents all other K⁺ currents. The Na⁺ current density was represented using a Hodgkin‐Huxley formalism according to Luo & Rudy, (1991, 1994) with modifications proposed by Livshitz & Rudy (2009) as:

$$i_{\mathrm{Na}}=g_{\mathrm{Na}}\times m^{3}hj\times (V_{\mathrm{m}}-E_{\mathrm{Na}}),$$ (4)

with g _Na being the maximum conductance per unit area (23 mS cm⁻²; Luo & Rudy, 1991), m the activation gating variable, h and j the inactivation gating variables, and E _Na the Nernst potential for Na⁺. E _Na was set to +55 mV.

The peak I _Na lasts only a few milliseconds and subsides before other time‐dependent ionic currents arise. Therefore, to focus on the interactions between V _e and I _Na, we lumped all other currents into one single repolarizing linear K⁺ current as:

$$i_{\mathrm{K}}=g_{\mathrm{K}}\times (V_{\mathrm{m}}-E_{\mathrm{K}}),$$ (5)

with g _K = 0.3 mS cm⁻² and E _K = −85 mV. This formulation sets the resting membrane potential at E _K.

As previously shown, the density of Na⁺ channels is higher in intercalated discs than on the lateral membranes (Cohen, 1996; Maier et al. 2002; Leo‐Macias et al. 2016). The current consensus is that a proportion P of approximately 50% of the whole‐cell Na⁺ current is present in the intercalated disc membranes (Lin et al. 2011; Shy et al. 2013; Leo‐Macias et al. 2016). Compared to a uniform distribution over the entire cell surface, g _Na is therefore scaled (increased) in the disc membrane by a factor F_{g Na} defined as:

$$F_{g_{\mathrm{Na}}}=P\frac{A_{\mathrm{cell}}}{A_{\mathrm{discs}}},$$ (6)

with A _cell being the area of the cell and A _discs the area of the membranes adjacent to intercalated discs. This factor was incorporated as a multiplier into eqn (4). For a cylindrical cardiac cell with typical length L = 100 μm and radius r = 11 μm, this scaling factor is 5.05 for P = 50% and would be 10.09 for P = 100% in the extreme case of all channels being located in the intercalated discs. Therefore, in the simulations, g _Na was scaled by various factors ranging from 1 to 10.09.

Morphological studies have also shown that Na⁺ channels form clusters in intercalated discs (Rhett et al. 2013; Veeraraghavan et al. 2015; Leo‐Macias et al. 2016). Therefore, we investigated the specific effect of Na⁺ channel clustering in dedicated simulations in which g _Na was redistributed into selected membrane regions while keeping constant the total Na⁺ current conductance (the integral of g _Na over the entire membrane).

Numerical methods

Unless specified otherwise, the membranes were modelled as discs with a predefined radius. The model described by partial differential eqns (1) and (2) was discretized using triangular finite elements with piecewise linear basis functions (Johnson, 1987; Sundnes et al. 2006). Meshes were generated in MATLAB using the function ‘generateMesh’. The maximal edge length was set to 0.05 times the disc radius. From the finite elements, eqn (1) was approximated by a system of ordinary differential equations:

$$\mathbf{K}{\mathbf{V}}_{\mathrm{e}}=\mathbf{M}\frac{\mathrm{d}{\mathit{V}}_{\mathbf{m}}}{\mathrm{d}t}+{\mathbf{F}}_{i_{\mathrm{ion}}},$$ (7)

where V _e is the vector of the V _e values at the mesh vertices, K is the conductance matrix for the extracellular space (stiffness matrix), M is the capacitance matrix (mass matrix) computed using c, and ${\mathbf{F}}_{i_{\mathrm{ion}}}$ is the vector of ion currents at the vertices (load vector). We simulated voltage clamp protocols controlling intracellular voltage V_i (or V_{i ,1} and V_{i ,2}). During a voltage step, dV _m/dt in eqn (7) is therefore equal to −dV _e/dt. Because, compared to the cleft, the intracellular space is not confined and has a low resistance, V_i was assumed to be spatially uniform.

Similarly, eqn (2) was discretized as:

$$\mathbf{K}{\mathbf{V}}_{\mathrm{e}}={\mathbf{M}}_1\mathit{}\frac{\mathrm{d}{\mathit{V}}_{\mathbf{m},\mathbf{1}}}{\mathrm{d}t}+{\mathbf{F}}_{i_{\mathrm{ion},1}}+{\mathbf{M}}_2\frac{\mathrm{d}{\mathit{V}}_{\mathbf{m},\mathbf{2}}}{\mathrm{d}t}+{\mathbf{F}}_{i_{\mathrm{ion},2}},$$ (8)

in which M ₁ = M ₂ = M if the two membranes have the same shape and specific capacitance. Assuming that extracellular gradients and potentials are negligible in the bulk extracellular space (outside the cleft), the systems described by eqns (7) and (8) were subjected to a Dirichlet boundary condition V _e = 0 at the rim of the disc, where the narrow cleft space joins the extended bulk space. Another Dirichlet boundary condition was applied on the intracellular potentials (V_i, or V_{i ,1} and V_{i ,2}) by enforcing the predefined voltage clamp protocols. These protocols consisted of depolarizing steps starting at a holding potential of −85 mV (resting potential). As initial condition, V _e was set to 0 in the entire cleft space and the gating variables m, h, and j were set to their corresponding steady‐state values.

Equations (7) and (8) were integrated using an operator splitting method (Sundnes et al. 2006) with a constant time step Δt of 0.05 μs. The diffusive part of the system was integrated using the Crank‐Nicolson method (Crank & Nicholson, 1947) by solving the following system at each time step:

$$\left(\overline{\mathbf{M}}-\frac{1}{2}\overline{\mathbf{K}}\mathrm{\Delta }t\right){\mathbf{V}}_{\mathrm{e}}(t+\mathrm{\Delta }t)=\left(\overline{\mathbf{M}}+\frac{1}{2}\overline{\mathbf{K}}\mathrm{\Delta }t\right){\mathbf{V}}_{\mathrm{e}}(t),$$ (9)

where $\overline{\mathbf{M}}$ and $\overline{\mathbf{K}}$ are reduced matrices obtained from M and K (or M ₁, M ₂ and K) after having enforced the Dirichlet conditions and V _e is the vector of the unknown V _e values at the mesh vertices. Taking advantage from the fact that the lefthand side operator in eqn (9) is a sparse symmetric matrix, the system was solved using the Cholesky decomposition of this matrix, which needed to be computed only once at the beginning of each simulation. The gating variables were integrated using the method of Rush & Larsen (1978).

To obtain macroscopic Na⁺ currents, the Na⁺ current density was integrated over the entire disc membrane. Reference simulations without feedback of V _e on I _Na were run by maintaining V _e = 0 in the entire cleft.

Statistics

For experimental results, significance was assessed at the 0.05 level using the two‐tailed Wilcoxon signed rank test (non‐normal data distribution).

Results

Restricting the extracellular space has a dual activating and attenuating effect on I _Na with complex spatiotemporal dynamics

First, we set out to understand the behaviour of I _Na and its interaction with V _e in cells expressing Na⁺ channels that were brought close to a non‐conductive obstacle. Therefore, we simulated a disc‐shaped membrane with a uniform distribution of channels adjacent to a narrow extracellular space. Fig. 1 A illustrates the model circuit equivalent and the finite element mesh. The conduction scaling factor F_{g Na} was set to 10.09. This corresponds to the situation in which all channels are located at the extremity of the myocytes and is based on typical cell geometries in vivo. The intracellular side of the membrane was subjected to a voltage clamp activation protocol. Fig. 1 B illustrates the different spatiotemporal behaviours of I _Na, V _e, the product of the three activation gates (m ³) and the product of the inactivation gates hj for various cleft widths, for a step to −25 mV (far above the I _Na activation threshold) and −50 mV (near the threshold).

Figure 1. Dynamic interactions between I _Na and V _e in a disc‐shaped membrane (R _disc = 11 μm) separated from a non‐conducting obstacle by an extracellular cleft (uniform distribution of g _Na, F_{g Na} = 10.09).

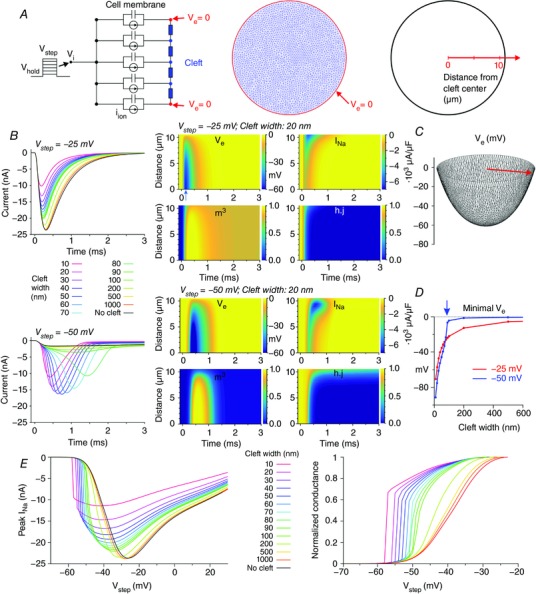
A, schematic representation of the model (left: cross‐section; middle: finite element mesh) with membrane capacitance, ion currents and extracellular resistive properties (blue). V _e at the rim of the disc was held at 0 (red). Due to radial symmetry (uniform Na⁺ channel distribution), the model behaviour does not depend on the azimuthal coordinate but only on the radial coordinate (right). B, left: total I _Na during an activation step from −85 mV to −25 mV (top) and to −50 mV (bottom), for various cleft widths. B, middle: corresponding colour maps of V _e, I _Na, m ³ and hj as a function of time and distance from the centre, for a 20‐nm‐wide cleft. C, spatial profile of V _e at the occurrence of the minimum (arrow in the middle panel of A) for V _step = −25 mV and a cleft width of 20 nm. D, minimal V _e registered in the cleft as a function of cleft width, for V _step = −25 mV and −50 mV. Note the abrupt behaviour for V _step = −50 mV (blue arrow). E, relationship between peak total I _Na and V _step for various cleft widths (left) and derived steady‐state activation curves (right).

At V _step = −25 mV, the restricted cleft decreased the peak of total I _Na. This effect increased with decreasing cleft width. I _Na decreased due to the diminished driving force (V _m – E _Na) resulting from the negative V _e in the cleft. In turn, this negative V _e was the consequence of the current flowing radially through the extracellular space. As shown in the corresponding colour plots and in Fig. 1 C, V _e was not spatially homogeneous but exhibited a radially symmetric concave profile, with a minimum in the cleft centre. Thus, the feedback of V _e on I _Na dynamics was stronger in the centre of the disc. The colour plots for V _step = −25 mV and a 20‐nm‐wide cleft (Fig. 1 B) and Movie S1 in Supporting information show that a substantially negative V _e first appeared in the centre of the disc. There, the strongly negative V _e (and thus the more positive V _m) precipitated I _Na inactivation. Because of the spatially heterogeneous behaviour of V _e and inactivation (product hj), the local I _Na density was also heterogeneous: local I _Na was maximal (in absolute value) and lasted longer in the periphery of the disc, and the self‐attenuation of I _Na was stronger in the centre.

At V _step = −50 mV, total I _Na was small in the absence of a cleft but strongly potentiated for cleft widths from 10 to 80 nm. For a 20‐nm‐wide cleft, as shown in the colour plots (Fig. 1 B) and in Movie S2, the negative V _e building up in the centre supported the activation of I _Na (product of gates m ³), whereas m ³ remained low in the periphery. Due to positive feedback, the increasing I _Na in the centre rendered V _e even more negative, until Na⁺ channels inactivated. In conjunction with the decreased driving force, I _Na in the centre was small and short lasting. In contrast, in the periphery, the driving force was reduced to a lesser extent and inactivation was not accelerated. As a result, I _Na was activated later but was more intense and lasted longer than in the centre of the disc. Thus, globally, the presence of a narrow cleft accelerated and increased I _Na in a self‐activating feedback mechanism. However, self‐attenuation still occurred. Consequently, peak total I _Na exhibited a biphasic behaviour with decreasing cleft width. For very narrow clefts, peak I _Na declined because of increasing self‐attenuation.

In conclusion, the dynamics were different at V _step = −25 mV and V _step = −50 mV. At −25 mV, decreasing cleft width caused a monotonic decrease of peak total I _Na, whereas at −50 mV, decreasing cleft width first caused an increase, followed by a decrease.

These dynamics can be further understood by examining the minimum of V _e as a function of cleft width (Fig. 1 D). At V _step = −25 mV, minimal V _e decreased progressively with cleft width. However, at V _step = −50 mV, V _e remained in the range of only a few millivolts for cleft widths ≥90 nm, and became abruptly negative only when cleft width was <80 nm (arrow in Fig. 1 D). This abrupt behaviour is explained by the fact that the self‐activating positive feedback mechanism described above appears only with sufficiently narrow clefts.

Fig. 1 E shows the relationships between peak total I _Na and V _step (I–V curves) for various cleft widths and corresponding steady‐state activation curves, which were reconstructed in the same way as patch clamp data. When total I _Na was considered, the self‐attenuating mechanism described above reduced peak I _Na (in absolute value) for potentials ≥20 mV more positive than the midpoint of activation of the control I–V curve without a cleft. Conversely, for potentials ≥10 mV more negative than this midpoint, peak I _Na was larger due to self‐activation. As for steady‐state activation curves, a narrow cleft caused a shift to more negative potentials and a steepening of the voltage dependence of activation.

Ephaptic effects are modulated by cleft width and size, cleft geometry and Na⁺ channel density

In intact myocardium, myocyte width and thus intercalated disc size varies between species and individual cells, and can be affected by certain conditions (e.g. hypertrophy). Moreover, the expression of Na⁺ channels within the disc and the proportion of Na⁺ channels located in disc membranes may also vary between cells. In the patch clamp experiments that we conducted, the Na⁺ channel expression in HEK cells and the contact area with the unexcitable obstacle varies as well. Therefore, we explored how differences in cleft size and geometry and the Na⁺ channel density in the membrane facing the restricted extracellular space would affect I _Na. We conducted simulations with the same model as in the previous section and varied the radius of the disc‐shaped membrane, the Na⁺ channel density (by varying F_{g Na}) and the width of the cleft. The Na⁺ channel distribution was kept uniform. In addition, we investigated the effect of changing the shape of the cleft from a disc to an elongated ellipse. This geometry mimics that of intercellular contacts in monolayer cultures of cardiomyocytes, where the length of the contact is several times larger than the thickness of the cultured cells (Jousset et al. 2016).

Fig. 2 A represents normalized peak total I _Na during an activation step from −85 to −25 mV and −50 mV as a function of cleft width for different F_{g Na} (1, 5.05 and 10.09, columns in Fig. 2 A). In each plot, normalized peak I _Na is represented for various disc‐shaped cleft radii (11, 7, 5.5 and 2.75 μm) as well as for an ellipse‐shaped cleft (semi‐major axis: 11 μm; semi‐minor axis: 2.75 μm). Peak I _Na was normalized to peak I _Na in the absence of a cleft. Values <1 signify that the absolute value of peak I _Na is smaller when the membrane is exposed to a cleft, which implies self‐attenuation, while values >1 imply self‐activation.

Figure 2. Effects of cleft size, cleft geometry and Na⁺ channel density on peak I _Na and V _e for a membrane separated from a non‐conducting obstacle by an extracellular cleft (uniform distribution of g _Na).

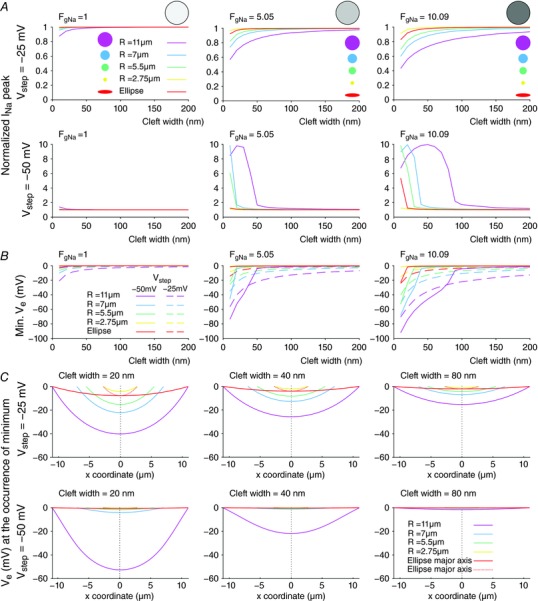
A, peak I _Na (normalized by peak I _Na in the absence of a cleft) as a function of cleft width for different disc‐shaped clefts (radii: see colour legend) and an elliptic cleft (semi‐major axis: 11 μm, semi‐minor axis: 2.75 μm), at V _step = −25 mV (top) and −50 mV (bottom), for F_{g Na} = 1 (left), F_{g Na} = 5.05 (middle) and F_{g Na} = 10.09 (right). B, corresponding minimal V _e (dashed lines: V _step = −25 mV; continuous lines: V _step = −50 mV). C, corresponding spatial profiles of V _e along the cleft diameter (or major/minor axis) at the occurrence of the minimum, for F_{g Na} = 5.05, at V _step = −25 mV (top) and −50 mV (bottom), and for cleft widths of 20 nm (left), 40 nm (middle) and 80 nm (right).

At V _step = −25 mV and F_{g Na} = 1, normalized peak I _Na was close to or just below 1 for all cleft geometries and cleft widths, indicating that peak I _Na was comparable to peak I _Na in the absence of a cleft. However, when F_{g Na} was increased to 5.05, normalized peak I _Na decreased to <1 for narrow clefts and decreased further as disc radius was increased. For the elliptic cleft, the behaviour of normalized peak I _Na resembled that with the disc‐shaped cleft with a radius of 2.75 μm. When F_{g Na} was further increased to 10.09, these observations were accentuated. These results indicate that increasing Na⁺ channel density decreases peak I _Na, indicating stronger self‐attenuation, in particular for narrow cleft widths. Additionally, peak I _Na clearly depends on the size of the cleft: the larger the cleft, the more negative peak I _Na is, and the more prominent self‐attenuation.

At V _step = −50 mV and for F_{g Na} = 1, normalized peak I _Na was close to or just above 1 for all cleft geometries and all cleft widths, indicating that peak I _Na was comparable to peak I _Na in the absence of a cleft. When F_{g Na} was increased to 5.05, normalized peak I _Na became >>1 for narrow clefts (≤50 nm). This increase was most notable for the largest cleft (R _disc = 11 μm). Increasing F_{g Na} further to 10.09 reinforced this effect. This indicates that increasing Na⁺ channel density in the cleft membrane potentiates the self‐activation of Na⁺ channels in narrow clefts. Similar to simulations with V _step = −25 mV, peak I _Na depended on cleft size at V _step = −50 mV, with larger clefts leading to more prominent self‐activation. Interestingly, the relationship between normalized peak I _Na and cleft width was highly non‐linear and biphasic: when cleft width was decreased, the onset of strong self‐activation depended jointly on Na⁺ channel density and cleft diameter. The behaviour of peak I _Na in the situation of the ellipse‐shaped cleft was closest to that for the disc‐shaped cleft with the same radius as its semi‐minor axis (2.75 μm).

The dependence of peak I _Na on Na⁺ channel density (F_{g Na}) can be understood by examining the minimal V _e that occurs in the cleft as a function of cleft width, F_{g Na}, and disc geometry for V _step = −25 and −50 mV, as shown in Fig. 2 B. The left plot of Fig. 2 B (F_{g Na} = 1) shows that, for V _step = −25 mV, the minimal V _e was very close to 0. Even for very small widths and large disc‐shaped clefts, V _e reached −20 mV. This V _e was not negative enough to decrease the driving force of I _Na and to cause any substantial self‐attenuation. For V _step = −50 mV, V _e did not decrease below −2 mV and, consequently, self‐activation was minimal. However, when F_{g Na} was set to 5.05 (middle plot), the negative V _e reached very negative values (up to −80 mV for R _disc = 11 μm) for both voltage steps. A further increase of F_{g Na} to 10.09 (right plot) resulted in even more negative V _e that exceeded several tens of millivolts for cleft widths <100 nm, which then led to substantial self‐activation and self‐attenuation, as reflected in Fig. 2 A.

While the dependence of self‐activation and self‐attenuation on Na⁺ channel density is relatively straightforward to understand, the modulation of I _Na by cleft size and geometry is more challenging. This challenge arises from the fact that V _e is not spatially uniform in the cleft, as illustrated in Fig. 2 C. This panel represents the spatial profiles of V _e (when the minimum V _e occurs) for F_{g Na} = 5.05, corresponding to the simulations shown in the middle plots in Fig. 2 A and B, for cleft widths of 20, 40 and 80 nm.

For disc‐shaped clefts, the spatial V _e profiles were similar (symmetric and concave) and had a similar gradient in the periphery, especially for V _step = −25 mV. Consequently, the minimal and average V _e was larger (in absolute value) for larger discs. This larger V _e can also be explained by the fact that the radial current in the cleft had to cover a larger distance. Due to the associated larger resistance, the potential difference increased, leading to stronger self‐activation and self‐attenuation as shown in Fig. 2 A. When cleft width was increased from 20 to 40 and 80 nm, V _e and its gradient decreased (in absolute value). This can be explained by the lower radial resistance of the extracellular cleft. These results show that large disc radii and narrow clefts both favour ephaptic interactions, considering the large negative V _e values.

For ellipse‐shaped clefts, the spatial profile of V _e depends on its direction (along the minor or major axis). Along the minor axis, the profile resembled that of small disc‐shaped clefts. This indicates that, for ellipse‐shaped clefts, the minimal V _e is essentially determined by the semi‐minor axis, i.e. by the shortest path (of lowest resistance) to the periphery of the cleft.

Restricting the extracellular space in patch clamp experiments reveals self‐attenuation and self‐activation of the Na⁺ current

To demonstrate self‐attenuation and self‐activation experimentally, we conducted patch clamp recordings of I _Na in HEK cells stably expressing human cardiac voltage‐gated Na_v1.5 channels. Cells were detached from the growth substrate and approached towards a non‐conducting obstacle to narrow the extracellular space near these cells, as illustrated in Fig. 3 A. In Fig. 3 B, I _Na traces of one representative cell are shown during an activation step far above activation threshold (left plot) and near the threshold (right plot). In each plot, three traces represent I _Na in the detached cell, the cell approached to the obstacle, and the cell subsequently moved away, respectively. For the step far above threshold, peak I _Na slightly decreased (in absolute value) when the cell was approached to the obstacle, and increased again when the cell was moved away. Thus, restricting the extracellular space near a portion of the membrane reversibly attenuated I _Na, as predicted by the simulations. This indicates self‐attenuation of Na⁺ channels. In contrast, for the voltage step near the activation threshold, approaching the cell to the obstacle led to an increase in peak I _Na, which receded again when the cell was moved away. Restricting the extracellular space thus reversibly increased I _Na in agreement with the simulations, indicating self‐activation. These effects on the total I _Na of the cell were small, most likely because only a small fraction of the membrane was facing the obstacle.

Figure 3. Experimental evidence of ephaptic effects in patch clamped HEK cells.

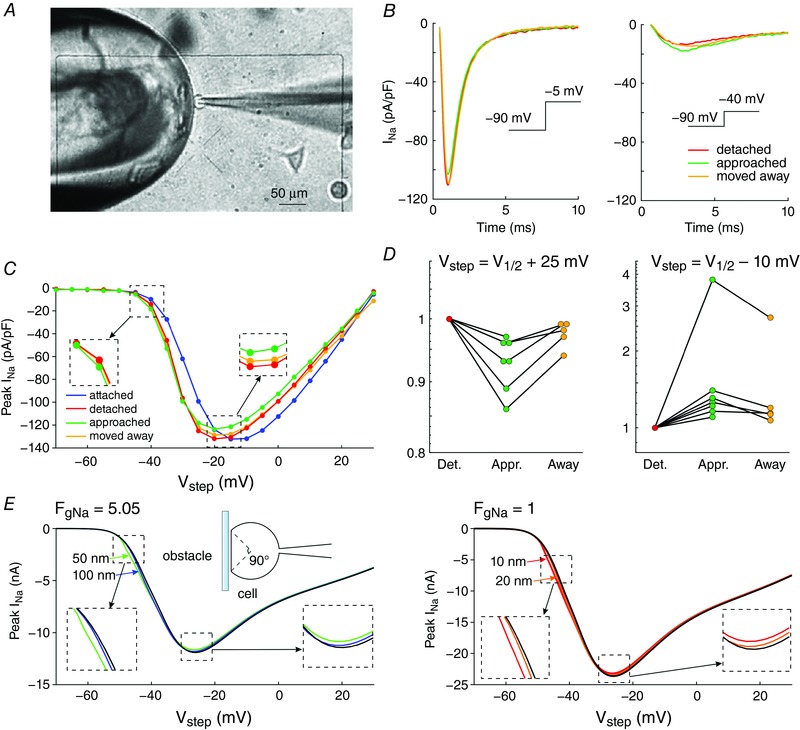
A, phase‐contrast microphotograph of a patch clamped HEK cell (pipette visible on the right) detached from its growth substrate and approached to a non‐conducting glass obstacle (left). B, I _Na recorded from the same cell during an activation step to −5 mV (far above threshold, left) and to −40 mV (near the activation threshold, right) under the following conditions; detached cell (red), cell approached to the obstacle (green) and cell subsequently moved away (yellow). C, I–V curves of the same cell under these three conditions as well as for the cell still attached to the growth substrate (blue). Insets illustrate the I–V curves near and far above the threshold. D, peak I _Na recorded in cells (n = 7) approached to the obstacle and in cells subsequently moved away normalized by corresponding peak I _Na in the detached cells before approaching them to the obstacle, for an activation step far above threshold (to V _1/2 = +25 mV, left) and near the activation threshold (to V _1/2 = −10 mV, right). Note the logarithmic scales. Lines connect measurements in the same cell. E, simulated I–V curves (V _step increments of 1 mV) using an F_{g Na} of 5.05 and cleft widths of 50 and 100 nm (left) and an F_{g Na} of 1 and cleft widths of 10 and 20 nm (right), assuming that the contact with the obstacle is subtended by an angle of 90° from the cell centre (schematic). R _disc = 11 μm. Insets illustrate the I–V curves near and far above the threshold.

In a series of experiments with 7 cells, a voltage clamp activation protocol was conducted on each cell that was subsequently attached, detached, approached to the obstacle, and moved away. I–V curves are shown in Fig. 3 C for one cell (same cell as in Fig. 3 B) under these four conditions. Of note, detaching the cell resulted in a shift of the I–V relationship towards more negative potentials. The cause of this shift is unclear. Possibly, the detachment of the cell and its subsequent change of shape from flat to spherical caused a remodelling of the cytoskeleton that, as shown in previous work (Dybkova et al. 2014), may affect the dynamics of Na⁺ channels. However, concerning ephaptic interactions, only experiments with the detached spherical cell are pertinent. A close‐up of the corresponding I–V curves (insets in Fig. 3 B) reveals that for potentials near −20 mV and above, peak I _Na was reversibly decreased when the cell was approached to the obstacle, which is compatible with ephaptic self‐attenuation. Conversely, for potentials near −35 mV, approaching the cell to the obstacle reversibly increased peak I _Na. These results strongly suggest ephaptic self‐activation of I _Na in the membrane in close proximity to the obstacle.

Fig. 3 D presents the analysis of these changes of peak I _Na in all 7 cells for a voltage step far above or near threshold. Because the half‐activation potential (V _1/2) varies between cells, these two voltage steps were determined relative to the V _1/2 of each individual cell as V _1/2 +25 mV and V _1/2 −10 mV, respectively (which were rounded to the next integer multiple of the voltage step increment of 5 mV). For these two voltage steps, Fig. 3 D depicts peak I _Na in the cells approached to the obstacle and in the cells subsequently moved away, normalized by corresponding peak I _Na in the detached cells before approaching them to the obstacle. For voltage steps far above threshold, close proximity to the obstacle decreased peak I _Na in all cells (values <1). In contrast, for voltage steps near the threshold, the proximity of the obstacle increased peak I _Na in all cells (values >1). Thus, changes suggesting ephaptic self‐attenuation and self‐activation were reproducibly observed in all 7 cells (P = 0.0156, Wilcoxon signed‐rank test). Detailed data of each individual cell are presented in the Appendix. These effects were reversible in 5 out of 5 cells (in the remaining two cells, the membrane seal was lost before the last steady‐state activation protocol could be completed). Although the magnitude of these effects greatly varied between cells, the results are in line with the computer simulations and support the hypothesis of ephaptic interactions between V _e and I _Na in a narrow extracellular space.

Fig. 3 E shows simulated I–V curves that consider the fact that only a small fraction of the membrane was facing the obstacle in the experiments. Assuming that the cells were spherical and that the contact with the obstacle was subtended by an angle of 90° as viewed from the cell centre, the relative areas of the membrane facing the obstacle and exposed to the bulk of the bath can be estimated to be 13% and 87%, respectively. Total I _Na was therefore simulated as a corresponding linear combination of I _Na in the presence and in the absence of the cleft. In HEK cells, I _Na density was variable from cell to cell but corresponded to values of F_{g Na} between 1 and 5. Corresponding I–V curves were therefore constructed for an F_{g Na} of 5.05 and 1 (Fig. 3 E). A good agreement with experimentally observed I–V curves (see Fig. 3 C) was obtained with 50‐ to 100‐nm‐wide clefts and F_{g Na} = 5.05, as well as with 10‐ to 20‐nm‐wide clefts and F_{g Na} = 1.

The spatial distribution of Na⁺ channels strongly affects ephaptic interactions

The simulations presented so far considered a homogeneous distribution of Na⁺ channels in the disc membrane. However, recent histological studies have shown that Na⁺ channels form clusters in intercalated discs (Rhett et al. 2013; Veeraraghavan et al. 2015; Leo‐Macias et al. 2016). The consequences of such Na⁺ channel clustering cannot be investigated using HEK cells, because the distribution of Na⁺ channels over their surface cannot be controlled and is presumably uniform.

Therefore, we took advantage of our high‐resolution model and the finite element method to explore the consequences of such channel clusters on ephaptic interactions. To simulate predefined spatial patterns of clusters, we modified the Na⁺ conductance in predefined regions of the disc without changing the total Na⁺ conductance of the disc membrane. This approach thus simulates a redistribution of the channels without changing the total number of channels (the total Na⁺ conductance is given by F_{g Na}).

We first investigated the effect of aggregating Na⁺ channels in one central cluster with a progressively decreasing radius (0.5, 0.25 and 0.125 times the disc radius R _disc), and compared the results with those obtained with a homogenous distribution (i.e. one cluster with a radius equal to R _disc (11 μm)), as shown in Fig. 4 A. For V _step = −25 mV and narrow clefts, peak I _Na decreased when the cluster size decreased, even with a low density of Na⁺ channels (F_{g Na} = 1). For an F_{g Na} of 5.05, the decrease in peak I _Na was even stronger. This indicates that self‐attenuation was stronger in the presence of smaller clusters of Na⁺ channels. Conversely, for V _step = −50 mV, peak I _Na increased when the cluster size was decreased. This increase was accentuated when F_{g Na} was also increased. Moreover, as cluster size decreased, peak I _Na increased over a larger range of cleft widths. Thus, self‐activation was stronger with smaller clusters. These stronger effects were due to a more negative minimal V _e when the channels were arranged in the centre of the disc in a cluster of decreasing size, even with F_{g Na} = 1. Fig. 4 B explains why the ephaptic effects were stronger for a small cluster by illustrating the spatial profiles of V _e at the occurrence of the respective V _e minima. For the uniform Na⁺ channel distribution, the profile of V _e was broad and concave. In contrast, for the Na⁺ channel clusters, the V _e profiles appeared narrower and deeper (for both voltage steps), and curvatures were different outside of the cluster. Fig. 4 C shows that the spatial profile was hyperboloid‐like outside the cluster region, while, for a uniform Na⁺ channel distribution, the profile was paraboloid‐like (Fig. 1 C). These hyperboloid‐like profiles can be explained by a strongly increasing density of radial cleft current near the current sink (the Na⁺ channel cluster viewed from the extracellular space) and the absence of any sink outside the cluster region. Thus, concentrating the sink into a smaller region resulted in a more negative V _e in that specific location.

Figure 4. Effects of Na⁺ channel clustering on ephaptic interactions in a disc‐shaped membrane (R _disc = 11 μm) separated from a non‐conducting obstacle by an extracellular cleft.

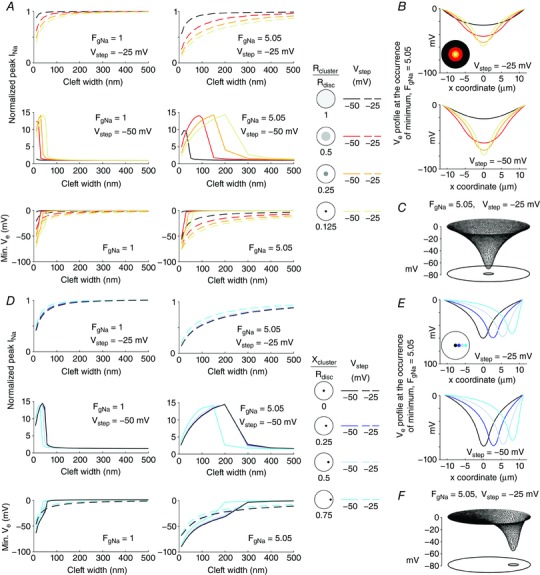
A, top and middle: peak I _Na (normalized by peak I _Na in the absence of a cleft) as a function of cleft width for V _step = −25 mV (top) and −50 mV (middle). Data are shown for different Na⁺ channel cluster sizes (cluster radius 1× (control uniform distribution), 0.5×, 0.25× and 0.125× that of R _disc, as shown on the right) with F_{g Na} = 1 (left) and F_{g Na} = 5.05 (right). A, bottom: corresponding minimal V _e as a function of cleft width for V _step = −25 mV (dashed lines) and V _step = −50 mV (continuous lines) for F_{g Na} = 1 (left) and F_{g Na} = 5.05 (right). B, spatial V _e profiles along the disc diameter (x‐coordinate) at the occurrence of the minimum (F_{g Na} = 5.05; cleft width: 40 nm), for different concentric Na⁺ channel cluster sizes (as in A), for V _step = −25 mV (top) and −50 mV (bottom). C, mesh of V _e at the occurrence of the minimum for a cleft width of 40 nm, a V _step to 25 mV, and an F_{g Na} of 5.05, for a central cluster having a radius of 0.125·R _disc. D, same as A, but for a Na⁺ channel cluster with a radius 0.125× that of the disc membrane positioned at increasing distances from the centre (ratio of the x‐coordinate of the cluster centre (x _cluster) to R _disc, legend on the right). E, same as B, but for different positions of a small cluster with a radius of 0.125·R _disc (as in D). F, same as C, but for a cluster (radius: 0.125·R _disc) shifted towards the periphery (x _cluster: 0.75·R _disc).

Movies S3 and S4 in Supporting information show V _e, I _Na density and gating parameters for a central cluster with a radius of 0.125·R _disc for a V _step to −25 and −50 mV, respectively (F_{g Na} = 5.05, 40‐nm‐wide cleft). These movies show that the time course of the gating variables (which were also computed outside the cluster where they did not generate any I _Na) was spatially heterogeneous, especially at a V _step to −50 mV (Movie S4), where m ³ remained near 0 and the product hj near 1 in the periphery but approached respectively 1 and 0 in the cluster. This heterogeneous evolution of gating parameters was due to the particular shape of the spatial profile of V _e (Fig. 4 C).

Next, in Fig. 4 D, we examined the effect of displacing a small cluster of Na⁺ channels towards the periphery. For V _step = −25 mV and for narrow cleft widths, the decrease in I _Na became less prominent when the cluster was moved towards the disc periphery, with F_{g Na} values of both 1 and 5.05. This reflects that self‐attenuation was strongest when the cluster was in the centre and decreased when the cluster was moved towards the periphery. Conversely, for V _step = −50 mV, peak I _Na became smaller (in absolute value) when the cluster was moved further from the centre, which indicates that self‐activation was the strongest for a centred cluster. With a cluster positioned at or near the centre of the disc, peak I _Na was also increased over a larger range of cleft widths. Similar to the situation of decreasing cluster size (Fig. 4 A), these stronger ephaptic interactions were due to an increasingly more negative minimal V _e when the cluster was more central, for both F_{g Na} values. Corresponding spatial V _e profiles are shown in Fig. 4 E and F. Moving the cluster towards the periphery skewed the V _e profile and rendered it asymmetric, while decreasing its minimum (in absolute value). This decrease was due to the shorter distance between the cluster and the edge of the disc, and thus to the presence of a path with a lower resistance for the radial current in the cleft.

These results show that V _e strongly depends on the spatial distribution of Na⁺ channels. Therefore, ephaptic effects are enhanced when Na⁺ channels are aggregated into a cluster, and this enhancement is most prominent for small and central clusters.

The activation of the Na⁺ current in an adjacent membrane depends on Na⁺ channel cluster size and relative position

To examine ephaptic interactions between two membranes that represent an intercalated disc, and to investigate the consequences of Na⁺ channel clustering on these interactions, we integrated a second excitable membrane in our computer model. The corresponding electric circuit is represented in Fig. 5 A. A voltage clamp activation protocol was applied on the intracellular side of the first membrane, while the potential on the intracellular side of the second membrane was held at the resting potential of −85 mV. In both membranes, two central Na⁺ channel clusters with predefined radii were incorporated (Fig. 5 A, right) and the behaviour of I _Na and V _e was compared to that obtained with a uniform Na⁺ channel distribution in both membranes. Note that no gap junctions were incorporated at this stage.

Figure 5. Effects of Na⁺ channel cluster size on I _Na and V _e in two membranes separated by a narrow cleft (R _disc = 11 μm).

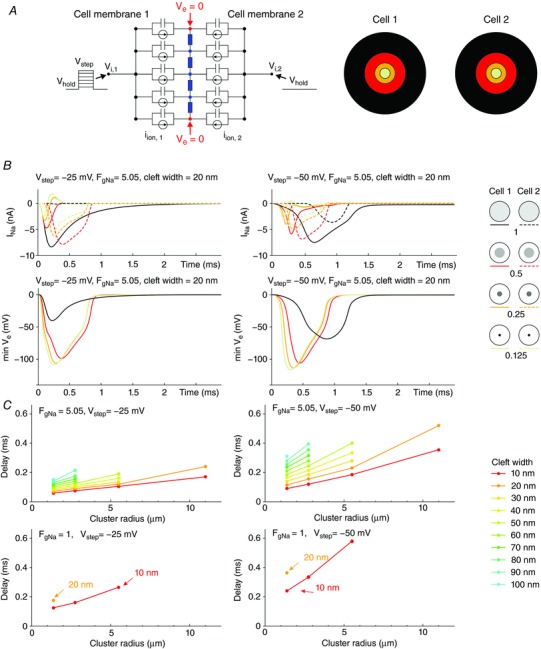
A, left: schematic of the two‐membrane model with membrane capacitance, ion currents and extracellular resistive properties. A, right: schematic of the two membranes, each containing a central cluster of a given radius (1x (control uniform distribution), 0.5×, 0.25× and 0.125× that of R _disc). B, top: total I _Na in membrane 1 (continuous lines) and membrane 2 (dashed lines) as a function of time, for different cluster radii (righthand legend) and a 20‐nm‐wide cleft, for a V _step to −25 mV (left) and −50 mV (right). B, bottom: corresponding time courses of minimal V _e for a V _step to −25 mV (left) and −50 mV (right). F_{g Na} = 5.05. C, delay between the onset of total I _Na in the two membranes as a function of cluster radius for different cleft widths (righthand legend), for a V _step to −25 mV (left) and −50 mV (right) and F_{g Na} = 5.05 (top) and F_{g Na} = 1 (bottom).

Fig. 5 B shows I _Na flowing through the two membranes for a 20‐nm‐wide cleft and an F_{g Na} of 5.05. Even though the intracellular side of the second membrane was clamped at −85 mV, the negative V _e, caused by the activation of I _Na in the first membrane, led to the activation of I _Na in the second membrane. This did not occur when Na⁺ channels were distributed uniformly at V _step = −25 mV. Smaller clusters led to shorter latencies of I _Na activation in the second membrane. Because the intracellular side of the second membrane was held at −85 mV, V _e reached very negative values when I _Na was activated there. Interestingly, with small Na⁺ channel clusters, these very negative V _e values resulted in a transiently positive driving force for I _Na in the first membrane, where it produced a net outward I _Na current.

The response of the second membrane and the delay between the onsets of I _Na in the two membranes is quantified in Fig. 5 C. For the two membranes, the onset of I _Na was defined by the time at which total I _Na passed a predefined threshold set to 0.25% of the total I _Na that would be generated if all channels were open. Fig. 5 C reports the delay between these onsets (absent data points or curves indicate that I _Na in the second membrane was not activated). For F_{g Na} = 5.05 (assuming that 50% of Na⁺ channels are in the intercalated disc), smaller clusters and narrower clefts resulted in shorter delays. Moreover, the range of cleft widths that allowed activation of I _Na in the second membrane was broader for smaller clusters. For large clusters and/or wide clefts, I _Na was not activated in the second membrane. These relationships were observed for both voltage steps to −25 and −50 mV. When F_{g Na} was set to 1 (assuming that Na⁺ channels are distributed uniformly over the entire surface of cardiomyocytes), the range of cleft widths and cluster radii permitting I _Na activation in the second membrane was considerably decreased: ephaptic activation occurred only for cleft widths of 10 and 20 nm.

We next examined the effect of changing the distance between the Na⁺ channel clusters in the two membranes such that the clusters are no longer facing each other. Fig. 6 A illustrates simulations in which one cluster (diameter: 1.375 μm = 0.125·R _disc) was incorporated in each membrane and the cluster centres were progressively moved away from the disc centre in opposite directions. For both step potentials, ephaptic activation of I _Na in the second membrane occurred only when the two clusters were co‐located or in close proximity (Movies S5 and S6) but not with separations between cluster centres ≥5.5 μm. I _Na activation in the second membrane caused a large additional negative deflection of V _e. This more prominently negative V _e is also visible in the spatial profiles of V _e. When I _Na was activated only in the first membrane, the site of the most negative V _e co‐located with the cluster in the first membrane. However, when I _Na was also activated in the second membrane, the site of the most negative V _e co‐located with the cluster in the second membrane. Interestingly, with clusters just in contact (distance between centres: 2.75 μm), total I _Na in the second membrane was smaller and V _e was more negative than with clusters facing each other.

Figure 6. Effects of relative Na⁺ channel cluster position on I _Na and V _e in two membranes separated by a narrow cleft (R _disc = 11 μm).

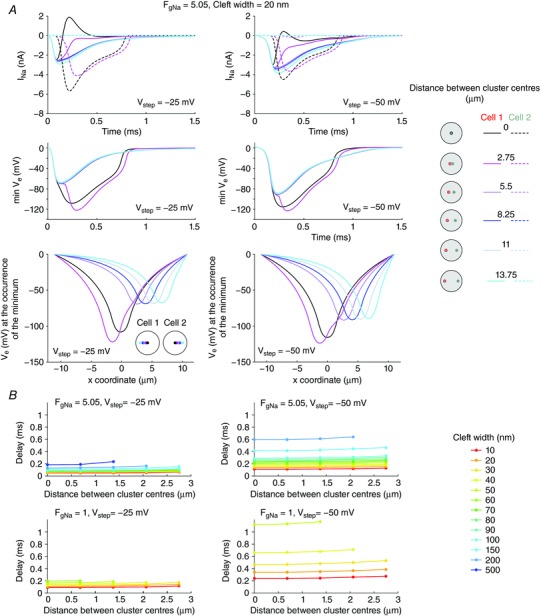
A, top: total I _Na in membrane 1 (continuous lines) and 2 (dashed lines) as a function of time for different relative positions of the clusters in the two membranes (see righthand legend; cluster radii: 1.375 μm; F_{g Na} = 5.05; cleft width: 20 nm), for a V _step to −25 mV (left) and−50 mV (right). A, middle: corresponding time courses of minimal V _e. A, bottom: corresponding spatial V _e profiles along the disc diameter at the time of occurrence of the minimal V _e. B, delay between the onset of total I _Na in the two membranes as a function of the distance between the cluster centres, for different cleft widths (legend), for a V _step to −25 mV (left) and −50 mV (right) and F_{g Na} = 5.05 (top) and F_{g Na} = 1 (bottom).

The delay between the onsets of I _Na in the two membranes (computed as in Fig. 5 B) is shown in Fig. 6 B. For both voltage steps and for both F_{g Na}, smaller distances between the clusters resulted in slightly shorter delays. However, the distance between clusters mostly determined the range of cleft widths allowing the activation of I _Na in the second membrane. For large distances between clusters and/or wide clefts, I _Na was not activated in the second membrane.

Thus, activation of I _Na in a second membrane is possible even when its intracellular potential is clamped at its resting value. Importantly, these results indicate that not only the density of Na⁺ channels but also the spatial distribution of the channels greatly influences ephaptic I _Na activation. This effect is potentiated by small central clusters and is optimal when the clusters in the two membranes face each other.

The distribution of Na⁺ channels modulates ephaptic interactions and action potential transfer between two cells coupled by a gap junctional resistance

In real cardiac tissue, cells are connected via gap junctions. Therefore, we adapted the model to investigate the interaction between ephaptic and gap junctional coupling during action potential transfer, and investigated how this transfer is influenced by the spatial distribution of Na⁺ channels. As illustrated in Fig. 7 A, we included a gap junctional resistance connecting the intracellular space of the two cells. In addition, we added on both sides of the intercalated disc an excitable element representing the bulk membranes of the cells (100 μm long cylinders with a radius of 11 μm). This arrangement permitted simulations of the potentials of the intracellular nodes under current clamp conditions. Numerically, this was done by considering the two intracellular potentials as additional variables and by adding two rows/columns constructed in accordance with charge conservation (Kirchhof current law) to the matrices K and M (see Methods). To elicit an action potential in the first cell, a rectangular current pulse was applied. The cleft width was 30 nm and an F_{g Na} of 5.05 was used. Gap junctional coupling was varied from a normal level of 100% (1.5 Ω·cm²; Shaw & Rudy, 1997) to 0%.

Figure 7. Interactions between ephaptic and gap junctional coupling between two cells.

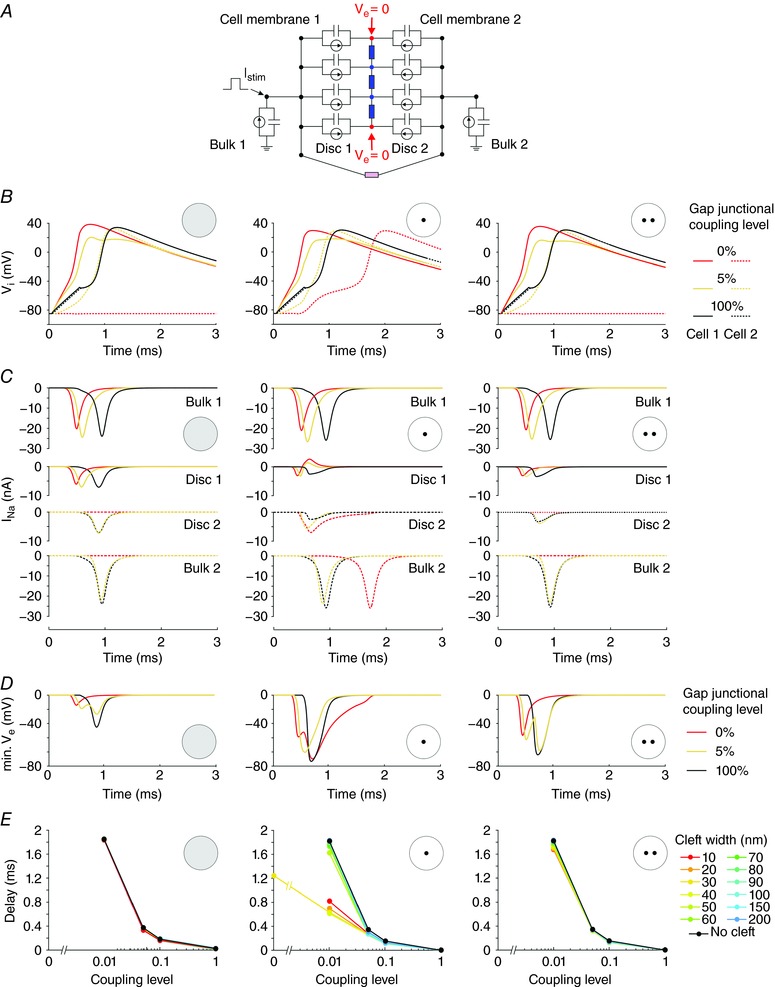
A, schematic representation of the 2‐cell model incorporating an intercalated disc (radius: 11 μm) and 2 disc membranes with membrane capacitance, ion currents and extracellular resistive properties (blue) and gap junctional resistance (pink). The discs were connected to elements representing the bulk membranes of the cells (100 μm long cylinders). The intracellular nodes were subjected to a current clamp protocol. The first cell was stimulated by a rectangular current pulse (duration: 0.5 ms; intensity: 11.5 nA). F_{g Na} = 5.05. Cleft width: 30 nm. B, intracellular potential as a function of time in cell 1 (continuous line) and cell 2 (dashed line) at different gap junctional coupling levels (100%, 5% and 0% of normal; righthand legend). Left: uniform Na⁺ channel distribution in both intercalated disc membranes. Middle: two aligned central Na⁺ channel clusters (R _cluster = 1.375 μm). Right: two misaligned Na⁺ channel clusters (R _cluster = 1.375 μm; distance between centres: 5.5 μm). C, corresponding I _Na through the bulk membrane of cell 1 (first row), the disc membrane of cell 1 (second row), the disc membrane of cell 2 (third row) and the bulk membrane of cell 2 (fourth row). D, corresponding minimal V _e. E, activation delay between the two cells as a function of gap junctional coupling level, for different cleft widths (legend) and for the three Na⁺ channel distributions.

Simulations were conducted for three scenarios: a uniform Na⁺ channel distribution in both intercalated disc membranes, two aligned central Na⁺ channel clusters, and two misaligned Na⁺ channel clusters. The corresponding intracellular potentials (V _i) are shown in Fig. 7 B for three levels of gap junctional coupling (100%, 5% and 0%). The corresponding I _Na in the bulk and disc membranes are shown in Fig. 7 C and the corresponding V _e in Fig. 7 D.

When the Na⁺ channels were uniformly distributed in the disc (first column), the second cell was not excited when the coupling level was 0 and ephaptic coupling alone was not sufficient to activate the second cell. Indeed, the V _e caused by the I _Na of the first disc was >−20 mV. The second cell was, however, excited at a coupling level of 5% after 0.4 ms (computed from the interval between the 0 mV crossings of the upstrokes). However, action potential transmission was essentially electrotonic because V _e caused by the I _Na of the first disc was also >−25 mV. At the normal coupling level, the cells were activated electrotonically and quasi‐synchronously due to the large coupling conductance. The very short delay was due to the absence of any electrotonic current load beyond the second cell. In contrast, when two aligned central Na⁺ channel clusters were simulated (second column), the second cell was activated by ephaptic interactions in the absence of coupling after 1.2 ms. Again, at a coupling level of 100%, action potential transfer was electrotonic and the upstrokes were almost synchronous. However, at a reduced but non‐zero level of coupling (5%), the aggregation of Na⁺ channels into central clusters facing each other led to ephaptic interactions that shortened the activation delay from 0.4 to 0.3 ms. This contribution of ephaptic interactions is witnessed by V _e reaching values <−50 mV and by the fact that I _Na in the second disc peaked before I _Na in the bulk membrane of the second cell. This I _Na in the second disc contributed to the depolarization of the bulk membrane of the second cell towards the threshold. When the clusters were misaligned (third column), these ephaptic interactions diminished. In the absence of gap junctional coupling, the second cell was no longer excited, and at a coupling level of 5%, the activation delay increased.

The effects of ephaptic coupling on the intercellular activation delay and the dependence of the delay on cleft width are summarized in Fig. 7 E. For the uniform Na⁺ channel distribution and for the case of misaligned clusters, ephaptic effects only slightly shortened this delay (almost superimposed curves). Action potential transfer was therefore essentially electrotonic. However, in the case of aligned clusters, ephaptic interactions in 10–30 nm clefts clearly shortened the delay for coupling levels ≤5%. These observations indicate that the distribution of Na⁺ channels greatly influences the ephaptic interactions and action potential transfer between two cells with a reduced gap junctional coupling.

Discussion

Although already proposed decades ago (Sperelakis & Mann, 1977), the existence of ephaptic interactions in the heart and the possibility of cardiac ephaptic conduction are still controversial. In this work, we report two findings that support ephaptic interactions. First, we used patch clamp experiments to demonstrate experimentally that ephaptic effects near a cell membrane containing human cardiac Na⁺ channels can modulate the Na⁺ current in a manner predicted by computer simulations. Second, using a new FEM model, we showed that the aggregation of Na⁺ channels into clusters greatly potentiates ephaptic effects, a finding which is important in the light of recent studies that demonstrate such Na⁺ channel clustering in intercalated discs (Leo‐Macias et al. 2016), notably in the perinexus (Rhett et al. 2013; Veeraraghavan et al. 2015).

In our patch clamp experiments with HEK cells expressing Na_v1.5 channels, we systematically observed that restricting the extracellular space near a part of the cell membrane causes two phenomena. At potentials far above the threshold, peak I _Na was decreased by this intervention (self‐attenuation), whereas at potentials near the threshold, peak I _Na was increased (self‐activation), in agreement with present and past simulation studies (Kucera et al. 2002; Tsumoto et al. 2011). These findings at the cellular level provide a proof‐of‐principle in favour of the existence of cardiac ephaptic effects.

Worth noting, the magnitude of these effects was characterized by a large intercellular variability. Here, it must first be noted that the level of Na⁺ channel expression also varied between cells (densities corresponding to F_{g Na} in the range 1–5). Second, we could not precisely control the size of the region in contact with the obstacle. Third, the width of the cleft was not known, and could also have been variable. As shown in Fig. 2, these three parameters jointly determine the magnitude of the effects on peak I _Na in a non‐linear manner. Thus, the variable magnitude of the ephaptic effects observed experimentally can be explained by the variability of these three parameters and the difficulty of controling them. Given the small sample size, these confounding factors represent a limitation of our study.

The simulations demonstrate that the spatial distribution of Na⁺ channels in two closely apposed excitable membranes exerts a crucial influence on ephaptic interactions. Specifically, our results indicate that Na⁺ channel clusters facing each other across the intercellular cleft potentiate ephaptic impulse transmission when intercellular coupling is reduced. This potentiation is due to the intricate spatiotemporal dynamic interactions between I _Na, V _e, and Na⁺ channel gating, as revealed by our high‐resolution modelling approach.

Ephaptic effects are spatially heterogeneous

Our simulations demonstrated that V _e in the cleft space varies as a function of position in the cleft. Even with a homogeneous distribution of Na⁺ channels, the changes in V _e were minimal near the junction of the cleft and the bulk extracellular space, and maximal near the centre of the cleft. This observation is in line with the previous results of Mori, Fishman and Peskin (Mori et al. 2008), who examined the spatial profiles of V _e in a model of ephaptic conduction assuming a radial symmetry of the cleft. Because of this spatially variable V _e, the effects of V _e on Na⁺ channel gating are not uniform but occur with different intensities and kinetics that depend on the position in the cleft, as visible in Fig. 1. Since V _e also directly determines the driving force of I _Na, the resulting spatial distribution of I _Na density is also influenced. Thus, an important finding of our study is that ephaptic effects (both self‐activation and self‐attenuation) are spatially heterogeneous.

Therefore, it appears logical that the spatiotemporal interaction between V _e, I _Na and channel gating is further determined by the distribution of Na⁺ channels. Changing this distribution directly influences the spatial pattern of V _e, rendering it more negative at locations with increased Na⁺ channel density. Consequently, because of the feedback of V _e on I _Na, the characteristic ephaptic interactions are potentiated at and near the cluster locations (Figs 4 and 5).

In addition, it should be considered that near Na⁺ channel clusters, extracellular [Na⁺] may transiently decrease while intracellular [Na⁺] may transiently increase due to I _Na. Both concentration changes are expected to decrease the Nernst potential of Na⁺ and thus to dampen self‐activation and to intensify self‐attenuation. In an ephaptic conduction model in which ion fluxes were represented using the Nernst‐Planck equation, Mori et al. (2008) reported a decrease of extracellular [Na⁺]. However, they observed that Na⁺ concentration changes play only a minor role, except for clefts narrower than 5 nm. Nevertheless, in the presence of Na⁺ channel clusters, the effects of extracellular Na⁺ depletion may be locally accentuated and become significant for wider clefts.

The physiological relevance of Na⁺ channel clusters and perinexi

Because V _e affects Na⁺ channel function on both sides of an intercellular cleft, ephaptic conduction across an intercalated disc is determined by the distribution of Na⁺ channels on both membranes. We found that ephaptic coupling is optimized by small Na⁺ channel clusters facing each other across the cleft space (Figs 6 and 7). This finding therefore strongly supports the notion that the localization of Na⁺ channels in the perinexus has a functional electrophysiological relevance, as proposed by Rhett and co‐workers (Rhett & Gourdie, 2012; Rhett et al. 2013). This notion is further supported by recent super‐resolution imaging studies of intercalated discs from adult myocardium demonstrating the presence of Na_v1.5 channel clusters adjacent to connexin 43 clusters (Veeraraghavan & Gourdie, 2016) and Na_v1.5 channels forming mixed clusters with N‐cadherin (Leo‐Macias et al. 2016). We therefore postulate that perinexi are privileged sites for ephaptic coupling in pathological situations where gap‐junctional coupling is decreased, e.g. consecutive to intracellular acidification and Ca²⁺ overload during ischaemia, or resulting from changes in connexin phosphorylation levels. Consequently, we suggest that any disease or clinical condition leading to a disruption of the perinexal arrangement of Na⁺ channels may have repercussions on cardiac conduction, considering that ephaptic conduction might act as a backup mechanism for AP propagation when gap‐junctional coupling is impaired.

While we did not examine the effects of spatially heterogeneous cleft widths and variations in extracellular resistivity due to adhesion proteins, we can nevertheless hypothesize that decreased conductivity in perinexal Na_v1.5 rich nanodomains with narrow clefts (Rhett et al. 2013) will additionally reinforce electrochemical transients and ephaptic interactions. Furthermore, the known heterogeneity in cleft width within the intercalated disc (Rhett et al. 2013; Veeraraghavan et al. 2015) raises the possibility that specific nanodomains within the intercalated disc constitute unitary structures for ephaptic coupling, somewhat similar to couplons in the context of excitation–contraction coupling (Asghari et al. 2012).

While the fact that Na⁺ channels form clusters in the intercalated disc is established (Leo‐Macias et al. 2016; Veeraraghavan & Gourdie, 2016), the detailed mechanisms of Na⁺ channel clustering in intercalated discs have not yet been fully elucidated. As shown in these studies, this clustering is likely to involve additional proteins such as N‐cadherin (Leo‐Macias et al. 2016), connexins (Veeraraghavan & Gourdie, 2016) and the formation of macromolecular complexes. However, these studies did not establish on what side of the intercalated disc these clusters were located. The question is therefore still open whether Na⁺ channels form clusters on corresponding face‐to‐face locations of the intercalated disc. Such co‐localization could occur even in regions remote from gap junction plaques, possibly facilitated by structural proteins.

Moreover, it is presently not known whether Na_v1.5 channels form clusters in the membranes of HEK cells. However, significant channel clustering seems unlikely because it is relatively straightforward to conduct single channel recordings in such cells (Tateyama et al. 2004). In simulations corresponding to HEK cells (Figs 1, 2, 3) we therefore considered a uniform distribution of Na⁺ channels. It is also not known whether α subunits cluster on their own or whether β subunits are required. We hope that further morphological studies will provide additional elements pertinent to the physiological role of Na⁺ channel distribution.

In the simulations, we did not consider tortuous intercalated disc shapes as observed in vivo (Leo‐Macias et al. 2015). Tortuosity is further expected to strengthen ephaptic effects by increasing the effective radial resistance of the cleft. We also assumed that the intracellular potential is spatially uniform. Therefore, it was not possible to assess the effects of different distributions of gap junctions. Such analysis would require the development of an explicit three‐dimensional modelling framework. All these considerations open prospects for further work.

Comparison with previous studies

To date, experimental studies aiming at proving or disproving cardiac ephaptic coupling are scarce. Suenson (1984) investigated interactions between two trabeculae or papillary muscles tightly apposed side by side and demonstrated that excitation of one preparation can induce the excitation of the other when the width of the extracellular solution layer was narrowed. However, in experiments with patch clamped isolated myocytes, Weingart & Maurer (1988) did not observe ephaptic impulse transmission when two isolated myocytes were gently brought in close lateral contact. At that time, the increased density of Na⁺ channels in intercalated discs was not yet known, and no experiments were conducted with cells brought in longitudinal contact. The insufficient density of Na⁺ channels in the lateral membranes may therefore explain the absence of ephaptic interactions in these experiments.

The involvement of ephaptic interactions in cardiac conduction was investigated in a series of studies combining optical mapping of impulse propagation in whole hearts by Poelzing's group and mathematical modelling of conduction with ephaptic interactions by Lin and Keener (Lin & Keener, 2010, 2013, 2014; George et al. 2015; Veeraraghavan et al. 2015, 2016). It was found that Na⁺ channel blockers, gap junctional uncouplers and changes in extracellular Na⁺ and K⁺ concentrations, in conjunction with interventions modifying the width of the intercellular space, exerted effects on conduction velocity and its anisotropy ratio that cannot be explained by electrotonic coupling alone, thus providing support for the involvement of ephaptic interactions in intact tissue.

In contrast, observations opposing ephaptic conduction were reported by Kléber's group, who investigated conduction in cultured strands of homozygous connexin 43 knock‐out murine ventricular myocytes (Beauchamp et al. 2004). These preparations exhibited very slow conduction (2.1 cm s⁻¹ vs. 52 cm s⁻¹ in wild‐type strands), which was attributed to a low level of connexin 45 expression. Exposing the knock‐out strands to the gap‐junctional uncoupler heptanol abolished conduction completely. However, it must be noted that according to our findings, the shape of intercellular contacts greatly influences ephaptic interactions. Fig. 2 shows that when the excitable disc is given an elongated shape, the magnitude of ephaptic effects is drastically reduced because they are essentially determined by the smallest dimension of this shape. The fact that cultured cardiomyocytes flatten on the growth substrate and assume a thickness of only a few micrometres (Jousset et al. 2016) therefore renders ephaptic conduction unlikely in such preparations. These considerations can explain the absence of ephaptic conduction in experiments with cultures of cardiomyocytes and suggest that such preparations are not an appropriate experimental model to study ephaptic impulse transmission.

Limitations

A question arises of why we did not compare I _Na in cells attached to the substrate to I _Na in detached cells, given the fact that in attached cells, the extracellular space between the cell and the substrate is also confined. However, detaching the cell involves a change in cell shape and thus a likely remodelling of the cytoskeletal architecture, which is known to influence the biophysical properties of I _Na (Dybkova et al. 2014). In addition, such a protocol would not permit us to examine whether changes in I _Na are reversible. For these reasons, we preferred to develop a protocol in which the change in cell shape is negligible and in which the extracellular space can be restricted rapidly and with minimal interference with the cell.

Beyder et al. (2010, 2012) have shown in HEK cells expressing Na_v1.5 channels that applying negative pressure to cell‐attached patches leads to an increase in I _Na. This mechanosensitivity of Na⁺ channels may have increased I _Na in our experiments when the cells were approached to the obstacle. However, such an increase would pertain to all depolarizing step potentials, both near threshold and far above threshold. The fact that we systematically observed a decrease in I _Na at potentials far above threshold indicates that another mechanism must have been involved. Although we did not observe any membrane deformation, we cannot fully exclude the possibility that at potentials near threshold, minor mechanical effects contributed to the increase in I _Na, in addition to ephaptic self‐activation.

Furthermore, because of the high computational expense of high‐resolution models, we did not investigate conduction in cell fibres but preferred to focus on resolving spatial features at the level of the single disc. Finally, we used a simplified membrane model incorporating only I _Na and a linear K⁺ current. Although this model did not take other currents or calcium dynamics into account, it offered the advantage of isolating the specific role of I _Na in ephaptic interactions without any confounding factors.

Conclusions

Our findings provide new insights into basic mechanisms of cardiac excitation and conduction and highlight the usefulness of the new mathematical model of the intercalated disc that we developed. By contributing to a greater understanding of the structure and function of the intercalated disc, our results may orient future experimental and modelling work to better encompass the conditions under which ephaptic interactions may influence cardiac electrical function in the healthy and diseased heart.

Additional information

Competing interests

The authors have no competing interests to disclose.

Author contributions

J.P.K. conceived and designed the study. E.H. conducted patch clamp experiments. J.P.K. and E.H. developed simulation code and conducted simulations. E.H. and J.P.K. analysed the data. H.A. provided advice and support in conducting the experiments and interpreting the data. E.H. and J.P.K. drafted the manuscript. All authors contributed to the interpretation of the data and to a critical review of the manuscript for important intellectual content. All authors approved the final version of the manuscript, agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved and all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by the Swiss National Science Foundation (grant number 31003A‐156738 to J.P.K.).

Translational perspective

Cardiac conduction disorders can result in arrhythmias, which are frequent and potentially life‐threatening complications of heart disease. Conduction relies on membrane depolarization by the sodium (Na⁺) current (I _Na) and on intercellular electrical coupling via gap junctions. Recent studies showed that Na⁺ channel density is high in intercalated discs and that Na⁺ channels aggregate near gap junctional plaques in regions called perinexi. These findings raised interest in another mechanism that could contribute to conduction, called ephaptic coupling. According to this mechanism, I _Na through the membrane on one side of the intercalated disc causes a substantial negative extracellular potential (V _e) in the narrow intercellular cleft. This negative V _e translates as membrane depolarization on the other side of the disc, where it contributes to Na⁺ channel activation and thus to conduction. However, ephaptic conduction is still controversial. We conducted proof‐of‐principle experiments with cells expressing human cardiac Na⁺ channels to demonstrate that cardiac I _Na is modulated by ephaptic interactions when the extracellular space is restricted. Using a high‐resolution model of the intercalated disc, we found that ephaptic impulse transmission from one cell to another is facilitated by clusters of Na⁺ channels facing each other across the intercellular cleft when gap junctional coupling is reduced. Our work contributes to the general understanding of cardiac excitation and indicates that perinexi are important functional elements for ephaptic coupling in pathological situations where gap junctional coupling is decreased. Conditions leading to a rearrangement of Na⁺ channels in intercalated discs may therefore have repercussions on cardiac conduction.

Supporting information

Disclaimer: Supporting information has been peer‐reviewed but not copyedited.

Movie S1. V _e, I _Na density, and products of activation gates m ³ and inactivation gates hj during a voltage step to −25 mV in the model of a disc‐shaped membrane (radius: 11 μm) separated from a non‐conducting obstacle by a 20‐nm cleft (uniform distribution of g _Na, F_{g Na} = 10.09).

Movie S2. V _e, I _Na density, and products of activation gates m ³ and inactivation gates hj during a voltage step to −50 mV in the model of a disc‐shaped membrane (radius: 11 μm) separated from a non‐conducting obstacle by a 20‐nm cleft (uniform distribution of g _Na, F_{g Na} = 10.09).

Movie S3. V _e, I _Na density, and products of activation gates m ³ and inactivation gates hj during a voltage step to −25 mV in the model of a disc‐shaped membrane (R _disc: 11 μm) separated from a non‐conducting obstacle by a 40‐nm cleft and containing a centred cluster of Na⁺ channels (F_{g Na} = 5.05; R _cluster = 0.125·R _disc).

Movie S4. V _e, I _Na density, and products of activation gates m ³ and inactivation gates hj during a voltage step to −50 mV in the model of a disc‐shaped membrane (R _disc: 11 μm) separated from a non‐conducting obstacle by a 40‐nm cleft and containing a centred cluster of Na⁺ channels (F_{g Na} = 5.05; R _cluster = 0.125·R _disc).

Movie S5. V _e, I _Na density in membranes 1 and 2 (I _Na1 and I _Na2), corresponding products of activation gates m ₁ ³ and m ₂ ³, and products of inactivation gates h₁j₁ and h₂j₂ during a voltage step to −25 mV in the model of 2 disc‐shaped membranes (R _disc: 11 μm) separated by a 20‐nm cleft (F_{g Na} = 5.05). Each membrane contains a cluster of Na⁺ channels outlined in red for cell 1 and green for cell 2 (R _cluster: 1.375 μm) and the distance between cluster centres is 2.75 μm.

Movie S6. V _e, I _Na density in membranes 1 and 2 (I _Na1 and I _Na2), corresponding products of activation gates m ₁ ³ and m ₂ ³, and products of inactivation gates h₁j₁ and h₂j₂ during a voltage step to −50 mV in the model of 2 disc‐shaped membranes (R _disc: 11 μm) separated by a 20‐nm cleft (F_{g Na} = 5.05). Each membrane contains a cluster of Na⁺ channels outlined in red for cell 1 and green for cell 2 (R _cluster: 1.375 μm) and the distance between cluster centres is 2.75 μm.

Appendix 1.

1. Sample set of Na⁺ currents recorded from one HEK293 cell detached from the growth substrate (raw currents and currents after P/4 processing)

Such a set of currents is shown in Fig. A1.

Figure A1. Currents recorded during an activation protocol from one HEK293 cell expressing Na_v1.5 channels detached from the growth substrate.

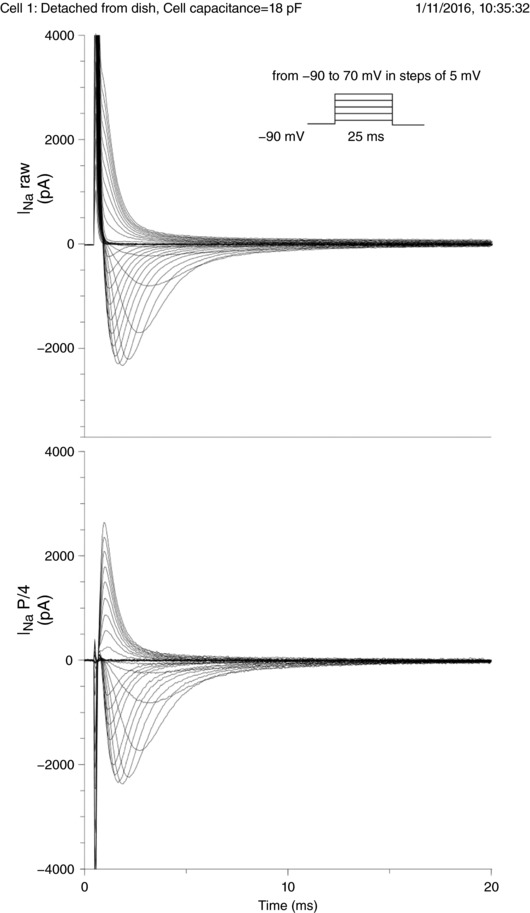
Top: raw currents. Bottom: currents after P/4 processing. Holding potential: −90 mV; step potentials: from −90 to +70 mV in increments of 5 mV.

2. Peak current–voltage (I–V) curves, Na⁺ currents (I _Na) at selected step potentials and analysis of peak I _Na for all 7 cells in the 4 different configurations investigated (attached to substrate, detached, approached to obstacle and moved away from obstacle)

In the following 7 sections, each section corresponds to one of the 7 cells for which the normalized peak I _Na is represented in Fig. 3 D in Results.

For every cell/experiment, the following data are reported:

• ‐Cell capacitance
• ‐Pipette and seal resistances
• ‐Remarks
• ‐ I–V curves (I _Na normalized to cell capacitance) for the 4 investigated configurations
• ‐Half‐activation potential (V _1/2) computed for the cell detached from the growth substrate
• ‐ I _Na traces at steps to V _1/2 = +25 mV and V _1/2 = −10 mV (dashed vertical lines in the I–V curve plots) rounded to the next integer multiple of 5 mV (vertical arrows)
• ‐Maximal peak I _Na density
• ‐Peak I _Na densities at V _1/2 = +25 mV and V _1/2 = −10 mV before normalization
• ‐Peak I _Na densities at V _1/2 = +25 mV and V _1/2 = −10 mV normalized by the corresponding peak I _Na density in the detached cell before approaching it to the obstacle. These are the data that are summarized in Fig. 3 D in Results.

The experiments are presented in chronological order.

Note that the seal resistance did not change during the experiments (the activation protocol was repeated only if the seal resistance did not change).

All experiments in which the activation protocol was successfully completed for at least the detached and approached configurations are presented and were considered for the summary analysis in Fig. 3 D in Results. No experiment was disregarded.

Cell 1 (01.11.2016, Fig. A2)

Figure A2.

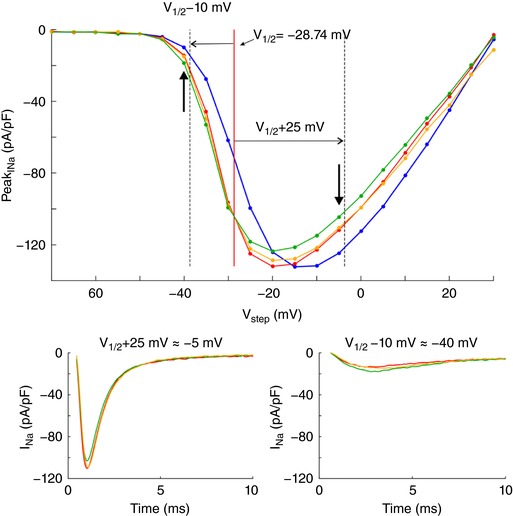
I–V curves and Na⁺ currents from cell 1.

• Cell capacitance (pF): 18.0

• Pipette resistance (MΩ): 2.5

• Seal resistance (GΩ): 1.1

• Remark: These are the data shown in Fig. 3 B and C. The raw I _Na is shown in Figure A1 for this cell.

• V _1/2 (detached configuration): −28.74 mV

• Maximal peak current density: −132.0 pA pF⁻¹ at −20 mV

Peak current densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−110.39	−13.59
Approached	−103.15	−17.89
Moved away	−109.3	−14.63
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.93	1.31
Moved away	0.99	1.07

Cell 2 (15.11.2016, Fig. A3)

Figure A3.

I–V curves and Na⁺ currents from cell 2.

• Cell capacitance (pF): 20.0

• Pipette resistance (MΩ): 1.9

• Seal resistance (GΩ): 3.4

• Remark: The pipette seal was lost before conducting the voltage clamp protocol in the cell moved away from the obstacle.

• V _1/2 (detached configuration): −27.24 mV

• Maximal peak current density: −147.9 pA pF⁻¹ at −15 mV

Peak currents densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−127.98	−34.82
Approached	−124.57	−38.54
Moved away	—	—
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.97	1.10
Moved away	—	—

Cell 3 (30.11.2016, Fig. A4)

Figure A4.

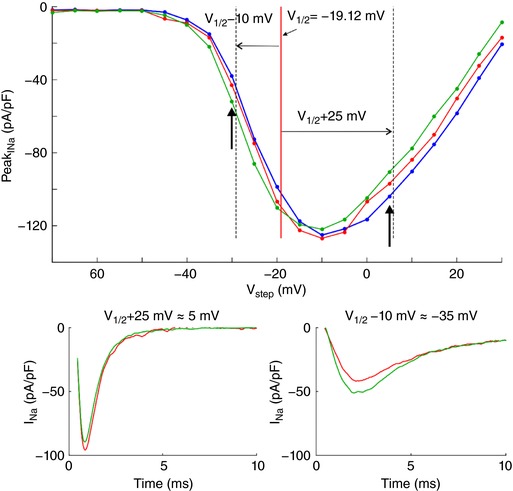
I–V curves and Na⁺ currents from cell 3.

• Cell capacitance (pF): 13.0

• Pipette resistance (MΩ): 2.3

• Seal resistance (GΩ): 6.0

• Remark: The pipette seal was lost before conducting the voltage clamp protocol in the cell moved away from the obstacle.

• V _1/2 (detached configuration): −19.12 mV

• Maximal peak current density: −126.9 pA pF⁻¹ at −10 mV

Peak currents densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−95.84	−41.82
Approached	−89.48	−51.13
Moved away	—	—
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.93	1.22
Moved away	—	—

Cell 4 (05.12.2016, Fig. A5)

Figure A5.

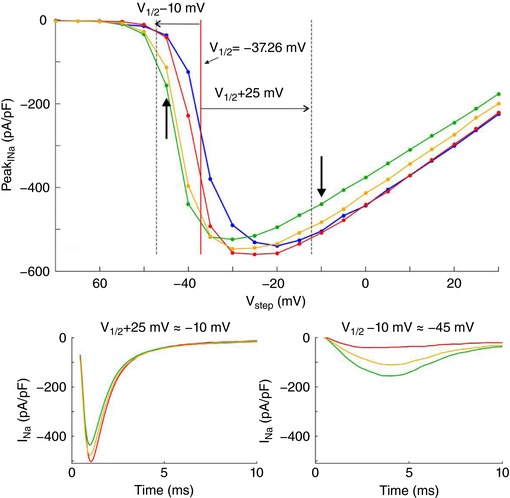
I–V curves and Na⁺ currents from cell 4.

• Cell capacitance (pF): 12.2

• Pipette resistance (MΩ): 2.3

• Seal resistance (GΩ): 2.0

• Remark: This cell had a particularly a large I _Na density.

• V _1/2 (detached configuration): −37.26 mV

• Maximal peak current density: −559.2 pA pF⁻¹ at −25 mV

Peak currents densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−503.41	−40.70
Approached	−435.46	−155.53
Moved away	−477.42	−110.79
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.86	3.82
Moved away	0.94	2.72

Cell 5 (07.03.2017, Fig. A6)

Figure A6.

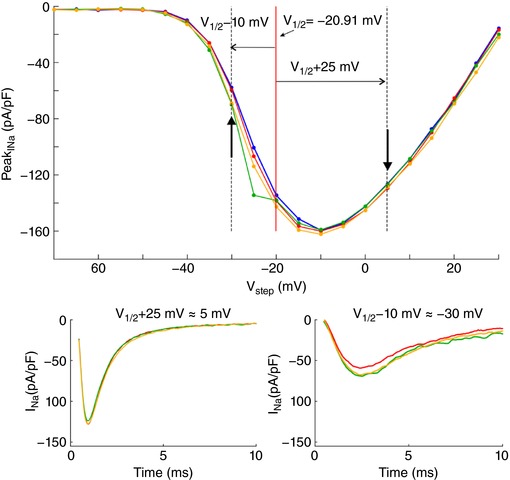
I–V curves and Na⁺ currents from cell 5.

• Cell capacitance (pF): 11.0

• Pipette resistance (MΩ): 2.3

• Seal resistance (GΩ): 1.4

• Remark: At V _step = −25 mV, when the cell was approached to the obstacle, a transient external perturbation artefactually increased I _Na.

• V _1/2 (detached configuration): −20.91 mV

• Maximal peak current density: −160.0 pA pF⁻¹ at −10 mV

Peak currents densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−128.11	−59.31
Approached	−123.91	−69.25
Moved away	−127.82	−67.71
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.96	1.16
Moved away	0.99	1.14

Cell 6 (20.06.2017, Fig. A7)

Figure A7.

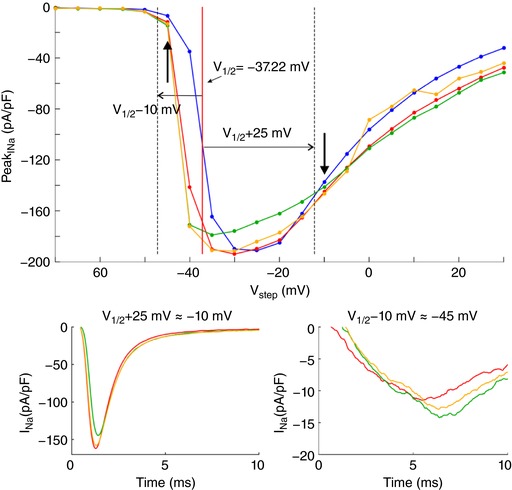
I–V curves and Na⁺ currents from cell 6.

• Cell capacitance (pF): 27.0

• Pipette resistance (MΩ): 2.3

• Seal resistance (GΩ): 1.0

• Remark: For the cell moved away from the obstacle, the cell became unstable for V _step >−10 mV.

• V _1/2 (detached configuration): −37.22 mV

• Maximal peak current density: −193.9 pA pF⁻¹ at −30 mV

Peak current densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−161.98	−11.50
Approached	−144.52	−14.55
Moved away	−158.00	−13.01
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.89	1.26
Moved away	0.97	1.13

Cell 7 (18.07.2017, Fig. A8)

Figure A8.

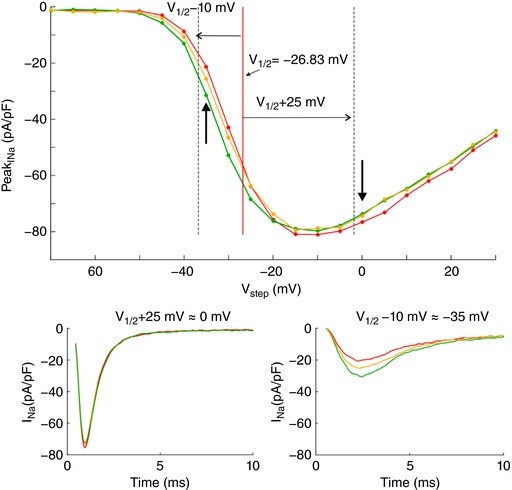
I–V curves and Na⁺ currents from cell 7.

• Cell capacitance (pF): 21.0

• Pipette resistance (MΩ): 1.8

• Seal resistance (GΩ): 1.2

• Remark: In this last experiment, the voltage clamp protocol was not conducted with the cell attached to the substrate.

• V _1/2 (detached configuration): −26.8 mV

• Maximal peak current density: −81.0 pA pF⁻¹ at −10 mV

Peak current densities	At V 1/2 +25 mV	At V 1/2 −10 mV
Values in pA pF−1
Detached	−75.60	−20.66
Approached	−72.65	−28.89
Moved away	−74.20	−25.00
Values normalized to the detached configuration
Detached	1.00	1.00
Approached	0.96	1.40
Moved away	0.98	1.21