Differential processing in modality‐specific Mauthner cell dendrites

Abstract

Key points

• The present study examines dendritic integrative processes that occur in many central neurons but have been challenging to study in vivo in the vertebrate brain. The Mauthner cell of goldfish receives auditory and visual information via two separate dendrites, providing a privileged scenario for in vivo examination of dendritic integration.

• The results show differential attenuation properties in the Mauthner cell dendrites arising at least partly from differences in cable properties and the nonlinear behaviour of the respective dendritic membranes.

• In addition to distinct modality‐dependent membrane specialization in neighbouring dendrites of the Mauthner cell, we report cross‐modal dendritic interactions via backpropagating postsynaptic potentials.

• Broadly, the results of the present study provide an exceptional example for the processing power of single neurons.

Abstract

Animals process multimodal information for adaptive behavioural decisions. In fish, evasion of a diving bird that breaks the water surface depends on integrating visual and auditory stimuli with very different characteristics. How do neurons process such differential sensory inputs at the dendritic level? For that, we studied the Mauthner cells (M‐cells) in the goldfish startle circuit, which receive visual and auditory inputs via two separate dendrites, both accessible for in vivo recordings. We investigated whether electrophysiological membrane properties and dendrite morphology, studied in vivo, play a role in selective sensory processing in the M‐cell. The results obtained show that anatomical and electrophysiological differences between the dendrites combine to produce stronger attenuation of visually evoked postsynaptic potentials (PSPs) than to auditory evoked PSPs. Interestingly, our recordings showed also cross‐modal dendritic interaction because auditory evoked PSPs invade the ventral dendrite (VD), as well as the opposite where visual PSPs invade the lateral dendrite (LD). However, these interactions were asymmetrical, with auditory PSPs being more prominent in the VD than visual PSPs in the LD. Modelling experiments imply that this asymmetry is caused by active conductances expressed in the proximal segments of the VD. The results obtained in the present study suggest modality‐dependent membrane specialization in M‐cell dendrites suited for processing stimuli of different time domains and, more broadly, provide a compelling example of information processing in single neurons.

Key points

• The present study examines dendritic integrative processes that occur in many central neurons but have been challenging to study in vivo in the vertebrate brain. The Mauthner cell of goldfish receives auditory and visual information via two separate dendrites, providing a privileged scenario for in vivo examination of dendritic integration.

• The results show differential attenuation properties in the Mauthner cell dendrites arising at least partly from differences in cable properties and the nonlinear behaviour of the respective dendritic membranes.

• In addition to distinct modality‐dependent membrane specialization in neighbouring dendrites of the Mauthner cell, we report cross‐modal dendritic interactions via backpropagating postsynaptic potentials.

• Broadly, the results of the present study provide an exceptional example for the processing power of single neurons.

Introduction

Research over half a century attributes processing power to single neurons and dendrites that goes beyond their classical role as passive integrators (Rall, 1959; Koch et al. 1983; Koch & Segev, 2000; Stuart & Spruston, 2015). Excitatory and inhibitory inputs to a neuron are distributed over the somato‐dendritic tree and the integration of these inputs depends upon a large number of factors, including the morphological and electrical properties of the dendritic tree and the spatio‐temporal distribution of the synaptic inputs that impinge on it (Rall, 1967; Jaffe & Carnevale, 1999). Indeed, the addition of voltage‐dependent conductances provide a number of higher order functions to dendrites, including logic operations, multiplication of independent inputs and multiplexing (Yuste & Tank, 1996; Gabbiani et al. 1999; Koch & Segev, 2000; London & Häusser, 2005; Branco & Häusser, 2010; Silver, 2010; Stuart & Spruston, 2015). However, much less is known about the role of such often theoretical dendritic functionality for processing relevant physiological stimuli in the intact brain or how distinct dendritic processes shape behaviour output (London & Häusser, 2005; Cuntz et al. 2013).

In fish, two identifiable brainstem neurons, the Mauthner cells (M‐cells), constitute the sensorimotor interface where sensory inputs converge to initiate startle escape behaviour. Specifically, M‐cells integrate multimodal inputs, most notably from the acoustico‐lateralis and visual systems, and a single action potential (AP) in one M‐cell reliably activates contralateral spinal motor execution networks causing a fast body‐bend (C‐start) away from a potential threat (Zottoli, 1977; Korn & Faber, 2005; Fetcho et al. 2008). In other words, the one‐to‐one link between M‐cell AP and escapes allows for a direct link between synaptic integration, M‐cell excitability, and behaviour (Preuss & Faber, 2003; Neumeister et al. 2008). Importantly, the M‐cell receives 8th nerve (acoustic) and visual excitatory inputs via two main separate dendrites, both accessible for in vivo intracellular recordings of synaptic responses to naturalistic stimuli (Preuss & Faber, 2003; Preuss et al. 2006; Szabo et al. 2006; Medan & Preuss, 2014). Numerous 8th nerve afferences impinge onto the distal part of the lateral dendrite (LD) via mixed electrical and chemical synapses providing massive and direct input to the high‐threshold M‐cell (Furshpan & Furukawa, 1962; Faber and Korn, 1978; Preuss et al. 2006; Szabo et al. 2006; Curti & Pereda, 2010). Much less is known, however, about the ventral dendrite (VD), which receives input from optic tectum afferences on its distal part (Zottoli et al. 1987, 1995; Canfield, 2003; Preuss et al. 2006; Flores et al. 2008a; Dunn et al. 2016). Indeed, both short, abrupt sound pips and long lasting gradually increasing visual (loom) stimuli effectively elicit M‐cell mediated startle escapes (Preuss & Faber, 2003; Preuss et al. 2006; Weiss et al. 2006; Medan & Preuss, 2014; Temizer et al. 2015; Dunn et al. 2016). Thus, the M‐cell dendrites process stimuli with fundamentally different dynamics (abrupt vs. gradual), which involve at least one order of magnitude difference in processing time (auditory ∼5 ms vs. 100s of ms for visual looms). In addition to excitatory inputs, both visual and auditory inputs mediate shunting feedforward inhibition (FFI), which tightly controls the threshold in the M‐cell (Korn & Faber, 1983; Faber et al. 1989; Preuss et al. 2006; Weiss et al. 2008). Thus, in the present study, we investigated whether electrophysiological membrane properties and dendrite morphology, studied in vivo, play a role in the selective sensory processing in the M‐cell.

Methods

Ethical approval

We acknowledge the ethical principles of The Journal of Physiology and confirm that all of our animal procedures were performed within these principles, as well as in accordance with the guidelines and regulations of the Institutional Animal Care and Use Committees of Hunter College, City University of New York and Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires.

Animals

Adult goldfish (Carassius auratus), 7–10 cm in body length, were purchased from Billy Bland Fishery (Taylor, AR, USA), Hunting Creek Fisheries (Thurmont, MD, USA) or FunFish (Córdoba, Argentina). Fish were allowed to acclimate for at least 1 week after transport in rectangular Plexiglas holding tanks (30 × 30 × 60 cm; 95 litres). Tanks were supplied with recirculating conditioned water maintained at 18°C. Water was conditioned as described in detail by Szabo et al. (2006). Ambient light was set to a 12:12 h light/dark photoperiod. Animals were fed floating pellets (Sera, Heinsberg, Germany) five times a week.

Electrophysiology

Intracellular responses of the M‐cell to visual and acoustic stimuli were studied in vivo using standard surgical and electrophysiological recording techniques (Preuss & Faber, 2003; Preuss et al. 2006; Medan & Preuss, 2011). To initiate anaesthesia, fish were immersed in ice water (1 litre) with 40 mg l⁻¹ of the general anaesthetic tricaine methanesulfonate (MS‐222), until fish ceased to swim, lost equilibrium and were unresponsive to a pinch on the tail (typically 10–15 min). They were next treated with topical anaesthetic (20% benzocaine gel; Ultradent, South Jordan, UT, USA) at incision sites and pressure points (pin placement) 5 min prior to surgical procedures. Fish were then stabilized in the recording chamber by two pins, one on each side of the head, and ventilated through the mouth with recirculating, aerated saline (6 litres) at 18°C (saline: sodium chloride 7.25 g l⁻¹, potassium chloride 0.38 g l⁻¹; monosodium phosphate monobasic 0.39 g l⁻¹, magnesium sulphate 0.11 g l⁻¹, Hepes 4.77 g l⁻¹; calcium chloride 0.24 g l⁻¹; dextrose 1.01 g l⁻¹, pH 7.2). The recording chamber was mounted inside an opaque, thin‐walled tank filled with saline covering the fish body up to eye level. The recirculating saline also included a maintenance concentration of the anaesthetic MS 222 (20 g l⁻¹) that does not interfere with auditory processing (Palmer & Mensinger, 2004; Cordova & Braun, 2007). In experiments where visual responses were recorded, the analgesic Fentanyl was injected i.m. [1 μg g⁻¹ body weight (bw)] (Bodnar & Bass, 1997; Cordova & Braun, 2007).

Because the M‐cell VD projects downwards, the animal was fixed in the chamber with its head pointing upward (∼15° respect to the horizontal plane) to improve chances of recording in distal VD locations. Next, the spinal cord was exposed with a small lateral incision at the caudal midbody. Bipolar electrodes were placed on the unopened spinal cord to transmit low‐intensity (5–8 V) electrical stimulation generated by an isolated stimulator (DS2A; Digitimer Ltd, Welwyn Garden City, UK). This allowed antidromic activation of the M‐cell axons, as confirmed by a visible muscular contraction (twitch). Surgical procedures were performed before the muscle paralysis agent was injected, which allows monitoring of the effectiveness the anaesthetic by watching for an increase of opercula movement frequency (which is largely reduced in deep anaesthesia) and movements/twitches in response to the surgical procedures. Shortly before the recordings started, the animals were injected i.m. with d‐tubocurarine (1 μg g⁻¹ bw; Abbott Laboratories, Abbott Park, IL, USA) or Flaxedil (10 μg g⁻¹ bw; gallamine triethiodide, Sigma, St Louis, MO, USA) and a small craniotomy exposed the medulla for intracellular recordings. Antidromic stimulation produces a negative potential in the M‐cell axon cap (typically 15–20 mV), which unambiguously identifies the axon hillock and allows intracellular recordings from defined locations along the M‐cell soma‐dendritic membrane (Furshpan & Furukawa, 1962; Furukawa, 1966; Faber et al. 1989). Furshpan & Furukawa (1962) established a map of the spatial variation of the extracellular antidromic response around the axon cap and LD membranes. In the present study, we established a similar mapping of dendritic locations along the VD.

Intracellular recordings were acquired using an Axoprobe‐1A amplifier (Axon Instruments, Foster City, CA, USA) in current clamp with borosilicate glass electrodes (7–10 MΩ). These are well established standard values for electrodes in this preparation and typically allow intracellular recordings for several hours (Korn et al. 1978; Korn & Faber, 2005). The electrodes were filled with 5 m potassium acetate to avoid leakage of chloride ions into the cell, which might influence the synaptic responses (Faber & Korn 1978). M‐cell responses were recorded on‐line with a G5 Macintosh (Apple Corp., Cupertino, CA, USA), using a data acquisition card (PCI E; National Instruments, Austin, TX, USA) at 25 kHz with acquisition software developed in the laboratory. Electrodes were advanced by means of motorized micromanipulators (MP‐285; Sutter Instruments, Novato, CA, USA) and their positions were established: first, the axon cap area was determined (defined as a site with an extracellular M‐cell AP field >10 mV), this point was set as the centre of co‐ordinates. Next the electrode was placed in the somatic region (±50 μm from axon cap) or at different locations along the dendrites. The x, y and z readings of the micromanipulators were recorded for each electrode penetration. Linear distance to soma for each recording site was calculated by trigonometry. Only one M‐cell was recorded and analysed in each animal although, in most cases, several penetrations (including one at the soma and several locations at the LD and or VD) were performed. Resting membrane potential (RMP) was monitored throughout the experiment and experiments where its value changed more than 10% during the recording session were not included in the analysis.

Acoustic stimuli

Sound stimuli consisted of single‐cycle sound pips (200 Hz) produced by a function generator (33210A; Agilent Technologies Inc., Santa Clara, CA, USA) connected to a shielded subwoofer (SA‐WN250; Sony Corp., Tokyo, Japan) located at a distance of 30 cm from the recording chamber. As a result of transfer loss through the media of the recording chamber, the maximum underwater sound intensity was 147 dB relative (re) to 1 μPa in water, which is typically subthreshold for evoking behavioural startle (Neumeister et al. 2008). Because we were interested on studying subthreshold propagation along dendrites, this limitation did not affect our results. Sound stimuli were recorded with a microphone positioned 10 cm over the head of the fish and stored together with intracellular recordings. A hydrophone (SQ01, Sensor) placed at the position of the fish was used for sound calibration but was removed during experiments.

Optic tectum stimulation

M‐cell responses were tested by electrical stimulation of the optic tectum by means of a bipolar electrode positioned in the anterior rim of the right or left tectum. Because tectum projections to the medulla are bilateral (Zottoli et al. 1987; Canfield, 2003; Dunn et al. 2016), stimulation on both tecti was effective to induce responses in the M‐cell. The shape and amplitude of the tectal stimulus (TS) response depends on the position of the stimulus electrode and the current applied, and we did not study this in a systematic way. However, once we found an effective configuration [i.e. a sizable postsynaptic potential (PSP)], we did not change electrode position or the current strength applied until the end of the experiment.

Synaptic responses and membrane properties

Postsynaptic responses to acoustic and visual stimuli were recorded at several loci along the soma‐dendritic membrane in both the LD and VD. This also included recordings of the acoustically evoked PSPs that spread antidromically into the VD and of TS evoked PSPs that spread antidromically in the LD, respectively. PSP peak amplitude was measured on individual responses and averages of 10 responses were used in the statistical analysis.

Transfer resistance (TR)

TR was determined by injecting current pulses (up to ±150 nA, 50 ms) or a positive current ramp (0–150 nA/20 ms; Wavetek Model 39; Wavetek, San Diego, CA, USA) into the M‐cell with one intracellular electrode when the membrane voltage response was recorded with a second intracellular electrode. A compensation circuit built into the amplifier eliminated cross‐talk between the electrodes. Depending on the distance between the two electrodes, we considered these measurements as input resistance (distance between electrodes smaller than 50 μm) or TR (electrodes larger than 50 μm apart), which incorporates the spatial current loss (Rall & Rinzel, 1973; Rinzel & Rall, 1974; Carnevale & Johnston, 1982; Carnevale et al. 1997). Input or TR were determined from the slope of the current/voltage (I–V) plots derived from a series of square pulses or from the initial parts of the I–V plots (first 2–5 ms of the ramp) that do not activate nonlinear conductances (see below). In 16 of 21 experiments, we measured TR by both methods (current ramp and square pulses) and found that they resulted in comparable resistance values (TOST equivalence test, t = –0.29; d.f. = 30, P = 0.61). In those experiments, the average TR obtained by either method was used for statistical comparisons.

Nonlinear properties of the M‐cell membrane

The M‐cell exhibits a well‐characterized voltage‐dependent potassium (K⁺) membrane conductance that inactivates when membrane depolarization exceeds 5 mV from resting membrane potential and thus increases M‐cell excitability for large membrane depolarization (Faber & Korn, 1986). This membrane nonlinearity can be characterized in a standardized way by injecting a positive current ramp (0–150 nA/20 ms; Wavetek Model 39) into the cell while recording membrane voltage with a second electrode (Neumeister et al. 2008; Medan & Preuss 2011). The resulting I–V plots reveal activation and inactivation of voltage‐dependent conductances over the entire range of membrane depolarization as a corresponding decrease and increase in membrane resistance, respectively.

Neuroanatomy

Following somatic intracellular recordings, left or right M‐cells were loaded with tetramethylrodamine‐dextran (3000 MW; Invitrogen, Carlsbad, CA, USA). Filling procedures were conducted in accordance with protocols previously used in the preparation (Flores et al. 2008b). Following the injection (20–30 nA square pulses of 500 ms, 1 Hz, over 20–60 min), dye was allowed to diffuse further for 10–40 min after which the animal was killed by cervical transection. The brain was dissected and fixed in 4% paraformaldehyde in 0.1 m phosphate buffer (pH 7.4) overnight and then washed five times for 20 min in phosphate buffer, embed in low melting agarose and cut into 100–200 μm sections (Vibratome 1000; Leica, Wetzlar, Germany), dehydrated in ethanol series and cleared in methyl salicylate. Cleared sections were scanned at 3 μm intervals with a confocal microscope equipped with a Helium/Neon laser (Fluoview 1000; Olympus, Tokyo, Japan). Images, saved as 3‐D stacks, were adjusted for brightness and contrast and illustrations were obtained by merging the individual serial sections with ImageJ, version 1.48d (NIH, Bethesda, MD, USA). For 3‐D neuronal reconstruction, stacks were aligned and M‐cell morphology was traced using Neurolucida (MBF Bioscience, Williston, VT, USA). Cells were divided in three sections: soma, defined as an area encompassing 30–60 μm at either side of the axon insertion point (Faber & Korn, 1978); the LD, ranging from the somatic origin of this laterally projecting dendrite to its distal end; and VD, ranging from the somatic origin of this anteroventral projecting dendrite to its distal end. Dendritic branch order was assigned using the shaft method of Neurolucida, which assumes that the neuronal tree is dominated by one main path and that all other portions of the tree are subsidiary to the main path. The resulting structure was then analysed with Neurolucida explorer to obtain various parameters of the reconstructed morphology. The parameters obtained were validated by comparison with previous work conducted using other staining methods (Nakajima, 1974; Zottoli et al. 1987).

Neuronal modelling

Intrinsic Mauthner neuron properties

To describe the passive and active properties of the M‐cell by computational means, we used Hodgkin–Huxley equations and cable theory. The dynamics of the membrane potential V(x, t) are:

$${\displaystyle C_{\mathrm{m}}\frac{\partial V}{\partial t}=\sum _{\mathrm{ionic}\mathrm{species}\mathrm{i}}{I}_{\mathrm{i}}+I_{\mathrm{app}}+\frac{a}{2R_{\mathrm{a}}}\frac{{\partial }^{2}V}{\partial x^2}}$$

where C _m is the membrane capacitance, a is the radius of the dendrite or axon, R _a is the axial resistance, I _app(x; t) is an external current applied to the cell at location x, and I _i(x; t) are the current variables that are specific to each ionic channel i. In the present study, we followed the formulation of the Hodgkin–Huxley equations as described in Renaud‐Le Masson et al. (2004) and Buhry et al. (2012). The dynamics of an ionic current are described as:

$$I_{\mathrm{i}(\mathrm{x},\mathrm{t})}=g_{\mathrm{i}}{m}_{\mathrm{i}}^{{\mathrm{q}}_{\mathrm{i}}}{h}_{\mathrm{i}}^{{\mathrm{p}}_{\mathrm{i}}}(V-E_{\mathrm{i}})$$

where g _i is the maximal channel conductance, q _i and p _i are constants describing the gating mechanisms of the ion channel, E _i is the ion reversal potential, and m _i and h _i represent activation and inactivation variables describing the state of the ion channel. The latter two are dynamical variables whose time courses are determined by:

$${\tau }_{\mathrm{m}}\frac{{\mathit{dm}}_{\mathrm{i}}}{\mathit{dt}}=\frac{1}{1+\mathit{exp}\left(\frac{V_{\mathrm{m},\mathrm{offset},\mathrm{i}}-V}{V_{\mathrm{m},\mathrm{slope},\mathrm{i}}}\right)}-m_{\mathrm{i}}$$

$${\tau }_{\mathrm{h}}\frac{{\mathit{dh}}_{\mathrm{i}}}{\mathit{dt}}=\frac{1}{1+\mathit{exp}\left(\frac{V-V_{\mathrm{h},\mathrm{offset},\mathrm{i}}}{V_{\mathrm{h},\mathrm{slope},\mathrm{i}}}\right)}-h_{\mathrm{i}}$$

Here, the parameters V _m;offset;i and V _h;offset;i are the threshold potentials for activation and inactivation, respectively, and the parameters V _m;slope;i and V _h;slope;i determine the sensitivities to crossing these thresholds. The parameters τ_m and τ_h are the time constants of the activation and inactivation dynamics. In addition to a passive leak current that is present everywhere in the cell, we equipped the axon cap of the neuron with a voltage‐gated Na⁺ current and a delayed rectifier K⁺ current, whereas the rest on the M‐cell was passive, unless otherwise stated. The Na⁺ channels are modelled as activating‐inactivating channels with q _Na = 3 and p _Na = 1, whereas the K⁺ channels are modelled using activating dynamics only, with q _K = 4.

Mauthner cell morphology for computational modelling

To obtain realistic signal propagation properties, we simulated the neuron activity using reconstructed neuron morphology. The detailed soma‐dendritic M‐cell morphology was reconstructed semi‐manually (D'Alessandro, 2007) from a confocal image stack of 120 layered 635 × 635 μm images, where the interval between the images was 3 μm. The whole dendritic morphology could be successfully reconstructed from the images, whereas, for the axon only the region around axon hillock (up to 57 μm from the soma) was reconstructed. For the rest of the axon morphology, we used information from the literature. Previous work reported axons of diameter 54 μm on average (Funch & Faber, 1982). We considered an axon of length 1 mm, and assumed it to be passive, whereas we equipped the distal part of the axon hillock (after the initial 30 μm) with active ionic conductances.

In addition to the detailed reconstruction, a simplified M‐cell morphology was used (Goldstein & Rall, 1974; Holmes & Rall, 1992; Holmes et al. 1992). This was achieved by replacing the reconstructed morphologies of VD and LD by cylindrical compartments of constant diameter that had the same length as the main dendrite (of VD and LD, respectively). The diameters of these cylindrical compartments were adjusted such that the total membrane areas of VD and LD and its subsidiary branches were conserved. The model neuron consisted of five segments of length 110 μm (VD) and five segments of length 106 μm (LD) and a passive somatic compartment of 50 by 50 μm. The passive axon consisted of three segments of length 333 μm (see below). In the simulations, all mentioned segments were further divided into three (in the model fittings) or 20 (in the signal propagation experiments) subsegments.

Neuron model construction

We fitted the model parameters C _m, g _Na, g _K, g _L, E _L, τ_m;Na, V _m;offset;Na, V _m;slope;Na, τ_h;Na, V _h;offset;Na, V _h;slope;Na, τ_m;K, V _m;offset;K and V _m;slope;K to reproduce membrane potential traces observed in a representative in vivo experiment, where the M‐cell was stimulated with square‐pulse and ramp currents. To do this, first approximate values that produce qualitatively correct spiking behaviour were identified by trial and error. Second, a cost function was formed that accounts for the difference in spike time (if any), as well as in membrane potential time courses, between the data and the model predictions. To find a local optimum, this cost function was minimized by sequentially adjusting (1 – dimensional minimization) each parameter in random order for a number of iterations. In these simulations, the model parameters were C _m = 2.5 μF cm⁻², g _L = 0.0087 S cm⁻², g _Na = 21 S cm⁻², g _K = 15.289 S cm⁻², g _L(axon) = 0.0003 S cm⁻², E _L = −83.4 mV, τ_m,Na = 0.018 ms, V _m,offset,Na = −56.7 mV, V _m,slope,Na = 8.1 mV, τ_h,Na = 0.21 ms, V _h,offset,Na = −64 mV, V _h,slope,Na = 6.06 mV, τ_m,K = 1.4 ms, V _m,offset,K = −67.5 mV and V _m,slope,K = 9.57 mV. The reversal potentials were assumed to be E _{rev Na} = 55 mV and E _{rev K} = –90 mV, and the axial resistance was assigned the value R _a = 120 Ωcm, as estimated by Funch & Faber (1982).

In addition to a model where dendrites are purely passive, we studied the contribution of active conductances along VD to signal propagation properties. The maximal conductances were scaled down from those at the spike initiation zone with the same factor α_i, (at spike initiation zone α = 1), thus retaining their relative proportion: g _(i)Na = α_ig_Na and g _(i)K = α_ig_K where g _(i)Na and g _(i)K represent the maximal conductances of Na⁺ and K⁺ channels at the ith segment. These factors were chosen as α₀ = 0.035 (soma), α₁ = α₂ = α₃ = α₄ = 0.035 and α₅ = 0 (distal VD segment is passive), where the factors α₁, α₂, α₃, α₄ and α₅ correspond from soma to distal end to segments of lengths 50 μm, 120 μm, 149 μm, 172 μm and 108 μm, respectively, on the VD main branch. To preserve the fit of the active model to the experimental data described above, some of the model parameters were refitted. The values of these parameters were g _Na = 9.033 S cm⁻², g _K = 4.381 S cm⁻², g _L(axon) = 0.0002 S cm⁻², τ_m,Na = 0.020 ms, V _m,offset,Na = −55.8 mV, V _m,slope,Na = 8.1 mV, τ_h,Na = 0.17 ms, V _h,offset,Na = −64 mV, V _h,slope,Na = 6.04 mV, τ_m,K = 1.41 ms, V _m,offset,K = −67.4 mV and V _m,slope,K = 9.56 mV in all our simulations with active dendrites, whereas the rest of the parameters were the same as in the simulations with passive dendrites.

We also simulated alternative distribution patterns of active conductances along the two dendrites and their impact on orthodromic and antidromic signal propagation. We considered three situations: (i) the same amount of active conductances in all compartments of the dendrite (i.e. homogeneous distribution); (ii) a maximal density at soma and progressively smaller amounts towards the distal dendrite; and (iii) minimal density at soma and progressively larger amounts towards the distal dendrite. The distribution of space constants is defined by mean density (c _μ, x‐axis) and distribution gradient (c _δ, y‐axis) such that the conductances of the active ion channels are the downscaled by factors (c _μ – 2 × c _δ, c _μ – c _δ, c _μ, c _μ + c _δ, c _μ + 2 × c _δ) in the soma and four first compartments along the VD, respectively, compared to the corresponding values in the axon initial segment (factors smaller than zero were however, replaced by zero). For orthodromic signal propagation, a 50 ms square‐pulse current with amplitude of 1, 1.5, 2, 2.5, 3, 4 or 5 nA, was injected at the distal end of the VD or LD and the voltage response was recorded along the main branch of the respective dendrite to calculate spatial decay constant. For antidromic signal propagation, a 50 ms square pulse current was injected at the soma (1, 1.5, 2, 2.5 or 3 nA) to simulate antidromic signal decay along the two dendrites, and the spatial decay constants were calculated by recording along the main branch of both dendrites.

NEURON (Carnevale & Hines, 2006) was used for simulating the model. A NEURON implementation of our model is publicly available at http://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=189308.

Statistical analysis

MATLAB, OriginPro 8 (OriginLab, Northampton, MA, USA) and SPSS (IBM Corp, Armon, NY, USA) were used for the statistical analysis. A significance level of α = 0.05 was used throughout the study. The results are reported as the mean ± SD unless otherwise noted. Boxplots were used for side‐by‐side comparison of several samples. To test whether datasets met assumptions of normality a Shapiro–Wilk test was applied. For experiments involving repeated measures a generalized estimating equations (GEE) analysis was used (SPSS). Regression hypotheses in GEE were tested using Wald chi‐squared statistics. To control for the expected proportion of false discoveries for multiple comparisons P values were adjusted using Benjamini–Hochberg correction (SPSS). The reported experiments were technically challenging, in some cases resulting in small samples (n = 3). However, the t test has been shown to be appropriate for samples as low as two given large effects (De Winter, 2013).

Results

M‐cell dendritic responses to tectal and auditory inputs show differential orthodromic decay

As noted, long lasting, ramped‐type visual stimuli (looms), as well as short, abrupt auditory stimuli (pips), are equally effective to trigger M‐cell initiated startle responses. We thus investigated whether there are modality specific processing traits that might be reflected in the membrane properties of the VD and LD. To test this idea, we compared the decay of TS and auditory PSPs travelling from the distal inputs site to the soma evoking responses with similar temporal patterns.

The traces in Fig. 1 A and B show responses to auditory (sound pip) and TS evoked PSPs measured sequentially along the LD and VD, respectively. Figure 1 A shows an example of an auditory PSP spreading from a distal input site in the LD to the soma indicating an ∼50% reduction in peak amplitude. To examine the signal spread along the VD with synaptic input with a time course similar to auditory PSPs, we stimulated the optic tectum, which evoked PSPs in the VD in a reliable way (Zottoli et al. 1987). Figure 1 B shows an example of a PSP evoked by TS spreading from a distal input site in the VD to the soma.

Figure 1. The VD shows a higher orthodromic spatial decay than the LD.

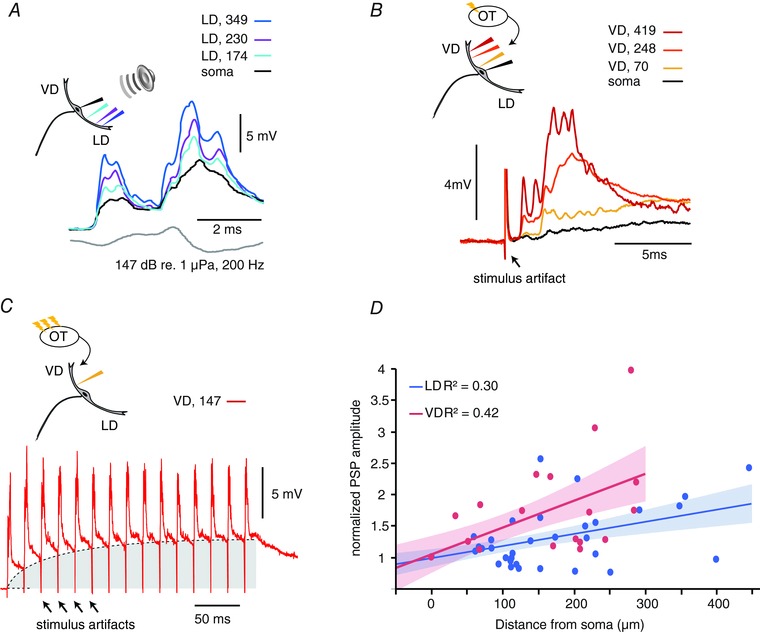
A, sample PSPs evoked by an auditory pip (grey lower trace) recorded at three LD locations and the soma. B, sample PSPs in response to single tectal stimulus. Note the short latency response (arrow). In (A) and (B), the colour code indicates the recording location with respect to the soma (μm). C, sample PSPs in response to a train (50 Hz, at 147 μm from soma) of tectal stimuli. Repetitive tectal stimulations evoke an underlying membrane depolarization (grey area) with superimposed EPSP (same neuron as in B). D, plot of the normalized PSPs amplitudes for the indicated recording locations along the VD (red dots) and LD (blue dots). Red (VD) and blue (LD) lines and shaded areas are linear fits and 95% confidence intervals, respectively. R ², coefficient of determination. [Color figure can be viewed at wileyonlinelibrary.com]

We recorded M‐cell responses to TS in 18 experiments. Response amplitude evoked by TS was stable for each cell and recording site but significantly variable between cells. The maximum amplitude of TS‐evoked responses that we recorded was 24.6 mV, 197 μm in the VD. Latency to TS was less than 1 ms (mean ± SD: 0.55 ± 0.14 ms, n = 18). Latency did not change with tectal electrode position or stimulation strength, suggesting that the tectal connections to the M‐cell are monosynaptic and may also involve electrical synapses, as demonstrated for auditory input (Zottoli et al. 1987; Pereda et al. 2003, 2013). Long lasting, high frequency TS stimuli produced temporal summation of the response (Fig. 1 C) and, in some experiments, evoked an M‐cell spike. The summation of the PSPs provide indirect evidence for chemical synapses between visual afferents and the M‐cell, thus resembling the mixed electrical/chemical synapses for 8th nerve inputs to the LD (Lin & Faber, 1988; Pereda et al. 2004; Szabo et al. 2006).

The results show a sizable attenuation and signal filtering of fast components for both PSPs as they propagate towards the soma; however, the size reduction of the visual PSP appears relatively larger than that of the auditory PSP. Figure 1 D shows the relationship between the amplitude of single visual (red) and auditory (blue) PSPs as a function of the distance from the soma along the LD and VD (VD: n _cells = 18, n _sites = 52; LD: n _cells = 21, n _sites = 65), respectively. The PSPs values were normalized relative to their amplitude at the soma. A repeated measure GEE (SPSS) with dendrite identity and distance as factors showed a significant interaction (P = 0.032; Wald chi‐squared), implying a difference in the rate of PSP amplitude change between the two dendrites. To compare decay ratio in the two dendrites, we fit the data with a linear function of the form y = Cx + a, where y is the normalized PSP amplitude and x is the distance from the recording site to soma (t test on the regression slope, LD: C _LD = 0.002, t = 4.48, d.f. = 47, P < 0.001; VD: C _VD = 0.004, t = 4.46, d.f. = 28, P < 0.001) and computed the distance factor (DF) defined as the distance at which the normalized PSP was 50% larger than that measured at the soma, i.e. solving the equation for y = 1.5). The DF in the LD (DF_ortho,LD = 273 μm) was about twice that in the VD (DF_ortho,VD = 108 μm), implying a larger decay in the VD compared to the LD (Fig. 1 D).

Interestingly, we found that auditory evoked PSPs originating in the LD also invaded the VD (Fig. 2 A) and, vice versa, tectal PSPs invaded the LD (Fig. 2 B). As indicated in Fig. 2 A and B, the somatic PSP in response to tectal stimuli was on average smaller compared to that evoke by auditory stimuli (mean ± SD: tectal: 4.66 ± 1.48 mV, n = 12; auditory: 6.76 ± 2.36 mV, n = 26; P > 0.0001; GEE; Wald chi‐squared). Note that the tectal somatic PSPs shown in Fig. 2 B is larger than the shown in Fig. 1 B, although it falls within the variability expressed in Fig. 1 D. Recordings along the two dendrites showed that both tectal and auditory evoked PSPs remained of sizable amplitude even in the distal parts of the cross‐modal dendrite (Fig. 2 A and B).

Figure 2. Auditory PSPs show higher cross‐modal backpropagation than VD PSPs.

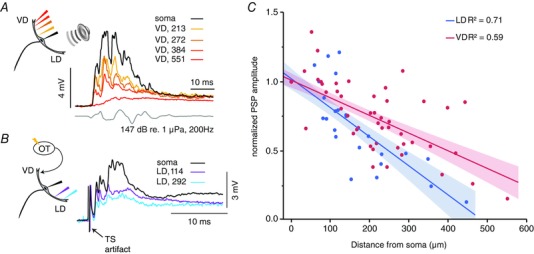
A, sample PSPs evoked by an auditory pip (grey lower trace) recorded after propagating from the LD into the VD. Note: the still sizeable auditory PSP in the distal VD 550 μm away from soma. B, sample traces of PSPs evoked by TS as they propagate into the LD. In (A) and (B), the colour code indicates recording location with respect to the soma in μm. C, plot of the normalized amplitudes of auditory evoked PSPs in the VD (red dots) and tectal evoked PSP in the LD (blue dots) at the indicated recording locations. Red (VD) and blue (LD) lines and shaded areas are linear fits and 95% confidence intervals, respectively. R ², coefficient of determination. [Color figure can be viewed at wileyonlinelibrary.com]

We quantified the magnitude of these antidromically propagating PSPs with sequential recordings along the cross‐modal dendrites using the same methods as those descibed above (Fig. 1). Figure 2 C shows the normalized PSPs for the auditory responses in the VD (n _cells = 26, n _sites = 72; red) and for visual responses in the LD (n _cells = 14, n _sites = 36; blue). As with orthodromic PSPs, we estimated the antidromic decay (DF) in the VD and LD with a linear fit to the cross‐modal PSPs (t test of regression, C _{LD_anti} = –0.00021, t = –9.07, P < 0.001; C _{VD_anti} = –0.0013, t = –9.97, P < 0.001).

By contrast to the propagation of orthodromic PSPs (Fig. 1), cross‐modal PSPs suffer less decay in the VD (DF_anti,VD = 402 μm) compared to the LD (DF_anti,LD = 249 μm) (Fig. 2 C). In support, a repeated measure GEE showed a significant interaction between the factors dendrite identity and distance (P = 0.006; Wald chi‐squared). These results suggest that compared to tectal PSPs, auditory PSPs not only attenuate less when travelling orthdromically to the soma, but also when invading the VD. Functionally, these cross‐modal PSPs could provide an underlying membrane depolarization that could increase the likelihood of an appropriately timed orthodromic PSP to reach threshold (Canfield, 2003, 2006).

Exploring possible causes for differential orthodromic signal decay in two dendrites

Tectal and auditory evoked FFI is similar in the LD and VD

Both visual and auditory stimuli evoke FFI at the perisomatic region of the M‐cell through a population of inhibitory interneurons, the so‐called passive hyperpolarizing potential cells (Diamond et al. 1973; Faber & Korn, 1978; Zottoli et al. 1987; Preuss et al. 2006; Weiss et al. 2008). Thus, differences in the strength of the evoked FFI between the two modalities may contribute to the observed differential orthodromic decay of the PSPs in the VD and LD (Fig. 1). Inhibition in the M‐cell is of the shunting type (i.e. it involves the activation of an inhibitory conductance in the postsynaptic membrane that channels incoming synaptic currents out of the cell) (Furukawa & Furshpan, 1963). The resulting reduction in M‐cell input resistance can be measured as a fractional amplitude reduction of a backpropagating AP (antidromic propagation), which is not regenerative in the M‐cell soma or dendrite (Faber & Korn, 1982). Thus, evoking an AP at specific times (2–250 ms) following a sensory stimulus (AP_test) allows quantification of the time course and magnitude of FFI (FFI effect = AP_test/AP_control × 100) (Fig. 3 A) (Faber & Korn, 1982). The results (n = 4) show a trend for tectally‐evoked FFI (TS‐FFI) being slightly stronger and peaking earlier than auditory evoked FFI (Fig. 3 B, inset). However, differences in FFI peak magnitude (TS: 24 ± 10%; Aud: 13 ± 4%, paired t test, P = 0.15) and FFI peak time (TS: 8 ± 7 ms; Aud: 19 ± 4 ms; n = 4, paired t test, P = 0.08) did not reach statistical significance. Thus, it might be concluded that the overall effectiveness of FFI is comparable for both modalities, suggesting that FFI probably plays no significant role for the differential decay of PSPs in VD and LD.

Figure 3. Tectal and auditory‐evoked FFI is similar in LD and VD.

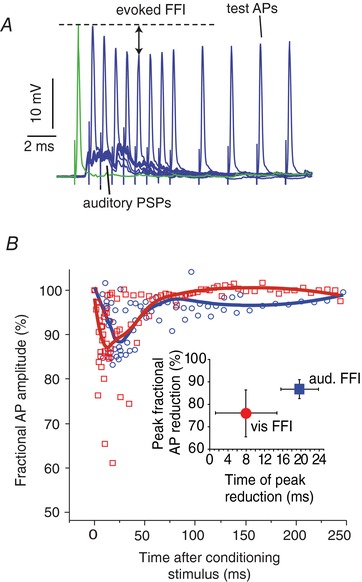
A, sample superimposed traces from a single experiment of intrasomatic recorded PSPs in response to auditory pips paired with a subsequent antidromically test AP evoked at different time points (2–20 ms) after the pip. The fractional amplitude reduction of the test APs was compared with a control AP without a preceding auditory pip (green trace) to derive the evoked FFI. Similar methods were used to accessing TS evoked FFI. B, scatter plots showing the fractional AP reductions (%) from all experiments (n = 4) in response to pip (red squares) and TS (blue circles) stimuli over a range of lead times (0–250 ms). The measurements were fitted with a polynomial function to indicate the time course of visually (red) and auditory (blue) evoked FFI. Inset: mean ± SD (n = 4) AP peak reduction and peak time of FFI evoked by TS (red) and pip (blue) stimuli. [Color figure can be viewed at wileyonlinelibrary.com]

LD and VD show differential cable properties

To evaluate differences in the cable properties between the VD and LD we next compared their transfer resistance (TR = V _soma/I _dend) (i.e. the attenuation a signal suffers as it travels from the input site towards a distant site) (Rinzel & Rall, 1974; Carnevale & Johnston, 1982; Holmes et al. 1992; Carnevale et al. 1997). To measure TR, we injected current pulses or current ramps in the dendrite when measuring the voltage response at the soma with a second electrode (Fig. 4 A and Ba). TR was quantified for each dendrite from voltage current plots derived from current pulses (±0–150 nA) (Fig. 4 Bb) or current ramps (0–150 nA in 20 ms; see Methods). The distance between the injection electrode and the somatic recording was varied (Fig. 4 C), however, as a result of the challenge of performing these simultaneous intracellular recordings, the range of the tested distances was limited between 83 to 247 μm in the LD (n = 6, mean ± SD: 162 ± 64 μm) and between 57 to 340 μm in the VD (n = 8; mean ± SD: 202 ± 111 μm) and only one type of TR experiment was obtained per cell (i.e. VD TR or LD TR). The distribution of TR across distance for those 14 experiments in the VD or LD is shown in Fig. 4 C. Cable theory states that TR decreases in passive dendrites with increasing distance between the injecting and recording electrode (Holmes & Rall, 1992; Golding et al. 2005); however, the change in TR is predicted to be relatively moderate for shorter inter‐electrode distances (London et al. 1999) or for relatively isodiametric cylinders (Jaffe & Carnevale, 1999). Indeed, we did not find a correlation between the TR value and distance in our measurements (R ² LD = 0.002 LD; R ² VD = 0.08); thus, we pooled the data and compared the mean TR in the LD (77.9 ± 33.4 kΩ, n = 6) and the VD (31.8 ± 19.8 kΩ, n = 8). As the box plot in Fig. 4 D shows, the VD had consistently lower TR values than the LD (two‐tailed two sample t test, t = 3.23; d.f. = 12, P = 0.007).

Figure 4. Differences in transfer resistance between LD and VD.

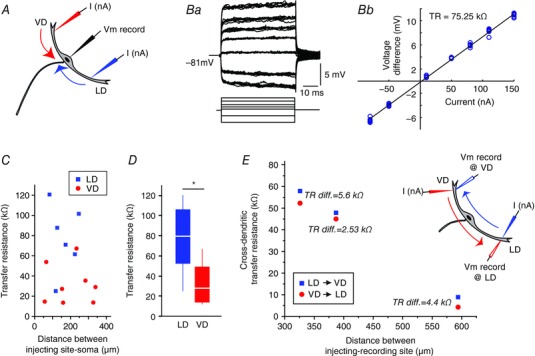
A, current ramps or square pulses were injected in different locations along the LD or VD (I nA) and the evoked voltage response was measured at the soma (Vm). B, sample traces showing membrane response to a family of current pulses (Ba) and the resulting I–V plot for determining TR (Bb) in the same experiment. C, plot of the individual TR measurements vs. soma‐dendritic distance for the LD (blue) or VD (red) and soma. Each symbol represents a different cell (n _LD = 6, n _VD = 8). D, box plots of TR obtained for the LD (blue, n = 6) and VD (red, n = 8) for all experiments. ^* P = 0.007. E, cross‐dendritic TR (n = 3) for LD → VD (blue squares) and VD → LD (red circles) for three experiments with the indicated difference in TR in the two reciprocal injection and recording directions. The current injected was the same in all sites tested. [Color figure can be viewed at wileyonlinelibrary.com]

As noted, PSPs originating in the LD and VD showed differential cross‐modal interactions (Fig. 2). To further substantiate these results, we tested for corresponding differences in cross‐modal TR between the two dendrites. Accordingly, in three additional M‐cells, current pulses were injected in one dendrite (e.g. LD) when recording voltage in the VD, thus obtaining, for the same cell, TR in both directions, LD → VD and VD → LD TR (n = 3). This method allowed a comparison of TR in both directions for similar dendritic loci in a given experiment (Fig. 4 E, inset). The dendritic injection/recording sites in the LD and VD ranged between 191–363 μm and 135–355 μm from soma, yielding inter‐electrode distances in the range 326–594 μm. The results showed that, in all experiments, TR LD →  VD was larger than the TR VD → LD (paired sample t test, t = 4.72, d.f. = 2, P = 0.02) (Fig. 4 E). Note that, in contrast to Fig. 4 C, when inter‐electrode distances exceeded 300 μm, TR dependence with distance was evident.

Together, our results suggest differential membrane properties in the two dendrites that putatively shape information processing, as well as cross‐modal interactions between LD and VD.

LD and VD show differences in voltage‐dependent membrane properties

Previous studies revealed a voltage‐dependent conductance in the proximal LD and M‐cell soma; namely, a putative K⁺ inward rectifier that rapidly inactivates at membrane depolarizations 5 mV above the resting potential. Inactivation of this conductance progressively increases M‐cell input resistance as its membrane potential approaches firing threshold (Faber & Korn, 1986; Neumeister et al. 2008; Medan & Preuss, 2011). However, it is not known whether the membrane of the VD contains similar conductance(s). Indeed, a differential expression of voltage‐gated conductances in the LD and VD might contribute to the observed differences in decay of postsynaptic responses in the two dendrites.

To reveal such membrane non‐linarites, current ramps were injected at the soma when recording the voltage response in the VD (n = 4, sites range 210–301 μm from soma) or LD (n = 8, sites range 200–334 μm from soma) with a second electrode (for details, see Methods) (Fig. 5 A). We next measured membrane resistance (i.e. the slope of voltage/currents plots) close to resting membrane potential (Fig. 5 Aa, slope 1) and in the depolarized cell (Fig. 5 Aa, slope 2). The ratio between slope 2/slope 1 was used to quantify the magnitude of the membrane non‐linearity in the two dendrites and was compared with a hypothetical ratio of 1 (i.e. to a strictly linear I–V relationship). Figure 5 B indicates that both dendrites display membrane nonlinearities during depolarization (i.e. mean ± SD slope 2/slope 1 ratios significantly larger than 1) (VD: 1.33 ± 1.9%, t = 3.46, d.f. = 3, P = 0.02; LD: 1.12 ± 0.12%, t = 3.16, d.f. = 7, P = 0.015). In addition, the results show that the nonlinearity is more substantial in the VD (two sample t test, t = 2.4, d.f. = 10, P = 0.02).

Figure 5. LD and VD show differences with respect to dendritic membrane non‐linearity.

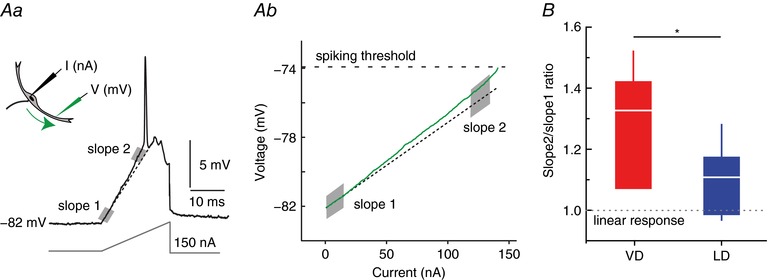
A, to reveal voltage‐dependent membrane properties in the VD and LD, we injected current ramps (I nA) in the soma when recording membrane voltage (Vm) in the LD or VD with a second electrode (Aa). Ab, putative changes in resistance during membrane depolarizations where analysed in voltage current plots by comparing the I–V slopes close to RMP (slope 1 shaded region) and for depolarizations 2–3 mV below threshold (slope 2 shaded region). The sample traces show the response recorded in LD, 172 μm away from soma with a values of 34  and 43 kΩ for slope 1 and slope 2, respectively. Dashed line indicates a linear fit to slope 1. B, box plot of slope 2/slope 1 ratios for the VD (red, n = 4) and LD (blue, n = 8) indicate a higher value for the former (^* P = 0.02). Dashed line indicates a hypothetical linear response of the membrane. [Color figure can be viewed at wileyonlinelibrary.com]

Differences in dendritic morphology might contribute to differences in signal propagation

The observed differential membrane properties between the VD and LD might be a result of morphological differences. Although the morphology of the LD has been studied in some detail (Bartelmez, 1915; Nakajima, 1974; Zottoli & Faber, 1979; Flores et al. 2008a), relatively sparse information exists about the VD (Nakajima, 1974; Zottoli et al. 1987; Preuss et al. 2006; Flores et al. 2008b). Here, we injected dye in six M‐cells obtaining three completely stained cells (Fig. 6 A, left), which were used for the 3‐D reconstruction (see Methods). Figure 6 A (right) shows the morphology and relative position of the dendrites in a 3‐D reconstruction based on confocal image stacks. As our stack microphotographs and reconstructions show, the M‐cell lacks a clearly defined soma. Consistent with previous accounts, we operatively defined the soma as the area encompassing 30–60 μm at either side of the axon insertion point, depending on the total length of the cell (Fig. 6 A, arrowheads) (Bartelmez, 1915; Bodian, 1937; Furshpan & Furukawa, 1962; Nakajima, 1974; Faber & Korn, 1978; Flores et al. 2008a,b). After defining the three main compartments of the somato‐dendritic tree (soma, LD and VD), we constructed diagrams of the LD and VD using the shaft order method (see Methods) to compare their branching patterns and obtain length and average diameter of distinct dendritic segments (Fig. 6 B). Table 1 summarizes these and other parameters measured in the three stained cells, which belong to animals with body lengths of 15 (cell 1) and 10 cm (cells 2 and 3). Dimension of the soma and dendrites appears to scale with body length (Zottoli, 1978). The number and location of secondary branches of the LD and VD (5–7 and 4–5 respectively) were similar in the three cells analysed. Figure 6 C shows that, compared to the LD, in all stained cells, the VD is longer (mean ± SD difference 31 ± 19%, n = 3, Cohen effect size = 0.52, paired t test: t = –5.41, d.f. = 2, P = 0.033) and has a smaller cross‐sectional area (mean ± SD difference 56 ± 13%, n = 3, Cohen effect size = 0.80, paired t test: t = 4.46, d.f. = 2, P = 0.047). The larger length and smaller cross‐sectional area of the VD is consistent with the differences observed in spatial attenuation of PSPs (Fig. 1).

Figure 6. VD and LD show differences in dendritic morphology.

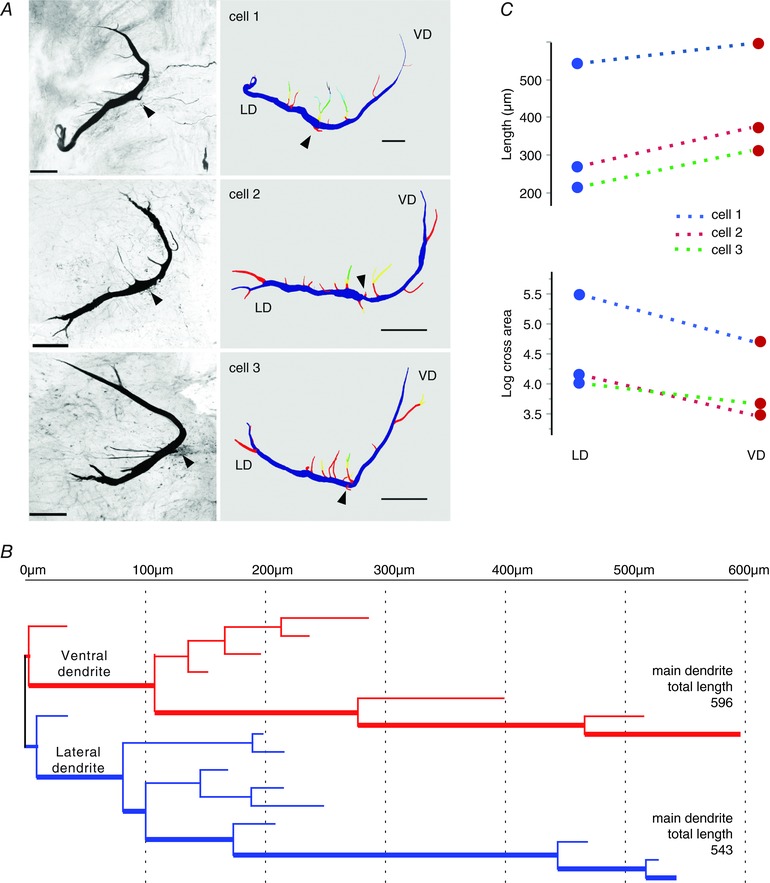
A, anatomical characterization of the M‐cell obtained by iontophoretic injection of rhodamine‐dextran dye followed by confocal imaging and 3‐D reconstruction using Neurolucida. Each row shows a different preparation (cells 1–3). Left: flattened anatomical stacks of stained M‐cells. Right: 3‐D reconstructions of the same cells coloured by branch order. Scale bars in all pictures = 100 μm. Arrowheads indicate the axon or its insertion point. B, dendritic branching pattern of cell 1 (top row in A). Red and blue lines define the branching pattern of VD and LD, respectively. The length of the main branch for each dendrite is indicated. The thick line denotes the main branch of the VD or LD. C, measurements of dendritic length (upper) and log cross area (lower) for the three cells showing consistent differences between LD and VD. [Color figure can be viewed at wileyonlinelibrary.com]

Table 1.

Morphometric parameters of M‐cell soma and dendrites based on 3‐D reconstructions of three stained cells

	Soma1				Lateral dendrite						Ventral dendrite
	Length (μm)	Average diameter (μm)	Surface (μm2)	Volume (μm3)	Length (μm)	Proximal dendrite2 average diameter (μm)	Number of secondary branches	Surface (μm2)	Volume (μm3)	Surface /volume ratio	Length (μm)	Proximal dendrite2 average diameter (μm)	Number of secondary branches	Surface (μm2)	Volume (μm3)	Surface/volume ratio
Cell 1	118	27	9908	66205	543	24	6	28428	131094	0.22	596	18	4	18618	65860	0.28
Cell 2	70	13	3206	11562	270	10	7	7051	17153	0.41	373	6	4	6729	12116	0.56
Cell 3	63	10	2012	5101	215	11	5	5323	11855	0.45	312	10	5	6568	12283	0.53

¹The soma is defined as the area encompassing 60 μm (cell 1) or 30 μm (cells 2 and 3) at either side of axon insertion point. The difference of soma size accounts for the difference in total cell length.

²Proximal dendrite average diameter is defined as the diameter of the segments included in the proximal third of the total extension of the dendrite (i.e. if the main dendrite is 600 μm long, this is the average diameter of segments included in the first 200 μm; see example in Fig. 1 B).

We also analysed anatomical information about the dendrites that was based on the x‐y‐z co‐ordinates of the recording electrodes during our electrophysiological experiments. In 16 out of 63 experiments, we recorded from the soma and both dendrites in the same neuron. In these cases, the angle between two vectors originating at the soma and ending at the respective LD or VD recording sites was calculated by dot product. The results showed LD/VD angles ranging from 113° to 157° with a mean ± SD of 132°± 13° (n = 16). The latter is consistent with angles that can be inferred from the literature (Zottoli et al. 1987). Information from our anatomical reconstructions and recording loci confirmed the lateral and slightly upwards projection of the LD, whereas the VD projects anterior and downwards (Faber & Korn, 1978; Zottoli et al. 1987). The angles that the LD and VD define with respect to the dorsoventral plane are 15° ± 3° and –40° ± 3° (mean ± SEM, n _LD = 30, n _VD = 34, dorsal positive). The latter explains why tilting the head of the animal upward increases the chances of impaling the distal portions of the VD (see Methods) (Zottoli et al. 1987; Preuss et al. 2006).

Modelling suggest that dendritic morphology may account for the differential orthdromic decay in the LD and VD

To test whether a distinct dendritic morphology can account for the observed propagation differences in the two dendrites, we used a Hodgkin–Huxley type neural model of the M‐cell based on realistic morphology. Figure 7 Aa illustrates the reconstructed dendritic morphology and the applied axon morphology; note that this neuron is the same as that shown in Fig. 6 A (cell 1).

Figure 7. Dendritic morphology may account for observed orthodromic propagation differences.

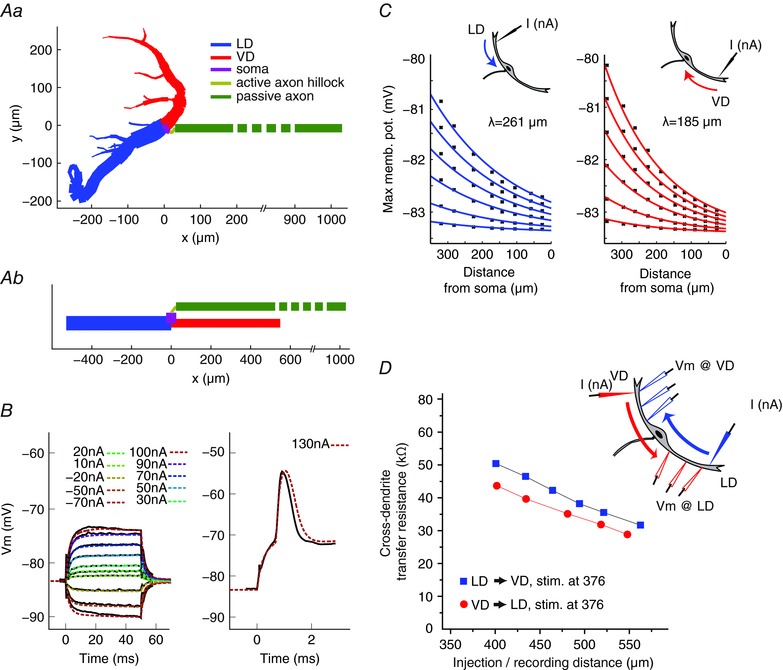
Aa, neuronal M‐cell model based on realistic anatomy (cell 1 in Fig. 6). Axon morphology is based on data from the literature (see Methods). Ab, simplified neural model where the dendritic branches, axon hillock area and axon are represented by individual cylindrical compartments, which have the same length and total membrane area as the reconstructed cell 1 above. B, M‐cell somatic membrane responses to physiological (solid black line) and modelled (coloured dashed line) sub‐threshold (left) and supra‐threshold (right) current injections. C, plots of simulated membrane depolarization along the LD (left) and VD (right) in response to distal current injections of various strengths (see text). The theoretical dendritic space constants were determined by fitting the responses to the exponential form Â(x) = K exp(–cx) + E _L on the logarithmic scale, where K is a constant that depends on the input current amplitude, c is the spatial decay, x is the distance from soma and E _L is the leak reversal potential (resting state membrane potential). D, simulations of cross‐dendritic TR measured along the LD → VD (blue squares) and VD → LD (red circles) for an injecting electrode positioned 376 μm from soma. Note the steady decrease of TR with increasing inter‐electrode distance and that the LD → VD TR is always higher than the VD → LD TR. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 7 B shows model responses to somatic current injections of sub‐ and suprathreshold intensities (dashed coloured lines) superimposed on recorded responses (continuous lines). The model correctly predicts not only the responses to subthreshold stimuli (Fig. 7 B, left), but also the timing and shape of the action potential (Fig. 7 B, right). We next tested the model predictions for orthodromic propagation of signals evoked by square current pulses (50 ms) of increasing amplitude (1, 3, 6, 9, 12 and 15 nA), injected at the distal end of the main branch of the LD and VD. The modelling results showed, consistent with our physiological results (Fig. 1), a smaller orthodromic decay in the LD (Fig. 7 C, left, λ_ortho,LD = 261 μm) than in the VD (Fig. 7 C, right, λ_ortho,VD = 185 μm). We repeated these experiments using a reconstruction from another neuron, and obtained qualitatively similar results (data not shown).

To investigate the possible contribution of dendritic branching on signal propagation (Holmes et al. 1992), we also implemented a simplified model of the M‐cell where the LD and VD dendritic arbors were replaced by single cylindrical compartments (see Methods) (Fig. 7 Ab). Accordingly, the differences in the spatial decays between the two dendrites will stem only from the difference in their length and diameter. This simplified model produced slightly higher space constants (λ_ortho,LD = 333 μm; λ_ortho,VD = 203 μm) but qualitatively reproduced the differences in spatial decay between the two branches (i.e. less spatial decay in the LD than in the VD). Together, the results support the notion that morphological differences between the dendrites might at least partly account for the differences in orthodromic space decay.

In addition, we tested whether our model can reproduce the asymmetry observed for the cross‐modal TR between the LD and VD (Fig. 4 E) (i.e. a larger cross‐dendritic TR for the LD compared to the VD). A current pulse (150 nA, 50 ms) was injected at a distal site in LD or VD (376 μm from soma) and the evoked response calculated for five locations along the cross‐modal dendrite (Fig. 7 D, inset). The results showed that the TR in the LD → VD direction (blue squares) was larger than the TR in VD → LD direction (red dots) for all loci, thus reproducing the physiology results (Fig. 4 E). In addition, these modelling experiments allowed measuring the voltage drop in multiple steps at defined locations (something which would be extremely hard to achieved in vivo) and confirmed TR reduction for large distances between the injecting and recording electrode (Golding et al. 2005).

Cross‐modal signal propagation between the two dendrites may involve voltage‐dependent conductances

Antidromic signal propagation in the dendrites was assessed in the realistic morphology model (see above) using current pulses (duration 50 ms, amplitude 1, 1.5, 2, 2.5, 3, or 4 nA) injected into the soma. The results showed a slightly shorter antidromic spatial constant (λ_anti) for the VD than for the LD: λ_anti,VD = 367 μm vs. λ_anti,LD = 438 μm (Fig. 8 A). A second model cell based on another neuron predicts qualitatively similar results (i.e. a shorter space constant for the VD than for the LD) (data not shown). The same result was obtained with the model that used a branchless morphology (λ_anti,LD = 342 μm vs. λ_anti,VD = 254 μm). As such, the model did not reproduce the electrophysiological data, which showed higher antidromic signal attenuation (DF) in the LD than in the VD (Fig. 2 C). Interestingly, this contrasts with the findings of the orthodromic decay model (Fig. 7 C), which qualitatively reproduced the experimental data (Fig. 1 C).

Figure 8. Active conductances might contribute to differences in antidromic signal propagation in the LD and VD.

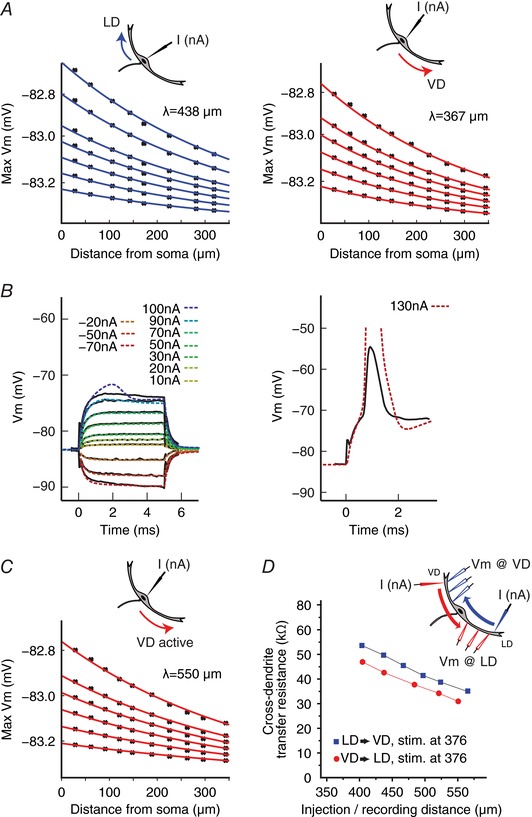
A, plots of simulated membrane depolarizations along the LD (left) and VD (right) in response to somatic current injection considering realistic morphology but purely passive dendrites. The theoretical antidromic dendritic space constants (λ) were determined as in Fig. 7 C. B, behaviour of an M‐cell model incorporating active conductances. Somatic membrane responses to physiological (solid black line) and modelled (coloured dashed line) sub‐threshold (left) and supra‐threshold (right) current injections. C, plots of simulated membrane depolarizations along the VD, which includes active conductances l. D, simulations of cross‐dendritic TR in the active model (details as in Fig. 7 D). [Color figure can be viewed at wileyonlinelibrary.com]

We next explored whether a differential expression of voltage‐dependent conductances in the proximal VD and LD can explain the mismatch between the purely passive model and the experimental data regarding antidromic spatial decays. Indeed, this notion is consistent with the more pronounced nonlinear behaviour of the VD membrane that we observed experimentally when injecting current ramps (Fig. 5). Accordingly, active Na⁺ and K⁺ conductances were added to the soma and proximal segments of the VD (see Methods) using the reconstructed morphology. As with the passive model (Fig. 7 B), the active M‐cell model correctly estimates responses to sub‐threshold stimuli (Fig. 8 B, left), as well as spike timing (Fig. 8 B, right; note that the model overestimates the amplitude of the AP). We next injected a 20 ms current ramp at the soma and recorded in the modelled VD or LD 150 μm from the current injection site (Fig. 5). The active model qualitatively reproduced the physiology results (i.e. a lower slope 2/slope 1 ratio in the LD than in the VD) (LD: slope 2/slope 1 = 1.354: VD: slope 2/slope 1 = 1.432). By contrast, the passive model showed similar voltage responses to the current ramp for both dendrites (LD slope 2/slope 1 = 1.135; VD slope 2/slope 1 = 1.135). Importantly, current pulse injection simulations demonstrated that an active VD reproduced qualitatively the experimentally observed orthodromic and antidromic space constants. Namely, a larger orthodromic decay in the VD compared to the LD (λ_ortho,VD = 214 μm vs. λ_ortho,LD = 312 μm, plots not shown) and a larger antidromic decay in the LD compared to VD (λ_anti,VD = 550 μm vs. λ_anti,LD = 438 μm) (Fig. 8 A and C). In addition, the active M‐cell model also reproduced the experimental data of a larger cross‐dendritic TR for PSPs propagating in the LD → VD direction compared to the VD → LD direction (Figs 4 E and 8 D).

To test how robust the above results are with respect to the relative amount and distribution of active conductances expressed in the VD, we performed additional simulations in which we systematically varied these two parameters (see Methods). Fig. 9 A shows the relationship between antidromic and orthodromic space constants in the two dendrites when active conductance density (c _μ, x‐axis) and distribution (c _δ, y‐axis) varies in the VD but the LD is kept passive. Hence, c _μ = 0 represents a passive dendrite and c _δ = 0 represents a homogeneous distribution (i.e. the same densities) of active conductances in all active dendritic compartments. Correspondingly, the passive model predicts a larger space constant for the LD in both antidromic and orthodromic directions (Fig. 9 A, blue square in solid orange area), whereas increasing active conductances in the VD leads to a higher antidromic space constant in the VD at the same time as not affecting the orthodromic space constant order (Fig. 9 A, white area where the black square corresponds to parameters of active model of Fig. 8). Indeed, the white area of Fig. 9 A depicts that a relatively large range of densities and distributions of active conductances in the VD will lead to the same order of decay constants as observed with the proposed active model (Fig. 8).

Figure 9. Model results are consistent for a wide range of densities and distribution of voltage‐dependent conductances in the VD and LD.

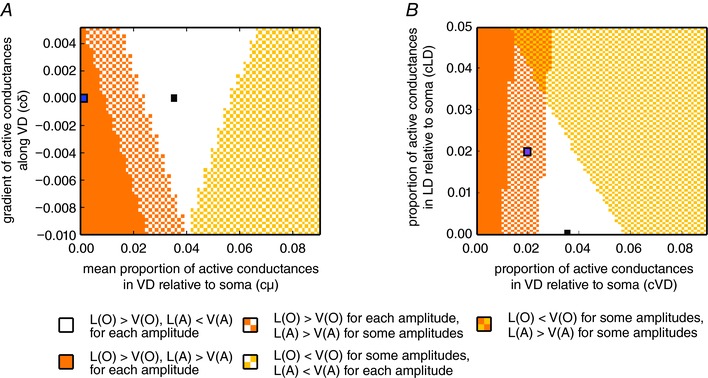
A, colour plot showing model predictions for the relationship between spatial decays in orthodromic (O) and antidromic (A) signal propagation as a function of the mean conductance density (c _μ, x‐axis) and distribution (c _δ, y‐axis) along VD. The black square represents the parameters used in the active model (Fig. 8), whereas the blue square represents the passive model (for the corresponding simulations, albeit with slightly different model parameters, Fig. 7; see also Methods). The white area shows the factors for which the spatial decay constants were qualitatively similar, as in experimental data for all amplitudes (i.e. the orthodromic spatial decay constant was larger in the LD and the antidromic spatial decay constant was larger in VD). The orange and yellow areas show the factors for which both spatial decay constants were larger in VD or LD, respectively. The checkerboard orange–white and yellow–white areas represent cases where either antidromic (orange–white) or orthodromic (yellow–white) propagation showed different qualitative results for different amplitudes, whereas the other type of propagation showed results that were consistent with the experiments for all amplitudes. B, robustness analysis on the quality of the model predictions when both dendrites possess active conductances. The colour plot is identical to that of (A), although only cases with c _δ = 0 are considered here. The x‐axis shows the factors for the active conductances in the soma and four first compartments along the VD and the y‐axis shows the factors for those in the five first compartments along LD. For the default active model (black square) and models with sufficiently similar factors cVD and cLD (white area), the qualitative results for the spatial decays from the experiments were reproduced. The purple square represents a point were VD and LD have the same amount of active conductances and where the order of spatial decays depends on stimulus amplitude. [Color figure can be viewed at wileyonlinelibrary.com]

The results shown above (Fig. 5) suggest that the LD may also contain voltage‐dependent conductances. Accordingly, we next systematically varied the densities of active conductances in both the LD and VD (c _LD and c _VD, respectively), keeping their distribution homogeneous (i.e. c_{δ LD} = c_{δ VD} = 0), and monitored the effect on the orthodromic and antidromic space constants in both dendrites. As shown in Fig. 9 A, the black square corresponds to model parameters used in the active model of Fig. 8 [purely passive LD (c_LD = 0) and 3.5% of active conductances in VD, c_VD = 0.035]. Similar to Fig. 9 A, the white area represents the combinations of parameters that predict higher orthodromic space constant for the LD and higher antidromic space constant in VD. Thus, it can be noted that, for the range between c _VD = 0.03–0.05, the model reproduces our physiological experiments even if the LD is, to a certain degree, active. When c _VD falls below 0.03 (parameter combinations falling in the orange checkerboard area), the orthodromic space constant will always be larger for the LD but the antidromic space constant will be larger for VD or larger for LD depending on the amplitude of the stimulus. For example, in the specific case where the amount of active conductances is the same in both dendrites (blue square, c _LD = c _VD = 0.02), the antidromic space constants will still be larger in the VD than in the LD for smaller stimulus amplitudes. The reason for this is the smaller cross‐sectional area of the distal segments of the VD that functionally expands the range at which smaller andidromic PSPs propagate in the VD. Taken together, these results confirm the robustness of our active model predictions and, more importantly, illustrate how introducing an asymmetry on the expression of active conductances can influence orthodromic and antidromic propagation in the dendrites beyond predictions based on geometry.

Discussion

Dendritic integration of synaptic inputs determines, to a large extent, the output response of a neuron. Hence, the effectiveness of any stimulus will depend on the degree of attenuation imposed by the specific properties of the dendritic tree. The M‐cell is shown to be a well‐suited preparation where such elementary questions can be examined in detail in an intact animal. The results of the present study show differential attenuation properties in the VD and LD arising at least partly from differences in cable properties and nonlinear behaviour of the respective dendritic membranes. As discussed below, these putative dendritic specializations, together with the observed cross‐modal dendritic interactions, match the requirements for processing realistic multimodal stimuli for predator avoidance.

Differential cable properties in M‐cell dendrites

We first tested whether PSPs with comparable transient waveforms are propagated differently in two main M‐cell dendrites. Sequential recordings along each dendrite showed that distally evoked transient PSPs attenuated more substantially in the VD than in the LD as they spread towards the soma (i.e, VD and LD showed a differential spatial decay of the signal) (Fig. 1). Consistent with the differential attenuation, we found that the orthodromic (dendro‐somatic) TR was lower in the VD compared to the LD (Fig. 4). Indeed, cable theory predicts that the consequence of a lower TR is a larger current loss and, consequently, a reduction in amplitude and slowing of the time course of the PSP along the VD compared to the LD (Rall, 1967; Rinzel & Rall, 1974).

Along with membrane resistance, geometry has been shown to be a major passive dendritic property determinant of signal propagation efficacy (Goldstein & Rall, 1974; Rinzel & Rall, 1974; Vetter et al. 2001; Gulledge et al. 2005). Consequently, attenuation differences between the dendrites might be partly explained by morphology asymmetries. We found that, once animal size difference is taken into account, dendritic morphology of the M‐cells is strikingly similar from animal to animal suggesting that the VD is slightly but consistently longer and thinner than the LD (Fig. 6 and Table 1). Both geometrical factors could account for differences in spatial decay as a result of its direct dependence on branch length and diameter (Rinzel & Rall, 1974; Holmes et al. 1992). Our anatomical results are in accordance with earlier morphological observations (Bartelmez, 1915; Bodian, 1952; Nakajima, 1974; Flores et al. 2008a).

That the observed differences in length and cross‐sectional area between the dendrites play a role for the higher spatial signal decay in the VD was tested further using a computational model of the M‐cell. This first model incorporates realistic morphology and assumed homogeneous membrane properties with no active conductances in the dendrites (i.e. passive membrane). Although the latter is probably unrealistic, the results suggest that morphological differences alone can qualitatively account for the differential spatial attenuation rates observed in the VD and LD.

The model was also informative about the contribution of secondary dendrites of the VD and LD. Providing the total dendritic surface is kept constant and the relative differences in main dendrite length and cross‐sectional area are preserved, a model that eliminates branching (i.e. secondary dendrites) still predicts a higher spatial decay rate in the VD, which implies that the higher decay ratio is not the result of a differential branching pattern between VD and LD (Goldstein & Rall, 1974). In addition, the fact that the M‐cell dendrites can be modelled as equivalent cylinders without losing predicting power considerably simplifies future modelling studies.

Possible contribution of active membrane properties and inhibition to dendritic filtering

Although the M‐cell dendrites are unable to generate dendritic spikes, our physiology results show that both the VD and LD behave nonlinearly above certain voltage depolarization (Fig. 5). The existence of this nonlinear voltage‐dependent behaviour is well documented for the soma and LD membrane (Faber & Korn, 1986; Neumeister et al. 2008; Medan & Preuss, 2011; Curtin et al. 2013). In the present study, we have demonstrated, for the first time, that the VD membrane not only shows similar voltage‐dependent properties as the LD when depolarized, but also the observed membrane nonlinearity appears to be more substantial in the VD than in the LD (Fig. 5 B). It has been proposed that the nonlinear behaviour of the LD is a result of the inactivation of voltage‐dependent inward rectifying K⁺ conductance (Faber & Korn, 1986), although the previous results could in principle also involve other types of K⁺ conductances. In either case, the inactivation of either conductance during sustained depolarization of the dendrites could increase the input resistance of the dendrites and effectively enlarge their space constant. Functionally, this could filter out small PSPs at the same time as boosting the large PSPs expected to be produced by massive sensory input signalling impending danger. Accordingly, this effect might play an important role in compensating the smaller space constant in the VD for visual stimuli with a sufficiently large amplitude (see below).

We also considered whether FFI plays a role in the differential decay rates observed in the VD and LD. However, we found that the inhibition evoked by tectal and sound stimuli to be comparable in magnitude and time‐course (Fig. 3). These similarities open up, at least hypothetically, the possibility that visual and auditory inputs activate a common pool of presynaptic inhibitory neurons, which are known in the M‐cell as passive hyperpolarizing potential cells (Diamond & Huxley, 1968; Korn & Faber, 2005).

Differential sensory processing in M‐cell dendrites

The size and time course of inputs to the LD and VD will depend on both stimulus characteristics and the engaged sensory pathways, which differ for the two modalities. The LD receives direct (di‐synaptic) from numerous (75–100) 8th nerve afferences that impinge onto the distal part of the dendrite via large (10 μm) mixed synapses (large club endings) comprised of gap junctions and chemical synapses (Bodian, 1952; Nakajima, 1974; Lin & Faber, 1988, 1988; Pereda et al. 2003). Particularly, electrotonic transmission has been shown to provide for massive synchronized input in response to an intense transient stimulus (e.g. sound pip or body blow) that can overcome the constrains impeded by the low input resistance (80–100 kΩ), high spiking threshold (RMP ≈ −82 mV; threshold ≈ −65 mV) of the M‐cell, as well as the action of FFI (Lin & Faber, 1988; Szabo et al. 2006; Weiss et al. 2008; Curti & Pereda, 2010). In the present study, we demonstrated that the passive and active membrane properties of the LD are probably well suited to propagate such transient PSPs.

The sensory pathway in the VD is less well understood than in the LD. Here, visual inputs from the retina are conveyed through a polysynaptic pathway via the optic tectum to distal parts of the dendrite. Our finding that a single tectal stimulus evoked short latency, transient PSPs with a fast rise time suggests that these inputs are monosynaptic and may also involve electrical synapses (Fig. 1) (Zottoli et al. 1987; Canfield 2003; Flores et al. 2008b). However, our results indicate that such a transient PSPs decay more abruptly when spreading to the soma. By contrast, a train of TS evoked a ramped‐type PSP, which was sometimes sufficient to trigger firing of the M‐cell (Fig. 1 C). Such a ramped‐type PSP will also benefit from the above mentioned nonlinear boosting effect that enhances the space constant in the VD. Indeed, visual loom stimuli, which reliably initiate startle escapes in goldfish, evoke PSPs that are characterized by fast components superimposed onto a ramped membrane depolarization (Preuss et al 2006) and are comparable to those evoked by the train of tectal stimulation. Looming sensitive neurons in the optic tectum are the probable source for such repetitive activity in the VD (Sajovic & Levinthal, 1983; Temizer et al. 2015; Dunn et al. 2016).

In sum, our results are consistent with the notion that postsynaptic membrane properties and synaptic specializations combine to preferentially propagate stronger and longer lasting stimuli in the M‐cell VD.

Cross‐dendritic propagation in the M‐cell

It is widely accepted that backpropagating APs can play a key role in information processing and synaptic plasticity (Goldstein & Rall, 1974; Stuart et al. 1997; Linden, 1999). AP backpropagation is strongly dependent on the number of branching points, dendrite morphology and expression of voltage‐gated channels (Goldstein & Rall, 1974; Vetter et al. 2001). Much less understood, however, is the potential role of backpropagating dendritic PSPs on information processing. As such, our result of a cross‐modal spread of visual and auditory evoked PSPs in the M‐cell dendrites provides a clear example of such a phenomenon. Specifically, we found that tectal and auditory evoked PSPs remain of sizeable amplitude in the cross‐modal dendrite. Such a cross‐dendritic PSP could putatively add to an appropriately timed orthodromic PSP (Canfield, 2003; Mu et al. 2012; Lacoste et al. 2015). Given that the M‐cell is a high threshold neuron that initiates startle behaviour via a single AP, such a summation probably provides for multimodal interactions that could change behavioural threshold. The functional significance of such a cross‐dendritic interactions is further enhanced through membrane non‐linearites in the LD and VD (see above) that, in principle, can account for supralinear multimodal integration in the M‐cell (C. McIntyre and T. Preuss, unpublished data).

Interestingly, our results show that the cross‐modal dendritic spread was asymmetric. Specifically, we found that the antidromic decay for PSPs is lower in the VD than in the LD, which was supported by consistent differences in cross‐dendritic transfer resistance (Figs 2 and 4 D). Functionally, this suggests a sensory order bias for multimodal interactions, namely, a larger effect if visual stimulus precedes an auditory stimulus, rather than the reverse. The former scenario might be indeed of value (e.g. when the fish process visual and auditory input provided by an approaching bird that hits the water surface).

Several non‐exclusive factors could explain the difference in antidromic propagation in the M‐cell dendrites. The first is geometry; however, our modelling results showed that M‐cell dendritic morphology alone is not sufficient to explain the differences between antidromic signal propagation in the two dendrites. An additional source for a differential modulation of antidromic signal propagation in dendrites is voltage‐dependent channels (Vetter et al. 2001; Johnston & Narayanan, 2008). Indeed, when active conductances were added to soma and proximal parts of the VD, our active model qualitatively reproduces the experimentally‐observed antidromic decay ratios, as well as the cross‐dendritic decay ratios and differences in cross‐dendritic TR (Fig. 8). We further tested how sensitive to variation in density and distribution of active conductance the predictions of the model were (Fig. 9 A). These additional simulations show that there is a relatively wide range of densities and types of distributions of the active conductances in the VD that will still produce higher orthodromic decay in the VD and higher antidromic decay in the LD.

It could also be possible that both dendrites express a similar pattern of active conductances, which nevertheless become engaged differently because of the size of the somatic PSP. As noted, similar sized synaptic responses produced at the distal VD or LD will undergo differential attenuation, effectively making LD inputs more easily engage active conductances in the VD. Although the PSP amplitude could certainly be part of the reason for the antidromic propagation differences, the difference in the nonlinear membrane behaviour upon depolarization of the VD and LD argues in favour of an additional mechanism (Fig. 5). In those experiments, we injected the same input at soma and measured the voltage response at about the same distance (200–300 μm) in either dendrite. The results showed that the VD has a significantly higher nonlinear behaviour implying a different (higher) excitability that was independent of stimulus amplitude because, in those experiments, we not only tested along range of stimulus intensities, but also used exactly the same stimulus (current ramp) for either dendrite.

Finally, our model implemented Na+ voltage‐dependent conductances that most probably do not represent the only type of active conductances the M‐cell express. Although we are aware that our model oversimplifies the diversity of putative voltage‐gated conductances expressed in the M‐cell, our proof‐of‐concept results emphasize the importance of voltage‐dependent conductances in signal processing as described in other neuronal types (Angelo & Margrie, 2011; Branco & Häusser, 2011; Harnett et al. 2012; Xu et al. 2012; Smith et al. 2013).

The present study shows that several factors probbaly contribute to differential propagation of visual and auditory inputs in the M‐cell including morphology, active conductances and the input dynamics of the stimulus. The larger orthodromic attenuation obtained for brief inputs in the VD could be counteracted by activation of nonlinear conductances only when inputs are sufficiently strong. In the LD, smaller passive attenuation would allow for effective propagation and boosting of brief PSPs. The combination of these mechanisms could functionally operate as a ‘selector’ ensuring only the appropriate stimulus (those unequivocally signalling an impending danger) triggers an M‐cell escape.

Contribution to signal processing by differences in dendrite properties has been extensively studied in vitro in neocortical pyramidal neurons (Stuart & Spruston, 1998), cerebellar Purkinje cells (Roth & Häusser, 2001; Branco & Häusser, 2011) and in modelled cortical and hippocampal interneurons (Emri et al. 2001; Eyal et al. 2014; Singh & Zald, 2015; Tran‐Van‐Minh et al. 2015). In vivo studies of dendritic processing using behaviourally relevant sensory stimuli are less common but include studies on the properties of pyramidal and cerebellar neurons (Jia et al. 2010; Xu et al. 2012; Smith et al. 2013; Ishikawa et al. 2015; Petersen, 2017), barrel cortex neurons (Varga et al. 2011), central complex neurons of Drosophila (Seelig & Jayaraman, 2013) and visual looming detectors of locust (Peron et al. 2009). In the present study, we performed in vivo intracellular recordings to investigate the dendritic filtering applied to behaviourally relevant sensory stimuli in the M‐cell. As such, our results provide an important contribution to the understanding of dendritic processing in an intact animal.

All animals face potentially dangerous situations, when the right decision taken at the right time is the difference between life and death. A predatory attack is an obvious example: sensory cues have to be integrated to decide when it is the right time to escape. When the neural integration of visual and auditory cues is accomplished by a single neuron, then dendrites should accommodate for those differences in stimulus dynamics. In the present study, we have found evidence for such dendritic specialization in the Mauthner cell. More generally, our results provide a compelling example of sensory specialization in neighbouring dendrites in a single neuron.

Additional information

Competing interests

The authors declare that they have no competing financial interests.

Author contributions

Experiments were performed at the Department of Psychology, Hunter College, City University of New York and Departamento de Fisiología y Biología Molecular y Celular, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires. VM and TP contributed to the conception and design of the work. VM, TMM, JS and TP contributed to acquisition, analysis and interpretation of the data. All authors contributed to drafting and revising the manuscript and approved the final version of the manuscript. All authors agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by a CONICET (PICT 20121578), Universidad de Buenos Aires (UBACyT 20020130300008BA and Thalmann Award, (VM)), as well as by a National Science Foundation Grant IOS 1147172, and awards from the Professional Staff Congress and the Research Foundation of the City University of New York (TP).