Learning Activity Predictors from Sensor Data: Algorithms, Evaluation, and Applications

Abstract

Recent progress in Internet of Things (IoT) platforms has allowed us to collect large amounts of sensing data. However, there are significant challenges in converting this large-scale sensing data into decisions for real-world applications. Motivated by applications like health monitoring and intervention and home automation we consider a novel problem called Activity Prediction, where the goal is to predict future activity occurrence times from sensor data. In this paper, we make three main contributions. First, we formulate and solve the activity prediction problem in the framework of imitation learning and reduce it to a simple regression learning problem. This approach allows us to leverage powerful regression learners that can reason about the relational structure of the problem with negligible computational overhead. Second, we present several metrics to evaluate activity predictors in the context of real-world applications. Third, we evaluate our approach using real sensor data collected from 24 smart home testbeds. We also embed the learned predictor into a mobile-device-based activity prompter and evaluate the app for 9 participants living in smart homes. Our results indicate that our activity predictor performs better than the baseline methods, and offers a simple approach for predicting activities from sensor data.

1 Introduction

Learning and understanding observed activities is at the center of many fields of study. An individual’s activities affect that individual, society, and the environment. Over the past decade, the maturing of data mining and pervasive computing technologies has made it possible to automate activity learning from sensor data. This activity information is now commonly utilized in applications from security systems to computer games. As a result of this technology push and application pull, robust approaches exist for labeling activities that occurred in the past or may be occurring in the present. In this paper, we propose to extend this recent work to look at activities that will occur in the future.

We study a novel problem called Activity Prediction, where the goal is to predict the future activity occurrence times from sensor data, and introduce a data-driven method for performing activity prediction. Activity prediction is valuable for providing activity-aware services including energy-efficient home automation, prompting-based interventions, and anomaly detection. However, activity prediction faces challenges not found in many other data mining tasks. In particular, sensor data are noisy, activity labels provided by activity recognition algorithms are subject to error, and the data contains rich relational and temporal relationships that must be exploited to be able to make highly-accurate predictions.

We formulate and solve the activity prediction problem as an instance of the imitation learning framework, where the training data provided by an activity recognition algorithm serves as the expert demonstrations. We provide a reduction of activity prediction learning to simple regression learning. This reduction allows us to leverage powerful off-the-shelf regression learners to learn an effective activity predictor that can reason about relational and temporal structure among the activities. Our approach naturally facilitates life-long learning, where the predictor can be improved based on new user data.

Selecting performance metrics for activity prediction is also challenging because there are multiple parameters that influence the desirability of the algorithm’s performance. We provide several evaluation metrics and discuss their usefulness in the context of real-world applications. We evaluate our activity prediction learning algorithms on twenty-four smart home sensor datasets and find that our proposed imitation-based methods not only outperform baseline predictors but predict a majority of the activities within minutes of their actual occurrence.

In addition, we embed our activity predictor inside an activity prompting algorithm and demonstrate the effectiveness of the prompting app for multiple participants living in smart homes. This prompting application demonstrates a potential real-world use of our prediction algorithms. The predictions are used to remind the users to perform certain daily activities. These interactions can help users live more independently and even positively influence their behavior.

We summarize our contributions as follows:

• Study a novel problem called Activity Prediction motivated by diverse real-world applications.

• Novel formulation of learning activity predictors in the framework of imitation learning and reduction to simple regression learning.

• Provide an evaluation methodology to measure the performance of a given activity predictor.

• Demonstrate good experimental results with our imitation-learning-based activity predictor on real sensor data collected from 24 smart home testbeds.

• Embed the learned predictor into a mobile-device-based activity prompter and evaluate the app on multiple participants living in smart homes.

In the next section, we formally describe the problem setup. This is followed by a description of both our independent and recurrent activity predictors. Next, we describe how activity recognition algorithms can be used to generate training data for learning activity predictors. Then, we describe various metrics for measuring the prediction performance, and provide experimental results comparing different predictors and analyze their performance. Finally, we describe an activity prompting mobile application we have used with a number of participants.

2 Problem Setup

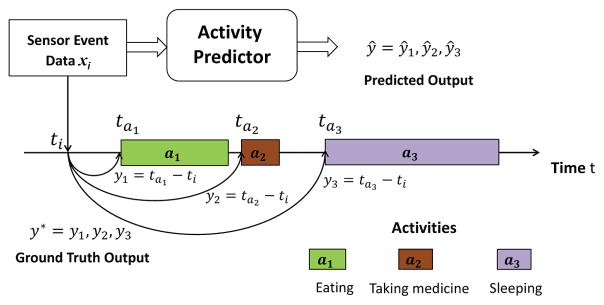
We consider the problem of Activity Prediction from sensor data. Let A = {a₁, a₂, ⋯, a_K} be a set of K activities, where a_j corresponds to the j^th activity class. Given features x ∈ ℜ^d extracted from the sensor data as input, an activity predictor generates ŷ = (ŷ₁, ŷ₂, ⋯, ŷ_K) as output. ŷ_j ∈ ℜ is the predicted relative next occurrence time of activity a_j, or the predicted number of time units that will pass until a_j occurs again. Fig. 1 provides an illustration of the activity prediction problem. Note that both the input features and output predictions correspond to individual sensor events occurring at specific points in time.

Fig. 1.

A high-level overview of the activity prediction problem. Given features x_i ∈ ℜ^d extracted from the current sensor event at time t_i as input, the activity predictor needs to predict the relative occurrence time of each activity. In this example, we have three activities: a₁ (eating); a₂ (taking medicine); and a₃ (sleeping). The starting times of activities a₁, a₂, and a₃ are t_a1, t_a2, and t_a3, respectively. Therefore, the ground-truth output is y^* = (y₁, y₂, y₃), where y_j = t_aj − t_i stands for the correct relative next occurrence time of activity a_j.

Our training data consists of a sequence of raw sensor events Λ = (λ₁, λ₂, ⋯, λ_N), where event λ_i corresponds to a sensor reading or sensor value with an associated timestamp t_i. We assume that an activity recognition (AR) algorithm is available to label each sensor event with its corresponding activity class and we use this information to train the activity predictor. An activity recognition algorithm learns a mapping from Λ to the corresponding activity labels, A_Λ. We first label the raw sensor events Λ using the activity recognizer and use this to generate training data for activity prediction at each time step t_i as illustrated in Fig. 1. We employ the AR algorithm from Cook et al. [1] that yields 95% recognition accuracy via 3-fold cross validation on the activities evaluated in this paper.

We further assume the availability of a feature function Φ that computes a d-dimensional feature vector Φ(λ_i) ∈ ℜ^d for any sensor event λ_i using the context of recent sensor events. We also assume a non-negative loss function L such that L(x, ŷ, y^*) ∈ ℜ⁺ is the loss associated with labeling a particular input x ∈ ℜ^d by output ŷ ∈ ℜ^K when the true output is y^* ∈ ℜ^K (e.g., RMSE). Our goal is to return a function/predictor whose predicted outputs have low expected loss.

3 Learning Algorithms

In this section we describe two algorithms for learning activity predictors: 1) The Independent Predictor (IP), a simple baseline approach, and 2) The Recurrent Activity Predictor (RAP), which is intended to improve on the baseline.

3.1 Independent Predictor

The Independent Predictor is our baseline activity predictor. As the name suggests, this predictor completely ignores the relational and temporal structure of the problem, and makes predictions using only the information from the most recent sensor events at a given time. The independent predictor is trained as follows. For each sensor event λ_i in the training sequence Λ, we extract the features x_i = Φ(λ_i) ∈ ℜ^d listed in Table 1 (input) and the ground-truth activity predictions ${\mathbf{y}}_i^{\ast }\in {\Re }^K$ (output) from the labeled activity segments (see Fig. 1 for an illustration). We learn an independent regressor Π_j for each activity a_j ∈ A as follows: for each sensor event λ_i in the training sequence Λ, we collect the input x_i and output $y_{ij}^{\ast }$ (the ground truth prediction for activity a_j), and give the aggregate set of input-output pairs ${\{{\mathbf{x}}_i,y_{ij}^{\ast }\}}_{i=1}^N$ (training examples) to a regression learner to minimize the given loss function L.

TABLE 1.

Activity prediction features.

Feature	Description
lastSensorEventHours+*	Hour of day for current event
lastSensorEventSeconds+*	Seconds since the beginning of the day for the current event
windowDuration+*	Window duration (sec)
timeSinceLastSensorEvent+*	Seconds since previous event
prevDominantSensor1+*	Most frequent sensor in the previ- ous window
prevDominantSensor2+*	Most frequent sensor in the win- dow before that
lastSensorID+*	Current event sensor
lastLocation+*	Most recent location sensor
sensorCount+**	Number of events in the window for each sensor
sensorElTime+**	Time since each sensor fired
timeStamp+*	Normalized time since beginning of the day
laggedTimeStamps*	Previous event timeStamps
laggedPredictions***	Previous event predictions
timeSinceLastPrediction****	Time since previous predictions
maximumValue#	Maximum value of sensor
minimumValue#	Minimum value of sensor
sum#	Sum of sensor values
mean#	Mean of sensor values
meanAbsoluteDeviation#	Average difference from mean
medianAbsoluteDeviation#	Avg. difference from median
standardDeviation#	Value standard deviation
coeffVariation#	Coefficient of value variation
numZeroCrossings#	Number of median crossings
percentiles#	Number below which a percent- age of values fall
sqSumPercentile#	Sq. sum values < percentile
interQuartileRange#	Difference between 25th and 75th percentiles
binCount#	Values binned into 10 bins
skewness#	Symmetry of values
kurtosis#	Measure of value “peakedness”
signalEnergy#	Sum of squares of values
logSignalEnergy#	Sum of logs of squares
signalPower#	SignalEnergy average
peakToPeak#	Maximum - minimum
avgTimeBetweenPeaks#	Time between local maxima
numPeaks#	Number of peaks

⁺Used for activity recognition.

^*Local features Ψ_local, one of each.

^**Local features Ψ_local, one sensorCount and one sensorElTime for each sensor used.

^***Context features Ψ_context, one per activity per context spot.

^****Context feature Ψ_context, one per context spot.

^#Based on window of recent values for each sensor.

During testing (or inference), we employ the K learned regressors independently on a given input x = Φ(λ) ∈ ℜ^d to compute the predicted output ŷ = (ŷ₁, ŷ₂, ⋯, ŷ_K), where ŷ_j = Π_j(x). The test-time complexity of this predictor is very low, which is valuable for making real-time predictions. However, the main weakness of this approach is that the recent sensor events may not provide sufficient context to make highly-accurate activity predictions, and it ignores the rich temporal structure of the problem.

3.2 Recurrent Activity Predictor

Notice that the independent predictor only uses the most recent sensor event data at a given time to make its predictions. To address this limitation, one could consider joint models by reasoning about the relationships between different activities and accounting for the temporal structure of the problem. It is important to note that the activity prediction problem can be viewed as a generalization of sequence labeling, where each output token is a vector of K values corresponding to the next activity occurrence time of each activity (K is the number of activities).

A natural solution would be to define a graphical model to encode the relationships between input and output variables at different time steps and learn the parameters from the training data [2]. However, such a graphical model may be very complex (large branching factor) and can pose severe learning and inference challenges. We may consider simplifying the model to allow for tractable learning and inference, but that can be detrimental to prediction accuracy. An alternate solution is to employ a heuristic inference method (e.g., loopy belief propagation or variational inference) with the complex model. Even though these methods have shown some success in practice, it is very difficult to characterize their solutions and predict when they will work well for a new problem. Therefore, we provide a simpler but effective solution that is based on imitation learning.

Imitation Learning Formulation

We formulate and solve the activity prediction problem in the framework of imitation learning. In traditional imitation learning, the goal of the learner is to learn to imitate the behavior of an expert performing a sequential-decision making task (e.g., playing a video game) in a way that generalizes to similar tasks or situations. Typically this is done by collecting a set of trajectories of the expert’s behavior (e.g., games played by the expert) on a set of training tasks. Then supervised learning is used to find a predictor that can replicate the decisions made on those trajectories. Often the supervised learning problem corresponds to learning a mapping from states to actions and off-the-shelf classification tools can be used. In our activity predictor learning problem, the expert demonstration corresponds to the correct activity predictions at different time steps (available for training data) and the expert behavior corresponds to predicting the best output ${\mathbf{y}}_i^{\ast }\in {\Re }^K$ at each time step i (see Fig. 1). In recent work, imitation learning techniques are successfully applied to solve a variety of structured prediction tasks in natural language processing and computer vision [3], [4], [5], [6], [7], [8]. However, to the best of our knowledge, imitation learning has not been used to solve activity learning tasks.

Main Challenges

The main challenge in applying imitation learning for solving the activity prediction problem is that the different output variables have structural dependencies as activities are related to each other. Therefore, the predictor Π should jointly reason about all the activities to compute the predicted output ŷ = (ŷ₁, ŷ₂, ⋯, ŷ_K). Unfortunately, the size of the joint output space is exponential, which renders the straightforward application of the above imitation learning formulation impractical.

Pseudo-Independent Predictors

To address the aforementioned challenges, we employ pseudo-independent predictors to achieve tractability without losing accuracy. Specifically, we assign one predictor Π_j to each activity a_j. These predictors are not completely independent, but are pseudo-independent in the sense that each predictor predicts the output for only a single activity but has the previous predictions from all the other predictors available as part of the input (context) while making predictions. The main advantage of this pseudo-independent formulation is that it allows us to encode arbitrary relationships between activities and the temporal structure as context features, and is highly efficient in terms of training and testing without much loss in accuracy.

Algorithm 1.

RAP Learning via Exact Imitation

Input: Λ = Training sequence of sensor event data labeled with activity segments, L = Loss function
Output: Π, the recurrent predictor
1:	for each activity predictor j = 1 to K do
2:	Initialize the set of regression examples 𝒟j = ∅
3:	end for
4:	for each time step i = 1 to N do
5:	for each activity predictor j = 1 to K do
6:	Compute Ψlocal(i) = Φ(λi)
7:	Compute Ψcontext(i, j)
8:	Joint features Ψij = Ψlocal(i) ⊕ Ψcontext(i, j)
9:	Compute best output $y_{ij}^{\ast }\in \Re$ using L
10:	Add regression example (Ψij, $y_{ij}^{\ast }$) to 𝒟j
11:	end for
12:	end for
13:	for each activity predictor j = 1 to K do
14:	Πj =Regression-Learner(𝒟j)
15:	end for
16:	return learned predictor Π = (Π1,Π2, ⋯,ΠK)

Pseudo-Independent Representation

For learning and making predictions, we need a feature representation for each of our pseudo-independent predictors. The predictor Π_j for activity a_j will employ both local features Ψ_local(i) = Φ(λ_i) (see Table 1) and prediction context features Ψ_context(i, j). The context features Ψ_context(i, j) consist of the activity time predictions ŷ for H previous events. We exclude the predictions for the activity being predicted (a_j) while including a separate feature indicating the seconds that elapsed since each of the H previous events. The context feature vector is of size H · K.

Exact-Imitation Approach

Algorithm 1 provides the pseudo-code for our recurrent activity predictor learning via exact imitation of the correct activity prediction trajectory. At each time step i, for each activity predictor Π_j, we compute the joint features Ψ_ij = Ψ_local(i) ⊕ Ψ_context(i, j) (input) and the best activity prediction $y_{ij}^{\ast }\in \mathfrak{R}$ (output) from the training data, where ⊕ refers to the vector concatenation operator. Note that for the exact imitation training, context features consist of ground-truth labels from the previous events. The aggregate set of input-output pairs ${\{{\mathrm{\Psi }}_{ij},y_{ij}^{\ast }\}}_{i=1}^N$ (training examples) for each activity predictor Π_j is given to a regression learner to learn Π_j by minimizing the given loss function L. Typically, incorporating L entails using labeled training data to learn a mapping from the feature vector to activity predictions y_ij. However, using L allows for flexibility in learning the output labels (coarser or finer) for a given application. If we can learn a function Π = (Π₁, Π₂, ⋯, Π_K) that is consistent with all these imitation examples, then it can be proved that the learned function will generalize and perform well on new instances [9].

DAgger Algorithm

One issue with exact imitation training is error propagation: errors in early time steps can propagate to downstream decisions and can lead to poor global performance [10]. Therefore, we employ a more advanced imitation learning algorithm called DAgger (Dataset Aggregation) [9] to learn robust predictors. DAgger is an iterative algorithm that can be viewed as generating a sequence of predictors (one per iteration), where the first iteration corresponds to exact imitation training. In each subsequent iteration, DAgger makes decisions with the predictor from the previous iteration, and generates additional training examples to learn to recover from any errors. A new predictor is learned from the aggregate set of training examples. In the end, the final predictor is selected based on a validation set. DAgger has valuable theoretical properties and can be seen as a no-regret online learning algorithm [9]. If we deploy the learned recurrent predictor in a real-life application, then the predictor can be adapted in real time based on feedback from the users, and the DAgger algorithm can be employed to naturally facilitate a life-long learning setting.

Algorithm 2 provides the pseudo-code for recurrent activity predictor learning via DAgger. In each iteration k of DAgger, we combine the predictor from previous iteration Π̂^k and the oracle predictor Π^* (predicts correctly using the training data) using a mixture parameter β_k ∈ [0, 1] to form the current policy Π^k that will be used to make the decisions. At each decision step, we flip a coin with bias β_k. If the coin turns up heads, we get the correct prediction from the oracle predictor Π^*. Otherwise, we ask predictor Π^k to make the prediction. Intuitively, the mixture parameter β_k allows us to generate diverse training examples.

At each time step i, for each activity predictor Π_j, we use the local features Ψ_local(i) (these features do not change during training) and the context features Ψ_context(i, j) based on the predictions of the current policy Π^k (these features can change as they depend on the previous predictions) to compute the predicted output ŷ_ij. We compare the predicted output ŷ_ij with the correct output $y_{ij}^{\ast }$ using the error threshold ε_j. If the difference between the predicted time and correct time for an activity class a_j is more than the allowed error ε_j, we call it a mistake. For each mistake, we use the input vector with context features from Π^k that was used to form the prediction, along with the ground-truth activity time ${\mathbf{y}}_i^{\ast }$, to generate a new training example and add it to the aggregate set of examples 𝒟_j.

At the end of each DAgger iteration k, the aggregate set of training examples 𝒟_j for each activity predictor Π_j is given to a regression learner to learn a new Π_j by minimizing the given loss function L. Π̂^k+1 = (Π₁, Π₂, ⋯, Π_K) is the new recurrent predictor, where Π_j is the new regressor learned from the aggregate set of training examples 𝒟_j. In the end, the final recurrent predictor is selected from the sequence of predictors based on the validation data.

Regression Learner

Recall that both of our activity predictor learning algorithms need a cost-sensitive regression learner. We have a hard learning problem at hand, which means linear functions will not suffice. Individual regression trees did not effectively learn these predictions due to high variance in activity times. Hence, we employ a random forest of 100 regression trees for this task [11].

Algorithm 2.

RAP Learning via DAgger

Input: 𝒟 = Training examples, dmax = dagger iterations, ε = (ε1, ε2, ⋯, εK) = error threshold vector
Output: Π, the recurrent predictor
1:	for each activity predictor j = 1 to K do
2:	Initialize 𝒟j with regression examples from exact imitation
3:	Πj =Regression-Learner(𝒟j)
4:	end for
5:	Initialization: Π̂1 = (Π1,Π2, ⋯,ΠK)
6:	for each dagger iteration k = 1 to dmax do
7:	Current Policy: Πk = βkΠ*+(1−βk)Π̂k//Π* is the oracle predictor
8:	for each time step i = 1 to N do
9:	for each activity predictor j = 1 to K do
10:	Compute Ψlocal(i) = Φ(λi)
11:	Compute Ψcontext(i, j) using context predictions from Πk
12:	Joint features Ψij = Ψlocal(i) ⊕ Ψcontext(i, j)
13:	Compute predicted output ŷij ∈ ℜ using Πk from Ψij
14:	Compute correct output $y_{ij}^{\ast }\in \Re$ using oracle predictor Π*
15:	if |Πk(Ψij) − Π*(Ψij)| ≥ εj then
16:	Add regression example (Ψij, $y_{ij}^{\ast }$) to 𝒟j
17:	end if
18:	end for
19:	end for
20:	for each activity predictor j = 1 to K do
21:	Πj =Regression-Learner(𝒟j)//learn from aggregate data
22:	end for
23:	Π̂k+1 = (Π1,Π2, ⋯,ΠK)//new recurrent predictor
24:	end for
25:	return best predictor Π̂k on the validation data

4 Training Data Generation via Activity

Recognizer

Time series forecasting uses a model to predict future values of a target variable based on previously observed values of the variable. In the case of activity forecasting, or activity prediction, the target variable is the number of time units that will elapse until a particular activity of interest will occur again. In order to base this prediction on previously observed values, we need to know when the activity occurred in the past. For this we rely on automated activity recognition. The challenge of activity recognition is to map sensor events to a label that indicates the corresponding activity the individual is performing. As with activity prediction, the activity recognition data consists of raw sensor events, Λ (see Section 2). Features x_i are extracted from the sensor events at time t_i and a supervised learning algorithm maps the features onto a value from A which indicates the activity that is being performed.

Our activity recognizer builds on the AR algorithm from Krishnan and Cook [12] to perform real-time activity labeling on streaming data. AR extracts features from a sliding window containing w consecutive sensor events, λ_i–w … λ_i, and learns a function that maps the feature vector x_i onto an activity label indicating the activity that is performed at the time of the last event in the window, or time t_i. The features that are used for the activity models in this paper are listed in Table 1. While the size of the window can be adjusted based on the most likely current activities, for our experiments we set the window size w to be 30.

Because of the insight that automated activity recognition sheds on human behavior and the valuable context activity labels bring to technology customization, activity recognition is a highly-investigated area of research [13], [14], [15], [16], [17]. Methods have been developed that encompass a diversity of sensor platforms including ambient sensors, wearable or phone sensors, and audio or video data. While AR utilizes a decision tree to learn activity models, these models can be created from a variety of learning approaches including support vector machines, Gaussian mixture models, and probabilistic approaches such as naïve Bayes, hidden Markov models, and conditional random fields [13], [14], [18], [19], [20], [21]. These models trade off computational cost, the type of sensor data that can be processed, and recognition accuracy/sensitivity. Unlike many of these earlier efforts, AR handles data that is collected in real-world settings with no data segmentation or participant scripting. It handles recognition in environments with multiple residents and with interwoven activities [12].

To train AR, we provide labels for at least one month of sensor data from each smart home location. Human annotators label the sensor events in each dataset with corresponding activities based upon interviews with the residents, photographs of the home, and a floorplan highlighting the locations of sensors in the space. Sensor events are labeled with the activity that was determined to be occurring in the home at that time. The datasets contain 120 activity classes in total, but many of them appear infrequently. For our experiments, we focus on 11 core activities that occur daily in a majority of the datasets. These activities, listed in Table 3, represent complex activities of daily living that are reflective of the resident’s daily health and functioning [22]. Sensor events that do not fit into one of the core activity classes are labeled as “Other Activity” and provide context for AR as well as for the activity predictor. To maximize consistency of ground truth labels, multiple annotators look at the datasets and disagreements between labels are resolved via discussion. The annotators demonstrate an overall interannotator agreement of κ = 0.85.

TABLE 3.

Activity classes.

Activity	Sensor Events
Bathe	208,119
Bed-Toilet Transition	174,047
Cook	2,614,836
Eat	585,377
Enter Home	174,486
Leave Home	311,164
Personal Hygiene	1,916,646
Relax	2,031,609
Sleep	732,785
Wash Dishes	1,139,057
Work	2,028,419

We evaluate the accuracy of AR using two methods and utilize the accuracy results in the analysis of our activity predictor. First, we measure AR recognition performance using 10-fold cross validation on the annotated sensor data for the 11 activities. Using this method, AR achieves a 96% accuracy for the datasets analyzed in this paper.

Our second evaluation method pairs AR with ecological momentary assessment (EMA) [23]. EMA is considered a reliable measurement technique in the psychology and sociology literature for recording events and behavior data in a natural setting [24], [25]. The idea is to query participants about the activity they are currently performing in order to obtain the most accurate, in-the-moment information about their behaviors. We collect this information using an EMA app that brings up an activity query at random times throughout the day, as shown in Fig. 2. The queried activity label is provided by AR. If AR does not guess the current activity correctly, the user can optionally provide the correct current activity label in order to better train the model. We collected 291 query responses from 8 smart home sites. From the results we observe an 86% accuracy rate for AR. We will utilize both of these baseline performance results as we evaluate our activity predictors.

Fig. 2.

Example prompt for the EMA app.

5 Evaluation Methodology

In this section, we will review and introduce several metrics to evaluate activity prediction algorithms in the context of real-world applications. To compare the effectiveness of different solution approaches for a given problem, the evaluation metrics must be carefully chosen. The quality and usefulness of a particular metric will vary based on the application and specific evaluation criteria. Many metrics tend to emphasize particular aspects of the results, so choosing multiple metrics can be necessary to completely understand the effectiveness of an approach.

Challenges

Selecting performance metrics for activity prediction is challenging because there are multiple parameters that influence the desirability of the algorithm’s performance. Activity predictors can be evaluated in multiple ways, depending upon the type of performance that is desired. First, activity prediction can be viewed as a type of classification task in which any prediction that has nonzero error (or error greater than a threshold) is considered a mis-labeled data point. In this case, traditional classifier-based performance measures can be utilized. Second, activity prediction can be considered as a type of forecasting algorithm. Viewed in this light, error is proportionate to the numeric distance between the predicted and actual values. In addition, activity prediction relies on the effectiveness of an online activity recognition algorithm. The performance of the activity predictor is not anticipated to exceed the reliability of the activity recognizer that is being used to train the predictor. The activity recognizer, in turn, is trained using hand-annotated data which may be inconsistently labeled.

Evaluation Metrics

We introduce several evaluation metrics and employ them to validate our prediction algorithms. Using our previous notation, ŷ_i represents a vector of predicted outputs for a sensor event in the evaluation dataset with elements ŷ_ij. ${\mathbf{y}}_i^{\ast }$ is the vector of true values for the same event with elements $y_{ij}^{\ast }$. Note that we have K activities in total. Each evaluation metric takes a predicted output ŷ_i and ground truth output ${\mathbf{y}}_i^{\ast }$ as input, and returns a real-value indicating the quality of the prediction. One could perform macro-averaging of metric values over different testing instances and datasets to compute aggregate values.

Mean absolute error (MAE), as defined in (1), provides a measure of the average absolute error between the predicted output and ground-truth output. It is similar to another well-known metric, root mean squared error (RMSE), defined in (2). Both of these measures provide the average error in real units and quantify the overall error rate, with a value of zero indicating a perfect predictor and no upper limit. Because RMSE squares each term, it does bring a disadvantage in effectively weighting large errors more heavily than small ones.

$$\text{MAE}=\frac{\sum \mid {\widehat{y}}_{ij}-y_{ij}^{\ast }\mid }{K}$$ (1)

$$\text{RMSE}=\sqrt{\frac{\sum {({\widehat{y}}_{ij}-y_{ij}^{\ast })}^2}{K}}$$ (2)

If the activities have varying levels of importance, we may want to use an error measure that places more emphasis on some activities than others (e.g., weighted RMSE). This might be the case if a particular activity needs to be predicted very accurately, for example. Additionally, we may need to compare results across activities or datasets where the time spacing between activity occurrences may be different. In these cases, measures such as MAE and RMSE do not give an indication of the relative error. For example, an error of 60 minutes in predicting a time-critical activity (e.g., taking medicine) may be unacceptable, but may be acceptable for other activities that do not need to happen at a certain time (e.g., housekeeping). In such situations, we may want to use a normalized error, such as range-normalized RMSE (NRMSE), defined in (3). Here, the minimum and maximum functions are computed over all ground-truth values of the test instances we are evaluating. This metric would usually be applied on each activity or dataset that we wish to separate. While NRMSE is convenient for comparing results from different sets, it does not have a well-defined normalization factor with which we can evaluate the actual magnitude of the errors.

$$\text{NRMSE}=\frac{\mathit{RMSE}}{max(y_{ij}^{\ast })-min(y_{ij}^{\ast })}$$ (3)

Another useful normalized metric is mean absolute percentage error (MAPE), defined in (4). MAPE normalizes each error value for each prediction by the true value $y_{ij}^{\ast }$ we are trying to predict. This metric allows us to normalize the error individually for each prediction. We can also quickly determine approximately how large the error is since it is a percentage of the true activity time. However, as $y_{ij}^{\ast }$ approaches zero (i.e., the activity is about to occur), an error of any insignificant amount can cause the element in the summation to become large. This leads to inflation of the MAPE value due to a few outlier cases where the error is small but the true activity time is even smaller.

$$\text{MAPE}=\frac{\sum \frac{\mid {\widehat{y}}_{ij}-y_{ij}^{\ast }\mid }{y_{ij}^{\ast }}}{K}$$ (4)

Since the metrics we have listed so far are based on finding the averages of all errors, they are sensitive to possible distortion by outliers. As a result, the metrics can often have large values. In order to analyze the effects of outliers, other evaluation metrics can be used. One metric we introduce for this purpose is the error threshold fraction (ETF), defined in (5). $I({\widehat{y}}_{ij},y_{ij}^{\ast })=1$ if $\mid {\widehat{y}}_{ij}-y_{ij}^{\ast }\mid \le v$ and 0 otherwise. Note that the numerator of the fraction is a count of the number of events with error below the threshold v. This metric indicates the fraction of the errors that are below the time threshold v. v should be non-negative, and lim_v→∞ ETF(v) = 1. By varying v we can ascertain how the errors are distributed; if we find that the ETF does not approach 1 until v is large, this may indicate that there are a significant number of large-error outliers. ETF(0) indicates the number of predictions which had zero error.

$$\text{ETF}(v)=\frac{\sum I({\widehat{y}}_{ij},y_{ij}^{\ast })}{K}$$ (5)

Yet another metric to consider is Pearson’s r, i.e., the correlation coefficient between the predicted and actual activity occurrence times. This measure, shown in (6), does not quantify the amount of error but does indicate the relationship between the predicted and actual values.

$$\mathrm{r}=\frac{\sum ({\widehat{\mathrm{y}}}_{\text{ij}}-\overline{{\widehat{\mathrm{y}}}_{\text{ij}}})({\mathrm{y}}_{\text{ij}}^{\ast }-\overline{{\mathrm{y}}_{\text{ij}}^{\ast }})}{\sqrt{\sum ({\widehat{\mathrm{y}}}_{\text{ij}}-\overline{{\widehat{\mathrm{y}}}_{\text{ij}}})\sqrt{\sum ({\mathrm{y}}_{\text{ij}}^{\ast }-\overline{{\mathrm{y}}_{\text{ij}}^{\ast }})}}}$$ (6)

In addition, during evaluation we need to consider the following sources of error and imprecision in the data:

1. Ground truth labels. Inaccurate class labels represent a source of error that exists in many datasets. We estimate the amount of error in ground truth activity labels by measuring inter-annotator agreement, or the degree of agreement of the activity labels between multiple annotators. This is typically represented using Cohen’s kappa [26].

2. Activity recognition accuracy. In general, the activity recognition model is trained using a limited set of training data. The trained model will then be used to generate activity labels for previously-unseen data. The model itself may be subject to error due to representational limitations, small training set, or shortcomings of the employed learning algorithm.

3. Predictor error. In the same way that the activity recognition algorithm will likely experience some error, so also an imperfect activity prediction algorithm will generate erroneous predictions.

Unlike classification algorithms, where an accuracy of 100% is expected, in this case the expected accuracy will be limited based on the quality of the labels. As a result, the evaluation metrics that are discussed here can be κ-normalized to reflect the same accuracy range that would be considered for a perfect dataset, while being sensitive to label noise that is known to be present in the data.

6 Experiments and Results

In this section we empirically evaluate and compare our activity predictors on real-world data using the evaluation metrics introduced in Section 5.

6.1 Experimental Setup

Datasets

We evaluate our activity prediction algorithm using sensor and activity data collected from 24 CASAS smart homes¹. Descriptions of the datasets are provided in Table 2. Each CASAS smart home test bed used in this evaluation includes at least one bedroom, a kitchen, a dining area, and at least one bathroom. While the sizes and layouts of the apartments vary, each home is equipped with combination motion/light sensors on the ceilings as well as combination door/temperature sensors on cabinets and external doors. Sensors unobtrusively and continuously collect data while residents perform their normal daily routines. Fig. 3 shows a sample layout and sensor placement for one of the smart home test beds. Each smart home sensor event is labeled by AR; these labels are collectively used to determine the ground-truth activity predictions y^* at any given time. The predictors were trained and tested separately for each dataset. The 11 activities used by both AR and the predictors are shown in Table 3.

TABLE 2.

CASAS smart home datasets used to evaluate activity predictors.

ID	Residents	Time Span	Sensors	Sensor Events
1	1	2 months	36	219,784
2	1	2 months	54	280,318
3	1	2 months	26	112,169
4	1	2 months	66	344,160
5	1	2 months	60	146,395
6	1	2 months	60	201,735
7	2	1 month	54	199,383
8	1	2 months	54	284,677
9	1	2 months	44	399,135
10	1	1 month	38	98,358
11	1	2 months	54	219,477
12	1	4 months	40	468,477
13	1	12 months	58	1,643,113
14	1	1 month	32	133,874
15	1	10 months	40	1,591,442
16	1	2 months	38	386,887
17	1	12 months	32	767,050
18	1	1 month	46	178,493
19	1	1 month	36	92,000
20	1	2 months	40	217,829
21	2	10 months	62	3,361,406
22	1	2 months	56	247,434
23	1	1 month	32	106,836
24	1	2 months	34	216,245

Fig. 3.

Floor plan of one CASAS smart home testbed. The location of each sensor is indicated with the corresponding motion (M), light (LS), door (D), or temperature (T) sensor number.

Activity Prediction Algorithms

We evaluate two forms of our Recurrent Activity Predictor (RAP). The first is RAP with Exact Imitation (RAP-EI), which uses the exact-imitation approach described in Section 3.2. The second version is RAP with DAgger (RAP-DAgger), using the DAgger approach to improve the predictor with new training values. We also evaluate the Independent Predictor (IP) as a informed baseline.

For all three algorithms, we employ the local features Ψ_local(i) described in Table 1. These features are generated directly from recent sensor events and highlight in- formation contained in those events. For the RAP-EI and RAP-DAgger algorithms, we also use context features Ψ_context(i, j) listed in Table 1. For each activity’s predictor model, these context features consist of the previous predictions for all activities except for the activity being predicted. The number of previous predictions used is determined by the context size H. To account for uneven time spacing between events, the time since each set of previous predictions is also included.

We also create a second baseline called Exponential, which is uninformed. This method does not learn a complex model of activity times. Instead, it models the relative times of each occurrence for each activity as an exponential distribution. The Exponential method then samples from the distribution in order to generate activity predictions.

6.2 Evaluation Procedure

To evaluate the performance of our predictors on these temporal datasets, we employ a sliding window validation procedure. This method is similar to k-fold cross-validation, but allows us to maintain the temporal ordering of the sensor event data. We select a window of N=2000 events which we use along with the corresponding ground-truth values as the training examples ${\{{\mathbf{x}}_i,{\mathbf{y}}_i^{\ast }\}}_{i=1}^{N=2000}$. We learn a predictor from this training data and employ it to make predictions for the next 5000 events after the window. The window is then shifted forward by 1000 events and the process is repeated. For exact-imitation training, the lag (context) values are provided using the ground-truth values from the training data, while the predicted values are employed during testing.

6.3 Varying Context Size

The performance of the recurrent predictors varies based on the the context size. In order to determine the optimal context size, we vary the size and observe the effects on the RAP-EI and RAP-DAgger predictors. These tests are performed using the first month of data from each dataset.

The average MAE for both methods (aggregated across all one-month datasets) is shown in Fig. 4. As context size increases, performance for both RAP-EI and RAP-DAgger improve until performance plateaus. Beyond this point, adding more context features does not further improve performance. For RAP-EI, this point is around H = 20. RAP-DAgger continues to see improvement up until H = 40, however the most of the improvement has been achieved by a context size of H = 20.

Fig. 4.

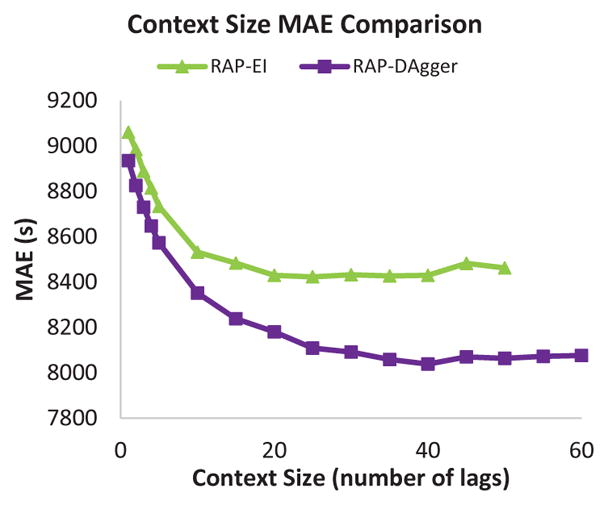
Average MAE based on context size aggregated over one-month subsets of all datasets.

Based on these results, we find a context size of H = 20 previous events to be a good choice. This provides the majority of the benefit gained from a larger context size. Increasing the context size further may provide a small benefit, however the complexity increases as the context size increases.

6.4 Comparison of Different Predictors

Building on the results of the previous section, we now compare the performance of each predictor method using a context size of H = 20 previous predictions for the recurrent predictors. For these tests, we use the full datasets described in Table 2 and activity labels provided by AR. We compare the following four methods:

• Exponential Baseline

• Independent Predictor (IP)

• RAP-EI with context H = 20

• RAP-DAgger with d_max = 5 iterations, β = 0, and H = 20

For RAP-DAgger, we chose d_max = 5 based on previous experience with DAgger which indicates most performance gains are acheived by the 5^th iteration. Previous experience has also indicated that β close to zero usually provides the best results.

IP vs RAP-EI

Table 4 shows the average MAE and RMSE results for each of the methods. IP had an average MAE of 9,294 seconds (about 2.5 hours). The RAP-EI method improves on this, reducing the MAE by about 630 seconds. The RMSE is improved by about 1,900 seconds, or about one half-hour. We also note that the RMSE values can be dramatically influenced by the outliers. There are a few datapoints in which the predicted activity time is off by almost a day. RMSE squares each error there by the average performance measure can be biased by these few outliers. We conclude that to examine the overall performance of the predictors, MAE is a better measure.

TABLE 4.

MAE and RMSE results for predictors in seconds, averaged over all datasets. RAP predictors use context size H=20. A one-way ANOVA indicates that the performance differences are extremely significant (p < .01).

Method	MAE	RMSE
Exponential	13,709.05	27,772.89
IP	9,294.48	21,370.18
RAP-EI	8,661.30	19,439.62
RAP-DAgger	8,402.01	19,114.13

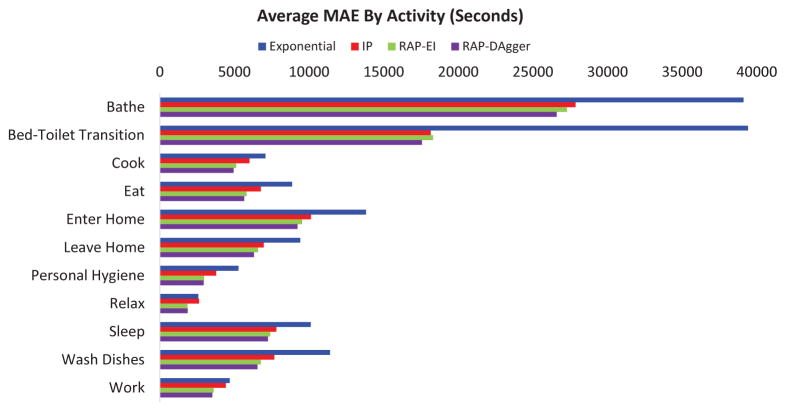
The average MAE results for each activity are shown in Fig. 5. RAP-EI outperforms IP on all activities except for Bed-Toilet Transition. This activity is one which can occur at different times during the night, usually unrelated to other activities. Hence, the activity context features used in RAP-EI do not provide any additional information for predicting Bed-Toilet Transitions and may result in higher error. We note that the performance of RAP-EI shows increased improvement over IP for activities such as Cook, Eat, Personal Hygiene, and Wash Dishes. These activities tend to be highly related to each other (e.g., the resident cooks and then eats their meal, followed closely by washing dishes and then brushing their teeth). The context features allow the recurrent predictor to discover these activity relationships to improve its performance over the independent predictor. As with the overall results, these MAE values show that RAP-EI generally has better performance compared to IP.

Fig. 5.

Average MAE for each activity. These values were averaged for each activity across all datasets.

We also note that the amount of tolerated error may be different for each activity. For example, an error of a few hours may be acceptable when predicting the Relax activity, while it may be intolerable when predicting Work. The amount of tolerable error will be dependent on the context in which the predictions will be used. However, the error seen here is small enough to be useful for many applications such as activity prompting and energy-efficient home automation [27].

Fig. 6 shows the ETF values for varying thresholds. The independent predictor has about 9% of its errors below 30 seconds. RAP-EI has about twice as many errors (17%) below 30 seconds. Similarly, 45% of RAP-EI errors are below 30 minutes, compared to only 37% of IP errors. These results indicate that not only does RAP-EI provide improved overall performance, but it also is able to have a greater number of its errors below one hour compared to IP. We also note that the majority of both IP and RAP-EI predictions are within one hour of the actual time, which is sufficient for many applications.

Fig. 6.

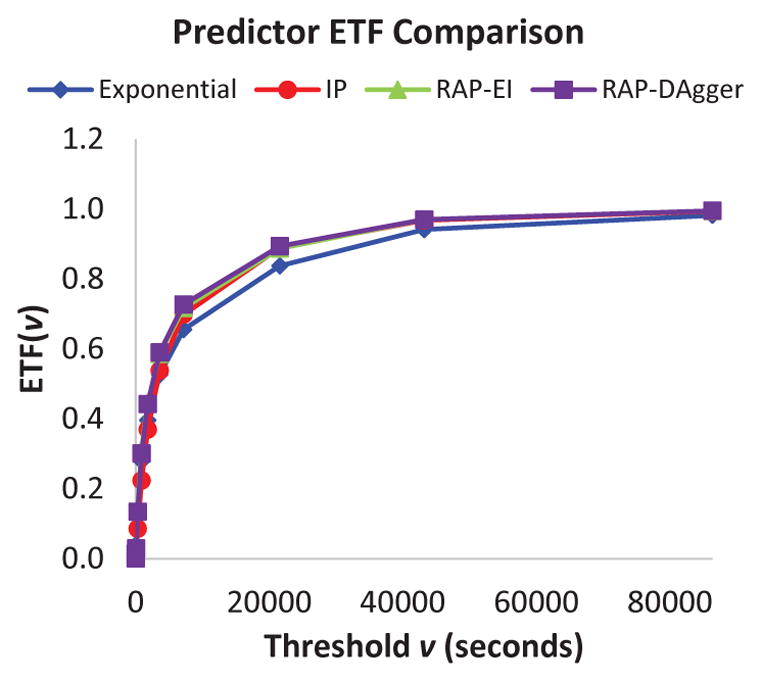
ETF plotted for each predictor. Threshold values range from one second up to one day.

We note that both IP and RAP-EI outperform the random Exponential predictor in most respects. They show significant improvement in terms of overall MAE and RMSE. The Exponential predictor outperforms IP on the Relax activity. However, this is likely due to the fact that the Relax activity occurs frequently throughout the day, resulting in the actual activity times being similar to the mean of the random distribution. Consequentially, the Exponential predictor is able to form predictions that are, on average, closer to the actual times. However, the ETF values indicate that more of the Exponential errors are larger than one hour, as the baseline does not actively adjust its predictions for smaller time differences. Thus, the informed predictions from IP and the RAP predictors show an improvement over the uninformed baseline prediction.

RAP-IE vs RAP-DAgger

We also examine the performance improvement that can be gained using DAgger to refine the exact imitation predictor. RAP-DAgger shows a greater overall performance in terms of both MAE and RMSE compared to RAP-EI. This indicates that the diversification of training examples gained through DAgger allows the predictor to increase its ability to correct from errors. This is also demonstrated by the results in Fig. 5, where RAP-DAgger outperforms RAP-EI for almost all activities. We note that the performance improvement is small compared to that between IP and RAP-EI. However, adding more DAgger iterations or increasing the context size should lead to increased performance.

The ETF plot of Fig. 6 indicates that RAP-EI slightly outperforms RAP-DAgger for smaller error sizes. However, RAP-DAgger has more of its errors below larger thresholds such as 6 hours. This indicates that the improvements from DAgger reduce the number of larger outlier errors. Furthermore, the fraction differences between the two predictors are small for the lower thresholds.

Area Under ETF Curves

We note the similarity between the ETF curves in Fig. 6 and a standard ROC curve. In this case, the discrimination threshold is based on the time-based threshold for prediction error. As with the Area Under a ROC Curve, a perfect predictor will have an Area Under the ETF Curve (AUETF) of 1.0. The AUETF values for our predictors are given in Table 5. Consistent with the ETF plots, the RAP-EI and RAP-DAgger methods outperform IP and all informed predictors outperform the Exponential method.

TABLE 5.

Area under the ETF curve (AUETF) values for each predictor.

Method	AUET F
Exponential	0.8672
IP	0.8946
RAP-EI	0.9008
RAP-DAgger	0.9036

Behavior Over Time

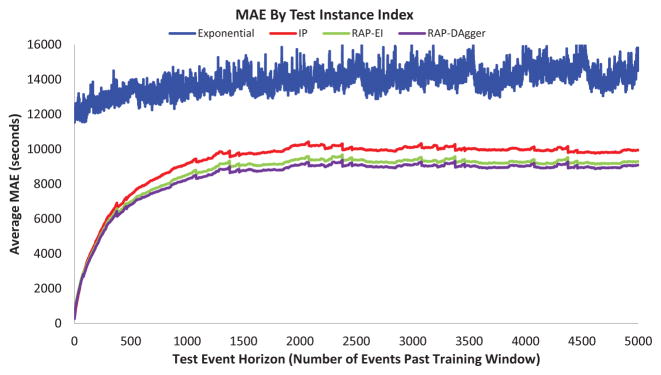
It is also of interest to examine how the error for each method changes as we move further from the training window. Fig. 7 shows the average MAE at each test horizon against how far that horizon was from the training window. For all methods except the Exponential, the average error is relatively low just after the training window (around 5 minutes). The error generally increases as the test event gets further from the training window. IP has a slightly higher error than RAP-EI, which in turn has a slightly higher error than RAP-DAgger. All three have much lower error at all event horizons compared to the random Exponential.

Fig. 7.

MAE plotted for each predictor against the test horizon. The test horizon indicates how far (in number of events) the test event is from the end of the training window. MAE values are averaged over all activities and datasets at each test horizon.

For all predictors, the error tends to increase as the event horizon moves away from the training window. However, IP and both RAP predictors stabilize after about 2,000 events at error values of about 2 hours, respectively. We suspect that the error rates are partially related to the size of the training window used. While the event frequency is different for each dataset, 5000 events is approximately a day or two in length. At 2000 events, the training window is relatively small compared to the size of the datasets, but this window size was chosen to provide a sufficient number of test windows for computing the evaluation metrics. It is likely that increasing the training window size (and thus allowing more of the residents’ activities to be observed) may reduce the error rates for the predictors. This hypothesis is supported by the results from the prompting app evaluation, shown in the next section. The predictors used for the app were trained with more than a month of data and had error rates below an hour even at more than two weeks beyond the training window.

7 Activity Prompting

The ability to predict, or forecast, future occurrences of activities can play a central role in activity prompting. Activity prompting can be used to remind a memory-impaired individual of an activity they typically perform or to encourage integration of a new healthy behavior into a normal routine. Prompting technologies have been shown to increase adherence to medical interventions, decrease errors in activities of daily living, and increase both independence and engagement for individuals with cognitive impairment [28], [29], [30], [31]. While limited context-based prompt methods have been explored for medication adherence and activity initiation [32], [33], [34], [35], [36], [37], [38], [39], [40], these approaches do not employ knowledge of current and upcoming activities when delivering prompts. Similarly, while commercially-available time or location-based prompting may help individuals use the aid, they typically require that the user learn how to program the prompts [30], [34], [41], [42] which may reduce use [43]. Activity awareness may reduce these limitations of current prompting systems [44].

We evaluated our IP activity predictor in the context of an activity prompting app called CAFE (CASAS Activity Forecasting Environment). Rather than relying on manual setting of reminder times or hand construction of reminder rules [36], [45], CAFE prompts individuals based on the predicted times that the activities will occur. The iOS-based app periodically queries a server for the predicted times of selected activities. An activity recognition algorithm [12] and our activity predictor both reside on the server and generate real-time labels and predictions as sensor data arrive from the smart homes. When the predicted occurrence time is reached, CAFE issues a notification, as shown in Fig. 8.

Fig. 8.

Interface for the CAFE app.

We evaluate CAFE with two sets of smart home residents. The first set (Group 1) consisted of two smart homes with young adult participants, while the second (Group 2) consisted of seven smart homes with adult residents over age 65, as described in Table 6. These homes are instrumented with sensors for motion, temperature, light, and door usage. Sensor data is automatically labeled using the AR activity recognition algorithm. For all homes, we utilize the generalized AR model that was trained from the datasets described in Table 2 to generate training data. None of the homes were part of the training set, so the training labels rely on the generalization power of the learned activity recognizer. Using the training data labeled by AR, we then trained a separate independent activity prediction model for each site to form predictions for use in CAFE. The participants responded to CAFE activity prompts over periods that ranged from one week to one month.

TABLE 6.

Description of CAFE testbeds.

Testbed	Residents	Sensors	Training Data	Prompting Time	Activities	Prompts
Group 1: Young Adults
kyoto	2	81	2 months	2 weeks	Bathe, Cook, Eat, Leave Home, Relax, Sleep, Work	22
navan	1	28	4 months	2 weeks		90
Group 2: Older Adults
ihs06	2	26	3 weeks	1 month	Bed-Toilet Transition, Relax, Work	615
ihs07	1	29	3 weeks	3 weeks	Cook, Leave Home	226
ihs08	2	28	3 weeks	1 month	Bathe, Sleep	173
ihs09	2	22	3 weeks	1 month	Eat, Sleep	414
ihs12	1 + 1 pet	23	5 weeks	2 weeks	Eat, Wash Dishes	27
ihs14	4 + 2 pets	29	4 weeks	1 week	Cook, Leave Home	8
ihs21	1	23	4 weeks	3 weeks	Leave Home, Relax	44

The participants in Group 1 were prompted for seven activities. The participants in Group 2 were each prompted for a different set of two or three activities chosen by the participants. They provided a total of 1619 responses, distributed as shown in Fig. 9.

Fig. 9.

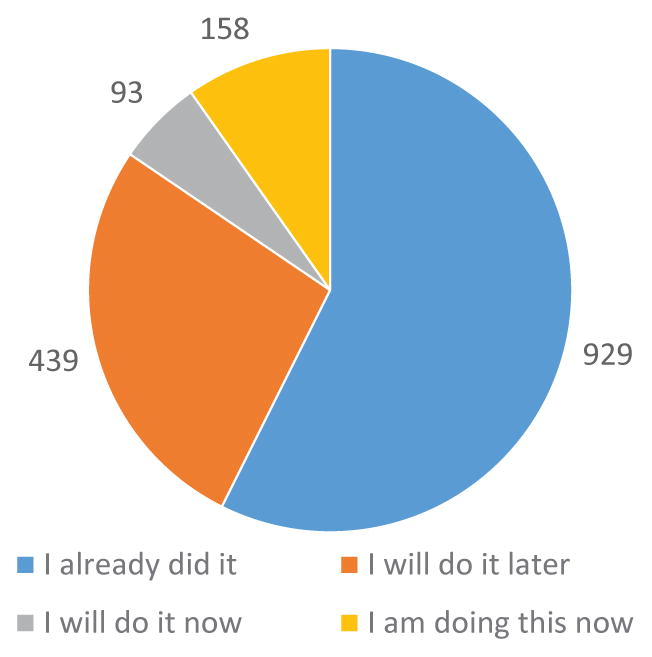
Distribution of CAFE responses for all participants.

We note that delays may occur between the activity occurring and the prompt being generated. This is partly due to the fact that the database is updated every 15 minutes, after which new prompts are generated. Furthermore, participants would often not respond to a prompt for a minute or so. As a result, they sometimes had already started an activity before they responded to the prompt, even if the prompt arrived at the correct time. Therefore, they respond with “I already did it” or “I will do it later”.

Given the nature of the current notification generation, we also evaluated the prompt timings based on MAE and range-normalized MAE, as summarized in Table 7. These values are calculated by comparing the predicted activity times with the activity start times labeled by the activity recognizer. Each activity occurred at least once a day and MAE values were normalized based on a maximum error of 43,200 seconds, or half of a day. As shown in Table 7, the MAE averaged over all participants in both groups is 933.73 seconds (about 16 minutes). The average prediction error aligns closely with the database update and participant response delays on average. To further assess the error we calculate the ETF value using 30 minutes, the maximum database and participant delay, as our threshold value.

TABLE 7.

Evaluation of CAFE prompts (in seconds).

MAE	Normalized MAE	ETF	κ-Normalized ETF
933.73	0.02	0.84	0.92

Finally, we obtained ground truth activity labels during the same period that participants in Group 1 received activity prompts. This was accomplished through the use of the EMA app. Using the EMA app, participants are queried every 15 minutes about the activity they are currently performing. The responses are stored in the database and used to validate our activity recognition algorithms. From the collected responses, we report AR accuracy of 92% for the seven activities used. We use this information to generate the κ-normalized values summarized in Table 7.

Interestingly, the participants noted that the app sometimes actually created a modification in their behavior. One resident recalled a time when he was debating between leaving home to get groceries or watching television. Upon receiving a CAFE prompt to leave home, he left immediately to perform his errands. On another occasion, a participant started working earlier than originally planned due to the prompt notification. Integrating activity prompts into daily behavioral routines thus raises interesting challenges for intervention design that need to be carefully considered in future work.

8 Related Work

Activity learning has been investigated over the last decade for a plethora of sensor platforms, including ambient sensors, wearable sensors, phone sensors, and audio/video data [13], [16]. In addition to activity recognition, activity discovery has been extensively studied utilizing techniques such as zero-shot learning, topic models, and sequence discovery [1], [46], [47], [48], [49]. In the work by Koppula and Saxena, the predicted next activity was supplied to robots in order to provide better assistance.

While activity prediction is not as heavily investigated as these other areas of activity learning, there are some representative first efforts in this area. Many of these techniques focus on sequence prediction, which can be adapted to predict the label of the activity that will occur next in the sequence. This work includes the Active LeZi algorithm [50] which is used to predict the identifier of the sensor in a home that will generate the next event. Other researchers [51], [52], [53] have investigated the use of probabilistic graph models to predict next events in video data.

In contrast with the emerging area of activity prediction, activity prompting systems have been developed and evaluated for quite a while. The majority of existing approaches are rule-driven or rely upon manually-generated user schedules [36], [39], [54]. Some recent work has focused on providing prompts to keep an individual on task when they fail to complete critical activities [30], [38], [41], [42], [55], [56], although these require extensive training for each activity. Other approaches [40] use sensed locations to generate reminders that are associated with those places. While these systems may adjust prompts based on user activities, they require substantial manually-generated information about an individual’s routine and locations where activities are performed. In contrast with these approaches, the method we propose is data-driven. By utilizing activity-labeled sensor events to learn an individual’s normal routine, our algorithm can automatically generate activity predictions and associated activity prompts.

Some work related to activity prediction has occurred in location-based social networks (LBSNs). Research in this area typically uses information about a user’s location and social context to predict a user’s future location [57], [58], [59]. These methods are simliar to our work in that they utilize multiple pieces of contextual information to predict user activity. However, many of these works focus on predicting only the next location a user will check in at [60], [61], [62], a form of sequence prediction. In contrast, the method presented here is used to predict the number of time units until all activities of interest will occur, enabling prediction beyond just the next activity. Scellato et al. [63] predict the timing and duration of user locations by looking for similar sequences in historic data. While this method is able to predict user locations at different future times, it relies on the averages of previous data to make its prediction. In contrast, our method uses nonlinear models to learn relationships between activities and context, allowing it to adapt more readily to changes in user behavior.

As an area for continued research, we hypothesize that activity prediction techniques can benefit from segmenting sensor data into sequences that represent single activity types. A number of techniques have been proposed for this task. Some approaches are unsupervised and utilize object-use fingerprints [64], [65] or statistical change point detection [66], [67].

9 Summary and Future Work

We studied a data-driven approach for predicting future occurrences of activities from sensor data. We showed how powerful regression learners can be leveraged to learn an effective activity predictor that can reason about relational and temporal structure among the activities in an efficient manner. Our extensive experiments on twenty-four smart home datasets validate that our recurrent activity predictor is effective at forecasting upcoming activity occurrences. Additionally, we illustrated the use of the predictor as part of our CAFE activity prompting app.

In the future, we will enhance our approach by incorporating iterative prediction refinement as well as smoothing, and perform a large-scale user study. In this paper, we limited our evaluation to consider only activity initiation, but an exciting direction will be to predict the length of the activity as well as individual activity steps. We will study the theoretical properties of our approach and apply it to more general prediction problems.

Biographies

Bryan Minor received his B.S. and Ph.D. from Washington State University. He is a research associate at Washington State University. His research interests include activity prediction, smart environments, and human-computer interaction.

Janardhan Rao Doppa received his M.Tech. from IIT Kanpur and his Ph.D. from the Oregon State University. He is an Assistant Professor at Washington State University. His research interests include artificial intelligence, machine learning, and data-driven science and engineering. His work on structured prediction received an outstanding paper award at the AAAI 2013 conference.

Diane J. Cook received her B.A. from Wheaton College and her M.S. and Ph.D. from the University of Illinois. She is a Huie-Rogers Chair Professor at Washington State University. Her research interests include machine learning, smart environments, and automated health assessment and intervention.