A Community Challenge for Inferring Genetic Predictors of Gene Essentialities through Analysis of a Functional Screen of Cancer Cell Lines

SUMMARY

We report the results of a DREAM challenge designed to predict relative genetic essentialities based on a novel dataset testing 98,000 shRNAs against 149 molecularly characterized cancer cell lines. We analyzed the results of over 3,000 submissions over a period of 4 months. We found that algorithms combining essentiality data across multiple genes demonstrated increased accuracy; gene expression was the most informative molecular data type; the identity of the gene being predicted was far more important than the modeling strategy; well-predicted genes and selected molecular features showed enrichment in functional categories; and frequently selected expression features correlated with survival in primary tumors. This study establishes benchmarks for gene essentiality prediction, presents a community resource for future comparison with this benchmark, and provides insights into factors influencing the ability to predict gene essentiality from functional genetic screens. This study also demonstrates the value of releasing pre-publication data publicly to engage the community in an open research collaboration.

Graphical abstract

INTRODUCTION

Although genetic alterations of human tumors have become increasingly well characterized, the application of this knowledge to clinical therapy has been limited. The promise of targeted cancer therapy requires both effective treatments and accurate, easily tested biomarkers to identify patient populations likely to respond to those treatments. Genes that are required for the survival of tumor cells, but not for normal cells, may provide an opportunity for specific targeting. This category of essential genes creates preferential vulnerabilities only in the context of a tumor’s specific genetic and epigenetic background, but not in contexts lacking those alterations. For example, the PARP1 gene has been shown to be essential in tumors deficient in BRCA1 or BRCA2, thus making PARP inhibitors a candidate for treating selective subtypes of breast and ovarian cancers (Bryant et al., 2005; Farmer et al., 2005; Drew, 2015). Therefore, a critical need exists to accurately predict differences in gene essentiality across a wide variety of cancer genetic subtypes from molecular features.

Large-scale functional screening of molecularly characterized cancer cell lines is a promising approach to generate pre-clinical hypotheses of tumor subtypes associated with sensitivity to functional perturbations. Several recent studies have identified small numbers of validated biomarkers of preferential gene essentiality based on statistical analysis of large-scale genetic screens (Schlabach et al., 2008; Cheung et al., 2011; Koh et al., 2012; Marcotte et al., 2012; Nijhawan et al., 2012; Ren et al., 2012; Rosenbluh et al., 2012; Shain et al., 2013; Shao et al., 2013; Marcotte et al., 2016). However, no study has yet conducted a systematic analysis of modeling approaches designed to infer predictive models of relative gene essentiality of cancer cells from such functional screening projects. Such a study is not only a challenging scientific problem, but one that emphasizes the need for a community of scientists with a range of expertise in data generation, predictive modeling, and biologic interpretation.

The DREAM challenges (http://www.dreamchallenges.org/) aim to assess computational models, contributed by researchers across the world, to prediction tasks focused mainly on biomedical research problems. Participating research teams develop and fine-tune their predictive models during one or more model building rounds. In the final round, each research team submits their best models, and, after the challenge is closed, an unbiased assessment using standardized metrics is performed on a blinded set of test data. Each challenge results in a rigorous assessment of the provided solutions to problems being addressed together with a performance ranking of teams and methods.

We used DREAM challenges to study the predictability of relative gene essentiality by leveraging Project Achilles, which has created one of the largest publicly available datasets containing genome-wide RNAi-mediated screens in molecularly characterized cancer cell lines (Luo et al., 2008; Cheung et al., 2011; Barbie et al., 2009; Cowley et al., 2014). Here, we simultaneously release a new set of Project Achilles data (constituting one of the largest public releases to date of RNAi screening data) together with the results of an open community challenge in which participants throughout the world were invited to assess modeling approaches on pre-publication data, which was released in tranches throughout the challenge.

RESULTS

Summary of Datasets and Challenge

We previously published an assessment of the impact on proliferation and viability of 55,000 small hairpin RNAs (shRNAs) targeting 11,000 genes in 216 cancer cell lines (Cowley et al., 2014). Here, we extended this study with an additional 149 cell lines tested for gene essentiality by a library of 98,000 shRNAs targeting 17,000 genes. Cell line screening data went through quality control including testing replicate reproducibility and confirming cell line identity as described previously (Cowley et al., 2014). To avoid teams predicting off-target effects of RNAi screens, relative gene essentiality scores were calculated using the DEMETER algorithm, which models out and corrects for off-target miRNA seed effects (STAR Methods, Tsherniak et al., 2017). Scores from DEMETER are relative gene essentiality measures, as each gene is compared with the mean cell line score (STAR Methods). The challenge also utilized molecular feature data from these 149 cell lines (genome-wide gene expression and copy-number data, in addition to mutational profiling of 1,651 genes) from the Cancer Cell Line Encyclopedia (Barretina et al., 2012). Based on these data, participants were tasked with training a predictive model on a subset of lines with both molecular feature and relative gene essentiality data and applying it to infer the relative gene essentiality values for an additional batch of cell lines for which participants could only access molecular feature data. Relative gene essentiality values were hidden and subsequently compared with predictions to assess model accuracy.

The challenge was conducted in three successive phases, during which participants were provided with progressively larger portions of the data to use for training, and predictions were evaluated using an independent test dataset. Conducting multiple challenge phases allows participants to iteratively evolve their modeling strategies based on the performance of models tested in previous phases, and allows organizers to perform a post-hoc analysis of the consistency of model performance across independent evaluations. The three phases of the challenge, respectively, used 45, 66, and 105 cell lines as the training set, and 22, 33, and 44 cell lines as the test set. During the first two challenge phases, participants could submit an unlimited number of models (Table S1 gives the number of models submitted in each phase), and received real-time feedback through a leader-board displaying the scores of all submitted models. In the final phase, participants were limited to a maximum of two models per team submitted for final scoring. All data used in this challenge was previously unpublished and are made available together with information about the data generation, challenge details, leaderboards, and source codes used to generate the results at https://www.synapse.org/Broad_DREAM_Gene_Essentiality_Prediction_Challenge. Teams’ solutions together with corresponding descriptions for each sub-challenge can be accessed in the Final Results section of the same web site.

Each phase consisted of three related sub-challenges, including: (1) building a model that best predicts all relative gene essentiality scores in the held-out test set using any feature data (including gene expression, copy number, and/or mutation features, as well as any additional external information), (2) predicting a subset of relative gene essentiality scores using only ten gene expression, copy number, or mutation features per gene being predicted, and (3) predicting a subset of relative gene essentiality scores using only a total of 100 gene expression, copy number, or mutation features across all genes being predicted (Figure 1A). For sub-challenges 2 and 3, a smaller list of 2,647 genes was selected for prediction by three main criteria (STAR Methods): (1) interesting profiles of the relative gene essentiality data itself (e.g., subset of cell lines displaying strong relative essentiality), (2) cancer-related genes (Futreal et al., 2004; Ciriello et al., 2013), and (3) some evidence of the gene as a known or potential drug target (Basu et al., 2013; Patel et al., 2013). The prediction tasks were designed to both obtain the best models for predicting relative gene essentiality using the genetic characteristics of the cancer cell lines and to gain insight into which genetic features were most informative for these models.

Figure 1. Overview of the Broad-DREAM Gene Essentiality Prediction Challenge and Performance Results.

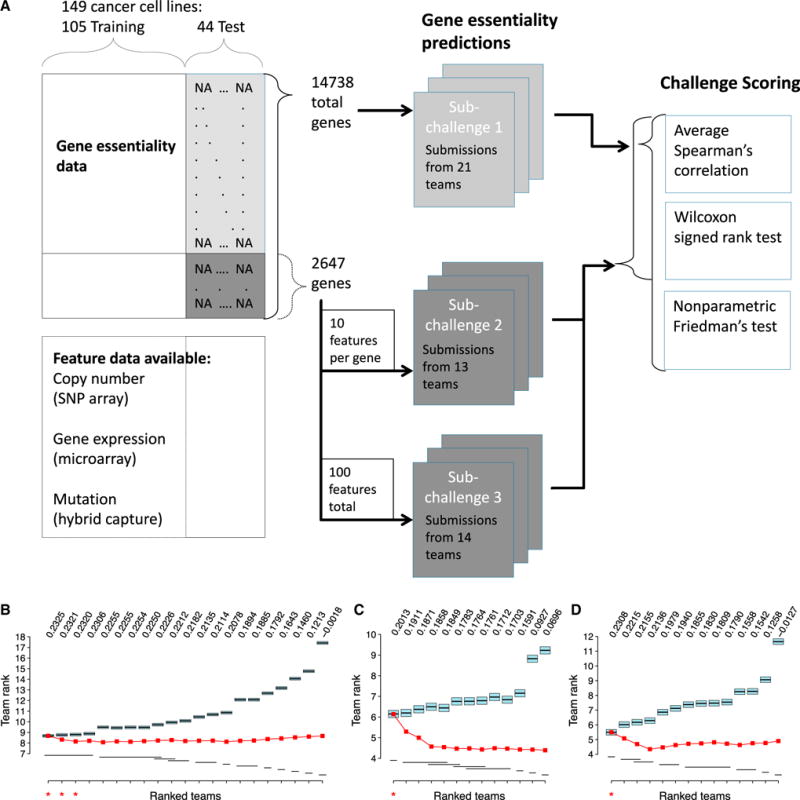
(A) Schematic of the Broad-DREAM gene essentiality prediction challenge. The challenge consisted of three related sub-challenges. Sub-challenge 1 addressed building a model that best predicts all gene essentiality scores in the held-out test set, using any feature data. Sub-challenge 2 addressed predicting a subset of gene essentiality scores using only 10 gene expression, copy number, or mutation features per gene. Sub-challenge 3 addressed predicting a subset of gene essentiality scores using only 100 gene expression, copy number, or mutation features in total. Teams’ performances for (B) sub-challenge 1, (C) sub-challenge 2, and (D) sub-challenge 3 are summarized as the average Spearman correlation across all predicted genes at the top. Black lines in the middle of blue boxes (“team rank”) display the average rank of each team’s scores across 14,738 genes (for sub-challenge 1) and 2,647 genes (for sub-challenges 2 and 3), and the width of each blue box is the critical difference reported by the Wilcoxon signed rank test. The critical differences for sub-challenges 1, 2, and 3 are 0.2580, 0.3545, and 0.3856, respectively. Black lines below the boxplots summarize the Wilcoxon signed rank test results by dividing the teams into groups. Each group is denoted by a distinct black line, which contains the teams with no statistically significant difference. The red line displays the rank of an ensemble model constructed from all models with rank less than or equal to the corresponding point on the x axis.

Evaluating Relative Gene Essentiality Predictions

Predictions by 48 teams were scored by Spearman’s rank correlation coefficient for each gene between the measured and predicted relative gene essentiality scores (Figures S1A–S1C). The mean Spearman correlation scores across all submissions and all predicted genes for final round submissions were 0.1957, 0.1649, and 0.1732 for sub-challenges 1, 2, and 3, respectively. Overall team scores were ranked based on the average correlation across all genes, and the statistical significance of the difference between team scores (Figures 1B–1D) was assessed using the Wilcoxon signed rank test (Figures S1D–S1F). Sub-challenges 2 and 3 showed one statistically significantly best-performing team. For sub-challenge 1, the scores of the top 4 teams displayed statistically significantly improved performance from the fifth ranked team, but were not statistically significantly different from each other. A more stringent post-hoc test (nonparametric Friedman’s test) determined that the top three teams achieved improved performance from the fourth ranked team (Figure S1G).

We tested whether the submitted predictions were better than those of standard approaches by comparing them with the predictions of a baseline algorithm. For sub-challenge 1, we trained a baseline regression algorithm (Lasso regression), on the set of training cell lines from the final challenge round and measured its performance on the test cell lines (Figure S2A). The majority (77.09%) of genes (i.e., 11,362 genes out of 14,738) were only weakly predicted (Spearman correlation between 0 and 0.4), although a subset of genes were predicted with relatively high accuracy (5.79% of genes, i.e., 853 genes, achieved Spearman correlations above 0.4). We assessed the statistical significance of model scores based on a permutation test in which the trained baseline regression algorithm was tested on 10,000 randomly re-sampled test cell line collections with shuffled cell line labels. As expected, the distribution of Spearman correlations for this null model was centered around 0 (Figure S2B), where the baseline model achieved average correlation of 0.1528. Twenty out of the 21 predictions submitted to this sub-challenge achieved scores outside of the 95% confidence interval of the null model (i.e., 0.0211 Spearman correlation), suggesting that genetic correlates with statistically significant predictive power can be inferred from functional screens. The same type of analysis revealed similar results for other sub-challenges (not shown here).

Ensemble Models Give Consistently High Performance

We next assessed whether relative gene essentiality prediction could benefit from constructing ensemble models that average results across numerous diverse modeling approaches used in the challenge (the so-called wisdom of the crowd effect, Tables S2, S3, and S4). For each sub-challenge, we constructed ensemble models consisting of all individual models with ranks 1 through N, for each N up to the number of models submitted in the final scoring round (Figures 1B–1D and S1). For each gene (i.e., prediction task) the rank of each cell line in the ensemble model was calculated as the average rank of the cell line across the constituent models in the ensemble. For sub-challenge 1, ensemble models performed better than or equal to the individual best model (the best model and the ensemble of all models were equivalent to the second significant digit in both Spearman correlation, 0.23, and average rank, 8.67). For sub-challenges 2 and 3, ensemble models significantly outperformed all individual models. However, we suggest that this strong performance should not be over-interpreted, because individual models were limited to 10 or 100 predictive features whereas ensemble models could implicitly utilize more features by averaging across models.

Sub-challenge 1 Results

Sub-challenge 1 was the most open-ended task of this DREAM challenge; participants had to predict all relative gene essentiality scores across all cell lines in the test set. Although any feature data and prior knowledge was allowed, the top two best-performing teams did not use the provided mutation data. The best-performing team used a combination of representation learning and kernel-based regression (STAR Methods). The second best-performing approach was an ensemble of multiple kernel learning and random forest regression algorithms, but utilized a restricted gene list based on literature (STAR Methods). The third best-performing approach started with a series of feature selection criteria to choose features from provided input data and then scaled these selected features before feeding them into a nonlinear regression algorithm (STAR Methods).

All three methods employed strategies consistent with successful approaches reported in previous DREAM challenges, including sharing information across response variables (Costello et al., 2014; Eduati et al., 2015), constructing ensembles of multiple models (Bilal et al., 2013), selecting features based on prior information or additional datasets (Costello et al., 2014; Bilal et al., 2013), and capturing nonlinear input/output relationships (Costello et al., 2014; Eduati et al., 2015) (Discussion).

Sub-challenge 2 Results

The best-performing approach for sub-challenge 2 leveraged features that are informative across many genes. The motivation of this approach was that the most correlated features for a specific gene may be subject to overfitting based on the small sample size and noise within the experiment (STAR Methods). Thus, selecting features correlated with multiple response variables may enrich in features associated with true biological subtypes. Sub-challenge 2 also yielded a clear interpretation of the best-performing model, based on a simple biologically motivated insight: always including one feature corresponding to the copy-number status of the gene whose essentiality is being predicted, in addition to nine features selected by statistical criteria. All 13 teams in sub-challenge 2 used variations of the same strategy of selecting features based on simple statistical tests (generally univariate correlation with the response variable), and applying a regression model to the pre-filtered features, including most commonly used models, such as linear, ridge, random forest, Gaussian process, and support vector machine regression. Interestingly, the fourth ranked team employed nearly the same strategy as the best-performing team, without using the hand-selected copy-number feature, which included selecting features for model inclusion based on their correlation with the response variable, and applying a simple linear model to the selected features. The statistically significant improvement of the best-performing team over the fourth ranked team suggests that this improvement is attributable to the inclusion of the copy-number feature. Overall, 8 out of 13 submitted methods outperformed a baseline model which selected the top 10 gene expression features based on Lasso regression on the training dataset.

Sub-challenge 3 Results

The best-performing approach for sub-challenge 3 also employs the best practices observed in previous DREAM challenges (Costello et al., 2014; Eduati et al., 2015) of including shared information across response variables (known as multi-task learning). Instead of performing feature selection separately for these related prediction problems, joint modeling approaches can be used to capture the commonalities between the problems. The best-performing team’s methodology selects the list of 100 genomic features iteratively by looking at the prediction performances on all 2,647 genes the teams were asked to predict (STAR Methods).

Characteristics of Gene Predictability

Although each sub-challenge revealed modeling approaches leading to statistically significant improvements, the difficulty of the prediction task (i.e., the gene that was being predicted) had a much greater effect on prediction accuracy than differences among modeling approaches (Figure S3). We refer to the Spearman correlation between predicted and observed essentiality scores for a given model applied to a given gene as the “predictability” score. We applied a random effects model to quantify the percent of variance in predictability scores attributable to differences between prediction tasks versus modeling approaches (STAR Methods).

For sub-challenges 1, 2, and 3, respectively, 61.65%, 43.62%, and 44.47% of the variance in predictability scores was explained by the gene for which relative essentiality was being predicted (Figures 2A–2C). By contrast, only 10.40%, 4.95%, and 12.16% of predictability scores were explained by differences in modeling approaches. Related to this, the predictability of genes also showed some correlation to the standard deviation in relative gene essentiality scores across cell lines (Figures 2D–2F). Genes with a higher standard deviation in their relative essentiality scores seem to be better predicted overall, compared with the average across all teams. This was an even stronger effect for the best-performing team in each sub-challenge (Figure S4).

Figure 2. Analysis of Gene Predictability.

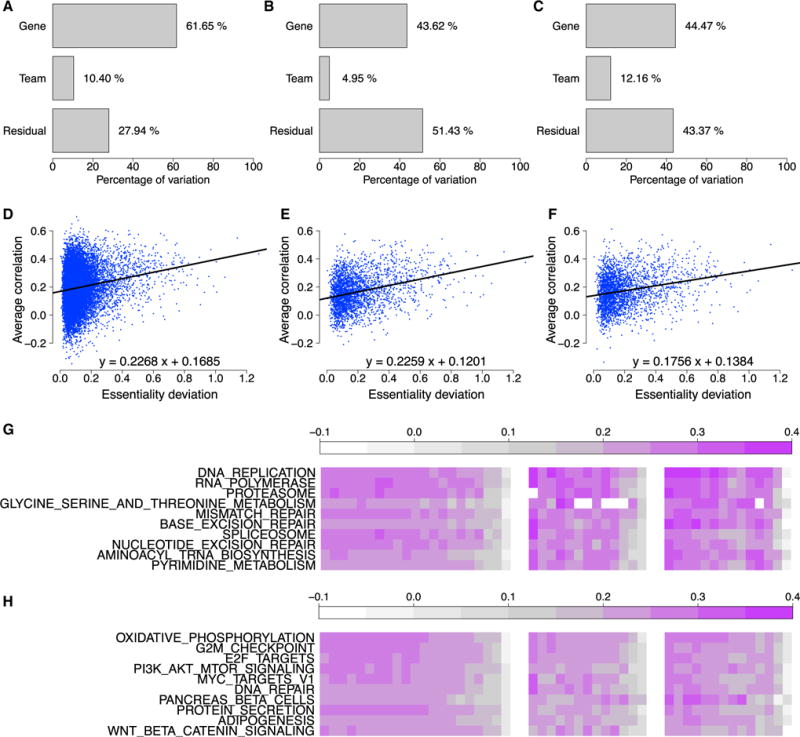
The proportions of variance explained by “gene” and “team” factors using the random effects model are shown for (A) sub-challenge 1, (B) sub-challenge 2, and (C) sub-challenge 3. The relationship between the standard deviations of gene essentiality scores and predictability scores (i.e., correlations between predicted and observed essentiality scores), averaged over all teams, are shown for (D) sub-challenge 1, (E) sub-challenge 2, and (F) sub-challenge 3. (G and H) The predictability scores of the top 10 gene sets (rows) that are best predicted over all teams and sub-challenges (columns) from (G) “KEGG” gene set collection and (H) “Hallmark” gene set collection. The score of a gene set for a team and sub-challenge pair is defined as the average predictabilities obtained by this team in this sub-challenge for the genes involved in this gene set.

We assessed whether genes that are well predicted correspond to certain biological processes. We ranked all genes by their average predictability score across models and used gene set enrichment analysis (GSEA) to calculate the enrichment of each KEGG and Hallmark gene set in the Molecular Signatures Database (MSigDB) relative to this ranked list (STAR Methods) (Subramanian et al., 2005). Well-predicted genes fall into gene sets that represent common biological processes or essential cellular functions such as DNA replication and repair, or essential cellular complexes such as the proteasome, spliceosome, or ribosome (Figures 2G, 2H, S5, and S6; Tables 1 and S5, S6, and S7).

Table 1.

Top 10 GSEA Results of Gene Predictability Averaged over All Teams in each Sub-challenge

Gene Set Name	Size	Normalized Enrichment Score	FDR q Value
Sub-challenge 1
KEGG proteasome	40	1.5332443	0.32170543
KEGG apoptosis	74	1.4924165	0.38147435
KEGG homologous recombination	25	1.5532851	0.3887445
KEGG renal cell carcinoma	62	1.4211984	0.4181525
KEGG renin angiotensin system	15	1.4481847	0.4225843
KEGG Parkinson’s disease	100	1.4281346	0.44821626
KEGG DNA replication	32	1.4569446	0.4559137
KEGG RNA polymerase	28	1.5906658	0.5116125
KEGG spliceosome	123	1.3328333	0.5146515
KEGG focal adhesion	164	1.3115251	0.5323963
Sub-challenge 2
KEGG proteasome	26	1.7807523	0.028672058
KEGG spliceosome	73	1.5590596	0.3131918
Hallmark adipogenesis	39	1.4641638	0.38694927
Hallmark DNA repair	48	1.406141	0.43439645
Hallmark MYC targets V1	111	1.4734303	0.43642634
KEGG cell cycle	55	1.4341469	0.44051114
HALLMARK E2F targets	75	1.3867909	0.46594828
KEGG nucleotide excision repair	17	1.4118508	0.47002134
KEGG pyrimidine metabolism	20	1.3697011	0.4960722
KEGG Huntington’s disease	60	1.3488446	0.50220245
Sub-challenge 3
KEGG proteasome	26	1.6273592	0.34336427
KEGG oocyte meiosis	39	1.452181	0.3463302
KEGG Huntington’s disease	60	1.4954373	0.38429984
Hallmark DNA repair	48	1.4548242	0.3926697
KEGG apoptosis	29	1.4718503	0.39337313
KEGG oxidative phosphorylation	25	1.4237828	0.4079552
KEGG nucleotide excision repair	17	1.5160906	0.41208157
KEGG Parkinson’s disease	33	1.3633572	0.4446588
KEGG chemokine signaling pathway	41	1.3515177	0.45927873
KEGG pyrimidine metabolism	20	1.3680565	0.4637498

Characteristics of Feature Selection

In addition to assessing how predictable each gene was in a team’s model, sub-challenges 2 and 3 were also designed to gain insight into the types and identity of genetic features that lead to good overall predictions. Teams were asked to construct predictive models for 2,647 selected genes (STAR Methods) using at most 10 features per gene (sub-challenge 2) or 100 features common to all genes (sub-challenge 3) from all the available gene expression, copy number, and mutation data.

All teams used gene expression features almost exclusively; copy number or mutation features were much less commonly utilized (Figures 3A and 3B). This implies that gene expression features encode the most useful information for the prediction of phenotypic effect of genetic perturbations, consistent with previous studies on predicting the effect of drug perturbations in cancer cell lines (Costello et al., 2014; Eduati et al., 2015; Nikolova et al., 2017; Jang et al., 2014) and predicting survival in primary tumors (Yuan et al., 2014; Margolin et al., 2013; Neapolitan and Jiang, 2015).

Figure 3. Analysis of the Influence of Different Molecular Feature Types on Model Performance.

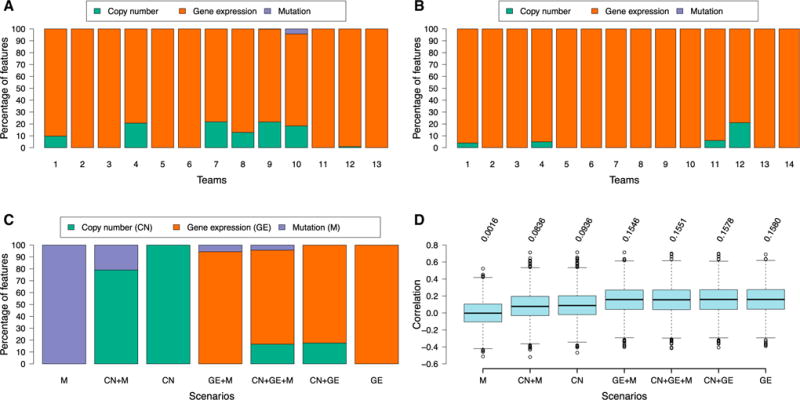
(A and B) Percentage of feature types (copy number, gene expression, and mutation) used by each team, for (A) sub-challenge 2 and (B) sub-challenge 3. (C and D) Percentage of feature types (C) and predictive performance (D) by Lasso on sub-challenge 2 using copy number, gene expression, and/or mutation.

We performed a controlled experiment to further test the observation that gene expression data was the most informative feature type in predictive models. Specifically, for each prediction task in sub-challenge 2, we calculated the test error of a commonly used regression model (Lasso) trained using each combination of feature types. All four models that included gene expression performed significantly better than the models that contained only mutation or copy-number data alone or in combination (Figure 3D). The best-performing model utilized gene expression alone, although models including other feature types in addition to gene expression had comparable performance with the gene-expression-only model. Indeed, in agreement with teams’ submissions, gene expression features were predominantly selected by all Lasso models that included gene expression as a feature type (Figure 3C).

We then looked into what gene expression features were used most commonly by teams in their models. Among the gene expression data, certain features were chosen more often across teams (in both sub-challenges) and across genes to be predicted (in sub-challenge 2). One such feature, EIF2C2 (also known as AGO2), is a component of the RNAi machinery of the cell (Liu et al., 2004; Meister et al., 2004; Rand et al., 2004). In sub-challenge 2, EIF2C2 expression was utilized in multiple gene models (n = 2–395) by 10 out of the 13 teams. EIF2C2 copy number, or other components of the RNAi machinery (such as EIF2C1, EIF2C3, EIF2C4, DICER1, etc.) were much less frequently used. In sub-challenge 3, 7 out of 14 teams also used EIF2C2 gene expression as one of their 100 predictive features. The fact that the expression of this gene is often used in these predictions implies that information about each cell line’s RNAi machinery level is informative for overall prediction of relative gene essentiality data from shRNA screens. This is consistent with the relationship of screen performance with AGO2 expression described in previous reports (Hart et al., 2014). When the top selected gene features are examined as a group, from either sub-challenge, GSEA analysis shows enrichment for both cancer-related and epithelial-mesenchymal transition gene sets (STAR Methods; Tables 2, S8, and S9). These imply that the cell state, whether it is more epithelial or mesenchymal, also encodes information about relative gene essentiality in that cell line.

Table 2.

Top 10 Gene Sets by GSEA Analysis of Features Commonly Chosen from Sub-challenges 2 and 3 Using “Hallmark” and “KEGG” Gene Sets

Gene Set Name	FDR q Value
Sub-challenge 2
Hallmark epithelial-mesenchymal transition	3.28 ×10−56
Hallmark TNF-α signaling via NF-κB	2.46 ×10−37
KEGG pathways in cancer	3.88 ×10−33
Hallmark UV response DN	1.09 ×10−29
Hallmark estrogen response late	1.09 ×10−29
KEGG focal adhesion	1.10 ×10−28
Hallmark IL-2 STAT5 signaling	5.43 ×10−27
Hallmark estrogen response early	3.56 ×10−26
Hallmark interferon gamma response	3.56 ×10−26
Hallmark apoptosis	1.89 ×10−24
Sub-challenge 3
Hallmark epithelial-mesenchymal transition	1.24 ×10−29
Hallmark estrogen response late	9.78 ×10−10
Hallmark hypoxia	9.78 ×10−10
Hallmark TNF-α signaling via NF-κB	1.28 ×10−7
Hallmark IL-2 STAT5 signaling	1.25 ×10−5
Hallmark coagulation	5.52 ×10−5
Hallmark apical junction	6.91 ×10−5
Hallmark estrogen response early	6.91 ×10−5
KEGG focal adhesion	6.91 ×10−5
KEGG cytokine-cytokine receptor interaction	8.56 ×10−5

We then looked further into the specific gene features used for some of the best gene predictions in sub-challenge 2, to see whether a more in-depth examination of a single predicted gene could be informative. We selected the genes with a predictability score greater than 0.4 for each team and examined the gene features (Table S10). Looking at these predicted genes, we noticed that TP53 was well predicted by the top two teams. Except for a single copy-number feature (TP53 copy number) chosen by the best-performing team, the rest were gene expression features, including features chosen by both teams (SAMM50, MDM2, and RPS27L). Both MDM2 and RPS27L are in TP53 pathways; MDM2 is regulated by TP53 and targets tumor suppressor genes for proteasomal degradation, and RPS27L is a direct p53 inducible target and its degradation requires binding by MDM2. The second best-performing team picked additional gene expression features that interact with TP53 (BAX, DDB2) and well predicted the essentiality of MDM2 by picking a similar set of gene expression features.

We also looked at the standard deviations of all gene expression features together with the standard deviations of gene expression features that were frequently used in sub-challenges 2 and 3. Figure S7 shows the density plots of these three sets of gene expression features. While teams picked gene expression features with both high and low standard deviations, features with higher standard deviations were preferentially included in the models.

Features Inferred from Cell Line Screens Predict Aggressiveness of Primary Tumors

We next assessed whether predictive features inferred from cell line screens relate to the aggressiveness of primary lung adenocarcinoma human tumor samples (given that a large proportion of cell lines in our panel, 65 out of 149, were lung adenocarcinomas). We selected the top 100 frequently selected features in sub-challenge 2 as the signature and clustered 495 lung adenocarcinoma patients with available survival data from The Cancer Genome Atlas (TCGA) into two groups using hierarchical clustering on mRNA expression data of this signature (Figure 4A). We found that this signature separated the patients into two groups with a significant survival difference (p = 0.0004). To assess whether this effect was significant, we generated 10,000 random 100 gene signatures from TCGA mRNA expression and performed the same survival analysis. The signature derived from cell line predictions achieved better survival classification than 9,823 of the 10,000 random signatures (p = 0.0177, Figure 4B). We also generated 10,000 random cluster assignments for our signature and performed the same survival analysis using these assignments. The signature derived from cell line predictions achieved better survival classification than 9,998 of the 10,000 random cluster assignments (p = 0.0002, Figure 4C).

Figure 4. Survival Analysis on TCGA Lung Adenocarcinoma Cohort Using the Predictive Signature Obtained from Sub-challenge 2 Submissions.

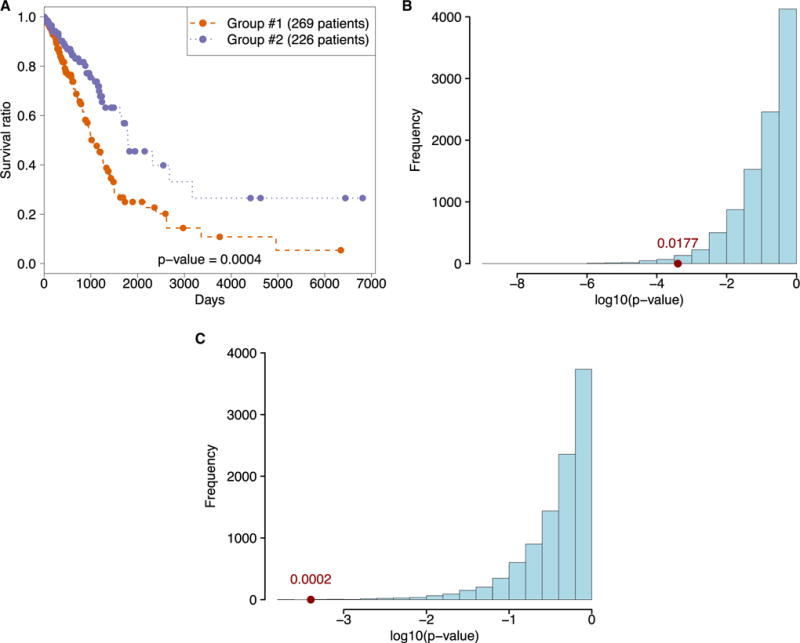
(A) Kaplan-Meier curve for two groups obtained using hierarchical clustering on mRNA expression data of signature genes.

(B and C) Distribution of Kaplan-Meier p values of null distribution models. Bootstrapping results over 10,000 randomly generated 100 gene signatures (B). Bootstrapping results over 10,000 randomly generated clustering labels (C). The x axis positions of the dots in (B) and (C) show the p-value obtained by the predictive signature extracted from the challenge submissions, whereas the numbers above them show the p-value of the improvement of this model compared to the bootstrapped models.

DISCUSSION

High-throughput genomic and functional genomic datasets on large numbers of tumor samples hold the promise to rapidly accelerate our ability to systematically characterize the molecular drivers of carcinogenesis and identify novel therapeutic targets associated with a tumor’s genetic background. However, unlocking the discovery potential of such highly complex datasets will require matching this data explosion with a concurrent expansion of our collective knowledge related to the relative strengths of myriad analytic strategies, the interpretation of statistical findings, and the inherent strengths and limitations of each dataset in elucidating a biological question.

The traditional publication model impedes the community’s ability to achieve rapid learning cycles to optimally advance such collective knowledge in at least two ways. First, any individual group can only address a fraction of the valuable questions enabled by such large datasets, and restricting data access until post-publication inherently precludes all other lines of investigation, often by a year or more. Second, even after large datasets are publicly available, the lack of established benchmarks and standardized assessment criteria can lead to a phenomenon known as the self-assessment trap in which a multitude of publications independently claim to achieve superior performance to other approaches (Norel et al., 2011), yet deriving robust learnings through meta-analysis of these independent results is often challenging or uncovers conflicting or irreproducible results (Venet et al., 2011).

The Broad-DREAM gene essentiality challenge explores an alternate research methodology in which any researcher is invited to engage as an active participant in the analysis of a novel large-scale dataset throughout the course of its generation. Our study builds on the community challenge paradigm established through the DREAM challenges, and represents the first time that such an open challenge has been tightly coupled with data generation at this scale. We believe this methodology demonstrated improvements in both of the inefficiencies referenced above. First, we were able to assess over 3,000 different models over a 4-month period, representing a speed and scale of model evaluation that would be impossible for a single research group. Second, by establishing pre-defined assessment criteria and blinding participants to the data used for assessment, we were able to perform unbiased post-hoc analysis of all model results and derive multiple conclusions that can inform future studies aiming to interpret high-throughput shRNA screens. Perhaps more importantly, by following a methodology similar to DREAM challenges and other benchmarking studies run over the past 9 years, we were able to identify recurring insights related to the best modeling approaches across many challenges exploring interpretation of diverse biomedical datasets. Below, we highlight several conclusions with supporting evidence from other benchmarking studies.

In multiple previous DREAM challenges, the best-performing methods intelligently incorporated domain-specific prior knowledge into their algorithm (Costello et al., 2014; Bilal et al., 2013; Margolin et al., 2013). Three of the five best-performing methods from our challenge employed this strategy during feature selection. These strategies include restricting predictive features to cancer-relevant genes based on previous publications. Another method restricted feature selection to genes associated with important pathways, showing high correlation with essentiality across many perturbations, having expression levels correlated with copy number, and having high expression levels across cell lines. One team employed the simple insight that the copy-number status of a given gene is likely predictive of preferential essentiality when the same gene is targeted by shRNAs. This performed better than another team’s similar method that lacked adding the copy-number status to their model. Although the influence of copy number on relative gene essentiality measures may be complex, this probably captured specific gene classes where the copy number (and by proxy, in some cases, the gene expression) of the gene itself is the best predictor of its own preferential gene essentiality. Genes where the amplification or overexpression of the gene leads to an “addiction” to that gene would be predicted by using gene expression or copy-number information of that gene. Conversely, cell lines with homozygous deletions in a given gene should not respond to targeting the deleted gene. Another specific copy-number-driven class are CYCLOPS genes, where deletion of one copy of the gene can lead to an increased dependency on that gene upon RNAi knockdown (Nijhawan et al., 2012).

Another finding from previous DREAM challenges is that for prediction problems containing multiple response variables for the same set of samples (e.g., phenotype measurements for multiple perturbations), the best-performing methods often build predictors that share information across response variables, rather than build independent models for each prediction task (Costello et al., 2014; Eduati et al., 2015). This strategy may reduce noise inherent in each response measurement by amplifying response patterns that are shared across multiple perturbations that affect similar cellular processes (Gönen and Margolin, 2014a; 2014b). Both the top-performing method in sub-challenge 1 and the top-performing method in sub-challenge 3 utilized this strategy, known as multi-task learning.

Taken together, all five of the top-performing methods either incorporated domain-specific prior knowledge or employed multitask learning. The common theme of all approaches is to leverage additional information beyond the data provided for a given prediction task (e.g., feature matrix and response vector). Such approaches may increase the statistical power of an inference problem by effectively increasing the sample size through incorporation of additional information. This interpretation would be consistent with multiple previous studies arguing that the size of a dataset trumps differences in analytic approaches in influencing model accuracy (Halevy et al., 2009).

Perhaps the most consistent finding from previous DREAM challenges is that ensemble modeling robustly achieves performance on par with the best individual modeling approaches (Boutros et al., 2014). Both the best- and second best-performing teams in sub-challenge 1 employed this insight and utilized ensemble approaches in their algorithms. More generally, an ensemble model constructed from all submissions in sub-challenge 1 achieved a virtually identical score to the best-performing model (as noted in the main text, ensemble models for sub-challenges 2 and 3 outperformed all submitted models for these challenges, although we caution against over-interpreting this result).

Gene expression features were most frequently used in predictions from the methods of all the challenge participants in sub-challenges 2 and 3. Although expression data could be most familiar to participants and therefore used most often, a baseline method also performed best when expression data was used in a controlled experiment. In addition, this has been seen in other studies, including other DREAM challenges (Costello et al., 2014; Eduati et al., 2015; Margolin et al., 2013; Neapolitan and Jiang, 2015). Mutation data, although attractive as predictive or clinical biomarkers, seem to be limited in their use in predicting gene essentialities across large numbers of genes and were rarely used in this challenge. The mutation data provided, in addition to being sparse (for both genes and cell lines) likely has an additional impediment to its use. Not all mutations are equivalent and both biological knowledge and validation are needed to determine the functional consequences of each genetic change, something not readily available for most mutations. It is likely that gene expression measures the cancer cell state to some extent, and therefore, on average across all genes, it is a better predictor of relative gene essentiality quantified by RNAi knockdown. Consistent with this hypothesis, the most common gene expression features across all genes and teams, taken as a group, are enriched for cancer-related signaling pathways and epithelial-mesenchymal transition genes. These imply that large differences in cell state, such as whether it is more epithelial or mesenchymal, or whether a particular signaling pathway is up-regulated, encode information about the overall gene essentiality in that cell line.

One of the most common single expression features chosen was EIF2C2 (AGO2), a component of the RNAi machinery, which likely has an overall impact on the range of gene knockdown possible in each cell line (Hart et al., 2014). This implies that some predictive features may pick up signals specific to the RNAi assay, and should be interpreted with caution when extending such biomarker/gene essentiality relationships to other means of inhibiting the target gene (e.g., pharmacologic).

Survival analysis of TCGA lung adenocarcinoma data also suggests that the gene expression features commonly utilized in the challenge contain information relevant to primary tumors. These might be genes most likely involved in tumor pathogenesis and therefore also related to poor survival. Lung adenocarcinoma was the only tumor type where a post-bootstrapping significant survival difference was found after those expression features were used to split samples into two groups. The majority of cell lines in the challenge dataset were non-small-cell lung cancers, so this may indicate that a specific lung cancer disease state which correlates with survival is captured by these common expression features.

Taken together, the conclusions listed above, supported by previous publications, yield a principled set of recommendations for the interpretation of shRNA screens. Overall, baseline genetic data contains some predictive value for most shRNA perturbations, with the essentiality of some genes far more predictable than others. Gene expression data should be used as key features in a predictive model. The specifics of a modeling approach have less impact on performance than the factors listed above, although improved performance can be obtained by sharing information across prediction tasks, incorporating relevant external data, or intelligently utilizing domain-specific knowledge in the model specification. Finally, constructing an ensemble of models developed by many different groups is a robust strategy for achieving predictive accuracy on par with the best individual modeling approach. We hope that the conclusions derived from this community challenge, together with the associated dataset and benchmarking resource, will contribute a meaningful brick upon which future studies can build to progressively enhance the growing edifice of knowledge related to interpreting high-throughput genetic screens.

STAR*METHODS

Detailed methods are provided in the online version of this paper and include the following:

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Cell line mutation data	(Barretina et al., 2012)	https://www.broadinstitute.org/ccle
Cell line DNA copy number data	(Barretina et al., 2012)	https://www.broadinstitute.org/ccle
Cell line microarray expression data	(Barretina et al., 2012)	https://www.broadinstitute.org/ccle
Project Achilles gene essentiality data	This paper	https://www.synapse.org/Broad_DREAM_Gene_Essentiality_Prediction_Challenge
Software and Algorithms
DEMETER algorithm
R version 3.3.3	(Tsherniak et al., 2017)	https://www.r-project.org/
GSEA software	(Subramanian et al., 2005)	http://software.broadinstitute.org/gsea/
lme4 R package	(Bates et al., 2015)	https://cran.r-project.org/package=lme4
glmnet R package	(Friedman et al., 2010)	https://cran.r-project.org/package=glmnet
survival R package	(Therneau and Grambsch, 2000)	https://cran.r-project.org/package=survival

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Adam A. Margolin (margolin@ohsu.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

This information can be obtained from Tsherniak et al. (2017).

METHOD DETAILS

Challenge Data

RNAi screening data from Project Achilles represents a large-scale loss-of-function screen involving ~98,000 shRNA reagents, targeting ~17K genes, lentivirally delivered in a pooled format to each cancer cell line in replicate (n = 3 or 4), in parallel (Tsherniak et al., 2017). This data was provided for a total of 149 cancer cell lines throughout the challenge, and went through quality control and processing as described in detail previously (Cowley et al., 2014). In brief, normalized log2 read counts were compared to the initial DNA plasmid pool to calculate a log2 fold change score per shRNA per replicate cell line sample, then quantile normalized across cell lines.

The DEMETER algorithm was used to calculate relative gene essentiality data, which are mean centered per gene and divided by the global standard deviation of the data set (Tsherniak et al., 2017). Given the observed phenotypic effects produced by RNAi reagents which share genes and seed regions, DEMETER fits an additive model combining contributions from the targeted gene as well as contributions from seed effects. Two seeds per shRNA were considered, where the seeds are defined by the sequence in the regions 11-17 nt and 12-18 nt. A reagent may have multiple gene effects, as determined by aligning the shRNA. Any shRNAs which targeted more than ten genes were omitted from the fitting process. In addition, any seed or gene with fewer than two observations were also omitted and not fit by this process.

Molecular feature data from these 149 cell lines (genome-wide gene expression and copy number data, in addition to mutational profiling of 1,651 genes) from the Cancer Cell Line Encyclopedia (Barretina et al., 2012) was downloaded from the CCLE portal (https://portals.broadinstitute.org/ccle/home).

All data used for the challenge including relative gene essentiality data, molecular features, and cell line annotations are available through Synapse under ID syn2384331 after registering to the system and joining to the challenge.

Gene Lists for Sub-challenges 2 and 3

A shorter list of genes was created for sub-challenges 2 and 3. Criteria 1 was to look for very high-quality DEMETER gene solutions and those gene solutions that had an outlier profile. High quality gene solutions required the third best shRNA for each gene to have a gene solution R² of >30%, meaning that the third best shRNA has to have at least 30% of its effects explained by the gene (rather than the off-target seed sequence). Outlier DEMETER profiles were defined as those genes where a small subset of cell lines (50 > n > 3) showed a strong relative essentiality (absolute values of DEMETER gene score > 1.5), but the majority of cell lines showed little effect. The second criteria filtered the gene list based on known genomic alterations of human tumors, based on the presence of genes on lists for either the Cancer Gene Census (Futreal et al., 2004) or the pan-cancer mutation analysis from TCGA projects (Ciriello et al., 2013). The third criteria filtered based on the ‘druggability’ of genes by incorporating information from two publications/databases of genes that are or have potential to be drug targets (Basu et al., 2013; Patel et al., 2013).

QUANTIFICATION AND STATISTICAL ANALYSIS

Best Performing Methods for Sub-challenge 1

The underlying regression algorithm of the best performing approach for sub-challenge 1 was kernel ridge regression (KRR) (Schölkopf and Smola, 2001; Shawe-Taylor and Cristianini, 2004). Multiple KRR models were trained on different representations, which are estimated by kernel canonical correlation analysis (KCCA) (Lai and Fyfe, 2000; Akaho, 2001) or kernel target alignment (KTA) (Cristianini et al., 2001) using both input and output data. KCCA is a kernel-based extension of standard CCA, which extracts maximally correlated subspaces from two different representations, namely genomic data and gene essentiality scores. KTA approximates an “ideal” kernel function, which can be used to predict a target variable perfectly. The ideal kernel function between cell lines is defined on gene essentiality scores of the training data set cell lines. In both KCCA and KTA, Gaussian kernel (GK) was used for input data, whereas both Gaussian kernel and linear kernel (LK) were used for outputs. There were two choices of kernel functions for output data and two ways of learning representations (KCCA or KTA), which resulted in four KRR models. The final prediction was the average over the outputs of the four models, and this averaging can alleviate instability, which can be caused by the small sample size. The baseline model, i.e., KRR without representation learning component, achieved 0.2255 average correlation score for the final test set. The average correlation score of the four different representation learning methods was 0.2325, whereas KTA + LK, KTA + GK, KCCA + LK, and KCCA + GK were 0.2321, 0.2301, 0.2188, and 0.2321, respectively. Representation learning provided significantly better performance than the baseline KRR, except KCCA + LK, and the final averaged model outperformed all other models according to the Wilcoxon signed rank test (p < 0.01).

The second best performing team started with feature selection on gene expression and copy number data using variance filters and restricting to genes of established cancer importance from a recent PanCancer study (Ciriello et al., 2013). The random forest (RF) predictor used the selected gene-level features directly whereas the multiple kernel learning (MKL) predictor transformed the original training features into kernel pathways represented by sets of genes each taken from a specific genetic pathway. The final gene essentiality predictions were computed by averaging the outputs of the MKL and RF models. The ensemble achieved better performance (0.2321 average correlation score) than either of the individual RF (0.2190) or MKL (0.2293) predictors, suggesting each approach captured sufficiently distinct biological information about the problem. Using gene expression and copy number features together provided improved prediction performance over either data type alone. In addition, the use of a larger collection of pathways in the MKL predictor led to an improvement in accuracy – pathway kernels were derived from three Molecular Signatures Database (MSigDB) collections (Subramanian et al., 2005) (canonical pathways, C2_CP, 1320 gene sets; chemical and genetic perturbations, C2_CGP, 3402 gene sets; and GO, C5_GO, 1454 gene sets (Ashburner et al., 2000)) in our final ensemble predictor improved performance over using the C2_CP collection alone (MKL: 0.2098, ensemble: 0.2220) or C2_CP in combination with C5_GO (MKL: 0.2192, ensemble: 0.2284).

Feature selection criteria used by the third best performing team include: (i) genes that have high overall expression levels across cell lines; (ii) mutations in genes associated with important cellular pathways; (iii) features that have high correlation with gene essentiality score of each gene or all the genes in general; (iv) genes whose expression levels have high correlation with corresponding copy numbers. These criteria were combined to select features with cutoffs chosen by cross validation. According to cross-validation and two other guiding principles listed below, a vector of scaling factors was determined to scale the feature matrix. The two guiding principles are: (i) features that have higher correlation with gene essentiality scores within the training set should have smaller scaling factor; (ii) genes with higher general expression level across all cell lines should have smaller scaling factor. Then, principal component analysis was carried out to reduce the number of features. Finally, Gaussian process for regression was used to predict gene essentiality, where a radial basis function kernel on the principal component matrix was used to represent the similarity between cell lines.

Best Performing Method for Sub-challenge 2

The best performing approach for sub-challenge 2 used the following three-step procedure to perform feature selection on expression data for each predicted gene. (i) They first ranked all expression features using the magnitude of correlation between gene essentiality values and expression levels for all predicted genes. This ranking was denoted by R1. (ii) They then ranked all expression features using their selection frequencies in the top 50 features in the first step. This ranking was denoted by R2. (iii) They then combined these two rankings R1 and R2 to find a unified ranking with weights 0.7 and 0.3, respectively; R = 0.7R1 + 0.3R2. The first nine features were selected this way. The tenth feature was the copy number value of the same gene for which essentiality was being predicted. This was based on the rationale that gene essentiality would heavily be influenced by the dosage (copy number) of that gene existing in the cell line system. Finally, for each gene being predicted, a linear support vector machine was trained using the corresponding ten features.

Best Performing Method for Sub-challenge 3

The best performing approach for sub-challenge 3 applied a greedy regularized least squares (RLS) model (Pahikkala et al., 2012) to solve the prediction task as a multilabel learning problem. Multitarget greedy regularized least-squares (MT-GRLS) (Naula et al., 2014) is a wrapper-based learning algorithm that constructs multilabel ridge regression model based on a given budget restriction on the number of common features to be selected. The method performs stepwise greedy forward selection by adding at each step the feature whose addition leads to the largest increase in leave-one-out cross-validation performance over all the target genes. The algorithm is highly scalable having a linear time training complexity, and it directly optimizes the predictive performance of the learned model subject to the budget constraints, making it ideal for this sub-challenge. An open-source implementation of the method is available in the RLScore software library at https://github.com/aatapa/RLScore. The best performing team evaluated the performance of MT-GRLS model internally using a nested-cross validation (CV) approach. They first applied the model over a range of regularization parameters with seven-fold inner CV to select the most predictive regularization parameter. Then, the predictive accuracy of the model was evaluated using a three-fold outer CV loop. The nested CV provided an accurate estimate of the prediction accuracy on the independent test set. The final prediction model was based on the best regularization parameter learned from the complete training data set using seven-fold CV. The prediction performance of the MT-GRLS did not benefit from any prior filtering of the features, probably due to its efficient feature selection procedure.

Percent of Variation Analysis

To see the effect of different factors on the prediction performance, we used “random effects model” on the prediction results of all three sub-challenges. The two factors we tested were “gene” factor and “team” (or “method”) factor. For each sub-challenge, we used the correlation scores calculated on each gene for each team as the dependent variables, and the gene predicted and the team were the independent variables. We fit the random effects model using the lme4 R package (Bates et al., 2015). After fitting the model, we calculated the proportion of variance explained for each factor together with residual variance.

GSEA/MSigDB Overlap Analyses

GSEA (Gene Set Enrichment Analysis) and MSigDB overlap analyses using a hypergeometric distribution were performed using “Hallmark” (Subramanian et al., 2005; Liberzon et al., 2015) and “KEGG” gene sets (Kanehisa and Goto, 2000; Kanehisa et al., 2014). GSEA analyses of gene predictability scores used average correlation scores of each gene over all teams to rank genes and performed enrichment analysis using this pre-ranked list of genes. MSigDB overlap analyses of commonly chosen features used genes chosen by teams at least 25 times in sub-challenge 2, and by at least 2 teams in sub-challenge 3. The FDRs for MSigDB overlap analyses listed are the false discovery rate analog of hypergeometric p-value after correction for multiple hypothesis testing according to Benjamini and Hochberg.

Baseline Lasso Regression Method

To establish a baseline performance for sub-challenge 2, we used the Lasso algorithm from the glmnet R package (Friedman et al., 2010). We restricted the Lasso algorithm to use at most ten features for each gene predicted in line with the sub-challenge 2 settings. We tried two different scenarios: (i) considering all training cell lines (105 in total) and (ii) considering cell lines with available mutation data (83 in total). For the first scenario, we trained copy number or gene expression only models together with joint model. For the second scenario, we trained single source models as well as model for pairs of data sources and full model that uses all three data sources.

TCGA Survival Analysis

We picked the top 100 frequently selected features in sub-challenge 2 as the predictive signature of cell viability. We downloaded mRNA expression data of TCGA lung adenocarcinoma patients with available survival data (Cancer Genome Atlas Research Network, 2014), which results in a data set of 495 samples. We found that 95 out of these 100 predictive genes were reported in TCGA gene expression assay. We clustered these 495 patients into two groups using hierarchical clustering with Ward’s minimum variance method on mRNA expression data of these 95 genes. We calculated the Kaplan-Meier survival curve using this clustering result and then find the corresponding p-value using the survival R package (Therneau and Grambsch, 2000). To assess the statistical significance of the results, we performed two different bootstrapping simulations:

1. We picked 10,000 random signatures of size 95 by selecting 95 genes out of 20,531 available in the TCGA cohort. We run the same clustering analysis on each signature and calculated the corresponding p-values. We then counted the number random signatures with better p-values than the predictive signature extracted from the challenge submissions.

2. We randomly shuffled the clustering labels obtained from the predictive signature extracted from the challenge submissions 10,000 times. We calculated the p-value from the Kaplan-Meier curve for each random labeling. We then count the random labels with better p-values than the labels obtained from the predictive signature extracted from the challenge submissions.

DATA AND SOFTWARE AVAILABILITY

All data used in this challenge was previously unpublished and are made available together with information about the data generation, challenge details, leaderboards, and source codes used to generate the results reported here at https://www.synapse.org/Broad_DREAM_Gene_Essentiality_Prediction_Challenge.

Highlights.

• An open-participation challenge to assess the ability to predict gene essentiality

• A novel dataset testing 98,000 shRNAs against 149 cancer cell lines

• Over 3,000 predictions submitted over a period of 4 months were analyzed

• This study establishes benchmarks for gene essentiality prediction