Extending the Propagation Distance of a Silver Nanowire Plasmonic Waveguide with a Dielectric Multilayer Substrate

Abstract

Chemical synthesized silver nanowires have been proved to be the efficient architecture for Plasmonic waveguides, but the high propagation loss prevents their widely applications. Here, we demonstrate that the propagation distance of the plasmons along a silver nanowire can be extended if this nanowire was placed on a dielectric multilayer substrate containing a photonic band gap, but not placed on a commonly used glass substrate. The propagation distance at 630 nm wavelength can reach 16 μm even that the silver nanowire is as thin as 90 nm in diameter. Experimental and simulation results further show that the polarization of this propagating plasmon mode was nearly parallel to the surface of the dielectric multilayer, so it can be excited by a transverse-electric polarized Bloch surface wave propagating along a polymer nanowire with diameter at only about 170 nm on the same dielectric multilayer. Numerical simulations were also carried out and are consistent with the experiment results. Our work provides a platform to extend the propagation distance of plasmonic waveguide and also for the integration between photonic and plasmonic waveguides on the nanometre scale.

Graphical Abstract

Figure.

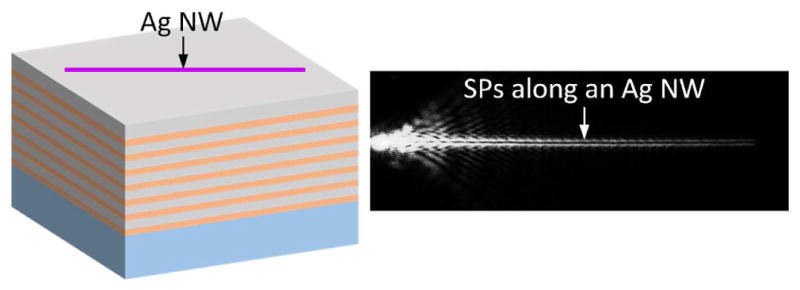
An Ag NW with diameter less than 100 nm was placed on a dielectric multilayer containing the photonics band gap. The LRM image of the SPs propagating along this Ag NW.

Silver nanowires (Ag NWs) synthesized using wet chemistry approaches have unique properties, such as their single crystallinity and atomic surface smoothness, which makes them particularly useful for constructing the plasmonic waveguides. ^{1, 2} Each Ag NW can functions as a plasmonic waveguide, meaning that surface plasmon polaritons (SPPs) can be excited and propagate along the NW. ^3–5 Till now, chemically synthesized crystalline Ag NWs show low scattering losses for wave guiding and are widely used for the development of nanophotonics devices. ⁶ For examples, Ag NWs can be assembled to form branched structures to carry out the functions of routers and logic gates, ^7–10 to form hybrid photon–plasmon nanowire lasers, ¹¹ and to form hybrid nanophotonic components and circuits with subwavelength confinement and reduced losses. ¹²

Ag NWs are very thin and soft and have a large aspect ratio; hence they are placed on solid substrates for practical applications. Typically, a bulk substrate or a single layer of a material is used as a substrate; for example, glass (SiO₂) or MgF₂ layer. Based on the localization character of the SPPs, there are two kinds of supported modes for an Ag NW on a single layer substrate. ¹³ The first one is a plasmonic bound mode where the field is localized at the nanowire–glass (or MgF₂) interface, where the effective refractive index is larger than that of the substrate. The bound mode shows high spatial confinement, but its propagation distance is much short due to the high absorption loss of the metal materials. The second one is the plasmonic leaky mode where the field extends into both the metal–air and metal–glass interfaces. The propagation constant β for the leaky mode is much smaller than that for the bound mode. The effective refractive index of the leaky modes is smaller than that of the substrate; therefore, the leaky mode can couple to photons in the substrate. As described in Ref. 13, this Plasmonic leaky mode will disappear in the case of thinner silver nanowire, due to the high leakage radiation loss into the glass substrate. So, previous reports on the imaging of plasmonic leaky mode of Ag NWs using the leakage radiation microscope (LRM) only studied thick Ag NWs, such as that the diameter is larger than 100 nm (sometimes even above 200 nm) and incident wavelength is in the visible light band.^13–18 In this letter, we will show that this plasmonic leaky mode can be maintained with long propagation distance in the case of thin Ag NW (70 or 90 nm in diameter), only that this NW was placed on a dielectric multilayer substrate (DMS) containing a photonic band gap (PBG), but not the commonly used single layer glass or silicon substrate.

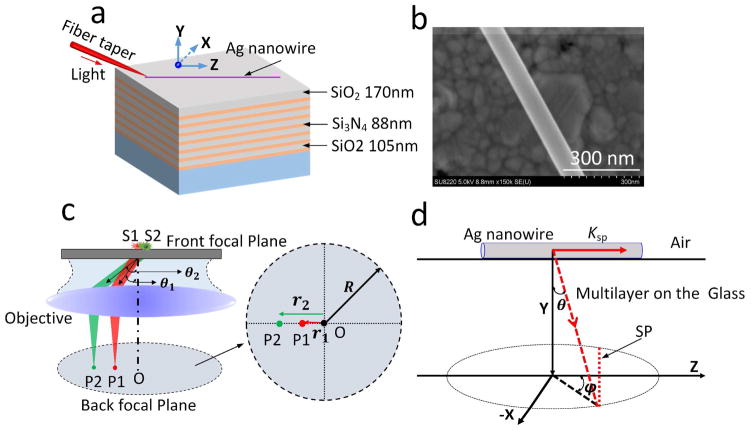
This dielectric multilayer (made of alternating SiO₂ and Si₃N₄ layers) was fabricated using plasma-enhanced chemical vapour deposition. The thickness of each layer is shown in Figure 1(a). Here, SiO₂ is the low (L) refractive index dielectric and Si₃N₄ is the high (H) refractive index dielectric. The thicknesses of these dielectric layers were 105 and 88 nm, respectively. In total fourteen layers were deposited on top of a cover glass. The thickness of the top SiO₂ layer was approximately 170 nm. By using these structural parameters, this dielectric multilayer can contain the PBG and support two-dimensional Bloch surface waves (2DBSW) at short wavelengths, such as at 590 nm. The 2DBSW can propagate freely across the two dimensional surface, the X-Z plane in Figure 1 (a). When the wavelength is increased (620 nm or longer), the 2DBSW will disappear (See Figure S1). ¹⁹ Ag NWs (from Nanjing XFNANO Materials Tech Co., Ltd., China) with a diameter of approximately 90 nm were synthesized using a wet chemistry approach (Figure 1(b)). ¹ We deposited an individual NW on the above-mentioned DMS. A laser beam (from a SuperK supercontinuum source, NKT Photonics, Denmark) was used for the excitation; it was first lens-coupled into a standard single mode silica fibre and then directed into the nanofiber through a fibre taper yielding quasi-circular-polarization guided modes with fractional evanescent fields. The silica fibre taper was then brought into contact with the Ag NW (Figure 1(a)) by a micromanipulator. The light propagating along the NW was characterized by a home-built leakage radiation microscope (LRM) system with both a front focal plane (FFP) and back focal plane (BFP) imaging modules.¹⁶

Figure 1. Schematic illustration of the experiment.

(a) An Ag NW was placed on a dielectric multilayer consisting of alternating layers of SiO₂ (105-nm-thick) and Si₃N₄ (88-nm-thick). There were fourteen layers in total, with a top SiO₂ layer with a thickness of 170 nm. A fibre taper was used to couple the laser beam into the nanowire. (b) SEM image of an Ag NW (diameter of 90 nm). (c) Illustration of the formation of BFP image. S1 and S2 denote the point emitters which is put on a glass substrate (the front focal plane of the objective). Their emitting angles are defined as ϑ₁ and ϑ₂, then two spots (P1 and P2) appear on the BFP, with distance to the centre spot O as r₁ and r₂, respectively. (d) Illustration of the BFP imaging formation for the plasmonic leaky mode propagating along an Ag NW. The plasmons with wave-vector (K_sp) propagate along the NW and leakage radiate simultaneously into the substrate with the angle at (ϑ and φ). Based on the momentum matching condition, this mode will be represented as a line (red dashed line lab led with SP) on the BFP image.

The FFP image is very common for an optical microscope, and provides the spatial distribution of the targets placed on the FFP of the objective. Whereas, the BFP imaging module is not always equipped on a commercial microscope. A schematic illustration of the formation of BFP image is shown in Figure 1 (c). At first, we should keep in mind that every spot on the BFP image represents the information of an angle (it can be the leakage radiation angle of the SP, ²¹ or emitting angle from a dye molecule, ²²). Then, the following will explain how to derive the value of this angle from the corresponding spot on the BFP image. For examples, when two emitters (S₁ and S₂) with different emission wavelengths were placed on the FFP of an objective, and let’s assume their emission is directional and along a particular angle (it is not practical, just an assumption for making an example). These angles into the substrate can be defined as ϑ₁ and ϑ₂. Subsequently, on the BFP of the objective, two spots (P1 and P2) will appear. The radial distance between the two points (P1 and P2) and the centre spot (O) on the BFP is defined as (r₁ and r₂). Based on the known radius of the R (that is determined by the known numerical aperture (NA) of the oil-immersed objective) of the imaging system, and measured r₁ and r₂ from BFP image, the emitting angles ϑ₁ and ϑ₂ can be derived with the equation ϑ_{1, 2} = arcsin ((N.A *r_{1, 2})/(R * n)), where n is the refractive index of the oil or substrate. It is easy to understand that the BFP image can give out information of the angular distribution of the emission or leakage radiation (which is also called as the Fourier plane imaging, meaning the Fourier transformation of the FFP image).

In the following experiment, the LRM is used to measure the SP propagating along an Ag NW placed on the DMS. The image formation can be illustrated simply in Figure 1(d). The SP propagates along the NW (Z-axis) with wavevector as k_sp. Due to the leaky property of this plasmonic leaky mode, the SP would become a photon (light) in the multilayer and then coupled into the lower glass substrate (Figure 1 (a)). The magnitude of the wavevector of light (in the glass below the multilayer) parallel to the axis of the NW is k_z/k₀ = n* sin (ϑ) cos(φ), which should be equal to the k_sp/k₀, due to the requirement of momentum matching for the excitation and leakage radiation of SP wave, where k₀ =2π/λ is the free space wavevector of the light at wavelength λ. This analysis shows that, on the BFP, the SP would appear as a line perpendicular to the reciprocal space vector corresponding to the long axis of the NW (red dashed line on Figure 1(d)). ^{13, 17} Using the measured angle ϑ and φ by the BFP image (Figure 1 (c) denotes how to derive the angle ϑ from the BFP image, and φ is defined on Figure 1 (d) which can be easily derived out), the propagation constant of the plasmonic leaky mode (k_sp/k₀) can be derived out. The schematic of the experimental setup (Figure S2) shows the light paths for both FFP and BFP imagings.

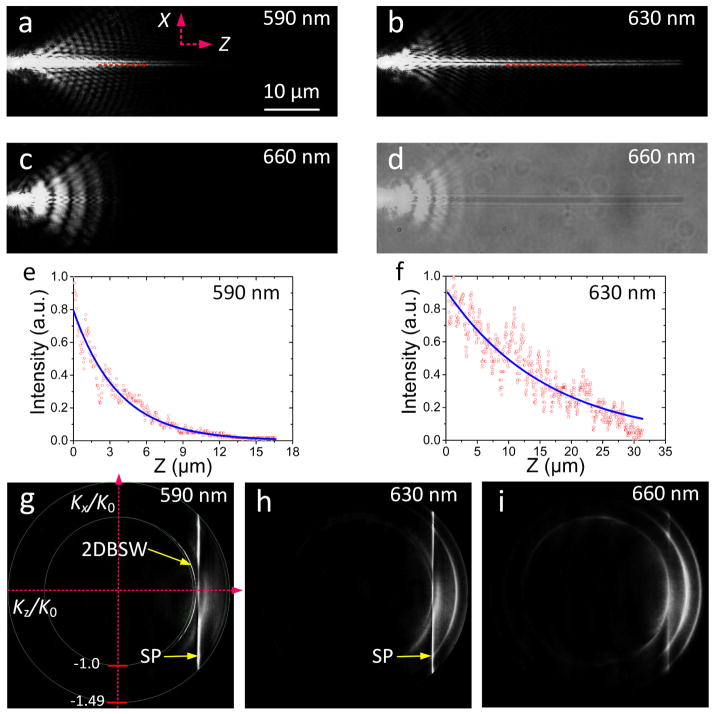
Experimental FFP images of the laser beam propagating along the 90 nm diameter Ag NW are shown in Figure 2(a) and (b) at incident wavelengths of 590 and 630 nm, respectively. Figure 2(c) and (d) shows the laser beam and white light images for an incident wavelength of 660 nm. The length of the Ag NW was approximately 53 μm. The FFP images demonstrate that the plasmonic leaky mode can be sustained on the thin Ag NW on the DMS at both 590 and 630 nm wavelength. The propagation lengths at 590 and 630 nm could be derived out with exponential curve fits and were found to be 4 and 16 μm, respectively, based on the intensity profiles along the NW (Figure 2(e) and (f)). The BFP images at these two wavelengths display another difference: at 590 nm a 2DBSW excited by the laser from the fibre taper is visible in the form of bright circles (Figure 2(g)). ²¹ At a wavelength of 630 nm these circles are not present (Figure 2 (h)). The vertical bright lines on Figure 2(g) and Figure 2(h) are a unique but relatively unrecognized feature of BFP images that correspond to the leaky mode along an Ag NW, ^15–18 whose formation is illustrated in Figure 1 (d). These bright lines (labelled “SP”) in Figure 2(e) and (f) can be used to derived the effective index of the plasmonic leaky mode (also referred to as the real part of the propagation constant), which was determined to be 1.05 at 590 nm and 1.02 at 630 nm. When the incident wavelength was increased to 660 nm, we did not observe any propagation along the NW in either the FFP (Figure 2(c), and 2(d)) or BFP images (Figure 2(i)). When a NW with the same diameter (90 nm) was placed on a glass substrate, no leaky propagating mode could be observed, similar to that shown in Figure 2(c) and (d).

Figure 2. Plasmonic mode of the Ag NW on the DMS.

FFP image of the light beam propagating along the Ag NW at three incident wavelengths, namely at (a) 590 nm, (b) 630 nm, and (c) 660 nm. (d) shows the same image area as that in (c), but here a white light source was placed above the sample to illuminate the NW to show the relative position of the coupled fibre taper and the Ag NW which appears as a darker line. The intensity distribution along the NW (Z-direction, red dashed lines) in (a) and (b) are shown in (e) and (f), respectively. The blue solid line is an exponential fit to the data (red dots) and was used to extract the propagation distance of the plasmonic leaky mode. (g) (h) and (i) show the corresponding BFP images at 590, 630 and 660 nm wavelength, respectively. The scale bar in (a) is also applicable for the images in (b)–(d).

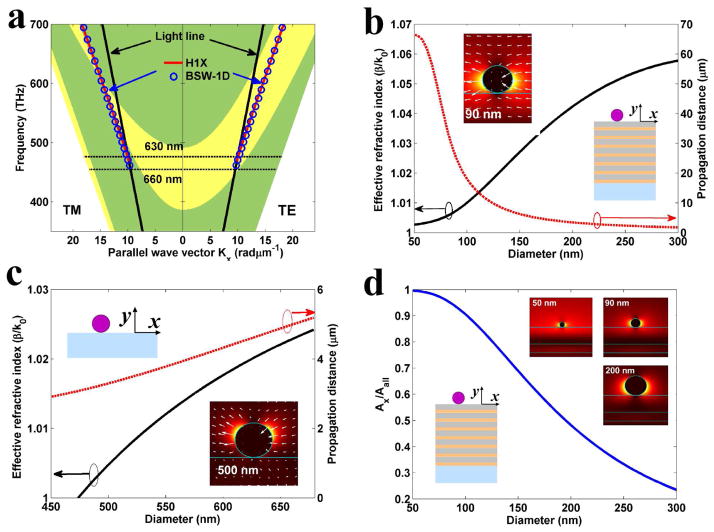
To clearly explain the experimental results, the projected band structure of the dielectric multilayer (shown in Figure 3(a) was calculated for transverse-electric (TE) and transverse-magnetic (TM) waves based on the dispersion equation for Bloch waves) using the finite element method. ^{22, 23} The permittivity of Ag NWs at different wavelengths was set based on experimental values. ²⁴ Owing to the surface scattering and grain boundary effects in real thin films, in the simulation, the refractive indices of SiO₂ and Si₃N₄ are n_SiO2 = 1.46 + i × 10⁻³ and n_Si3N4 = 2.14 + i5 × 10⁻³, respectively. The refractive index of the glass substrate was n_glass = 1.515. It should be noted that generally chemically prepared Ag NWs have pentagonal cross-section, but in our work, this NW is very thin (the diameter is less than 100 nm) and the incident wavelength (around 600 nm) is more than six times of this diameter, so in our simulations, we assume the cross section of the Ag NW is to be circular, which does not affect the modes sustained by the Ag NW.

Figure 3. Numerical simulation of the plasmonic mode.

(a) The projected band structure of the dielectric multilayer for TE and TM polarizations. The yellow zone denotes the stop band. The red solid lines and blue circles denote the dispersion relation for H1X mode of Ag NW with diameter 90 nm and BSW-1D mode of polymer NW with diameter 170 nm, respectively. (b), (c) show the effective refractive index and propagation distance of the H1X mode versus the diameter of the Ag NW placed on the DMS (b) or on the glass substrate (c). The incident wavelength was 630 nm. The inset in (b) shows the electric field distribution of the H1X mode for the 90-nm-diameter NW on the DMS. The inset in (c) shows the electric field distribution of the H1X mode of the 500-nm-diameter NW on the glass substrate. The arrows in the inset graphs (electric field distribution) denote the direction of the electric field vectors. (d) The ratio of the electric field energy (A_x/A_all) for the H1X mode versus the diameter. The electric field distributions for H1X mode of Ag NW with diameter 50 nm, 90 nm and 200 nm are shown in the inset, respectively.

The dispersion relation for plasmonic leaky mode of Ag NW with a diameter of 90 nm is shown in Figure 3(a) with a red solid line. Based on the electric field distribution and vector directions of electric field on the inset graph of Figure 3 (b), this mode can be attributed to the H1X mode. ²⁵ For an excitation wavelength of 660 nm, the dispersion curve of the H1X mode disappears and the mode is cut off because it moves across the light line (Figure 3 (a)). Therefore, the electromagnetic waves at this frequency cannot be guided by the NW. As noted in Figure 3(a), the dispersion curve of H1X mode is in the stop band for TE polarization. The bandgap effect of dielectric multilayer can inhibit the leakage radiation of H1X mode, and thus increase the propagation distance of H1X mode. Figure 3(b) and 3(c) demonstrate the diameter-dependent dispersion relation of the H1X mode for a NW placed on the DMS and on the glass substrate, respectively. It is clearly shown that the H1X mode of Ag NWs placed on the glass substrate has a larger cut-off diameter and shorter propagation distance compared with that of NWs placed on the DMS. For examples, when the diameter of the Ag NW is smaller than 480 nm, the H1X mode on the glass substrate is cut off at the incident wavelength of 630 nm. The H1X mode on the DMS can exist even when the diameter of the NW is decreased to 50 nm (as shown by inset graph in Figure 3 (d)). What is more, the comparison between Figure 3 (b) and (c) shows that the propagation distance of the plasmonic signal is highly increased if the Ag NW was placed on the DMS.

Here we give a note on the comparisons between the plasmonic modes of an Ag NW placed on a bare glass substrate and that on a DMS. As shown in Figure S3, three related plasmonic modes of an Ag NW placed on a bare glass substrate were simulated with the incident wavelength fixed at 630 nm. The H0 mode is the plasmonic bound mode with effective refractive index larger than the refractive index of the glass substrate (Figure S3 (a)), although it can sustained at a very thin Ag NW, its propagation distance is much lower (Figure S3 (b)). For example, when the diameter of the Ag NW is 90 nm, the propagation is less than 2 μm (Figure S3 (b)). But this mode has high spatial confinement (Figure S3 (c)). There are another two plasmonic leaky modes, the H1X, and H1Y (Figure S3), they are the typical plasmonic leaky modes which have also been presented in Figure 2d of Reference 18. They are of different polarization states (as noted by the white arrows in Figure S3 (c)). From Figure S3, we can find these two modes cannot sustain in the case of thin NW and also their propagation distances are much short. For examples, the H1X mode is cutoff when the diameter is less than 440nm, and the H1Y mode is cutoff when the diameter is less than 110 nm. The propagation distance of these two modes are both less than that of the plasmonic mode reported here.

Here, we also give a note on why H1Y mode does not exist when the thin Ag NW was placed on the DMS. Firstly, as shown in Figure 3 (a), the DMS used here contains the broad PBG mainly for the TE polarized light at the investigated wavelengths and larger wavenumber (the wavenumber of the guided mode is larger than that of light in vacuum of the same frequency). The TM polarized light of larger wavenumber will transmit through the DMS. Secondly, as shown in Figure S3 (c), for H1X mode, its main component is of TE polarization (the electric field parallel to the interface of DMS), the leakage radiation of H1X mode is inhibited by the PBG of the DMS, so it can be maintained in the case of a very thin Ag NW placed on the DMS. However, for the H1Y mode, its main component is of TM polarization (the electric field vertical to the interface of DMS), its signals will leaky heavily into the DMS, as a result this H1Y mode cannot be sustained in the case of a thin Ag NW placed on the DMS.

As described in Figure. 1 of Reference 25, there is also a plasmonic mode between the H0 and H1Y, but based on our simulations, this mode will disappear when the incident wavelength is longer than 400 nm (the diameter of the NW is 200 nm, the same as that used in Reference 25). Whereas, in our experiments and simulations, the investigate wavelength is longer than 550 nm, so we do not use this mode for comparisons. Based on the polarization direction and electric field distribution, we find that the H1X mode on a glass substrate (Figure S3 (c)) is similar as the plasmonic leaky mode of the Ag NW on the DMS (inset graph of Figure 3 (b)). So we also name this plasmonic leaky mode on the DMS that we investigated here as the H1X mode. In the comparison, we have not quantitatively compared the confinement of these plasmonic modes, because it is not precise to define the mode area for a plasmonic leaky mode, and our aim of this paper is mainly focused the longer propagation distance of plasmons sustained on a very thin Ag NW.

Furtherly, when we take a close look at the diameter-dependent propagation distances for Ag NWs on a glass substrate (Figure S3 (b)) and that on a DMS (Figure 3 (b)), we can find that the propagation distance decreases with the diameter of the Ag NWs when the NWs were placed on a DMS (Figure 3 (b)), whereas, this dependence is opposite in the case of Ag NWs on a glass (Figure S3). This phenomenon can be analyzed as following. Considering that the H1X mode is a hybrid mode, ²⁵ the field components of the H1X mode can be decomposed into TE- and TM-polarized components in the dielectric multilayer. The TE- and TM-polarized component of H1X mode can experience difference leaky loss in the DMS due to the different photonic band structure for TE and TM polarizations as shown in Figure 3(a). For an excitation wavelength of 630 nm, the dispersion curve of H1X mode is in the stop band for TE polarization. Then, the DMS can effectively decrease the leaky radiation of the TE-polarized component of H1X mode based on the photonic bandgap effect. However, the dispersion curve of H1X mode is in the transmission band for TM polarization as noted in Figure 3(a). The TM-polarized component of H1X mode will propagate through the dielectric multilayer and radiate into the glass substrate. To qualitatively understand the wave guiding behaviour of the H1X mode on the dielectric multilayer, the ratio of the electric field energy (A_x) with TE-polarized component to the total electric field energy (A_all) are calculated and is shown in Figure 3(d). A_x and A_all are defined as follows (1) and (2): ²⁶

$$A_x=\int \underset{-\infty }{\overset{+\infty }{\int }}\frac{1}{2}\left(\frac{d\left(\epsilon (r)\omega \right)}{d\omega }{\left|E_x(r)\right|}^2\right)d^{2}r$$ (1)

$$A_{\mathit{all}}=\int \underset{-\infty }{\overset{+\infty }{\int }}\frac{1}{2}\left(\frac{d\left(\epsilon (r)\omega \right)}{d\omega }{\left|\mathit{E}(r)\right|}^2\right)d^{2}r$$ (2)

where |E_x(r)|² and |E(r)|² are the intensity of the X-component of electric fields and the total electric fields, respectively. ε is the permittivity. r denotes a spatial position. With the decreasing of the NW diameter, the ratio of A_x/A_all is increased, and finally approaches to one. This means that the H1X mode on the dielectric multilayer is gradually transformed into the “pure” TE-polarized mode with decreasing of the NW diameter. For TE-polarized mode, the dielectric multilayer can effectively decrease the leaky radiation of mode due to the bandgap effect. Moreover, as the diameter of NW is decreased, the electric field energy of H1X mode on the dielectric multilayer is increasingly localized into the local environment as noted in the inset of Figure 3(d), which can decrease the loss from the absorption of material and increase the effects of the environment or solution outside the NW. Therefore, the propagation distance of H1X mode on the dielectric multilayer is sharply increased with decreasing of the NW diameter.

In contrast, when the Ag NW was placed on a bare glass substrate, and as the diameter of NW is decreased, the energy of corresponding H1X mode (Figure 3 (c)) is gradually diffused into the environment due to the decreasing of the effective refractive index of mode (Figure 3 (c) and Figure S3). The leakage loss of this H1X mode is enhanced (there is no band gap effect for the bare glass substrate), which decreases the propagation distance of the H1X mode on the bare glass substrate.

In our experiment, an Ag NW of smaller diameter (at approximately 70 nm) placed on the same DMS was also investigated and the results are shown in Figure S 4. The propagation distance can be derived as about 12 μm with the incident wavelength at 590 nm, and 18 μm at 600 nm. These propagation distances are longer than those from the Ag NW with the diameter at 90 nm, which are consistent with the above numerical simulations.

Finally, we will show the polarization state of the H1X mode of an Ag NW on the DMS, and its coupling with another kind of surface wave. When a polarizer was placed before the camera for BFP images, experimental results (Figure S 4 (g) and (f)) show that this H1X mode presents the similar polarization state as the reported BSW mode of a polymeric NW placed on a DMS. ²¹ This polarization similarity was also verified by the numerical simulation as shown in Figure S5. ^{21, 27}, thus providing the possibility of coupling between the plasmonic mode on an Ag NW and the BSW mode on a polymeric NW. Similar to the Ag NW, the thin polymer NW is also very soft and should also be placed on a solid substrate for practical use. When the polymer NW is too thin and placed on a glass substrate, such as a diameter less than 250 nm, it also cannot transport optical signals. Our previous work and other published paper shows that if we placed this thin polymeric NW on a dielectric multilayer, it can transport optical signals, which is the Bloch surface wave along a dielectric NW or stripe. ^{21, 27}

Here, to show this nanowires coupling, a polymer NW with a diameter of 170 nm was selected. The dispersion relation of the corresponding BSW mode along this polymer NW was simulated as shown in Figure 3 (a) (labelled as BSW-1D). The coupling behaviours between the BSW mode and the plasmonic mode are numerically simulated as shown in Figure S6. The theoretical details of coupling efficiency were shown and discussed in Figure S7. In experiments, a polymer NW with a diameter of about 170 nm was fabricated and placed on the same multilayer substrate (Figure 1(a)); then, an Ag NW (90 nm in diameter) was placed close to the polymer NW (Figure 4(a)). The BSW propagating along the polymer NW was excited via a silica fibre taper, and the BSW was coupled into the SP (Figure 4(b)). The propagation paths of the optical signals along both the polymer and Ag NWs can be clearly observed (Figure 4(b)), which demonstrate that the BSW mode can be coupled into the SP mode. This structure containing two contacted NWs (Figure 4(b)) works as a beam splitter. The original BSW is divided into two paths; the first one sends the BSW along the polymer NW, while the second one changes the BSW into a SP along the Ag NW. Known to all, polymer and metal NWs both have their particular properties, such as polymer NWs can be doped with various functional units, metal Ag NWs might provide high electric field enhancement or sensitivity, so the integration between these two kinds of NWs for signals transportation will open new opportunities for NW devices. Obviously, this kind of modes coupling (between BSWs and SPs on the NWs) is different from the traditional coupling between a dielectric NW and a metal NW, because the NWs on a traditional glass or silicon substrate cannot transport optical signals in the case of a small diameter.

Figure 4. Coupling between the plasmonic and BSW modes.

(a) White light image of the Ag NW and polymeric NW on the multilayer. The diameter of the polymer NW is about 170 nm and that of Ag NW is 90 nm. The location of the Ag and polymer nanowires are the darker lines. (b) FFP image of the light beam propagating along the two NWs with the incident wavelength at 630 nm.

In conclusion, we report the use of a dielectric multilayer containing a PBG as a substrate for the Ag NW. When comparing with the plasmonic bound mode of an Ag NW placed on the glass substrate, the plasmonic mode of an Ag NW on the DMS presents much longer propagation distance but less spatial confinement. When comparing with the plasmonic leaky mode of an Ag NW on the glass substrate, the plasmonic mode of the Ag NW on a DMS can be sustained even that its diameter is as low as 70 nm or 90 nm, and keeps a longer propagation distance. Both experimental and simulation results show that this thin Ag NW on a DMS can provide longer propagation distance than that of a thicker one. Although it is a plamonic leaky mode, its propagation distance is extended due to the PBG inside the DMS. This propagation distance can be further increased if the number of the dielectric layer is increased ²³. The long propagation distance is favourable for plasmon signals delivery for remote sensing or integrated circuits. This DMS can also tune the polarization state of the plasmonic mode of the Ag NW, so that it can be coupled with the polymer NW in the nanometre scales. Whereas, the optical signals cannot be coupled between these two thin NWs if they are placed on a commonly glass substrate. This DMS provides new parameters to manipulate the propagation properties of an Ag NW plasmonic waveguide mode. Except for the chemical synthesized Ag NWs, this DMS can also be used for other plasmonic waveguide made of other metallic NWs, such as the NWs made with focused ion beam or electron beam lithography. So, our work provides a platform for the development of NWs devices and will bring opportunities in the field of nanophotonics.²⁸