Stretch activation properties of Drosophila and Lethocerus indirect flight muscle suggest similar calcium-dependent mechanisms

Abstract

Muscle stretch activation (SA) is critical for optimal cardiac and insect indirect flight muscle (IFM) power generation. The SA mechanism has been investigated for decades with many theories proposed, but none proven. One reason for the slow progress could be that multiple SA mechanisms may have evolved in multiple species or muscle types. Laboratories studying IFM SA in the same or different species have reported differing SA functional properties which would, if true, suggest divergent mechanisms. However, these conflicting results might be due to different experimental methodologies. Thus, we directly compared SA characteristics of IFMs from two SA model systems, Drosophila and Lethocerus, using two different fiber bathing solutions. Compared with Drosophila IFM, Lethocerus IFM isometric tension is 10- or 17-fold higher and SA tension was 5- or 10-fold higher, depending on the bathing solution. However, the rate of SA tension generation was 9-fold faster for Drosophila IFM. The inverse differences between rate and tension in the two species causes maximum power output to be similar, where Drosophila power is optimized in the bathing solution that favors faster muscle kinetics and Lethocerus in the solution that favors greater tension generation. We found that isometric tension and SA tension increased with calcium concentration for both species in both solutions, reaching a maximum plateau around pCa 5.0. Our results favor a similar mechanism for both species, perhaps involving a troponin complex that does not fully calcium activate the thin filament thus leaving room for further tension generation by SA.

stretch activation (SA) is a delayed rise in force following rapid muscle lengthening (stretch) (38) that supplements the force level that can be achieved by calcium activation alone. A four-phase tension response is produced by a muscle with prominent stretch activation that is first calcium activated and then rapidly lengthened and held isometric at the new length: an immediate force increase (phase 1), a force decay (phase 2), a secondary force increase (phase 3), and a slow force recovery (phase 4) (Fig. 2). The phase 3 force increase is delayed with respect to the fiber length change and is defined as SA. SA is a transient response to a length increase. The steady-state Abbott effect (also known as “Force Enhancement) occurs following a slower and longer stretch of an active muscle which causes steady-state tension to be higher than when the muscle is activated at the same final stretched length (1, 21, 30). SA is an inherent property of the sarcomere, and almost all striated muscles display some level of SA, but it is most prominent and beneficial in muscle types that generate work and power through repetitive cyclical contractions (26). In the context of a muscle that is cyclically lengthening and shortening to generated work and power, the timing of the delayed activation is synchronized with the cyclical muscle length change so that the increased force generation by the muscle occurs during active shortening. SA’s opposite and complementary phenomenon is shortening deactivation (SD), a delayed drop in force following shortening, which decreases resistance during muscle lengthening (26). These delayed force changes in response to length change increase muscle power and efficiency (41).

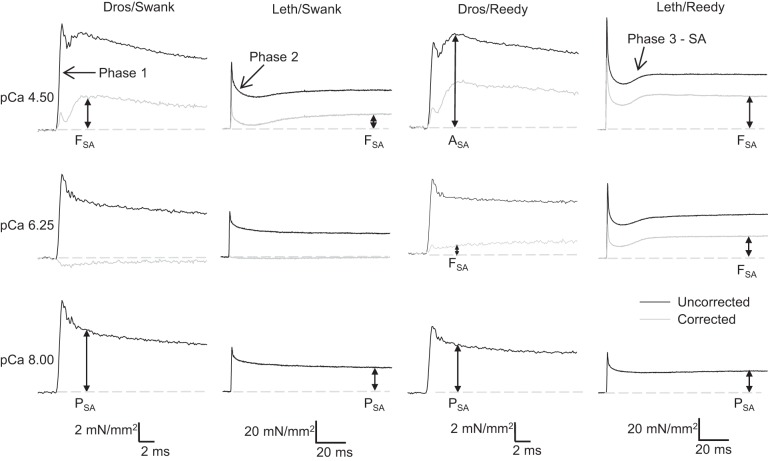
Fig. 2.

Representative traces of Drosophila and Lethocerus indirect flight muscle (IFM) tension transients following a 1% muscle length increase over 0.5 ms at three calcium concentrations: pCa 4.5, 6.25, and 8.0. The gray trace is the resultant tension trace after the passive tension trace, pCa 8.0, has been subtracted. This resultant trace shows the active stretch activation (SA) component (F_SA). Phases 1–3 of the tension transient are labeled along with the different measures of SA tension: A_SA: total SA tension, P_SA: passive SA tension, F_SA: active SA tension. The dashed gray line highlights the isometric tension value before the length step. Note the different scale bars for time and tension for Lethocerus traces compared with Drosophila traces.

Muscle types vary in the magnitude of their stretch activation response. Vertebrate heart muscle possesses moderate stretch activation, which likely increases force production during systole (6, 40, 42, 45). In the extreme case of asynchronous insect indirect flight muscle (IFM), where the wings beat faster than the nerve impulses arrive, calcium cycling during each contraction is not required because SA and SD modulate force levels (27). Without SA and SD, insect flight muscle would absorb work and hence not be able to power flight. In contrast, skeletal muscle types generally only have a small SA response; therefore, variation in force levels during function relies almost entirely on intracellular calcium cycling with minor input from SA and SD (34). However, while critical to muscle function, the mechanisms behind SA and SD are not well understood.

One possible reason for the lack of understanding may be that there are different mechanisms for SA and SD in various muscle types and/or species. For example, differences in the optimal calcium concentration the produces maximal SA tension (F_SA) and the ratio of F_SA to calcium-activated isometric tension (F₀) at different calcium concentrations have been reported (2, 25, 32, 47). These differences have important implications for the SA mechanism. For example, the finding that intermediate calcium concentrations produce the highest F_SA in Lethocerus IFM (2, 32) has led to the proposal that a low level of F₀, brought about by a relatively low calcium concentration, is required to leave room for SA to increase tension, while higher levels of isometric tension at high calcium concentrations reduce the amount of F_SA that can be generated (32). However, contrary findings by other investigators do not support an intermediate calcium concentration-dependent mechanism. Some Lethocerus (25, 36) and all Drosophila studies (36, 47) have found that the same high calcium concentration that produced maximum F₀ also produced maximum F_SA.

Studies suggest that SA evolved several times (10), perhaps with different physiological, morphological, and ecological constraints influencing the optimal SA characteristics and mechanism for a given species (46). For example, tiny Drosophila IFM are strongly influenced by ambient temperature, unable to sustain a thermal gradient between core temperature and the environment greater than a fraction of a degree (20). But, some larger insects, such as those in the genus Apis, cannot shed the heat generated by working IFM during flight rapidly enough to escape substantial warming of IFM. Instead, they use the heat generated to increase muscle power. Lethocerus is an example of a large insect that requires preflight warmup by sustained maximum tetanus to reach working flight muscle temperature. Thus, Lethocerus IFM may require the ability to generate high-force, isometric contractions, while Drosophila IFM may not need to produce isometric contractions. Another important constraint is wing beat frequency which is ~10-fold higher in Drosophila than Lethocerus (23, 31). Drosophila IFM kinetics presumably should be much higher to power the faster wing beating of its smaller surface area wings while the much larger Lethocerus wings beat slower and support a much larger body mass (10).

Alternatively, the reported differences in SA characteristics may be due to variation in experimental protocols, apparatuses, or solutions (2, 25, 32, 37, 47). In particular, the components of skinned IFM fiber bathing solutions such as ATP concentration, ionic strength, and the inclusion or absence of an ATP regeneration system, could be leading to the appearance that SA differs between insect species.

To determine actual muscle mechanical differences between species, particularly in the SA response, we compared the performance of Drosophila and Lethocerus IFM skinned fibers on the same muscle mechanics apparatus following an identical experimental protocol. We also compared the influence of the different bathing solutions used previously by our two research groups (37, 47). Our results suggest that there are distinct species differences, most notably the magnitude of F_SA and rate of F_SA generation; however, the F_SA response to calcium is very similar. For both species, F_SA increases with calcium concentration, in proportion to calcium-activated F₀, with maximum F_SA occurring at the same calcium concentration as maximum F₀.

METHODS

Fiber preparation.

Fibers from the dorsal-longitudinal muscle (DLM) of 3-day-old Oregon-R Drosophila were dissected as previously described (43). Briefly, the thorax was split along the sagittal plane and fibers were removed from a half thorax while in skinning solution (pCa 8.0, 12 mM MgATP, 1 mM free Mg²⁺, 5 mM EGTA, 300 mM CP, 300 U/ml CPK, 20 mM N,N-bis(2-hydroxyethyl)-2-aminoethanesulfonic acid (BES, pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT, 50% glycerol, and 0.5% Triton X-100) at 4°C. Fibers were split lengthwise to decrease diameter and mounted to the mechanics apparatus using aluminum T-clips (17).

Live specimens of Lethocerus indicus were imported from Thailand and housed temporarily in aquaria in the Reedy laboratory. Fibers for mechanics were prepared as previously described (37). Briefly, the head, abdomen, and appendages were removed. The thorax was rinsed with cold Ringer’s solution through the central hole where the alimentary canal formerly passed and then cut into dorsal/ventral halves with small surgical scissors. The DLMs were left in the dorsal hemi-thorax for mechanical protection, and then chemically skinned with 18 ml of solution. The base skinning solution was alternately aqueous or made in 50–75% glycerol and contained 20 mM MOPS, 5 mM MgAcetate, 5 mM ATP, 5 mM EGTA, 5 mM NaN3, 20 mM NaPhosphate, pH 6.80 adjusted with NaOH. Skinning the fibers required two days with the glycerol and aqueous solutions exchanged several times. The first three exchanges included anti-protease treatment and 1% Triton X-100. Final solution was prepared in 75% glycerol with 5 mM DTT added. In the final solution, hemi-thoraces can be stored at −100°C for many years with no apparent degradation of structure or mechanics. DLMs were subdissected into straplike fascicles of a few hundred fibers. Single fascicles were placed in microcentrifuge tubes with 1 ml of storage solution, transported on dry ice to the Swank laboratory, and stored there at −80°C until use. For dissecting single fibers and T-clipping, fascicles were warmed to 4°C in storage solution and individual fibers were then peeled off the fascicle with forceps. The 15-mm-long fibers were cut to ~0.5 mm with iris scissors and then fitted with T-clips (17) that were 25% smaller than those used for Drosophila fibers due to the smaller diameter of Lethocerus fibers. The resulting length of the fiber between the clips averaged ~0.3 mm, which was similar to clipped Drosophila fibers.

Muscle mechanics.

IFM fibers from either species were set up on the mechanics apparatus identically and as previously described (43). Briefly, an isolated fiber was mounted to the apparatus in relaxing solution, either Reedy relaxing solution (Table 1) or Swank relaxing solution (Table 1), using aluminum T-clips. The fiber was stretched until just taut, the fiber length between the clips was measured, and the fiber was lengthened by 5%. Using a mirror to image the fiber from below and from the side, the two widths were measured and the fiber area was calculated assuming an elliptic cross section. The fiber was activated at pCa 5.0 with the corresponding activating solution (Table 1). The fiber was stretched by 2% muscle length increments until power output, as determined by sinusoidal analysis (see below), was maximized. IFM fibers that did not produce maximum power greater than 80 W/m³ were discarded and not analyzed. Isometric tension, step analysis, and sinusoidal analysis protocols were subsequently performed at this optimal length at 15°C. Separate sets of fibers were used for each bathing solution, resulting in four sets of results, rather than subjecting a fiber to both Reedy and Swank solutions. This avoided a lengthy protocol that would have excessively run down the fibers.

Table 1.

Stock fiber-bathing solutions

Solution	pCa	IS	pH	ATP	BES	MOPS	EGTA	CaCl2	MgCl2	MgOAc	Na2CP	CPK
Swank Relaxing	8	200	7.0	12	20		5	0.1	14		30	600
Reedy Relaxing	9.67	100	6.8	15		20	5			15
Swank Activating	4	200	7.0	12	20		5	5.5	14		30	600
Reedy Activating	4.5	100	6.8	15		20	5	5.0		15

All units are mM except CPK, which is U/ml. Ionic strength (IS) was kept constant between activating and relaxing solutions by using sodium methane sulfonate (NaMs) for Swank solutions, 6.9 mM in relaxing and 18.4 mM in activating, and by adding 10 mM NaCl to Reedy activating solution. Additionally, 1 mM DTT was added to both Swank solutions and 5 mM NaN₃ to both Reedy solutions. pH was adjusted with KOH for Swank solutions and NaOH for Reedy solutions. Free calcium was calculated using either MaxChelator (3) or Calcium (15).

Isometric and SA tension measurements.

After the optimal length for power production was found, the fiber was shortened to slack length to determine baseline (zero force), then relengthened to the optimal length. Isometric tension was recorded 2 min later. To measure the SA response at pCa 5.0, the fiber was then run through a trapezoid-shaped lengthening and shortening protocol consisting of a 1% length increase over 0.5 ms, a 500-ms plateau at this length, followed by a 0.5-ms return to the starting length. Calcium concentration was lowered to pCa 8.0 by exchanging sufficient relaxing solution. Subsequently, appropriate volumes of either Swank or Reedy activating solution (Table 1) were exchanged into the fiber-bathing chamber to reach the next pCa. After 1 min to allow tension to stabilize, isometric tension was measured (without a change in length), then the lengthening and shortening step protocol was performed. Isometric tension was measured again to determine if damage occurred to the fiber as result of the length steps. This was repeated for 13 calcium concentrations until pCa 4.5 was reached. A final exchange was back into pCa 5.0 where F_0, F_SA, and sinusoidal analysis measurements were repeated to determine if fiber degradation (rundown) occurred. To account for the effect of fiber degradation on isometric and SA tension, the pCa 5.0 values at the end were subtracted from the starting pCa 5.0 values and a correction factor was determined by dividing this value by the number of runs. This value times the run number was then added to all in between tension values under the assumption that fiber degradation was linear over time. Typical fiber degradation over the entire protocol was ~15% for F_SA and ~30% for isometric tension. To make sure fiber degradation was not qualitatively influencing our results, we tested a subset of fibers starting at high calcium instead of low calcium and a random calcium concentration order. All experiments produced the same results (before and after correction): F_SA was highest at the high calcium concentrations. For measurements in the Reedy solutions (both Lethocerus and Drosophila IFMs), pCa 9.67 was also included. In all cases, values at pCa 9.67 were not statistically different from pCa 8.0 and, for simplicity, are not always reported or shown.

SA analysis.

The total SA tension (A_SA) was measured for a given calcium concentration by subtracting the total calcium-activated isometric tension, A₀ (immediately before the step), from the peak value of the delayed force increase [phase 3 (13)] following stretch. This tension level was corrected to show only active components (F_SA) by subtracting passive phase 3 tension (P_SA) which we measured at pCa 8.0; therefore, F_SA = A_SA − P_SA. P_SA was measured at the same time point after the lengthening step as the A_SA phase 3 peak amplitude at pCa 4.5. Tension and F_SA versus pCa plots were fitted with the Hill equation, F = A/[1 + 10^{B*(x − C)}], where F = the observed force and the variable x = pCa. Parameters B and C represent the Hill coefficient and the pCa at half-maximal force, respectively, which we report in Tables 2 and 3 for isometric and stretch-activated tension. The parameter A represents the maximal force and is necessary to account for potentially incomplete saturation at pCa 4.5. Because this parameter effectively extrapolates the observed data, we do not report it. The rates associated with the SA tension transients were obtained by fitting the tension trace following the initial spike, Huxley and Simmon’s phases two through four (22), to the sum of three exponential curves: a₃[1 − exp(−r₃t)] + a₂exp(−r₂t) + a₄exp(−r₄t) + offset.

Table 2.

Isometric tension

Species/Solution	n	A0, mN/mm2	P0, mN/mm2	F0, mN/mm2	Hill Coefficient	pCa50
Dros/Swank	11	4.2 ± 0.3LS LR	2.8 ± 0.4LR	1.4 ± 0.2LS LR	2.36 ± 0.58DR LS LR	6.15 ± 0.07LS
Leth/Swank	10	35.1 ± 3.8DS DR LR	18.1 ± 2.3DS DR	17.0 ± 1.7DS DR LR	0.99 ± 0.06DS	5.60 ± 0.06DS DR LR
Dros/Reedy	9	4.4 ± 0.4LS LR	2.5 ± 0.5LS LR	1.9 ± 0.2LS LR	1.17 ± 0.12DS	6.34 ± 0.10LS
Leth/Reedy	10	60.8 ± 2.9DS DR LS	20.8 ± 3.1DS DR	40.1 ± 3.3DS DR LS	0.88 ± 0.05DS	6.06 ± 0.09LS

All values are means ± SE. A₀, total active isometric tension (pCa 5.0); P₀, passive isometric tension (pCa 8.0); F₀, corrected active isometric tension (F₀ = A₀ − P₀). Graphs of the relationship between isometric tension and calcium concentration from individual fibers were fit with the Hill equation to obtain Hill coefficient and pCa₅₀ values for each fiber, which were then averaged. The n values for both sets of Drosophila Hill coefficients and pCa₅₀ values are 3 fibers less than for the isometric tension values. Superscript letters indicate statistical difference between the four sets of fibers based on one-way ANOVA with Holm-Sidak pairwise multiple comparisons, P < 0.05. DS = Drosophila fibers bathed in Swank solutions; DR = Drosophila fibers bathed in Reedy solutions; LS = Lethocerus fibers bathed in Swank solutions; LR = Lethocerus fibers bathed in Reedy solutions.

Table 3.

Stretch-activated tension

Species/Solution	ASA	PSA	FSA	Hill coefficient	pCa50
Dros/Swank	9.2 ± 0.8 [12]LS LR	5.7 ± 0.4 [12]LS LR	3.5 ± 0.5 [12]LS LR	1.92 ± 0.24 [9]DR LS LR	6.05 ± 0.05 [9]LS
Leth/Swank	38.8 ± 2.6 [10]DS DR LR	23.0 ± 1.8 [10]DS DR	15.8 ± 1.0 [10]DS DR LR	1.01 ± 0.03 [10]DS	5.60 ± 0.04 [10]DS DR LR
Dros/Reedy	10.8 ± 1.2 [10]LS LR	6.5 ± 0.8 [10]LS LR	4.3 ± 0.6 [10]LS LR	1.29 ± 0.19 [9]DS	6.09 ± 0.14 [9]LS
Leth/Reedy	52.5 ± 1.1 [10]DS DR LS	21.4 ± 0.9 [10]DS DR	31.1 ± 1.1 [10]DS DR LS	1.14 ± 0.03 [10]DS	6.29 ± 0.04 [10]LS

All values are means ± SE. A_SA, total active stretch tension (pCa 5.0); P_SA, passive stretch tension (pCa 8.0); F_SA, corrected active stretch tension (F_SA = A_SA − P_SA). Graphs of the relationship between stretch-activated tension, F_SA, and calcium concentration from individual fibers were fit with the Hill equation to obtain the average Hill coefficient and pCa₅₀ values. Square brackets indicate number of fibers tested. Superscript letters indicate statistical difference between the four sets of fibers based on one-way ANOVA with Holm-Sidak pairwise multiple comparisons, P < 0.05. DS = Drosophila fibers bathed in Swank solutions; DR = Drosophila fibers bathed in Reedy solutions; LS = Lethocerus fibers bathed in Swank solutions; LR = Lethocerus fibers bathed in Reedy solutions.

Power measurements.

We used sinusoidal analysis (29, 43) to measure power generation and the frequency at which maximum power was generated (f_max). A 0.25% peak-to-peak strain amplitude and frequencies ranging from 0.5 to 650 Hz were applied to the fiber. Power and f_max were determined as previously described (44, 48). Drosophila sinusoidal analysis used the following frequencies: 0.5, 1, 2.5, 5, 7.5, 10, 15, 20, 30, 40, 50, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 130, 140, 150, 160, 170, 190, 210, 220, 230, 245, 255, 265, 280, 295, 315, 345, 365, 385, 400, 425, 450, 475, 500, 525, 550, 575, 615, 625, 650, while Lethocerus analysis used these frequencies: 0.5, 0.75, 1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4, 2.6, 2.8, 3, 3.2, 3.4, 3.6, 3.8, 4, 4.5, 5, 5.5, 6, 7, 8, 9, 12, 15, 20, 25, 30, 35, 40, 45, 55, 65, 75, 85, 100, 115, 130, 150, 175, 200, 225, 250, 300, 350, 400, 450, 500. The different frequency sets ensured optimal coverage of positive power producing frequencies for the different muscle kinetics of each species.

Statistical analysis.

One-way ANOVA (P < 0.05) with Holm-Sidak pairwise multiple comparisons were performed using Sigma Plot.

RESULTS

Calcium-activated isometric tension.

Lethocerus fibers generated higher tension regardless of the solution. At pCa 5.0, Lethocerus generated 8-fold higher total active isometric tension (A₀) in Swank solution and 14-fold higher A₀ while in Reedy solution than Drosophila (Table 2). Lethocerus net active isometric tension (F₀) was 12-fold and 21-fold higher than Drosophila in Swank and Reedy solutions, respectively. Passive tension (P₀) was ~8-fold higher for Lethocerus fibers than Drosophila in both solutions. The Reedy solution increased the amount of both A₀ and F₀ generated by the Lethocerus fibers, but there was not a statistically significant increase for Drosophila fibers.

Tension values can be influenced by how much the fibers are lengthened before measuring tension. The fibers’ lengths were all set by lengthening until maximum power was generated. In Swank solutions, Drosophila fibers were stretched 17.2 ± 2.5% and Lethocerus fibers were stretched 17.2 ± 2.2%. In Reedy solutions, fibers were stretched 14.6 ± 2.2% and 13.8 ± 3.0%, respectively. There were no significant differences between these stretch amounts (one-way ANOVA). Thus, fiber length had minimal impact on isometric tension values.

Isometric tension of Drosophila and Lethocerus IFMs both increased with increasing [Ca²⁺] (Fig. 1). There are some slight differences between species at the higher calcium concentrations. Saturation of tension occurred around pCa 5.5 for Drosophila, while Lethocerus saturation occurred around pCa 4.5 or perhaps tension is still slightly increasing at pCa 4.5. Drosophila fibers lost tension at pCa 4.5 in the Reedy solution. Drosophila fibers in Swank solution had the steepest tension-pCa curve as determined by fitting the normalized active tension curve. In this solution, Drosophila fibers had 3.6-fold higher Hill coefficients and 1.08-fold higher pCa₅₀ values than Lethocerus fibers (Table 2). However, when measured in Reedy solution, Drosophila Hill coefficients were not significantly different from Lethocerus IFM values and neither were the pCa₅₀ values. That is, in Swank solutions, Drosophila IFM are slightly more calcium sensitive and have a much steeper slope (higher cooperativity) than Lethocerus IFM, but these differences are not apparent in the Reedy solutions.

Fig. 1.

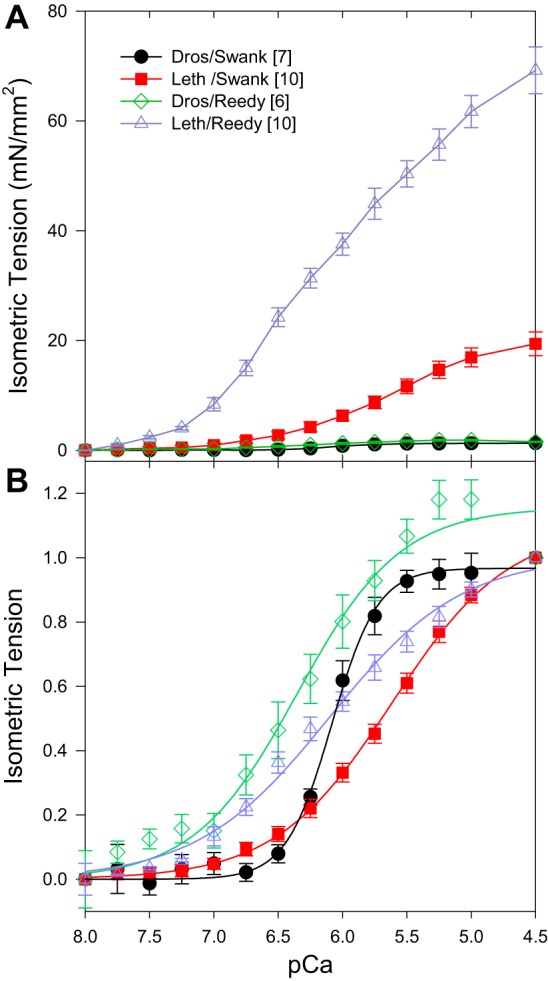
Influence of calcium concentration on isometric tension (F₀). A: isometric tension versus pCa. pCa 8.0, passive tension, has been set to zero so that only cross-bridges are responsible for the active isometric tension values shown. B: Hill fits of the average active tension values of each data set. Isometric tension values, normalized to 1 at pCa 4.5, versus pCa. Square brackets in the legend indicate number of fibers tested. Error bars are SE. Dros, Drosophila; Leth, Lethocerus.

Stretch-activated tension.

To quantify the stretch activation response, muscle-lengthening steps of 1% were applied over 0.5 ms to skinned IFM fibers. Tension responses from both insect’s IFMs at pCa 5.0 showed the classic stretch-activation response composed of an immediate tension rise concomitant with stretch (phase 1), a quick tension decay (phase 2), a slower, delayed, increase in tension (phase 3 or stretch-activation), and a very slow decay in tension (phase 4) (Fig. 2) (13). Total stretch-activated tension, A_SA (phase 3), is the increase in tension above calcium-activated tension. We separated out the active (F_SA) component of stretch-activated tension by subtracting the passive elastic component (P_SA), measured at pCa 8.0, from A_SA: F_SA = A_SA − P_SA (Fig. 2 and Table 3).

Overall, Lethocerus produced higher SA tension compared with Drosophila for all three measures of SA tension in both solutions (Table 3). The solutions influenced A_SA and F_SA values, but P_SA was similar in either Swank or Reedy relaxing solutions. Interestingly, Lethocerus F_SA was only 5-fold higher than Drosophila F_SA when measured in Swank solutions, but 7-fold higher than Drosophila F_SA when measured in Reedy solutions. In contrast, the solutions made no significant changes to any SA tension values for Drosophila IFM, similar to what we observed with isometric tension.

SA calcium response.

The response of both species’ F_SA values to calcium concentration was very similar to the isometric tension response to calcium concentration (compare Figs. 3 and 1). All fibers showed an increase in F_SA with increasing calcium. Saturation of SA tension occurred around pCa 5.5 to 4.5, for three of the four cases, while for Lethocerus in Reedy solutions saturation may have occurred around pCa 4.5. The Drosophila fibers in Swank solutions again showed the steepest response to calcium. These fibers also had higher Hill coefficients suggesting increased cooperativity and were more sensitive to calcium as shown by higher pCa₅₀ values. The Reedy bathing solutions increased the Lethocerus pCa₅₀ value by 1.12-fold, but did not change Drosophila pCa₅₀. In contrast, the Reedy solutions decreased the Drosophila Hill coefficient values by almost half, but did not influence the Lethocerus Hill coefficient (Table 3). Thus, both solutions and species influenced the SA response to calcium, but F_SA increased with calcium concentration under all conditions tested.

Fig. 3.

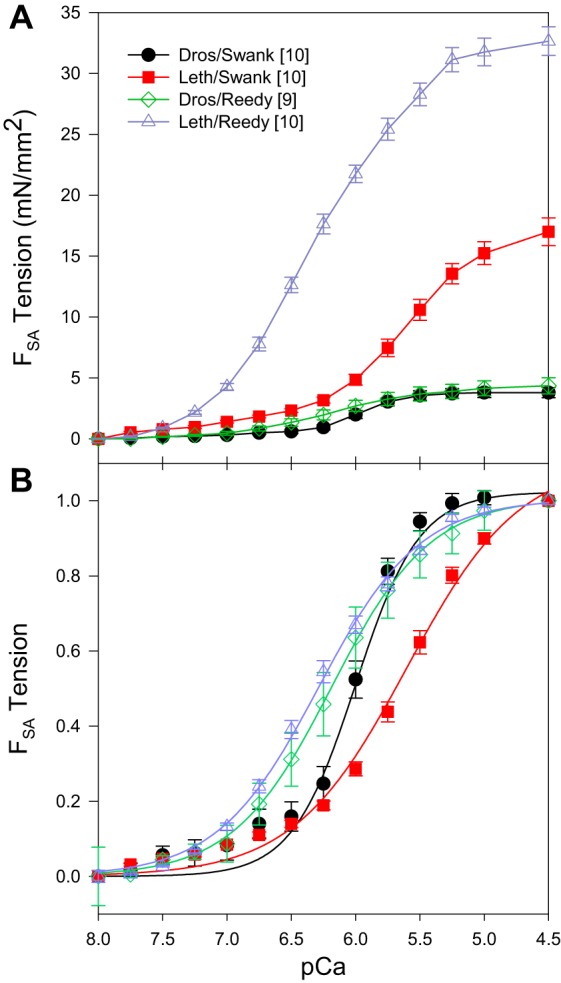
A: effect of calcium concentration on SA tension (F_SA). pCa 8.0 has been set to zero so that only cross-bridges are responsible for the tension shown. B: Hill fits of the average of each data set. F_SA tension values normalized to 1 at pCa 4.5. Square brackets in the legend indicate number of fibers tested. Error bars are SE.

SA rates.

To help compare cross-bridge and muscle kinetics, we measured the rate (r₃) of the delayed force increase (phase 3) following the lengthening step. Solution conditions did not significantly alter r₂ and r₃. Drosophila r₃ was 9-fold higher under both solution conditions as solutions did not significantly alter r₃. The results were very similar for r₂, a 7- to 9-fold higher r₂ value for Drosophila. Rate constant r₄ was decreased by the Reedy solution, but again the Drosophila rate was significantly faster than Lethocerus (Table 4).

Table 4.

Small muscle length amplitude, power, optimum muscle speed, and SA rates

Species/Solution	n	Pmax	fmax	n	r2	r3	r4
Dros/Swank	12	254 ± 18DR LS	162.5 ± 8.9DR LS LR	12	1,423 ± 53LS LR	1,370 ± 49LS LR	139 ± 75DR LS LR
Leth/Swank	10	133 ± 13DS LR	18.5 ± 1.5DR LR	10	153 ± 11DS DR	151 ± 12DS DR	53 ± 7LS DR LR
Dros/Reedy	10	141 ± 18DS LR	94.5 ± 3.9DS LS LR	10	1,343 ± 98LS LR	1,285 ± 98LS LR	101 ± 70LS LR
Leth/Reedy	10	325 ± 53DR LS	28.5 ± 2.9DS LS	8	177 ± 18DS DR	142 ± 15DS DR	4 ± 3DS LS DR

All values are means ± SE. Power was measured under small amplitude conditions, 0.125% muscle length; f_max is the frequency at which maximum power was produced. The rates of phase 2, 3, and 4, r₂, r₃, and r₄, respectively, of the tension transients following stretch are shown. Superscript letters indicate statistical differences between the four sets of fibers based on one-way ANOVA with Holm-Sidak pairwise multiple comparisons, P < 0.05. DS = Drosophila fibers bathed in Swank solutions; DR = Drosophila fibers bathed in Reedy solutions; LS = Lethocerus fibers bathed in Swank solutions; LR = Lethocerus fibers bathed in Reedy solutions.

Stretch tension relative to isometric tension.

To determine how much of a boost in tension the SA response gives to the muscle fibers, we normalized F_SA to maximum isometric tension, F_0,max (Fig. 4). This showed that the Drosophila IFM percent increase in tension is greater than Lethocerus at all active tension generating pCas. At pCa 4.5, Drosophila tension transiently increased 2.4 to 2.9-fold depending on solution, while Lethocerus only increased 1.5 to 1.8-fold. In both species the increase was greater in Swank solution than Reedy solution.

Fig. 4.

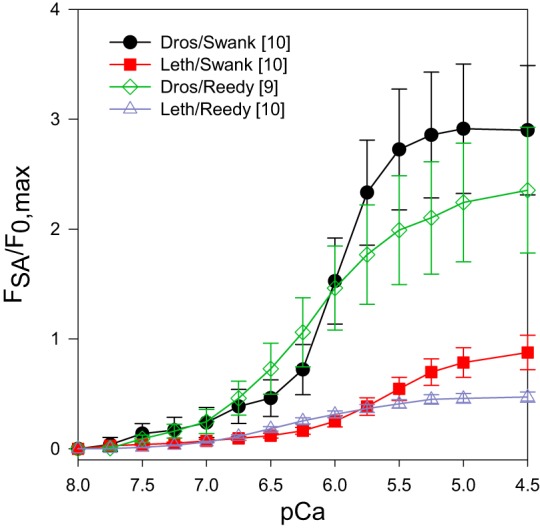
The percent increase in tension above isometric due to the phase 3 SA response: F_SA/F_0,max. For each of the four plots, the F_SA value for each pCa from Fig. 3A was divided by the maximum isometric tension value, F_0,max, from Fig. 1A.

Power generation.

Each species generated about the same amount of maximum power (P_max) at pCa 5.0. However, their P_max values occurred at different oscillation frequencies and bathing solutions. That is, the solutions and muscle length change frequencies both had a significant impact on the amount of IFM power generated (Table 4 and Fig. 5). Drosophila fibers generated 1.9-fold higher power in Swank solutions than the Lethocerus fibers, but Lethocerus fibers generated 2.4-fold higher power in Reedy solutions than Drosophila fibers. The frequency at which maximum power was generated, f_max, was much higher for Drosophila fibers than Lethocerus in both solutions. As expected based on the wing beat frequencies, Drosophila IFM are clearly much faster with 3.3-fold and 8.8-fold higher f_max values for Swank and Reedy solutions, respectively. However, Drosophila had a higher f_max in Swank solutions than in Reedy solutions, 1.8-fold higher, while Lethocerus had a 1.5-fold higher f_max in Reedy solutions compared with Swank solutions.

Fig. 5.

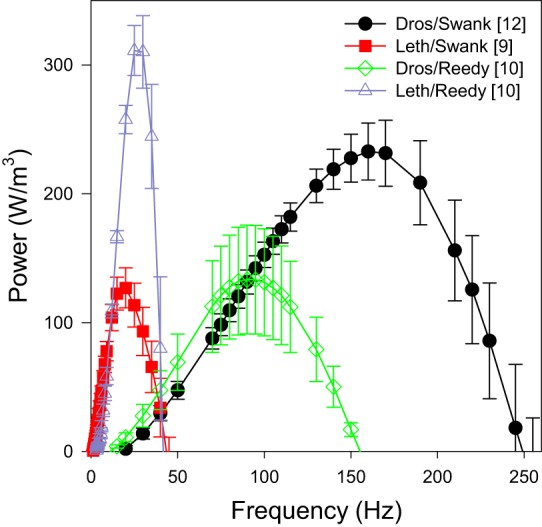
Power generated by Drosophila and Lethocerus fibers at pCa 5.0. Power was measured by oscillating the muscle length by 0.125% in a sinusoidal pattern over a range of frequencies: 0.5 to 650 Hz for Drosophila and 0.5 to 500 Hz for Lethocerus. Frequencies that did not generate positive power are not shown. Square brackets in the legend indicate number of fibers tested. Error bars are SE.

DISCUSSION

The main goal of this work was to compare the stretch activation response of Lethocerus and Drosophila IFM under identical experimental conditions to gain insight into the stretch activation mechanism or possibly multiple mechanisms. Since these species may have evolved SA independently (10), their SA mechanisms might vary. If this is the case, investigators studying the SA mechanism might be deducing alternative conclusions simply because multiple mechanisms exist. Alternatively, experimental conditions might be contributing to reported variation in SA characteristics and proposed mechanisms.

Species differences in F_SA and F₀.

The defining characteristic of the stretch activation response is a delayed increase in force following a rapid lengthening step. We focused primarily on characterizing the magnitude of the delayed force increase, F_SA, because it is critical for positive power generation and flight. Our results show that Lethocerus F_SA is 5- to 10-fold higher, depending on the fiber-bathing solutions, than Drosophila F_SA. We also observed that isometric tension, F₀, is 12- to 21-fold greater in Lethocerus IFM. Thus, the higher SA tension response could be due to Lethocerus IFM being able to generate more tension in general than Drosophila IFM. When we normalized F_SA to maximum F₀, we observed that the percent increase in tension above F₀ was higher for Drosophila, ~2.5–fold, for all pCas, and ~1.75-fold for Lethocerus. In other words, Drosophila has a greater relative tension increase due to SA than Lethocerus, but the amount tension changes is greater for Lethocerus.

One reason for the greater F₀ and F_SA values for Lethocerus is likely a higher myosin duty ratio, the time myosin spends bound to actin relative to total cross-bridge cycle time. More time strongly bound to actin means more cross-bridges are attached to actin at any given time, resulting in higher force generation. However, increasing the time myosin takes to move through strongly actin-bound states decreases muscle contraction speed. The 9-fold faster rate of the SA response, r₃, and optimal muscle speed for generating power, f_max, for Drosophila compared with Lethocerus IFM supports the idea of a large difference in duty ratio. Thus, at least part of the reason for the greater Lethocerus tension values is that its myosin spends a longer time strongly bound to actin.

Another reason for the tension differences could be that the thin filament of Lethocerus is better activated by calcium and thus has more myosin-binding sites exposed for cross-bridges to form. The Bullard laboratory has found that there are two troponin C (TnC) isoforms in Lethocerus and Drosophila IFMs that differentially affect F₀ and F_SA (2). TnC4 only binds one calcium ion while TnC1 binds two calcium ions when calcium saturated. Experiments altering the ratios of these TnC isoforms in Lethocerus IFM revealed that fibers with mostly TnC4 produce high F_SA but low F₀, while fibers with predominately TnC1 produce high F₀ but low F_SA. These results suggest that TnC1 enables better calcium activation of the thin filament than TnC4. Studies suggest Drosophila and Lethocerus have different ratios of the two isoforms. Western blot measurements by the same group suggest a 5 to 1 ratio of TnC4 to TnC1 for Lethocerus (39) compared with a 10 to 1 ratio for Drosophila (11). Another laboratory only found a very faint trace of TnC1 in a blot of Drosophila IFM (8). Another possibility is that Drosophila TnC versions might not activate the thin filament in response to calcium to the same degree as the Lethocerus versions.

While these reasons could explain higher active tension, Lethocerus passive tension was also 8-fold higher. The difference in passive tension is not due to the amount the fibers were stretched because we stretched out the fibers an equal percentage of total fiber length. Passive insect muscle sarcomere elasticity is primarily set by the physical properties of titin-like connecting filaments such as projectin and products of the Sallimus gene (4, 5). These gene products vary in length in different muscle types of Drosophila primarily through alternative splicing (5). A direct comparison of Drosophila and Lethocerus kettin, a product of the Sallimus gene, found that Lethocerus kettin is larger and extends further along actin from the Z-disk into the I-band than Drosophila (4, 5). Additionally, the Z-disks are wider in Lethocerus.

Influence of calcium on F_SA.

A confusing aspect of the IFM stretch activation response is that a few earlier studies have found that maximum F_SA occurs at intermediate calcium concentrations, where F₀ is low, rather than saturating calcium concentrations where F₀ is high. Linari et al. (32) and Krizc and colleagues (2) found the highest F_SA for Lethocerus IFM fibers at intermediate calcium concentrations and very low F_SA at pCa 4.5 (saturating calcium concentration). However, other Lethocerus studies indirectly indicate that F_SA is maximal at high calcium concentrations. While not measuring Lethocerus F_SA over a range of calcium concentrations, Iwamoto and colleagues (24, 25) found that Lethocerus F_SA was greater than F₀ at saturating calcium concentration. An earlier study agrees with Iwamoto et al. (25), finding Lethocerus F_SA to be twice as high as F₀ at high calcium concentration (36). For Bombus and Ctenacroscelis, Iwamoto et al. (25) found that F₀ was relatively large while F_SA was modest at saturating calcium concentration, pCa 4.0–4.5. Two previous Drosophila studies of SA showed about the same F_SA and F₀ levels at saturating calcium (36, 47).

To better determine the influence of calcium on SA, we have eliminated variables due to different laboratories, physiology rigs, and mounting techniques so we could accurately compare F₀ and F_SA calcium responses in both Lethocerus and Drosophila. We compared isometric tension and stretch-activated tension as a function of pCa in the two solutions sets used by our laboratories. We found the responses to calcium were, in general, not species specific. Both species IFMs, in both bathing solutions, showed increasing F₀ and F_SA with increasing calcium concentration. There were some species differences. In the Swank solutions, Lethocerus showed a slightly rightward pCa shift compared with Drosophila, suggesting lower calcium affinity. In some instances, Lethocerus had a slightly lower Hill coefficient, suggesting lower cooperativity. These differences are likely due to functional properties of the respective troponin complexes. TnI and tropomyosin in Drosophila and Lethocerus IFM have different structures. Lethocerus TnI has a proline-alanine-rich COOH-terminal extension which is lacking in Drosophila. Instead a similar sequence is fused to a tropomyosin isoform in Drosophila (9). A comparison of Drosophila and Lethocerus TnC found that the noncoordinating residues in the calcium-binding loops differ, which may result in different calcium-binding affinities, and there is also sequence variation outside the calcium-binding loop (39). Another contributing factor could be the higher duty ratio of the Lethocerus IFM myosin. We have previously observed a shift to earlier activation when we transgenically expressed an embryonic myosin (EMB) with a higher duty ratio in the Drosophila jump muscle (12). Overall though, we found that for both Lethocerus and Drosophila IFM, calcium-activated tension is required for F_SA, that both F_SA and F₀ increase with increasing calcium concentration, and that maximum F_SA occurs at high calcium concentrations rather than intermediate concentrations.

Why have some investigators observed, contrary to our findings, that intermediate calcium concentrations give higher F_SA than saturating calcium concentrations? We thought that the most likely cause was different fiber-bathing solution compositions, particularly [ATP], ionic strength, and the presence or absence of an ATP regeneration system (CK and CPK). The two solutions we used differed in all three of these components, but perhaps the differences were not great enough to qualitatively change the pCa results. Therefore, we explored greater changes in component amounts and other modifications to our mechanics protocol (data not shown, typically 2–3 fibers for each protocol variation). We focused on Lethocerus fibers because results showing maximum F_SA at intermediate calcium concentrations were found by investigators using Lethocerus fibers and because this has never been reported, to our knowledge, for Drosophila IFM.

Modifications to our protocol included fiber-bathing solutions nearly identical to those used by Linari et al. (32). This change alone caused no significant qualitative differences in the F_SA calcium response. Next, we tested if fiber length and hence sarcomere length at which the experiments were performed made a difference. Instead of setting of initial fiber length to the length that generates maximum power, we tried setting it at shorter lengths such as at just taut tension, which was the starting length used by Linari et al. (32). We also tried length steps greater than 1%, returning to relaxing solution (pCa 9.67) between each pCa, working at 20°C instead of 15°C, and testing if end-compliance was an issue by fixing the ends of fibers with glutaraldehyde before T-clipping the fibers (7, 33). When done singly, none of these changes resulted in our objective: significantly higher F_SA at lower calcium compared with higher calcium.

However, by combining some of these modifications we could produce an F_SA tension curve that was leftward shifted and, most importantly, peak stretch-activated tension occurred around pCa 6.5 (Fig. 6). To obtain this result, we used a pair of fibers T-clipped together and a shorter starting fiber length (less passive stiffness). We only lengthened the muscle 2% above just taut tension compared with our typical 12% increase. We used a bathing solution that should increase the percentage of myosin heads in the strongly bound state, including the rigor state: 5 mM ATP, 50 mM ionic strength, and no ATP regeneration system. In these solutions, it took longer for isometric tension to plateau and reach its peak value after new solutions were exchanged. We also increased the bathing solution temperature to 20°C. These alterations did not produce as large of a decline in F_SA tension at high calcium as reported by some investigators, instead, only about a 30% decline in F_SA. However, these results show that we could obtain results similar to investigators who have found that intermediate calcium concentrations produce the highest F_SA.

Fig. 6.

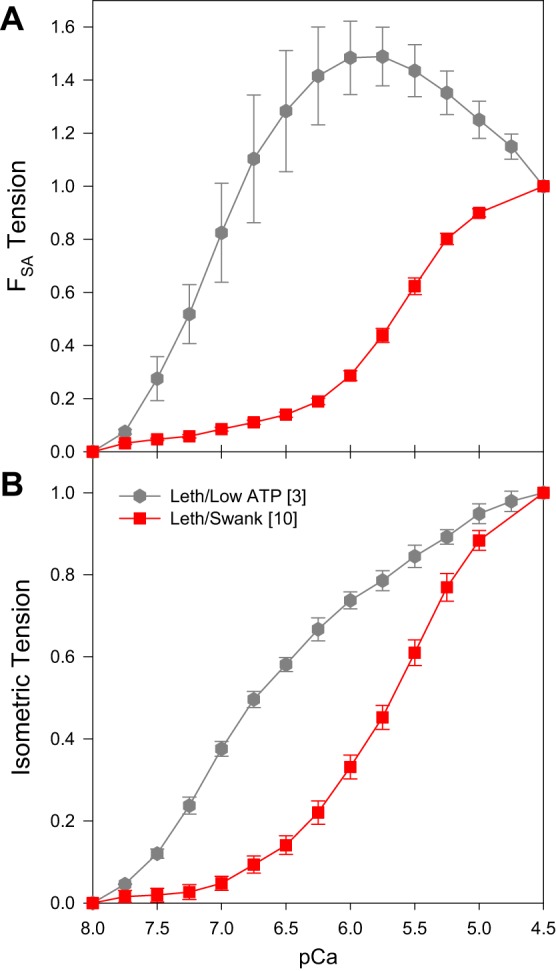
High F_SA at intermediate calcium concentrations in Lethocerus fibers. This result was induced by decreasing [ATP] to 5 mM, decreasing ionic strength to 50 mM, setting fiber starting length 2% above just taut, not including an ATP regeneration system, and raising the bathing solution temperature to 20°C (gray hexagons). For comparison, we copied the Lethocerus in Swank solution plots from Figs. 1B and 3B into these graphs (red squares). All tension values were normalized to 1 at pCa 4.5. A: SA tension (F_SA) versus calcium concentration. B: isometric tension (P₀) versus calcium concentration. Square brackets in the legend indicate number of fibers tested. Error bars are SE.

We think the main reason for why this combination of protocol alterations changed the F_SA versus calcium concentration response involves depleting ATP concentration and working at a lower ionic strength. Most investigators agree that the increase in tension from SA is due to a transient increase in the number of myosin heads strongly bound to actin, and that a key component is making more heads available to participate in the SA response. The low ionic strength, low [ATP], and increased buildup of ADP (due to lack of a regeneration system and the higher temperature) cause more cross-bridges to be strongly bound under isometric tension conditions. An increased number of heads binding before stretch means there are fewer heads available to respond to stretch and bind to actin. More heads can be made available for SA by working at lower calcium concentrations where the thin filament is not fully activated and fewer heads are binding to actin before stretch.

However, the conditions that produced maximum F_SA at intermediate calcium concentrations are likely not physiological. While we do not know the ionic strength of IFM, 200 mM ionic strength is physiological for many muscle types (16) and IFM contains an ATP regeneration system, the phosphoarginine and phosphoarginine kinase system (46). We previously found that muscle speed in Drosophila IFM is highly ATP concentration dependent. To obtain a muscle speed (f_max value) that matches the wing beat frequency of the flies, at least 12 mM ATP is required in the bathing solution plus a high ATP regenerating system of 30 mM CP and 600 U/ml CPK (44). The regeneration system decreases buildup of ADP inside the muscle fiber by converting it back to ATP, and decreases the concentration gradient of ATP inside the fiber (35).

A way to indirectly determine which pCa causes maximum F_SA would be to stimulate live IFM fibers over a range of frequencies. This would release different amounts of calcium into the IFM. A live muscle preparation has not been developed for Drosophila or Lethocerus. However, experiments with live, asynchronous Continus mutabilis IFM suggest maximum F_SA at high calcium concentrations. When its flight muscle was tetanically stimulated to produce maximum isometric tension, F_SA was about about 2-fold higher than F₀ (26, 28).

Mammalian heart muscle possesses a modest stretch activation response. A study of skinned mouse myocardium found that the highest F_SA (P₃ in their paper) occurs at saturating calcium for isometric tension (42). This finding agrees with our results and suggests that the F_SA response to calcium in the heart is similar to the IFM mechanism.

Power generation.

Some studies of IFM power generation indirectly suggest that maximum F_SA occurs at high calcium concentrations. For example, Gilmour and Ellington’s study, which showed that bumblebee’s asynchronous flight muscle could generate enough power to meet the requirements for aerodynamic power generation, a pCa value of 4.7 was used in their skinned fiber preparations (14). F_SA has to be prominent at this high calcium concentration in order for the flight muscle to generate the required power for flight. We have previously measured power versus pCa in Drosophila IFM. Power increased with calcium concentration and was proportional to F_SA (47).

Our current study found that Drosophila and Lethocerus IFMs produce similar amounts of peak power at pCa 5.0 even though F_SA and F₀ values differed greatly. The reason is fairly straightforward given that power equals force times velocity. Drosophila takes a low-force, high-speed approach to power production, while Lethocerus fibers generate much more force but operate at a much slower speed. Thus, the Swank solutions that enable faster kinetics work better for Drosophila, while those that help produce more F₀ and F_SA, Reedy solutions, are better suited for Lethocerus IFM.

Comparing Swank and Reedy solutions.

The Reedy solutions had a lower ionic strength, lower ATP, and lacked an ATP regeneration system compared with the Swank solutions. While the Reedy solutions increased Lethocerus maximum F_SA and F₀ by 1.4- and 2.3-fold, respectively, they had little or no effect on Drosophila maximum F_SA and F₀. The increase in Lethocerus tension values are most likely because the Reedy solutions slowed down cross-bridge detachment rate, due to lower ATP concentration plus ADP accumulation, and thus more myosins are bound to actin at any given time. In contrast, Drosophila IFM force generation might be more limited by accessibility of myosin-binding sites on actin, due to its TnC4 isoform, rather than myosin kinetics (11, 39). By not fully calcium activating the thin filament, TnC4 might reduce the number of cross-bridges by limiting the availability of myosin-binding sites on actin. Perhaps only a small number of cross-bridges can bind at a given time even when solution conditions would promote more being bound. Under these conditions, those cross-bridges that can find a binding site on actin cycle more slowly and thus slow muscle kinetics. Another possibility is that the Reedy solutions are increasing Drosophila F_SA and F₀, but that the change is not large enough to be statistically significant given the degree of error in our measurements of the much lower Drosophila tension values.

The solutions also made a difference in Hill coefficients and pCa₅₀ values. The Reedy solution slopes of pCa versus F₀ and F_SA were generally less steep, activation started at a lower calcium concentration, and they were often leftward shifted. This is probably due to the lack of a regeneration system and/or lower ionic strength. Rigor bridges, slower detaching bridges or stronger binding cross-bridges (effect of reduced ionic strength) can likely start activating the thin filament at lower calcium concentration. The ionic strength difference could also be directly affecting regulatory protein function, resulting in an altered response to calcium (18).

Implications for flight and the SA mechanism.

Previous findings that suggest maximum F_SA occurs at intermediate calcium concentrations and that there is very little F_SA at saturating calcium concentration have led to the idea that the SA mechanism needs some calcium activation of the thin filament, but not too much activation (32). The thin filament cannot be fully activated or most cross-bridges will be contributing to isometric tension with only a few left to contribute to F_SA. Thus, IFMs could not be operating at high calcium concentrations to power flight since they would generate very little muscle power.

However, our current finding that F_SA is optimal at maximum calcium concentration suggests that IFMs generate the most power for flight at saturating calcium concentrations. Work by the Dickinson and Swank laboratories suggests that Drosophila varies its IFM calcium concentration to alter both aerodynamic and IFM power generation. Measurements of relative calcium concentration and aerodynamic power during tethered flight revealed that both aerodynamic power and calcium concentration varied about two-fold, and that maximum aerodynamic power occurred at high calcium concentrations (19). Measurements of IFM power generation when calcium was varied showed that a two- to three-fold variation in power could easily be achieved by varying calcium if maximum power occurred at saturating calcium concentrations (47). The actual concentration of calcium in the IFMs during flight is not known for either Drosophila or Lethocerus, but our current work suggests that both could be using a similar calcium-based mechanism to vary power for flight.

Given our current results, we propose a slightly different mechanism with functional properties of thin filament proteins isoforms playing a role in determining the ratio of F₀ to F_SA rather than calcium level setting the ratio. Recent stretch-activation investigations suggest a thin filament-based cross-bridge recruitment mechanism (2, 25, 37). The stress or strain on the thin filaments from lengthening a fiber under load may cause a greater number of myosin-binding sites to become available on the thin filament than are initially made available by calcium binding. The troponin/tropomyosin complex is likely important in this proposed SA mechanism (2, 11, 37), in particular, that TnC4 is critical for F_SA and that it contributes minimally to F₀ generation, while TnC1 may be required for substantial F₀. These results suggest that TnC4 does not fully activate the thin filament which keeps isometric tension generation low, even at high calcium concentrations. Therefore, there are plenty of myosin heads available to contribute to F_SA. Even if this mechanism is not correct, our results suggest that the SA mechanism in both Lethocerus and Drosophila responds the same to changes in calcium concentration.

GRANTS

Supported by NIH National Institute of Arthritis and Musculoskeletal and Skin Diseases Grants AR064274 (to D. M. Swank) and AR062135 (to M. K. Reedy and R. J. Edwards).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

B.M.G., M.K.R., R.J.E., and D.M.S. conceived and designed research; B.M.G., C.C.E., C.Z., M.K.R., and R.J.E. performed experiments; B.M.G., C.C.E., L.C.S., and R.J.E. analyzed data; B.M.G., R.J.E., and D.M.S. interpreted results of experiments; B.M.G. prepared figures; B.M.G., L.C.S., R.J.E., and D.M.S. edited and revised manuscript; B.M.G., C.C.E., L.C.S., C.Z., M.K.R., R.J.E., and D.M.S. approved final version of manuscript; D.M.S. drafted manuscript.