Shifting gears: dynamic muscle shape changes and force-velocity behavior in the medial gastrocnemius

During movement, skeletal muscles contract and bulge in thickness or width. These shape changes play a key role in modulating the performance of skeletal muscle by increasing its range of operating velocities. Yet to date the underlying mechanisms associated with muscle shape change remain largely unexplored. This study identified muscle force, and not velocity, as the mechanistic driving factor to allow for muscle gearing to vary depending on the contractile conditions during human cycling.

Abstract

When muscles contract, they bulge in thickness or in width to maintain a (nearly) constant volume. These dynamic shape changes are tightly linked to the internal constraints placed on individual muscle fibers and play a key functional role in modulating the mechanical performance of skeletal muscle by increasing its range of operating velocities. Yet to date we have a limited understanding of the nature and functional implications of in vivo dynamic muscle shape change under submaximal conditions. This study determined how the in vivo changes in medial gastrocnemius (MG) fascicle velocity, pennation angle, muscle thickness, and subsequent muscle gearing varied as a function of force and velocity. To do this, we obtained recordings of MG tendon length, fascicle length, pennation angle, and thickness using B-mode ultrasound and muscle activation using surface electromyography during cycling at a range of cadences and loads. We found that that increases in contractile force were accompanied by reduced bulging in muscle thickness, reduced increases in pennation angle, and faster fascicle shortening. Although the force and velocity of a muscle contraction are inversely related due to the force-velocity effect, this study has shown how dynamic muscle shape changes are influenced by force and not influenced by velocity.

NEW & NOTEWORTHY During movement, skeletal muscles contract and bulge in thickness or width. These shape changes play a key role in modulating the performance of skeletal muscle by increasing its range of operating velocities. Yet to date the underlying mechanisms associated with muscle shape change remain largely unexplored. This study identified muscle force, and not velocity, as the mechanistic driving factor to allow for muscle gearing to vary depending on the contractile conditions during human cycling.

when muscles contract and shorten, they must increase in girth to maintain (or nearly maintain) their volume; this occurs at the level of the myofilament lattice (14, 63), muscle fibers (26), muscle fiber bundles (54), and whole muscle (9, 13). Pennate muscles can increase their girth in thickness (the distance between the aponeuroses), in width (the distance orthogonal to thickness), or in some combination of both dimensions (65). Studies have shown that whole muscle undergoes variable changes in thickness and width during both isometric and dynamic contractions (5, 30, 48) and that individual muscle fascicles undergo transverse expansions during shortening (61). These dynamic shape changes are thought to play an important functional role in modulating the mechanical performance of skeletal muscle by enhancing the range of velocities over which a fascicle can shorten (6, 48) and may even help to explain the decline in muscle performance that occurs with age (24, 48). However, to date, our understanding of dynamic muscle shape change during submaximal dynamic tasks is limited.

Shape changes are tightly linked to the muscle’s architecture. In pennate muscles, fascicles shorten and rotate to greater pennation angles during contraction (10, 19, 20, 41, 48). These rotations decouple the length changes of the fascicles from the length changes of the whole muscle in a process known as gearing v_MTU/v_f (6). In a muscle-tendon unit (MTU) with a compliant tendon, gearing is the product of two components, v_MTU/v_b and v_b/v_f, where v_MTU, v_b, and v_f are the shortening velocities of the MTU, the muscle belly, and the muscle fascicles, respectively (60). Studies have shown that gearing changes in response to the mechanical demands of the task, thereby allowing fascicles to operate at more favorable velocities for force and power production across a range of MTU velocities (6, 8, 48, 60). For example, low force-high velocity contractions are associated with large fascicle rotations and high gearing, whereas high force-low velocity contractions are associated with smaller fascicle rotations and low gearing (6, 48, 60). It has been suggested that the structural and material properties of surrounding connective tissues contribute to dynamic muscle shape changes, gearing, and the overall mechanical behavior of skeletal muscles (3, 6, 7, 24, 39, 45), yet the underlying mechanisms still remain unknown.

For a muscle to remain isovolumetric, muscle shortening must be accompanied by an increase in width, an increase in thickness, or changes in both dimensions (Fig. 1). Previous studies have shown that pennate muscles bulge asymmetrically during shortening (e.g., see Refs. 6, 44, and 48); however, the direction of muscle bulging depends on the mechanical demands of the contraction. For example, Randhawa et al. (48) have shown that the medial gastrocnemius (MG) gets thinner during isovelocity ankle plantarflexion contractions but undergoes much smaller decreases in thickness during isotonic plantarflexions, whereas others have shown that the MG does not change in thickness across a range of ankle angles or contraction levels (30, 40, 48). Furthermore, Narici et al. (40) found that although the changes in thickness were not significant, they varied depending on both the level of contractile force and the region of the muscle where the thickness measurement was taken. These in vivo results are similar to in situ animal studies that have demonstrated that fiber shortening in the MG is accompanied by increases in muscle thickness at low force levels but relatively small changes in thickness at high-force levels (6).

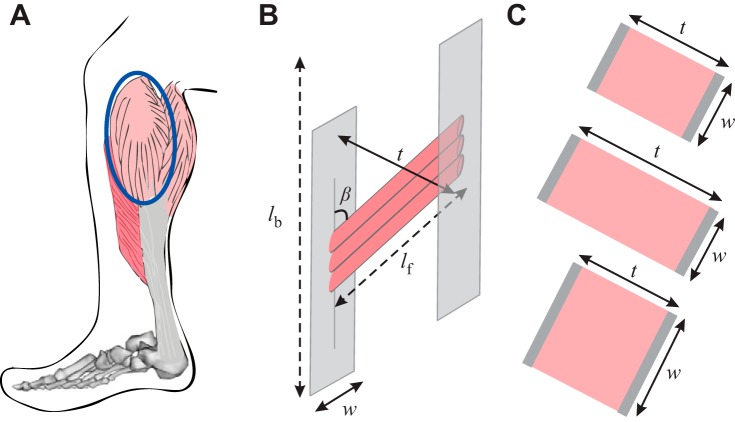
Fig. 1.

A: representation of the human medial gastrocnemius (MG). B: side view of muscle belly where fascicles (red) lie at an angle [pennation angle (β)] relative to the muscles line of action; fascicles insert into the superficial and deep aponeuroses (gray). Muscle belly length (l_b) and fascicle length (l_f) are indicated by dashed lines. C: top view of MG muscle belly illustrates that when pennate muscles contract (rest; top) they bulge in thickness [the distance between the two aponeuroses (t); middle] or in width [the distance orthogonal to thickness (w); bottom] to maintain a nearly constant volume [styled after Azizi et al (6)].

These variable shape changes are also linked to the internal constraints placed on the muscle fibers. When muscle actively shortens, cross-bridges develop forces that cause fibers to shorten and myofilaments to compress in girth (63). However, to maintain a (nearly) isovolumetric state, fibers develop additional forces that oppose the decreases in fiber girth and instead act to expand the fibers in their transverse direction (39, 45). These expansions require muscle fibers to rotate to higher pennation angles to fit within the same volume. Fiber expansions also depend on the properties of the surrounding connective tissues that both cover the whole muscle belly and wrap around individual muscle fibers. In pennate muscles, fascicles insert via the sheet-like aponeuroses that cover the superficial and deep portions of the muscle belly (62). When a muscle shortens, a component of the fascicle force acts to pull the superficial and deep aponeuroses together and effectively resists the muscle’s tendency to expand in thickness (39). However, muscle fascicles are wrapped by myofascial connective tissue that contributes additional stiffness that functions to resist increases in muscle girth (24). Thus, when fascicles shorten, the interplay between compressive fascicle forces and connective tissue resistance results in stress asymmetries within the contracting fibers that lead to the variable dynamic shape changes observed within skeletal muscle (6, 24, 39). Therefore, the ability of fascicles to rotate and operate at high gearing will be limited in situations where fascicle compressive forces and myofascial and aponeurosis stiffness constrain increases in muscle thickness. Although these ideas are derived from a range of different studies, there have not yet been any studies that integrate the varying muscle forces that occur with submaximal and voluntary contractions with the set of measurements (fascicle lengths, pennation angles, and muscle thicknesses) required to test this mechanism of muscle shape change and gearing.

Therefore, the purpose of the present study was to 1) determine the in vivo changes in fascicle velocity, pennation angle, and muscle thickness in the MG as a function of velocity and force and 2) determine how these dynamic muscle shape changes are linked to muscle belly gearing under varied levels of force and velocity. We hypothesized that 1) shortening contractions that develop higher forces would be associated with smaller changes in muscle thickness and decreased fascicle rotations and 2) increases in force would be accompanied by decreased muscle gearing.

MATERIALS AND METHODS

Acquisition of experimental data.

We collected a comprehensive set of kinematic, kinetic, EMG, and ultrasound data from 10 competitive cyclists (6 males, 4 females, age 33 ± 6 yr; Fig. 2). Subjects pedaled on a stationary cycle ergometer (Indoor Trainer; SRM, Julich, Germany) at cadences between 80 and 140 rpm and crank loads between 14 and 44 N m while we recorded ultrasound images of the MG muscle belly and muscle-tendon junction (MTJ), the three-dimensional (3D) trajectories of 32 LED markers, reaction forces effective and ineffective (normal and radial) to the crank, and surface EMG patterns from 10 muscles. All subjects gave informed consent, and protocols were approved by the Institutional Review Boards at Simon Fraser University and Harvard University.

Fig. 2.

A: experimental setup where we collected kinematic, kinetic, EMG, and ultrasound data from 10 competitive cyclists. B: we used B-mode ultrasound imaging of the medial gastrocnemius (MG) muscle belly to determine fascicle length (l_f), muscle thickness, and pennation angle during pedaling. We used ultrasound imaging of the MG muscle-tendon junction and a motion capture marker on the calcaneus to estimate tendon length (l_t). A scaled musculoskeletal model was used together with the motion capture data to determine the time-varying MG muscle-tendon unit length (l_MTU). The difference between the time-varying MTU length from the scaled musculoskeletal model and tendon length from tracked ultrasound images was used to determine muscle belly length (l_b).

Subjects pedaled at nine combinations of cadence and crank torque: 80 rpm at 14 N m, 80 rpm at 26 N m, 80 rpm at 35 N m, 80 rpm at 44 N m, 100 rpm at 13 N m, 100 rpm at 26 N m, 120 rpm at 13 N m, 120 rpm at 24 N m, and 140 rpm at 13 N m, corresponding to crank powers of 115, 220, 290, 370, 135, 270, 165, 300, and 200 W, respectively. Crank torques were calculated as the average torque for both legs per pedal cycle. The average maximum cadence and crank power for the 10 subjects tested here was 185 ± 17 rpm and 908 ± 240 W, respectively. Each trial lasted 15 s, and each block of nine experimental conditions was presented in a random order and repeated twice so that we could separately image both the MG muscle belly and the MG MTJ. Subjects rested for 5 min in between blocks of conditions. While pedaling, subjects wore sport sandals with cleats that were secured to clipless instrumented pedals (Powerforce; Radlabor, Freiburg, Germany); the sandals had a stiff sole and allowed markers on the ankle and foot to be placed directly over bony landmarks on the skin.

A B-mode ultrasound probe (7 MHz, 60-mm field of view, Echoblaster; Telemed, Vilnius, Lithuania) was secured over either the MG muscle belly or the MG MTJ on the right limb using a stretchy adhesive bandage, and an ultrasound gel pad (Parker Laboratories) was placed between the probe and skin to enhance image quality and allow the muscle to bulge (Fig. 2B). Ultrasound images were recorded at 40 Hz (and subsequently pooled for 10 consecutive cycles), and prior calibration (42) determined the position of the ultrasound scanning plane relative to a triad of optical markers on the probe so that two-dimensional (2D) ultrasound images of the MTJ could be projected into the 3D laboratory coordinate system.

On the left limb, bipolar Ag/AgCl surface EMG electrodes (10-mm diameter, 21-mm spacing, Norotrode; Myotronics) were placed over the mid-bellies of the MG, lateral gastrocnemius (LG), soleus (SOL), tibialis anterior (TA), and six other muscles (not reported here). EMG signals were sampled at 2,000 Hz (bandwidth 10–500 Hz; Biovision, Wehrheim, Germany), amplified (gain 1,000), and band-pass filtered as described elsewhere (e.g., see Refs. 11 and 59). “Maximum effort” sprint trials (high power and cadence) were collected at the beginning and end of each session in an effort to elicit maximum muscle activity, and we used these data as a reference when normalizing the muscles’ EMG intensities (e.g., see Ref. 50).

We used an optical motion capture system (Certus Optotrak; NDI, Waterloo, ON, Canada) sampling at 100 Hz to track the 3D locations of 32 LED markers placed bilaterally on the lower extremities and the pedals and on the ultrasound probe. Markers were placed bilaterally over the greater trochanter, lateral epicondyle, lateral malleolus, calcaneus, and fifth metatarsal. Five markers were positioned on the pelvis, and two were fixed on each pedal, and rigid marker triads were secured to the right thigh, shank, and ultrasound probe. Six “virtual” markers were defined based on the measured marker motions, segment lengths determined from 3D spatial data acquired via motion capture during a static trial, and known bike dimensions; these markers located the subjects’ hip centers (53), lateral epicondyles, and pedal centers of pressure. Static calibration trials were collected in cycling posture to scale a musculoskeletal model to each subject (OpenSim version 3.3) (16).

Pedal reaction forces effective and ineffective (normal and radial) to the right and left cranks were recorded at 2,000 Hz (Powerforce; Radlabor, Freiburg, Germany), and in a previous study, we verified that plantarflexion moments estimated from ultrasound-based measures of tendon strain were consistent with the net ankle moments determined from inverse dynamics (17).

Analysis of experimental data.

Ultrasound images from the MG muscle belly and MTJ were manually digitized in a blinded fashion (ImageJ; National Institutes of Health, Bethesda, MD) to estimate time-varying fascicle lengths, pennation angles, muscle thickness, and tendon lengths during cycling (Figs. 2B and 3). Eight points in each ultrasound image were digitized: three points on each of the superficial and deep aponeuroses and two points on the same representative muscle fascicle in each image. The aponeuroses were defined based on a linear fit of the three points. Pennation angle was calculated in each image as the mean of the two angles made by the fascicle with the deep and superficial aponeuroses. Thickness was defined as the distance between the superficial and deep aponeurosis. Fascicle lengths, pennation angles, and muscle thickness from 10 complete crank revolutions were fit with 2-harmonic Fourier series for each subject in each condition (Figs. 2B and 3).

Fig. 3.

EMG and ultrasound-based experimental data collected in this study. Plots show the time-varying normalized muscle activation with raw EMG recordings, muscle-tendon unit (MTU) length, tendon length, belly length, fascicle length, pennation angle, and muscle thickness for the medial gastrocnemius (MG) over one complete crank cycle. Data are shown for one representative subject pedaling at 80 rpm at 44 N m averaged over 10 pedal cycles.

Ultrasound images from the distal MTJ were manually digitized to estimate time-varying Achilles tendon (AT) lengths during pedaling (Figs. 2B and 3). AT length was determined by the distance from the 3D coordinates of the AT insertion on the calcaneus (after correcting for LED marker dimensions and skin thickness) to the digitized MG MTJ. MG tendon force was estimated based on the measured AT length changes, tendon stiffness, and slack length. We used these methods to calculate force, as described and validated previously (17), rather than traditional inverse dynamics due to the presence of coactivation between the plantarflexors and the dorsi-flexors (TA), which occurs at the highest cadences. Tendon stiffness was estimated from ramped isometric tests where we quantified the total stiffness of the AT (17, 35). We determined the proportion of the total AT stiffness contributed by the MG based on the ratio of the maximum force-generating capacity F_max of the MG to the combined triceps surae maximum force. Tendon slack length was measured at 310° of the crank cycle, which was averaged over all cycles; this choice was motivated by tendon buckle data showing this point to occur before the tendon begins to stretch (17, 21). The time-varying tendon force from 10 cycles was used to compute a mean force trace for each condition.

Time-varying MG MTU lengths were determined using a subject-specific scaled musculoskeletal model together with the experimental LED marker data via inverse kinematics (OpenSim version 3.3 (4, 16) (Fig. 2B). The model we used is based on existing models (1, 4, 15) and characterizes the geometry of the bones, the kinematics of the hip, knee, ankle, subtalar, and metatarsophalangeal joints, and the paths of the muscles (Fig. 2B). We constrained the path of the MG “wrap” over the posterior femoral condyles (4), and we verified that the scaled models have plantar flexion moment arms that are similar to moment arms published in the literature (17). Time-varying MG muscle belly lengths were calculated as the difference between MTU length from the scaled musculoskeletal model and tendon length from the tracked ultrasound images (Figs. 2B and 3).

Instantaneous muscle belly velocity (v_b) and fascicle velocity (v_f) were calculated as the first time-derivative of the changes in 1_b and l_f, respectively. Muscle belly gearing v_b/v_f was determined at the time when belly shortening velocity, v_b, was maximum. Maximum belly shortening velocity, v_b, and fascicle shortening velocity, v_f, occurred within 8° of each other. Shortening velocities are indicated by negative values.

EMG intensities of the muscles were calculated across a 10- to 450-Hz frequency band using an EMG-specific wavelet analysis (58) and were normalized for each muscle by the maximum intensity detected during the “maximum effort” reference cycling trials. Muscle force is linearly related to the EMG amplitude and not its power (33), so we used the square-root of the normalized EMG intensity as a measure of muscle excitation (ê) We used a first-order differential equation to determine normalized muscle activation [â(t)] from normalized muscle excitation[ê(t)] (64) that is commonly used for modeling human muscle. This choice was motivated partly by a parallel project that will compare the muscle models from this study to muscle force predictions from the OpenSim musculoskeletal simulation enviroN ment (16) that also uses this transfer function. However, it should be noted that other transfer functions are capable of estimating better activation dynamics (23, 28, 49) but require additional model parameters that are currently unknown for muscle in humans:

$$\frac{d}{dt}\left(\stackrel{}{\mathit{â}}\right)+\left[\frac{1}{{\tau }_{\text{act}}}\left(\beta +\left[1-\beta \right]\stackrel{}{\mathit{ê}}\left(t\right)\right)\right]\stackrel{}{\mathit{â}}\left(t\right)=\left(\frac{1}{{\tau }_{\text{act}}}\right)\stackrel{}{\mathit{ê}}\left(t\right)\mathrm{.}$$ (1)

The activation time constant τ_act was 35 ms, and the ratio of the activation to deactivation time constant β was 0.6 (Fig. 3); these values were derived from tetanic contraction data (27). The maximum activation and force values used in the analysis were chosen as the peak values in pedal cycle, which coincides with the timing of peak belly shortening velocity within 12 ± 4°.

Statistics.

A general linear model ANOVA was conducted to determine whether differences in the experimental measurements [belly shortening velocity, fascicle shortening velocity, rate of pennation angle change, change in muscle thickness, activation, gearing, tendon strain, and tendon force (unnormalized)] existed between the different pedaling conditions (load and cadence) and subject (random factor). Additionally, because we obtained experimental estimates of muscle-tendon force and MTU velocity, we conducted a general linear model ANCOVA with tendon force and MTU velocity as covariates and subject (random factor) to determine how the muscle parameters varied with force and velocity. The results within the text are reported for the ANCOVA; however, Figs. 4 and 5 are based on the ANOVA results. A general linear model ANCOVA was also conducted to test for significant associations between activation and gearing, tendon strain and gearing, and tendon force and gearing, with fascicle-shortening velocity, pennation angle, and thickness as covariates. Linear regression was used to determine the association between activation and tendon force and, additionally, an ANCOVA to determine whether the association (slope of regression lines) between activation and tendon force differed between pedaling conditions with increasing crank load at a constant cadence (80 rpm) and those with increasing cadence at a constant crank load (13–14 N m). Finally, we used multiple regression analysis to determine whether activation or force (independent variables) had an effect on each of the dependent variables: maximum belly shortening velocity, maximum fascicle shortening velocity, maximum rate of pennation angle change, change in thickness, and gearing. A linear relationship between the dependent variable and each of the covariates was confirmed before the ANCOVAs were conducted. Differences were considered significant at the P < 0.05 level. Data are reported as means ± SE.

Fig. 4.

Changes in peak muscle-tendon unit (MTU) shortening velocity (A), tendon strain (B), tendon force (C), and muscle activation (D) across the range of conditions tested in this study. Data are presented as means ± SE for 10 subjects. Tendon forces were normalized to the maximum isometric force (F_max) of the MG that was calculated using the estimated muscle volume (V_m) from regression equations (22), optimal fiber length (l_f,opt; from each scaled musculoskeletal model), a specific tension, σ₀, of 225 kPa (51, 55), and the average MG pennation angle, β, where $F_{\text{max}}=\left(\frac{V_{\text{m}}}{l_{\text{f},\text{opt}}}\right)\hspace{0.17em}\times \hspace{0.17em}{\sigma }_0\hspace{0.17em}\times \hspace{0.17em}cos\beta$. The normalized muscle activations were determined from the surface EMG using wavelet analysis and a first-order differential equation (64) and normalized to maximum muscle activation recorded during reference cycling trials.

Fig. 5.

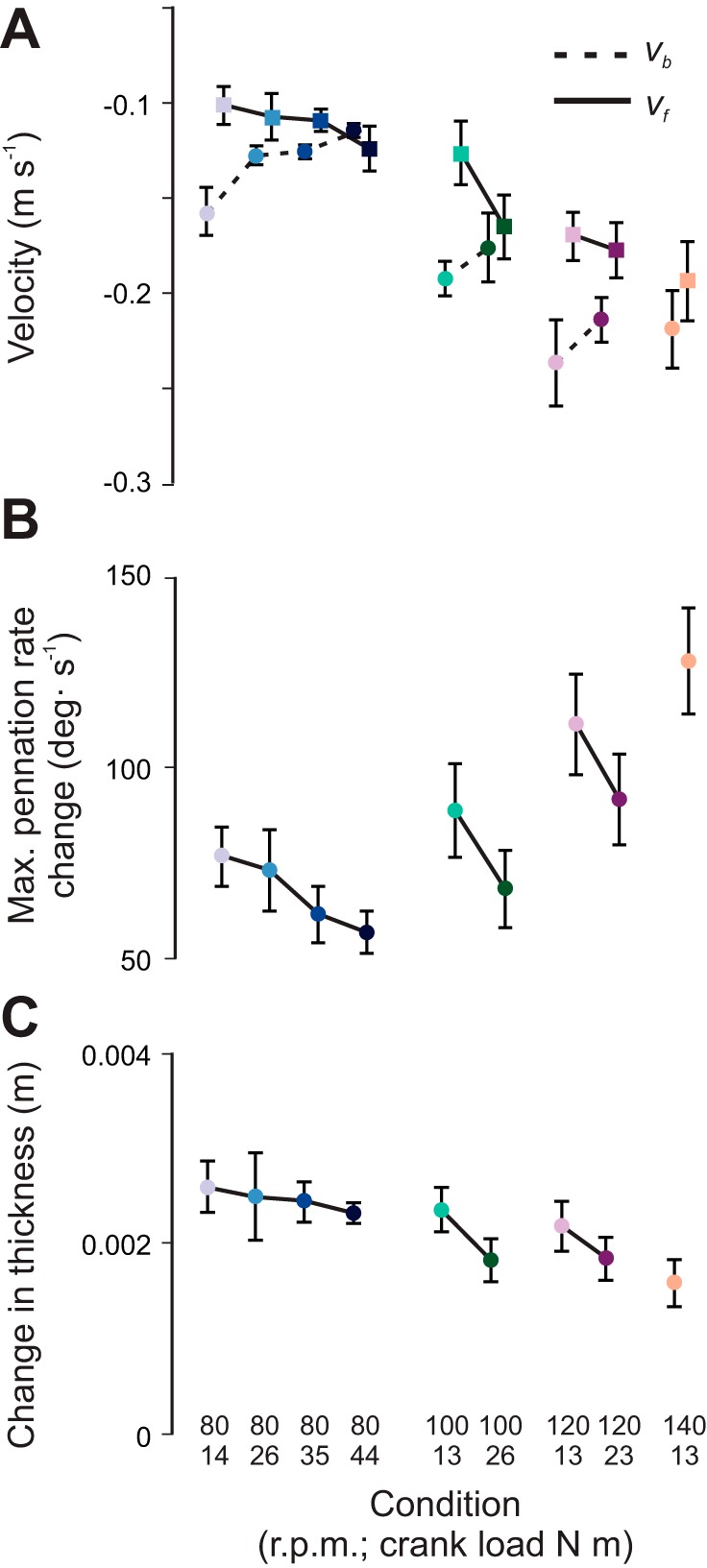
Changes in muscle belly and fascicle behavior across the range of conditions tested in this study. A: variation in maximum muscle belly-shortening velocity (v_b; circles, dashed lines) and fascicle shortening velocity (v_f; squares, solid lines). B: rate of pennation angle change. C: change in muscle thickness. Data are presented as means ± SE for 10 subjects.

RESULTS

Our results show that the cadence and crank torque tested in this study independently altered the muscle’s contractile mechanics. During pedaling, increases in cadence were accompanied by increases in MTU velocity (P < 0.05) but not significant increases in muscle force, whereas increases in crank load were accompanied by increases in force (P < 0.05) but not MTU velocity (Fig. 4, A and C). MTU velocity ranged from −0.19 ± 0.01 m/s at 80 rpm to −0.32 ± 0.02 m/s at 140 rpm. On average, peak tendon strains varied from 3.1 ± 0.14% at the lowest load to 5.1 ± 0.16% at the highest load (Fig. 4B). Subjects’ estimated peak tendon forces increased, with load ranging from 27 to 30% of F_max at the lowest loads to nearly 50% of F_max at the highest load (Fig. 4C). Muscle activation also varied with the mechanical conditions of the task. Peak muscle activation ranged from 32 to 45% (Fig. 4D). Activation increased with both force and MTU velocity, with the minimum activation 32 ± 3.1% at the low-velocity/low-force condition and the maximum activation at both the low-velocity/high-force condition (45 ± 2.7% at 80 rpm at 44 N m) and the high-velocity/low-force condition (45 ± 3.3% at 140 rpm at 13 N m).

The shortening behavior of the muscle fascicles was uncoupled from the shortening behavior of the muscle belly. Maximum belly shortening velocity decreased with force (Fig. 5A). Maximum belly shortening velocity ranged from −0.24 ± 0.02 m/s at 120 rpm at 13 N m to −0.11 ± 0.004 m/s at 80 rpm at 44 N m. Maximum fascicle shortening velocity followed an opposite trend compared with the muscle belly and increased with force (Fig. 5A). Maximum fascicle shortening velocity ranged from −0.11 ± 0.01 m/s at 80 rpm at 14 N m to −0.20 ± 0.01 m/s at the high-velocity/low-force condition, 140 rpm at 13 N m (Fig. 5A). The measured belly and fascicle shortening velocities were tightly linked to the dynamic muscle shape changes. Across the range of mechanical conditions, fascicle shortening was accompanied by an increase in pennation angle and an increase in muscle thickness within the MG (Fig. 3). The increase in fascicle shortening velocity with force (P < 0.05) was accompanied by decreases in the extent and rate at which the fascicles rotated (P < 0.05) (range: 57–128°/s) (Fig. 5B). The changes in muscle thickness (range: 1.6–2.6 mm) were also related to the associated belly and fascicle velocities. Average muscle thickness was 15.3 ± 1.6 mm, and the change in muscle thickness decreased with force (P < 0.05; Fig. 5C). These results are in support of our first hypothesis.

Muscle belly gearing was linked to the measured shape changes. Gearing varied from 0.97 ± 0.09 to 1.46 ± 0.14 across the range of conditions (Fig. 6A). The maximum gearing was 1.46 ± 0.14 and occurred at the intermediate-velocity/low-force condition, 100 rpm at 13 N m. Force, tendon strain, and activation were all significantly associated with gearing (P < 0.05). In support of our second hypothesis, gearing decreased with increasing force (P < 0.05) but did not vary significantly with MTU velocity (Fig. 6, B and C). This finding remained unchanged when gearing was determined at the time of maximum fascicle shortening velocity rather than at the time of maximum belly shortening velocity (these time points are within 8° of each other across all conditions and trials).

Fig. 6.

Gearing varies, depending on the mechanical demands of the task. A: muscle belly gearing across the range of conditions tested in this study. B: gearing did not significantly vary with peak MTU shortening velocity. C: gearing significantly decreased (P < 0.05) with increasing force. Gearing values for each trial were calculated as v_b/v_f at the timing of maximum v_b.

Activation and force were uncoupled in our experiments, which was in part due to the intrinsic force-velocity relationship of a muscle. Across the nine conditions, there was a weak association between peak muscle activation and peak force (r² = 0.29; Fig. 7). For example, in the high-cadence/low-load condition, the MG had a relatively high activation (45 ± 3.3%) but low force (29 ± 1.3% F_max), whereas at the low-cadence/high-load condition, the MG had a relatively high activation (45 ± 2.1%) and also a high force (52 ± 1.1% F_max). When we separated the pedaling conditions into two distinct groups, 1) constrained MTU velocity with increasing force and 2) constrained force with increasing MTU velocity, we observed the independent effects of force (group 1) and MTU velocity (group 2) on the relationship between activation and force (Fig. 7). These results show that although there was a strong association between activation and force within each group of mechanical conditions (group 1: r² = 0.94; group 2: r² = 0.92), there was a significant difference between this relationship, which was apparent by the difference in the slopes between the two groups (slopes of normalized activation/force of 0.51 and 6.19).

Fig. 7.

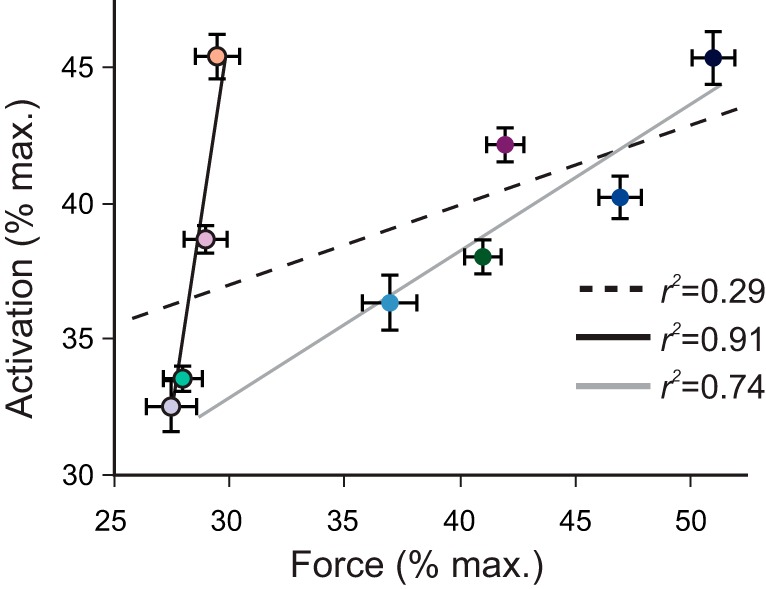
Force and muscle activation were uncoupled across the range of mechanical conditions tested in this study. Data points represent average peak tendon force normalized to the maximum isometric force of the MG (x-axis) vs. average peak muscle activation normalized to maximum muscle activation recorded during reference cycling trials (y-axis) for 10 subjects at the different conditions. SE bars are shown for both mean peak activation and mean peak normalized force. Slopes and r² values are shown for 1) all 9 pedaling conditions (dashed black line), 2) 4 conditions with constrained MTU velocity with increasing force (blue colored circles and solid gray line), and 3) constrained force with increasing MTU velocity (outlined light colored circles and solid black line). Data point colors correspond to the conditions listed in Figs. 4–6.

The multiple regression analysis showed that force was a significant predictor of maximum belly shortening velocity (r² = 0.64, P < 0.05), maximum fascicle shortening velocity (r² = 0.59, P < 0.05), and gearing (r² = 0.56, P < 0.05); however, activation was only a significant predictor of maximum belly shortening velocity (r² = 0.58, P < 0.05).

DISCUSSION

In this study, we used ultrasound-based measurements of muscle architecture and tendon length change to determine how a muscle’s dynamic shape changes and contractile behavior are influenced by force and velocity. We have shown that dynamic muscle shape changes and the uncoupling of the shortening behavior of muscle fascicles from the shortening behavior of the whole muscle belly (i.e., gearing) are influenced by force but not velocity. Specifically, increases in force were accompanied by reduced changes in muscle thickness, reduced fascicle rotations, and increased fascicle shortening velocities. Yet due to the increased strain in the series elastic tendon, increases in force were also accompanied by decreases in muscle belly shortening velocity. Our results provide some of the first in vivo experimental data to support theorized mechanisms of muscle shape change and contribute to our understanding about the independent mechanical effects of force and velocity on muscle behavior.

Dynamic muscle shape changes.

The shape changes reported in this study are related to the internal constraints placed on the muscle fibers. During active shortening, cross-bridges develop forces that cause fibers to shorten in length and compress in girth (63). Yet to remain (nearly) isovolumetric, forces develop that oppose these decreases in fiber girth (39, 45), thereby requiring fiber rotation, as shown here. However, the fiber rotation is affected by additional forces caused by myofascial connective tissue that wraps around muscle fibers (24), surrounding aponeuroses and nearby structures such as bones and neighboring muscles.

Modeling studies have shown that asymmetries in fiber bulging reflect asymmetries in the transverse stresses acting on the fibers (when fibers are considered transversely isotropic; 39, 45). For example, finite-element models of the gastrocnemii have shown that during shortening contractions, an asymmetric stress distribution will develop across the muscle belly, in particular with a higher compressive force between the superficial and deep aponeuroses. This is in large part due to the longitudinal fiber forces having a component that draws the aponeuroses together that is not matched by an equivalent compressive force in the width-wise direction. Therefore, the compressive forces during shortening are greater in the direction bound by the aponeuroses (thickness) in comparison to the width direction, where there are no aponeuroses bounding the muscle.

The mechanical properties of the aponeurosis may also play a key role in modulating dynamic shape changes and internal muscle geometry (6, 7, 43–45). When muscles bulge, the aponeurosis stretches longitudinally, with reported strains varying from 1 to 12% (2, 7, 18, 25, 29, 31, 32, 34, 36, 37, 52, 56), and to a greater extent transversely (width-wise), with reported strains of up to 8% (3, 6, 7, 31, 46, 52, 56). These biaxial properties have been suggested to play an important functional role in variable muscle shape change, allowing longitudinal aponeurosis stiffness to be modulated by the amount of width-wise bulging (7). In the context of our results, it is plausible that the increases in muscle force, which were likely associated with increases in muscle width, would have resulted in greater transverse aponeurosis strains and subsequent increases in the longitudinal stiffness. This is supported by the observed decreases in MG fascicle rotation that occurred with increased force. However, the influence of the aponeurosis strain on internal muscle geometry (shortening and rotations) is likely only as important as far as the aponeurosis can stretch. Under the highest activation levels measured here and assuming the aponeuroses strain 6% at maximum force (based on the average strain from literature values), we predict that the aponeuroses would stretch ∼5 mm, which is considerably less than the amount fascicles shorten (up to 20 mm; Fig. 3). Although the presence of aponeurosis does indeed lead to stress asymmetries developing within the muscle belly, the effect of aponeurosis properties alone (e.g., biaxial stiffness) on variable muscle shape change is potentially minor.

Our results support the idea that variable muscle shape changes during fascicle shortening are in part due to the stress asymmetries that result from the interplay between the compressive forces and the connective tissue resistance (7, 24, 43). These stress asymmetries additionally depend on the base material properties of the muscle tissue (45), but to date little remains known about this effect. The changes in muscle thickness and pennation observed within this study are consistent with the mechanisms put forward in both in situ animal studies (6, 24) and modeling studies (43, 44). Specifically, we found a reduction in the increases in muscle thickness and a decrease in fascicle rotation with increasing force. At higher muscle forces (where there is greater compressive force between the aponeuroses), it would be expected that the thickness of the MG would remain steady or even decrease, and this is consistent with the results from previous studies in man (30, 40, 48).

Gearing.

Gearing within the gastrocnemii has been studied in different experimental contexts but with conflicting results. The muscle belly gearing results for the MG reported here differ from those reported for the MG, LG, and SOL measured in a previous cycling study under similar mechanical conditions (60). In particular, our results show that muscle belly gearing was relatively unaffected by MTU velocity (Fig. 6B), whereas it was previously shown that muscle belly gearing increased with increasing cadence (See Table 2 in Ref. 60). This may be related to differences in the experimental methods used to calculate gearing. Here, we directly measured tendon length changes using ultrasound and then estimated time-varying muscle belly lengths as the difference between MTU lengths, which were derived from kinematics and a scaled musculoskeletal model, and tendon lengths, which were measured using ultrasound. Previously, Randhawa et al. (48) estimated the belly velocity using the implicit assumption that the aponeurosis stretch was negligible. Additionally, modeling results suggest that the effects of velocity on gearing may only come into play at high MTU velocities, so the lack of association between gearing and MTU velocity seen in this study could be related to the fact that the peak MTU velocities reached by elite cyclists may be less than MTU velocities in the general population.

It should also be noted that muscle force is related to its velocity through the force-velocity relationship, and in this context the findings of higher gearing at high velocity/low forces are consistent with lower gearings occurring at low velocity/high forces (6). The variable nature of the force and velocity during cycling makes these experimental conditions different from those elicited within typical in situ experiments, where gearing and shape changes are determined at constant force or constant MTU velocity (6, 8, 24). However, in vivo cycling data are advantageous in that we are able to test the independent effects of force, velocity, and activation, which has not been possible in previous studies. The range of conditions, varied levels of activation, and detailed experimental techniques in the current study have allowed us to identify muscle force, and not velocity, as the mechanistic driving factor to allow for the gearing to vary between these in vivo contractile conditions.

The variations in gearing during pedaling observed in this study are not solely a result of the changes in fascicle shortening velocity. Changes in gearing are related to alterations in the shortening velocity of the muscle belly. During cycling, it is not possible to maintain constant belly velocity while altering load due to the series elasticity of the AT. Our data show that increases in load at a constant cadence result in decreases in gearing; this is related to the increased fascicle shortening velocity as well as the decreased belly shortening velocity. With increasing loads, the AT underwent larger strains that uncoupled length changes of the MTU from length changes of the muscle belly, leading to the observed decrease in belly shortening velocity. This has previously been defined as tendon gearing (60). We must note that our ultrasound measurements are in one plane and assumed that the fascicles are linear, following paths from the superficial to the deep aponeurosis. However, muscle fascicles are in fact curvilinear (38, 39, 47) to maintain mechanical stability within the muscle (57). However, 2D B-mode ultrasound measurements of pennate muscles report errors of less than 6% for fascicle length (38) and less than 1° for pennation angle (47) when treating fascicles as linear rather than curvilinear structures, and thus the effects of this assumption on our results are likely minor.

Measuring in vivo muscle forces in humans remains challenging. In this study, we used tendon strains measured using B-mode ultrasound together with subject-specific values of tendon stiffness and slack length to estimate time-varying forces. These methods for estimating forces have previously been evaluated and are consistent with ankle moments derived from inverse dynamics (17). When comparing this method with previous approaches that estimate muscle forces using moments derived from inverse dynamics together with moment arms and physiological cross-sectional areas, one advantage of our method is that it accounts for the relative contributions of the MG, LG, and SOL to tendon force based on their EMG intensities (17). However, this method is not without limitations. First, tendon force estimates vary with tendon stiffness and tendon slack length, and thus errors in either of these two parameters could result in errors in the time-varying forces. For example, a ± 10% error in tendon stiffness would result in a ± 10% error in tendon force, whereas a ±1% error in tendon slack length could lead to a ±20% error in tendon force as well as a substantial delay in the onset of force (17). Because of this sensitivity, we determined tendon slack length on a subject-specific basis during the cycling trials and verified that these lengths were consistent with those derived from each subject’s net ankle moments (from inverse dynamics) vs. the subject’s AT lengths measured using ultrasound during pedaling (17).

Second, we assumed that tendon force-length properties remain constant across knee angles, and we did not characterize the nonuniform length changes that may occur between the MG, LG, and SOL. It is possible that at different knee angles, where the relative lengths of these muscles are affected differently as a result of the biarticular nature of the LG and MG vs. the uniarticular nature of the SOL, we may get a different value of stiffness and thus a different value of force. In the context of this study, the effects of this assumption are likely to be small given that the knee reaches 130° of flexion at a crank angle of 90°, and this matches the isometric test conditions under which we measured tendon stiffness (17, 35) and coincides with the time where measurements of interest for this study were taken. However, extending this method to locomotor tasks with fewer kinematic constraints such as walking and running may introduce additional challenges, such as noisy tendon strain measurements, that were minimized in this study given that subjects were seated (knee angles constrained) and wore clipless pedals (ankle angles constrained) during measurements. Deriving individual muscle forces from inverse dynamics during periods of co-contraction is limited, and although we are most interested in MG behavior at the time of the peak shortening velocity when any force from co-contraction between the triceps surae muscles and the TA is likely to be negligible, we believe our methods of estimating force are appropriate for this study.

Conclusions.

The mechanisms governing dynamic muscle shape change and their influence on the mechanical behavior of skeletal muscle during submaximal activation levels remain largely unexplored. In this study, we used human cycling to uncouple and understand the independent mechanical effects of force and velocity on the behavior of skeletal muscle. We found that dynamic muscle shape changes are influenced by force but not velocity, such that muscle belly gearing decreases with increasing levels of force. Previous studies have suggested that there are a range of factors that contribute to dynamic muscle shape changes, and here we provide a comprehensive set of in vivo data that support the myriad of theorized mechanisms of muscle shape change from both animal studies (e.g., see Ref. 6) and human muscle modeling (e.g., see Ref. 43). The complex interactions between the contractile and elastic machinery under varied mechanical conditions warrant further investigation. Future work should aim to both use advanced imaging techniques to characterize dynamic muscle shape change in three dimensions (e.g., see Ref. 12) and develop continuum-based muscle models to explore the mechanical effects of the base material properties of muscle tissue (e.g., see Ref. 45).

GRANTS

This work is supported by National Institutes of Health Grant no. R01-2R01-AR-055648 and an National Sciences and Engineering Research Council Graduate Research Fellowship to T. J. M. Dick.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

T.J.M.D. and J.M.W. conceived and designed research; T.J.M.D. and J.M.W. performed experiments; T.J.M.D. analyzed data; T.J.M.D. and J.M.W. interpreted results of experiments; T.J.M.D. prepared figures; T.J.M.D. drafted manuscript; T.J.M.D. and J.M.W. edited and revised manuscript; J.M.W. approved final version of manuscript.