Stability of hand force production. I. Hand level control variables and multifinger synergies

We extended the idea of hierarchical control with referent spatial coordinates for the effectors and explored two types of synergies stabilizing multifinger force production tasks. We observed synergies among finger forces as well as synergies between hypothetical control variables that stabilized performance under visual feedback but failed to stabilize it after visual feedback had been removed. Indexes of two types of synergies correlated with each other. The data suggest the existence of multiple mechanisms stabilizing motor actions.

Abstract

We combined the theory of neural control of movement with referent coordinates and the uncontrolled manifold hypothesis to explore synergies stabilizing the hand action in accurate four-finger pressing tasks. In particular, we tested a hypothesis on two classes of synergies, those among the four fingers and those within a pair of control variables, stabilizing hand action under visual feedback and disappearing without visual feedback. Subjects performed four-finger total force and moment production tasks under visual feedback; the feedback was later partially or completely removed. The “inverse piano” device was used to lift and lower the fingers smoothly at the beginning and at the end of each trial. These data were used to compute pairs of hypothetical control variables. Intertrial analysis of variance within the finger force space was used to quantify multifinger synergies stabilizing both force and moment. A data permutation method was used to quantify synergies among control variables. Under visual feedback, synergies in the spaces of finger forces and hypothetical control variables were found to stabilize total force. Without visual feedback, the subjects showed a force drift to lower magnitudes and a moment drift toward pronation. This was accompanied by disappearance of the four-finger synergies and strong attenuation of the control variable synergies. The indexes of the two types of synergies correlated with each other. The findings are interpreted within the scheme with multiple levels of abundant variables.

NEW & NOTEWORTHY We extended the idea of hierarchical control with referent spatial coordinates for the effectors and explored two types of synergies stabilizing multifinger force production tasks. We observed synergies among finger forces and synergies between hypothetical control variables that stabilized performance under visual feedback but failed to stabilize it after visual feedback had been removed. Indexes of two types of synergies correlated with each other. The data suggest the existence of multiple mechanisms stabilizing motor actions.

human movement occurs in a changing unpredictable environment: we can never predict perfectly the shape of a pebble we step on or the weight of a cup we are about to lift. This makes dynamical stability (an ability to return to a state or trajectory following a small transient perturbation) crucial for successful execution of goal-directed actions. Two approaches have been developed to address the stabilization of movements. One of them assumes that neural internal models predict interactions within the body and between the body and the environment; these internal models are quickly updated in cases of unexpected perturbations (Kawato 1999; Shadmehr and Wise 2005; Wolpert et al. 1998). The alternative hypothesis is that dynamical stability of salient performance variables (cf. the notion of task-specific stability, Schöner 1995) is ensured by neural organizations termed synergies that do not perform computations but involve few to many mappings within a neural hierarchy of control (reviewed in Latash et al. 2007; Latash 2010). A method to quantify such synergies has been developed within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999). Most commonly, this method analyzes intertrial variance in the space of elemental variables (those produced at a hierarchically lower, high dimensional level) in directions that do not affect a salient performance variable (the UCM) and directions orthogonal to the UCM (ORT), which do affect performance.

Recently, the idea that synergies are a means to ensure the task-specific stability of actions has been coupled with the idea of the neural control of movements using spatial referent coordinates (RCs; Latash 2010, 2016). Within the latter hypothesis, voluntary actions are consequences of changes in spatial RCs for effectors at all levels of analysis, whereas mechanical effects and muscle activation patterns emerge as results of interactions between the centrally specified RC(t) patterns and the time-varying external force field. For the neural control of a single muscle, RC is equivalent to the threshold of stretch reflex, λ, introduced within the equilibrium-point hypothesis (Feldman 1966, 1986).

Because every human effector is controlled by at least two groups of muscles, agonists and antagonists for a given task, even one-effector natural tasks are abundant (cf. Latash 2012) at the level of control. For example, single-finger force (F) production in isometric conditions may be viewed as a consequence of a change in RCs for the two opposing muscle groups: agonists and antagonists. Two main commands have been introduced to describe unidirectional and counterdirectional shifts of the two RCs, reciprocal (r-command) and coactivation (c-command) (Feldman 1980). In particular, the c-command changes the spatial range where the two opposing muscle groups are active simultaneously. At the level of mechanical behavior, in isometric condition, a change in the r-command effectively shifts RC for the fingertip while a change in the c-command leads to changes in the fingertip apparent stiffness, k: F = k(AC – RC), where AC is the actual coordinate of the fingertip. Note that this scheme of control does not assume direct neural specification of apparent stiffness (cf. impedance control, Hogan 1985) but leads to modification of k in specific (isometric) external conditions. We assume here that the force-coordinate characteristic may be approximated as a linear function, which is a nontrivial assumption and will be addressed in more detail in the discussion. If there is a synergy at the level of two elemental variables, RC and k, which stabilizes F, one can expect high intertrial variability of the {RC; k} data points along the hyperbolic UCM for this task compared with variability orthogonal to this UCM. Such {RC; k} synergies have been demonstrated in recent studies (Ambike et al. 2016a, 2016b), although typical linear methods for quantifying intertrial variance are inapplicable because of the hyperbolic UCM in the {RC; k} space.

In this study, we use the term hand action to refer to the total force (F_TOT) and total moment of force (M_TOT) produced by the hand; F_TOT production can be viewed as the result of specification of RC and k for the hand (hence “hand level” analysis). Alternatively, this action can be analyzed as a result of the combined mechanical effect of forces produced by each finger individually, “finger force level” analysis; such analysis was performed in several earlier studies (Latash et al. 2001; reviewed in Zatsiorsky and Latash 2008). Additionally, it is possible to analyze hand action as a combination of {RC; k} pairs for each finger (“finger level” analysis). The former two analyses are addressed in the current paper, whereas the latter, which involves a more complex analysis in the eight-dimensional space of {RC; k} variables for each finger, may be carried out in a follow-up paper. The finger forces result from the mechanical effects of numerous muscles in the hand, wrist, and forearm. We have decided not to perform a muscle-level analysis to avoid using invasive methodology, such as intramuscular electromyogram, which would likely affect natural behavior of our subjects.

The {RC; k} synergies stabilizing F_TOT during hand force production tasks have been reported in earlier studies (Ambike et al. 2016a, 2016b). The present study extends the findings of Ambike and colleagues to combined force-moment production tasks that may be viewed as building blocks for a range of prehensile actions. We explored whether {RC; k} synergies ensured stability of F_TOT as reflected in other phenomena related to stability of hand action such as multifinger force-stabilizing synergies and unintentional force drifts in the absence of visual feedback (Ambike et al. 2015; Vaillancourt and Russell 2002). We also explored possible drifts in the {RC; k} space under full visual feedback, i.e., when accuracy of F_TOT production was not compromised.

We hypothesized that, under visual feedback, there would be strong {RC; k} synergies and strong multifinger synergies stabilizing F_TOT (cf. Ambike et al. 2016a). Our second hypothesis was that removing visual feedback would lead to a drift in F_TOT to lower values (cf. Ambike et al. 2015; Vaillancourt and Russell 2002), reflecting its loss of stability, and that this performance drift would be accompanied by disappearance of F_TOT-stabilizing synergies at both four-finger and {RC; k} levels (cf. Parsa et al. 2016, 2017a, 2017b). Our third hypothesis was that the indexes of the two types of synergies, {RC; k} at the hand level and among individual finger forces, would correlate with each other. Note that a strong correlation between the two synergy indexes would suggest that the two synergies might reflect a single neural action-stabilizing mechanism. If the two indexes are unrelated to each other, this would point to at least two parallel, and largely independent, mechanisms stabilizing hand action.

In the present experiment, we used a task that required accurate production of a combination of hand F_TOT and M_TOT in isometric conditions (as in Parsa et al. 2016, 2017a). We used the inverse piano device (Martin et al. 2011) to introduce smooth controlled perturbations of the hand AC, recorded F_TOT changes, and used regression analysis to compute RC and k (cf. Ambike et al. 2016a). Although it was not the subject of a specific hypothesis, the combined F_TOT and M_TOT production task allowed us to determine whether having visual feedback on one of the two performance variables could help to avoid drift in the other variable and loss of corresponding synergies.

METHODS

Subjects

Ten adult subjects (5 female; ages 20–35 yr) participated in the current study. All subjects were right handed according to hand use during daily activities. Subjects reported no upper limb injuries or neurological disorders that would interfere with their ability to perform the study. Subjects provided written informed consent in accordance with procedures approved by the Office for Research Protections at The Pennsylvania State University.

Apparatus

This study was conducted using the “inverse piano” device (Martin et al. 2011), which allows finger forces to be recorded while fingers are raised and lowered. The device uses four piezoelectric uniaxis force transducers (208C01; PCB Piezotronics, Depew, NY) to measure finger pressing force. Four signal conditioners (PCB 484B11) provide excitation and amplification to each transducer individually. Analog force data are sampled at a rate of 1,000 Hz using a 16-bit analog-to-digital card (PCI-6052; National Instruments, Austin, TX). The sensors are mounted on linear actuators (PS01-23 × 80; Linmot, Spruitenbach, Switzerland) that allow each sensor to be raised and lowered along a vertical axis. The actuators are controlled by a four-channel servo drive (Linmot E400-AT) through which each actuator can be controlled individually. The linear motors are mounted such that they can be adjusted in an anterior-posterior direction to fit individual subjects’ hands. The distance between the centers of adjacent sensors is 3 cm.

Each subject sat with his or her right forearm in a sagittal plane, approximately parallel to the ground, and placed each finger of their right hand on a corresponding force sensor of the inverse piano device. Sensor positions were adjusted so that each finger was slightly curved when the fingertip was on the sensor face, and the hand formed a natural dome. A 19-in. monitor placed ~0.8 m from the subject’s face provided visual feedback on F_TOT and M_TOT production, as described below. A customized program running in the LabVIEW programming environment (National Instruments) provided visual feedback, controlled motor positions, and logged data for offline processing.

Procedure

The procedure of the present study consisted of three parts. First, subjects produced four-finger maximal voluntary contraction (MVC) trials. During this part of the procedure, subjects received feedback on F_TOT; they were instructed to increase F_TOT smoothly to maximum and given a 6-s time window during which they could produce this maximal force. Subjects were given one practice MVC trial, waited for ~30 s, and then produced a test MVC value. This second MVC value was used to normalize task forces as described in the following text.

The second part of the procedure consisted of single-finger force ramps. During these trials, subjects were instructed to keep all four fingers on the force sensors, but to press with only one finger at a time to follow a 12-s force profile. The force profile began with 3 s at 5% of the instructed finger’s peak force during the four-finger MVC trial (MVC_f), followed by a 6-s ramp to 50% of the finger’s MVC_f, and finally 3 s at 50% MVC_f. Subjects performed four ramp trials, one for each finger. Data from these trials were not analyzed in the present study.

The final part of the procedure consisted of the main experimental trials. During this part of the procedure, subjects were required to produce accurate F_TOT and M_TOT magnitudes according to a visual target. A cursor on the screen moved up the screen with F_TOT, and the cursor moved left and right with M_TOT. M_TOT was computed with respect to a virtual pivot passing between the middle and ring fingers of the hand: pressing with the index and middle fingers moved the cursor to the left (pronation moment) while pressing with the ring and little fingers moved the cursor to the right (supination moment). Moment arms were computed according to the physical location of the centers of the corresponding sensors and were 4.5, 1.5, −1.5, and −4.5 cm for the index, middle, ring, and little fingers, respectively. No effects of tangential forces and no changes in the point of force application were considered; as a result, M_TOT represented a computed variable, not the actual total moment of force.

The initial position of the cursor was set when subjects rested their fingers on the sensors without pressing; as such, the sensors measured active force production only. The initial position of the cursor (which was always in the center of the screen) corresponded to F_TOT = 20% of MVC, and M_TOT into supination moment with the magnitude equal to 7% of the index finger MVC_f multiplied by its 4.5-cm moment arm. These values were selected based on earlier studies (Park et al. 2010; Parsa et al. 2016, 2017a) so that subjects could repeatedly produce the required force and moment levels without fatigue but also such that these levels were high enough to induce force and moment drifts.

Each trial was 21 s long. Upon trial onset, subjects were instructed to move the cursor to the target as quickly as possible and maintain its position in the target. After 5 s, the inverse piano raised and lowered all four fingers by 1.0 cm at a rate of 2.0 cm/s (cf. Ambike et al. 2016a). Subjects were instructed not to react to the movement of their fingers; when their fingers returned to the initial position, the subjects were reminded to bring the cursor back to the initial position. Eight seconds after the trial initiation, feedback was removed according to one of three conditions as follows: in the no feedback condition, the cursor disappeared completely; in the force-feedback condition, the movement of the cursor was constrained along the horizontal axis such that subjects received feedback only on F_TOT; and in the moment-feedback condition, cursor movement was constrained along the vertical axis such that subjects received feedback only on M_TOT. In all cases, subjects were asked to maintain both the F_TOT and M_TOT magnitudes, “keep doing what you have been doing,” after feedback was removed. After 11 s, the fingers were raised by 1.0 cm at 2.0 cm/s (again under the instruction not to voluntarily intervene) and returned to their initial position, at which point the target changed color to indicate that the trial was over. Subjects performed practice trials (typically 3–4 trials) until they felt comfortable with their ability to comply with all instructions. Subjects performed 24 trials in each condition, for a total of 72 trials. Presentation of trial conditions was fully randomized according to a predetermined scheme, which the experimenter could not view during the experiment. No mandatory rest intervals were imposed during the experimental trials, but subjects were invited to take any rest interval desired between trials. Figure 1 shows a detail of the experimental setup and a schematic of the trial structure noting times of sensor movement and feedback disappearance.

Fig. 1.

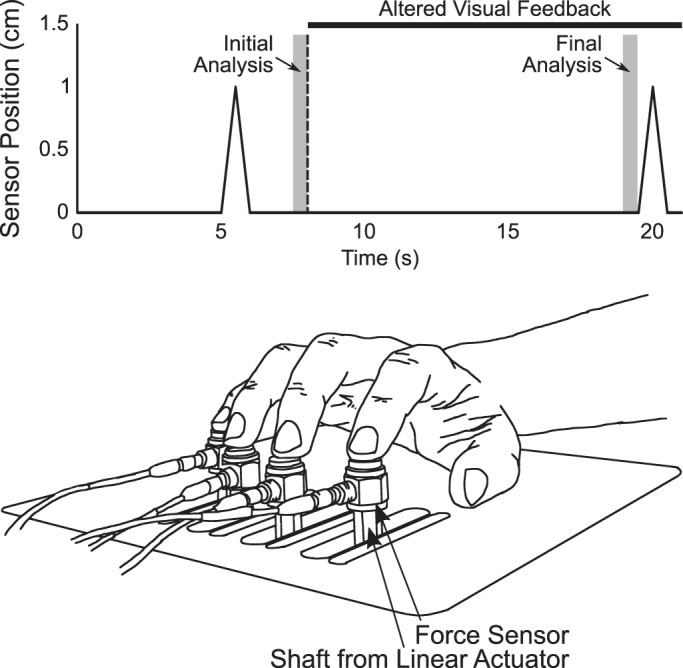
Schematic of the sensor motion during the experimental trials (top) and illustration of the inverse piano apparatus (bottom). On the sensor motion illustration, the vertical broken line represents the time at which visual feedback was removed (8 s after trial onset), whereas the two shaded areas indicate the times over which response variables were computed for initial and final comparisons. The inverses piano apparatus is shown with all four fingers raised by means of linear actuators, which are mounted under the table and therefore not visible in the illustration.

Data Analysis

Data were processed offline using Python 3 (Python Software Foundation) and packages from the SciPy library (Jones et al. 2001). Data were low-pass filtered using a forward-and-reverse 4th-order Butterworth filter with a cutoff frequency of 10 Hz. Data were visually inspected for subjects’ failure to adhere to instructions; the largest number of trials removed per condition for an individual subject on this basis was three.

Analysis of performance drifts.

To quantify F_TOT drifts, we compared average F_TOT during an episode from 7.5 to 8 s from trial onset (just before visual feedback was removed) with F_TOT from 18.5 to 19 s after trial onset (just before the fingers were raised a second time). M_TOT values were also computed during these two episodes to quantify drifts in M_TOT production. For the purposes of these comparisons, F_TOT was normalized to the target value of 20% MVC_f [yielding force unit (FU)], and M was normalized to the target value of 7% maximal index finger moment [yielding moment unit (MU)].

Computation of RC and k.

The hypothetical control variables RC and k were computed two times for each experimental trial, according to methods used by Ambike et al. (2016a). First, we verified that the force changes during the time when the fingers had been raised were a linear function of the time-varying finger coordinate. For this purpose, we only accepted trials in which the correlation coefficient between F_TOT and finger coordinate was >0.9 in both episodes of finger raising. Across subjects, an average of 19 trials/condition was accepted; this number varied from 13 to 24.

Upon ensuring a linear F_TOT response to change in finger position, the initial F_TOT over 50 ms before the fingers were raised was computed. We also computed a final value of F_TOT as the average F_TOT during the final 10 ms of upward sensor motion. Subtracting the final value of F_TOT from its initial value, we obtained ΔF_TOT. We then computed apparent stiffness k = ΔF_TOT/1.0, where 1.0 cm is the change in position of the fingertips, yielding apparent stiffness in Newtons per centimeter, and the referent coordinate of the hand RC = –F_TOT/k, in centimeters. Note that our choice of coordinate frame, where we take the initial position of the fingers = 0, results in RC < 0. To check whether subjects might become acclimated to onset time of the inverse piano and vary their responses to the perturbation imposed (despite being instructed not to do this), we explored possible changes in RC and k with the trial number and found no effects in any of the conditions and phases of analysis.

We computed mean values of RC and k pre- and postdrifts, as well as the range of RC and k values across trials for each subject and each condition separately. Finally, for each subject, we computed the change in RC and k for each acceptable trial: ΔRC = RC_f − RC_i and Δk = k_f − k_i, where the subscripts f and i refer to the final and initial episode of finger-raising within a trial; we then compared across-trial mean values of ΔRC and Δk.

Permutation analysis for RC and k.

To test whether values of RC and k covaried across trials to stabilize F_TOT, we used random permutation to generate surrogate data (cf. Müller and Sternad 2003). The purpose of the permutation analysis is to determine whether or not covariation of RC and k across trials helped to reduce F_TOT variability. Because the UCM in the two-dimensional {RC; k} space is hyperbolic, F_TOT = –k × RC, linear methods of analysis cannot be used. The permutation analysis estimates F_TOT variability expected if RC and k did not covary across trials. Note that the unavoidable variability in F_TOT allows variance in both RC and k that do not have to covary, for example, the subjects could select a stereotypical solution and reproduce it with minimal variance and no covariance between RC and k.

For each subject, we randomly generated {RC; k} pairs using actual values within a condition and computed the corresponding force values (F_SUR). Furthermore, SD of sets of F_SUR was computed. This permutation procedure was carried out 10,000 times per subject per condition, and average SD of each surrogate dataset (SD_SUR) was computed and compared with the SD of the actually observed forces (SD_ACT): R_SD = SD_SUR/SD_ACT. Note that R_SD > 1 means that the original dataset contained covariations of RC and k that helped to keep intertrial F_TOT variability lower than expected from a dataset without such covariation.

Hyperbolic regression analysis.

Because our hypothesis predicted that {RC; k} pairs from individual trials would vary mostly along the corresponding hyperbolic UCM, we fit hyperbolas to each subject’s RC and k sets of data. The coefficient of determination (R²) for these best-fit hyperbolas was computed separately for the initial and final values of {RC; k} pairs of data points within each trial. For further statistical analysis, R² were transformed to z-scores.

UCM-based analysis of variance.

We quantified intertrial variance in two subspaces, the UCM and the space orthogonal to the UCM (ORT), according to the framework of the UCM hypotheses (Scholz and Schöner 1999). Briefly, this method quantifies the component of intertrial variance, which affects a salient performance variable (V_ORT), and the component that does not (V_UCM). The UCM for F_TOT was computed as the null space of the Jacobian matrix corresponding to total force: J = [1 1 1 1]; to compute UCM with respect to M_TOT, J = [−4.5 −1.5 1.5 4.5], which corresponded to the physical location of the fingers in the medial-lateral direction. Detailed descriptions of the methods involved in computation of V_UCM and V_ORT are available in Latash et al. (2001) and Scholz et al. (2002). To quantify the relative amount of V_UCM and V_ORT observed, we calculated an index of synergy, ΔV = (V_UCM/3 − V_ORT)/(V_TOT/4), where V_UCM, V_ORT, and V_TOT are normalized by the dimensionality of the respective spaces. For statistical analyses, ΔV was z-transformed to account for its computational bounds, yielding ΔV_Z. These computational bounds for a four-finger task are 1.33 ≥ ΔV ≥ −4, so ΔV_Z = 0.5 × ln[(ΔV + 4)/(1.33 − ΔV)] and, therefore, the critical value of ΔV_Z ≈ 0.55 corresponds to ΔV = 0.

Statistics

Our first specific hypothesis was that, under visual feedback, strong F_TOT-stabilizing synergies would be observed in the space of the theoretical control variables {RC; k} for the whole hand and for four-finger force production using the UCM-based variance analysis. We compared R_SD, a measure of the increase in SD of F_TOT when data were randomly permuted, with 1 (the value of R_SD that would indicate permutation had no effect) to test this hypothesis for the {RC; k} data. Similarly, we compared ΔV_Z with its critical value, ≈0.55, to verify whether F_TOT-stabilizing variation of individual finger forces was present.

Our second main hypothesis was that performance drifts would be accompanied by drifts in {RC; k} and UCM synergies. As such, first we used the two-way repeated-measures ANOVA Time (2 levels: initial and final) × Feedback (3 levels: no feedback, force feedback, and moment feedback) on F_TOT and M_TOT to assess the presence of drifts in task performance. We then ran the same ANOVA on R_SD and z-scores of R² of best-fit hyperbolas for the {RC; k} data to investigate drifts in {RC; k} synergies and on ΔV_Z to investigate whether performance drifts were accompanied by changes in UCM synergies stabilizing F_TOT and/or M_TOT.

To investigate potential relations between the indexes of F_TOT-stabilizing synergies quantified at the {RC; k} level and at the interfinger level (hypothesis 3), we correlated R_SD with F_TOT-stabilizing ΔV_Z. We performed this correlation analysis for each subject across feedback (no-feedback, force-feedback, and moment-feedback) and time (initial and final) conditions.

Although not the subject of specific hypotheses, we also investigated how the computed control variables RC and k changed during performance drifts. For these analyses, we again applied the Time × Feedback ANOVA to mean values of RC and k and their ranges to assess how these variables change over time intervals when performance drifts were observed. In addition, we used the one-way ANOVA, feedback, on across-trial changes in RC and k (ΔRC and Δk).

Some of the response variables we used, particularly ranges of RC and k values, are very sensitive to outliers. Because of this concern, before analyzing {RC; k} data, values of RC and k for each subject that were >3 SD from the average during a given condition were removed. On average, less than one value per dataset was removed because of this criterion. All statistics were run in SAS 9.4 (The SAS Institute, Cary, NC). Repeated-measures ANOVAs were run using the MIXED procedure and variance components variance-covariance structure. F-test degrees of freedom were computed using the Kenward-Roger method (Kenward and Roger 1997). Normality of fitted data was verified using quantile-quartile plots. When significant main effects of factors with more than two levels or interactions were observed, we explored them with pairwise comparisons with Bonferroni corrections. Significance is assumed when P < 0.05. Unless otherwise stated, all numerical data are presented as means ± SE.

RESULTS

Performance Drifts

All subjects were able to satisfactorily complete the full experimental procedure. When visual feedback on F_TOT and/or M_TOT was removed, subjects showed drifts in the variables without feedback. In particular, when feedback on F_TOT was removed, we observed a drop in the F_TOT magnitude; when feedback on M_TOT was removed, we observed a change in M_TOT from the prescribed supination moment to the production of a pronation moment, which could reach higher magnitudes than the original supination M_TOT. None of the subjects reported fatigue during the experimental procedure. Within each feedback condition, paired t-tests indicated that the magnitude of force drift was unchanged from the first three trials to the last three trials (no feedback: t₉ = 0.40, P > 0.5; force feedback: t₉ = 0.06, P > 0.5; moment feedback: t₉ = 1.68, P = 0.13). Time series plots of across-subjects average F_TOT and M_TOT with SE shades are presented in Fig. 2.

Fig. 2.

Across-subjects average force (F_TOT) and moment (M_TOT) production performance. Large deviations at 5 and 19.5 s result from fingers being lifted to measure referent coordinate (RC) and apparent stiffness (k) values. Visual feedback was removed at 8 s after trial onset (vertical broken line). Note the drifts in performance variables (F_TOT and M_TOT) when feedback on that variable was removed. Error shades show SE.

The visual impressions from Fig. 2 were borne out in the two-way repeated-measures ANOVA Feedback × Time, which showed a significant interaction for both F_TOT [F(2,45) = 14.81, P < 0.001] and M_TOT [F(2,45) = 27.34, P < 0.001]. Pairwise comparisons indicated that, with visual feedback, average values of F_TOT and M_TOT did not change. Additionally, values of F_TOT and M_TOT remained unchanged when feedback on that particular variable was left intact (in the force-feedback and moment-feedback conditions, respectively). However, without feedback on force, F_TOT decreased significantly to 0.79 ± 0.05 FU when all feedback was turned off and to 0.89 ± 0.04 FU when only moment feedback was presented. These two values of F_TOT were significantly different from one another. Similarly, M_TOT changed to pronation values: −1.02 ± 0.25 MU in the no-feedback condition and −1.70 ± 0.45 MU in the force-feedback condition (values are negative because subjects switched from supination to pronation moments). These values of M_TOT were not significantly different from one another.

{RC; k} synergies stabilizing F_TOT

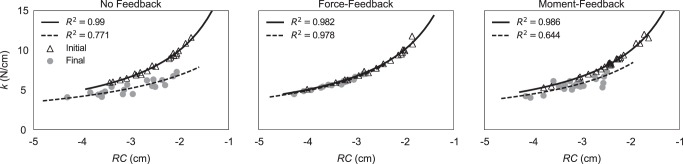
Under full visual feedback on both F_TOT and M_TOT, RC and k values were closely aligned along hyperbolic contours corresponding to the task F_TOT value. These observations support our first specific hypothesis. Coefficients of determination for best-fit hyperbolas under full visual feedback ranged from 0.99 to 0.88; R² was only lower than 0.90 one time, for a single subject in one condition. After feedback on F_TOT was removed, R² values became lower, ranging from 0.95 to 0.19 in the no-feedback condition and from 0.89 to 0.34 in the moment-feedback condition. Figure 3 shows {RC; k} data and hyperbolic fits for a representative subject before and after visual feedback was turned off for all three feedback conditions.

Fig. 3.

The {RC; k} values from a representative subject for each trial during initial (open triangles) and final (gray circles) time points, before and after, respectively, visual feedback was removed in the three visual feedback conditions: no feedback, force feedback, and moment feedback. R² values refer to best-fit hyperbolas computed for initial (solid line) and final (broken line) {RC; k} datasets.

Surrogate sets of {RC; k} pairs (see methods) produced F_TOT values that showed much higher SD across trials (SR_SUR) compared with the actual datasets (SD_ACT). Analysis of surrogate datasets produced high values of the ratio R_SD = SR_SUR/SD_ACT; across subjects, R_SD ranged from 14.18 ± 2.21 (no-feedback condition) to 13.22 ± 1.53 (moment-feedback condition). The values of R_SD were significantly greater than 1 (P < 0.001).

We also correlated R² values with R_SD for each subject across time periods and conditions. Correlation coefficients ranged from 0.98 to 0.79; a single-tailed t-test on z-transformed correlation coefficients confirmed that, across subjects, these correlations were greater than zero (t₉ = 8.27; P < 0.001).

Drifts in RC and k

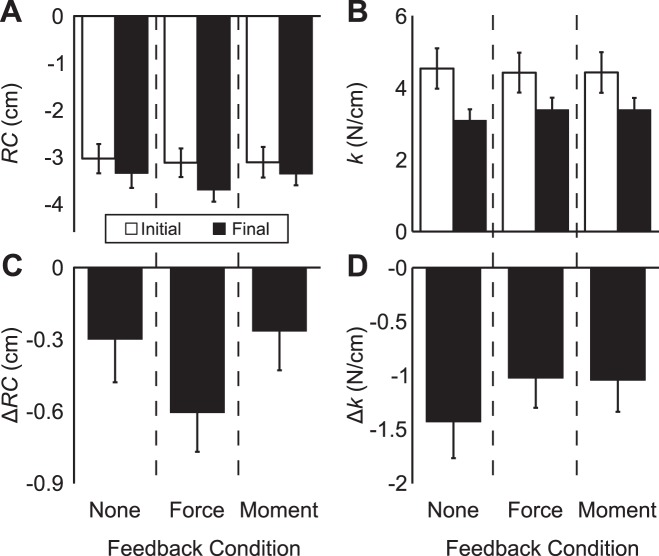
For each subject in each feedback condition, we analyzed the across-trial average values of RC and k during the initial (full visual feedback) and final (partial or no visual feedback) states, as well as average within-trial changes in RC (ΔRC) and k (Δk). On average, values of RC moved farther from the actual fingertip coordinate when feedback was removed while values of k decreased. For RC, the two-way ANOVA Feedback × Time showed a significant effect of Time [F(1,45) = 25.51, P < 0.001] without significant interactions. The main effect of Feedback was just over the significance criterion [F(2,45) = 3.18, P = 0.051]. A similar ANOVA on k showed a significant effect of Time only [F(1,45) = 80.51, P < 0.001]. These data are shown in Fig. 4, A and B.

Fig. 4.

Average values of RC (A) and k (B) for each feedback condition before (open bars) and after (filled bars) performance drifts occurred, as well as average within-trial changes in RC (C) and k (D) during these drifts. Error bars are SE.

Changes in RC and k were compatible with the patterns observed in mean values but indicated more task specificity in the central nervous system’s (CNS) choice of RC and k values. In particular, the lack of F_TOT drift in the force-feedback condition was associated with a larger shift of RC away from the hand coordinate: the one-way ANOVA with factor feedback on ΔRC showed a significant effect of Feedback [F(1,18) = 4.32, P = 0.029], and pairwise contrasts indicated that ΔRC during the force-feedback condition (−0.61 ± 0.16 cm) was significantly farther from the hand coordinate than during the moment-feedback condition. However, ΔRC during the force-feedback condition and no-feedback condition were not significantly different (P = 0.083). Similarly, the no-feedback condition could be distinguished from the conditions with feedback on force or moment by larger decrease in k: the one-way ANOVA on Δk showed a significant effect of Feedback [F(1,18) = 9.53, P < 0.01]. This occurred because Δk was larger for no-feedback (−1.43 ± 0.34 N/cm) than force-feedback or moment-feedback conditions, whereas moment- and force-feedback conditions (−1.02 ± 0.27 and −1.04 ± 0.29 N/cm, respectively) were not different from one another. These data are presented in Fig. 4, bottom.

We also investigated whether the range of RC and k values employed by subjects across trials within a condition changed during the performance drifts. The range of RC values showed an increase after feedback was turned off in the no-feedback condition only: the two-way ANOVA Feedback × Time showed a significant Feedback × Time interaction [F(2,45) = 3.96, P = 0.026]. Pairwise comparisons indicated that the range of RC values increased during the no-feedback condition and that this final range of RC values was larger than the final range of RC values during the force-feedback condition; no other significant differences were observed.

The range of k values showed a consistent decrease during performance drifts. In all conditions, the range of k values was smaller after some or all feedback was turned off compared with full visual feedback; the two-way ANOVA Feedback × Time indicated a significant main effect of time [F(1,45) = 35.98, P < 0.001] without other significant effects or interactions. These results are shown in Fig. 5.

Fig. 5.

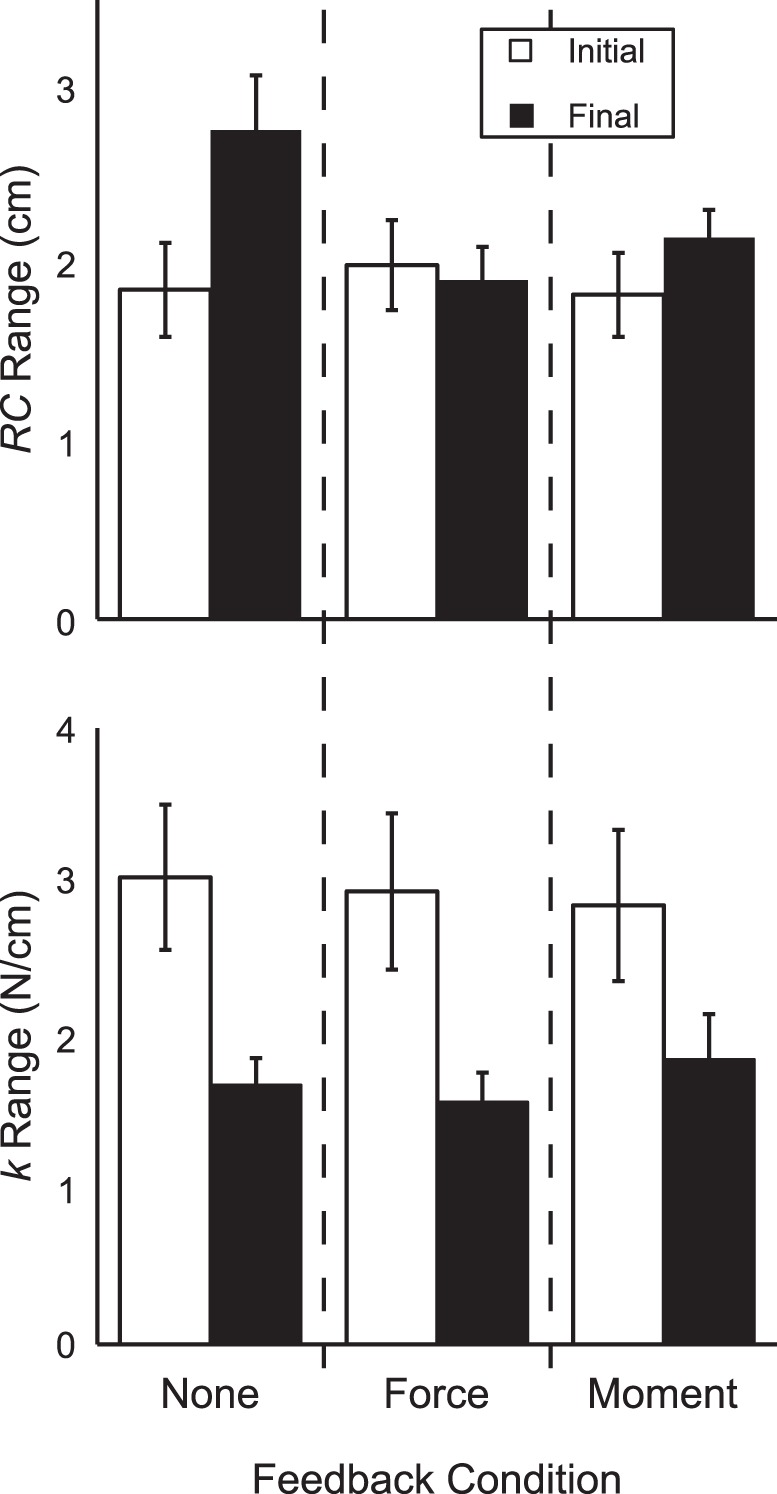
Average values of the ranges of RC (top) and k (bottom) during full visual feedback (open bars) and partial or no visual feedback (filled bars) for different feedback conditions. Error bars are SE.

After performance drifts, R_SD dropped to 2.66 ± 0.35 in the no-feedback condition and to 2.24 ± 0.21 in the moment-feedback condition. Under the force-feedback condition, R_SD remained high at 11.41 ± 1.22. The two-way ANOVA Feedback × Time confirmed a significant Feedback × Time interaction [F(2,45) = 10.17, P < 0.001]. Pairwise comparisons showed that R_SD did not differ between the two time intervals with F_TOT feedback. In contrast, R_SD was significantly lower in the moment-feedback and no-feedback conditions. It is notable, however, that R_SD ≈ 2 was significantly higher than 1; in other words, RC and k covaried to some extent across all feedback conditions, but the magnitude of this covariation differed between conditions with and without force feedback. The data presented in Fig. 6A support our second hypothesis although they suggest that F_TOT-stabilizing {RC; k} synergies are merely attenuated and do not disappear completely.

Fig. 6.

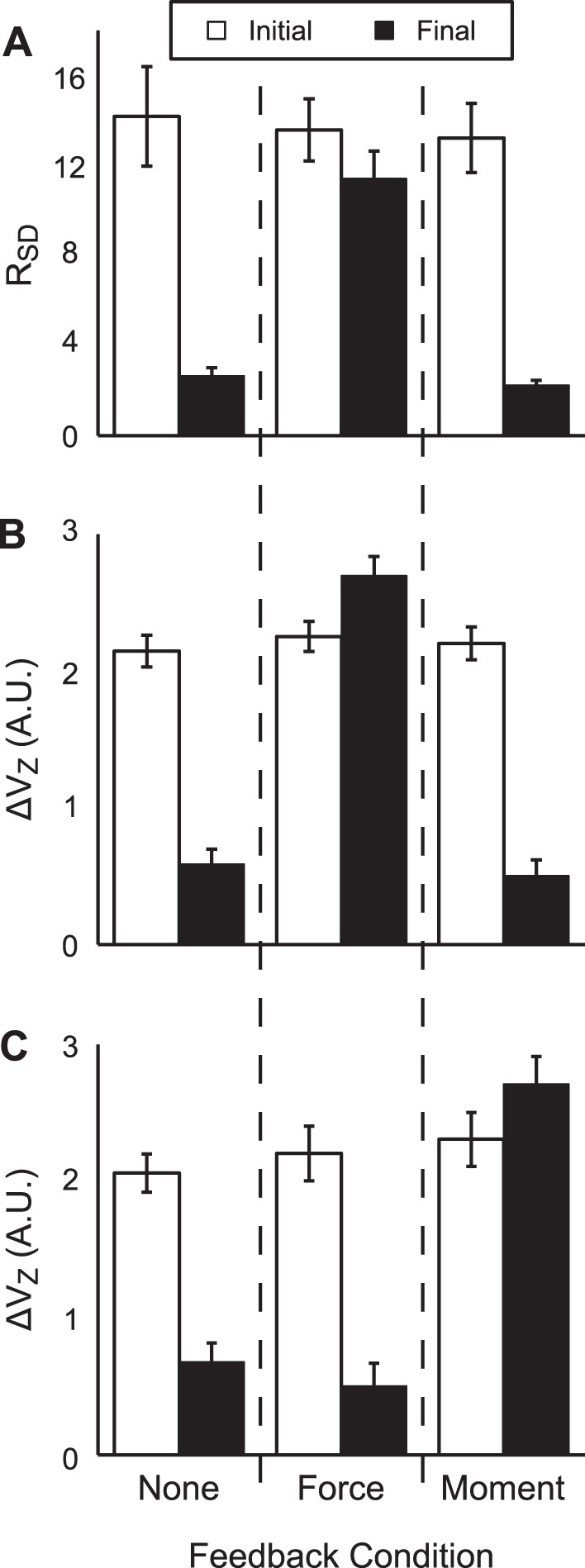
A: results of permutation analysis quantifying F_TOT-stabilizing covariation of {RC; k} values, R_SD. R_SD is the ratio of SD of force produced by permuted datasets to force produced in experimental trials. B and C: uncontrolled manifold (UCM)-based ANOVA with respect to F_TOT (B) and M_TOT (C): ΔV_Z is the z-transformed ∆V index. Error bars are SE.

UCM-Based Analysis of Variance

We analyzed the intertrial variance using the framework of the UCM hypothesis to investigate whether finger forces covaried across trials to stabilize F_TOT. When full visual feedback was available, the z-transformed index of synergy (ΔV_Z) was high (ranging from 2.25 ± 0.11 to 2.02 ± 0.12 across conditions, significantly greater than the critical value ≈0.55, P < 0.001), indicating the presence of an F_TOT-stabilizing synergy. When visual feedback on F_TOT was removed, ΔV_Z decreased to 0.50 ± 0.12 in the moment-feedback condition and to 0.59 ± 0.11 in the no-feedback condition, both not different significantly from the critical value of ΔV_Z ≈ 0.55. This means that the force-stabilizing synergy disappeared over the force drift time interval in support of our second specific hypothesis.

When visual feedback on M_TOT was removed (force-feedback condition), however, ΔV_Z increased from its initial value to 2.69 ± 0.14. The two-way ANOVA Feedback × Time showed a significant Feedback × Time interaction [F(2,45) = 76.42, P < 0.001]. Pairwise comparisons confirmed that ΔV_Z did not differ across feedback conditions under full visual feedback but decreased significantly when feedback on F_TOT was removed and increased significantly when feedback on M_TOT was removed. These results are shown in Fig. 6B.

We also investigated whether finger forces covaried across trials to stabilize M_TOT. Similar to the stabilization of F_TOT, M_TOT was stabilized only when visual feedback on M_TOT was provided. ΔV_Z values ranged from 2.28 ± 0.18 to 2.16 ± 0.16 when all visual feedback was presented (ΔV_Z greater than the critical value, P < 0.001). Under the force-feedback condition, ΔV_Z dropped to 0.50 ± 0.17, whereas, under the no-feedback condition, ΔV_Z was 0.68 ± 0.14, both not different significantly from the critical value of ΔV_Z ≈ 0.55. In contrast, ΔV_Z increased to 2.71 ± 0.2 when only feedback on M_TOT was presented. The two-way ANOVA Feedback × Time showed a significant Feedback × Time interaction [F(2,45) = 43.94, P < 0.001]. Pairwise comparisons indicated that, when all feedback was available, ΔV_Z with respect to M_TOT was similar for all conditions. However, ΔV_Z decreased significantly under the force-feedback and no-feedback conditions, whereas ΔV_Z remained unchanged for the moment-feedback condition. ΔV_Z values for force-feedback and no-feedback conditions were not significantly different from one another. These data are presented in Fig. 6C.

Comparison of UCM and Permutation Analysis Results

Visual inspection of R_SD and ΔV_Z results (Fig. 6, A and B, respectively) suggests that permutation analysis and UCM-based ANOVA produced correlated indexes. Figure 7 shows the aggregate R_SD and ΔV_Z data across all subjects (for a total of 60 data points). There is an evident logarithmic relation between these variables; the best-fit logarithmic regression (shown in Fig. 7) was ΔV_Z = 0.9414 × ln(R_SD) – 0.1043, which yielded R² = 0.78.

Fig. 7.

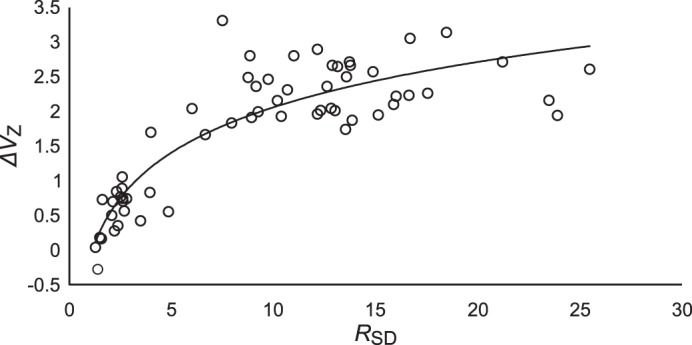
Z-transformed synergy index, ΔV_Z, plotted against R_SD for all subjects. Each subject contributes 6 values of R_SD and ΔV_Z to the plot measured before and after feedback was removed across the three feedback conditions.

To investigate this possibility further, we correlated R_SD with ΔV_Z for each subject across feedback conditions. This was done by retrieving six R_SD and ΔV_Z values for each subject (initial and final values for each feedback condition). The correlation coefficients derived from this analysis ranged from 0.99 to 0.74; 7 of the 10 subjects showed a significant correlation between R_SD and ΔV_Z (R ≥ 0.81; P < 0.05). A t-test on z-transformed correlation coefficients confirmed that, across subjects, these values were significantly greater than zero (t₉ = 6.94, P < 0.001). These results support our third specific hypothesis.

DISCUSSION

The results of our study provide support for the three specific hypotheses formulated in the Introduction, although the second hypothesis has been supported only in part. Our first hypothesis predicted that strong {RC; k} synergies and strong multifinger synergies would stabilize F_TOT under full visual feedback. The analysis of {RC; k} synergies (cf. Ambike et al. 2016a) supported this hypothesis by showing both intertrial data points that were fit well with hyperbolic regression lines and the much smaller F_TOT SD compared with the SD computed from surrogate datasets (cf. Müller and Sternad 2003). In addition, the UCM-based analysis of intertrial variance in the space of finger forces showed high synergy indexes for both salient variables, F_TOT and M_TOT (cf. Latash et al. 2001; Parsa et al. 2016).

Our second hypothesis predicted that removing visual feedback would lead to a drift in F_TOT to lower values (as in earlier studies, Ambike et al. 2015; Vaillancourt and Russell 2002), reflecting its loss of stability, and that this performance drift would be accompanied by disappearance of F_TOT-stabilizing synergies at both four-finger and {RC; k} levels. The UCM-based analysis of intertrial variance provides full support for this hypothesis: F_TOT drifted to lower values without visual feedback, and the high synergy index values observed under full visual feedback dropped to levels that were not statistically distinguishable from the critical value (indicating the lack of F_TOT-stabilizing synergy). The results of {RC; k} synergy analysis also confirmed a drop in the synergy index, but this drop led only to attenuation of the synergy, not its complete disappearance. These results may be seen as mostly confirmatory of the cited earlier observations and extending them to a wider range of tasks (combined F_TOT and M_TOT production).

Our third hypothesis was that the indexes of the two types of synergies (interfinger and {RC; k}) would correlate with each other. This hypothesis was supported showing a nonlinear (close to logarithmic) relation between the two indexes (Fig. 7). Overall, these results provide support for our main idea that {RC; k} synergies ensure stability of the hand action in force production tasks, and, when stability is challenged (e.g., by removing visual feedback), the synergies get weaker and may even disappear.

With respect to our exploratory goal, the results showed no benefit of having visual feedback on one of the task-specific variables (F_TOT or M_TOT) for organizing synergies stabilizing the other variable. In fact, most of the effects on the drift magnitudes and synergy indexes for one of the two task-specific variables were similar between the no-feedback condition and a condition with feedback on the other variable. To the extent that differences in stability of one variable were altered because of stabilization of the other variable, feedback on one variable appeared to decrease the stability of the other variable. In the following sections, we discuss the implications of these observations for synergic control of action stability, synergies in different spaces of elemental variables, and the role of visual feedback for stability of salient variables.

Hierarchical Control with Referent Spatial Coordinates

A primary advantage of the account of the neural control of voluntary actions as the specification of time-varying RCs is its foundation in physics and physiology of the system (reviewed in Feldman 2015; Latash 2017). This approach avoids problems associated with specification of muscle forces and joint torques assumed in alternative approaches (e.g., Hinder and Milner 2003; reviewed in Shadmehr and Wise 2005). In contrast, it relies on the natural coupling between kinetic and kinematic variables, e.g., muscle force and length, which may be viewed as a biological law of nature parametrized by the CNS using RCs, i.e., coordinates for an effector when it does not produce force against the environment. When an effector reaches its RC (λ for a single muscle, Feldman 1986), it reaches a state of minimal potential energy. When the effector’s actual coordinate differs from its RC, it displays motion toward the RC, if this motion is unimpeded, or produces force on the environment if the movement is blocked. Control with parameters such as RC avoids problems associated with neural specification of forces and/or muscle activation levels (which is impossible, see Bernstein 1935, 1967) and allows action stability to be ensured by the negative feedback effects (reviewed in Feldman 2015).

According to this theory, any natural movement is associated with setting a time profile of a task-level low-dimensional set of referent coordinates (RC_TASK) by the CNS. From the task level, a sequence of neural few-to-many mappings leads to lower-level RCs for individual effectors down to λ values for all of the involved muscles. Because every joint is controlled by at least two muscles, joint-level RCs can be conceptualized as two commands, reciprocal (r) and coactivation (c) (Feldman 1980, 1986). The r-command effectively shifts RC for the joint, whereas the c-command reflects common spatial activation zones of muscles with antagonistic actions leading to changes in the joint apparent stiffness (Latash and Gottlieb 1991). For example, for the hand involved in a force-production task, the r- and c-commands define its referent coordinate and apparent stiffness, RC and k.

The presence of at least two commands for isometric force production makes the task abundant and affords numerous solutions. All ecological tasks have numerous solutions, and two main approaches to understanding the performance of such tasks have dominated the field of motor control. One of them assumes that the CNS facilitates solutions that are optimal in the sense that they minimize a cost function (reviewed in Latash and Zatsiorsky 2016; Prilutsky and Zatsiorsky 2002). The other approach assumes that no single solution is selected by the CNS, but rather the abundant space of elemental variables (e.g., RC and k) is organized by the CNS to exhibit high stability in directions that change a potentially important variable (F_TOT is the hand pressing example) and relatively low stability in directions that do not change this variable (the UCM for that variable, Schöner 1995). According to the latter approach, repeating an action multiple times is expected to show relatively high variance along the UCM. Our results show that subjects do not stick to a single solution but rather show large intertrial variability along the hyperbolic UCM (see Fig. 3 and Ambike et al. 2016a) when provided with full visual feedback. Although the spread of the data is much larger along the UCM compared with directions that deviate from the UCM, preferred ranges for the RC and k variables are observed. As such, it appears that some degree of stability exists along the UCM as well, and it has been suggested that the midpoint of the data range may indicate a preferred, possibly optimal, solution (see Park et al. 2010).

We take care to note that synergies stabilizing performance at one level of a hierarchically organized task do not guarantee the presence of synergies stabilizing performance at other levels. Previous studies of two-hand multifinger pressing tasks and one-hand prehensile tasks (Gorniak et al. 2007, 2009) have indicated that there may be a trade-off between synergies at the task level and at the effector level. In particular, the studies of two hand-pressing tasks showed two-hand synergies stabilizing performance and no within-a-hand synergies stabilizing that hand’s contribution to the task. We also analyzed synergies at two levels, between the two hypothetical control variables stabilizing F_TOT at the hand level and among the four individual finger forces. We did not observe a trade-off in the present study: synergies among the hypothetical control variables stabilizing F_TOT at the hand level coexisted with four-finger synergies at the level of finger forces. This happened despite the fact that accurate production of F_TOT does not necessitate that individual finger forces will covary to stabilize it (e.g., finger contributions could be stereotyped across trials). We should note that our levels of analysis are related to each other in a more complex way compared with the cited Gorniak studies; the issue of multiple hierarchical levels relevant to our study may be explored and discussed in the future.

Stability of Action by an Abundant System

The problem of defining a set of neural variables, RC_TASK, to match mechanical constraints imposed by the task is an example of the problem of motor redundancy (Bernstein 1967). Redundancy has classically been seen as a computational problem for the CNS, to be solved with optimization or other computational means (reviewed in Latash and Zatsiorsky 2016; Prilutsky and Zatsiorsky 2002). Relatively recently, this problem has been reformulated using the concept of abundance (Gelfand and Latash 1998; Latash 2012), which views the numerous degrees of freedom available for task performance as a useful feature that allows various performance variables to be stabilized. It has also been suggested that the presence of abundant solutions could be conducive to further refinement of actions according to additional criteria, secondary tasks (Parsa et al. 2017b; Zhang et al. 2008). This latter aspect may be the cause of the observed increase in ΔV_Z for one performance variable when feedback on the other performance variable was removed.

The concept of abundance and the idea of task-specific controllable stability of action have been developed within the UCM hypothesis (Scholz and Schöner 1999). The UCM hypothesis assumes that the controller can ensure different stability properties in different directions of an abundant space of elemental variables (those produced by individual elements) leading to a particular structure of intertrial variance. Different mechanisms have been suggested for ensuring such variance patterns, including computational schemes based on ideas of optimal feedback control (Diedrichsen et al. 2010; Todorov 2004; Todorov and Jordan 2002) and physiological schemes assuming tunable back-coupling loops (Latash et al. 2005; Martin et al. 2009). Note that the tunable back-coupling schemes assume the existence of two classes of neural variables involved in the neural control of movement. Action characteristics, seen in averaged across-trial performance variables, are defined by time profiles of RCs. Action stability is defined by the gains within the back-coupling loops; these gains can be changed independently of RCs, leading to changes in stability properties of actions without a change in their overall characteristics as seen in averaged across-trial patterns. The existence of this class of neural variables is supported by the phenomena of anticipatory synergy adjustments (a drop in the synergy index in preparation to a quick change in the performance variable, Olafsdottir et al. 2005) and by contrasting changes in performance and synergy indexes seen in neurological patients with cortical and subcortical disorders (reviewed in Latash and Huang 2015).

Although most earlier studies used the framework of the UCM hypothesis to explore elemental variables at the level of individual effectors (digits, joints, muscle groups, etc.; reviewed in Latash 2008), the idea of {RC; k} synergies shows that this framework can also be used to explore mapping from a hypothetical higher-dimensional control level to a low-dimensional effector performance space. Earlier studies have typically shown that the combined action of multiple elements can be organized to stabilize a particular mechanical variable to which all of the elements contribute. In contrast, our study (as well as some earlier studies: Ambike et al. 2016a, 2016b) shows that two variables at a control level can be organized to stabilize a single effector variable at the level of mechanical performance. This is a novel extension of the UCM framework making a step from purely mechanical movement analysis to the realm of neural variables.

For linear systems and systems that can be linearized given the natural intertrial motor variability, the UCM hypothesis offers a tool to quantify stability in different directions within abundant spaces using intertrial variance as a proxy of stability. This method cannot be applied when the UCM cannot be linearized given typical data spreads as in the essentially nonlinear {RC; k} data analyzed in the present study (cf. Fig. 3). As such, we use an alternative method that compares accuracy of performance between an actual dataset and a surrogate dataset created using similar distribution of the elemental variables deprived of their possible covariation (Müller and Sternad 2003). For the aforementioned analysis, we used the metric R_SD, which reflects the ratio of the SDs of F_TOT for the surrogate and actual datasets.

In the present study, we observed task-specific stability at two very different levels of physical organization. The hand {RC; k} pairs were observed to covary to stabilize the desired magnitude of F_TOT (Fig. 5A); in addition, the covariation of finger forces stabilized the same F_TOT (Fig. 5B). These are not trivial observations. The task prescribed low variance of performance for F_TOT, but it did not prescribe higher or lower variability in directions that did not affect F_TOT (i.e., within the corresponding UCMs). The subjects could use stereotypical combinations of both {RC; k} and individual finger forces to achieve good performance without intertrial covariations. The two groups of elemental variables could also show different covariation patterns, possibly stabilizing F_TOT at one level and not stabilizing it at the other level of analysis. Given the importance of action stability during natural behavior in the unpredictable environment, the existence of multiple neural subsystems involved in stabilizing salient mechanical variables may be a natural means of guaranteeing stability. Note that a previous study (Reschechtko et al. 2017) has implicated the existence of different parallel processes for ensuring performance and stability of performance.

Although the two-outcome indexes of synergy analysis, R_SD and ΔV, show similar statistical effects, they may not reflect the activity of a single overarching stability-guaranteeing system. For example, they may be moderated by different feedback modalities. Evidence for the dissimilar origins or mechanisms of these behaviors includes the different effects of removal of visual feedback: whereas the covariation of finger forces disappeared entirely (ΔV_Z was not significantly greater than its critical value), covariation of {RC; k} merely decreased and remained above the chance level (R_SD was always >1). Additionally, when R_SD and ΔV_Z were plotted against one another (Fig. 7), correlation between these indexes was strong within a range of values, but after R_SD exceeded ≈10, ΔV_Z plateaued. This result may also be attributable in part to two distinct clusters of data: one cluster during the initial time period during which feedback was available (high ΔV_Z) and one when feedback was removed (low ΔV_Z). It is also notable that ΔV_Z was sensitive to the multitasking requirement (when all feedback was available): after visual feedback on F_TOT or M_TOT was removed, ΔV_Z on the other variable increased; in contrast, R_SD was unaffected by the availability of visual feedback on the other task component.

Loss of Stability Without Visual Feedback

It is well known that force production tends to decrease in isometric conditions when visual feedback on force is removed. Some of the first studies showing this effect (Slifkin et al. 2000; Vaillancourt and Russell 2002) attributed it to the limited capacity of working memory. Subsequent studies using neuroimaging and electrophysiological techniques (Coombes et al. 2011; Poon et al. 2012; Vaillancourt et al. 2003) appear to further this hypothesis. A few recent studies, however, cast doubt on this interpretation by showing that subjects are able to reproduce memorized force level without a drift under conditions similar to those when continuous force production shows a significant force drop (Jo et al. 2016; Solnik et al. 2017).

In the context of control of action with RCs, this phenomenon of force drift has been explained as a natural tendency of systems to move toward states with lower potential energy (Ambike et al. 2015; Latash 2016). Such a state could be achieved when the RC for an effector coincides with its actual configuration. As such, the notion of RC back-coupling has been introduced to account for drifts in both force production and limb position (Zhou et al. 2015). This process may be viewed as a reflection of lost stability of the desired magnitude of F_TOT. Our results provide direct support for this interpretation: without visual feedback, the drift in F_TOT was accompanied by a rather dramatic drop in both synergy indexes, R_SD and ∆V. Removal of visual feedback on M_TOT led to its drift accompanied by a drop in the respective ∆V index. Note that one cannot explore M_TOT stability at the level of hand {RC; k}; this can be done at the level of {RC; k} for individual fingers, which may be addressed in a follow-up study.

Although the CNS has many sensory modalities at its disposal for the stabilization of F_TOT and M_TOT, our results indicate a primary role for visual feedback. Only visual feedback was manipulated in the current experiment, and removing this single modality resulted in complete loss of F_TOT- and M_TOT-stabilizing covariation of individual finger forces, and a decrease in the F_TOT-stabilizing covariation of {RC; k} by an order of magnitude. Note that the drifts in F_TOT and M_TOT happened despite the availability of veridical somatosensory feedback. We would like to emphasize the dramatic drift in M_TOT, which led to reversal of its direction from supination to pronation. Whereas large M_TOT drifts were reported earlier (Parsa et al. 2017a), the current study is the first to document an unintentional switch in the M_TOT direction. This switch could be secondary to the drifts in individual finger forces. Indeed, force drifts are known to be larger for higher initial force magnitudes, even when expressed in relative units, while at low forces the drift may be all but absent (Ambike et al. 2015; Vaillancourt and Russell 2002). The supination task required the relatively weak little-ring finger pair to produce a large fraction of their MVC force while the antagonist fingers (index and middle) produced much smaller forces. As a result, the ring-little fingers showed a large force decline, ultimately leading to lower absolute force magnitudes compared with the index-middle forces, resulting in the switch in the M_TOT direction. This issue may be further developed in our planned paper focusing on individual finger level {RC; k} analysis.

An earlier study exploring {RC; k} changes during the force drifts reported consistent RC drifts across subjects with relatively inconsistent drifts in k (Ambike et al. 2016b). In contrast, we observed a consistent and large decline in k while drifts in RC were modest (Fig. 4). Note that k reflects a mechanical effect of the c-command (Feldman 1980), which modulates the common spatial zone of activation of agonist-antagonist muscles and results in muscle cocontraction in isometric conditions. Hence, our results suggest that the subjects were consistently decreasing the amount of muscle cocontraction over the trial duration. These phenomena are similar to the slow drop in muscle coactivation after a quick action (reviewed in Gottlieb et al. 1989) interpreted as a consequence of a slow drift in the c-command (reviewed in Feldman 2015). In our study, this happened in the absence of any quick action, even under the force-feedback conditions, when a drop in k was accompanied by a compensatory shift in RC so that F_TOT level remained unchanged.

Muscle cocontraction has been viewed as both a positive and a negative factor in motor control. For many years, cocontraction has been viewed as a means of stiffening the joint (effector) and ensuring its higher mechanical stability (Apps et al. 2016; Hirokawa et al. 1991; Humphrey 1982). On the other hand, cocontraction has no net effect on performance and, therefore, may be considered as energetically wasteful, so a drop in k may be viewed as a drift of the system toward a more energetically efficient more optimal solution (cf. Parsa et al. 2017b). When visual feedback is available, RC is adjusted to ensure proper task performance. In the absence of visual feedback, the RC adjustment is insufficient, and a drop in F_TOT is observed. The drop in k also led to a drop in its range across trials (in contrast to the RC range, Fig. 5), which could be a consequence of a “floor effect” or a reflection of a specific neural strategy yet to be discovered.

The c-Command and Computation of RC and k

Our computations of RC and k values from experimental data assumed that the force produced by an effector could be described as a linear function of the difference between the actual and referent configuration, F = k(AC − RC). Note that individual muscle force-length characteristics are typically nonlinear, despite the linearizing action of the stretch reflex (Nichols and Houk 1976). However, when agonist and antagonist muscles show nonzero cocontraction, the overall effector (e.g., joint or fingertip) characteristic becomes closer to linear within the cocontraction range. In steady isometric conditions, muscle cocontraction is a function of the c-command, which reflects the spatial zone between the activation thresholds for agonist (λ_ag) and antagonist (λ_ant) muscle groups (Fig. 8). We assumed that the linear approximation was adequate in our study. Although we did not directly measure muscle activations, we expected significant antagonist (extensor) activity for two main reasons. First, modeling has demonstrated the necessity of extensor activity to ensure the fingers do not collapse during isometric pressing (Li et al. 2000, 2001); in addition, several studies provided experimental evidence for nonzero antagonist activation during steady-state isometric force production (Corcos et al. 1990; Ghez and Gordon 1987). Our observations of strong linear correlations between force and coordinate (R² > 0.9) used to compute {RC; k} values also suggests that the linear approximation was justified.

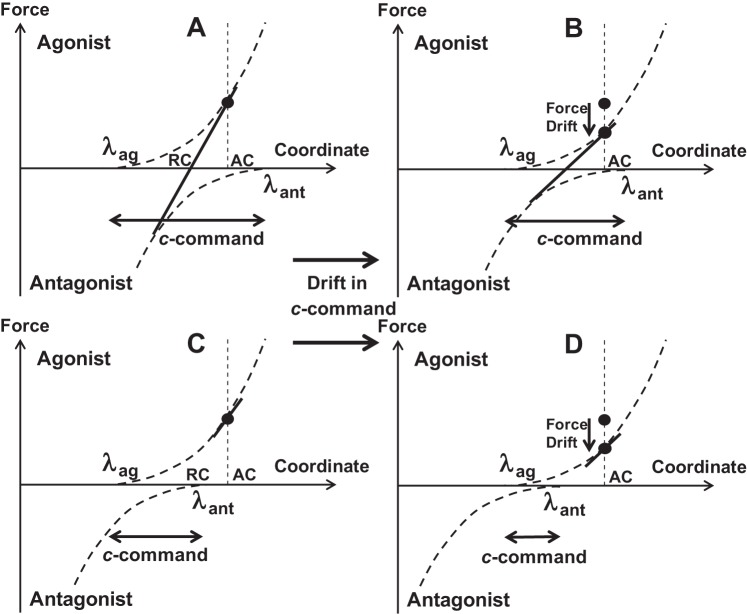
Fig. 8.

Schematic of force-coordinate characteristics for the agonist and antagonist muscle groups (curved broken lines) and for the effector (fingertip, straight solid lines). The neural control of the system may be described with changes in activation thresholds for the opposing muscle groups [activation thresholds for agonist (λ_ag) and antagonist (λ_ant)]. The c-command defines the spatial range where both muscle groups are active. Force production in isometric conditions [actual coordinate (AC)] is shown with black filled circles. If the c-command is large (A), both muscles are active, and the force-coordinate characteristic is close to linear. If the c-command is small (C), only agonist muscles are active, and the force-coordinate characteristic is nonlinear. In both cases, a drift in the c-command (B and D) results in a force drop, a drop in the slope (k) of the tangential line to the force-coordinate characteristic, with or without a change in the referent effector coordinate (RC, midpoint between λ_ag and λ_ant).

As illustrated in Fig. 8, if the overlap of λ_ag and λ_ant is sufficiently large (A), the force-coordinate characteristic is relatively linear in the range of agonist-antagonist cocontraction despite the strongly nonlinear individual characteristics. Next, a drift in the c-command can be expected to lead to a drop in the apparent stiffness k (the slope of the overall characteristic) as shown in Fig. 8B, resulting in a force drop. To avoid the force drop, a compensatory change in RC is needed (as shown in Fig. 3, middle).

If, however, in the initial conditions, the c-command is smaller such that there is no antagonist cocontraction (Fig. 8C), the force-coordinate characteristic is likely to be nonlinear. Even if local analysis produces large R² values for linear regression (shown with the short straight line), extrapolation of this line may produce erroneous estimates of RC. After a drift in the c-command (Fig. 8D), a similar effect is expected, i.e., a drop in force associated with a drop in the estimated k with or without a shift in RC. As mentioned in the opening paragraph of this section, we believe that published data support the assumption that the c-command in our experiment was large enough to produce significant antagonist cocontraction. In the absence of electromyographic confirmation, this assumption remains a potential weakness of the study, which we hope to fix in the future.

Concluding Comments

The present study is the first to show a potential relation between force-stabilizing covariation patterns in the space of mechanical effectors (finger forces) and in that of hypothetical control variables (RC and k values for the hand). We found that both {RC; k} values at the hand level and individual finger forces covaried to stabilize F_TOT. Furthermore, these patterns of covariation were coupled to performance drifts elicited by the removal of visual feedback on performance variables: drifts in performance were accompanied by the interfinger covariation metric ΔV_Z decreasing to its critical value (indicating that no F_TOT-stabilizing and M_TOT-stabilizing synergy was present) and R_SD decreasing by an order of magnitude (indicating much less covariation of RC and k values to stabilize F_TOT).

A few potential problems remain related to the method of estimating RC and k. One of them, related to linearization of the force-length characteristic, has been discussed in the previous subsection. Another one is the fact that both RC and k could be drifting during the second episode of finger lifting by the inverse piano. This caveat must be acknowledged. We would like to note, however, that the exponential time constants of force drift in such tasks have been reported to be within the range from 10 to 20 s (Ambike et al. 2015), whereas we estimated RC and k over 0.5-s intervals. These short intervals were not expected to be associated with significant drifts in RC and k. Furthermore, the first episode of finger lifting within each trial was performed under visual feedback, when no force drift took place, and data recorded during the two episodes showed similar goodness of fit with linear regressions (R² > 0.9).

GRANTS

This work was supported by National Institute of Neurological and Communicative Disorders and Stroke Grant R21-NS95873 to M. L. Latash.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.R. and M.L.L. conceived and designed research; S.R. performed experiments; S.R. and M.L.L. analyzed data; S.R. and M.L.L. interpreted results of experiments; S.R. and M.L.L. prepared figures; S.R. and M.L.L. drafted manuscript; S.R. and M.L.L. edited and revised manuscript; S.R. and M.L.L. approved final version of manuscript.