The divisive normalization model of V1 neurons: a comprehensive comparison of physiological data and model predictions

Abstract

The physiological responses of simple and complex cells in the primary visual cortex (V1) have been studied extensively and modeled at different levels. At the functional level, the divisive normalization model (DNM; Heeger DJ. Vis Neurosci 9: 181–197, 1992) has accounted for a wide range of single-cell recordings in terms of a combination of linear filtering, nonlinear rectification, and divisive normalization. We propose standardizing the formulation of the DNM and implementing it in software that takes static grayscale images as inputs and produces firing rate responses as outputs. We also review a comprehensive suite of 30 empirical phenomena and report a series of simulation experiments that qualitatively replicate dozens of key experiments with a standard parameter set consistent with physiological measurements. This systematic approach identifies novel falsifiable predictions of the DNM. We show how the model simultaneously satisfies the conflicting desiderata of flexibility and falsifiability. Our key idea is that, while adjustable parameters are needed to accommodate the diversity across neurons, they must be fixed for a given individual neuron. This requirement introduces falsifiable constraints when this single neuron is probed with multiple stimuli. We also present mathematical analyses and simulation experiments that explicate some of these constraints.

the primary visual cortex (V1) is the most studied cortical area. Beginning with the seminal studies of Hubel and Wiesel (1959, 1962), V1 neurons have been studied extensively in physiology for half a century (see Albrecht et al. 2003; Andoni et al. 2013; Angelucci and Shushruth 2013; Ferster and Miller 2000; Fitzpatrick 2000; Hubel and Wiesel 1977; Lamme 2003; Lennie and Movshon 2005 for reviews). A wide range of models have been proposed to account for various properties of V1 neurons at various levels of analysis (see Albrecht et al. 2002; Carandini et al. 1999, 2005; Graham 1992, 2011; Grossberg 1988; Hubel and Wiesel 1977; Priebe and Ferster 2008; Sompolinsky and Shapley 1997 for reviews).

These models of V1 neurons can be classified into three types: functional, structural, and descriptive (Albrecht et al. 2003, p. 759; see also Herz et al. 2006). A functional model aims to characterize a variety of response properties within the context provided by a visual information-processing algorithm. For example, a simple cell can be modeled approximately as a linear filter followed by rectification (e.g., Movshon et al. 1978c). Ideally, a functional model can take the stimulus image as input and calculate the response. This makes it possible to perform simulation experiments with a functional model by presenting it with a set of stimuli and examining the predicted responses. Typically, functional models of V1 neurons involve various combinations of linear and nonlinear operations defined via algebraic equations. The goal of a functional model is to characterize the neuron’s response to a given stimulus. All models discussed in the present article are of this type. Note that a functional model can be regarded as an intermediate step toward a structural model for better understanding of the neuron’s mechanism (Marr 1982, chapter 1.2).

A structural model aims to characterize some aspect of the biophysical and/or biochemical processing mechanisms in the early visual system. Typically, it is formulated either as an algorithm representing a neural circuit or as a system of differential equations (see Ben-Yishai et al. 1995; Brosch and Neumann 2014; Chance and Abbott 2000; Ellias and Grossberg 1975; Grossberg 1988; Izhikevich 2007; Kouh and Poggio 2008; Schwabe et al. 2006; Shapley and Xing 2013; Somers et al. 1995, 1998; Zhaoping 2011 for reviews and examples). Structural models are beyond our scope here.

A descriptive model applies statistical regression techniques to summarize and regularize a set of empirical measurements with a mathematical equation. These measurements can be characterized by a small number of parameters of this equation. For example, the tuning bandwidth of a V1 neuron can be estimated by fitting a Gaussian function to its empirical tuning curve. A purely descriptive model neither provides theoretical explanation of the measurements nor infers any mechanism behind them.

Note that both functional and descriptive models involve curve-fitting to experimental data. The most important difference between the two types is that a functional model should be falsifiable as a scientific theory (Popper 1959; Roberts and Pashler 2000), whereas a descriptive model does not have to be. A functional model incorporates some theoretical commitments that constrain the range of data patterns that it can predict and/or account for. The predictions must follow from the theoretical commitments of the model and be testable experimentally.

The present review is based on a functional model of the static (steady state) properties of simple and complex cells in V1. The temporal dynamics of the neuronal response is beyond our present scope. (See, e.g., Albrecht et al. 2002, 2003; Heeger 1993 for reviews on temporal dynamics; we revisit this issue in General Discussion.) Most experiments discussed below used prolonged (steady state) stimuli such as drifting and/or flickering gratings with relatively long durations (e.g., a few seconds). Under these conditions, the transient response triggered by the stimulus onset can be bracketed out of the analysis to a good approximation, and the most important dependent variable is the steady-state firing rate of the neuron as measured by a poststimulus time histogram. The models discussed below are functional models that take a single grayscale image as input and produce a single number for each neuron simulated that we take to be “the response” to a given stimulus.

An adequate functional model of the V1 neurons should satisfy the conflicting desiderata of falsifiability (Popper 1959) and flexibility at the same time. On one hand, the model needs to be flexible enough to accommodate the variety of V1 neurons with some adjustable parameters. The data reviewed below were recorded from neurons from different species (e.g., cats, New/Old World monkeys, rabbits, rodents, and ferrets) under different conditions (e.g., anesthesia vs. alertness) and different experimental protocols. Furthermore, there is substantial variability within a sample of neurons recorded from a single animal under constant conditions. Clearly, adjustable parameters are needed to accommodate this diversity. It should also be noted that it is easy to make the model more flexible by adding more parameters. On the other hand, if the model becomes so flexible as to be able to fit any response pattern, it would become devoid of all empirical content (Roberts and Pashler 2000). Whereas it might still be useful as a descriptive formalism for a succinct characterization of properties such as tuning bandwidths, such a model would not constrain our theories about the functional organization of the visual system. To have empirical content, the model must be restrictive enough to rule out at least some possible data patterns.

There is “a fairly well agreed on standard model of V1 response properties,” usually involving a combination of linear filtering, half-wave rectification and exponentiation, and response normalization (Carandini et al. 2005, p. 10590). Whereas it is still unknown how well this divisive normalization model (DNM) can account for the full complexity of the V1 population code for time-varying naturalistic stimuli (Olshausen and Field 2005; but see Rust and Movshon 2005), it is consistent with much of the available data to a good approximation. The DNM was developed over a number of years, during which it combined experimental (e.g., De Valois et al. 1982a; Hubel and Wiesel 1959; Movshon et al. 1978c) and theoretical (e.g., Grossberg 1973) contributions, as well as interdisciplinary explorations of the correspondence between the physiological data and the mathematical formalisms (e.g., Albrecht and Geisler 1991; Carandini and Heeger 1994; Heeger 1992b). Versions of this model have been applied to a broad spectrum of data ranging from single-cell recordings (see, e.g., Albrecht et al. 2003; Carandini and Heeger 2011; Heeger 1992b for reviews) to multielectrode population recordings (e.g., Busse et al. 2009; Goris et al. 2009; Ruff et al. 2016), EEG brain imaging data (e.g., Candy et al. 2001; Zhang et al. 2008), fMRI brain imaging data (e.g., Boynton et al. 1999; Brouwer and Heeger 2011; Moradi and Heeger 2009), and psychophysical data (e.g., Boynton and Foley 1999; Foley and Chen 1999, 1997; Itti et al. 2000; Malo and Laparra 2010; Meese et al. 2007, 2009; Meese and Holmes 2002; Neri 2011, 2015; Olzak and Thomas 1999, 2003; To et al. 2010).

Unfortunately, there is no standard formulation of the DNM as a functional model. Various authors and publications customized the DNM by using different mathematical expressions and idiosyncratic parameterizations. There is a clear family resemblance across these model variants—the verbal description quoted above summarizes the core DNM ideas—but allowing such customization makes the DNM more flexible and thereby weaker as a scientific theory. The customization introduces hidden degrees of freedom because it involves a choice among a variety of formulations. Also, many of the published DNM variants are formulated in terms of variables that characterize the stimuli in particular experiments (e.g., the luminance contrasts of two gratings in two spatially separate regions). This practice makes those DNM variants hard to generalize to novel stimuli.¹

Here, we propose a standard formulation of the DNM as a functional model that takes images as inputs, test its validity with respect to a comprehensive suite of empirical phenomena (listed in Table 1), and identify falsifiable predictions of the DNM based on mathematical analysis of the standard formulation. The key idea that allows the identification of falsifiable predictions is this: While the model parameters may have to be adjusted flexibly to accommodate the diversity across neurons, they must be fixed for a given individual neuron. This introduces falsifiable constraints when this single neuron is probed with a judiciously chosen suite of stimuli. The standardization also allows us to unify and consolidate a large amount (though certainly not all) of DNM-related research scattered across dozens of journal articles spanning decades of experimental and theoretical development.

Table 1.

Phenomena accounted for by divisive normalization model (Eq. 15) in simulation experiments

Number	Phenomenon	Figure
1	Size tuning: The RF has limited spatial extent.	5
2	The measured RF diameter increases as the grating contrast decreases.	6
3	The measured RF diameter decreases for nonpreferred orientations.	7
4	The measured RF diameter decreases for nonpreferred spatial frequencies.	8
5	The response decreases monotonically as the hole in an annular grating increases.	9
6	The response relationship with hole size is nearly invariant to stimulus contrast.	9
7	The CF has a characteristic sigmoidal shape.	3
8	Supersaturation effect: The CF can slope downward at very high contrasts.	10
9	The CF is affected by visual noise added to the grating stimulus.	11
10	The CF is scaled down for gratings with nonpreferred orientations.	3
11	The CF is scaled down for gratings with nonpreferred spatial frequencies.	3
12	The CF is affected by the size of the grating patch.	12
13	Orientation tuning: The response is maximal for the preferred orientation.	2
14	Spatial-frequency tuning: The response is maximal for the preferred frequency.	2
15	Orientation bandwidths become narrower as the size of grating patch increases.	13
16	Frequency bandwidths become narrower as the size of grating patch increases.	13
17	Orientation bandwidths tend to be invariant with respect to the grating contrast.	14
18	Frequency bandwidths tend to become narrower as the contrast decreases.	14
19	The spatial-frequency tuning function has a secondary peak for square gratings.	15
20	The CF shifts leftward for square gratings compared with sinusoidal ones.	15
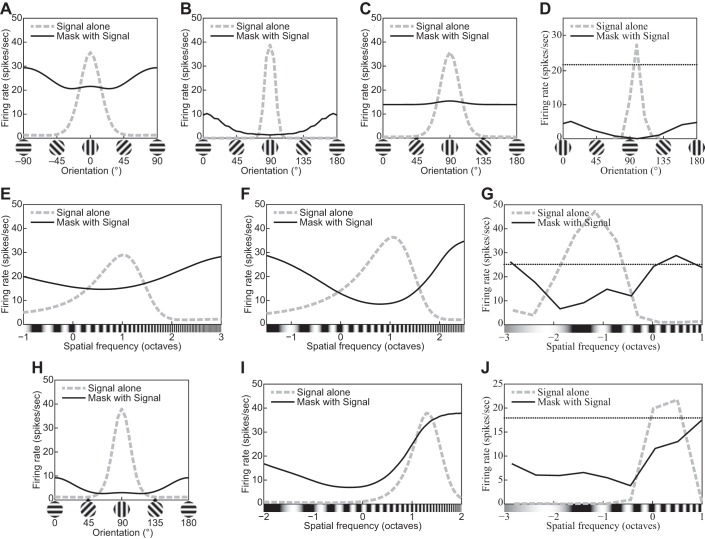
21	Cross-orientation suppression: orientation tuning of the mask grating	16
22	Cross-orientation suppression: spatial-frequency tuning of the mask grating	16
23	Cross-orientation suppression: The mask contrast affects the CF.	18
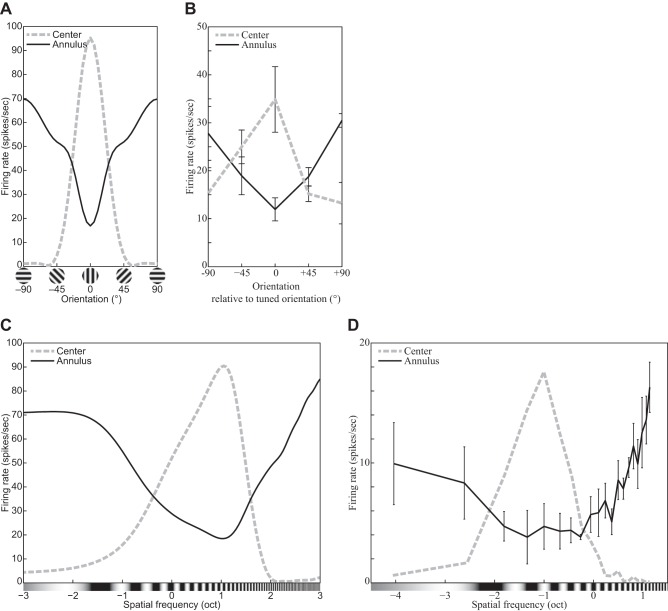
24	Surround suppression: orientation tuning of the surrounding grating	19
25	Surround suppression: spatial-frequency tuning of the surrounding grating	19
26	Surround suppression: The contrast of an annular grating affects the CF.	20
27	Surround suppression: The orientation of an annular grating affects the CF.	21
28	Mapping the RF of a simple cell with a light spot	23
29	Mapping the RF of a simple cell with the reverse correlation method	24
30	Comparison of the mapped RF of a simple cell and its spatial-frequency tuning	25

RF, receptive field, CF, contrast response function.

This article is organized around a series of figures with side-by-side comparisons between data patterns illustrating various properties of real V1 neurons and the corresponding patterns simulated with the DNM. On the basis of side-by-side examination of dozens of phenomena, we identify relationships between certain model parameters and the phenomena. These relationships in turn generate falsifiable predictions. This type of analysis focuses on the qualitative patterns that can be produced by a model under a given parameterization (Pitt et al. 2006). It contrasts with the typical approach in the experimental literature where, with some notable exceptions (e.g., Tadmor and Tolhurst 1989), one or more models were compared in terms of their quantitative fits to physiological data pertaining to a single phenomenon.

Our review is of potential interest to several groups of readers. First, readers interested in the neurophysiology of simple and complex cells in V1 will find a systematic series of figures with representative data from classic experiments, as well as their interpretation under the DNM. Single-cell data published over a 50-year span were digitized from select figures in the original reports and are replotted here. Second, readers interested in functional modeling of the early visual system will find systematic exposition and motivation of the DNM, as well as its empirical grounding. Third, expert modelers of the early visual system will find mathematical derivations and simulation experiments that identify novel falsifiable predictions of the DNM. Last but not least, modelers who need an off-the-shelf front end to a larger model (e.g., Jacobs 2009; Petrov et al. 2005, 2006) will find a general-purpose parameterization of the DNM and a standard parameter set (Table 2) that is consistent with almost all phenomena listed in Table 1. The model was implemented as a software program for MATLAB (The MathWorks 2015). This software takes a static grayscale image as input and produces a matrix of firing rate responses for a population of DNM neurons centered on a single retinal location and tuned for a range of orientations and spatial frequencies.

Table 2.

Parameters of divisive normalization model (Eq. 15)

Parameter	Equation	Value
Free parameters
Firing rate, spikes/s	15	M = 40
Semisaturation contrast (dimensionless)	15	α = 0.1
Baseline (a.k.a. maintained discharge) (dimensionless)	15	β = 0.02
Stimulus drive exponent	15	nn = 2
Suppressive drive exponent	15	nd = 2
Orientation FWHH bandwidth of the Gabor WF, °	2, 3	hθ = 40
Spatial-frequency FWHH bandwidth of the Gabor WF, oct	2, 4	hf = 1.5
FWHH of the radial spatial-pooling kernel, cyc	19	hR = 2.0
Orientation pooling FWHH bandwidth, °	21, 22	hΘ = 60
Spatial-frequency pooling FWHH bandwidth, oct	20	hF = 2.0
Constants calculated from the free parameters
FWHH size of the Gabor WF, perpendicular to grating, °/cyc	2, 4	$h_{\stackrel{⌣}{x}}$ ≈0.92
FWHH size of the Gabor WF, parallel to grating, °/cyc	2, 3	$h_{\stackrel{⌣}{y}}$ ≈1.26
Concentration parameter of the orientation pooling kernel	21, 22	κΘ ≈1.22
Stimulus drive calibration constant (implementation dependent)	15, 16	kn = 0.25
Suppressive drive calibration constant (implementation dependent)	15, 16	kd ≈ 0.011
Implementation specifications chosen a priori
No. of orientation channels, evenly spaced around the circle	18	NΘ = 12
No. of (main + auxiliary) spatial-frequency channels	18	NF = 5 + 2
Spacing of the frequency channels, oct		δF = 0.5
Preferred orientation of the stimulus drive, °	16	Θ* = 0
Preferred frequency of the stimulus drive, cyc/°	16	F* = 2.0
Size of a “large” (128 × 128) input image, °	5	5.76
Size of a “small” (64 × 64) input image, °	5	2.88

The values for the 10 free parameters are compatible with typical neurophysiological measurements of representative simple and complex cells. Moreover, the model under this standard parameterization accounts qualitatively for the phenomena in Table 1. All simulation results in this article were produced with these parameter values unless explicitly stated otherwise. FWHH, full width at half height; WF, weighting function; cyc, wave cycle; oct, octave = log[cyc/°].

The rest of the article is organized as follows: Models presents the DNM, its proposed parameterization, and computational implementation. Simulation Experiments reviews over two dozen empirical phenomena and interprets them through the lens of the DNM. It also reports mathematical analyses, simulation results, and some novel predictions. Finally, there is a General Discussion followed by mathematical appendices.

Models

The essential components of the divisive normalization model (DNM) are the linear filters, the static nonlinearities, and divisive normalization. These components are described below, but, before this is done, we must acknowledge an important preprocessing step, namely, light adaptation (or luminance gain control). The adaptation is primarily accomplished in the retina (Shapley et al. 1993; Shapley and Enroth-Cugell 1984; see also Virsu et al. 1977; Virsu and Lee 1983). It matches the limited dynamic range of the neurons to the locally prevalent luminance. The DNM does not model this light adaptation explicitly. It simply assumes it has been incorporated into the encoding of the input images. This assumption is justified in situations when the stimuli are embedded in a large uniform gray background and when the visual system has adapted to the baseline luminance level L_b. The input to the model is a matrix I(x, y) of local contrast around this fixed baseline:

$$I\left(x,y\right)=\left[L\left(x,y\right)-L_{\text{b}}\right]/L_{\text{b}}$$ (1)

where L(x, y) is the luminance at coordinates x and y. In this notation, a sinusoidal grating with contrast c modulates between I_min = −c and I_max = +c and has zero mean. The maximal possible contrast (c_max = 1) of a grating is attained when the lowest intensity is zero and the highest intensity is twice the mean.

Linear rectification model of simple cells and energy model of complex cells.

The majority of V1 neurons respond selectively to a variety of stimulus features including position, size, orientation, and spatial frequency (e.g., De Valois et al. 1982a; Hubel and Wiesel 1959, 1968; Pollen and Ronner 1982; Watkins and Berkley 1974). A typical V1 neuron responds to stimulation within a circumscribed region called the (classical) receptive field (RF). Different neurons have RFs centered on different positions, and V1, as a whole, forms a topographic map (e.g., Schwartz et al. 1985). This population code is beyond our scope. We are modeling a representative individual neuron. Note that in this article the origin of the xy coordinate system is placed conventionally at the center of the neuron’s RF.

Hubel and Wiesel (1959, 1962) introduced the influential distinction between simple and complex cells in V1. According to their original definition (Hubel and Wiesel 1962), simple cells have four characteristic properties: 1) distinct excitatory (bright-excitatory) and inhibitory (dark-excitatory)² subregions within the RF; 2) spatial summation within a given subregion; 3) mutual antagonism between subregions; and 4) responses to novel stimuli can be predicted to a good approximation on the basis of the spatial arrangement of the subregions. These four properties would be expected from a linear spatio-temporal filter, and they would motivate the application of linear systems theory (e.g., Lathi 2005) to the study of spatial vision (e.g., De Valois and De Valois 1988; Graham 1989; Maffei and Fiorentini 1973; Shapley and Lennie 1985). Quantitative tests have identified a subpopulation of V1 neurons that exhibit these linear properties to a good approximation (e.g., Andrews and Pollen 1979; Movshon et al. 1978c; Pollen and Ronner 1982; see Albrecht et al. 2003 for review). This linear systems approach is reinforced by a rich body of psychophysical data (e.g., Campbell and Robson 1968; Cornsweet 1970) and theory that supports the existence of channels selective for orientation and spatial frequency (De Valois and De Valois 1988; Graham 1989). However, two caveats should be kept in mind here (Albrecht et al. 2003). First, the match between the measured single-cell responses and the linear systems predictions is always approximate, never exact, because they are systematic nonlinearities (discussed below). Second, the simple vs. complex cell distinction probably denotes the end points of a continuum rather than a sharp dichotomy (see The Stimulus Drive for a discussion). These caveats notwithstanding, this distinction has proven its theoretical utility and is widely used in V1 models.

The spatial layout of simple-cell RFs has been mapped out with local stimulus probes (e.g., light and dark spots and bars) and the reverse correlation method (see receptive fields of simple cells). The RF of a typical simple cell consists of alternating bright- and dark-excitatory subregions (De Valois et al. 1982a; Hubel and Wiesel 1962; Maffei and Fiorentini 1973; Sengpiel et al. 1997). This two-dimensional (2D) spatial pattern can be approximated well by the Gabor function in Eq. 2 (Daugman 1980, 1985; Field and Tolhurst 1986; Jones and Palmer 1987a, 1987b; Kulikowski et al. 1982; Marĉelja 1980; Ringach 2002). Mathematically, a Gabor function G_XYFΘΦ(x,y) is a product of a Gaussian envelope and a sinusoidal grating:

$$|\begin{array}{l}{G}_{XYF\Theta \Phi }\left(x,y\right)=\text{exp}\left[-4\text{ln}2\left(\frac{{\stackrel{⌣}{x}}^2}{h_{\stackrel{⌣}{x}}^2}+\frac{{\stackrel{⌣}{y}}^2}{h_{\stackrel{⌣}{y}}^2}\right)\right]\text{cos}\left(F\stackrel{⌣}{x}-\Phi \right)\\ \stackrel{⌣}{x}=\left(y-Y\right)\text{sin}\Theta +\left(x-X\right)\text{cos}\Theta \\ \stackrel{⌣}{y}=\left(y-Y\right)\text{cos}\Theta -\left(x-X\right)\text{sin}\Theta \end{array}$$ (2)

where x and y (degrees of visual angle, °) are positions across the image and X and Y define the center of the RF.³ The grating has spatial⁴ frequency F (cycles/°, cpd), phase Φ, and orientation Θ. The parameters $h_{\stackrel{⌣}{x}}$ and $h_{\stackrel{⌣}{y}}$ control the full width at half height (FWHH) of the Gaussian envelope along the orthogonal and parallel directions as shown in Fig. 1. See appendix a for more details.

Fig. 1.

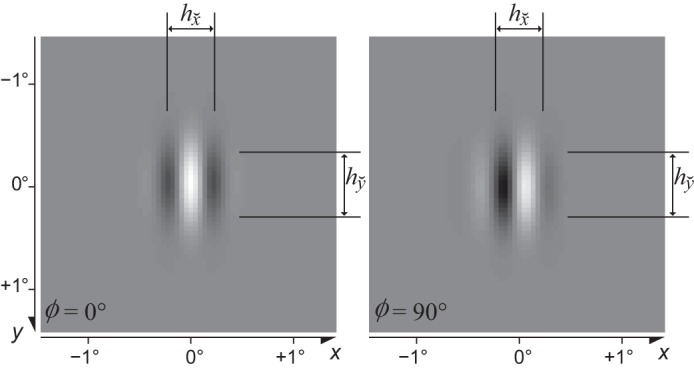
Examples of Gabor patches with phase Φ = 0° and Φ = 90°, vertical orientation (Θ = 0°), and spatial frequency F = 2 cpd (Eq. 2). The parameters $h_{\breve{x}}$ and $h_{\breve{y}}$ control the full width at half height (FWHH) of the Gaussian envelope along the directions that are perpendicular and parallel to the grating, respectively.

The alternating arrangement of bright- and dark-excitatory RF regions makes the simple cell selectively responsive (or tuned) to the orientation and frequency of the stimuli. It is very informative to probe the neuron with a battery of sinusoidal gratings covering a range of orientations and frequencies. Such probing in the frequency (Fourier) domain complements the local probing in the space domain for simple cells and is necessary when studying complex cells because their RFs cannot be segmented into bright- and dark-excitatory subregions by means of local probes. In this study, we consider only excitatory neurons in V1 that are tuned for both orientation and spatial frequency (e.g., De Valois et al. 1982a; see orientation and spatial-frequency tuning for further references).⁵

Figure 2 illustrates typical empirical⁶ tuning curves with respect to orientation and spatial frequency. For example, the tuning curve in Fig. 2A has a peak at 0° and FWHH of ~45°, which measure this neuron’s preferred orientation and the orientation bandwidth, respectively.

Fig. 2.

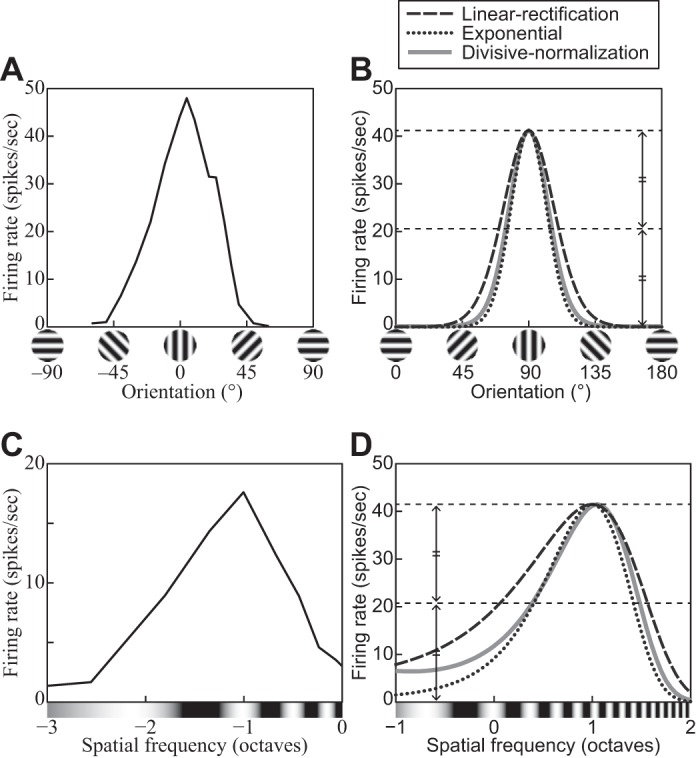
A: a representative orientation tuning curve—in this case from a V1 complex cell of an anesthetized cat. Replotted from Fig. 1 in Rose and Blakemore (1974). B: orientation tuning curves of 3 models introduced in the main text: linear rectification (Eq. 6), exponential (Eq. 11), and divisive normalization (DNM, Eq. 15). Each model neuron was probed with gratings with 100% contrast, 5.76° size, and the neuron’s preferred phase and frequency. All 3 models used the same weighting function for the linear filtering stage and DNM’s standard bandwidth parameters (see Standard parameter set). The stimulus drive exponent of the exponential model (n_Ex = n_n = 2) was set to its counterpart in the standard DNM parameter set (Table 2). C: a representative spatial-frequency tuning curve—in this case from a V1 simple cell of an anesthetized cat. Replotted from Li and Li (1994, Fig. 7C). D: spatial-frequency tuning curves of the 3 models described in C. The grating probes had 100% contrast, 5.76° size, and the neuron’s preferred phase and orientation. Dotted lines depict the full and half heights of the curves. (See phenomena 13 and 14 in Table 1.)

With a perfectly linear filter (Lathi 2005), the response profile in the space domain completely determines the tuning in the frequency domain (via the Fourier transform) and vice versa (via the inverse Fourier transform). Specifically, consider a linear filter whose weighting function is a Gabor patch in the space domain (Eq. 2). The tuning function of this filter is a bivariate Gaussian in the frequency domain (Graham 1989, p. 85). Moreover, for a given frequency F, the orientation bandwidth h_θ (in °) is inversely proportional to the size $h_{\stackrel{⌣}{y}}$ of the patch along the direction parallel to the grating:

$$h_{\stackrel{⌣}{y}}{h}_{\theta }F=\frac{720}{{\pi }^2}\text{ln}2=const$$ (3)

where the constant 720ln(2)/π² comes from the conversion from degrees to radians and from FWHH to standard deviation. See appendix a for details. The reason for this inverse relationship is intuitively clear from Fig. 1: To estimate the stimulus orientation with high precision (low h_θ), it is necessary to have a large baseline for measurement along the length of the bars. An analogous inverse relationship exists between the frequency bandwidth h_f and the perpendicular size $h_{\stackrel{⌣}{x}}$. Intuitively, to estimate the stimulus frequency with high precision (low h_f), it is necessary to be able to “count” many cycles within the width of the filter. It is more convenient to express the frequency bandwidth h_f in octaves on a log₂ scale instead of linear units. The exact relationship (derived in appendix a) is

$$h_{\stackrel{⌣}{x}}=\frac{\left(2^{h_f}+1\right)2\text{ln}2}{\left(2^{h_f}-1\right)\pi F}$$ (4)

Real neurons are never perfectly linear, but the orientation- and frequency-tuning properties of simple and complex cells are in approximate qualitative agreement with the predictions of the linear theory. “The two-dimensional tuning curves are mostly moderately elongated along a radial axis [in the Fourier plane], and extreme or amorphous shapes (e.g., sausages, amoebas) are rare” (Lennie and Movshon 2005, p. 2020). Typically, the preferred orientation does not depend much on the frequency of the test grating, and vice versa (Webster and De Valois 1985). This means that the joint orientation-by-frequency tuning curve can be modeled as the product of two orthogonal dimension-specific curves (cf. Fig. 2), which is in agreement with the linear prediction.

The output E_S of a linear filter to a stimulus image I is a scalar quantity equal to the dot product⁷ of the image with the weighting function (WF), which determines the properties of the filter. All models discussed in this article use Gabor WFs (G_XYFΘΦ; see Eq. 2), and the filter can be written as

$$E_{S:XYF\Theta \Phi }\left(I\right)={\displaystyle \int I\left(x,y\right)G_{XYF\Theta \Phi }\left(x,y\right)\text{d}x\text{d}y}$$ (5)

The center XY of the Gabor patch determines the center of the receptive field (RF) of the filter (in image space), the frequency F of the patch determines the preferred frequency of the filter (in Fourier space), and analogously for the orientation Θ and phase Φ. Of all images with a given energy (i.e., fixed variance of the intensity distribution), the output is maximized by the stimulus that exactly matches the WF (Cauchy-Schwarz inequality; Encyclopedia of Mathematics, https://www.encyclopediaofmath.org//index.php?title=Cauchy-Schwarz_inequality). In this sense, the preferred stimulus of the filter in Eq. 5 is the Gabor patch in Eq. 2. The absolute value of the output can be interpreted as the similarity between the stimulus and the preferred template, and the sign indicates whether the two are in phase or out of phase. (An image is in phase with a WF when the bright spots on the image line up with the bright-excitatory regions of the WF and the dark spots line up with the dark-excitatory regions; it is out of phase if the alignment is the other way around.)

The linear rectification model of a simple cell consists of a linear filtering stage (Eq. 5) followed by half-wave rectification (Eq. 6). The linear stage is motivated by the extracellular recordings surveyed above, as well as by intracellular recordings (e.g., Jagadeesh et al. 1993), suggesting that the fluctuations in membrane potential of simple cells around the resting potential can be modeled quantitatively in terms of linear summation of synaptic potentials. For our purposes, the output of the linear stage is referred to as the stimulus drive E_S to the simple cell. The stimulus drive can be positive or negative, but the firing rate of a real neuron is always nonnegative. This is modeled by a rectifying nonlinearity

$$R_{LN}\left(I\right)=M_{LN}\lfloor E_{S:XYF\Theta \Phi }\left(I\right)\rfloor$$ (6)

where R_LN is the response of the cell (in spikes/s, sps) and M_LN is a parameter that, under certain calibration assumptions, defines the maximum firing rate to a preferred grating. The half-wave rectification operator $\lfloor E\rfloor =\text{max}\left(0,E\right)$ passes positive values unchanged and converts negative values to zero.

The weighting function of a linear neuron coincides with its receptive field. Consequently, the terms WF and RF are sometimes used interchangeably in the literature. We keep them distinct because the corresponding referents are distinct for nonlinear models. WF is a theoretical term that is defined only with respect to a model with a linear filtering stage (Eq. 5). By contrast, the RF is defined operationally by systematically probing the responses of the (real or simulated) neuron according to some specific experimental protocol.⁸ The RF is often smaller than the WF in models involving nonlinearity and/or suppression as discussed below.

Complex cells differ from simple cells because of the absence of distinct bright- and dark-excitatory subregions in their RFs (Hubel and Wiesel 1962; Watkins and Berkley 1974). Complex cells are relatively invariant to the phase of the stimuli (De Valois et al. 1982a; Ibbotson et al. 2005; Maffei and Fiorentini 1973; Movshon et al. 1978c; Sengpiel et al. 1997). For example, they respond indiscriminately to light and dark bars, as long as the bar stands out from the gray background. They are sensitive to the stimulus orientation and spatial frequency, however, and their tuning curves are very similar to those of simple cells (De Valois et al. 1982a).

Complex cells are usually modeled in terms of several linear filters whose outputs are nonlinearly transformed and then combined (see Bair 2005; Martinez and Alonso 2003; Mechler and Ringach 2002; Spitzer and Hochstein 1988 for reviews). “A key feature of these models is that the underlying linear filters—not the later nonlinearities—determine the set of stimuli to which the neuron will respond” (Lennie and Movshon 2005, p. 2023). The most influential model of this class is the energy model (Adelson and Bergen 1985; Pollen and Ronner 1983; Spitzer and Hochstein 1985; Watson and Ahumada 1985):

$$E_{C:XYF\Theta }\left(I\right)=\sqrt{E_{S:XYF\Theta ,0\text{°}}{\left(I\right)}^2+E_{S:XYF\Theta ,90\text{°}}{\left(I\right)}^2}$$ (7)

where E_S:XYFΘ,0° and E_S:XYFΘ,90° are linear filters (Eq. 5) whose WFs have identical parameters XYFΘ but orthogonal phases. The energy model (Eq. 7) produces phase-invariant output E_C via the trigonometric identity sin²Φ + cos²Φ = sin²Φ + sin²(Φ + 90°) = 1. The firing rate R_LN(I) of the complex cell can be modeled by substituting E_C for E_S in Eq. 6 (see, e.g., Emerson et al. 1992; Heeger 1992b; Lehky et al. 2005; Szulborski and Palmer 1990 for similar formulations). It is tempting to interpret Eq. 7 as a formalization of the hierarchical feedforward simple-to-complex arrangement proposed by Hubel and Wiesel (1962). The physiological evidence, however, is more consistent with a nonhierarchical interpretation in terms of a continuum from strongly phase-sensitive (simple) cells to nearly phase-invariant (complex) cells (Bair 2005; De Valois and De Valois 1988; Martinez and Alonso 2003; Mechler and Ringach 2002). For our present purposes, it suffices to treat Eq. 7 as a mathematically convenient functional description of the stimulus drive E_C to complex cells.

As a notational convenience, it is often useful to bundle the long subscripts into a tuning preference vector

$$P_i=〈X_i{Y}_i{F}_i{\Theta }_i{\Phi }_i〉$$ (8)

where the phase Φ_i can take a special nonnumerical value to indicate a phase-invariant (complex) cell. In this notation, an image I induces stimulus drive $E_{{\text{P}}_i}\left(I\right)$ to a neuron with index i and preferences P_i:

$$E_{P_i}\left(I\right)=\{\begin{array}{l}{E}_{S:X_i{Y}_i{F}_i{\Theta }_i{\Phi }_i}\left(I\right)\text{\hspace{1em}for\hspace{0.17em}a\hspace{0.17em}simple\hspace{0.17em}cell},\\ E_{C:X_i{Y}_i{F}_i{\Theta }_i}\left(I\right)\text{\hspace{1em}for\hspace{0.17em}a\hspace{0.17em}complex\hspace{0.17em}cell}\end{array}$$ (9)

Note that $E_{{\text{P}}_i}$ is a linear operator for the simple cell. That is, for a fixed $i,\hspace{0.17em}{E}_{{\text{P}}_i}\left(I\prime +I″\right)=E_{{\text{P}}_i}(I\prime )+E_{{\text{P}}_i}(I″)$ for any pair of images I′ and I″ and $E_{{\mathbf{P}}_i}\left(cI\right)=c{E}_{{\mathbf{P}}_i}\left(I\right)$ for any number c ≥ 0. The latter equality also holds for the complex cell.

The linear rectification model $R_{LN}\left(I\right)=M_{LN}\lfloor E_{{\text{P}}_i}\left(I\right)\rfloor$ provides a quantitative account of the selectivity of V1 neurons’ responses to bars, edges, and gratings. Moreover, it provides “a credible account of the responses to a variety of more complicated targets, including checkerboards (De Valois et al. 1979), random dot textures and Glass patterns (Smith et al. 2002)” (Rust and Movshon 2005, p. 1647). It dominated the field until the mid-1980s and set the stage for subsequent research that uncovered systematic departures from linearity. Various types of nonlinear operations have been considered, including thresholding

$$R_{\text{Th}}\left(I\right)=M_{Th}\lfloor {\beta }_{Th}+E_{P_i}\left(I\right)\rfloor ,$$ (10)

exponentiation

$$R_{Ex}\left(I\right)=M_{Ex}{\lfloor E_{P_i}\left(I\right)\rfloor }^{n_{Ex}},$$ (11)

and hyperbolic ratio transformation (Eq. 12 in Hyperbolic ratio model), where M_Th, β_Th, M_Ex, and n_Ex are free parameters and $\lfloor \cdot \rfloor$ is the rectification operator from Eq. 6. Note that these nonlinear operations are not mutually exclusive and the divisive normalization model incorporates them into Eq. 15 below (following Heeger 1992b). The hyperbolic ratio model is discussed next, and exponentiation and thresholding is discussed in Summary and discussion.

Hyperbolic ratio model.

The contrast response function (CF⁹) describes how a neuron’s response depends on the contrast of the stimulus. Consider a family of stimuli {cI_T}_c∈[0,1] based on the same template image I_T but varying in contrast c. We assume throughout this section that the template I_T is normalized so that its contrast is 1.0 (cf. Eq. 1). The CFs of neurons have been measured for various templates, cortical areas, species, and conditions (e.g., Albrecht et al. 2002; Albrecht and Geisler 1991; Albrecht and Hamilton 1982; Carandini et al. 1997; Dean 1981; Derrington and Lennie 1984; Geisler and Albrecht 1997; Li and Creutzfeldt 1984; Sclar et al. 1990; see Albrecht et al. 2003; Carandini et al. 1999; Graham 2011; Heeger 1992a; Lennie and Movshon 2005 for reviews). Furthermore, as Albrecht et al. (2002) pointed out, “although there is a great deal of heterogeneity from cell to cell, it is possible to provide a description of the basic properties of the contrast response function that applies to the overwhelming majority of neurons: As the contrast increases from zero, the response increases in an accelerating fashion, remains dynamic over some limited range of contrasts, and then saturates” (p. 888). Figure 3 illustrates the characteristic sigmoidal shape of a typical CF.

Fig. 3.

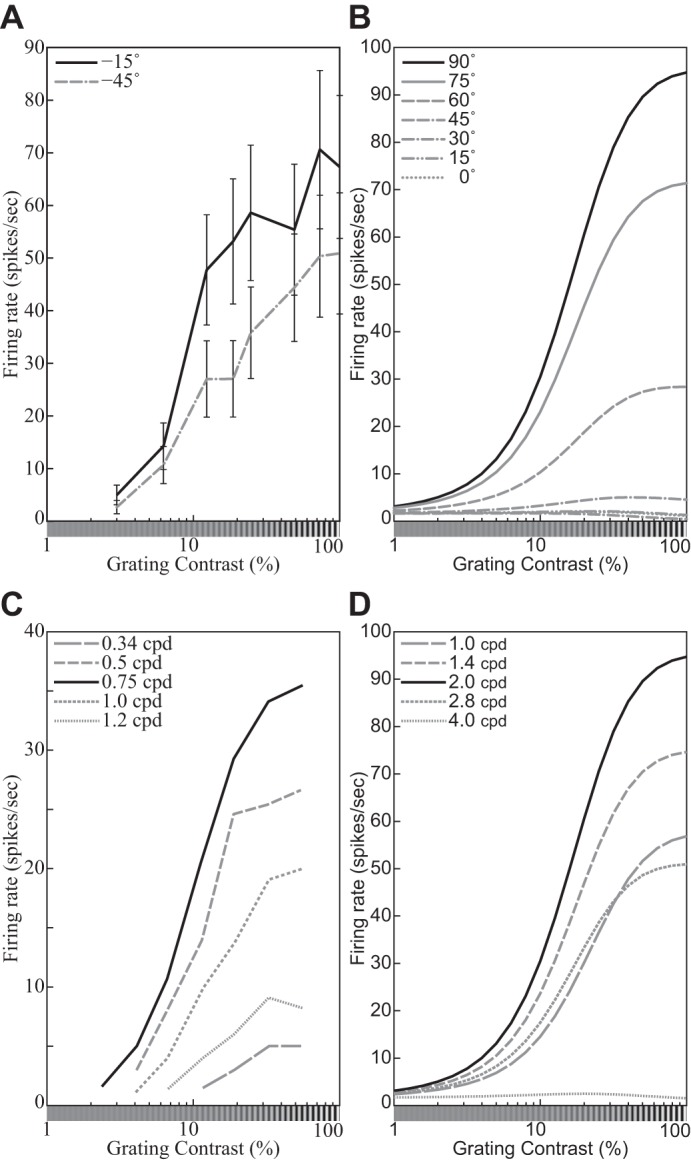
Representative contrast response functions (CFs). A: responses of a simple cell to drifting sinusoidal gratings spanning a range of contrasts at 2 orientations (see key). Replotted from Carandini et al. (1997, Fig. 4B, anesthetized macaque; error bars =  ±SE). B: CFs of the DNM neuron with default parameters, probed with gratings with the neuron’s preferred frequency (1.0 oct) and orientations shown in key. The size of the stimuli was equal to the measured RF diameter (0.81°). C: responses of a V1 neuron to drifting sinusoidal gratings with the neuron’s preferred orientation and spatial frequencies shown in key. Replotted from Albrecht and Hamilton (1982, Fig. 7A). D: CFs of the divisive normalization model (DNM, defined in text) neuron with default parameters, probed with gratings with the neuron’s preferred orientation (0°) and spatial frequencies shown in key. The size of the stimuli was equal to the measured RF diameter (0.81°). (See phenomena 7, 10, and 11 in Table 1.)

The hyperbolic ratio model has been widely used as a descriptive model to fit these data (e.g., Albrecht and Hamilton 1982; see also Graham 2011; Legge and Foley 1980; Naka and Rushton 1966).¹⁰ The response R_HB of this model to a stimulus cI_T with contrast c and template I_T is

$$R_{HB}\left(c{I}_T\right)=M_{HB}\left(I_T\right)\frac{c^{n_{HB}}}{{\alpha }_{HB}{}^{n_{HB}}+c^{n_{HB}}}$$ (12)

where the semisaturation contrast parameter α_HB expresses the contrast of the image that produces one-half of the saturation level M_HB(I_T).¹¹ Note that the latter depends on the template I_T. When contrast is plotted on a log axis, the exponent n_HB controls the slope of the CF and α_HB controls its location (Fig. 4; Graham 2011; see appendix b for properties of the CF plotted on a linear contrast axis). Note also that the response to a stimulus with zero contrast (i.e., a uniform gray field) is assumed to be zero.

Fig. 4.

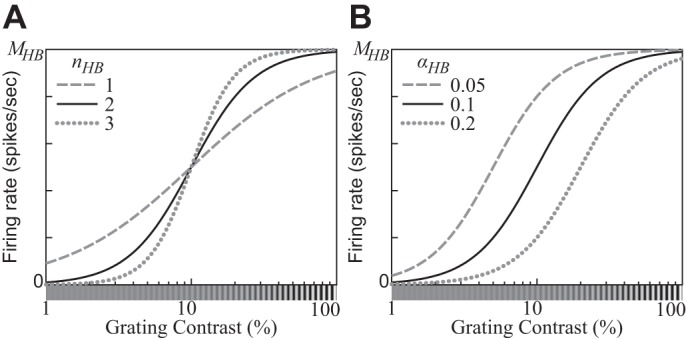
Contrast response functions (CFs) produced by the hyperbolic ratio model (Eq. 12). A: the exponent parameter n_HB controls the slope of the CF as a function of the log contrast of the stimulus. B: the semisaturation contrast parameter α_HB controls the location of the CF. A stimulus with contrast α_HB elicits one-half of the saturation level M_HB. (α_HB = 0.1 for A; n_HB = 2 for B.)

The hyperbolic ratio model (Eq. 12) involves two nonlinear operations: exponentiation and division. The former accounts for the accelerating shape of the CF at low contrasts—that is, for the fact that the CF slope gets steeper and steeper as the contrast increases from zero. Using the logarithmic scale of the contrast c, the maximal slope is n_HB/4 at c = α_HB. The divisive operation of the hyperbolic ratio model saturates the CF at high contrasts. The CF of the hyperbolic ratio model with these properties can represent shapes of CFs of real neurons well. Note that the asymptotic limit c→∞ has no physiological interpretation because the luminance contrast c cannot be greater than 1 (Eq. 1).

Equation 12 predicts that all CFs measured for the same neuron are multiplicatively scaled replicas of each other across the entire contrast range. That is, the ratio of the neuron’s responses to images with identical contrast but different templates I_T′ and I_T″ is invariant with respect to c:

$$\frac{R_{\text{HB}}\left({cI}_{\mathit{T\prime }}\right)}{R_{\text{HB}}\left({cI}_{T″}\right)}=\frac{M_{\text{HB}}\left(I_{\mathit{T\prime }}\right)}{M_{\text{HB}}\left(I_{T″}\right)}$$ (13)

The empirical CFs (Fig. 3) of typical simple and complex cells in V1 are consistent with this prediction in many cases (e.g., Albrecht and Hamilton 1982; Carandini et al. 1997; see contrast response function for further references). In particular, when I_T′ and I_T″ are gratings with different orientations, Eq. 13 accounts for the approximate contrast invariance of the orientation tuning curves of typical V1 neurons (e.g., Sclar and Freeman 1982; Skottun et al. 1987; see orientation and spatial-frequency tuning for further references). Note, however, that the spatial-frequency tuning curves of many V1 neurons have a slight but systematic dependence on contrast (e.g., Albrecht and Hamilton 1982; Skottun et al. 1987; see phenomenon 17 in orientation and spatial-frequency tuning for further discussion).

Cortical neurons have a limited dynamic range, and their firing rates saturate at high contrasts (e.g., Albrecht and Hamilton 1982). It is important to note that this saturation is not simply an output nonlinearity because it occurs at a fixed contrast rather than at a fixed response level for different stimuli. Consider the CFs plotted in Fig. 3C, for example. The responses to gratings whose frequency is 0.34 cpd saturate below 10 sps even though the same neuron can sustain firing rates above 30 sps when stimulated at its preferred frequency (0.75 cpd). Each neuron is characterized by an entire family of CFs—one for each stimulus template. It is for this reason that this type of divisive normalization is called contrast-set gain control (or simply contrast gain control).

The contrast gain control should not be confused with luminance gain control (Eq. 1) or contrast adaptation. These are different mechanisms in the visual system (Frazor and Geisler 2006; Mante et al. 2005). The luminance gain control (or light adaptation) is primarily accomplished in the retina (Shapley et al. 1993; Shapley and Enroth-Cugell 1984; see also Virsu et al. 1977; Virsu and Lee 1983). On the other hand, the contrast gain control encompasses retinal (Baccus and Meister 2002; Scholl et al. 2012; Shapley et al. 1993; Shapley and Enroth-Cugell 1984), subcortical (Kaplan et al. 1987), and cortical (Bex et al. 2007; Ohzawa et al. 1982, 1985; Solomon et al. 2004) contributions (Sclar et al. 1990; Truchard et al. 2000; see also The suppressive drive). Because of the luminance gain control, the maximal contrast is c_max = 1. The semisaturation contrast parameter α_HB in Eq. 12 is in light-adapted units. Note that the hyperbolic ratio is not clearly saturated for c ≈ 1 unless (α_HB ≪ 1). There are recordings from real V1 neurons whose CFs show no clear saturation at high contrasts (see Busse et al. 2009; Vaiceliunaite et al. 2013 for examples).

The hyperbolic ratio model requires the extraction of two distinct pieces of information about the stimulus. One is the contrast c, which is an intrinsic property of the image. The other is the degree of match between the input template I_T and the weighting function of the neuron. Both pieces of information are available in the image, but they cannot be extracted by the application of a single filter. The stimulus drive extracted by a linear filter (Eq. 5) is a single number that confounds contrast information and degree-of-match information. If either of them is known, the other can be decoded from the stimulus drive. The two models discussed so far are complementary in this regard: The linear rectification model characterizes stimulus selectivity, whereas the hyperbolic ratio model describes the dependence on contrast. When an arbitrary stimulus is presented, however, both pieces of information are unknown and multiple filters must be applied to resolve this ambiguity. The divisive normalization model pools the (half-squared) outputs of filters with diverse tuning preferences to estimate the intrinsic properties of the image. This pooled estimate is then used to normalize the stimulus drives to the individual units.

Divisive normalization model.

The notion of a normalization pool is pivotal to the divisive normalization model (DNM) and sets it apart from the simpler models discussed above. The introduction of a normalization pool is motivated by three convergent lines of evidence. The first line comes from the experimental data on the contrast-set gain control outlined above (Fig. 3), coupled with the need to pool across filters with diverse tuning preferences to estimate the stimulus contrast. A second, related line comes from a priori considerations involving the so-called noise-saturation dilemma (Grossberg 1988). Individual neuronal responses are noisy, and they have a limited dynamic range. The brain needs to represent signals across very wide dynamic ranges. Hence the dilemma: “If the [activations of individual neurons] are sensitive to large inputs, then why do not small inputs get lost in internal system noise? If the [activations] are sensitive to small inputs, then why do they not all saturate at their maximum values in response to large inputs?” (Grossberg 1988, p. 33). The proposed solution relies on pooled inhibition¹² within a network of interacting neurons to normalize the individual responses relative to a dynamically adjustable baseline. Such divisive normalization has been proposed (e.g., Carandini and Heeger 2011) as a canonical type of neural computation in a wide variety of sensory modalities, brain regions, and species. The divisive nonlinearity in the hyperbolic ratio model (Eq. 12) is an instantiation of this general principle.

The third and most direct line of evidence motivating the introduction of a normalization pool consists of experimental demonstrations of various broadly tuned suppressive effects in V1. In cross-orientation suppression, for example, the response to a grating (signal) is suppressed by another grating (mask) superimposed onto the signal within the neuron’s receptive field (e.g., DeAngelis et al. 1992; Morrone et al. 1982; see cross-orientation suppression for further references and discussion). In surround suppression, the response is suppressed by masks presented outside the classical RF (e.g., Cavanaugh et al. 2002b; Li and Li 1994; see surround suppression).

Thus modeling the responses of a single individual neuron requires filtering the input image with multiple linear filters that have diverse weighting functions. Let this diverse set be indexed by i, the filters in the normalization pool have preferences P_i, and P* denote the tuning preference vector (Eq. 8) of the stimulus drive of the target neuron.

Heeger (1992b) combined all theoretical ideas introduced above into a single equation. His formulation of the divisive normalization model has been very influential (see Carandini and Heeger 2011 for a recent review). In our notation, which is different from Heeger’s, this equation is

$$R_{DN}\left(I\right)=M_{DN}\frac{{\lfloor E_{\mathbf{\text{P}}*}\left(I\right)\rfloor }^{n_{\text{DN}}}}{\alpha D{N}^{{\mathit{n}}_{\text{DN}}}+{\Sigma }_{i\in \mathcal{N}}{E}_{{\mathbf{\text{P}}}_i}{\left(I\right)}^{n_{DN}}}$$ (14)

where the summation in the denominator encompasses the normalization pool $\mathcal{N}$. The exponent n_DN and the semisaturation contrast α_DN are free parameters analogous to their counterparts in the hyperbolic ratio Eq. 12 (Fig. 4). Note that the firing rate parameter M_DN is a constant that does not depend on the stimulus I. This parameter determines the stimulus drive E_P*(I) to the target neuron, which can be either a simple or a complex cell (Eq. 9).

The suppressive drive ${\Sigma }_{i\in \mathcal{N}}{E}_{{\text{P}}_i}{\left(I\right)}^{n_{DN}}$ in the denominator represents the aggregated inhibitory influence impinging on the target neuron. There is evidence that this inhibitory influence combines lateral inhibition from other neurons in V1, feedforward inhibition from and within the lateral geniculate nucleus (LGN), and feedback inhibition from higher cortical areas (e.g., Angelucci and Shushruth 2013; Sengpiel et al. 1998; see The suppressive drive for further references and a brief discussion). These sources have different temporal and spatial properties (e.g., Bair et al. 2003; see The suppressive drive). This is an active research area that is beyond our present scope. Equation 14 models this suppressive drive as a sum of (exponentiated) homogeneous terms $E_{{\text{P}}_i}$, each of which is analogous to the stimulus drive E_P* in the numerator. Note that various authors have interpreted the divisive normalization equation as a descriptive (e.g., Sengpiel et al. 1998), functional (e.g., Heeger 1992b), or structural model. (The structural interpretation is often related to shunting inhibition, e.g., Carandini et al. 2002; Carandini and Heeger 1994) The present article focuses on the functional aspect only. From the present point of view, Eq. 14 entails no commitment about what neurophysiological mechanisms produce the suppressive effect. The formula itself suggests a three-stage sequence of linear filtering followed by exponentiation followed by divisive normalization, and this is indeed how Eq. 14 is implemented on a computer. This sequential scheme, however, is not physiologically possible because the unnormalized intermediate terms $E_{{\text{P}}_i}$ cannot be represented by substrates with a limited dynamic range such as membrane potentials or firing rates. This constraint is at the core of Grossberg’s (1988) noise-saturation dilemma. Instead, the normalization almost certainly involves dynamic inhibitory interactions within a recurrent network (e.g., Brosch and Neumann 2014; Chance and Abbott 2000; Ellias and Grossberg 1975; Heeger 1993; Kouh and Poggio 2008) in conjunction with other regulatory mechanisms (e.g., Carandini et al. 2002; Freeman et al. 2002).

Various variants of Eq. 14 have been used to account successfully for extracellular recordings (e.g., Heeger 1992b; Carandini and Heeger 2011), multielectrode population recordings (e.g., Busse et al. 2009; Goris et al. 2009; Ruff et al. 2016), EEG brain imaging data (e.g., Candy et al. 2001; Zhang et al. 2008), fMRI brain imaging data (e.g., Boynton et al. 1999; Brouwer and Heeger 2011; Moradi and Heeger 2009), and psychophysical data (e.g., Boynton and Foley 1999; Foley and Chen 1999, 1997; Itti et al. 2000; Malo and Laparra 2010; Meese et al. 2007, 2009; Meese and Holmes 2002; Neri 2011, 2015; Olzak and Thomas 1999, 2003; To et al. 2010). Unfortunately, many of these applications use different mathematical formulations and idiosyncratic parameterizations. This practice makes it difficult to compare the results across studies despite the clear family resemblance of the model variants.

Aiming to consolidate this scattered literature, we propose Eq. 15 as the standard formulation of the divisive normalization model (DNM). This equation is the centerpiece of the present review. It is used to simulate a comprehensive suite of empirical phenomena that are listed in Table 1 (Simulation Experiments). By adjusting its parameters, Eq. 15 can represent or approximate many (though not all¹³) of the main variants in the DNM literature. It was chosen on the basis of theoretical analysis and simulation experiments with several model variants that were compared informally on their ability to account for the phenomena in Table 1. In our opinion, the following formulation achieves a good balance between flexibility and parsimony:

$$R\left(I\right)=M\frac{{\lfloor \beta +k_n{E}_{\text{P}*}\left(I\right)\rfloor }^{n_n}}{{\alpha }^{n_{\text{d}}}+k_{\text{d}}{\Sigma }_{i\in \mathcal{N}}{w}_i{E}_{{\text{P}}_i}{\left(I\right)}^{n_{\text{d}}}}$$ (15)

The firing rate parameter M and the semisaturation contrast α have the same interpretation as their counterparts in Heeger’s (1992b) proposal (Eq. 14, Fig. 4). There are separate exponents n_n and n_d for the numerator and denominator, respectively. The baseline parameter β allows for nonzero responses when the stimulus drive E_P*(I) is zero. The maintained discharge of the DNM neuron—its response to a blank stimulus (uniform gray field)—is $M{\lfloor \beta \rfloor }^{n_{\text{n}}}/{\alpha }^{n_{\text{d}}}$ sps. Note that the firing rate of an actual simple cell in V1 can be less than its maintained discharge when the dark-excitatory regions in the cell’s receptive field are stimulated by a light spot (Hubel and Wiesel 1959). This property can be modeled by Eq. 15, assuming β > 0, but not by Eq. 14. Conversely, setting β < 0 within the scope of the half-wave rectification operator $\lfloor \cdot \rfloor$ amounts to setting a threshold on the stimulus drive (Heeger 1992a; Sceniak et al. 2002; Tadmor and Tolhurst 1989). The constraint that β must be fixed for a given neuron entails falsifiable predictions for the model (see contrast response function and appendix c).

The calibration constants k_n and k_d are not free parameters. Conceptually, they are factored into the weights w_i in Eq. 15 and the weighting function of the linear filter E_P* (Eq. 5). Both constants are defined with respect to a single calibration image I_cal:

$$|\begin{array}{l}{k}_{\text{n}}={\left(E_{\mathbf{\text{P}}*}\left(I_{\text{cal}}\right)\right)}^{-1}\\ k_{\text{d}}={\left({\Sigma }_{i\in \mathcal{N}}{w}_i{E}_{{\mathbf{\text{P}}}_i}\left(I_{\text{cal}}\right)\right)}^{-1}\end{array}$$ (16)

The calibration image is chosen a priori as the grating whose frequency and orientation (and phase for a simple cell) match the preferences P* of the stimulus drive of the target neuron. The contrast of I_cal is 1, and its spatial extent is large enough to fill both the classical receptive field and the suppressive surround. Calibrating the model in terms of an explicit image is convenient because it establishes a standardized scale for the substantive parameters α and β—they can be interpreted as equivalent contrasts. To see why, consider the calibration family of gratings {cI_cal}_c∈[0,1] that use I_cal as a template and sweep a range of contrasts c. For this special family, Eqs. 15 and 16 reduce to the following variant of the hyperbolic ratio model (Eq. 12; see also appendix c):

$$R\left(c{I}_{\text{cal}}\right)=M\frac{{\lfloor \beta +c\rfloor }^{n_{\text{n}}}}{{\alpha }^{n_{\text{d}}}+c^{n_{\text{d}}}}$$ (17)

Then a positive baseline (β > 0) can be interpreted as the contrast of the counter-phase grating that cancels the maintained discharge of a simple cell and a negative baseline (β < 0) as the contrast of the preferred (in phase) grating that barely elicits a response.

To complete the specification of the divisive normalization model, we need to define the suppressive drive ${\Sigma }_{i\in \mathcal{N}}{w}_i{E}_{{\text{P}}_i}{\left(I\right)}^{n_{\text{d}}}$ in the denominator of Eq. 15. This is an important aspect of the DNM. Our simulations indicate that changing the composition of the suppressive drive can affect the overall model performance as much as manipulating the parameters in Eq. 15. We need to specify three things: the weighting functions of the linear filters $E_{{\text{P}}_i}$, the composition of the normalization pool $\mathcal{N}$ encompassed by the sum, and the pooling weights w_i. We followed the common practice (e.g., Itti et al. 2000; Reynolds and Heeger 2009) with respect to all three. First, we assume all linear filters have the same spatial-frequency bandwidth h_f (Eq. 4) and the same orientation bandwidth h_θ (Eq. 3). These h_f and h_θ are assumed for the stimulus drive E_P* as well. Second, we assume that the normalization pool tiles the space of frequencies and orientations. There is evidence (DeAngelis et al. 1992, 1994) that the suppressive effects are approximately invariant with respect to the phase of the mask grating. We model this by including only phase-invariant components E_C (Eq. 7) into $\mathcal{N}$. Third, we adopt the common simplifying assumption that the pooling weights w_i can be separated¹⁴ into independent pooling kernels with respect to space, frequency, and orientation:

$${\displaystyle \sum _{i\in \mathcal{N}}{w}_i{E}_{P_i}{\left(I\right)}^{n_{\text{d}}}}={\displaystyle \sum _{X_i{Y}_i\in {\mathcal{N}}_{XY}}{\displaystyle \sum _{F_i\in {\mathcal{N}}_{\text{F}}}{\displaystyle \sum _{{\Theta }_i\in {\mathcal{N}}_{\Theta }}{w}_{X_i{Y}_i}{w}_{F_i}{w}_{{\Theta }_i}{E}_{C:X_i{Y}_i{F}_i{\Theta }_i}{\left(I\right)}^{n_{\text{d}}}}}}$$ (18)

where ${\mathcal{N}}_{XY}$ is a grid of image locations, ${\mathcal{N}}_F$ is a set of frequency channels, and ${\mathcal{N}}_{\Theta }$ is a set of orientation channels. This specification is constrained by empirical data on various forms of suppression¹⁵ (surveyed in Results) and by considerations of symmetry, parsimony, and computational efficiency.

The spatial pooling weights $w_{X_i{Y}_i}$ are defined by a radially symmetric 2D Gaussian kernel

$$w_{X_i{Y}_i}\propto \text{exp}\left[-4\text{ln}2\frac{{\left(X_i-X*\right)}^2+{\left(Y_i-Y*\right)}^2}{{\left(h_R/F*\right)}^2}\right]$$ (19)

where X* and Y* are the coordinates of the center of the spatial integration field of the stimulus drive and F* is the preferred frequency of the stimulus drive. The weights are defined up to a scaling factor and then calibrated by k_d in Eq. 16. The diameter at half height of the kernel is proportional to the preferred wavelength 1/F* of the stimulus drive of the target neuron. The spatial pooling bandwidth h_R (in number of cycles) is a free parameter common to all channels. Note that the overall suppressive field of the model is produced by a combination of two types of spatial summation. First, the individual components $E_{{\text{P}}_i}$ perform summation within elliptical Gabor receptive fields whose spatial dimensions $h_{\breve{x}}$ and $h_{\breve{y}}$ also are proportional to the respective channel wavelengths (Eqs. 3 and 4). Second, after nonlinear rectification with exponent n_d, there is another summation across components centered on multiple locations X_iY_i. Equation 19 defines the weighting function of the latter summation.

The frequency pooling weights $w_{F_i}$ are defined by a Gaussian kernel along the log-frequency (octave) dimension:

$$w_{F_i}\propto \text{exp}\left[-4\text{\hspace{0.17em}ln\hspace{0.17em}}2\frac{{\left({\text{log}}_2{F}_i-{\text{log}}_2{F}^{*}\right)}^2}{h_{F^2}}\right]$$ (20)

The pooling kernel is centered on the preferred frequency F* of the stimulus drive of the target neuron. (This restriction may have to be relaxed—see appendix e.) The frequency pooling bandwidth h_F (in octaves) controls the FWHH of the kernel. This parameter is distinct from the bandwidth h_f of the weighting functions of the individual components $E_{{\text{P}}_i}$. Because of the pooling, the frequency tuning of the suppressive effects is broader than h_f, in agreement with the data (DeAngelis et al. 1994; Li and Li 1994).

Finally, the orientation pooling weights $w_{{\Theta }_i}$ are defined by a von Mises kernel

$$w_{{\Theta }_i}\propto \text{exp}\left[{\kappa }_{\Theta }\text{cos}2\left({\Theta }_i-{\Theta }^{*}\right)\right]$$ (21)

where Θ* is the preferred orientation of the stimulus drive of the target neuron. The von Mises distribution is the circular analog of the normal distribution (Fisher 1996). The dimensionless concentration parameter κ_Θ is intuitively similar to inverse variance. Equation 21 assigns $w_{\max }\propto e^{{\kappa }_{\Theta }}$ to the preferred orientation and $w_{\min }\propto e^{-{\kappa }_{\Theta }}$ to the orthogonal orientation. The two points whose height is halfway between these two extremes occur at orientations Θ* ± h_Θ/2, where

$$\text{cos}\left(h_{\Theta }\right)=\frac{1}{{\kappa }_{\Theta }}\text{ln}\left[\frac{e^{{\kappa }_{\Theta }}+e^{-{\kappa }_{\Theta }}}{2}\right]$$ (22)

This equation establishes an invertible relationship in which h_Θ monotonically increases as κ_Θ decreases. The circular uniform distribution $w_{{\Theta }_i}\propto \text{1}$ is the special case for κ_Θ = 0, h_Θ = 90°. It is convenient to parameterize the DNM in terms of its orientation pooling bandwidth h_Θ (in °). Again, this parameter is distinct from the bandwidth h_θ of the weighting functions of the individual components $E_{{\mathbf{\text{P}}}_i}$. Because of the pooling, the tuning of cross-orientation suppression is broader than h_θ, in agreement with the data (DeAngelis et al. 1992; Morrone et al. 1982). Unfortunately, κ_Θ cannot be expressed as a closed-form function of h_Θ, but in practice Eq. 22 is easy to solve numerically.

Overall, our formulation of the divisive normalization model has 10 free parameters: M, α, β, n_n, and n_d in Eq. 15, the tuning bandwidths h_f and h_θ of the linear filters (Eq. 5), and the pooling bandwidths h_R, h_F, and h_Θ of the suppressive drive (Eq. 18). Five auxiliary constants ($h_{\stackrel{⌣}{x}}$, $h_{\stackrel{⌣}{y}}$, κ_Θ, k_n, and k_d) are calculated from the free parameters (cf. Table 2).

Simulation Experiments

The divisive normalization model (DNM, Eq. 15) was implemented and tested on a wide range of stimuli designed to replicate a comprehensive suite of published neurophysiological studies (Table 1).

Computational implementation and calibration.

We developed MATLAB (The MathWorks 2015) software that takes a static grayscale image as input and produces a matrix of firing rate responses for a population of DNM neurons. The neurons in this population have receptive fields at a single retinal location, and they are tuned for a range of orientations and spatial frequencies. The details of this implementation are given in appendix f. Briefly, the software provides tools for accomplishing two main computational tasks: constructing a DNM object for a given parameter set and calculating the responses of a model for a given input image.

A DNM object is a data structure that encapsulates the model’s parameters, weighting functions (WFs) for all linear filters, pooling weights for the suppressive drive, and various auxiliary information. Our implementation used $N_{\Theta }=12$ orientation channels spaced evenly at 15° increments around a circle. It used the following set of spatial-frequency channels: ${\mathcal{N}}_F=\{\sqrt{2}/2,1,\sqrt{2},2,2\sqrt{2},4,4\sqrt{2}\}\text{cyc/°}$. The first and last channels in this set were auxiliary. They were included to contribute to the normalization of the five main channels in the middle. The WF of each channel was a Gabor function (Eq. 2). Two WFs were constructed per channel: one in sine (Φ = 90°) and one in cosine (Φ = 0°) phase (Fig. 1), for a total of 168 = 12 × 7 × 2 Gabor patches. The sizes $h_{\stackrel{⌣}{x}}$ and $h_{\stackrel{⌣}{y}}$ of their Gaussian envelopes were calculated from the free parameters h_f and h_θ according to Eqs. 4 and 3. All images were rendered on a square 128 × 128 grid subtending 5.76 degrees of visual angle. To improve efficiency, we also used a “small” 64 × 64 grid for some simulations that did not involve stimuli with extensive surrounds.

The calibration constants k_n and k_d were calculated according to Eq. 16 with the aid of a calibration grating I_cal with unit contrast, vertical orientation (Θ* = 0°), frequency F* = 2.0 cyc/°, phase Φ* = 0°, and spatial extent covering the entire grid.

The calibrated model can be applied to an arbitrary grayscale input image. The computationally expensive operation is the calculation of the suppressive drive in Eq. 18. The stimulus is convolved with each of the 168 Gabor filters to produce 84 phase-invariant suppressive terms $E_{{\text{P}}_i}$ in Eq. 15. The software uses the FFT algorithm (fast Fourier transform; Lathi 2005) to compute these convolutions efficiently (see appendix f for details). The suppressive drives of multiple simulated neurons can be computed as weighted linear combinations of the same $E_{{\text{P}}_i}$ with different pooling kernels $w_{X_i{Y}_i}$, $w_{F_i}$, and $w_{{\Theta }_i}$ centered on different orientations and frequencies (Eqs. 18–21). Our software calculates the responses of 60 DNM complex cells and 240 DNM simple cells. The former are phase invariant (Eq. 7) and span the 12 orientations × 5 frequencies listed above (excluding the auxiliary frequencies). The latter vary also in phase: Φ = 0°, 90°, 180°, and 270°.

The channel with Θ* = 0° and F* = 2.0 cyc/° is singled out as the target and used to generate the DNM predictions in most figures below. Note, however, that it is only marginally more expensive to compute an entire population code of the input image (deCharms and Zador 2000; Pouget et al. 2003). Our software can be used as off-the-shelf front end to larger models utilizing population codes. In fact, an earlier version of the software has been incorporated into such larger models (Jacobs 2009; Petrov et al. 2005, 2006).

Standard parameter set.

We propose the values listed in Table 2 as a standard parameterization of the DNM. These values were used to generate almost all of the DNM results in this article, with a few exceptions noted explicitly below. They are compatible with typical neurophysiological measurements of representative simple and complex cells and with the phenomena in Table 1. Thus these values are good defaults when the DNM is used as a building block for the construction of larger models of the visual system. The explicit reliance on a calibration image (Eq. 16) is designed to facilitate the reusability of parameter values across multiple applications.

A limitation inherent in the notion of standard parameterization must be acknowledged: Real V1 neurons have diverse properties (e.g., see Busse et al. 2009; De Valois et al. 1982a; Goris et al. 2015; Peirce 2007) that are impossible to subsume under a single parameter set. We reviewed single-cell recordings from different species (e.g., cats, New/Old World monkeys, rabbits, rodents, and ferrets) obtained under different conditions (e.g., anesthesia vs. alertness: Bereshpolova et al. 2011; Chen et al. 2009; Disney et al. 2007; Ecker et al. 2014; Goltstein et al. 2015; Niell and Stryker 2010; Pisauro et al. 2013; Vaiceliunaite et al. 2013) and different experimental protocols (see Mukherjee and Kaplan 1995; Smyth et al. 2003 for examples). Furthermore, there is substantial variability within a sample of neurons recorded from a single animal under constant conditions. Clearly, model parameters need to vary substantially to accommodate this diversity. The standard set in Table 2 is proposed as an estimate of the central tendency of a broad distribution. Our goal is to produce a qualitative account of the phenomena in Table 1 rather than a quantitative fit of a specific data set.

Now, let us discuss briefly the 10 free parameters in Table 2. The firing rate parameter M converts the dimensionless ratio of Eq. 15 into physiologically observable units (spikes/s). This parameter plays no role in accounting for the qualitative patterns that are our focus here but is indispensable for quantitative fitting of actual neuronal firing rates. The semisaturation contrast α was discussed in Hyperbolic ratio model and illustrated in Fig. 4B. Under the DNM calibration (Eq. 15), it is expressed in dimensionless units and can be interpreted as equivalent contrast. The proposed value (α = 0.1) is consistent with empirical estimates obtained via hyperbolic ratio fits to the contrast response functions of V1 neurons (Albrecht and Hamilton 1982; Busse et al. 2009; Gardner et al. 1999; Sclar et al. 1990). The exponents n_n and n_d control the slope of the CF (Fig. 4A). Exponents > 1 are needed to account for the accelerating nonlinearity at low contrasts discussed in appendix b. The standard value n_n = n_d = 2 is consistent with empirical estimates (e.g., Albrecht et al. 2003, p. 752; Busse et al. 2009, p. 933) and implements Heeger’s (1992a) half-squaring operator ${\lfloor \cdot \rfloor }^2$. Note that Eq. 15 has separate exponents for the numerator and denominator. This additional flexibility is needed for quantitative fits of physiological (e.g., Carandini and Heeger 2011) and psychophysical (e.g., Itti et al. 2000) data.

The baseline parameter β can be interpreted as equivalent contrast as discussed in Divisive normalization model. The interpretation depends on its sign. Negative values effectively impose a threshold on the stimulus drive (cf. Eq. 11), whereas positive values produce a maintained discharge in response to a blank stimulus (uniform gray field). Many real neurons in V1 emit spikes in the absence of external stimulation, although the spontaneous firing rates typically are quite low (Allison and Bonds 1994; De Valois et al. 1982a; Hubel 1959; Hubel and Wiesel 1959; Nassi et al. 2015; Pettigrew et al. 1968; Squatrito et al. 1990). For example, Hubel and Wiesel (1959) recorded maintained discharges between 0.1 and 10 spikes/s in V1 neurons of anesthetized cats. Under the standard parameterization, Eq. 15 produces $M{\lfloor \beta \rfloor }^{n_n}/{\alpha }^{n_d}$ = 1.6 spikes/s. The β parameter is in the focus of the mathematical analyses below (see Eq. 23 and appendix c) and several simulations (e.g., Fig. 10) that explore nonstandard values.

Fig. 10.

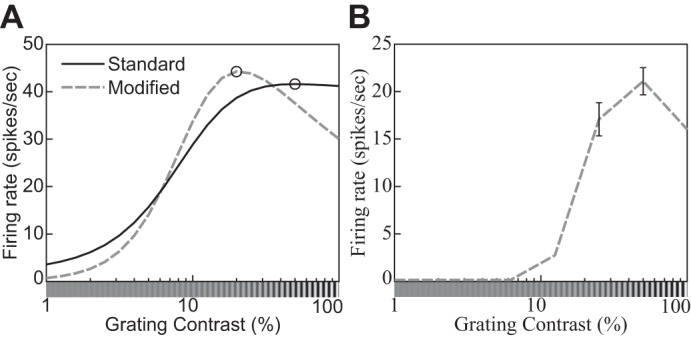
An example of the supersaturation effect (phenomenon 8 in Table 1). A: contrast response function of a DNM neuron with standard (solid line) and modified (n_d = 2.35, β = 0, M = 30, dashed line) parameterization. The stimulus frequency and orientation matched the DNM preferences. The size of the grating patch was 2.88°. B: contrast response function of a real neuron (replotted from Peirce 2007, Fig. 2e, anesthetized macaque).

The remaining five free parameters control various bandwidths. They have diverse units (listed in Table 2) and should be interpreted with care because their empirically observable analogs depend on complex interactions among the DNM components as discussed in orientation and spatial-frequency tuning. For instance, the orientation tuning bandwidth of the model as a whole is 31.8° under the standard parameters (Figs. 13 and 14). Note that this is smaller than the bandwidth h_θ = 40° of the linear filtering stage and much smaller than the pooling bandwidth h_Θ = 60° of the suppressive drive. Analogously, the frequency tuning bandwidth of the standard model as a whole is 1.11 oct, which is smaller than both h_f = 1.5 and h_F = 2.0 oct. The overall model bandwidths are within the reported ranges of neurophysiological measurements (Busse et al. 2009; De Valois et al. 1982a; Kulikowski and Bishop 1981; Movshon et al. 1978a; Rose and Blakemore 1974; Schiller et al. 1976a, 1976b; Watkins and Berkley 1974). Finally, the standard FWHH of the radial spatial-pooling kernel (Eq. 19) covers h_R = 2.0 cycles of the neuron’s preferred frequency. This value is consistent with surround-suppression measurements (see size tuning and surround suppression for references).

Fig. 13.

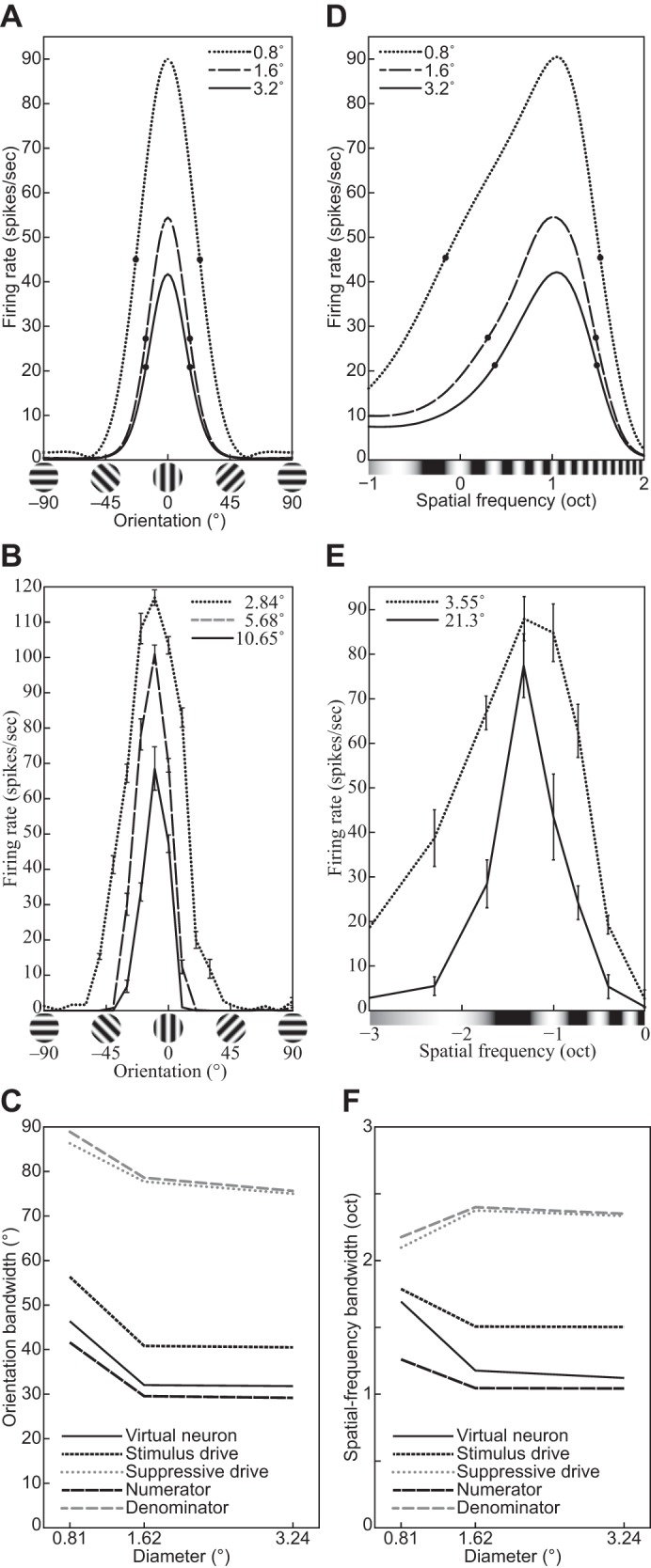
Orientation and spatial-frequency tuning functions of the divisive normalization model (DNM) neuron with standard parameters (A and D), a V1 neuron (replotted from Okamoto et al. 2009, Fig. 1, anesthetized cat; error bars =  ± SE) (B), and a V1 simple cell (replotted from Osaki et al. 2011, Fig. 5B, anesthetized cat; error bars =  ± SE) (E) for gratings with different diameters (indicated in key). C and F: effect of stimulus size on the bandwidths of the DNM neuron, the numerator and denominator in Eq. 15, the stimulus drive (Eq. 9), and the suppressive drive (Eq. 18). The contrast of the grating was 100% for A and D, its frequency was 2.0 cpd for A, and its orientation was 0° for D. The full widths at half height are indicated by pairs of bold dots in A and D. (See phenomena 15 and 16 in Table 1).

Fig. 14.

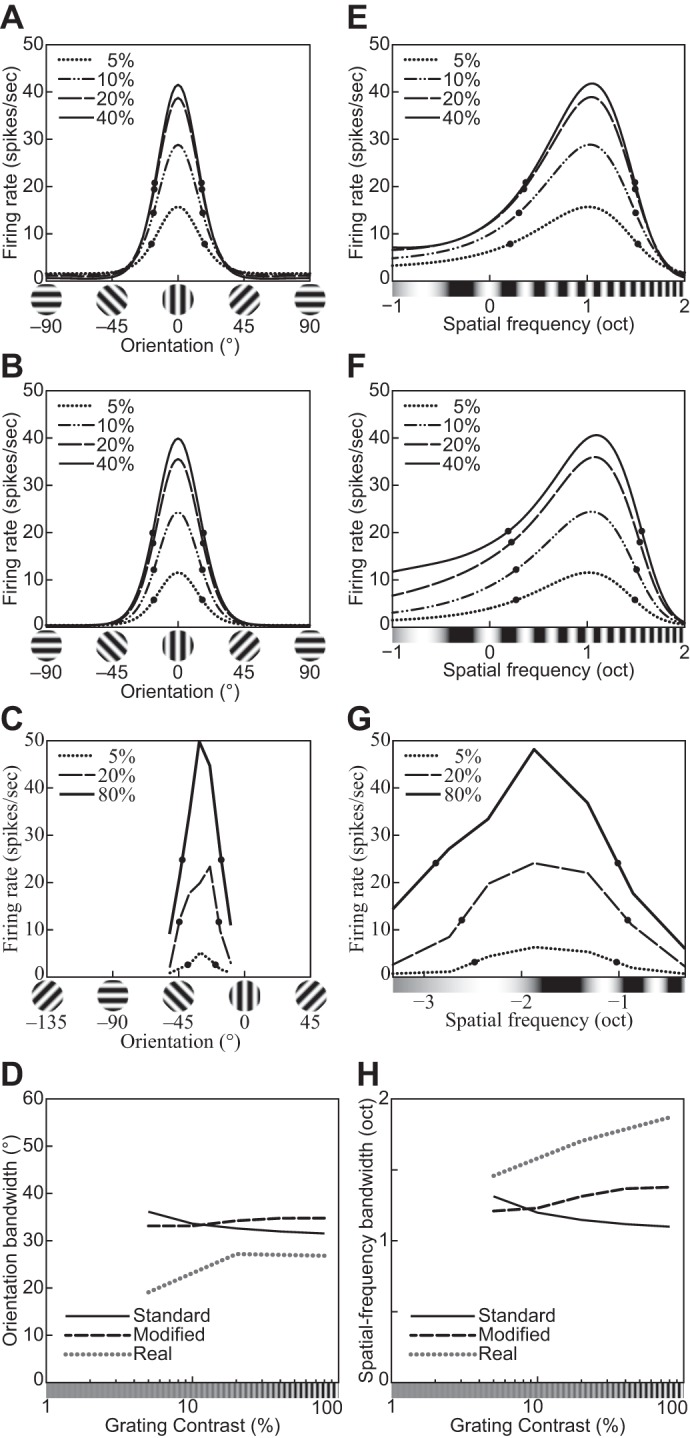
Orientation and spatial-frequency tuning functions for gratings with different contrasts (indicated in key). A and E: the divisive normalization model (DNM) neuron with the standard parameter set. B and F: the DNM neuron with a modified parameter set (h_Θ = 40°, h_F = 1.0 oct). C: orientation tuning of a simple striate cell (replotted from Skottun et al. 1987, Fig. 3A, anesthetized cat). G: frequency tuning of a simple striate cell (replotted from Skottun et al. 1987, Fig. 4A, anesthetized cat). D and H: effect of stimulus contrast on the bandwidths of the real neurons in C and G and of the DNM neuron in the orientation (D) and frequency (H) domains for the 2 parameter sets (key). A, B, E, and F: the size of the grating patch was 2.88°. The spatial frequency of the grating was 2.0 cpd for A and B, and its orientation was 0° for E and F. (See phenomena 17 and 18 in Table 1.)

Results.

A systematic series of simulation experiments replicated the qualitative patterns characterizing the phenomena in Table 1. The simulated DNM patterns are plotted alongside single-cell recording data from representative experiments. The physiological data were captured from the figures in their respective publications with PlotDigitizer (http://plotdigitizer.sourceforge.net) and replotted here in a unified format. All simulations used the standard parameters listed in Table 2 unless explicitly indicated otherwise.

size tuning.

Our first simulation measured the responses of a DNM complex cell as a function of the stimulus diameter.¹⁶ All stimuli were gratings whose orientation Θ* = 0° and frequency F* = 2 cpd matched the cell’s tuning preferences. The resulting size tuning function is plotted in Fig. 5A for gratings with maximal contrast c = 1. The responses increased as stimulus size increased at first, reached a peak, decreased, and finally settled to an asymptote. This matches the qualitative pattern observed in single-cell recordings of V1 neurons (Gieselmann and Thiele 2008; Jones et al. 2001; Schwabe et al. 2010; Sengpiel et al. 1997).

Fig. 5.

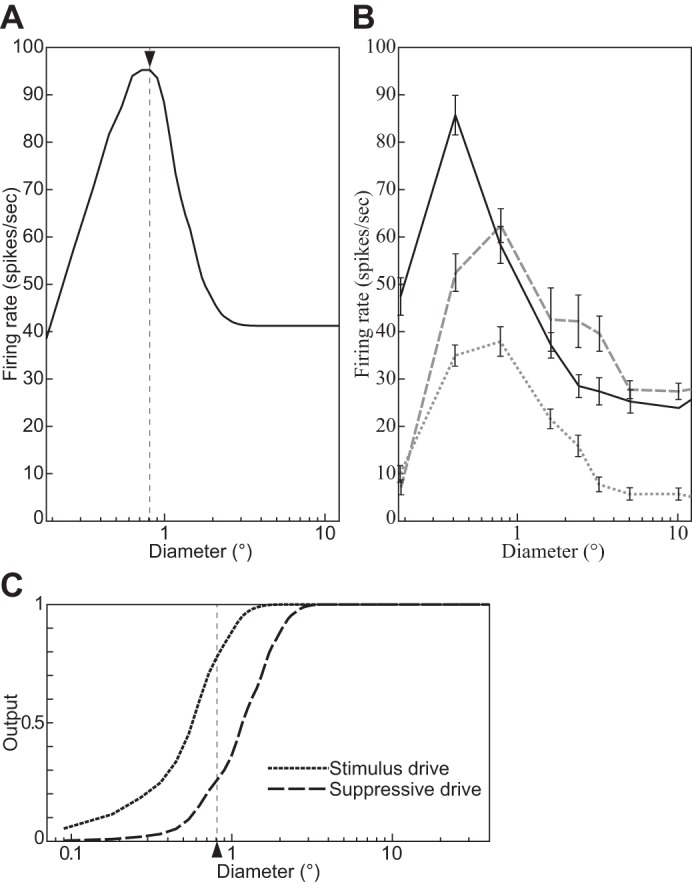
Size tuning functions of a divisive normalization model (DNM) complex cell with standard parameters (A), 3 V1 complex cells (B) (replotted from Schwabe et al. 2010, Fig. 2, anesthetized macaque; error bars =  ±SE), and the stimulus and suppressive drive terms of the DNM equation (C). The measured RF diameter of the DNM neuron is 0.81° (indicated by arrowhead in A). All stimuli were gratings with maximal contrast (c = 1) and orientation and frequency that matched the preferences of the respective neuron. (See phenomenon 1 in Table 1.)

The nonmonotonic response pattern in Fig. 5 indicates that the neuron’s RF has limited spatial extent (phenomenon 1 in Table 1). The diameter of the grating that induces the maximal response is often used in physiological studies to operationalize the size of the classical RF. For the DNM neuron, this measured RF diameter (MRFD) is ≈0.81° (marked by arrowhead in Fig. 5A). Note that it is narrower than the FWHH sizes of the elliptical contour of the weighting function of the model’s linear stage ($h_{\breve{x}}$ = 1.26° and $h_{\breve{y}}$ = 0.92°, Table 2; see also Fig. 1). Other parameter sets were also tested, and the MRFD tended to expand as n_n, α, h_Θ, or h_F increased or β, n_d, h_θ, or h_f decreased. As a consistency check, note also that the measured asymptotic response rate (≈41.2 spikes/s) matched the prediction of the hyperbolic ratio Eq. 17. This is because the gratings with very large diameters in this simulation became identical to the calibration image I_cal, thereby satisfying the condition for applicability of Eq. 17.

The nonmonotonic response pattern in the model arises from the interplay between the numerator and denominator in Eq. 15. As the stimulus diameter increases, the stimulus drive (Eq. 9) rises faster but saturates earlier than the suppressive drive (Eq. 18, Fig. 5C; Gieselmann and Thiele 2008).

The MFRDs of real neurons depend on the parameters of the grating. The MRFD increases as the stimulus luminance contrast decreases (phenomenon 2, Fig. 6B; Cavanaugh et al. 2002a; Kapadia et al. 1999; Nienborg et al. 2013; Sceniak et al. 1999; Schwabe et al. 2010; Sengpiel et al. 1997; Tailby et al. 2007). Also, the MRFD decreases for gratings with nonpreferred orientations (phenomenon 3, Fig. 7B; Tailby et al. 2007). The DNM neuron reproduces both phenomena (Figs. 6A and 7A). The simulation that produced Fig. 7A was designed to emulate the method of Tailby et al. (2007). Specifically, the stimuli in the Opt condition (gray solid line, Fig. 7A) were gratings of the preferred orientation (0°). We determined the MRFD for the DNM neuron in the Opt condition (0.81°, vertical dashed line, Fig. 7A) and then determined the orientation tuning curve for gratings with this diameter (see Fig. 13A). The orientation in the Ori_Δ condition (15.9°) was determined by the half-height points of this (symmetric) tuning curve. Probing the DNM neuron with gratings at this suboptimal orientation produced the dotted black line in Fig. 7A. It replicates the qualitative pattern of the neurophysiological data in Fig. 7B.

Fig. 6.

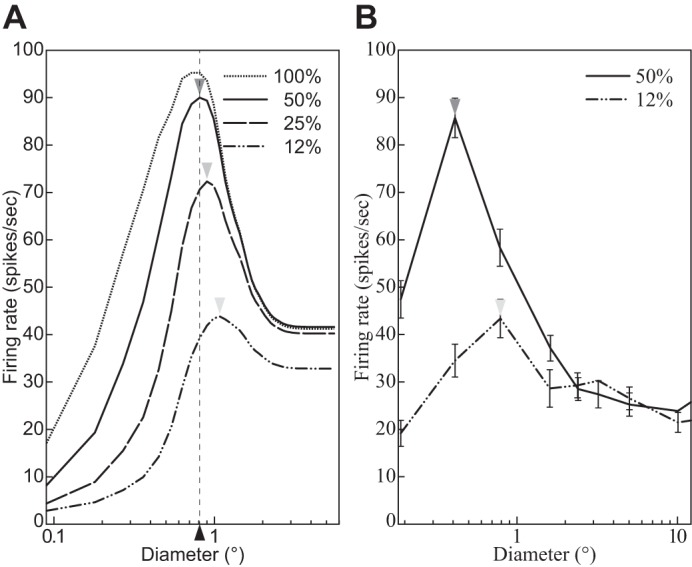
The size tuning function depends on the contrast of the stimulus grating. A: divisive normalization model (DNM) complex cell with standard parameters. B: V1 complex cell (replotted from Schwabe et al. 2010, Fig. 2a, anesthetized macaque; error bars =  ±SE). The measured RF diameter (depicted by arrowheads) increases as the stimulus contrast (shown in key) decreases. Stimulus orientation and frequency matched the preferences of the respective neuron. (See phenomenon 2 in Table 1).

Fig. 7.

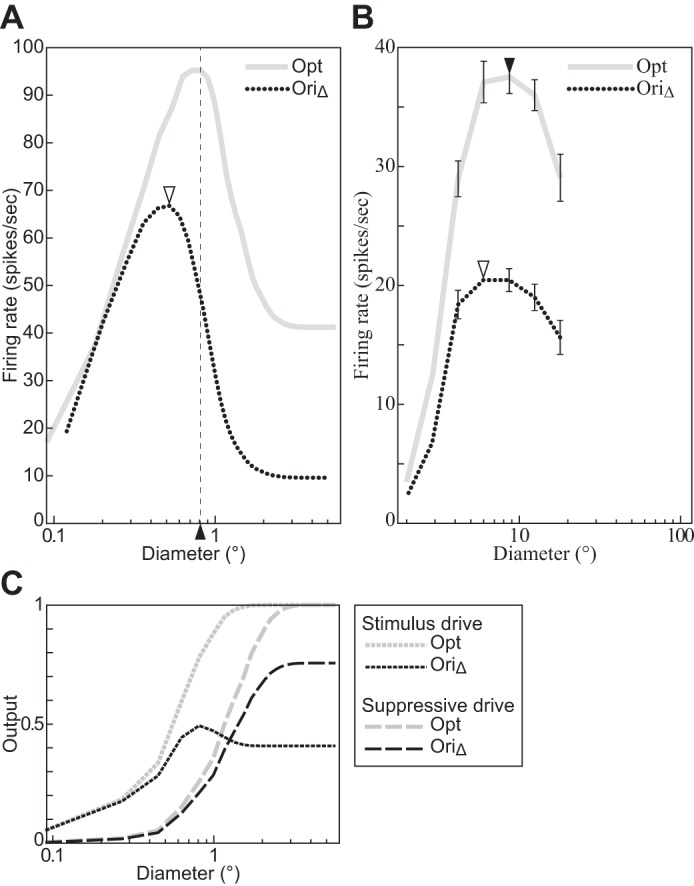
The size tuning function depends on the orientation of the stimulus grating. A: divisive normalization model (DNM) complex cell with standard parameters. B: V1 complex cell (replotted from Tailby et al. 2007, Fig. 2b, anesthetized cat; error bars =  ±SE). C: the stimulus and suppressive drive terms of the DNM equation. The grating orientation in the Opt condition matched the preferences of the respective neuron. The orientation in the Ori_Δ condition was determined by the half-height point of the orientation tuning function (Tailby et al. 2007). See text for details. All gratings had maximal contrast (c = 1), and their frequency matched the preference of the respective neuron. (See phenomenon 3 in Table 1.)

The MRFD of the model is also affected by the spatial frequency of the grating. It decreases if the frequency is either lower or higher than the DNM neuron’s preferred frequency, with stronger decreases for lower frequencies (Fig. 8A). The nonoptimal stimulus frequencies (Spf_L = −0.21 oct, 0.86 cpd; Spf_H = 1.52 oct, 2.87 cpd) for this simulation were chosen at the half-height points of the model frequency-tuning curve (see Fig. 13D; Tailby et al. 2007). The available recordings from real V1 neurons suggest that their MRFD tends to decrease as the stimulus frequency becomes higher than the preferred frequency, but no clear trend has been observed when the stimulus frequency becomes lower (Fig. 8B; Osaki et al. 2011; see also Tailby et al. 2007). This qualitative pattern may be somewhat different from the DNM prediction. The shift in MRFD for nonoptimal frequencies is a complex effect that depends on the size tuning of both the stimulus and suppressive drives. Their size tuning curves are affected differently by the stimulus frequency manipulation because of the different composition of the two kinds of drives in the DNM. The stimulus drive is a single Gabor filter, whereas the suppressive drive is composed of multiple filters (or channels, Eq. 18). The channels of the suppressive drive are tuned to a range of frequencies, and the lower-frequency channels have Gabor weighting functions with larger spatial integration fields (see Eqs. 3 and 4 and appendix f). We discuss the relationships among channel properties, stimulus size, and stimulus frequency in Summary and discussion.

Fig. 8.

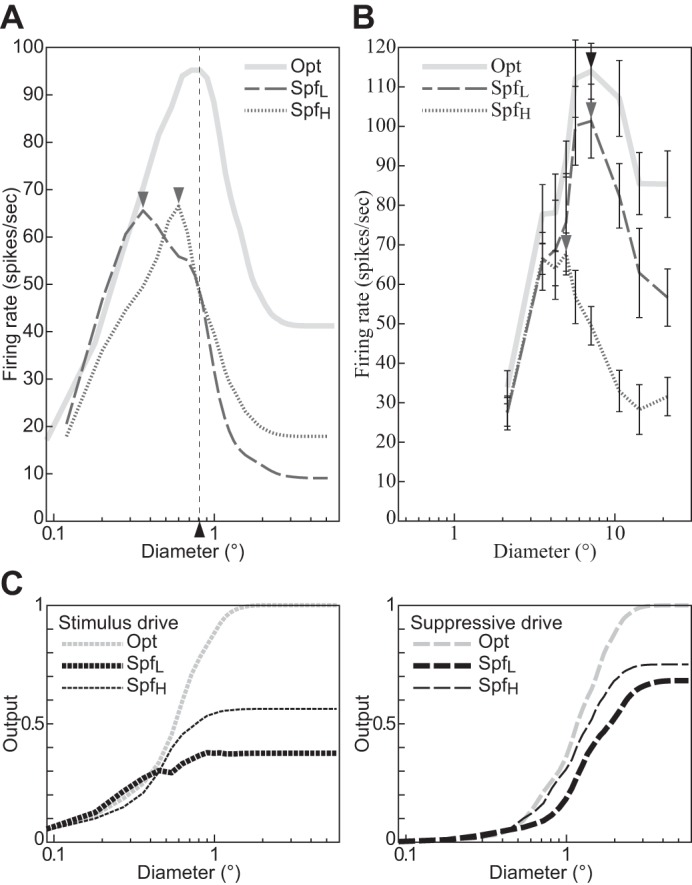
The size tuning function depends on the spatial frequency of the stimulus grating. A: divisive normalization model (DNM) complex cell with standard parameters. B: a real V1 neuron (replotted from Osaki et al. 2011, Figs. 2A and 4A, anesthetized cat; error bars =  ±SE). C: the stimulus and suppressive drive terms of the DNM equation. The stimulus frequency matched the preference of the respective neuron in the Opt condition, was lower in the Spf_L condition, and was higher in the Spf_H condition. The side frequencies in A were determined by the half-height points of the DNM frequency tuning curve. See text for details. The data in B were collected with Spf_L = 0.10 cpd, Opt = 0.20 cpd, and Spf_H = 0.30 cpd (Osaki et al. 2011). All gratings had maximal contrast (c = 1), and their orientation matched the preference of the respective neuron. (See phenomenon 4 in Table 1.)

The size tuning of V1 neurons has also been measured with annular stimuli that overlay a circular gray “hole” in a larger circular grating with the neuron’s preferred orientation and frequency (Cavanaugh et al. 2002a; Jones et al. 2001; Sengpiel et al. 1997). The recordings from V1 neurons decreased monotonically as the diameter of the hole increased and then leveled off at an asymptotic level that was similar to the spontaneous discharge of the cell (Fig. 9B, phenomenon 5). It is instructive to compare the hole diameter for which the responses become nearly constant with the RF diameter measured with disk stimuli as discussed above. The two procedures yield comparable results for the DNM neuron with the standard parameter set (Fig. 9A). This pattern is common for neurons in anesthetized cat V1 (Sengpiel et al. 1997) and in anesthetized macaque V1 (Jones et al. 2001; Fig. 9B). On the other hand, in another sample from anesthetized macaque V1 (Cavanaugh et al. 2002a) the hole diameter of many neurons (162/217) was substantially larger (47% on average) than the RF diameter (Cavanaugh et al. 2002a; Fig. 9D). The DNM can reproduce this pattern (Fig. 9C) with a modified parameter set (M = 25, n_d = 2.5, β = 0.005, α = 0.04). Recall that when disk stimuli (with no holes) are used to measure the RF diameter, the latter depends on stimulus contrast for both real and model neurons (Fig. 6). When annular stimuli are used, however, the DNM predicts approximate invariance with respect to the contrast of the grating inside the annular envelope (Fig. 9A, phenomenon 6).

Fig. 9.

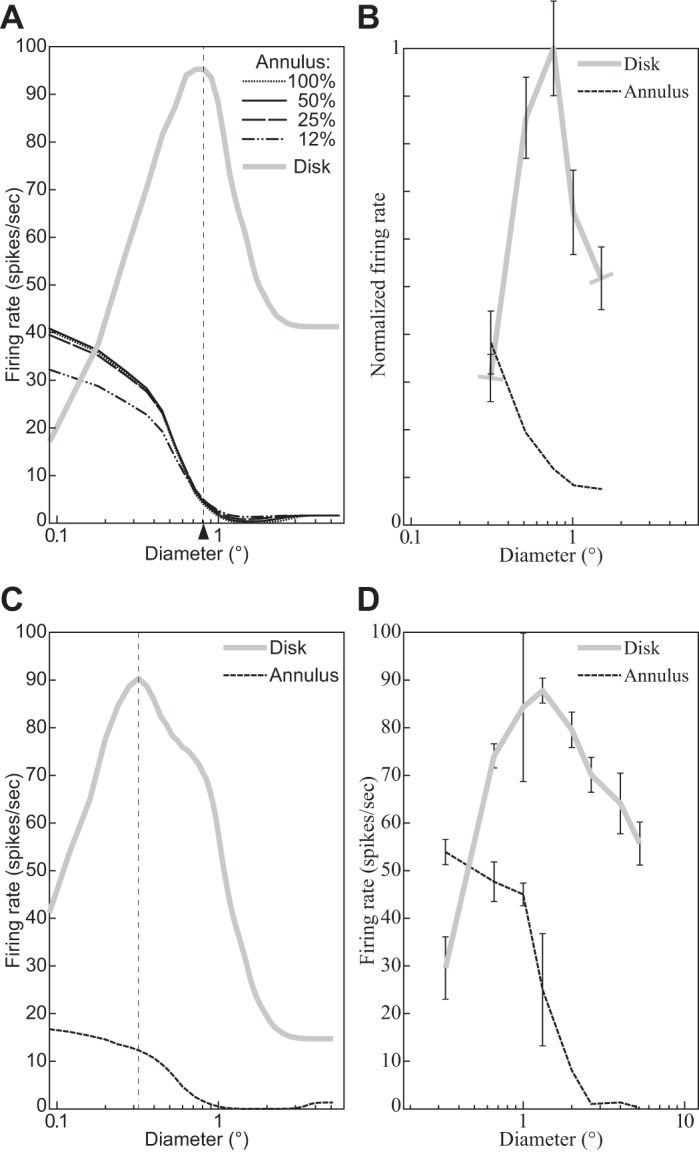
Responses to annular stimuli containing a circular gray “hole” inside a large circular grating. x-Axis specifies the diameter of the hole for annular stimuli and the outside diameter for disk stimuli (cf. Fig. 5). A: DNM complex cell with standard parameters. Key indicates the contrast of the annular stimuli; the disk had 100% contrast. The measured RF diameter (0.81°) is indicated by arrowhead. B: V1 neuron for which the 2 operational procedures yield comparable diameters (replotted from Jones et al. 2001, Fig. 1, anesthetized macaque; error bars =  ±SE). C: DNM complex cell with a modified parameter set (M = 25, n_d = 2.5, β = 0.005, α = 0.04). Both disk and annulus had 100% contrast. The measured RF diameter (0.36°) is indicated by vertical dashed line. D: V1 neuron for which the annulus-measured diameter is larger than the disk-measured diameter (replotted from Cavanaugh et al. 2002a, Fig. 4, anesthetized macaque). All stimuli are based on gratings whose frequency and orientation matched the preference of the respective neuron. (See phenomena 5 and 6 in Table 1.)

contrast response function.

Recall from Hyperbolic ratio model that the contrast response function (CF) describes how a neuron’s response depends on the contrast of the stimulus. When probed with simple gratings, the DNM includes the hyperbolic ratio model as a special case (Eq. 17; see also appendix c). Thus the hyperbolic ratio fits to the CFs of real neurons (e.g., Albrecht et al. 2003; Albrecht and Hamilton 1982) can be reinterpreted as support for the DNM. Moreover, variants of these two models were developed to explain change of the CFs under different conditions (Carandini et al. 1997; Cavanaugh et al. 2002a; Heeger 1992b; Peirce 2007; Sengpiel et al. 1998).

Our simulations measured the CF of the DNM neuron with gratings whose orientation and frequency matched the neuron’s preferences and whose size was large enough (5.58°) to cover the neuron’s suppressive field. The model responses are plotted in Fig. 10A (solid curve) as a function of stimulus contrast (phenomenon 7). The slope of the CF becomes maximal when the contrast is at 9%, above 0. It may be relevant to the psychophysical literature that a differential threshold of a grating contrast becomes minimal above the contrast detection threshold (see Itti et al. 2000; Wilson 1980 for a comparison between human and model performance on luminance contrast discrimination).

Note that the CF of the DNM neuron slightly decreases if the contrast is higher than 50% with the standard parameter set (indicated by a solid curve and an open circle in Fig. 10A). An analogous pattern is also observed from some real neurons (Li and Creutzfeldt 1984; Peirce 2007; Somers et al. 1998; Tyler and Apkarian 1985). This is called the supersaturation effect (phenomenon 8). This effect could be emulated only weakly by the DNM neuron with the standard parameter set. Some V1 neurons, however, do show the supersaturation effect very clearly (Fig. 10B). Mathematical analysis (appendix c) indicates that the model produces this effect when the baseline parameter β exceeds the following critical value:

$$\beta >\frac{n_{\mathrm{n}}}{n_{\mathrm{d}}}\left(1+{\alpha }^{n_{\mathrm{d}}}\right)-1$$ (23)

This inequality suggests that the supersaturation effect becomes stronger as β increases, α decreases, and n_n/n_d decreases (Fig. 10A; see also Sawada and Petrov 2015 for supersaturation plots produced with a different parameter set).

When visual noise is added to the preferred grating of a real neuron, the neuron’s responses tend to scale down by a multiplicative factor (phenomenon 9; Carandini et al. 1997). This effect was observed in the model when the contrast of the tuned grating was high (e.g., 50%, 25%, and 12% in Fig. 11, A and B). When the contrast of the grating was zero or very low, adding noise increased the response of the DNM neuron (Fig. 11, A and B). The response of the real neurons was also increased by the noise alone (from 0.8 ± 0.3 to 2.0 ± 0.6 spikes/s; Carandini et al. 1997). This effect of the noise without any grating can depend on the neurons (Squatrito et al. 1990). In the simulations, the addition of visual noise increased the DNM firing rate but decreased the slope of the CF for near-zero grating contrasts (Fig. 11A). Decreasing the slope is expected to increase the threshold of the model neuron for detecting the grating. However, if the output of one model neuron is relayed as excitatory input to another model neuron, it is possible that adding noise to the stimulus elevates the responses of the first neuron enough to trigger a response in the second neuron. In this way, moderate amounts of additive stimulus noise can improve the detection performance of the entire ensemble, despite the fact that the noise decreases the CF slope in the first stage (Funke et al. 2007). This effect is called stochastic resonance (Moss et al. 2004). Some psychophysical studies have claimed that stochastic resonance can be measured behaviorally (Moss et al. 2004; Sasaki et al. 2006a; Simonotto et al. 1997), but others have proposed alternative explanations (Perez et al. 2007).

Fig. 11.

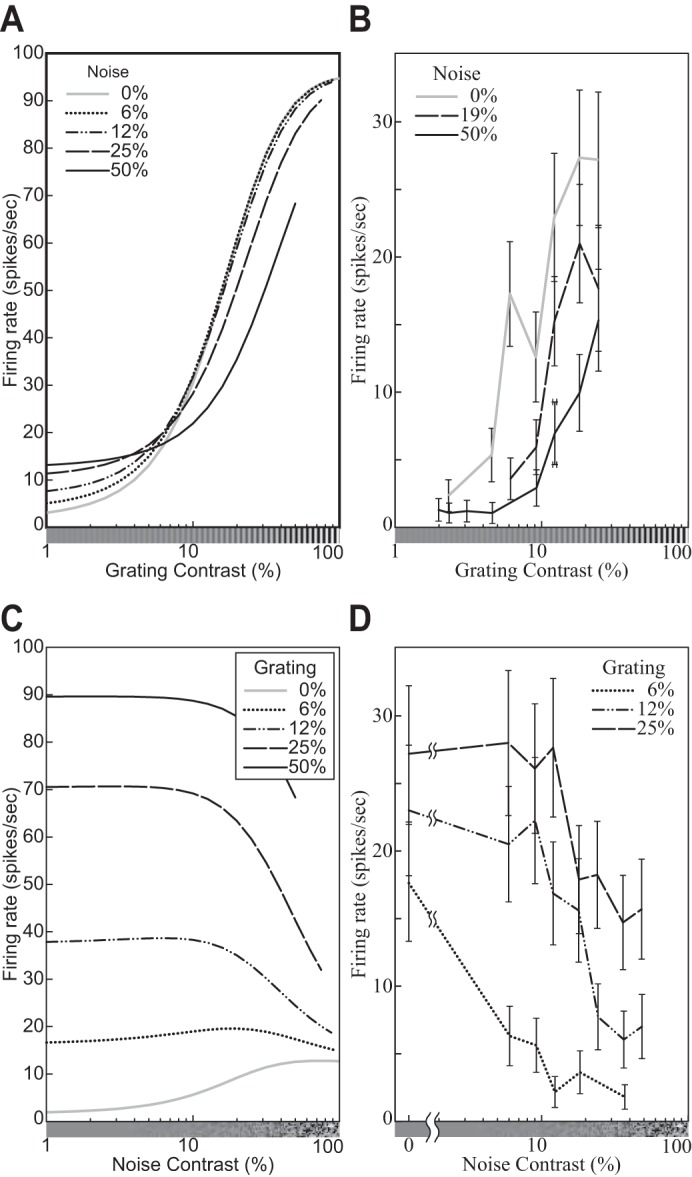
Responses of the model neuron (A and C) and a V1 simple cell (replotted from Carandini et al. 1997, Fig. 14, D and C, anesthetized macaque; error bars =  ±SE) (B and D) to a grating with a random noise pattern superimposed. The graphs in A and B are plotted against the contrast of the grating, whereas those in C and D are plotted against the contrast of the noise. A and C: the size of the stimuli was equal to the measured RF diameter (0.81°), and orientation and frequency matched the tuning preferences of the model neuron. (See phenomenon 9 in Table 1.)

The CFs of real neurons were affected by the orientation (phenomenon 10; Carandini et al. 1997; Tolhurst and Dean 1991) and the spatial frequency (phenomenon 11; Albrecht et al. 2003; Albrecht and Hamilton 1982; Carandini et al. 1997) of the stimulus grating. The CFs of real V1 neurons were multiplicatively scaled down if the orientation or the frequency of the grating was different from the neuron’s preferred orientation or frequency (Fig. 3; Carandini et al. 1997). These trends are also observed in the model (Fig. 3, B and D; see appendix d for the mathematical analysis).

Our simulation experiments showed that the CF of the model neuron was also affected by the size of the grating patch (Fig. 12). As stimulus diameter increases up to 0.8°, the overall firing rate increases, the CF slope at low contrasts becomes steeper, and the function becomes more saturating at high contrasts. Then, the asymptotic firing rate decreases while the slope at low contrasts is unchanged up to 3.2°. The function is unchanged even if stimulus diameter becomes larger than 3.2°. These simulation results can be explained by the mathematical analysis of the DNM in appendix d. Note that an analogous trend was recorded from LGN neurons and was explained in terms of a divisive operation (Bonin et al. 2005). To the best of our knowledge, however, the phenomenon has never been observed in V1 neurons with grating patches as stimuli (see Schumer and Movshon 1984). Note also that the supersaturation effect is observed from the DNM neuron if the stimulus diameter is 1.6° or larger.

Fig. 12.

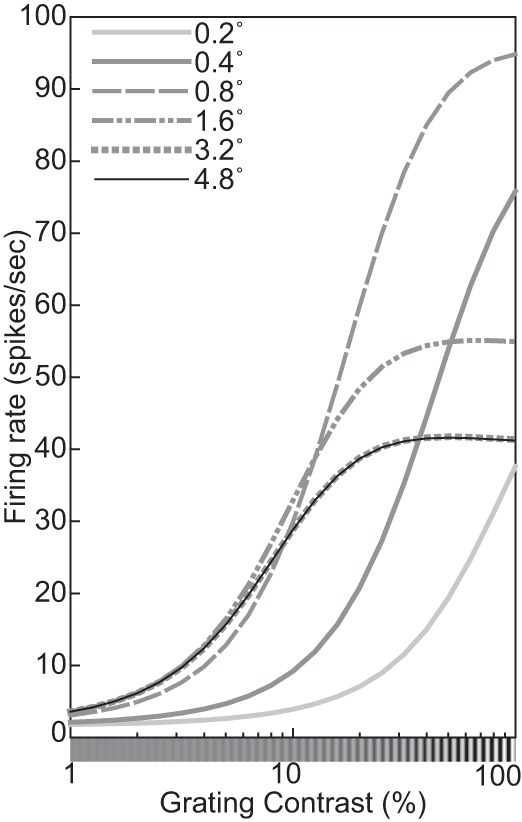
Contrast response functions of the model neuron for gratings with different diameters (indicated in key). The contrast, orientation, and spatial frequency of the grating were 100%, 0°, and 2.0 cpd. (See phenomenon 12 in Table 1.)

orientation and spatial-frequency tuning.

The orientation and spatial-frequency tuning functions of the DNM neuron are shown in Fig. 2 (phenomena 13 and 14). The measured peaks of the tuning functions were consistent with the weighting function of the stimulus drive (Eq. 2). The measured bandwidths of the tuning functions were 31.8° in the orientation domain and 1.11 oct in the frequency domain. Other parameter sets of the model were also tested, and the measured bandwidths tended to become narrower as n_n, α, h_Θ, or h_F increases or β, n_d, h_θ, or h_f decreases. Note that the measured bandwidths were substantially narrower than those of the weighting function of the linear filter in Eq. 5 (h_θ = 40°, h_f = 1.5 oct). This narrowing effect is attributed to the rectification and the expansive nonlinearity (n_n > 1) in the numerator of Eq. 15.

Note that the bandwidths of the numerator of Eq. 15 are a little narrower (29.2° and 1.04 oct) than those of the DNM neuron itself (31.8° and 1.11 oct). This occurs because the denominator of Eq. 15, which represents suppression, tends to widen the tuning curves of the DNM neuron. The tuning functions of the denominator are unimodal and become maximal at the same orientation and frequency as those of the numerator. The divisive operation then has a widening effect and becomes stronger as the denominator becomes more sharply tuned. This is why the bandwidths of the DNM neuron become wider as α, h_Θ, or h_F decreases or as n_d increases because they make the tuning functions of the denominator narrower. In particular, the h_Θ and h_F parameters (Table 2) allow an almost independent control of the widening of the orientation and frequency tuning, respectively.

There is evidence that the orientation (Li and Li 1994; Okamoto et al. 2009; see also Maffei and Fiorentini 1976 for a report of a few exceptional neurons) and spatial-frequency (Maffei and Fiorentini 1976; Osaki et al. 2011) bandwidths of real neurons become narrower when the size of the grating patch increases. The model simulated this effect well (Fig. 13A). The stimulus drive (Eq. 9) has a similar effect on both kinds of bandwidths, whereas the suppressive drive (Eq. 18) has different effects. Figure 13, E and F, plot the effect of stimulus size on the FWHH bandwidths of the DNM neuron, the numerator and denominator in Eq. 15, and the stimulus and suppressive drives. The orientation bandwidth profiles of these various terms unfold essentially in parallel (Fig. 13E). The overall inverse relationship between stimulus size and orientation bandwidth arises because the weighting function of the linear stage of the model is partially hidden by the surround suppression. This leads to a systematic underestimation of the measured RF (De Valois et al. 1985). Then, the measured bandwidths become wider if the grating patch just fills the underestimated RF.

On the other hand, surround suppression does modulate the relationship between DNM’s frequency bandwidth and the size of the grating patches. Note the nonmonotonic frequency bandwidth profile of the suppressive drive (Eq. 18) in Fig. 13F. The drop at small stimulus sizes arises because the suppressive channels tuned to very low spatial frequencies cannot be stimulated well by a small grating patch (see also Fig. 8C and Fig. 22). The low-frequency channels have larger spatial integration fields (Linear rectification model of simple cells and energy model of complex cells). The overall effect is to broaden the frequency tuning curve of the DNM neuron as the patch size decreases (Fig. 13D). Note that the peak of the frequency tuning curve of real neurons tends to shift to a higher frequency as the size of the stimulus decreases (Osaki et al. 2011; Teichert et al. 2007). However, the model neuron did not show this trend. The peak of its frequency tuning curve was not affected by the size of the grating patch in our simulations.

Fig. 22.

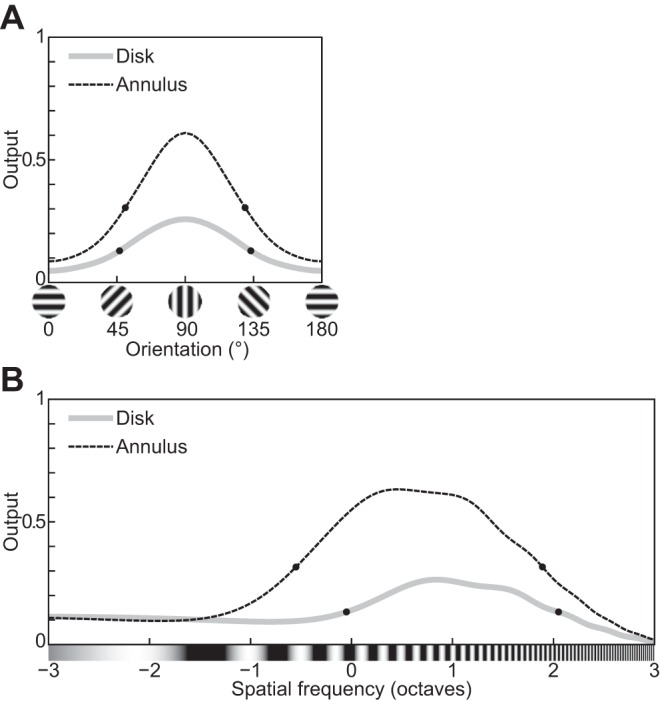
Tuning curves of the divisive normalization model (DNM) suppressive drive term (Eq. 18) with standard parameters when probed with stimuli that are typically used to induce cross-orientation and surround suppression—a circular grating patch (Disk) and an annular grating (Annulus), respectively: orientation tuning (A) and spatial-frequency tuning (B) of the suppressive drive with respect to these 2 types of inducers. Frequency of all gratings was set to 2 cpd while measuring the orientation tuning, and their orientation was set to 0° while measuring the frequency tuning in agreement with the preferences of the DNM neuron. The diameter of Disk and the inner diameter of Annulus matched the measured receptive field diameter (0.81°). The outer diameter of Annulus was 5.76°. Compare with Fig. 16, A and E, Fig. 19, A and C, Fig. 7C, and Fig. 8C.

The orientation and frequency bandwidths of real neurons are invariant from the contrast of the grating patches to a good approximation. This fact was an important motivation for the development of the divisive normalization model (Heeger 1992b). The invariance of the orientation bandwidth has been replicated in many physiological results (phenomenon 17, Fig. 14, C and D; Alitto and Usrey 2004; Anderson et al. 2000; Li and Creutzfeldt 1984; Sclar and Freeman 1982; Skottun et al. 1987; Somers et al. 1995; Troyer et al. 1998). On the other hand, some physiological studies identified a relatively weak but statistically significant trend in the direction of narrowing the spatial-frequency bandwidths of many real neurons as the contrast decreases (phenomenon 18, Fig. 14, G and H; Albrecht and Hamilton 1982; Sceniak et al. 2002; Skottun et al. 1987). These trends in the neurophysiological data could be emulated to some extent by the model neuron with a nonstandard parameter set with smaller h_Θ (40°) and h_F (1.0 oct). Under the standard parameterization, the bandwidths of the DNM neuron in both domains became slightly wider as the contrast decreased (Fig. 14). Note that these trends in the neurophysiological data are rather weak and that a significant subset of the neurons in V1 show opposite trends (Alitto and Usrey 2004; Kim 2011; Sceniak et al. 2002; Sclar and Freeman 1982).

The effect of stimulus contrast on the orientation and frequency bandwidths depends on the β parameter in the numerator and in the denominator of Eq. 15. The bandwidths of the numerator become narrower as the contrast decreases if β < 0 (the iceberg effect; Heeger 1992a; Sceniak et al. 2002; Tadmor and Tolhurst 1989) and become wider if β > 0. The bandwidths of the model neuron are also widened by the denominator depending on stimulus contrast. Recall that the widening effect of the denominator becomes stronger as the denominator becomes more sharply tuned. The tuning function of the denominator broadens as the contrast decreases, and it becomes a constant (${\alpha }^{n_d}$) at zero contrast. This contrast dependence of the widening effect of the denominator is consistent with the trend that the bandwidths of the model neuron become narrower as the contrast decreases.

Pollen and Ronner (1982) measured the spatial-frequency tuning of real neurons using sinusoidal and square gratings. They observed that, when measured with square gratings, the tuning function showed two peaks in the spatial-frequency domain (phenomenon 19). The primary peak appeared at the neuron’s preferred frequency, and the secondary peak appeared at one-third of the preferred frequency (Fig. 15B). The height of the secondary peak was between 0.6 and 0.8 times the height of the primary peak for most neurons. The secondary peak of some neurons was even as high as the primary peak. These observations partly agree with the predictions of the linear rectification model (see Linear rectification model of simple cells and energy model of complex cells). According to Fourier series decomposition, a square grating with frequency f_sq can be represented by a sum of sinusoidal gratings at the odd harmonics of f_sq with magnitudes proportional to reciprocals of the orders of the harmonics: ${{\displaystyle {\sum }_{j=0}^{\infty }\left(2j\text{+}1\right)}}^{-1}\sin \left(f_{sq}\text{/}\left(2j\text{+}1\right)\right)$. Thus if a neuron satisfying the assumption of the linear rectification model is tuned to a sinusoidal grating with frequency f_sin, it is predicted that its tuning function to a square grating should show multiple local maxima in the spatial-frequency domain. The positions of these maxima are f_sin/(2j + 1) and their heights are 1/(2j + 1) of the global maximum at f_sin, where j is a nonnegative integer. However, the results of Pollen and Ronner (1982) showed some deviations from the linear predictions. Only the primary (j = 0) and secondary peaks (j = 1) of the tuning functions could be reliably identified in the data, and the heights of the observed secondary peaks were higher than the predicted height. The DNM neuron with a nonstandard parameter set (h_f = 0.8, h_F = 0.4) can emulate these results, including the discrepancy to some extent (Fig. 15A). The tuning function of the model neuron shows the secondary peak at one-third of the tuned frequency, and its height is ~0.9 of the height of the primary peak. On the other hand, the model neuron also showed the tertiary peak at one-fifth of the tuned frequency (j = 2). Note also that the DNM neuron responds more strongly to the square grating than the sinusoidal grating, especially when their contrast is moderately low (Fig. 15C). The contrast response function of the DNM neuron with the square grating shifts horizontally to the left (phenomenon 20). This is because the outputs of both stimulus and suppressive drives are always larger to the square grating than to the sinusoidal grating with the same frequency and orientation (see Eq. 5).¹⁷

Fig. 15.

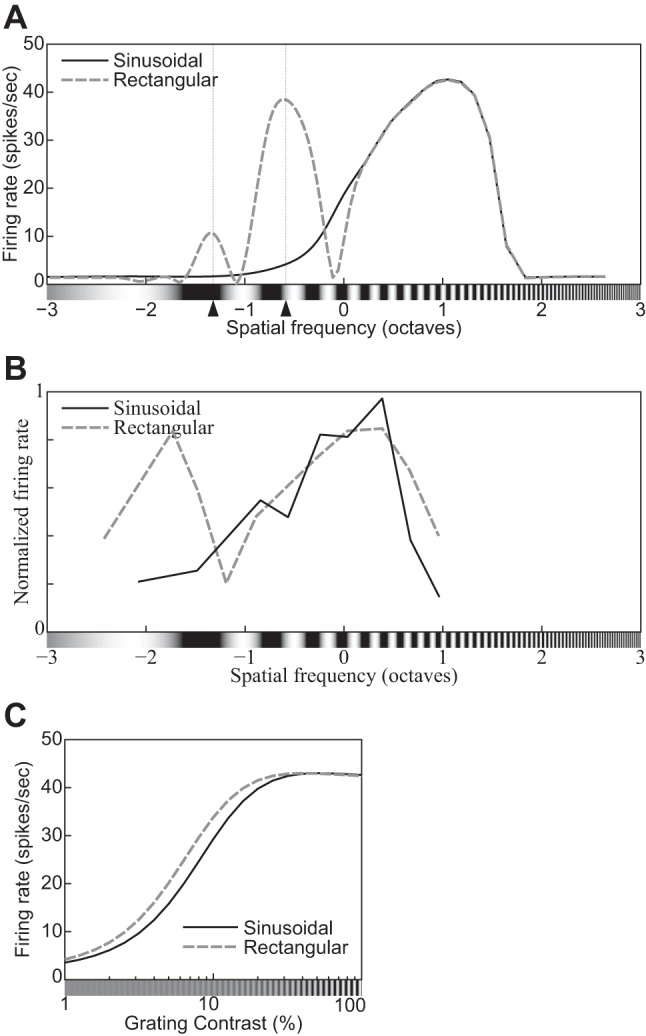
Spatial-frequency tuning functions for sinusoidal and square gratings of the model neuron with a modified parameter set (h_f = 0.8, h_F = 0.4) (A) and of a complex cell (replotted from Pollen and Ronner 1982, Fig. 6E, anesthetized cat) (B). Note the secondary peak at one-third of the tuned frequency for square gratings (dashed line). C: contrast response functions of the model neuron with the modified parameter set for sinusoidal and square gratings (indicated in key). (See phenomena 19 and 20 in Table 1.)

cross-orientation suppression.

The responses of real neurons in V1 to a grating (signal) tend to be suppressed by another grating (mask) superimposed on the signal grating within the neuron’s measured RF. This cross-orientation suppression is a topic of active investigation (e.g., Bonds 1989; DeAngelis et al. 1992; De Valois and Tootell 1983; Li et al. 2006; Koch et al. 2016; Morrone et al. 1982; Priebe and Ferster 2006; see The suppressive drive for additional references and discussion). Figure 16D provides a paradigmatic example (DeAngelis et al. 1992). The dashed line In Fig. 16D plots the orientation tuning curve (cf. Fig. 2A) of a complex cell measured with a simple grating with the cell’s preferred frequency and spatial extent; the solid line plots the responses of the same cell to plaid stimuli composed of two superimposed gratings: a signal and a mask. The strength of the suppression effect is measured relative to the baseline response to the signal alone (depicted by the horizontal dotted line in Fig. 16D). The signal always has the cell’s preferred orientation and frequency, whereas the parameters of the mask are manipulated to estimate the tuning properties of the suppression effect. To isolate the latter, experimentalists use masks that elicit little or no response when presented alone. The default choice is to use a mask whose orientation is orthogonal to the neuron’s preferred orientation. When the goal is to measure the orientation tuning of the suppressive effect, however, the mask must differ from the signal in spatial frequency (e.g., DeAngelis et al. 1992) and/or temporal frequency (e.g., Bonds 1989).

Fig. 16.

Tuning functions of the cross-orientation suppression effect. In all panels, the dashed gray line plots the excitatory tuning function obtained with nonmasked signal gratings, whereas the solid black line plots the neuron’s response to a plaid stimulus consisting of a preferred (fixed) signal and a superimposed mask grating. The horizontal axis represents the orientation/frequency of the signal or mask, respectively. The empirical tuning functions (D, G, and J) were measured in separate sessions with different grating contrasts. The horizontal dotted lines in these graphs represent the neuron’s response to a nonmasked signal with the same contrast as the signal component of the plaids in the suppression sessions (see DeAngelis et al. 1992 for details). The cross-orientation suppression effect is the mask-induced decrement relative to this baseline. A: orientation tuning of the DNM neuron with standard parameters (signal c = 15%, mask c = 25%). B: orientation tuning of a DNM neuron with modified parameters (n_n = n_d = 10, h_Θ = 55, M = 11; signal c = 15%, mask c = 25%). C: orientation tuning of a DNM neuron with modified parameters (h_Θ = 90, h_f = 1.0; signal c = 15%, mask c = 25%). D: orientation tuning of a complex cell (replotted from DeAngelis et al. 1992, Fig. 7, C and D, anesthetized cat; signal f = 1.25, mask f = 0.6 cpd). E: frequency tuning of the DNM neuron with standard parameters (cf. A; signal c = 10%, mask c = 25%). F: frequency tuning of a DNM neuron with modified parameters (h_F = 1.0, h_Θ = 90, R = 50; signal c = 10%, mask c = 25%). G: frequency tuning of a simple cell (DeAngelis et al. 1992, Fig. 3, A and B; signal c = 10%, mask c = 25%). H and I: orientation and frequency tuning of an augmented DNM neuron that had an extra parameter μ_F so that the pooling kernel of the suppressive drive could be set independently from the preferred frequency of the stimulus drive (appendix e; μ_F = −1 oct, h_F = 1.0, α = 0.03, M = 3; signal c = 15%, mask c = 25%). Note that the preferred frequency of the augmented DNM neuron with μ_F = −1 oct is 2.46 cpd and is clearly different from the preferred frequency of the stimulus drive F* = 2.0 cpd. J: frequency tuning of the same complex cell as D (DeAngelis et al. 1992, Fig. 3, C and D; signal c = 15%, mask c = 25%). All frequency tuning functions were obtained with plaids with orthogonal signal and mask orientations. All simulated orientation tuning functions were obtained with signal f = 2, mask f = 1 cpd (except for H: signal f = 2.46, mask f = 1.23 cpd). Stimulus size was 2.88° in all simulations. (Note: signal/mask f = frequency of the respective component of a plaid, c = contrast.) (See phenomena 21 and 22 in Table 1.)

The basic empirical result is that for many V1 cells it is possible to find a broad range of orientations and frequencies such that a mask with these parameters elicits no response from the neuron when presented alone but suppresses the response when superimposed on the signal grating. This suggests there is a suppression mechanism (or, more likely, a combination of several mechanisms as discussed in The suppressive drive) that operates in a broad region of the Fourier domain that envelops and exceeds the excitatory tuning of the neuron along both orientation and frequency dimensions. The DNM accounts for this by positing separate bandwidth parameters (h_Θ and h_F in Table 2) for the respective pooling weights of the suppressive drive (Eqs. 21 and 20). Note that the cross-orientation suppression mechanism should be distinguished from the cross-orientation suppression effect. The former is a theoretical construct that is reified in the suppressive drive of the DNM, whereas the latter is a measurable mask-induced reduction of the firing rate relative to a baseline. We probe the tuning properties of the suppression effect to test the model and to estimate physiologically plausible ranges for various model parameters, keeping in mind that the effect depends on nonlinear interactions among multiple mechanisms.

The strength of suppression depends on orientation for some V1 neurons (e.g., the complex cell in Fig. 16D).¹⁸ In nearly all such cases, the suppression is weakest at mask orientations that are orthogonal to the preferred signal orientation (DeAngelis et al. 1992). The most suppressive region is centered on the preferred orientation. This motivates the DNM specification that the peak of the orientation pooling kernel of the suppressive drive is centered on the preferred orientation Θ* of the stimulus drive (Eq. 21). The DNM performance with standard parameters is plotted in Fig. 16A. The model can account for the qualitative features of the orientation tuning curves of cross-orientation suppression (phenomenon 21 in Table 1; see Busse et al. 2009; Heeger 1992b for earlier accounts based on alternative formulations of the DNM).

The strength of the suppression effect also provides valuable information. It can be quantified by a suppression index SI = 1 − R(I_* + I _× )/R(I_*), where R is the firing rate of the neuron and I_* and I _×  are the signal and mask gratings (see Koch et al. 2016). The suppression index ranges from SI = 0 when the mask has no effect to SI = 1 when the mask shuts down the neuron completely. For example, SI of the maximum suppression effect observed from the V1 neuron in Fig. 16D exceeds 0.95 (see appendix e for details), whereas that from the DNM with the standard parameter set in Fig. 16A is ~0.43. Note that SI depends strongly on the experimental protocol (see, e.g., Table 1 in Priebe and Ferster 2006 for descriptive statistics). Following DeAngelis et al. (1992), we used 25% mask contrast and 15% signal contrast in our simulations of Fig. 16, A–C, H, and I. The DNM can leverage this difference in contrasts to produce near-complete suppression (Fig. 16B). However, this requires implausibly high values for the exponent parameters (e.g., n_n = n_d = 10; see appendix e for details).

The model’s difficulty in producing strong cross-orientation suppression can be traced also to the restrictive specification of the frequency pooling weights $w_{F_i}$ of the suppressive drive. Note that Eq. 20 specifies a Gaussian kernel centered on the preferred excitatory frequency F*. There are indeed real V1 neurons for which the most suppressive frequency is close to the preferred excitatory frequency, e.g., the simple cell in Fig. 16G (DeAngelis et al. 1992), and the model can reproduce this pattern (phenomenon 22, Fig. 16F). However, the assumption that the most suppressive frequency always coincides with the preferred signal frequency is too restrictive, because the two frequencies have been shown to diverge for many V1 neurons (DeAngelis et al. 1992; De Valois and Tootell 1983; Morrone et al. 1982). For the complex cell in Fig. 16J, for example, the most suppressive mask frequency (0.6 cyc/°) was one full octave below the preferred frequency (1.25 cyc/°; Fig. 3, C and D in DeAngelis et al. 1992). Such large eccentricities cannot be emulated by the standard DNM, but it is straightforward to add a free parameter to Eq. 20 to offset the center of the pooling kernel. (See Eq. E3 in appendix e, where the new parameter is denoted μ_F.) The augmented model can emulate both the eccentric frequency curve (Fig. 16I) and the near-complete suppression in the orientation curve (Fig. 16H) with a common parameter set with default exponents (n_n = n_d = 2, μ_F = −1, h_F = 1, α = 0.03, M = 3). Note that the augmented model’s ability to emulate both effects with common parameters is important because the respective physiological data in Fig. 16, D and J, were recorded from a single complex cell (DeAngelis et al. 1992).

Consider the cross-orientation suppression for orthogonal plaids composed of signal and mask gratings with equal contrasts and equal frequencies. The suppression effect produced by the DNM becomes stronger as the grating contrast of such an isocontrast orthogonal plaid increases (Fig. 17). The effect produced by the DNM with the standard parameter set is relatively weak (Bonds 1989) compared with many real V1 neurons (Koch et al. 2016; Priebe and Ferster 2006). The median SI in one sample of 32 simple cells in cat V1 (Priebe and Ferster 2006) was SI = 0.23 for low-contrast (8%) plaids and SI = 0.32 for high-contrast (32%) plaids. In the DNM framework, the relative weakness of the suppression effect can be traced in part to the orientation pooling weights $w_{{\Theta }_i}$ (Eq. 21) in the standard parameter set. The pooling weights are maximal for the channels tuned to the preferred orientation of the stimulus drive and are minimal for those tuned to the orthogonal (i.e., mask) orientation. The weights for the channels stimulated by the mask grating increase as the orientation pooling bandwidth parameter h_Θ increases. In the limit when h_Θ = 90°, the weights become uniform and the DNM can produce SIs in the range 0.2 < SI < 0.4 (dashed line in Fig. 17B), which is consistent with the median SIs reported by Priebe and Ferster (2006).

Fig. 17.

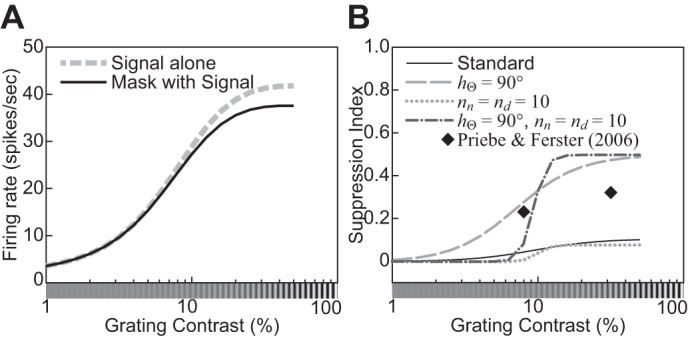
A: contrast response functions of the model neuron with standard parameters for a signal grating alone (dashed line, cf. Fig. 3) and for an orthogonal plaid composed of signal and mask gratings with equal contrasts (solid line). B: the suppression index (SI, defined in text) for the model neuron with 4 different parameter sets is plotted as a function of the contrast of either grating in an isocontrast plaid. Key indicates which parameters have been modified from their standard values (Table 2). The 2 diamonds depict the median SIs measured for 2 contrasts in a sample of 32 simple cells (Priebe and Ferster 2006, Table 1, anesthetized cat).

The mask grating affects the contrast response function (CF) of V1 neurons (phenomenon 23; Carandini 2004; Freeman et al. 2002; Morrone et al. 1982). It has been shown that variants of the DNM can account for this effect (Carandini et al. 1997; Carandini and Heeger 2011; Freeman et al. 2002; Heeger 1992b). Figure 18B shows representative physiological data (Freeman et al. 2002), and Fig. 18A shows our simulation results of a DNM neuron with the standard parameter set. Note that the empirical CFs in Fig. 18B are truncated on the left because the experimental protocol did not include stimuli with near-zero grating contrasts. The CF of the DNM neuron shifts rightward/downward¹⁹ as the mask contrast c_m increases. The amount of this shift depends nonlinearly on c_m: the shift is negligible for c_m < 12% and substantial for c_m ≥ 12%. This pattern agrees with the physiological results. When the neuron’s response is plotted as a function of the mask contrast c_m (Fig. 18, C and D), the resulting graphs shift upward and scale up vertically as the contrast of the signal grating increases.

Fig. 18.

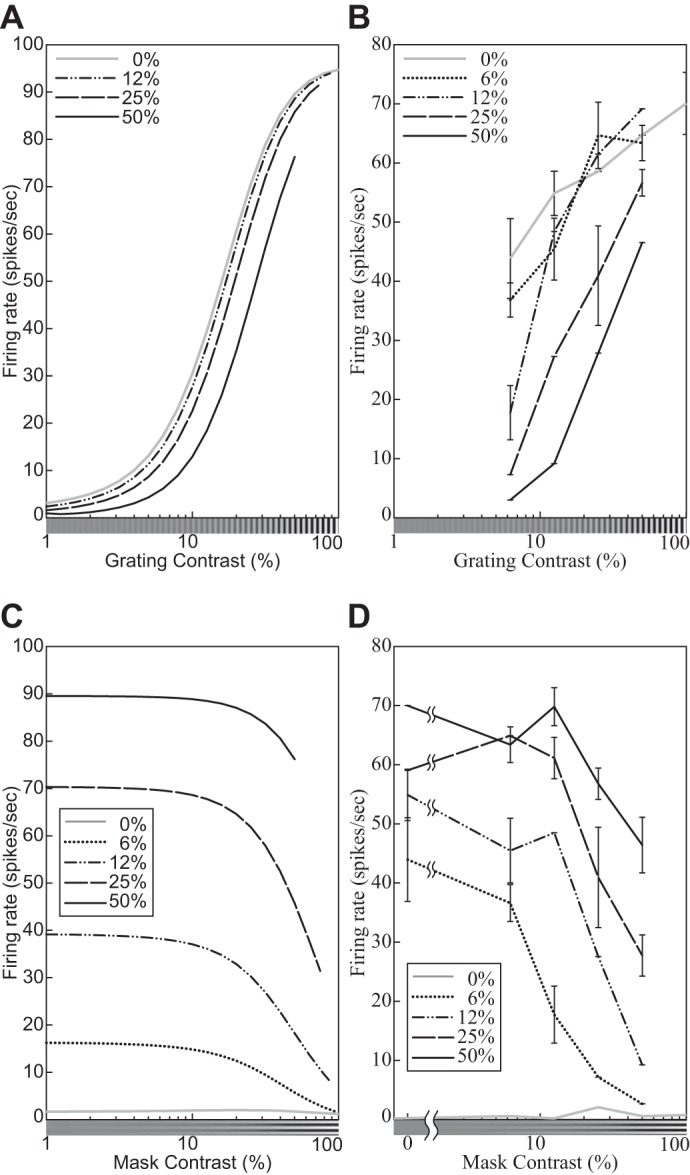
Effect of cross-orientation suppression on the contrast response functions of the model neuron with standard parameters (A and C) and a V1 neuron (replotted from Freeman et al. 2002, Fig. 6, anesthetized cat) (B and D). In A and B, the responses of the model and real neurons are plotted against the contrast of the signal grating, with mask contrast shown in key. In C and D, the responses are plotted against the contrast of the mask grating, with signal contrast in key. A and C: the size of the stimuli was equal to the measured RF diameter (0.81°). The orientations of the signal and mask gratings were 0° and 90°, and their spatial frequency was 2.0 cpd. (See phenomenon 23 in Table 1.)

surround suppression.

The responses of real neurons to a grating patch within the neurons’ measured RF tend to be suppressed by an annular grating surrounding the RF. This surround suppression tends to be strongest when the orientation and frequency of the annular grating are the same as those the neuron is tuned to (phenomena 24 and 25; Blakemore and Tobin 1972; Cavanaugh et al. 2002b; DeAngelis et al. 1994; Li and Li 1994; Nelson and Frost 1978; Ozeki et al. 2004, 2009; Self et al. 2014; Sillito et al. 1995). The experimental protocols are similar to those for cross-orientation suppression, except that the mask (annular) grating surrounds the signal rather than being superimposed on top of it. The ranges of the surround suppression in both orientation and frequency are wider than the respective tuned bandwidths. These trends were captured by the DNM neuron with standard parameters (Fig. 19).

Fig. 19.

The effect of surround suppression on the response of the model neuron with standard parameters (A and C), a V1 complex cell (replotted from Cavanaugh et al. 2002b, Fig. 2B, anesthetized macaque; error bars =  ±SE) (B), and a V1 simple cell (replotted from Li and Li 1994, Fig. 7C, anesthetized cat; error bars =  ±SE) (D) in the orientation and spatial frequency domains. In all panels, the solid line plots the neuron’s response to a composite stimulus consisting of a center grating and a surrounding annulus, whereas the dashed line plots the standard tuning function as probed with the center alone. x-Axis represents the orientation (A and B) or frequency (C and D) of the surrounding annulus for composite stimuli (solid lines) or that of the center for simple stimuli (dashed lines). A and C: the contrast of the center grating was 100%, and its diameter was 0.81° (the measured RF). The contrasts of the annulus grating were 100% and 5.76°. The frequency of the center and annular gratings was 2.0 cpd for A. Their orientation was 0° for C. (See phenomena 24 and 25 in Table 1.)

The contrast response function (CF) of real neurons is affected by the contrast (phenomenon 26, Fig. 20; Carandini 2004; Cavanaugh et al. 2002a; DeAngelis et al. 1994) and the orientation (phenomenon 27, Fig. 21; Cavanaugh et al. 2002b) of an annular grating surrounding the classical RF. The CF of the DNM neuron shifts rightward/downward as the contrast of the annular grating increases (Fig. 20A; see Carandini and Heeger 2011 for an alternative DNM variant fitted to the same type of physiological data). This shift is larger when the annular grating is parallel to the preferred orientation of the DNM neuron than when it is orthogonal (Fig. 21A). These trends agree with the physiological results in Fig. 20B and Fig. 21B. The slope of the CF of the model neuron can be modulated by the annular grating, too. With a different parameter set (n_n < n_d), the CF of the DNM neuron became shallower as the contrast of the annular grating increased (Fig. 20C). The same trend has been observed for some V1 neurons (Fig. 20D; Carandini 2004). It is worth pointing out that that the contrast affects the strength of surround suppression and its orientation tuning. Specifically, Fig. 21A shows that the suppression effect of the DNM neuron is weaker and more orientation dependent at higher contrasts (e.g., by factors of 0.72 for parallel and 0.93 for orthogonal at 100% contrast) compared with lower contrasts (e.g., 0.34 for parallel and 0.45 for orthogonal at 10% contrast). The same trend is detectable for the V1 simple cell in Fig. 21B.

Fig. 20.

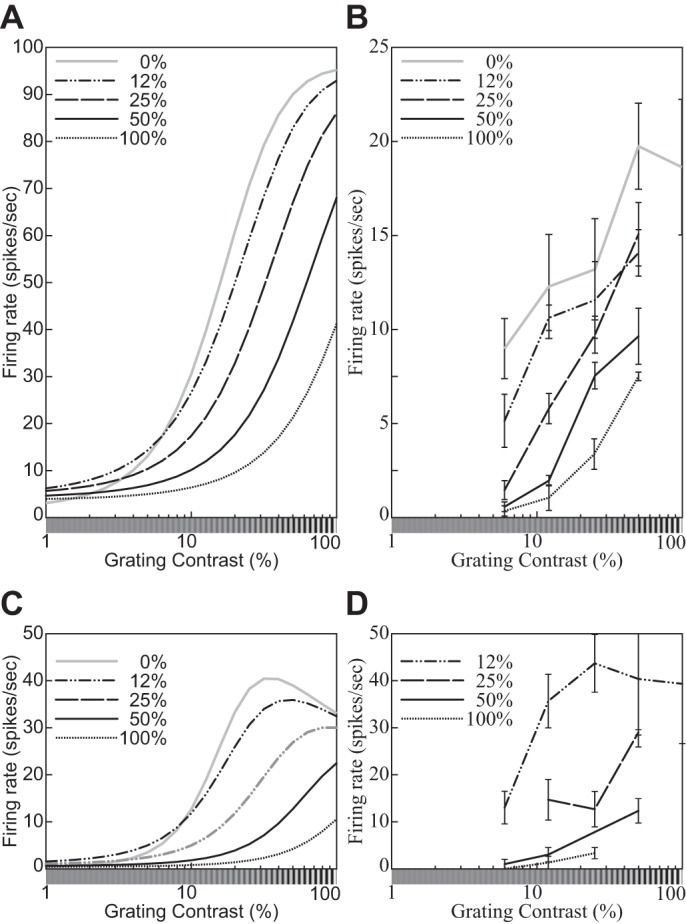
Surround-suppression effects on the contrast response functions for different contrasts of the annular grating. The contrast of the central disk is plotted on the x-axes, and the contrast of the annular surround is indicated in the key. A: the model neuron with the standard parameter set (cf. Table 2). B: a complex cell in cat V1 (replotted from Carandini 2004, Fig. 6). C: the model neuron with a modified parameter set (n_n = 2.8, n_d = 3.0, M = 10). D: a complex cell in cat V1 (replotted from Carandini 2004, Fig. 7). A and C: orientation and spatial frequency of the center and annulus gratings were 0° and 2.0 cpd. Diameter of the center grating patch was 0.81° and is equal to the measured RFs of the model neuron for both parameter sets. Size of the annulus grating was 5.76°. (See phenomenon 26 in Table 1.)

Fig. 21.

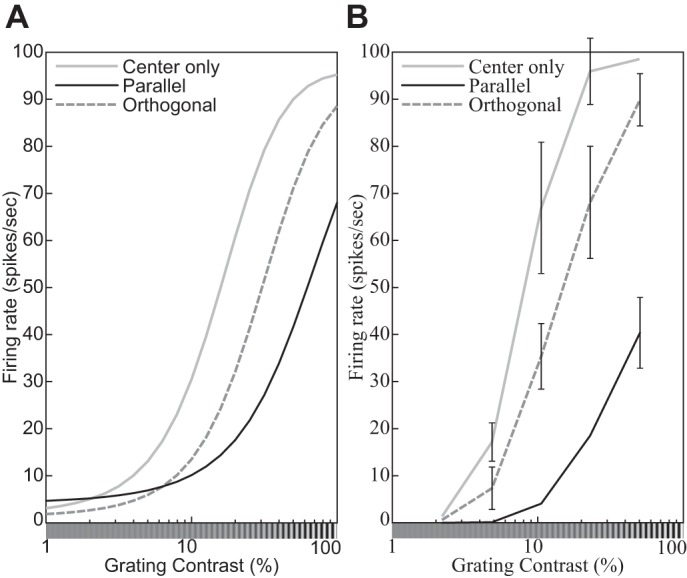
Surround-suppression effects on the contrast response functions for different orientations of the annular grating (indicated in key). A: the divisive normalization model (DNM) neuron with standard parameters. B: a simple cell (replotted from Cavanaugh et al. 2002b, Fig. 5A, anesthetized macaque; error bars =  ±SE). A: orientation of the center grating was 0°. Spatial frequency of the center and annulus gratings was 2.0 cpd. Size of the center grating patch was equal to the measured RF diameter (0.81°). Size of the annulus grating was 5.76°. (See phenomenon 27 in Table 1.)

Because cross-orientation and surround suppression show analogous trends in real V1 neurons, they are modeled jointly by the aggregate suppressive drive in Eq. 18. Our simulations showed that Eq. 15 as presently formulated can account for many signature patterns of the static (steady state) responses associated with both cross-orientation and surround suppression to some extent. A strong cross-orientation suppression effect could be emulated by the DNM with a modified parameter set (Fig. 16, B and F) or with an augmentation of the model specification itself (appendix e; Fig. 16, H and I). In fact, converging physiological evidence suggests that the two types of suppression arise from distinct mechanisms (see The suppressive drive for references and discussion). We need more systematic studies that compare these two types of suppression to determine whether and how they can be integrated into a single functional model.

It is also worth pointing out that even though Eq. 15 has only one suppressive term, this term produces quantitatively nonidentical response patterns when probed with a circular grating patch (cross-orientation suppression) compared with an annular grating with a gray “hole” (surround suppression). Figure 22 compares the orientation and spatial-frequency tuning of the suppressive drive for the grating patch and the annular grating with the standard DNM parameters. The orientation bandwidth is slightly wider for the patch (86.4°, cross-orientation suppression) than the annulus (78.9°, surround suppression), whereas the frequency bandwidth is narrower for the patch (2.10 oct) than the annulus (2.44 oct). These effects arise from differences in the visual stimuli used in the respective experimental protocols rather than from separate suppressive terms in Eq. 15. The grating patch is not large enough to cover the entire spatial integration fields of the channels tuned to low spatial frequencies (Eqs. 3 and 4).

receptive fields of simple cells.

The RF of a real simple cell is composed of bright- and dark-excitatory subregions. This composition has been mapped with local stimulus probes such as a light spot (Hubel and Wiesel 1959; Volgushev et al. 1996), light and dark spots (Lampl et al. 2001), a light bar (Andrews and Pollen 1979), light and dark bars (Glezer et al. 1982; Kulikowski and Bishop 1981; Kulikowski and Vidyasagar 1986; Movshon et al. 1978b; Tadmor and Tolhurst 1989), and the reverse correlation method (DeAngelis et al. 1993a, 1993b; Gardner et al. 1999; Jones and Palmer 1987b; Moore and Freeman 2012; Nishimoto et al. 2006; Ringach 2002; Smyth et al. 2003). The classical RF of the DNM simple cell was also mapped with these methods (Figs. 23 and 24, phenomena 28 and 29). Note that the firing rate of a real simple cell becomes lower than its maintained discharge ($M{\lfloor \beta \rfloor }^{n_{\mathrm{n}}}/{\alpha }^{n_{\mathrm{d}}}$) when the light spot stimulates its dark-excitatory subregions (Hubel and Wiesel 1959; Fig. 23) or the light and dark bars stimulate its dark- and bright-excitatory subregions, respectively (Andrews and Pollen 1979; Fig. 25C). This effect can be observed with the DNM simple cell only when its maintained discharge in the absence of external stimulation is high enough to reveal the inhibitory effect of a light-spot probe. This occurs when $M{\lfloor \beta \rfloor }^{n_{\mathrm{n}}}/{\alpha }^{n_{\mathrm{d}}}\gg 0$.

Fig. 23.

Receptive field maps obtained with a light spot as a probe for 3 divisive normalization model (DNM) simple cells (standard parameters) with different phases ϕ. Grayscale levels indicate firing rates. Maintained discharge (the response to a uniform gray field) was the same for the 3 cells and is indicated by arrowhead on color bar. The size of the light-spot probe was 0.045° × 0.045° (1 pixel). Stimulus background was uniform gray, and luminance of the spot was twice as high as the background gray. (See phenomenon 28 in Table 1.)

Fig. 24.

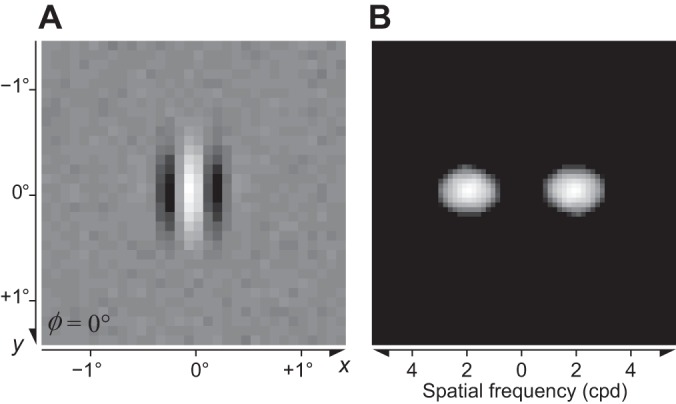
A: the receptive field of a divisive normalization model (DNM) simple cell (standard parameters) obtained via the reverse correlation method. Brighter and darker regions represent bright- and dark-excitatory regions, respectively. B: 2D Fourier spectrum energy distribution of the RF pattern in A. The stimuli were 32 × 32 mosaics of random luminance spots (white noise). Size of the stimuli was 2.88°, and that of the spots was 0.090° (2 × 2 pixels). (See phenomenon 29 in Table 1.)

Fig. 25.

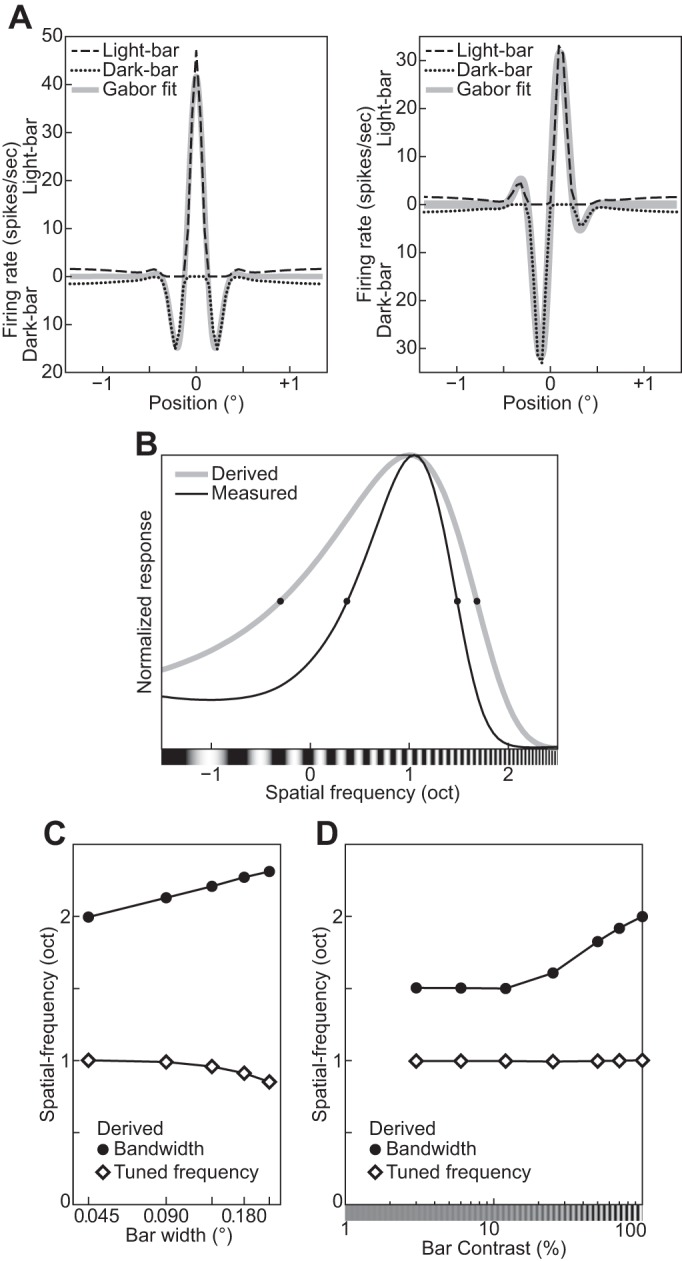
A: measured 1D distributions of the responses to light and dark bars parallel to the tuned orientation of the divisive normalization model (DNM) simple cells with different phases Φ: 0° (left) and 90° (right). x-Axis represents positions of the bars along an orientation perpendicular to the tuned orientation. Top half of the graph is for the light bar, and bottom half of the graph is for the dark bar. The best-fitting 1D Gabor pattern is superimposed (in gray) for comparison. The background of the stimulus was uniform gray, and the luminance of the bars was 0 (dark) or twice as high as the background gray (light). The width of the bars was 0.045° (1 pixel). B: spatial-frequency tuning functions of the DNM simple cell derived (gray line) from the 1D pattern of its RF in A and measured (black line) with a grating. C: effect of the width of the bars on the tuned spatial frequency derived from the measured RF as in A. D: effect of the contrast of the bars. (See phenomenon 30 in Table 1.)

Consider a hypothetical simple cell that acts as a purely linear filter of the visual stimulus. Under this linearity assumption (cf. Linear rectification model of simple cells and energy model of complex cells), the bandwidths in the orientation and spatial frequency-domains can be derived from the 2D composition of its bright- and dark-excitatory subregions in its RF in the image domain (Eqs. 3 and 4; Graham 1989; Lathi 2005). However, the derived bandwidths of real simple cells tend to be wider than these measured directly with gratings of various orientations and frequencies (Gardner et al. 1999; Nishimoto et al. 2006; Ringach 2002; Tadmor and Tolhurst 1989; see also orientation and spatial-frequency tuning). These results suggest that real simple cells are nonlinear. This discrepancy of the bandwidths is also observed with the model simple cell (Fig. 24 and Fig. 25B). The derived bandwidths in the orientation and the frequency domains were 42.6° and 1.53 oct with the reverse correlation method and were wider than those measured with a grating (31.8° and 1.11 oct). This trend could be observed from the DNM cell if n_n > 1 (see Gardner et al. 1999). Note that the derived bandwidths were rather close to the specified bandwidths of the stimulus drive (40° and 1.5 oct). Several other parameter sets (including n_n < 1) were tested, and this similarity was observed reliably.

Note that the stimulus probe itself could also affect the results. Recall that the RF could be measured with a bar as the probe. However, as the bars become wider, the derived bandwidth became wider and the tuned frequency derived was lower (Fig. 25C). This underestimation of the tuned frequency was also observed in the physiological data (Tadmor and Tolhurst 1989). The derived bandwidth was also affected by the contrast between the black and white bars (Fig. 25D).

Summary and discussion.

The results of our simulation experiments show that the model neuron based on the divisive normalization Eq. 15 can account for many physiological phenomena (Table 1) with a standard parameter set (Table 2). A few other phenomena can also be accounted for, but they require customized parameter sets. Certain aspects of the frequency tuning function of the cross-orientation suppression effect require an additional free parameter (Fig. 16, H and I; see appendix e for details). On the basis of these simulation results and of mathematical analyses, we can make some falsifiable predictions that can be used to test the divisive normalization model (DNM).

All predictions involve probing a single neuron with multiple stimuli. The theoretical constraints stem from the fact that the model parameters must be fixed for each individual neuron. Thus certain patterns are expected to occur together in the responses of a given neuron because they all depend on a single model parameter. In particular, the baseline parameter β in Eq. 15 gives rise to interesting constraints. We have shown that the following three phenomena can be produced by the model only when β is sufficiently large:

1) The dark-excitatory subregions of a simple cell probed with a single light spot (Hubel and Wiesel 1959) can be observed only when $M{\lfloor \beta \rfloor }^{n_{\mathrm{n}}}/{\alpha }^{n_{\mathrm{d}}}\gg 0$. This condition ensures that the DNM simple cell has a substantial maintained discharge in the absence of external stimulation. This is necessary to reveal the inhibitory effect of a light-spot probe (phenomenon 28, Fig. 23).

2) The supersaturation effect (phenomenon 8, Fig. 10) can occur in the model only when $\beta >(1+{\alpha }^{n_{\mathrm{d}}})n_{\mathrm{n}}/n_{\mathrm{d}}-1$ (Eq. 23). Recall from contrast response function that this effect refers to the nonmonotonicity of the contrast response function of some V1 neurons. (Note that the majority of V1 neurons have monotonically increasing CFs.)

3) Finally, the widening of the bandwidths in the orientation and spatial-frequency domains with decreasing stimulus contrast (phenomenon 18, Fig. 14, D and H; see also phenomenon 17) can occur in the model only when β > 0.

Because of their dependence on a common parameter, the DNM predicts a correlation among these three phenomena if they are tested for each individual cell in a sample of V1 neurons recorded in a physiological experiment.

These interlocking patterns are methodologically important because they show that the DNM is constrained enough to be falsifiable even though it has 10 free parameters that give it the flexibility it needs to account for the diversity of V1 neurons. This novel theoretical result emerges from the examination of a comprehensive suite of phenomena within the framework of a single model with consistent parameters.

The model also provided alternative interpretations of a few phenomena observed in physiological studies. For example, the effect of stimulus size on the orientation and frequency bandwidths of real V1 neurons (see Fig. 13). The measured bandwidths depend on the size of the grating patch, and the size that maximizes the bandwidths is larger than the measured RF of the neuron. This occurs because RF mapping methods tend to underestimate the true extent of the weighting function (WF) of the linear filtering stage of the model neuron. The periphery of the WF of the model neuron is hidden by an annular region of the surround suppression, which narrows down the measured RF of the model neuron. This means that the stimulus patch must be larger than the measured RF to fill the true WF. Note that our simulations show that the surround suppression itself actually makes the bandwidths of the DNM neuron wider (see orientation and spatial-frequency tuning).

The tuning bandwidths of real simple cells are often narrower when measured directly in the orientation and spatial-frequency domains compared with those derived from the mapped spatial patterns of the RFs (see Fig. 25). This discrepancy from linearity has often been explained by the exponentiation of the stimulus drive with n_n > 1 (DeAngelis et al. 1993b; Gardner et al. 1999; Moore and Freeman 2012; see also Fig. 2) and/or by the so-called iceberg effect, which occurs in our model when β < 0 (Carandini and Ferster 2000; Sompolinsky and Shapley 1997; Tadmor and Tolhurst 1989; Volgushev et al. 2000). If β < 0, the measured bandwidths of the model neuron become narrower because its tuning curves shift downward (Tadmor and Tolhurst 1989), and the bandwidths derived from the measured RF of the model neuron become wider because the measured RF itself becomes smaller in size (Bringuier et al. 1999). Note that $\beta \gg -1$ and the iceberg effect cannot be very large. Otherwise, it would not be possible to measure the RF of the model neuron with a local stimulus probe or the reverse correlation method because the outputs of the stimulus drive to these images would be too small. The present simulations (Fig. 25) show that the model can produce such discrepancy from linearity even when β > 0. Across its parameter range, the model produces discrepancy from linearity due to the exponentiation with n_n > 1 in the numerator of Eq. 15 (DeAngelis et al. 1993b; Gardner et al. 1999; Moore and Freeman 2012). Besides, the denominator of the DNM also plays an important role for the discrepancy. The tuning curves of the DNM can be wider than those of the stimulus drive even with n_n > 1 if the tuning curves of the denominator (see Fig. 22) are narrowly tuned.

A few studies have shown that the size of the grating patch also bears some relationship to the preferred frequency of real neurons. The peak of the frequency tuning curve of real neurons tends to shift to a higher frequency as the size of the grating patch decreases (Osaki et al. 2011; Teichert et al. 2007). Also, the peak of the size tuning curve of the real neuron tends to shift to a smaller size if the spatial frequency of the grating is higher than the preferred frequency of the neuron (Osaki et al. 2011). These trends were not observed with the DNM neuron used in the simulation experiments. Such trends, however, can be emulated by a model with some additional flexibility. For example, the suppressive drive of the DNM model can be modified so that the suppression in the spatial-frequency domain changes depending on the eccentricity from the center of the RF. These trends can also be expected to be emulated by the modified DNM if the peak of the suppression in the spatial-frequency domain shifts to a higher frequency as eccentricity increases. Another possible modification involves the stimulus drive. Note that Naito and Sato (2015) pointed out that model neurons should be composed of multiple Gabor filters to model these trends. These filters can be tuned to different spatial frequencies, and the sizes of their WFs can be correlated with the tuned frequencies, i.e., smaller WFs are tuned to higher frequencies. Also, following the suggestions of Naito and Sato (2015), analogous modifications can be made to the DNM, composing its stimulus drive from multiple Gabor filters. This latter modification would change the properties of the DNM quite radically.

It is instructive to compare the stimulus and suppressive drives in the DNM Eq. 15. These two terms were differently affected in our simulations by the size and spatial frequency of a grating (see phenomena 4 and 16; Fig. 5C, Fig. 8C, Fig. 13, C and F, and Fig. 22). The frequency bandwidth of the stimulus drive becomes narrower as the diameter of the grating patch increases, whereas that of the suppressive drive becomes wider (Fig. 13). This difference arises because the stimulus drive is a single Gabor filter (Linear rectification model of simple cells and energy model of complex cells) whereas the suppressive drive comprises multiple filters (or channels, Divisive normalization model) in our formulation of the DNM. The channels have different preferred frequencies but the same frequency bandwidth. Because of the common bandwidth, the size of the spatial integration field varies inversely with the preferred frequency across channels (Eq. 4). Consequently, stimuli with intermediate diameters cannot stimulate the lower-frequency channels well but do stimulate the higher-frequency channels. The DNM can be modified so that its stimulus drive incorporates multiple Gabor filters tuned to different spatial frequencies (see The Stimulus Drive for a review of physiological studies suggesting this idea). This would make the DNM considerably more flexible and hence able to fit a wider range of physiological data. However, it might also produce some undesirable predictions. For example, the frequency bandwidth of such a modified DNM is predicted to become wider as the diameter of the grating patch increases, which would be inconsistent with the overall trend observed in V1 neurons (Osaki et al. 2011; Fig. 13, phenomenon 16). See The Stimulus Drive for further discussion.

General Discussion

Our simulation experiments demonstrated that the divisive normalization model (DNM) can account for a comprehensive set of neurophysiological studies of both simple and complex cells in V1 (Table 1). Moreover, a mathematical analysis of Eq. 15 predicts interdependence between certain observable phenomena. In Simulation Experiments, we explained how these predictions can be tested experimentally, which establishes that the standard formulation of the DNM specified in Divisive normalization model is a falsifiable theory. If this formulation, especially Eq. 15, is modified, the concrete mathematical results proven in the appendices will no longer apply. It seems plausible, however, that analogous results would hold for any formulation based on similar principles. In other words, our theoretical conclusions probably extend to the entire class of models based on a combination of linear filtering, half-wave rectification and squaring, and response normalization (Carandini et al. 2005). Our results ultimately rest on the fact that although adjustable parameters are needed to accommodate the diversity across neurons, they must be fixed for each individual neuron. This fixedness gives rise to falsifiable constraints when a single neuron is probed with a judiciously chosen battery of stimuli.

The DNM qualitatively emulates most of the empirical phenomena listed in Table 1 with the standard parameter set in Table 2. Quantitative comparisons of the DNM with real neurons are also possible, but it would require quantitative estimation of all parameters of the DNM for individual neurons from physiological data. Potentially, the quantitative evaluation of the DNM allows us to compare it with other models of V1 neurons. The interpretability of such quantitative tests, however, would depend on the qualitative validity of the models.

Correlation among model parameters.

The parameters of the model are conceptually independent from one another, but physiological studies have shown correlations among their empirical counterparts. These correlations can potentially decrease the number of independently adjustable parameters or limit the ranges of these parameters. This subsection briefly reviews some studies that suggest correlations among various DNM parameters.

The preferred spatial frequency F of the divisive normalization model correlates with some parameters of the contrast response function (CF). Dean (1981) reported that the preferred spatial frequencies of neurons in cat striate cortex correlated positively with their contrast threshold and negatively with the slope of their CF. Consider the hyperbolic ratio model for simplicity (Eq. 12). Its mathematical analysis shows that the hyperbolic ratio model can account for both these correlations if the semisaturation contrast parameter α_HB correlates positively with the preferred frequency F across the population of model neurons (see Hyperbolic ratio model). Some studies have shown that the bandwidths of V1 neurons tend to be narrower in neurons with higher preferred spatial frequencies (De Valois et al. 1982a; Kulikowski and Bishop 1981; Kulikowski and Vidyasagar 1986; Yu et al. 2010). This effect can be emulated by the DNM if either β, n_d, or h_f decreases or α, n_n, or h_F increases as the preferred frequency F increases. (See Table 2 for the meaning of these symbols.) Note that the tuning bandwidths with respect to spatial frequency and orientation correlate with one another (Zhu et al. 2010). Both of these bandwidths would be affected together if α, β, n_n, or n_d covaries with F.

The RF locations of V1 neurons affect their orientation and frequency tuning. The DNM can emulate this by introducing a correlation between the RF location parameters (X, Y) in Eq. 2 and the tuning preference parameters Θ and F. First, as the retinal eccentricity of the locations increases the preferred frequencies of real neurons decrease (Henriksson et al. 2008; Movshon et al. 1978b; Yu et al. 2010), and this correlation can be represented well by the cortical magnification factor (Daniel and Whitteridge 1961; Duncan and Boynton 2003; Schwartz 1980; Swindale 1996; Tootell et al. 1982). Next, the observed distribution of preferred orientations has a preponderance of vertical or horizontal preferences for neurons with RFs in or near the fovea (De Valois et al. 1982b; Henry et al. 1974) and a preponderance of radial orientations for neurons in the visual periphery (Schall et al. 1986; see also Sasaki et al. 2006b for fMRI results). The results of an fMRI study suggest that human V1 contains more vertically tuned neurons than horizontally tuned neurons (Yacoub et al. 2008). On the other hand, the numbers of the vertical and horizontal neurons found in cat striate cortex are almost equal (Li et al. 2003), whereas rat V1 apparently has a preponderance of neurons with horizontal preferences (Girman et al. 1999). Note also that the neurons tuned to vertical or horizontal orientations, and to high spatial frequencies, have narrower bandwidths in the orientation domain compared with neurons tuned to oblique orientations (Li et al. 2003; Orban and Kennedy 1981).

The stimulus drive.

The present formulation of the divisive normalization model specifies the weighting function of simple cells as a 2D Gabor filter (Eq. 5). There are, however, some other filters that can fit physiological data better than the Gabor filter does (see Stork and Wilson 1990; Wallis 2001 for reviews). All those models of simple cells use a linear filtering stage (cf. Eq. 5) as their first processing step. This linear filtering predicts that the cell’s response will be maximal for a square-wave grating with their preferred frequency, orientation, and phase.

Simple and complex cells are represented in qualitatively different ways in the present formulation of the DNM (see Linear rectification model of simple cells and energy model of complex cells). Hubel and Wiesel’s (Hubel and Wiesel 1959, 1962, 1968; also Bishop and Henry 1972) original classification was based on 2D patterns of the classical RFs. Another classification method was proposed later on the basis of the temporal modulation of the firing rates evoked by a drifting grating (e.g., Andrews and Pollen 1979; Maffei and Fiorentini 1973; Movshon et al. 1978a, 1978c). The key discriminating factor is that simple cells show greater modulation than complex cells. One line of empirical support for this idea is the finding that the magnitude of the temporal modulation tends to have a bimodal distribution across V1 cells. The classifications based on these two methods often agree with one another (Dean and Tolhurst 1983; De Valois et al. 1982a; Henry and Hawken 2013; Mata and Ringach 2005; Sengpiel et al. 1997), but the agreement is not always complete (see Chen et al. 2009; Skottun et al. 1991 for reviews). Also, there are always some neurons whose behaviors fall between the “pure” types defined by either method (Crowder et al. 2007; Hietanen et al. 2013; Kagan et al. 2002; Mata and Ringach 2005; Meffin et al. 2015; Van Kleef et al. 2010). Note that some recent physiological studies (Chance et al. 1999, 2000; Martinez and Alonso 2003; Priebe et al. 2004; see also Mechler and Ringach 2002 for a review) have suggested that the simple and complex cells are better conceptualized as end points of a continuum rather than as a categorical distinction. Mechler and Ringach (2002) showed that the bimodal distribution can be explained by a nonlinear monotonic transformation of the signal and that a bimodal distribution does not necessarily imply two qualitatively different types of neurons. Also, the temporal modulation of the firing rates can be affected by other properties of the visual stimuli. For example, some complex cells show temporal modulation if the contrast of the drifting grating is low (Crowder et al. 2007; Van Kleef et al. 2010; see also Henry and Hawken 2013). The temporal phase of the modulation also changes as a function of stimulus contrast (Albrecht 1995). The temporal modulation of firing rate is also affected by stimulation of the surround regions of the neuron’s classical RF (Bardy et al. 2006). The effect of the surround stimulation on the modulation can be either facilitatory or suppressive depending on the individual neurons.

The numerator of our DNM Eq. 15 includes two types of nonlinear operations: exponentiation and thresholding (see also Eqs. 11 and 10). Both have been considered as possible explanations of various physiological phenomena. These two operations are not mutually exclusive (Finn et al. 2007; Heeger 1992a, 1992b; Priebe and Ferster 2008). The exponentiation (with n_n > 1) has strong empirical support in the measured slopes of the contrast response functions of V1 neurons (Albrecht and Hamilton 1982; Busse et al. 2009), but the support for the thresholding operation is not as clear cut. These two nonlinear operations have been used to explain the observed discrepancy between the tuning curves of real neurons measured directly in the frequency domain with test gratings and the tuning curves derived from the empirical RFs, especially with respect to spatial frequency (phenomenon 30; see Summary and discussion for further discussion). The thresholding operation (β < 0) predicts that both orientation and spatial frequency bandwidths should become wider as the contrast of the stimulus grating increases.²⁰ The opposite trend is predicted when β > 0. On the other hand, the exponential operation predicts contrast invariance of both bandwidths. Thus neither operation by itself can fully explain the empirically observed relations between the stimulus contrast and the two tuning bandwidths. The orientation bandwidths of the real neurons tend to be invariant (Alitto and Usrey 2004; Anderson et al. 2000; Li and Creutzfeldt 1984; Sclar and Freeman 1982; Skottun et al. 1987; Somers et al. 1995; Troyer et al. 1998), whereas there is a weak trend that their frequency bandwidths become narrower as the contrast decreases (Albrecht and Hamilton 1982; Sceniak et al. 2002; Skottun et al. 1987). Note that these are population-level trends and there are many individual neurons that show effects contrary to the prediction based on β < 0 (Alitto and Usrey 2004; Kim 2011; Sceniak et al. 2002; Sclar and Freeman 1982). We have shown that the suppressive drive of the denominator also makes both bandwidths wider and that this widening effect becomes stronger as the contrast increases. This widening effect can be controlled with respect to orientation and frequency individually by adjusting the parameters of the suppressive drive. In sum, the present DNM formulation has enough flexibility to account qualitatively for the observed trends in both orientation and frequency bandwidths.

The stimulus drive in our DNM formulation is composed of a single linear filter for simple cells (Eq. 5) and a pair of linear filters for the complex cell (Eq. 7). The classic reverse correlation method (DeAngelis et al. 1993a, 1993b; Gardner et al. 1999; Jones and Palmer 1987b) allowed mapping of the receptive fields (RFs) of simple cells only. Recent theoretical developments of the reverse correlation make it possible to analyze the RFs of complex cells as well, revealing pairs of Gabor-like image filters in individual complex cells (e.g., Sasaki and Ohzawa 2007; Touryan et al. 2002, 2005). These filters are called subunits. Interestingly, such subunits have also been observed in simple cells, too, and there can be more than two subunits per cell (Chen et al. 2007; Fournier et al. 2014; Rust et al. 2004, 2005; Vintch et al. 2015). Note that various other physiological phenomena can be explained in terms of such subunits. For example, the preferred spatial frequencies of some neurons depend on the size of the test grating patch (Osaki et al. 2011; Teichert et al. 2007). This trend can be explained by multiple subunits tuned to different frequencies (Naito and Sato 2015; see also Summary and discussion). The spatial-frequency tuning (Bredfeldt and Ringach 2002; Frazor et al. 2004; Mazer et al. 2002) and the orientation tuning (Schummers et al. 2007) of some neurons change temporally relative to the onset of the stimulus grating. This temporal effect can be modeled by subunits with different temporal properties. Neurons with weak orientation selectivity (e.g., Tan et al. 2011) also respond to a grating whose orientation is orthogonal to the neuron’s preferred orientation. Such neurons can be modeled by adding a subunit with a radially symmetric weighting function resembling the on/off-center units in the LGN (Goris et al. 2015). Note also that some intracortical interactions among V1 neurons can be modeled better with an additive/subtractive operation in the numerator of the DNM equation than in the denominator (Nassi et al. 2015; Sato et al. 2014). If two differently tuned neurons interact linearly, they can appear as subunits of each other.

Neurons in V1 are tuned to gratings with particular orientations in static images, and many neurons are selective to the motion direction of drifting gratings with specific temporal frequencies (e.g., Jones et al. 2001; Livingstone 1998). Neurons with strong direction selectivity can be modeled by a drifting Gabor filter, which is a 2D Gabor filter whose phase changes over time, whereas neurons with no direction selectivity can be modeled by a 2D Gabor filter whose amplitude modulates temporally between alternating polarities (Adelson and Bergen 1985; Heeger 1992a, 1993). It has been shown that these two 3D filters (temporal sequences of 2D filters) agree with the spatial-temporal RFs of real neurons measured in physiological studies (DeAngelis et al. 1993a, 1993b; McLean et al. 1994). The spatial-temporal RFs that were measured in these studies were qualitatively consistent with the preferred directions and the preferred temporal frequencies of the neurons, but nonlinear operations were required for quantitative fit. Heeger (1993) used 3D filters in his version of the DNM, but it was too simple to account for various other temporal properties. Some of these temporal properties can be captured by introducing temporal dynamics of the CF-related parameters of the DNM (Albrecht et al. 2002), the orientation tuning (Schummers et al. 2007), the spatial-frequency tuning (Bredfeldt and Ringach 2002; Frazor et al. 2004; Mazer et al. 2002), and some interactions among them (e.g., Livingstone and Conway 2007). The various normalization mechanisms in the DNM—gain control, cross-orientation suppression, and surround suppression—differ in their individual temporal properties (see The suppressive drive for some examples). Studying the temporal properties of the neurons can allow us to disentangle these multiple mechanisms and to understand their respective roles (e.g., Butts et al. 2011; Fournier et al. 2014; Levy et al. 2013).

The suppressive drive.

In our formulation of the DNM, both surround suppression and cross-orientation suppression are aggregated in a single suppressive drive (Eq. 18) for simplicity. These two forms of suppression show some analogous properties, and these properties were captured by the DNM to some extent. On the other hand, the simulation experiments show some limitations of our formulation (cf. appendix e). Indeed, there is converging evidence that the two forms of suppression arise from different neurophysiological mechanisms (Angelucci and Bullier 2003; Li et al. 2005; Sengpiel et al. 1998). It has been suggested that cross-orientation suppression consists of multiple components: monocular components from LGN (Li et al. 2006; see also Bauman and Bonds 1991) and between LGN and V1 (DeAngelis et al. 1992; Freeman et al. 2002; Li et al. 2006; Priebe and Ferster 2006; Smith 2006) as well as binocular components from LGN (Sengpiel et al. 1995; Walker et al. 1998) and from intracortical connections within V1 (Endo et al. 2000; Li et al. 2005; Sengpiel and Blakemore 1994; Sengpiel and Vorobyov 2005). Note that the monocular components play a major role in cross-orientation suppression (DeAngelis et al. 1992; Li et al. 2005; Sengpiel and Vorobyov 2005). It has also been suggested that surround suppression consists of multiple components (Angelucci et al. 2002; Angelucci and Bressloff 2006; Angelucci and Bullier 2003; Nurminen and Angelucci 2014; Webb et al. 2005): from LGN (Naito et al. 2007; Ozeki et al. 2004), between LGN and V1 (Webb et al. 2005), from intracortical connections within V1 itself (Ozeki et al. 2009), as well as top-down feedback (Angelucci and Bullier 2003; Bair et al. 2003; Li et al. 2001) from V2/V3 (Nassi et al. 2013, see also Hupé et al. 2001a) and from MT (Hupé et al. 2001b). These various components of cross-orientation and surround suppression have different temporal and spatial properties (e.g., Bair et al. 2003; Knierim and van Essen 1992). Any version of the DNM that aims to model the temporal dynamics of neurons’ responses (and not just their steady-state responses as our version does) will have to take into account the diverse temporal properties of these various suppression mechanisms. The following paragraphs provide some entry points to this rich and growing literature.

Cross-orientation suppression is mostly (though not exclusively) monocular (DeAngelis et al. 1992; Li et al. 2005; Sengpiel and Vorobyov 2005), while surround suppression is mostly binocular (DeAngelis et al. 1994). These two types of suppression also differ in other respects. Consider their latencies. The latency of cross-orientation suppression is substantially shorter than that of surround suppression and even shorter than that of the response to optimal excitatory stimuli measured in the same cells (Smith et al. 2006). The latency of surround suppression depends on its sources. For example, the corticocortical feedback contribution to surround suppression in V1 lagged behind the initial responses of the neurons by ~20 ms from V2 and V3 (Nassi et al. 2013, alert macaque) and by <10 ms from MT (Hupé et al. 2001b, anesthetized macaque). The latency of surround suppression also depends on the distance between the classical RF of the target neuron and the location of the inducing stimulus—the farther out the surrounding inducer, the slower and weaker the suppressive influence (Bair et al. 2003). These effects are consistent with the basic fact that the latency and strength of the connection between two cortical neurons depend on the distance between them (Bringuier et al. 1999; Grinvald et al. 1994). There is also evidence that the surround suppression with a short delay (~7 ms) after the initial response is isotropic, whereas that with a long delay (20 ms) is selective to the orientation of the surround stimuli (Knierim and van Essen 1992). The LGN is a plausible source for the faster isotropic suppression, given the (nearly) orientation invariance of many LGN neurons (see Bonin et al. 2005; Zaltsman et al. 2015 for reviews). Note that both types of suppression can be induced by a drifting grating whose temporal frequency is above 10–15 Hz for most neurons (Durand et al. 2007). This frequency is too high to elicit excitatory response in most V1 neurons (Ikeda and Wright 1975; Movshon et al. 1978b; Saul and Humphrey 1992). This high temporal resolution of the surround suppression can be explained by feedforward signals from LGN and/or feedback signals from MT. Neurons in LGN and MT have higher temporal resolution than those in V1. On the other hand, only LGN seems to play a major role in the cross-orientation suppression considering the short latency of the latter.

The responses of some neurons are facilitated in a nonlinear manner by stimuli outside their classical RFs (Cavanaugh et al. 2002b; Jones et al. 2001; Kapadia et al. 1995; Levitt and Lund 1997; Li and Li 1994; Maffei and Fiorentini 1976; Nelson and Frost 1985; Polat et al. 1998; Sillito et al. 1995; Vinje and Gallant 2000; see Fitzpatrick 2000 for a review) as well as by stimuli within the classical RFs (Bonds 1989; De Valois and Tootell 1983; Walker et al. 1998). The facilitatory stimuli differ depending on the individual neurons. The facilitatory effect can arise from intracortical connections within V1 and/or feedback from higher cortical areas. Optogenetic stimulation of neurons in V1 facilitates the responses of other V1 neurons (Li et al. 2013; Nassi et al. 2015; Sato et al. 2014;). The facilitatory (as well as the suppressive) effect was not affected by inactivation of V2 (Hupé et al. 2001a), but it was weakened (or eliminated) by inactivation of V2 and V3 (Nassi et al. 2013). Also, the surround stimuli themselves can cause an excitatory signal and evoke firing responses in many neurons without any stimulation within the classical RFs with a very long latency (≥100 ms; Li et al. 2001; Rossi et al. 2001). The latency of this excitatory effect from the surround stimuli does not depend on the distance of the surround stimuli from the RFs (Rossi et al. 2001). This constant latency of the excitatory effect suggests that this effect cannot be attributed to intracortical connections because the temporal delay of a signal mediated by these connections depends on the distance on the retina.

In this article, the spatial pooling weights of the DNM suppressive drive are specified for simplicity according to a radially symmetric 2D Gaussian kernel (Eq. 19). The spatial properties of surround suppression in real V1 neurons, however, are not so homogeneous. Different regions surrounding the classical RF of a V1 neuron can cause suppression with different magnitudes (DeAngelis et al. 1994; Vinje and Gallant 2000) and can have different patterns of suppression with respect to orientation (Cavanaugh et al. 2002b; Li and Li 1994; Nurminen and Angelucci 2014; Shushruth et al. 2013). The suppression and facilitation from the surround region can also depend on the spatial context within and outside the classical RF (Jones et al. 2001; Kapadia et al. 1995; Polat et al. 1998). A judicious combination of surround suppression and surround facilitation with appropriate temporal and spatial characteristics can account for a neuron’s tuning to more complex visual features (e.g., Craft et al. 2007; Fitzpatrick 2000; Grossberg and Mingolla 1985; Li 1998, 2000).

Directions for future work.

In this study, we considered only simple synthetic stimuli within a limited spatial context under static (or steady state) experimental conditions. We did not assess the performance of the model under a more ecologically valid stimulation. Of course, the visual system has evolved to deal with natural visual stimuli rather than synthetic stimuli such as gratings. There is ample physiological evidence in support of this idea. For example, natural stimuli produced more reliable response patterns across trials compared with those produced by synthetic gratings. In addition, the spike trains induced by natural stimuli had more consistent timing across trials, greater sparseness, and higher signal-to-noise ratio than those induced by gratings (Baudot et al. 2013; see also Touryan et al. 2005). Sparse spike trains with high signal-to-noise ratio are evidence for efficient coding of the visual stimuli. It has been shown that suppression plays a critical role for improving the reliability, precision, signal-to-noise ratio, and sparseness of individual neurons (Haider et al. 2010; Vinje and Gallant 2000; Zhu et al. 2015; see also Butts et al. 2011 for analogous results in LGN neurons). The suppression also contributes to the sparseness at the population level (Vinje and Gallant 2000). That is, the number of the responding neurons decreases and the interneuronal correlations decrease. This tuning to natural visual stimuli allows the visual system to efficiently encode visual information in our everyday life (Barlow 2001; Simoncelli and Olshausen 2001). On the other hand, Rust and Movshon (2005) warned about the interpretative difficulties inherent in the use of such complex stimuli. One important direction for future work is to identify which aspects of natural stimuli are the basis for their preferential treatment by the visual system compared with synthetic stimuli. For example, the reliability of the neuronal responses improves when the spectral power distribution of the natural stimuli follows the statistics of natural images (Rikhye and Sur 2015). It can be interesting to test whether any synthetic visual stimulus with the natural spectral power distribution (Field 1987) can improve the reliability of the neuronal responses in a similar manner. Experiments of this sort can test whether the natural spectral power distribution is necessary or sufficient for the improvement in reliability. Such knowledge would help to improve the DNM specification and especially the composition of its normalization pool.

Our review is focused on relatively simple (first order) properties of the stimuli, despite the fact that the responses of many real neurons can be affected by higher-order visual information including figure-ground organization (Hupé et al. 1998; Lamme et al. 1999; Lee et al. 1998; Rossi et al. 2001; Zhang and von der Heydt 2010; Zhou et al. 2000), 3D context (Murray et al. 2002, 2006), perceptual filling-in (Fiorani Júnior et al. 1992; Komatsu 2006), and visual illusions (Ramsden et al. 2001; see also Jancke et al. 2004 for a brain imaging study). This means that no model can fully replicate the response of a neuron to natural stimuli unless such higher-order information is taken into account. On the other hand, extracting such higher-order information from a retinal image is an open research problem. One practical way to circumvent this problem would be to prepare the higher-order information in advance and make it available to the model as its inputs from a top-down process.

The divisive normalization model (DNM) has also been used to fit physiological results of populations of neurons in V1 (Busse et al. 2009; Goris et al. 2009). Note that modeling populations is different from modeling single cells, for several reasons: First, a population may be able to process visual information better than individual neurons by forming a population code in which different neurons specialize in encoding different aspects of the input signal (deCharms and Zador 2000; Pouget et al. 2003). For example, the neuronal population in V1 can systematically represent the second-order visual information, while only a subset of the individual cells in V1 respond selectively to second-order stimuli (e.g., An et al. 2014). This complicates the derivation of model predictions about the population response because a given physiological phenomenon may have two possible explanations: one in terms of a population code and another in terms of the properties of individual neurons. Another difficulty arises from the selective sampling of neurons in physiological experiments. It has been pointed out that recordings from some neurons are often excluded from the data set, producing a selection bias that can affect the experimental results (Olshausen and Field 2005). Therefore, the physiological results of the population can change depending on which neurons are included/excluded in the population. This can add extra parameters to the model of the population. On the other hand, selection bias is less critical for single-cell recording because the model aims to account for the response properties of individual neurons. These differences suggest that different approaches may be required to model populations of neurons as opposed to modeling individual neurons. One fruitful area for future research is to explore the degree to which the divisive-normalization equation is applicable to both cases.

In conclusion, the DNM provides a useful functional characterization of the responses of simple and complex cells in V1. It deserves to be designated as “the standard” model for many present purposes (e.g., Carandini and Heeger 2011). We hope that the standard formulation proposed here, the standard parameter set, and the accompanying software implementation will facilitate future research based on this influential and successful model. Of course, the DNM will be supplanted and/or subsumed by future, more advanced models, just as it subsumed the “standard” linear model of the 1980s (Rust and Movshon 2005). It seems particularly desirable to augment the DNM with mechanisms to account for the temporal dynamics of neuronal responses (e.g., Brosch and Neumann 2014; Heeger 1993). Accounting for this temporal dimension, however, poses interesting challenges. It is hard to see, for example, how a simple functional model can account for the temporal properties of surround suppression (and facilitation), which are attributable to several different sources as discussed above. Such an augmented model would need additional components and new adjustable parameters. Ideally, the components and parameters should have biologically plausible interpretations that relate to physiological and/or anatomical data. Developing the DNM along those lines will bring it closer to a structural model.

GRANTS

This project was supported by National Eye Institute Research Grant R21 EY-022745-01.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

T.S. and A.A.P. conceived and designed research; T.S. performed experiments; T.S. analyzed data; T.S. interpreted results of experiments; T.S. prepared figures; T.S. drafted manuscript; T.S. and A.A.P. edited and revised manuscript; T.S. and A.A.P. approved final version of manuscript.

APPENDIX A: TUNING FUNCTIONS OF A 2D GABOR FILTER

Consider the orientation and spatial-frequency tuning functions of a 2D Gabor filter (Eqs. 2 and 5) with preferred frequency F (cycles/°, cpd) and preferred orientation Θ (°). The orientation tuning function of this filter is cyclic and becomes maximal at Θ and Θ + 180°. The two peaks have the same shape, and the orientation bandwidth h_θ (°) is defined as the width of each peak at its half height. The orientation tuning function for a grating with spatial frequency F is equivalent to a circular cross section of the 2D Fourier transform of the filter, taken along a circle centered in the origin of the Fourier space and having a radius that corresponds to F. Note that a Fourier spectrum energy distribution of a 2D Gabor filter is a 2D Gauss distribution (see Figs. 2.10 and 2.11 in Graham 1989). Then, the relation between the orientation bandwidth h_θ and the bandwidth $h_{\breve{y}}$ of the Gabor filter at its preferred frequency F can be written as follows (see Tables 2.2 and 2.4 in Graham 1989; see also our Fig. 1 for an illustration of $h_{\breve{y}}$):

$$h_{\stackrel{⌣}{y}}=\frac{4\ln 2}{\pi F\frac{\pi h_{\theta }}{180}}=\frac{720\ln 2}{{\pi }^{2}F{h}_{\theta }}$$ (A1)

The spatial-frequency tuning function is unimodal and has a maximum at the preferred frequency F (cpd; cf. Fig. 2D). Its bandwidth h_f (oct) is defined as the distance between two frequencies F_low and F_high (cpd) at the half height of the function where F_low < F_high. Then, the relation among F, F_low, F_high, and h_f is

$$\{\begin{array}{l}{F}_{\mathrm{l}\mathrm{o}\mathrm{w}}+F_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}=2F\\ F_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}/F_{\mathrm{l}\mathrm{o}\mathrm{w}}=2^{h_f}\end{array}$$ (A2)

From Eq. A2, the bandwidth F_high − F_low in cycles per degree can be derived as follows:

$$F_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-F_{\mathrm{l}\mathrm{o}\mathrm{w}}=2F\frac{2^{h_f}-1}{2^{h_f}+1}$$ (A3)

Recall that the Fourier spectrum energy distribution of a 2D Gabor filter is a 2D Gauss function. The spatial-frequency tuning function of the filter for a grating with orientation θ is equivalent to a radial cross section of the Gauss function along a ray from the origin and with orientation θ + 90°. Then, the relation between the frequency bandwidth F_high − F_low and the bandwidth $h_{\breve{x}}$ of the Gabor filter at its preferred orientation Θ can be written as follows (see Tables 2.2 and 2.4 in Graham 1989; see also our Fig. 1 for an illustration of $h_{\breve{x}}$):

$$h_{\stackrel{⌣}{x}}=\frac{4\ln 2}{\pi \left(F_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-F_{\mathrm{l}\mathrm{o}\mathrm{w}}\right)}$$ (A4)

From Eqs. A3 and A4, the relation between $h_{\breve{x}}$ and h_f can be written as follows:

$$\{\begin{array}{l}{h}_f={\log }_2\frac{\pi F{h}_{\stackrel{⌣}{x}}+2\ln 2}{\pi F{h}_{\stackrel{⌣}{x}}-2\ln 2}\\ h_{\stackrel{⌣}{x}}=\frac{\left(2^{h_f}+1\right)2\ln 2}{\left(2^{h_f}-1\right)\pi F}\end{array}$$ (A5)

These derivations are the basis of Eqs. 3 and 4 in Linear rectification model of simple cells and energy model of complex cells.

APPENDIX B: CONTRAST RESPONSE FUNCTION OF HYPERBOLIC RATIO MODEL ALONG A LINEAR CONTRAST AXIS

We analyze the contrast response function (CF) of the hyperbolic ratio model (Eq. 12) on a linear contrast axis. The CF is a function of the luminance contrast c of a grating stimulus. We assume that the orientation and spatial frequency of the grating are consistent with the tuning of the model and that the diameter of the grating is sufficiently large to fill the entire receptive field of the model.

The model’s sensitivity to small local changes in contrast is maximized at the contrast difference threshold c*, which corresponds to the point of steepest slope of the CF (see Itti et al. 2000; Wilson 1980; see also contrast response function). The maximal CF slope is

$$\frac{{\left(n_{\mathrm{H}\mathrm{B}}+1\right)}^{\frac{n_{\mathrm{H}\mathrm{B}}+1}{n_{\mathrm{H}\mathrm{B}}}}{\left(n_{\mathrm{H}\mathrm{B}}-1\right)}^{\frac{n_{\mathrm{H}\mathrm{B}}-1}{n_{\mathrm{H}\mathrm{B}}}}}{4{\alpha }_{\mathrm{H}\mathrm{B}}{n}_{\mathrm{H}\mathrm{B}}}$$ (B1)

This maximum occurs for contrast

$$c^{*}={\alpha }_{\mathrm{H}\mathrm{B}}{\left(\frac{n_{\mathrm{H}\mathrm{B}}-1}{n_{\mathrm{H}\mathrm{B}}+1}\right)}^{\frac{1}{n_{\mathrm{H}\mathrm{B}}}}$$ (B2)

if n_HB > 1 and for c* = 0 otherwise (Fig. 26). If n_HB > 1, the CF is convex downward around c = 0. This trend of the model CF can account for the shapes of CFs of real neurons around c = 0 (Albrecht et al. 2003; Albrecht and Hamilton 1982).

Fig. 26.

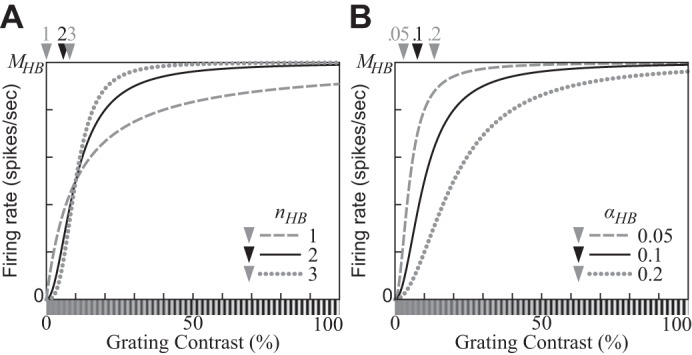
Contrast response functions (CFs) produced by the hyperbolic ratio model (Eq. 12) on a linear contrast axis. Positions of maximal slopes of the CFs are indicated by arrowheads. A: CFs with 3 different values of the exponent parameter n_HB. B: CFs with 3 different values of the semisaturation contrast parameter α_HB. A stimulus with contrast α_HB elicits one-half of the saturation level M_HB. (α_HB = 0.1 for A; n_HB = 2 for B.)

APPENDIX C: SHAPE OF CONTRAST RESPONSE FUNCTION OF DIVISIVE NORMALIZATION MODEL

In this appendix we analyze mathematically the shape of the contrast response function (CF) of the divisive normalization model (DNM). Consider the DNM Eq. 15 and a grating g(c) with contrast c, the model’s preferred orientation and frequency (and phase for a simple cell), and spatial extent large enough to fill both the entire receptive and suppressive fields of the model. For this special choice of stimuli g(c) within the calibration family of Eq. 16, the CF of the DNM becomes

$$R\left(g\left(c\right)\right)=M\frac{{\lfloor \beta +c\rfloor }^{n_{\mathrm{n}}}}{{\alpha }^{n_{\mathrm{d}}}+c^{n_{\mathrm{d}}}}$$ (C1)

(Note that this equation is equivalent to Eq. 17 in Divisive normalization model.) The first derivative of Eq. C1 with respect to c is

$$\frac{\mathrm{d}}{\mathrm{d}c}R\left(g\left(c\right)\right)=\frac{\left(c^{n_{\mathrm{d}}}\left(n_{\mathrm{n}}-n_{\mathrm{d}}\right)-\beta n_{\mathrm{d}}{c}^{n_{\mathrm{d}}-1}+n_{\mathrm{n}}{\alpha }^{n_{\mathrm{d}}}\right)}{M^{-1}{\left({\alpha }^{n_{\mathrm{d}}}+c^{n_{\mathrm{d}}}\right)}^2{\left(\beta +c\right)}^{1-n_{\mathrm{n}}}}$$ (C2)

for 0 ≤ c ≤ 1 if β > 0 and −β < c ≤ 1 if β ≤ 0. Note that dR(g(c))/dc > 0 at c = 0 if β > 0 and at c → −β + 0 (the right-hand limit at −β) if β ≤ 0. This means the CF is increasing at low contrasts.

We differentiate the numerator of Eq. C2 one more time:

$$\frac{\mathrm{d}}{\mathrm{d}c}\left(c^{n_{\mathrm{d}}}\left(n_{\mathrm{n}}-n_{\mathrm{d}}\right)-\beta n_{\mathrm{d}}{c}^{n_{\mathrm{d}}-1}+n_{\mathrm{n}}{\alpha }^{n_{\mathrm{d}}}\right)=c^{n_{\mathrm{d}}-2}{n}_{\mathrm{d}}\left(c\left(n_{\mathrm{n}}-n_{\mathrm{d}}\right)-\beta \left(n_{\mathrm{d}}-1\right)\right)$$ (C3)

The derivative of the numerator becomes 0 at c = 0 and c = c_ex, where

$$c_{\mathrm{e}\mathrm{x}}=\beta \frac{n_{\mathrm{d}}-1}{n_{\mathrm{n}}-n_{\mathrm{d}}}$$ (C4)

Hence, the numerator has two local extrema: $n_{\mathrm{n}}{\alpha }^{n_{\mathrm{d}}}$ at c = 0 and

$$-{\beta }_{n_{\mathrm{d}}}\frac{{\left(n_{\mathrm{d}}-1\right)}^{n_{\mathrm{d}}-1}}{{\left(n_{\mathrm{n}}-n_{\mathrm{d}}\right)}^{n_{\mathrm{d}}-1}}+n_{\mathrm{n}}{\alpha }^{n_{\mathrm{d}}}$$ (C5)

at c = c_ex. Besides, the denominator of Eq. C2 is always positive between $\lfloor -\beta \rfloor$ and 1, exclusive.

In light of these analytic results, the possible shapes of the contrast response functions of the DNM in the range from $\lfloor -\beta \rfloor$ to 1 can be categorized into the following three types:

1) The CF is unimodal and convex-upward if dR(g(c))/dc < 0 at c = 1. This condition is satisfied when β is sufficiently large:

$$\beta >\frac{n_{\mathrm{n}}}{n_{\mathrm{d}}}\left(1+{\alpha }^{n_{\mathrm{d}}}\right)-1$$ (C6)

The CF is decreasing at high contrasts and must have a local maximum between $\lfloor -\beta \rfloor$ and 1, exclusive. In other words, in this regime the model produces the supersaturation effect. This inequality, which is reproduced as Eq. 23 in contrast response function, is a sufficient condition for the supersaturation effect for g(c).

2) The CF has both a local maximum and a local minimum if dR(g(c))/dc > 0 at c = 1, dR(g(c))/dc < 0 at c = c_ex (see Eq. C5), and $\lfloor -\beta \rfloor <c_{\mathrm{e}\mathrm{x}}<1$. The local maximum lies between $\lfloor -\beta \rfloor$ and c_ex, and the local minimum lies between c_ex and 1. Note that in practice, the CF may not be conditioned sufficiently well to check these conditions on the basis of physiological data. Many physiological studies have shown that the DNM can fit data well under an assumption that n_n = n_d. Then, n_n − n_d can be too small compared with n_d − 1 to have stable estimates of c_ex and dR(g(c))/dc at c = c_ex (Eq. C5).

3) The CF is monotonically increasing otherwise.

APPENDIX D: CONTRAST RESPONSE FUNCTION FOR NONPREFERRED STIMULI

We expand the analysis of appendix c to stimuli g̃(c) that do not necessarily match the tuning parameters of the DNM neuron. Specifically, we consider here the DNM response (Eq. 15) as a function of the contrast c of a circular grating patch with nonpreferred orientation and/or nonpreferred spatial frequency and/or diameter that is not large enough to cover the entire receptive and suppressive fields of the model.

Let g̃(c) be any circular grating patch. Our analysis is based on the simple observation that g̃(c) = cg̃(1). As discussed in Linear rectification model of simple cells and energy model of complex cells (cf. Eq. 9), the stimulus drive Eq. 5 is a linear operator for simple cells. The corresponding Eq. 7 for complex cells is nonlinear, but it too scales in direct proportionality for any contrast c ≥ 0. This proportionality holds even when the orientation, spatial frequency, and/or diameter of g̃(c) differ from their optimal values. Note also that the suppressive drive ${\displaystyle {\sum }_{i\in \mathcal{N}}{w}_i{E}_{P_i}{(I)}^{n_d}}$ in Eq. 18 is a linear combination of stimulus drive terms $E_{P_i}(I)$ raised to power n_d. In light of these considerations and of Eq. 17 in the main text (see also Eq. C1 above), the DNM contrast response function for an arbitrary grating g̃(c) becomes

$$R\left(\tilde{g}\left(c\right)\right)=M\frac{{\lfloor \beta +p_{\tilde{g}}c\rfloor }^{n_{\mathrm{n}}}}{{\alpha }^{n_{\mathrm{d}}}+{\left(q_{\tilde{g}}c\right)}^{n_{\mathrm{d}}}}$$ (D1)

where p_g̃ and q_g̃ depend on the grating g̃ but not on the contrast c. Equation D1 can be modified as follows:

$$R\left(\tilde{g}\left(c\right)\right)=M\frac{{\lfloor \beta +\frac{p_{\tilde{g}}}{q_{\tilde{g}}}{10}^{\left({\text{log}}_{10}c+{\text{log}}_{10}{q}_{\tilde{g}}\right)}\rfloor }^{n_{\mathrm{n}}}}{{\alpha }^{n_{\mathrm{d}}}+{10}^{n_{\mathrm{d}}\left({\text{log}}_{10}c+{\text{log}}_{10}{q}_{\tilde{g}}\right)}}$$ (D2)

Equation D2 shows that a relation between plots of R(g̃(c)) and R(g(c)) (Eq. C1) can be represented by the following transformations assuming $\text{|}\beta \text{|}\ll p_{\tilde{g}}c$: translation for −log₁₀q_g̃ along the log-contrast axis and scaling by a factor of ${\left(p_{\tilde{g}}/q_{\tilde{g}}\right)}^{n_{\mathrm{n}}}$ along the response axis. Note that the assumption $\text{|}\beta \text{|}\ll p_{\tilde{g}}c$ is hardly satisfied if the contrast c is low.

APPENDIX E: DECOUPLING POOLING KERNEL OF SUPPRESSIVE DRIVE FROM PREFERRED FREQUENCY OF STIMULUS DRIVE

In this appendix we consider the addition of a new free parameter to Eq. 20 to relax the restriction that the frequency pooling weights of the suppressive drive must be centered on the preferred frequency of the stimulus drive of the DNM neuron. This augmentation is needed to account for certain aspects of cross-orientation suppression introduced in cross-orientation suppression. As we discuss there, very strong suppression effects have been observed for many V1 neurons (DeAngelis et al. 1992; Koch et al. 2016; see Fig. 16D), whereas the DNM with the standard parameters can produce only relatively modest suppression under the standard parameterization (Fig. 16A).

Let us consider in detail the orientation tuning function of the cross-orientation suppression effect observed for the real V1 neuron in Fig. 16D (replotted from Fig. 7, C and D, of DeAngelis et al. 1992). This neuron was probed with stimuli composed of a signal grating $I_{\text{*}}$ and a mask grating $I_{\text{×}}$. The frequency (1.25 cyc/°) and orientation (190°) of $I_{\text{*}}$ were approximately the same as the neuron’s excitatory preferences. The frequency of $I_{\text{×}}$ was about one-half of the preferred frequency (0.6 cyc/°), and $I_{\text{×}}$ elicited no response from the neuron when presented alone. Consider the condition in which$I_{\text{×}}$ had the same orientation as $I_{\text{*}}$ (and hence both were equal to the neuron’s preferred orientation). The data in Fig. 16D show that the neuron responded at a rate of >20 spikes/s (sps) to the signal $I_{\text{*}}$ alone, but <1 sps to the composite stimulus $I_{\text{*}}$ + $I_{\text{×}}$. This relation can be written using the DNM as follows:

$$\{\begin{array}{l}1>R\left(I_{*}+I_{\times }\right)=M\frac{{\lfloor \beta +k_{\mathrm{n}}{E}_{{\mathbf{\text{P}}}^{*}}\left(I_{*}+I_{\times }\right)\rfloor }^{n_{\mathrm{n}}}}{{\alpha }^{n_{\mathrm{d}}}+k_{\mathrm{d}}{E}_{\Sigma }\left(I_{*}+I_{\times }\right)}\\ 20<R\left(I_{*}\right)=M\frac{{\lfloor \beta +k_{\mathrm{n}}{E}_{{\mathbf{\text{P}}}^{*}}\left(I_{*}\right)\rfloor }^{n_n}}{{\alpha }^{n_{\mathrm{d}}}+k_{\mathrm{d}}{E}_{\Sigma }\left(I_{*}\right)}\end{array},$$ (E1)

where E_Σ(I) denotes the suppressive drive (${\displaystyle {\sum }_{i\in \mathcal{N}}{w}_i{E}_{{\text{P}}_i}{(I)}^{n_{\mathrm{d}}}}$). Recall that the mask grating elicited a negligible response from the neuron when presented alone. Hence, we can assume $E_{P*}\left(I_{*}+I_{\times }\right)\approx E_{P*}\left(I_{*}\right)$. Then

$$E_{\Sigma }\left(I_{*}+I_{\times }\right)>20E_{\Sigma }\left(I_{*}\right)+19{\alpha }^{n_{\mathrm{d}}}/k_{\mathrm{d}}$$ (E2)

where ${\alpha }^{n_{\mathrm{d}}}/k_{\mathrm{d}}$ is a positive constant. In other words, the output of the suppressive drive to $I_{\text{*}}$ + $I_{\text{×}}$ is at least 20 times larger than its output to $I_{\text{*}}$. To quantify the strength of the suppression effect, we use the suppression index SI = 1 − R($I_{\text{*}}$ + $I_{\text{×}}$)/R($I_{\text{*}}$) defined by Koch et al. (2016). The neuron in Fig. 16D has SI ≈ 0.95.

The near-complete cross-orientation suppression in Fig. 16D can be emulated by the DNM, provided that the mask has greater contrast than the signal. Our simulations used contrasts 15% and 25% for $I_{\text{*}}$ and $I_{\text{×}}$, respectively.²¹ The emulation requires significant modifications to the parameter set: n_n = n_d = 10, h_Θ = 55, M = 11. Note in particular that the two exponents are much larger than their standard setting (n_n = n_d = 2). This modification magnifies the contrast difference between $I_{\text{*}}$ and $I_{\text{×}}$ and makes E_Σ($I_{\text{*}}$ + $I_{\text{×}}$) substantially stronger than E_Σ($I_{\text{*}}$). These large exponents also make the contrast response function (CF) of the model neuron very steep, which renders this approach implausible because such steep CFs are hardly observed for real V1 neurons (Albrecht and Hamilton 1982; Busse et al. 2009).

Another approach for accounting for the observed near-complete suppression effects is to modify one of the DNM equations. We interpret such strong suppression effects as evidence that the suppressive drive pooling weights (Eq. 20) are much larger for the channels stimulated by the mask $I_{\text{×}}$ than for the channels stimulated by the signal $I_{\text{*}}$. Such pooling weights would produce very strong suppression $E_{\Sigma }\left(I_{*}+I_{\times }\right)\gg E_{\Sigma }\left(I_{*}\right)$ in a straightforward manner. Recall that in the standard DNM formulation (Eq. 20), the pooling weights of the suppressive drive are defined so that the most suppressive frequency coincides with the preferred frequency F* of the stimulus drive. The analogous restriction for orientation pooling (Eq. 21) works well and agrees with the physiological data (see cross-orientation suppression and surround suppression). However, the present formulation apparently is too restrictive with respect to the frequency pooling weights, because there are real V1 neurons whose most suppressive frequencies for cross-orientation (DeAngelis et al. 1992) or surround suppression (DeAngelis et al. 1994; Li and Li 1994) differ significantly from their preferred signal frequencies. The complex cell in Fig. 16D happens to be one such case. Its most suppressive frequency F^× is roughly 1 oct below its preferred frequency F* (Fig. 16J). The gratings $I_{\text{×}}$ and $I_{\text{*}}$ were chosen with these frequencies because the experimental procedure of DeAngelis et al. (1992) searched for masks that maximized the suppressive effect. The most natural way for decoupling F^× from F* in the DNM is to introduce a new free parameter μ_F into Eq. 20. The augmented specification of the spatial-frequency pooling weights ${}^{w}F{}_i$ becomes

$$w_{F_i}\propto \text{exp}\left[-4\text{ln}2\frac{{\left({\text{log}}_2{F}_i-{\text{log}}_2{F}^{*}-{\mu }_F\right)}^2}{h_{F^2}}\right]$$ (E3)

where μ_F parameterizes the difference between the center of the frequency pooling kernel of the suppressive drive and the preferred frequency of the stimulus drive. Recall that the outputs of the two drives are normalized by calibration constants k_n and k_d determined with the help of calibration images (Eq. 16). Only one such image suffices for the standard DNM formulation, but the augmented version requires separate calibration images for the stimulus and suppressive drives when μ_F ≠ 0. Specifically, the calibration image for the suppressive drive has to be a grating with frequency $F^{*}/2^{{\mu }_F}$ cpd. This augmented equation allows the DNM to account for the cross-orientation suppression data (Fig. 16, H and I) that were problematic for the standard formulation.

The modified Eq. E3 complicates the interpretation of the parameter F* of the stimulus drive. It no longer coincides with the preferred excitatory frequency of the model neuron as a whole. For example, the most excitatory frequency of the model neuron in Fig. 16I is measured to be 2.46 cpd (1.30 oct), even though the preferred frequency of the stimulus drive is F* = 2.0 cpd (1.0 oct). One way to demonstrate this inconsistency is to measure the frequency tuning function of the DNM directly with gratings and compare it to the Fourier transform of the receptive field of the DNM measured with local stimulus probes (cf. Fig. 23 and Fig. 25B). The peaks of the measured and derived tuning functions occur at different frequencies (Fig. 27A). Such divergent frequency preferences have been observed experimentally in real V1 neurons (DeAngelis et al. 1993b; Smyth et al. 2003). Note also that the difference between the two preferred frequencies of the DNM neuron depends on the contrast of the grating (Fig. 27B).

Fig. 27.

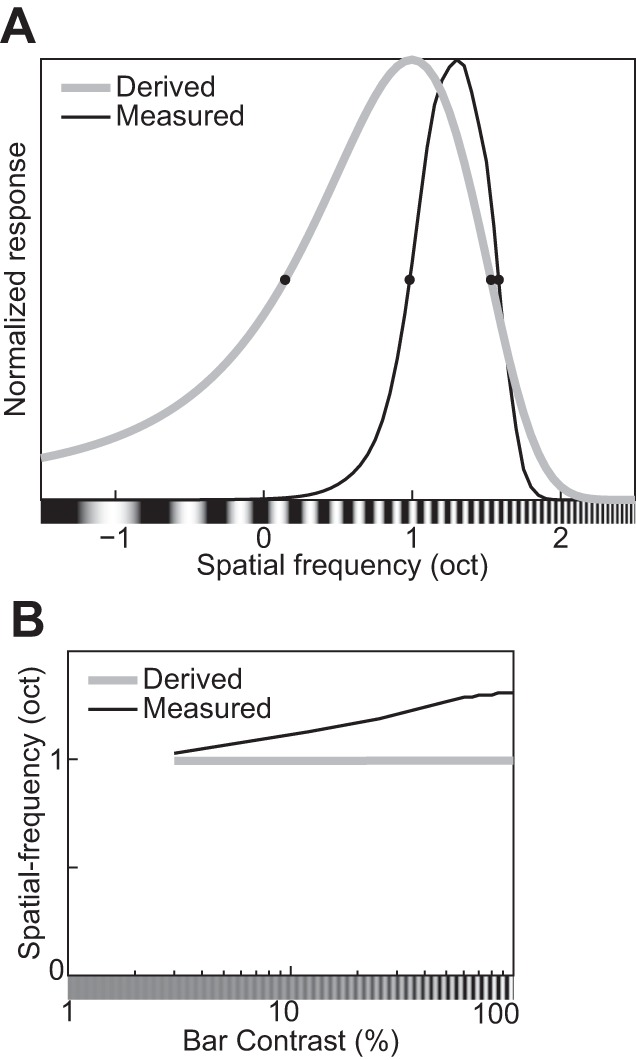
Two alternative procedures for estimating the spatial-frequency tuning function yield diverging results for the augmented divisive normalization model (DNM) neuron (in which the standard Eq. 20 is replaced with Eq. E3). The first procedure (black lines) measures the frequency tuning directly with gratings. The second procedure (gray lines) derives the frequency tuning indirectly via the Fourier transform of the neuron’s receptive field probed with light and dark bars (see phenomenon 30 in Table 1, receptive fields of simple cells, and Fig. 25B). A: spatial-frequency tuning functions obtained via the direct (Measured) and indirect (Derived) procedures. Contrasts of the grating and the bars were 100%. B: effect of the contrasts of the grating and the bars on the peak frequencies of the derived and measured frequency tuning functions.

Finally, note also that the revised Eq. E3 still satisfies the assumption that the pooling weights in Eq. 18 can be factored into independent kernels with respect to space, frequency, and orientation. This assumption simplifies the model specification and reduces the number of free parameters but may prove too restrictive for some purposes. Concretely, the discrepancy between the orientation tuning bandwidths of the surround suppression effect (Fig. 19B) and of the cross-orientation suppression effect (Fig. 16D) suggests inseparability in space and orientation. This is a topic for future research.

APPENDIX F: COMPUTATIONAL IMPLEMENTATION OF DIVISIVE NORMALIZATION MODEL

The computational implementation of the divisive normalization model (DNM, Eq. 15) allows the model to be applied to any visual stimulus used in physiological or psychophysical studies. Its computational efficiency and practical usage have also been taken into consideration.

The suppressive drive of the DN model (Eq. 18) is computationally demanding. It is represented as a weighted sum of $E_{C:X_i{Y}_i{F}_i{\Theta }_i}{(I)}^{n_d}$ (Eq. 7) in the orientation, spatial frequency, and 2D retinal space domains, where $E_{C:X_i{Y}_i{F}_i{\Theta }_i}(I)$ is a square root of a sum of $E_{S:X_i{Y}_i{F}_i{\Theta }_i,0°}{(I)}^2$ and $E_{S:X_i{Y}_i{F}_i{\Theta }_i,90°}{(I)}^2$ (Eq. 5). A part of the weighted sum of the suppressive drive in the 2D retinal space domain can be computed with 2D cross-correlation of a retinal image I(x, y) (Eq. 1) with two 2D Gabor filters $G_{X_i{Y}_i{F}_i{\Theta }_i,{\Phi }_i}$ in Eq. 2:

$${\displaystyle \sum _{X_i{Y}_i}{w}_{X_i{Y}_i}{E}_{C:X_i{Y}_i{F}_i{\Theta }_i}{\left(I\right)}^{n_{\mathrm{d}}}}={\displaystyle \iint w_{X_i{Y}_i}{\left({\left(I\left(x,y\right)\otimes G_{X_i{Y}_i{F}_i{\Theta }_i{0}^{°}}\left(x,y\right)\right)}^2+{\left(I\left(x,y\right)\otimes G_{X_i{Y}_i{F}_i{\Theta }_i{90}^{°}}\left(x,y\right)\right)}^2\right)}^{\frac{n_{\mathrm{d}}}{2}}\mathrm{d}\mathrm{x}\mathrm{d}\mathrm{y}}$$ (F1)

where an operator $\otimes$ represents cross-correlation. This is equivalent to computing $E_{C:X_i{Y}_i{F}_i{\Theta }_i}$ at every pixel of the input image. Then, the number of the 2D spatial grid N_X × N_Y becomes equivalent to that of pixels in the filtered image.

The computational cost for one cross-correlation operation is of order O(N_XN_Y log (N_XN_Y)), and N_Θ × N_F such operations are needed to compute the suppressive drive for one input image. Thus the total cost is O(N_IN_ΘN_FN_XN_Ylog(N_XN_Y)), where N_I denotes the number of images. This computation can be optimized with convolution theory, namely, the filter kernels in Eq. 2 are applied to the input image in a 2D Fourier space:

$$I\left(x,y\right)\otimes G_{X_i{Y}_i{F}_i{\Theta }_i{\Phi }_i}\left(x,y\right)={\mathcal{F}}^{-1}\left(\mathcal{F}\left(I\left(x,y\right)\right)\text{*}\mathcal{F}\left(G_{X_i{Y}_i{F}_i{\Theta }_i{\Phi }_i}\left(x,y\right)\right)\right)$$ (F2)

where operators F and F⁻¹ denote the Fourier transform and its inverse and * denotes conjugation. The Fourier transforms of the filter kernels G_XYFΘΦ can be computed in advance and used for processing every input image. This brings the total cost down to O(N_IN_XN_Ylog(N_XN_Y)), which still is the most expensive computation in the model.

Note that Eqs. F1 and F2 are only approximate in practice because the sizes of I and G_XYFΘΦ are both finite. The approximation improves if I and G_XYFΘΦ are surrounded by sufficiently large regions of uniform gray. The size of I with the surrounding region should be the same as that of G_XYFΘΦ and be $2^{m_x}\times 2^{m_y}$ where m_x and m_y are positive integers. It allows the model to process the image efficiently with the fast Fourier transform algorithm in Eq. F2.

The processing is further optimized so that the model can compute the suppressive drives of multiple model neurons to a common input image at once. The results of the image filtering process in Eq. F2 can be shared among all model neurons. It generates a set of N_Θ × N_F × N_X × N_Y different channels. The suppressive drives of multiple neurons can be computed from the same set of the channels with different neuron-specific pooling weights $w_{{\Theta }_i}$, $w_{F_i}$, and $w_{X_i{Y}_i}$ in Eq. 18.

In the process of computing the suppressive drives, the software calculates N_Θ × N_F × N_X × N_Y × 2 different E_S:XYFΘΦ and N_Θ × N_F × N_X × N_Y different E_C:XYFΘ. They can be also used as the stimulus drives of multiple neurons. Note that in practice we only need a much smaller number N_C, instead of N_X × N_Y, of the 2D spatial positions of the model neurons, especially when the resolution of the input image is high. Also, not all N_F spatial frequencies are appropriate for the stimulus drives because of the edge effect. Theoretically, the domain of spatial frequencies is unbounded, but in practice E_S:XYFΘΦ and E_C:XYFΘ can only be sampled within a limited range. Consider the model neurons whose preferred frequencies are on the upper (or lower) bound of the sampling range. They cannot be suppressed by channels outside of the sampled range because these channels are truncated in the implementation. The edge effect can be alleviated by removing some neurons whose tuned frequencies are close to the bounds of the sampling range. Hence, there are N_Θ × (N_F − Δ_F) × N_C × 3 model neurons generated in total: N_Θ × (N_F − Δ_F) × N_C complex cells and N_Θ × (N_F − Δ_F) × N_C × 2 simple cells (see Eq. 7), where Δ_F is the number of channels removed for the edge effect.