Interacting networks of brain regions underlie human spatial navigation: a review and novel synthesis of the literature

Abstract

Navigation is an inherently dynamic and multimodal process, making isolation of the unique cognitive components underlying it challenging. The assumptions of much of the literature on human spatial navigation are that 1) spatial navigation involves modality independent, discrete metric representations (i.e., egocentric vs. allocentric), 2) such representations can be further distilled to elemental cognitive processes, and 3) these cognitive processes can be ascribed to unique brain regions. We argue that modality-independent spatial representations, instead of providing exact metrics about our surrounding environment, more often involve heuristics for estimating spatial topology useful to the current task at hand. We also argue that egocentric (body centered) and allocentric (world centered) representations are better conceptualized as involving a continuum rather than as discrete. We propose a neural model to accommodate these ideas, arguing that such representations also involve a continuum of network interactions centered on retrosplenial and posterior parietal cortex, respectively. Our model thus helps explain both behavioral and neural findings otherwise difficult to account for with classic models of spatial navigation and memory, providing a testable framework for novel experiments.

INTRODUCTION

Navigation, particularly involving the real world, is an inherently multimodal process involving a dynamic interplay between perception, memory, decision-making, attention to landmarks and other features, and short-term memory for a goal (Ekstrom et al. 2014; Garling et al. 1984; Montello 1998; Spiers and Gilbert 2015). For example, when we enter a new environment, we often “survey” our surroundings, much like a rat does when it rears on its legs, to try to gain some initial estimation of our position relative to other objects and features within the environment. In this way, our ability to perceive objects relative to our immediate position is useful for detecting what objects we might select to navigate to, with both our facing direction and distance from these objects helpful as information to encode. At the same time, we typically have a navigational goal in mind, such as finding a supermarket or store we are searching for, and what we attend to will be highly dependent on our navigational goal. As we begin to ambulate, we must update our position as we move relative to other landmarks, and thus make decisions about which objects and landmarks are relevant for reaching our goal. Importantly, at any given time, all of these cognitive processes can be at play simultaneously.

In addition to the cognitive processes underlying navigation being highly dynamic, the cues that we use to navigate are inherently multimodal. On one hand, as humans, we are primarily visual creatures, and there is ample evidence that we strongly favor the visual modality, both behaviorally and neurally, when we navigate (Ekstrom 2015). At the same time, as we take steps, we engage our path integration system, which involves integrating information from our vestibular system and, to a lesser extent, our motor and proprioceptive systems (Angelaki and Cullen 2008). Our path integration system thus provides a running estimate of how many degrees we have turned and approximately how many steps we have taken (Loomis et al. 1993; Mittelstaedt and Mittelstaedt 1980). Visual information, via optic flow, can override vestibular-based path integration (Warren et al. 2001), and almost all models of navigation assume a dynamic interplay between path integration and visual systems as important to updating our current position. For example, some models of navigation propose that visual information can be used to remove accumulated error from the path integration system (Gallistel 1990; McNaughton et al. 1991; Wang 2016), a process referred to as recalibration, thus further highlighting the multimodal nature of spatial representations. Vision alone can also guide navigation in the absence of the need for any spatial representations, a process termed “beaconing,” “response learning,” or, when a seen landmark is first used to find an unseen landmark, “piloting” (Morris et al. 1986; Mou and Wang 2015; Packard et al. 1989).

Yet, whereas visual and vestibular components form a core foundation of how we navigate, somatosensory and proprioceptive cues are also important for counting steps and estimating turn angles (Angelaki and Cullen 2008). Indeed, sighted individuals perform similarly when learning simple routes either by touching or seeing them (in a small-scale rendering), and blind participants form comparable haptic representations to sighted individuals (Giudice et al. 2011). This argues that both visual and somatosensory/proprioceptive input can be used to form a similar quality of spatial representations. In addition, auditory cues are also important, for example, in providing additional information about our gait and the relative distance of objects based on echoes. As one more extreme example of this, some blind individuals, and even those with normal vision who undergo training, can navigate quite effectively using echolocation (Kolarik et al. 2014). In this way, navigation involves using available sensory cues, which will most often be visual but do not necessarily have to be. Together, these cues allow us to derive spatial representations that will provide us with information about the relative distances and directions of objects in our environment.

ISOLATING COGNITIVE PROCESSES DURING NAVIGATION?

Our discussion so far reveals that the study of human spatial navigation involves a dynamic interplay of cognitive functions and sensory input. As is often argued in the field of navigation, multimodal input operates on modality independent “spatial” representations of a similar nature, as our examples from blind individuals above illustrate. In other words, regardless of how we learned a spatial layout and navigated it in the first place, all forms of input, including using text (for example, reading vs. visually acquiring routes, e.g., Taylor and Tversky 1992), should distill to the same fundamental spatial representations. One elemental representation, in particular, termed the cognitive map, provides us with the relative direction and distance of objects within our environment (Gallistel 1990; Hegarty et al. 2006; O’Keefe and Nadel 1978; Taylor and Tversky 1992; Tolman 1948; Wolbers et al. 2011). Critically, the cognitive map, an idea first coined by Tolman, was subsequently extended by O’Keefe and Nadel to involve a metric, Cartesian-like, Euclidean representation of the positions of landmarks relative to each other, supported by neural activity in the hippocampus.

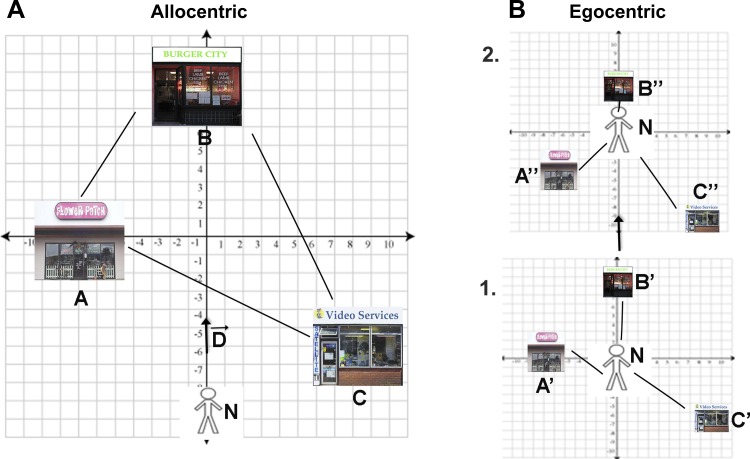
The cognitive map, a fundamentally allocentric representation (O’Keefe 1991; O’Keefe and Nadel 1978), differs from more commonly formed egocentric representations in that the location, bearing, and velocity of the observer, in principle, do not matter. This is because his/her position can be inferred on the basis of the relative positions of stable landmarks (Fig. 1). In other words, as the navigator moves in an allocentric reference frame, he/she can use his/her position relative to landmarks to infer his/her location without having to keep track of the distance and direction moved, as would be necessary in an egocentric reference frame (for a detailed discussion, see Wang 2017). In this way, we might consider the idea that egocentric and allocentric representations make up two fundamentally different forms of navigation (Klatzky 1998; O’Keefe and Nadel 1978). Specifically, an allocentric representation involves employing a stable coordinate system using the positions relative to each other (Fig. 1A), whereas an egocentric representation involves those same objects but relative to our body position, and thus changes continuously as we navigate (Fig. 1B). However, there is also a large area of overlap between egocentric and allocentric representations, and determining which one a navigator employs is not obvious. Two of the reasons for this, which we will discuss in detail shortly, are because both how we measure egocentric and allocentric representations and consider them mathematically suggest a significant degree of overlap between the two (Ekstrom et al. 2014; Wang 2017).

Fig. 1.

Fundamental similarities between allocentric and egocentric coordinate systems. A: within an allocentric coordinate system, A, B, and C are landmark coordinates, N is the position of the navigator, and D is the displacement vector (movement of the navigator). AB, AC, and BC are therefore vectors that indicate both the direction and distance of landmarks to each other. The positions of landmarks stay stable with displacements of the navigator. B: in an egocentric coordinate system, in contrast, the positions of landmarks change continuously with movements of the navigator (i.e., movement from frame 1 to frame 2). The position of the navigator, however, is always centered at the origin. A′, B′, and C′ are positions of landmarks in egocentric frame 1, A″, B″, and C″ are positions of landmarks in egocentric frame 2. These correspond to vectors A′N, B′N, C′N, etc. Within this framework, egocentric to allocentric conversion can be accomplished many different ways. For example, AB, BC, AC in allocentric coordinates can be approximated with vector subtraction (A′N − B′N or A″N − B″N); see McNaughton et al. (1991) for more details. This conversion can also be solved using estimation of the Pythagorean theorem [e.g., AB = sqrt(A′N² + B′N²) or AB = sqrt(A″N² + B″N²)]. This is because vectors AB = A′B′ = A″B″ and the displacement vector (D) are the same in allocentric (A) and egocentric (B) space. This also means the two subspaces have the same basis set.

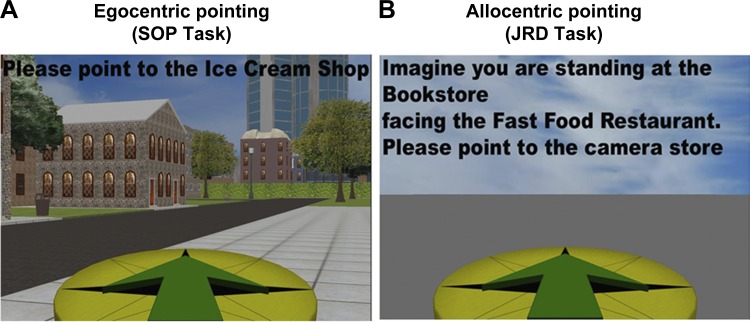
Two of the most common ways of assessing egocentric and allocentric representations involve the scene and orientation-dependent pointing (SOP) task and the judgments of relative direction (JRD) task. These two tasks are illustrated in Fig. 2. However, as readily shown in Fig. 2 and as discussed extensively in a recent review (Ekstrom et al. 2014), both of these tasks involve overlap in the need for both egocentric and allocentric coordinates. For example, the JRD necessitates knowledge of one’s position in the environment, which can be influenced, in part, by one’s memory for preferred facing angles when navigating (e.g., McNamara et al. 2003). Even a cartographic map, which might seem to be the purest form of an allocentric representation, shows biases in terms of the egocentric direction at which we encoded it in the first place, which must be accounted for (Evans and Pezdek 1980; Shelton and McNamara 2004). The SOP task, though heavily dependent on one’s memory for orientation when the targets disappear, could also be solved using knowledge about the relative positions of objects to each other, particularly when one is disoriented (Waller and Hodgson 2006). In this way, we lack a “process pure” measure of representations formed during navigation. Although this is true of a variety of different cognitive measures in psychology, this poses a problem for navigation if we want to isolate the specific brain regions involved, because it can be difficult to know if a participant in a study is using primarily one form of representation or another.

Fig. 2.

Canonical tasks used to assay egocentric and allocentric representations. A: the scene and orientation pointing (SOP) task. Components include 1) current location and bearing during navigation and 2) location of probed store (Ice Cream Shop). Whereas the SOP task is most easily solved based on knowledge of one’s egocentric position relative to the target, the SOP task can also be solved with knowledge of the current location relative to a second store and its relationship to the probe (Ice Cream Shop). In this way, allocentric knowledge can be used to solve the SOP task, in some situations. B: the judgments of relative direction (JRD) task. Components include 1) imagined location and direction of one target (Bookstore) relative to a second (Fast Food) and 2) imagined location and direction of a second target (Fast Food) relative to the probe (Camera Store). Whereas the JRD task is most easily solved based on knowledge about the relative positions of the three stores (allocentric knowledge), it can also be solved using one’s memory for a visual snapshot that includes the two imagined target stores (Bookstore, Fast Food) and probe (Camera Store); see Wolbers and Wiener (2014) for more details. In this way, egocentric knowledge can also contribute to solving the JRD task.

A second issue involves the extent to which the two representations, egocentric and allocentric, themselves may often be dynamic and interchangeable (Byrne et al. 2007; Gramann et al. 2005; Kolarik and Ekstrom 2015). What is the primary difference between an egocentric and allocentric representation? As illustrated in Fig. 1A, this appears to be reference to self vs. other landmarks. As such, reference to self then necessitates continuous updating of one’s positions relative to landmarks. As pointed out, by Wang, however, and also as illustrated in Fig. 1B, this means that the primary difference between the two involves tracking the displacement of the navigator (Wang 2017), a point also discussed in some forms in earlier work (Klatzky 1998; Nigro and Neisser 1983; Wang et al. 2006). In fact, the two can be considered functionally equivalent, as long as the navigator subtracts the distance and angle that they move egocentrically (Fig. 1B; see also Wang 2017).

The interchangeability of egocentric and allocentric representations has both mathematical and neural implications (see Fig. 2 for more details). Mathematically, as shown in Fig. 1B, an allocentric representation is a linear transformation of an egocentric one involving subtracting one’s displacement vector. Neural networks, based on realistic physiological data, can readily perform basis set computations. For example, both V1 orientation-selective responses and grid cells in the entorhinal cortex, when employed in a neural network model, can extract the basis set of an N-dimensional space (Blair et al. 2007; Rao and Ballard 1999). Because the basis sets of egocentric and allocentric space are identical (since they are a simple linear transformation of each other), and mechanisms exist in the brain for performing this computation in other contexts, this implies that conversion between the two coordinate systems in the brain should be possible. Overall, the facts that 1) we lack process pure assays of egocentric and allocentric representations (i.e., they are not discrete) and 2) the two are highly dynamic and partially interchangeable (based on the displacement vector) are increasingly acknowledged in most modern theories of spatial computation.

For example, most modern theories of spatial computation argue against process pure accounts of spatial navigation (Dabaghian et al. 2014; Ekstrom et al. 2014; Geva-Sagiv et al. 2016). Such models differ from classic “stage” models of spatial cognition that assume dissociable, hierarchical steps of spatial knowledge acquisition in which egocentric route knowledge necessarily precedes allocentric cognitive maps (Piaget and Inhelder 1967; Siegel and White 1975). Though such stage models accurately pointed out that topological (nonmetric) knowledge often occurs during spatial navigation, the idea of discrete stages of knowledge acquisition has been challenged in numerous theoretical and empirical studies (Ekstrom et al. 2014; Golledge 1999; Ishikawa and Montello 2006; Jafarpour and Spiers 2017; Montello 1998; Wang, 2017; Zhang et al. 2014). Specifically, these studies and theoretical papers suggest that egocentric route and allocentric topological knowledge often emerge early during learning and in parallel with an additional emerging consensus from this work that topological knowledge can often exist in both egocentric and allocentric forms, with no requirement for metric Euclidean knowledge.

An important question then regards whether egocentric and allocentric representations necessarily exist in “hybrid” forms and whether it is possible to measure one preferentially compared with the other? One approach often taken in the human spatial navigation literature is to attempt to partially dissociate them by selectively studying factors such as how information is acquired (e.g., route or survey information), the context of the experimental task (e.g., navigating, pointing, map drawing), or the fidelity of the spatial information that has been acquired and integrated into the representation of the environment. As pointed out in past work, “purely” egocentric representations may dominate in situations involving peripersonal space, for example, knowing what is on your right side as you move through an environment (Làdavas et al. 1998). In practice, though, during active wayfinding this information will be somewhat uninformative as increasing distance leads to a degradation in egocentric representations obtained from path integration (Souman et al. 2009). Similarly, a purely allocentric representation, as we have argued above, is also challenging to study during active navigation, although one approach is to employ experimental paradigms that “tip” the spectrum toward largely egocentric or allocentric representations.

In one such example of a study, Mou et al. (2006) had participants learn arrays of objects in a cylindrical area from a specific viewpoint, walk to the center of the cylinder, and point to various objects in one of three conditions (facing the learned viewpoint, rotated but not disoriented, and disoriented). Results demonstrated that participants learned both egocentric and allocentric information (they were able to point accurately from a nonlearned viewpoint but performed best when that viewpoint was the imagined facing direction for their pointing judgments). In addition, participants’ pointing was only affected by disorientation when the array of objects did not have a salient, intrinsic axis. The authors interpreted this result as evidence that allocentric reference frames are ideal for such tasks but that egocentric information can be used as a sort of backup strategy when reliable allocentric information is not available. In this way, the authors showed that both allocentric and egocentric forms of representation often coexist during navigation, with some conditions (geometric regularity) resulting in preference for allocentric representation, but, in the absence of this, a preference for egocentric representation. Thus the results of Mout et al. (2006) suggest that emphasizing certain conditions, such as orientation vs. salient axes, can favor one form of representation over another, suggesting that although the two coexist on a spectrum, under some conditions they are at least partially dissociable.

MUST WE HAVE METRIC KNOWLEDGE OF SPACE TO SUCCESSFULLY NAVIGATE AND REASON ABOUT SPACE?

A next important question regards the nature of egocentric and allocentric representations for space. One frequent assumption that we make when considering these two forms of spatial coordinate systems is that they must always involve Euclidean, metric representations of space when we navigate, in terms of both direction and distance, just like we might draw a spatial environment on graph paper. In fact, a fundamental assumption of many neural models of spatial navigation, such as cognitive map theory, involves exactly this idea. For example, as O’Keefe and Nadel (1978) state (p. 10): “. . . [we will be] sticking our necks out and taking the strong position that the metric of the cognitive map is Euclidean.” However, there is no reason to assume that our spatial representations formed during navigation need always be metric representations like a Cartesian graph, and instead, there is substantial evidence that direction, distance, or both can instead be topological (Dabaghian et al. 2014; Moar and Carleton 1982; Poucet 1993; Tobler 1979). In support of this, our spatial representations are often distorted by various factors that vary as a function of task and are not simply the result of an imprecise metric representation (Fujita et al. 1993; Huttenlocher et al. 2004; Jafarpour and Spiers 2017; Okabayashi and Glynn 1984; Shelton and McNamara 2001; Stevens and Coupe 1978; Thompson et al. 2004). A more accurate way to phrase how we represent space is perhaps a “just good enough representation” for the task at hand, often preserving sequential (topological) relationships but frequently violating metric, continuous properties of space (Ekstrom and Ranganath 2017). This definition aligns with that used in the field of human language (Ferreira et al. 2002; Mata et al. 2014) and visual perception in terms of our extensive use of “heuristics” (Moar and Bower 1983; Tversky 1981; Wolfe 2006), an idea we will return to shortly.

What is the evidence for spatial topology instead of Euclidean metrics? In one of the most widely cited and discussed examples of our spatial representations often lacking precise metrics and instead often relying on heuristics, Stevens and Coupe (1978) asked participants to indicate which cities from a list were farther west. Although participants made many of these judgments correctly, one particular error occurred for decisions involving Reno and San Diego (Reno is farther west due to the geography of the United States). Participants consistently indicated that San Diego was further west, suggesting that category heuristics about distance (that California is farther west than Nevada) overrode metric Euclidean knowledge of maps in some cases (Okabayashi and Glynn 1984; Stevens and Coupe 1978). Note that this assumption will often work (e.g., Los Angeles is farther west than Las Vegas) but sometimes will not. This finding was an early hint that category heuristics can often compete with, override, or operate in the absence of precise metric knowledge of spatial locations.

In another such study demonstrating the importance of heuristics to spatial representations, Huttenlocher et al. (1991, 2004) asked participants to remember dots within a circle. They then drew the positions of these dots on a circle from recall. Huttenlocher and colleagues found that participants consistently showed a pattern of regression to the mean such that the positions of the dots were closest to the center of spaces between category boundaries, i.e., 0°, 90°, 180°, 270° (Huttenlocher et al. 1991, 2004). In other words, participants remembered the locations of the dots, even when clustered around those lines (0°, 90°, 180°, 270°), as being shifted closer to the center of imaginary partitions of the circle whose boundaries were presumably defined by participants as imaginary lines at 0°, 90°, 180°, 270° (Fig. 3A). Thus category, heuristic knowledge overrode metric directional knowledge of space. To be clear, the study also supported the idea that some metrics of space were in fact preserved, because participants’ dot placements were accurate in some cases (i.e., when remembering those close to 45°), but that in many other cases, the category heuristic of “between 0° and 90°” overrode more precise metric knowledge of the positions of the dots.

Fig. 3.

Heuristics override metric Euclidean knowledge of space. A: schematic of results from 2 different studies by Huttenlocher et al. (1991, 2004). These studies involved participants encoding and then drawing the locations of dots within a circle. Participants showed a significant tendency toward drawing dot locations that were encoded at or near 0°, 90°, 180°, or 270° as closer to 45°, 135°, 225°, and 315°. These findings demonstrated a tendency to use category heuristics (“somewhere in between 0° and 90°”) rather than precise metric knowledge. B: schematic of findings from Moar and Bower (1983). When participants estimated the angles of the intersections between 3 well-known streets, they tended to draw the angles as closer to 90° than their actual angles. Because the sum of angles of a triangle must not exceed 180°, this violates the rules of Euclidean geometry. C: Alignment effects, demonstrated in numerous studies cited within the main text. Participants pointed to the imagined locations of targets (using the JRD task) more accurately when imagining themselves facing parallel to main axes of a rectangle than when misaligned. These findings suggest that the category heuristic of “rectangle,” in this case, aids in the memory for the locations of stores, without which spatial memory is significantly less precise.

We might argue, however, that the above examples are of spaces that are not typically navigable; for example, although we can draw maps of “geographical space” (Montello 1993), we rarely navigate through such actual large environments in their entirety (Wolbers and Wiener 2014). Similarly, drawing circles taps into our object representation system and, as argued above, involves spatial reasoning, but it typically employs representations in immediate, figural space (Montello 1993). However, there is also a large body of research that suggests that representations we form during spatial navigation are typically neither consistently metric nor Euclidean. Instead, similar to spatial cognition, representations formed during spatial navigation involve distortions and heuristics based on task demands.

For example, a commonly used task in spatial navigation is to have people estimate directions or distances based on navigating a recent space. When estimating distance, participants often make systematic errors, either over- or underestimating the actual distances, depending on the familiarity of the environment (Jafarpour and Spiers 2017; Knapp and Loomis 2004; Philbeck and Loomis 1997; Thompson et al. 2004). When returning to the origin after completing two legs of a triangle, blindfolded participants tend to both underestimate their turning angle and the distance they need to walk, despite their ability to egocentrically update their position using their path integration system (Loomis et al. 1993). Thus our knowledge of both distance and direction, acquired via either navigation or direct perception, are often not metrically accurate and are distorted by task demands (i.e., how many turns did I take? see Moar and Carleton 1982).

However, the above examples simply indicate that our metric knowledge from navigable space is not particularly accurate and is often distorted. It could simply be that this knowledge is erroneous and distorted by task demands but could still be Euclidean. However, this assertion also does not appear to be the case. In one study, participants were asked to estimate the angle of three different road intersections, each on separate trials, that participants had visited frequently. The sum of the angles of the road intersection consistently exceeded 180°, violating the rules of Euclidean geometry (Moar and Bower 1983). These findings suggested that this was because participants estimated angles as closer to 90° rather than the true angle, which was often less than that, and thus the sum of these angles (90° + 90° + 90°) readily exceeded 180° (Fig. 3B). In particular, the use of right angles to remember navigated space suggests that heuristics play a strong role in how directional knowledge is stored, rather than metric or Euclidean knowledge.

Further consistent with a tendency to use geometrical shape heuristics with right angles, such as rectangles, to code spatial knowledge, numerous studies in both real-world and virtual environments demonstrate that we are more accurate in remembering the direction of objects in a spatial layout when aligned with the axes of the surrounding boundaries of the environment than when misaligned (Fig. 3C). Specifically, if we navigate a large-scale park (McNamara et al. 2003), learn a virtual layout of objects following active navigation (Chan et al. 2013), remember a well-known city (Frankenstein et al. 2012), or remember a cartographic map (Shelton and McNamara 2004), participants remember the relative positions and directions of objects better when parallel to the axes of a square or rectangle (90°, 180°, 270°) than when misaligned (45°, 135°, 225°; Fig. 3C). These effects, termed “alignment effects,” appear to be a ubiquitous property of both encoding and retrieving spatial layouts, both actively and passively encoded (Tversky 1981; Waller et al. 2002). These findings also suggest that heuristics, such as the shape of the surrounding environment, often form a core component of how we accurately represent the metrics of space, without which our metric knowledge is significantly degraded and error prone.

BRAIN REGIONS UNDERLYING SPATIAL NAVIGATION IN HUMANS: CLASSIC MODELS

We have argued so far that the assumptions of 1) discrete egocentric and allocentric representations and 2) unique, separable cognitive processes underlying them have significant shortcomings, as does the further assumption 3) that such representations must always be metric and Euclidean. However, these have been among the core assumptions of many classic neural models of spatial navigation. For example, one of the most frequently discussed dichotomies in the literature involves the idea that the hippocampus stores metric allocentric representations of space whereas parietal cortex stores metric egocentric representations (Aguirre and D’Esposito 1999; Byrne et al. 2007; O’Keefe and Nadel 1978). Evidence for this basic idea is copious and is only briefly reviewed here (for a more complete review, see Ekstrom et al. 2014 and Kolarik and Ekstrom 2015). Lesions to the hippocampus of the rat induce profound deficits in learning the Morris water maze, which involves remembering the position of a hidden location by triangulating it from the positions of landmarks outside the maze (Morris et al. 1982). These same lesions, however, generally leave the ability to navigate using a response and/or egocentric strategy intact (Eichenbaum et al. 1990; Pearce et al. 1998). Lesions to the human hippocampus also tend to disrupt the ability to use distal landmarks to navigate (Astur et al. 2002; Bartsch et al. 2010), although the effects are decidedly more variable across studies (Ekstrom et al., 2014). Lesions to human parietal cortex disrupt the ability of patients to imagine objects relative to one side vs. another (Bisiach and Luzzatti 1978) and navigation involving sequences of turns, tending to leave allocentric forms of navigation intact (Ciaramelli et al. 2010; Weniger et al. 2009). Thus there is substantial evidence in the literature that lesions to hippocampus and parietal cortex can have different effects depending on how we navigate space.

As we have pointed out before, based on discussion of past work, egocentric and allocentric forms of navigation involve a linear transform of each other based on the displacement vector. Could it be that a brain region, perhaps situated between parietal cortex and hippocampus, performs such a transformation? Indeed, one influential model, termed the BBB model, argues that retrosplenial cortex performs precisely this function, allowing a transformation between the two coordinate systems (Byrne et al. 2007). Consistent with this argument, lesions to retrosplenial cortex profoundly impair one’s ability to compute heading direction (Hashimoto et al. 2010), which is essential for transforming between the two coordinate systems. In addition, neuroimaging findings argue that retrosplenial cortex often activates during tasks that involve transformation between different coordinate systems, such as solving the JRD task after navigating or transforming different viewpoints (Dhindsa et al. 2014; Zhang et al. 2012).

CHALLENGES TO CLASSIC MODELS

Whereas the studies reviewed thus far provide evidence that is largely consistent with classical models of the neural basis of egocentric and allocentric navigation, the results of other studies are more difficult to accommodate with these models. For example, in humans at least, hippocampal lesions produce variable impairments in the virtual Morris water maze and other tasks involving the ability to use distal landmarks. In many cases, patients with hippocampal damage show some preserved ability to navigate in situations that would appear to require allocentric navigation (Banta Lavenex et al. 2014; Bohbot et al. 2004; Hirshhorn et al. 2012; Kolarik et al. 2016; Rosenbaum et al. 2000), and in other cases, little impairment at all (Bohbot and Corkin 2007; Bohbot et al. 1998). If the hippocampus is necessary for all forms of allocentric navigation, however, even small amounts of damage should severely impair the ability to use an allocentric strategy. In addition, posterior parietal cortex damage, often taken as the center for egocentric representation, results in some impairment in tasks that appear to require allocentric navigation (Ciaramelli et al. 2010; DiMattia and Kesner 1988; Kesner et al. 1989; Save and Poucet 2000, 2009).

Another issue that we encounter, although well recognized historically in the literature, is that the hippocampus, in particular, is important for a much wider range of tasks than simply allocentric navigation. Specifically, lesions to the hippocampus in humans produce profound amnesia, with an inability to encode and retrieve new events and experiences, as well as those experienced before the insult (Scoville and Milner 1957; Squire et al. 2004). There is now growing consensus that the role of the human hippocampus extends beyond a purely navigational function, instead playing a more general role in the binding of contextual details in the service of episodic memory, our memory for unique events (Eichenbaum et al. 2007; Tulving 1987). However, although the role of the hippocampus in human memory may be biased toward spatiotemporal processing and binding, critical components of our memory for events, it can also include other dimensions, such as auditory or emotion domains, depending on task demands (for a recent review, see Ekstrom and Ranganath 2017). Similarly, there is now growing consensus that posterior parietal and retrosplenial cortices also play roles in memory that extend beyond navigation (Valenstein et al. 1987; Vann et al. 2009). The more general role of the hippocampus in memory, and even perception (Erez et al. 2013; Yonelinas 2013), thus complicates arguments that the hippocampus should be specialized for allocentric navigation and/or metric representations of space.

RODENT STUDIES

Place cells, which are neurons in the hippocampus that fire at specific spatial locations during navigation (Ekstrom et al. 2003; Matsumura et al. 1999; Muller et al. 1987; O’Keefe and Dostrovsky 1971), are often taken as the neural instantiation of the metric, Euclidean cognitive map (Burgess and O’Keefe 2011; O’Keefe and Nadel 1978). The issue directly relevant to our current considerations, however, is that place cells alter their firing depending on a variety of factors, including what the navigational goal is, and thus cannot be considered purely allocentric. For instance, several studies have shown that when a rat runs on a linear track, place cells remap (i.e., the place fields for individual cells differ) when a rat runs in one direction compared with another (Gothard et al. 1996; Redish et al. 2000). Perhaps more fundamentally problematic for the idea of a global, metric map of space, place cells also change their preferred location of firing depending on the future goal of the animal (Ainge et al. 2007; Ferbinteanu and Shapiro 2003; Lee et al. 2006; Wood et al. 2000).

The results from such paradigms in both rats and humans demonstrate that the same location in space can be referenced to competing hippocampal place cell maps depending on the behavioral context; similar findings have also been shown in humans and nonhuman primates (Ekstrom et al. 2003; Wirth et al. 2017). Furthermore, place cells in the bat hippocampus have been shown to remap between vision- and echolocation-based navigation (Geva-Sagiv et al. 2016). Finally, place cells were recently demonstrated in the rodent retrosplenial cortex and proposed to play a role in episodic memory and navigation (Mao et al. 2017), with other studies suggesting location-specific coding in rodent visual cortex (Haggerty and Ji 2015; Ji and Wilson 2007), prefrontal cortex (Fujisawa et al. 2008), claustrum (Jankowski and O’Mara 2015), and even the human amygdala (see Fig. 2C in Miller et al. 2013). In this way, place cells are neither uniquely localized to the hippocampus nor “GPS-like” (Eichenbaum and Cohen 2014); however, we also acknowledge that this does not preclude some degree of specialization within these brain areas.

Head direction cells, another class of cells active during navigation, similarly are often taken as an example of a neural code for allocentric facing direction (Moser and Moser 2008; Ranck 1984; Taube 2007). Like place cells, empirical studies suggest that head direction cells manifest in several different brain regions, including the subiculum, dorsal thalamus, retrosplenial cortex, hippocampus, and entorhinal cortex (for reviews, see Moser et al. 2008; Taube 2007). Head direction cells typically fire for facing directions linked to distal landmarks; thus a head direction cell will fire whenever an animal moves toward the top of the maze (“north”). If the landmarks are rotated 90°, however, this cell will instead fire for eastward directions. In this way, head direction cells can be considered “allocentric” because they are yoked to the positions of distal landmarks. Because vestibular input is necessary for normal head direction cell function (Stackman and Taube 1997), however, and are involved in path integration (Taube 2007), they also have some egocentric correlates. Thus head direction cells also do not show discrete egocentric or allocentric properties when their inputs are modulated, although they do appear to show an allocentric bias.

Together, these findings are inconsistent with the idea that 1) there is a single location within the brain for metric allocentric representation and that 2) the representation is necessarily modular, in other words, that such cells in a single specialized brain region calculate the Euclidean spatial metric. For demonstrations of how entorhinal grid cells similarly do not fit with the localization perspective, see Hales et al. (2014) and Kanter et al. (2017). However, more research is needed on both fronts before we can determine how spatial coding in humans depends on place cells and grid cells, and we return to these issues when we outline specific predictions of our model.

A POSSIBLE WAY FORWARD: TOWARD A NETWORK CONCEPTUALIZATION OF NAVIGATION

As we have argued so far, human spatial navigation is better conceived of, behaviorally at least, as a highly dynamic process that more closely involves the use of heuristics and a continuum of egocentric and allocentric topological spatial representations rather than discrete, modular, metric representations. These considerations then also pose a significant problem for isolating a specific brain region unique to a given process. As we have argued so far, these attempts generally have not held up very well either. Lesions to hippocampus and, indeed, most brain areas rarely impair one aspect of behavioral function and lead to only subtle impairments in what many have termed allocentric navigation. Similarly, brain regions often “activate” across a variety of different tasks when studied with noninvasive functional neuroimaging (Poldrack 2011). If, instead, we reconceptualize navigation as a fundamentally network-based phenomenon, we then take the onus off one specific brain region housing the necessary machinery for representing spatial aspects of navigation and move the burden to how multiple brain regions interact as fundamental to this process. We also allow, more naturally, for a continuum of interactions of egocentric and allocentric representations involving different scales of space and different heuristics, as necessitated by the current task demands.

The core of our proposed theoretical model argues that the retrosplenial region serves as a hub for spatial navigation involving other critical, interacting nodes such as hippocampus, posterior parietal cortex, posterior parahippocampal cortex, and dorsolateral prefrontal cortex (Fig. 4). Before we begin our discussion of our theoretical model, though, it is worth mentioning that we are not arguing for the idea that these brain regions lack any unique neural machinery. In fact, there is ample evidence from both neuroanatomy and neurophysiology suggesting that there are differences in cell type, how cells are connected within different brain regions, and how these different regions respond during tasks (Felleman and Van Essen 1991; Lavenex and Amaral 2000). For example, place cells within the hippocampus respond at specific spatial locations as an animal navigates, suggesting a neural code for location within the brain (Ekstrom et al. 2003; Muller et al. 1987; O’Keefe and Dostrovsky 1971; Wilson and McNaughton 1993). These findings make it clear that there is indeed some specialization within the brain, at least for higher order cognitive function. Instead, what we are arguing is that there is more redundant coding across brain regions than previously recognized in some models and that interactions, mediated by low-frequency oscillations between brain regions, are critical for the emergence of topological spatial representations.

Fig. 4.

Schematic of our network model of allocentric and egocentric representation. Network conceptualization shows allocentric (A) and egocentric (B) representations centered on the retrosplenial region (RSR; retrosplenial cortex and retrosplenial complex) and posterior parietal cortex (PPC), respectively. EC, entorhinal cortex; HC, hippocampus; IT, inferotemporal cortex; PFC, prefrontal cortex; PR, parahippocampal region; Thal, thalamus; VC, visual cortex. Allocentric and egocentric representations involve information processing centered on different hubs yet still involve largely overlapping brain regions. The model thus allows for a continuum of allocentric and egocentric representations, as well as hybrid versions of the two, which will depend on the degree of hubness and shared computations across brain regions within the network. The model also allows for heuristics, which will involve additional contributions from areas such as IT.

Indeed, there is now growing evidence for some degree of redundant, distributed coding across brain areas, an idea that was fundamental to early computational models of learning (Hopfield 1995; Rumelhart et al. 1987). One of the early findings from neuroimaging studies of spatial navigation was in fact that a range of different brain regions typically activate in contrasts involving egocentric and allocentric navigation (Committeri et al. 2004; Galati et al. 2000; Neggers et al. 2006; Sulpizio et al. 2014), similar to the findings of rodent studies reviewed above (e.g., the presence of place cells outside of the hippocampus). Additionally, there is also growing consensus that cells within the hippocampus respond to a larger variety of variables than just location, including viewing landmarks, spatial goals, and conjunctions of these variables with spatial location (Ekstrom et al. 2003; Rolls and O’Mara 1995; Wirth et al. 2017; Wood et al. 1999). The presence of location-specific neural codes outside of the hippocampus and cells coding variables other than purely spatial ones within the hippocampus suggests a degree of redundant and conjunctive coding across networks of brain regions. Importantly, a network conceptualization, as we have argued in past work (Ekstrom et al. 2014), takes the onus off of unique brain regions with highly specialized neural machinery as central to navigation and instead allows us to reconceive of this function in a more distributed fashion based on highly connected and interacting “hubs” of brain areas.

LESION STUDIES SUGGEST THAT SPATIAL NAVIGATION IS A NETWORK PHENOMENON

We believe that one of the strongest forms of evidence arguing for a network-based perspective on spatial navigation comes from lesion studies, as we have begun to discuss above. The notion that localized lesions can give rise to widespread neural changes, a process termed “diaschisis” by Von Monakow in 1902 (for a historical review, see Finger et al. 2004), has been around for over 100 years and has received increased attention in recent years, partly because of the availability of new techniques for studying large-scale changes following localized lesions (Carrera and Tononi 2014). Several recent studies in the rodent have revealed that localized lesions to brain regions implicated in spatial navigation and declarative memory cause widespread changes in the activation of other cortical areas within these same networks. For example, hippocampal lesions have been found to cause widespread cortical hypoactivity, indexed by the immediate-early genes c-fos and zif268, including regions of the medial temporal lobe [postrhinal cortex (the rodent homolog of primate parahippocampal cortex), perirhinal cortex, and entorhinal cortex] and the anterior thalamic nuclei (Jenkins et al. 2006). All of these regions are thought to play roles in spatial navigation and declarative memory. Additionally, lesions to the hippocampus (Albasser et al. 2007) and anterior thalamic nucleus (Jenkins et al. 2002a, 2002b, 2004) result in dramatic decreases in activity (of immediate-early genes) in the retrosplenial cortex and, in the case of lesions to the anterior thalamic nuclei, the hippocampus. Moreover, damage to the mammillothalamic tract, which connects the mammillary bodies and the anterior thalamic nuclei, results in widespread decreases in activation (of the immediate-early gene c-fos), including within the hippocampus, retrosplenial cortex, and prefrontal cortex (Albasser et al. 2007). These findings support the idea that individual brain regions do not function as isolated modules, but instead are highly connected and integrated with each other.

A recent study investigated the effects of hippocampal damage on network interactions in the human brain (Henson et al. 2016). As a result of medial temporal lobe lesions, patients showed decreased functional connectivity between the hippocampus and the posterior cingulate cortex, as well as between other regions of this subnetwork, such as between thalamus, medial prefrontal cortex, and parietal cortex compared with controls. Moreover, a large-scale network analysis (716 regions of interest) revealed that hippocampal damage resulted in widespread changes in functional connectivity, including changes between regions outside of this hippocampal circuit. These results complement the findings in the rodent, together suggesting that hippocampal damage, via its connectivity to other brain regions, has far-reaching effects beyond simply altering local interactions (see also Gratton et al. 2012).

Recent computational modeling studies have begun to incorporate full-brain connectivity, both mono- and polysynaptic, by using graph theory to investigate structural and functional brain networks, respectively. For example, Alstott et al. (2009) found that virtual lesions to hub regions of the brain caused widespread changes in functional connectivity between many regions of the brain. Interestingly, the lesions that were consistently associated with widespread changes were those that strongly affected a network of brain regions connected either anatomically or functionally to the hippocampus, such as the posterior cingulate cortex, medial prefrontal cortex, precuneus, and lateral parietal cortex. Given that patients with hippocampal damage exhibited decreased functional connectivity within these same regions (Henson et al. 2016), hippocampal lesions might be better understood by the disruptions that they cause to a broader network, including other influential nodes within areas previously associated with spatial cognition. Moreover, although graph theory analysis of structural brain networks initially failed to find evidence that the hippocampus serves as an anatomical hub, more recent studies demonstrated its hublike properties when instead taking functional dynamics into account (Mišić et al. 2014a, 2014b). These findings point to the importance of studying functional (i.e., putative polysynaptic) interactions (in addition to structural connectivity) between brain regions to elucidate the hubs of network-wide interactions. In support of the modeling results, recent studies from our laboratory have suggested that the medial temporal lobe (Watrous et al. 2013), and the hippocampus in particular (Schedlbauer et al. 2014), serves as a functional hub during spatiotemporal episodic memory retrieval.

NEUROIMAGING STUDIES SUGGEST THAT SPATIAL NAVIGATION AND MEMORY ARE NETWORK PHENOMENA

As we have discussed previously (Ekstrom et al. 2014), it appears reasonable to decompose egocentric and allocentric representations into landmark (e.g., landmark location, landmark identity), direction (e.g., heading, the angle between landmarks), and distance (e.g., distance between landmarks, distance to a goal location), as some models have attempted in some forms (Aguirre and D'Esposito 1999; Siegel and White 1975). In fact, recent functional magnetic resonance imaging (fMRI) studies using univariate analysis (e.g., activation analysis, adaptation analysis) and multivariate pattern analysis (MVPA; e.g., classification analysis, representational similarity analysis) have provided evidence for some degree of specialization in the brain regions that code information about these three components, which we will discuss in turn. However, as we will argue, these studies also suggest that multiple brain regions code information about landmark identity, direction, and distance, suggesting that these core components of spatial representations likely have distributed and partially redundant representations rather than highly localized and unique ones.

Before we begin our review of such studies, it is important to summarize the anatomical and functional differences between some of the brain regions we will be discussing that are relevant to navigation. Specifically, there are numerous labels used for anatomical and functional areas within retrosplenial and parahippocampal cortex, and it is useful to define these terms. Both retrosplenial cortex and posterior parahippocampal cortex (PHC) are anatomically defined regions, whereas retrosplenial complex and parahippocampal place area (PPA) are functionally defined regions (i.e., based on activation rather than strictly using anatomical landmarks). The most generally accepted definition of the retrosplenial cortex corresponds to Brodmann areas 29 and 30 (Vann et al. 2009). PHC is a subregion of the parahippocampal gyrus, with its anterior boundary defined as the perirhinal cortex and its posterior boundary typically defined as the splenium of the corpus callosum (Law et al. 2005). In contrast, retrosplenial complex tends to lie posterior to retrosplenial cortex (i.e., beginning in retrosplenial cortex and extending caudally), and PPA tends to lie posterior to parahippocampal cortex (i.e., beginning in posterior PHC and extending to the anterior lingual gyrus) (Epstein 2008; Huffman and Stark 2017; Marchette et al. 2014); however, given that these are functionally defined regions, in at least a subset of participants, these regions might not overlap with retrosplenial cortex and PHC.

With regard to the functional role of these brain regions in navigation, several studies have investigated the representation of landmark and location information in the human brain and found roles for these areas. For example, Marchette et al. (2015) found that patterns of activity in retrosplenial complex, PPA and occipital place area (OPA) could be used to “cross decode” landmark identity between exterior and interior images of buildings on a university campus. Regarding the representation of location per se, the results of a multivariate pattern classification analysis suggested that the hippocampus (both anterior and posterior subregions), retrosplenial complex, and PPA code information about location within a room-sized virtual environment (Sulpizio et al. 2014). Similar results have been reported for large-scale environments. For example, patterns of activity in the retrosplenial complex and the left presubiculum were more similar in response to photographs that depicted the same location on a university campus than those that depicted different locations (Vass and Epstein 2013). Additionally, similar analyses have suggested that the retrosplenial complex, the PPA, and parietal-occipital sulcus carry information about location during performance of variants of the JRD task (Marchette et al. 2014; Vass and Epstein 2017; see Fig. 2). Moreover, Brown et al. (2016) reported successful classification of “prospective” goal locations, based on the associative memory of the location with which a cued object was paired, in the hippocampus, PHC, perirhinal cortex, and retrosplenial complex in a virtual environment (Brown et al. 2016), suggesting that these regions activate place-selective responses during route planning. The results of these studies reveal that many regions carry landmark- and location-related information, including the hippocampus, retrosplenial cortex, retrosplenial complex, PPA, PHC, and OPA, among other cortical regions.

Studies have also investigated the representations of direction, supporting similar conclusions of distributed neural codes. For example, an adaptation analysis revealed greater blood oxygen level-dependent (BOLD) activation of the retrosplenial complex for trials with different headings than trials with repeated headings in a virtual environment (Baumann and Mattingley 2010). Similarly, Shine et al. (2016) had participants encode a virtual environment in the presence of real-world head and body rotations (subjects wore a head-mounted display; translations were controlled via joystick), and during a retrieval task they found that non-repeated headings were associated with greater BOLD activation relative to repeated headings in both the retrosplenial cortex and the thalamus. A whole brain analysis also revealed adaptation effects in the precuneus, caudate, brain stem, superior frontal gyrus, and inferior frontal gyrus (Shine et al. 2016). Vass and Epstein (2013) found that patterns of activity were more similar in response to trials with the same heading than trials with different headings in the retrosplenial complex and right presubiculum, and Vass and Epstein (2017) reported similar effects in the retrosplenial complex, entorhinal cortex, left precuneus, left superior frontal gyrus, and left middle temporal gyrus (see also Marchette et al. 2014; Vass and Epstein 2013, 2017). Furthermore, the results of a multivariate pattern classification analysis revealed that the hippocampus (both anterior and posterior subregions), retrosplenial complex, and PPA code heading within a room-sized virtual environment (Sulpizio et al. 2014). Finally, tasks involving computations of the angle between a navigator’s heading and the goal location (i.e., egocentric angle) have shown that activity in posterior parietal cortex correlates with the magnitude of this angle (Howard et al. 2014; Spiers and Maguire 2007), suggesting that this region could be involved in representing the egocentric angle to the goal location. Thus many regions have been shown to carry directional information, including the hippocampus, retrosplenial region, PPA, thalamus, precuneus, and posterior parietal cortex, among other subcortical and cortical regions.

Studies regarding the neural code for spatial distance in humans support similar conclusions regarding distributed neural codes. For example, Spiers and Maguire (2007) reported an association between the Euclidean distance to a goal location and BOLD activation in both the medial prefrontal cortex (activity increased as the distance to the goal decreased) and the right subicular/entorhinal region (activity decreased as the distance to the goal decreased) in London taxi drivers who performed a navigation task in a virtual version of London (Spiers and Maguire 2007). Howard et al. (2014) extended these results to the hippocampus proper, reporting that activity in the hippocampus was modulated by both the Euclidean distance (anterior hippocampus) and path distance (posterior hippocampus) to a goal location during performance of a navigation task in a virtual version of London (activity decreased with decreasing distance to the goal, similar to the previous results in the subicular/entorhinal region). Similarly, an adaptation analysis revealed a relationship for the Euclidean distances between locations on a university campus, with activity reported in the left anterior hippocampus, left inferior insula, left anterior superior temporal sulcus, and the right posterior inferior temporal sulcus (Morgan et al. 2011). Decoding analyses using fMRI data revealed similar findings. For example, the dissimilarity of patterns of activity in the hippocampus (both anterior and posterior subregions), PPA, and retrosplenial complex related to the physical distance between locations in a room-sized virtual environment, i.e., greater dissimilarity for locations that were further apart (Sulpizio et al. 2014). Relatedly, an intracranial EEG study revealed that low-frequency oscillations in the human hippocampus could be used to decode the distance traveled during teleportation (Vass et al. 2016). Similarly, an fMRI study found that the similarity of patterns of activity in the hippocampus was related to both the remembered spatial distance between objects and the remembered temporal distance between objects (Deuker et al. 2016). Thus the results of these studies suggest that many regions code distance-related information, including the hippocampus, retrosplenial complex, PPA, and entorhinal cortex, among other cortical regions.

To be clear, the studies discussed in this section suggest that there is some specialization in the involvement of brain regions in the representation of landmarks, direction, and distance information. Importantly, however, the results also provide clear evidence for shared, distributed representations across brain regions; for example, the hippocampus, parahippocampal place area, and retrosplenial complex all carry information about location, heading, and the distance between locations (Sulpizio et al. 2014). Altogether, the emerging pattern of results suggests a sharing of computations related to spatial processing across many brain regions, rather than being the specialized focus of a single brain region. This presence of some amount of redundant coding with brain regions also argues against a purely localizationist perspective on spatial navigation and instead for a network-based conceptualization.

MECHANISTIC BASIS OF OUR MODEL: MULTIPLE INTERACTING, DYNAMICALLY CONFIGURABLE BRAIN REGIONS

The core of our model argues that spatial navigation is an emergent property of network interactions between a number of key regions, including the retrosplenial region (e.g., retrosplenial cortex, retrosplenial complex), parahippocampal region (e.g., PHC, PPA), hippocampus, entorhinal cortex, posterior parietal cortex, precuneus, thalamus, occipital place area, and prefrontal cortex. This list might seem to be virtually exhaustive because we are proposing that several different brain regions in multiple lobes, as well as several subcortical areas, are involved in parallel in coding representations underlying human spatial navigation. However, there are some key network properties that we hypothesize will be dissociable across the performance of different spatial navigation tasks relative to other cognitive tasks. For example, overlapping brain regions can play a role in multiple cognitive tasks because of differences in the “neural contexts” that arise from interregional interactions (Bressler 2004; Bressler and McIntosh 2007; McIntosh 2000, 2004; Phillips and Singer 1997; Watrous and Ekstrom 2014). We hypothesize that the retrosplenial region will serve as a functional hub of the spatial “navigation network,” particularly, but not limited to, spatial processing involving world-referenced, allocentric computations. Nonetheless, we also acknowledge the importance of some specialization, with our model restricting critical navigation-related function to a core set of brain regions within the navigation network (Fig. 4). Additionally, and perhaps most importantly, we emphasize the importance of highly interconnected, functional hubs, such as retrosplenial cortex, as critical areas for computations favoring allocentric coordinates, compared with posterior parietal cortex, which will serve as a critical hub biased toward egocentric computations. Note that we emphasize that these two regions have a bias toward either form of representation, but given that egocentric and allocentric representations emerge from network interactions including these two brain regions, neither exclusively dominates at any time.

Consistent with some of our previous proposals, we suggest that, mechanistically, low-frequency oscillations in the 1–12 Hz range (which includes the canonical theta range) will be critical for these network interactions. Our past work has suggested that low-frequency oscillations are greater across a network of different brain regions during correct compared with incorrect memory retrieval (Watrous et al. 2013). These low-frequency oscillations likely activate specific ensembles of neurons, which may manifest at higher frequencies in an asynchronous manner (Burke et al. 2015), thereby coding various aspects of the task via “spectral fingerprinting” (Siegel et al. 2012; Watrous and Ekstrom 2014). The idea is that the relative balance of egocentric and allocentric representations along a continuum of such representations will involve slightly differently frequencies of coherent oscillations between brain regions.

For example, when a participant utilizes a primarily egocentric representation, which will depend on memory for one’s displacement, a cluster of head-direction, place-specific, and velocity representations in retrosplenial, hippocampus, and posterior parietal cortex become simultaneously active, with posterior parietal cortex showing the greatest numbers of interactions with these different sites because of the predominance of the need for “self” representation. Note, though, that the representation at this time is a continuous mixture of different cell types, some of which may even be redundant between the different brain regions. As a participant switches to a more allocentric frame of reference, heuristics, such as whether the boundaries are in a square or circular shape, will likely come into play within areas such as inferior temporal cortex, with a further switch to predominance within retrosplenial cortex and place cell/head direction cell responses. Importantly, we suggest that both the specific brain hubs (posterior parietal vs. retrosplenial cortex) and frequencies of interactions will differ along a continuum between the two types of representations (see Ekstrom and Watrous 2014).

Critically, this network conceptualization also allows a continuous, hybrid form of an egocentric-allocentric representation that would otherwise be difficult to conceptualize in a scenario where one brain region does one function (Wang 2017). In this way, both forms of representations can simultaneously coexist and be called on to solve a task, depending on the current demands. We note that this could be additive or nonadditive, dependent on what cells are recruited redundantly vs. uniquely between different brain regions (Arnold et al. 2016; Bassett and Gazzaniga 2011; Ekstrom et al. 2014). Importantly, as retrosplenial regions become more of a hub, we have a relative tilt toward an allocentric form of processing. As we include inferior temporal cortex and anterior temporal areas (e.g., perirhinal cortex) to a greater extent in the interactions, we allow for a greater predominance of shape heuristics in processing.

In this way, we can think of the specific cellular response in specific brain regions more as complex conjunctions of signals that might be useful computationally for solving a task in terms of best capturing its unique components (Ekstrom and Ranganath 2017). There will likely be multiple different cellular responses involving variables such as geometric shape templates (e.g., squares, rectangles, and triangles) with other conjunctions of responses that include landmarks, heading direction, cardinal directions, and major and minor axes within the environment. These responses will likely manifest much like we might observe in the hidden layer of a “deep” neural network that can solve complex tasks (Mnih et al. 2015). The relative mix and conjunctions of these different cell types both within and across brain regions can then be optimized for the task, thus providing a means of configuring “on the fly.” At the same time, these conjunctive representations, in their purest sense, are not readily decomposable to a single feature, but rather exist on a continuum of conjunctions and interactions that are flexible and dynamic during the task (Ekstrom et al. 2003; Wirth et al. 2017).

PREDICTIONS OF OUR MODEL

Our model, in contrast to classic localizationist perspectives on spatial navigation, emphasizes the importance of redundant, distributed coding across different brain regions rather than computations within specific, dedicated modules in isolation. This in turn puts the emphasis on parallel interactions between different brain regions, via low-frequency oscillations, rather than the activity of a single brain region in relative isolation. At the same time, our model is not an “extreme” distributed model in that all neurons in all brain regions are the same, and as we have attempted to make clear, and consistent with decades of work in neuroscience, we readily acknowledge specialization within specific brain regions. Thus our model focuses on multimodal areas that have been shown to be strongly linked to spatial navigation, specifically, retrosplenial cortex, retrosplenial complex, parahippocampal gyrus (PHC, PPA, and entorhinal cortex), prefrontal cortex, posterior parietal cortex, and other subcortical areas specified in Fig. 4. As studies on human spatial navigation continue, specifically those that test our model, we will be able to validate or falsify specific aspects.

The first critical prediction that our model makes is that the retrosplenial region, rather than the hippocampus, is the most critical hub for navigation. In turn, this hypothesis allows us to make several novel predictions. First, the hypothesis that the retrosplenial region is a hub for spatial navigation could be tested by using a graph theory analysis of whole brain functional connectivity. Such an analysis should compare differences in how “hublike” its functional connectivity is between different cognitive tasks. We predict that the retrosplenial region will stand out as a particularly influential hub during performance of a spatial navigation task (i.e., its “hub score” will be in the top 5% of all nodes) compared with all other hubs in the navigation network (see Fig. 4). Note that we still predict the involvement of other critical hubs, such as hippocampus and posterior PHC, as well (Arnold et al. 2014), just to a lesser extent than retrosplenial cortex. Further, we predict that the retrosplenial region will exhibit greater hub scores for tasks that preferentially involve allocentric representations relative to egocentric representations, which we instead predict to rely to a greater extent on posterior parietal cortex as the relative hub (see Fig. 4).

Specifically, tasks requiring estimation of location based on multiple, stable landmarks should result in the retrosplenial cortex serving as a hub (regardless of modality), whereas those requiring updating of positions based on current body position should result in primarily posterior parietal cortex serving as a hub. In other words, as we tip the scales along the allocentric to egocentric spectrum in favor of one representation over another, we should also see a correlation with the degree of change in hub score from retrosplenial to posterior parietal cortex. As a null control condition, we predict that both allocentric and egocentric tasks will elicit greater hub scores in the retrosplenial region compared with a nonnavigation baseline task, which should tap these navigation-related areas minimally (Stark and Squire 2001). In addition, we predict that task-dependent changes in the “hubness” of the retrosplenial region, via changes in connectivity patterns (either directly or indirectly), will correlate with task performance, which provides insight into the degree to which participants might successfully utilize one form of representation over another (e.g., average error on the JRD task; see Fig. 2). The observation of a relationship between these network measures and behavior would provide more direct evidence that network interactions within the spatial navigation network support behavioral performance.

Some of these predictions have been partially validated. In one study, the retrosplenial region was shown to be a functional hub within a spatial navigation network during the resting state, and the degree to which it served as a hub was predictive of participants’ subjective navigational ability (Kong et al. 2017). Additionally, the retrosplenial region increases its functional connectivity with other cortical regions during performance of a spatial navigation task relative to a resting baseline task (Boccia et al. 2016), suggesting that the retrosplenial region alters its connectivity in the service of spatial navigation. Finally, the retrosplenial region is anatomically extremely well situated to integrate information from visual cortex with other multimodal information, as well as to combine information from the medial temporal lobes (Maguire 2001; Vann et al. 2009). However, several of the predictions of our model remain to be tested, specifically those related to the JRD and SOP tasks and the relative shifting of hub scores in a task-related fashion. The application of MVPA and network connectivity analyses is particularly attractive for understanding both the types of information that are represented within different regions of the spatial navigation network and the interactions between these regions. Furthermore, techniques that implement MVPA-based functional connectivity, such as informational connectivity (Coutanche and Thompson-Schill 2013), offer an exciting new way to study how information and computations are shared across multiple brain regions. Moreover, classification analysis can be applied to whole brain functional connectivity matrices to study the computational benefits of network interactions over local computations (Shirer et al. 2012).

A second critical prediction of our model is that damage to human retrosplenial cortex will result in more devastating impairments to spatial navigation than lesions to other brain regions, such as the hippocampus. This prediction has already been partially validated. Specifically, patients with strokes affecting retrosplenial cortex suffer profound navigation deficits (Hashimoto et al. 2010; Ino et al. 2007; Maguire 2001; Takahashi et al. 1997), including aspects that can be characterized as somewhere within an overlapping spectrum of egocentric and allocentric representations. This stands in contrast to lesions to the hippocampus, which typically result in more mild impairments affecting the precision of spatial memories or, in some cases, few navigational impairments at all, as discussed above. However, we believe that further testing of this idea is needed. Specifically, our model makes two additional predictions about retrosplenial vs. other lesions within the navigation network. First, patients with retrosplenial lesions should not only suffer profound navigation deficits, but these should be more pronounced for allocentric than egocentric biased tasks. Second, when patients attempt these tasks, they should also show a relative shifting in hubness to areas such as the hippocampus and parahippocampal cortex, which will thus play partially compensatory roles. Third, patients with damage to posterior parietal cortex should show profound deficits in egocentrically based navigation, with some allocentric deficits, but with a relative shifting of hubness scores to retrosplenial cortex compared with controls. Finally, and perhaps most critically, patients with lesions to multiple hubs within the navigation network, relative to patients with lesions to a single hub, should show the most profound and pronounced deficits in tasks such as the JRD and SOP.

Our model also makes specific predictions about redundant coding of navigation-related information throughout the navigation network, which we have outlined in Fig. 4. Specifically, we predict that we will see cellular responses to core aspects of navigation (distance, direction, location, and velocity) that are not localized to single brain regions but present, to different degrees, in multiple brain regions. As we discussed above in rodent studies, we believe this finding has been supported, in part, by single-cell recordings in rodents and humans showing place and head-direction responses in multiple brain regions. As we have also reviewed, fMRI has strongly implicated distributed coding mechanisms in allocentric and egocentric coding, but although it is a good indicator of this phenomenon, it lacks the resolution to depict cell-specific responses. Critically, we believe that in vivo recording studies in human patients and nonhuman primates will likely find higher distributions of place and head direction cells (in addition to velocity cells) within core areas of the navigation network compared with other brain regions. The presence of redundant cellular coding is critical to our model and remains to be fully tested, particularly in primates, for whom our model is most directly relevant.

Finally, and perhaps most importantly, mechanistic aspects of our model remain to be fully tested. Specifically, we hypothesize that low-frequency oscillations are critical for coordinating groups of task-relevant neural responses across brain regions within the navigation network important to performing a task. For example, when the JRD task is performed, we predict that cells responsive to location and direction (particularly imagined location) will be active across multiple areas of the navigation network, with the highest concentration in the retrosplenial region. Critically, we predict the presence of low-frequency oscillations as a means of coordinating between these brain regions. Thus disruption of these oscillations, which is possible with invasive stimulation (Kim et al. 2016), should disrupt this coordination. We predict that such a disruption will cause performance decrements but will not completely abolish performance, because distributed single-neuron responses will still be active, although insufficiently coordinated. Similarly, electrical stimulation applied directly to a brain region such as hippocampus or retrosplenial cortex (Jacobs et al. 2016) should disrupt task performance but not abolish it, as long as some coding and interactions between other brain regions are possible. Thus a final critical prediction, which remains to be fully tested, regards the importance of interactions between redundant coding mechanisms in a task-specific manner across the navigation network.

CONCLUSIONS

Despite the appeal of and evidence for localized spatial representations within brain regions such as retrosplenial cortex, posterior parietal cortex, hippocampus, and prefrontal cortex, there is also substantial evidence for distributed interactions among these regions as critical to spatial representations underlying navigation. Whereas some spatial metrics can be important in some instances (estimating how far one is from campus), we often use heuristics either in place of or in conjunction with spatial metrics. Our copious use of heuristics when reasoning about space makes it is difficult to distill navigation to discrete forms of spatial representations to any given task (egocentric vs. allocentric). Instead, such modality-independent representations seem better characterized by a spectrum of possible contributions, including topological and heuristic components that operate in the absence, in many cases, of “pure” metric knowledge. As such, it is difficult to assign a single brain region to a single function in navigation, and instead, we argue that a network conceptualization more naturally accomplishes the dynamic nature of spatial representation. Our model proposes that allocentric and egocentric representations involve a continuum behaviorally and are mediated by dynamic interactions via low-frequency oscillations between multiple brain regions centered on retrosplenial and posterior parietal cortex, respectively. Specifically, we hypothesize that the degree to which one of these regions serves as a hub will be associated with where on the egocentric-allocentric spectrum behavioral performance falls. Network-based conceptualizations of navigation also more naturally allow for contributions of shape heuristics and specific task demands, such as using rectangles to remember target locations. Together, these ideas provide a novel and testable framework for understanding the neural basis of human spatial navigation.

GRANTS

We acknowledge funding from National Institute of Neurological Disorders and Stroke Grants NS076856 and NS093052 (to A. D. Ekstrom) and National Science Foundation Award BCS-1630296.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.D.E. and D.J.H. prepared figures; A.D.E., D.J.H., and M.S. drafted manuscript; A.D.E., D.J.H., and M.S. edited and revised manuscript; A.D.E. approved final version of manuscript.