Abstract
We studied the effects of aminoglycosides and changing Mg2+ ion concentration on the accuracy of initial codon selection by aminoacyl-tRNA in ternary complex with elongation factor Tu and GTP (T3) on mRNA programmed ribosomes. Aminoglycosides decrease the accuracy by changing the equilibrium constants of ‘monitoring bases’ A1492, A1493 and G530 in 16S rRNA in favor of their ‘activated’ state by large, aminoglycoside-specific factors, which are the same for cognate and near-cognate codons. Increasing Mg2+ concentration decreases the accuracy by slowing dissociation of T3 from its initial codon- and aminoglycoside-independent binding state on the ribosome. The distinct accuracy-corrupting mechanisms for aminoglycosides and Mg2+ ions prompted us to re-interpret previous biochemical experiments and functional implications of existing high resolution ribosome structures. We estimate the upper thermodynamic limit to the accuracy, the ‘intrinsic selectivity’ of the ribosome. We conclude that aminoglycosides do not alter the intrinsic selectivity but reduce the fraction of it that is expressed as the accuracy of initial selection. We suggest that induced fit increases the accuracy and speed of codon reading at unaltered intrinsic selectivity of the ribosome.
INTRODUCTION
Intracellular protein synthesis relies on ribosomal translation of messenger RNA (mRNA) encoded genetic information to sequences of amino acid (aa) residues (1–4). For maximal fitness, the bacterial ribosome is composed of few large RNA chains and a large number of ribosomal proteins of small and uniform size (5) and it translates mRNA with high speed and accuracy (2,6–9). The elongation factor GTPases Tu (EF-Tu) and G (EF-G) increase the rates of binding of aminoacyl-tRNA to the ribosomal A site and translocation of mRNA and tRNAs along the ribosomal frame by five (9,10) and four (11) orders of magnitude, respectively.
Aminoacyl-tRNA (aa-tRNA) in ternary complex with EF-Tu and GTP (T3) binds to the ribosomal A/T site (1,2). In response to matching or non-matching mRNA codon in the A site, the T3-bound GTP is rapidly hydrolyzed allowing aa-tRNA to accommodate into the A/A site or, alternatively, intact T3 in the GTP form rapidly leaves the ribosome (1). Initial codon selection by T3 ends upon GTP hydrolysis (12). The accuracy of initial selection is provided by codon-anticodon interactions and amplified by activation of the monitoring bases A1492, A1493 and G530 of 16S ribosomal RNA (rRNA) for binding to the codon-anticodon helix (1,13,14). The accuracy of bacterial mRNA translation into peptide sequence is further amplified by proofreading (15–18), which occurs after hydrolysis of GTP in T3 and leads to high-probability-dissociation of near-cognate aa-tRNA (10,19,20). Together, initial selection and proofreading ensure a remarkably high accuracy of genetic code translation in vivo (21,22), but there are also notably high error ‘hot spots’, often involving U:G mismatches (9,21,22).
Ribosome speed (11) and translation errors (7,9,12,23) are sensitive to the concentration, [Mg2+], of free Mg2+ ions. Increasing [Mg2+] is deleterious. It reduces the accuracy of codon reading by an incoming aa-tRNA in both initial and proofreading codon selection steps (9,10,12,24), transforms near-cognate ternary complex into competitive inhibitors of cognate codon reading (8,25) and inhibits the EF-G dependent translocation (11,26). At the same time, Mg2+ ions are essential for the stability of the 70S ribosome structure (27), suggesting that the intracellular Mg2+ concentration is fine tuned for high viability and rapid growth of bacteria (27,28). Free [Mg2+] in E. coli has been estimated to be in the 1–2 mM range (29), slightly below the [Mg2+] value of 2.3 mM which, together with polyamines and other components of the ‘polymix’ buffer (23), calibrates the accuracy of translation in the test-tube (28) to that in the bacterial cell (22).
Aminoglycosides corrupt the accuracy of initial codon selection and proofreading in genetic code translation (30–32) and inhibit EF-G dependent translocation of mRNA and tRNAs (26,33,34). They induce hyper-activation of the monitoring bases A1492, A1493 and G530 of 16S rRNA (14,35–37) for contact not only with cognate (13,14) but also with near-cognate codon-anticodon helices in the decoding center of the ribosome (14). It has been suggested that increasing [Mg2+] induces hyper-activation of the monitoring bases, thereby corrupting the accuracy of codon selection and inhibiting translocation by a similar mechanism (7,11,14). It has also been proposed that the accuracy of initial codon selection is greatly enhanced by a particular induced fit mechanism (38–40) conferring a much smaller rate constant for GTPase activation on EF-Tu in near-cognate than cognate cases (24,40,41) and, furthermore, that aminoglycosides increase the near-cognate GTPase rate constant and leaves the cognate one unaltered (30,32).
Here, we used a cell free system for ribosomal protein synthesis with E. coli components (12) to quantify the effects of [Mg2+] and aminoglycosides on the accuracy of initial codon selection. We also measured a mean dissociation time of an A-site bound T3, assembled with Phe-tRNAPhe and a GTPase deficient His84Ala EF-Tu mutant (42). The experiments were performed in absence of aminoglycosides or presence of paromomycin, gentamicin or neomycin. In contrast to earlier proposals (7,14), including our own (11), we found that high [Mg2+] and aminoglycosides corrupt the accuracy of initial codon selection by different mechanisms. Both agents affect T3-bound ribosomal complexes in a codon-anticodon independent manner but, while increasing [Mg2+] selectively stabilizes the initial T3•ribosome complex, aminoglycosides selectively stabilize the pre-GTPase T3•ribosome complex with activated monitoring bases. We use our data to estimate the upper thermodynamic limit to the accuracy, the ‘intrinsic selectivity’ of the ribosome. Aminoglycosides and [Mg2+] do not affect the intrinsic selectivity but, instead, decrease the fraction of it that is expressed as current accuracy. We also conclude that although an induced fit mechanism leaves the intrinsic selectivity unaltered, it may enhance both the accuracy and speed of initial codon selection on the ribosome.
MATERIALS AND METHODS
Reagents and buffer conditions
Purified Escherichia coli components including initiation factors, elongation factors, 70S ribosomes (MRE 600) and f[3H]Met-tRNAfMet as well as synthetic mRNAs were prepared as described previously (9) and references therein. Native tRNAPhe were from Chemical Block. [3H]Met and [3H]GTP were from Perkin Elmer. Other chemicals were either from Sigma-Aldrich or Merck. All experiments were performed at 37°C in polymix buffer (23) containing 95 mM KCl, 5 mM NH4Cl, 0.5 mM CaCl2, 8 mM putrescine, 1 mM spermidine, 5 mM potassium phosphate, 1 mM DTE and 5 mM Mg(OAc)2. The buffer also contained 1 mM ATP + 1 mM GTP for the ribosome mixture or 2 mM ATP for the ternary complex mixture and energy regenerating components: 10 mM phosphoenolpyruvate (PEP), 50 μg/ml pyruvate kinase (PK), and 2 μg/ml myokinase (MK). Extra Mg(OAc)2 was added to adjust the free Mg2+ concentration in the reaction. Free [Mg2+]varies from 1.3 to 25 mM with addition of 0 to 30 mM extra Mg(OAc)2 assuming that one ATP or GTP molecule chelates one Mg2+ and PEP chelates Mg2+ with a Kd-value of 6 mM (43).
Measurement of kcat/Km for cognate initial selection reaction
Ribosome mixture contained 70S ribosomes (0.3–2 μM), f[3H]Met-tRNAfMet (0.45–2.5 μM), mRNA (0.45–2.5 μM), IF1 (0.45–2.5 μM), IF2 (0.15–0.5 μM), IF3 (0.45–1.5 μM) in polymix buffer with the energy regeneration components and varying concentrations of extra Mg(OAc)2. Ternary complex mixture contained tRNAs (2–5 μM), EF-Tu (0.15–1 μM), [3H]GTP (0.15–0.5 μM), amino acid (0.2 mM) and aa-tRNA synthetase (1.5 units/μl) in polymix buffer with energy regeneration components and varying concentrations of extra Mg(OAc)2. When studying the effects of aminoglycosides, 10 μM of paromomycin, gentamicin or neomycin were added to the both mixes. All the concentrations here refer to the component concentrations in the final reaction mixture.
Pre-initiated 70S ribosomes, with f[3H]Met-tRNAfMet in the P site, were formed by incubation of the ribosome mixture at 37°C for 10 min. Ternary complexes were formed by incubating the ternary complex mixture at 37°C for 15 min. Ribosome and ternary complex mixtures were rapidly mixed in a quench-flow instrument (RQF-3, KinTek Corp.) and quenched with 17% formic acid (final concentration) at specific time points. In order to estimate the concentration of active 70S initial complexes, equal volumes (10 μl) of ribosome and ternary mixtures were also mixed with addition of EF-Ts (1.5 μM). The reaction was incubated at 37°C for 1 min followed by quenching with formic acid (17% final). All samples were centrifuged at 20 000 × g for 15 min at 4°C, and the fractions of [3H]GTP and [3H]GDP, or the extent of [3H]dipeptide formed for the control experiments, were quantified using ion-exchange or reversed phase HPLC equipped with a β-RAM model 3 radioactivity detector (IN/US Systems) as described previously (9).
Measurement of kcat/Km for near-cognate initial selection
Near-cognate reactions were performed identically to the cognate reactions except that, in cases where near-cognate GTP hydrolysis reactions were slow, the mixing was performed manually rather than in a quench flow instrument. Transformation of [3H]GDP to [3H]GTP by the energy regeneration system was limited by the slow dissociation rate of GDP from EF-Tu, kex_GDP, (∼0.01 s−1 in absence of EF-Ts). Furthermore, the slow rate of exchange of [3H]GTP for unlabeled GTP on the ternary complex (kex_GTP) decreased the [3H]GDP signal. For precise parameter estimation a cognate reaction was always performed in parallel with the near-cognate one (12). Two ribosome mixtures, containing mRNAs with either cognate or near-cognate A-site codon, were prepared as described above. A ternary complex mixture was also prepared as described above, and divided into two mixtures for cognate and near-cognate reaction. Ribosome and ternary complex mixtures were mixed and quenched by 17% (final) formic acid after varying incubation times. The two resulting curves (Figure 1, black and red curves), sharing the plateau of GTP hydrolysis, kex_GDP, and kex_GTP, were jointly fitted (12) (see also SI, Eq. S46 for details). To estimate active ribosome concentration for near-cognate reactions, a separate ternary complex mixture was prepared with the corresponding cognate tRNA in the presence of EF-Ts (1.5 μM), and reacted with the ribosome complex in equal volumes (10 μl). Analysis of all 3H-labeled products was performed as described for the cognate reactions.
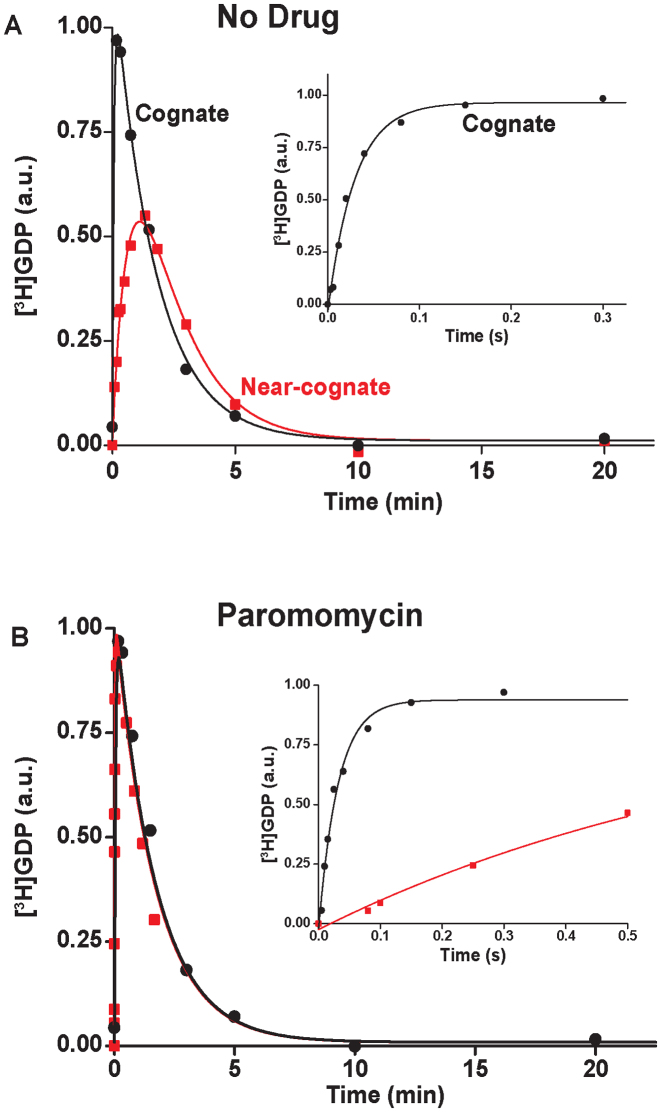
Figure 1.
Effects of paromomycin on the kinetics of GTP hydrolysis on ternary complexes reading cognate (UUC) and near-cognate (CUC) codons. Time courses of [3H]GDP accumulation after mixing ternary complexes [3H]GTP·EF-Tu·Phe-tRNAPhe with excess of mRNA programmed 70S ribosomes with cognate codon UUC (black squares) or near-cognate codon CUC (red circles) in the A-site. Cognate and near-cognate reactions were conducted in parallel at 1.3 mM free Mg2+ concentration (high accuracy condition). [3H]GDP accumulation in fast time scale is shown in inserts. Actual rates, k, of GTP hydrolysis for T3 reading UUC and CUC codons were obtained from fits of the corresponding curves (see M&M for details). Panel A: (no drug) k = 34 s−1 for UUC and k = 0.024 s−1 for CUC reading. Panel B: (with Paromomycin) k = 32 s−1 for UUC and k = 1.3 s−1 for CUC reading.
Chase of T3(H84A) by wild type T3
A GTPase deficient EF-Tu mutant (H84A) (42) was used to prepare a a ternary complex, T3(H84A), mixture as described above in the section ‘Measurement of kcat/Km for cognate initial selection reaction’. T3(H84A) was pre-bound to mRNA programmed ribosomes with a cognate codon in the A site in the absence of drug or presence of 10 μM Par, Gen or Neo. The mean dissociation time, 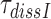 of T3(H84A) was estimated in chase experiments by addition of native cognate T3 with wild type EF-Tu in a five-fold smaller concentration than T3(H84A) in the absence and in equal concentration in the presence of drugs. The time course of dipeptide formation was then measured essentially as described above in the section ‘Measurement of kcat/Km for cognate initial selection reaction’ except that the mixing was done manually. The experiments were performed at 2.3 mM free [Mg2+], a concentration at which the accuracy of our cell-free protein synthesis system matches that in the living E. coli cell (22,28). To obtain the mean dissociation time,
of T3(H84A) was estimated in chase experiments by addition of native cognate T3 with wild type EF-Tu in a five-fold smaller concentration than T3(H84A) in the absence and in equal concentration in the presence of drugs. The time course of dipeptide formation was then measured essentially as described above in the section ‘Measurement of kcat/Km for cognate initial selection reaction’ except that the mixing was done manually. The experiments were performed at 2.3 mM free [Mg2+], a concentration at which the accuracy of our cell-free protein synthesis system matches that in the living E. coli cell (22,28). To obtain the mean dissociation time, 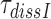 , of T3(H84A), the mean time of dipeptide formation was multiplied by a factor of six in the absence and by a factor of two in the presence of aminoglycosides. The rationale behind such a correction is that at the native T3 concentration 5-fold below that of T3(H84A) the probability of native T3 binding after T3(H84A) dissociation and, hence, of dipeptide formation is only one per six. This effectively slows dipeptide formation rate in the absence of drug by a factor of six making it possible to conduct the experiment ‘by hand’. At equal T3 and T3(H84A) concentrations the probability of native T3 binding after T3(H84A) dissociation is one per two and the dipeptide formation rate is slowed by the same factor. Details of this procedure are provided in SI (see Eq. S33).
, of T3(H84A), the mean time of dipeptide formation was multiplied by a factor of six in the absence and by a factor of two in the presence of aminoglycosides. The rationale behind such a correction is that at the native T3 concentration 5-fold below that of T3(H84A) the probability of native T3 binding after T3(H84A) dissociation and, hence, of dipeptide formation is only one per six. This effectively slows dipeptide formation rate in the absence of drug by a factor of six making it possible to conduct the experiment ‘by hand’. At equal T3 and T3(H84A) concentrations the probability of native T3 binding after T3(H84A) dissociation is one per two and the dipeptide formation rate is slowed by the same factor. Details of this procedure are provided in SI (see Eq. S33).
RESULTS
Accuracy of initial codon selection and its tuning by Mg2+ ions and aminoglycosides
We studied the effects of varying free [Mg2+] in the 1.3–25 mM interval and aminoglycoside addition on the kinetic efficiency, 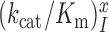 , of cognate (x = c) UUC (Phe) or near-cognate (x = nc1) CUC (Leu), (x = nc2) UCC (Ser) or (x = nc3) UUA (Leu) codon reading by Phe-tRNAPhe in ternary complex (T3) with EF-Tu and GTP. The experiments were performed in the absence of aminoglycoside (I = 0) or in the presence of paromomycin (I = P), gentamicin (I = G) or neomycin (I = N). A single T3 solution was prepared for mixing with each one of solutions containing mRNA programmed ribosomes with fMet-tRNAfMet in the P site and a UUC, CUC, UCC or UUA codon in the A site (see Materials and Methods). GTP hydrolysis reactions were started by mixing equal volumes of T3 and ribosome solutions. The reactions were quenched by formic acid at different incubation times and the extent of GTP hydrolysis was quantified as described in Materials and Methods. The mRNA programmed 70S ribosomes were always present in excess over T3, and the rate of GTP hydrolysis (k), defined as the inverse of the mean time for the hydrolytic reaction (44), was measured at several concentrations, [R1], of active ribosomes. Conditional on proportionality between k and [R1], (kcat/Km)-values were estimated as k/[R1] (12). In cognate cases, hydrolysis of [3H]GTP was much faster than regeneration of [3H]GTP from EF-Tu bound [3H]GDP, allowing for estimation of the k parameter directly from single exponential fitting (Figure 1A, insert). In near-cognate cases, GTP hydrolysis reaction was much slower (Figure 1A). Therefore estimation of k required concomitant determination of the rate of [3H]GTP regeneration from EF-Tu bound [3H]GDP and the rate of exchange of [3H]GTP in T3 with unlabeled, free GTP (see Materials and Methods for details). The addition of paromomycin had negligible effect on the rate, k, of GTP hydrolysis reaction in the cognate cases (Figure 1B, insert) but increased greatly the k-values of the near-cognate reactions (Figure 1B and B insert). Also gentamicin and neomycin addition had negligible effect on the cognate k-value but increased the rate of near-cognate GTP hydrolysis reaction by even larger factors than paromomycin (see Supplementary Figure S1).
, of cognate (x = c) UUC (Phe) or near-cognate (x = nc1) CUC (Leu), (x = nc2) UCC (Ser) or (x = nc3) UUA (Leu) codon reading by Phe-tRNAPhe in ternary complex (T3) with EF-Tu and GTP. The experiments were performed in the absence of aminoglycoside (I = 0) or in the presence of paromomycin (I = P), gentamicin (I = G) or neomycin (I = N). A single T3 solution was prepared for mixing with each one of solutions containing mRNA programmed ribosomes with fMet-tRNAfMet in the P site and a UUC, CUC, UCC or UUA codon in the A site (see Materials and Methods). GTP hydrolysis reactions were started by mixing equal volumes of T3 and ribosome solutions. The reactions were quenched by formic acid at different incubation times and the extent of GTP hydrolysis was quantified as described in Materials and Methods. The mRNA programmed 70S ribosomes were always present in excess over T3, and the rate of GTP hydrolysis (k), defined as the inverse of the mean time for the hydrolytic reaction (44), was measured at several concentrations, [R1], of active ribosomes. Conditional on proportionality between k and [R1], (kcat/Km)-values were estimated as k/[R1] (12). In cognate cases, hydrolysis of [3H]GTP was much faster than regeneration of [3H]GTP from EF-Tu bound [3H]GDP, allowing for estimation of the k parameter directly from single exponential fitting (Figure 1A, insert). In near-cognate cases, GTP hydrolysis reaction was much slower (Figure 1A). Therefore estimation of k required concomitant determination of the rate of [3H]GTP regeneration from EF-Tu bound [3H]GDP and the rate of exchange of [3H]GTP in T3 with unlabeled, free GTP (see Materials and Methods for details). The addition of paromomycin had negligible effect on the rate, k, of GTP hydrolysis reaction in the cognate cases (Figure 1B, insert) but increased greatly the k-values of the near-cognate reactions (Figure 1B and B insert). Also gentamicin and neomycin addition had negligible effect on the cognate k-value but increased the rate of near-cognate GTP hydrolysis reaction by even larger factors than paromomycin (see Supplementary Figure S1).
Estimates of cognate 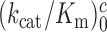 and
and 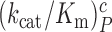 as well as near-cognate
as well as near-cognate 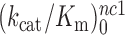 and
and 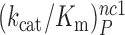 parameters at different [Mg2+] values are plotted in Figure 2. The [Mg2+] dependencies of cognate
parameters at different [Mg2+] values are plotted in Figure 2. The [Mg2+] dependencies of cognate  parameters and near-cognate
parameters and near-cognate 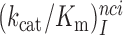 parameters for reading the CUC, UCC and UUA near-cognate codons in the absence of aminoglycosides and in the presence of paromomycin, gentamicin or neomycin are shown in Supplementary Figures S2 and S3. In the cognate cases, the [Mg2+] dependent parameters
parameters for reading the CUC, UCC and UUA near-cognate codons in the absence of aminoglycosides and in the presence of paromomycin, gentamicin or neomycin are shown in Supplementary Figures S2 and S3. In the cognate cases, the [Mg2+] dependent parameters 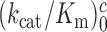 and
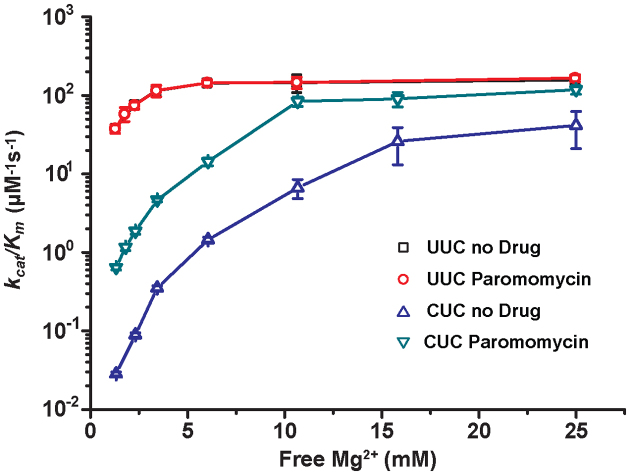
and 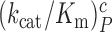 are virtually identical (Figure 2) as they increase from 37
are virtually identical (Figure 2) as they increase from 37  at 1.3 mM free [Mg2+] to a plateau value of 150
at 1.3 mM free [Mg2+] to a plateau value of 150  at 25 mM [Mg2+]. At the same time, the [Mg2+] dependencies of near–cognate
at 25 mM [Mg2+]. At the same time, the [Mg2+] dependencies of near–cognate 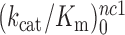 and
and 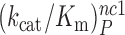 differ greatly (Figure 2). At 1.3 mM [Mg2+],
differ greatly (Figure 2). At 1.3 mM [Mg2+], 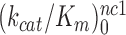 is more than three orders of magnitude smaller than
is more than three orders of magnitude smaller than 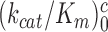 while
while 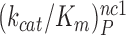 is about 20-fold larger than
is about 20-fold larger than 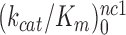 . At increasing [Mg2+] all curves in Figure 2 converge towards similar plateau values. The cognate
. At increasing [Mg2+] all curves in Figure 2 converge towards similar plateau values. The cognate 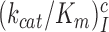 values are very similar for I = 0, P, G and N and inequalities
values are very similar for I = 0, P, G and N and inequalities 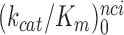
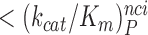 <
<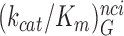 <
<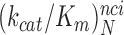 hold for all studied near-cognate codons (CUC (i = 1), UCC (i = 2) and UUA (i = 3)) at all values of [Mg2+] (Figure 2, Supplementary Figures S2 and S3). From these data we infer that the error induction mechanisms of Mg2+ ions and aminoglycosides are distinct (see Discussion).
hold for all studied near-cognate codons (CUC (i = 1), UCC (i = 2) and UUA (i = 3)) at all values of [Mg2+] (Figure 2, Supplementary Figures S2 and S3). From these data we infer that the error induction mechanisms of Mg2+ ions and aminoglycosides are distinct (see Discussion).
Figure 2.
Effects of [Mg2+] and paromomycin on the kinetic efficiency (kcat/Km) of cognate and near-cognate GTPase reactions. Log10-values of kcat/Km of GTP hydrolysis in T3 ([3H]GTP·EF-Tu·Phe-tRNAPhe) reading cognate (UUC) or near-cognate (CUC) codonplotted as functions of [Mg2+] in the presence ( , UUC;
, UUC;  , CUC) or absence (
, CUC) or absence ( , UUC;
, UUC;  , CUC) of paromomycin.
, CUC) of paromomycin.
Impact of aminoglycosides on efficiency-accuracy trade-off in initial codon selection
Using data presented in the previous section the cognate codon reading efficiency, 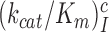 , was plotted versus the initial codon selection accuracy,
, was plotted versus the initial codon selection accuracy, 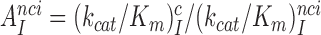 in the absence (I = 0) or presence of different aminoglycosides (I = P, G or N) and near-cognate codons CUC (i = 1), UCC (i = 2) or UUA (i = 3) at varying [Mg2+] (Figure 3). Linear efficiency-accuracy trade-off plots (9,12) were obtained in all cases as shown for i = 1, 2 or 3 in Figure 3A, B or C, respectively. All trade-off lines are accounted for by Equation (1) (derived in SI, Eq. S14) with [Mg2+]-independent k1 and
in the absence (I = 0) or presence of different aminoglycosides (I = P, G or N) and near-cognate codons CUC (i = 1), UCC (i = 2) or UUA (i = 3) at varying [Mg2+] (Figure 3). Linear efficiency-accuracy trade-off plots (9,12) were obtained in all cases as shown for i = 1, 2 or 3 in Figure 3A, B or C, respectively. All trade-off lines are accounted for by Equation (1) (derived in SI, Eq. S14) with [Mg2+]-independent k1 and 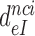 parameters (12):
parameters (12):
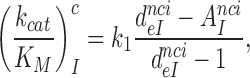 |
(1) |
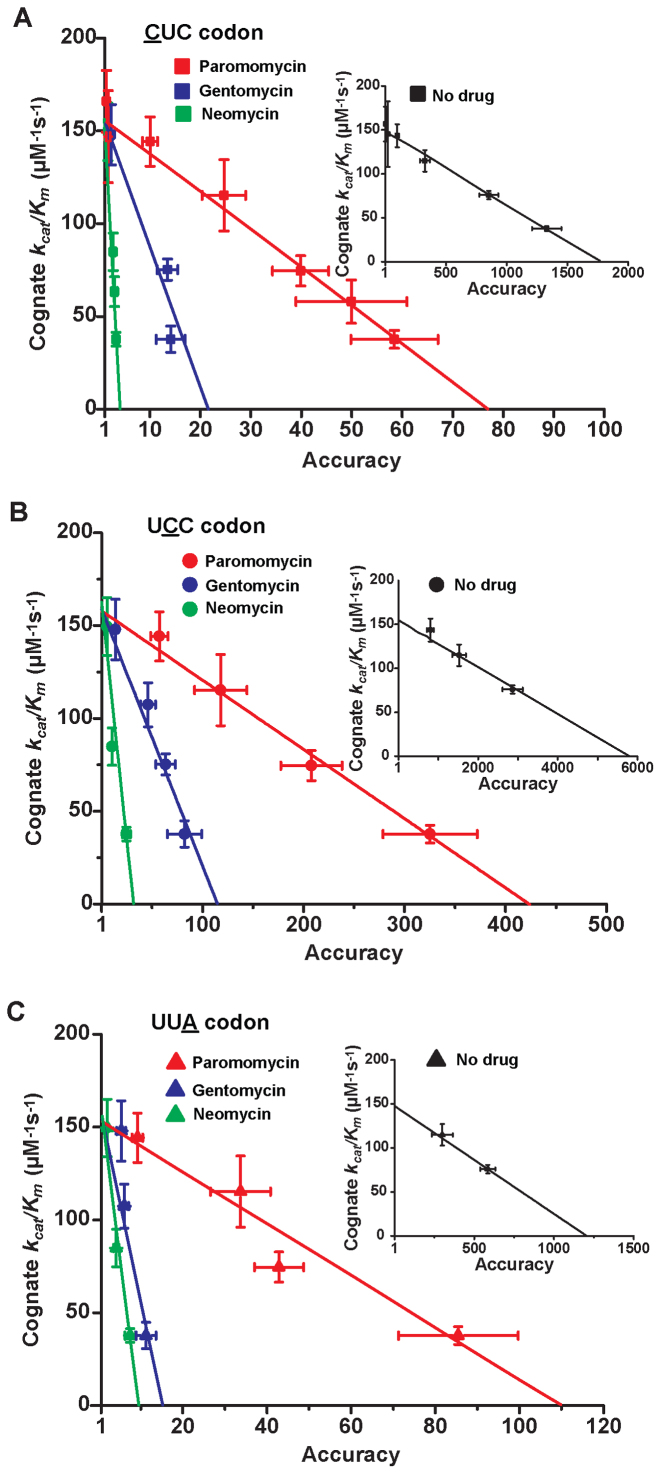
Figure 3.
The effect of aminoglycosides on the efficiency-accuracy trade-off. Kinetic efficiency (kcat/Km)c of the reaction of GTP hydrolysis on EF-Tu·GTP·Phe-tRNAPhe ternary complex reading its cognate UUC codon was plotted versus accuracy of initial selection for the same ternary complex reading its near-cognate codons in the presence of paromomycin, gentamicin and neomycin or in their absence (inserts). The intercepts of straight lines with the accuracy axis (A-value when (kcat/Km)c = 0) give the effective selectivity values 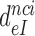 compiled in Table 1. Panel A: CUC near-cognate codon; Panel B: UCC near-cognate codon; Panel C: UUA near-cognate codon.
compiled in Table 1. Panel A: CUC near-cognate codon; Panel B: UCC near-cognate codon; Panel C: UUA near-cognate codon.
The rate constant for association of ternary complex to the ribosome, k1, is estimated as the value of 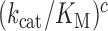 at the intercept of a trade-off line with the vertical A = 1 axis. The effective selectivity parameter,
at the intercept of a trade-off line with the vertical A = 1 axis. The effective selectivity parameter, 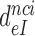 , is operationally defined from the A-value of the intercept of each trade-off line with the horizontal
, is operationally defined from the A-value of the intercept of each trade-off line with the horizontal 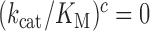 axis (Figure 3). From the plots in Figure 3k1 was estimated as 150
axis (Figure 3). From the plots in Figure 3k1 was estimated as 150 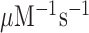 and the
and the 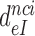 values in the absence of drugs as
values in the absence of drugs as 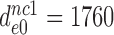 ,
, 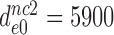 and
and 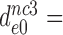 1200. The latter estimates are very similar to those obtained in previous work for the same tRNA and near-cognate codons (9). The
1200. The latter estimates are very similar to those obtained in previous work for the same tRNA and near-cognate codons (9). The 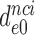 -value decreased to
-value decreased to 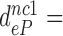 75,
75, 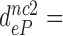 420 and
420 and 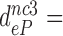 110 by addition of paromomycin; to
110 by addition of paromomycin; to 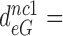 17,
17, 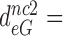 100 and
100 and 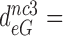 15 by addition of gentamicin; and to
15 by addition of gentamicin; and to 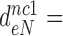 3.9,
3.9, 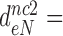 30 and
30 and 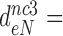 9 by addition of neomycin (Table 1). The fold decrease in
9 by addition of neomycin (Table 1). The fold decrease in 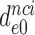 upon aminoglycoside addition was in each case quantified as a
upon aminoglycoside addition was in each case quantified as a 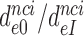 ratio, as shown for i = 1, 2, 3 and I = P, G, N in Table 1. Importantly, the
ratio, as shown for i = 1, 2, 3 and I = P, G, N in Table 1. Importantly, the 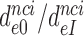 ratios in Table 1 also quantify the fold of aminoglycoside-induced decrease in current accuracy of initial codon selection (
ratios in Table 1 also quantify the fold of aminoglycoside-induced decrease in current accuracy of initial codon selection (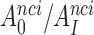 ) at any Mg2+ ion concentration. This follows from linearity of the trade-off plots in Figure 3 and from the aminoglycoside-insensitivity of the cognate
) at any Mg2+ ion concentration. This follows from linearity of the trade-off plots in Figure 3 and from the aminoglycoside-insensitivity of the cognate 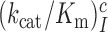 parameters (Figure 2 and Supplementary Figure S2). Therefore, these ratios also estimate the effects of aminoglycosides on the initial selection accuracy in the living cell. The
parameters (Figure 2 and Supplementary Figure S2). Therefore, these ratios also estimate the effects of aminoglycosides on the initial selection accuracy in the living cell. The 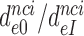 ratios are similar for different near-cognate codons (different i-values). We defined average ratios,
ratios are similar for different near-cognate codons (different i-values). We defined average ratios, 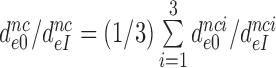 , to estimate the decrease in effective selectivity of codon reading by paromomycin (
, to estimate the decrease in effective selectivity of codon reading by paromomycin (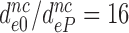 ), gentamicin (
), gentamicin (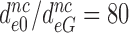 ) and neomycin (
) and neomycin (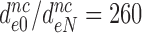 ) (Table 2). Although neomycin and paromomycin induce similar structural arrangements of the decoding center (45), neomycin reduces the effective selectivity by a much larger factor than does paromomycin (Table 2).
) (Table 2). Although neomycin and paromomycin induce similar structural arrangements of the decoding center (45), neomycin reduces the effective selectivity by a much larger factor than does paromomycin (Table 2).
Table 1. Dissociation time, 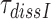 , of the GTPase deficient cognate ternary complex and effective selectivity,
, of the GTPase deficient cognate ternary complex and effective selectivity, 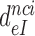 , for different near-cognate codons with and without drugs.
, for different near-cognate codons with and without drugs.
| No drug | Paromomycin | Gentamicin | Neomycin | |
|---|---|---|---|---|
Dissociation time, 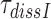 (s) (s) |
2±0.1 | 26±1 | 130±4 | 320±15 |
| Fold increase by drug | 13±1 | 65±4 | 160±11 | |
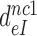 -value on CUC -value on CUC |
1760±180 | 75 ± 10 | 17 ± 4 | 3.9 ± 0.6 |
| Fold decrease by drug | 23± 4 | 104± 27 | 451±84 | |
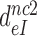 -value on UCC -value on UCC |
5900±970 | 420 ± 76 | 103 ± 20 | 30 ± 5 |
| Fold decrease by drug | 14± 4 | 57± 15 | 197± 46 | |
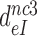 -value on UUA -value on UUA
|
1200±190 | 111 ± 22 | 14.6 ± 0.8 | 9 ± 1.7 |
| Fold decrease by drug | 11± 3 | 82± 14 | 133± 33 |
Table 2. Average fold decrease, 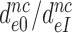 , in effective selectivity compared with fold increase in dissociation time,
, in effective selectivity compared with fold increase in dissociation time, 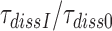 , of the GTPase deficient cognate T3 upon aminoglycoside addition.
, of the GTPase deficient cognate T3 upon aminoglycoside addition.
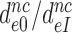
|
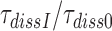
|
|
|---|---|---|
| No drug | 1 | 1 |
| Paromomycin | 16 ± 2 | 13 ± 1 |
| Gentamicin | 81 ± 12 | 65 ± 4 |
| Neomycin | 260 ± 34 | 160 ± 11 |
Aminoglycoside addition reduces the rate of cognate ternary complex dissociation from the ribosome
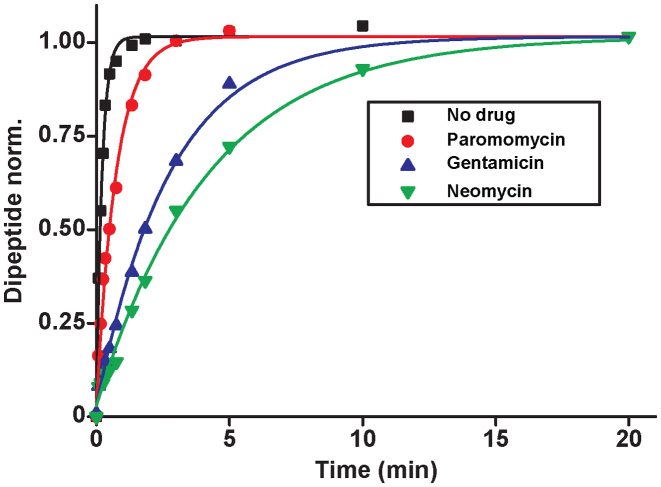
A possible explanation for the observed aminoglycoside specific reduction of the accuracy of initial selection is a change in the equilibrium constant connecting the ‘inactive conformation’ of the monitoring bases with their active conformation in which they contact the codon-anticodon helix (1,2,14). These contacts are expected to stabilize cognate compared to near-cognate T3 binding (14). To quantify the magnitude of such aminoglycoside induced stabilization of cognate T3 binding we studied the effect of aminoglycosides on the mean-time of dissociation of a GTPase deficient ternary complex, T3(H84A), from mRNA programmed ribosomes with (initiator) fMet-tRNAfMet in P site and cognate UUC (Phe) codon in A site. This ternary complex contained Phe-tRNAPhe, the GTPase deficient EF-Tu mutant, H84A, (42) and GTP. T3(H84A) was pre-bound to the ribosome and then chased from it by addition of GTPase proficient T3 assembled with native EF-Tu and GTP. The mean time for T3(H84A) dissociation,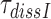 , was estimated from the mean time of fMet-Phe-tRNAPhe dipeptide formation (Figure 4) as described in Materials and Methods. Estimates of
, was estimated from the mean time of fMet-Phe-tRNAPhe dipeptide formation (Figure 4) as described in Materials and Methods. Estimates of 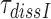 obtained in the absence of aminoglycoside (I = 0) or in the presence of paromomycin (I = P), gentamicin (I = G) or neomycin (I = N) are summarized in Table 1 and presented as ratios
obtained in the absence of aminoglycoside (I = 0) or in the presence of paromomycin (I = P), gentamicin (I = G) or neomycin (I = N) are summarized in Table 1 and presented as ratios 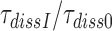 for I = P, G and N in Table 2. It is seen that ratios
for I = P, G and N in Table 2. It is seen that ratios  are very similar to ratios
are very similar to ratios 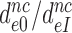 for I = P, G and N (Table 2). From the close similarity of these ratios we propose that the origin of error induction by aminoglycosides is, indeed, a shift of equilibrium of the monitoring bases from their inactive to their active states, and that the underlying relative change in equilibrium constant is the same for cognate and near-cognate codon–anticodon interactions, as explained in detail in Discussion.
for I = P, G and N (Table 2). From the close similarity of these ratios we propose that the origin of error induction by aminoglycosides is, indeed, a shift of equilibrium of the monitoring bases from their inactive to their active states, and that the underlying relative change in equilibrium constant is the same for cognate and near-cognate codon–anticodon interactions, as explained in detail in Discussion.
Figure 4.
The effects of aminoglycosides on the dissociation-mean-time of GTPase-deficient cognate ternary complex. Time traces of dipeptide formation mirrow slow dissociation of GTPase deficient T3 (EF-Tu(H84A)·GTP·Phe-tRNAPhe), pre-bound to the A site of mRNA programmed ribosomes. The chase of GTPase deficient cognate T3 by native cognate T3 was conducted in the absence of aminoglycoside or in the presence of paromomycin, gentamicin or neomycin (see Materials and Methods for details).
DISCUSSION
Key observations of the present work
The kinetic efficiency, kcat/Km, of the cognate GTP hydrolysis reaction is unaffected by aminoglycosides but increases four-fold as the free [Mg2+] increases from 1.3 to 25 mM (Figure 2, Supplementary Figure S2).
The corresponding near-cognate kcat/Km-values increase by orders of magnitude in response to aminoglycoside addition in the low Mg2+ concentration range and increase further with increasing [Mg2+] up to the cognate kcat/Km-values (Figure 2, Supplementary Figure S3).
The efficiency-accuracy trade-off plots (Figure 3) are linear for all near-cognate codons both in the absence and presence of the aminoglycosides (Figure 3).
In response to aminoglycoside addition the mean dissociation time of a cognate, GTPase deficient ternary complex increase by the very same aminoglycoside specific factors (Figure 4, Table 2) as those seen for the decrease in the accuracy-axis intercepts of the efficiency-accuracy lines (Figure 3, Table 2).
To account for these key observations we have developed a kinetic model for initial codon selection by ternary complex.
Kinetic modeling of initial codon selection
Initial selection of ternary complex proceeds through sequential formation of at least three structurally distinct T3-bound ribosome complexes (2–4,46). Therefore, realistic modeling of this kinetic process requires a scheme with at least four steps (47,48), leading from free T3 and free ribosome (R1) to GTP hydrolysis in complex C4 (Figure 5). R1 is here the mRNA-programmed ribosome with a P-site peptidyl-tRNA and an empty A site. Binding of T3 to R1 leads to reversible formation of the first T3-bound complex, C2, with association and dissociation rate constants k1 and 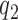 , respectively. T3 has the same classical, ‘straight’ conformation in C2 as in its free state (49), and is unable to make codon-anticodon contact (24,47,50). Therefore rate constants k1 and
, respectively. T3 has the same classical, ‘straight’ conformation in C2 as in its free state (49), and is unable to make codon-anticodon contact (24,47,50). Therefore rate constants k1 and 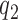 are codon unspecific and the same for cognate and near-cognate T3. More recently, cryo electron microscopy (cryo-EM) has confirmed the lack of codon-anticodon contact in C2 (structure I or T in the cryo-EM nomenclature) (46), and shown the decoding center of the ribosome in C2 to be very similar to that in the mRNA-programmed ribosomes with P-site tRNA and empty A site (51). In complex C3, emerging from C2 with rate constant k2, the aa-tRNA of T3 is ‘bent’, allowing for proper codon-anticodon contact (52–54), and the 30S subunit has an ‘open’ conformation (14), like in C2. Complex C3 has been observed by single molecule FRET (47) and more recently by cryo-EM (structure II or A*/T in the cryo-EM nomenclature) (46). In C3 there is codon-anticodon contact, monitoring base A1493 is more ordered than in C2 and makes contact with the codon-anticodon helix, but otherwise the decoding centers of C2 and C3 are similar (46). Complex C3 may move backward to complex C2 or forward to complex C4 with rate constants
are codon unspecific and the same for cognate and near-cognate T3. More recently, cryo electron microscopy (cryo-EM) has confirmed the lack of codon-anticodon contact in C2 (structure I or T in the cryo-EM nomenclature) (46), and shown the decoding center of the ribosome in C2 to be very similar to that in the mRNA-programmed ribosomes with P-site tRNA and empty A site (51). In complex C3, emerging from C2 with rate constant k2, the aa-tRNA of T3 is ‘bent’, allowing for proper codon-anticodon contact (52–54), and the 30S subunit has an ‘open’ conformation (14), like in C2. Complex C3 has been observed by single molecule FRET (47) and more recently by cryo-EM (structure II or A*/T in the cryo-EM nomenclature) (46). In C3 there is codon-anticodon contact, monitoring base A1493 is more ordered than in C2 and makes contact with the codon-anticodon helix, but otherwise the decoding centers of C2 and C3 are similar (46). Complex C3 may move backward to complex C2 or forward to complex C4 with rate constants 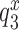 or
or 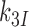 , respectively, where index x signifies cognate (c) or near-cognate (nc) codon-anticodon interaction and index I signifies the absence (I = 0) or presence (I = P,G or N) of drug. Rate constant
, respectively, where index x signifies cognate (c) or near-cognate (nc) codon-anticodon interaction and index I signifies the absence (I = 0) or presence (I = P,G or N) of drug. Rate constant 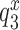 is determined by the stability of codon-anticodon interaction in the absence of monitoring base contribution. The rate constant for monitoring bases activation,
is determined by the stability of codon-anticodon interaction in the absence of monitoring base contribution. The rate constant for monitoring bases activation, 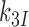 , increases in response to aminoglycoside addition but is neutral to the cognate or near-cognate status of the codon-anticodon contact. In complex C4, the interactions between codon-anticodon helix and monitoring bases A1492, A1493 and G530 are fully developed (13) and the 30S subunit is ‘closed’ (14) with monitoring bases G530 and A1492 now hydrogen-bonded (13,14). Complex C4, in which the decoding center has similar geometry for cognate and near-cognate tRNAs, has been observed in structures of the mRNA programmed 70S ribosome with P- and A- site tRNAs (55,56). In recent cryo-EM work (46) C4 was visualized also for near-cognate T3 and its striking similarity with the cognate C4 complex, previously observed in crystallographic (54) and cryo-EM (57) studies, has been confirmed. Complex C4 moves backward to complex C3 with rate constant
, increases in response to aminoglycoside addition but is neutral to the cognate or near-cognate status of the codon-anticodon contact. In complex C4, the interactions between codon-anticodon helix and monitoring bases A1492, A1493 and G530 are fully developed (13) and the 30S subunit is ‘closed’ (14) with monitoring bases G530 and A1492 now hydrogen-bonded (13,14). Complex C4, in which the decoding center has similar geometry for cognate and near-cognate tRNAs, has been observed in structures of the mRNA programmed 70S ribosome with P- and A- site tRNAs (55,56). In recent cryo-EM work (46) C4 was visualized also for near-cognate T3 and its striking similarity with the cognate C4 complex, previously observed in crystallographic (54) and cryo-EM (57) studies, has been confirmed. Complex C4 moves backward to complex C3 with rate constant  or forward to GTP hydrolysis with rate constant
or forward to GTP hydrolysis with rate constant 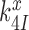 . The value of rate constant
. The value of rate constant 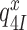 for monitoring bases de-activation upon their dissociation from the codon-anticodon helix and ‘re-opening’ of the 30S subunit depends on the cognate or near-cognate status of the codon-anticodon interaction and the presence or absence of aminoglycosides. The equilibrium constants connecting ribosomal states (C2, C3) and (C3, C4) are defined as
for monitoring bases de-activation upon their dissociation from the codon-anticodon helix and ‘re-opening’ of the 30S subunit depends on the cognate or near-cognate status of the codon-anticodon interaction and the presence or absence of aminoglycosides. The equilibrium constants connecting ribosomal states (C2, C3) and (C3, C4) are defined as 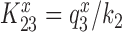 and
and 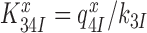 , respectively. We stress here that state C4 in Figure 5 is the last ground state on the pathway to GTP hydrolysis with activation free energy barrier
, respectively. We stress here that state C4 in Figure 5 is the last ground state on the pathway to GTP hydrolysis with activation free energy barrier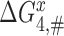 . The GTP hydrolysis rate constant,
. The GTP hydrolysis rate constant, 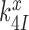 is therefore given by
is therefore given by 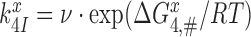 , where
, where 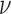 is a frequency factor (39) and the
is a frequency factor (39) and the 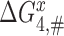 barrier accounts for conformational changes in EF-Tu that organize its catalytic center and the chemistry of GTP hydrolysis (42,58). Whether
barrier accounts for conformational changes in EF-Tu that organize its catalytic center and the chemistry of GTP hydrolysis (42,58). Whether 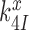 is neutral or sensitive to the cognate or near-cognate nature of the codon-anticodon contact and the presence or absence of aminoglycosides will be discussed below, but first we outline pertinent kinetics and accuracy characteristics of the codon recognition scheme in Figure 5.
is neutral or sensitive to the cognate or near-cognate nature of the codon-anticodon contact and the presence or absence of aminoglycosides will be discussed below, but first we outline pertinent kinetics and accuracy characteristics of the codon recognition scheme in Figure 5.
Figure 5.
Four steps scheme of initial codon selection by ternary complex on mRNA programmed ribosomes. R1 is the mRNA-programmed ribosome with empty A-site and peptidyl-tRNA in the P-site; T3 is free ternary complex. Binding of T3 to R1 results in initial complex C2 in which the anticodon of aa-tRNA in T3 lacks contact with the mRNA codon. In complex C3 aa-tRNA in T3 is ‘bent’, its anticodon is in contact with the mRNA codon and monitoring bases A1492, A1493 and G530 are in ‘inactive conformation’. In complex C4, the monitoring bases are activated and interact with the codon-anticodon helix promoting a ‘closure’ of the 30S subunit (see main text for details).
Mg2+ ions and aminoglycosides have orthogonal effects on the accuracy of initial codon selection
The kcat/Km value for ribosome dependent GTP hydrolysis in a ternary complex is, firstly, determined by the rate constant, k1, of T3 association to the ribosome and, secondly, by the probability,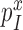 , that formation of initial complex C2 between the ribosome and a cognate (x = c) or near-cognate (x = nc) T3 leads to GTP hydrolysis on EF-Tu rather than dissociation of intact T3 from the ribosome (8). The cognate kcat/Km-value for the kinetic scheme in Figure 5 is given by
, that formation of initial complex C2 between the ribosome and a cognate (x = c) or near-cognate (x = nc) T3 leads to GTP hydrolysis on EF-Tu rather than dissociation of intact T3 from the ribosome (8). The cognate kcat/Km-value for the kinetic scheme in Figure 5 is given by
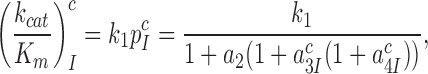 |
(2) |
where 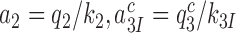 and
and 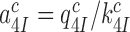 are discard parameters (see SI, Eq. S6, for details). Crystallographic studies have shown that aminoglycoside binding displaces the monitoring bases A1492 and A1493 from their binding sites in helix h44 of 16S rRNA greatly favoring their active, ‘flipped out’ conformations, in which they interact with the codon-anticodon helix (13,45,59). Aminoglycosides are, therefore, expected to increase the forward rate constant
are discard parameters (see SI, Eq. S6, for details). Crystallographic studies have shown that aminoglycoside binding displaces the monitoring bases A1492 and A1493 from their binding sites in helix h44 of 16S rRNA greatly favoring their active, ‘flipped out’ conformations, in which they interact with the codon-anticodon helix (13,45,59). Aminoglycosides are, therefore, expected to increase the forward rate constant  for monitoring bases binding to the codon-anticodon helix. By this mechanism, they decrease both the cognate discard parameter
for monitoring bases binding to the codon-anticodon helix. By this mechanism, they decrease both the cognate discard parameter 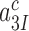 and the equilibrium constant
and the equilibrium constant 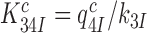 between complexes C3 and C4, thereby shifting their equilibrium further towards C4. This equilibrium shift is here observed as an aminoglycoside specific increase in the mean-time of dissociation of a GTPase deficient T3 originally in cognate complex C4 (Figure 4 and Discussion below). We note that aminoglycoside dependent reductions in
between complexes C3 and C4, thereby shifting their equilibrium further towards C4. This equilibrium shift is here observed as an aminoglycoside specific increase in the mean-time of dissociation of a GTPase deficient T3 originally in cognate complex C4 (Figure 4 and Discussion below). We note that aminoglycoside dependent reductions in 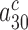 do not affect the cognate
do not affect the cognate 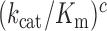 parameter at any Mg2+ concentration (Figure 2 and Supplementary Figure S2). This implies that
parameter at any Mg2+ concentration (Figure 2 and Supplementary Figure S2). This implies that 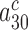 and the product
and the product 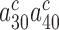 are much smaller than one also in the absence of aminoglycosides, so that their further reduction by aminoglycosides has no effect on the cognate kcat/Km-value and Equation (2) is approximated by:
are much smaller than one also in the absence of aminoglycosides, so that their further reduction by aminoglycosides has no effect on the cognate kcat/Km-value and Equation (2) is approximated by:
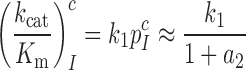 |
(3) |
The lack of sensitivity of the cognate kcat/Km and, hence, a2 parameter, to aminoglycosides suggests that neither 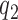 nor
nor 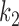 is aminoglycoside sensitive. The increase in cognate kcat/Km-value with increasing [Mg2+] can now be explained by a decrease in the discard parameter a2 caused by decreasing dissociation rate constant
is aminoglycoside sensitive. The increase in cognate kcat/Km-value with increasing [Mg2+] can now be explained by a decrease in the discard parameter a2 caused by decreasing dissociation rate constant 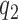 . We note that in an early study of the initial ribosome binding state for T3, the decrease in
. We note that in an early study of the initial ribosome binding state for T3, the decrease in 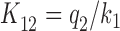 with increasing [Mg2+] was identified but originally ascribed to increasing association rate constant k1 (60).
with increasing [Mg2+] was identified but originally ascribed to increasing association rate constant k1 (60).
Near-cognate kcat/Km-values are given by (see SI, Eq. S6, for details):
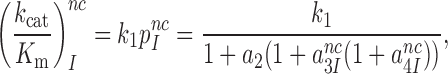 |
(4) |
where 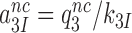 and
and 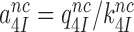 are near-cognate discard parameters. The current accuracy, A, of initial codon selection is defined by the ratio between cognate and near-cognate kcat/Km-values (39):
are near-cognate discard parameters. The current accuracy, A, of initial codon selection is defined by the ratio between cognate and near-cognate kcat/Km-values (39):
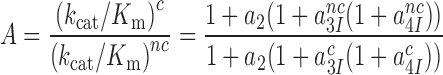 |
(5) |
Accordingly, small a2-value at high [Mg2+] renders low accuracy of initial codon selection (8,12,24,50), and large a2-value at low [Mg2+] renders high accuracy (12), approaching the effective initial codon selectivity, defined as A in the limit where a2 goes to infinity in Equation (5):
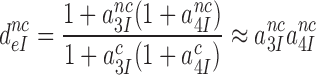 |
(6) |
The effective selectivity, 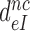 , can be operationally defined as the A-axis intercept of a linear efficiency-accuracy plot (Figure 3) (12). Large values of
, can be operationally defined as the A-axis intercept of a linear efficiency-accuracy plot (Figure 3) (12). Large values of 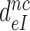 (Table 1) imply that the discard parameters
(Table 1) imply that the discard parameters 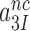 and
and 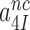 are much larger than one, allowing for the simplifying
are much larger than one, allowing for the simplifying 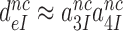 approximation in Equation (6).
approximation in Equation (6).
All efficiency-accuracy plots in the present work are linear both in the presence and absence of aminoglycosides (Figure 3), implying that neither the 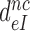 -parameter (see Equation 1) nor the
-parameter (see Equation 1) nor the 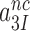 and
and 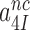 parameters vary with changing [Mg2+]. It has been suggested that Mg2+ ions and aminoglycosides affect the accuracy of initial codon selection similarly by occupying the aminoglycoside binding site in h44, thereby driving the monitoring bases to their ‘flipped out’, activated conformation (7,11,14). Contrary to these previous speculations, the present results mean that increasing [Mg2+] does not activate A1492 and A1493, and only reduces the dissociation rate constant q2. From this follows that Mg2+- ions and aminoglycosides affect different steps of the initial selection process and thus have ‘orthogonal’ modes of action. This conclusion is also in line with the strikingly different effects of Mg2+ ions and aminoglycosides on the Michaelis-Menten rate constant,
parameters vary with changing [Mg2+]. It has been suggested that Mg2+ ions and aminoglycosides affect the accuracy of initial codon selection similarly by occupying the aminoglycoside binding site in h44, thereby driving the monitoring bases to their ‘flipped out’, activated conformation (7,11,14). Contrary to these previous speculations, the present results mean that increasing [Mg2+] does not activate A1492 and A1493, and only reduces the dissociation rate constant q2. From this follows that Mg2+- ions and aminoglycosides affect different steps of the initial selection process and thus have ‘orthogonal’ modes of action. This conclusion is also in line with the strikingly different effects of Mg2+ ions and aminoglycosides on the Michaelis-Menten rate constant, 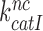 of the GTPase reaction for near-cognate ternary complex. That is, while large [Mg2+] variation had only small effect on
of the GTPase reaction for near-cognate ternary complex. That is, while large [Mg2+] variation had only small effect on 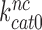 , paromomycin addition increased
, paromomycin addition increased 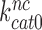 by more than one order of magnitude (see Supplementary Figure S4).
by more than one order of magnitude (see Supplementary Figure S4).
Aminoglycosides do not affect the intrinsic selectivity of the ribosome
In the present context (Figure 5) the intrinsic (ultimate) selectivity of the ribosome, 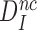 , is defined as:
, is defined as:
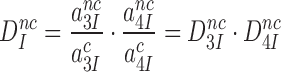 |
(7) |
This corresponds to the current accuracy, A, in the limit where discard parameters 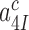 and
and 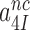 in Equation (5) go to infinity at unaltered
in Equation (5) go to infinity at unaltered 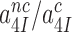 ratio. In this limit the concentrations of the ribosomal complexes in Figure 5 are in thermodynamic equilibrium not only in near-cognate but also in cognate cases, so that
ratio. In this limit the concentrations of the ribosomal complexes in Figure 5 are in thermodynamic equilibrium not only in near-cognate but also in cognate cases, so that 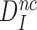 can be defined in terms of standard free energies, as in Equation (8) below. The intrinsic selectivity
can be defined in terms of standard free energies, as in Equation (8) below. The intrinsic selectivity 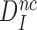 does not depend on discard parameter a2 and, hence, on [Mg2+]. Ratios
does not depend on discard parameter a2 and, hence, on [Mg2+]. Ratios 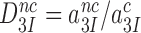 and
and 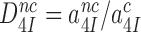 are the intrinsic selectivity arising from codon-anticodon interactions alone and the selectivity amplification by activated monitoring bases, respectively. Parameter
are the intrinsic selectivity arising from codon-anticodon interactions alone and the selectivity amplification by activated monitoring bases, respectively. Parameter 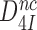 , previously ascribed to a ‘geometric’ selectivity amplification (13,14), has more recently been ascribed to the creation of a water free environment around the codon-anticodon helix (61). In this environment the lack of base-to-base H-bonds in near-cognate codon-anticodon helices cannot be compensated by base-to-water H-bonds, resulting in a larger standard free energy gap between a near-cognate and a cognate codon-anticodon helix than in bulk water (39,61).
, previously ascribed to a ‘geometric’ selectivity amplification (13,14), has more recently been ascribed to the creation of a water free environment around the codon-anticodon helix (61). In this environment the lack of base-to-base H-bonds in near-cognate codon-anticodon helices cannot be compensated by base-to-water H-bonds, resulting in a larger standard free energy gap between a near-cognate and a cognate codon-anticodon helix than in bulk water (39,61).
Recasting Equation (7) in terms of the equilibrium and rate constants of Figure 5 leads to (see SI, Eq. S20, for details):
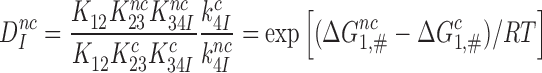 |
(8) |
It follows that 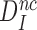 is a fundamental parameter determined by the difference in standard free energy for near-cognate and cognate substrates to reach their transition states on the enzyme from their free states (39).
is a fundamental parameter determined by the difference in standard free energy for near-cognate and cognate substrates to reach their transition states on the enzyme from their free states (39). 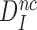 provides, therefore, an upper, thermodynamic bound for the accuracy of initial codon selection on the ribosome.
provides, therefore, an upper, thermodynamic bound for the accuracy of initial codon selection on the ribosome.
Although aminoglycosides greatly reduce accuracy, A, and effective selectivity, 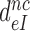 , of initial codon reading they leave the intrinsic selectivity,
, of initial codon reading they leave the intrinsic selectivity, 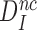 , unaltered. This inference follows from our finding that the factors
, unaltered. This inference follows from our finding that the factors 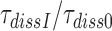 by which aminoglycosides increase the mean dissociation times,
by which aminoglycosides increase the mean dissociation times, 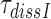 , of cognate, GTPase deficient T3 are very similar to the factors
, of cognate, GTPase deficient T3 are very similar to the factors 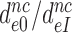 by which they decrease effective selectivity
by which they decrease effective selectivity 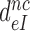 (Table 2). It follows, therefore, that:
(Table 2). It follows, therefore, that:
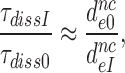 |
(9) |
for I = P, G and N (Table 2). Taking into account that 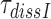 can be approximated as (see SI, Eq. S31, for details):
can be approximated as (see SI, Eq. S31, for details):
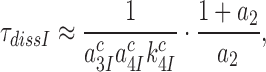 |
(10) |
one obtains from Equations (6), (7) and (9) that:
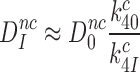 |
(11) |
This means, in other words, that the intrinsic selectivity in the presence of aminoglycosides, 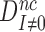 , is equal to that in their absence,
, is equal to that in their absence, 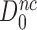 , multiplied by the ratio
, multiplied by the ratio 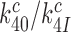 of cognate GTPase rate constants. At 37°C, the rate constant
of cognate GTPase rate constants. At 37°C, the rate constant 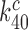 is larger than 900 s−1 but a precise estimate of its value is difficult to obtain (44). In line with previous suggestions, we deem it likely that rate constant
is larger than 900 s−1 but a precise estimate of its value is difficult to obtain (44). In line with previous suggestions, we deem it likely that rate constant 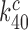 has been maximized by optimization of the interaction between rRNA (A2662 in the sarcin-ricin loop) and the GTPase center of EF-Tu for maximal rate of GTP hydrolysis (46,54,61,62). Furthermore, structures of the mRNA programmed ribosome with cognate tRNA in the A site or of the 30S subunit with cognate ASLs have shown paromomycin to have but a marginal effect on the geometry of the decoding center and virtually no effect on the geometry of the codon-anticodon helix (13,14,55,56). To the extent that these structural features pertain also to the ternary complex in state C4, which we deem as likely (48), they suggest that aminoglycoside addition leaves the cognate GTPase rate constant
has been maximized by optimization of the interaction between rRNA (A2662 in the sarcin-ricin loop) and the GTPase center of EF-Tu for maximal rate of GTP hydrolysis (46,54,61,62). Furthermore, structures of the mRNA programmed ribosome with cognate tRNA in the A site or of the 30S subunit with cognate ASLs have shown paromomycin to have but a marginal effect on the geometry of the decoding center and virtually no effect on the geometry of the codon-anticodon helix (13,14,55,56). To the extent that these structural features pertain also to the ternary complex in state C4, which we deem as likely (48), they suggest that aminoglycoside addition leaves the cognate GTPase rate constant 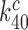 unchanged, i.e.
unchanged, i.e. 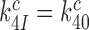 . It then follows from Equation (11) that
. It then follows from Equation (11) that 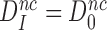 , which means that aminoglycosides greatly reduce the effective selectivity,
, which means that aminoglycosides greatly reduce the effective selectivity, 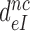 , but leave the intrinsic selectivity,
, but leave the intrinsic selectivity, 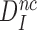 , of the ribosome unaltered.
, of the ribosome unaltered.
How aminoglycosides reduce the effective selectivity of initial codon reading
To see how the reduction of 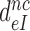 -values by aminoglycosides (Table 2) comes about we recast Equation (6) in terms of equilibrium and rate constants (see SI, Eq. S16, for details):
-values by aminoglycosides (Table 2) comes about we recast Equation (6) in terms of equilibrium and rate constants (see SI, Eq. S16, for details):
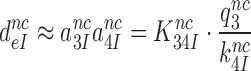 |
(12) |
Further, from Equation (10) it follows that 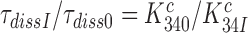 (see SI, Eq. S32, for details) and then from Equations (9) and (12) that:
(see SI, Eq. S32, for details) and then from Equations (9) and (12) that:
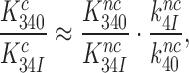 |
(13) |
Here the left hand side corresponds to 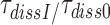 and the right hand side to
and the right hand side to 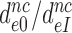 in Equation (9). Accordingly, the
in Equation (9). Accordingly, the 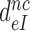 reduction may be due to a decrease in the equilibrium constant
reduction may be due to a decrease in the equilibrium constant 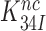 , an increase in the rate constant,
, an increase in the rate constant, 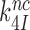 or a combination thereof.
or a combination thereof.
In the previous section we concluded that 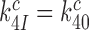 , but what about the near-cognate GTPase rate constants appearing in Equation (13)? An answer to this question is provided by crystallographic data showing virtually no structural changes of the decoding center or the geometry of the codon-anticodon helix in state C4 in response to aminoglycoside addition in near-cognate cases (51,56). Following the same logic as in the previous section we propose from these structural data that aminoglycosides leave not only cognate but also near-cognate GTPase rate constants unaltered (
, but what about the near-cognate GTPase rate constants appearing in Equation (13)? An answer to this question is provided by crystallographic data showing virtually no structural changes of the decoding center or the geometry of the codon-anticodon helix in state C4 in response to aminoglycoside addition in near-cognate cases (51,56). Following the same logic as in the previous section we propose from these structural data that aminoglycosides leave not only cognate but also near-cognate GTPase rate constants unaltered (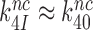 ). Then, it follows from Equation (13) that aminoglycosides reduce equilibrium constants
). Then, it follows from Equation (13) that aminoglycosides reduce equilibrium constants 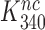 and
and 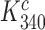 by the very same factor. The
by the very same factor. The 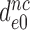 -value reductions are then completely explained by the aminoglycoside-induced reductions in
-value reductions are then completely explained by the aminoglycoside-induced reductions in 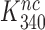 at unaffected
at unaffected 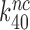 .
.
The premise 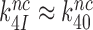 leads, however, to an apparent problem: if aminoglycosides only affect
leads, however, to an apparent problem: if aminoglycosides only affect 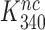 and
and  how then can paromomycin increase the Michaelis-Menten constant,
how then can paromomycin increase the Michaelis-Menten constant,  , of the near-cognate GTP hydrolysis reaction from about 6 s−1 to about 80 s−1 (see Supplementary Figure S4)? To explain this result we first note that
, of the near-cognate GTP hydrolysis reaction from about 6 s−1 to about 80 s−1 (see Supplementary Figure S4)? To explain this result we first note that  for the scheme in Figure 5 is given by (see SI, Eq. S8, for details):
for the scheme in Figure 5 is given by (see SI, Eq. S8, for details):
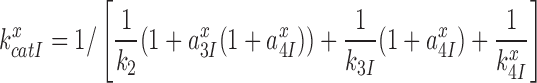 |
(14) |
In cognate cases the discard parameters 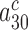 and
and 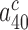 are much smaller than one and decrease further upon aminoglycoside addition, so that:
are much smaller than one and decrease further upon aminoglycoside addition, so that:
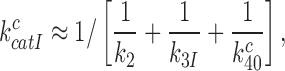 |
(15) |
where we used that 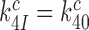 (see above in Discussion). This suggests that the cognate
(see above in Discussion). This suggests that the cognate  will display but a moderate increase in response to aminoglycoside addition due to increased k3I-value. In near-cognate cases, in contrast, the discard parameters
will display but a moderate increase in response to aminoglycoside addition due to increased k3I-value. In near-cognate cases, in contrast, the discard parameters 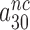 and
and 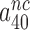 are much larger than one but become greatly reduced by aminoglycosides. These features explain (see Equation 14) why
are much larger than one but become greatly reduced by aminoglycosides. These features explain (see Equation 14) why 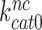 is so much smaller than
is so much smaller than 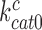 and why aminoglycosides greatly increase
and why aminoglycosides greatly increase 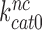 at unaltered
at unaltered 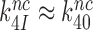 . It also follows (see SI, Eq. S10, for details) that when
. It also follows (see SI, Eq. S10, for details) that when 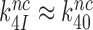 the increase in
the increase in 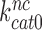 by aminoglycosides is near proportional to the aminoglycoside-induced decrease in
by aminoglycosides is near proportional to the aminoglycoside-induced decrease in 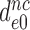 . Indeed, the 14-fold increase in
. Indeed, the 14-fold increase in 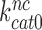 by paromomycin (from 6 s−1 to about 80 s−1) is close to the 16 fold decrease in
by paromomycin (from 6 s−1 to about 80 s−1) is close to the 16 fold decrease in 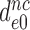 by this drug (Table 2).
by this drug (Table 2).
Above we concluded that the reduction in 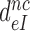 by aminoglycosides is caused by a reduction in
by aminoglycosides is caused by a reduction in 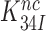 (see Equation 12). It follows from Equations (6) and (7) that
(see Equation 12). It follows from Equations (6) and (7) that 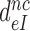 can also be written as:
can also be written as:
 |
(16) |
Equation (16) implies that any reduction in 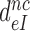 at unaltered
at unaltered 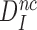 must be mirrored by a corresponding reduction in the combined discard parameter
must be mirrored by a corresponding reduction in the combined discard parameter 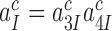 for cognate codon reading. At 2.3 mM free [Mg2+], at which the dissociation times,
for cognate codon reading. At 2.3 mM free [Mg2+], at which the dissociation times, 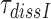 , for GTPase deficient cognate T3 were measured (Table 1) the discard parameter
, for GTPase deficient cognate T3 were measured (Table 1) the discard parameter 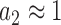 (28). Also taking into account that
(28). Also taking into account that 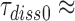 2 s (Table 1) and
2 s (Table 1) and 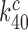 > 900 s−1 (44) Equation (10) can be used to estimate an upper bound for
> 900 s−1 (44) Equation (10) can be used to estimate an upper bound for 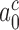 as 10−3. This means that the fraction of the intrinsic selectivity that is expressed in the effective selectivity is smaller than 1 per mille and that aminoglycosides reduce this remarkably small fraction even further. We note that these extremely small values of
as 10−3. This means that the fraction of the intrinsic selectivity that is expressed in the effective selectivity is smaller than 1 per mille and that aminoglycosides reduce this remarkably small fraction even further. We note that these extremely small values of 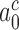 and
and 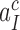 can be traced to the near irreversibility of the cognate reaction upon formation of codon-anticodon contact in state C3. With
can be traced to the near irreversibility of the cognate reaction upon formation of codon-anticodon contact in state C3. With 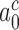 = 10−3 and
= 10−3 and 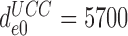 (Table 1) and use of Equation (16) we estimate
(Table 1) and use of Equation (16) we estimate  as 5.7.106. This value is surprisingly high and, yet, in good agreement with the value
as 5.7.106. This value is surprisingly high and, yet, in good agreement with the value 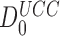 = 2.7 ×106 calculated from the rate constants of initial selection, as reported by Rodnina and collaborators (7) and also with the value of
= 2.7 ×106 calculated from the rate constants of initial selection, as reported by Rodnina and collaborators (7) and also with the value of 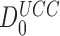 in the range 0.6 × 106 – 3.4 × 106, as estimated from molecular dynamic simulations by Åqvist et al. (61) for T3 with Phe-tRNAPhe reading its near-cognate UCC codon.
in the range 0.6 × 106 – 3.4 × 106, as estimated from molecular dynamic simulations by Åqvist et al. (61) for T3 with Phe-tRNAPhe reading its near-cognate UCC codon.
Past results in the context of the present study
Ramakrishnan and co-workers measured the effect of paromomycin (Par) on the affinity of anticodon stem-loop (ASL) constructs to 70S ribosomes programmed with short mRNA analogues (14). They found that Par increased the ribosome affinity to a cognate ASL about 15-fold (14), similar to the Par induced increase in dissociation time of a GTPase-deficient cognate T3 from the 70S ribosome observed here (Table 2). They also found that the effect of Par on near-cognate ASLs was insignificant (14). Also the latter result is perfectly in line with the present data, provided that the equilibrium constant 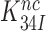 remained considerably larger than one after a 15-fold decrease in response to Par addition (see SI, Eq. S40, for details).
remained considerably larger than one after a 15-fold decrease in response to Par addition (see SI, Eq. S40, for details).
Rodnina and collaborators used fast kinetics and T3s with fluorescence labeled tRNA to study the effects of Par on codon reading (30). These studies were conducted with a low fidelity (LoFi) buffer (7), which lacked the polyamines required for cell-free protein synthesis of physiological relevance (23,24,27,63–65). Since there was virtually no initial codon selection either with or without Par (i.e.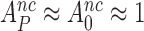 ), the effects of Par on the elemental rate constants they observed (30) could not be related to the Par-induced decrease in the accuracy of initial selection that occurs under physiological conditions. Namely, under conditions where the accuracy of our in vitro translation matches that in vivo (28), Par decreased the accuracy of initial selection on the UCC codon by a Phe-tRNAPhe containing T3 from
), the effects of Par on the elemental rate constants they observed (30) could not be related to the Par-induced decrease in the accuracy of initial selection that occurs under physiological conditions. Namely, under conditions where the accuracy of our in vitro translation matches that in vivo (28), Par decreased the accuracy of initial selection on the UCC codon by a Phe-tRNAPhe containing T3 from 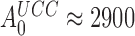 down to
down to 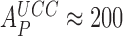 (Figure 3B). We also note that while we used a four state scheme to describe initial codon selection (Figure 5), Rodnina and collaborators used a three-state scheme (Equation 17) to describe the same process. In essence, this amounts to a contraction of our states C3 and C4 in Figure 5 to a single state C34, in which the distinction between active and inactive monitoring bases is blurred:
(Figure 3B). We also note that while we used a four state scheme to describe initial codon selection (Figure 5), Rodnina and collaborators used a three-state scheme (Equation 17) to describe the same process. In essence, this amounts to a contraction of our states C3 and C4 in Figure 5 to a single state C34, in which the distinction between active and inactive monitoring bases is blurred:
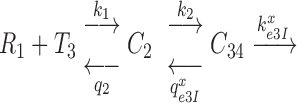 |
(17) |
Rodnina et al. concluded that Par decreased k2 in both cognate and near-cognate cases about trice (30). It can also be calculated from their elemental rate constants (Table 2 in (30)) that because of this k2 reduction the Michaelis-Menten constant kcat of the near-cognate GTP hydrolysis reaction was increased by Par only slightly, from 30 s−1 to 34 s−1. From the present data follows that k2 was insensitive to aminoglycosides, and that Par induced an increase in the near-cognate kcat-value for GTP-hydrolysis from 6 to 80 s−1 (Supplementary Figure S4). One explanation for these discrepancies could be their low temperature (20°C) and polyamine deficient conditions compared to our high temperature (37°C) and polyamine proficient conditions. Another explanation could be the approximate nature of the elemental rate constant estimations from their fluorescence based data (see Supplementary Discussion for details).
Rodnina and collaborators also concluded that Par decreased the near-cognate dissociation rate constant 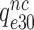 (their k-2) in Equation (17) from 17 to 3.5 s−1 and increased the near-cognate GTPase rate constant
(their k-2) in Equation (17) from 17 to 3.5 s−1 and increased the near-cognate GTPase rate constant 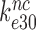 (their k3) from 50 to about 500 s−1 at unchanged cognate GTPase rate constant
(their k3) from 50 to about 500 s−1 at unchanged cognate GTPase rate constant 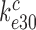 (about 500 s−1) (30). Concerning Par-induced changes in these parameters, we first note that
(about 500 s−1) (30). Concerning Par-induced changes in these parameters, we first note that 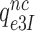 and
and 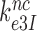 in Equation (17) are related to the elemental rate and equilibrium constants of the scheme in Figure 5 as
in Equation (17) are related to the elemental rate and equilibrium constants of the scheme in Figure 5 as 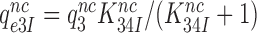 and
and 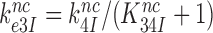 , respectively (see SI, Eq. S44, for details). A large reduction in
, respectively (see SI, Eq. S44, for details). A large reduction in  by Par leads, therefore, directly to a large decrease in
by Par leads, therefore, directly to a large decrease in 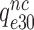 and a large increase in
and a large increase in 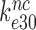 even at unaltered near-cognate GTPase rate constant
even at unaltered near-cognate GTPase rate constant 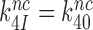 . It is, we propose, the contraction of the four-state kinetic scheme in Figure 5 to the three-state scheme in Equation (17) that is the main reason for the apparent discrepancy between the present conclusion that Par has no effect on
. It is, we propose, the contraction of the four-state kinetic scheme in Figure 5 to the three-state scheme in Equation (17) that is the main reason for the apparent discrepancy between the present conclusion that Par has no effect on 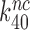 and only decreases equilibrium constant
and only decreases equilibrium constant 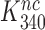 for monitoring bases activation and the previous conclusion that Par increases the near-cognate GTPase rate constant by an order of magnitude (30,32).
for monitoring bases activation and the previous conclusion that Par increases the near-cognate GTPase rate constant by an order of magnitude (30,32).
The role of induced fit in initial codon selection
The notion of induced fit generally refers to reorganization of the catalytic center of an enzyme in response to substrate binding (38,39). The present four-state scheme (Figure 5) describes an induced fit mechanism of initial codon selection in which the binding of cognate and near-cognate T3s lead to similar reorganizations of the ribosome decoding center. In this respect the present mechanism differs significantly from previously suggested induced fit mechanisms of initial codon selection, as explained below.
We first note that in the absence of drugs the compounded GTPase rate constant 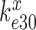 in the contracted scheme of Equation (17) is approximated by
in the contracted scheme of Equation (17) is approximated by 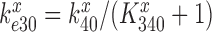 (see SI, Eq. S44, for details). Accordingly, even in the case when
(see SI, Eq. S44, for details). Accordingly, even in the case when  , the comparatively small values observed for
, the comparatively small values observed for 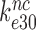 (7,24,41) are easily explained by comparatively large values of
(7,24,41) are easily explained by comparatively large values of 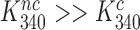 . Those reflect a comparatively large standard free energy cost for binding of the monitoring bases A1492, A1493 and G530 to a near-cognate compared to a cognate codon-anticodon helix and concomitant ‘closure’ of the 30S subunit (14). In contrast, Rodnina and collaborators explained small
. Those reflect a comparatively large standard free energy cost for binding of the monitoring bases A1492, A1493 and G530 to a near-cognate compared to a cognate codon-anticodon helix and concomitant ‘closure’ of the 30S subunit (14). In contrast, Rodnina and collaborators explained small 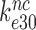 values by suggesting that GTP hydrolysis in near-cognate cases occurs in the ‘open’ state of the 30S subunit with inactive monitoring bases, i.e. in a state corresponding to C3 in Figure 5 (24,40). This ‘induced fit’ mechanism favors cognate in relation to near-cognate T3s (38) by allowing only cognate T3s to reach state C4 and from there proceed to GTP hydrolysis via an optimal transition state. Near-cognate T3s, in contrast, are only able to reach state C3, from which they proceed to a suboptimal transition state for GTP hydrolysis (1,14,24,40). It has also been suggested that aminoglycosides greatly reduce the standard free energy cost to reach state C4 from state C3 thereby redirecting near-cognate T3s to follow the pathway of cognate T3s to rapid GTP hydrolysis via state C4 (1,66). This particular induced fit mechanism was challenged by crystal structures of the mRNA programmed ribosome with near-cognate, deacylated tRNAs in their A sites (51,56,67–70) and more recently by cryo-EM structures of near-cognate ternary complexes bound to mRNA programmed ribosomes (46). These structures demonstrate that even in the absence of drugs near-cognate T3 can reach state C4 in Figure 5 with a near-cognate codon-anticodon helix in authentic contact with the monitoring bases and the 30S subunit closed around the ASL of the tRNA. The implication here is that cognate and near-cognate T3 can proceed to GTP hydrolysis via structurally very similar ground states in C4 and, hence, have very similar transition state free energy barriers for GTP hydrolysis (i.e.
values by suggesting that GTP hydrolysis in near-cognate cases occurs in the ‘open’ state of the 30S subunit with inactive monitoring bases, i.e. in a state corresponding to C3 in Figure 5 (24,40). This ‘induced fit’ mechanism favors cognate in relation to near-cognate T3s (38) by allowing only cognate T3s to reach state C4 and from there proceed to GTP hydrolysis via an optimal transition state. Near-cognate T3s, in contrast, are only able to reach state C3, from which they proceed to a suboptimal transition state for GTP hydrolysis (1,14,24,40). It has also been suggested that aminoglycosides greatly reduce the standard free energy cost to reach state C4 from state C3 thereby redirecting near-cognate T3s to follow the pathway of cognate T3s to rapid GTP hydrolysis via state C4 (1,66). This particular induced fit mechanism was challenged by crystal structures of the mRNA programmed ribosome with near-cognate, deacylated tRNAs in their A sites (51,56,67–70) and more recently by cryo-EM structures of near-cognate ternary complexes bound to mRNA programmed ribosomes (46). These structures demonstrate that even in the absence of drugs near-cognate T3 can reach state C4 in Figure 5 with a near-cognate codon-anticodon helix in authentic contact with the monitoring bases and the 30S subunit closed around the ASL of the tRNA. The implication here is that cognate and near-cognate T3 can proceed to GTP hydrolysis via structurally very similar ground states in C4 and, hence, have very similar transition state free energy barriers for GTP hydrolysis (i.e. 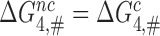 ). In this new picture, similar to that suggested by Åqvist and collaborators (61),
). In this new picture, similar to that suggested by Åqvist and collaborators (61), 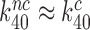 but the standard free energy cost to reach the pre-GTP hydrolysis state C4 is much higher for near-cognate than cognate T3. Moreover, when
but the standard free energy cost to reach the pre-GTP hydrolysis state C4 is much higher for near-cognate than cognate T3. Moreover, when  , it follows from Equation (8) that
, it follows from Equation (8) that 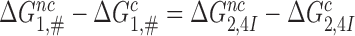 (see SI, Eq. S21 for details). Since in state C2 cognate and near-cognate T3s have the same standard free energy, it also follows that the intrinsic selectivity
(see SI, Eq. S21 for details). Since in state C2 cognate and near-cognate T3s have the same standard free energy, it also follows that the intrinsic selectivity 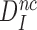 is solely determined by the difference in standard free energy between near-cognate and cognate T3s in state C4. Thus, induced fit per se does not conjure increased intrinsic selectivity
is solely determined by the difference in standard free energy between near-cognate and cognate T3s in state C4. Thus, induced fit per se does not conjure increased intrinsic selectivity 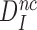 (39).
(39).
Now, if the intrinsic, ultimate, selectivity, 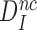 , is unaffected by induced fit, what about the effective selectivity,
, is unaffected by induced fit, what about the effective selectivity, 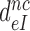 ? To answer this question we recast Equation (12) for
? To answer this question we recast Equation (12) for 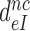 (see SI, Eq. S16, for details) in the form:
(see SI, Eq. S16, for details) in the form:
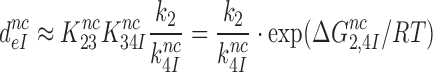 |
(18) |
It is seen that at a constant 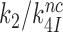 ratio, the effective selectivity
ratio, the effective selectivity 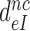 increases with increasing
increases with increasing 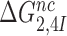 gap size. We further note that in state C2 of the present induced fit model (Figure 5) there is no codon-anticodon contact, monitoring bases are inactive and the 30S subunit is in the open form. It is only in state C4 the three conditions for GTP hydrolysis are fulfilled, i.e. codon-anticodon contact is established, monitoring bases are all active and the 30S subunit closed. This implies that the near-cognate standard free energy cost,
gap size. We further note that in state C2 of the present induced fit model (Figure 5) there is no codon-anticodon contact, monitoring bases are inactive and the 30S subunit is in the open form. It is only in state C4 the three conditions for GTP hydrolysis are fulfilled, i.e. codon-anticodon contact is established, monitoring bases are all active and the 30S subunit closed. This implies that the near-cognate standard free energy cost, 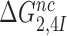 , to move from state C2 to state C4 is comparatively large (2,14), and, hence, according to Equation (18),
, to move from state C2 to state C4 is comparatively large (2,14), and, hence, according to Equation (18), 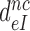 -value is also comparatively large. In contrast, in a hypothetical situation without induced fit, the monitoring bases could be activated and the 30S subunit closed already in state C2 in the absence of the codon-anticodon contact. Accordingly, without the induced fit, the near-cognate standard free energy gap
-value is also comparatively large. In contrast, in a hypothetical situation without induced fit, the monitoring bases could be activated and the 30S subunit closed already in state C2 in the absence of the codon-anticodon contact. Accordingly, without the induced fit, the near-cognate standard free energy gap 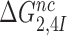 from state C2 to C4 would be smaller, the
from state C2 to C4 would be smaller, the 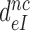 -value also smaller and the frequency of initial codon selection errors would be larger. In general, the more similar the structures of the decoding center in states C2 and C4, the smaller the free energy gap,
-value also smaller and the frequency of initial codon selection errors would be larger. In general, the more similar the structures of the decoding center in states C2 and C4, the smaller the free energy gap, 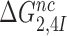 , and the smaller the
, and the smaller the 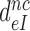 -value, the error induction by aminoglycosides described here being a special case of this general principle.
-value, the error induction by aminoglycosides described here being a special case of this general principle.
Another inference from the statement that 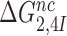 is the main determinant of the effective selectivity,
is the main determinant of the effective selectivity, 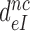 (Equation 18) is that the existence of an intermediate state C3, with codon-anticodon contact in an aqueous environment (Figure 5), or of other putative states between C2 and C4, will not affect the
(Equation 18) is that the existence of an intermediate state C3, with codon-anticodon contact in an aqueous environment (Figure 5), or of other putative states between C2 and C4, will not affect the 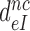 -value. It follows, therefore, that the induced fit mechanism without state C3 proposed by Yusupov/Yusupova and collaborators (51,67) has the same effective selectivity
-value. It follows, therefore, that the induced fit mechanism without state C3 proposed by Yusupov/Yusupova and collaborators (51,67) has the same effective selectivity 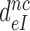 as the mechanism in Figure 5, provided that the
as the mechanism in Figure 5, provided that the 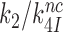 ratio and
ratio and 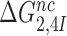 are the same. In their mechanism the rearrangement of the decoding center proceeds directly from state C2 to C4 as the A-site tRNA bends and its ASL enters the decoding center. In particular, they suggested that the entering ASL disrupts the stacking between A1492 and A1913, thereby activating A1492 to interact with the second position of the codon-anticodon helix (51,67). Subsequently, interaction between G530 and activated A1492 induces ribosome closure for both cognate and near-cognate T3s alike, so that the codon-anticodon contact occurs in the water-free environment of state C4 (67). In cognate cases this contact is stable and complex C4 rapidly moves forward to GTP hydrolysis. In near-cognate cases this contact is unstable and complex C4 rapidly moves backward to complex C2 (51,67). However attractive, this ‘direct induced fit’ mechanism seems to be at odds with a recent cryo-EM study, in which state C3 was directly observed (46). It is tempting to speculate that the intermediate state C3 confers a kinetic advantage to the mechanism in Figure 5 by providing an indirect but faster route from C2 to C4 that avoids a predictably difficult ‘one step’ water expulsion from the ‘tight and rigid’ decoding center (51) by the incoming ASL of tRNA (14).
are the same. In their mechanism the rearrangement of the decoding center proceeds directly from state C2 to C4 as the A-site tRNA bends and its ASL enters the decoding center. In particular, they suggested that the entering ASL disrupts the stacking between A1492 and A1913, thereby activating A1492 to interact with the second position of the codon-anticodon helix (51,67). Subsequently, interaction between G530 and activated A1492 induces ribosome closure for both cognate and near-cognate T3s alike, so that the codon-anticodon contact occurs in the water-free environment of state C4 (67). In cognate cases this contact is stable and complex C4 rapidly moves forward to GTP hydrolysis. In near-cognate cases this contact is unstable and complex C4 rapidly moves backward to complex C2 (51,67). However attractive, this ‘direct induced fit’ mechanism seems to be at odds with a recent cryo-EM study, in which state C3 was directly observed (46). It is tempting to speculate that the intermediate state C3 confers a kinetic advantage to the mechanism in Figure 5 by providing an indirect but faster route from C2 to C4 that avoids a predictably difficult ‘one step’ water expulsion from the ‘tight and rigid’ decoding center (51) by the incoming ASL of tRNA (14).
In summary, we suggest that initial codon selection benefits from an induced fit mechanism which increases the effective selectivity, current accuracy and speed of codon reading at unaltered intrinsic selectivity of the ribosome. By this mechanism (Figure 5), aminoglycosides reduce the effective selectivity and the current accuracy of initial codon selection by an equal reduction of the standard free energy cost for ribosome movement from state C2 to state C4 in cognate and near-cognate cases.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Drs Joseph Puglisi and Magnus Johansson for critical reading of the manuscript. We are grateful to Dr Suparna Sanyal for providing us with purified H84A EF-Tu mutant protein.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Knut and Alice Wallenberg foundation (RiboCORE); Swedish Research Council and the Human Frontier Science Program (to M.E.). Funding for open access charge: Knut and Alice Wallenberg foundation (RiboCORE); Swedish Research Council and the Human Frontier Science Program (to M.E.).
Conflict of interest statement. None declared.
REFERENCES
- 1. Ogle J.M., Carter A.P., Ramakrishnan V.. Insights into the decoding mechanism from recent ribosome structures. Trends Biochem. Sci. 2003; 28:259–266. [DOI] [PubMed] [Google Scholar]
- 2. Ogle J.M., Ramakrishnan V.. Structural insights into translational fidelity. Annu. Rev. Biochem. 2005; 74:129–177. [DOI] [PubMed] [Google Scholar]
- 3. Schmeing T.M., Ramakrishnan V.. What recent ribosome structures have revealed about the mechanism of translation. Nature. 2009; 461:1234–1242. [DOI] [PubMed] [Google Scholar]
- 4. Voorhees R.M., Ramakrishnan V.. Structural basis of the translational elongation cycle. Annu. Rev. Biochem. 2013; 82:203–236. [DOI] [PubMed] [Google Scholar]
- 5. Reuveni S., Ehrenberg M., Paulsson J.. Ribosomes are optimized for autocatalytic production. Nature. 2017; 547:293–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ehrenberg M., Kurland C.G.. Costs of accuracy determined by a maximal growth rate constraint. Q. Rev. Biophys. 1984; 17:45–82. [DOI] [PubMed] [Google Scholar]
- 7. Gromadski K.B., Daviter T., Rodnina M.V.. A uniform response to mismatches in codon-anticodon complexes ensures ribosomal fidelity. Mol. Cell. 2006; 21:369–377. [DOI] [PubMed] [Google Scholar]
- 8. Johansson M., Lovmar M., Ehrenberg M.. Rate and accuracy of bacterial protein synthesis revisited. Curr. Opin. Microbiol. 2008; 11:141–147. [DOI] [PubMed] [Google Scholar]
- 9. Zhang J., Ieong K.W., Johansson M., Ehrenberg M.. Accuracy of initial codon selection by aminoacyl-tRNAs on the mRNA-programmed bacterial ribosome. Proc. Natl. Acad. Sci. U.S.A. 2015; 112:9602–9607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ieong K.W., Uzun U., Selmer M., Ehrenberg M.. Two proofreading steps amplify the accuracy of genetic code translation. Proc. Natl. Acad. Sci. U.S.A. 2016; 113:13744–13749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Borg A., Ehrenberg M.. Determinants of the rate of mRNA translocation in bacterial protein synthesis. J. Mol. Biol. 2015; 427:1835–1847. [DOI] [PubMed] [Google Scholar]
- 12. Johansson M., Zhang J., Ehrenberg M.. Genetic code translation displays a linear trade-off between efficiency and accuracy of tRNA selection. Proc. Natl. Acad. Sci. U.S.A. 2012; 109:131–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ogle J.M., Brodersen D.E., Clemons W.M. Jr, Tarry M.J., Carter A.P., Ramakrishnan V.. Recognition of cognate transfer RNA by the 30S ribosomal subunit. Science. 2001; 292:897–902. [DOI] [PubMed] [Google Scholar]
- 14. Ogle J.M., Murphy F.V., Tarry M.J., Ramakrishnan V.. Selection of tRNA by the ribosome requires a transition from an open to a closed form. Cell. 2002; 111:721–732. [DOI] [PubMed] [Google Scholar]
- 15. Hopfield J.J. Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. U.S.A. 1974; 71:4135–4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ninio J. Kinetic amplification of enzyme discrimination. Biochimie. 1975; 57:587–595. [DOI] [PubMed] [Google Scholar]
- 17. Ehrenberg M., Blomberg C.. Thermodynamic constraints on kinetic proofreading in biosynthetic pathways. Biophys. J. 1980; 31:333–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Freter R.R., Savageau M.A.. Proofreading systems of multiple stages for improved accuracy of biological discrimination. J. Theor. Biol. 1980; 85:99–123. [DOI] [PubMed] [Google Scholar]
- 19. Thompson R.C., Stone P.J.. Proofreading of the codon-anticodon interaction on ribosomes. Proc. Natl. Acad. Sci. U.S.A. 1977; 74:198–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Ruusala T., Ehrenberg M., Kurland C.G.. Is there proofreading during polypeptide synthesis. EMBO J. 1982; 1:741–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kramer E.B., Farabaugh P.J.. The frequency of translational misreading errors in E. coli is largely determined by tRNA competition. RNA. 2007; 13:87–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Manickam N., Nag N., Abbasi A., Patel K., Farabaugh P.J.. Studies of translational misreading in vivo show that the ribosome very efficiently discriminates against most potential errors. RNA. 2014; 20:9–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Jelenc P.C., Kurland C.G.. Nucleoside triphosphate regeneration decreases the frequency of translation errors. Proc. Natl. Acad. Sci. U.S.A. 1979; 76:3174–3178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Gromadski K.B., Rodnina M.V.. Kinetic determinants of high-fidelity tRNA discrimination on the ribosome. Mol. Cell. 2004; 13:191–200. [DOI] [PubMed] [Google Scholar]
- 25. Wohlgemuth I., Pohl C., Mittelstaet J., Konevega A.L., Rodnina M.V.. Evolutionary optimization of speed and accuracy of decoding on the ribosome. Philos. Trans. R Soc. Lond. B Biol. Sci. 2011; 366:2979–2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Studer S.M., Feinberg J.S., Joseph S.. Rapid kinetic analysis of EF-G-dependent mRNA translocation in the ribosome. J. Mol. Biol. 2003; 327:369–381. [DOI] [PubMed] [Google Scholar]
- 27. Nierhaus K.H. Mg2+, K+, and the ribosome. J. Bacteriol. 2014; 196:3817–3819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Zhang J., Ieong K.W., Mellenius H., Ehrenberg M.. Proofreading neutralizes potential error hotspots in genetic code translation by transfer RNAs. RNA. 2016; 22:896–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Alatossava T., Jutte H., Kuhn A., Kellenberger E.. Manipulation of intracellular magnesium content in polymyxin B nonapeptide-sensitized Escherichia coli by ionophore A23187. J. Bacteriol. 1985; 162:413–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Pape T., Wintermeyer W., Rodnina M.V.. Conformational switch in the decoding region of 16S rRNA during aminoacyl-tRNA selection on the ribosome. Nat. Struct. Biol. 2000; 7:104–107. [DOI] [PubMed] [Google Scholar]
- 31. Rodnina M.V., Wintermeyer W.. Fidelity of aminoacyl-tRNA selection on the ribosome: kinetic and structural mechanisms. Annu. Rev. Biochem. 2001; 70:415–435. [DOI] [PubMed] [Google Scholar]
- 32. Gromadski K.B., Rodnina M.V.. Streptomycin interferes with conformational coupling between codon recognition and GTPase activation on the ribosome. Nat. Struct. Mol. Biol. 2004; 11:316–322. [DOI] [PubMed] [Google Scholar]
- 33. Cabanas M.J., Vazquez D., Modolell J.. Inhibition of ribosomal translocation by aminoglycoside antibiotics. Biochem. Biophys. Res. Commun. 1978; 83:991–997. [DOI] [PubMed] [Google Scholar]
- 34. Tsai A., Uemura S., Johansson M., Puglisi E.V., Marshall R.A., Aitken C.E., Korlach J., Ehrenberg M., Puglisi J.D.. The impact of aminoglycosides on the dynamics of translation elongation. Cell Rep. 2013; 3:497–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Fourmy D., Recht M.I., Blanchard S.C., Puglisi J.D.. Structure of the A site of Escherichia coli 16S ribosomal RNA complexed with an aminoglycoside antibiotic. Science. 1996; 274:1367–1371. [DOI] [PubMed] [Google Scholar]
- 36. Recht M.I., Fourmy D., Blanchard S.C., Dahlquist K.D., Puglisi J.D.. RNA sequence determinants for aminoglycoside binding to an A-site rRNA model oligonucleotide. J. Mol. Biol. 1996; 262:421–436. [DOI] [PubMed] [Google Scholar]
- 37. Carter A.P., Clemons W.M., Brodersen D.E., Morgan-Warren R.J., Wimberly B.T., Ramakrishnan V.. Functional insights from the structure of the 30S ribosomal subunit and its interactions with antibiotics. Nature. 2000; 407:340–348. [DOI] [PubMed] [Google Scholar]
- 38. Koshland D.E. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. U.S.A. 1958; 44:98–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Fersht A. Enzyme Structure and Mechanism. 1977; 1977 ednNY: W.H. Freeman and Company. [Google Scholar]
- 40. Daviter T., Gromadski K.B., Rodnina M.V.. The ribosome's response to codon-anticodon mismatches. Biochimie. 2006; 88:1001–1011. [DOI] [PubMed] [Google Scholar]
- 41. Pape T., Wintermeyer W., Rodnina M.V.. Complete kinetic mechanism of elongation factor Tu-dependent binding of aminoacyl-tRNA to the A site of the E. coli ribosome. EMBO J. 1998; 17:7490–7497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Daviter T., Wieden H.J., Rodnina M.V.. Essential role of histidine 84 in elongation factor Tu for the chemical step of GTP hydrolysis on the ribosome. J. Mol. Biol. 2003; 332:689–699. [DOI] [PubMed] [Google Scholar]
- 43. Wold F., Ballou C.E.. Studies on the enzyme enolase. I. Equilibrium studies. J Biol Chem. 1957; 227:301–312. [PubMed] [Google Scholar]
- 44. Johansson M., Bouakaz E., Lovmar M., Ehrenberg M.. The kinetics of ribosomal peptidyl transfer revisited. Mol. Cell. 2008; 30:589–598. [DOI] [PubMed] [Google Scholar]
- 45. Borovinskaya M.A., Pai R.D., Zhang W., Schuwirth B.S., Holton J.M., Hirokawa G., Kaji H., Kaji A., Cate J.H.. Structural basis for aminoglycoside inhibition of bacterial ribosome recycling. Nat Struct Mol Biol. 2007; 14:727–732. [DOI] [PubMed] [Google Scholar]
- 46. Loveland A.B., Demo G., Grigorieff N., Korostelev A.A.. Ensemble cryo-EM elucidates the mechanism of translation fidelity. Nature. 2017; 546:113–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Blanchard S.C., Gonzalez R.L., Kim H.D., Chu S., Puglisi J.D.. tRNA selection and kinetic proofreading in translation. Nat. Struct. Mol. Biol. 2004; 11:1008–1014. [DOI] [PubMed] [Google Scholar]
- 48. Pavlov M.Y., Liljas A., Ehrenberg M.. A recent intermezzo at the ribosome club. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2017; 372:20160185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Nissen P., Kjeldgaard M., Thirup S., Polekhina G., Reshetnikova L., Clark B.F., Nyborg J.. Crystal structure of the ternary complex of Phe-tRNAPhe, EF-Tu, and a GTP analog. Science. 1995; 270:1464–1472. [DOI] [PubMed] [Google Scholar]
- 50. Pape T., Wintermeyer W., Rodnina M.. Induced fit in initial selection and proofreading of aminoacyl-tRNA on the ribosome. EMBO J. 1999; 18:3800–3807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Demeshkina N., Jenner L., Westhof E., Yusupov M., Yusupova G.. New structural insights into the decoding mechanism: translation infidelity via a G.U pair with Watson-Crick geometry. FEBS Lett. 2013; 587:1848–1857. [DOI] [PubMed] [Google Scholar]
- 52. Valle M., Sengupta J., Swami N.K., Grassucci R.A., Burkhardt N., Nierhaus K.H., Agrawal R.K., Frank J.. Cryo-EM reveals an active role for aminoacyl-tRNA in the accommodation process. EMBO J. 2002; 21:3557–3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Stark H., Rodnina M.V., Wieden H.J., Zemlin F., Wintermeyer W., van Heel M.. Ribosome interactions of aminoacyl-tRNA and elongation factor Tu in the codon-recognition complex. Nat. Struct. Biol. 2002; 9:849–854. [DOI] [PubMed] [Google Scholar]
- 54. Schmeing T.M., Voorhees R.M., Kelley A.C., Gao Y.G., Murphy F.V.t., Weir J.R., Ramakrishnan V.. The crystal structure of the ribosome bound to EF-Tu and aminoacyl-tRNA. Science. 2009; 326:688–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Selmer M., Dunham C.M., Murphy F.V.t., Weixlbaumer A., Petry S., Kelley A.C., Weir J.R., Ramakrishnan V.. Structure of the 70S ribosome complexed with mRNA and tRNA. Science. 2006; 313:1935–1942. [DOI] [PubMed] [Google Scholar]
- 56. Demeshkina N., Jenner L., Westhof E., Yusupov M., Yusupova G.. A new understanding of the decoding principle on the ribosome. Nature. 2012; 484:256–259. [DOI] [PubMed] [Google Scholar]
- 57. Fischer N., Neumann P., Konevega A.L., Bock L.V., Ficner R., Rodnina M.V., Stark H.. Structure of the E. coli ribosome-EF-Tu complex at <3 A resolution by Cs-corrected cryo-EM. Nature. 2015; 520:567–570. [DOI] [PubMed] [Google Scholar]
- 58. Rodnina M.V., Fricke R., Kuhn L., Wintermeyer W.. Codon-dependent conformational change of elongation factor Tu preceding GTP hydrolysis on the ribosome. EMBO J. 1995; 14:2613–2619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Panecka J., Mura C., Trylska J.. Interplay of the bacterial ribosomal A-site, S12 protein mutations and paromomycin binding: a molecular dynamics study. PLoS One. 2014; 9:e111811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Rodnina M.V., Pape T., Fricke R., Kuhn L., Wintermeyer W.. Initial binding of the elongation factor Tu.GTP.aminoacyl-tRNA complex preceding codon recognition on the ribosome. J. Biol. Chem. 1996; 271:646–652. [DOI] [PubMed] [Google Scholar]
- 61. Satpati P., Sund J., Aqvist J.. Structure-based energetics of mRNA decoding on the ribosome. Biochemistry. 2014; 53:1714–1722. [DOI] [PubMed] [Google Scholar]
- 62. Schuette J.C., Murphy F.V.t., Kelley A.C., Weir J.R., Giesebrecht J., Connell S.R., Loerke J., Mielke T., Zhang W., Penczek P.A. et al. . GTPase activation of elongation factor EF-Tu by the ribosome during decoding. EMBO J. 2009; 28:755–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Ehrenberg M., Kurland C.G.. Measurement of translational kinetic parameters. Methods Enzymol. 1988; 164:611–631. [DOI] [PubMed] [Google Scholar]
- 64. Bartetzko A., Nierhaus K.H.. Mg2+/NH4+/polyamine system for polyuridine-dependent polyphenylalanine synthesis with near in vivo characteristics. Methods Enzymol. 1988; 164:650–658. [DOI] [PubMed] [Google Scholar]
- 65. Igarashi K., Kashiwagi K.. Modulation of cellular function by polyamines. Int. J. Biochem. Cell Biol. 2010; 42:39–51. [DOI] [PubMed] [Google Scholar]
- 66. Rodnina M.V., Wintermeyer W.. Ribosome fidelity: tRNA discrimination, proofreading and induced fit. Trends Biochem. Sci. 2001; 26:124–130. [DOI] [PubMed] [Google Scholar]
- 67. Rozov A., Demeshkina N., Westhof E., Yusupov M., Yusupova G.. Structural insights into the translational infidelity mechanism. Nat. Commun. 2015; 6:7251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Rozov A., Demeshkina N., Westhof E., Yusupov M., Yusupova G.. New structural insights into translational miscoding. Trends Biochem. Sci. 2016; 41:798–814. [DOI] [PubMed] [Google Scholar]
- 69. Rozov A., Westhof E., Yusupov M., Yusupova G.. The ribosome prohibits the G*U wobble geometry at the first position of the codon-anticodon helix. Nucleic Acids Res. 2016; 44:6434–6441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Rozov A., Demeshkina N., Khusainov I., Westhof E., Yusupov M., Yusupova G.. Novel base-pairing interactions at the tRNA wobble position crucial for accurate reading of the genetic code. Nat. Commun. 2016; 7:10457. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.