Nonselective Wiring Accounts for Red-Green Opponency in Midget Ganglion Cells of the Primate Retina

Abstract

In primate retina, “red-green” color coding is initiated when signals originating in long (L) and middle (M) wavelength-sensitive cone photoreceptors interact antagonistically. The center-surround receptive field of “midget” ganglion cells provides the neural substrate for L versus M cone-opponent interaction, but the underlying circuitry remains unsettled, centering around the longstanding question of whether specialized cone wiring is present. To address this question, we measured the strength, sign, and spatial tuning of L- and M-cone input to midget receptive fields in the peripheral retina of macaque primates of either sex. Consistent with previous work, cone opponency arose when one of the cone types showed a stronger connection to the receptive field center than to the surround. We implemented a difference-of-Gaussians spatial receptive field model, incorporating known biology of the midget circuit, to test whether physiological responses we observed in real cells could be captured entirely by anatomical nonselectivity. When this model sampled nonselectively from a realistic cone mosaic, it accurately reproduced key features of a cone-opponent receptive field structure, and predicted both the variability and strength of cone opponency across the retina. The model introduced here is consistent with abundant anatomical evidence for nonselective wiring, explains both local and global properties of the midget population, and supports a role in their multiplexing of spatial and color information. It provides a neural basis for human chromatic sensitivity across the visual field, as well as the maintenance of normal color vision despite significant variability in the relative number of L and M cones across individuals.

SIGNIFICANCE STATEMENT Red-green color vision is a hallmark of the human and nonhuman primate that starts in the retina with the presence of long (L)- and middle (M)-wavelength sensitive cone photoreceptor types. Understanding the underlying retinal mechanism for color opponency has focused on the broad question of whether this characteristic can emerge from nonselective wiring, or whether complex cone-type-specific wiring must be invoked. We provide experimental and modeling support for the hypothesis that nonselective connectivity is sufficient to produce the range of red-green color opponency observed in midget ganglion cells across the retina. Our nonselective model reproduces the diversity of physiological responses of midget cells while also accounting for systematic changes in color sensitivity across the visual field.

Introduction

The central retina in primates is dominated by an intricate “midget” ganglion cell circuitry, with the critical role of encoding the high spatial resolution of foveal vision. A private-line pathway connects single-cone photoreceptors to single midget ganglion cells (Fig. 1A) (Kolb and Dekorver, 1991; Calkins et al., 1994; Jusuf et al., 2006), which preserves the exquisite acuity afforded by the array of foveal cones sampling the visual image (Fig. 1B,C) (Williams and Coletta, 1987; Rossi and Roorda, 2010). This pathway also plays a fundamental role in “red-green” color vision, characteristic of trichromatic human and nonhuman primates: midget cells uniquely exhibit color opponency, arising from antagonistic interaction between long (L) and middle (M) wavelength-sensitive cones within the receptive field (De Monasterio and Gouras, 1975; Derrington et al., 1984; Crook et al., 2011). The underlying circuitry, however, has remained difficult to determine and centers on the longstanding question (Wiesel and Hubel, 1966) of whether cone-specific antagonistic wiring is present in the midget circuit (Crook et al., 2014).

Figure 1.

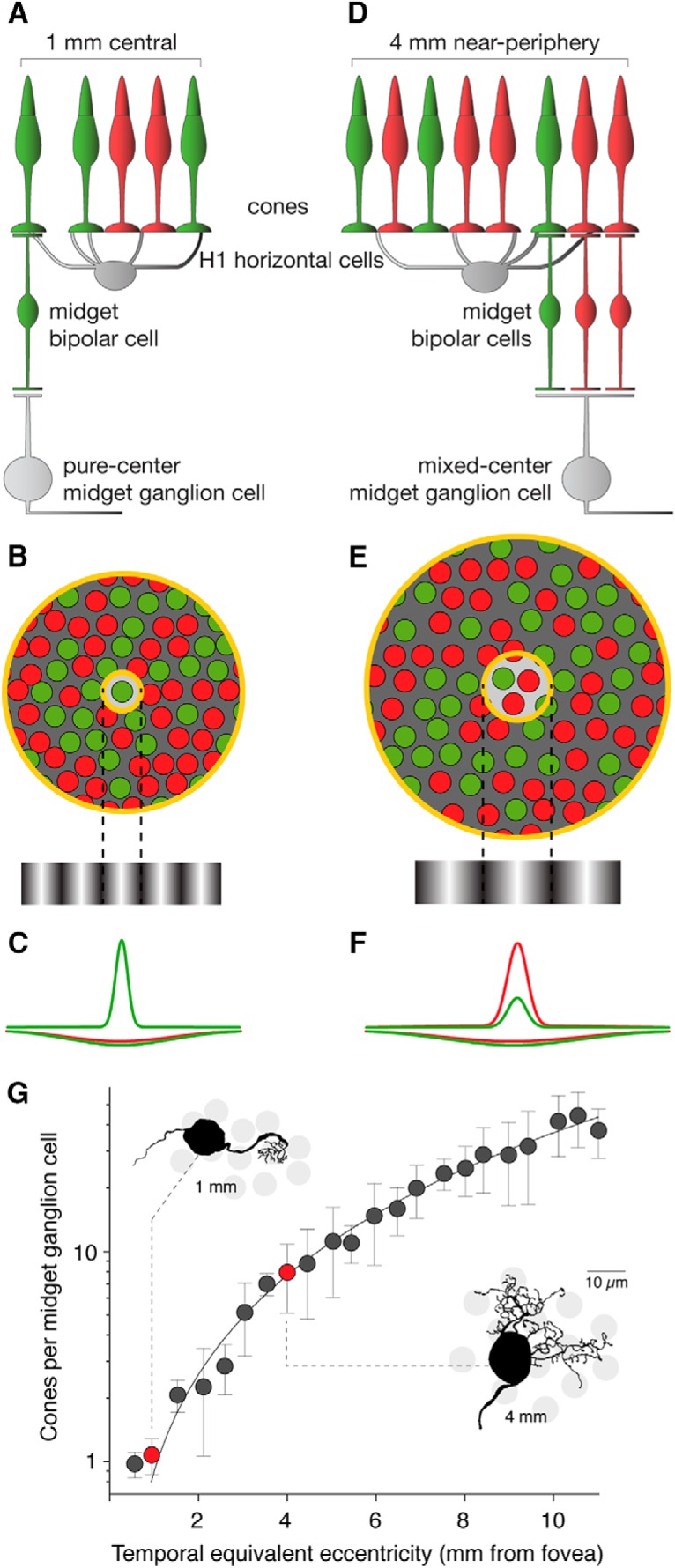
Midget circuitry in fovea and periphery. A, A midget ganglion cell in the fovea (<1 mm eccentricity) is characterized by “private-line” circuitry: a receptive field center comprises a single cone connected via a single midget bipolar cell, whereas the receptive field surround has broad, indiscriminate L- and M-cone inputs via H1 horizontal cells. B, This example cell shows a peak spatial frequency tuning on the order of a single cone. C, The single M-cone center has a response profile opposite that of the mixed L- and M-cone inputs to the receptive field surround, which is sufficient to drive an L–M cone-opponent response. D, The receptive field center of a more peripheral midget cell (4 mm eccentricity) no longer exhibits private-line circuitry, as multiple cone-bipolar inputs converge onto the larger midget ganglion cell dendritic field. H1 inputs to the receptive field surround also increase. E, A larger receptive field center shows reduced spatial frequency tuning. F, Mixed L and M inputs to center and surround response profiles diminish the likelihood of cone-opponent sensitivity. G, The convergence of cones to the midget dendritic field increases monotonically with eccentricity and can be fit with the function y = 0.29x² + 0.83x − 0.28. Inset, Example midgets from 1 and 4 mm eccentricity, along with their sampling of the underlying cone mosaic. Error bars indicate SEM. Adapted with permission from Crook et al. (2014).

In the central retina, L- versus M-cone opponency has been shrewdly modeled as a consequence of the same private-line circuitry underlying high acuity: a single L- or M-cone input to the receptive field center is antagonized by the opposite cone type found only in the mixed, nonselective surround (Paulus and Kröger-Paulus, 1983; Lennie et al., 1991; Mullen and Kingdom, 1996). This is supported by nonselective connections from L- and M-cones to horizontal cells (Boycott et al., 1987; Wässle et al., 1989; Dacey et al., 1996, 2000b; Crook et al., 2011) and a similar lack of cone specificity in inhibitory amacrine cell input to midget cells (Calkins and Sterling, 1996; Crook et al., 2011). The private-line midget circuit, coupled with nonselective surround wiring, can underlie both acuity and cone opponency in foveal midget ganglion cells, eliciting responses to high-spatial frequency luminance stimuli that isolate the receptive field center and responses to low-spatial frequency color stimuli that engage center-surround antagonism (Ingling and Martinez-Uriegas, 1983).

Outside the fovea, however, private-line circuitry is lost as ganglion cell dendritic trees enlarge to receive convergent signals from multiple cones (Fig. 1D). Nonselective wiring thus predicts a diminished likelihood of cone opponency (Lennie et al., 1991; Mullen and Kingdom, 1996) as L- and M-cone inputs combine (Fig. 1E,F), as a function of the rate of convergence of cones to midget dendritic trees (Fig. 1G, adapted from Crook et al., 2014). Midget ganglion cells lacking cone opponency in the periphery have been reported (Dacey, 1999; Diller et al., 2004; Field et al., 2010), but other reports of cone opponency in peripheral midgets (Field et al., 2010) or their parvocellular equivalents in the LGN (Martin et al., 2001, 2011; Solomon et al., 2005; Buzás et al., 2006) suggest that specific connectivity (Reid and Shapley, 1992) or physiological bias (Buzás et al., 2006; Field et al., 2010) is required. Whether it is necessary to invoke cone-specific connectivity, however, depends on the degree of opponency accounted for by a random-wiring model, and whether this is sufficient to account for opponency observed in the periphery.

To assess cone selectivity, we recorded from a large population of midget cells in vitro and measured the sign, strength, and spatial tuning of L- and M-cone inputs to receptive fields. We found that the incidence and strength of a cone-opponent response were variable and related to the relative strength of L- and M-cone input to the receptive field center versus surround. This variation could be well accounted for with a nonselective connectivity model, which reproduced the local properties of cone-opponent receptive fields, predicted the incidence of cone-opponent cells across the retina, and correlated with psychophysical measures of chromatic sensitivity. We conclude that nonselective wiring can mediate cone-opponent signaling in midget cells and, importantly, account for the variation in this property across the retina.

Materials and Methods

In vitro preparation.

Eyes were removed from deeply anesthetized macaque monkeys (Macaca nemestrina, Macaca fascicularis, or Macaca mulatta, of either sex) serving the Tissue Distribution Program of the National Primate Research Center at the University of Washington. After enucleation, the anterior chamber of the eye was removed, the vitreous drained, and the remaining eyecup placed in oxygenated Ames' medium. The retina, choroid, and pigment epithelium were then dissected away from the sclera with care not to cause retinal detachment from the supporting layers. Radial cuts were made in the retina to create a flatmount that was adhered, ganglion cell layer up, to the glass bottom of a steel superfusion chamber that had been coated with poly-L-lysine (Sigma P1399, 10 mg in 10 ml H₂O). A perfusion inlet tube, outlet tube, agar bridge, and thermistor were inserted into the bath. The retina was continuously superfused with Ames' medium (pH 7.37; constant oxygenation with 95% O₂/5% CO₂; temperature was thermostatically maintained, TC-344B; Warner Instruments, at ∼36°C). Visual stimuli were delivered to the photoreceptors from the vitreal (ganglion cell) side of the retina as in situ, via the microscope objective lens as described further below.

In vitro electrophysiology.

Ganglion cells were observed using a 60× water-immersion objective under infrared illumination. Midget ganglion cells were visually identified and differentiated from parasol cells by their relatively high density and small soma size (Dacey and Lee, 1994). Cell type identity was confirmed by mapping receptive field size, as midget ganglion cells showed the smallest receptive field center diameters of any primate ganglion cell (30–150 μm). We found that maintained spike discharge recorded in vivo (Troy and Lee, 1994) was a reliable indicator of overall retinal sensitivity and adherence to the retinal pigment epithelium; we therefore characterized the cone inputs to ganglion cells that showed maintained activity in the range of 20–30 s. Using the “loose-patch” method, extracellular recordings were made with glass micropipettes (5–8 mΩ) filled with Ames' medium.

Stimulus generation.

A digital light projector (Christie Digital Systems) was used to project the visual stimuli (VSG, Cambridge Research Systems) through an optical relay to the microscope camera port and bring the image into focus at the photoreceptor layer. The irradiance spectra for red, green, and blue primaries were measured with a spectroradiometer (PR705; Photo Research); peak wavelengths and integrated photon fluxes were 636, 550, and 465 nm and 2.7 × 10⁶, 6.9 × 10⁵, and 1.8 × 10⁵ photons s⁻¹ μm⁻², respectively. To compute the effectiveness of the light delivered by each primary to the cone aperture, we calculated the products of each primary irradiance spectrum and each cone spectral sensitivity function (Baylor et al., 1987). We corrected for the spectrally broadening effects of self-screening by assuming a pigment density of 0.016 μm (Baylor et al., 1987) and a cone outer segment length of 5 μm: while cones at ∼8 mm have an outer segment length of 20 μm (Banks et al., 1991), we correct for the fact that peripheral cones in vitro lay obliquely to the optical axis of the objective, thus shortening the effective path length and reducing light capture. Each product was then summed across wavelength giving units of “effective” photons s⁻¹ μm⁻² (irradiance corrected by cone spectral sensitivity). Effective photons s⁻¹ μm⁻² were then converted to photoisomerizations s⁻¹ cone⁻¹ by multiplying by the area of the cone aperture. In previous studies involving transverse illumination of the cone outer segment (Baylor et al., 1979), where funneling of the inner segments plays no role, the conversion factor commonly used is 0.37 μm². The efficiency of photoisomerization (0.67) (Dartnall, 1972) is included in this value. In the in vitro macaque retina, as in vivo, light is incident upon the vitreal surface of the retina and funneling by the inner segment would tend to increase the effective area of the cone aperture. We therefore consider the use of 0.37 μm² as a very conservative estimate of cone aperture to make the conversion to photoisomerizations s⁻¹ cone⁻¹. To achieve cone isolation, both modulation depth and irradiances of the primary lights were adjusted; cone isolation was confirmed by direct recordings from macaque cones and is reported elsewhere (Packer et al., 2010).

Often the intensity of stimuli used in human visual psychophysics or in physiological experiments in the intact primate eye are expressed in units of retinal illuminance, or Trolands (Td). To aid comparison with our data, we previously calculated that for a peripheral cone with an inner segment aperture of 9 μm, 1 Troland (Td) was equivalent to ∼30 photoisomerizations s⁻¹ cone⁻¹ (Crook et al., 2009).

Cone contrast was defined as the peak excursion from the background, divided by the mean light level, expressed as a percentage. Computed contrast for cone-isolating stimuli was 16% around a background comprising equal quantal catches for the three cone types (i.e., L = M = S) or 75% around a background with unequal catches. The L and M components of midget-cell receptive fields were characterized using cone-isolating spots of different diameter and drifting gratings of varying spatial frequency. To center the stimulus on the cell's receptive field, the cell body was first placed in the middle of the stimulus field. Fine-diameter horizontal and vertical slits (10 or 25 μm wide) were then systematically moved in the x and y directions to locate the most sensitive point of the receptive field. The location of the maximum spike response was defined as the receptive field midpoint; stimuli were positioned relative to this point. When possible, eccentricity was determined for recorded midgets. All eccentricities are reported as temporal equivalent eccentricity (Watanabe and Rodieck, 1989).

Computing cone-specific contributions to the receptive field.

L- and M-cone-specific stimuli (modulated at 2 Hz) were presented as spots (9–2000 μm diameter, contrast 75%) or as drifting sine-wave gratings (spatial frequency 0.047–15 cycles/degree [cpd], contrast 45%). Spike rate amplitude and phase were calculated from the first Fourier harmonic at the stimulus frequency. Spatial frequency tuning curves to stimuli were fit using a difference-of-Gaussians model incorporating response amplitude and phase (Enroth-Cugell et al., 1983) to determine L- and M-cone contributions to the receptive field center and surround. Response weight and radius of the receptive field center and surround were computed from the amplitude and 1 σ of the Gaussian fit functions, respectively. Details and application of this model have been described previously (Dacey et al., 2000a; McMahon et al., 2004). The dataset includes a subset of midget cells recorded for a different purpose in a previous publication (Crook et al., 2011) and reanalyzed here. We used the weight parameters from the fits to L- and M-cone spatial frequency tuning functions to calculate the proportion of L- or M-cone input to the receptive field center [L_c/(L_c + M_c)] and surround [L_s/(L_s + M_s)]. For this cone purity index, a value of 1 indicates a pure L-cone input and a value of 0 indicates a pure M-cone input.

Classifying chromatic and achromatic cells.

For the lowest spatial frequency grating (0.047 cpd) or largest spot size (2000 μm) presented at 2 Hz, the ON response phase is ∼0° and OFF response phase is ∼180°. By comparing the response phase during low-spatial-frequency L- and M-cone stimulus presentation, we called midget cells chromatic (i.e., exhibiting L–M cone opponency) when responses to L- and M-cone stimuli were separated across the ON and OFF response phases (L–M phase difference ∼180°), and achromatic (i.e., lacking cone opponency) when responses were not separated (L–M phase difference ∼0°). Because cells rarely responded equally to L- and M-cone stimuli, we computed a response-strength ratio, where the weaker response amplitude to one stimulus condition (L or M) was divided by the other, stronger response amplitude. Cells with balanced responses to L and M stimuli have a response magnitude near 1, whereas the most unbalanced cells show values near 0.

Computing contrast response functions.

Achromatic contrast sensitivity for midget and parasol cells was also measured. Spatial frequency tuning curves using additive L + M stimuli were similarly fitted as described above to determine for each cell the spatial frequency that evoked the peak response. Contrast sensitivity was evaluated for each cell at this spatial frequency and at the lowest spatial frequency tested. Gratings were presented at contrasts ranging from 1% to 45% or 2% to 38%, depending on the background light level. Cells' contrast response curves were fitted with a Naka–Rushton function as follows:

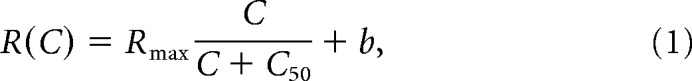where R_max is the maximal response in spikes s⁻¹, C is the Michelson contrast, C₅₀ is the semisaturation constant (the contrast at which r = 1/2 R_max), and b is the baseline response in spikes s⁻¹. Contrast response fits were characterized by the semisaturation constant, C₅₀ (Kaplan and Shapley, 1986).

Receptive field modeling.

We implemented a difference-of-Gaussians receptive field model (Enroth-Cugell et al., 1983) wherein a midget cell's receptive field center and surround response fields are represented as 2D circularly symmetric Gaussians of opposite sign, which sum all the cones that fall within the area of the receptive field. Our model adopts the same simplification of others previously, which sets aside the bipolar cell layer and considers the cones as direct contributors to the receptive field (e.g., Lennie et al., 1991; Reid and Shapley, 1992, 2002; Crook et al., 2011; Lee et al., 2012). The basis for the receptive field center is the summed cone inputs via midget bipolar centers, and the basis for the surround is the summed cone inputs via midget bipolar surrounds, formed by H1 horizontal cell feedback (Verweij et al., 2003) (Fig. 1). Nonselective connectivity was implemented based on the preponderance of anatomical and physiological evidence for nonselectivity throughout the midget circuit (Boycott et al., 1987; Wässle et al., 1989; Calkins and Sterling, 1996; Dacey et al., 2000b; Diller et al., 2004; Jusuf et al., 2006; Crook et al., 2011). For any given eccentricity, the model generated cells with biologically plausible 2D receptive fields, from which L- and M-cone contribution to receptive field center and surround was computed. Fourier analysis was used to assess spatial frequency tuning. Model scripts were written in MATLAB R2015b (The MathWorks).

For each modeled cell, a unique patch of retinal mosaic was first generated by randomly assigning L- and M-cones to a triangular grid, with random jitter. To reflect the variation of L:M cone ratios across individual retinas, the relative number of L and M cones in each patch was drawn from a lognormal distribution of L:M ratios observed empirically (Dacey et al., 2000b). For simplicity, S cones were omitted from model cone mosaics. Photopic light levels were assumed; thus, rod input to the midget ganglion cell circuit was disregarded. Cone radius and packing density (Packer et al., 1989) were parameterized as a function of eccentricity. We modeled the sensitivity of each cone input as the central 1σ of a 2D Gaussian, where σ is equal to the cone radius. Midget dendritic-field size and cone-to-midget convergence (Crook et al., 2014) were also parameterized as functions of eccentricity, to determine the number of cones in a receptive field center (n_c) and surround (n_s). The receptive field center radius (σ_c) of a model midget cell was taken as the dendritic-field radius and given a normalized response gain of k_c = 1. The receptive field surround radius was assigned as six times larger than the center; normalized response gain, k_s, was varied between 0.5 and 0.9 (Lennie et al., 1991; Croner and Kaplan, 1995).

Cone contributions to receptive field centers were determined by applying a Gaussian kernel to the mosaic and weighting all cones falling within 1σ (Field et al., 2010) as follows:

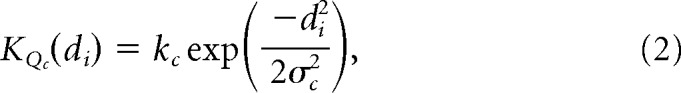where, for all center cones of type Q, d_i is the distance of a single cone lying between the origin and the receptive field center radius, σ_c. The same holds for surround cones and their distance, d_j, lying between the origin and the surround radius, σ_s, as follows:

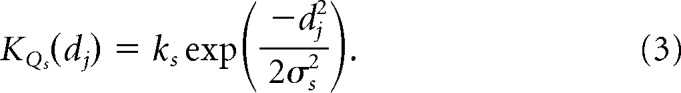For the arrays of all the L- or M-cones in the mosaic that contribute to a single ganglion cell, G, the 2D spatial response profiles are expressed as follows:

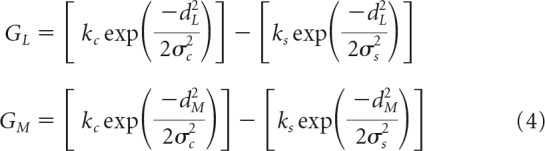The total contribution of L- and M-cones to the receptive field center and surround can be expressed as the sum of individual cone weights as follows:

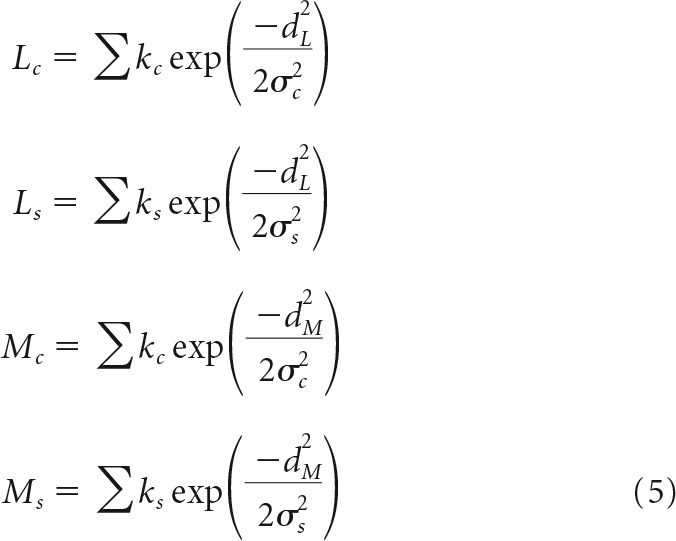Parameters and the source of their estimates are listed in Table 1.

Table 1.

Parameter values for the DoG model

Parameter	Value	Reference
Cones per mm2	M = ⌈19890x−0.6331⌉	Packer et al., 1989
Global retinal L:M PDF	G = $\frac{1}{0.74w\sqrt{2\pi }}\times \exp \left\{\frac{-{\left(\ln w-0.47\right)}^2}{1.09}\right\}$	Where w = L/M weight; Dacey et al., 2000b
Dendritic field radius (mm)	D = 0.002738x1.327	Crook et al., 2014; current study
Center radius	Rc = D
Surround radius	Rs = 6D	Croner and Kaplan, 1995
RF σ	σc = Rc; σs = Rs	Field et al., 2010
RF μ	μ = 0	All centered around zero
Cones to center	nc = ‖0.29x2 + 0.83x − 0.28‖	Crook et al., 2014
Cones to surround	ns = $n_c\times {\left(\frac{R_s}{R_c}\right)}^2$
Cone radius	H = 3.995 × exp(0.0163x) − 3.149 × exp( − 1.288x)	Packer et al, 1989
Center weighting	kc = 1
Surround weighting	ks = [0.5, 0.9]	Croner and Kaplan, 1995 (0.5); Lennie et al., 1991 (0.91)
Center Gaussian weighting kernel	KQc(di) = $K_c\times \exp \left(\frac{-d_i^2}{2{\sigma }^2}\right),d_i=\left[0,R_c\right]$	Where d is the distance of a single cone, i, from the origin
Surround Gaussian weighting kernel	KQs(dj) = $K_c\times \exp \left(\frac{-d_j^2}{2{\sigma }^2}\right),d_j=\left[0,R_s\right]$	Where d is the distance of a single cone, j, from the origin

x, Retinal location, expressed in millimeters of temporal equivalent eccentricity (Watanabe and Rodieck, 1989).

Experimental design and statistical analysis.

We used several statistical tests to quantify some comparisons between groups of empirical and model cells. First, we used Levene's test to assess the equality of variances for measurements of center and surround cone purity (two groups, df = 1) for empirical chromatic midget cells (n = 96), empirical achromatic midget cells (n = 72), empirical parasol cells (n = 50), model chromatic cells (n = 2231), and model achromatic cells (n = 2769). Second, we compared response sensitivity between chromatic (n = 23) and achromatic (n = 32) empirical midget cells to a luminance grating stimulus at the peak spatial frequency tuning, using a Student's unpaired, two-tailed t test, with the assumption of equal variance (two groups, df = 53). Third, we assessed the contrast response properties of empirical retinal ganglion cells, by fitting Naka–Rushton functions to contrast-response data from chromatic midget cells (n = 24), achromatic midget cells (n = 34), and parasol cells (n = 14) and comparing the C₅₀ parameters from these fits across cell groups using a one-way ANOVA (three groups, df = 2). All statistical tests were done using MATLAB R2015b (The MathWorks). The outcomes of these tests are detailed in Results.

Results

In the periphery, the coextensive appearance of cone-opponent (“chromatic”) and nonopponent (“achromatic”) midget cells in retina (e.g., Field et al., 2010) or their parvocellular counterparts in LGN (e.g., Buzás et al., 2006; Martin et al., 2011) could be evidence that an opponent mechanism is selectively applied to a category of cells, or it could be evidence that the opponent mechanism itself is a variable property. While we characterized cells using the classical descriptors “chromatic” and “achromatic” to focus our presentation, our results largely demonstrate that cone opponency in midget ganglion cells is not a categorical, hard-wired property, but rather a locally variable feature related to the random spatial distribution and variable ratio of L and M cones sampled by the midget receptive field.

Chromatic opponency is a variable property of the midget ganglion cell population

To characterize the chromatic properties of midget cells, we sought to determine the contributions of L and M cones to receptive field centers and surrounds. To do this, we mapped the spatial frequency tuning of L- and M-cone inputs to 168 ON and OFF midget ganglion cells at 15°–45° eccentricity (3–9 mm from the foveal center), measuring spike discharges to L- and M-cone isolating stimuli presented as spots of increasing diameter or drifting gratings of increasing spatial frequency. Spatial frequency tuning curves were fit with a difference-of-Gaussians function, and the relative contributions of L and M inputs to receptive field centers and surrounds were then determined from the weight parameters of the fits. From these weights, we computed a cone purity index for the receptive field center and surround.

A majority of midget ganglion cells were characterized as chromatic, showing a response phase difference between low-spatial frequency L- and M-cone stimuli near 180° (188 ± 38°, mean ± SD [here and throughout, unless specified], n = 96). However, more than one-third of cells did not exhibit cone-opponent responses, with a phase difference near 0° (−3 ± 55°, n = 72). The response phase difference of these achromatic cells was similar to the response phase difference computed for a sample of ON and OFF parasol cells (1 ± 46°, n = 50) recorded in the same eccentricity range.

The distributions of retinal locations of chromatic and achromatic midgets were broadly overlapping across the recording range, with the median eccentricity of achromatic midgets (6.89 ± 1.46 mm median absolute deviation [MAD], n = 52) slightly more peripheral than the median eccentricity for chromatic midgets (5.47 ± 1.37 mm MAD, n = 76). This heterogeneity has been reported previously (Buzás et al., 2006; Martin et al., 2011) and supports the view that chromatic and achromatic midgets are not spatially segregated to different retinal regions (Solomon et al., 2005; Martin et al., 2011).

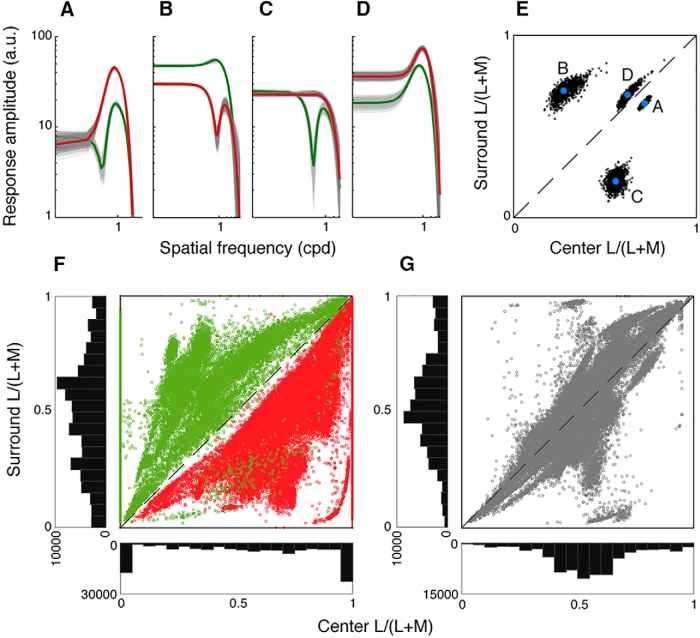
The L- and M-cone spatial frequency tuning curves showed characteristic differences between chromatic (Fig. 2A,B) and achromatic cells (Fig. 2C,D), demonstrating how cone opponency is created by a mismatch in L- and M-cone input strength to center versus surround. The receptive field centers of chromatic midgets (n = 96) either comprised a single cone type or were weighted toward one cone type, while receptive field surrounds were always a mix of L and M inputs. An example OFF midget cell with pure L input to the center, shown in Figure 2A, exhibited a bandpass L-cone response in the OFF phase (red), whereas M cones, present only in the surround, drove a low-pass response in the opposite ON phase (green). In comparison, an example ON midget cell with strongly weighted L center inputs, shown in Figure 2B, also showed a bandpass L-cone response in the ON phase (red), whereas the M-cone spatial frequency tuning curve (green) exhibited phase-reversing behavior at an intermediate spatial frequency. Reported previously as the “spatiochromatic notch” (Crook et al., 2011), a weak M-cone contribution to the ON center was observed in phase with the dominant L input at high spatial frequencies, when the receptive field center was isolated. However, at low spatial frequencies that engaged the full receptive field, this center contribution was attenuated by the much-stronger contribution of M cones to the surround, causing a response null and a reversal to the OFF phase (Fig. 2B, arrow).

Figure 2.

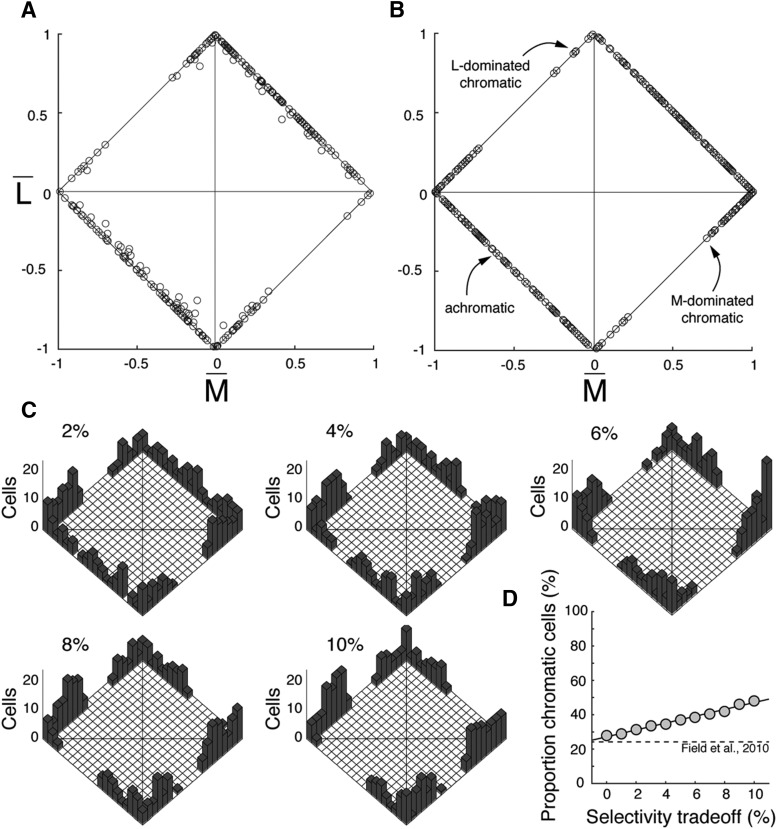
Chromatic and achromatic receptive field characteristics. Cone-isolating stimuli revealed chromatic midget cells with cone-opponent responses or achromatic midgets cells, which resembled parasol cells in their lack of cone-opponent responses. A, B, Chromatic midgets (n = 96) either comprised a single cone type (A) or were strongly weighted toward one cone type (B) in the receptive field center, whereas receptive field surrounds were always a mix of L and M inputs. Insets, Illustrative difference-of-Gaussians. A, An example OFF midget cell with pure L input to the center exhibited a bandpass L-cone response in the OFF phase (red), whereas M cones, present only in the surround, drove a low-pass response in the opposite ON phase (green). B, An example OFF midget cell with dominant L input to the center also showed a bandpass L-cone response in the OFF phase (red), whereas the M-cone spatial tuning curve (green) exhibited phase-reversing behavior. A weak M-cone contribution to the OFF center was observable in phase with the dominant L input at high spatial frequencies, but the stronger M-cone contribution to the surround produced a response null (arrowhead) and a reversal to the ON phase at lower spatial frequencies. C, D, Achromatic midgets (C) showed mixed L and M inputs to both center and surround and exhibited in-phase, bandpass tuning for both L- and M-cone stimuli across all spatial frequencies. Similarly, parasol cells (D) showed mixed L and M inputs to both center and surround, albeit with lower spatial frequency cutoffs. Insets, Illustrative difference-of-Gaussians. E, Chromatic cells (red, green) were characterized by an L–M phase difference of ∼180°, whereas achromatic (gray) and parasol cells (black) were characterized by a phase difference of ∼0°. While the phase difference was stereotyped across cells with and without a cone-opponent response, cells rarely responded equally to L- and M-cone-isolating stimuli; various response ratios between the two stimuli suggest various distributions of L- and M-cone inputs to receptive fields. F, For chromatic midgets, plotting the cone purity index of the receptive field center (x axis) versus surround (y axis) shows a disparity between center and surround cone weights, indicated by points below (L-dominated centers, red) or above (M-dominated centers, green) the diagonal. Example cells from A and B are labeled. G, Both achromatic midgets (gray) and parasols (black) show balanced cone purity index values between center and surround, indicated by clustering along the diagonal. Example cells from C and D are labeled. H–J, A subset of midget cells where eccentricity was recorded (n = 118) is plotted as a function of eccentricity. Chromatic cells, with unequal cone purity index values, are more likely in nearer retinal locations (H), whereas intermediate (I) and far peripheral (J) locations show a greater proportion of achromatic cells with balanced cone purity index values.

Achromatic midgets (n = 72) always showed mixed L and M inputs to both center and surround, exhibiting in-phase, bandpass tuning curves for both L- and M-cone stimuli across all spatial frequencies (Fig. 2C). Parasol cells, recognized as the primate equivalent of the mammalian Y-cell (Crook et al., 2008) and whose responses to achromatic stimuli are well described (e.g., Lee et al., 1988; Diller et al., 2004), also demonstrated mixed L and M inputs to center and surround, exhibiting similar bandpass tuning curves (Fig. 2D).

Cells were called chromatic or achromatic based on the response phase difference between low-spatial frequency L- and M-cone stimuli, but we observed that cells rarely responded equally to these two stimuli, suggesting that L and M inputs varied greatly across receptive fields. To illustrate this, we plotted the L–M phase difference for each cell, along with the response-strength ratio, where the weaker response amplitude to one stimulus condition (L or M) was divided by the other, stronger response amplitude (Fig. 2E). While the phase difference between L and M responses was stereotyped for chromatic and achromatic cells (clustering around 180° or 0°, respectively), the response strength was variable from cell to cell. This continuum of L versus M responses, from maximally balanced and opposed (180°, 1) to maximally unbalanced (origin) to maximally balanced and unopposed (0°, 1), suggests that a continuum of L and M inputs to the receptive field subsequently produces a continuum of chromatic and achromatic responses properties in individual cells.

Specifically, the distribution of L and M inputs across the receptive field center and surround largely impacts these properties. For chromatic cells, cone opponency arises when one cone type contributes more strongly to the center than it does to the surround, and the other cone type's contribution to the surround is stronger than its contribution to the center. Plotting the cone purity index of chromatic cells' center versus surround illustrates this relationship (Fig. 2F). The cone purity index of midget receptive field centers showed a range of values, but skewed toward pure M (0) or pure L (1) (x axis histogram), resulting in a large variance (0.56 ± 0.34). By comparison, the cone purity index of receptive field surrounds (y axis histogram) tended to be more mixed (0.48 ± 0.21). The purity index of the receptive field center was significantly more variable than that of the surround for chromatic cells (Levene's test, F = 38.6, p = 3.21 × 10⁻⁹). This greater variance can be explained by a difference in size: a center:surround size ratio of ∼1:6 (Croner and Kaplan, 1995) suggests a midget receptive field center has ∼36× fewer inputs than the receptive field surround. The high variance of these few inputs affords a greater likelihood of an L:M ratio unequal to the L:M ratio of the larger and less-variable receptive field surround. Indeed, the cone purity index for a given chromatic midget tended to be unequal between center and surround. M-dominant cells, with weak or absent L input to the center (Fig. 2F, green), showed stronger L inputs to the surround, thus positioned above the diagonal line. L-dominant cells, with weak or absent M input to the center (red), showed stronger M inputs to the surround, thus situated below the diagonal.

Conversely, plotting the cone purity index of surround versus center for achromatic midgets (Fig. 2G, gray) shows receptive field centers (0.55 ± 0.17) tended to be more equitably composed of L and M (gray, x axis histogram), as did receptive field surrounds (0.54 ± 0.20) (gray, y axis histogram). Unlike chromatic cells, the difference in variance between center and surround was not statistically significant for achromatic cells (Levene's test, F = 2.59, p = 0.11), and a cell's cone purity index tended to be equal between receptive field center and surround, illustrated by clustering along the diagonal. The lower variance of cone purity for receptive field centers of achromatic cells, more closely matching that of their surrounds, can be explained by increased inputs to midget dendritic fields, which is consistent with the increase in achromatic midgets more peripherally, where dendritic fields are larger (Diller et al., 2004). In other words, the increased cone inputs to receptive field centers (and thus smaller variance in the cone purity index) of cells at greater retinal eccentricities means that such cells have a greater likelihood of being achromatic. Parasol cells (Fig. 2G, black) also exhibited equitable L and M inputs to center (0.50 ± 0.15, black, x axis histogram) and surround (0.47 ± 0.17; black, y axis histogram) with variances that were not statistically significantly different (Levene's test, F = 0.81, p = 0.37). To illustrate the effect of retinal location on the likelihood of chromatic tuning, a subset of chromatic and achromatic midget ganglion cells (n = 118), for which retinal eccentricity was recorded, are plotted in Figure 2H–J. Chromatic cells with unequal cone purity index values tend to be more central, but with increasing retinal eccentricity, the cone purity index of cells tends to become more equitable, resulting in the increased appearance of achromatic cells.

Notably, both chromatic and achromatic midget cells showed in-phase or nonopponent L- and M-cone responses to stimuli presented at the peak of the cell's spatial sensitivity, where the receptive field center is isolated and activation of the receptive field surround is minimized. To examine how well midget cells could encode a spatial response to luminance stimuli, we measured spike discharges in a subset of cells (n = 71) to cone-additive (L + M) drifting gratings of increasing spatial frequency. All cells exhibited bandpass spatial tuning, with a peak of 0.78 ± 0.36 cpd for chromatic cells (n = 23) and 0.64 ± 0.25 for achromatic cells (n = 32). The sensitivity (quantified as the amplitude of the first harmonic) of achromatic cells (53.9 ± 19.9 spikes s⁻¹) was somewhat higher than for chromatic cells (38.8 ± 13.1 spikes s⁻¹) at the peak spatial frequency (Student's two-sample, two-tailed t test, T = −3.19, p = 0.002). By comparison, parasol cells (n = 16) showed similar bandpass tuning but with a lower peak spatial frequency (0.35 ± 0.10 cpd) and higher sensitivity (70.3 ± 17.0 spikes s⁻¹) than midget ganglion cells. Using the L + M grating spatial frequency that evoked the peak response for each cell, we measured that cell's response for contrasts in the range of 2%–45%. We fitted Naka–Rushton functions to these contrast-response data and compared the C₅₀ parameters from these fits across cell types. We observed that both chromatic midgets (C₅₀ = 32.7 ± 26.2%; n = 24) (Fig. 3A) and achromatic midgets (C₅₀ = 31.5 ± 24.3%; n = 34) (Fig. 3B) have robust, compressive responses to increasing L + M contrast, which strongly resemble the responses of parasol cells (C₅₀ = 31.3 ± 33.0%; n = 14) (Fig. 3C). Although midget cells had overall lower firing rates than parasol cells, we found there was a similar degree of compression in the achromatic contrast response functions across chromatic midget, achromatic midget, and parasol cells: C₅₀ fit parameter values did not differ significantly across cell types (one-way ANOVA, F = 0.29, p = 0.75). We conclude that all midget ganglion cells successfully encode achromatic stimuli at high spatial frequencies, regardless of their responses to chromatic or achromatic stimuli at very low spatial frequencies. This result supports the hypothesis that midget ganglion cells set the limit for spatial resolution across the retina (Thibos et al., 1987; Dacey, 1993; Rossi and Roorda, 2010; Watson, 2014; Wilkinson et al., 2016). Previous in vivo studies found extremely low contrast sensitivity in central retina (3°–13°) (Kaplan and Shapley, 1986), which contrasts with our findings at slightly greater eccentricities (15°–45°). Although it is possible that there is a sharp and dramatic decline in contrast sensitivity between 15° and 10° eccentricity (across 1 mm of retina), we have argued previously (Crook et al., 2008) that a potentially critical technical limitation shared by studies in the acutely anesthetized animal is the natural blurring of the extrafoveal retinal image (Williams et al., 1996), compounded by the recognized difficulty of optimizing and maintaining image quality. In many of these experiments, spatial frequencies of ≥10 cpd may be difficult to achieve and/or greatly attenuated in the optical image cast on the retina (Crook et al., 2008). Given that the highest contrast sensitivity requires stimuli presented at the peak of the spatial tuning function, reduced contrast sensitivity might thus be expected in parafoveal midget cells, which may attain peak spatial frequency tuning as high as 40 cpd (Merigan et al., 1991).

Figure 3.

Both chromatic and achromatic midgets respond to high-spatial frequency achromatic stimuli. A, Chromatic midget cells (n = 24) are highly sensitive to L + M contrast at the peak spatial frequency, showing robust, saturating contrast response curves. The mean firing rate of all cells at each contrast (2%–45%) is plotted (black circles). Error bars indicate SD. Each cell's contrast response curve was fitted with a Naka–Rushton function of three parameters: R_max, C₅₀, and b. The average fit of all cells (with parameters R_max = 86.6 spikes s⁻¹, C₅₀ = 32.7%, b = 0.83 spikes s⁻¹) is shown (solid line). B, Achromatic midgets (n = 34) are also highly sensitive to L + M contrast at the peak spatial frequency. Mean firing rates are plotted as in A, along with the average Naka–Rushton fit (R_max = 101 spikes s⁻¹, C₅₀ = 31.5%, b = 0.51 spikes s⁻¹). C, The contrast response functions for parasol cells (n = 14) have a higher response gain than midget cells, but similar saturating behavior over the contrast range. Mean firing rates are plotted as in A, along with the average Naka–Rushton fit (R_max = 144 spikes s⁻¹, C₅₀ = 31.3%, b = 2.3 spikes s⁻¹). Comparing the C₅₀ fit parameters for all cells shows that the degree of contrast-response compression is not significantly different across cell types (one-way ANOVA, p = 0.75).

Bootstrap analysis for fitting reliability

We sought to confirm the reliability of our difference-of-Gaussians fitting protocol in assigning relative L and M input strength to the receptive field center and surround. Because these fits are critical for us to characterize the cone inputs receptive field, we used a bootstrap analysis to assess the variability with which difference-of-Gaussian functions were fitted to the spike data. For each of our 168 midget cells, tuning curves of L- and M-cone drifting gratings of various spatial frequencies were bootstrapped 1000 times. Using the original spike train from a cell's response to an L- or M-isolating grating or spot size (a 1 × n vector of spike times, n, that occurred during stimulus presentation), a bootstrapped spike train was generated by drawing with replacement n times from the original spike-time vector. For each of the 1000 new spike trains generated for a particular stimulus presentation, spikes were binned and the first harmonic (F1) component of the response was calculated. This process was repeated for all cells, over all spatial frequencies tested to build a bootstrapped spatial frequency tuning curve for both L- and M-cone stimuli. Each bootstrapped tuning curve was fitted with a difference-of-Gaussians function. From each of these fits, the relative L- and M-cone weight parameters were retrieved and a cone purity index to center and surround was recomputed. Figure 4 shows the refitted bootstrapped spatial tuning curves for three chromatic cells (Fig. 4A–C) and one achromatic cell (Fig. 4D). The cone purity index to center and surround, computed for each bootstrap, is shown for each cell in Figure 4E. The clustering of values from the bootstrap analysis confirms that L and M input weights to the receptive field can be reliably determined from our difference-of-Gaussians fitting protocol. Figure 4F plots the cone purity index for all bootstraps of M-dominated (green) and L-dominated (red) chromatic cells. The distribution of bootstrapped cone purity index values for center (0.57 ± 0.36, x axis histogram) versus surround (0.49 ± 0.24, y axis histogram) recapitulated the distribution from the original fits of chromatic cells (Fig. 2F); the same tendency of unequal index values between center and surround is illustrated by plotted points above or below the diagonal. By contrast, bootstraps of achromatic cells (Fig. 4G) showed equitable cone purity indices between center (0.55 ± 0.18, x axis histogram) and surround (0.54 ± 0.21, y axis histogram), much like the original fits of achromatic cells (Fig. 2G); this is illustrated by a clustering of points along the diagonal. Our bootstrap analysis illustrates that our fitting protocol is reliable for reporting the relative L and M input strength to the receptive field center and surround, and therefore indicates that this relative inequality between center and surround cone purity is a robust and reliable way to differentiate chromatic from achromatic cells.

Figure 4.

Bootstrap analysis confirms center-surround disparity in chromatic cells. For 168 midget cells, spike trains of L- and M-cone spatial tuning curves were bootstrapped 1000 times. Each bootstrapped tuning curve was then fitted with a difference-of-Gaussians function, from which the relative L- and M-cone weight parameters were retrieved and a cone purity index to center and surround recomputed. A–D, Examples of refitted bootstrapped spatial tuning curves are shown for three chromatic cells (A–C) and one achromatic cell (D). E, The cone purity index to center versus surround, computed for each bootstrap, is plotted for each cell. F, Center versus surround cone purity index for all bootstraps of M-dominated (green) and L-dominated (red) chromatic cells. Index values to center (0.57 ± 0.36, x axis histogram) versus surround (0.49 ± 0.24, y axis histogram) showed the same pattern of disparity as the original fits of chromatic cells, illustrated by plotted points above (green) or below (red) the diagonal. G, Center versus surround cone purity index for all bootstraps of achromatic cells. Equivalent cone purity index values between center (0.55 ± 0.18, x axis histogram) and surround (0.54 ± 0.21, y axis histogram), similar to the original fits of achromatic cells, are illustrated by a clustering of points along the diagonal.

Generating cells with a nonselective receptive field model

Anatomical evidence within the midget circuit overwhelmingly favors nonselective connectivity (for review, see Crook et al., 2014). We aimed to test whether midget cells that nonselectively sample a random cone mosaic could produce sufficient cone bias within the midget receptive field to drive color-opponent signals, similar to that observed in our empirical population. We deployed a difference-of-Gaussians model to generate a large population of model midget cells at a range of simulated retinal eccentricities, and assessed whether this model could fully account for the diversity of receptive field profiles we observed for empirical cells. We further aimed to test how chromatic sensitivity changes as a function of eccentricity.

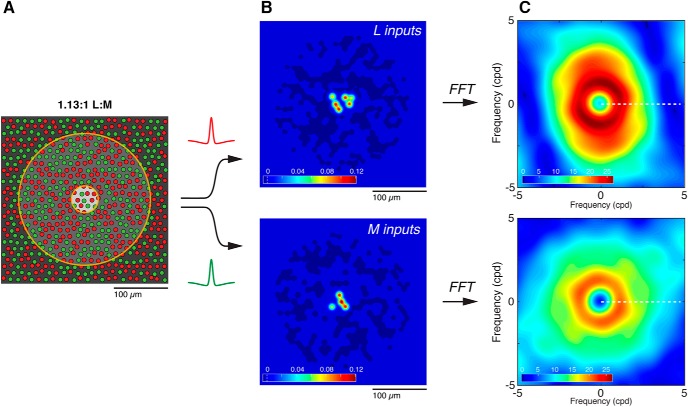
We generated 5000 model cells sampled uniformly over an eccentricity range of 1.25°–50° (0.25–10 mm), using the parameters outlined in Table 1 and in Materials and Methods. For each cell's unique cone mosaic, a receptive field center and surround radius was assigned based on eccentricity (Fig. 5A). An input weight was assigned to each L and M cone in the receptive field; weights to center and surround Gaussians were summed, and cone purity indices for both were computed. To evaluate isolated L- and M-cone sensitivity, receptive field profiles for L inputs (Fig. 5B, top) and M inputs (Fig. 5B, bottom) were separated and then Fourier-transformed to the frequency domain. Response amplitude and phase were determined from the real and imaginary components of the complex transform, evaluated along a continuous range of spatial frequencies from 1/128 to 32 cpd (Fig. 5C, dotted line). Because midget cell responses to L + M stimuli are well described by the linear combination of their responses to L- and M-cone-isolating stimuli separately (data not shown), Fourier analysis of the sum of L and M receptive field profiles was used to evaluate achromatic (L + M) sensitivity, and Fourier analysis of the difference of L and M receptive field profiles was used to evaluate opponent chromatic (L–M) sensitivity.

Figure 5.

Generating model receptive fields. A, A simulated patch of cone mosaic for a model cell at 5 mm eccentricity. The mosaic was generated on a triangular grid with random jitter; L and M cones were then randomly assigned. Overall L:M cone ratio for the patch was drawn from a distribution of ratios observed empirically, and cone density and diameter were assigned as a function of eccentricity. Receptive field size was also assigned as a function of eccentricity; this model cell's receptive field center (light gray circle) and surround (dark gray circle) are shown. B, To evaluate isolated L- and M-cone sensitivity, receptive field profiles for L and M inputs were separated and a difference-of-Gaussians kernel applied to weight the contribution of every cone in the receptive field. Heat maps illustrate the normalized strength of weighted L (top) and M (bottom) inputs to the cell's receptive field. Very strong inputs from 10 cones contribute to the receptive field center (red, yellow), whereas ∼350 cones comprise a much weaker input of the opposite sign to form the surround (dark blue). Color bars represent the normalized contribution of each cone ranges from approximately −0.05 (surround cones) to 0.12 (center cones). C, Fourier transforms of the spatial maps were used to evaluate the frequency tuning of L and M inputs to the cell. Response amplitude (top, L inputs; bottom, M inputs) and phase (data not shown) were determined from the real and imaginary components of the complex transform, respectively. Values were evaluated along a single axis, representing a continuous range of spatial frequencies (dotted line).

The strength of chromatic tuning was determined by computing the chromatic gain ratio, G_C = (R_L−M)/(R_L+M), of L + M and L–M response amplitudes at the lowest spatial frequency, and confirmed by the phase relationship of L- and M-cone responses. Cells were considered color-opponent if G_C > 1 and L and M response phases were separated by 180°. Chromatic cells were designated L-dominated if L-cone responses occurred at 0° (M-cone response at 180°) and M-dominated if M-cone responses occurred at 0° (L-cone response at 180°). Model cells with G_C < 1 and 0° L–M response phase separation were characterized as achromatic. Our model produced a largely heterogeneous population of chromatic (n = 2231) and achromatic (n = 2769) cells, with broadly overlapping distributions of chromatic and achromatic model cells as a function of eccentricity. When evaluated over an equivalent range to that of our empirical data (3–10 mm), median eccentricity for achromatic model cells (7.03 ± 1.63 mm MAD, n = 2264) was more peripheral than for chromatic model cells (5.83 ± 1.60 mm MAD, n = 1636), which is comparable with the ∼1.5 mm separation seen in our empirical dataset.

Characterizing receptive field profiles of model midget cells

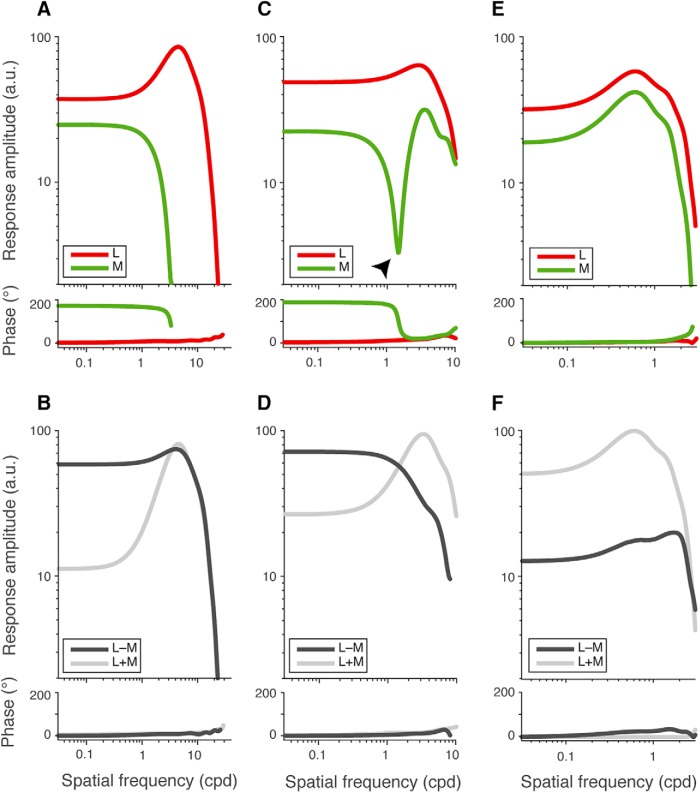
The receptive field properties of both chromatic and achromatic cells generated by the model closely resembled those of our empirical population, with examples illustrated in Figure 6. Chromatic model midgets comprised either pure (Fig. 6A,B) or strongly weighted input from one cone type (Fig. 6C,D) to the receptive field center, and showed mixed L and M inputs to the surround. An example chromatic model cell with pure L input to the center, shown in Figure 6A, showed a bandpass response in one phase (Fig. 6A, red), whereas M-cones, present only in the surround, showed a low-pass response in the opposite phase (Fig. 6A, green). As such, this cell showed dominant opponent (L–M) sensitivity at the lowest spatial frequencies (<3 cpd; Fig. 6B, dark gray), with enhanced achromatic (L + M) sensitivity emerging at high spatial frequencies, when the receptive field center is isolated (≥3 cpd; Fig. 6B, light gray). By comparison, an example model cell with dominant L-cone inputs to center, shown in Figure 6C, showed a bandpass L-cone response in one phase (Fig. 6C, red), whereas the M-cone response (Fig. 6C, green) showed a phase reversal at an intermediate spatial frequency (arrowhead): weak contribution to the center was observable as a small in-phase response with the dominant input at high spatial frequencies but was attenuated at low spatial frequencies by a much stronger surround, causing a response null and a phase reversal. This cell also exhibited dominant opponent (L–M) sensitivity at low spatial frequencies (<1 cpd; Fig. 6D, dark gray) but enhanced achromatic sensitivity at high spatial frequencies with the isolation of the receptive field center (≥1 cpd; Fig. 6D, light gray).

Figure 6.

Chromatic and achromatic midget receptive fields are reproduced with a nonselective wiring model. Frequency analysis of receptive field inputs is shown for three model cells. Chromatic model midgets were composed of a single cone type (A, B) or were strongly biased toward one cone type (C, D) in the receptive field center, and showed mixed L and M inputs to the receptive field surround. A, An example model cell with pure L input to the center exhibited a bandpass L-cone response of one phase (red), whereas M-cones, present only in the surround, showed a low-pass response in the opposite phase (green). B, As such, this cell showed dominant opponent (L–M) sensitivity at low spatial frequencies (dark gray), with enhanced achromatic (L + M) sensitivity emerging at high spatial frequencies, with the isolation of the pure-cone center (light gray). C, An example model cell with dominant L inputs to center exhibited a bandpass L-cone response in one phase (red), whereas the M cone spatial tuning curve (green) exhibited phase-reversing behavior. A weak M-cone contribution to the center was in phase with the dominant L input at high spatial frequencies, but at lower spatial frequencies, the stronger M-cone contribution to the surround caused a response null (arrowhead) and a phase reversal. D, Like pure-center cells, these model chromatic cells also exhibited spatial-frequency-dependent chromatic and achromatic responses, showing dominant opponent (L–M) sensitivity at low spatial frequencies (dark gray) but enhanced achromatic sensitivity at high spatial frequencies (light gray). E, By comparison, achromatic model cells showed mixed L and M inputs to both the receptive field center and surround, and showed bandpass, in-phase tuning for L (red) and M (green) inputs across all spatial frequencies. F, Correspondingly, such cells showed weak L–M sensitivity (dark gray), and high L + M sensitivity (light gray) across all spatial frequencies, with no cone-opponent behavior.

By comparison, achromatic model cells showed mixed L and M inputs to both the receptive field center and surround, and showed bandpass, in-phase tuning for both L and M inputs across all spatial frequencies with no cone-opponent responses (Fig. 6E). Correspondingly, such cells showed weak L–M sensitivity (Fig. 6F, dark gray), and high L + M sensitivity (light gray) at all spatial frequencies.

Formalizing the chromatic criteria for midget cells

The receptive field profiles of model cells closely emulated those of empirical cells; because the strength of L and M inputs was explicitly quantified during the generation of each model cell, we evaluated the distribution of these weights across our model population to compare with our empirical data. As a rule, model cells show chromatic sensitivity under the same conditions as empirical cells: when (1) one cone type contributes more strongly to the center than it does to the surround, and (2) the other cone type contributes more strongly to the surround than it does to the center. This rule can be formalized with an equation for chromatic gain of the net L or M input (L_T, M_T) to the receptive field as follows:

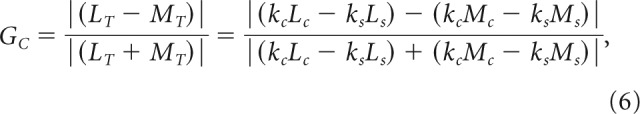where L_c and M_c are cone input weights to the center, L_s and M_s are input weights to the surround, and k_c and k_s are center and surround response gain constants. Chromatic gain is maximized when either L_T or M_T is negative; this is achieved when the surround dominates for one cone type (either k_sL_s > k_cL_c or k_sM_s > k_cM_c). Chromatic gain is minimized as L_T = M_T is approached, when neither cone type dominates in the surround (k_sL_s < k_cL_c and k_sM_s < k_cM_c). Plotting the cone purity index for center and surround for each cell shows distinct patterns for chromatic versus achromatic cells.

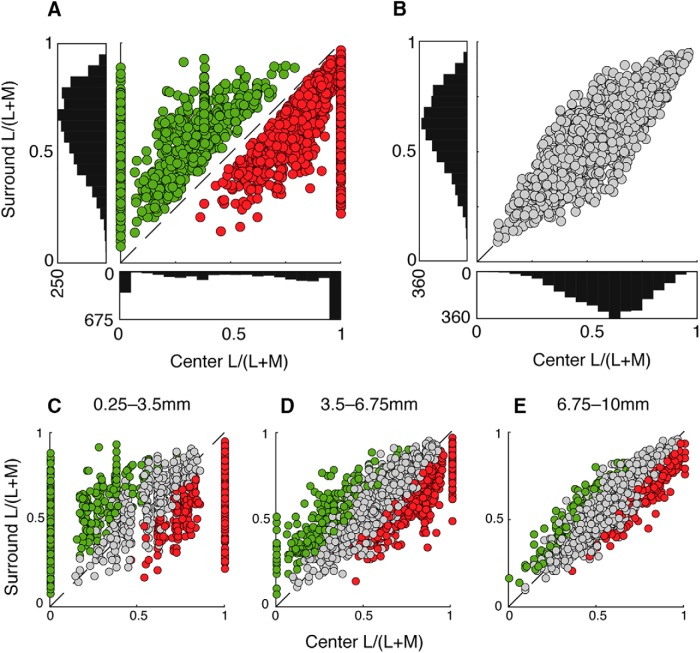
For model cells with a sufficient cone bias between center and surround, the chromatic criteria are satisfied: the dominant center cone type is always stronger than its contribution to a mixed surround of L and M, and the absence or weakness of the second cone type to the center means its contribution to the surround will always be greater. Plotting each model cell's cone purity index for center and surround shows that all L-dominated cells (where L_T > 0 and M_T < 0) fall below the diagonal, and M-dominated cells (where M_T > 0 and L_T < 0) fall above the diagonal (Fig. 7A). The distributions of cone purity index values for center (x axis histogram) and surround (y axis histogram) closely replicate those seen for our population of empirical chromatic cells (Fig. 2F, histograms). As with our empirical population, cone purity index values exhibited greater variance for the center (0.64 ± 0.36) than surround (0.62 ± 0.17). This difference in variance between center and surround was statistically significant for chromatic model cells (Levene's test, F = 1970, p < 10⁻¹⁰).

Figure 7.

L- versus M-cone disparity between receptive field center and surround determines cone opponency. Chromatic opponency is afforded to model cells with a sufficient cone disparity between center and surround. A, For chromatic model cells demonstrating cone opponency, plotting the cone purity index of center (x axis) versus surround (y axis) shows that all cells with L-dominated centers (red) fall below the diagonal, where M dominates to the surround. Conversely, cells with M-dominated centers (green) fall above the diagonal, where L dominates to the surround. Cone purity index values to center were highly variable and skewed toward 1 (pure L) or 0 (pure M). B, For achromatic model cells, plotting each cell's cone purity index to center (x axis) and surround (y axis) shows balanced L- and M-cone inputs between center and surround, indicated by points clustered along the diagonal. C–E, Binning model cells by eccentricity reveals more chromatic cells (with unequal cone purity index values) at near retinal locations (C), gradually supplanted by weakly chromatic and achromatic cells (more balanced cone purity index values) at intermediate (D) and far (E) eccentricities.

Conversely, achromatic cells that demonstrate balanced cone inputs to center and surround fail the chromatic criteria (Fig. 7B), showing equal cone purity indices to center and surround. Just like for empirical achromatic cells (Fig. 2G), model achromatic cells (where k_cL_c > k_sL_s and k_cM_c > k_sM_s) demonstrate clustering along the diagonal. The distribution of cone purity index values for the center (0.59 ± 0.16; Fig. 7B, x axis histogram) matched the distribution of those for the surround (0.60 ± 0.16; Fig. 6B, y axis histogram). The difference in variance between center and surround cone purity distributions was not statistically significant for achromatic cells (Levene's test, F = 0.18, p = 0.67). We binned cells by retinal location (Fig. 7C–E) to compare eccentricity-dependent chromatic behavior to that observed in empirical cells. Similar to empirical cells (Fig. 2G–I), chromatic cells with unequal cone-purity index values for center and surround are more likely at central retinal locations (Fig. 7C), whereas at intermediate (Fig. 7D) and far (Fig. 7E) eccentricities, the cone-purity indices of the two receptive field mechanisms tend to be less disparate, resulting in weaker chromatic tuning and the increased appearance of achromatic cells.

Although the chromatic rule is satisfactory for identifying cells as either having or lacking a cone-opponent response between center and surround, the scatter of chromatic and achromatic cells plotted in Figure 7 suggests that chromatic tuning is not a category but a continuum. The variability of chromatic and achromatic cells seen in our and others' data (e.g., Solomon et al., 2005; Buzás et al., 2006; Martin et al., 2011) suggests that there is biological variability within the midget pathway that shapes this continuum. As our model permits us to emulate aspects of biological variation reported in the literature (for instance, relative strength of receptive field center and surround, or overall L:M-cone ratio), we modulated parameters to evaluate the effect of such variation would have on the distribution of chromatic and achromatic cells.

Relative center-surround gain impacts the generation of chromatic cells

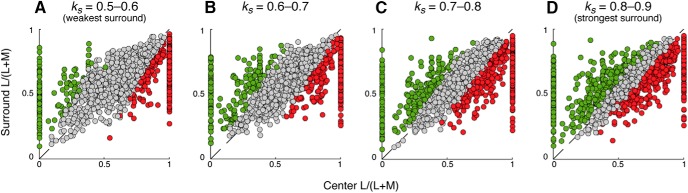
The formalization of the chromatic rule (Eq. 6) not only permits us to relate our modeling output to previous papers that use chromatic gain as a measure of chromatic tuning, while also allowing us to explicitly highlight the large impact of relative center-surround strength (k_c and k_s) on the chromatic behavior of a cell. Because chromatic gain can fluctuate strongly in the face of this single parameter, we can examine this compared with the more agnostic characterization of cells by their cone purity to receptive field center and surround. Figure 8 shows how we parametrically explored relative center-surround strength and its effect on chromatic tuning. While direct measurements of midget receptive field center and surround strength have been done (Derrington et al., 1984; Croner and Kaplan, 1995) and different values for relative center-surround gains have been proposed (Lennie et al., 1991; Mullen and Kingdom, 1996), there is not much experimental precedent for a single value of surround strength in midget cell receptive fields, which gave us the opportunity to use modeling to explore its influence on chromatic behavior in the face of limited experimental data. To account for the variability of values across the literature, our model generated cells with different k_s values along the uniform range of 0.5–0.9× that of the center. To systematically examine the effect of this single parameter on the generation of chromatic model cells, we rebinned the data as a function of surround response gain: k_s = 0.5–0.6, k_s = 0.6–0.7, k_s = 0.7–0.8, and k_s = 0.8–0.9 (Fig. 8). Of model cells with k_s values of 0.5–0.6, 30% of cells (379 of 1276) were chromatic (Fig. 8A), compared with 38% (481 of 1251) of model cells with k_s values of >0.6–0.7 (Fig. 8B), 48% (616 of 1291) of model cells with k_s values of >0.7–0.8 (Fig. 8C), and 64% (757 of 1182) of model cells with k_s values of >0.8–0.9 (Fig. 8D). Generally, achromatic cells were generated more frequently in simulations that used the lowest k_s values, and these achromatic cells plot farther from the diagonal (i.e., greater inequality between cone purity indices for center and surround). Conversely, simulations with higher values of k_s more frequently produced cells with chromatic sensitivity, with achromatic cells only found closely clustered to the diagonal (i.e., much smaller cone disparities between center and surround). Simulations with stronger k_s values reduce the amount of cone disparity between a receptive field center and surround that is required to generate a cone-opponent response. By comparison, weaker k_s values attenuate the overall cone contribution to the surround, increasing the likelihood that the center will dominate for both L and M inputs, thus producing an achromatic cell. Our model was not heavily dependent on a precise value of surround gain to generate chromatic cells, and any number of biologically driven values appear to suffice. However, stronger cone opponency across model cells was observed in simulations when center and surround gains were more equal. This highlights the requirement of center-surround antagonism within the midget receptive field to produce cone opponency, and is consistent with results showing that pharmacologically blocking the receptive field surround abolishes cone-opponent signals in midget cells altogether (Crook et al., 2011).

Figure 8.

Effect of relative center-surround response gain on the generation of chromatic cells. A total of 5000 model cells were generated with a relative surround gain, k_s, randomly assigned as 0.5–0.9 times the response gain of the center. Cells were binned as a function of their relative surround gain and cone purity index plotted for receptive field center (x axis) versus surround (y axis). A, Distribution of chromatic and achromatic cells with k_s equal to 0.5–0.6 times that of the center; 30% of cells (379 of 1276) were chromatic. B, Distribution of chromatic and achromatic cells with k_s equal to 0.6–0.7 times that of the center; 39% of cells (481 of 1251) were chromatic. C, Distribution of chromatic and achromatic cells with k_s equal to 0.7–0.8 times that of the center; 48% (616 of 1291) of cells were chromatic. D, Distribution of chromatic and achromatic cells with k_s equal to 0.8–0.9 times that of the center; 64% (757 of 1182) of cells were chromatic.

Overall L:M cone ratio does not impact the generation of chromatic cells

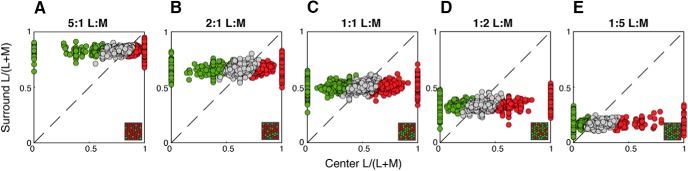
Our model generated a unique cone mosaic for each model cell, each with an L:M ratio independently drawn from the distribution observed across a large sample of macaque retinas from spectral ERG and physiological measurements (L/(L + M) = 0.61 ± 0.16, or ∼1.55:1 L:M) (Jacobs and Deegan, 1997; Dacey et al., 2000b). However, this does not provide direct insight about the population of achromatic and chromatic midget cells in a single retina. Both physiological and human imaging (Roorda and Williams, 1999; Hofer et al., 2005) studies have shown that L:M cone ratios vary widely across individual retinas, so we evaluated how specific L:M ratios affect the generation of chromatic and achromatic model midget cells. Using a single value of k_s = 0.75, we generated 1500 model cells for each of five discrete retinal L:M ratios: 5:1, 2:1, 1:1, 1:2, and 1:5, and plotted the cone purity index of center versus surround for each retina (Fig. 9). We found that the distribution of cone purity indices to center and surround are shifted based on a retina's overall weight of L and M cones. For each retina, the cone purity index values for surround exhibited low variance around a mean that closely reflected the overall L:M ratio (Fig. 9A–E, y axes). This stability of purity can be explained by the large number of inputs to the receptive field surround, which reduces the variability of L and M inputs. The center cone purity index values also reflected the overall L:M ratio for each retina but spanned the entire range from pure M (0) to pure L (1) for all conditions (Fig. 9A–E, x axes). The much larger variance of center purity index values can be explained by the far fewer cone inputs to receptive field centers than to surrounds. Despite a relatively stable range of surround purity index values, the highly variable center alone was sufficient to produce a cone disparity between the receptive field center and surround of many model cells, thereby generating cone opponency. The model outputs show comparable proportions of chromatic cells across all retinal L:M ratios, suggesting that overall L:M ratio of an individual retina has little bearing on the generation of chromatic cells. Furthermore, L:M-ratio-constrained model populations show the same eccentricity-dependent effects of chromatic tuning: that is, regardless of L:M ratio, the number of pure-cone center cells decrease with eccentricity and are supplanted by weakly chromatic and achromatic cells with more balanced cone purity indices. Our model is broadly immune to effects of retinal cone ratio; the number of chromatic cells does not appreciably differ from retina to retina, nor does eccentricity appear to affect cells from one retina differently from another. Critically, this reifies what has been seen psychophysically: human observers have highly stereotyped color detection and discrimination despite large variations in retinal L:M ratio from person to person (Brainard et al., 2000).

Figure 9.

Effect of overall L:M cone ratio on the generation of chromatic cells. A total of 1500 model cells were generated for five different L:M-cone ratio ranges. Distribution of chromatic and achromatic cells from retinas with L:M ratios of (A) 5:1, (B) 2:1, (C) 1:1, (D) 1:2, and (E) 1:5 are plotted as described in Figures 7 and 8. Insets, Illustrative diagrams of L:M ratio. For each retina, the cone purity index in the surround exhibited low variance around a mean that closely reflected the overall L:M ratio (y axes). The distribution of center cone purity also reflected the overall L:M ratio for each retina, but exhibited higher variance, and so spanned the entire range from pure M (0) to pure L (1) for all conditions (x axes). Notably, chromatic and achromatic cells were generated in all conditions, regardless of L:M ratio.

Spatial frequency-dependent chromatic and achromatic tuning changes with eccentricity

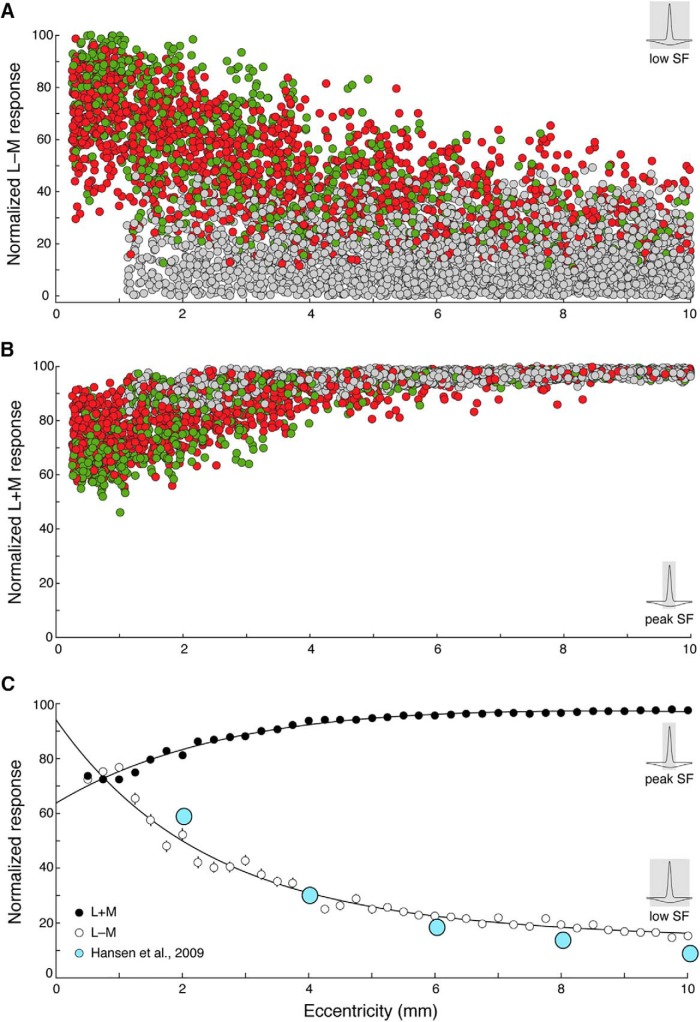
To better understand the effect of eccentricity on chromatic sensitivity of our model cells, we plotted the L–M response at the lowest spatial frequency for each model cell as a function of retinal location (Fig. 10A). We observed that central eccentricities produced the highest density of chromatic cells (red, green), which exhibited the strongest opponent L–M responses. Chromatic sensitivity decreased gradually with eccentricity, giving way to more achromatic cells (gray) in the periphery, with the lowest opponent L–M responses. This continuous decline in chromatic cells is precisely the prediction of previous models of nonselectivity (Lennie et al., 1991; Mullen and Kingdom, 1996): because of the increased cone inputs to midget cells in the retinal periphery, this produces fewer chromatic cells with cone-purity imbalance between center and surround, and more achromatic cells with balanced cone purity to center and surround. However, despite this decline in chromatic midgets, it is not complete; at even the farthest eccentricities modeled, ∼20% of our model population still showed cone-opponent responses. This suggests that a nonselective model is sufficient to explain the maintained appearance of chromatic cells (Martin et al., 2001; Solomon et al., 2005; Buzás et al., 2006), while also explaining the increased appearance of achromatic cells in the periphery (Diller et al., 2004; Field et al., 2010). Previous studies in parafovea, which identified L- or M-dominant input to the receptive field surround in addition to the center, have posited that the fovea possesses its own mechanism of specificity to enhance the cone purity of receptive field surrounds (Reid and Shapley, 1992, 2002; Lee et al., 2012). By contrast, our nonselective wiring model suggests that L- or M-dominant foveal surrounds could too be a product of nonselectivity, considering the size of foveal receptive fields. Compared with the ∼350 surround inputs to a peripheral midget cell at 25°, a foveal midget cell surround is expected to be much smaller, comprising as few as six cones. There is therefore a much greater likelihood of encountering a foveal midget with an L- or M-dominant surround in addition to its L- or M-pure center. This low-input wiring scheme is supported by recent connectomic reconstructions of cones and horizontal cells at the precise center of the human fovea: foveal horizontal cells connect indiscriminately to all cones, like their peripheral counterparts, and foveal cones are connected strongly to their neighbors by a spatially restricted horizontal cell network (Dacey et al., 2017; Packer et al., 2017).

Figure 10.

Chromatic and achromatic responses across eccentricity. A, Each model cell's opponent L–M responses at the lowest spatial frequency was plotted as a function of eccentricity. The density of chromatic cells (red, green) was highest closest to the fovea and exhibited the strongest opponent L–M responses. L–M responses decreased gradually with eccentricity, giving way to more achromatic cells (gray) in the periphery, with the lowest opponent L–M responses. B, Each model cell's response to L + M stimuli at the peak spatial frequency was plotted as a function of eccentricity. All model cells, both chromatic and achromatic, showed high L + M responses at high spatial frequencies, at all eccentricities. C, Model cells were binned across the eccentricity range (bin width = 0.25 mm); mean L–M response at the lowest spatial frequency (open circles) and mean L + M response at peak spatial frequency (closed circles) were computed and plotted as a function of eccentricity. Overall chromatic responses decline with increasing distance from fovea, whereas achromatic responses are consistently strong across all retinal locations. The decline in average chromatic strength is consistent with the decline of human L–M chromatic detection sensitivity measured psychophysically by Hansen et al. (2009) (blue circles). SF, Spatial frequency. Error bars indicate SEM.

In contrast to the gradual loss of chromatic sensitivity at low spatial frequencies, L + M sensitivity at the peak spatial frequency is maintained in both chromatic and achromatic model cells, across all eccentricities (Fig. 10B). Although peak spatial frequency predictably declines with eccentricity (a function of increasing receptive field center size), our simulations are consistent with the high-spatial-frequency achromatic sensitivity observed empirically in both chromatic and achromatic midget cells (Fig. 3). A nonselective model thus supports the hypothesis that the midget pathway can encode an achromatic acuity signal, thus setting the limit for spatial resolution in the retina.

Notably, although only a proportion of model cells across the modeled eccentricity range were classified as chromatic (showing overt cone opponency), many achromatic cells showed L–M responses well above zero. Despite no overt opponency, residual responses to L–M stimuli were still observed due to slight overall biases of L or M cones to the receptive field. The overlap of responses of chromatic and achromatic cells in Figure 10A is in keeping with the view that midget ganglion cells form a single population, with L–M responses falling along a continuum. All model midget cells demonstrated strong responses to high spatial frequency L + M stimuli (Fig. 10B). To understand how the response of a population of midgets would change across eccentricity, we binned the responses of model midget cells across retinal location and computed the mean L–M and L + M response for each bin (Fig. 10C). At low spatial frequencies, the mean low-frequency L–M sensitivity of the population declines nearly fivefold from fovea to the far periphery (open circles), driven by the overall decrease of chromatic cells, but also by a reduced chromatic sensitivity within each cell. To relate this population behavior to color processing more broadly, the mean low-frequency L–M sensitivity serves as good indication of what a hypothetical low-pass filter could extract at a later stage in visual processing. Evidence for such a low-pass filter can be found psychophysically: this decline in average chromatic strength is consistent with the decline of L–M chromatic detection sensitivity in human observers, measured by Hansen et al. (2009) (blue circles). The mean high-frequency L + M sensitivity of the population is consistently strong across all retinal locations (black circles). The gradual decrease with eccentricity of chromatic (L–M) sensitivity at low spatial frequencies, paired with the stable achromatic (L + M) sensitivity at high spatial frequencies, is consistent with the view that midget cells are the primary substrate of high-acuity achromatic tuning, with L–M opponent signals variably applied. Thus, midget cells appear to deploy spatial frequency-dependent encoding of chromatic and achromatic information. The strength of this multiplexing is predicted to decrease in peripheral cells.

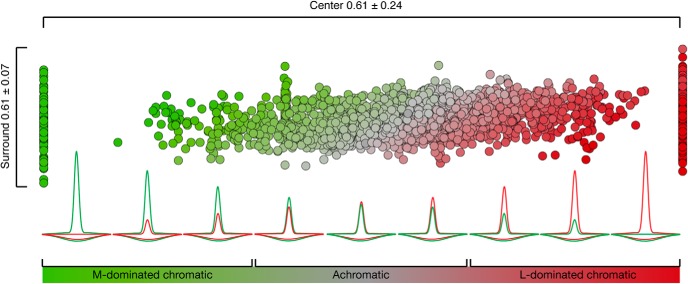
Figure 11 summarizes how both chromatic and achromatic model midget cells, generated under a constrained L:M ratio, as would be the case for a single retina, differentially respond to L–M opponent stimuli. Because the number of inputs to a midget-cell receptive field center is small, there is large variability in center purity, illustrated by the spread of points ranging from pure M (left) to pure L (right) along the x axis. By comparison, the larger number of inputs to the receptive field surround renders its purity much less variable, and it more closely reflects the L:M ratio of the cone mosaic (y axis). The result is that a continuum of possible receptive fields with highly variable centers and highly stable surrounds are produced (inset illustrations). Receptive fields with strongly unbalanced L and M inputs to center show cone opponency, where one cone type dominates the center while the other cone type dominates the surround. These cells exhibit the strongest responses to L–M stimuli (saturated red and green points). Receptive fields with more balanced L and M inputs to center do not show this disparity and thus show weak, or absent, opponency (desaturated red and green points). Because of the high variability of center inputs, most cells, regardless of opponency, have a small bias of either L or M to the center, thereby showing a residual response to L–M chromatic stimuli. The continuum of receptive field profiles observed in model midget cells emulates the diversity of profiles observed in our empirical population, strongly suggesting that a single wiring paradigm, which samples a random cone mosaic nonselectively, is sufficient to generate a heterogeneous population of both chromatic and achromatic midget ganglion cells across the visual field. Notably, this single wiring paradigm also generates midget ganglion cells that all exhibit high achromatic sensitivity to high spatial frequency stimuli, regardless of the chromatic tuning at low spatial frequencies.

Figure 11.

The response continuum of model midget cells. Random variation in the receptive field profiles means that model cells generated for a single retina form a continuum of responses to L–M opponent stimuli. Drawn from cone mosaics with L:M ratios between 1:1 and 2.3:1, a subsample of 2154 model cells were plotted as a function of center cone purity index (x axis) versus surround cone purity index (y axis). The relatively small number of inputs to a midget-cell receptive field center underlies a large variance (0.61 ± 0.24) in cone purity index values, from pure M to pure L (left to right, respectively; x axis). The larger number of inputs to receptive field surrounds produces considerably less variance (0.61 ± 0.07), so the cone purity index is stable around a mean that reflects the L:M cone ratio of the sample cone mosaics (y axis). This combination produces a broad, continuous range of possible receptive field profiles (difference-of-Gaussians profiles, bottom inset) with highly variable centers and highly stable surrounds. Receptive fields with dominant L or M input to center show chromatic opponency, where one cone type dominates the center while the other cone type dominates the surround. These cells exhibit the strongest responses to L–M stimuli (saturated red and green points). Receptive fields with more balanced L and M to center do not show this disparity and thus show weak, or absent, opponency (desaturated red and green points). Because of the high variability of center inputs, most cells, regardless of opponency, have a small bias of either L or M to the center, thereby showing a residual response to L–M stimuli. The continuous distribution of possible L- and M-cone contributions to center and surround is randomly sampled to generate a heterogeneous population of chromatic and achromatic midget ganglion cells across the visual field.

Testing model predictions in the retinal periphery

As is the inherent nature of single-cell recordings, our electrophysiological recordings consist of cells recorded at disparate, noncontiguous locations in a number of different retinas, each with presumably different overall L:M cone ratios (Dacey et al., 2000b). Given these constraints, it is difficult to make a direct comparison between our empirical data and our model to assess how well the model captures the activity of the retina-wide midget population. To compare our model's performance directly to electrophysiological data, we looked to the multielectrode array recordings of Field et al. (2010). Their method's concurrent recording of hundreds of midget cells enables a good approximation of a population's sensitivity over a contiguous area, at a particular eccentricity range, in a single retina, all while still being able to characterize the receptive fields of individual cells. From their recordings in peripheral primate retina, the authors reported a non-normal, fat-tailed distribution of cone weights to the receptive field center (i.e., a greater frequency of cells with dominant L- or M-cone centers), compared with a normal distribution of cone weights to the receptive field surround. This departure of receptive field center weights from a normal distribution was taken as evidence for functionally specific wiring. However, despite this enhanced cone purity at the receptive field center, the authors reported very few cone-opponent cells in their dataset. We compared the number of chromatic cells found in their population to that generated in our model for a similar retina (Fig. 12). Opponency in model cells was quantified and plotted as L̄ = (L_c − L_s)/(L_T + M_T) versus M̄ = (M_c − M_s)/(L_T + M_T) (Field et al., 2010), where the relative center-surround input of each cone type (L_c−L_s, M_c−M_s) is normalized by the sum of total L (L_T) and M (M_T) input to the entire receptive field. Respectively, positive L̄ or M̄ values indicate L- or M-cone dominance to the receptive field center, whereas negative L̄ or M̄ values indicate L- or M-cone dominance to the surround. Cells that plot in the second and fourth quadrants are cone-opponent, whereas cells located in the first and third quadrants are not. To compare our model output to the sample of 263 cells recorded at 6.75 mm (average cone ratio of 2:1 L:M, eccentricity span of ∼1.5 mm) (Field et al., 2010, their Fig. 4H), we took model cells generated for a retina with a 2:1 L:M ratio (Fig. 9B), then selected the subset that fell within a 6–8 mm eccentricity range (n = 312). We found the sample of Field et al. (2010) (Fig. 12A, modified from Field et al., 2010, their Fig. 4H) to be similar (63 of 263, 24%) to the proportion of opponent cells predicted by our model (Fig. 12B) for the same retinal location (87 of 312, 28%). In the dataset of Field et al. (2010), not only is the overall incidence of cone-opponent cells quite low, but the strength of the opponent response in individual cells is reduced as well. This is illustrated by an absence of cells in the center of the diagonals of the second and fourth quadrants, with clustering of cells toward the corners. A similar clustering is apparent in our model cell population, itself a recapitulation of the prediction of Lennie et al. (1991) for peripheral parvocellular units (their Figure 5.10C). We take this as compelling support that a functionally specific wiring paradigm is not required to produce peripheral chromatic cells on the order observed empirically. However, suggesting that a nonselective model is sufficient to describe the data is not the same as proving that a selective model is not required. We thus imparted a parameter of selectivity to the model to test the possibility that selectivity may occur at the receptive field center by way of synaptic strengthening, that is, strengthening connections of one cone type at the expense of the other (“tradeoff”). To do this, we assessed each cell in our same peripheral model population (n = 312) for whether it was L-cone dominant (L_c > L_s) or M-cone dominant (M_c > M_s). Although not all cells showed chromatic behavior, all cells showed at least slight cone bias (Fig. 10A). Once the dominant cone type was identified in the cell, its receptive field center contribution was increased by a percentage (1%–10% of the original contribution) and a corresponding amount was subtracted from the weaker cone type. The results of parametrically enhancing the receptive field center selectivity have a small but observable effect on the distribution of chromatic and achromatic cells, indicated by the migration of cells from the first and third quadrants (achromatic) to the second and fourth quadrants (chromatic) (Fig. 12C). Furthermore, introducing even mild selectivity quickly produced model populations with higher proportions of chromatic cells than reported in our original model (Fig. 12D, 0% selectivity tradeoff) or in Field et al. (2010, dashed line). We take these results as a strong indication that very little, if any, selectivity is required at the receptive field synapse to generate a population of cells in keeping with that observed empirically.

Figure 12.

Comparison of model and empirical cells in the retinal periphery. Opponency in individual model cells was quantified by calculating the relative strengths of the total input from L and M cones across the entire receptive field, and the normalized weights [x axis, (M_C − M_S)/(L_T + M_T); y axis, (L_C − L_S)/(L_T + M_T)] were plotted as in Field et al. (2010; their Fig. 4H). Cells that plot in the first and third quadrants do not show cone-opponent responses, whereas cells located in the second and fourth quadrants do show cone-opponent responses. A, Chromatic and achromatic cells identified in a single recording at 6.75 mm temporal eccentricity, modified from Field et al. (2010, their Fig. 4H). A third axis quantifying the orthogonal departure of some cells from the L and M axes (illustrating putative S-cone input) has been removed for clarity. Sixty-three of 263 total midget cells (24%) showed L–M opponent responses, characterized by their location in the second and fourth quadrants. Notably, the opponent responses of these cells is weak, illustrated by an absence of cells at the midpoints of the diagonals (where L and M weights are equal and opposite) and a clustering of cells toward the x and y axis endpoints, where an overall L- or M-cone bias to the receptive field is demonstrated. B, In a population of model cells generated on the range of 6–8 mm eccentricity, 87 of 312 total cells (28%) were opponent, similarly demonstrating both an absence of strongly opponent cells at the midpoints of the diagonals and clusters of weakly opponent cells toward the x and y axis endpoints. C, D, To test the effects of synaptic strengthening as a mechanism for selectivity, the model population was subject to “tradeoff,” in which amplitude for the dominant cone type in the receptive field center was enhanced at the expense of the nondominant cone type. Tradeoff is represented as a percentage of the total response amplitude. C, As synaptic tradeoff increased, the number of chromatic cells in the population increased, indicated by the migration of cells from the first and third quadrants (achromatic) to the second and fourth quadrants (chromatic). Populations after adding 2%, 4%, 6%, 8%, and 10% selectivity are shown (histograms). Axes are the same as A and B. D, The effect of mild selectivity quickly produced model populations with higher proportions of chromatic cells that reported in the original model (0% selectivity tradeoff) or in Field et al. (2010, dashed line).

Our modeling provides a parsimonious explanation for the variable chromatic tuning of peripheral midget cells, and is well supported by the electrophysiological data presented here and in other studies. As our model also predicts the appearance of achromatic cells beginning at 1 mm eccentricity (a region more foveal than our own dataset), extant studies of central retina and LGN can be used, at least cursorily, to assess the validity of our predictions. Qualitative studies of fovea that describe only chromatic midget cells (Reid and Shapley, 1992; Smith et al., 1992) seem to contradict our model's predictions specifically for locations <2 mm eccentricity, but we acknowledge that, in such studies, it is not always trivial to determine the retinal location of recorded units, the number of cells, or the stimuli used to classify them. In studies where recording location is specified and the cell population quantified, there are reports of achromatic cells at <2 mm (10°) eccentricity, and their numbers vary. For instance, chromatic LGN cells comprised 93% of the population reported by Reid and Shapley (2002) at a mean location of 1.6 mm (8°) eccentricity, while 61% of units recorded by Martin et al. (2011) at 1.3 mm (6.5°) eccentricity demonstrated chromatic tuning. Indeed, variably opponent LGN units were earlier reported by Derrington et al. (1984), which suggests that chromatic tuning is a variable property of cells in the central 10° of vision the same way it is in the periphery. While our peripheral recordings are insufficient to test our model's predictions of the central retina, there also does not seem to be any definitive contradiction between extant foveal studies and our model.

Discussion

This study addressed whether midget ganglion cells of the primate retina are specially wired for color, or whether chromatic sensitivity arises without the need for cone type-selective circuits. We mapped the tuning curves of individual cells using cone-isolating gratings varied in spatial frequency, then fit these curves with difference-of-Gaussian functions, to determine the L- and M-cone inputs to midget receptive fields. We found that peripheral midget receptive fields comprised multiple mixed L and M inputs to the surround, and either pure or mixed L- and M-cone inputs to the center. Our findings concur with others (Reid and Shapley, 2002; Buzás et al., 2006; Field et al., 2010; Martin et al., 2011) showing opponency arises when input from one of the cone types is weighted more strongly to the receptive field center. However, while many propose selective wiring to account for the data, we find a receptive field model that nonselectively samples a realistic cone mosaic provides a parsimonious explanation for our electrophysiological recordings.

Thanks to the private-line midget circuit, cone-opponent responses in central retina are easily accounted for with nonselective wiring (Lennie et al., 1991) because the single L- or M-cone input to the receptive field center is always antagonistic with the opposite cone type, present only in the receptive field surround. But understanding the persistence of cone-opponent midget cells well into periphery, where multiple cone inputs sum to the receptive field center, has been less intuitive. On the whole, anatomical studies have not identified a locus of selectivity in the midget circuit. Peripheral midget cell dendritic trees collect excitatory input from all proximal L- and M-cone-connecting midget bipolar cells with similar contact areas (Jusuf et al., 2006), and their receptive field surrounds appear dependent on feedback from horizontal cells (Crook et al., 2011) that nonselectively sample L and M cones (Dacey et al., 2000b). Moreover, blocking inhibitory glycinergic and GABAergic transmission has no effect on L versus M opponency in midget ganglion cells (Crook et al., 2011), consistent with a lack of cone type-selective amacrine cell circuitry (Calkins and Sterling, 1996).

Although nonselectivity underlies some models of opponency in retina (Momiji et al., 2006, 2007), many more emphasize functional specialization to differentially strengthen L or M inputs to the receptive field, as a way to emulate the central private-line circuit (Reid and Shapley, 1992; Martin et al., 2001, 2011; Buzás et al., 2006; Field et al., 2010; Lee et al., 2012). Such selectivity is proposed to explain the observation of cone-opponent cells in periphery because nonselective models, such as Mullen and Kingdom (1996), predict a steep decay in chromatic sensitivity with eccentricity. Our model can account for these two apparently conflicting observations. At any given retinal location, our electrophysiology and modeling show that midget cells vary widely from strongly chromatic to achromatic (Fig. 10A), a typical feature of recordings in near peripheral retina (Martin et al., 2001, 2011; Solomon et al., 2005; Buzás et al., 2006; Field et al., 2010). But while cell-to-cell variability is high, our model predicts a decrease in chromatic sensitivity of the overall population with eccentricity (Fig. 10C), which recapitulates previous predictions and corresponds with psychophysical measures of chromatic sensitivity across the visual field (Hansen et al., 2009). These two aspects of the data are consistent with a probabilistic interpretation of cone opponency: as midget dendritic fields enlarge with increasing eccentricity, the likelihood of chromatic behavior declines systematically but is not completely abolished.

Functional selectivity seems tractable as a strategy for increasing the likelihood of chromatic tuning in midget cells at any retinal location. Indeed, this is what we observed when introducing a mechanism of synaptic strengthening to our model (Fig. 12C). Our simulations indicate that even mild bias at the receptive field center enhances chromatic tuning across the population. It is most relevant, then, to compare our result with Field et al. (2010), who offer a data-driven argument for slight functional bias in L- or M-cone assignment to receptive field centers, but show no concomitant increase in cone-opponent cells (Fig. 12A,B). While it would be remiss to disregard the possibility of very small bias to receptive fields, its functional relevance in the absence of any change to chromatic tuning (especially when considered within the canon of anatomical nonselectivity) therefore remains unclear.

A random wiring model provides an elegant framework for the dual role of the midget circuit in color and form vision (Lennie and Movshon, 2005). In our recordings, midget cells exhibited high achromatic sensitivity at high spatial frequencies and variable chromatic sensitivity at low spatial frequencies; this spatial frequency-dependent tuning was captured in our receptive field model. The separation of chromatic and achromatic sensitivity (i.e., the “spatiochromatic notch”) appears to be a simple consequence of differentially weighted L- or M-cone inputs to the receptive field center versus surround. Our results are consistent with the idea of the midget pathway as the substrate for high-acuity achromatic vision that, with the evolution of separate L- and M-cone types in primate, produced trichromatic color vision by harnessing the preexisting center-surround antagonism of receptive fields (Mollon, 1989; Lennie et al., 1991; Merigan et al., 1991; Wässle et al., 1993; Crook et al., 2014). Such “unprincipled” sampling (Lennie, 2000) also generates similar proportions of chromatic cells regardless of L:M ratio (Fig. 9), which informs why large interindividual cone-type variability (Roorda and Williams, 1999; Hofer et al., 2005) does not elicit variable color perception (Brainard et al., 2000).

Center-surround receptive fields capable of transmitting both spatial and chromatic signals were well characterized in both foundational (Wiesel and Hubel, 1966; DeValois et al., 1977; Derrington et al., 1984) and more recent studies (Benardete and Kaplan, 1999; Blessing et al., 2004; Martin et al., 2011) in parvocellular LGN cells. As such, spatial frequency-dependent multiplexing has long been proposed as a mechanism for encoding color and luminance signals (Ingling Jr and Martinez-Uriegas, 1983). This seems economical given the degree of anatomical nonselectivity observed in the midget circuit and corroborates our results showing that a simple low-pass filter can retrieve a color-opponent signal whose strength covaries with psychophysical measures of color sensitivity (Fig. 10C). Indeed, measures of both color and luminance acuity in human observers seem to adhere to the principle of spatial frequency-dependent decomposition of color and luminance information, with the acuity for chromatic stimuli nearly half that of luminance stimuli (Anderson et al., 1991; Sekiguchi et al., 1993). This is consistent with center-surround activation by a broad stimulus for color opponency, whereas high achromatic acuity is achieved by isolated activation of the spatially resolved receptive field center.

Our proposition that decomposition of color and luminance occurs with simple low and bandpass filters (Fig. 10A,B) has been proposed to occur in striate cortex (V1) with selective combination of retinogeniculate afferents (D'Zmura and Lennie, 1986; Lennie and D'Zmura, 1988; Billock, 1995). Compared with the local homogeneity of midget cells' spatial properties, spatial frequency tuning is highly variable from cell to cell in localized regions of V1 (De Valois et al., 1982). Local sets of variably-tuned cortical filters could differentially capture color and/or luminance information in a given region of the visual field, as a function of each cell's spatial tuning and the chromatic properties of its retinogeniculate inputs. Modeling using independent component analysis revealed that such filters naturally emerge as a product of redundancy reduction, without imposing selective combination (Doi et al., 2003). This cell-by-cell basis for demultiplexing color and luminance offers a possible explanation for the variability of electrophysiological results showing V1 neurons tuned for color, luminance, or both (Lennie et al., 1990; Johnson et al., 2001, 2004; Jansen et al., 2015).

Renewed speculation about the retinal origins of color vision has come with the application of adaptive optics to psychophysics (Marcos et al., 2017). Recently, experiments in which perceptual judgements were elicited by the stimulation of identified cone types in the parafovea identified local interactions between cones suggestive of center-surround antagonism, and moreover concluded that these local interactions reflect nonselective wiring of receptive field surrounds in the foveal region (Tuten et al., 2017). By contrast, related experiments that find a minority of chromatic percepts elicited by single-cone stimulation (Sabesan et al., 2016) has reinvigorated the hypothesis that a small subset of retinal cells are specialized for color vision only. However, no model consistent with the known retinal circuitry has yet been offered to support such speculation.

In conclusion, the nonselective wiring model recapitulates the hallmark cone opponency of midget cells and accounts for the decline and variability of this property across the retina, all while preserving midget cells' fundamental role in spatial vision. Moreover, it is consistent with the emerging picture of synaptic organization of the midget circuit in both central and peripheral retina. That a nonselective model so well consolidates findings from physiology, anatomy, and psychophysics has broad implications for how other prominent features of perception may trace their origins to nonselective circuits (Lee and Reid, 2011; Morgan et al., 2016).