Semiautomatic determination of arterial input function in DCE-MRI of the abdomen

Abstract

The goal of this study was to develop a semiautomatic segmentation technique of the abdominal aorta to determine the arterial input function (AIF). A total of 24 patients having therapy naïve abdominal cancers were imaged using DCE-MRI on a 3T MR scanner. DCE-MRI continued for 4.2 minutes with 2.1 seconds temporal resolution (120 acquisitions). Gadoteridol (0.1 mmol/kg) was infused intravenously at 30 seconds after starting DCE-MRI, and flushed with 20-ml saline (2 ml/s). Patients were instructed to hold breath after maximal inhalation, and repeat as needed to full inspiration. The location of the abdominal aorta was manually identified, but its segmentation and motion tracking were automatically implemented. AIFs determined in the aortic region with and without tracking motion were statistically compared. The aortic region was further segmented into multiple smaller regions, and the AIF change according to the size of the region of interest (ROI) was examined. The displacement of the abdominal aorta during DCE-MRI was 3.4±2.3 (mean±SD) mm. The root mean square error (RMSE) of AIF from the best fitting curve was 0.110±0.010 mM after motion correction, which was significantly smaller than that before motion correction (0.134±0.016 mM; p<0.001). The amplitude of AIF varied up to 15% according to the ROI size. However, when the radius of ROI was reduced more than 3 mm, the variation in AIF amplitude was less than 5%. Therefore the ROI having smaller radius than that of aorta will need to be used to determine a reliable AIF in abdominal DCE-MRI.

1 Introduction

Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) is a non-invasive method that has been extensively utilized to quantitate the tissue perfusion parameters for diagnosis and prognosis of various diseases including cancers [1-3] and inflammations [4-6]. Arterial input function (AIF) is the measure of contrast concentration in arterial blood during and after intravenous bolus injection of a paramagnetic contrast agent [7], which is critical to retrieve pharmacokinetic perfusion parameters in quantitative DCE-MRI [8-10]. The microvascular perfusion is determined by the transfer of the contrast agent from the blood plasma to the target tissue. In upper abdominal DCE-MRI, a large abdominal aorta (about 2 cm in diameter) is seen in axial image slices, thus AIF can be determined by measuring the time-dependent contrast concentration within the aortic region. The region of interest (ROI) of the aorta is manually determined in usual. However, due to the partial volume effect that mainly occurs at the edge of aorta and the displacement associated with breathing and patient body motion, the manual segmentation may induce operator-dependent variation in determining AIF.

Several methods have been proposed to extract AIF automatically in brain [11-13], breast [14, 15], and prostate DCE-MRI [16]. Most of these methods identify voxels belonging to artery based on the known characteristics of AIF such as early bolus arrival time (BAT), early time to reach the peak signal (TTP) and large maximum peak concentration (MPC). However, the AIF shape can be changed according to injection rate, cardiac output and arterial pathology [17, 18], and furthermore commonly distorted by pulsate inflow effect [19, 20]. Therefore AIF may not follow the known characteristics, limiting the accuracy and applicability of the aforementioned automated segmentation methods.

In this study, we introduce a new method to extract AIF from the abdominal aorta. An optimal thresholding technique automatically determines the ROI based on the signal contrast between the ROI and the background. The ROI is determined at each time frame tracking the motion of the aorta, and AIF is retrieved by averaging contrast concentration in the ROI at each time frame. Also, we examined the variation of AIF according to the ROI size, which demonstrates error that can be induced by manual ROI segmentation, and determined the appropriate size of ROI to retrieve a reliable AIF in the abdominal DCE-MRI.

2 Materials and Methods

The institutional review board at the University of Alabama at Birmingham approved this clinical imaging study. All patients signed informed consents, and the health insurance portability and accountability act (HIPAA) was strictly observed.

2.1 Human subjects

A total of 24 patients with therapy naïve abdominal cancers were accrued (14 patients with pancreatic adenocarcinoma; 5 patients with gastrointestinal stromal tumors; 5 patients with hepatocellular carcinoma). DCE-MRI was applied for all patients prior to treatment. Thirteen patients were male, and eleven patients were female. The average age of the patients was 62 years.

2.2 Clinical MRI protocol

All patients were imaged with a single 3T MR scanner (Philips Achieva, Philips Medical Systems, Best, Netherlands). A torso phased array coil was placed around the upper abdomen of each patient. All images were acquired in axial planes. Prior to DCE-MRI, T1 weighted imaging at three different flip angles (5°, 10°, and 15°) was performed for T1 mapping [21]. A three-dimensional (3D) fast spoiled gradient echo sequence (THRIVE) with fat suppression was employed with the following parameters: TR/TE = 5/2.3 ms, FOV = 400 × 400 mm, NEX = 1, thickness/gap = 6/0 mm, 10 slices, frequency/phase encoding = 192/154, matrix size = 256 × 256, and SENSE factor = 2. Temporal resolution was 2.1 seconds, and imaging at each flip angle was conducted at maximum inhalation. DCE-MRI was applied for patients using the same imaging sequence and parameters, but with a fixed flip angle (FA = 15°). DCE-MRI was continued for 4.2 minutes (120 imaging). Each patient was instructed to stop breathing at maximum inhalation and repeat it as needed during DCE-MRI. The duration of each breath hold was about 20 seconds. At 30 seconds after starting DCE-MRI, gadoteridol (0.1 mmol/kg; Bracco Diagnostics Inc., Princeton, NJ) was intravenously infused at the rate of 2 ml/sec and followed by 20-ml saline flush.

2.3 Image processing

Figure 1 shows the procedure of semiautomatic segmentation of the abdominal aorta. In this study, the sixth image slice was used, since it was located 30 mm away from the first slice (the first slice was at superior position); AIF obtained from one of the first five slices (0∼30 mm) was likely overestimated due to blood unsaturation [22]. Among the 120 DCE-MR images, the one having the maximum peak signal in the abdominal aorta was chosen. When a user selected a pixel within the aortic region, a small image window (40 × 40 mm) containing the aorta at the center was created (Fig. 1a). Then the pixel size of the image window (1.56 × 1.56 mm) was interpolated to 0.2 × 0.2 mm (Fig. 1b). The aortic region was segmented using Otsu's method [23] (Fig. 1c), and a circle fitting to the segmented image was found. This fitting circle was used as the region of interest (ROI). The overlay of the fitting circle on the aortic image is shown in Fig. 1d. This process was repeated for all images acquired at different time frames; the diameter of the ROI was invariant, but the displacement of the ROI center position was traced. AIF was extracted by averaging the contrast concentration in the ROI at each time frame. The best fitting curve to the AIF was driven from the population-based AIF (pAIF) [24]. pAIF was modified by a scaling factor and an offset factor like apAIF+b to fit into the AIF obtained, and the root mean square error (RMSE) of the AIF from the fitting curve was calculated. For comparison, the RMSE of the AIF obtained without tracking motion from the fitting curve was also obtained. pAIF was given by Dr. Geoffrey Parker at the University of Manchester (Manchester, UK).

Figure 1.

Semiautomatic segmentation of the abdominal aorta. (a) An image window (40 × 40 mm) containing abdominal aorta at the center (pixel size: 1.56 × 1.56 mm). (b) The interpolated image window (pixel size: 0.2 × 0.2 mm). (c) The binary image of the abdominal aorta segmented by Otsu's method. (d) Overlay of the best fitting circle on the aortic image.

The ROI was further segmented into multiple smaller regions. The radius of the original ROI was 1 mm decreased to create the second ROI, and the radius of the second ROI was 1 mm decreased to create the third ROI, etc. This was repeated until the ROI radius became equal to or less than 1 mm. The abdominal aorta was categorized into six groups according to its radius (group 1 (radius: 6∼7 mm) (n=3); group 2 (radius: 7∼8 mm)(n=2); group 3 (radius: 8∼9 mm) (n=5); group 4 (radius: 9∼10 mm) (n=6); group 5 (radius: 10∼11 mm) (n=6); group 6 (radius: 11∼12 mm) (n=2)). AIFs were extracted from the original ROI and sub-ROIs. The amplitudes of AIFs were normalized to that in the core ROI, and then averaged over imaging time. These amplitude-normalized and temporal-mean AIFs were compared to one another, examining the AIF variation according to the ROI size in each group.

All image processing and analysis were performed using an in-house computer software package made of Labview (National Instruments Co., Austin, TX).

2.4 Statistical analysis

One-way ANOVA (analysis of variance) was utilized to compare the root mean square error (RMSE) of AIF from the best fitting curve before tracking motion of the aorta with that after tracking motion [25]. P values less than 0.05 were considered significant. All data were presented as mean ± standard deviation. Statistical analysis was conducted using SAS, version 9.4 (SAS Institute Inc., Cary, NC).

3 Results

Figure 2 shows the motion of the abdominal aorta during DCE-MRI. Figure 2a shows the boundary of the aortic region (ROI) of a representative patient, while its center position was varying for 187 seconds (89 time frames; 2.1 second per frame). The ROI center was initially located at (0, 0), and its radius was 9 mm. The mean radius of all 24 abdominal aortas was 9.06±1.25 mm. The color scale represents the overlay of the ROI boundaries. Figure 2b shows the trace of the center position of the aorta shown in Fig. 2a. Figure 2c shows two box plots of maximum and mean aorta displacements from the initial position, respectively, during DCE-MRI (n=24). The centerline within each box represents the median value, the top and bottom of the box show the interquartile data range, and the whiskers attached on the box show the entire data range. The mean displacement was 3.36±2.34 mm, while the minimum and maximum displacements were 0.70 mm and 10.79 mm, respectively.

Figure 2.

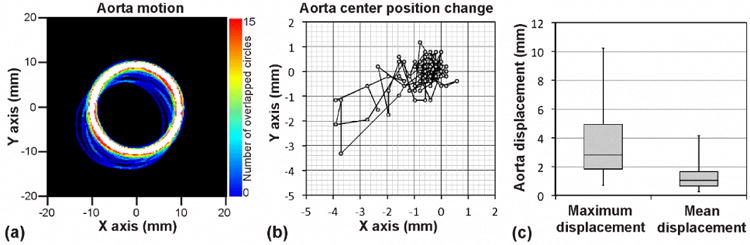
Motion of the abdominal aorta during DCE-MRI. (a) Abdominal aorta motion during 187 seconds of DCE-MRI (89 time frames) of a representative patient. Each circle represents the edge of the segmented aortic region at each time frame. Initial center position of the aorta was (0, 0), and its radius was 9 mm. Color scale represents the number of overlapped circles. (b) Trace of center position of the aorta shown in Fig. 2a. (c) Box plots of aorta maximum and mean displacements from the initial aortic position

Figure 3 shows an arterial input function (AIF) retrieved from a representative abdominal aorta before and after tracking the aorta motion together with the fitting curve. In Fig. 3, the root mean square error (RMSE) of the AIF from the fitting curve was 0.104 mM after tracking motion, whereas that before tracking motion was 0.130 mM. The mean RMSE was 0.110±0.010 mM (mean±SD; n=24) after tracking motion, which was significantly lower than that before tracking motion (0.134±0.016 mM) (p<0.001).

Figure 3.

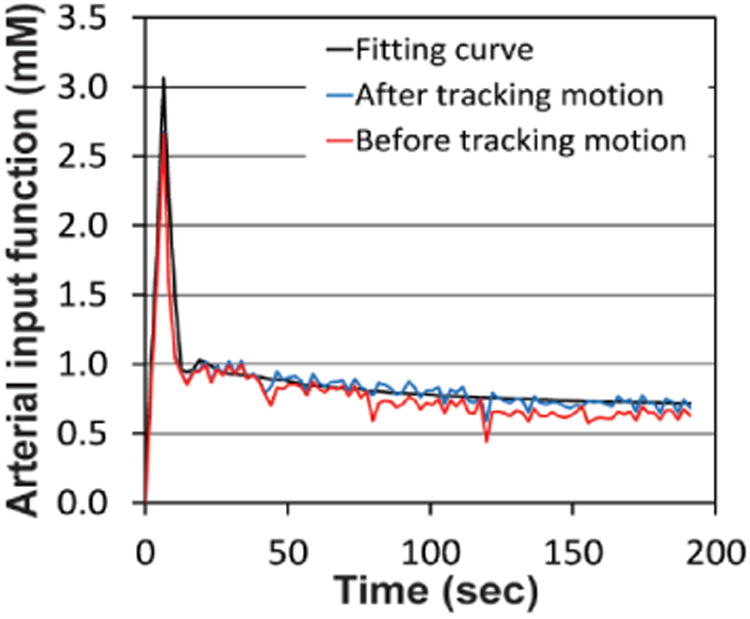
Arterial input function before (red) and after tracking motion (blue) with the fitting curve (black).

Figure 4 shows the variation in AIF according to the ROI size. Figure 4a shows the AIFs extracted from each of seven ROIs (original ROI plus six sub-ROIs) of a representative aortic image. The amplitude of AIF was lowest in the original ROI (ROI radius: 7 mm), but became higher when a smaller ROI was employed. Figure 4b shows the amplitude-normalized and temporal-mean AIFs of six groups. The amplitude of AIF in the original ROI was 10∼15% lower than that in the core ROI regardless of the groups. When a sub-ROI having 3-mm smaller radius than that of the original ROI was used, the AIF amplitude was less than 5% different from that in the core ROI regardless of the groups.

Figure 4.

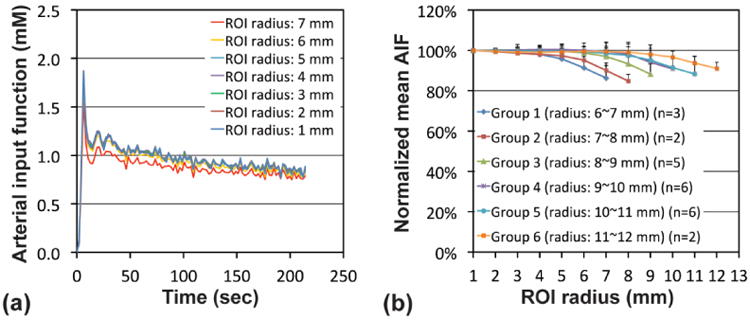
Arterial input function (AIF) according to the ROI size. (a) AIFs at seven ROIs (original ROI plus six sub-ROIs) of a representative aortic image. (b) The normalized mean AIFs of six groups; the amplitudes of AIFs were normalized to that in the core ROI (1 mm radius) and then averaged over imaging time. Abdominal aorta was categorized into six groups according to its radius (groups 1-6).

4 Discussion

A novel semiautomatic technique to segment the abdominal aorta was developed to extract the arterial input function (AIF). Unlike brain, breast or prostate imaging, a large aorta is seen in all axial image slices of the abdominal DCE-MRI, which enables us to calculate the time-dependent contrast concentration within the artery without suffering from partial volume effect [26]. The abdominal aorta moved about 3 mm during DCE-MRI in average, which was about 17% of its diameter, therefore the automatic segmentation of the ROI at each time frame tracking its motion would be important to enhance the accuracy in determining AIF. In this study, we demonstrated that the AIF accuracy was significantly increased after aorta motion tracking. We employed a repeated breath-hold method, but if a free breathing mode had been used, the aorta motion might have been more severe.

We also demonstrated that the amplitude of AIF varies up to 15% according to the ROI size within the aorta. However, the AIF variation was minimal, when the radius of ROI was reduced more than 3 mm. This represents that the AIF variation was mainly induced by partial volume effect at the aorta boundary. In this study, the original pixel size was 2.08 mm × 2.60 mm (FOV: 400 × 400 mm; frequency/phase encoding: 192×154), thus the signal reduction due to partial volume effect within the 3-mm outmost shell is reasonable. Therefore, the ROI size should be determined according to the pixel size; the larger the pixel size is, the smaller the ROI should be. In this study, the ROI having 3-mm smaller radius than that of the aorta yields a reliable AIF. But, the smaller the ROI is, the more the AIF will be vulnerable to noise.

The segmentation of the ROI was conducted using Otsu's method, an optimal thresholding technique. Several optimal thresholding techniques have been utilized including Otsu's method [23], maximum entropy thresholding [27], isodata method [28] and mixture modeling [29]. In this study, Otsu's method was empirically chosen based on the visual assessment. Optimal thresholding is to determine a global threshold to separate background and foreground pixels with minimal misclassification. However, since each technique employs a unique approach to estimate which pixels belong to background or foreground, the threshold is likely to change according to the technique even for the same image. Therefore the aortic boundary determined by optimal thresholding is just estimation, not the ground truth. Another concern is that the segmentation protocol in this study was established using images obtained from a single MR scanner. The threshold is determined by the mean signal difference between the foreground and the background, number of pixels belonging to each group, and signal-to-noise ratio (SNR). MRI signal and SNR are subject to change in relation to imaging sequence/parameters and magnetic field strength. Therefore the segmentation protocol in this study may not be optimal for images from other MR scanners that may use different imaging sequence and parameters. Thus the segmentation protocol may need to be revalidated using images obtained from multiple MR scanners.

Alternatively, an edge detection technique might be used to determine the aortic boundary. Various edge detection techniques have been utilized including Canny [30], Sobel [31] and Laplacian operators [32]. Edge detection is to determine the boundary of an object based on the rapid signal change near the boundary, and it is quite efficient in high SNR images. However, abdominal MR images are often distorted by motion artifact associated with respiratory and peristalsis, thus MRI artifacts and/or noise should be sufficiently suppressed prior to applying an edge detection technique for optimal performance.

5 Conclusions

We developed a semiautomatic technique to determine the AIF in breath-hold DCE-MRI of the abdomen. The error in determining AIF was significantly reduced by tracking the aorta motion. The variation in AIF was up to 15% according to the ROI size within the aortic region mainly due to partial volume effect. Therefore the smaller ROI than the aortic region should be used to retrieve a reliable AIF, while the ROI size will be determined according to the pixel size.