Reporting and methodological quality of survival analysis in articles published in Chinese oncology journals

Abstract

Survival analysis methods have gained widespread use in the filed of oncology. For achievement of reliable results, the methodological process and report quality is crucial. This review provides the first examination of methodological characteristics and reporting quality of survival analysis in articles published in leading Chinese oncology journals.

To examine methodological and reporting quality of survival analysis, to identify some common deficiencies, to desirable precautions in the analysis, and relate advice for authors, readers, and editors.

A total of 242 survival analysis articles were included to be evaluated from 1492 articles published in 4 leading Chinese oncology journals in 2013. Articles were evaluated according to 16 established items for proper use and reporting of survival analysis.

The application rates of Kaplan–Meier, life table, log-rank test, Breslow test, and Cox proportional hazards model (Cox model) were 91.74%, 3.72%, 78.51%, 0.41%, and 46.28%, respectively, no article used the parametric method for survival analysis. Multivariate Cox model was conducted in 112 articles (46.28%). Follow-up rates were mentioned in 155 articles (64.05%), of which 4 articles were under 80% and the lowest was 75.25%, 55 articles were100%. The report rates of all types of survival endpoint were lower than 10%. Eleven of 100 articles which reported a loss to follow-up had stated how to treat it in the analysis. One hundred thirty articles (53.72%) did not perform multivariate analysis. One hundred thirty-nine articles (57.44%) did not define the survival time. Violations and omissions of methodological guidelines included no mention of pertinent checks for proportional hazard assumption; no report of testing for interactions and collinearity between independent variables; no report of calculation method of sample size. Thirty-six articles (32.74%) reported the methods of independent variable selection. The above defects could make potentially inaccurate, misleading of the reported results, or difficult to interpret.

There are gaps in the conduct and reporting of survival analysis in studies published in Chinese oncology journals, severe deficiencies were noted. More endorsement by journals of the report guideline for survival analysis may improve articles quality, and the dissemination of reliable evidence to oncology clinicians. We recommend authors, readers, reviewers, and editors to consider survival analysis more carefully and cooperate more closely with statisticians and epidemiologists.

1. Introduction

As applications of survival analysis have gone rapidly and seen wide applications in clinical oncology in the last several decades,^[1] its correct application and presentation is critically relevant to the medical literature. As we have observed,^[2] survival analyses are used to investigate time-to-event outcomes which are common in medical research as they offer more information than simply whether or not an event occurred. Clinical outcomes come in a variety of statistical forms. If it is desired to estimate the proportion surviving by any time, Kaplan–Meier can be used.^[3] And if we wish to compare curves from different groups, the log-rank test can be used. While a life table accounts for survival times of censored observations both across and within fixed intervals, in many aspects the life table estimates approximate those generated from the Kaplan–Meier and the Nelson–Aalen approaches. In survival analysis, regression models are used for analyzing the causal linkage between an outcome lifetime variable (such as the hazard rate, the event time, or the survival function) and 1 or more independent variables, with 1 or more variables serving as controls. There are several popular families of parametric time distributions, including the exponential survival, Weibull, gamma, lognormal, log-logistic, and other distributions. In the year 1972, Cox et al^[4] masterfully developed a proportional hazard model, which derives robust, consistent, and efficient estimates of covariate effects using the proportional hazards assumption while leaving the baseline hazard rate unspecified. Since then, the Cox proportional hazard model, often simply referred to as the Cox model, has become the most widely applied regression perspective in survival analysis.

However, failure to conduct survival analysis appropriately, which is manifested, for example, violating or neglecting assumptions of PH for Cox model and preconditions, or ambiguous coding of variables, can potentially lead to inaccurate, misleading, or even erroneous conclusions; or render the conclusions difficult to interpret. As early as 1995, Altman et al^[5] first carried out a systematic review of the research articles published in clinical oncology journals that proposed the reporting quality problems of survival analysis in 5 cancer research journals, found that almost half of the articles did not give any summary of length of follow-up; that in 62% of articles at least 1 end point was not clearly defined; and that both log-rank test and multivariate analyses were frequently reported at most only as P values (63/84 (75%) and 22/47 (47%) respectively) in total 132 articles. Simone et al^[6] evaluated the reporting of survival end points in cancer randomized control trials in 8 medical journals, and found that 33 end points reported optimally of 10 publications in 125 selected articles. Hence, a majority of articles failed to provide a complete reporting of survival end points. Christophe et al^[7] support the need to standardize the selection, definition, and reporting of time-to-event end points in clinical trials. The following years, there are a large number of such articles emerged,^[8,9] but the reporting quality of survival analysis articles is uneven. In China, Xiuyue^[10] summarized problems of applications of survival analysis in a lecture paper.

So far, research on methodological and reporting quality evaluation of survival analysis in articles is rare worldwide, and has not been available in Chinese literature. Thus, we evaluated studies using survival analysis published in 4 leading Chinese oncology journals in 2013 according to 16 established items, hoping to provide reference for reasonable application of survival analysis and correct reporting of results for authors, reviewers, and journal editors.

2. Methods

2.1. Data collection

The 4 journals were selected due to their high Chinese journal citation reports impact factor (IF) and used more methods of survival analysis published in oncology journals of: Chinese Journal of Clinical Oncology (CJCO, IF = 0.338 of year 2013), Chinese Journal of Radiation Oncology (CJRO, IF = 0.803 of year 2013), Chinese Journal of Cancer Prevention and Treatment (CJCPT, IF = 0.774 of year 2013), and Chinese Journal of Oncology (CJO, IF = 0.960 of year 2013). We performed a manual search of all articles published in 2013. A total of 242 articles that contained survival analysis in the title, abstract, statistics analysis, or results, published in CJCO (91 articles), CJRO (36 articles), CJCPT (57 articles), CJO (58 articles) were included in the research.

2.2. Criteria for literature inclusion and exclusion

Criteria for literature inclusion: the title described in using survival analysis method; methodology section of abstract described in using survival analysis method; methodology section of text described in using survival analysis method.

Criteria for literature exclusion: review and conference abstract; introduction of survival analysis methodology; the object of study of the literature is animals.

2.3. Assessment items of reporting quality

With reference to related research,^{[2,5,10–13]} we applied 16 items to evaluate the quality of reporting of survival analysis in each articles. These items were (Table 1):

Table 1.

The items of evaluating the quality of reporting of survival analysis in articles published in 4 Chinese oncology journals in 2013.

2.3.1. Whether reported assumption of proportional hazard (assumption of PH) for Cox proportional hazards regression model (Cox model)

In the Cox model, in which the risk or “hazard” of an independent variable is assumed to be constantly proportional (the relative risk does not change with time). The problem can be illustrated by considering survival curves with a binary variable that identifies patients in groups A and B, representing 2 forms of treatment. If the hazard is proportional, the survival curve of 1 group will not cross the survival curve of the other group. If assumption of PH is met, a set of stratified log-log survival functions will be parallel. If the assumption of PH is violated for a given covariate, 1 popular approach is to stratify on this covariate, fitting a proportional hazard model for each stratified group, or by including time-dependent covariates.

2.3.2. Selection of independent variables for Cox model

Independent variable selection can seriously affect the model estimation. Therefore, it should be justified. Usually, variables are selected according to professional knowledge and previous studies, or statistically significant association in a univariate analysis.

2.3.3. Interactions of independent variables for Cox model

When the effect of an independent variable on the outcome variables can be affected by other variables, we have interactions among independent variables. This can conceal the true correlation between independent and dependent variables.^[14] Generally, their statistical significance and effect on the model must be tested and reported, according to professional knowledge or previous studies. Articles including explicit tests for interaction, mentioning the concept of interaction anywhere in the text, or justifying the exclusion of interaction from the final model were regarded as fulfilling the criterion.

2.3.4. Collinearity of independent variables for Cox model

Collinearity is high correlation between 2 or more covariates. Multicollinearity would occur if some covariates are partially or totally explained by other covariates. Collinearity is necessary to be checked before establishing Cox models, otherwise unreliable estimates of coefficients and wide confidence intervals (CIs) may appear. Methods for tackling the multicollinearity can be found in the textbook by Ziegel.^[15] However, collinearity is often ignored. The item was considered to be fulfilled as long as the concept of collinearity was discussed anywhere in article.

2.3.5. Whether multivariate analysis was performed

Univariate analysis as length of survival was examined with only 1 explanatory variable at a time, thus ignoring the effects of other variables simultaneously. And multivariate analysis was examined with at least 2 explanatory variables. We recorded the type of information presented to summarize the results.

2.3.7. Reporting survival endpoints (such as overall survival, disease-free survival, local control survival, etc., whether survival endpoints were defined)

Survival process describes the length of time measured from some specified starting time point to the occurrence of a life event. According to this specification, the measurement of an event time should start from a well-defined origin of time and ends at the time when a particular event of interest occurs. Surrogate time-to-event end points were defined as all time-to-event end points except overall survival and disease-specific survival.^[16] We recorded the number of time-to-event end points studied in each article and whether end points were reported clearly.

2.3.10. Reporting of follow-up information (such as end time of follow-up, mode of follow-up, the median of follow-up time, the mean of follow-up time, range of follow-up time, follow-up rate, and dealing with missing data)

Survival analysis must have sufficiently long follow-up durations to capture enough events to reveal meaningful patterns in the data. A short follow-up duration is appropriate for studying very severe cancers with poor prognoses, whereas a long follow-up duration is better suited to studying less-severe disease, or participants with good prognoses.^[17] We checked whether the terminal time of follow-up was reported and also whether the length of follow-up (such as a median) was given. We also recorded whether follow-up rates were reported and also whether articles reported if any studies were lost to follow-up and, if so, whether they reported how these were treated in the methods of articles.

2.3.11. Whether the sample size and the method of calculating sample size were reported

We kept a record of the quantity of subjects studied and the maximum and minimum quantity of events.

2.3.14. Whether the survival curves were drawn

We checked whether survival curves were drawn and also recorded whether annotated censored data in the analysis.

2.3.15. Reporting the application of statistics software

Reporting the statistics software application can help other researchers to reproduce and test the survival analysis.

2.3.16. Whether statisticians and epidemiologists were included in authors

Proper use of statistical methods combined with professional knowledge can avoid bias and reduce defects during statistical analysis and reporting procedures. Similar studies have indicated that inadequate reporting was less frequent if an author was affiliated with a department of statistics, epidemiology, or public health.^[18] Therefore, the participation of statisticians and epidemiologists is important for properly using and appropriately reporting survival analysis. There was participation of epidemiologist and statisticians in studies if 1 of authors was affiliated with a department of statistics, epidemiology or public health, and statisticians or epidemiologists were appreciated in the acknowledgments section of the article.

2.4. Statistical analysis

The items were evaluated by 2 authors and the disagreement was discussed for solution. The data were described with frequency, rate, and proportion. The comparison of rate and proportion among groups by χ² test. All calculations were operated in IBM SPSS Statistics 18.0 and P value <.05 was considered significant.

3. Results

3.1. The use of survival analysis in 1492 articles published in 4 Chinese oncology journals

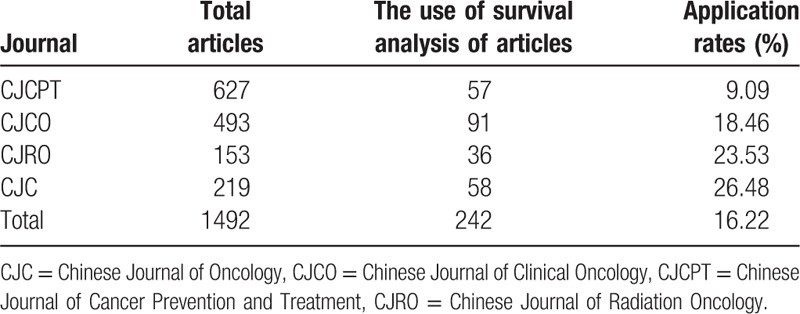
From January 2013 to December 2013, in 1492 articles, 242 (16.22%) ones used survival analysis. Among them, CJCPT has the lowest application rate, 9.09%, CJO has the highest application rate, 26.48%. Differences in application of survival analysis in 4 Chinese oncology journals have statistical significance (χ² = 48.26, P < .001) (Table 2).

Table 2.

The application of survival analysis in articles published in 4 Chinese oncology journals in 2013.

3.2. Cox proportional hazard regression model

Cox model was used in 112 articles, no paper reported the assumption of PH. All 112 articles reported significance probability, 87 articles reported RR (or HR), 36 articles reported the methods of independent variable selection (Table 3).

Table 3.

The status of the Cox model in articles published in 4 Chinese oncology journals in 2013.

Notes: PH, proportional hazard; RR, relative risk; HR, hazard ratio

3.3. Survival information

Seventy-four articles (30.6%) reported median survival time, 4 articles (1.7%) reported mean of survival time, 20 articles (8.3%) reported range of survival time, 78 articles (32.2%) reported median survival time among groups, 7 articles (2.9%) reported different mean survival times among groups, 8 articles (3.3%) reported different ranges of survival time among groups, 99 articles (40.9%) reported survival rates of different years, 109 articles (45.0%) reported different survival rates of different years among groups (Table 4).

Table 4.

The survival information in articles published in 4 Chinese oncology journals in 2013.

3.4. Methods of survival analysis applied in the articles

Twenty-two articles (91.74%) used Kaplan–Meier to calculate survival rates, 9 articles (3.72%) used life table to calculate survival rates, 190 articles (78.51%) use log-rank test and 1 article (0.41%) used Breslow test to make groups comparison, 112 articles (46.28%) used Cox model to make multivariate analysis. One hundred six articles (43.80%) made univariate analysis. One hundred ten articles (45.45%) made both univariate and multivariate analyses. Two articles (0.83%) did not make a univariate analysis, but made multivariate analysis. Twenty-four articles (9.92%) made neither univariate nor multivariate analysis (Table 5).

Table 5.

Methods of survival analysis applied in articles published in 4 Chinese oncology journals in 2013.

3.5. The types of survival time

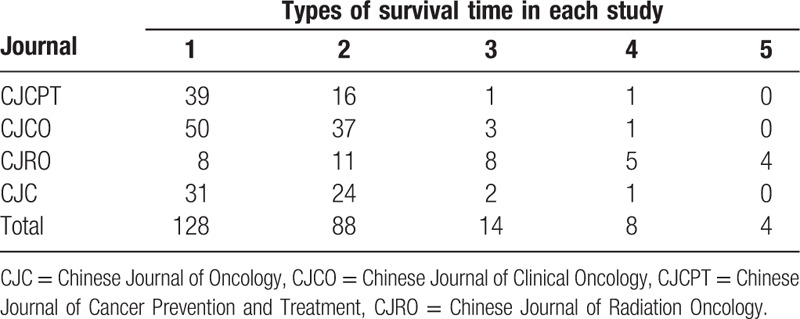
At the most of 5 types and at least 1 of survival time were reported in each article. One hundred twenty-eight articles (52.89%) reported 1 type of survival time. Eighty-eight articles (36.36%) reported 2 types of survival time. Four articles (1.65%) reported 5 types of survival time. A total of 396 end points and 10 different types of survival time were reported in 242 articles (Table 6).

Table 6.

The types of survival time reported in 242 articles.

The report rates of overall survival, progression-free survival, disease-free survival, and local control survival were 92.15%, 23.97%, 15.29%, and 10.33%, respectively. The report rates of all types of survival endpoint were lower than 10%. Among them, the event-free survival and postrelapse survival has the lowest reporting rate, all being only 0.41%. One hundred fifty-eight end points (39.90%) of 103 articles (42.56%) defined survival endpoint (Table 7).

Table 7.

Survival time used in the 242 survival analysis articles.

3.6. The information of follow-up

The report rates of end time of follow-up, mode of follow-up, and median of follow-up time were 71.90%, 53.30%, and 51.24%, respectively. Eleven ones (4.55%) reported mean of follow-up time. One hundred twenty-six articles (52.07%) reported range of follow-up time. Follow-up rates were mentioned in 155 articles (64.05%), of which 4 articles were under 80% and the lowest was 75.25%, 55 articles were100% (Table 8). Eleven of 100 articles which reported a loss to follow-up had stated how to treat it in the analysis.

Table 8.

Follow-up information in 242 articles.

3.7. Sample size

The smallest sample size is 6, while the largest sample size is 14,802. Sixty-two articles (25.21%) had sample size≤50, 6 articles (2.48%) had sample size > 1000, and 175 articles (72.31%) had sample size of 50–1000 (Table 9). No paper reported calculation method of sample size.

Table 9.

Distribution of sample size in 242 articles.

3.8. Drawing of survival curves

Sixty-four articles (67.8%) drew survival curves.

3.9. Application of statistics software for survival analysis

The most frequently used program is SPSS (91.32%), followed by STATA (2.07%) (Table 10).

Table 10.

The application of statistics software for survival analyses in 242 articles.

3.10. The cooperation with statisticians and epidemiologists

The authors of 5 articles (2.07%) included statistical professionals.

3.11. Interactions

No articles reported the item. The product term was included as an independent variable in all models to isolate the interaction and examine its impact.

3.12. Collinearity

No article reported collinearity among independent variables. BKW^[19] was used to assess the degree of collinearity.

3.13. Participation of statisticians and epidemiologists

Only 5 articles (2.07%) reported participation of statisticians and epidemiologists.

4. Discussion

Survival analysis is no replaceable for analysis of survival data, especially for those containing censored data. So far, survival analysis has formed a relatively perfect theory system. Hence, survival analysis should be enhanced and widely used. There are differences in application rates of survival analysis for the 4 journals in our study.

In our study, the method to calculate survival rate is mainly the Kaplan–Meier, and the minority was life table. Kaplan–Meier is both applicable to small sample materials and large sample materials, while the life table method is only applicable to large sample (n > 100) data.^[2,10,11] However, the sample size of 4 articles using the life table was less than 100. The study^[20] has only 22 cases, which may influence the reliability of results, it was advisable to use the Kaplan–Meier.

In comparison of multigroup survival data, only 1 study used the Breslow test, the others used the log-rank test. The 2 tests were distinct, the log-rank test emphasizes long-term effect, while the Breslow test concerned recent-effect relatively.^[21] The researchers can select the method according to the purpose of research, or use the 2 methods. When their results are the same, the long-term effect and recent effect can all be regarded as different. If log-rank test rejects H₀ while Breslow test does not reject H₀, this indicates long-term effect is different while recent effect is not different.

In survival analysis, the research on influencing factors of sufferers’ survival condition should consider influence of confounding and interaction of other factors rather than a certain factor. The model of multivariate analysis should be established to make further research on the medical problem. This research shows that 106 (43.8%) articles only used univariate analysis, and 24 (9.92%) articles did use neither univariate analysis nor multivariate analysis.

For the Cox model, the assumption of PH must be met, otherwise results may be led to severe bias, wrong inference, or lower power of a test.^[22,23] In the 112 studies using the Cox model, checks for PH assumption were not mentioned, it may be due to the lack of statistical knowledge, unskillful software application, or absence of guidelines for appropriate reporting and should be attached importance to authors, reviewers, and editors of journal. This item may have been violated in these papers, the accuracy of the estimates of risk is therefore uncertain. Some scholars have summarized the hypothetical test method and then put forward some methods, such as Schoenfeld residual plot method and score residual method.^[24–26] For Cox mdoel in the multiple factor analysis research, the report of interaction between independent variables is propitious to understand the results for readers.

Compared with semiparameter model, parameter model can utilize more data information, especially when sample size is limited. Compared with survival rate of nonparametric method, the survival rate of parametric calculation method considers influence of other correlative factors, leading to a more accurate result.^[27,28] In this research, 221 (91.3%) articles used SPSS (Statistical Product and Service Solutions) software for statistical analysis but none used parametric technique for familiar with SPSS but not familiar with SAS (Statistical Analysis System) or Stata (Statistical Software). While SURVIVAL menu of SPSS does not provide items for corresponding parameter regression, parameter regression analysis can be done using LIFEREG course of SAS.

In this research, 223 end points (56.4%) are about overall survival, similar to findings of Simone et al.^[6] However, relative to survival endpoint of other types, overall survival needs more sample size and follow-up visit time. The studies^[6,16] suggest that the definition of events has important influence on the results of the study. Different research does not have the same definition for survival endpoint, and a great deal of research does not only have 1 type of survival endpoint. Hence to clearly define survival endpoint is conductive to better understanding of research content and result by readers. 39.9% of end points define survival endpoint. Simone et al^[6] also indicated only 27% of end points define survival endpoint. Therefore, detailed definition of survival endpoint should arouse the attention of the scholars around the world.

For medical research, follow-up survey information is very important and should be elaborated.^[16] Only 55.7% report central tendency of follow-up time, and 11 articles use mean of follow-up survey time to represent central tendency of follow-up survey time. Generally, the follow-up survey time does not meet normal distribution, and the median of follow-up time in reporting is accurate. Ninety (31%) ones do not report the loss to follow-up, with reporting rate of follow-up survey rate being 64%. In this research, only 11 articles report treatment condition of loss to follow-up. Follow-up mode, the end time of follow-up survey, and dispersion tendency of follow-up survey time, etc., are very important information, while many articles fail to describe them.

In medical research, it is very important to estimate sample size, too large sample size can lead to wasting of resources, while too small sample size can lead to very low power of the test. So we should estimate the sample size in advance. The articles should describe the method of estimating sample size. There are no articles reporting estimation method of sample size. Considering the survival data at the same time survival outcome and survival endpoint, and survival endpoint may contain censored data, the distribution of survival endpoint and common statistical distribution are obviously different, so it is relatively complicated to estimate sample content.^[29] Many scholars put forward a great many methods of estimation method of sample size for survival analysis.^[30,31]

Censoring of survival data is also of important influence on research result. Too high rate of censor will be lower accuracy and effectiveness of analysis result of an analytical model, increasing risk of bias. Hence, the rates of censor should be reported in articles. The result shows no articles report the censoring rate, but many articles have the phenomenon of excessive rate of censoring. For example, the calculation shows the study done by Xuexia et al^[32] has censored rate up to 84%, severely influencing the results.

Undoubtedly, there are limitations in our study. We evaluated only articles from 4 leading journals. This is not likely to reflect conformance with the criteria comprehensively. Moreover, we cannot ensure whether certain data were missing due to actual failure to perform the corresponding test, or space limitations in the article.^[33] The authors might feel that it was unnecessary to perform these tests or had good reasons to make exemptions.^[34] Finally, a comparison study between Chinese and non-Chinese journals may be necessary to decide whether this is a global issue.

To sum up, there are some common deficiencies were noted about survival analysis articles in Chinese clinical oncology journals. The main reasons behind these deficiencies may be: lack of statistical expertise and software application ability; no availability of automatic option for complex analysis in current statistical software; inadequate training in statistical methods among medical researchers or medical professionals; and absence of guidelines for appropriate reporting. Moreover, researchers may occasionally be unwilling to perform complex statistical tests and collaborate with biostatisticians.

The reporting quality and reliability of survival analysis can be improved by editorial amendments, peer review, and a statistical review system.^[35,36] When survival analysis is inaccurately constructed and improperly reported, it is difficult for researchers and readers to understand the results, and reproduce the models for future research. Hence, we recommend authors, readers, reviewers, and editors to become more acquainted with the use and reporting of survival analysis. Journal editors should be more specific and proactive about the requirements for the publication of survival analysis and relax the word limit in the statistical analysis section. Moreover, journals develop statistical reporting guidelines concerning survival analysis and encourage researchers to collaborate with statisticians and epidemiologists to improve accuracy and the quality of reporting.