Abstract
Schapire and Singer’s improved version of AdaBoost for handling weak hypotheses with confidence rated predictions represents an important advance in the theory and practice of boosting. Its success results from a more efficient use of information in weak hypotheses during updating. Instead of simple binary voting a weak hypothesis is allowed to vote for or against a classification with a variable strength or confidence. The Pool Adjacent Violators (PAV) algorithm is a method for converting a score into a probability. We show how PAV may be applied to a weak hypothesis to yield a new weak hypothesis which is in a sense an ideal confidence rated prediction and that this leads to an optimal updating for AdaBoost. The result is a new algorithm which we term PAV-AdaBoost. We give several examples illustrating problems for which this new algorithm provides advantages in performance.
Keywords: boosting, isotonic regression, convergence, document classification, k nearest neighbors
1. Introduction
Boosting is a technique for improving learning by repeatedly refocusing a learner on those parts of the training data where it has not yet proved effective. Perhaps the most successful boosting algorithm is AdaBoost first introduced by Freund and Schapire (1997). Since its publication AdaBoost has been the focus of considerable study and in addition a large number of related boosting algorithms have been put forward for consideration (Aslam, 2000; Bennett, Demiriz, & Shawe-Taylor, 2000; Collins, Schapire, & Singer, 2002; Duffy & Helmbold, 1999, 2000; Friedman, Hastie, & Tibshirani, 2000; Mason, Bartlett, & Baxter, 2000; Meir, El-Yaniv, & Ben-David, 2000; Nock & Sebban, 2001; Ratsch, Mika, & Warmuth, 2001; Ratsch, Onoda, & Muller, 2001; Schapire & Singer, 1999)(see also http://www.boosting.org). Our interest in this paper is the form of AdaBoost using confidence-rated predictions introduced by Schapire and Singer (1999). For clarity we will refer to this form of AdaBoost as CR(confidence-rated)-AdaBoost as opposed to the binary form of AdaBoost originally introduced by Freund and Schapire (1997).
In the CR-AdaBoost setting a weak hypothesis not only votes for the category of a data point by the sign of the number it assigns to that data point, but it provides additional information in the magnitude of the number it assigns. CR-AdaBoost combines the confidence-rated weak hypotheses that are generated into a linear combination with constant coefficients to produce its final hypothesis. While this approach works well in many cases, it is not necessarily ideal. A particular weak hypothesis may erroneously invert the order of importance attached to two data points or if the order is not inverted it may still assign an importance that is not consistent between two data points. As a potential cure for such problems we here consider the Pool Adjacent Violators algorithm (Ayer et al., 1954; Hardle, 1991). This algorithm makes use of the ordering supplied by a weak hypothesis and produces the isotonic regression which in a sense is the ideal confidence-rated prediction consistent with the ordering imposed by the weak hypothesis. We show how this may be converted into a resulting weak hypothesis which produces optimal improvements at each step of what we term PAV-AdaBoost. Our algorithm is a type of real AdaBoost, as Friedman, Hastie, and Tibshirani (2000) use the general term, but their realization involves trees, while our development is in the direction of linearly ordered structures. Isotonic regression (PAV) could potentially play a role in other approaches to boosting provided the weak hypotheses generated have the appropriate monotonicity property. We chose CR-Adaboost because the confidence of a prediction h(x) is assumed to go up with its magnitude and this is exactly the condition where isotonic regression is appropriate.
In the most general setting PAV-AdaBoost may be applied exactly parallel to CR-AdaBoost. However, there are situations where one is limited to a certain fixed number of weak hypotheses. To deal with this case we propose a modified form of PAV-AdaBoost which repeatedly cycles through this finite set of weak hypotheses until no more improvement can be obtained. The result is a type of back-fitting algorithm, as studied by Buja, Hastie, and Tibshirani (1989) but the fitting is nonlinear and convergence does not follow from their results. For CR-AdaBoost with a fixed finite set of weak hypotheses, Collins, Schapire, and Singer (2002) have recently given a proof of convergence to the optimum under mild conditions. While our algorithm does not satisfy their hypotheses we are able to prove that it also converges to the optimum solution under general conditions.
The first part of this paper (Sections 2 and 3) deals with theoretical issues pertinent to defining the algorithm. Section 2 consists of an introduction to the PAV algorithm together with pseudocode for its efficient implementation. Section 3 recalls CR-AdaBoost (Schapire & Singer, 1999), describes how PAV is used with CR-AdaBoost to yield the PAV-AdaBoost algorithm, and proves several optimality results for PAV-AdaBoost. The second part of the paper (Sections 4 and 5) deals with the learning capacity and generalizability of the algorithm. Section 4 gives three different examples where PAV-AdaBoost is able to learn on training data more successfully than confidence-rated AdaBoost. In its full generality PAV-AdaBoost has infinite VC dimension as shown in an appendix. In Section 5 we show that an approximate form of PAV-AdaBoost has finite VC dimension and give error bounds for this form of PAV-AdaBoost. All the results in this paper are produced using the approximate form of PAV-AdaBoost. The final sections present examples of successful applications of PAV-AdaBoost. In Section 6 we consider a real data set and a simulated problem involving two multidimensional normal distributions. Both of these examples involve a fixed small set of weak hypotheses. For these examples we find PAV-AdaBoost outperforms CR-AdaBoost and compares favorably with several other classifiers tested on the same data. The example in Section 7 deals with a real life document classification problem. CR-AdaBoost applied to decision tree weak hypotheses has given perhaps the best overall document classification performance to date (Apte, Damerau, & Weiss, 1998; Carreras & Marquez, 2001). The method by which CR-AdaBoost (Schapire & Singer, 1999) deals with decision tree weak learners is already optimized so that PAV-AdaBoost in this case does not lead to anything new. However, there are examples of weak learners unrelated to decision trees and we consider two types for which PAV-AdaBoost is quite effective, but CR-AdaBoost performs poorly. Section 8 is a discussion of the practical limitations of PAV-AdaBoost.
2. Pool adjacent violators
Suppose the probability p(s) of an event is a monotonically non-decreasing function of some ordered parameter s. If we have data recording the presence or absence of that event at different values of s, the data will in general be probabilistic and noisy and the monotonic nature of p(s) may not be apparent. The Pool Adjacent Violators (PAV) Algorithm (Ayer et al., 1954; Hardle, 1991) is a simple and efficient algorithm to derive from the data that monotonically non-decreasing estimate of p(s) which assigns maximal likelihood to the data. The algorithm is conveniently applied to data of the form where si is a parameter value, ωi is the weight or importance of the data at i, and pi is the probability estimate of the data associated with i. We may assume that no value si is repeated in the set. If a value were repeated we simply replace all the points that have the given value si with a single new point that has the same value si, for which pi is the weighted average of the contributing points, and for which ωi is the sum of the weights for the contributing points. We may also assume the data is in order so that i < j ⇒ si < sj. Then the si, which serve only to order the data, may be ignored in our discussion.
We seek a set of probabilities such that
| (1) |
and
| (2) |
is a maximum. In other words we seek a maximal likelihood solution. If the sequence is a constant value q, then by elementary calculus it is easily shown that q is the weighted average of the p’s and this is the unique maximal likelihood solution. If the q’s are not constant, they in any case allow us to partition the set N into K nonempty subsets defined by a set of intervals on each of which q takes a different constant value. Then we must have
| (3) |
by the same elementary methods already mentioned. We will refer to these intervals as the pools and ask what properties characterize them. First, for any k, r(j) ≤ k ≤ t(j)
| (4) |
This must be true because if one of the ≥’s in inequality (4) could be replaced by < for some k, then the pool could be broken at the corresponding k into two pools for which the solutions as given by Eq. (3) would give a better fit (a higher likelihood) in Eq. (2). Let us call intervals that satisfy the condition (4) irreducible. The pools then are irreducible. They are not only irreducible, they are maximal among irreducible intervals. This follows from the fact that each successive pool from left to right has a greater weighted average and the irreducible nature of each pool.
It turns out the pools are uniquely characterized by being maximal irreducible intervals. This follows from the observation that the union of two overlapping irreducible intervals is again an irreducible interval. It remains to show that pools exist and how to find them. For this purpose suppose I and J are irreducible intervals. If the last integer of I plus one equals the first integer of J and if
| (5) |
we say that I and J are adjacent violators. Given such a pair of violators it is evident from condition (4), for each interval, and from condition (5) that the pair can be pooled (a union of the two) to obtain a larger irreducible set. This is the origin of the PAV algorithm. One begins with all sets consisting of single integers (degenerate intervals) from 0 to N − 1. All such sets are irreducible by default. Adjacent violators are then pooled until this process of pooling is no longer applicable. The end result is a partition of the space into pools which provides the solution (3) to the order constrained maximization problems (1) and (2).
As an illustration of irreducible sets and pooling to obtain them consider the set of points:
One pass through this set of points identifies two pairs {p1, p2} and {p4, p5} as adjacent violators. When these are pooled they result in single points of weight 2 with the values and , respectively. A second pass through the resulting set of four points shows that {p1, p2} and p3 are now adjacent violators. These may be pooled to produce the pool {p1, p2, p3} and the value . Examination shows that there are no further violations so that the irreducible pools are {p0}, {p1, p2, p3}, and {p4, p5}.
In order to obtain an efficient implementation of PAV one must use some care in how the pooling of violators is done. A scheme we use is to keep two arrays of pointers of length N. An array of forward pointers, F, keeps at the beginning of each irreducible interval the position of the beginning of the next interval (or N). Likewise an array of backward pointers, B, keeps at the beginning of each interval the position of the beginning of the previous interval (or −1). Pseudocode for the algorithm follows.
2.1. PAV algorithm
| #Initialization |
| A. Set F[k] ← k + 1 and B[k] ← k − 1, 0 ≤ k < N. |
| B. Set up two (FIFO) queues, Q1 and Q2, and put all the numbers, 0, …, N − 1, in order into Q1 while Q2 remains empty. |
| C. Define a marker variable m and a flag. |
| #Processing |
| While (Q1 nonempty){ |
| Set m ← 0. |
| While (Q1 nonempty){ |
| k ← dequeue Q1. |
| If(m ≤ k){ |
| Set flag ← 0. |
| While (F[k] ≠ N and intervals at k and F[k] are adjacent violators){ |
| Pool intervals beginning at k and F[k]. |
| Set u ← F[F[k]]. |
| Redefine F[k] ← u. |
| If (u < N) redefine B[u] ← k. |
| Update m ← u. |
| Update flag ← 1. |
| } |
| } |
| If (flag = 1 and B[k] ≥ 0) enqueue B[k] in Q2. |
| } |
| Interchange Q1 and Q2. |
| } |
This is an efficient algorithm because after the initial filling of Q1 an element is added to Q2 only if a pooling took place. Thus in a single invocation of the algorithm a total of no more than N elements can ever be added to Q2 and this in turn limits the number of tests for violators to at most 2N. We may conclude that both the space and time complexity of PAV are O(N). See also Pardalos and Xue (1999).
PAV produces as its output the pools described above and these define the solution as in Eq. (3). It will be convenient to define p(si) = qi, i = 1, …, N and we will generally refer to the function p.
A simple example of the type of data to which the algorithm may be applied is a Bernoulli process for which the probability of success is a monotonic function of some parameter. Data generated by such a process could take the form of tuples such as (s, 3, 2/3). Here the parameter value is s and at this value there were 3 trials and 2 of these were a success. PAV applied to such data will give us a prediction for the probability of success as a function of the parameter. The PAV algorithm may be applied to any totally ordered data set and assigns a probability estimate to those parameter values that actually occur in the data set. For our applications it will be important to interpolate and extrapolate from these assigned values to obtain an estimated probability for any parameter value. We do this in perhaps the simplest possible way based on the values of p just defined on the points .
2.2. Interpolated PAV
Given the function p defined on the set , assume that the points come from a totally ordered space, S, and are listed in increasing order. Then for any s ∈ S define p(s) by
Case 1. If s = si, set p(s) = p(si).
Case 2. If s < s1, set p(s) = p(s1).
Case 3. If si < s < si+1, set .
Case 4. If sN < s, set p(s) = p(sN).
While one could desire a smoother interpolation, 2.2 is general and proves adequate for our purposes. In cases where data is sparse and the parameter s belongs to the real numbers, one might replace Case 3 by a linear interpolation. However, there is no optimal solution to the interpolation problem without further assumptions. The definition given has proved adequate for our applications and the examples given in this paper.
PAV allows us to learn a functional relationship between a parameter and the probability of an event. The interpolation 2.2 simply lets us generalize and apply this learning to new parameter values not seen in the training data.
3. AdaBoost
The AdaBoost algorithm was first put forward by Freund and Schapire (1997) but improvements were made in Schapire and Singer (1999). We first review important aspects of CR-AdaBoost as detailed in Schapire and Singer (1999), and then describe how PAV is used with AdaBoost. The AdaBoost algorithm as given in Schapire and Singer (1999) follows.
3.1. AdaBoost algorithm
Given training data with xi ∈ X and yi ∈ {1, −1}, initialize D1(i) = 1/m. Then for t = 1, …, T:
Train weak learner using distribution Dt.
Get weak hypothesis ht: X → ℝ.
Choose αt ∈ ℝ.
-
Update:where
(6) Output the final hypothesis:(7) Schapire and Singer establish an error bound on the final hypothesis.
Theorem 1
The training error of H satisfies:
| (8) |
From inequality (8) it is evident that one would like to minimize the value of Zt at each stage of AdaBoost. Schapire and Singer suggest two basic approaches to accomplish this. The first approach is a straightforward minimization of the right side of Eq. (6) by setting the derivative with respect to αt to zero and solving for αt. They observe that in all interesting cases there is a unique solution which corresponds to a minimum and may be found by numerical methods. We shall refer to this as the linear form of AdaBoost because it yields the sum
| (9) |
which is a linear combination of the weak hypotheses.
The second approach to optimization presented in Schapire and Singer (1999) is applicable to the special case when the weak learner produces a partition of the training space into mutually disjoint nonempty sets . Here α is absorbed into h, h is assumed to be a constant cj on each set Xj, and one asks how to define the cj in order to minimize Z in Eq. (6). Let us define a measure μ on all subsets of X by
Then we may set
| (10) |
The solution (Schapire & Singer, 1999) is then given by
| (11) |
and we may write
| (12) |
provided we define
3.2. PAV-AdaBoost algorithm
The AdaBoost Algorithm 3.1 is modified from step (iii) on. The weak hypothesis coming from step (ii) is assumed to represent a parameter so that si = ht (xi). Each data point (xi, yi) may thus be transformed to a tuple
| (13) |
PAV is applied to this set of tuples to produce the function pt (s). With the use of pt (s) we can define another function
| (14) |
Clearly this function is monotonic non-decreasing because pt (s) is. There is one difference, namely, kt (s) may assume infinite values. Through the formula (11) this leads to the replacement of Eq. (9) by
| (15) |
and Eq. (12) becomes
| (16) |
where μ(s) is the measure induced on ht [X] by μ through ht. Based on Eq. (16) and the inequality
we may obtain the bound
Further we have the following theorem.
Theorem 2
Among all monotonic non-decreasing functions defined on ht [X], kt is that function which when composed with ht produces the weak hypothesis with minimum Zt.
Proof
By its construction pt (s) partitions the set ht [X] into a family of subsets on each of which pt, and hence kt, is a constant. For each j set . Then referring to the defining relations (10) we see that the function achieves its unique minimum when c is the constant value of kt on Sj. Now let g be a monotonic non-decreasing function that when composed with ht produces the minimum Zt. We first claim that g is constant on each set Sj. Suppose that g is not constant on some Sj and let the minimal value of g be c′ and maximal value of g be c″ on Sj. Let S′ and S″ be those subsets of Sj that map to c′ and c″, respectively, under g. Then in turn set and and define , etc., in the obvious way as in Eq. (10). Then we have the inequality
| (17) |
which follows from the constancy of pt on Sj (see inequality (4) above). Now suppose c′ is less than the constant value of kt on Sj. Then because the function is convex with a strictly positive second derivative it decreases in value in moving c from c′ to the value of kt as a consequence of inequality (17). Thus we can decrease the value of Zt arising from g by increasing c′ to the next greater value of g or to kt whichever comes first. This contradicts the optimality of g. We conclude that c′ cannot be less then the value of kt on Sj. Then c″ must be greater than the constant value of kt on Sj. But the dual argument to that just given shows that this is also impossible. We are forced to the conclusion that g must be a constant on Sj. Now if g were not equal to kt on Sj, we could decrease the value of Zt arising from g by changing its value on Sj to that of kt, which we know is optimal. This may cause g to no longer be monotonic non-decreasing. However if we make this change for all Sj the result is kt, which is monotonic non-decreasing. The only conclusion then is that kt is optimal.
There are practical issues that arise in applying PAV-AdaBoost. First, we find it useful to bound pt away from 0 and 1 by ε. We generally take ε to be the reciprocal of the size of the training set. This is the value used in Schapire and Singer (1999) for “smoothing” and has the same purpose. If we assume that 0 < ε < 1/2 and define λ = ln[(1 − ε)/ε], then this approach is equivalent to truncating kt at size λ. Define
| (18) |
Based on the proof of Theorem 2 we have the following corollary.
Corollary 1
Among all monotonic non-decreasing functions defined on ht [X] and bounded by λ, kλt is that function which when composed with ht produces the weak hypothesis with minimum Zt.
Proof
Theorem 2 tells us that among monotonic non-decreasing functions, kt is that function that minimizes Zt. Let W be a pool of points from ht [X] on which kt takes the constant value β(>λ). We already know that β minimizes the function
| (19) |
Because this function has a strictly positive second derivative and achieves its minimum at β the value that minimizes it within [−λ, λ] is λ. A similar argument applies if β < −λ. Thus kλt must be that function which is monotonic non-decreasing and constant on each pool and minimizes Zt. The only question that remains is whether there could be a monotonic non-decreasing function bounded by [−λ, λ] but not constant on the pools and which yields a smaller Zt. That this cannot be so follows by the same argument used in the proof of the Theorem.
In some applications we apply the weak learner just as outlined above. This seems appropriate when there is an unlimited supply of weak hypotheses ht produced by the weak learner. Just as for standard AdaBoost we try to choose a near optimal weak hypothesis on each round. In other applications we are limited to a fixed set of weak hypotheses. In this case we seek a set of monotonic non-decreasing functions bounded by λ that minimize the expression
| (20) |
Because each kλj in expression (20) acts on only the finite set hj [X] and the result is bounded in the interval [−λ, λ], compactness arguments show that at least one set must exist which achieves the minimum in (20). We propose the following algorithm to achieve this minimum.
3.3. PAV-AdaBoost.finite algorithm
Assume a fixed set of weak hypotheses and a positive real value λ. For any set of monotonic non-decreasing functions bounded by λ and where each kλj is defined on hj [X] define
| (21) |
To begin let each kλj be equal to the 0 function on hj [X]. Then one round of updating will consist of updating each kλj, 1 ≤ j ≤ n, in turn (not in parallel) according to the following steps:
-
Define
(22) where(23) Apply the PAV algorithm as described under 3.2 and Corollary 1 to produce the optimal kλj which . Replace the old by the new kλj.
At each update step in this algorithm either kλj is unchanged or it changes and the sum in (20) decreases. Repetition of the algorithm converges to the minimum for expression (20).
Theorem 3
Let denote the functions produced on the tth round of Algorithm 3.3. Let denote any set of functions that produces the minimum in expression (20). Then we have
| (24) |
pointwise on X.
Proof
Clearly for the update procedure of Algorithm 3.3 can produce no change. Let denote the result of (21) applied to , where t denotes the result of the tth round. By compactness we may choose a subsequence {t(r)} for which each converges pointwise to a function kλj. For this set of functions let { } denote the values defined by Eq. (21). We claim that the set is invariant under the update procedure of the algorithm. If not suppose that the update procedure applied to this set of functions produces an improvement when kλj′ is updated and decreases the sum (20) by an ε > 0. Then because the update procedure is a continuous process, there exists an integer M > 0 such that when r > M the update procedure applied in the t(r) + 1th round to must produce an improvement in the sum (20) by at least ε/2. However, the sums converge downward to so that we may choose an N >for which r > N implies
| (25) |
It follows then that
| (26) |
But this latter relation contradicts the fact that the sum must be a lower bound for any such sum produced by the algorithm because of the monotonically decreasing nature of these sums in successive steps in the algorithm. We thus conclude that must indeed be invariant under the algorithm’s update procedure.
The next step is to show that an invariant set under the algorithm’s update procedure defines a unique function on X. For any α, 0 ≤ α ≤ 1, consider the set of functions . This is again a set of monotonic functions to be considered in taking the minimum of expression (20). Define
| (27) |
By assumption F(1) is the true minimum of (20) while . Let us suppose that F(1) < F(0). Because e−x is a convex function it follows that F is also and we have
| (28) |
From this relation it follows that
| (29) |
Now define
| (30) |
and note that with αj = α, 1 ≤ j ≤ n, we have
| (31) |
It then follows that
| (32) |
Then some one of the partials of G in Eq. (32) must be negative, say the one corresponding to j′. But then the nature of the derivative ensures that for some α > 0
| (33) |
This, however, contradicts the invariance of the set under the update procedure applied at j′. We are forced to the conclusion that F(0) = F(1). Now suppose there were an i with
| (34) |
Then because e−x is strictly convex we would have for any α, 0 < α < 1, the relation
| (35) |
But this contradicts the minimality of F(1). We conclude that inequality (34) does not occur. At this point we have shown that
| (36) |
where the convergence is pointwise on X. It now follows easily that convergence holds as in Eq. (36) not just for the subsequence , but also for the original sequence. If not we could choose a subsequence of the original sequence that for some particular xi converged to a value other than . By compactness we could then choose a subsequence of this subsequence to take the place of in the above arguments. The end result must then be a contradiction because inequality (34) must be true in this case. This establishes the convergence stated in Eq. (24).
For evaluation purposes we generally work with f(x) as defined in Eq. (15) rather than H(x) = sign(f (x)). In this way we not only use confidence-rated predictions as input, but produce a confidence-rated prediction as output. We believe this allows for a more sensitive analysis of performance. The function f(x) is used as a ranking function. This allows measures such as recall and precision to be applied. If there are a total of A items with label +1 and if among the r top scoring items there are a that have label +1, then the precision and recall at rank r are calculated as
| (37) |
Both precision and recall vary between 0 and 1, but not all values are taken for any given data set. This has led to the concept of an interpolated precision corresponding to a prescribed recall level. If R is any number between 0 and 1 the interpolated precision at recall level R is defined
| (38) |
The 11-point average precision (Witten, Moffat, & Well, 1999) is defined as the average of IPR over the eleven R values 0, 0.1, 0.2, …, 0.9, 1.0. In all the results that we will report here we have applied the 11-point average precision as a summary statistic by which to judge performance. There is one minor problem. The score is used to rank but in some cases the same score is repeated for a number of ranks. In that case the score does not completely determine the rank. Our approach is to divide the total number of objects labeled +1 in those ranks by the number of ranks and consider this quotient as the precision at each of the ranks. For example if three objects labeled +1 occur over ten ranks with the same score we consider that 0.3 objects labeled +1 occur at each of the ten ranks. Finally, training gives explicit values for pt on the set ht [X]. We use the interpolation of 2.2 to extend pt (and hence kt) to new values. In this way the hypothesis f(x) is defined over the entire space.
4. The PAV training advantage
From Theorem 2 we can expect that PAV-AdaBoost enjoys a training advantage over linear AdaBoost. This is not just an advantage in the speed with which PAV-AdaBoost learns but also in an absolute sense. PAV-AdaBoost can learn things (about the training set) that linear AdaBoost cannot learn at all. The purpose of this section is to give simple examples illustrating this fact. Because we are not concerned here with the generalizability of learning, but rather with what can be learned about the training set, we will not need to consider a test space separate from the training space. The examples will involve a training space and we will examine the performance on the training space.
One setting in which we find boosting useful is to combine several different scorings in an attempt to produce a scoring superior to any one of them. Suppose we are given a labeled training set X and a set of scoring functions where each scoring function tends to associate higher scores with the +1 label. Then we can apply the PAV-AdaBoost.finite algorithm, 3.3, to combine the scores to produce a final output score f as defined in Eq. (15). Whether this is successful will depend on the scores , but we may expect some success if they come from different sources or express different aspects of the data that are important for distinguishing the two classes. For comparison purposes we also optimize linear AdaBoost by repeated application of the algorithm to the same limited set of scores (weak hypotheses) until convergence. In the case of linear AdaBoost convergence is assured by a slight modification of the proof of Theorem 3 or by Collins, Schapire, and Singer (2002). We find there are many examples where PAV-AdaBoost is successful but linear AdaBoost is not.
4.1. Example
We assume that the training space X consists of four mutually disjoint subsets A, B, C, and D each of which contains 100 objects. Table 1 gives the details. If we assume a scoring function will take a constant value on each of the subsets, then the best possible scoring function will order the sets in increasing order as they appear in the first row of the table. For such a scoring function the precision (11-point average) will be 0.860. When PAV-AdaBoost.finite is applied to this example in one round (processing s1 and s2 in turn) it produces an f giving this ideal order and a precision of 0.860. However, linear AdaBoost produces a precision of 0.823. In fact it is clear that linear AdaBoost can never give the ideal ordering because in α1s1 + α2s2, we must have α1 > α2 in order to score points in D above points in C, but then points in A will necessarily score above points in B unless both α’s are negative. But if both α’s are negative, then B points will score above D points.
Table 1.
Training set X = A ∪ B ∪ C ∪ D. Two scoring functions are defined, but no linear combination of them can order the sets in the order of the probability of +1 labels.
| Subset | A | B | C | D |
|---|---|---|---|---|
| +1 labels | 1 | 50 | 51 | 99 |
| Score s1 | s1 = 3 | s1 = 1 | s1 = 4 | s1 = 5 |
| Score s2 | s2 = 1 | s2 = 2 | s2 = 4 | s2 = 3 |
4.2. Example
Here we use a training set X similar to that used in the previous example composed of four mutually disjoint subsets A, B, C, and D each of which contains 100 objects. The details are given in Table 2. The ideal order for this space is D at the top followed by B and C in either order and lowest A. This order is produced in one round by PAV-AdaBoost.finite with a precision of 0.698. When linear AdaBoost is applied the α’s produced are zero leading to a random performance with a precision of 0.300.
Table 2.
Training set X = A ∪ B ∪ C ∪ D. Two scoring functions are defined, and a linear combination of them can produce the ideal order of the probability of +1 labels.
| Subset | A | B | C | D |
|---|---|---|---|---|
| +1 labels | 0 | 20 | 20 | 80 |
| Score s1 | s1= 0 | s1= 1 | s1 = 0 | s1 = 1 |
| Score s2 | s2= 0 | s2= 0 | s2 = 1 | s2 = 1 |
4.3. Example
Here we consider a more conventional problem, namely, boosting naïve Bayes’. We use the binary or multivariate form as our weak learner, though superior performance has been claimed for the multinomial form of naïve Bayes’ (McCallum & Nigam, 1998). We find the binary form more convenient to use for simulated data as one need not assign a frequency to a feature in a document, but simply whether the feature occurs. Our goal is not the best absolute performance, but rather to compare different approaches to boosting. For simplicity we will consider a document set that involves only three words. We assume any document has at least one word in it. Then there are seven kinds of documents: {x, y, z}, {x, y}, {x, z}, {y, z}, {x}, {y}, {z}. We assume that the training space X consists of 700 documents, 100 identical documents of each of these types. To complete the construction of the training space we randomly sample a number from a uniform distribution on the 101 numbers from 0 to 100 inclusive and assign the +1 label that many times. This is repeated for each of the seven document types to produce the labeling on all of X. Such a random assignment of labels may be repeated to obtain as many different versions of X as desired. We repeated this process 1000 times and learned on each of these spaces with several different algorithms and the results in summary are given in Table 3. The different methods of learning examined are naïve Bayes’, PAV-AdaBoost, and linear AdaBoost with naïve Bayes’ as weak learner, and lastly stump AdaBoost. Stump AdaBoost is boosting with decision trees of depth 1 as weak learner (Carreras & Marquez, 2001; Schapire & Singer, 1999). We included stump AdaBoost because it, along with Bayes’ and linear AdaBoost, is a linear classifier which produces a weighting of the individual features. On the other hand PAV-AdaBoost is nonlinear. The ideal category in the table is the result if document groups are ordered by the probability of the +1 label. The random category is the precision produced by dividing the total number of +1 labels by 700. Examination of the data shows that all the classifiers perform well above random. While PAV-AdaBoost seldom reaches the ideal limit, in the large majority of training spaces it does outperform the other classifiers. However, one cannot make any hard and fast rules, because each classifier outperforms every other classifier on at least some of the spaces generated.
Table 3.
Performance comparisons between different classification methods on 1000 simulated training spaces. The second column gives the average over all training spaces of the 11-point average precision for each of the different methods. The counts listed in a given row and column give the number of training spaces on which the performance of the method listed on that row outperformed/equaled/fell below the method listed at the top of that column.
| 11-pap | PAV-Ada | LinAda | StmpAda | Bayes’ | |
|---|---|---|---|---|---|
| Ideal | 0.7721 | 962/38/0 | 993/7/0 | 990/10/0 | 993/7/0 |
| PavAda | 0.7321 | 949/41/10 | 885/37/78 | 954/44/2 | |
| LinAda | 0.7053 | 10/41/949 | 220/534/246 | 67/901/32 | |
| StmpAda | 0.7047 | 78/37/885 | 246/534/220 | 284/494/222 | |
| Bayes’ | 0.7042 | 2/44/954 | 32/901/67 | 222/494/284 | |
| Random | 0.5039 | 0/0/1000 | 0/0/1000 | 0/0/1000 | 0/0/1000 |
5. The learning capacity and generalizability of PAV-AdaBoost
The previous examples suggest that PAV-AdaBoost is a more powerful learner than linear AdaBoost and the question naturally arises as to the capacity of PAV-AdaBoost and whether PAV-AdaBoost allows effective generalization. First, it is important to note that the capacity of the individual hypothesis h(x) to shatter a set of points is never increased by the transformation to k(h(x)) where k comes from the isotonic regression of +1 labels on h(x). If h cannot distinguish points, then neither can h composed with a monotonic non-decreasing function. However, what is true of the output of a single weak learner is not necessarily true of the PAV-AdaBoost algorithm. In the appendix we show that the hypothesis space generated by PAV-AdaBoost.finite, based on the PAV algorithm defined in 2.1 and the interpolation 2.2, has in many important cases infinite VC dimension. For convenience we will refer to this as the pure form of PAV-AdaBoost. In the remainder of this section we will give what we will refer to as the approximate form of PAV-AdaBoost. This approximate form produces a hypothesis space of bounded VC dimension and allows a corresponding risk analysis, while yet allowing one to come arbitrarily close to the pure PAV-AdaBoost.
Our approximation is based on a finite set of intervals for each t, which partition the real line into disjoint subsets. For convenience we assume these intervals are arranged in order negative to positive along the real line by the indexing j. The Bt will be used to approximate the pt(s)(defined earlier by 2.1 and 2.2) corresponding to a weak hypothesis ht. For each t the set Bt is assumed to be predetermined independent of what sample may be under consideration. Generally in applications there is enough information available to choose Bt intelligently and to obtain reasonable approximations. Assuming such a predetermined , then given define
| (39) |
The result is a new set of hypotheses, , that approximate . We simply apply the PAV-AdaBoost algorithms to this approximating set. The theorems of Section 3 apply equally to this approximation. In addition we can derive bounds on the risk or expected testing error for the binary classification problem. First we have a bound on the VC dimension of the hypothesis space.
Theorem 4
Let denote the set of partitions to be applied to T hypotheses defined on a space X as just described. Let ℋ denote the set of all hypotheses defined on X where varies over all sets of monotonically nondecreasing functions whose ranges are within [−λ, λ]. Then the VC dimension of ℋ satisfies
| (40) |
Proof
Define sets
| (41) |
Note that these sets partition the space X and that any function of the form is constant on each such set. Then it is straightforward for the family of all such functions H(x) that we have the stated bound for the VC dimension.
Vapnik (1998), p. 161, gives the following relationship between expected testing error (R) and empirical testing error (Remp).
| (42) |
which holds with probability at least 1 − η, where E(N) depends on the capacity of the set of functions and involves η and the sample size N.
Corollary 2
Let denote the set of partitions to be applied to T hypotheses. If S is any random sample of points from X of size and η > 0 and if represents T rounds of PAV-AdaBoost learning or the result of AdaBoost.finite applied to S, then with probability at least 1 − η the risk (R) or expected test error of H satisfies inequality
| (43) |
where
| (44) |
and
| (45) |
in the case of PAV-AdaBoost or equivalently
| (46) |
in the case of PAV-AdaBoost.finite.
Proof
First note that relation (42) can be put in the form (43) by a simple algebraic rearrangement where E(N) corresponds to E′ and Remp corresponds to R′. It is evident that the right side of (43) is an increasing function of both E′ and R′ when these are nonnegative quantities. Vapnik (1998), p. 161, gives the relationship
| (47) |
The relation (43) then follows from inequality (40) and the bound on N, which insures that E(N) ≤ E′ and the fact that Remp ≤ R′. The latter is true because relations (45) and (46) are simply different expressions for the same bound on the training error (empirical error) for PAV-AdaBoost, but only the second is defined for PAV-AdaBoost.finite.
In practice we use approximate PAV-AdaBoost with a fine partitioning in an attempt to minimize R′. This does not benefit E′ but we generally find the results quite satisfactory. Two factors may help explain this. First, when the PAV algorithm is applied pooling may take place and effectively make the number of elements in a partition Bt smaller than nt. Second, bounds of the form (43) are based on the VC dimension and ignore any specific information regarding the particular distribution defining a problem. Thus tighter bounds are likely to hold even though we do not know how to establish them in a particular case (Vapnik, 1998). This is consistent with (Burges, 1999; Friedman, Hastie, & Tibshirani, 2000) where it is pointed out that in many cases bounds based on the VC dimension are too loose to have practical value and performance is much better than the bounds would suggest. However, we note that even when N is not extremely large, E′ can be quite small when T is small. Thus the relation (43) may yield error bounds of some interest when PAV-AdaBoost.finite is used to combine only two or three hypotheses.
6. Combining scores
We have applied PAV-AdaBoost to the real task of identifying those terms (phrases) in text that would not make useful references as subject identifiers. This work is part of the electronic textbook project at the National Center for Biotechnology Information (NCBI). Textbook material is processed and phrases extracted as index terms. Special processing is done to try to ensure that these phrases are grammatically well formed. Then the phrases must be evaluated to decide whether they are sufficiently subject specific to make useful reference indicators. Examples of phrases considered useful as index terms are muscles, adenosine, beta2 receptors, cerebral cortex, fibroblasts, and vaccine. Examples of terms considered too nonspecific are concurrent, brown, dilute, worsening, suggestive, cent, and roof. The specific terms are used to index the text in which they occur. If a PubMed® user is looking at a MEDLINE® record and wishes more information about the subject of the record he can click a button that marks up the record with hotlinks consisting of all those specific phrases that occur in the text and also occur as index terms to book sections. If he follows one of these links he will be allowed to choose from, usually several, textbook sections that are indexed by the selected term. By following such links he may gain useful information about the subject of the PubMed record.
In order to study the problem of identifying those terms that are not useful as subject indicators or reference markers, we randomly selected 1000 PubMed records and had two judges with biological expertise examine each marked up record. The judges worked independently and selected any terms that they considered unsuitable for reference and marked them so. This resulted in two sets of judgments which we will refer to as A and B. The number of terms judged totaled 11,721. Independently of the work of these judges we produced several different scorings of the same set of terms. These scorings are detailed in Table 4. The methods for calculating the strength of context and database comparison scores are described in Kim and Wilbur (2001).
Table 4.
Performance of individual scoring methods designed to provide information on a terms usefulness as a reference link to textbook material. The random entry at the bottom simply shows the proportion of terms marked as not useful by the two judges.
| Scoring method | 11-pap, A | 11-pap, B |
|---|---|---|
| s1 =-strength of context | 0.4737 | 0.2918 |
| s2 =-database comparison | 0.4198 | 0.2505 |
| s3 =-number of words | 0.2240 | 0.1373 |
| s4 =-number of letters | 0.2548 | 0.1500 |
| s5 = ambiguity | 0.2884 | 0.1907 |
| s6 = -coherence | 0.2932 | 0.1882 |
| random | 0.2031 | 0.1272 |
Briefly the more context is associated with a term the more likely that term is useful in representing the subject. The minus sign is because we are trying to identify the terms that are not useful. The database comparison score comes from comparing the frequency of a term in MEDLINE with its occurrence in a database not focused on medicine. If the term is seen much more frequently in a medical database it is more likely to be useful. Again the sign is switched because of our negative purpose. Terms with more words or more letters tend to be more specific and hence more likely to be useful. Ambiguity is a measure of how frequently the term co-occurs with two other terms significantly when these two terms tend to avoid each other. Terms that are ambiguous tend to be poor subject indicators. Likewise coherence is a method of assessing the extent to which terms that co-occur with the given term imply each other. It is computed somewhat differently than ambiguity and does not have the same performance.
We applied five different methods to combine these scores to produce a superior scoring of the data. In addition to PAV-AdaBoost.finite and linear AdaBoost we applied Mahalanobis distance (Duda, Hart, & Stork, 2000), a log-linear model (Johnson et al., 1999), and the Cmls wide margin classifier described by Zhang and Oles (2001). For judge A we applied all methods in a 10-fold cross validation to see how well they could learn to predict A’s judgments on the held out test material. The same analysis was repeated based on B’s judgments. Results for the different methods applied to the two judgement sets, A and B, are given in Table 5. The log-linear, Cmls, and linear AdaBoost methods are linear classifiers. Mahalanobis distance is nonlinear but designed to fit multivariate normal distributions to the +1 and −1 labeled classes and use the optimal discriminator based on these fittings. None of these methods work as well as PAV-AdaBoost.finite.
Table 5.
The 11-point average precisions of different classifiers tested through 10-fold cross validation separately on judgment sets A and B.
| Train/test | Mahalanobis | Log-linear | Cmls | Lin-Ada | PAV-Ada |
|---|---|---|---|---|---|
| A/A | 0.5402 | 0.5667 | 0.5634 | 0.5140 | 0.6023 |
| B/B | 0.3461 | 0.3632 | 0.3614 | 0.3520 | 0.3640 |
In order to examine the performance of PAV-AdaBoost.finite in another environment, we simulated two three dimensional multivariate normal distributions. Distribution N1 was derived from the covariance matrix
and the points obtained were labeled as +1. Distribution N−1 was derived from the covariance matrix
and points were labeled as −1. Five hundred points were sampled from each distribution to produce a training set of 1000 points. Another 1000 points were sampled in the same manner to produce a test set. The location of the means for distribution N1 and N−1 were varied to be either closer to each other or farther apart to produce learning challenges of varying difficulty. Training and testing sets of three levels of difficulty were produced and the same five classifiers applied to the previous data set were applied here. The results are given in Table 6. Sets 1, 2, and 3 are of increasing level of difficulty. Since this problem is ideal for the Mahalanobis distance method, we are not surprised to see that it outperforms the other methods in all cases. However, among the other four methods PAV-AdaBoost.finite gives the best performance on two cases and is a close second to the Log-Linear method on the third case.
Table 6.
Eleven point average precisions for classifiers trained to discriminate between two three-dimensional normal distributions. Training took place on one sample and testing on an independently generated sample from the same distributions. The weak learners for boosting are the three co-ordinate projections.
| N1 mean | N2 mean | Mahalanobis | Log-linear | Cmls | Lin-Ada | PAV-Ada | |
|---|---|---|---|---|---|---|---|
| Set 1 | (−1, −1, −1) | (2, 2, 2) | 0.8556 | 0.7973 | 0.8235 | 0.8341 | 0.8357 |
| Set 2 | (0,0,0) | (1, 1, 1) | 0.7250 | 0.5980 | 0.5961 | 0.5950 | 0.6107 |
| Set 3 | (0,0,0) | (1/2, 1/2, 1/2) | 0.7014 | 0.5653 | 0.5606 | 0.5568 | 0.5624 |
7. Document classification
We are concerned with the rating of new documents that appear in a large database (MED-LINE) and are candidates for inclusion in a small specialty database (REBASE®). The requirement is to rank the new documents as nearly in order of decreasing potential to be added to the smaller database as possible, so as to improve the coverage of the smaller database without increasing the effort of those who manage this specialty database. To perform this ranking task we have considered several machine learning approaches and have developed a methodology of testing for the task. The version of REBASE (a restriction enzyme database) we study here consists of 3,048 documents comprising titles and abstracts mostly taken from the research literature. These documents are all contained in MEDLINE and we have ignored that small part of the database not contained in MEDLINE. We have applied naïve Bayes’ (binary form) to learn the difference between REBASE and the remainder of MEDLINE and extracted the top scoring 100,000 documents from MEDLINE that lie outside of REBASE. We refer to this set as NREBASE. These are the 100,000 documents which are perhaps most likely to be confused with REBASE documents. We have set ourselves the task of learning to distinguish between REBASE and NREBASE. In order to allow testing we randomly sampled a third of REBASE and called it RTEST and a third of NREBASE and called it NRTEST. We denote the remainder of REBASE as RTRAIN and the remainder of NREBASE as NRTRAIN. Thus we have training and testing sets defined by
| (48) |
We have applied some standard classifiers to this data and obtained the results contained in Table 7. Here naïve Bayes’ is the binary form and we discard any terms with weights in absolute value less than 1.0. Such a cutting procedure is a form of feature selection that often gives improved results for naïve Bayes’. We also use the binary vector representation for Cmls (Zhang & Oles, 2001) and use the value 0.001 for the regularization parameter λ as suggested in Zhang and Oles, (2001). KNN is based on a vector similarity computation using IDF global term weights and a tf local weighting formula. If tf denotes the frequency of term t within document d and dlen denotes the length of d (sum of all tf′ for all t′in d) then we define the local weight
Table 7.
Results of some standard classifiers on the REBASE learning task.
| Classifier | Naïve Bayes’ | KNN | Cmls |
|---|---|---|---|
| 11-pap | 0.775 | 0.783 | 0.819 |
| (49) |
where α = 0.0044 and λ = 0.7. This formula is derived from the Poisson model of term frequencies within documents (Kim, Aronson, & Wilbur, 2001; Robertson & Walker, 1994) and has been found to give good performance on MEDLINE documents. The similarity of two documents is the dot product of their vectors and no length correction is used as that is already included in definition (49). KNN computes the similarity of a document in the test set to all the documents in the training set and adds up the similarity scores of all those documents in the training set that are class +1 (in RTRAIN in this case) in the top K ranks. We use a K of 60 here.
One obvious weak learner amenable to boosting is naïve Bayes’. We applied linear AdaBoost and obtained a result on the test set of 0.783 on the third round of boosting. With naïve Bayes’ as the weak learner PAV-AdaBoost does not give any improvement. We will discuss the reason for this subsequently. Our interest here is to show examples of weak learners where PAV-AdaBoost is successful.
One example where PAV-AdaBoost is successful is with what we will call the Cmass weak learner.
7.1. Cmass algorithm
Assume a probability distribution D(i) on the training space . Let P denote that subset of X with +1 labels and N the subset with −1 labels. To produce h perform the steps:
Use D(i) to weight the points of P and compute the centroid c⃗p.
Similarly weight the points of N and compute the centroid c⃗n.
Define ω⃗ = c⃗p − c⃗n and h(x⃗) = ω⃗ · x⃗ for any x⃗.
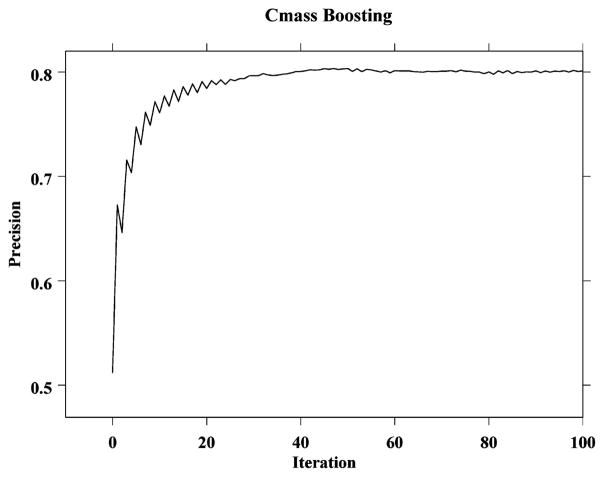
With the Cmass weak learner PAV-AdaBoost gives the results depicted in Figure 1. PAV-AdaBoost reaches a peak score just above 0.8 after about 60 iterations. Since Cmass is very efficient to compute it takes just under eleven minutes to produce one hundred rounds of boosting on a single 500 MH Pentium Xeon processor. There is some similarity here to wide margin classifiers such as SVM or Cmls in that those data points that are easily classified are progressively ignored (are not support vectors) as the processing continues to focus on those vectors which are eluding the classifier. Linear AdaBoost fails to boost with Cmass. It does this by first producing an alpha of approximately 0.86 and then proceeding to produce negative alphas which converge rapidly to zero. The scores produced in these steps actually decrease slightly from the initial Cmass score of 0.512.
Figure 1.
PAV-AdaBoost with Cmass as weak learner. Precision is 11-point average precision.
Another weak learner where PAV-AdaBoost is able to boost effectively is what we term Nscore (neighbor score).
7.2. Nscore algorithm
Assume a probability distribution D(i) on the training space . Let P denote that subset of X with +1 labels and N the subset with −1 labels. Let t −1 denote the number of times we have already applied the algorithm. Then if t is even choose the member x⃗i of P with greatest D(i) (or one of the greatest in a tie). If t is odd, make the same choice from N instead. If t is even define ht (x⃗) = sim(x⃗i, x⃗), while if t is odd define ht (x⃗) = −sim(x⃗i, x⃗), for any x⃗. Here sim(x⃗i, x⃗) is the similarity computation used in KNN above and defined in (49) and by IDF weighting.
PAV-AdaBoost applied with Nscore as weak learner reaches a score of 0.822 at around 4,000 iterations and remains at 0.82 at 10,000 iterations. The 4,000 iterations take 30 minutes on a single 500 MH Pentium Xeon processor. The result is shown in Figure 2. Attempts to apply linear AdaBoost with Nscore as defined in 7.2 fail. The program locks onto a small subset of the space and repeats these elements as the alphas move to zero and boosting becomes ineffective. In order to perform linear AdaBoost effectively we added a parameter that would only allow Nscore to repeat a point after xlap iterations. We tried values for xlap of 100, 1,000, and 3,000. The results are shown in Figure 2. While PAV-AdaBoost clearly peaks in the first 10,000 iterations, linear AdaBoost does not. We continued the linear AdaBoost (xlap = 3,000) calculation for a total of 50,000 iterations and reached a final score of 0.795. During the last 6,000 iterations it did not increase its peak level so that it appears nothing more could be gained by continuing an approximately day long calculation.
Figure 2.
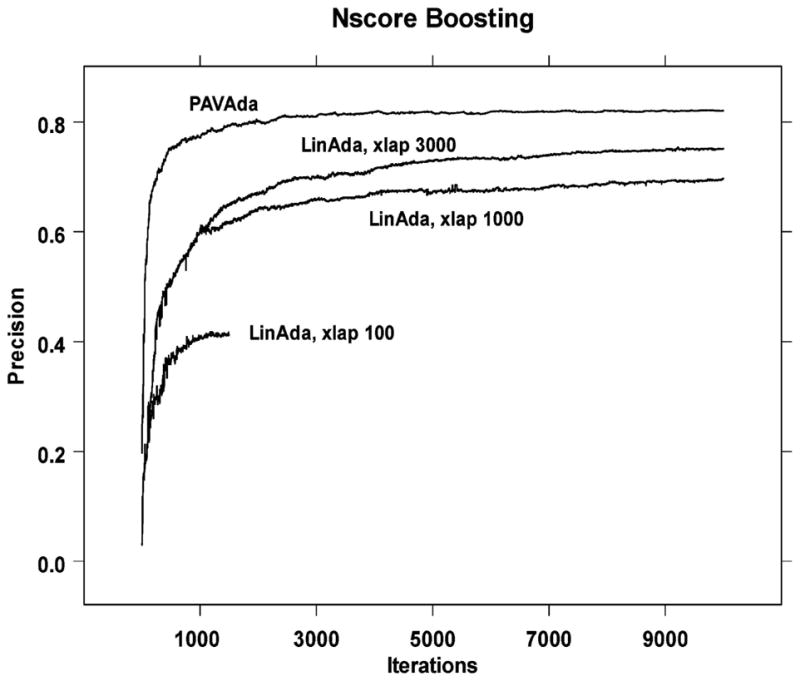
Boosting Nscore with PAV-AdaBoost compared with several different attempts to boost Nscore with linear AdaBoost.
8. Discussion
We are not the first to attempt a reweighting of weak hypotheses in boosting depending on an assessment of the quality of training for different regions of the data. Several have done this based on properties of the data which are outside of or in addition to the information to be gained from the values of the individual weak hypotheses themselves (Maclin, 1998; Meir, El-Yaniv, & Ben-David, 2000; Moerland & Mayoraz, 1999). The bounds on expected testing error in (Meir, El-Yaniv, and Ben-David, 2000) are based on a partition of the space and show a dependency on the dimension of that space very similar to our results in Theorem 4 and Corollary 2. Our general approach, however, is more closely related to the method of Aslam (2000) in that our reweighting depends only on the relative success of each weak hypothesis in training. Aslam evaluates success on the points with positive and negative label independently and thereby decreases the bound on training error. In a sense we carry this approach to its logical limit and decrease the bound on the training error as much as possible within the paradigm of confidence rated predictions. Our only restriction is that we do not allow the reweighting to reverse the order of the original predictions made by a weak learner. Because our approach can be quite drastic in its effects there is a tendency to over train. Corollary 2 suggests that in the limit of large samples results should be very good. However in practical situations one is forced to rely on experience with the method. Of course this is generally the state of the art for all machine learning methods.
An important issue is when PAV-AdaBoost can be expected to give better performance than linear AdaBoost. The short answer to this question is that all the examples in the previous two sections where PAV-AdaBoost is quite successful involve weak hypotheses that are intrinsic to the data and not produced by some optimization process applied to a training set. As an example of this distinction let the entire space consist of a certain set X of documents and let ω be a word that occurs in some of these documents but not others. Suppose that some of these documents that are about a particular topic have the +1 label and the remainder the −1 label. Then the function
| (50) |
is what we are referring to as an intrinsic function. Its value does not depend on a sample from X. On the other hand if we take a random sample Y ⊆ X which is reasonably representative of the space, then we can define the Bayesian weight bω associated with ω. If we define the function
| (51) |
Then it is evident that depends on the sample as well as the word ω. It is not intrinsic to the space X of documents. We believe this distinction is important as the non-intrinsic function is already the product of an optimization process. Since PAV is itself an optimization process it may be that applying one optimization process to the output of another is simply too much optimization to avoid over training in most cases.
We believe naïve Bayes’ provides an instructive example in discussing this issue. Bayesian scores produced on a training set do not correspond to an intrinsic function because the same data point may receive a different score if the sample is different. Thus it is evident that there is already an optimization process involved in Bayesian weighting and scoring. In applying PAV-AdaBoost with naïve Bayes’ as weak learner we find poor performance. Because PAV-AdaBoost is a powerful learner, poor generalizability is best understood as a consequence of overtraining. In the case of PAV-AdaBoost applied to naïve Bayes’ such overtraining appears as PAV approximates a generally smooth probability function with a step function that reflects the idiosyncrasies of the training data in the individual steps. We might attempt to overcome this problem by replacing the step function produced by PAV by a smooth curve. The PAV function derived from naïve Bayes’ training scores (learned on TRAIN) and a smooth approximation are shown in Figure 3. The smooth curve has the formula
Figure 3.
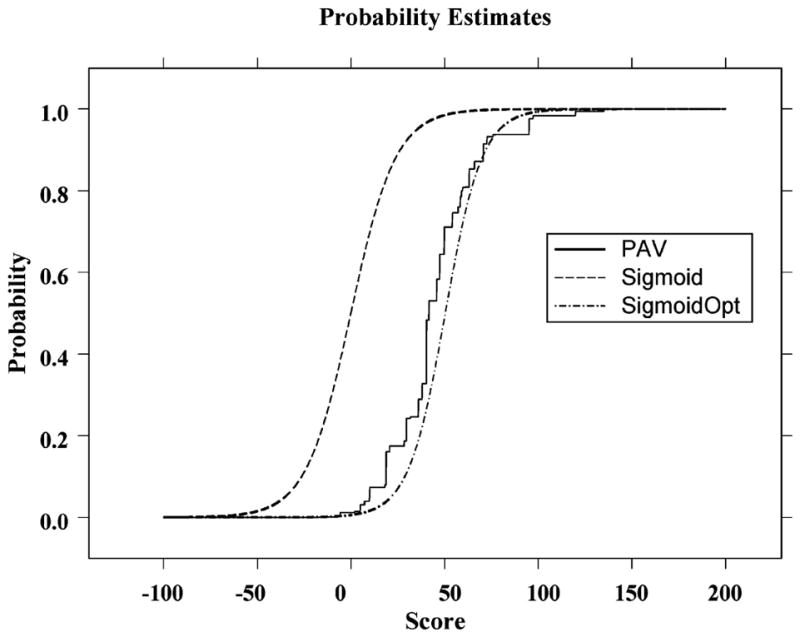
Probability of label class +1 as a function of score as estimated by PAV and by sigmoid curves. The curve marked Sigmoid is the estimate implicitly used by linear AdaBoost and is clearly not the optimal sigmoid minimizing Zt. SigmoidOpt is the result of optimization over both ω and b in definition (52).
| (52) |
and is the sigmoid shape commonly used in neural network threshold units (Mitchell, 1997). The parameters ω and b have been optimized to minimize Z. If we use this function as we do p(s) in definition (14) we obtain
| (53) |
Thus if we set b = 0 and optimize on ω alone to minimize Z, we find that the function (52) gives the probability estimate used implicitly by linear AdaBoost with α = ω/2. The resultant sigmoid curve is also shown in Figure 3. From this picture it is clear that neither PAV-AdaBoost nor linear AdaBoost are ideal for boosting naïve Bayes’. PAV-AdaBoost because it over trains and linear AdaBoost because it is too far from optimal. A better choice would be what we may call optimal linear AdaBoost which is the result of optimizing formula (52) over both ω and b. The results of these three different strategies applied to boost naïve Bayes’ are shown in Figure 4. While optimal linear AdaBoost outperforms the other methods on this problem, it is evident that none of the methods perform very well. We attribute this to the fact that once individual term weights are added into the Bayes’ score it is not possible for Boosting to ameliorate the effects of the dependency between terms. It has been known for some time (Langley & Sage, 1994) that dealing with inter-term dependencies can improve the performance of naïve Bayes’. We hypothesize that to be most effective this must take place at the level of individual terms.
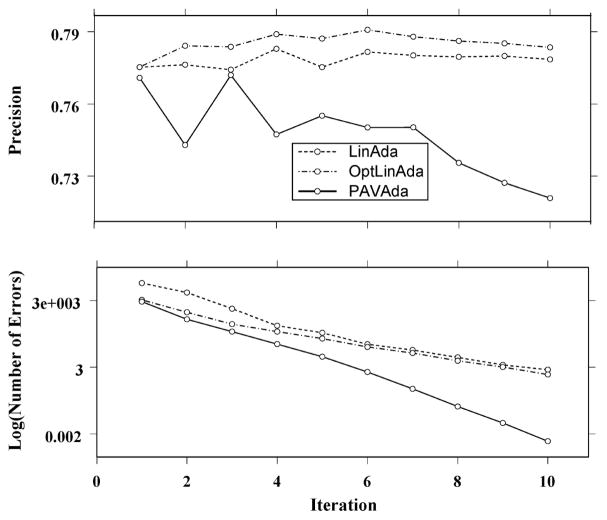
Figure 4.
Boosting naïve Bayes (binary form) with three different algorithms. PAV-AdaBoost gives the lowest error on the training space (lower panel), but optimal linear AdaBoost gives the best generalizability (upper panel).
Let us return to the main issue here, namely, when is linear AdaBoost preferable to PAV-AdaBoost. In examining Figure 3 it is not obvious that linear AdaBoost would perform better than PAV-AdaBoost. Each method fails to be optimal. In order to obtain more insight we repeatedly resampled the training and testing sets and performed boosting by the two methods. We found that generally linear AdaBoost outperformed PAV-AdaBoost. It was common that neither method worked very well, but generally linear AdaBoost had the edge. This leads us to the general conclusion that when a weak learner produces a logodds score linear AdaBoost may be a good choice for boosting. Of course in this situation optimal linear AdaBoost may be even better. When the score is not a logodds score a sigmoid curve may not give a good approximation and in that situation PAV-AdaBoost may give the better result.
Finally, there is the question of why PAV-AdaBoost applied to Nscore produces such a good result. The score of 0.822 is superior to the results in Table 7. We have only been able to produce a higher score on this training-testing pair by applying AdaBoost to optimally boost over 20,000 depth four decision trees. By this means we have obtained a score just larger than 0.84, but the computation required several days. While this is of theoretical interest it is not very efficient for an approximately 2% improvement. We believe the good result with PAV-AdaBoost applied to Nscore is a consequence of the fact that we are dealing with a large set of relatively simple weak learners that have not undergone prior optimization. We see the result of PAV-AdaBoost applied to Nscore as a new and improved version of the K-nearest neighbors algorithm.
Acknowledgments
The authors would like to thank the anonymous referees for very helpful comments in revising this work.
Appendix
Here we examine the VC dimension of the set of hypotheses generated by the PAV-AdaBoost.finite algorithm based on the pure form of PAV defined by 2.1. This presupposes a fixed set of weak hypotheses and the set of functions under discussion is all the functions obtained by applying PAV-AdaBoost.finite to possible finite training samples with any possible labeling of the sample points and then extending the results globally using the interpolation of 2.2. Let us denote this set of functions by ℋ. Different weightings for points are allowed by PAV-AdaBoost.finite, but to simplify the presentation we will assume that all points have weight 1.
To begin it is important to note that the algorithm actually acts on samples of the fixed set of points {(h1(x), h2(x), …, hT (x))}x∈X in Euclidean T-space. Thus for this purpose we may disregard the set of weak hypotheses and focus our attention on finite subsets of Euclidean T-space where the role of the weak hypotheses is assumed by the co-ordinate projection functions. We may further observe that whether a set of points can be shattered by ℋ does not depend on the actual co-ordinate values, but only on the orderings of the points induced from their different co-ordinate values. Finally we observe that if a set of points contains points A and B and A is less than or equal to B in all co-ordinate values, then ℋ cannot shatter that set of points. The regressions involved must always score B equal to or greater than A if B dominates A. It will prove sufficient for our purposes to work in two dimensions. In two dimensions the only way to avoid having one point dominate another is to have the points strictly ordered in one dimension and strictly ordered in the reverse direction in the other dimension. Thus we may consider a set of N points to be represented by the N pairs where is any strictly increasing set of real numbers and b is an arbitrary real number that may be determined by convenience. We will refer to the ordering induced by the first co-ordinate as the forward ordering, and the ordering induced by the second co-ordinate as the backward ordering. For a given labeling of such a set of points (which must contain both positive and negative labels) the PAV-AdaBoost.finite algorithm may be applied and will always yield a solution. This solution will depend only on the number of points, the ordering, and the labels, but not on the actual numbers ri used to represent the points.
In order to shatter sets of points we must examine the nature of solutions coming from PAV-AdaBoost.finite. Clearly for any labeling of the points we may consider the points as contiguous groups labeled negative or labeled positive and alternating as we move up the forward order. Let the numbers of points in these groups be given by . We will assume that the lowest group (m1) in the forward order is labeled negative and the highest group (mK) is labeled positive. This will allow us to maintain sufficient generality for our purposes. Then K must be an even integer and it will be convenient to represent it by 2k − 2. Our approach will be to assume a certain form for the solution of the PAV-AdaBoost.finite scoring functions and use the invariance of these functions under the algorithm to derive their actual values. For the regression induced function k1obtained from the forward ordering we assume without loss of generality the form
| (54) |
Here k1(mp) denotes the value of k1 on all the points in the group mp. Likewise the k2 obtained from the backward ordering is assumed to have the form
| (55) |
By definition (54), αk corresponds to the single group m2k−2 with positive label. As a result of the forward isotonic regression it follows that α1 = −λ and αk = λ. Now appealing to the invariance of k1 and k2 under the algorithm (apply one round of PAV-AdaBoost.finite and k1 and k2 are unchanged) we may derive the relations
| (56) |
These relations are valid for αj, 2 ≤ j ≤ k − 1 and for all βj, 1 ≤ j ≤ k − 1. By simply adding to the appropriate expressions in (56) we obtain expressions for the scores over the various mi.
| (57) |
The important observation here is that the odd and even groups will be separated provided the αj+1 − αj are all positive and not overwhelmed by the log terms. If this can be arranged properly it will also guarantee that the regressions are valid as well. By repeated substitutions using Eqs. (57) it can be shown that
| (58) |
One crucial result that comes from this relationship is that if all the mi are equal then all the log terms disappear in Eq. (58) and because α1 = −λ and αk = λ we may conclude from Eqs. (57) that the score of all positive labeled elements is λ/(k − 1) while the score of all negative labeled elements is −λ/(k − 1). If the mi are all equal to two, let us refer to the resulting function k1 + k2 as a binary solution. Such solutions may be used to shatter two dimensional sets of any number of points.
Let be any strictly increasing set of real numbers and the corresponding set of points in two dimensions. Let a labeling be given that divides the set into contiguous same label groups with the sizes as one moves up the forward ordering. For definiteness let the group corresponding to n1 have the positive label and the group corresponding to nJ have the negative label. Our strategy is to sandwich each group corresponding to an nj between two elements that form a binary group in a new system of points for which the binary solution defined above will apply. For any ε > 0 define the strictly increasing set of numbers by
| (59) |
Label the two dimensional set of points coming from in groups of two starting with negative from the left end and ending in positive at the far right end. Then this set of points has a binary solution and its extension by the interpolation 2.2 separates the positive labeled and negative labeled points of corresponding to the groupings . The construction (59) will vary slightly depending on the labeling of the end groups of , but the same result holds regardless. We have proved the following.
Theorem 5
For any choice of λ and in any Euclidean space of dimension two or greater, if all points have weight one and the weak hypotheses are the co-ordinate projections, then the VC dimension of the set ℋ of all hypotheses that may be generated by PAV-AdaBoost.finite over arbitrary samples with arbitrary labelings is infinite.
The construction of the sets of points and the set of points corresponding to as defined in (59) can all be carried out within any open subset of E2 for any N by simply choosing ε small enough and adjusting b appropriately.
Corollary 3
Let denote a fixed set of weak learners defined on a space X and define U: X → ET by U(x) = (h1(x), h2(x), …, hT (x)). Assume that all points have weight one. If the image of X under U contains an open subset of a 2-dimensional hyperplane parallel to two of the co-ordinate axes in ET, then for any λ the set of hypotheses coming from PAV-AdaBoost.finite applied to over all possible samples of X and arbitrary labelings has infinite VC dimension.
References
- Apte C, Damerau F, Weiss S. Text mining with decision rules and decision trees. Conference Proceedings The Conference on Automated Learning and Discovery; CMU; 1998. [Google Scholar]
- Aslam J. Improving algorithms for boosting. Conference Proceedings 13th COLT; Palo Alto, California. 2000. [Google Scholar]
- Ayer M, Brunk HD, Ewing GM, Reid WT, Silverman E. An empirical distribution function for sampling with incomplete information. Annals of Mathematical Statistics. 1954;26:641–647. [Google Scholar]
- Bennett KP, Demiriz A, Shawe-Taylor J. A column generation algorithm for boosting. Conference Proceedings 17th ICML.2000. [Google Scholar]
- Buja A, Hastie T, Tibshirani R. Linear smoothers and additive models. The Annals of Statistics. 1989;17(2):453–555. [Google Scholar]
- Burges CJC. A tutorial on support vector machines for pattern recognition. Bell Laboratories, Lucent Technologies; 1999. (Available electronically from the author) [Google Scholar]
- Carreras X, Marquez L. Boosting trees for anti-spam email filtering. September 5–7, 2001; Conference Proceedings RANLP2001; Tzigov Chark, Bulgaria. 2001. [Google Scholar]
- Collins M, Schapire RE, Singer Y. Logistic regression, AdaBoost and Bregman distances. Machine Learning. 2002;48(1):253–285. [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. 2. New York: John Wiley & Sons, Inc; 2000. [Google Scholar]
- Duffy N, Helmbold D. Potential boosters?. Conference Proceedings Advances in Neural Information Processing Systems; 1999. p. 11. [Google Scholar]
- Duffy N, Helmbold D. Leveraging for regression. Conference Proceedings 13th Annual Conference on Computational Learning Theory; San Francisco. 2000. [Google Scholar]
- Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal or Computer and System Sciences. 1997;55(1):119–139. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Additive logistic regression: A statistical view of boosting. The Annals of Statistics. 2000;38(2):337–374. [Google Scholar]
- Hardle W. Smoothing Techniques: With Implementation in S. New York: Springer-Verlag; 1991. [Google Scholar]
- Johnson M, Geman S, Canon S, Chi Z, Riezler S. Estimators for stochastic “unification-based” grammars. Conference Proceedings Proceedings ACL’99; Univ. Maryland. 1999. [Google Scholar]
- Kim W, Aronson AR, Wilbur WJ. Automatic MeSH term assignment and quality assessment. Conference Proceedings Proc. AMIA Symp; Washington, D.C. 2001. [PMC free article] [PubMed] [Google Scholar]
- Kim WG, Wilbur WJ. Corpus-based statistical screening for content-bearing terms. Journal of the American Society for Information Science. 2001;52(3):247–259. [Google Scholar]
- Langley P, Sage S. Induction of selective Bayesian classifiers. Conference Proceedings Tenth Conference on Uncertainty in Artificial Intelligence; Seattle, WA. 1994. [Google Scholar]
- Maclin R. Boosting classifiers locally. Conference Proceedings Proceedings of AAAI.1998. [Google Scholar]
- Mason L, Bartlett PL, Baxter J. Improved generalizations through explicit optimizations of margins. Machine Learning. 2000;38:243–255. [Google Scholar]
- McCallum A, Nigam K. A comparison of event models for naive bayes text classification. Conference Proceedings AAAI-98 Workshop on Learning for Text Categorization.1998. [Google Scholar]
- Meir R, El-Yaniv R, Ben-David S. Localized boosting. Conference Proceedings 13th COLT; Palo Alto, California. 2000. [Google Scholar]
- Mitchell TM. Machine learning. Boston: WCB/McGraw-Hill; 1997. [Google Scholar]
- Moerland P, Mayoraz E. DynamBoost: combining boosted hypotheses in a dynamic way. IDIAP Switzerland; 1999. (Technical Report RR 99-09) [Google Scholar]
- Nock R, Sebban M. A Bayesian boosting theorem. Pattern Recognition Letters. 2001;22:413–419. [Google Scholar]
- Pardalos PM, Xue G. Algorithms for a class of isotonic regression problems. Algorithmica. 1999;23:211–222. [Google Scholar]
- Ratsch G, Mika S, Warmuth MK. On the Convergence of Leveraging. London: Royal Holloway College; 2001. (NeuroCOLT2 Technical Report 98) [Google Scholar]
- Ratsch G, Onoda T, Muller KR. Soft margins for AdaBoost. Machine Learning. 2001;42:287–320. [Google Scholar]
- Robertson SE, Walker S. Some simple effective approximations to the 2-Poisson model for probabilistic weighted retrieval. Conference Proceedings. 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.1994. [Google Scholar]
- Schapire RE, Singer Y. Improved boosting algorithms using confidence-rated predictions. Machine Learning. 1999;37(3):297–336. [Google Scholar]
- Vapnik V. Statistical Learning Theory. New York: John Wiley & Sons, Inc; 1998. [Google Scholar]
- Witten IH, Moffat A, Bell TC. Managing Gigabytes. 2. San Francisco: Morgan-Kaufmann Publishers, Inc; 1999. [Google Scholar]
- Zhang T, Oles FJ. Text categorization based on regularized linear classification methods. Information Retrieval. 2001;4(1):5–31. [Google Scholar]