Acoustic-Based Proton Range Verification in Heterogeneous Tissue: Simulation Studies

Abstract

Acoustic-based proton range verification (protoacoustics) is a potential in vivo technique for determining the Bragg peak position. Previous measurements and simulations have been restricted to homogeneous water tanks. Here, a CT-based simulation method is proposed and applied to a liver and prostate case to model the effects of tissue heterogeneity on the protoacoustic amplitude and time-of-flight range verification accuracy. For the liver case, posterior irradiation with a single proton pencil beam was simulated for detectors placed on the skin. In the prostate case, a transrectal probe measured the protoacoustic pressure generated by irradiation with five separate anterior proton beams. After calculating the proton beam dose deposition, each CT voxel's material properties were mapped based on Hounsfield Unit values, and thermoacoustically-generated acoustic wave propagation was simulated with the k-Wave MATLAB toolbox. By comparing the simulation results for the original liver CT to homogenized variants, the effects of heterogeneity were assessed. For the liver case, 1.4 cGy of dose at the Bragg peak generated 50 mPa of pressure (13 cm distal), a 2× lower amplitude than simulated in a homogeneous water tank. Protoacoustic triangulation of the Bragg peak based on multiple detector measurements resulted in 0.4 mm accuracy for a δ-function proton pulse irradiation of the liver. For the prostate case, higher amplitudes are simulated (92-1004 mPa) for closer detectors (<8 cm). For four of the prostate beams, the protoacoustic range triangulation was accurate to ≤1.6 mm (δ-function proton pulse). Based on the results, application of protoacoustic range verification to heterogeneous tissue will result in decreased signal amplitudes relative to homogeneous water tank measurements, but accurate range verification is still expected to be possible.

1. Introduction

Clinical use of proton therapy for cancer treatment is complicated by proton range uncertainty(Paganetti, 2012; Knopf and Lomax, 2013). As protons interact with material, they deposit energy (dose) and slow down. Because of the inverse square relationship between speed and stopping power, a large fraction of a proton beam's energy is deposited in the last few millimeters of travel. This increased dose deposition results in the characteristic Bragg peak (BP). Due to the absence of dose beyond this Bragg peak, proton therapy is theoretically advantageous relative to photon therapy, which undergoes exponential attenuation. Although the range of protons in water is known with sub-millimeter accuracy, changes in patient anatomy, errors in converting CT Hounsfield Units (HU) to proton stopping power, and imaging errors cause proton range uncertainty when tissue is irradiated(Paganetti, 2012; Knopf and Lomax, 2013). As a result, the dosimetric advantage of proton therapy is partially compromised by the necessity of using large margins (up to 1-3 mm + 3.5% of the range) and avoiding treatment plans that place organs-at-risk behind the target(Knopf and Lomax, 2013).

To reduce the proton range uncertainty, a number of in vivo range verification techniques have been proposed and studied. Proton irradiation activates nuclei and results in the emission of photons (prompt gamma) and positrons, whose annihilation can be localized through PET measurements. Despite significant developments in both PET and prompt gamma (including gamma camera(Polf et al., 2015), nanosecond spectrally-resolved(Verburg and Seco, 2014), and time-of-flight techniques(Golnik et al., 2014)), neither of these methods has achieved broad clinical adoption beyond preliminary testing(Priegnitz et al., 2016). For both PET and prompt gamma, the maximum depth of emitted, measured photons does not coincide with the Bragg peak, and biological washout limits the collectable PET signal(Knopf and Lomax, 2013). Proton radiography and tomography are both promising(Schneider and Pedroni, 1995), but scattering reduces the resolution of the acquired images.

Protoacoustics (also known as ionoacoustics (Assmann et al., 2015; Kellnberger et al., 2016) and RACT(Alsanea et al., 2015)) is a potential in vivo proton range verification technique that measures the acoustic pressure waves generated by proton dose deposition(Sulak et al., 1979; Tada et al., 1991; Hayakawa et al., 1995; Albul et al., 2001; Jones et al., 2015; Patch et al., 2016; Jones et al., 2016b). As a thermoacoustic technique, the volume heated by the deposited dose emits pressure waves whose amplitude, frequency, and shape depend on the dose deposition and material. Due to the characteristic proton dose deposition, two macroscopic pressure waves are generated: the cylindrical α-wave is emitted by the pre-peak Bragg curve dose deposition, and the spherical γ-wave is emitted by the Bragg peak(Albul et al., 2004; Jones et al., 2014). By measuring the arrival time of the acoustic γ-wave (τ^γ), the distance between a detector and the Bragg peak (l) can be calculated based on a time-of-flight (TOF) calculation if the speed of sound (c) is known: l = cτ^γ. A proof-of-principle experiment using proton beams of clinically-relevant energies has shown that protoacoustic range verification can achieve 2 mm precision (standard deviation) in a water phantom(Jones et al., 2016b).

In order to assess the possibility of in vivo protoacoustic range verification, protoacoustics must be studied in heterogeneous materials. Heterogeneity affects both the generation of protoacoustic waves (different materials produce different pressure amplitudes from the same deposited energy) and the propagation of the emitted waves (the speed, attenuation, and reflectivity). For example, sound travels slower through fat than through muscle, which may introduce error if an incorrect c is used in the TOF distance calculation.

Here, a method is presented for simulating protoacoustic generation and propagation based on the CT. This model is first applied to a liver case in order to predict the effects of tissue heterogeneity on the measured protoacoustic signal amplitude and arrival times. For the liver case, three scenarios are simulated using the same dose deposition and the same detector positions, but different materials: (1) a homogeneous water phantom (WATER, HU = 0), (2) a homogeneous patient phantom (HOM, all material with HU > -200 is replaced with HU = 0), and (3) a heterogeneous patient phantom (HET). By comparing the results from (1) and (2), the effect of skin/air reflections on the protoacoustic signal can be identified. By comparing the results from (2) and (3), the effects of tissue heterogeneity can be identified.

Finally, for a prostate case irradiated with five different proton beams, the protoacoustic signal at a row of transrectal detectors is simulated and analyzed to show another possible clinical application of protoacoustic proton range verification.

The presented simulation results are made under the assumption that the literature material properties are correct. By accepting these assumptions, the calculated proton dose deposition and simulated pressure waves are considered “ground truth” for the study, and the accuracy of the protoacoustic range verification technique can be assessed. Due to the scarcity of the literature reported values, validation will require future, direct comparison of protoacoustic experiments to simulations. This is beyond the scope of this paper. Rather, we seek to propose a simulation technique and use it to predict the effects of applying protoacoustics to heterogeneous materials.

2. Methods

As a thermoacoustic process in which deposited heat causes expansion and the emission of pressure waves, protoacoustic simulations start with the proton dose deposition and assume that the dose is transformed into heat. Eclipse v11 (Varian Medical Systems, Palo Alto, CA) was used to calculate the proton dose deposition for a single pencil beam scanned (PBS) spot. The source pressure resulting from this energy deposition was used to seed the acoustic propagation simulation, which was performed with the k-Wave MATLAB toolbox(Treeby and Cox, 2010a), a program that numerically solves the wave equation with a k-space psuedospectral method. k-Wave considers the properties of each voxel, and attenuation and reflections are modeled. All simulations were performed using a publically available, anonymized CT dataset. The simulation method is shown in the flow chart in Fig. 1.

Figure 1.

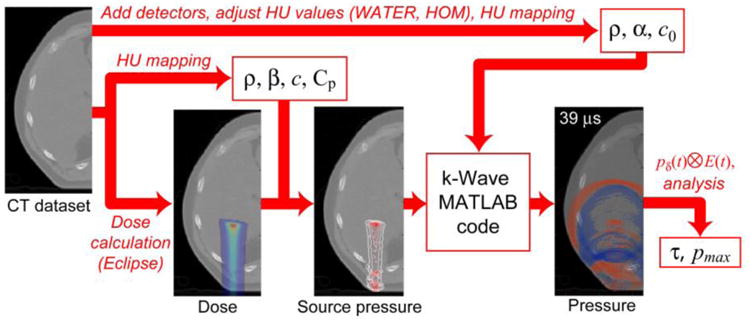
The simulation method is shown. The dose and source pressure are calculated based on the CT after mapping the necessary material properties of each voxel based on the HU. For the acoustic simulation, the CT dataset is modified for the detectors (liver case - add cylinders at skin surface and/or convert to the WATER or HOM phantom; prostate case - add the endorectal probe) before mapping the acoustic material properties. After simulation, the pressure waves resulting from a delta-function excitation proton pulse (p_δ) are convolved with the proton pulse of interest (E(t)). The protoacoustic pressure waves' maximum pressure and arrival times are analyzed.

2.1. Dose Deposition

The dose deposition, D(r) [J kg^-1], resulting from irradiation of a heterogeneous CT with a single, monoenergetic proton pencil beam was calculated using Eclipse. The deposited dose is related to the energy per volume, E(r) [J m^-3], by multiplying by the density, ρ: E(r) = ρD(r). E(r) specifies the energy per volume that is deposited in a voxel at r. For a proton pulse with normalized time-dependence $E(t)[s^{-1}]({\int }_{-\infty }^{\infty }E(t)dt=1)$, the energy deposition rate is given by the product of the spatial and temporal functions, E(r)E(t) [J m^-3 s^-1].

2.2. Source Pressure: c, ρ, β, C_p

The thermoacoustic source pressure generated by this energy dose deposition, p_source [Pa s^-1], is given by:

$$p_{\mathit{\text{Source}}}(\mathbf{r},t)=\mathrm{\Gamma }E(\mathbf{r})E(t)$$ (1)

where Γ = c²β/C_p is the Grüneisen coefficient, which depends on the speed of sound, c [m/s], the thermal expansion coefficient, β [K^-1], and the specific heat capacity, C_p [J K^-1 kg^-1]. Although important for quantitative photoacoustic and other thermoacoustic studies, the Grüneisen coefficient is difficult to measure, and its value for different tissue types is rarely reported in the literature(Cox et al., 2009; Yao et al., 2014).

Calculating the p_source generated in a heterogeneous material requires specifying ρ (to calculate E(r) from D(r)), c, β, and C_p for each voxel. Here, all of these parameters are mapped based on the Hounsfield Unit (HU) of the simulation CT. The density and speed of sound are calculated using the built-in k-Wave function, which is based on an empirical mapping(Schneider et al., 1996; Mast, 2000). To determine the thermal expansion coefficient and heat capacity, each CT voxel was assigned to a particular tissue type based on its HU. For simplicity and due to the scarcity of these values in the literature, the tissue type of each CT voxel was assigned to lung, fat/adipose, various organs, cancellous bone, or cortical bone based on the HU ranges given in Table 1 and plotted in Fig. 2. For voxels with an intermediate HU value, the material properties were assigned assuming the voxel was a mixture of the two closest tissue types (according to HU value), and a linear interpolation was performed to find the appropriate weighting. For example, a voxel with HU = -125 would be assigned a β = (β_lung + β_fat/adipose)/2. From the material properties mapped as described above, the p_source for each voxel was calculated based on eq. (1).

Table 1.

The HU ranges, thermal expansion coefficient (β), heat capacity (C_p), attenuation coefficient (α₀), and attenuation coefficient power (d) are shown in the rows and columns with bold headers. For voxels with HU values intermediate between the given ranges, the different parameters are linearly interpolated. The speed of sound and HU reported in the literature for the different materials is also given and compared to the speed of sound mapped with the HU relationship used here(Duck, 1990).

Tissue Type	HU Range	β Sourcea	β value (K-1 × 104)a	Cp (J kg-1 K-1)b	c (m s-1)b	HUc	cHU (m s-1)e	α0 (Np (MHz)-d m1)b	dreportedb	d
Lung	-1000 – -150		0	3886	949.3	-741	682	230.94	1	1.05
Fat/Adipose	-100 – -50	Fat, Human	9.2	2348.3	1440	-70	1453	4.3578	1.0861	1.05
Various Organs	20 – 85	mean(Blood, Muscle)	3.835	3585.3				6		1.05
Blood		Blood: whole	4	3617	1578	55	1580	2.3676	1.0498
		Muscle, rabbit	3.44
Muscle		Muscle, dog	3.9	3421.2	1588	42	1567	7.1088	1.0827
Kidney				3763	1554	43	1568	2.0867	1.022
Liver				3540	1586	53	1578	6.195	1
Bone (cancellous)	125 – 300	Bone, Cow	1.97	2274	2118	260	1716	47	1.2	1.05
Bone (cortical)	>1000			1312.8	3515	1376	2544	54.553	1	1.05

^aRef. (Duck, 1990)

^bRef.(Hasgall et al., 2014)

^cRef. (Schneider et al., 1996)

^eRef. (Mast, 2000)

Figure 2.

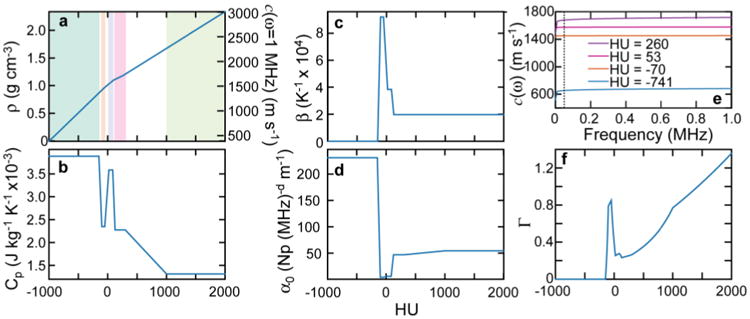
The simulation HU-to-material property maps are shown for density (a, left axis) and speed of sound at 1 MHz (a, right axis), heat capacity (b), thermal expansion coefficient (c), and attenuation coefficient (d). The frequency dependent speed of sound calculated with eq. (3) is shown for four HU values (bone(cancellous): 260 HU; liver: 53 HU; fat: -70 HU; lung: -741 HU) (e). In e, the average ω_max (50 kHz for the liver case, δ function proton pulse) calculated from the simulated protoacoustic pressure waves is shown with the dashed vertical line. The calculated Grüneisen coefficient, Γ = c²β/C_p, is shown in f. The five HU ranges associated with each tissue type are shown in a: lung, fat/adipose, various organs, bone (cancellous), and bone (cortical).

For the k-Wave simulations, a delta-function (δ) proton pulse was assumed, and the time-integrated p_source, ΓE(r), was input into k-Wave. To calculate the pressure waves that result from arbitrary proton pulse shapes, the pressure wave simulated for the δ-function proton pulse, p_δ(t), was convolved with the desired proton pulse E(t)(Paltauf et al., 1998; Jones et al., 2016a). For the results reported here, the pressure waves resulting from a δ-function proton pulse and a FWHM 14 μs Gaussian proton pulse were analyzed. Proton pulses of ∼14 μs FWHM have been generated experimentally for the generation of protoacoustic waves(Jones et al., 2015; Jones et al., 2016b). Because of the millimeter length scales encountered in the clinical proton dose deposition, proton pulses of < ∼5 μs maintain stress confinement, and thus are δ-function-like(Jones et al., 2016a). The simulations were performed for pulses of 1 × 10⁷ protons, which corresponds to a dose of 1.0-1.4 cGy at the Bragg peak for the 124.9-136.3 MeV beams simulated here.

2.3. Acoustic Properties: ρ, c₀, α₀, d

The above description results in the starting point for the acoustic k-Wave simulations: the source pressure is defined. But, the acoustic properties of each voxel must be assigned to properly model the acoustic propagation. Each voxel must have a specified density (defined as described above), zero-frequency speed of sound (c₀), attenuation power law prefactor (α₀ [Np (rad s^-1)^-d m^-1]), and attenuation power law exponent (d), where the frequency-dependent acoustic attenuation (α [Np m^-1]) is calculated (implicitly by k-Wave) as:

$$\alpha ={\alpha }_0{\omega }^d$$ (2)

where ω [rad s^-1] is the acoustic frequency(Treeby and Cox, 2010b). As with β and C_p above, α₀ is defined for each voxel based on the HU tissue-type assignment (Table 1). Attenuation and dispersion are linked through Kramers-Kronig relations(Treeby, 2013), and both the attenuation and speed of sound are frequency dependent. If the speed of sound at one frequency is known, the speed of sound at other frequencies is given by:

$$\frac{1}{c_2({\omega }_2)}-\frac{1}{c_1({\omega }_1)}={\alpha }_{0}tan(\stackrel{\pi d}{}/\underset{2}{})({\omega }_2^{d-1}-{\omega }_1^{d-1}).$$ (3)

For the simulations, the attenuation power law exponent was chosen as d = 1.05. The c assigned above (for calculating Γ) from the empirical mapping is assumed to be measured at 1 MHz. For the k-Wave simulations, from this c(ω = 1 MHz), the zero-frequency speed of sound, c₀ = c(ω = 0 MHz), was calculated for each voxel based on eq. (3). From the input c₀, k-Wave calculates the required frequency-dependent speed of sound for each voxel during the simulation. As shown in Fig. 2e for some selected HU values, based on the model and Table 1 values used here, the speed of sound at 1 MHz changes by less than 0.3% at 50 kHz (representative of the protoacoustic pressure wave frequencies simulated here) for liver and fat. For cancellous bone and lung, however, the change can be up to 4.3% due to their larger assigned attenuation.

Some of the simulations (the liver WATER and HOM) were performed under homogeneous conditions through a water medium. These simulations were run without attenuation (the absorption coefficient of water is ∼0) and without dispersion: the speed of sound was constant at all frequencies.

2.4. Analysis

Thermoacoustic emissions have a bipolar structure in which a positive pressure compression peak precedes a negative pressure rarefaction peak. Based on previous simulations in water(Jones et al., 2016a), the arrival time of the γ-wave compression peak, ${\tau }_{\mathit{\text{comp}}}^{\gamma }$, is offset from the l/c by:

$${\tau }_{\mathit{\text{comp}}}^{\gamma }=l/c+S_{\mathit{\text{pulse}}}+S_{\mathit{\text{comp}}}+S_{\theta }$$ (4)

where S_pulse is due to the proton pulse shape (longer Gaussian proton pulses result in later arriving ${\tau }_{\mathit{\text{comp}}}^{\gamma }$ due to loss of thermoacoustic stress confinement), S_comp is due to the choice of measuring the arrival time at the compression peak (due to interference between the positive and negative pressure waves, the positive compression peak arrives early because it is largely a result of emission from the Bragg peak volume closer to the detector), and S_θ is due to the Bragg peak asymmetry (the pressure wave arrival time depends on the angle, θ, between the proton propagation axis, Bragg peak, and the detector). Based on previous protoacoustic simulations in water(Jones et al., 2016a), the S_pulse = 0 and 3.1 μs and S_comp = -2.2 and -7.2 μs for the cases of a delta-function and 14 μs FWHM Gaussian proton pulses simulated here, respectively. S_comp is parameterized for detectors placed within a 30° cone beyond the BP and close to the propagation axis. For these detectors, S_θ≈0. For detectors at larger angles relative to the beam axis, S_θ is non-zero. Because the BP position – and, by extension, S_θ – is unknown during range verification calculation, no attempt to correct for S_θ was made here (S_θ is assumed to be zero). Therefore, TOF calculations based on data simulated for more laterally placed detectors are expected to have higher errors (up to ±2.6 mm for a δ-function proton pulse (Jones et al., 2016a)) than for distal detectors closer to the propagation axis.

For each simulated pressure wave measured at the detector position r, a polynomial was fit to the first arriving, positive compression peak. The ${\tau }_{\mathit{\text{comp}}}^{\gamma }$ was measured based on the time when the polynomial fit reached its maximum. The protoacoustic-determined distance between detector and Bragg peak, l_PA, was then calculated through eq. (4) by subtracting S_pulse and S_comp (determined according to excitation proton pulse based on previous simulations (Jones et al., 2016a)) and multiplying ( ${\tau }_{\mathit{\text{comp}}}^{\gamma }$-S_pulse - S_comp) by c.

Two speeds of sounds were considered for the distance calculation: the speed of sound of HU = 0 (c_H2O = 1523.9 m/s, the speed of sound of water at 37 °C) and the average speed of sound interpolated over the CT between the Bragg peak and detector and calculated based on dispersion (eq. (3)) using the maximum amplitude frequency in the protoacoustic pressure spectrum, ω_max(c_CT). By using c_H2O, a common assumption in ultrasound is tested; a single speed of sound - that attributed to tissue - is used to convert arrival times into distance. By using c_CT, the CT is used to inform the speed of sound. Because the speed of sound in tissue is material- and frequency-dependent, the c_CT is calculated based on the acoustic wave frequency and the material between detector and Bragg peak.

The protoacoustic triangulated position of the Bragg peak, ${\mathbf{r}}_{\mathit{\text{BP}}}^{\mathit{\text{PA}}}$, was calculated by finding the point that minimizes $\sum _i{|l_{\mathit{\text{PA}}}^i-|{\mathbf{r}}_{\mathit{\text{BP}}}^{\mathit{\text{PA}}}-{\mathbf{r}}_{det}^i\left|\right|}^2$, where i detectors are used in the calculation, $l_{\mathit{\text{PA}}}^i$ Is the protoacoustic-calculated distance between detector i and the BP, and ${\mathbf{r}}_{det}^i$ is the detector position. The ${\mathbf{r}}_{\mathit{\text{BP}}}^{\mathit{\text{PA}}}$ was calculated in two ways: unrestricted, in which x, y, and z are allowed to change, and restricted, in which the x and z BP positions are fixed to the actual values. The restricted calculation assumes that the lateral position of the proton beam is known, as is the case in the clinic (only the depth of penetration along the beam axis is uncertain).

2.5. Liver

The liver was chosen as a site to study because it represents a relatively homogeneous part of the body devoid of air pockets between irradiated material and detector. Proton beam arrangements for liver irradiation are chosen based on the tumor location. If present, ribs and air pockets (bowels or stomach) are avoided to minimize range uncertainty. Although less common than posterior oblique beams, the posterior arrangement chosen here is used clinically (Yuan et al., 2013), and it is ideal for these studies because the entrance surface is perpendicular to the beam and detectors may be placed at many different angles surrounding the beam. From the same starting dose and source pressure deposition, three different sets of simulations were run: (1) the water phantom case (WATER), in which all CT values were set to HU = 0, (2) the homogeneous patient phantom (HOM) in which all soft tissue and bone voxels (HU values for voxels originally > -200) were set to HU = 0, and the heterogeneous patient phantom (HET) in which no HU values were modified from the original (except for detector placement - see below). For the WATER and HOM phantoms, there was no attenuation and no dispersion, so c (and c₀) was always set to c_H2O = 1523.9 m/s, the speed of sound in water at 37 °C. For each phantom case, CT projections integrated along the superior-inferior direction (averaging the transverse slices within the simulation volume) are shown in Fig. 3 to illustrate the presence of ribs and lung.

Figure 3.

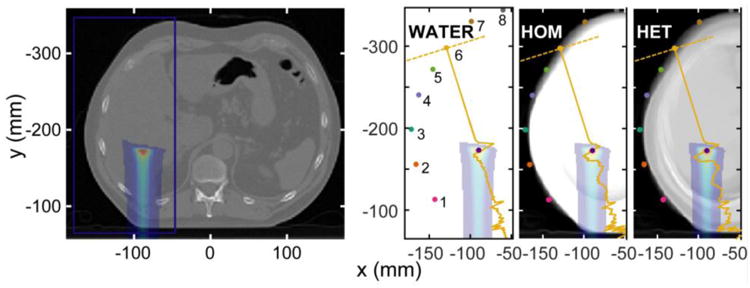
A transverse slice through the liver CT is shown (left) with the single PBS spot dose deposition and simulation volume boundary. The average HU of each simulation volume for the three cases are shown at right. The average x,y position of each detector set is shown along with a characteristic protoacoustic trace superimposed on the image. The detector sets are numbered counterclockwise from the lower left (as labeled in the WATER image).

For the liver simulation, 8 sets of 12 detectors were placed at various points on the skin surrounding the liver, which was irradiated posteriorly with a 124.9 MeV beam. The detectors within each set are spaced (∼6 mm) along a row in the superior-inferior direction (z) on the CT patient's skin. The average x,y position of the 12 detectors in each set are shown in Fig. 3.

In the k-Wave simulation, detectors are simply voxels whose time-dependent pressure is recorded. They are therefore ideal, point detectors that do not affect the simulation. Digitally placing a detector outside the CT patient's skin in an air voxel results in unrealistically low simulation pressures because pressure waves within the patient volume are heavily reflected at the skin/air interface. On the other hand, digitally placing a detector in an interfacial skin voxel or at a skin depth of a few millimeters within the tissue also presents a problem: incoming pressure waves interfere with themselves after reflecting off the skin/air interface, resulting in unrealistic simulated pressures. Realistic detectors have a finite size, are coupled to the skin by coupling gel, and do not reflect appreciable signal back into the patient. In order to simulate detectors more realistically, each of the 8 sets of detectors was simulated individually, and each detector was placed 6 mm away from the skin in a digitally generated 8 mm radius cylinder of material extending perpendicular to the skin surface (see supplementary data). The material of the cylinder was set to the average HU of the local skin. These cylinders approximate circular or spherical detectors coupled to the skin. By extending the cylinders to the edge of the simulation volume, no pressure entering the detector volume is reflected back into the patient because the edge of the simulation volume absorbs all incident pressure.

2.6. Prostate

To simulate the protoacoustic signal measured by a row of transrectal detectors, a 60 mm long, 24 mm diameter probe was digitally inserted into the patient's rectum by replacing the probe volume voxels with HU = 0. Nine detectors were defined at voxels centrally located along the probe and placed at 6 mm spacing, as shown in Fig. 4. Air pockets (HU < -150) within the rectum were replaced with HU = 0 to approximate filling with a rectal balloon to simplify the results by preventing acoustic reflections.

Figure 4.

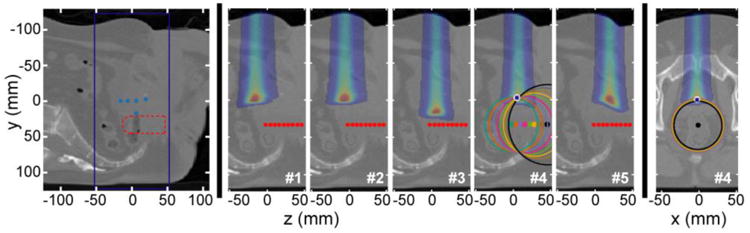
A sagittal slice through the prostate CT is shown (left) with the simulation volume boundary. The BP depth of the five simulated proton beams is shown (dots) along with the outline of the digitally-inserted transrectal probe volume. At center, the simulation volume is shown with dose deposition and detector points for the five separately simulated proton dose depositions. Beams #1,2,4,5 have the same energy (125.6 MeV), but different sup-inf propagation axes. Beam #3 has a higher energy (136.3 MeV), but the same propagtion axis as beam #4. At right, a transverse slice shows the beam #4 dose deposition. The triangulation process is illustrated for beam #4 (δ proton pulse excitation). Converting the arrival time to distance specifies a sphere. After setting the x and z beam coordinates based on the known beam axis position, the penetration depth can be calculated (restricted triangulation). The actual BP and protoacoustically-triangulated positions are indicated with a white dot and blue asterisk, respectively.

To assess the proton range verification potential, five acoustic simulations were run with five different PBS spots on the HET phantom, as shown in Fig. 4. The triangulation process for beam #4 is also illustrated.

2.7. Simulation details

Eclipse simulations were performed with 1 mm grid spacing. k-Wave simulations were performed with voxel size 1.5 × 1.5 × 1.5 mm³ and a time step of ≤ 98 ns. The volumes of the liver and prostate simulation volumes were 89 × 189 × 53 and 77 × 165 × 71 voxels, respectively. To prevent reflections from the sides of the simulation volume, a perfectly matched layer of 10 voxels was added to each side of the volume. To decrease computational time, the MATLAB k-Wave toolbox was used to generate C++ input files, which were then run on a computer with 32 Gb of RAM and two Intel Xeon CPU E5-2620 2.00 GHz processors. Heterogeneous liver and prostate simulations were computed in ∼12 and ∼14 minutes, respectively.

The consistency of the k-Wave simulations was tested for different time steps and voxel sizes. Decreasing the time step generated the exact same results. For the HET liver simulations, decreasing the voxel size from 1.5 × 1.5 × 1.5 mm³ to 0.5 × 0.5 × 0.5 mm³ resulted in an arrival time difference of 0.24 ± 0.18 μs, an amplitude difference of 8 ± 3% (mean ± standard deviation), and an increase in computation time to ∼8.5 h (40× slower). The voxel-size dependence is attributed to CT interpolation effects (see supplementary data).

3. Results

Liver

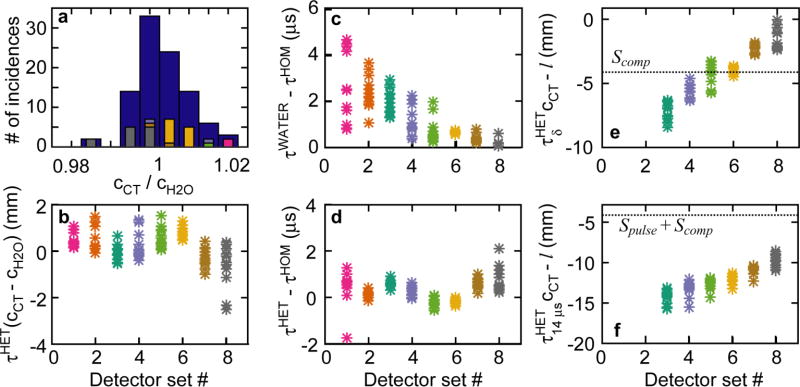
To compare the speed of sound in water and in heterogeneous tissue, a histogram of c_CT / c_H2O is plotted in Fig. 5a. For each detector, the average, frequency-dependent speed of sound was calculated along a ray through the HET phantom between the Bragg peak and detector. The histogram shows that the average speed of sound in the heterogeneous phantom is within 2.2% (mean = 100.3%, std. dev = 0.65%) of the c_H2O for the liver case studied here.

Figure 5.

The liver case arrival time results are shown for the δ excitation proton pulse (unless noted). (a) The ratio of CT-mapped speed of sound averaged over the BP-to-detector path to water speed of sound is shown as a histogram for all detectors (blue) and each individual detector set (foreground, color). (b) The difference in τ*c - the uncorrected TOF distance - calculated with c_CT and c_H2O is plotted for each detector set. (c) The difference between arrival times measured in the WATER and HOM phantoms are shown. (d) The difference between arrival times measured in the HET and HOM phantoms are shown. The difference between uncorrected TOF distance for the δ-function (e) and 14 μs FWHM Gaussian (f) proton pulse are plotted.

A characteristic simulated protoacoustic pressure trace is plotted on Fig. 3 (right). The pressure trace is recorded as a function of time, but, in the figure, it is plotted on a t*c_CT axis extending from detector to Bragg peak (the detector position corresponds to t = 0). Similar plots have been used previously to visualize how the pressure wave reports on the Bragg peak position(Hayakawa et al., 1995; Patch et al., 2016). As shown, the positive compression pressure peak arrives before (it is closer to the detector) the Bragg peak. The negative rarefaction peak arrives after the positive peak. All arrival times, τ, reported here are measured from the peak of a polynomial fit of the first-arriving, positive compression peak (τ_comp). For the shown characteristic pressure traces, calculating the detector-to-BP distance (l_PA) from l_PA =τ_comp *c_CT would result in an underestimate (l_PA < l; the plotted pressure peak is short of the BP in Fig. 3). This underestimation has been characterized in previous simulations, and S_pulse and S_comp are used in an attempt to compensate(Jones et al., 2016a).

The difference in arrival times, Δτ_comp, simulated for the WATER, HOM, and HET phantoms are shown in Fig. 5c-d. From comparisons of the WATER and HOM phantom, the simulated pressure waves arrive 0.1 to 4.7 μs later in the HOM phantom than in the WATER phantom, despite both simulations having the same speed of sound and initial pressure distribution. The simulated pressure waves arrive -1.8 to 2.1 μs later in the HET phantom than in the HOM phantom.

From HET phantom simulations, the difference in TOF distances calculated using the CT-derived speed of sound, c_CT, and average water speed of sound, c_H2O, span -2.5 to 1.5 mm (Fig. 5b). The largest difference is observed for detectors that are both far from the BP (set #7 and set #8) and for those whose average speed of sound differs from c_H2O.

The difference in TOF-calculated distance and actual BP-to-detector distance is shown in Fig. 5e-f Before correcting for S_comp and S_pulse, the actual distance between BP and detector, l, is 8.4 to 0 mm greater than the TOF-calculated τ_comp·c_CT for the delta-function proton pulse, and 8.6 to 15.6 mm greater for the 14 μs FWHM Gaussian proton pulse.

The pressure amplitudes measured at each detector for WATER, HOM, and HET simulations of a δ-function excitation proton pulse are shown in Fig. 6a. The simulated pressure amplitude generally decreases with increasing distance between BP and detector, although more pressure is observed distal to the BP due to constructive interference from the broad, relatively flat distal dose deposition. The WATER simulations result in 1.4 to 4.8 times higher simulated pressure at the detectors than when the waves propagate through the HOM phantom. The attenuation-less WATER and HOM phantoms result in higher pressure than in the HET phantom. From 1 × 10⁷ protons (1.4 cGy at the BP), 50 mPa of pressure is expected in the HET phantom (at 13 cm distal, detector set #6) for the δ-function excitation proton pulse. The ratio of pressure simulated in the HET and HOM simulations is shown in Fig. 6b. Aside from detector sets #7 and 8, which show lower than expected pressure amplitudes, the pressure amplitude scales with the average attenuation between BP and detector. For the 14 μs Gaussian excitation proton pulse, there is little (<20%) amplitude difference between HOM and HET phantom simulation amplitudes, but a large drop in pressure (5 mPa expected at detector set #6) relative to the δ-function proton excitation pulse (see supplementary data).

Figure 6.

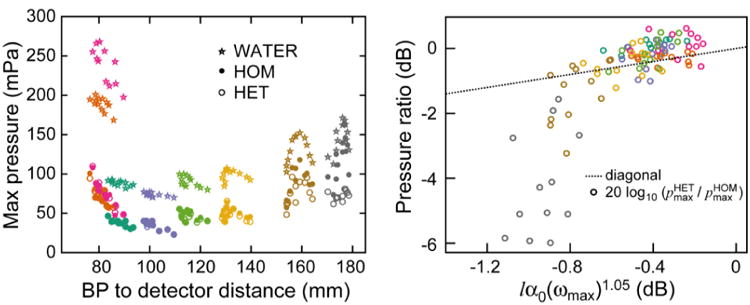
The liver case maximum pressures are shown for the δ excitation proton pulse (left). The ratio of maximum pressures from the HET and HOM phantoms is shown (right) as a function of the CT-mapped attenuation averaged over the BP-to-detector path. The HOM phantom simulation has no attenuation. Data points are color-coded based on detector set (as in Figs. 3+5).

The protoacoustic-triangulated BP position was calculated from the HET simulations using c_CT and c_H2O for a δ-function and 14 μs FWHM Gaussian proton pulse from the pressure waves simulated for each detector set (Table 2). The distance between true and protoacoutic-calculated Bragg peak positions, $|{\mathbf{r}}_{\mathit{\text{BP}}}^{\mathit{\text{PA}}}-{\mathbf{r}}_{\mathit{\text{BP}}}|$, are reported for the unrestricted (Δr) and restricted (Δy) calculations. The 12 detectors in each of the 8 sets of detectors represent a small detection region, which does not allow for triangulation from a single set. Therefore, in order to perform an unrestricted triangulation, the measurements from all 96 detectors are used, and result in errors of 4.2 and 7.5 mm (δ and 14 μs, respectively). When all detectors are used, assuming that the x and z positions of the BP are known results in protoacoustic range verification errors of 0.4 and 5.8 mm (δ and 14 μs, respectively). For the δ-function excitation proton pulse, using c_CT rather than c_H2O results in a slight improvement in BP position determination accuracy. For the 14 μs FWHM Gaussian excitation proton pulse, use of c_H2O or c_CT result in almost identical results.

Table 2.

The error in protoacoustic-based triangulation of the Bragg peak position in the liver case. Δr is the distance between the actual BP position and the protoacoustic-determined position based on an unrestricted triangulation. Δy is the error in proton range calculated with the protoacoustic arrival time under the restricted conditions.

Proton Pulse	Speed of Sound		Detectors
			Set 3	Set 4	Set 5	Set 6	Set 7	Set 8	All
δ	cH2O	Δr (mm)							4.2
		Δy (mm)	18.9	3.1	0.6	0.6	1.1	1.4	0.4
	cCT	Δr (mm)							4.2
		Δy (mm)	18.2	3.0	0.5	0.5	1.2	1.5	0.3
14 μs FWHM	cH2O	Δr (mm)							7.5
		Δy (mm)	25.9	10.3	7.3	5.8	4.6	3.5	5.8
	cCT	Δr (mm)							7.4
		Δy (mm)	25.9	10.3	7.3	5.8	4.6	3.4	5.8

Prostate

The process of triangulation is illustrated in Fig. 4 and the results are reported in Table 3. Each circle corresponds to the intersection of the shown image slice with the sphere of radius l_PA calculated from the arrival time simulated for each detector. If the x and z BP positions are known, the protoacoutic range verification accuracy is < 1.6 mm (δ-function proton pulse) for beams #2-5 and 4.3 mm for beam #1. There is little observed difference in accuracy for the calculations based on simulations with the δ-function or 14 μs FWHM excitation proton pulses.

Table 3.

For each simulated prostate proton beam, the BP range was calculated based on the protoacoustic arrival times measured at all the transrectal detector points under the restricted conditions.

Proton Pulse	Speed of Sound		PBS Beam
			#1	#2	#3	#4	#5
δ	cH2O	Δy (mm)	3.9	1.3	0.2	0.6	1.6
	cCT	Δy (mm)	4.3	0.7	0.2	0.3	1.1
14 μs FWHM Gaussian	cH2O	Δy (mm)	0.3	0.6	1.3	0.8	3.0
	cCT	Δy (mm)	0.0	1.2	1.3	0.5	2.6

The simulated pressure amplitudes are higher for the prostate than the liver case. The maximum simulated pressure (δ proton pulse) is 1000 mPa for beam #3 (1.3 cGy at BP, closest detector at 16.6 mm) and the minimum is 110 mPa for beam #1 (1.0 cGy at BP, furthest detector at 71 mm). For the 14 μs FWHM Gaussian excitation proton pulse, the maximum pressures span 160 to 50 mPa for the same detectors as above (see supplementary data).

4. Discussion

For envisioned clinical application of protoacoustics, transducers placed on or in the patient will be identified and registered to the treatment room, proton beam, and patient coordinates by a pre-treatment cone-beam CT (CBCT). Protoacoustic pressure waves recorded by the transducers will be used to calculate the proton beam range within the patient (by virtue of the co-registered coordinates) using an average speed of sound (like c_H2O). Currently, range uncertainty is limited by inter-fraction patient anatomy changes, set-up error, and CT-to-stopping power conversion error. Instead of relying on dose calculations, in vivo range verification techniques are attractive because they remove many of these errors through measurement. Through the proposed protoacoustic technique, which seeks to measure distance between detector and Bragg peak, realtime in vivo range verification would replace the current, limiting errors with protoacoustic-specific errors, which are due to (eq. (4)): heterogeneity (c), non-ideal proton pulses (S_pulse), arrival time definitions (S_comp), asymmetric Bragg peak depositions (S_ϕ), and noise. With the exception of heterogeneity, the other errors have been investigated experimentally (Jones et al., 2016b) and in simulation (Jones et al., 2016a). For the proposed clinical application, another additional complexity is intra-fraction patient motion, which will add error into the registration between protoacoustic and patient (CBCT) coordinate system. A possible solution is to create a dual ultrasound-protoacoustic probe, which would, in theory, allow for the protoacoustically-identified Bragg peak to be registered with anatomy identified on a real-time ultrasound image ((Patch et al., 2016)).

Through the presented simulations, the “ground truth” proton beam range is compared to the protoacoustic-calculated range with the goal of characterizing the protoacoustic errors, particularly the effect of heterogeneous tissue on the speed of sound (c) and signal amplitude. The simulations are based on acoustic parameters drawn from literature. Experimental validation is required to assess the underlying assumptions, but the simulations represent an informed attempt to model and assess the protoacoustic technique in tissue given the available data.

4.1. Assumptions

The simulations presented here are based on a number of assumptions. If the simulation results are compared to experiment, there are assumptions in the dose deposition calculation -converting the CT to proton stopping power (up to 4.6% error, hence one of the reasons for in vivo range verification(Paganetti, 2012)). Even if the dose deposition is taken to be correct, the source pressure depends on β, C_p, and c and the acoustic pressure wave propagation depends on c₀, ρ, and α. All of these variables are mapped based on the voxels' HU values, and β, C_p, and α are assigned discretely from five possible values (Fig. 2). Of these, the expansion coefficient (β) is the least well known in the literature, but erroneous assignment only causes a change in pressure amplitudes, which have little effect on arrival times (and TOF-based range verification). Of the acoustic variables, we speculate that the simulation results are most sensitive to c because the speed of sound dictates the arrival time and the complex interference effects. Mapping c based on HU is reported to have a standard deviation of 20 m/s, but this mapping was performed over a limited density range (0.95-1.12 g cm^-3) of soft tissues at ∼1 MHz, and c is frequency dependent (based on dispersion, which is itself linked to attenuation: α₀ and d). Ultimately, comparison between simulations and experimental protoacoustic results from heterogeneous materials are required to validate the acoustic parameters. CT-based acoustic models have been proposed previously to aid in image registration(Wein et al., 2008), increase ultrasound accuracy(Fontanarosa et al., 2011) and assess the biological origin of sound production(Aroyan et al., 2000; Narasimhan et al., 2004), but validation in these cases does not necessarily extend to the applications proposed here.

The simulation sites – liver and prostate – were chosen to minimize the uncertainty introduced by the underlying simulation assumptions. Because c is calibrated in soft tissue, the liver and prostate sites were chosen for study because of their homogeneity and the minimal presence of air pockets and bone. For liver, the simulation volume predominately contains liver tissue with additional muscle, fat/adipose tissue, a small portion of lung, ribs, and the surrounding air. The 1 MHz c mapping used in the simulation assigns a speed of sound of 1578 m/s to liver, which is close to the 1586 m/s reported in the literature (Table 1). From ultrasound, bone and air pockets are known to be poor transmitters due to attenuation and high reflectivity. Due to its lower frequency (<500 kHz (Jones et al., 2016a)), the penetration of protoacoustic pressure waves is expected to be higher than >1 MHz ultrasound waves, which may make protoacoustic brain studies viable even though skull attenuation prevents ultrasound imaging(Tavakoli and Evans, 1991; Nie et al., 2012). Acoustic simulations with bone were avoided here, however, as the accuracy of simulation results is questionable given the lack of study of bone acoustic parameters(James et al., 2017). For example, the correlation between bone density and sound speed is reported to be different than the soft tissue correlation(Lees et al., 1983; Mast, 2000). The properties of soft tissues are better characterized, and the variation in density, speed of sound, and attenuation is smaller than in bone, which leads to lower expected errors in the presented simulations. Unfortunately, the presence of bone is often correlated with high range uncertainties, and these sites would benefit the most from in vivo range verification. Some high uncertainty sites - in which the proton beam passes through bone, but there is not bone between Bragg peak and detector - can be simulated without needing bone acoustic properties, but further characterization experiments are required to simulate and assess protoacoustic propagation through cranial structures. Even without this knowledge, however, cranial experiments may provide an acceptable average speed of sound that can be used to convert protoacoustic arrival time into accurate distances; the clinical application of protoacoustics does not rely on CT-based acoustic parameters, only the simulations of acoustic propagation rely on the assumed CT mapping. Despite the underlying assumptions, the goal here is to propose a CT-based heterogeneous simulation method and, as best as can be achieved given available data, predict the effects of heterogeneity on the amplitude and arrival times of the protoacoustic signal.

The simulations also assume ideal, point detectors. Ideal detectors were chosen to keep the results general, as realistic corrections are specific to the chosen transducers. Despite the large physical sizes of detectors (up to 2 cm for larger hydrophones) that have been used in previous experimental studies, sub-millimeter accuracy has been reported (Lehrack et al., 2017). Aside from physical sizes, which will limit their placement and the number that can be used, realistic transducers may have three effects on the measured acoustic signal: limited bandwidth, directionality, and non-coincidence of acoustic and physical center (a frequency-specific phase shift). The limited bandwidth cuts out portions of the frequency spectrum and, as peaks are distorted (generally, broadened if higher frequencies are removed), results in a possible change in measured arrival time (Assmann et al., 2015). Because the simulated protoacoustic signals have low frequencies (the simulated spectrum for the δ function proton-induced signal peaks at 50 kHz), frequency filtering the heterogeneous liver-simulated protoacoustic waves with the bandwidth of a Bruel & Kjaer 8105 (BK) hydrophone ((Jones et al., 2015), maximum sensitivity at 125 kHz, diminishing to 50% relative sensitivity at 150 kHz) causes negligible changes in arrival times (δ proton pulse: change in arrival time ± standard deviation = -0.12 ± 0.44 μs; 14 μs proton pulse: -0.7 ± .13 μs). Thus, for the ideal detector simulations presented here, applying a realistic bandwidth will have negligible effects on the range verification results (0.12 μs shift translates into <200 μm) because real hydrophones capture the majority of the expected bandwidth. It should be noted that because protoacoustic signals are low, future application-optimized hydrophones/transducers might sacrifice broad bandwidths for sensitivity (e.g. tuning the resonance more drastically to the protoacoustic bandwidth), at which point the resulting limited frequency response is expected to have a more significant impact on arrival times. For directionality, the experimentally-used omnidirectional BK hydrophone was well modeled by a simulated point detector when submerged in a water bath (Jones et al., 2016b), but use of a flat, non-spherical transducer will create directional dependence in the response, which effectively narrows the detector field-of-view. To approximate the directionality imposed by coupling a spherical detector to the skin (e.g. with coupling gel), cylinders of material were added to the simulations (as discussed in the methods section). Simulating the directionality of a non-spherical detector can be achieved by approximating the detector as its constituent voxels, and averaging the signal simulated at each individual voxel. The third difference between an ideal and realistic detector – the frequency-dependent phase response or non-coincidence between acoustic and physical center – results in a delay between waves measured with an ideal and real detector. This offset can be measured experimentally (Jones et al., 2016b; Lehrack et al., 2017)and then added in post-processing. To summarize the above, realistic detectors will result in a calibration-correctable delay, and the limited bandwidth is not expected to appreciably affect the range verification accuracy (assuming sensitivity up to ∼150 kHz). If the transducer bandwidth is severely limited (at low or high frequencies), then arrival times may be shifted, and the effect must be considered.

4.2. Qualitative Effects of Heterogeneity

Proton dose deposition causes heating that generates thermoacoustic pressure waves (protoacoustics). The characteristic simulated pressure waves shown in Fig. 3 display the expected bipolar wave shape (positive followed by negative peaks), but they are more complex than the waves simulated and measured previously for a dose deposition in a water tank (Jones et al., 2016a; Jones et al., 2016b). The reason for this complexity is the material heterogeneity. The source pressure, from which the protoacoustic waves propagate, is not continuous and cylindrically symmetric, as it is in the water tank case. The source pressure depends on the dose deposition and the Grüneisen parameter of the material, both of which are different for heterogeneous materials. For example, fat is measured to have a Γ = 0.8(Yao et al., 2014), while soft tissue is expected to be Γ = 0.25-0.28 (Fig. 2). Thus, for the same deposited energy, fat will generate ∼2.8 times more thermoacoustic pressure than soft tissue. Both the dose deposition and the Grüneisen parameter vary in heterogeneous materials, which creates a complex source pressure with areas of higher and lower pressure. As described in the methods section, for the purposes of this study, the dose deposition and source pressure were calculated on the HET phantom and then transferred to the WATER and HOM phantoms to seed the simulations of acoustic propagation. Thus, the liver case is focused on understanding how heterogeneity affects the acoustic propagation, not the acoustic generation. Due to the complexity of the generated pressure waves, the arrival time of the first, positive compression peak was used for the TOF calculations because it is the least susceptible to interference (it arrives first) and has the largest amplitude.

4.3. c_H2O vs c_CT

For the liver case, the average speed of sound measured between the Bragg peak and each detector in the HET phantom, c_CT, only varies by <2.2% from the speed of sound in water c_H2O (Fig. 5a). Although the variation in speed of sound ranges from 1304 to 2024 m/s along the path between detector and Bragg peak, these deviations cancel out when the average is taken. This suggests that, as is assumed in ultrasound, a single speed of sound may be adequate for protoacoustic TOF calculations. Because a CT is always collected for treatment planning in proton therapy, the c_CT may also be calculated based on the anticipated proton beam penetration without upsetting the clinical workflow and without the acquisition of additional images. If the average errors in converting HU to speed of sound along the path between Bragg peak and detector are greater than the errors in converting HU to stopping power (a question requiring experimental study), however, c_CT-based protoacoustic calculations will not beat out careful Monte Carlo-calculated range predictions. Because c_CT is close to c_H2O, the distance calculated with each only differ by < 2.5 mm (Fig. 5b). The further the distance between detector and BP, the later the arrival time, and the greater error will be introduced if c_H2O is assumed in place of c_CT (2% of 10 cm > 2% of 1 cm). The largest differences between c_CT and c_H2O are observed herefor some detectors from set #1 and #8 where interceding ribs and fat, respectively, skew the average speed of sound along the acoustic pathlength.

4.4. Effect of Body Contour

Although the non-air parts of the WATER and HOM phantoms are composed of the same material (HU = 0), the arrival times differ by 0.1 to 4.7 μs (Fig. 5c) and there is a significant decrease in pressure amplitude for WATER versus HOM phantoms (Fig. 6a). The only difference between the two phantoms are the air spaces: WATER is a solid rectangular volume while HOM is formed based on the patient's body. Therefore, the difference in arrival times are attributed to two effects: interference between (i) waves from different portions of the dose deposition – in the HOM case, detectors have a limited field-of-view – and (ii) between the acoustic waves reflecting off of the skin-air interface in the HOM phantom. As described in the methods section above, in the HOM (and HET) phantom each set of detectors is simulated separately with the addition of cylinders of material extending normal to the skin surface and centered on the detectors (see supplementary data). These cylinders approximate the effect of coupling an absorbing detector on the skin surface. For detectors placed lateral to the Bragg peak (sets #1 and #2 in particular, Fig. 3), the cylinders enforce a direction-dependent detector sensitivity: the protoacoustic waves from the beam entrance do not reach detector sets #1 and #2 because there is air in the path between beam entrance and detector due to the curvature of the body. The reduced field-of-view of the dose deposition volume created by the body curvature causes the drop in amplitude reaching the detectors in the HOM versus WATER phantoms (Fig. 6a).

4.5. Effect of Heterogeneity: arrival time and amplitude

The difference in arrival time and pressure amplitude simulated at identical detectors in the HOM and HET phantoms can be attributed to the effect of heterogeneity. Although the c_CT in the HET phantom varies over +/- 2.2% of the c_H2O of the HOM phantom, the HET pressure waves almost all arrive after the HOM simulated waves. Based on the c_CT/c_H2O ratio, one would expect that Δτ (Fig. 5d) would also vary between positive and negative values. The reason for the positive Δτ values can be explained by interference - the fact that the waves take multiple paths from the dose deposition to the detector. The acoustic waves propagate in all three dimensions, and c_CT only represents the direct path between Bragg peak and detector. In the simulation (and reality), the acoustic waves take many paths to reach the detector, and the interference between multiple path waves arriving at the detector at slightly delayed times will likely cause the compression peak to arrive later than in the homogeneous case - the compression peak from the first arriving wave will be shifted to later time by the constructive interference from a second arriving (slightly delayed) wave.

For most of the considered detectors, the difference in amplitude between the HOM and HET simulations can be explained by the average attenuation of the material between BP and detector. Detector set # 8, however, displays a lower amplitude for the HET simulation relative to the HOM simulation than would be expected based on the attenuation alone. The other causes of amplitude loss are reflections and interference. Reflections occur at interfaces with mismatched acoustic impedance. There are no unusual interfaces (compared to the other detector paths) along the path between the Bragg peak and the detectors in set #8. For detector sets #7 and #8, the drop in amplitude between HOM and HET phantoms is largely attributed to destructive interference due to the fat/adipose tissue (lower sound speed causes slower propagation of part of the wave) observed in the -y,+x corner of the transverse image (see supplementary data movie). Also, at the skin surface, a strong negative pressure wave is generated by the air interface reflection, and it is funneled by the body curvature towards detectors sets # 7 and #8 (supplementary movies), which may also cause a drop in amplitude.

For the 14 μs Gaussian excitation proton pulse, the small difference between HOM and HET simulated pressure amplitudes can be attributed to the lower frequency (δ:mean(ω_max) = 50kHz; 14 μs: mean(ω_max) = 37 kHz), which results in lower attenuation and less significant destructive interference due to c-dependent delays because of the temporally broad pressure peaks: a few microseconds of heterogeneity-induced relative delay between ∼20 μs pressure peaks still generates constructive interference while it results in destructive interference for ∼5 μspressure peaks.

4.6. Range Verification Accuracy: liver case

For the liver case, the Bragg peak positions calculated based on the simulated protoacoustic waves are given in Table 2. Each set of detectors consists of a row of 12 detectors placed superior-inferiorly along the skin. Without assuming the lateral (x,z) position of the beam, the Bragg peak position cannot be determined from a single set of 12 detectors because they are close together - approximating a point - and only report a distance to the Bragg peak (not a direction), which specifies a sphere of possible BP positions. When all sets are considered, the BP position can be determined to within Δr = 4.2 mm of the true position (for the δ-function like excitation proton pulse) based on distances provided from multiple points around the BP. Sets #1 and #2 are not considered, because they are lateral to the dose deposition, and therefore primarily report on the distance to the beam axis (α-wave)(Jones et al., 2014) rather than distance to the BP. In the clinic, the lateral position of the proton beam is known with submillimeter accuracy relative to the room coordinates. Therefore, as long as the protoacoustic detector is properly registered to the beam delivery/room coordinates (through identification of the detectors on pre-treatment CBCTs, for example), the BP lateral positions are known within imaging tolerances (±1 mm), and the protoacoustic triangulation process can be restricted from determining the BP x, y, and z to just the BP range depth (y in this case). Intra-fraction patient movement is a problem for this restricted calculation, as it will introduce errors in the registration between room/beam, detector, and/or patient coordinates, but, even with a few millimeters of unintended patient shift, the calculated Δy is expected to be more accurate than if no a priori information of the beam coordinate is used in the calculation. When it was assumed that the proton beam axis is known, this restriction was applied, and the BP depth can be determined from a single set of detectors. Set #3 produced less accurate results than the other sets. This can be attributed to their respective positions: measuring from a more lateral position is expected to be less accurate than measuring from a more distal position closer to the beam propagation axis (S_pulse is calibrated for detectors in a 30° cone distal to the beam propagation axis)(Jones et al., 2016a). Combining the protoacoustic measurements from many view points (many detector sets), resulted in a further increase in accuracy down to <0.4 mm. Use of c_CT in the TOF calculation provided similar results as when c_H2O was used, which is expected given the similarity between the two values(Fig. 5a). The protoacoustic waves generated by δ-function and 14 μs FWHM Gaussian excitation proton pulses are different. For proton pulses with rise times > ∼5 μs, stress confinement is lost, and the resulting emitted protoacoustic waves are broadened, decrease in amplitude, decrease in frequency, and arrive later in time. As shown in Fig. 5e+f, the S_pulse andS_comp correction factors change. For the 14 μs FWHM Gaussian excitation proton pulses, there is a larger error in the range verification process, which is expected to be due to the additional corrections (S_pulse) - and therefore larger chance of error - required for non delta-function proton pulse excitations. Even before triangulation, Fig. 5f shows that the S_pulse + S_comp is too high, and does not properly correct the difference between l and the τ*c simulated for the protoacoustic waves generated by the 14 μs FWHM Gaussian excitation proton pulses.

4.7. Prostate Case

The prostate site was chosen to show another possible clinical application of protoacoustic based range verification. By using a transrectal array of detectors, the position of the Bragg peak may be triangulated. The amplitude of the simulated pressure waves is higher in the prostate case than in the liver case because the detectors are closer to the BP and, because the detectors are surrounded by tissue rather than on the skin, they do not suffer from a restricted field-of-view of the dose deposition, as in the liver case. Because the transducers are limited to a line within the transrectal probe, the triangulation process can only determine a circle of potential BP positions if the BP x and z positions are not assumed. Therefore, only the restricted triangulation calculation was applied, and Δy is reported.

When the prostate is irradiated with the δ-function excitation proton pulse, the y position of the BP is calculated to within 1.6 mm for beams #2-5 (using c_H2O or c_CT). For beam #1, the BP is laterally displaced from the detectors (> 15 mm along z), and the Δy error is up to 4.3 mm (c_CT). Previous simulations in water have predicted 1-2 mm errors in range verification when the detector is placed lateral to the BP, and S_comp was determined based on detectors placed within a 30° cone distal to the BP(Jones et al., 2016a). Only one (the closest) detector falls within this cone (24.6°) for beam #1. While beam #2's BP is also slightly displaced from the detectors (4.5 mm along z), three of the nine detectors fall within the cone, and the range verification is calculated with <1.3 mm. Another disadvantage of laterally placed detectors is that the 9 detectors represent a less varied set of observation points. When the BP is directly above the detectors (eg, beam #4), angular variations in the TOF calculation errors may be canceled out by combining the results from multiple detector vantage points. Although beam #5 is centrally located relative to the line of detector points, its Δy error is slightly higher than for beams #2, 3, and 4. This may be because of the tilt in the Bragg peak caused by the uneven entrance surface. As with the liver site, the range calculations using c_H2O and c_CT were similar. In general (beam #1 being the exception), TOF calculations using the 14 μs Gaussian excitation proton pulse simulation results yielded less accurate BP positions. As described above, the longer excitation proton pulses introduce errors. The corrections for these errors are based on simulations performed in water tanks with cylindrically symmetric dose depositions. In heterogeneous materials, the dose deposition is distorted, and the simulation-derived corrections (S_pulse) may no longer be sufficient, with increasing errors expected for increasing excitation pulse widths.

4.8. General Discussion

General observations can be drawn from the presented simulations. Lower pressure amplitudes are expected for protoacoustic measurements in heterogeneous tissues versus homogeneous water tanks. In the considered soft tissue liver and prostate cases, the amplitude decrease is largely due to patient contour-related, restricted detector field-of-views and destructive interference, not attenuation; the low protoacoustic wave frequency (ω_max < 50kHz) means lower attenuation relative to > 1 MHz ultrasound techniques. TOF-based protoacoustic range verification is predicted to achieve <1.6 mm accuracy when δ-function irradiation proton pulses are used and the beam propagation axis (here, the BP x and z coordinates) is known, but this accuracy depends on detector placement - multiple distal detectors are preferred. When longer proton pulses are used, the range verification accuracy and pressure amplitudes tend to decrease, although lower frequency waves are less sensitive to attenuation and destructive interference. For the considered soft tissue cases, the average speed of sound between detector and BP calculated from CT mapping (c_CT) is close to the speed of sound in water at 37°C (c_H2O), and TOF calculations based on both were similar. Thus, approximating the speed of sound in tissue as c_H2O may not lead to appreciable loss of accuracy in protoacoustic range verification. Here, c_H2O was used as the representative value, but further investigations are required to determine whether a different value – such as the c_saline = 1540 m/s used in ultrasound diagnostic imaging – may provide more accurate results. The TOF range calculation requires correction terms (S_pulse, S_comp) calibrated by simulation or experiment. Experimental measurements are needed both to validate the presented model and to test the generalizability of these conclusions to other anatomical sites and beam/patient geometries. The robustness of the technique to intra-fraction patient movement must also be assessed.

Previous experimental water tank studies have shown that the precision of the protoacoustic range verification technique is limited by the dose-restricted signal-to-noise ratio(Jones et al., 2016b). Although the noise-less simulations predict that under certain conditions < 1.6 mm accuracy is achievable in heterogeneous tissue, the up-to ∼5× drop in pressure amplitude associated with moving from a water tank to a patient presents a challenge for clinical translation. Placing the detectors as close to the BP as possible (as with the transrectal probe) and using < 5 μs proton pulses will maximize the measured pressure amplitudes. The SNR/dose is maximized at ∼5 μs FWHM proton pulses, so sub-1 μs proton pulses may be overly short (Jones et al., 2016a).

5. Conclusions

A CT-based method for simulating the protoacoustic signal in heterogeneous materials is presented. For the considered liver and prostate cases, accurate ≤1.6 mm time-of-flight based protoacoustic range verification may be possible under ideal conditions when multiple detectors are placed distal to the Bragg peak and the lateral beam position is known. The pressure amplitude decreases in heterogeneous tissue relative to homogeneous water phantoms by up to 5 times primarily due to reduced detector field-of-view and destructive interference.