Abstract
The purpose of this study was to investigate the feasibility of incorporating linear energy transfer (LET) into the optimization of intensity modulated proton therapy (IMPT) plans. Because increased LET correlates with increased biological effectiveness of protons, high LETs in target volumes and low LETs in critical structures and normal tissues are preferred in an IMPT plan. However, if not explicitly incorporated into the optimization criteria, different IMPT plans may yield similar physical dose distributions but greatly different LET, specifically dose-averaged LET, distributions. Conventionally, the IMPT optimization criteria (or cost function) only includes dose-based objectives in which the relative biological effectiveness (RBE) is assumed to have a constant value of 1.1. In this study, we added LET-based objectives for maximizing LET in target volumes and minimizing LET in critical structures and normal tissues. Due to the fractional programming nature of the resulting model, we used a variable reformulation approach so that the optimization process is computationally equivalent to conventional IMPT optimization. In this study, five brain tumor patients who had been treated with proton therapy at our institution were selected. Two plans were created for each patient based on the proposed LET-incorporated optimization (LETOpt) and the conventional dose-based optimization (DoseOpt). The optimized plans were compared in terms of both dose (assuming a constant RBE of 1.1 as adopted in clinical practice) and LET. Both optimization approaches were able to generate comparable dose distributions. The LET-incorporated optimization achieved not only pronounced reduction of LET values in critical organs, such as brainstem and optic chiasm, but also increased LET in target volumes, compared to the conventional dose-based optimization. However, on occasion, there was a need to tradeoff the acceptability of dose and LET distributions. Our conclusion is that the inclusion of LET-dependent criteria in the IMPT optimization could lead to similar dose distributions as the conventional optimization but superior LET distributions in target volumes and normal tissues. This may have substantial advantage in improving tumor control and reducing normal tissue toxicities.
1. Introduction
In clinical practice, proton therapy treatments to date have been prescribed at physical doses 10% lower than those used in photon therapy. This paradigm is based on an assumption that doses deposited by protons are 10% more biologically effective than those by photons. In other words, the relative biological effectiveness (RBE) of protons versus photons is considered to have a constant value of 1.1. However, it is known that RBE is a complex variable dependent on many factors, including dose per fraction, linear energy transfer (LET), tissue type, biological endpoint, etc. Nevertheless, proton therapy practitioners continue to use the simplistic constant RBE due, in part, to the lack of reliable and accurate predictive RBE models (Paganetti et al., 2002).
The LET, defined as the average energy transfer (ionization) per unit distance traveled by charged primary particles (ICRU, 2011), increases slowly at first and then exponentially near the end of proton range. It is shown that increased LET leads to increased RBE, especially at the end of range of protons (Wilkens and Oelfke, 2004; Guan et al., 2015a), where the RBE value can be 1.3 or higher at the Bragg peak and 1.6 or higher in the fall off region (in a few millimeters). Precautions in this respect have been taken into account in current proton treatment planning by avoiding the use of beams whose distal edge may end up in or close to a critical structures. In this way, the possible overshooting due to uncertainties in dose distributions and the resulting damage of high LET/RBE protons to healthy tissues could be prevented. However, this measure may prevent the selection of potentially beneficial beam angles and could diminish the therapeutic value of proton therapy.
In passively scattered proton therapy (PSPT) and single field optimized intensity modulated proton therapy (SFO-IMPT), high LET protons at the distal edge of each beam are unavoidably placed in normal tissues just beyond the distal edges of target volumes. In multiple field optimized intensity modulated proton therapy (MFO-IMPT), denoted as IMPT hereafter, intensities of beamlets from all incident beams are simultaneously optimized to meet dosimetric requirements. IMPT thus has much higher degree of freedom for modulation than PSPT and SFO-IMPT. Previous studies have shown that highly modulated fields in IMPT can produce equivalent physical dose distributions but greatly different LET distributions (Grassberger et al., 2011; Giantsoudi et al., 2013). Therefore, in theory it is feasible for IMPT to produce satisfactory dose distributions while achieving desirable LET distributions, e.g., placement of high LET protons inside target volumes and away from critical normal tissues, guided by innovative planning or optimization techniques.
Although treatment planning and optimization methods that incorporate variable RBE of protons have been explored (Wilkens and Oelfke, 2005; Frese et al., 2011), they have not yet been implemented clinically. This may be due to the reluctance to accept the resulting physical dose (i.e., RBE of 1.1) distributions from such methods, which may not be consistent with conventional practice. However, recent clinical data have reported unforeseen normal tissue complications from proton treatments (Sabin et al., 2013; Gunther et al., 2015) and their positive correlation with high LETs (Peeler et al., 2016). Subsequently, considering the RBE dependence on LET in treatment planning while preserving the physical dose prescribed in current practice has been focused in recent studies (Bassler et al., 2010; Giantsoudi et al., 2013; Bassler et al., 2014; Fager et al., 2015; Unkelbach et al., 2016). We will discuss these methods in the Discussion section.
The present study aimed to investigate the impact of incorporating LET criteria directly into IMPT optimization. Both dose and LET distributions could be optimized simultaneously in the proposed approach. Dose-averaged LET was used to indicate LET values in this study. The goal of this optimization was set to not only produce satisfactory dose distributions but also to achieve reduced LET distributions (thus lower biologically effective dose distributions) in critical structures and increased LET in target volumes compared to plans created using conventional objectives.
2. Methods and materials
2.1 LET-incorporated Optimization
The goal of LET-incorporated IMPT optimization in this study was to optimize dose and LET distributions simultaneously. The objectives and constraints on doses were consistent with those used in conventional IMPT optimization. The calculation and planning criteria of dose here implicitly included a RBE of 1.1, as in current clinical practice. The optimization of variable RBE was not within the scope of this study. The additive objectives of LET were, straightforwardly, maximization of LET in tumor targets and minimization of LET in critical tissues and normal tissues.
Given that Dij and Lij indicate the dose and LET contribution, respectively, from beamlet j to voxel i in unit intensity and wj indicates the intensity of beamlet j, the total dose Di and dose-averaged LET (LETd) Li in voxel i are calculated as follows:
| (1) |
| (2) |
The calculation of Dij and Lij was carried out by a previously validated fast Monte Carlo system (Yepes et al., 2016). Although LET is typically quantified in two averaging variants, i.e., track-averaged and dose-averaged LET (Grassberger and Paganetti, 2011; Guan et al., 2015b), only the latter was used in this study for consistency with most biological dosimetric analyses.
The general optimization model in radiation therapy including IMPT can be represented as follows in (3)–(5):
| (3) |
| (4) |
| (5) |
The minimization cost function is formulated by the deviation between the delivered (Di) and prescribed doses of each voxel. Also a priority factor (λi) is assigned to each voxel or structure in order to control the tradeoff between competing objectives. The lower and upper bounds of the doses are LBi and UBi, which are adjusted for different structures and specific applications. It has been established that quadratic (i.e., p = 2) and linear (i.e., p = 1) forms of the cost function (3) are effective in optimizing dose distributions for radiation therapy (Bortfeld, 1999; Chan et al., 2006; Jia et al., 2011; Cao et al., 2013). In this study, a linear cost function (6) was used for performing the conventional dose-based optimization (DoseOpt):
| (6) |
where T, O, N are the set of voxels in target volumes, organs at risk (OARs), and normal tissues, respectively. Optimization priority factors for penalizing over-dosing and under-dosing on target, OAR doses over the limit , and normal tissue doses are , , λO, and λN, respectively.
By adding two terms for maximizing dose-averaged LET in the target and minimizing it in OARs, the cost function for LET-incorporated optimization (LETOpt) was formulated as shown in (7). The optimization priority factors for the two objectives are θT and θO.
| (7) |
Note that threshold LET values and objectives for normal tissue LETs were not used in this study, but they can be easily added for applications. Constraints on doses were identical in DoseOpt and LETOpt.
Solving the LET-incorporated optimization problem as formulated above essentially requires linear fractional programming (LFP) techniques, because the LET component in the cost function is a ratio of two linear questions, i.e., Σj Dij Lij wj and Σj Dij wj, with regard to the optimization variable wj. Due to the linearity, the problem is quasiconvex and can be conveniently reformulated to a linear programming (LP) problem. Here we apply the Charnes and Cooper variable transformation (Charnes and Cooper, 1962) by defining the original variable wj with two new variables xj and t,, e.g., wj = xj⁄t. Assuming and for our problem analogically, where is the transposed dose contribution vector for voxel i for computing one objective term in a cost function like (7), an equivalent linear cost function can be formed as
| (8) |
The reformulated LP model of LETOpt thus has an optimization variable xj, instead of the original beamlet intensity wj, and an auxiliary variable t. Meanwhile, the dose constraints defined by wj are changed to ones such as
| (9) |
| (10) |
After solving the reformulated LP for LETOpt, i.e., (8)–(10), and obtaining the optimal solution of xj, the beamlet intensity can be post-processed using wj = xj⁄t for the final dose and LETd calculation. In this study, both DoseOpt and LETOpt models were solved by the interior point method using a commercial solver CPLEX v12.3 (IBM, NY, USA).
2.2 Patients and Treatment Planning
Five brain tumor patients that had been treated with proton therapy (PSPT or SFO-IMPT) at our institution were selected for this study, including one glioblastoma, one anaplastic astrocytoma and three ependymoma cases. Although the tumor size and location varied from one patient to another, in all cases, one or more critical structures, e.g., brainstem or optic chiasm, were adjacent to or overlapped with gross target volumes (GTVs) and clinical target volumes (CTVs). The prescriptions to target volumes and field arrangements were the same as those used in the clinical treatments. The doses prescribed to all OARs are set to zero in optimization. Table 1 lists patient information and specific treatment planning parameters for the five patient cases.
Table 1.
Patient information and treatment planning parameters.
| Patient # |
Type of Cancer | Prescription Dose (Gy/fx) | Number of Fractions | Number of Beams (non-coplanar) | OARs included in Optimization |
|---|---|---|---|---|---|
| 1 | Glioblastoma | 2 (GTV) 1.67 (CTV) |
30 | 2 | Brainstem, Optic Chiasm, Rt Cochlea, Rt Optic Nerve, Brain |
| 2 | Anaplastic Astrocytoma |
1.8 (GTV) 1.6 (CTV) |
30 | 3 | Brainstem, Optic Chiasm, Lt Cochlea, Lt Optic Nerve, Brain |
| 3 | Ependymoma | 1.8 (GTV) | 30 | 3 | Brainstem, Optic Chiasm, Brain |
| 4 | Ependymoma | 1.8 (GTV) | 28 | 3 | Brainstem, Optic Chiasm, Rt Cochlea, Rt Temp Lobe, Brain |
| 5 | Ependymoma | 1.8 (GTV) | 30 | 3 | Brainstem, Rt Hippocampus, Spinal Cord, Brain |
Two IMPT plans were created for each patient case, one using the conventional dose-based optimization and the other using the proposed LET-incorporated optimization. Each plan was based on 3D modulation delivery (Lomax, 1999). The intensities of all beamlets from all treatment fields were simultaneously and independently optimized, that is, MFO was applied. The simulation of plan delivery and dose/LET distributions was based on a discrete pencil beam scanning system commissioned at our institution (Gillin et al., 2010).
It should be noted that all plans optimized by either DoseOpt or LETOpt were tailored to produce dose distributions as similar as possible to those of the previous clinical plans. If necessary, multiple optimization runs were performed as trial and error, with adjustment to criteria or priority factors, until the plans were reviewed and found to be acceptable. Our goal in this study was to investigate the impact of LET-incorporated optimization on the ability to manipulate LET distributions, not to improve dose distributions. The detailed results of the patient studies, i.e., primarily the dosimetric data, are discussed in the next section.
3. Results
Table 2 summarizes six key indices each of dose and LETd based on the IMPT plans optimized by DoseOpt and LETOpt for the five patient cases: dose and LETd for 1% and 99% of the GTV, the maximum of dose and LETd for the brainstem, dose and LETd that are exceeded in 0.1 cc of the brainstem, and the maximum and mean of dose and LETd for the optic chiasm. There were only minor differences in those indices of dose between the DoseOpt and LETOpt plans. Meanwhile, there were pronounced differences in LETd. The maximum LETd and LETd to 0.1 cc of the brainstem were reduced from DoseOpt to LETOpt by an average of 19.4% and 23.7%, respectively. The maximum and mean LETd for the optic chiasm were reduced by 21.1% and 21.9%, respectively, and the LETd for 1% and 99% of the GTV were increased by 27.2% and 18.4%.
Table 2.
Dose (Gy) and Dose-averaged LET, i.e., LETd, (keV/μm) indices of the IMPT plans optimized by DoseOpt and LETOpt for five brain tumor patients. Max and mean values for dose and LETd are based on all voxels in corresponding structures, and the dose and LET to 0.11cc of the brainstem are reported. Dose and LETd to 1% and 99% of the GTV are also reported.
| Patient # |
Dose Optimization | LET Optimization | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Brainstem | Chiasm | GTV | Brainstem | Chiasm | GTV | ||||||||
| Max | 0.1cc | Max | Mean | 1% | 99% | Max | 0.1cc | Max | Mean | 1% | 99% | ||
| 1 | Dose | 2.0 | 1.9 | 1.8 | 1.3 | 2.2 | 2.0 | 1.9 | 1.9 | 1.8 | 1.3 | 2.2 | 1.9 |
| LETd | 8.1 | 7.1 | 6.8 | 4.9 | 3.5 | 1.4 | 7.9 | 6.2 | 1.8 | 1.4 | 3.7 | 1.6 | |
| 2 | Dose | 2.0 | 1.8 | 2.0 | 1.2 | 2.1 | 1.8 | 1.9 | 1.8 | 2.0 | 1.2 | 2.1 | 1.8 |
| LETd | 10.0 | 8.9 | 8.2 | 5.8 | 5.1 | 2.0 | 8.5 | 7.5 | 8.2 | 5.8 | 5.1 | 2.8 | |
| 3 | Dose | 2.0 | 1.9 | 0.1 | 0.1 | 2.0 | 1.8 | 2.0 | 1.9 | 0.1 | 0.1 | 2.0 | 1.9 |
| LETd | 9.3 | 9.0 | 5.1 | 3.6 | 4.2 | 2.6 | 6.8 | 6.3 | 4.5 | 3.3 | 7.0 | 3.0 | |
| 4 | Dose | 2.0 | 1.9 | 0.2 | 0.1 | 2.0 | 1.8 | 2.0 | 1.9 | 0.3 | 0.2 | 2.0 | 1.8 |
| LETd | 5.1 | 4.7 | 4.4 | 3.0 | 3.8 | 2.3 | 4.6 | 4.3 | 3.5 | 2.1 | 5.1 | 2.3 | |
| 5 | Dose | 2.0 | 1.9 | – | – | 2.0 | 1.7 | 2.0 | 1.9 | – | – | 2.0 | 1.7 |
| LETd | 13.5 | 12.4 | – | – | 4.7 | 2.2 | 7.7 | 6.0 | – | – | 6.1 | 2.7 | |
|
| |||||||||||||
| Mean of % difference of LETd between DoseOpt and LETOpt | −19.4 | −23.7 | −21.1 | −21.9 | 27.2 | 18.4 | |||||||
Plans optimized by DoseOpt and LETOpt for one glioblastoma case (Patient 1), are compared in Figure 1. Both the dose distributions and dose volume histograms (DVHs) confirmed that the doses generated by the DoseOpt and LETOpt plans were comparable for this case. In terms of LETd, as shown by LETd distributions and LETd volume histograms (LVHs), the sparing of the brainstem and the optic chiasm was significantly improved. For the optic chiasm, the max LETd was reduced from 6.8 keV/μm to 1.8 keV/μm. However, the magnitude of the LETd increase in the GTV was not as pronounced as that of the LETd decrease in the brainstem or the optic chiasm. Another comparison is shown in Figure 2 for one of the ependymoma cases (Patient 3). The DoseOpt and LETOpt plans again had similar doses, although the DoseOpt plan was worse for sparing of the brainstem in the low-dose region than the LETOpt plan was. LETd hotspots in normal tissues and the brainstem were greatly reduced by LETOpt, and LETOpt plans had a larger area with high LETd distributed in the GTV and CTV than did DoseOpt plans. The DVHs and LVHs for three other patient cases are included in Appendix A.
Figure 1.
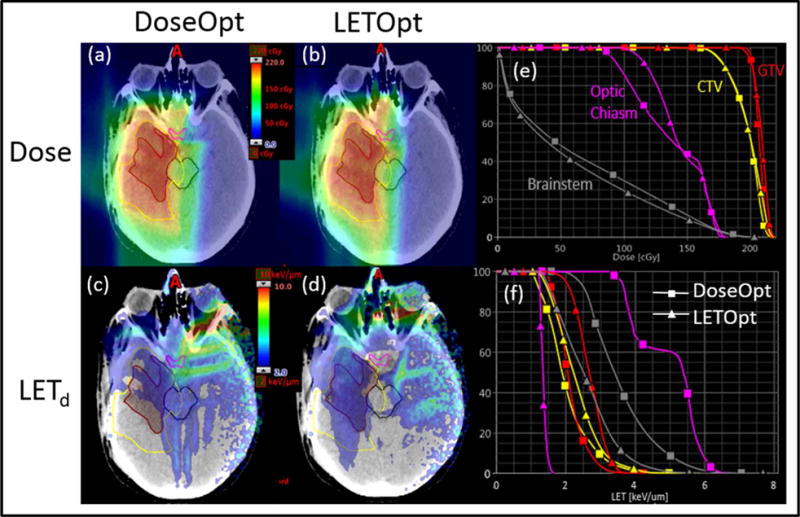
Comparison of DoseOpt and LETOpt plans for Patient 1. Panels (a) and (b) show dose distributions (based on a constant RBE of 1.1) for the DoseOpt and LETOpt plans. Panels (c) and (d) show dose-averaged LET distributions for the DoseOpt and LETOpt plans. Panels (e) and (f) are dose- and LET-volume histograms for the GTV (red contour), CTV (yellow contour), brainstem (black contour), optic chiasm (magenta contour).
Figure 2.
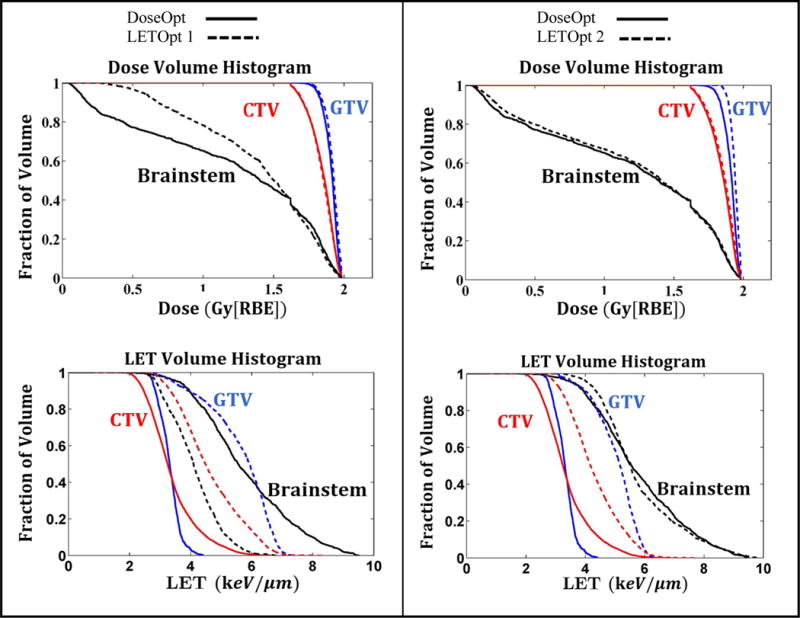
Dose (RBE=1.1) and dose-averaged LET volume histograms of the IMPT plans optimized by DoseOpt (solid lines) and LETOpt (dashed lines) for Patient 3. Two LETOpt plans (1 and 2) are shown here to illustrate the trade-off effect between dose and LET objectives. Each LETOpt plan is compared to the DoseOpt plan. The ratio of the optimization priority factor between the dose and LET objectives is 1 for the LETOpt plan 1 and 10 for the LETOpt plan 2.
Optimized plans for the Patient 3 as a representative case are further compared in DVHs and LVHs in Figure 2. One DoseOpt plan and two LETOpt plans (1 and 2) are shown and compared. The ratio of the optimization priority factor of the dose and LET objectives was set at one for the LETOpt plan 1 and ten for LETOpt plan 2. In other words, plan 1 was optimized with ten times less priority given to dose objectives, including ones for target volumes and critical normal tissues, than plan 2. For plan 1, although the brainstem was not well spared at low doses by LETOpt compared to DoseOpt, its exposure to high LETs was greatly reduced with a decrease of 3 keV/μm from the maximum LETd. Note that the similar behavior was observed in Patient 4 and 5. For plan 2, the dose sparing of the brainstem was similar for LETOpt and DoseOpt, but the benefit of LET sparing could not be achieved as it was in plan 1. Pronounced increases of LETd in target volumes were achieved by both LETOpt plans. However, the magnitude of increase was modestly lower for plan 2 than for plan 1 because higher optimization priority was given to dose instead of LET in plan 2. The choice between plan 1 and 2 in clinic should be determined by physician’s preference on different metrics such as maximum or mean dose to brainstem, and boost in target dose, etc. We should note that the tradeoff effect between dose and LET metrics was observed in all patient cases, while its magnitude and sensitivity to changing optimization priorities varied among cases (as seen in examples shown in Figure 1, 2 and 4).
4. Discussion
Proton therapy is increasingly accessible to cancer patients (Chang et al., 2014; Schuemann et al., 2014). Continuous improvement of this cutting-edge technology, including treatment planning, will allow its theoretical benefits to be fully realized and its associated risks to be minimized. Currently, the biological uncertainties of protons remain a significant challenge to realize the full potential of proton therapy (Mitin and Zietman, 2014). Despite extensive ongoing research to better understand the biological effectiveness of protons and other heavy particles, including in vitro and in vivo animal studies as well as patient response analyses, a variable RBE model, especially one dependent on tissue type and clinical endpoint, has yet not been agreed upon for use in clinical treatment planning. From an alternative perspective, incorporation of LET in treatment planning assuming the dependence of RBE on LET, while ensuring no or minimal changes to the dose distributions used in current practice (with its simplistic constant RBE of 1.1), can be implemented straightforwardly and immediately in the clinic to benefit patients. At our center, we have begun evaluating the LET-incorporated optimization presented here in a clinical setting for selected patients and expect to generate LET-optimized plans together with conventionally optimized plans in the clinical routine for physicians to choose.
The present study demonstrated that the LET-incorporated IMPT optimization can create preferred dose-averaged LET distributions while maintaining satisfactory dose distributions. Optimization of LET, i.e., maximization in target volumes and minimization in critical normal tissues as shown in our patient studies, is expected to boost the differential benefits of increasing the biological effect of protons in tumor and/or reducing it in healthy tissues compared to the current standard for brain tumor cases. Within dose-exposed volumes, evaluation of LET can be used as another measure of plan quality, in addition to dose. Moreover, one can also choose to use radiobiological models as additional indicators of plan quality, such as the linear quadratic (LQ) cell survival model, tumor control probability (TCP), normal tissue complication probability (NCTP), and RBE models. For example, Figure 3 shows the DVHs from variable RBE-weighted doses based on a recently published RBE model (McNamara et al., 2015) for a representative case (Patient 1). This demonstrates that the LET-incorporated optimization not only increased the variable RBE-weighted dose for target volumes but also reduced it for critical structures compared to a plan conventionally optimized using constant RBE. Similar DVHs for other patient cases can be found in Appendix B.
Figure 3.
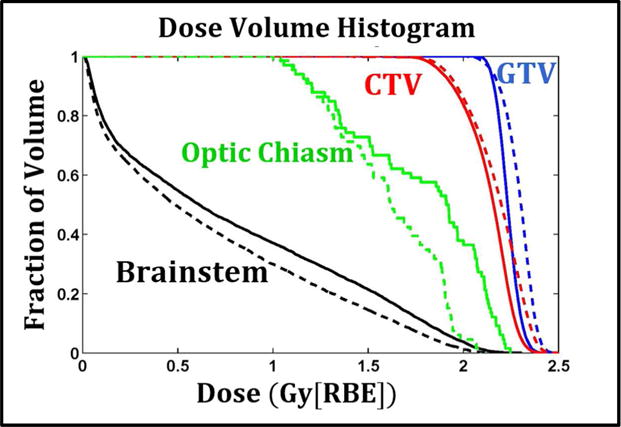
Dose volume histograms of the IMPT plans optimized by DoseOpt (solid lines) and LETOpt (dashed lines) for Patient 1. The RBE here is variable and calculated based on a recently published RBE model (McNamara et al., 2015). The required tissue parameters are obtained from literature (Frese et al., 2011).
LET painting approaches have been investigated for ion (Bassler et al., 2010; Bassler et al., 2014) and proton (Fager et al., 2015) therapies, in which planning methods such as splitting targets or adopting opposite beam arrangements are used to allocate the high LET protons within target instead of normal tissues. However, those techniques may require greater effort in planning, quality assurance, and delivery than does the current practice because they use more planning volumes and beam angles. In contrast, incorporating LET directly into the optimization process may have certain practical advantages over the LET painting techniques and it could be easily implemented in clinical settings. Such an approach as presented in this work can adopt the same target volumes and beam arrangements that are used in conventional PSPT and IMPT treatment plans. Meanwhile, ideas in LET painting such as avoiding the distal edge in target boundary regions could be used to improve the benefits of LET-incorporated optimization.
One recent study discussed a multi criteria optimization approach in which a set of IMPT plans were created using various dose based objectives and constraints, then plans with superior dose and LET distributions were selected (Giantsoudi et al., 2013). While the advantage of this method is that multiple competing plans can be generated, the disadvantage is that the performance on finding improved LET distributions may be compromised because LET criteria are not included in optimization.
In another recent study, a two-step prioritized optimization approach was proposed: first a plan was optimized using conventional dose criteria, and, in the second step, the plan was optimized solely based on the product of LET and dose as a surrogate of variable RBE weighted dose with constraints to limit the change to physical dose distribution from the first step (Unkelbach et al., 2016). Prioritized optimization may be an effective approach to managing the trade-off effect between dose and LET. However, the optimality of LET optimization may be affected by the local minimum problem in nonconvex optimization, as the second round of prioritized optimization uses a warm start. This is less of a problem for simultaneous optimization approaches such as the one proposed in this study. However, our approach has the drawback of requiring determination of good optimization priority factors to balance gains in dose and LET. The comparison of the effectiveness and efficiency of different optimization strategies is also of interest and will be an area of future study.
Our study confirms that the redistributed LET maps may compensate the cut of quality dose distributions achieved by IMPT (Unkelbach et al., 2016). This was seen in Patient 3 and 5 where brainstem dose was increased in the LET optimized plans at the low dose region compared to the dose optimized plan. However, this is not always the case. For example, the LET optimized plan for Patient 1 in this study achieved a greatly improved LET distribution without degrading the physical dose distribution. The varying magnitude of the benefit of LET optimization may be attributed to patient anatomies and beam arrangements. The trade-off effect between dose and LET merits should be thoroughly investigated in future research. Methods such as multi-criteria optimization and beam angle optimization can be highly helpful in the search for superior dose and LET distributions.
5. Conclusion
In this study, a LET-incorporated IMPT optimization method was introduced. This method was able to produce clinically satisfactory dose distributions while increasing dose-averaged LET in target volumes and reducing it in critical normal tissues for five selected brain tumor patient cases. The clinical application of this method requires no changes to the current treatment protocols using a constant RBE and therefore has a potential to bring an immediate improvement to IMPT in enhancing tumor control and reducing normal tissue toxicities.
Acknowledgments
Authors would like to thank Amy Ninetto for providing editorial assistance to improve this manuscript. This work was supported in part by the National Cancer Institute of the National Institutes of Health (2U19CA021239-35) and the Cancer Prevention and Research Institute of Texas (RP160232).
Appendix A
DVH and LVH for plans optimized by DoseOpt and LETOpt for patient 2, 4 and 5.
Figure 4.
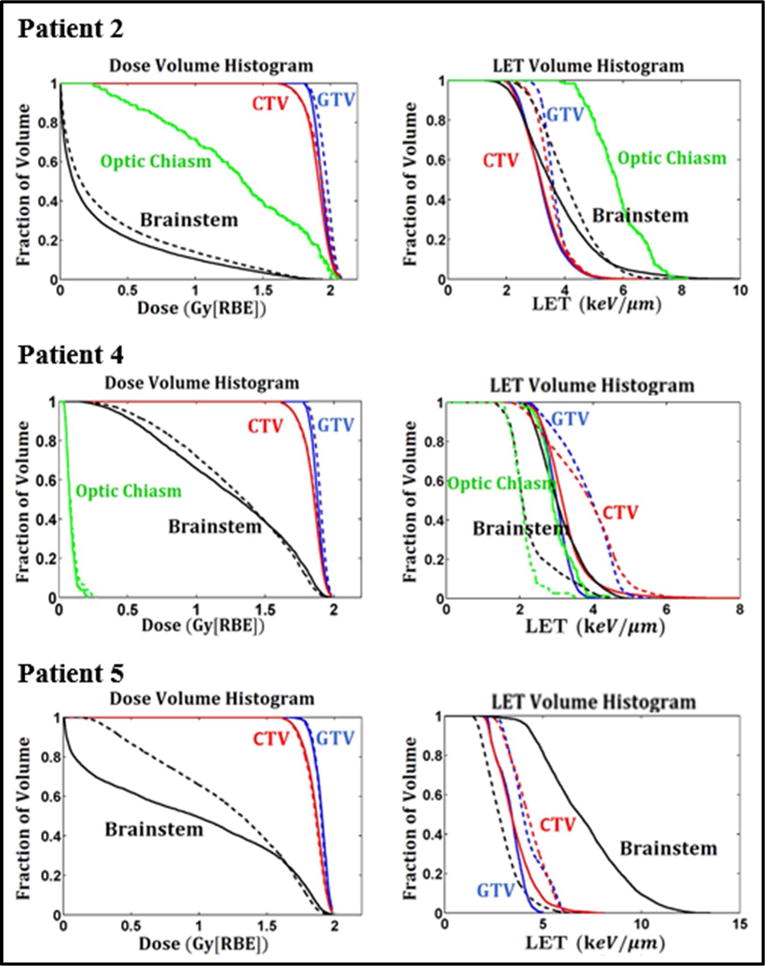
Dose- and LETd-volume histograms of the IMPT plans optimized by DoseOpt (solid lines) and LETOpt (dashed lines) for Patient 2, 4 and 5.
Appendix B
DVH in terms of variable RBE for plans optimized by DoseOpt and LETOpt for patient 2, 3, 4 and 5.
Figure 5.
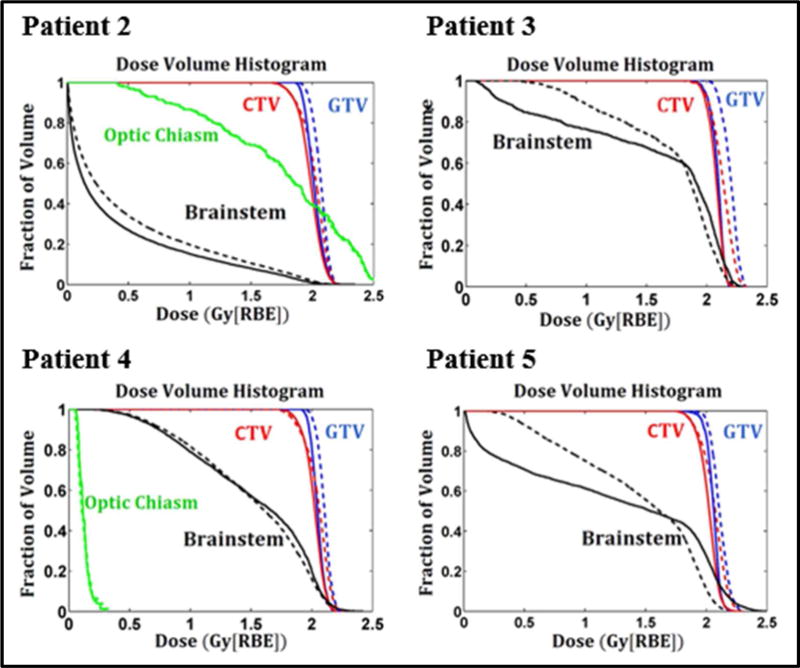
Dose volume histograms of the IMPT plans optimized by DoseOpt (solid lines) and LETOpt (dashed lines) for Patient 2, 3, 4 and 5. The RBE here is variable and calculated based on a recently published RBE model (McNamara et al., 2015). The required tissue parameters are obtained from literature (Frese et al., 2011).
References
- Bassler N, Jäkel O, Søndergaard CS, Petersen JB. Dose- and LET-painting with particle therapy. Acta Oncologica. 2010;49:1170–6. doi: 10.3109/0284186X.2010.510640. [DOI] [PubMed] [Google Scholar]
- Bassler N, Toftegaard J, Lühr A, Sørensen BS, Scifoni E, Krämer M, Jäkel O, Mortensen LS, Overgaard J, Petersen JB. LET-painting increases tumour control probability in hypoxic tumours. Acta Oncologica. 2014;53:25–32. doi: 10.3109/0284186X.2013.832835. [DOI] [PubMed] [Google Scholar]
- Bortfeld T. Optimized planning using physical objectives and constraints. Semin Radiat Oncol. 1999;9:20–34. doi: 10.1016/s1053-4296(99)80052-6. [DOI] [PubMed] [Google Scholar]
- Cao W, Lim G, Li X, Li Y, Zhu XR, Zhang X. Incorporating deliverable monitor unit constraints into spot intensity optimization in intensity-modulated proton therapy treatment planning. Phys Med Biol. 2013;58:5113–25. doi: 10.1088/0031-9155/58/15/5113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan TC, Bortfeld T, Tsitsiklis JN. A robust approach to IMRT optimization. Phys Med Biol. 2006;51:2567–83. doi: 10.1088/0031-9155/51/10/014. [DOI] [PubMed] [Google Scholar]
- Chang AL, Yock TI, Mahajan A, Hill-Kaiser C, Keole S, Loredo L, Cahlon O, McMullen KP, Hartsell W, Indelicato DJ. Pediatric Proton Therapy: Patterns of Care across the United States. International Journal of Particle Therapy. 2014;1:357–67. [Google Scholar]
- Charnes A, Cooper WW. Programming with linear fractional functionals. Naval Research logistics quarterly. 1962;9:181–6. [Google Scholar]
- Fager M, Toma-Dasu I, Kirk M, Dolney D, Diffenderfer ES, Vapiwala N, Carabe A. Linear Energy Transfer Painting With Proton Therapy: A Means of Reducing Radiation Doses With Equivalent Clinical Effectiveness. Int J Radiat Oncol Biol Phys. 2015;91:1057–64. doi: 10.1016/j.ijrobp.2014.12.049. [DOI] [PubMed] [Google Scholar]
- Frese MC, Wilkens JJ, Huber PE, Jensen AD, Oelfke U, Taheri-Kadkhoda Z. Application of constant vs. variable relative biological effectiveness in treatment planning of intensity-modulated proton therapy. Int J Radiat Oncol Biol Phys. 2011;79:80–8. doi: 10.1016/j.ijrobp.2009.10.022. [DOI] [PubMed] [Google Scholar]
- Giantsoudi D, Grassberger C, Craft D, Niemierko A, Trofimov A, Paganetti H. Linear Energy Transfer-Guided Optimization in Intensity Modulated Proton Therapy: Feasibility Study and Clinical Potential. Int J Radiat Oncol Biol Phys. 2013;87:216–22. doi: 10.1016/j.ijrobp.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillin MT, Sahoo N, Bues M, Ciangaru G, Sawakuchi G, Poenisch F, Arjomandy B, Martin C, Titt U, Suzuki K, Smith AR, Zhu XR. Commissioning of the discrete spot scanning proton beam delivery system at the University of Texas M.D. Anderson Cancer Center, Proton Therapy Center, Houston. Med Phys. 2010;37:154–63. doi: 10.1118/1.3259742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassberger C, Paganetti H. Elevated LET components in clinical proton beams. Phys Med Biol. 2011;56:6677. doi: 10.1088/0031-9155/56/20/011. [DOI] [PubMed] [Google Scholar]
- Grassberger C, Trofimov A, Lomax A, Paganetti H. Variations in Linear Energy Transfer Within Clinical Proton Therapy Fields and the Potential for Biological Treatment Planning. Int J Radiat Oncol Biol Phys. 2011;80:1559–66. doi: 10.1016/j.ijrobp.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan F, Bronk L, Titt U, Lin SH, Mirkovic D, Kerr MD, Zhu XR, Dinh J, Sobieski M, Stephan C, Peeler CR, Taleei R, Mohan R, Grosshans DR. Spatial mapping of the biologic effectiveness of scanned particle beams: towards biologically optimized particle therapy. Sci Rep. 2015a;5:9850. doi: 10.1038/srep09850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan F, Peeler C, Bronk L, Geng C, Taleei R, Randeniya S, Ge S, Mirkovic D, Grosshans D, Mohan R, Titt U. Analysis of the track- and dose-averaged LET and LET spectra in proton therapy using the geant4 Monte Carlo code. Med Phys. 2015b;42:6234–47. doi: 10.1118/1.4932217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunther JR, Sato M, Chintagumpala M, Ketonen L, Jones JY, Allen PK, Paulino AC, Okcu MF, Su JM, Weinberg J, Boehling NS, Khatua S, Adesina A, Dauser R, Whitehead WE, Mahajan A. Imaging Changes in Pediatric Intracranial Ependymoma Patients Treated With Proton Beam Radiation Therapy Compared to Intensity Modulated Radiation Therapy. Int J Radiat Oncol Biol Phys. 2015;93:54–63. doi: 10.1016/j.ijrobp.2015.05.018. [DOI] [PubMed] [Google Scholar]
- ICRU. Fundamental quantities and units for ionizing radiation (ICRU Report 85) J ICRU. 2011;11:1–31. doi: 10.1093/jicru/ndr011. [DOI] [PubMed] [Google Scholar]
- Jia X, Men C, Lou Y, Jiang SB. Beam orientation optimization for intensity modulated radiation therapy using adaptive l(2,1)-minimization. Phys Med Biol. 2011;56:6205–22. doi: 10.1088/0031-9155/56/19/004. [DOI] [PubMed] [Google Scholar]
- Lomax A. Intensity modulation methods for proton radiotherapy. Phys Med Biol. 1999;44:185–205. doi: 10.1088/0031-9155/44/1/014. [DOI] [PubMed] [Google Scholar]
- McNamara AL, Schuemann J, Paganetti H. A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data. Phys Med Biol. 2015;60:8399–416. doi: 10.1088/0031-9155/60/21/8399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitin T, Zietman AL. Promise and Pitfalls of Heavy-Particle Therapy. Journal of Clinical Oncology. 2014;32:2855–63. doi: 10.1200/JCO.2014.55.1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paganetti H, Niemierko A, Ancukiewicz M, Gerweck LE, Goitein M, Loeffler JS, Suit HD. Relative biological effectiveness (RBE) values for proton beam therapy. International Journal of Radiation Oncology*Biology*Physics. 2002;53:407–21. doi: 10.1016/s0360-3016(02)02754-2. [DOI] [PubMed] [Google Scholar]
- Peeler CR, Mirkovic D, Titt U, Blanchard P, Gunther JR, Mahajan A, Mohan R, Grosshans DR. Clinical evidence of variable proton biological effectiveness in pediatric patients treated for ependymoma. Radiotherapy and oncology : journal of the European Society for Therapeutic Radiology and Oncology. 2016;121:395–401. doi: 10.1016/j.radonc.2016.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabin ND, Merchant TE, Harreld JH, Patay Z, Klimo P, Qaddoumi I, Armstrong GT, Wright K, Gray J, Indelicato DJ, Gajjar A. Imaging Changes in Very Young Children with Brain Tumors Treated with Proton Therapy and Chemotherapy. American Journal of Neuroradiology. 2013;34:446. doi: 10.3174/ajnr.A3219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuemann J, Dowdell S, Grassberger C, Min CH, Paganetti H. Site-specific range uncertainties caused by dose calculation algorithms for proton therapy. Phys Med Biol. 2014;59:4007–31. doi: 10.1088/0031-9155/59/15/4007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unkelbach J, Botas P, Giantsoudi D, Gorissen BL, Paganetti H. Reoptimization of Intensity Modulated Proton Therapy Plans Based on Linear Energy Transfer. Int J Radiat Oncol Biol Phys. 2016;96:1097–106. doi: 10.1016/j.ijrobp.2016.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkens JJ, Oelfke U. A phenomenological model for the relative biological effectiveness in therapeutic proton beams. Phys Med Biol. 2004;49:2811–25. doi: 10.1088/0031-9155/49/13/004. [DOI] [PubMed] [Google Scholar]
- Wilkens JJ, Oelfke U. Optimization of radiobiological effects in intensity modulated proton therapy. Med Phys. 2005;32:455–65. doi: 10.1118/1.1851925. [DOI] [PubMed] [Google Scholar]
- Yepes PP, Eley JG, Liu A, Mirkovic D, Randeniya S, Titt U, Mohan R. Validation of a track repeating algorithm for intensity modulated proton therapy: clinical cases study. Phys Med Biol. 2016;61:2633. doi: 10.1088/0031-9155/61/7/2633. [DOI] [PubMed] [Google Scholar]


