Abstract
Drying of garlic slices in thin-layer have been studied with Infrared (IR) at 0.075, 0.15, 0.225 and 0.3 W cm−2 radiation intensity and 0.75 and 1.25 m s−1 air flow velocity. The results showed increasing in drying rate and decreasing at the time of drying with decreasing air flow velocity and increasing IR radiation intensity. The effective moisture diffusivity (Deff) was obtained using Fick’s diffusion equation and its mean values ranged between 5.83×10−11 and 7.66×10−10 m2 s−1 for all investigated conditions. In addition, a third-order polynomial equation linking the effective moisture diffusivity and moisture content was found. Average activation energy increased with the decrease of IR radiation and increase of air flow velocity. Thirteen different mathematical models were verified with non-linear regression analysis for describing the garlic drying process. Modified Henderson and Pabis model presented the best prediction of the drying of garlic slices.
Keywords: Garlic, Infrared drying, Radiation intensity, Moisture diffusivity, Activation energy
Nomenclature
- a, b, c, g, h, y
empirical constants
- k, k1, k2
drying rate constants (1/s)
- IR
infrared
- Deff
effective moisture diffusivity (m2/s)
- (Deff)avg
average effective moisture diffusivity (m2/s)
- D0
pre-exponential factor of the Arrhenius equation (m2/s)
- Ea
activation energy (kJ mol−1)
- R
universal gas constant (8.3143 kJ/kmol K)
- L
thickness of the sample (slab) (m)
- Me
equilibrium moisture content (g water/g dry matter)
- M0
initial moisture content (g water/g dry matter)
- Mt
moisture content at time t (g water/g dry matter)
- MR
moisture ratio (dimensionless)
- MRExp
experimental moisture ratio (dimensionless)
- MRPre
predicted moisture ratio (dimensionless)
the average predicted moisture ratio
- ln (MR)
natural logarithm of moisture ratio
- N
number of observations
- n
positive integer
- p
number of constants
- RMSE
root mean square error
- R2
coefficient of determination
- %E
the average percentage error
- χ2
reduced chi-square
- T
temperature of drying air (°C)
- Tabs
absolute temperature (K)
- t
drying time (s)
- v
air flow velocity, m/s
- I
infrared radiation intensity, W cm−2
1. Introduction
Garlic (Allium sativum L.) has several uses in addition to its main function as a spice and a flavoring agent for food it also has some medicinal benefits (Lawson and Wang, 2001). Garlic crop is exposed to pronounced losses due to metabolic processes and microbial activity during storage. Most likely thirty percent of the freshly harvested garlic is lost due to improper means of transference and storage (Aware and Thorat, 2010).
Food products drying is usually used for preserving food safety as it greatly reduces the microbial and enzymatic changes through the storage period, hence, extending the shelf life of the produce (Sacilik and Unai, 2005, Barrozo et al., 2001). Also, the demand has increased on Garlic powder, one of the most popular commercial garlic products, which can be produced by drying garlic cloves or slices. The dried samples are then ground into powder (Litaiem et al., 2015, Figiel, 2009).
Yilbas et al. (2003) indicated that drying of moist products is a complex process comprising coinciding heat and mass transfer. The practice of drying a product sample in a single layer of particles or slices is known as thin-layer drying. At present, three types of mathematical models are used to define thin-layer drying process of agricultural produce, viz., theoretical models which merely study the internal resistance for transferring the moisture between heating air, semi-theoretical and experimental models which only take into account the external resistance (Panchariya et al., 2002, Midilli et al., 2002).
Celma et al. (2008) highlighted that IR drying is based on the IR radiation emitted from a source, which reacts with the internal structure of the samples thus increases its temperature and vaporizes the humidity. In addition, IR energy transfers from its source to the produce without heating the adjacent air. In this process, the internal layers of the sample would be warmer than the surrounding air. Accordingly, the sample drying occurs from internal to external layers by both convection and radiation and therefore the rate of heat transfer is greater as compared to the conventional drying. IR drying method is mostly effective for products having a considerable moisture content, as long-wave radiation (over 3 µm) is nearly fully absorbed by the moist of the product (Celma et al. (2009). However, dry materials have high radiation permeability. There are some merits in favor of IR radiation heating regarding conventional drying, e.g. decreased drying time, reduced air flow velocity thru the product and higher energy efficiency (Togrul, 2005).
Mathematical modeling is the best and appropriate approach for describing the kinetics of the drying process. Precise modeling of the behavior of drying of agricultural products requires specific correlation and regression statistical methods in order to attain a set of equations that give an accurate explanation of the process (Celma et al., 2008). Numerous experimental models for drying kinetics in falling rate drying period are available in the literature. The models used were linear, power, exponential, Arrhenius and logarithmic, which represent the most common mathematical functions (Togrul, 2006). In addition to polynomial models which are used when the aforesaid forms get small determination coefficients (Celma et al., 2008).
The present study was undertaken to investigate and evaluate the influence of different levels of IR radiation intensity and air flow velocity on the thin-layer drying characteristics of garlic slices. Moreover, to determine the effective moisture diffusivity and activation energy of garlic slices and testing thirteen different drying models for describing and predicting drying process of garlic slices.
2. Materials and methods
2.1. Materials
Freshly harvested cloves of garlic (Allium sativum) were obtained from a local variety store for study in this research work. The garlic cloves were unpeeled and cut into slices of (2.5 ± 0.5 mm) thickness. garlic slices. The initial moisture content of the garlic slices was determined according to the standard procedure of the Association of Official Analytical Chemists (AOAC) (AOAC, 2005), where the samples were dried at 70 °C for 24 h under a vacuum of 85 kPa (Vacutherm model VT 6025, Heraeus Instrument, D-63450. Hannover, Germany). The initial moisture content of the garlic was between 70 and 72.5% (w.b.). Garlic pieces were placed in perforated plastic bags and stored at 1 °C and RH of 80% during conducting the drying experiments which continued until the moisture content reached 6 (% w.b).
2.2. Experimental set-up and procedure
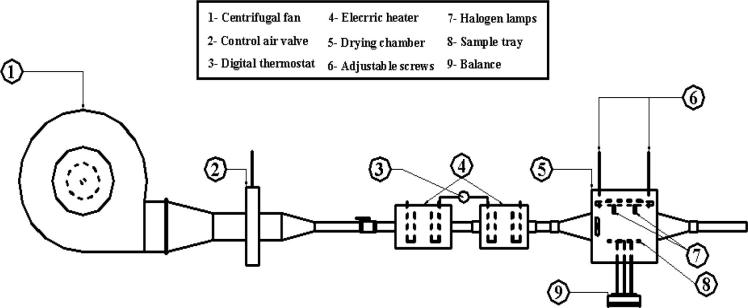
An IR dryer (Fig. 1) was used for the drying process of the garlic slices samples with IR radiation. The device consists mainly of two electric heaters (1.35 kW each) for heating the drying air, a centrifugal fan for supplying the air flow and a drying chamber made of 1.5 mm sheet of galvanized metal of 40 × 28 × 40 cm in dimensions. The chamber was shielded from inside with aluminum foil sheets for reflecting the IR radiation over garlic slices. The IR radiation sources are two IR halogen lamps (500 W) installed inside the chamber. A solar radiation sensor (pyrometer, model H-201) was used for the measurement of radiation intensity
Fig. 1.
Schematic diagram of infrared dryer used in drying garlic slices.
Garlic samples were placed on a holding tray of 20 × 20 × 1 cm in the chamber. The tray was put facing to the IR lamps, and the space between the lamps and the sliced of garlic samples was set at 15 cm. The samples were uniformly spread as a thin-layer in the holding tray. The experiments were carried at an inlet air temperature fixed at 40 °C (Abe and Afzal, 1997). Samples of 100 g of sliced garlic were used in the experiments. Four IR radiation intensities namely, 0.075, 0. 15, 0.225, and 0.3 W cm−2 and two air flow velocity of 0.75 and 1.25 m s−1 were used in the experiments. Changes in the samples mass were noted each 5 min in the first hour and each 10 min in the next hour then each 20 min until the samples reached to about 6 (% w.b). The experiments were replicated three times. Moisture ratio (MR) was calculated from the obtained experimental moisture content values. MR which is typically defined as: . Though, it might be abbreviated to Mt/Mo, as in IR the samples could be dried to the dry matter content (Midilli, 2001).
2.3. Modeling of the IR thin-layer drying data
The experimental drying data were tested to find the most suitable model among thirteen different models defining drying process set by a number of authors (Table 1). The different constants in the tested models were determined using non-linear regression procedure using IBM SPSS software package (IBM SPSS version 22).
Table 1.
Mathematical models used to describe the thin-layer drying curve.
| No. | Model name | Analytical expression | Reference |
|---|---|---|---|
| 1 | Lewis | MR = exp(−kt) | Bruce (1985) |
| 2 | Page | MR = exp(−kty) | Page (1949) |
| 3 | Modified page | MR = exp(−(kt)y) | White et al. (1981) |
| 4 | Henderson and Pabis | MR = a exp(−kt) | Henderson and Pabis (1961) |
| 5 | Wang and Singh | MR = 1 + at + bt2 | Wang and Singh (1978) |
| 6 | Logarithmic | MR = a exp(−kt) + c | Togrul and Pehlivan (2002) |
| 7 | Tow term | MR = a exp(−k1t) + b exp(−k2t) | Henderson (1974) |
| 8 | Tow term exponential | MR = a exp(−kt) + (1 − a) exp(−kat) | Sharaf-Eldeen et al. (1980) |
| 9 | Modified Henderson and Pabis | MR = a exp(−kt) + b exp(−gt) + c exp(−ht) | Karathanos (1999) |
| 10 | Midilli | MR = a exp(−ktn) + bt | Midilli et al. (2002) |
| 11 | Approximation of diffusion | MR = a exp(−kt) + (1 − a) exp(−kbt) | Kassem (1996) |
| 12 | Verma et al. | MR = a exp(−kt) + (1 − a) exp(−gt) | Verma et al. (1985) |
| 13 | Simplified Fick’s diffusion | MR = a exp(−c(t/L2)) | Diamante and Munro (1991) |
The coefficient of determination (R2), reduced chi-square (χ2), root mean square error (RMSE) and the average percentage error (%E) were used to inspect the good fitness of the selected mathematical models to the experimental data. A model is considered more suitable the higher values of R2 and the lower the values of χ2, RMSE and %E (Midilli and Kucuk, 2003, Akpinar et al., 2006). The following equations were used to calculate the above-mentioned parameters:
| (1) |
| (2) |
| (3) |
| (4) |
2.4. Calculation of the effective moisture diffusivity
Effective moisture diffusivity (Deff) is usually used to describe the drying characteristics of foodstuffs. Assuming that the sliced garlic samples were taking slab shape, Fick’s second diffusion equation can be used to determine the effective moisture diffusivity of the garlic slices. Fick’s diffusion equation for particles with a slab geometry is defined by the following equation (Crank, 1975):
| (5) |
Taking the natural logarithm of both sides of Eq. (5) the following equation was obtained:
| (6) |
Eq. (6) is estimated arithmetically by putting (Fourier number for diffusion):
| (7) |
| (8) |
Then (Deff) was determined from the following equation:
| (9) |
2.5. Calculation of the activation energy
Activation energy (Ea) is the comparative easiness with which water molecules overcome the energy obstacle during their transfer through the samples The reliance of the effective moisture diffusivity on the temperature can be described by an Arrhenius-type equation (Akgun and Doymaz, 2005, Sanjuan et al., 2003) as follows:
| (10) |
Taking natural logarithm of both sides of Eq. (10) it could be written as follows:
| (11) |
In order to obtain the values of the activation energy (Ea), the values of ln (Deff) were plotted versus the reciprocal of the absolute temperature (1/Tabs) and the slope of the fitted straight line is equal to (−Ea/R).
3. Results and discussion
3.1. Drying process behavior
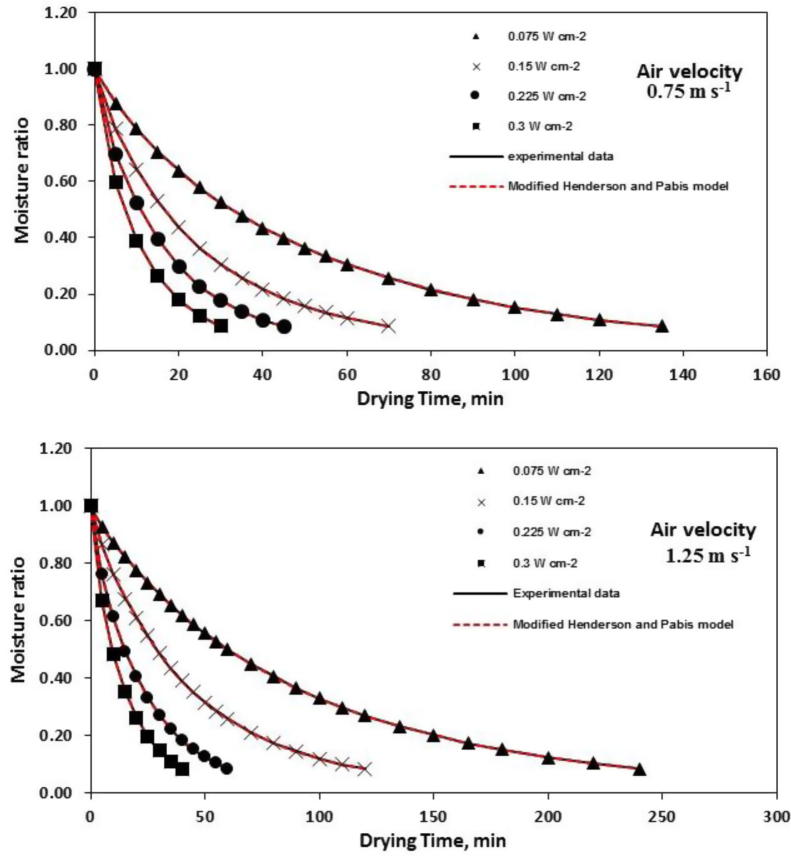
The variations of moisture ratio with the time of drying at different IR radiation intensity and air flow velocity are depicted in Fig. 2. The garlic slices moisture ratio decrease with increasing time of drying. Each time air flow velocity decreased and the intensity of radiation increased, a high heat flow is delivered by the IR heating resulting in a rapid surge of the samples temperature toward the completion of the drying process causing a remarkable drop in the time of drying. The drying time reduced from 135 to 30 min by increasing the radiation intensity from 0.075 to 0.3 W cm−2 at the air flow velocity of 0.75 m s−1, whereas, it decreased from 240 to 40 min at 1.25 m s−1.
Fig. 2.
Variation of the experimental and the predicted moisture ratio by the best fitting model with drying time at different radiation intensity and air flow velocity.
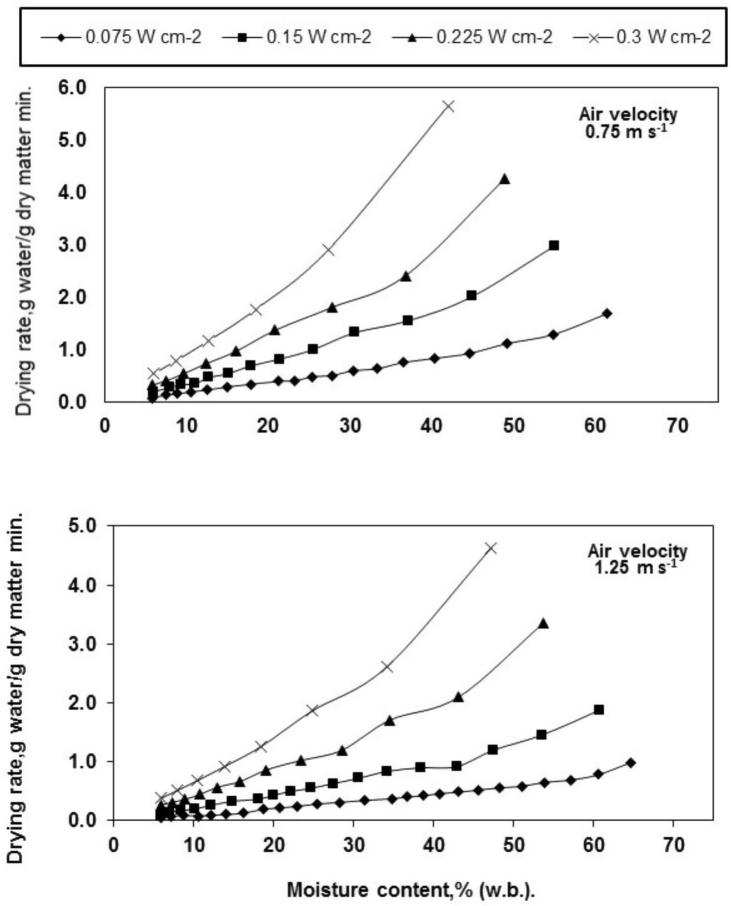
Correspondingly, the effect of moisture content on the drying rate at different air flow velocity and IR intensity is presented in Fig. 3. From the figure, it can be said that the drying rate reduced with the decrease of the moisture content in the garlic slices and increase of the drying time, or in other words, it has been decreased with the decrease of IR intensity and the increase in air flow velocity. These findings are in agreement to other published works in the drying of food products (Madamba et al., 1996, Doymaz, 2004, Akgun and Doymaz, 2005, Celma et al., 2009).
Fig. 3.
The effect of moisture content on the drying rate of garlic slices at different radiation intensity and air flow velocity.
3.2. Fitting of the thin-layer drying curves
The thirteen models listed in (Table 1) were used for predicting the changes in the garlic slices moisture content with the drying time.
The obtained statistical parameters for data fitting for the thirteen models are presented in Table 2. The thirteen models revealed high values of R2 varied between 0.977575 and 0.999948. Accordingly, all tested models could adequately describe the behavior of drying garlic slices using IR system. Nevertheless, Modified Henderson and Pabis model displayed the highest average value of R2 (0.999948) and the lowest values of χ2 (1.5 × 10−6), RMSE (0.00101) and %E (0.0131). Consequently, this model is the best one among the tested models that accurately express the thin-layer drying behavior of garlic slices under the studied conditions. The constants of the best model for describing the thin-layer garlic slices drying curves are revealed in Table 3.
Table 2.
Statistical results obtained for the thin layer drying models for garlic slices.
| Model name | R2 | Χ2 | RMSE | E |
|---|---|---|---|---|
| Lewis | 0.97945 | 0.0016656 | 0.03714 | 0.6225 |
| Page | 0.999948 | 0.0000138 | 0.00176 | 0.0282 |
| Modified page | 0.999949 | 0.0000043 | 0.00176 | 0.0282 |
| Henderson and Pabis | 0.992901 | 0.0006351 | 0.02249 | 0.2795 |
| Wang and Singh | 0.977575 | 0.0020418 | 0.04117 | 0.7325 |
| Logarithmic | 0.999116 | 0.0000828 | 0.00808 | 0.1482 |
| Tow term | 0.999930 | 0.0000059 | 0.00205 | 0.0297 |
| Tow term exponential | 0.999700 | 0.0000288 | 0.00486 | 0.0791 |
| Modified Henderson and Pabis | 0.999948 | 0.0000015 | 0.00101 | 0.0131 |
| Midilli | 0.994713 | 0.0005245 | 0.01951 | 0.1765 |
| Approximation of diffusion | 0.999926 | 0.0000061 | 0.00203 | 0.0597 |
| Verma et al. | 0.999925 | 0.0000080 | 0.00208 | 0.0597 |
| Simplified Fick’s diffusion | 0.996875 | 0.0008285 | 0.01528 | 0.2615 |
Table 3.
Values of the drying constant and coefficients of the best model (Modified Henderson and Pabis).
| Air flow velocity, m S−1 | Radiation intensities, W cm−2 | R2 | a | k | b | g | c | h |
|---|---|---|---|---|---|---|---|---|
| 0.75 | 0.075 | 0.999980 | −0.05464 | 0.078292 | 0.858571 | 0.017277 | 0.194526 | 0.078292 |
| 0.150 | 0.999990 | 0.032785 | 23.9443 | 0.46867 | 0.025948 | 0.498544 | 0.0572262 | |
| 0.225 | 0.999990 | 0.068664 | 13.97198 | 0.047448 | 0.0112722 | 0.883887 | 0.060954 | |
| 0.300 | 0.999999 | −0.89364 | 0.307836 | 0.79639 | 0.074489 | 1.097247 | 0.3037576 | |
| 1.25 | 0.075 | 0.999991 | 0.8151439 | 10.92615 | 0.8015159 | 0.0093420 | 0.18334003 | 0.024588 |
| 0.150 | 0.999935 | 0.027725 | 31.2562 | 0.0152427 | 0.0152427 | 0.517667 | 0.0319941 | |
| 0.225 | 0.999710 | 0.0297217 | 5.6398614 | 0.8597122 | 0.0385008 | 0.1105659 | 0.146296 | |
| 0.300 | 0.999992 | 0.05176108 | 37.35448 | 0.6796835 | 0.0526023 | 0.268555 | 0.1187397 | |
Fig. 2 depicts the plots of the variations of the experimental and the predicted moisture ratio by the best model i.e. Modified Henderson and Pabis with the drying time of garlic slices. From the plots, it is clear that the Modified Henderson and Pabis model gives an accurate prediction for the drying process of garlic slices under the tested settings.
3.3. Effective moisture diffusivity (Deff)
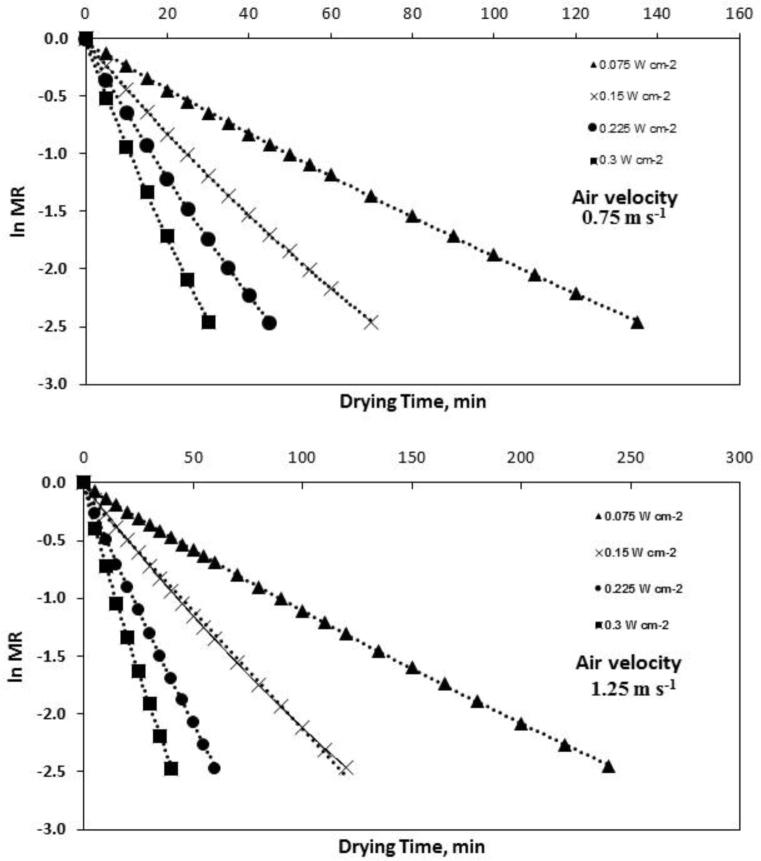
The values of ln(MR) were drawn versus the mean drying time (t) of garlic slices at the various experimental condition and the plots for the IR drying curves are illustrated in Fig. 4. The figure revealed that plots have slightly deviated from the linearity for all studied drying conditions. This deviation might be due to various causes e.g. the initial moisture content is not uniformly distributed, a variation of the product temperature during drying, change in moisture diffusivity with moisture content and shrinkage of the product (Adu and Otten, 1996, Khraisheh et al., 1997).
Fig. 4.
Values of ln(MR) versus the mean drying time (t) of garlic slices at the various experimental condition.
The deviation from linearity of the experimental logarithmic drying curve indicates that Deff is dependent on the moisture content (Celma et al., 2009). Thus, using non-linear regression a second order polynomial equation relating ln (MR) and the drying time (t) was established with a good fitting of the experimental results (Eq. (12)):
| (12) |
The regression coefficients A0, A1, and A2 of Eq. (12) and the resultant R2 are offered in Table 4.
Table 4.
Regression coefficients and coefficient of determination (R2) of Ln (MR) for different IR drying conditions.
| Air flow velocity (m S−1) | IR radiation intensity (W cm−2) | A0 | A1 | A2 | R2 |
|---|---|---|---|---|---|
| 0.75 | 0.075 | −0.0348 | −0.0204 | 0.00002 | 0.9997 |
| 0.15 | −0.0231 | −0.0419 | 0.0001 | 0.9998 | |
| 0.225 | −0.0234 | −0.0636 | 0.0002 | 0.9997 | |
| 0.3 | −0.0234 | −0.095 | 0.0005 | 0.9994 | |
| 1.25 | 0.075 | −0.0246 | −0.0114 | 0.000006 | 0.9999 |
| 0.15 | −0.0211 | −0.0242 | 0.005 | 0.9999 | |
| 0.225 | −0.0352 | −0.0445 | 0.0000005 | 0.9996 | |
| 0.3 | −0.0269 | −0.0709 | 0.0003 | 0.9996 | |
3.3.1. Effect of moisture content on the effective moisture diffusivity
The effective moisture diffusivity (Deff) of food materials describes the moisture mass transfer property through the food produce The change in Deff with the reduction in moisture content is a complicated process consist of molecular diffusion, liquid diffusion, vapor diffusion, hydrodynamic flow and other mechanisms (Karathanos et al., 1990).
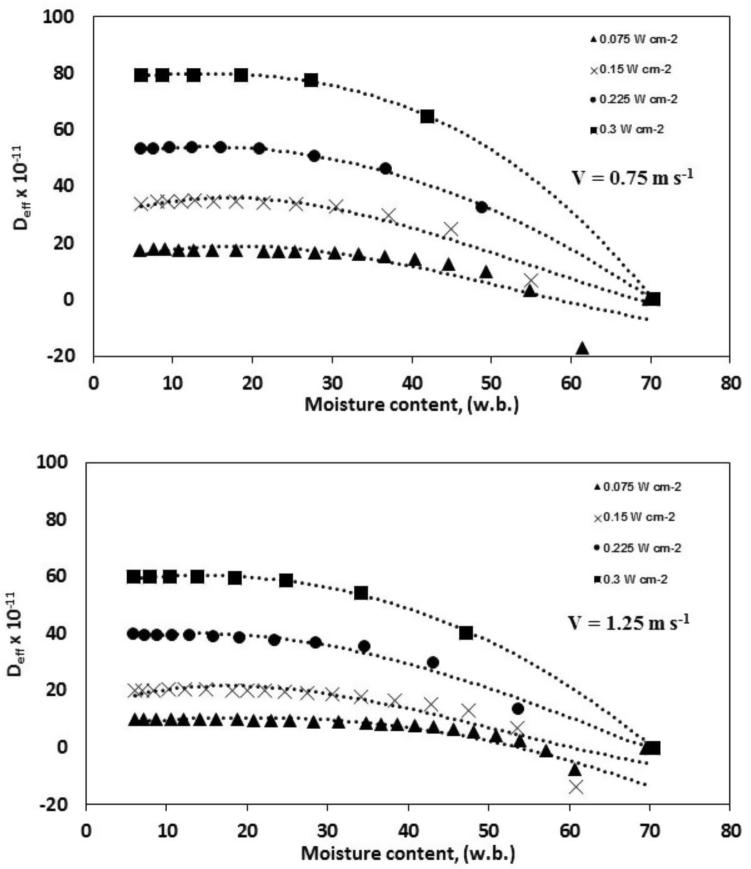
The calculated Deff values by Eq. (6) were plotted versus moisture content and are shown in Fig. 5. It is seen that Deff values increased as the moisture content decreased for all tested conditions. The dependency of the effective moisture diffusivity on moisture content may be due to the varied kinetics that causes moisture moving during the drying process. In the starting of the drying process, when the samples have a great amount of moisture, the moisture movement is mainly by liquid diffusion. During the progressing of the drying process and the sample surface gets more dried a permeable structure is shaped and the moisture transference may be due vapor diffusion. The pores in the garlic slices surface are enlarged as the water vapor pressure inside them increase. Hence Deff increases at higher moisture contents and decreases at lower ones. Comparable findings regarding the changes of Deff were stated by different authors for different food stuff (Sharma et al., 2005, Celma et al., 2009).
Fig. 5.
Changes in effective moisture diffusivity (Deff) with moisture content for garlic slices at different IR radiation and air flow velocity.
(Deff) was correlated versus moisture content (Mt) of garlic slices and establish a third order polynomial relationship as shown below:
| (13) |
The regression constants A, B, C, D of for IR drying of product at conditions of drying are shown in Table 5. The higher values of R2 reveals better fitting of the empirical equation in describing the changes of the effective moisture diffusivity (Deff) with the corresponding moisture content (Mt) at the different conditions of the thin-layer IR drying of the garlic slices.
Table 5.
Regression coefficients and coefficient of determination (R2) of Deff for different IR drying conditions.
| Air flow velocity (m S−1) | IR radiation intensity (W cm−2) | A | B | C | D | R2 |
|---|---|---|---|---|---|---|
| 0.75 | 0.075 | 11.73 | 0.8548 | −0.0283 | 0.0002 | 0.7682 |
| 0.15 | 27.73 | 1.0388 | −0.0363 | 0.0002 | 0.9669 | |
| 0.225 | 50.41 | 0.5051 | −0.0178 | 0.000006 | 0.9992 | |
| 0.3 | 77.926 | 0.2268 | −0.0035 | 0.0002 | 0.9999 | |
| 1.25 | 0.075 | 7.2374 | 0.3172 | −0.00071 | −0.00002 | 0.6291 |
| 0.15 | 13.969 | 0.9293 | −0.0317 | 0.0002 | 0.817 | |
| 0.225 | 35.742 | 0.6074 | −0.0234 | 0.0001 | 0.9808 | |
| 0.3 | 57.214 | 0.4253 | −0.0137 | 0.00005 | 0.9994 | |
3.3.2. Influence of IR drying variables on the average effective moisture diffusivity
The arithmetic mean of (Deff) at the different moisture content of the samples throughout the IR drying of garlic slices was calculated to determine the average effective moisture diffusivity (Deff)avg. the obtained data is tabulated and offered in Table 6. It is evident from this table that (Deff)avg increased gradually with the increase of IR radiation intensity for the same values of air flow velocity. At the air flow velocity of 0.75 m s−1 the values of (Deff)avg increased from 1.379 × 10−10 to 7.663 × 10−10 m2 s−1 with the increase of IR intensity from 0.075 to 0.300 W cm−2. This reduces the time of drying significantly. The increase of IR radiation resulted in fast heating of the garlic slices and the vapor pressure in the garlic slices increased which speed up the moisture diffusion to the samples surface. Still, Table 6 shows that (Deff)avg values reduced when the air flow velocity increased from 0.75 to 1.25 m s−1. This could be owing to that the samples were cooled by the higher air flow velocity since the samples temperature is higher than adjacent air.
Table 6.
Average effective moisture diffusivity ((Deff)avg) during infrared drying conditions.
| Air flow velocity, m s−1 | Infrared radiation intensity, W cm−2 | Average effective moisture diffusivity, m2 s−1 |
|---|---|---|
| 0.75 | 0.075 | 1.379 × 10−10 |
| 0.150 | 3.113 × 10−10 | |
| 0.225 | 4.996 × 10−10 | |
| 0.300 | 7.663 × 10−10 | |
| 1.25 | 0.075 | 0.5834 × 10−10 |
| 0.150 | 1.634 × 10−10 | |
| 0.225 | 3.559 × 10−10 | |
| 0.300 | 5.652 × 10−10 | |
Analyzing (Deff)avg values with the IR drying variables through linear regression provided this equation:
| (14) |
3.4. Activation energy
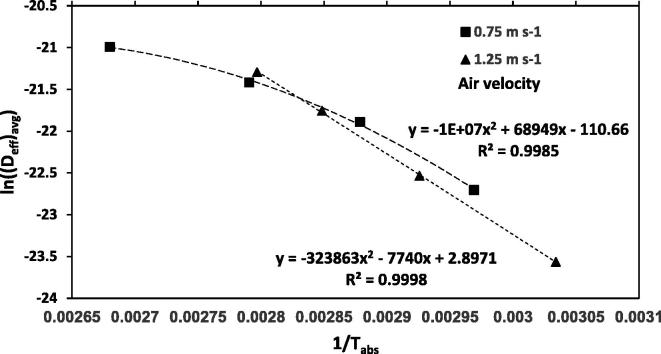
The values of the activation energy (Ea) in the IR drying of garlic slices were determined from the slope of Fig. 6 and they are tabulated and given in Table 7. Ea values for all the experimental condition ranged from 3.05 to 45.13 kJ mol−1. In the IR drying technology smaller Ea values indicates greater Deff values of the product. In drying methods, Ea values were lower than those for the conventional heating for moisture diffusivity of vegetables and varied from 130 to 280 kJ mol−1 (Feng et al., 1999). Ea values increased with the increased of air flow velocity from 0.75 to 1.25 m s−1 at all levels of IR radiation intensity. This displays that the drying rate decreased as the air velocity increased from 1.25 to 0.75 m s−1 during IR drying procedures. the values of Ea of a process decrease due to the increase in the average energy of the molecules. Hence, the above outcomes point out that the detected increasing of the drying rates throughout the IR drying of garlic slices resulted from the decreasing of the Ea values for moisture desorption. However, Ea values decreased with the increased of IR radiation intensity 0.075 to 0.3 W cm−2, for the two tested air flow velocities. Equivalent results in the change of Ea values during soybeans drying by microwave were stated (Adu and Otten, 1996).
Fig. 6.
Values of ln (Deff) versus the reciprocal of the absolute temperature (1/Tabs).
Table 7.
Average activation energy during infrared drying conditions.
| Air flow velocity, m s−1 | Infrared radiation intensity, W cm−2 | Average activation energy, kJ mol−1 |
|---|---|---|
| 0.75 | 0.075 | 25.38 |
| 0.150 | 12.29 | |
| 0.225 | 06.79 | |
| 0.300 | 03.05 | |
| 1.25 | 0.075 | 45.13 |
| 0.150 | 20.64 | |
| 0.225 | 16.62 | |
| 0.300 | 06.38 | |
4. Conclusions
Infrared radiation drying of garlic slices in thin-layer at radiation intensity ranging from 0.075 to 0.3 W cm−2 and two air flow velocity of 0.75 and 1.25 m s−1 was experimentally studied. the results showed an increase in the drying rate and a decrease in drying time with the increase of IR intensity and decrease of air flow velocity. The Modified Henderson and Pabis model is able to satisfactory describe the performance of garlic drying and well predicting the changes in moisture content of garlic slices. The effective moisture diffusivity (Deff) varied from 5.837 × 10−11 to 7.663 × 10−10 m2 s−1. The Deff was correlated versus moisture content of slices and a third order polynomial relationship was found. The Activation energy (Ea) increased with the increase of air flow velocity and the decreasing of IR radiation intensity.
Acknowledgements
The authors are grateful to the Deanship of Scientific Research, King Saud University for funding through Vice Deanship of Scientific Research Chairs.
Footnotes
Peer review under responsibility of King Saud University.
References
- Abe T., Afzal M. Thin-layer infrared radiation drying of Rough rice. J. Agr. Eng. Res. 1997;67:289–297. [Google Scholar]
- Adu B., Otten L. Microwave heating and mass transfer characteristics of white beans. J. Agr. Eng. Res. 1996;64:71–78. [Google Scholar]
- Akgun N.A., Doymaz I. Modeling of olive cake thin-layer drying process. J. Food Eng. 2005;68:455–461. [Google Scholar]
- Akpinar E.K., Bicer Y., Cetinkaya F. Modelling of thin layer drying of parsley leaves in a convective dryer and under open sun. J. Food Eng. 2006;75:308–315. [Google Scholar]
- Association of Official Analytical Chemists – International [AOAC] 18th ed. AOAC; Gaithersburg, MD, USA: 2005. Official Methods of Analysis. [Google Scholar]
- Aware R.S., Thorat B.N. Proceedings of the 17th International Drying Symposium. Magdeburg; Germany: 2010. Garlic drying by various methods and its impact onallicin retention. 1587–1585. [Google Scholar]
- Barrozo M.A.S., Souza A.M., Costa S.M., Murata V.V. Simultaneous heat and mass transfer between air and soybean seeds in a concurrent moving bed. Int. J. Food Sci. Tech. 2001;36(4):393–399. [Google Scholar]
- Bruce D.M. Exposed-layer barley drying, three models fitted to new data up to 150 °C. J. Agr. Eng. Res. 1985;32:337–347. [Google Scholar]
- Celma A.R., Cuadros F., Lopez-Rodriguez F. Review: characterization of industrial tomato by-products from infrared drying process. Food Bioprod. Process. 2009;87:282–291. [Google Scholar]
- Celma A.R., Rojas S., Lopez-Rodriguez F. Mathematical modelling of thin-layer infrared drying of wet olive husk. Chem. Eng. Process. 2008;47:1810–1818. [Google Scholar]
- Crank J. second ed. Clarendon press; Oxford, UK: 1975. The mathematics of diffusion. [Google Scholar]
- Diamante L.M., Munro P.A. Mathematical modeling of hot air drying of sweet potato slices. Int. J. Food Sci. Technol. 1991;26:99–109. [Google Scholar]
- Doymaz I. Convective air drying characteristics of thin layer carrots. J. Food Eng. 2004;61(3):359–364. [Google Scholar]
- Feng H., Tang J., Cavalieri R.P. Combined microwave and spouted bed drying of diced apples: effect of drying conditions on drying kinetics and product temperature. Dry Technol. 1999;17(10):1981–1998. [Google Scholar]
- Figiel A. Drying kinetics and quality of vacuum-microwave dehydrated garlic cloves and slices. J. Food Eng. 2009;94:98–104. [Google Scholar]
- Henderson S.M., Pabis S. Grain drying theory. II. Temperature effects on drying coefficients. J. Agr. Eng. Res. 1961;6:169–174. [Google Scholar]
- Henderson S.M. Progress in developing the thin layer drying equation. Trans. ASAC. 1974;17:1167–1172. [Google Scholar]
- Karathanos V.T., Villalobos G., Saravacos G.D. Comparison of two methods of estimation of the effective moisture diffusivity from drying data. J. Food Sci. 1990;55(1):218–231. [Google Scholar]
- Karathanos V.T. Determination of water content of dried fruits by drying kinetics. J. Food Eng. 1999;39:337–344. [Google Scholar]
- Kassem, A.S., 1996. Comparative studies on thin layer drying models for wheat. In: Proceedings of the 13th International Congress on Agricultural Engineering, vol. 6, 2–6 February, Morocco.
- Khraisheh M.A.M., Cooper T.J.R., Magee T.R.A. Shrinkage characteristics of potatoes dehydrated under combined microwave and convective air conditions. Dry. Technol. 1997;15(3–4):1003–1022. [Google Scholar]
- Lawson L.D., Wang Z.J. Low allicin release from garlic supplements: a major problem due to the sensitivities of alliinase activity. J. Agric. Food Chem. 2001;49:2592–2599. doi: 10.1021/jf001287m. [DOI] [PubMed] [Google Scholar]
- Litaiem J., Mihoubi D., Touil1 A., Zagrouba F. Experimental and theoretical investigation of drying behavior of garlic in infrared dryer. J. New Sci., Agric. Biotechnol., JS-INAT. 2015;6:861–867. [Google Scholar]
- Madamba P.S., Driscoll R.H., Buckle K.A. The thin layer drying characteristics of garlic slices. J. Food Eng. 1996;29:75–97. [Google Scholar]
- Midilli A., Kucuk H. Mathematical modelling of thin layer drying of pistachio by using solar energy. Energ. Convers. Manage. 2003;44:1111–1122. [Google Scholar]
- Midilli A. Determination of pistachio drying behaviour and conditions in a solar drying system. Int. J. Energy Res. 2001;25:715–725. [Google Scholar]
- Midilli A., Kucuk H., Yapar Z. A new model for single layer drying. Dry. Technol. 2002;20(7):1503–1513. [Google Scholar]
- Page G.E. Department of Mechanical Engineering; Purdue University, Purdue, USA: 1949. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin Layers. M.S. Thesis. [Google Scholar]
- Panchariya P.C., Popovic D., Sharma A.L. Thin-layer modeling of black tea drying process. J. Food Eng. 2002;52:349–357. [Google Scholar]
- Sacilik K., Unai G. Dehydration characteristics of Kastamonu garlic slices. Biosys. Eng. 2005;92(2):201–215. [Google Scholar]
- Sanjuan N., Lozano M., Garcia-Pascal P., Mulet A. Dehydration kinetics of red pepper (Capsicum annuum L. var. Jaranda) J. Sci. Food Agric. 2003;83:697–701. [Google Scholar]
- Sharaf-Eldeen Y.I., Blaisdell J.L., Hamdy M.Y. A model for ear corn drying. Trans. ASAE. 1980;23(5):1261–1265. [Google Scholar]
- Sharma G.P., Verma R.C., Pathare P.B. Thin layer infrared radiation drying of onion slices. J. Food Eng. 2005;67:361–366. [Google Scholar]
- Togrul H. Simple modeling of infrared drying of fresh apple slices. J. Food Eng. 2005;71:311–323. [Google Scholar]
- Togrul H. Suitable drying model for infrared drying of carrot. J. Food Eng. 2006;77:610–619. [Google Scholar]
- Togrul I.T., Pehlivan D. Mathematical modelling of solar drying of apricots in thin layers. J. Food Eng. 2002;55:209–216. [Google Scholar]
- Verma L.R., Bucklin R.A., Endan J.B., Wratten F.T. Drying effects of drying air parameters on rice drying models. Trans. ASAE. 1985;85:296–301. [Google Scholar]
- Wang C.Y., Singh R.P. Use of variable equilibrium moisture content in modeling rice drying. Trans. ASAE. 1978;11:668–672. [Google Scholar]
- White G.M., Ross I.J., Ponelert R. Fully exposed drying of popcorn. Trans. ASAE. 1981;24:466–468. [Google Scholar]
- Yilbas B.S., Hussain M.M., Dincer I. Heat and moisture diffusion in slab products to convective boundary condition. Heat Mass Transf. 2003;39:471–476. [Google Scholar]