On the complex dynamics of savanna landscapes

Significance

This paper makes a significant contribution both to ecological theory and to an understanding more generally regarding how complex dynamics can emerge in mathematical models from quite simple underlying assumptions. Empirical and theoretical work has suggested that savanna–forest systems exhibit bistability, potentially flipping from one state to another in the face of environmental change. Here, we show that the dynamics of those systems may be much more complicated (periodic and endogenously driven) and present surprising responses to environmental variability. From a mathematical point of view, the models that we explore exhibit a rich array of behaviors and responses to random perturbations, and we suggest that such dynamics may arise in a variety of contexts.

Abstract

Simple mathematical models can exhibit rich and complex behaviors. Prototypical examples of these drawn from biology and other disciplines have provided insights that extend well beyond the situations that inspired them. Here, we explore a set of simple, yet realistic, models for savanna–forest vegetation dynamics based on minimal ecological assumptions. These models are aimed at understanding how vegetation interacts with both climate (a primary global determinant of vegetation structure) and feedbacks with chronic disturbances from fire. The model includes three plant functional types—grasses, savanna trees, and forest trees. Grass and (when they allow grass to persist in their subcanopy) savanna trees promote the spread of fires, which in turn, demographically limit trees. The model exhibits a spectacular range of behaviors. In addition to bistability, analysis reveals (i) that diverse cyclic behaviors (including limit and homo- and heteroclinic cycles) occur for broad ranges of parameter space, (ii) that large shifts in landscape structure can result from endogenous dynamics and not just from external drivers or from noise, and (iii) that introducing noise into this system induces resonant and inverse resonant phenomena, some of which have never been previously observed in ecological models. Ecologically, these results raise questions about how to evaluate complicated dynamics with data. Mathematically, they lead to classes of behaviors that are likely to occur in other models with similar structure.

It has long been recognized that even simple mathematical models can give rise to very complex behaviors. Lorenz (1), more than a half-century ago, showed that such issues could confound weather prediction, and Ricker (2) and May (3) both illustrated analogous complications for the prediction of the dynamics of biological populations. This should not be interpreted so much as a criticism of models, but rather, it is a recognition that even simple underlying relationships can lead to very complicated dynamics. Quite surprisingly, more complex relationships do not in general produce more complex outcomes. Moreover, rich dynamics emerging from simple models do not necessarily prevent the establishment of predictable macroscopic properties that emerge, as in the ergodic theory of chaos (4). Such considerations make clear the importance of understanding the range of behaviors that simple models of biological systems can exhibit, even when explicit prediction is impossible. Knowledge of the range of possible biological outcomes can be a first step toward coarse-graining that can lead to more robust prediction.

Simple models that exhibit complex dynamics have proved to be invaluable in motivating and advancing work in dynamical systems, as for the Lorenz equations and the Belousov–Zhabotinsky reaction (5, 6). Equally important, however, is to understand the biological relevance of complex dynamics, the mechanisms that give rise to them, and their robustness in the face of model simplification (7) or in response to noise. Simple dynamical systems may indeed show surprising and sometimes paradoxical responses in noisy environments.

In this paper, we explore a set of simple, yet realistic, models of savanna dynamics based on simple ecological principles and classify the spectacular range of dynamic behaviors that they produce. We focus on the dynamics and distributions of biomes—the broadest organizational unit for vegetation globally. Biomes include, for example, deserts, temperate forests, and savannas. Ecologists have long recognized that climate is the primary determinant of the distribution of biomes on Earth (8, 9). However, we also increasingly recognize that the relationship between climate and vegetation distributions is not strictly deterministic (even accounting for differences in, for example, soils) (10, 11). Dynamic systems where vegetation–environment feedbacks are significant—such as savannas, defined by the coexistence of trees and grasses—present a particular challenge. Recent work suggests that, over large parts of their range, savannas persist where climate can support forests, because fire limits tree cover (10, 11). Low tree cover, in turn, facilitates the accumulation of grass, which fuels frequent fires in savannas, such that savannas potentially represent a distinct and stable alternative to forests maintained by a positive feedback with fire (11, 12).

Here, our model captures these dynamic features of savanna–forest systems, where the relationship between biome and climate is not deterministic. It describes the proportions of grass, forest trees, and savanna trees and distinguishes between saplings that are easily burnt by fire and adult savanna trees more resistant to fire. We examine the complex dynamics of this system and the dynamical structures that organize its behavior, including families of periodic behaviors, heteroclinic orbits connecting as many as three distinct equilibria, and bifurcations of periodic orbits as well as the coexistence thereof. Those dynamics may be real but of little biological importance, and we explore this aspect. More fundamentally, we explore the mechanisms that give rise to the observed behaviors, illustrate the richness that can arise from these simple assumptions, and show how to decompose the dynamics to understand their fundamental nature more deeply. In particular, we show how these dynamics are impacted by the presence of noise and exhibit a surprising effect of random ecological fluctuations either in promoting the emergence of large-amplitude periodic behaviors at specific noise levels or even more paradoxically, in collapsing periodic dynamics onto an equilibrium, stopping oscillations where fluctuations have specific SDs (stochastic resonance or inverse stochastic resonance). All of these mathematical properties provide a better understanding of the complex interaction between savanna and forest biomes and of the key elements of their stability.

Grass/Savanna Trees Dynamics

Our model describes the interplay in savanna–forest systems between grass and trees. We base our model on two simple ecological observations. The first is that the emergence of large trees in savanna is limited by fire: indeed, saplings are fire-susceptible but resprout readily (13, 14), such that fire does not kill saplings but rather, limits their transition to the adult size class (15); after trees are large, they are mostly resistant to the relatively mild fires (16, 17) that characterize savanna systems (18). This observation lends itself to a size-structured model, in which we distinguish saplings $S$ and adult trees $T$ together with a sapling-to-tree recruitment rate $\omega$ that depends on the occurrence of fire.

The second key observation is that fire is limited, in turn, by tree cover (19). The response of fire to tree cover is nonlinear; fire spreads readily in systems with some tree cover but quickly stops spreading above a threshold in tree cover [evaluated to around 40% in remotely sensed tree cover datasets (19)], which reflects the dependence of fire spread on sufficient grass biomass (20, 21). Although fire spread can be modeled explicitly (22), a simpler model can be formalized. We base the model on units of aerial cover (where G, S, and T represent the fractional covers of grass, saplings, and trees, respectively), incorporating the threshold response of fire to grass cover $G$ into the sapling-to-tree recruitment term $\omega$. At high $G$, fire spreads, and sapling-to-tree recruitment $\omega$ is low; at low $G$, fire cannot spread, and $\omega$ is high. This yields the following 3D system (11):

$$\{\begin{array}{cc}\dot{G}=\mu S+\nu T-\beta GT\hfill & \\ \dot{S}=\beta GT-(\omega (G)+\mu )S\hfill & \\ \dot{T}=\omega (G)S-\nu T\hfill & \end{array},$$ [1]

where $\mu$ and $\nu$ are the mortality rates of savanna saplings and adult trees, respectively; $\beta$ is the birth rate of savanna saplings; and the sapling-to-tree recruitment coefficient $\omega$ is a decreasing sigmoidal function of grass (Table 1 shows the formula sigmoidal function used in our simulations). Because they represent fractions of landscape cover, the variables $(G,S,T)$ are such that $G+S+T=1$, allowing us, by expressing one of the variables as a function of the other two, to reduce the system to a 2D equation with no constraint on the variables. The analysis of this system (details are in SI Savanna and Woodlands) reveals that, depending on parameter values, the system can have multiple equilibria resulting from the general sigmoidal response of $\omega$ to $G$ but largely independent of its precise functional form (11). We elucidate analytically and numerically the dependence on the parameters of the emergence of these multiple stable equilibria in Fig. 1. This analysis shows that, depending on the birth and mortality rates of trees, the landscape can develop into grassland or alternatively, into a completely wooded landscape; and both states can coexist and be stable in a wide region of parameters delineated by codimension-one saddle node bifurcations (23, 24). These bifurcations merge tangentially and disappear at cusp bifurcation points (ref. 24, chap. 8.2), beyond which the two equilibria can no longer coexist; as parameters vary further, the landscape changes gradually.

Table 1.

Parameters interpretation and default value (unless specified otherwise)

Symbol	Ecological interpretation	Default value
$\alpha$	Forest tree birth rate	0.2
$\beta$	Savanna saplings birth rate	0.3
$\gamma$	Fire propagation through savanna relative to grass	$\in [0,1]$
$\omega$	Savanna sapling-to-adult recruitment rate	$\omega (G,S,T)={\omega }_0+\frac{{\omega }_1-{\omega }_0}{1+e^{-(G+\gamma (S+T)-{\theta }_1)/s_1}}$
		${\omega }_0=0.9$, ${\omega }_1=0.4$, ${\theta }_1=0.4$, $s_1=0.01$
$\phi$	Forest tree mortality rate	$\phi (G,S,T)={\phi }_0+\frac{{\phi }_1-{\phi }_0}{1+e^{-(G+\gamma (S+T)-{\theta }_2)/s_2}}$
		${\phi }_0=0.1$, ${\phi }_1=0.9$, ${\theta }_2=0.4$, $s_2=0.05$
$\mu$	Savanna sapling mortality rate	0.1
$\nu$	Adult savanna tree mortality rate	0.5

Fig. 1.

Codimension-one (A) and -two (B–F) bifurcation diagrams of model Eq. 1 (ω₁ = 0.2, µ = 0.2, and ν = 0.1, black lines in panels B–E) with respect to all pairs of parameters. Blue regions, bistability between the two regimes; green regions, only the grassland state is stable; yellow regions, only the woodland state is stable. (A) Equilibria are plotted in blue: stable, solid line; unstable, dashed line. Default parameters are the same as in Table 1. SN, saddle node (pink); Tc, transcritical bifurcation (purple).

From the ecological viewpoint, the dynamical structure underlying bistability results in the fact that dramatic changes in the ecological landscape and ecosystems may occur from small perturbations, arising, for instance, from natural fluctuations, climatic events, or human-related interactions. These can lead to persistent switches between grassland and wooded landscapes. In these regions, landscape structure strongly depends on its history and is hysteretic, and over time, in the presence of ecological fluctuations, the relative times spent in the grassland or wooded landscapes are a monotonic function of the birth rate of savanna saplings (Fig. S8).

In this simplest model, high tree cover—loosely corresponding to forest—is stable for some regions of parameter space. However, these “forests” have little in common with real forests, which differ from savannas in more than just the density and cover of trees. Forest trees differ from savanna trees in that they are actually killed by fires (not just “topkilled” and able to readily resprout) (25–27) and are susceptible to fires at much larger sizes (25, 28). Forest trees also shade out grasses completely (20, 21, 29), while savanna trees are more variable (30, 31) but can have very open canopies (30, 31). Forests of savanna trees are more similar to what ecologists sometimes call woodland, although this is itself a somewhat ambiguous term for something that may be relatively rare in nature (32); we will use this terminology here.

Adding a Forest Tree Functional Type

To consider these trait differences among savanna and forest trees, we add a dimension to our model to include an additional forest tree functional type $F$, the mortality of which $\phi$ depends on whether fire can spread. We also allow savanna trees ($S$ and $T$) to vary in the degree to which they exclude grasses (33, 34), thereby preventing fire to spread. We denote this with $\gamma \in [\mathrm{0,1}]$, with the convention that $\gamma =1$ corresponds to savanna trees that allow fire to spread as well as grass alone and that $\gamma =0$ corresponds to perfectly shady savanna trees:

$$\{\begin{array}{cc}\dot{G}=\mu S+\nu T-\beta GT+\phi (G+\gamma (S+T))F-\alpha GF\hfill & \\ \dot{S}=\beta GT-(\omega (G+\gamma (S+T))+\mu )S-\alpha SF\hfill & \\ \dot{T}=\omega (G+\gamma (S+T))S-\nu T-\alpha TF\hfill & \\ \dot{F}=(\alpha (1-F)-\phi (G+\gamma (S+T)))F\hfill & \end{array},$$ [2]

where $\alpha$ is the forest tree birth rate. We note that the savanna dynamics given by equations in Eq. 1 correspond to a subsystem of this generalized model with $F=0$ and $\gamma =0$. We show in SI Savanna and Forests the intuitive result that this subsystem is stable as soon as the average forest tree mortality rate in time along a trajectory $(G(t),S(t),T(t))$ is strictly larger than its birth rate. From an ecological viewpoint, we observe that, given the sigmoidal decreasing shape of the forest tree mortality rate map, forests are more likely to invade savanna landscapes with little grass than landscapes dominated by grass, which is a natural consequence of the fact that fires tend to be less frequent in these regimes, leaving opportunities for forest trees to emerge.

We now analyze in detail the dynamics of the full system given by Eq. 2, first investigating the tension between the establishment of grass and forest in the absence of savanna trees before investigating how the degree to which savanna trees and saplings prevent fire spread qualitatively affects the dynamics of this system.

Grass/Forest Tree Dynamics.

The global ecological system 2 contains a description of the interplay between grass and forest trees in the absence of savanna trees ($S=T=0$) given by the 1D dynamics

$$\dot{G}=\phi (G)F-\alpha GF,$$

with $F=1-G$. We investigate in detail this subsystem in SI Savanna and Forests and show that this system generically displays one or three fixed points: for a small forest tree birthrate $\alpha$, compared with the mortality rate, the landscape develops into a grassland, while for high birth rates, the landscape develops into a forest dominated by forest-type trees; for intermediate values, the system displays bistability between these two regimes. Similar to the savanna equilibria in the reduced system, the system shows sharp transitions between the different equilibria associated with a pair of saddle node bifurcations, which collapse into codimension-two cusp bifurcations as other parameters are varied, implying the presence of hysteresis and noise-induced attractor switching (Fig. S8). Furthermore, we also show that the subspace is stable, irrespective of the value of $\gamma$, as soon as the product of the rates of increase of $S$ and $T$ is smaller than the product of their removal rates, an intuitive condition from the ecological viewpoint.

The Complex Dynamics of Composite Landscapes.

The subsystems exhibited above are constrained by their effective low dimensionality, and the dynamics reduce to relatively simple attractors. These savanna, woodland, and forest equilibria coexist with possible composite states, where all ecological species are present. In particular, these states naturally emerge where forest tree birth rates are low. In the extreme case where $\gamma =0$, such that savanna trees and saplings do not propagate fire, the system was examined in ref. 12; in that work, cursory numerics hinted toward the emergence of complex cyclic behavior requiring more sophisticated analysis. We provide here a study of the dynamics and bifurcations of that system as multiple parameters vary to reveal the underlying dynamical structures of the system.

We examine in detail the dynamics of this system and its bifurcations as a function of savanna and forest trees birth rates $\alpha$ and $\beta$, which are key parameters of ecological systems. In particular, these parameters, still not well-constrained in the empirical literature, are the ones around which we have the most uncertainty and are likely to vary between different ecological conditions.

This analysis reveals a very sensitive dependence on the parameters of the dynamics. Complex dynamics appear, including in addition to a variety of equilibria, families of periodic orbits undergoing complex transformations, including folding and collisions with branches of neutrally stable equilibria at homoclinic or heteroclinic points. These phenomena are summarized in the codimension-two bifurcation diagram in Fig. 2, displayed together with sample codimension-one bifurcation diagrams and individual trajectories (SI Composite Landscapes and Fig. S2 have more details). In the codimension-two bifurcation diagram, we observe the changes in the number and stability of equilibria and periodic orbits as a function of $\alpha$ and $\beta$. Of course, saddle node bifurcations of the savanna and forest subsystems identified above are present in the bifurcation diagram; since these only depend on one of two birth rates, they form straight lines parallel to the axes. In addition to these already identified bifurcations, the diagram is organized around a complex Hopf bifurcation curve associated with the emergence of families of periodic orbits, with stability that depends on the supercritical or subcritical nature of the bifurcation (23, 24) (generating locally stable or unstable limit cycles, respectively). Here, we observed that the nature of the Hopf bifurcation is not constant along the bifurcation line and changes at four points of the plane $(\alpha ,\beta )$. The points at which the criticality of the Hopf bifurcation changes correspond to codimension-two Bautin bifurcations (ref. 24, chap. 8.3). The universal unfolding of this bifurcation contains a fold of limit cycles, along which a branch of stable and a branch of unstable limit cycles collide and disappear. The changes in the sub- or supercritical nature of the Hopf bifurcations are visible in the codimension-one bifurcation diagrams in that the local stability of the cycles near the bifurcations is modified as we change parameters and the presence of folds of limit cycles also clearly affects the dynamics of the system. In these diagrams, we observe that the system may present diverse dynamics, including stable grassland, savanna, forest, and woodland, or composite equilibria, multistability, and periodic orbits. Note that the folds of limit cycles (pink curves in Fig. 2) play a particularly important role in shaping the region of oscillations of the system. They will also have a crucial and surprising effect of silencing oscillations in the presence of noise, as we will show below.

Fig. 2.

Bifurcation diagram of the full system. (A) Codimension-two bifurcation diagram as a function of $\alpha$ and $\beta$. Orange regions indicate the presence of stable oscillations, and yellow regions indicate the presence of unstable oscillations. Parameters are the same as in Table 1. Blue lines, homoclinic bifurcations; dashed black lines, subcritical Hopf bifurcation; GH, generalized Hopf bifurcation (Bautin); green lines, saddle node; purple lines, transcritical; solid black lines, supercritical Hopf bifurcation. (B) Codimension-one slices of the above bifurcations for fixed $\beta =0.4$ (B1) or $\alpha =0.4$ (B2). Blue solid (dashed) lines correspond to stable (unstable) fixed points, solid (dashed) pink lines correspond to the maximum and minimum G values on a stable (unstable) cycle, and circles correspond to heteroclinic orbits (blue stars depict the fixed points belonging to the orbit). Bifurcations indicated on the graph split the diagram into four regions (woodland, oscillations, bistability, and forest; B1) or grassland, woodland, and oscillations (B2). C1 (β = 0.2) and C2 (parameters as in B2) represent a selection of typical dynamics in the regions depicted in B1 and B2.

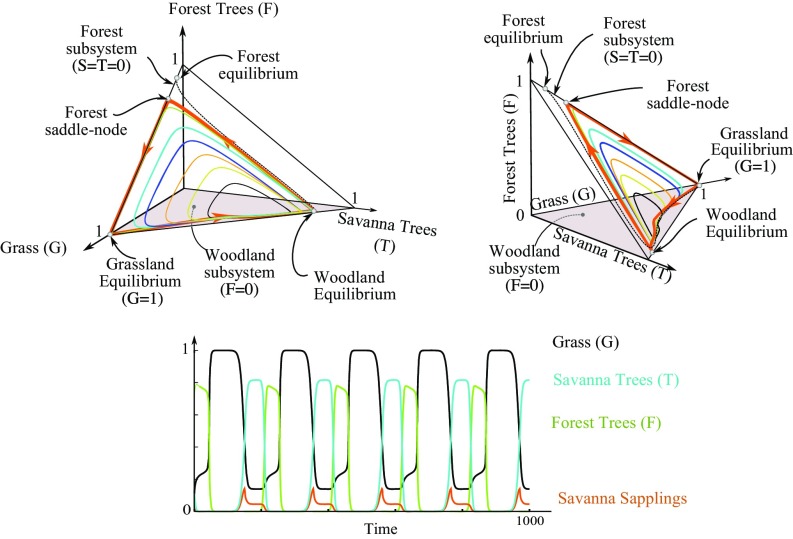
The supercritical Hopf bifurcation line delineates a wide region where the system displays stable oscillations and varies regularly between different landscapes. As we investigated the persistence of these oscillations as a function of the parameters, we found that they undergo a dramatic transition at the saddle node bifurcation associated with the forest subsystem. At this point, the orbit expands and approaches the three coexisting unstable equilibria of the system. This results in sharp, large-amplitude, slow oscillations, leading the system from almost stabilizing to a regime completely invaded by grass $G=1$ before rapidly switching to approaching a savanna or woodland equilibrium with no forest tree and then jumping suddenly to a forest equilibrium when savanna trees are absent, itself leading to the grass equilibrium where this slow dynamic starts anew. These trajectories are depicted in Fig. 3. As parameters are varied, these trajectories collapse to a heteroclinic loop formed from branches of invariant manifolds exactly connecting (i) the full-grass equilibrium ($G=1$) to (ii) a savanna or woodland equilibrium (unstable saddle landscape with grass, savanna saplings and trees, and no forest tree) to (iii) a forest saddle node equilibrium (with grass and forest trees in the absence of savanna saplings and trees). This family of heteroclinic loops persists for a wide range of parameter values with fixed forest tree birthrate as soon as the savanna sapling birth rate is sufficiently large.

Fig. 3.

Family of stable periodic orbits and heteroclinic loop. The heteroclinic joins the grassland equilibrium, the forest saddle node, and the woodland equilibrium. Parameters are the same as in Fig. 2 with $\beta =0.4$. (Upper) The heteroclinic loop (orange bold cycle) and associated stable cycles ($\alpha$ ranging from $0.2$ to $0.565$) in the phase space $(S,T,F)$. One trajectory for $\alpha$ larger than the value of the heteroclinic loop is plotted as a dashed black line: it converges toward the forest equilibrium. (Lower) Dynamics in time near the heteroclinic cycle show long transient stabilizations near grassland, forest, and woodland equilibria.

In ecological terms, heteroclinic cycles arise when all of the three following conditions are satisfied.

• i)The grass equilibrium is unstable to invasion by savanna trees $\beta \omega (1)>\nu (\mu +\omega (1))$ [i.e., when savanna sapling birthrate $\beta$ and/or savanna sapling-to-adult tree recruitment rate at high grass $\omega (1)$ are large enough in comparison with savanna trees mortality].
• ii)The woodland or savanna equilibrium is unstable to invasion by forest trees [i.e., the birth rate of forest trees is larger than their death rate at the equilibrium grass level $G_w$: $\alpha >\phi (G_w)$].
• iii)The full-grass equilibrium is stable for the savanna–forest subsystem [i.e., the birth rate of forest trees is smaller than their mortality rate when the landscape is only composed of grass $\alpha <\phi (1)$].

Because $\phi$ is nondecreasing, it is clear that these three conditions are simultaneously valid for a wide range of parameters. In these situations, one can understand the origin of the periodic and heteroclinic behaviors. Let us, for instance, assume that the landscape is initially almost completely covered by grass. Because of the high birth rate of savanna saplings and high recruitment rate to adult savanna trees (condition i), savanna trees progressively invade the landscape, while forest trees remain initially at a low level (condition iii). The establishment of a woodland makes fires less frequent, such that the forest tree death rate drops. Eventually, forest tree death rates are swamped by their birth rate, and the forest tree population starts expanding at the expense of savanna trees (condition ii). However, forest trees, more sensitive to fires than savanna trees (conditions i and iii), are in turn replaced by grass, and the system returns to a landscape dominated by grass, where the process starts afresh.* Oscillations are thus the result of a winnerless competition, wherein grass landscapes are invaded by savanna woodlands, themselves invaded by forest trees; in turn, they are overrun by grass because of their sensitivity to fire. This heteroclinic cycle arising in a winnerless competition is evocative of classical results of the competition between three species dating back to May and Leonard (35). Generally, heteroclinic cycles are not structurally stable, and it is the specific structure of ecological models in ref. 35 and probably in our model, particularly the presence of invariant subspaces, that may be at the root of the observed robustness. Symmetries can also stabilize heteroclinic cycles as shown in systems equivariant with respect to a symmetry group in ref. 36. We refer to the review in ref. 37 for a complete discussion on robust heteroclinic cycles in systems featuring invariant subspaces.

For completeness, we mention the presence of a family of homoclinic orbits on a saddle composite equilibrium (light-blue curve in Fig. 2). These orbits are repulsive and thus, do not affect the dynamics in a visible way. They are described in more detail in SI Composite Landscapes and Fig. S3.

When Savanna Trees Propagate Fire.

The above bifurcation diagram is valid when neglecting that savanna trees can propagate fire. We investigate in this section the persistence and breakdown of oscillatory dynamics when savanna trees propagate fire. In the extreme (and somewhat unrealistic) case that savanna trees propagate fire with the same intensity as grass, the system is ecologically qualitatively similar to the 2D system that we consider above. Indeed, we show in SI When Savanna Trees Can Propagate Fire that the system admits a maximum of two stable equilibria: (i) a savanna landscape with high grass plus savanna tree cover, which spreads fire and keeps forest tree density low via a positive feedback, and (ii) a forest—this time a more realistic forest composed of forest trees—that prevents fire from spreading, thereby keeping forest tree mortality low via another positive feedback. Formally, in this system, the forest trees satisfy an autonomous differential equation, and the other variables can only display equilibria by a simple application of Bendixson’s criterion (SI When Savanna Trees Can Propagate Fire).

In reality, savanna trees vary quite substantially in the degree to which they exclude grasses, thereby preventing fire spread (38, 39). Intermediate values of $\gamma$ are thus of interest, and explicit analysis with respect to $\gamma$ reveals that this parameter substantially modifies the dynamics through complex bifurcations that organize the way in which the variety of oscillations observed in the system with $\gamma =0$ disappear as $\gamma$ increases. To characterize this dependence, we computed the bifurcation diagram of the system as a function of the three relevant parameters $\alpha$, $\beta$, and $\gamma$. We found that a complex codimension-three bifurcation diagram organizes the system and by computing multiple codimension-two bifurcations diagrams, show that, in the vicinity of this point, the unfolding of the dynamical structures is consistent with a degenerate Bogdanov–Takens bifurcation of the elliptic type described in ref. 40, chap. VI.C (details are in SI When Savanna Trees Can Propagate Fire and Fig. S5). To represent the complex mechanisms associated with this singularity, we display in Fig. 4 various codimension-two bifurcation diagrams with respect to the parameters $(\beta ,\gamma )$ for distinct values of the parameter $\alpha$. For fixed $\gamma =0$, we have observed in Fig. 2 that the curve of Hopf bifurcations switches from sub-to supercritical through a Bautin bifurcation, which implies in particular that, beyond this bifurcation, the bifurcation diagram for fixed $\alpha$ displayed a supercritical Hopf bifurcation and a subcritical Hopf bifurcation. As $\gamma$ is varied, we observed two distinct scenarios depending on the value of $\alpha$ relative to two critical values ${\alpha }_{c1},{\alpha }_{c2}$ corresponding first to a fold of the curve of Bogdanov–Takens bifurcation and second to the codimension-three point numerically identified as a degenerate Bogdanov–Takens bifurcation mentioned above. These two critical values split the parameter space into three main types of codimension-two bifurcations diagrams. For $\alpha <{\alpha }_{c1}$, the upper branch of subcritical Hopf bifurcations undergoes a Bautin bifurcation and turns supercritical before merging with the branch of supercritical Hopf bifurcations, forming a closed curve within which the system features oscillations. For $\alpha >{\alpha }_{c1}$, the curve of Hopf bifurcation splits into two parts, with the upper branch possibly displaying a change in the sub- or supercritical nature through a Bautin bifurcation when $\alpha <{\alpha }_{c2}$; each branch of Hopf bifurcation merges on a saddle node curve through Bogdanov–Takens bifurcations, which are classically associated with the presence of homoclinic orbits.

Fig. 4.

Impact of fire propagated by savanna trees. (A) Codimension-two bifurcation diagrams as a function of $\beta$ and $\gamma$ for various values of $\alpha$ (colors). Solid lines indicate supercritical Hopf, dashed lines indicate subcritical Hopf, and dotted–dashed lines indicate saddle node bifurcations. (B) Codimension-one bifurcation diagrams as a function of $\gamma$ for fixed values of $\alpha =0.4$ and $\beta =2$ (B1) or $\beta =0.5$ (B2) or of $\alpha =0.3$ and $\beta =1.3$ (B′1). The codimension-one bifurcations are depicted with blue circles for bifurcations of equilibria or with orange circles for bifurcations of periodic orbits. They split the parameter space into four types of regions: composite equilibria (green region), oscillations (yellow region), woodland (pink region), and bistability (B′1; light blue). Sample dynamics for each subregion are shown in C1–C3, corresponding to parameter values associated with B1, B2, and B′1, respectively, and with $\gamma$ indicated along the top. BT, Bogdanov–Takens bifurcation; FLC, fold of limit cycles; GH, generalized Hopf bifurcation (Bautin); Hom, homoclinic; SNT, saddle node transcritical; Tc, Hopf and transcritical.

From an ecological viewpoint, this diagram shows that the capacity of savanna trees to propagate fire has major effects on landscape dynamics. We notice that, for all of the values of $\alpha$ considered, the upper branch of the Hopf bifurcation curve is initially increasing, implying that fire propagating through savanna trees can be the source of oscillating landscapes, even where the effects of fire do not vary through time. We have extracted three codimension-one bifurcation diagrams to illustrate the role of $\gamma$. For large birthrates of forest and savanna trees, we observe that increasing $\gamma$ indeed induces the emergence of massive oscillations of the system appearing through a subcritical Hopf bifurcations and after a fold of limit cycles and that these oscillations persist until a homoclinic loop, where they collapse with a saddle fixed point (Fig. 4B1). These dynamics are sensitive to modifications of the birthrates of trees. For smaller values of savanna saplings birthrates $\beta$, in sharp contrast with the previous case, large oscillations are present in the system for $\gamma =0$ and progressively vanish as $\gamma$ is increased through a supercritical Hopf bifurcation (Fig. 4B2). For smaller values of the forest trees birthrate and associated decrease in the savanna trees birthrates, we found distinct dynamics with periodic orbits emerging and disappearing through Hopf bifurcations (Fig. 4C1). Note that extensive numerical analysis did not identify other types of bifurcations, such as possible period doublings in the continuation of branches of limit cycles, and that no chaotic dynamics were observed.

Role of Ecological Noise

These very simple models for savanna and forest can be criticized on a number of fronts. Most notably, they are based on the implicit assumption that rates are deterministic and constant through time. In savannas especially, this assumption is obviously flawed; savannas are subject to multifarious variability, which may be fundamental to their long-term ecological functioning (15, 41). For starters, fire is to some extent a stochastic event. Most savannas experience fires at most once per year and often, on average, at a much lower frequency (19, 42); the timing of these partially depends on climatic variability but is probably also partially stochastic (43). Growth rates of both savanna and forest trees can also vary from year to year (31, 44, 45), driven by variability in water and nutrient limitation and by shifting landscape patterns of herbivory; as a result, the timing of tree establishment in savannas changes significantly through time (46–48).

A common assumption of relevant models is that all of these sources of variability tend to average out, such that global dynamics are well-described by average effective parameters. However, tackling variability in demographic parameters may be crucial to evaluating whether the dynamics described above have any relevance to savannas or in fact, to any system, and we ask this explicitly in this system by introducing stochastic fluctuations in the system 2 (details are in SI Role of Noise: Stochastic and Inverse Stochastic Resonances).

It is natural to assume that random perturbations of this dynamical system may have a limited effect on the observed dynamics in regions where the system displays single attractive equilibria. In the case of multistability, it is well-known that the system will wander from one equilibrium to another with dwell times that depend on the geometry of the dynamical system, particularly on the attraction basins of each equilibrium and on the attractivities of these (Fig. S8). At the other extreme, a noise of very large variance generally overwhelms the dynamics. Between these two regimes, noise may interact in a subtle way with the nonlinearities and yield dynamics not predicted in the deterministic system. This is particularly true in the vicinity of global bifurcations, where the dynamics can be very sensitive to perturbations and where noise elicits alternative dynamics.

Noise in Nonlinear Dynamical Systems.

Understanding the effect of random perturbations on nonlinear systems near these transitions has been a challenge across many scientific disciplines and particularly in biology (49–52). For instance, coherence resonance first shown 20 y ago (53) describes the phenomenon, whereby small noise applied to a system near (but before) a Hopf bifurcation threshold generates coherent oscillatory responses. This is a quite general phenomenon (ref. 54 has a review) that naturally occurs in this system near Hopf bifurcations. The noisy oscillations generated by this phenomenon are of relatively modest amplitude and do not necessarily induce a significant footprint in the dynamics that would be visible in data. Instead, we will focus our attention on two phenomena identified more recently that possibly have a massive impact on the dynamics.

• i)Stochastic resonance, whereby noise induces large-amplitude optimally periodic responses in systems with no periodic orbit. These phenomena were chiefly identified in so-called excitable dynamical systems (55), which feature an equilibrium (or rest) state, an excited state corresponding to a large transient excursion from the resting state, and a refractory (or recovery) period. These states are organized in such a way that, in the absence of noise, the system is at rest, but in response to perturbations, it goes through the excited state and then to the refractory state before returning to rest. Stochastic resonance is naturally associated with multiple timescale dynamics, such as nerve spikes (56–58), where they have been confirmed experimentally (59–61).
• ii)Inverse stochastic resonance, whereby noise optimally cancels oscillatory responses. This phenomenon was recently evidenced in specific regimes of systems featuring a bistability between a periodic orbit and an equilibrium (62, 63) as well as in data (52).

Here, we show that the system displays both phenomena in the vicinity of its global bifurcations: stochastic resonance around the heteroclinic orbit and inverse stochastic resonance in the vicinity of folds of limit cycles, here arising from the unfolding of Bautin bifurcations. In these regimes, noise thus interacts in a complex way with the nonlinearities and yields dynamics not predicted in the deterministic system.

Stochastic Resonance near Heteroclinic Cycles.

Consistent with the ecological problem modeled, we have assumed that the different ecological functional types change at comparable timescales, and thus, the system does not explicitly display multiple timescale excitable dynamics. However, we show here that the presence of heteroclinic cycles endows the system with effective excitable dynamics. This is in particular the case in the vicinity of the stable heteroclinic cycle described above, with a forest tree birth rate sufficiently large to stabilize the forest equilibrium. In that case, small perturbations are compensated exponentially quickly, and the system returns to the forest equilibrium after short transients; however, larger perturbations may lead the system to values of grass covers that induce fire-driven mortality of forest trees greater than their birth rate, leading to an almost complete disappearance of forest trees in favor of grass. This is progressively replaced by savanna saplings and then adult savanna trees, which are themselves replaced by forest trees, leading the system back to equilibrium. In this situation, the dynamics thus feature a resting state (forest equilibrium), an excited state (full-grass unstable equilibrium), and recovery through the savanna–woodland regime, endowing the system with dynamics largely comparable with an excitable structure (SI Role of Noise: Stochastic and Inverse Stochastic Resonances and Fig. S6).

We thus stochastically perturbed the system at equilibrium in parameter regions near the heteroclinic cycle to investigate whether synchronizing effects similar to stochastic resonance occurred in this region of the parameter space. Fig. 5 depicts the result of these simulations as a function of the SD $\sigma$ of a white noise perturbation of the system modeling ecological noise. While small perturbations indeed induced little qualitative change in the dynamics and large values substantially modified the dynamics (Fig. 5C, Left and Right), intermediate values of noise induced striking structured, large-amplitude oscillations, similar to the vanished heteroclinic cycle, that occurred at regularly spaced time intervals (Fig. 5C, Center). We quantified this phenomenon by computing the statistics of the peak amplitude of the Fourier transform and indeed found a very clear stochastic resonance phenomenon associated with a peak in the maximal amplitude of the Fourier transform (Fig. 5A). We confirmed in SI Role of Noise: Stochastic and Inverse Stochastic Resonances that this structure is robust and persists away from the heteroclinic bifurcation.

Fig. 5.

Stochastic resonance near the heteroclinic cycle (parameters as in Fig. 3 with $\alpha =0.55$); the deterministic system reaches a forest equilibrium. (A) Maximal amplitude of the Fourier transform as a function of noise level in log scale shows a clear peak at the stochastic resonance ($\sigma \sim 0.01$). (B) Heteroclinic cycle (red curve) and dynamics for $\sigma =0.01$ (blue curve) in phase space $(G,S,T)$. (C) Trajectories of the variables $(G,S,T)$ in time for the three sample values of $\sigma$ highlighted with pink squares in A.

Inverse Stochastic Resonance.

In the bifurcation diagram provided in Fig. 2, we reveal a number of parameter regions where a stable periodic orbit coexists with a stable fixed point, particularly in the vicinity of the codimension-two Bautin bifurcations. Noise may have important qualitative effects in these regions, and in particular, inverse stochastic resonance may occur. We stochastically perturbed the periodic behaviors in these regions and observed a massive impact of ecological noise on the resulting dynamics in sharp contrast with the increased periodicity reported in the previous section. Instead of triggering oscillations, we show in Fig. 6 that there exists an optimal level of noise at which oscillations disappear and a forest landscape establishes. At this level of noise, the number of oscillations drops and the amplitude of the fluctuations declines as visible in the significant dip in the statistics of the number of small oscillations at a specific value of the ecological noise level (Fig. 6A).

Fig. 6.

Inverse stochastic resonance. (A) Number of oscillations in the time interval $[0,1000]$ for various values of the noise $\sigma$. Statistics were computed over 100 independent realizations. (B and C) Sample trajectories for three values of $\sigma :{10}^{-4},{10}^{-3},0.025$ in the phase space $(G,S,F)$ (B) or as a function of time (C). Same parameters as in Fig. 5 with $\alpha =0.34$ and $\beta =1.5$ in the vicinity of the fold of limit cycles.

Trajectories of the system (Fig. 6C) clearly evidence this effect. For small ecological noise, the system only slightly deviates from the deterministic oscillation, and a close-to-periodic behavior emerges. However, for a larger ecological noise level, oscillations almost completely disappear, and the system stabilizes around the forest state. This effect disappears for larger ecological perturbations, and the forest state is replaced by large-amplitude oscillations between grassland, woodland, and forest landscapes. This emergence of large oscillations is quite surprising in the context of inverse stochastic resonance and contrasts with classical models, where oscillations comparable with the deterministic cycle emerge for larger noise levels. Here, oscillations are sharper and of larger amplitude than the deterministic cycle, and they evoke the vanished heteroclinic orbit as visible in the 3D plots of the trajectories (Fig. 6B): while the deterministic cycle is smooth and of small amplitude (black trajectory in Fig. 6B) and the small noise trajectories are small perturbations of the cycle (green trajectory in Fig. 6C), trajectories for intermediate noise (orange trajectory in Fig. 6C) collapse quickly to the fixed point, and larger noise trajectories show large-amplitude spiky trajectories that approach the full-grass and the composite equilibria repetitively (blue trajectory in Fig. 6C). This finding is a demonstration that inverse stochastic resonance may also arise in ecological systems.

Discussion

We have thoroughly explored the dynamics of a simple model for the landscape dynamics of grass, savanna trees, and forest trees in interaction with fire. The model assumes that fire spread has a threshold response to tree cover (19, 64); it admits, however, that savanna trees can vary in the degree to which they exclude fires (33, 34) and that fire, in turn, impacts tree population dynamics by preventing savanna saplings from maturing into adult trees (15, 17) and by killing forest trees, regardless of their size (27).

Previous analyses have shown that bistability in vegetation structure (between grassland or savanna and woodland or forest) is a persistent feature of this type of model (10, 11, 65, 66). In this paper, analysis additionally reveals (i) that diverse cyclic behaviors (including limit and homo- and heteroclinic cycles) occur for broad ranges of parameter space, robust to introducing more ecological realism into the model; (ii) that large shifts in landscape structure can result from endogenous dynamics, not just from external drivers; and (iii) that introducing noise into this system induces (inverse) resonant phenomena, some of which have never been previously observed in ecological models.

The question of whether cyclic behaviors in ecological models are predictive of real ecological dynamics is an open question. Certainly, savannas are often described as theoretically rich systems, both here and elsewhere (67–69), but predictions of complex temporal dynamics have generally not penetrated the empirical literature beyond an emerging recognition that savannas represent a potential stable alternative to forests in some climate regimes (10, 70). Empirically evaluating whether the diverse cyclic behaviors observed herein actually occur in real savanna–forest systems presents a real challenge, primarily because of the timescales of structural change. For instance, well-studied savannas in South Africa are populated with trees that range in lifespan from $\sim$100 y old (46) up to as many as 500–1,000 y old (71); meanwhile, paleoecological studies indicate that vegetation change can be characterized by millennia of stasis (72). The century to millennium is probably the appropriate timescale on which to test these predictions; unfortunately, observational data are patchy and hard to interpret on these long scales. In other more data-rich systems, the question has received more direct attention. Classically, predictions of cycles from simplified Lotka–Volterra predator–prey cycles are borne out in observations of real predator–prey systems [e.g., among populations of lynx and hare (73)], with notable departures that are the subject of intense debate. Similarly, an extensive literature has searched for and sometimes found evidence of the chaotic population dynamics that models often predict (74, 75).

Complex temporal dynamics clearly do occur in nature. Yet, evidence for temporal cycles is more scant than models tend to predict. Some have suggested that, despite high species and functional diversity, natural dynamics are more “low dimensional” than models tend to predict (76). Whether this is true and why are fundamental questions in ecology. By extension, we do not know whether to expect our predictions of widespread cycles in vegetation dynamics herein to be borne out in real savanna–forest systems. Regardless, empirical consideration of vegetation dynamics in savannas and across savanna–forest boundaries should certainly more explicitly admit the possibility of complex temporal dynamics—a significant shift away from a current narrow focus on vegetation dynamics that are the deterministic product of exogenous changes in environment.

The most immediate and obvious prediction—with major implications for how we think about ecosystem transitions—is that large changes in vegetation structure may not necessarily reflect critical transitions between alternative stable states. Here, large fluctuations were endogenous and endogenously reversible. For instance, heteroclinic cycles appear as long periods of relatively slow change (that resembles stability) near one unstable equilibrium punctuated by a rapid change (that resembles a phase transition) to another unstable equilibrium during another part of the cycle. This suggests a note of caution; currently, a proliferating literature considers major shifts in structure to be reliable indicators of state transitions. This assumption predicates, for instance, the literature on early warning signals (77–80)—but if large shifts in structure are not always state transitions, the more fundamental question is how to differentiate, in data, phase transitions from other types of dynamics that produce large changes in system state. Direct comparison of data with mechanistic models for system dynamics may be necessary.

Despite important literature in stochastic systems for ecology, the qualitative effects of noise on nonlinear ecological dynamics remain quite poorly understood. Here, we have pushed this analysis one step further by revealing how noise can affect complex dynamics observed in this ecological system. Beyond attractor switching phenomena classically observed in systems with multiple equilibria, we have revealed in an ecological system two opposite roles of noise in the dynamics: a stochastic resonance phenomenon near a heteroclinic cycle and an inverse stochastic resonance in the vicinity of the folds of limit cycles. From the mathematical viewpoint, this ecological system provides an original situation where this phenomenon occurs. Indeed, while stochastic resonance was mostly evidenced in excitable systems with multiple timescales, we showed here that the heteroclinic cycles present in the system endowed the dynamics with a structure comparable in many ways with those excitable systems and in particular, induced the presence of a stochastic resonance phenomenon. This observation has several implications for theoretical ecology. In particular, this underlines the fact that ecological noise, even when its amplitude is small, can generate complex macroscopic dynamics in systems with trivial equilibrium dynamics in the absence of noise. This emphasizes the crucial importance of (i) incorporating stochastic effects in dynamical models as well as (ii) considering evanescent complex deterministic dynamical structures, since noise may increase their extent and impact. Our findings also underline the fact that noise may also have a strong stabilizing effect on ecological equilibria through inverse stochastic resonance, a surprising effect not considered before in ecological systems, which may have important implications for observing oscillatory behaviors in realistic ecological situations. Both phenomena occur within the same specific noise regimes. These two observations argue for the importance of taking into account in models and in field observations the associated levels of ecological variations to discover the determinants of the establishments of a specific landscape.

Hence, this paper contributes both to the ecological literature on forest–savanna dynamics and to the general theoretical literature exploring the emergence of complex behaviors from simple dynamics. On the ecological side, it raises challenges regarding how data can be used to sort out the real world relevance of mathematical phenomena, the relevant timescales involved, and the consequences of embedding such phenomena within a spatial mosaic, in which parameters change along gradients or patchily. From a mathematical viewpoint, the model presents a fascinating demonstration of how simple models can lead to highly complex and nonequilibrium behaviors; because of the simplicity of the model, it seems certain that similar behaviors should be observed in a variety of other systems. Thus, regardless of whether the described phenomena can be observed in ecological systems, they are likely to be important in other applications.

Materials and Methods

Numerical Simulations and Bifurcation Diagrams in the Absence of Noise.

Simulations of the ordinary differential equations were done using Matlab R2015b. Deterministic trajectories and codimension-one bifurcation diagrams were obtained using the XPP software (81), and codimension-two bifurcation diagrams were obtained with the Matcont package (82). Codimension-two continuation of homoclinic and transcritical bifurcations was drawn connecting multiple points obtained through extensive computations of codimension-one bifurcation diagrams. Construction points are indicated along the lines. The codimension-two curves of transcritical bifurcations were computed likewise. Unless specified otherwise, we used for our parameters a choice consistent with previous literature (11, 12), which is summarized in Table 1.

Stochastic Simulations and Resonances.

Stochastic systems were implemented using the Euler–Maruyama scheme with a small time step ($dt={10}^{-4}$) on Matlab. The stochastic resonance phenomenon was illustrated computing the Fourier transform of the solution (Matlab command fft). For the inverse stochastic resonance, we computed the total number of oscillations performed by the system through the number of peaks of the grass variable $G$ above a threshold (${\theta }_G=0.33$, Matlab command findpeaks, signal processing toolbox). This choice avoids emphasizing small oscillations of the system. Similar results are obtained with the maximal modulus of the Fourier transform.