Landau–Ginzburg theory of cortex dynamics: Scale-free avalanches emerge at the edge of synchronization

Significance

The human cortex operates in a state of restless activity, the meaning and functionality of which are still not understood. A fascinating, though controversial, hypothesis, partially backed by empirical evidence, suggests that the cortex might work at the edge of a phase transition, from which important functional advantages stem. However, the nature of such a transition remains elusive. Here, we adopt ideas from the physics of phase transitions to construct a general (Landau–Ginzburg) theory of cortical networks, allowing us to analyze their possible collective phases and phase transitions. We conclude that the empirically reported scale-invariant avalanches can possibly come about if the cortex operated at the edge of a synchronization phase transition, at which neuronal avalanches and incipient oscillations coexist.

Abstract

Understanding the origin, nature, and functional significance of complex patterns of neural activity, as recorded by diverse electrophysiological and neuroimaging techniques, is a central challenge in neuroscience. Such patterns include collective oscillations emerging out of neural synchronization as well as highly heterogeneous outbursts of activity interspersed by periods of quiescence, called “neuronal avalanches.” Much debate has been generated about the possible scale invariance or criticality of such avalanches and its relevance for brain function. Aimed at shedding light onto this, here we analyze the large-scale collective properties of the cortex by using a mesoscopic approach following the principle of parsimony of Landau–Ginzburg. Our model is similar to that of Wilson–Cowan for neural dynamics but crucially, includes stochasticity and space; synaptic plasticity and inhibition are considered as possible regulatory mechanisms. Detailed analyses uncover a phase diagram including down-state, synchronous, asynchronous, and up-state phases and reveal that empirical findings for neuronal avalanches are consistently reproduced by tuning our model to the edge of synchronization. This reveals that the putative criticality of cortical dynamics does not correspond to a quiescent-to-active phase transition as usually assumed in theoretical approaches but to a synchronization phase transition, at which incipient oscillations and scale-free avalanches coexist. Furthermore, our model also accounts for up and down states as they occur (e.g., during deep sleep). This approach constitutes a framework to rationalize the possible collective phases and phase transitions of cortical networks in simple terms, thus helping to shed light on basic aspects of brain functioning from a very broad perspective.

The cerebral cortex exhibits spontaneous activity even in the absence of any task or external stimuli (1–3). A salient aspect of this, so-called resting-state dynamics as revealed by in vivo and in vitro measurements, is that it exhibits outbursts of electrochemical activity characterized by brief episodes of coherence—during which many neurons fire within a narrow time window—interspaced by periods of relative quiescence, giving rise to collective oscillatory rhythms (4, 5). Shedding light on the origin, nature, and functional meaning of such an intricate dynamics is a fundamental challenge in neuroscience (6).

On experimentally enhancing the spatiotemporal resolution of activity recordings, Beggs and Plenz (7) made the remarkable finding that, actually, synchronized outbursts of neural activity could be decomposed into complex spatiotemporal patterns, thereon named “neuronal avalanches.” The sizes and durations of such avalanches were reported to be distributed as power laws [i.e., to be organized in a scale-free way, limited only by network size (7)]. Furthermore, they obey finite-size scaling (8), a trademark of scale invariance (9), and the corresponding exponents are compatible with those of an unbiased branching process (10).

Scale-free avalanches of neuronal activity have been consistently reported to occur across neural tissues, preparation types, experimental techniques, scales, and species (11–18). This has been taken as empirical evidence backing the criticality hypothesis (i.e., the conjecture that the awake brain might extract essential functional advantages—including maximal sensitivity to stimuli, large dynamical repertoires, optimal computational capabilities, etc.—from operating close to a critical point, separating two different phases) (19–22).

To make further progress, it is of crucial importance to clarify the nature of the phase transition marked by such an alleged critical point. It is usually assumed that it corresponds to the threshold at which neural activity propagates marginally in the network [i.e., to the critical point of a quiescent-to-active phase transition (7)], justifying the emergence of branching process exponents (23, 24). However, several experimental investigations found evidence that scale-free avalanches emerge in concomitance with collective oscillations, suggesting the presence of a synchronization phase transition (25, 26).

From the theoretical side, on the one hand, very interesting models accounting for the self-organization of neural networks to the neighborhood of the critical point of a quiescent-to-active phase transition have been proposed (27–30). These approaches rely on diverse regulatory mechanisms (31), such as synaptic plasticity (32), spike time-dependent plasticity (33), excitability adaptation, etc., to achieve network self-organization to the vicinity of a critical point. These models have in common that they rely on an extremely large separation of dynamical timescales [as in models of self-organized criticality* (36, 37)], which might not be a realistic assumption (27, 30, 38, 39). Some other models are more realistic from a neurophysiological viewpoint (17, 29), but they give rise to scale-free avalanches if and only if causal information—which is available in computational models but not accessible in experiments (40)—is considered. Thus, in our opinion, a sound theoretical model justifying the empirical observation of putative criticality is still missing.

On the other hand, from the synchronization viewpoint, well-known simple models of networks of excitatory and inhibitory spiking neurons exhibit differentiated synchronous (oscillatory) and asynchronous phases, with a synchronization phase transition in between (41–44). However, avalanches do not usually appear (or are not searched for) in such modeling approaches (18, 45, 46).

Concurrently, during deep sleep and also, under anesthesia, the cortical state has long been known to exhibit so-called “up and down” transitions between states of high and low neural activity, respectively (47, 48), which clearly deviate from the possible criticality of the awake brain and have been modeled on their own (29, 49, 50). Thus, it would be highly desirable to design theoretical models describing within a common framework the possibility of criticality, oscillations, and up–down transitions.

Our aim here is to clarify the nature of the phases and phase transitions of dynamical network models of the cortex by constructing a general unifying theory based on minimal assumptions and allowing us, in particular, to elucidate what the nature of the alleged criticality is.

To construct such a theory, we follow the strategy pioneered by Landau and Ginzburg. Landau proposed a simple approach to the analysis of phases of matter and the phase transitions that they experience. It consists of a parsimonious, coarse-grained, and deterministic description of states of matter in which—relying on the idea of universality—only relevant ingredients (such as symmetries and conservation laws) need to be taken into account and in which most microscopic details are safely neglected (9, 51). Ginzburg went a step further by realizing that fluctuations are an essential ingredient to be included in any sound theory of phase transitions, especially in low-dimensional systems. The resulting Landau–Ginzburg theory, including fluctuations and spatial dependence, is regarded as a metamodel of phase transitions and constitutes a firm ground on top of which the standard theory of phases of matter rests (9). Similar coarse-grained theories are nowadays used in interdisciplinary contexts—such as collective motion (52), population dynamics (53), and neuroscience (54–56)—where diverse collective phases stem out of the interactions among many elementary constituents.

In what follows, we propose and analyze a Landau–Ginzburg theory for cortical neural networks—which can be seen as a variant of the well-known Wilson–Cowan model, including crucially, stochasticity and spatial dependence—allowing us to shed light from a very general perspective on the collective phases and phase transitions that dynamical cortical networks can harbor. Using analytical and mostly, computational techniques, we show that our theory explains the emergence of scale-free avalanches as episodes of marginal and transient synchronization in the presence of a background of ongoing irregular activity, reconciling the oscillatory behavior of cortical networks with the presence of scale-free avalanches. Last but not least, our approach also allows for a unification of existing models describing diverse specific aspects of the cortical dynamics, such as up and down states and up and down transitions, within a common mathematical framework and is amenable to future theoretical (e.g., renormalization group) analyses.

Model and Results

We construct a mesoscopic description of neuronal activity, where the building blocks are not single neurons but local neural populations. These latter can be interpreted as small sections of neural tissue (57, 58) consisting of a few thousand cells (far away from the large number limit) and susceptible to be described by a few variables. Although this effective description is constructed here on phenomenological bases, more formal mathematical derivations of similar equations from microscopic models exist in the literature (59). In what follows, (i) we model the neural activity at a single mesoscopic “unit,” (ii) we analyze its deterministic behavior as a function of parameter values, and later, (iii) we study the collective dynamics of many coupled units.

Single-Unit Model.

At each single unit, we consider a dynamical model in which the excitatory activity, $\rho$, obeys a Wilson–Cowan equation (60) (that is, following the Landau approach, we truncate to third order in a Taylor series expansion^†):

$$\dot{\rho }(t)=[-a+R(t)]\rho (t)+b{\rho }^2(t)-{\rho }^3(t)+h,$$ [1]

where $a>0$ controls the spontaneous decay of activity, which is partially compensated for by the generation of additional activity at a rate proportional to the amount of available synaptic resources, $R(t)$. The quadratic term with $b>0$ controls nonlinear integration effects.^‡ Finally, the cubic term imposes a saturation level for the activity, preventing unbounded growth, and $h$ is an external driving field.

A second equation is used to describe the dynamics of the available synaptic resources, $R(t)$, through the combined effect of synaptic depression and synaptic recovery as encoded in the celebrated model of Tsodyks and Markram (61) for synaptic plasticity (32):

$$\dot{R}(t)=\frac{1}{{\tau }_R}(\xi -R(t))-\frac{1}{{\tau }_D}R(t)\rho (t),$$ [2]

where ${\tau }_R$ (${\tau }_D$) is the characteristic recovery (depletion) time and $\xi$ is the baseline level of nondepleted synaptic resources. Importantly, we have also considered variants of this model, avoiding the truncation of the power series expansion or including an inhibitory population as the chief regulatory mechanism: either of these extensions leads to essentially the same phenomenology and phases as described in what follows, supporting the robustness of the forthcoming results (SI Appendix).

Mean Field Analysis.

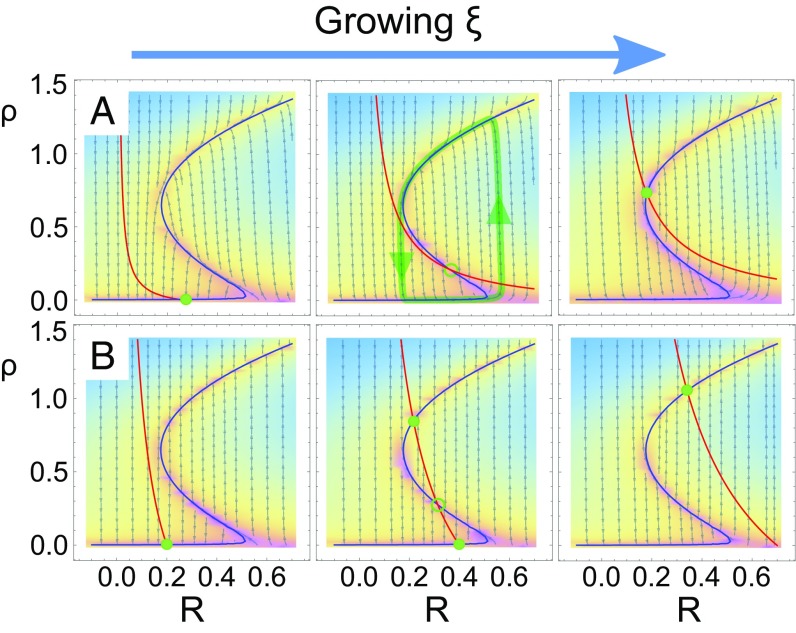
Here, we analyze, both analytically and computationally, the dynamics of a single unit as given by Eqs. 1 and 2. We determine the fixed points $({\rho }^{\ast },R^{\ast })$ (i.e., the possible steady states at which the system can settle) as a function of the baseline level of synaptic resources, $\xi$, which plays the role of a control parameter (all other parameters are kept fixed to standard nonspecific values as summarized in Fig. 1). For small values of $\xi$, the system falls into a quiescent or down state with ${\rho }^{\ast }\approx 0$ and $R^{\ast }\approx \xi$.^§ Instead, for large values of $\xi$, there is an active or up state with self-sustained spontaneous activity ${\rho }^{\ast }>0$ and depleted resources $R^{\ast }<\xi$. In between these two limiting phases, two alternative scenarios (as illustrated in Fig. 1 and summarized in the phase diagram in SI Appendix) can appear depending on the timescales ${\tau }_D$ and ${\tau }_R$.

• i)Case A. A stable limit cycle (corresponding to an unstable fixed point with complex eigenvalues) emerges for intermediate values of $\xi$ (in between two Hopf bifurcations) as illustrated in Fig. 1A. This Hopf bifurcation scenario has been extensively discussed in the literature (62), and it is at the basis of the emergence of oscillations in neural circuits.
• ii)Case B. An intermediate regime of bistability including three fixed points is found for intermediate values of $\xi$ (in between two saddle node bifurcations): the up and the down ones as well as an unstable fixed point in between (as illustrated in Fig. 1B). This saddle node scenario is the relevant one in models describing transitions between up (active) and down (quiescent) states (29, 49, 63).

Fig. 1.

Phase portraits and nullclines for the (deterministic) dynamics (Eqs. 1 and 2). Nullclines are colored in blue ($\dot{\rho }=0$) and red ($\dot{R}=0$), respectively; fixed points $({\rho }^{\ast },R^{\ast })$—at which nullclines intersect—are highlighted by green (open) circles for stable (unstable) fixed points. Background color code (shifting from blue to purple) represents the intensity of the vector field $(\dot{\rho },\dot{R})$, with local directions that are represented by small gray arrows. A trajectory illustrating a limit cycle is showed in green in A. The system exhibits either (A) an oscillatory regime or (B) a region of bistability in between a down (Left) state and an up (Right) state. It is possible to shift from case A to case B and vice versa by changing just one parameter [e.g., the timescale of resources depletion, ${\tau }_D^{-1}$ ($0.016$ and $0.001$ for cases A and B, respectively)]. Other parameter values: $h={10}^{-3},a=0.6,b=1.3,{\tau }_R={10}^3$. The control parameters in Left, Center, and Right are $\xi =0.3,1.6,2.3$, respectively, in A and $\xi =0.2,0.4,0.7$, respectively, in B.

Two remarks are in order. The first is that one can shift from one scenario to the other just by changing one parameter (e.g., the synaptic depletion timescale ${\tau }_D$).^¶ The second and very important one is that none of these two scenarios exhibit a continuous transition (transcritical bifurcation) separating the up/active from the down/quiescent regimes. Thus, at this single-unit/deterministic level, there is no precursor of a critical point for marginal propagation of activity.

Stochastic Network Model.

We now introduce stochastic and spatial effects in the simplest possible way. For this, we consider a network of $N$ nodes coupled following a given connection pattern as described below. Each network node represents a mesoscopic region of neural tissue or unit as described above. On top of this deterministic dynamics, we consider that each unit (describing a finite population) is affected by intrinsic fluctuations (55, 59, 64). More specifically, Eq. 1 is complemented with an additional term $+A(\rho )\eta (t)$, which includes a (zero mean, unit variance) Gaussian noise $\eta (t)$ and a density-dependent amplitude $A(\rho )$ ^# [i.e., a multiplicative noise (65)].

At macroscopic scales, the cortex can be treated as a 2D sheet consisting mostly of short-range connections (66).^‖ Although long-range connections are also known to exist and small world effects have been identified in local cortical regions (68), here we consider a 2D square lattice (size $N=L^2$) of mesoscopic units as the simplest way to embed our model into space. Afterward, we shall explore how our main results are affected by the introduction of more realistic network architectures, including additional layers of complexity, such as long-range connections and spatial heterogeneity.

Following the parsimonious Landau–Ginzburg approach adopted here, the coupling between neighboring units is described up to leading order by a diffusion term. This type of diffusive coupling between neighboring mesoscopic units stems from electrical synapses (57, 69), has some experimental backing (70), and has been analytically derived starting from models of spiking neurons (54).** Thus, finally, the resulting set of coupled stochastic equations is

$$\{\begin{array}{cc}\dot{{\rho }_i}(t)=(-a+R_i){\rho }_i+b{\rho }_i^2-{\rho }_i^3+h+D{\nabla }^2{\rho }_i+\sigma \sqrt{{\rho }_i}{\eta }_i\hfill & \\ \dot{R_i}(t)=\frac{1}{{\tau }_R}(\xi -R_i)-\frac{1}{{\tau }_D}{R}_i{\rho }_i\hfill & \end{array},$$ [3]

where for simplicity, some time dependences have been omitted; ${\rho }_i(t)$ and $R_i(t)$ are the activity and resources at a given node $i$ (with $i=\mathrm{1,2},\mathrm{\dots }N$) and time $t$, respectively. $D{\nabla }^2{\rho }_i\equiv D{\sum }_{j\in n.n.i}({\rho }_j-{\rho }_i)$ describes the diffusive coupling of unit $i$ with its nearest neighbors $j$ with (diffusion) constant $D$. The physical scales of the system are controlled by the values of the parameters $D$ and $\sigma$; however, given that, as illustrated in SI Appendix, results do not change qualitatively on varying parameter values (as long as they are finite and nonvanishing), here we take $D=\sigma =1$ for the sake of simplicity.

Eq. 3 constitutes the basis of our theory. In principle, this set of equations is amenable to theoretical analyses, possibly including renormalization ones (9). However, here we restrict ourselves to computational studies aimed at scrutinizing what is the basic phenomenology, leaving more formal analyses for the future. In particular, we resort to numerical integration of the stochastic equations (Eq. 3), which is feasible thanks to the efficient scheme developed in ref. 71 to deal with multiplicative noise. We consider $\delta t=0.01$ as an integration time step and keep, as above, all parameters fixed, except for the baseline level of synaptic resources, $\xi$, which works as a control parameter.

Phases and Phase Transitions: Case A.

We start analyzing sets of parameters within case A above. We study the possible phases that emerge as $\xi$ is varied. These are illustrated in Fig. 2, where characteristic snapshots and overall activity time series as well as raster plots are plotted. For a more vivid visualization, we have also generated videos of the activity dynamics in the different phases (Movie S1).

Fig. 2.

Illustration of the diverse phases emerging in the model (case A). The baseline of synaptic resources, $\xi$, increases from top to bottom: $\xi =0.4$ (down state), $\xi =1.2$ (synchronous regime), $\xi =2.47$ (critical point for the considered size $N={128}^2$), $\xi =2.7$ (asynchronous phase), and $\xi =5$ (active phase). The first column shows snapshots of typical configurations; the color code represents the level of activity at each unit as shown in the scale. The network spiking or synchronous irregular phase is characterized by waves of activity growing and transiently invading the whole system before extinguishing the resources and coming to an end. However, in the nested oscillation or asynchronous irregular (AI) regime, multiple traveling waves coexist, interfering with each other. In the up state, waves are no longer observed, and a homogeneous state of self-sustained activity is observed (Movie S1). The second column shows the time series of the overall activity averaged over the whole network. In the down state, activity is almost vanishing. In the synchronous phase, macroscopic activity appears in the form of almost synchronous bursts interspersed by almost silent intervals. At the critical point, network spikes begin to superimpose, giving rise to complex oscillatory patterns (nested oscillations) and marginally self-sustained global activity all across the asynchronous regime; finally, in the up state, the global activity converges to steady state with small fluctuations. The third column shows steady-state probability distribution $P(\rho )$ for the global activity: in the down state and the network spiking regime, the distributions are shown in a double-logarithmic scale; observe the approximate power law for very small values of $\rho$ stemming from the presence of multiplicative noise (10). The fourth column shows an illustration of the different levels of synchronization across phases: a sample of $200$ randomly chosen units is mapped into oscillators using their analytic signal representation (Materials and Methods); the plot shows the time evolution of their corresponding phases ${\varphi }_k^{\mathcal{A}}$. Observe the almost periodic behavior in the synchronous phase, which starts blurring at the critical point and progressively vanishes as the control parameter is further increased. Parameter values: $a=1,b=1.5,{\tau }_R={10}^3,{\tau }_D={10}^2,h={10}^{-7}$.

Down-state phase (A1).

If the baseline level $\xi$ is sufficiently small ($\xi \lesssim 0.75$), resources $R$ are always scarce, and the system is unable to produce self-sustained activity (i.e., it is hardly excitable), giving rise to a down-state phase characterized by very small values of the network time-averaged activity $\overline{\rho }\equiv \frac{1}{T}{\int }_0^{T}dt\frac{1}{N}{\sum }_{i=1}^N{\rho }_i(t)$ for large times $T$ (Fig. 2, first row). The quiescent state is disrupted only locally by the effect of the driving field $h$, which creates local activity, barely propagating to neighboring units.

Synchronous irregular phase (A2).

Above a certain value of resource baseline ($\xi \gtrsim 0.75$), there exists a wide region in parameter space in which activity generated at a seed point is able to propagate to neighboring units, triggering a wave of activity that transiently propagates through the network until resources are exhausted, activity ceases, and the recovery process restarts (Fig. 2, second row). Such waves or “network spikes” appear in an oscillatory, although not perfectly periodic, fashion, with an average separation time that decreases with $\xi$. In the terminology of Brunel (43), this corresponds to a synchronous irregular state/phase, since the collective activity is time-dependent (oscillatory) and single-unit spiking is irregular (as discussed below). This wax and wane dynamics resembles that of anomalous (e.g., epileptic) tissues (72).

Asynchronous irregular phase (A3).

For even larger values of resource baseline ($\xi \gtrsim 2.15$), the level of synaptic recovery is sufficiently high as to allow for resource-depleted regions to recover before the previous wave has come to an end. Thereby, diverse traveling waves can coexist and interfere, giving rise to complex collective oscillatory patterns [Fig. 2, fourth row, which is strikingly similar to, for example, EEG data of $\alpha$-rhythms (73)]. The amplitude of these oscillations, however, decreases on increasing network size (which occurs as many different local waves are averaged and deviations from the mean tend to be washed away). This regime can be assimilated to an asynchronous irregular (AI) phase of the work by Brunel (43) (see below).

Up-state phase (A4).

For even larger values of $\xi$, plenty of synaptic resources are available at all times, giving rise to a state of perpetual activity with small fluctuations around the mean value (Fig. 2, fifth row) (i.e., an up state). Let us finally remark that, as explicitly shown in SI Appendix, the AI phase and the up state cannot be distinguished in the infinite network size limit, in which there are so many waves to be averaged that a homogeneous steady state emerges on average in both cases.

Phase Transitions.

Having analyzed the possible phases, we now discuss the phase transitions separating them. For all of the considered network sizes, the time-averaged overall activity, $\overline{\rho }$, starts taking a distinctively nonzero value above $\xi \approx 0.75$ (Fig. 3), reflecting the upper bound of the down or quiescent state (transition between A1 and A2). This phase transition is rather trivial and corresponds to the onset on network spikes [i.e., oscillations; with characteristic time that depends on various factors, such as the synaptic recovery time (74) and the baseline level of synaptic resources].

Fig. 3.

Overall network activity state (case A) as determined by the network time-averaged value $\overline{\rho }$ ($h={10}^{-7}$). (A) Order parameter $\overline{\rho }$ as a function of the control parameter $\xi$ for various system sizes $N={64}^2,{128}^2,{256}^2,{512}^2$ [from bottom (blue) to top (orange)]; observe that $\overline{\rho }$ grows monotonically with $\xi$ and that an intermediate regime, in which $\overline{\rho }$ grows with system size, emerges between the up and down states. (B) SD of the averaged overall activity in the system multiplied by $\sqrt{N}$; $\chi ={\sigma }_{\rho }\sqrt{N}$ (in the text). The point of maximal variability coincides with the point of maximal slope in A for all network sizes $N$. (C) Finite-size scaling analysis of the peaks in B. The distance of the size-dependent peak locations ${\xi }_c(N)$ from their asymptotic value for $N\to \mathrm{\infty }$, ${\xi }_c^{\mathrm{\infty }}$, scales as a power law of the system size, taking ${\xi }_c^{\mathrm{\infty }}\approx 2.15$ and revealing the existence of true scaling at criticality.

More interestingly, Fig. 3 also reveals that $\overline{\rho }$ exhibits an abrupt increase at (size-dependent) values of $\xi$ between two and three, signaling the transition from A2 to A3. However, the jump amplitude decreases as $N$ increases, suggesting a smoother transition in the large-$N$ limit. Thus, it is not clear a priori, using $\overline{\rho }$ as an order parameter, whether there is a true sharp phase transition or whether there is just a cross-over between the synchronous (A2) and asynchronous (A3) regimes. To elucidate the existence of a true critical point, we measured the standard deviation of the network-averaged global activity $\overline{\rho }$, ${\sigma }_{\rho }$. Direct application of the central limit theorem (65) would imply that such a quantity should decrease as $1/\sqrt{N}$ for large $N$, and thus, $\chi \equiv \sqrt{N}{\sigma }_{\rho }$ should converge to a constant. However, Fig. 3B shows that $\chi$ exhibits a very pronounced peak located at the ($N$-dependent) transition point between the A2 and A3 phases; furthermore, its height grows with $N$ (i.e., it diverges in the thermodynamic limit), revealing strong correlations and anomalous scaling as occurs at critical points. Also, a finite-size scaling analysis of the value of $\xi$ at the peak [for each $N$; i.e., ${\xi }_c(N)$] reveals the existence of finite-size scaling as it corresponds to a bona fide continuous phase transition at ${\xi }_c^{\mathrm{\infty }}\simeq 2.15(5)$ in the infinite-size limit (Fig. 3C). Moreover, a detrended fluctuation analysis (75, 76) of the time series reveals the emergence of long-range temporal correlations right at ${\xi }_c$ (SI Appendix) as expected at a continuous phase transition.

To shed further light on the nature of such a transition, it is convenient to use a more adequate (synchronization) order parameter. In particular, we consider the Kuramoto index $K$—customarily used to detect synchronization transitions (77)—defined as $K\equiv \frac{1}{N}⟨\left|{\sum }_{k=1}^N{e}^{i{\varphi }_k(t)}\right|⟩$, where $i$ is the imaginary unit, $|\cdot |$ is the modulus of a complex number, $⟨\cdot ⟩$ here indicates averages over time and independent realizations, and $k$ runs over units, each of which is characterized by a phase, ${\varphi }_k(t)\in [0,2\pi ]$, that can be defined in different ways. For instance, an effective phase ${\varphi }_k^{\mathcal{A}}(t)$ can be assigned to the time series at unit $k$, ${\rho }_k(t)$, by computing its analytic signal representation, which maps any given real-valued time series into an oscillator with time-dependent phase and amplitude (Materials and Methods). Using the resulting phases, ${\varphi }_k^{\mathcal{A}}(t)$, the Kuramoto index $K_{\mathcal{A}}$ can be calculated. As illustrated in Fig. 4A, it reveals the presence of a synchronization transition: the value of $K_{\mathcal{A}}$ clearly drops at the previously determined critical point ${\xi }_c(N)$. An alternative method to define a time-dependent phase for each unit (details are discussed in Materials and Methods) reveals even more vividly the existence of a synchronization transition at ${\xi }_c(N)$ as shown in Fig. 4B. Finally, we have also estimated the coefficient of variation (CV) of the distance between the times at which each of these effective phases crosses the value $2\pi$; this analysis reveals the presence of a sharp peak of variability, converging for large network sizes to the critical point ${\xi }_c^{\mathrm{\infty }}\approx 2.15$ (Fig. 4B, Inset).

Fig. 4.

Synchronization transition elucidated by measuring the Kuramoto parameter as estimated using (A) the analytic signal representation ${\mathcal{A}}_k(t)$ of activity time series ${\rho }_k(t)$ at different units $k$ and for various system sizes [$N={128}^2$ (red), ${256}^2$ (orange), and ${512}^2$ (green)]. For illustrative purposes, A, Right Inset shows the analytical representation (including both a real part and an imaginary part) of five sample units as a function of time; A, Left Inset shows the time evolution of one node (gray) together with the amplitude of its analytic representation (blue). Both vividly illustrate the oscillatory nature of the unit dynamics. (B) Results similar to those in A but using a different method to compute time-dependent phases of effective oscillators (Materials and Methods). This alternative method captures more clearly the emergence of a transition; the point of maximum slope of the curves corresponds to the value of the transition points ${\xi }_c(N)$ in A. B, Inset shows the CV (ratio of the SD to the mean) of the times between two consecutive crossings of the value $2\pi$; it exhibits a peak of variability at the critical point ${\xi }_c(N)$.

Thus, recapitulating, the phase transition separating the down state from the synchronous irregular regime (A1–A2 transition) is trivial and corresponds to the onset of network spikes, with no sign of critical features. In between the asynchronous and up states (A3–A4), there is no true phase transition, as both phases are indistinguishable in the infinitely large size limit (SI Appendix). However, different measurements clearly reveal the existence of a bona fide synchronization phase transition (A2–A3), at which nontrivial features characteristic of criticality emerge.

Avalanches.

For ease of comparison with empirical results, we define a protocol to analyze avalanches that closely resembles the experimental one as introduced by Beggs and Plenz (7). Each activity time series of an individual unit can be mapped into a series of discrete time “spikes” or events as follows. As illustrated in Fig. 5A, a spike corresponds to a period in which the activity at a given unit is above a given small threshold in between two windows of quiescence (activity below threshold).^†† Hence, as illustrated in Fig. 5B, the network activity can be represented as a raster plot of spiking units. Following the standard experimental protocol, a discrete time binning $\mathrm{\Delta }t$ is chosen, and each individual spike is assigned to one such bin. An avalanche is defined as a consecutive sequence of temporally contiguous occupied bins preceded and ended by empty bins (Fig. 5 B and C). Quite remarkably, using this protocol, several well-known experimental key features of neuronal avalanches can be faithfully reproduced by tuning $\xi$ to a value close to the synchronization transition.

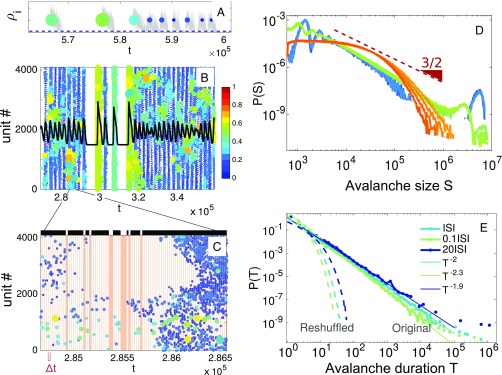
• i)The sizes and durations of avalanches of activity are found to be broadly (power law) distributed at the critical point; these scale-invariant avalanches coexist with anomalously large events or “waves” of synchronization as revealed by the heaps in the tails of the curves in Fig. 5 D and E.
• ii)Changing $\mathrm{\Delta }t$, power law distributions with varying exponents are obtained at criticality (the larger the time bin, the smaller the exponent) as originally observed experimentally by Beggs and Plenz (7) (Fig. 5E).
• iii)In particular, when $\mathrm{\Delta }t$ is chosen to be equal to the interspike interval (ISI; i.e., the time interval between any two consecutive spikes), avalanche sizes and durations obey—at criticality—finite-size scaling with exponent values compatible with the standard ones (i.e., those of an unbiased branching process) (Fig. 5 B and C and SI Appendix).
• iv)Reshuffling the times of occurrence of unit’s spikes, the statistics of avalanches is dramatically changed, giving rise to exponential distributions (as expected for an uncorrelated Poisson point process) and thus revealing the existence of a nontrivial temporal organization in the dynamics (Fig. 5E).
• v)Away from the critical point, both in the subcritical regime and in the supercritical regime, deviations from this behavior are observed. In the subcritical or synchronous regime, the peak of periodic large avalanches becomes much more pronounced; in the asynchronous phase, such a peak is lost, and distribution functions become exponential ones with a characteristic scale (Fig. 5D).

Fig. 5.

Avalanches measured from activity time series. (A) Illustration of the activity time series ${\rho }_i(t)$ (gray color) at a given unit $i$. By establishing a threshold value $\theta$ (dashed blue line close to the origin), a single “event” or “unit spike” is defined at the time of the maximal activity in between two threshold crossings (note that the forthcoming results are robust to changes in this criterion) (SI Appendix); a weight equal to the area covered in between the two crossings is assigned to each event (note the color code). This allows us to map a continuous time series into a discrete series of weighted events. The time distance between two consecutive events is called ISI. (B) Raster plot for a system with ${64}^2$ units obtained using the procedure above for each unit. Observe that large events coexist with smaller ones and that these last ones occur in a rather synchronous fashion. The overall time-dependent activity is marked with a black curve. (C) Zoomed-in view of a part of B illustrating the time-resolved structure and using a time binning $\mathrm{\Delta }t$ equal to the network-averaged ISI. Shaded columns correspond to empty time bins (i.e., with no spike). Avalanches are defined as sequences of events occurring in between two consecutive empty time bins, and they are represented by the black bars above the plot. (D) Avalanche size distribution (the size of the avalanche is the sum of the weighted spikes that it comprises) for diverse values of $\xi$ (from $1.85$ to $2.05$ in shades of blue, from $2.7$ to $2.9$ in shades of green, and from $3.3$ to $3.45$ in shades of orange) measured from the raster plot $\mathrm{\Delta }t=\text{ISI}$. The (red) triangle, with slope $3/2$, is plotted as a reference, illustrating that, near criticality, a power law with an exponent similar to the experimentally measured one is recovered. Away from the critical point, either in the synchronous phase (shades of blue) or in the asynchronous one (shades of orange), clear deviations from power law behavior are observed. Observe the presence of “heaps” in the tails of the distributions, especially in the synchronous regime; these correspond to periodic waves of synchronized activity (SI Appendix). They also appear at criticality but at progressively larger values for larger system sizes. (E) Avalanche duration distribution determined with different choices of the time bin. The experimentally measured exponent $\approx 2$ is reproduced using $\mathrm{\Delta }t=\text{ISI}$, whereas deviations from such a value are measured for smaller (larger) time bins in agreement with experimentally reported results. After reshuffling times, the distributions become exponential ones, with characteristic timescales depending on $\mathrm{\Delta }t$ (dashed lines).

Summing up, our model tuned to the edge of a synchronization/desynchronization phase transition reproduces all chief empirical findings for neural avalanches. These findings strongly suggest that the critical point alluded to by the criticality hypothesis of cortical dynamics does not correspond to a quiescent/active phase transition—as modeling approaches usually assume—but to a synchronization phase transition, at the edge of which oscillations and avalanches coexist.

It is important to underline that our results regarding the emergence of scale-free avalanches are purely computational. To date, we do not have a theoretical understanding of why results are compatible with branching process exponents. In particular, it is not clear to us if a branching process could possibly emerge as an effective description of the actual (synchronization) dynamics in the vicinity of the phase transition or whether the exponent values appear as a generic consequence of the way that temporally defined avalanches are measured (46). These issues deserve to be carefully scrutinized in future work.

The Role of Heterogeneity.

Thus far, we have described homogeneous networks with local coupling. However, long-range connections among local regions also exist in the cortex, and mesoscopic units are not necessarily homogeneous across space (68, 78). These empirical facts motivated us to perform additional analysis of our theory, in which slightly modified substrates are used. We considered small world networks and verified that our main results (i.e., the existing phases and phase transitions) are insensitive to the introduction of a small percentage of long-range connections (SI Appendix). However, details, such as the boundaries of the phase diagram, the shape of propagation waves, and the amplitude of nested oscillations, do change.

More remarkably, as described in detail in SI Appendix, a simple extension of our theory, in which parameters are not taken to be homogeneous but position-dependent (i.e., heterogeneous in space), is able to reproduce remarkably well empirical in vitro results for neural cultures with different levels of mesoscopic structural heterogeneity (79).

To further explore the influence of network architecture onto dynamical phases, in future work, we will extend our model using empirically obtained large-scale networks of the human brain, as their heterogeneous and hierarchical–modular architecture is known to influence dynamical processes operating on them (68, 80).

Phases and Phase Transitions: Case B.

Here, we discuss the much simpler scenario for which the deterministic/mean field dynamics predicts bistability (i.e., case B above), which is obtained, for example, considering slower dynamics for synaptic resource depletion. In this case, the introduction of noise and space does not significantly alter the deterministic picture. Indeed, computational analyses reveal that there are only two phases: a down state and an up one for small and large values of $\xi$, respectively. These two phases have the very same features as their corresponding counterparts in case A. However, the phase transition between them is discontinuous (much as in Fig. 1B), and thus, for finite networks, fluctuations induce spontaneous transitions between the up and down states when $\xi$ takes intermediate values in the regime of phase coexistence. Thus, in case B, our theory constitutes a sound Landau–Ginzburg description of existing models, such as those in refs. 29, 49, and 50, describing up and down states and up and down transitions.

Conclusions and Discussion

The brain of mammalians is in a state of perennial activity, even in the absence of any apparent stimuli or task. Understanding the origin, meaning, and functional significance of such an energetically costly dynamical state is the fundamental problem in neuroscience. The so-called criticality hypothesis conjectures that the underlying dynamics of cortical networks is such that it is posed at the edge of a continuous phase transition, separating qualitatively different phases or regimes, with different degrees of order. Experience from statistical physics and the theory of phase transitions teaches that critical points are rather singular locations in phase diagrams, with very remarkable and peculiar features, such as scale invariance (i.e., the fact that fluctuations of wildly diverse spatiotemporal scales can emerge spontaneously, allowing the system dynamics to generate complex patterns of activity in a simple and natural way). A number of features of criticality, including scale invariance, have been conjectured to be functionally convenient and susceptible to be exploited by biological (as well as artificial) computing devices. Thus, the hypothesis that the brain actually works at the borderline of a phase transition has gained momentum in recent years (20–22), even if some skepticism remains (46). However, what these phases are and what the nature of the putative critical point is are questions that still remain to be fully settled.

Aimed at shedding light on these issues, here we followed a classic statistical physics approach. Following the parsimony principle of Landau and Ginzburg in the study of phases of the matter and the phase transitions that they experience, we proposed a simple stochastic mesoscopic theory of cortical dynamics that allowed us to classify the possible emerging phases of cortical networks under very general conditions. For the sake of specificity and concreteness, we focused on regulatory dynamics—preventing the level of activity to explode—controlled by synaptic plasticity (depletion and recovery of synaptic resources), but analogous results have been obtained considering, for example, inhibition as the chief regulatory mechanism. As a matter of fact, our main conclusions are quite robust and general and do not essentially depend on specific details of the implementation, the nature of the regulatory mechanism.

The mesoscopic approach on which our theory rests is certainly not radically novel, as quite a few related models exist in the literature. For instance, neural mass (81–83) and neural field models (66, 67) and rate or population activity equations (58, 84) are similar in spirit and have been successfully used to analyze activity of populations of neurons and synapses and their emerging collective regimes at mesoscopic and macroscopic scales.

Taking advantage of experience from the theory of phase transitions, we introduce two important key ingredients: intrinsic stochasticity stemming from the noninfinite size of mesoscopic regions and spatial dependence. In this way, our theory consists of a set of stochastic (truncated) Wilson–Cowan equations and can be formulated as a field theory using standard techniques (85). A rather similar (field theoretic) approach to analyze fluctuation effects in extended neural networks has been proposed (54).

Such a theory turns out to include a continuous phase transition from a quiescent phase to an active phase, with a critical point in between, which is in contrast with our findings here. Note, however, that the authors of ref. 54 themselves open the door to more complex scenarios if refractoriness and thresholds are included. In any case, such a continuous phase transition picture can be easily recovered in our framework just by changing the sign of a parameter (i.e., taking $b<0$ in Eq. 1); with such a parameter choice, our theory constitutes a sound Landau–Ginzburg description of microscopic models of neural dynamics exhibiting criticality and a continuous phase transition from a quiescent phase to an active phase (27, 39). We believe, however, that this scenario does not properly capture the essence of cortical dynamics, as in actual networks of spiking neurons, there are spike integration mechanisms, meaning that many inputs are required to trigger further activity.

Using our Landau–Ginzburg approach, we have shown that the stochastic and spatially extended neural networks can harbor two different scenarios depending on parameter values: case A including a limit cycle at the deterministic level and the possibility of oscillations and case B leading to bistability (Fig. 1).

In the simpler case B, our complete theory generates either a down-state or a homogeneous up-state phase, with a discontinuous transition separating them, and the possibility of up–down transitions when the system operates in the bistability region. In this case, our theory constitutes a sound mesoscopic description of existing microscopic models for up and down transitions (29, 49, 63, 86).

However, in case A, we find diverse phases, including oscillatory and bursting phenomena: down, synchronous irregular, asynchronous irregular, and active states.

As a side remark, let us emphasize that we constructed a coarse-grained model for activity propagation, but our analyses readily revealed the emergence of oscillations and synchronization phenomena. Hence, our results justify the use of models of effective coupled oscillators to scrutinize the large-scale dynamics of brain networks. As a matter of fact, such models have been reported to achieve the best performance [e.g., reproducing empirically observed resting-state networks (68)] when operating close to the synchronization phase transition point (64, 87, 88).

Within our framework, it is possible to define a protocol to analyze avalanches resembling very closely the experimental one (7, 8, 11, 16, 17). Thus, in contrast with other computational models, causal information is not explicitly needed/used here to determine avalanches—they are determined from raw data—and results can be straightforwardly compared with experimental ones for neuronal avalanches without conceptual gaps (40).

The model reproduces all of the main features observed experimentally. (i) Avalanche sizes and durations distributed in a scale-free way emerge at the critical point of the synchronization transition. (ii) The corresponding exponent values depend on the time bin $\mathrm{\Delta }t$ required to define avalanches, but (iii) fixing $\mathrm{\Delta }t$ to coincide with the ISI, the same statistics as in empirical networks [i.e., the critical exponents compatible with those of an unbiased branching process (10)] are obtained. Finally, (iv) scale-free distributions disappear if events are reshuffled in time, revealing a nontrivial temporal organization.

Thus, the main outcome of our analyses is that the underlying phase transition at which scale-free avalanches emerge does not separate a quiescent state from a fully active one; instead, it is a synchronization phase transition. This is a crucial observation, as most of the existing modeling approaches for critical avalanches in neural dynamics to date rely on a continuous quiescent/active phase transition.

Consistent with our findings, the amazingly detailed model put together by the Human Brain Project Consortium suggests that the model best reproduces experimental features when tuned near to its synchronization critical point (89). In such a study, the concentration of calcium ions, Ca²⁺, needs to be carefully tuned to its actual nominal value to set the network state. Similarly, in our approach, the role of the calcium concentration is played by the parameter $\xi$, regulating the maximum level reachable by synaptic resources. Interestingly, the calcium concentration is well-known to modulate the level of available synaptic resources (i.e., neurotransmitter release from neurons) (32, 58, 61); hence, both quantities play a similar role.

Let us emphasize that we have not explored how potentially the network could self-organize to operate in the vicinity of the synchronization critical point, without having to resort to parameter fine tuning. Adaptive, homeostatic, and self-regulatory mechanisms accounting for this will be analyzed in future work. Also, here we have not looked for the recently uncovered neutral neural avalanches (40), as these require causality information to be considered, and such detailed causal relationships are blurred away in mesoscopic coarse-grained descriptions.

Summing up, our Landau–Ginzburg theory with parameters in case B constitutes a sound description of the cortex during deep sleep or during anesthesia, when up and down transitions are observed. However, case A, when tuned close to the synchronization phase transition, can be a sound theory for the awaked cortex in a state of alertness. A detailed analysis of how the transition between deep sleep (described by case B) and awake (or rapid eye movement sleep described by case A) states may actually occur in these general terms is beyond our scope here, but observe that, just by modifying the speed at which synaptic resources recover, it is possible to shift between the two cases, making it possible to investigate how such transitions could be induced.

A simple extension of our theory, including spatial heterogeneity, has been shown to be able to reproduce remarkably well experimental measurements of activity in neural cultures with structural heterogeneity, opening the way for more stringent empirical validations of the general theory proposed here.

Although additional experimental, computational, and analytical studies would certainly be required to definitely settle the controversy about the possible existence, origin, and functional meaning of the possible phases and phase transitions in cortical networks, we hope that the general framework introduced here—based on very general and robust principles—helps in clarifying the picture and in paving the way to future developments in this fascinating field.

Materials and Methods

Model Details.

In the Wilson–Cowan model, in its simplest form, the dynamics of the average firing rate or global activity, $\rho$, is governed by the equation

$$\dot{\rho }(t)=-a\rho \left(t\right)+(1-\rho (t))S\left(W\rho \left(t\right)-\mathrm{\Theta }\right),$$

where $W$ is the synaptic strength, $\mathrm{\Theta }$ is a threshold value that can be fixed to unity, and $S(x)$ is a sigmoid (transduction) function [e.g., $S(x)=\tanh (x)$] (59, 60). We adopt this well-established model and for simplicity, keep only the leading terms in a power series expansion; we rename the constants, yielding the deterministic part of Eq. 1. To this, we add noise $\sqrt{\rho (t)}\eta (t)$, which is a delta-correlated Gaussian white noise of zero mean and unit variance accounting for stochastic/demographic effects in finite local populations as dictated by the central limit theorem; a formal derivation of such an intrinsic or demographic noise starting from a discrete microscopic model can be found in ref. 59. A noise term could also be added to the equation for synaptic resources (50), but it does not significantly affect the results. Considering $N$ mesoscopic units and coupling them diffusively within some networked structure (e.g., a 2D lattice), we finally obtained the set of Eq. 3.

Analytic Signal Representation.

The Hilbert transform $\mathcal{H}(\cdot )$ is a bounded linear operator largely used in signal analysis, as it provides a tool to transform a given real-valued function $u(t)$ into a complex analytic function, called the analytic signal representation. This is defined as ${\mathcal{A}}_u(t)=u(t)+i\mathcal{H}[u(t)]$, where the Hilbert transform of $u(t)$ is given by $\mathcal{H}[u(t)]=h\times u=\frac{1}{\pi }{lim}_{ϵ\to 0}{\int }_{ϵ}^{\mathrm{\infty }}\frac{u(t+\tau )-u(t-\tau )}{\tau }d\tau$. Expressing the analytic signal in terms of its time-dependent amplitude and phase (polar coordinates) makes it possible to represent any signal as an oscillator. In particular, the associated phase is defined by ${\varphi }_k^{\mathcal{A}}=\arctan Im({\mathcal{A}}_k)/Re({\mathcal{A}}_k)$.

From Continuous Time Series to Discrete Events.

Local time series at each single unit, ${\rho }_k(t)$, can be mapped into time sequences of point-like (“unit spiking”) events. For this, a local threshold $\theta \ll 1$ is defined, allowing us to assign a state on/off to each single unit/node (depending on whether it is above/below such a threshold) at any given time. If the threshold is low enough, the procedure is independent of its specific choice. A single (discrete) event or spike can be assigned to each node $i$ (e.g., at the time of the maximal ${\rho }_i$ within the on state); a weight proportional to the integral of the activity time series spanned between two consecutive threshold crossings is assigned to each single event (Fig. 5A). Other conventions to define an event are possible, but results are not sensitive to it as illustrated in SI Appendix.

Phases from Spiking Patterns.

An alternative method to define a phase at each unit can be constructed after a continuous time series has been mapped into a spiking series. In particular, using a linear interpolation, ${\varphi }_k^{(\mathcal{B})}(t)=2\pi (t-t_n^k)/(t_{n+1}^k-t_n^k)$, where $t\in [t_n^k,t_{n+1}^k)$ and $t_n^k$ is the time of the nth spike of node/unit $k$.