RNA force field with accuracy comparable to state-of-the-art protein force fields

Significance

The complex and often highly dynamic 3D structures of RNA molecules are central to their diverse cellular functions. Molecular dynamics (MD) simulations have played a major role in characterizing the structure and dynamics of proteins, but the physical models (“force fields”) used for simulating nucleic acids are substantially less accurate overall than those used in protein simulations, creating a major challenge for MD studies of RNA. Here, we report an RNA force field capable of describing the structural and thermodynamic properties of RNA molecules with accuracy comparable to state-of-the-art protein force fields. This force field should facilitate the use of MD simulation as a tool for the study of biologically significant RNA molecules and protein–RNA complexes.

Abstract

Molecular dynamics (MD) simulation has become a powerful tool for characterizing at an atomic level of detail the conformational changes undergone by proteins. The application of such simulations to RNA structures, however, has proven more challenging, due in large part to the fact that the physical models (“force fields”) available for MD simulations of RNA molecules are substantially less accurate in many respects than those currently available for proteins. Here, we introduce an extensive revision of a widely used RNA force field in which the parameters have been modified, based on quantum mechanical calculations and existing experimental information, to more accurately reflect the fundamental forces that stabilize RNA structures. We evaluate these revised parameters through long-timescale MD simulations of a set of RNA molecules that covers a wide range of structural complexity, including single-stranded RNAs, RNA duplexes, RNA hairpins, and riboswitches. The structural and thermodynamic properties measured in these simulations exhibited dramatically improved agreement with experimentally determined values. Based on the comparisons we performed, this RNA force field appears to achieve a level of accuracy comparable to that of state-of-the-art protein force fields, thus significantly advancing the utility of MD simulation as a tool for elucidating the structural dynamics and function of RNA molecules and RNA-containing biological assemblies.

Long-timescale molecular dynamics (MD) simulations have been successfully used to characterize complex conformational transitions in proteins (1). In principle, MD simulation should also be a powerful tool for characterizing such conformational changes in RNA molecules, whose highly flexible 3D structures enable their diverse cellular functions (2–4). The physical models (“force fields”) used in RNA simulations, however, are widely considered to be much less accurate overall than the force fields used in protein simulations; artifacts have often been observed in simulations of even simple RNA systems (5–10). Improvements to the accuracy of RNA force fields would greatly facilitate the use of MD simulation to study the functional dynamics of biologically significant RNA molecules.

AMBER is currently the most widely used force field for MD simulations of RNA systems (11, 12). Over the last decade, efforts to improve the accuracy of the AMBER RNA force field have focused largely on refining backbone and glycosidic torsion parameters on the basis of quantum mechanical (QM) calculations (11, 13–17). These optimizations resulted in substantial improvements in the description of canonical double-helical RNA structures but did not fully resolve other key problems such as the overstabilization of nucleobase stacking and the underestimation of base-pairing strength, which are determined primarily by electrostatics and van der Waals (vdW) interactions (18–20). Chen and García (20) addressed this problem by adjusting the vdW parameters of nucleobase atoms to weaken stacking and strengthen base pairing. Their choice of parameters improved the simulated structural properties of RNA tetraloops, which are widely used for benchmarking the quality of RNA force fields, but did not improve the accuracy of simulations of some other model RNA systems such as ssRNAs (10, 20).

Here, using a combination of ab initio and empirical methods, we have modified electrostatic, vdW, and torsional parameters of the AMBER ff14 RNA force field (12) to more accurately reproduce the energetics of nucleobase stacking, base pairing, and key torsional conformers. We then performed MD simulations of both extended and structured RNA systems, including short and long ssRNAs, RNA duplexes, tetraloops, and riboswitches, using the revised parameters and the recently published TIP4P-D water model (21). The simulated structural and thermodynamic properties of these systems exhibited substantially improved agreement with experimental data, to the point that the accuracy of this revised AMBER RNA force field can be considered comparable to that of state-of-the-art fixed-charge protein force fields. We expect that this force field will enable the use of MD simulation to investigate the complex functional dynamics of a wide range of RNA molecules, as well as RNA-containing macromolecular machines.

Results

Reparameterization of the AMBER RNA Force Field.

We adopted a two-step approach to reparameterize the AMBER ff14 RNA force field (12). We first developed revised nucleobase nonbonded parameters to improve the description of base pairing and stacking, then derived revised terms for the γ, ζ, and χ torsions.

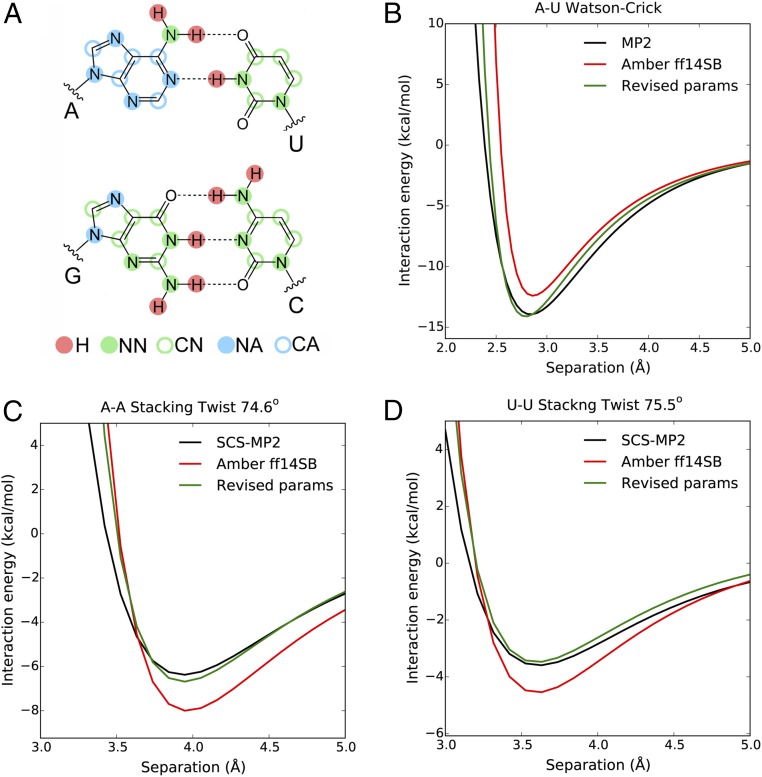
To tackle base pairing, we calculated the QM dimer interaction energy at the MP2 level as a function of intermolecular separation for six common types of base pairs (see Methods for details). This level of QM calculation has been shown to be adequate for describing base-pairing energies (22). Comparison of the QM and molecular mechanical (MM) interaction energy profiles shows that the AMBER ff14 parameters underestimate base-pairing strength, especially at distances smaller than 2.7 Å [where the repulsive C₁₂ component of the Lennard-Jones (LJ) potential becomes excessively steep] (Fig. 1B and SI Appendix, Fig. S1). We adjusted charges and vdW parameters of nucleobase nitrogen and polar hydrogen atoms to minimize the discrepancy between the QM and MM potential energy profiles (Fig. 1B, Tables 1 and 2, and SI Appendix, Fig. S1). Notably, splitting the nucleobase nitrogen atoms into two different vdW atom types on the basis of their aromatic character (Fig. 1A) and reducing the σ and ε values of polar hydrogens to zero (Table 1) greatly improved the quality of the fit to the QM data.

Fig. 1.

(A) The vdW atom types for nucleobase atoms in the revised force field. (B) Interaction energies of the A–U Watson–Crick base pair as functions of intermolecular separations. (C) Interaction energies of the A–A stacked dimer at 74.6° twist angle as functions of intermolecular separations. (D) Interaction energies of the U–U stacked dimer at 75.5° twist angle as functions of intermolecular separations. See SI Appendix, Figs. S1–S3 for the complete set of data included in the parameterization.

Table 1.

Charges of the nucleobase atoms in the revised force field

Base	Atom	Charges
		AMBER ff14	Revised
C	N4	−0.9530	−0.8716
	H41/H42	+0.4234	+0.3827
U	N3	−0.3549	−0.3913
	H3	+0.3154	+0.3518
G	N1	−0.4787	−0.5606
	H1	+0.3424	+0.4243
	N2	−0.9672	−1.0158
	H21/H22	+0.4364	+0.4607
A	N1	−0.7615	−0.7969
	H2	+0.0473	+0.0650
	N6	−0.9019	−1.0088
	H61/H62	+0.4115	+0.4738

Unlisted atoms have unchanged charges.

Table 2.

The vdW atom types and parameters for nucleobase atoms in the revised force field

vdW atom type	σ, Å		ε, kcal⋅mol−1
	AMBER ff14	Revised	AMBER ff14	Revised
H	1.0691	0.0000	0.0157	0.0000
NA	3.2500	3.2890	0.1700	0.1700
NN		3.3507
CA	3.3997	3.3004	0.0860	0.0636
CN		3.2850		0.0538

Nonpolar hydrogen and oxygen atoms (not listed) have unchanged parameters.

The AMBER ff14 parameters substantially overestimate the stacking energy with respect to the QM values (18, 20) (Fig. 1 C and D). To improve the description of stacking, we calculated the QM dimer interaction energies of A–A and U–U stacked dimers with varying relative orientations and separations using SCS(MI)-MP2, a semiempirical MP2-based method that allows the computation of accurate stacking energies (19, 23). We then adjusted the vdW parameters of the nucleobase carbon atoms to reproduce the QM interaction energies (Fig. 1 C and D and SI Appendix, Figs. S2 and S3).

Our modifications of the charges and vdW parameters for the nucleobases necessitated an adjustment to the glycosidic (χ) dihedral terms. Following the methods of previous parameterizations of the χ torsion (15, 17) (Methods and SI Appendix, Table S1), we generated the in vacuo QM potential energy profiles for the four nucleosides with either the C3′-endo or C2′-endo sugar pucker configuration (SI Appendix, Fig. S4). The χ dihedral terms were then parameterized to minimize the differences between the QM and MM potential energy profiles (SI Appendix, Table S2). Explicit-solvent MD simulations of mononucleosides showed that the pyrimidine nucleosides adopt the anti χ configuration to a greater extent than do purine nucleosides (SI Appendix, Table S3), qualitatively matching the results of earlier NMR experiments (24, 25).

The revised force field includes the nonbonded phosphate parameters published by Steinbrecher et al. (26), which have increased σ values for oxygen atoms. This change required the introduction of new backbone γ and ζ dihedral terms, which were previously shown to be critical for maintaining the stability of both DNA and RNA duplexes in simulation (14, 16, 27). Initial attempts at parameterizing the γ and ζ torsions to match the in vacuo QM potential energy profiles led to erroneous populations of the γ and ζ conformers in explicit-solvent simulations. We thus employed a hybrid approach that combined ab initio calculations with the COSMO implicit-solvent model (28) and explicit-solvent MD simulations (see Methods for details). The theoretical populations of the +gauche, −gauche, and trans conformers were first derived from the QM-COSMO potential energy profiles, and the dihedral terms were then adjusted to ensure that similar populations were reproduced in the simulations (SI Appendix, Figs. S5 and S6 and Tables S2, S3, and S4).

The Revised Parameters Recover the Solution Conformations of ssRNA Tetranucleotides.

The protein force fields currently in use for MD simulations are typically able to faithfully reproduce the solution conformations of short peptides and attain close agreement (χ² < 2) between the simulated and experimental NMR measurements (29–31). In contrast, MD simulations of comparably simple ssRNA tetranucleotides using currently available RNA force fields often result in structures that deviate significantly from the experimentally determined structures. These molecules tend to favor an intercalated conformation in simulation (5–10, 32) (Fig. 2A), but the large discrepancies between the simulated and experimental ³J scalar-coupling values (SI Appendix, Table S5) suggest that this intercalated conformation is probably a simulation artifact.

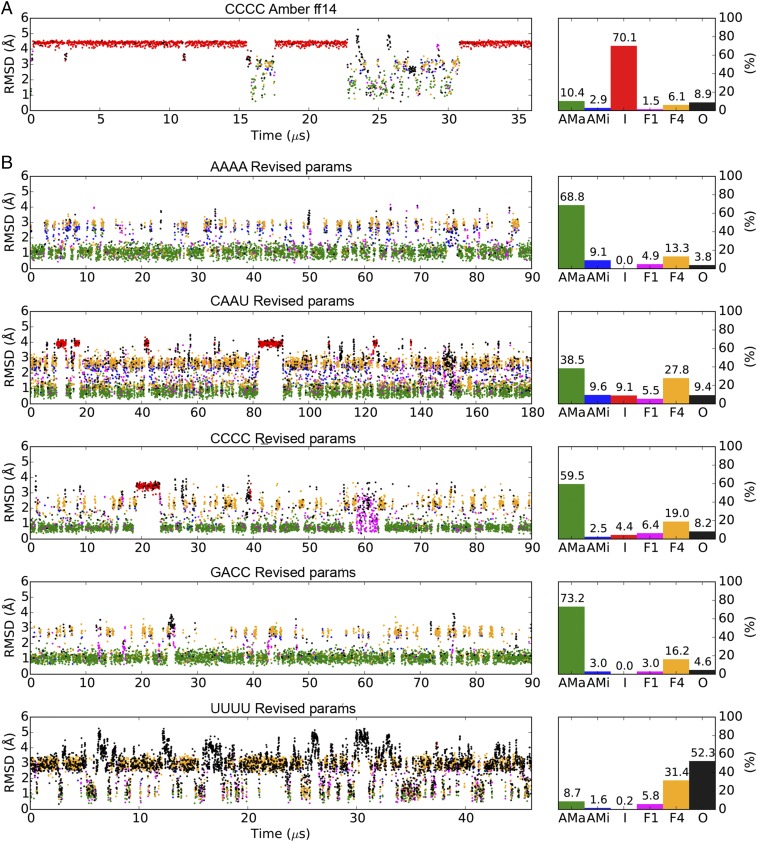
Fig. 2.

MD simulations of ssRNA tetramers using AMBER ff14 and the TIP3P water model (A) or the revised parameters (B). The scatter plots on the left indicate rmsds of the backbone (including the ribose) nonhydrogen atoms to the initial A-form structures. Based on the stacking patterns of the four nucleotides, the simulated conformations are categorized into six groups: A-form major (AMa, green), A-form minor (AMi, blue), Intercalated (I, red) Nucleotide-4 flipped (F4, yellow), Nucleotide-1 flipped (F1, magenta), and Others (O, black). See Methods for the detailed definitions of these conformations. Percentage populations of the six conformations in each simulation are shown on the right.

We evaluated the accuracy of our revised parameters for the AMBER RNA force field through long MD simulations of the AAAA, CAAU, CCCC, GACC, and UUUU ssRNA tetranucleotides, for which extensive NMR data are available. All except UUUU primarily adopted the experimentally observed A-form-like conformations, and intercalation was either completely eliminated or dramatically reduced (Fig. 2B). Consequently, the χ² errors between the simulated and experimental ³J scalar-coupling values were substantially improved to 1.4–2.2 (SI Appendix, Table S5), on par with the performance of most protein force fields. A substantially reduced amount of intercalation was also observed in a recent work (33) using a combination of the AMBER force field and the OPC water model (34), which is similar to the TIP4P-D water model used here, and it was suggested that a substantial fraction of the improvement should be ascribed to the water model. As a further test of this conclusion we performed a simulation with the OPC water model and found only ∼20% intercalation (SI Appendix, Fig. S9) and much improved agreement with experiment (SI Appendix, Table S5) compared with TIP3P. This result is in line with previous findings (33) and highlights the importance of the choice of water model for describing ssRNA.

Unlike the other tetranucleotides tested, UUUU predominantly adopts a minimally stacked random-coil conformation in solution (6). In the simulation of UUUU using the revised force field this random-coil conformation was reproduced in the majority of the frames (Fig. 2). The deviation between the simulated and experimental NMR observables for UUUU is larger (χ² ≈ 4) than those of the other tetranucleotides (SI Appendix, Table S5), possibly because UUUU visited the stacked states in a nonnegligible number of simulation frames (Fig. 2), resulting in a less disordered conformational ensemble than was observed experimentally.

The Revised Parameters Improve the Description of Long Disordered ssRNAs.

MD simulations of disordered proteins with several commonly used protein force fields together with the TIP3P water model result in more compact structures (characterized by much smaller radius of gyration values) than are observed experimentally (21). The TIP4P-D water model, however, largely corrects the overly compact simulated conformations of disordered proteins (21, 35).

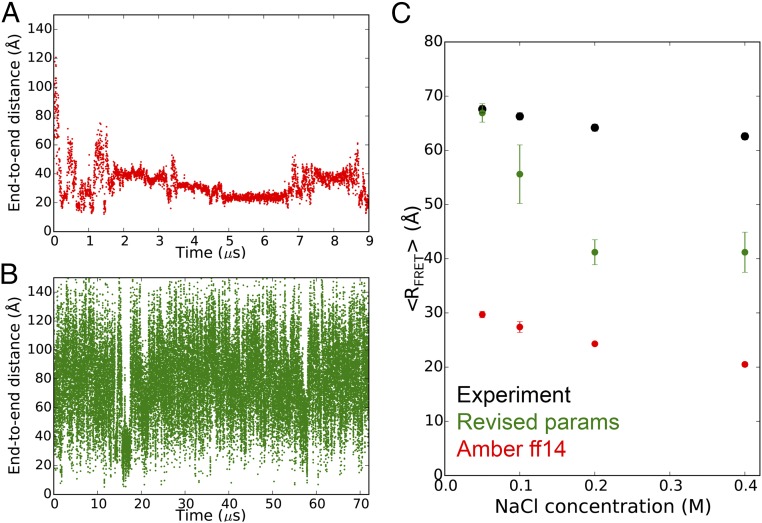
Similarly, the AMBER ff14 RNA force field and the TIP3P water model cause the highly extended rU₄₀ ssRNA to quickly collapse to an ensemble of globule-like structures with end-to-end distance values much smaller than those measured by single-molecule FRET experiments (〈R_FRET〉) (Fig. 3 A and C) (36). The combination of AMBER ff14 and the TIP4P-D water model is also unable to prevent rU₄₀ from collapsing (SI Appendix, Fig. S19). Simulations using our revised RNA parameters and the TIP4P-D water model, however, maintain the extended conformation of rU₄₀ and recapitulate the experimental 〈R_FRET〉 values at low salt concentration ([NaCl] < 0.1 M) (Fig. 3 B and C). In simulations under higher salt concentrations ([NaCl] ≥ 0.1 M), rU₄₀ alternates between extended and double-helical hairpin conformations containing up to 18 U–U base pairs, leading to lower 〈R_FRET〉 values (Fig. 3 and SI Appendix, Fig. S8). Experimental evidence supports the existence of such hairpin structures of polyuridylic acids, but only at temperatures of 280–290 K, which are lower than that of the simulations (300 K) (37, 38). The revised force field thus recapitulates well the properties of disordered ssRNAs but likely overstabilizes the double-helical conformation.

Fig. 3.

The end-to-end distance of the rU₄₀ long ssRNA simulated with AMBER ff14 and TIP3P (A) or the revised parameters and TIP4P-D (B) under 0.05 M NaCl at 300 K. See SI Appendix, Figs. S7 and S8 for other NaCl concentrations. (C) The 〈R_FRET〉 values of rU₄₀ under different NaCl concentrations. The experimental values were reported in ref. 36. See Methods for the procedure of calculating the simulated 〈R_FRET〉 values.

The Revised Parameters Can Reversibly Fold RNA Duplexes and Tetraloops to Subangstrom Resolution.

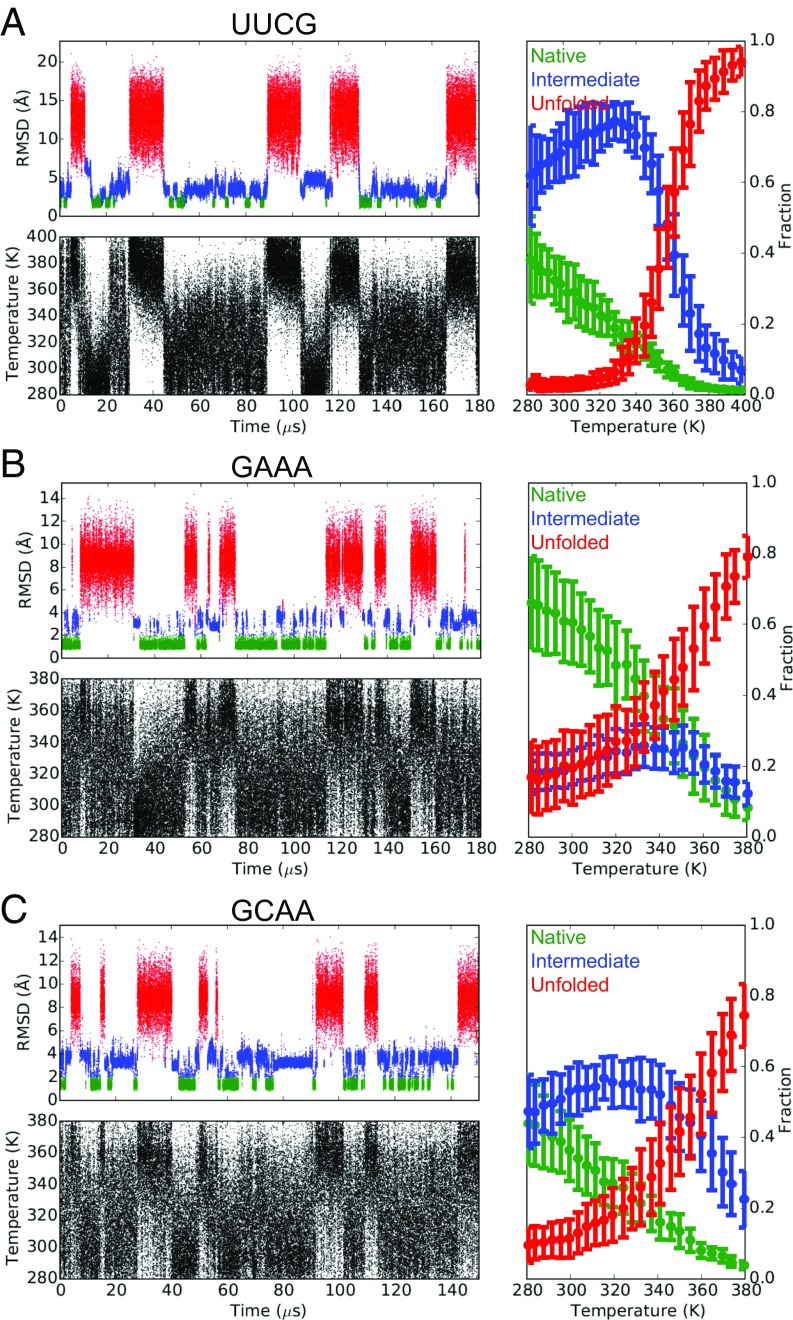
A major success of modern protein force fields is that they can fold many small protein domains to within 2 Å rmsd of the crystal structures, and can typically predict their melting temperatures (T_m) to within 50 K of the experimentally determined values (39–41). The reversible folding and unfolding of basic RNA structural elements such as duplexes and tetraloops in MD simulations, however, has proven more challenging due to inaccuracies in the RNA force fields. Although replica-exchange MD simulations using either the AMBER ff14 or Chen–García parameters have been shown to fold UUCG and GNRA tetraloops, the native conformations—which are observed in both X-ray and NMR structures, and thus presumably dominate in solution—only accounted for a small fraction (Chen–García: ∼10%, AMBER ff14: <1%) of the lowest-temperature (277 K) ensemble (10, 20, 42). Using a simulated tempering protocol (43, 44) and our revised parameter set we were able to simulate the reversible folding of eight RNA duplexes of varying sequences and lengths, as well as the ggcacUUCGgugcc, gccGAAAggc, and ggcGCAAgcc hyperstable tetraloops (Figs. 4 and 5 and SI Appendix, Figs. S11 and S12).

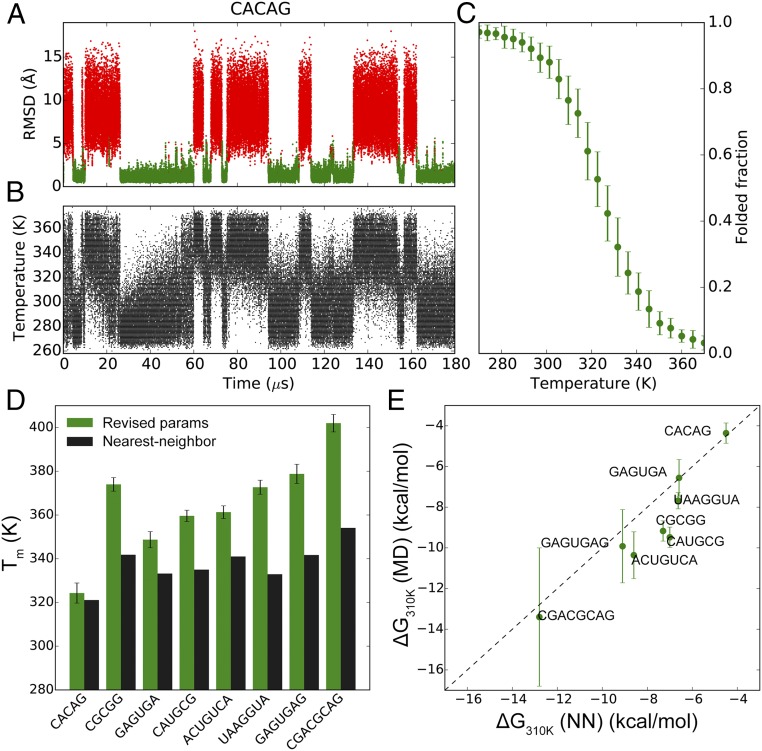
Fig. 4.

MD simulations of RNA duplexes. (A) Nonhydrogen rmsd trace of the CACAG RNA duplex. The folded (green) and unfolded (red) states of the duplex are indicated. (B) The time evolution of temperatures in the simulated tempering MD simulation of the CACAG duplex. (C) Melting curve of the CACAG duplex. The rmsd traces and melting curves of all eight RNA duplexes are in SI Appendix, Fig. S12. (D) T_m values of the eight RNA duplexes calculated from the MD trajectories. In black are the T_m values estimated with the NN model (45). (E) ΔG_{310 K} values calculated from the MD trajectories (by fitting to the nonlinear van’t Hoff equation) compared with those estimated with the NN model. The lowest temperatures in the simulated tempering simulations of GAGUGAG and CGACGCAG were higher than 310 K, so for these duplexes the ΔG_{310 K} values were extrapolated from the fitted lnK_eq – 1/T curves.

Fig. 5.

The nonhydrogen rmsd traces, the time evolutions of temperatures, and the melting curves of the ggcacUUCGgugcc (A), gccGAAAggc (B), and ggcGCAAgcc (C) RNA tetraloops. The native (green), intermediate (blue), and unfolded (red) states of the tetraloops are indicated. Error bars were estimated using a blocking analysis.

In the simulations of the duplexes at least eight reversible folding events were observed in each trajectory, allowing the estimation of thermodynamic quantities that can be compared with the corresponding values predicted by the relatively accurate, experimentally derived nearest-neighbor (NN) model (45). The folding free energies of the duplexes at 310 K (ΔG_{310 K}) calculated from the simulations were slightly more negative than the NN model (root-mean-square error = 1.4 kcal mol⁻¹, mean signed error = −1.1 kcal mol⁻¹; Fig. 4E), indicating that the revised parameters moderately overstabilize double-helical conformations, consistent with the results of the rU₄₀ simulations. The simulated T_m values were 5–50 K higher (mean signed error = +27.6 K) than the values predicted by the NN model. More stable duplexes tended to have larger discrepancies in T_m (Fig. 4D). This observation is related to an underestimation of the enthalpy of duplex formation in simulation, which leads to a less-steep melting curve, thus shifting the midpoint toward a higher temperature range. Underestimation of folding enthalpy has also been observed in protein-folding simulations (46). Simulations of the tetraloops each registered several reversible folding events to <1 Å rmsd of the experimental structures from completely unfolded conformations (Fig. 5). In particular, the single-stranded loop regions of the tetraloops repeatedly adopted conformations that were <0.8 Å rmsd from the experimental structures (SI Appendix, Fig. S11), suggesting that their native conformations have been successfully recapitulated in the simulations. The fraction of the native conformation of each tetraloop at the lowest-temperature (280 K) ensemble was at least 40% (Fig. 5 and SI Appendix, Table S6), a significant improvement compared with the values reported previously (10, 20, 42). As we observed for the RNA duplexes, the T_m values of the double-stranded segments of the tetraloops (Fig. 5) were 20–30 K higher than the experimental values (SI Appendix, Table S6) (47).

Reversible Ligand Binding to a Guanine Riboswitch Aptamer Domain.

The level of accuracy achieved in describing the conformational ensemble of relatively simple RNA systems encouraged us to assess whether the revised parameters can maintain the stability of larger, more complex RNA molecules such as the aptamer domains of riboswitches, which can fold into 3D structures having a degree of complexity comparable to that of protein domains (3).

The aptamer domain of the Bacillus subtilis xpt guanine riboswitch binds guanine and its analog hypoxanthine with high affinity (48, 49). Crystal structures show that the aptamer adopts a tuning-fork–like fold containing three double-helical regions (P1–P3) (SI Appendix, Fig. S13A) (50, 51). P2 and P3 are parallel to each other and are anchored together through the kissing-loop interactions between their hairpin loops L2 and L3. The single-stranded segments connecting the stems (J1/2, J2/3, and J3/1) form a three-way junction that acts as the binding pocket, where the ligand is specifically recognized by residues U22, U51, and C74 through multiple hydrogen bonds (SI Appendix, Fig. S13B) (50, 51).

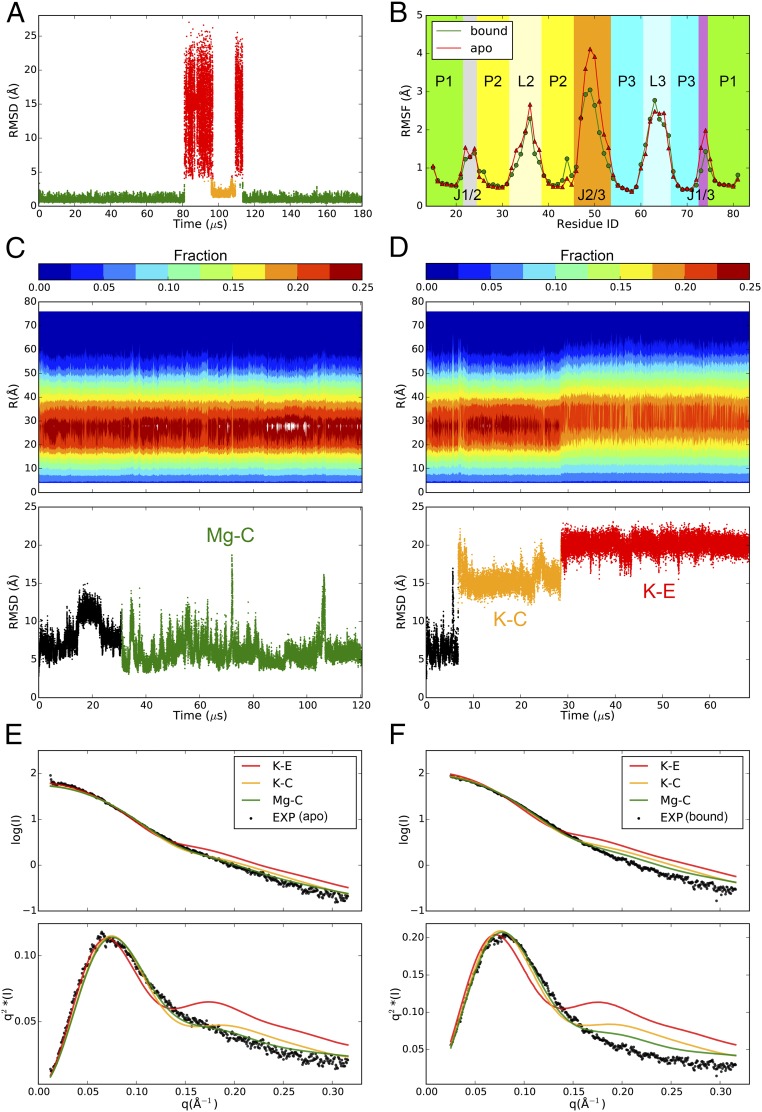
In the simulation of the guanine-bound aptamer, the guanine-binding pocket accurately maintained its native conformation for 81 µs, at which point guanine escaped from the binding pocket into the solvent (Fig. 6A). The ligand was briefly recaptured by the pocket at 97 µs but adopted a binding pose distinct from the crystal structure (Fig. 6A and SI Appendix, Fig. S13C) and stayed in this nonnative bound conformation for 13 µs before dissociating from the pocket. At 114 µs guanine again entered the binding pocket, and this time the native bound conformation was readopted and maintained until the end of the simulation (Fig. 6A). This result shows that the simulation is able to identify the correct binding pocket and binding pose in this complex system. Because the experimental affinity of guanine to the aptamer is less than 10 nM (49), the fact that we observed reversible ligand dissociation and reassociation within a 180-µs simulation starting from the bound structure indicates that the affinity of the ligand is probably underestimated in simulation, which may result from a suboptimal choice of parameters for the ligand (Methods). In a 90-µs simulation performed with the AMBER ff14SB force field the overall riboswitch structure was maintained, but the binding-pocket structure was not conserved: After 20 µs U51 rotated away from guanine and did not participate in the binding (SI Appendix, Fig. S16).

Fig. 6.

MD simulations of riboswitches. (A) The nonhydrogen rmsd trace of the binding pocket of the ligand-bound guanine riboswitch aptamer. Green, orange, and red colors indicate the native bound conformation, the nonnative bound conformation, and the unbound conformation, respectively. (B) Root-mean-square fluctuation (RMSF) values of the C1′ atoms in the simulations of the bound (green; only the frames where guanine was bound with the native conformation were included in the calculation) and apo (red) guanine riboswitch. The C1′ atoms in the double-helical regions were aligned against for the calculation. (C and D) The distribution of all nonhydrogen pairwise interatomic distances (Top) and the nonhydrogen rmsd to the crystal structure (PDB ID code 3IQR) (Bottom) calculated for the MD simulations of the apo SAM-I aptamer with magnesium (C) or only potassium (D). (E and F) The theoretical SAXS profiles, shown as scattering curves (Top) and Kratky plots (Bottom), of the simulated Mg–C, K–C, and K–E ensembles compared with the experimental SAXS profiles of the apo (E) and bound (F) SAM-I aptamer in the presence of magnesium.

Examining the conformational flexibility of the aptamer domain in its guanine-bound and apo states in simulation, we found the conformations of the three double-helical regions to be stable, whereas the single-stranded segments exhibited considerable conformational freedom (Fig. 6B). J2/3 was the most dynamic part of the molecule, and the binding of guanine considerably reduced its flexibility (Fig. 6B). The simulated global dynamics of the apo and bound aptamer domain are qualitatively consistent with the results of previous N-methylisatoic anhydride probing assays, with the exception that the J1/2 segment was less flexible in the simulations compared with the experimental results (52).

Magnesium-Dependent Dynamics of the Apo SAM-I Riboswitch Aptamer Domain.

As a model for a complex system that undergoes large-scale conformational changes, we focused on the aptamer domain of the Thermoanaerobacter tengcongensis SAM-I riboswitch. Stoddard et al. (53) used small-angle X-ray scattering (SAXS) experiments to demonstrate that the solution conformation of the SAM-I riboswitch is heavily influenced by magnesium. In the absence of magnesium the aptamer domain adopts extended and disordered structures regardless of the availability of the ligand. The addition of magnesium alone, in the absence of the ligand, is able to facilitate the formation of tertiary interactions within the apo aptamer, resulting in an ensemble of compact, yet heterogeneous, conformations. Ligand binding then further immobilizes the secondary structural elements and leads to a stable and well-defined structure (53).

We removed the ligand from the crystal structure of the ligand-bound aptamer domain (54) to generate the starting structure for our MD simulations. The theoretical SAXS profile of the starting structure suggests that it is representative of the solution conformation in the Mg(+), SAM-bound state (χ = 1.86) while being distinct from that of the Mg(+), apo ensemble (χ = 2.82) (SI Appendix, Table S7). After 30 µs of simulation with magnesium we observed an ensemble of compact conformations, Mg-C (Fig. 6C), whose theoretical SAXS profile instead exhibits better agreement with the Mg(+), apo profile (χ = 1.74) than with the Mg(+), bound profile (χ = 2.27) (Fig. 6 E and F and SI Appendix, Table S7). The simulated conformational transition of the SAM-I riboswitch from the bound to the apo state upon the removal of the ligand in the presence of magnesium is thus consistent with that observed experimentally.

In a simulation with potassium as the sole counter ion the aptamer domain first sampled compact structures (K–C) not observed in the Mg–C ensemble (see SI Appendix for a more detailed description of the conformational changes in this riboswitch) and later adopted more extended conformations (K–E) featuring disrupted tertiary interactions (Fig. 6D and SI Appendix). The SAXS profile of the K–E ensemble displays high intensities in the larger scattering angles, which is substantially different from both Mg(+) experimental profiles (Fig. 6 E and F and SI Appendix, Table S7) but shares similarities with those measured in the absence of magnesium (53). Since the complete unfolding of the aptamer domain might require milliseconds of simulation time (2), these results suggest that the K–E ensemble may represent an intermediate on the unfolding pathway.

In contrast to what would be expected based on the experimental results, we found that simulations of the SAM-I riboswitch performed with the AMBER ff14SB force field were not strongly influenced by Mg(+): The overall structure of the riboswitch was well maintained in 90-µs simulations performed either with or without Mg(+) (SI Appendix, Fig. S17).

Discussion

We have reparameterized the AMBER RNA force field to rebalance the stacking and base-pairing interactions, which are the primary stabilizing forces of RNA structures. In particular, we have modified the charges and vdW parameters of the nucleobase atoms, as well as the χ, γ, and ζ torsion potentials. Moreover, we have used the TIP4P-D water model (21), in which there is a better balance between the strengths of electrostatic and dispersive interactions, and where the dispersive interactions are not too weak relative to those in biomolecules. Similarly to its effect in simulations of disordered proteins, this water model helps to alleviate the problem of overly stable stacking interactions (33).

This revised set of parameters was tested for its ability to reproduce the structural and thermodynamic properties of RNA systems of varying structural complexity. The simulations were able to closely recapitulate the conformational ensembles of long and short single-stranded polynucleotides, the structures (to subangstrom rmsd) and stabilities (to within 1.5 kcal⋅mol⁻¹) of tetraloops and RNA duplexes, the conformational dynamics of complex RNA folds, and the binding pose of a small ligand. The level of accuracy we observed is comparable to that of state-of-the-art protein force fields, which can typically reproduce the conformational ensembles of small peptides and disordered proteins (21, 29, 30, 46), predict the structures of small fast-folding proteins to less than 2-Å resolution (39–41), accurately describe the dynamics of folded proteins (55, 56), and, in favorable cases, predict the binding poses of ligands (57). This substantial improvement in accuracy should allow MD simulation to play an expanded role as a tool for elucidating the structure and dynamics of biologically important RNA molecules and when used in combination with protein force fields may also facilitate the study of protein-RNA complexes.

We expect that the revised nucleobase nonbonded parameters will be largely transferable to DNA, but the absence of the 2′-hydroxyl group in deoxynucleotides has nonnegligible effects on the torsion profiles. It will thus be necessary to introduce DNA-specific dihedral terms to make this parameter set suitable for DNA simulations. [A similar distinction between DNA and RNA force fields already exists in the most recent AMBER16 package, which uses the χOL3 correction for RNA (15) and the bsc1 update for DNA (16).]

Like any MM force field, the parameterization described here has limitations. One issue is that it appears to modestly overstabilize the helical regions of RNAs, resulting in higher melting temperatures for the rU₄₀ long hairpin, the RNA duplexes, and the tetraloops. This overstabilization may also contribute to the excessive ordering of the UUUU tetranucleotide and the J1/2 segment of the guanine riboswitch aptamer domain. An area that we did not investigate is the accuracy of nonbonded parameters for charged species like ions and the phosphate group. The phosphate vdW parameters published by Steinbrecher et al. (26) were originally developed to ensure that the solvation free energies of bioorganic phosphates in TIP3P water matched the experimental values, and most of the current ion parameters were developed to be compatible with the standard TIP3P or TIP4P water models (58–60). In particular, it has been observed that the CHARMM22 parameters for magnesium, which were used in simulating the riboswitches, result in an exchange rate of water from the first solvation shell that is orders of magnitude smaller than the experimental estimate (61). Although it is unlikely that this limitation would significantly affect the results of the simulations in this work that included magnesium (the ions were expected to remain hydrated and not interact directly with the RNA), it would be desirable to derive new ion and phosphate parameters for better compatibility with the TIP4P-D water model.

Methods

Ab Initio Calculations.

Initial geometries of Watson–Crick A–U, Watson–Crick G–C, Hoogsteen A–U, Wobble G–U, Calcutta U–U, and Imino G–A base pairs, as well as the A–A and U–U stacked dimers with different orientations, were extracted from high-resolution crystal structures in the Protein Data Bank (PDB). The intermolecular separations of each nucleobase dimer were varied from 2.0 Å to 5.0 Å in 0.05-Å increments. For the base pairs, in vacuo QM counterpoise-corrected interaction energies were calculated at the MP2 level of theory, using density-fitting approximations (62), with an augmented triple-zeta basis set (aug-cc-pVTZ) using the MOLPRO program (63). The QM interaction energies of the stacked dimers were calculated with SCS(MI)-MP2, a semiempirical MP2-based method that is able to estimate the strength of nucleobase stacking only slightly less accurately than the much more computationally demanding CCSD(T) method (19, 23).

In vacuo potential energy surface (PES) scans of the χ (O4′-C1′-N9-C4 in purines and O4′-C1′-N1-C6 in pyrimidines) torsion were performed for the four ribonucleosides. PES scans of the γ (O5′-C5′-C4′-C3′) torsion for uridine and the ζ (C3′-O3′-P′-O5′) torsion for a model molecule mimicking the RNA backbone (SI Appendix, Fig. S6A) were performed either in vacuum or with the COSMO continuum solvent model (28). We left the α torsion unchanged, since the AMBER ff14 RNA force field reproduces the QM PES scan well. The torsions were varied between −180° and 180° in 10° increments. Each structure was relaxed at the MP2 level with a number of other dihedral angles constrained to ensure the smoothness of the PESs (SI Appendix, Table S1).

Parameter Fitting.

Charges of the hydrogen bond donors in base pairs and the N1 and H2 atoms in adenine, as well as the LJ parameters of nucleobase nitrogen and polar hydrogen atoms, were optimized to minimize the following function:

$$\epsilon ={\displaystyle \sum _{i=1}^N{\left(E_i^{QM}-E_i^{MM}\right)}^2\hspace{0.17em}{e}^{-E_i^{QM}}},$$

where E^MM and E^QM are the MM and QM interaction energies of the base-paired dimers. The differences between E^MM and E^QM were weighted by the factor $e^{-E_i^{QM}}$, where E_i^QM is in kilocalories per mole. We found that the agreement between the MM and the QM interaction energies greatly improved by the optimization of the σ and ε values of the polar hydrogen atoms, and by optimizing the vdW parameters of the aromatic ring N atoms (N1, N3, N7, and N9) in adenine and the N atoms in the five-member ring of guanine (N7 and N9) separately from all of the other nucleobase N atoms (Table 2). The LJ parameters of nucleobase carbon atoms were subsequently optimized based on the interaction energies of the stacked dimers.

New χ dihedral terms were obtained through fitting to the QM potential energy profiles with the same minimization method (SI Appendix, Fig. S3). The force field potential energy, E^MM, was calculated with the following equation:

$$E^{MM}\left(\phi \right)=E^{MM\left(no\hspace{0.17em}dih\right)}+{\displaystyle \sum _{m=1}^M{k}_m\left(1+\cos \left(m\phi -{\theta }_m\right)\right)}.$$

In this equation, E^{MM(no dih)} was calculated with the dihedral term to be optimized removed from the MM force field. k_m and θ_m are the parameters of the fit and represent the force constant and equilibrium dihedral angle for the mth term in the cosine expansion.

For the backbone γ and ζ torsions, considerable differences were observed between the profiles calculated in vacuum and with the COSMO continuum solvent (SI Appendix, Figs. S5 and S6). A combination of ab initio and empirical methods was thus used to derive the new dihedral terms. The populations of the +gauche, −gauche, and trans configurations were first calculated based on the MP2-COSMO profiles, and the dihedral terms were adjusted to ensure that similar populations were recapitulated in explicit-solvent MD simulations (SI Appendix, Tables S3 and S4).

The total number of terms, M, in the cosine expansion was four for the χ torsion and three for the γ and ζ torsions. The new k_m and θ_m values are summarized in SI Appendix, Table S2.

MD Simulations of ssRNA Tetramers.

The starting A-form structures of five ssRNA tetramers (AAAA, CAAU, CCCC, GACC, and UUUU) were generated with the program Coot (64) and solvated in cubic 40-ų boxes containing 0.15 M NaCl. The TIP4P-D water model (21) and the CHARMM22 force field (65) were used to parameterize the water molecules and ions, respectively. As a comparison, CCCC was also parameterized with AMBER ff14, which includes the bsc0 and χOL modifications (14, 15), and the TIP3P water model (66). The systems were first equilibrated at 275 K for 50 ps using the Desmond software (67), and production simulations were performed at 275 K in the NPT ensemble (68–70) using Anton (71). Conformations of the ssRNA tetramers were categorized based on their base-stacking patterns, which were analyzed by the program DSSR (72). In both the A-form major (AMa) and A-form minor (AMi) conformations the four nucleobases are sequentially stacked. The main difference between AMa and AMi is that the 3′-end backbone α-torsion is +gauche in AMa and trans in AMi. In the Nt1-flipped (F1) and Nt4-flipped (F4) conformations the ribose ring of the terminal nucleotide adopts the C2′-endo configuration and the base is flipped away from the other three. In the intercalated conformation (I), nucleotide j inserts between and stacks against nucleotides i and i + 1 (j < i or j > i + 1). Conformations other than the ones mentioned above (O) are mainly random coils.

MD Simulations of rU₄₀.

The initial linear A-form model of rU₄₀ was built with the program Coot. The molecule was solvated in 115-ų boxes containing 0.05 M, 0.1 M, 0.2 M, or 0.4 M NaCl. Production runs were performed at 300 K in the NPT ensemble with Anton. The distance between the O5′ atom of U1 and the O3′ atom of U40, R, was converted into FRET efficiency, E_FRET, with the equation $E_{FRET}=1/1+{\left(R/R_0\right)}^6$, where R₀ was set to 56.4 Å according to previous experimental results (36). The FRET-averaged end-to-end distance was calculated using 〈R_FRET〉 = R₀(1/〈E_FRET〉 − 1)^1/6. SEM of 〈E_FRET〉 was estimated using a blocking procedure (73).

MD Simulations of RNA Duplexes.

The double-stranded models of eight non-self-complementary RNA duplexes were generated with the program Coot. The systems were solvated in ∼55-ų boxes with 1 M KCl. Simulated tempering simulations following the protocol described in ref. 43 were performed on Anton. Exponentially distributed 24-rung temperature ladders spanning 100 K were used, with a temperature update interval of 18 ps.

The T_m value and the folding free energy at 310 K (ΔG_{310 K}) of an RNA duplex at 1 M standard concentration were estimated using the two-state model (45). The average folded fraction, f, in each rung was calculated based on the criterion that more than 50% of the original base pair hydrogen bonds should be present in the folded conformation. The data were then fitted to the nonlinear van’t Hoff equation:

$$\ln K_{eq}=\text{ln}\frac{2f}{{\left(1-f\right)}^2{C}_t}=\frac{\mathrm{\Delta }{H}_0-T_0\mathrm{\Delta }{C}_p}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)+\frac{\mathrm{\Delta }{C}_p}{R}\text{ln}\frac{T}{T_0}+\text{ln}{K}_0,$$

where C_t is the total concentration of single strands in the system, ΔC_p is the temperature-independent heat capacity change, T₀ is an arbitrarily selected reference temperature, and ΔH₀ and K₀ are the enthalpy and equilibrium constants at T₀ (45, 74).

MD Simulations of RNA Tetraloops.

The initial structures of the ggcacUUCGgugcc, gccGAAAggc, and ggcGCAAgcc tetraloops were extracted from PDB entries 2KOC, 1JJ2, and 1ZIH, respectively. The systems were neutralized with potassium cations, and the simulated tempering protocols were similar to those of the RNA duplex simulations, except that the simulation of ggcacUUCGgugcc used a 30-rung temperature ladder spanning 120 K.

The simulated structure of a tetraloop was categorized in the native, intermediate, or unfolded conformation based on the following criteria. (i) If not all of the Watson–Crick base pairs in the stem are formed, the structure is considered to be unfolded. (ii) If all of the Watson–Crick base pairs in the stem are formed, the overall rmsd value is lower than 2.5 Å, and all of the signature H-bond interactions in the loop in the experimental structure are formed, the structure is considered to be native. (iii) Structures that do not fall into either the unfolded or the native categories are designated intermediate.

MD Simulations of Riboswitches.

The structure of the B. subtilis xpt-pbuX guanine riboswitch was extracted from PDB entry 4FE5 (50). The original ligand hypoxanthine in 4FE5 was either replaced by guanine or removed. The guanine-bound and apo molecules were solvated in 88-ų boxes with 0.5 M NaCl and 0.1 M MgCl₂. The nonbonded parameters of the atoms in the guanine base were transferred from our revised RNA force field, except that the charge of atom H9 was adjusted to make the net charge of the ligand equal to zero.

The structure of the SAM-bound T. tencongensis SAM-I riboswitch was extracted from PDB entry 3IQR (53), and the SAM ligand was removed for the simulations. Residue A94, which was mutated to G in the crystal structure, was mutated back to A. The molecule was solvated in 91-ų boxes with either 0.5 M KCl or 0.5 M KCl and 0.1 M MgCl₂.

The systems were first equilibrated at 293 K for 50 ps using Desmond (67), and production simulations were performed at 293 K in the NPT ensemble (68–70) on Anton (71).

Calculation of the Theoretical SAXS Profiles.

Two hundred frames were randomly picked from each of the Mg–C, K–C, and K–E ensembles and converted to individual PDB files. The FoXS program (75) was used to calculate the SAXS profiles of these three model ensembles. The resulting theoretical scattering curves were then fitted to the experimental scattering curves of the Mg(+) apo or bound SAM-I aptamer retrieved from the BIOISIS database (www.bioisis.net). The fit between the theoretical and experimental scattering curves was evaluated with the χ value as defined by

$$\chi =\sqrt{\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(\frac{I_{exp}\left(q_i\right)-c{I}_{model}\left(q_i\right)}{{\sigma }_{I_{exp}}\left(q_i\right)}\right)}^2}},$$

where I_exp(q_i) and I_model(q_i) are the experimental and modeled SAXS intensities measured at wavevector q_i, respectively, c is the scaling factor to be fitted, and ${\sigma }_{I_{exp}}\left(q_i\right)$ is the measured error in I_exp(q_i).