Auxetic metamaterials from disordered networks

Significance

Recent work indicates that selective pruning of disordered networks of nodes connected by bonds can generate materials with nontrivial mechanical properties, including auxetic networks having a negative Poisson’s ratio $\nu$. Until now, auxetic networks created based on this strategy have not been successfully realized in experiment. Here a model that includes angle-bending forces and the experimental boundary conditions is introduced for pruning-based design of auxetic materials. By pruning the appropriate bonds, $\nu$ can be tuned to values approaching the lower mechanical limit of −1, and the corresponding laboratory networks exhibit good agreement with model predictions. Optimization algorithms are then used to show that highly auxetic materials can be engineered from inhomogeneous bonds and nodes that exhibit distinct mechanical characteristics.

Abstract

Recent theoretical work suggests that systematic pruning of disordered networks consisting of nodes connected by springs can lead to materials that exhibit a host of unusual mechanical properties. In particular, global properties such as Poisson’s ratio or local responses related to deformation can be precisely altered. Tunable mechanical responses would be useful in areas ranging from impact mitigation to robotics and, more generally, for creation of metamaterials with engineered properties. However, experimental attempts to create auxetic materials based on pruning-based theoretical ideas have not been successful. Here we introduce a more realistic model of the networks, which incorporates angle-bending forces and the appropriate experimental boundary conditions. A sequential pruning strategy of select bonds in this model is then devised and implemented that enables engineering of specific mechanical behaviors upon deformation, both in the linear and in the nonlinear regimes. In particular, it is shown that Poisson’s ratio can be tuned to arbitrary values. The model and concepts discussed here are validated by preparing physical realizations of the networks designed in this manner, which are produced by laser cutting 2D sheets and are found to behave as predicted. Furthermore, by relying on optimization algorithms, we exploit the networks’ susceptibility to tuning to design networks that possess a distribution of stiffer and more compliant bonds and whose auxetic behavior is even greater than that of homogeneous networks. Taken together, the findings reported here serve to establish that pruned networks represent a promising platform for the creation of unique mechanical metamaterials.

When one stretches a material along one axis, intuition suggests that the material will contract in the orthogonal lateral directions. For most natural and synthetic materials, this intuition is confirmed by experiment. This behavior is quantified by Poisson’s ratio, $\nu$, which for a deformed material is defined as the negative ratio of the material’s lateral strain to its axial strain. In linear elastic theory for an isotropic sample, Poisson’s ratio is a monotonic function of the ratio of the material’s shear modulus, $G$, to its bulk modulus, $B$. In two dimensions $\nu \to 1$ as $G/B\to 0$. In this limit, the material is “incompressible,” meaning that its volume does not change during this axial compression. In the limit $G/B\to \mathrm{\infty }$, $\nu \to -1$. In the range where $\nu$ is negative, materials become wider as they are stretched and thinner as they are compressed. Such materials, termed “auxetics,” show promise in applications that require structural elements (1–3), impact absorbers (4, 5), filters (6, 7), fabrics (8, 9), or other tailor-made mechanical responses. Many auxetic materials are metamaterials or materials constructed from building blocks with designed functionality. Metamaterials represent a growing area of research in soft matter physics (10).

Auxetic materials have been formed through a variety of preparation protocols. Under special processing conditions, polymer foams and fibers, for example, can exhibit negative Poisson’s ratios (4, 11–14). Auxetic foams, in particular, can be formed through a process of heating and sintering fine particles of ultrahigh molecular weight polyethylene (11, 15), leading to structures of nodes connected by thin fibrils which collapse isotropically when compressed. Such structures are termed “reentrant” and are a common motif in auxetic materials (11, 16). When compressed uniaxially, these nodes and fibrils undergo complex rearrangements that give rise to their auxetic behavior. As materials approach the lower limit of Poisson’s ratio, their hardness, or resistance to a small indentation, is predicted to increase rapidly (17). This prediction is confirmed in the case of ultrahigh molecular weight polyethylene, where the hardness of the auxetic material far exceeds that of a nonauxetic but otherwise equivalent foam (4).

The node and fibril structures common in auxetic polymer foams can be thought of as networks consisting of nodes connected by bonds. A central, common feature of past efforts to design auxetic materials in both theory and experiment, however, has been a reliance on regular, ordered lattices. Such lattices include the double-arrowhead structure (8, 18), star honeycomb structures (19), reentrant honeycombs (20, 21), and others (22). Building on recent theoretical arguments (23–25), in this work we focus on disordered, random networks.

In the linear regime, the bulk modulus, $B$, or the shear modulus, $G$, of a network is proportional to the sum of the potential energies that are stored in each bond when the network is compressed or sheared. The decrease in $B$ or $G$ when the $i\text{th}$ bond is removed is denoted $\mathrm{\Delta }{B}_i$ or $\mathrm{\Delta }{G}_i$, respectively. In a simple crystalline network, every bond responds in nearly the same manner to a global deformation. In contrast, in amorphous networks the response of individual bonds to a global deformation can span many orders of magnitude (23, 25).

Furthermore, there is little correlation between the values of $\mathrm{\Delta }{B}_i$ and $\mathrm{\Delta }{G}_i$ of a bond, $i$ (25). This suggests that, by selective removal or “pruning” of bonds with large or small values of $\mathrm{\Delta }{G}_i$ or $\mathrm{\Delta }{B}_i$, the ratio $G/B$ can be manipulated to reach a desired value; this would lead to disordered, “amorphous” materials with intriguing mechanical properties. Recent work has shown that similar pruning strategies could be used to design allosteric behavior into a network (where a deformation at a local source can produce a desired response at a distant target site). This behavior was demonstrated in experiments (26). Creating auxetic materials, however, is more challenging and success in creating experimental prototypes has been elusive. More specifically, simple models were used to design pruned networks with negative Poisson’s ratio but, when prepared in the laboratory, they failed to exhibit auxetic behavior. This state of affairs has led to the question of whether pruning-based approaches for design of auxetic materials are fundamentally flawed or whether it is indeed possible to engineer truly auxetic laboratory materials by relying on more sophisticated models.

Here we address that question by introducing a mechanical model of disordered networks that incorporates the effects of angle bending in a unique way. The model is minimally complex, and it is parameterized by comparison with experimental data for simple, random disordered networks. By adopting a pruning strategy that identifies and removes select bonds from these networks, it is shown that it is possible to reach Poisson’s ratios as low as $\nu =-0.8$. The 2D pruned networks designed in this manner are then prepared in the laboratory from rubber sheets that have been laser cut according to the simulated models. They are found to behave as predicted. Structural analysis shows that highly auxetic networks are marked by an abundance of concave polygons. When networks are compressed uniaxially, these concave polygons shrink in all dimensions. Collectively, the local deformations of these concave polygons yield global auxetic behavior. These structures also give rise to a sublinear stress–strain behavior, which is an important characteristic of impact-mitigating materials. We also investigate the effect of angle-bending stiffness, a parameter which plays a dominant role in ensuring agreement between simulation and experiment. This parameter also dramatically affects a material’s ability to be made auxetic, both in simulation and in experiment. Networks composed of bonds with angle-bending forces that are orders of magnitude weaker than those relevant to our experimental realizations can easily be tuned to show $\nu =-1$, while networks with much stiffer angle-bending forces cannot be tuned at all. Such changes are explained by the distributions and correlations of $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$. We conclude our discussion by designing highly auxetic materials through a materials optimization strategy. Specifically, by selectively manipulating the mechanical characteristics of a few select bonds, it is shown that the value of Poisson’s ratio can be further reduced from $\nu =-0.8$ to $-0.9$. The improved networks designed in this manner can then be successfully produced in the laboratory.

Models

Simulation Model.

To have well-defined starting configurations, we base our networks on jammed packings of frictionless spheres at zero temperature (27). We note, however, that the results are not necessarily confined to this choice of starting conditions. Spherical particles are initially placed at random positions within the simulation area. Particles $i$ and $j$ experience harmonic repulsions

$$V(r_{ij})=\frac{ϵ}{2}{(1-\frac{r_{ij}}{{\sigma }_{ij}})}^2\mathrm{\Theta }\left(1-\frac{r_{ij}}{{\sigma }_{ij}}\right),$$ [1]

where $r_{ij}$ is the center-to-center distance, ${\sigma }_{ij}$ is the sum of the radii of particles $i$ and $j$, and $\mathrm{\Theta }(x)$ is the Heaviside step function. $ϵ=1$ sets the energy scale. The energy is minimized to produce zero-temperature, mechanically stable configurations. Particles are randomly assigned one of four evenly spaced radii (namely 0.6, 0.74, 0.87, and 1.0), leading to an amorphous packing when compressed isotropically. In all calculations, the contacts of particles which are in contact with fewer than three adjacent particles are not counted toward the total $Z$, as these would not contribute to the modulus of a jammed system. Such particles are removed before bonds are formed.

Two particles are considered to be in contact when $r_{ij}<{\sigma }_{ij}$. The average number of contacts or bonds per particle, $Z$, plays a central role in a host of network characteristics (27–29). To set the value of $Z$, we create harmonic repulsive walls at the simulation box edges, whose positions are adjusted and the configuration is relaxed until the required number of particle contacts is achieved. Unstretched bonds of length $r_{ij}^0$ are then placed between the centers of pairs of contacting particles $i$ and $j$ and the soft-sphere potential is removed. The energy due to bond compression is thus

$$V_c(r_{ij})=\frac{1}{2r_{ij}^0}{(r_{ij}-r_{ij}^0)}^2.$$ [2]

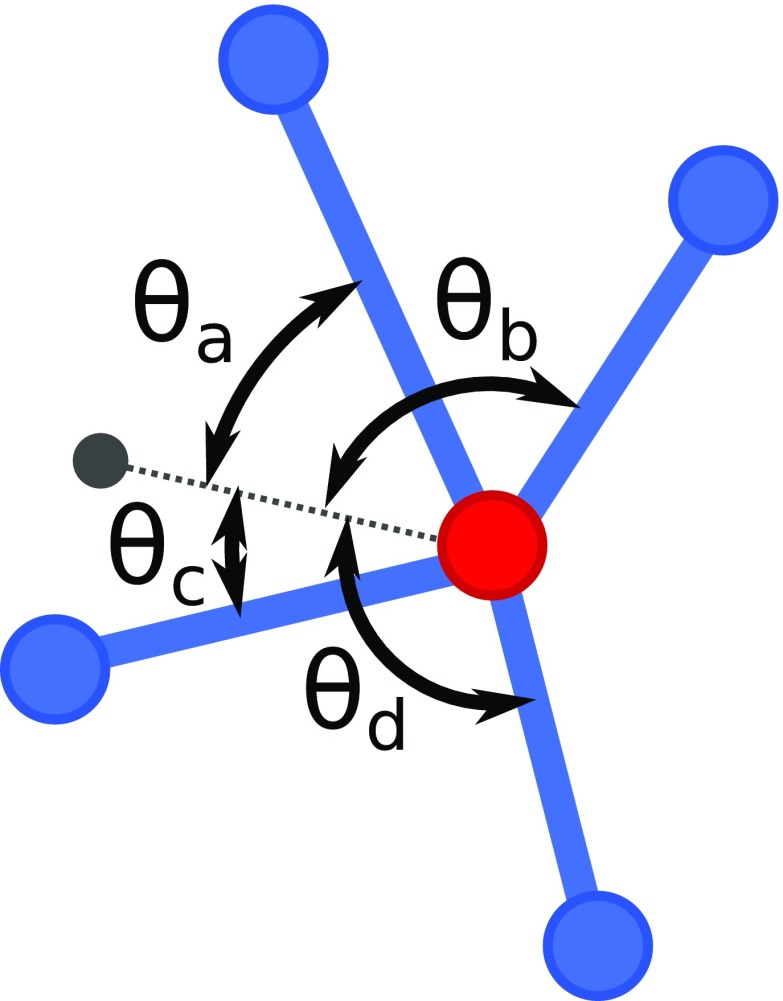
To include angle-bending constraints, we introduce a unit vector, ${\overrightarrow{s}}_i$, at each node $i$ of the network, as shown in Fig. 1. A bond connecting nodes $i$ and $j$ makes an angle ${\theta }_{ji{\overrightarrow{s}}_i}$ with the vector ${\overrightarrow{s}}_i$. When the system is relaxed, this angle adopts its equilibrium value, ${\theta }_{ji{\overrightarrow{s}}_i}^0$. The energy cost to change an angle is quadratic,

$$V_b({\theta }_{ji{\overrightarrow{s}}_i})=\frac{k_{ang}}{2}{({\theta }_{ji{\overrightarrow{s}}_i}-{\theta }_{ji{\overrightarrow{s}}_i}^0)}^2,$$ [3]

where $k_{ang}$ sets the energy scale for the angle-bending potential. During energy minimization, to obtain the ground state where the system is in mechanical equilibrium, the direction of $\overrightarrow{s}$ on each site is allowed to vary to minimize the total angular energy of a node. The coefficient $k_{ang}$ is determined by comparing the response of model networks to those prepared in experiments and depends on the material and shape of the bonds, as described in Methods.

Fig. 1.

Schematic describing how angular restraints are applied for the node shown in red. A director, shown in gray, is attached to each node with a harmonic bond potential. Harmonic angles potentials are added between each pair of bonded nodes and the director, as indicated by the angles ${\theta }_{a-d}$. The director is positioned such that ${\theta }_{a-d}$ are as far from 0° and 180° as possible. This scheme is applied at each node.

The total energy of a network under stress is the sum of two terms: a compressive component given by Eq. 2 and a bending component, given by Eq. 3. Note that the compressive strength is scaled by $1/r_{ij}^0$ as would occur in a physical mechanical strut of constant thickness.

Fig. 2 shows representative realizations of 2D disordered networks consisting of nodes connected by bonds, before and after pruning.

Fig. 2.

Examples of typical 500-node networks before and after pruning with $Z_0=4.0,5.2,5.9$. Top row shows unpruned networks, while Bottom row shows networks which have been pruned to $Z=3.0$. Unpruned networks show decreasing $\nu$ as $Z_0$ increases while pruned networks show a minimum $\nu$ at $Z_0=5.2$. This minimum $\nu$ at $Z_0=5.2$ corresponds to a high fraction of reentrant nodes which can collapse inward as the system is compressed.

In two dimensions, there are two independent shear moduli—one associated with simple shear and one with pure shear. The modulus associated with simple shear influences the value of $\nu$ that is measured when the material is deformed by pulling or pushing from opposite corners. The modulus associated with pure shear relates to the value of $\nu$ measured when the material is uniaxially compressed or expanded in $x$ or $y$, as shown in SI Appendix, Fig. S5. In this study we focus primarily on algorithms that influence only the modulus associated with pure shear since this can be more easily measured in our experiments. However, we also show that isotropic auxetic networks can be created using similar algorithms which consider bond contributions to both pure and simple shear. Such materials are auxetic with respect to any uniaxial deformation. $G$ and $B$ are measured as described in Methods.

Results

Bond Response Distributions.

In an amorphous network the distributions of $\mathrm{\Delta }{B}_i$ and $\mathrm{\Delta }{G}_i$, $P(\mathrm{\Delta }{B}_i)$ and $P(\mathrm{\Delta }{G}_i)$ can span many orders of magnitude. That is, when some bonds are removed, $G$ or $B$ may decrease significantly, while when others are removed, there may be only a negligible decrease. Our pruning procedure targets bonds that contribute little to the shear modulus but contribute strongly to the bulk modulus. It is therefore important that $P(\mathrm{\Delta }{B}_i)$ and $P(\mathrm{\Delta }{G}_i)$ be broad and extend to small values (23, 25).

A second crucial condition for successful pruning is that $\mathrm{\Delta }{B}_i$ and $\mathrm{\Delta }{G}_i$ be uncorrelated. Based on these two features, one can selectively remove bonds from a disordered network to drive $B$, $G$, and thus $\nu$ to a desired target value (23, 24).

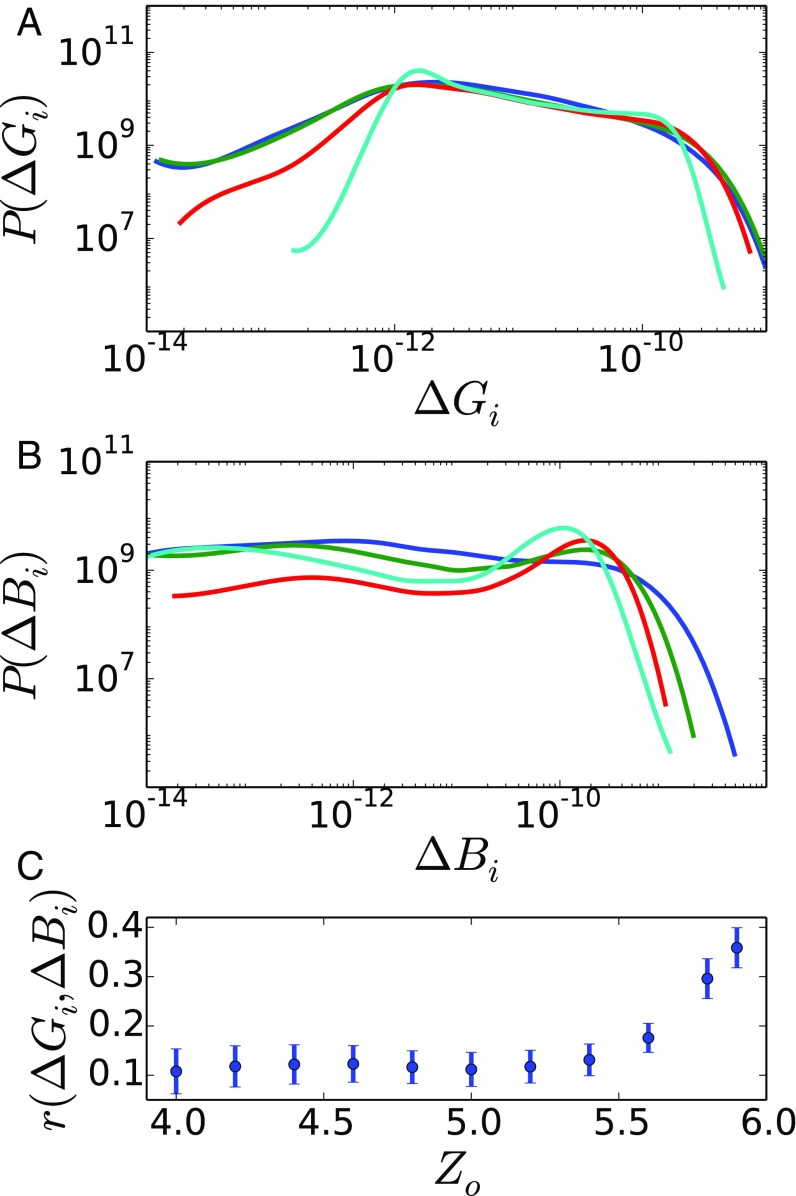
Fig. 3 A and B shows the probability distributions $P(\mathrm{\Delta }{B}_i)$ and $P(\mathrm{\Delta }{G}_i)$ for unpruned networks. Results are shown for networks with $Z_0$ ($Z$ of the network before pruning) between $4.0$ and $5.9$, with $k_{ang}=0.01$. The value of $k_{ang}$ is set as the value which best reproduces the deformation observed in experiment, as described in Methods. As $Z_0$ increases, both $P(\mathrm{\Delta }{B}_i)$ and $P(\mathrm{\Delta }{G}_i)$ become narrower. This suggests that networks with lower coordination numbers are more amenable to pruning. A peak in $P(\mathrm{\Delta }{B}_i)$ becomes apparent for $Z_0=5.9$.

Fig. 3.

Probability distributions and correlations of $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$ for unpruned 500-node networks with different $Z_0$. A shows probability distributions of $\mathrm{\Delta }{G}_i$, while B shows those for $\mathrm{\Delta }{B}_i$. Strains for both deformations are ${ϵ}_y=1\times {10}^{-4}$. Datasets as ($Z$, color) are (4.0, blue), (4.8, green), (5.2, red), and (5.9, cyan). Each dataset is taken from $100$ independent $500$-node networks. The bond bending strength is $k_{ang}=0.01$, a value which is experimentally realizable. As the coordination number increases, distributions narrow significantly, reducing the networks’ propensity to be pruned. C shows the correlation between $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$ for networks over a range of initial $Z$ values. SDs of $r$ values across $100$ independent configurations are shown.

To facilitate effective pruning, bond response distributions must be not only broad, but also uncorrelated. Fig. 3C shows the Pearson correlation coefficient for $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$ across a range of $Z_0$ values. While distributions are significantly uncorrelated between $Z_0=4.0$ and $5.2$, the level of correlation increases thereafter. As we will see, networks pruned from $Z_0=5.2$ lead to the lowest value of $\nu$.

Pruning.

For the iterative pruning strategy adopted here, at each iteration the lowest $\mathrm{\Delta }{G}_i$ bond is removed. Given the low correlation between $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$, pruning the lowest $\mathrm{\Delta }{G}_i$ bonds tends to increase $G/B$ and decrease $\nu$. At each iteration, $\mathrm{\Delta }G$ for a bond is measured by performing a trial removal of that bond and by measuring the resulting shear modulus, thereby resulting in $n_{bond}$ measurements of $G$. Each measurement of $G$ requires on the order of seconds or minutes of central processing unit (CPU) time, depending on network size. Creating a large auxetic network can therefore be computationally demanding. The calculation of $\mathrm{\Delta }{G}_i$ can be parallelized with one core per $\mathrm{\Delta }{G}_i$ measurement. We use the parallel workflow management software Swift/T to parallelize this process across several hundred CPU cores, thereby accelerating network creation (30).

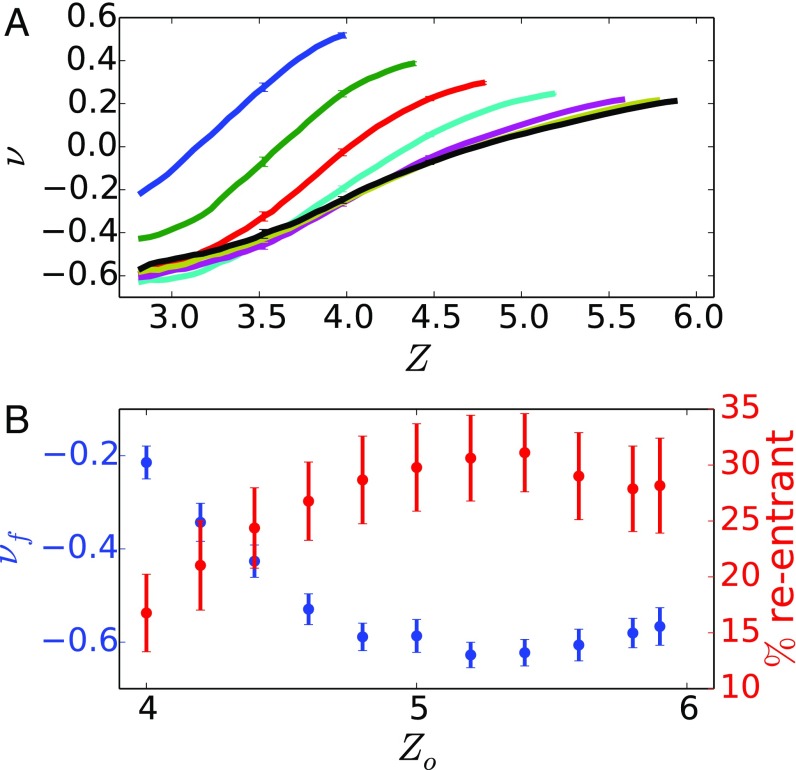
Fig. 4 shows Poisson’s ratios, $\nu$, for networks having different values of $Z_0$. Each dataset represents an average of $50$ independent pruned networks of $500$ nodes each.

Fig. 4.

(A and B) Poisson’s ratios resulting from pruning 500-node networks with different values of $Z_0$ shown in A and with resulting structural and mechanical properties shown in B. Data are taken from $50$ independent $500$-node networks. In A, 95% confidence intervals are shown. To prune, we remove the lowest $\mathrm{\Delta }G$ bond at each iteration. Networks are pruned until $Z=2.8$, at which point they become so sparse that $\nu$ fluctuates wildly with further pruning. In B, the blue dataset shows Poisson’s ratio reached at $Z=3.0$ with respect to $Z_0$, with $95\%$ confidence intervals shown. A minimum $\nu$ is observed at $Z_0=5.2$. Plotted in red is the fraction of nodes which are classified as reentrant. The data show that the most auxetic networks show the greatest degree of reentrant behavior, suggesting a structural origin for $\nu$.

Poisson’s ratio is determined by introducing a small strain of magnitude ${ϵ}_y=1\times {10}^{-4}$ in the $y$ dimension of the network, allowing the system to relax to an average force tolerance of $1\times {10}^{-13}$, and then measuring the resulting lateral deformation. Note that while simple bead-spring networks (those ignoring angle bending) lose rigidity below $Z=4$, the angular restraints in the model introduced here lead to rigid networks and to much lower values of $Z$. As shown in SI Appendix, Fig. S2, ${ϵ}_y=1\times {10}^{-4}$ is well within the linear regime.

Several interesting features are apparent in the pruning progression shown in Fig. 4. First, even before there is any pruning, Poisson’s ratio of the networks decreases from $0.51$ at $Z_0=4.0$ to $0.21$ at $Z_0=5.9$, revealing a wide variation of $\mathrm{\Delta }\nu =0.3$. A decrease in $\nu$ with increasing coordination has been observed previously in network systems (31). Second, the initial slope of the Poisson’s ratio curve as a function of pruning decreases from $d\nu /dZ=0.47$ to $0.14$ between $Z_0=4.0$ and $Z_0=5.9$ (as calculated by the average slope over the first $\mathrm{\Delta }Z=0.1$ pruning). The smaller value of $d\nu /dZ$ at higher $Z_0$ is consistent with the narrower distribution functions and higher correlations observed, as shown in Fig. 3. However, a higher $Z_0$ also implies that there are simply more bonds available for pruning. These factors conspire to produce the lowest pruned networks when $Z_0=5.2$. This also corresponds to the highest $Z_0$ before the correlation of $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$ begins to increase, as seen in Fig. 3C. Networks with $Z_0=5.2$ show a minimum average of $\nu =-0.62$. The lowest $\nu$ value achieved for an individual network, however, is $\nu =-0.79$.

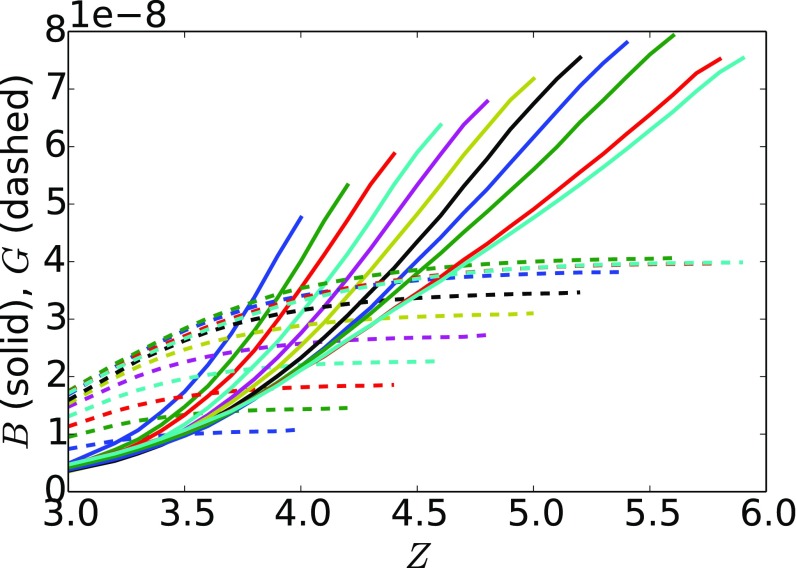
To explore further how $\nu$ changes with pruning, we examine $G$ and $B$ of networks as they are pruned, as shown in Fig. 5. In two dimensions, linear elastic theory states $\nu =(1-G/B)/(1+G/B)$. By pruning the lowest $\mathrm{\Delta }G$ bonds, our aim is to maintain a high value of $G$ while reducing $B$. During pruning, initially $B$ drops and $G$ remains nearly constant, resulting in the steepening slope of $\nu$ seen in Fig. 4. At some value of $Z$ along the pruning process, $G$ begins to decrease more rapidly, and the slope of $\nu$ decreases in magnitude until $\nu$ reaches its minimum. This accelerated decrease of $G$ can be attributed to the fact that few low-$\mathrm{\Delta }{G}_i$ bonds remain once pruning has progressed sufficiently.

Fig. 5.

Bulk and shear moduli of networks as low $\mathrm{\Delta }G$ bonds are pruned. Initially, the bulk moduli decrease while the shear moduli remain constant, resulting in the increasing magnitude of the slope of $\nu$ observed in Fig. 4. After significant pruning, $G$ begins to decrease. Near $Z=3.0$, $G/B$ plateaus and $\nu$ reaches its minimum.

Structural Features.

Fully pruned networks ($Z=3.0$) show a range of $\nu$ values that depend on their corresponding $Z_0$, suggesting that underlying structural differences exist between these pruned networks. Fig. 2 shows representative networks with $Z_0=4.0,5.2,5.9$ before and after pruning to $Z=3.0$. One can appreciate that these structures are in fact quite different from each other, despite having similar numbers of nodes and bonds. To quantify these structural differences, we calculate the percentage of nodes which are reentrant in pruned networks, as shown in Fig. 4B. Here, a reentrant node is defined as one having an angle between adjacent bonds that is greater than 180°. As can be seen in Fig. 2, reentrant nodes manifest as concave angles in polygons within the network. Such polygons tend to collapse inward at reentrant nodes when compressed. A sufficient number of such polygons could lead to globally auxetic behavior. As can be seen in Fig. 4B, more auxetic networks exhibit a higher percentage of reentrant nodes. This structural motif therefore provides a basis for design of amorphous or otherwise disordered networks that are auxetic and isotropic. In this calculation we did not classify nodes with only two bonds as reentrant, although we arrive at qualitatively the same conclusions if they are included.

Experimental Validation.

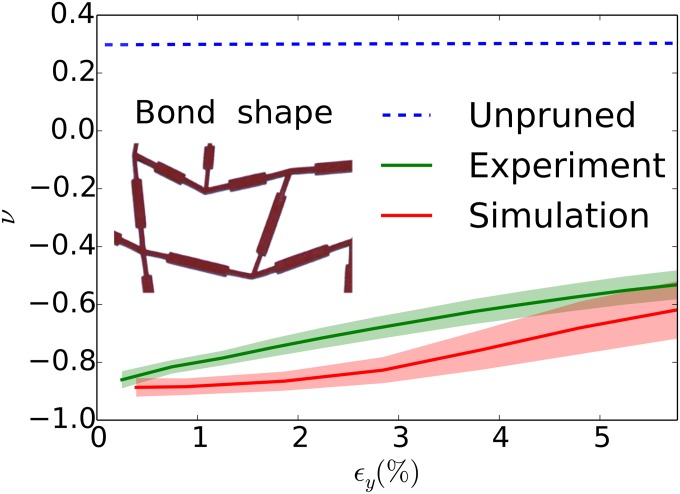
Experimental pruned networks are made of laser-cut sheets of rubber (26) as described in Methods. The strength of bond bending, $k_{ang}$ in simulation, is modified by controlling the thickness of the bonds at the point where they attach to the nodes as well as their aspect ratio as seen in Fig. 6, Inset. We focus on the bond shape shown in Fig. 6. The deformation of such networks can be described quantitatively by our model with the value $k_{ang}=9\times {10}^{-3}$, which we use for all networks composed of bonds of this shape. We uniaxially compress three independent networks with $Z_0=5.2$ pruned to $Z=3.0$ and measure $\nu$ in both simulation and experiment as shown in Fig. 6. At low strains, networks are strongly auxetic; however, $\nu$ increases monotonically with increasing strain.

Fig. 6.

Poisson’s ratios from simulation and experiment for pruned and unpruned networks. Shown in green and red is $\nu$ with uniaxial strain from three different networks pruned to $Z=3.0$ from $Z_0=5.2$. The solid lines represent the average $\nu$ for the three configurations and the shaded areas represent standard deviations. The dashed blue line shows $\nu$ for unpruned networks in simulation at low strain. A value of $k_{ang}=9\times {10}^{-3}$ in simulation is fitted to match this experimental bond shape (Inset). This $k_{ang}$ fits well for all networks which use this bond shape. A section of an experimental network is shown as an example of the individual bond shape used.

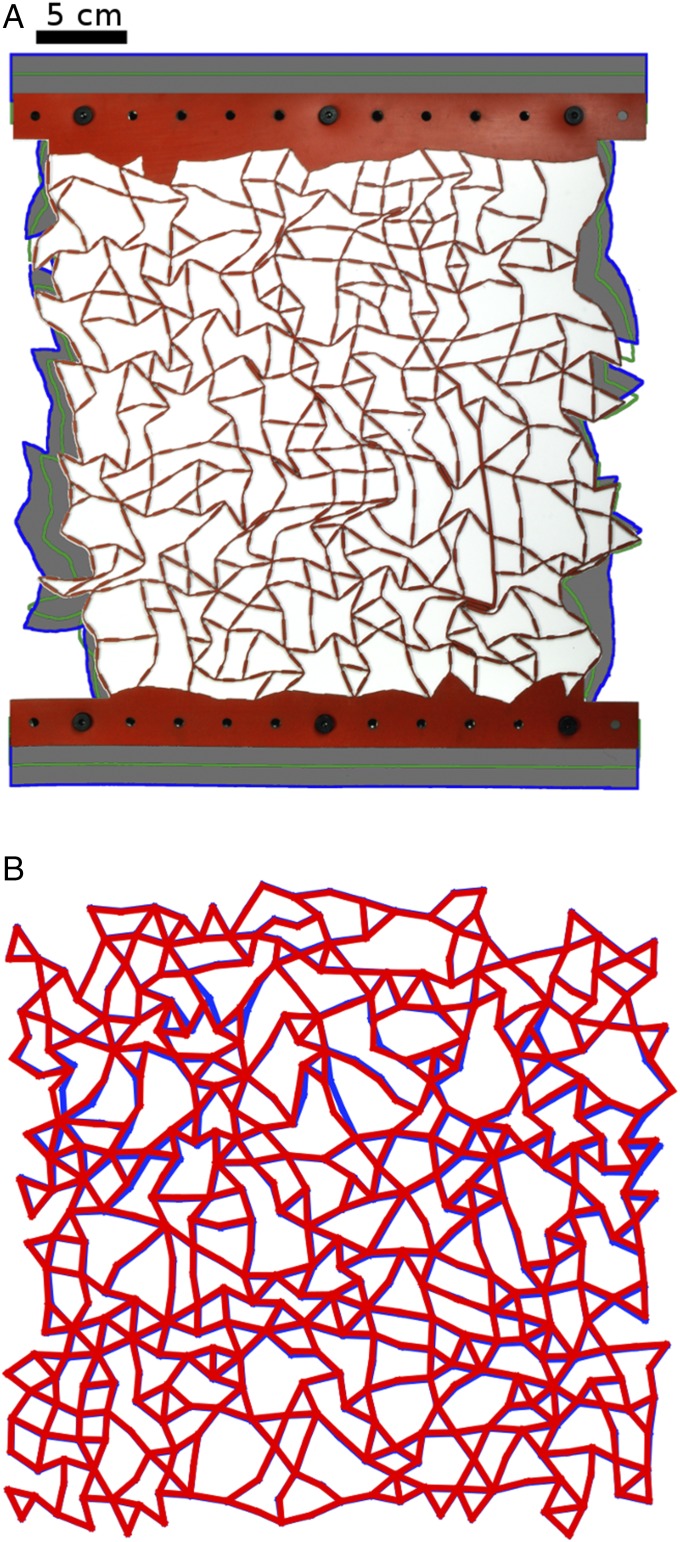
We now examine the response of a particular network formed with $k_{ang}=9\times {10}^{-3}$. Fig. 7A shows a network compressed with ${ϵ}_y=0.09$. The shape of the uncompressed network is shown in gray, serving to demonstrate its auxetic response. Fig. 7B directly compares experimental and simulated configurations at ${ϵ}_y=2\%$. The experimental configuration is shown in red, and the simulated configuration is shown in blue. At this strain, experiment and simulation are in good agreement. Note that the network shown in Fig. 7B is isotropic and will be auxetic with respect to any strain. By iteratively pruning the minimum $\mathrm{\Delta }{G}_{pure}+\mathrm{\Delta }{G}_{simple}$ bond, we achieve $\nu =-0.25$ for this network. For higher strains, our simulations are no longer able to accurately predict node positions, as they do not describe the behavior of physical bonds and nodes when they collide. However, despite this shortcoming, the trends of $\nu$ with ${ϵ}_y$ are captured well by our model, as shown in Fig. 6.

Fig. 7.

A compressed 500-node experimental network with comparison with simulation. (A) A compressed experimental network at a strain of ${ϵ}_y=9\%$. The gray shaded region indicates the shape of the uncompressed network, and the green outline represents the shape at ${ϵ}_y=5\%$. (B) Comparison of an experimental configuration with that predicted from simulation at ${ϵ}_y=2\%$. Note that this network is isotropic and will be auxetic with respect to any uniaxial strain, which is distinct from the other networks in this work. It shows $\nu =-0.25$ for deformations up to ${ϵ}_y=4\%$. In red is shown a rendering of the experimental configuration and in blue is shown the simulated configuration at the same strain.

Angle-Bending Stiffness.

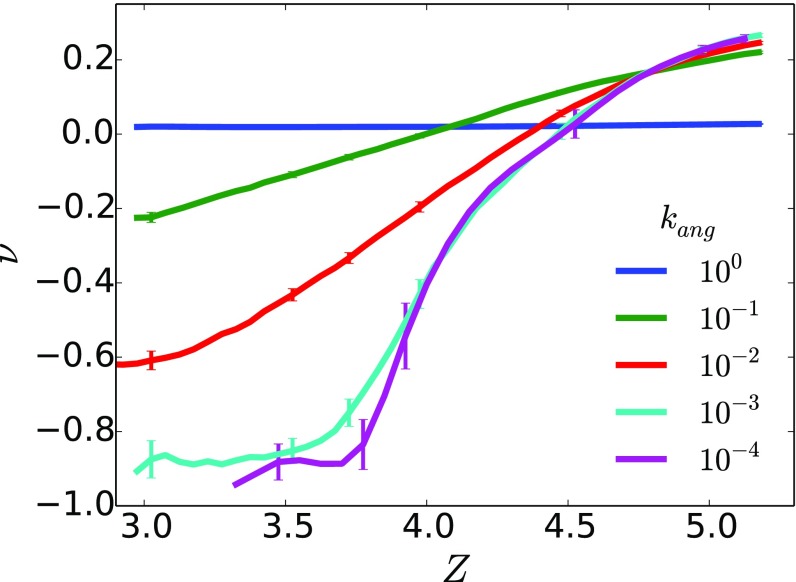
We have focused only on values of $k_{ang}$ within a relatively narrow range, but one could conceive of specially designed experimental realizations which would span a much wider range. This is of interest because networks with greater bond stiffness can withstand greater strains before failing. As such, we turn our attention to the effect that a wide range of bond-bending stiffness has on $\nu$. We study networks with $Z_0=5.2$, which yielded the lowest value of $\nu$ for $k_{ang}=0.01$. Fig. 8 shows $\nu$ resulting from low-$\mathrm{\Delta }G$ pruning of $500$-node networks with values of $k_{ang}$ that span five orders of magnitude, from ${10}^{-4}$ to ${10}^0$. Consistent with previous work (23), $\nu \to -1$ as $k_{ang}\to 0$ in fully pruned networks. Consistent with these results, we find that as $k_{ang}$ becomes smaller, bond response distributions become wider and are more easily modified by pruning, as shown in SI Appendix, Fig. S1.

Fig. 8.

Poisson’s ratios resulting from pruning $500$-node networks with $Z_0=5.2$ and $k_{ang}$ values which range from ${10}^{-4}$ to ${10}^0$. With larger $k_{ang}$, pruning becomes less effective due to narrower ranges of $\mathrm{\Delta }{G}_i$ and $\mathrm{\Delta }{B}_i$ and increased correlations between the two quantities. In the lower limit, $\nu$ approaches $-1.0$ as predicted in previous work (23).

Physical Insights from Model Improvement.

Three features distinguish the model used in this work from that of previous attempts: (i) the use of finite rather than periodic simulations, (ii) the use of fixed boundary conditions as used in experiment, and (iii) most importantly the addition of an angle-bending potential. To demonstrate the importance of the angle-bending term, we study a network which has been pruned to $\nu =-0.96$ at $Z=3.9$ with an extremely low angle-bending stiffness of $k_{ang}={10}^{-4}$. Increasing $k_{ang}$ to $k_{ang}={10}^{-2}$ increases Poisson’s ratio to $\nu =-0.36$. Increasing $k_{ang}$ past this experimentally determined value to $k_{ang}=1$ increases $\nu$ to $0.0$, as shown in SI Appendix, Fig. S8. By picking a value of $k_{ang}$ which does not correspond to the experimental realization, predictions from the simulation would be inaccurate.

Our results suggest that weaker angle-bending forces allow for more dramatic deformations of the concave polygons present in these networks. Assigning a larger $k_{ang}$ penalizes these deformations, which increases $\nu$. Therefore, to create auxetic experimental realization of networks, care should be taken to minimize the effect of angle-bending forces.

Stress–Strain Behavior.

For a variety of impact-mitigation applications, it is of interest to develop materials that display a relatively constant stress–strain behavior. Such materials can absorb more energy while maintaining lower applied forces and thus reduce the possibility of damage. As shown in SI Appendix, Fig. S3, pruned networks display nearly constant stress past $3\%$ strain. At such strains, linear response calculations are no longer accurate, as shown in SI Appendix, Fig. S2. We find that the linear response framework applies well until roughly $1\%$ strain.

Bond Strength Optimization.

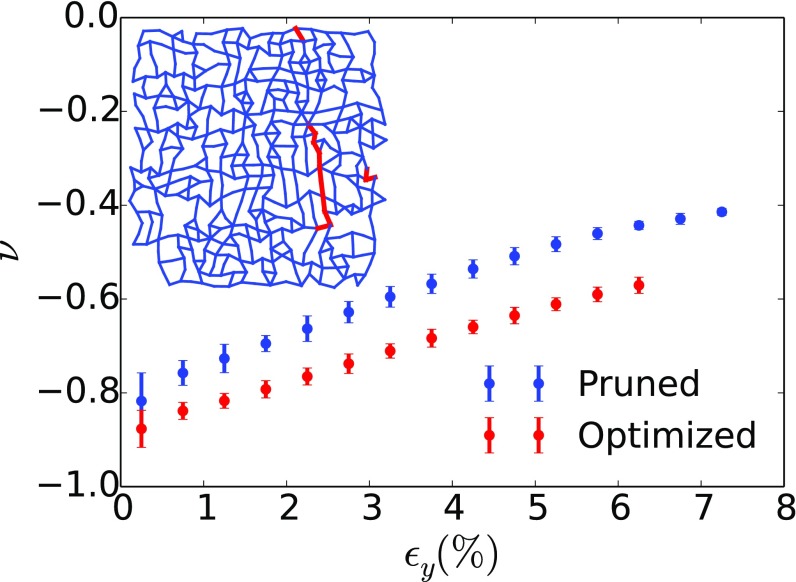
Up to this point, we have relied on homogeneous materials, with identical bonds, for all calculations and experiments. In what follows, we modify the strength of individual bonds as a means for decreasing $\nu$ in networks composed of bonds with different stiffnesses. This process can be mimicked in experiment by modifying the thickness or material of a given bond. We implement a simple optimization algorithm that iteratively strengthens by 10% the bond leading to the greatest decrease in $\nu$. Both the compressive modulus and the bending modulus of a particular bond are increased when a bond is strengthened. We examine a particular network with $k_{ang}={10}^{-2}$ and $\nu =-0.79$. By successively strengthening individual bonds in this network, we further decrease $\nu$ from $-0.79$ to $-0.91$ in simulation. Interestingly, after $430$ iterations with $649$ total bonds in the network (where one bond in strengthened by 10% at each iteration), $94\%$ of the bonds remained untouched, while a select few, $1.8\%$, are strengthened to more than five times their original strength, leading to an essentially bimodal distribution of bond strengths. These strengthened bonds are almost all connected as shown in Fig. 9, Inset.

Fig. 9.

Experimentally measured $\nu$ for an ordinary pruned network and an otherwise identical network in which several of the bonds have been strengthened. Error bars show $2.5\sigma$. The bonds which were strengthened were chosen in simulation to reduce $\nu$. In simulation, the networks with regular and strengthened bonds were predicted to show $\nu =0.79,0.91$, respectively, at small strains. Inset network configuration shows, in red, bonds which were strengthened in experiment and, in blue, unstrengthened bonds.

To validate the predictions of our simulations, we also prepared an experimental realization of this optimized network. For simplicity, bonds strengthened by a factor of 5 or greater were made thicker, and others were left unchanged. The corresponding experimental values of $\nu$ are shown in Fig. 9, showing a decrease in $\nu$ of $0.059$ at ${ϵ}_y=0.25\%$ and a decrease of $0.11$ at ${ϵ}_y=2.75\%$, in good agreement with predictions. Importantly, these optimized materials with a few significantly stronger bonds lend themselves to additive manufacturing. In such realizations, some bonds could be constructed of highly rigid materials, while the remainder would be more pliable, and more advanced optimization algorithms could readily be applied to this problem.

Conclusion

In summary, we have established that it is possible to create designer auxetic materials from amorphous networks. The pruning strategy that we have proposed does not depend on the initial configuration but rather relies on measuring aspects of local response to a globally applied deformation. As such, it may apply more generally to networks based on a variety of initial preparation protocols and not just those based on jamming. The models and concepts introduced in this work have been validated through a concerted program of design, computation, and laboratory experimentation. Amorphous networks are shown to offer a number of control parameters that can be tuned to achieve particular mechanical responses. It is found, for example, that a network’s propensity to be made auxetic depends on both the network’s original coordination number and the relative resistance to angle bending. More pliable networks yield the lowest Poisson’s ratios due to their wide bond response distribution and their low response correlation. Stiffer networks are less amenable to pruning and show only limited changes of their Poisson’s ratio through pruning. By relying on bond-strength optimization schemes, however, it is possible to alter Poisson’s ratio of networks with stiff bonds considerably, thereby providing a strategy to alter not only how auxetic a material is, but also its intrinsic stiffness. While the results presented here have been limited to 2D networks, the concepts and strategies proposed should be equally applicable to three dimensions, where we can use 3D printing to realize our computer models. We therefore anticipate that these networks could be potentially useful for applications involving additive manufacturing. Using appropriately designed nanoparticles, it is also conceivable that one could form auxetic materials through a self-assembly process.

Methods

Simulation Methods.

Simulated networks are generated as described in Models. A harmonic wall coefficient of $2.0$ is used to compress particles. To measure $\nu$, ${ϵ}_y=1\times {10}^{-4}$ is applied and the transverse strain of nodes at the left and right edges of the network is measured. Bulk properties are measured by applying uniform compressions of $1\times {10}^{-4}$. Shear properties are measured with ${ϵ}_x=-1\times {10}^{-4}$ and ${ϵ}_y=1\times {10}^{-4}$ or $\gamma =1\times {10}^{-4}$, for pure and simple shear, respectively. The average force is relaxed to $1\times {10}^{-13}$ for all measurements. To mimic experiment, particles along the top and bottom edges of networks are restrained in the $x$ dimension. The coefficient to describe bond bending, $k_{ang}$, is fitted by determining the value of $k_{ang}$ which minimized mean-square distance between nodes in uniaxially strained experimental and simulated networks at ${ϵ}_y=3\%$. The same $k_{ang}$ value is used to describe each class of experimental bonds.

Experimental Methods.

Experimental networks are constructed of laser-cut silicone rubber sheets with a Shore value of $A70$ and a thickness of $1.5$ mm as described in previous work (26). We can vary the relative resistance to angle bending (which is quantified by $k_{ang}$ in our simulation model), by narrowing or widening a section of the bond near the node (Fig. 6). To facilitate measurement, nodes at the top and bottom of the network are fused into a solid rubber piece, as shown in Fig. 7A. Poisson’s ratio is determined by applying a uniaxial compression in the $y$ direction and measuring the resulting lateral strain.