Statistical tests and identifiability conditions for pooling and analyzing multisite datasets

Significance

How can one efficiently combine experimental and observational predictive data from different laboratories into a single predictive model when the laboratories have differently calibrated measuring instruments and the study populations have different demographic distributions? When both differences exist in the data, important quantities may not be identifiable, but we provide sufficient conditions for when they are and practical plans to account for the differences, including subsampling. The methods are applied to two Alzheimer’s disease studies, where measured cerebral spinal fluid and demographic data show differences, and we seek to identify associations with a response variable. We provide tools to add to the armamentarium of the scientific experimenter and data analyst for efficient combination of information from diverse sources.

Abstract

When sample sizes are small, the ability to identify weak (but scientifically interesting) associations between a set of predictors and a response may be enhanced by pooling existing datasets. However, variations in acquisition methods and the distribution of participants or observations between datasets, especially due to the distributional shifts in some predictors, may obfuscate real effects when datasets are combined. We present a rigorous statistical treatment of this problem and identify conditions where we can correct the distributional shift. We also provide an algorithm for the situation where the correction is identifiable. We analyze various properties of the framework for testing model fit, constructing confidence intervals, and evaluating consistency characteristics. Our technical development is motivated by Alzheimer’s disease (AD) studies, and we present empirical results showing that our framework enables harmonizing of protein biomarkers, even when the assays across sites differ. Our contribution may, in part, mitigate a bottleneck that researchers face in clinical research when pooling smaller sized datasets and may offer benefits when the subjects of interest are difficult to recruit or when resources prohibit large single-site studies.

Many studies that involve human subjects are constrained by the number of samples that can be obtained when the disease population of interest is small, when the measurement of interest is difficult to obtain, or when other logistic or financial constraints are present that prohibit large-scale studies (1, 2). For example, in Alzheimer’s disease (AD) research, cerebrospinal fluid (CSF) measurements from lumbar puncture (LP) may be limited by participant willingness to undergo LP and institutional capability to routinely perform the procedure in a research setting. The assays for amyloid beta 1–42 and tau (the hallmark features of AD pathology) are known to vary widely between assay product type and within a specific type of assay from differences in batch composition (3). Similarly, the expense of imaging examinations may prohibit large-scale investigations. While the sample sizes may be sufficient to evaluate the primary hypotheses, researchers may want to investigate secondary analyses focused on identifying subtle associations between specific predictors and the response variable (3, 4). Such secondary analyses may be underpowered for the given sample sizes. One possible solution is to identify and pool several similar datasets across multiple sites (5). One hopes that the larger sample sizes of the pooled dataset will enable investigating potentially interesting scientific questions that may not otherwise be possible with smaller single-site cohorts.

In practice, we find that direct pooling of already collected datasets in a post hoc manner across multiple sites can be problematic due to differences in the distributions of one or more measures (or features) (6). In fact, even when data acquisition is harmonized across sites, we may still need to deal with site-specific or method-specific effects on the measurements, such as the above noted example with CSF (7), before the analysis can proceed (8, 9). For example, as discussed above, in AD studies, CSF measurements (10) may not be easily pooled in the absence of gold standard reference materials that are common across assays (or sites) (3). Such issues also arise in combining cognitive measures or transferring analysis results or models from one potentially large-sized dataset to another. For example, cohort studies may administer different cognitive tests that assess the same underlying cognitive domain; therefore, thresholds used to categorize individuals into different disease status groups may not be easily transferred from one site to the other (5, 11). These issues are not restricted to biomedical studies, and variously manifest in machine learning and computer vision, where distinct datasets must be pooled (e.g., for training a statistical model). While the literature on addressing sample selection bias and compensating for population characteristics differences is sizable (12, 13), statistical frameworks for resolving distributional shift to facilitate pooled analysis, essential in various applications, are less developed in comparison.

Deriving scientific conclusions from a unified analysis spanning multiple individual datasets is often accomplished in practice via so-called meta-analysis approaches. Such an approach carefully collects research analyses/findings separately performed on the datasets and then aggregates individual analysis results through statistical models to come up with a final estimate of the parameters (14). However, various assumptions in meta-analysis schemes may not always hold in practice, and simple violations can lead to inaccurate scientific conclusions (15, 16). Alternatively, if access to the actual data from individual studies is available, some preprocessing to harmonize the data followed by statistical analysis of the pooled data may be preferable in many cases. The preprocessing often uses methods that compensate (or correct) for distributional shift to the extent possible. For example, ideas related to domain shift in refs. 17 and 18 and other results describe sophisticated models to improve prediction accuracy by correcting domain shift. What is less developed is a formal treatment explaining how confident we are that the shift across datasets has been successfully corrected (and consequently, the analysis can safely proceed), whether the correction can be improved if we were able to acquire more samples, what mathematical assumptions are needed, and whether the residual (say, after a correction step) is due to fewer than necessary samples or other violations of the underlying assumptions. The primary goal of this paper is to offer a formal treatment of these problems and derive the theoretical basis that can guide practical deployments.

In this paper, we build and extend on our preliminary results (19), and we present an in-depth theoretical study of distributional shift correction across datasets. That includes consistency properties, an identifiability condition, and a hypothesis test to check model accuracy using a discrepancy measure popular in the domain adaptation literature (17, 18). We also provide an analysis based on a subsampling procedure, showing how these ideas can be modified to deal with the practical situation where the covariates for different sites (or studies) are not exactly the same (e.g., age range of cohorts may vary)—toward facilitating rigorous analysis of pooled datasets. Briefly, we (i) give a precise condition to evaluate whether a distributional shift correction is identifiable; (ii) derive a subsampling procedure to separate distributional shift from other sources of variations, such as sample selection bias and population characteristics differences; (iii) propose an algorithm based on a nonparametric quantity: maximum mean discrepancy (MMD); and (iv) present experiments showing how these ideas can facilitate AD biomarker research (Fig. 1).

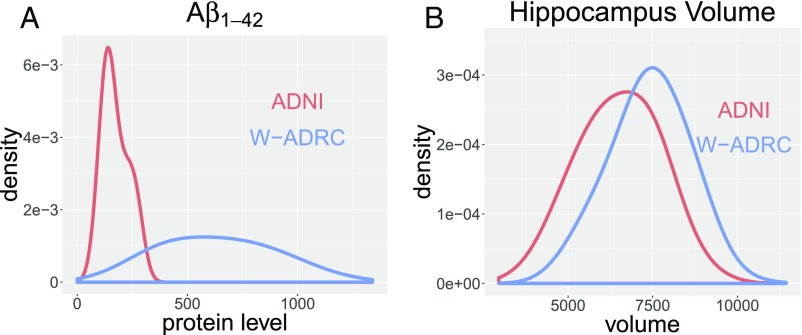
Fig. 1.

A shows the distributional shift of $A{\beta }_{1-42}$ across ADNI and W-ADRC. B shows the distributional shift of hippocampus volume across ADNI and W-ADRC.

Problem Setting

Let us assume that we have data from two sites $S$ and $T$, and the sitewise data correspond to $p$ different features. For presentation purposes, we will assume that the features include eight CSF protein levels, denoted as $X$, acquired from each participant via an LP. Since the absolute values of CSF measurements vary as a function of the assay instrumentation, we are interested in correcting the distributional shift to facilitate the analysis of the pooled dataset. However, notice that there are at least two other factors that can influence the correction. $S$ and $T$ may have participants with age distributions that are not identical. It is known that age influences protein-level measurements and therefore, will affect our distributional shift correction. We denote the population characteristics that cause differences in age distributions as $E_P$ (also called “transportability” in ref. 13). Similarly, while site $S$ may include an almost equal split of individuals with and without disease, healthy individuals may be overrepresented in site $T$. We denote this bias in sample selection between two datasets as $E_B$, which also influences $X$ (13). Therefore, the actual distributions of observed CSF protein levels in the two datasets, $X_S$ and $X_T$, are $P(X_S|E_P,E_B)$ and $P(X_T|E_P,E_B)$, respectively. If we only have access to $X_S$ and $X_T$ but no other variables related to $E_P$ and $E_B$, then correcting the distributional shift between $X_S$ and $X_T$ is difficult. However, the problem is identifiable when we have age and diagnosis status relevant for the variables $E_P$ and $E_B$. In fact, we can specify the condition when the correction is identifiable. We briefly review some concepts related to graphical causal model and d-separation rules and then state the identifiability condition.

Graphical Causal Model.

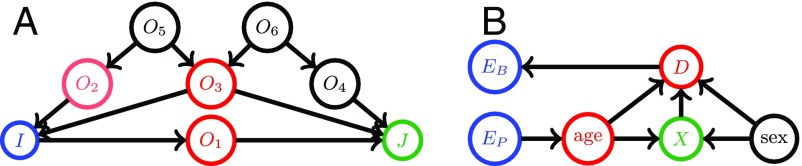
A graphical causal model is represented by a directed acyclic graph (DAG), which consists of three types of entities: variables (nodes), arrows (edges), and missing arrows. DAGs are useful visual representations of a domain expert’s assumptions regarding causal relationships explaining the data generation process (20). In Fig. 2A, we show an example. Arrows in the graph represent possible direct causal effects between pairs of variables. For example, the arrow from $I$ to $O_1$ means that $I$ exerts a direct causal influence on $O_1$. The absence of an arrow represents an assumption of no direct causal effect between the two variables (20). The missing arrow from $I$ to $J$ denotes the absence of a direct causal effect of $I$ on $J$. Fig. 2B shows an example for our data analysis task, where the DAGs depict causal relations between age, sex, CSF, diagnosis status, and other variables. Here, age, sex, and other endogenous variables influence the CSF measurements $X$, which influence the diagnosis status $D$. The population characteristic difference $E_P$ only has a direct causal effect on age, whereas the sample selection bias $E_B$ is only directly related to diagnosis status $D$ for each specific study or site. Note that a graphical causal model is nonparametric and makes no other assumptions about the distribution of variables, the functional form of direct effects, or the magnitude of causal effects.

Fig. 2.

A is an example of a graphical causal model. The colored nodes are an example of a d-separation rule, where $I$ and $J$ are d-separated by $\{O_1\text{,}{O}_2\text{,}{O}_3\}$. B is the graphical causal model for our CSF data analysis example. Here, the population characteristics difference $E_P$ only has a direct causal effect on the age distribution. The sample selection bias $E_B$ is only directly related to diagnosis status $D$ for each specific study. Nodes denoting age and sex influence the CSF measurements denoted by $X$, which then influence the diagnosis status $D$. The CSF measurements $X$ and the nodes $E_P$ and $E_B$ are d-separated by diagnosis status $D$ and age.

Next, we introduce a useful concept called d-separation (21) using the model in Fig. 2A as an example. If two variables $I$ and $J$ are d-separated by a set of variables $Z$, then they are conditionally independent given $Z$. A path is a sequential set of connected nodes independent of the directionality of the arrows. A “collider” on a path is a node with two arrows along the path pointing into it ($O_5\to O_3\leftarrow O_6$ in Fig. 2A). Otherwise, the node is a noncollider on the path.

Definition.

[d-separation (21)]: A path $p$ between two variables, $I$ and $J$ is said to be blocked by a set of variables $Z$ if either (i) $p$ contains a noncollider that is in $Z$ or (ii) $p$ contains a collider node that is outside $Z$ and has no descendant in $Z$. We say that $I$ and $J$ are d-separated by $Z$ if any path between them is “blocked” by $Z$.

For example, in Fig. 2A, $I$ and $J$ are d-separated by $Z=\{O_1,O_2,O_3\}$. After including $\{O_1,O_3\}$ in $Z$, all paths are blocked due to rule i, except the path $p_l:I\leftarrow O_2\leftarrow O_5\to O_3\leftarrow O_6\to O_4\to J$. The path $p_l$ stays unblocked, because (i) no noncollider on that path is in $Z$ and (ii) the only collider $O_3$ on $p_l$ is in $Z$. Therefore, we can include one of $\{O_2,O_5,O_6,O_4\}$ on the path into $Z$ to “block” it.

Identifiability Condition

We can now present a condition describing when distributional shift correction across sites is identifiable, even with the concurrent influence of sample selection bias and population characteristic differences on the measurements $X$.

Theorem 1.

The distribution shift correction is identifiable if there exists a known set of variables $Z$, such that the following three conditions are all concurrently satisfied.

• i)$Z$ d-separates $X$ and $E_B$ (sample selection bias) and also d-separates $X$ and $E_P$ (population characteristic difference).
• ii)The conditional probability $\mathbb{P}(X|Z)$, after appropriate transformations on $X$, is the same across multiple participating sites ($S$ and $T$).
• iii)The distribution of $Z$ has a nontrivial overlap across multiple sites ($S$ and $T$), which means that there exists an interval $[a,b]$, such that $\mathbb{P}(a\le Z\le b)\ge 0.5$ for all sites.

The proof is in SI Appendix, S.6. From Fig. 2B and Table 1, we can check that $Z=\{D,\text{age}\}$ satisfies Theorem 1. Condition i is satisfied by noticing that $Z$ d-separates $X$ and the nodes $E_P$ and $E_B$. If all sites collect samples similarly, $\mathbb{P}(X|Z)$ will be the same [e.g., $\mathbb{P}(X|D=AD,\text{age}=\mathrm{\hspace{0.17em}80})$]. From Fig. 2B, variations denoted by $E_P$ and $E_B$ only influence the marginal distributions of $D$ and age but have no effect on the causal relation/function among variables [e.g., $\mathbb{P}(X|Z)$]. The distributional shift of $X$ can be corrected after some transformation; therefore, condition ii holds. Finally, we will see (Table 1) that the disease status and age distributions have a nontrivial overlap across the two datasets; therefore, condition iii also holds.

Table 1.

Variations of age and diagnosis status across datasets

Description	ADNI	W-ADRC
Sample size	$284$	$125$
Age range ($\sim$55–65/$\sim$65–75/$\sim$75–85 yr), %	$11/43/46$	$44/34/22$
Diagnosis status (CN/AD), %	$60/40$	$76/24$

In practice, it is useful to seek a d-separating set of variables $Z$ with the fewest variables, such that we can sacrifice (or leave out) the fewest samples to separate distributional shift from the other variations $E_P$ and $E_B$. Finding a minimal d-separating set can be solved as a maximum flow problem (22). In practice, if the causal model is not too complicated, one may even find a d-separating set $Z$ manually. Then, it can be transformed into the problem of “blocking” two nodes in an undirected graph with the fewest blocks (23) (SI Appendix).

Tests for Correcting Distributional Shift

We now describe an algorithm to correct distributional shift if it is identifiable (Theorem 1). We start our discussion by first assuming that the two to-be-pooled datasets, $S$ and $T$, only include a distributional shift in the features (e.g., due to measurement or site-specific nuisance factors) and involve no other sampling biases or confounds (i.e., $E_P$ and $E_B$). Later, we present a subsampling framework to extend the algorithm to the case where other variations co-occur and also contribute to the shift. We calculate the distributional shift correction by identifying a parametric transformation on the sitewise samples from $S$ and $T$. We assume that site $S$ provides $n_S$ samples $X_S=(x_S^1,x_S^2,\mathrm{\dots },x_S^{n_S})$ given by a distribution $P_S$ and that $T$ provides $n_T$ samples $X_T$ with a distribution $P_T$.

Let us denote the transformation on $X_S$ as $h^{\lambda }(\cdot )$ and the transformation on $X_T$ as $g^{\theta }(\cdot )$ characterized by the unknown parameters $\lambda$ and $\theta$, respectively. For example, if we choose $h^{\lambda }(\cdot )$ to be an affine transformation with parameters $\lambda :=W$, it maps any value $x$ to $Wx$: that is, $h^W(\cdot ):x\to Wx$. The algorithm seeks to find a pair of transformations, such that distributions of two datasets are matched (corrected) after the transformations are applied. We use MMD as a measure of difference between the two (transformed) distributions. The MMD is expressed as a function of two distributions $P_S$, $P_T$ as

$$\mathcal{M}\mathcal{M}\mathcal{D}(P_S,P_T)={\parallel {𝔼}_{X\sim P_S}\mathcal{K}(X,\cdot )-{𝔼}_{X\sim P_T}\mathcal{K}(X,\cdot )\parallel }_{\mathcal{H}},$$

which is defined using a Reproducing Kernel Hilbert Space with norm $\parallel \cdot {\parallel }_{\mathcal{H}}$ and kernel $\mathcal{K}$. MMD can also be considered as the mean difference between two distributions after kernel embedding and has several desirable properties (for example, it is zero if and only if two distributions are identical) (24). One requirement, however, is that the kernel has to be characteristic, and specific choices may be guided by the application (24). The empirical version of MMD can be calculated with samples $X_S,X_T$ as

$$\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}(X_S,X_T)={\parallel \frac{1}{n_S}\sum _{i=1}^{n_S}\mathcal{K}(x_S^i,\cdot )-\frac{1}{n_T}\sum _{j=1}^{n_T}\mathcal{K}(x_T^j,\cdot )\parallel }_{\mathcal{H}}.$$

Recall that our algorithm is trying to match the two distributions after applying the parametric transformations $h^{\lambda }(\cdot )$ and $g^{\theta }(\cdot )$. Therefore, we estimate parameters $\lambda$ and $\theta$ using the empirical MMD by searching for a minimum value (e.g., using stochastic gradient descent):

$$(\widehat{\lambda },\widehat{\theta })=\arg \underset{\lambda \in {\mathrm{\Omega }}_{\lambda },\theta \in {\mathrm{\Omega }}_{\theta }}{\min }\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}(h^{\lambda }(X_S),g^{\theta }(X_T)).$$ [1]

The class of transformations that we will choose for a specific application should be informed by domain knowledge, but in general, simpler transformation classes are preferable.

We now show that the estimators $\widehat{\lambda }$ and $\widehat{\theta }$ are consistent.

Theorem 2.

Under mild assumptions (SI Appendix, S.2), if there is a ${\lambda }_0,{\theta }_0$ such that $h^{{\lambda }_0}(X_S)$ and $g^{{\theta }_0}(X_T)$ have the same distribution, then

$$\mathcal{M}\mathcal{M}\mathcal{D}(h^{\widehat{\lambda }}(X_S),g^{\widehat{\theta }}(X_T))\to \mathrm{\hspace{0.17em}0}$$

with the rate $\max (\frac{\sqrt{\log (n_S)}}{\sqrt{n_S}},\frac{\sqrt{\log (n_T)}}{\sqrt{n_T}})$. If ${\lambda }_0,{\theta }_0$ are unique, then the estimators $\widehat{\lambda },\widehat{\theta }$ are consistent.

Remark.

In various applications (including our experiments), we may choose one class of transformations $h^{\lambda }(x)$ to be the identity transformation and transform samples in the other dataset to match the reference dataset.

The foregoing discussion and Theorem 2 assume that the two distributions can be matched via some unknown transformation. This may not always be true, and it is important, in practice, to identify when the datasets cannot be pooled for the specified class of transformations. Next, we provide a hypothesis test to answer this question. Let us define

$$\begin{array}{l}{H}_0:\text{There exists}\hspace{0.17em}\lambda ,\theta \hspace{0.17em}\text{such that}\hspace{0.17em}{h}^{\lambda }(X_S)\text{and}\hspace{0.17em}{g}^{\theta }(X_T)\text{match}\\ H_A:\text{There is no}\hspace{0.17em}\lambda ,\theta \hspace{0.17em}\text{such that}\hspace{0.17em}{h}^{\lambda }(X_S)\text{and}\hspace{0.17em}{g}^{\theta }(X_T)\text{match}.\end{array}$$

The test statistics can be obtained by plugging $\widehat{\lambda }$, $\widehat{\theta }$ into the empirical MMD calculation as

$${\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}}_{\text{best}}=\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}(h^{\widehat{\lambda }}(X_S),g^{\widehat{\theta }}(X_T)).$$

We can show that the hypothesis test is consistent. Additional details for the small sample size case are in SI Appendix, S.3.

Theorem 3.

Under mild assumptions (SI Appendix, S.2), ${\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}}_{\text{best}}$ converges to zero with the rate $\max (\frac{1}{\sqrt{n_S}},\frac{1}{\sqrt{n_T}})$ when $H_0$ holds and converges to a positive constant with the rate $\max (\frac{\sqrt{\log (n_S)}}{\sqrt{n_S}},\frac{\sqrt{\log (n_T)}}{\sqrt{n_T}})$ when $H_A$ holds.

The test can provide guidance on whether the distributional shift has been successfully corrected. If the test suggests the alternative hypothesis, one may consider adjusting the transformation class $h^{\lambda }(\cdot )$ and $g^{\theta }(\cdot )$ or other factors, such as sample selection bias and population attribute difference, or one may decide against pooling. Next, we introduce a subsampling scheme to correct distributional shift when other contributors to the shift coexist, but the correction is still identifiable.

Subsampling Framework.

When the test chooses $H_A$, one reason may be that one or more cohort-specific factors contribute in significant ways to the observed distributional shift between $X_S$ and $X_T$. Recall that our earlier discussion suggests that the problem is identifiable if we can find a $Z$ satisfying the conditions in Theorem 1. Then, a subsampling procedure can potentially resolve the confound. The reason is that

$$\mathbb{P}(X|E_P,E_B)={𝔼}_{Z|E_P,E_B}[\mathbb{P}(X|Z,E_P,E_B)].$$

From Theorem 1, we know that $\mathbb{P}(X|Z,E_P,E_B)=\mathbb{P}(X|Z)$, which remains the same across sites after a suitable transformation. Therefore, simply by adjusting $\mathbb{P}(Z|E_P,E_B)$, the effects of the other factors on $X$ can be controlled, except distributional shift. Such a subsampling scheme is widely used in addressing sample selection bias in other applications (25) (information on the subsampling scheme for reducing computational burden is in ref. 26). In our setting, the motivation for using subsampling is similar, but it is used in the context of correcting distributional shift—after subsampling. Separately, since subsampling has been used in bagging to stabilize estimations and reduce variance [e.g., for random forests (27)], we can directly obtain stable estimators and calculate their variance.

Specifics of Subsampling.

We divide $X_S$ into $d$ groups with sample sizes given as $(n_S^1,\mathrm{\dots },n_S^d)$: i.e., $X_S=(x_S^{(\mathrm{1,1})},\mathrm{\dots },x_S^{(1,n_S^1)},\mathrm{\dots },x_S^{(d,1)},\mathrm{\dots },x_S^{(d,n_S^d)})$. Similarly, $X_T$ is divided into groups with sample sizes given as $(n_T^1,\mathrm{\dots },n_T^d)$: i.e., $X_T=(x_T^{(\mathrm{1,1})},\mathrm{\dots },x_T^{(1,n_T^1)},\mathrm{\dots },x_T^{(d,1)},\mathrm{\dots },x_T^{(d,n_T^d)})$. The subsample sizes are $(s_1,s_2,\mathrm{\dots },s_d)$, where $s_j\le \min (n_S^j,n_T^j)$ for any $j=\mathrm{\hspace{0.17em}1},\mathrm{\dots },d$. Then, we generate subsamples for $X_S$ and $X_T$ and apply Eq. 1 sequentially. We run subsampling with replacement $B$ times and denote each iteration’s estimators as ${\widehat{\lambda }}^b,{\widehat{\theta }}^b$. Then, our final transformation estimators are given as $\widehat{\lambda }=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\lambda }}^b$ and $\widehat{\theta }=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\theta }}^b$.

Infinitesimal Jackknife Confidence Interval.

In most scientific studies, we also want to obtain a confidence interval for the calculated transformations. In this case, however, there is no closed form solution, and therefore, we use a bootstrap type method. Since subsampling already involves bootstrapping, using a simple bootstrap results in a product of bootstraps. Fortunately, a similar issue was encountered in bagging, and an infinitesimal Jackknife (IJ) method (28) was provided for random forests, which works quite well (27, 29). Inspired by this result, we use the IJ to estimate the variances of estimators $\widehat{\lambda }$ and $\widehat{\theta }$. The method cannot be directly applied here, since it considers subsampling from one group, whereas we need subsampling from multiple groups. We, therefore, extend the results to multiple groups (proof is in SI Appendix, S.7).

Based on the subsampling scheme for $X_S$ and $X_T$ defined above, the multigroup IJ estimator of variance is given as the following theorem.

Theorem 4.

Define $g_{u(i,k)}^b$ to be the number of appearances of $x_u^{(i,k)}$ in iteration $b$. Define $ℂ𝕆𝕍(g_{u(i,k)},\lambda )=\frac{1}{B}{\sum }_{b=1}^B({\widehat{\lambda }}^b-\widehat{\lambda })(g_{u(i,k)}^b-\frac{s_i}{n_u^i})$. The IJ estimator of variance for $\widehat{\lambda }$ is

$$𝕍𝔸{ℝ}_{IJ}(\widehat{\lambda })=\sum _{u\in \{S,T\}}\sum _{i=1}^d\sum _{k=1}^{n_u^i}{(ℂ𝕆𝕍(g_{u(i,k)},\lambda ))}^2.$$

The procedure for $\widehat{\theta }$ is identical.

Algorithm 1.

Subsampling MMD Algorithm ($\mathcal{S}\mathbf{}\mathcal{S}\mathbf{}\mathcal{P}$)

1: Divide $X_S$ and $X_T$ separately into $d$ groups by $Z$

2: Decide subsample size $(s_1,s_2,\mathrm{\dots },s_d)$

3: For $b=\mathrm{\hspace{0.17em}1}$ to $B$, do

4: Generate subsamples $X_S^b$ from $d$ groups of $X_S$

5: Generate subsamples $X_T^b$ from $d$ groups of $X_T$

6: $({\widehat{\lambda }}^b,{\widehat{\theta }}^b)=\arg {\min }_{\lambda \in {\mathrm{\Omega }}_{\lambda },\theta \in {\mathrm{\Omega }}_{\theta }}\widehat{\mathcal{M}\mathcal{M}\mathcal{D}}(h^{\lambda }(X_S^b),g^{\theta }(X_T^b))$

7: Calculate and record $g_{u(i,k)}^b$ for all $u,i,k$

8: Set $\widehat{\lambda }=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\lambda }}^b$ and $\widehat{\theta }=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\theta }}^b$ and calculate $𝕍𝔸{ℝ}_{IJ}(\widehat{\lambda })$ and

$𝕍𝔸{ℝ}_{IJ}(\widehat{\theta })$

Applications to AD Study

We show the application of the framework to correct distributional shift between two AD datasets and show how such a strategy can lead to improved pooled data analysis. The two datasets come from the Alzheimer’s Disease Neuroimage Initiative (ADNI) project and the Wisconsin Alzheimer’s Disease Research Center (W-ADRC). Both studies follow similar protocols for acquiring CSF samples from participants and measuring protein levels (3). It is known that the CSF protein levels are indicative of neurofibrillary tangles and amyloid plaques, characteristic of AD pathology. The distributions of the protein measurements across the two datasets are different due to various reasons described in the literature (3), which makes pooled analysis and/or transferring results from one dataset to the other problematic. For example, a threshold derived for the ADNI dataset may not be applicable to the W-ADRC dataset. Both datasets included eight distinct CSF protein levels measured on seven proteins ($A{\beta }_{1-42}$ is measured by two methods), where the distributional shift needs to be corrected. In both W-ADRC and ADNI, the measured proteins include $A{\beta }_{1-38}$, $A{\beta }_{1-40}$, $A{\beta }_{1-42}$, $p{\mathit{\text{-tau}}}_{181}$, $t\mathit{\text{-tau}}$, NFL, and neurogranin. While the W-ADRC dataset provides 125 samples, the ADNI includes 284 samples (Table 1 and SI Appendix). After correcting the distributional shift, we fit statistical models, which include age, sex, and CSF proteins as covariates. As a response variable, we use hippocampus volume or diagnosis status. Here, other than correcting the CSF protein levels across the two datasets, we also correct distribution shift of hippocampus volumes, since they may be calculated with different image acquisition characteristics and potentially different software (Freesurfer in ADNI vs. FIRST/FSL in W-ADRC). Our workflow involves three tasks: (i) correct distributional shift across the datasets for CSF protein levels, (ii) transform thresholds in ADNI to W-ADRC, and (iii) pool the data together to predict the response variable (hippocampus volume and diagnosis status) within regression or classification.

Correct Distributional Shift of CSF.

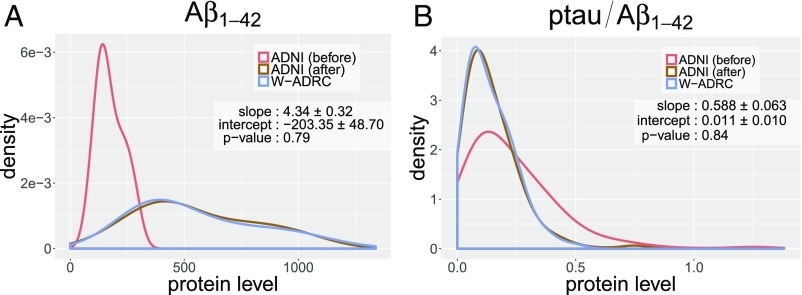
Table 1 shows that the age distributions as well as the proportions of participants who are healthy [control (CN)] and diseased (AD) in the two datasets are not exactly the same, which makes directly attempting a distributional shift correction in the CSF measures not very meaningful. However, when other variations (confounders) coexist together with distributional shift, as discussed earlier, we should check whether there exists a set of variables $Z$ satisfying conditions given in Theorem 1. We previously described how choosing $Z=\{D,\text{age}\}$ satisfies Theorem 1. Such a $Z$ is also the minimal d-separating set. To proceed with the analysis, we divide our samples in $d=\mathrm{\hspace{0.17em}6}$ groups based on all possible combinations of diagnosis status (AD/CN) and age ranges ($55\sim \mathrm{\hspace{0.17em}65}/65\sim 75/75\sim \mathrm{\hspace{0.17em}85}$). We can now run the subsampling MMD algorithm ($\mathcal{S}\mathcal{S}\mathcal{P}$) (see Algorithm 1) with $Z=\{D,\text{age}\}$ (iterations $B=\mathrm{\hspace{0.17em}2000}$) to correct the distributional shift in $X$. We show two representative results in Fig. 3. For each plot in Fig. 3, depending on the subsamples randomly collected from 10 iterations, we plot the distributions of protein levels and a protein ratio measure (widely used in the aging/AD literature) in ADNI before/after correction (red/brown) with respect to W-ADRC baseline (blue). We see that the distributions of raw measures are very different between ADNI (using the AlzBio3 xMAP assay) and W-ADRC (using the ELISA INNOTEST assay). After our correction, the distributions are matched for all eight CSF protein measurements and both protein ratios that are relevant in AD research ($p$-tau/$A{\beta }_{1-42}$ and $t$-tau/$A{\beta }_{1-42}$). We randomly select one iteration and apply the hypothesis test, which accepts the transformations with high p-values. We also use the IJ to estimate the SDs of parameters and report them in Fig. 3.

Fig. 3.

The plots of (A) $A{\beta }_{1-42}$ and (B) $p\mathit{\text{-tau}}/A{\beta }_{1-42}$ show the empirical distributions of W-ADRC samples (blue), ADNI samples (red), and transformed ADNI samples (brown). W-ADRC samples are nicely matched with transformed ADNI samples.

Transferring Thresholds for Disease Staging Across Datasets.

After performing our correction, CSF protein measurements across the two datasets can be analyzed together. We can evaluate the effect of using models (or thresholds) derived for the ADNI dataset on W-ADRC by transferring the criteria directly. For example, five CSF-based biomarker signatures (thresholds) developed for AD using ADNI participants (11) can now be transferred to the W-ADRC dataset. Given a threshold for any specific CSF protein, we can evaluate a sample in W-ADRC by comparing the corresponding measurements with the transformed threshold. The procedure produces sensitivity and specificity (for detection of AD) for each of eight CSF protein measurements and the two derived ratios. Our final thresholds, sensitivities, and specificities based on the experiments are shown in Table 2. The accuracy estimates suggest that all derived thresholds work well—we find that the sensitivity and specificity are competitive with the results reported for ADNI (11) and show how results/models from one dataset may be transferable to another dataset using our proposal.

Table 2.

The performance of thresholds in ADNI and W-ADRC

Dataset	$t$-tau	$A{\beta }_{1-42}$	$p$-tau181	$\frac{t\mathit{\text{-tau}}}{A{\beta }_{1-42}}$	$\frac{p{\mathit{\text{-tau}}}_{181}}{A{\beta }_{1-42}}$
W-ADRC
Threshold	568.08	629.39	48.86	0.77	0.07
Sensitivity, %	75.86	89.66	82.75	93.10	93.10
Specificity, %	92.23	69.90	67.96	86.41	79.61
ADNI
Threshold	93.00	192.00	23.00	0.39	0.10
Sensitivity, %	69.6	96.4	67.9	85.7	91.1
Specificity, %	92.3	76.9	73.1	84.6	71.2

The W-ADRC thresholds are derived from corresponding ADNI thresholds reported in the literature (11) using Algorithm.

Pooling and Analyzing the Two Datasets Together.

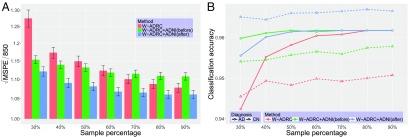
For the final experiment, we evaluate whether predictors from both datasets can be pooled for predicting hippocampus volume and diagnosis status (response variables) within regression and classification. We build a linear regression model based on age, sex, and CSF proteins (after distributional shift correction) to identify associations with hippocampus volume. To evaluate the accuracy of the model, we randomly choose $25$ samples ($20\%$) from W-ADRC data to serve as the test set. For evaluation purposes, we generate three different types of training datasets: W-ADRC samples only, W-ADRC plus raw (uncorrected) ADNI samples, and W-ADRC plus transformed ADNI samples. Note that the data used to generate the training set are based on all $284$ ADNI samples and the remaining $100$ W-ADRC samples. To obtain prediction errors for each of the three schemes with respect to varying training sample sizes, we vary the training sample size by choosing $b\%$ samples from each of the two datasets and then change $b$ from 30 to $90\%$ in $10\%$ increments. To avoid performance variation due to random choice of samples, after the test set is chosen, we run five bootstraps to select the training set and fit the model. Finally, we run 80 bootstraps to generate multiple test sets and evaluate the model performance. In this way, based on 400 bootstraps, we are able to obtain a more stable prediction error, and we are able to calculate the SD. The square root of mean squared prediction error (MSPE) scaled by a constant is shown in Fig. 4A. We can see that the prediction errors decrease as training sample size increases, while the W-ADRC plus transformed ADNI data consistently offer the best performance.

Fig. 4.

A shows the trend of MSPE for hippocampus volume as the sample size increases using 400 bootstraps. The bar plot covers the prediction error for three types of training set as depicted in the legend, including W-ADRC only (red), W-ADRC plus ADNI (green), and W-ADRC plus transformed ADNI (blue). The third model continues to perform the best. B shows the trend of classification accuracy with respect to patients with AD (solid lines) and healthy patients (dotted lines) as sample size increases using 400 bootstraps. An SVM model is used, and three types of training sets are shown in the legend. For samples with AD, the three methods converge to the same accuracy as the training sample size increases. For healthy CNs, the W-ADRC plus the transformed ADNI dataset is always better than the other two schemes. It is interesting to see that W-ADRC plus the raw ADNI data also performs better than W-ADRC alone, possibly because only 25 (24%) subjects from W-ADRC are diagnosed with AD—with few AD samples, even the uncorrected ADNI data nicely inform the classification model.

Next, the same setup is used to predict AD status with a support vector machine (SVM) classifier. Because the ratio of AD to CN is biased in the test set from W-ADRC, we set a uniform prior in SVM and separately report the classification accuracy for participants with AD and without AD in Fig. 4B.

Discussion

There is growing interest in the design of infrastructure and platforms that allow scientists across different sites and even continents to contribute scientific data and explore scientific hypotheses that cannot be evaluated on smaller datasets. Such efforts can be facilitated via the availability of theory and algorithms to identify whether pooling is meaningful, how the data should be harmonized, and later, how statistically meaningful and reproducible scientific conclusions can be obtained. We described a statistical framework that addresses some of the natural issues that arise in this regime, in particular, providing conditions where distributional shift between datasets can be corrected. The experimental results suggest promising potential applications of this idea in aging and AD studies. There remain several outstanding issues that are not fully addressed by this work. The procedure does not currently deal with discrete measurements, which are often encountered in some applications. It will also be interesting to more explicitly use information about the response variables—deciding when pooling is beneficial not only depends on the correction of distributional shift but may also be influenced by other factors, including sample size and noise level. On the computational side, special classes of kernels may lead to more efficient means of estimating the transformation to align the distributions. Finally, there are interesting deep learning algorithms for domain/data shift correction, and impressive empirical results are being reported, even for high-dimensional distributions. The University of Wisconsin Institutional Review board approved all study procedures and each subject provided signed informed consent before participation.