Significance
Understanding how structural order forms in matter is a key challenge in designing materials. In the 1920s, Pauling proposed packing as a mechanism for driving structural order based on observed correlations between the structure of crystals and the mathematical packing of hard spheres. We study the ordering of several systems of hard colloids in which structural order correlates with mathematical packing and find, surprisingly, that structural order cannot arise from packing. Our approach provides statistical mechanics approaches for investigating the mathematics of packing and raises questions about the role of packing in determining the structural order of matter.
Keywords: packing, assembly, colloids, shape entropy, digital alchemy
Abstract
Since the 1920s, packing arguments have been used to rationalize crystal structures in systems ranging from atomic mixtures to colloidal crystals. Packing arguments have recently been applied to complex nanoparticle structures, where they often, but not always, work. We examine when, if ever, packing is a causal mechanism in hard particle approximations of colloidal crystals. We investigate three crystal structures composed of their ideal packing shapes. We show that, contrary to expectations, the ordering mechanism cannot be packing, even when the thermodynamically self-assembled structure is the same as that of the densest packing. We also show that the best particle shapes for hard particle colloidal crystals at any finite pressure are imperfect versions of the ideal packing shape.
Why do atoms, molecules, or nanoparticles form the crystals that they form? In 1929, Pauling proposed an answer to this question for atoms by showing remarkable correlations between the sphere packing problem, the study of which dates back to Sanskrit writings in 499 CE (1), and the crystal structures of ionic solids (2). The packing problem asks the following question: given a set of hard, convex objects, such as spheres, what is the spatial arrangement of those objects that most densely fills space? Pauling argued that crystal structures could be explained by packings of spheres of appropriate atomic radii.
Variants of the packing problem have yielded solutions relevant not only to the rationalization of crystal structures (2) but also, in optimal information transmission (3), DNA in cell nuclei (4, 5), blood clots (6), plant morphology (7), and the stacking of oranges in the produce section (8). Packing rules were used by Frank and Kasper (9, 10) to rationalize complex crystal structures in intermetallic alloys, and the molecular packing parameter, a popular geometric measure in surfactant self-assembly, is also based on packing principles (11).
More recently, Pauling’s packing principles have been used to rationalize and predict colloidal crystals and nanoparticle superlattice structures by asserting packing as a causal mechanism. For example, packing rules explain many binary nanoparticle superlattice structures obtained from both spherical and nonspherical particle shapes (12–14). Packing rules are also successfully used to design DNA-functionalized gold nanospheres (15, 16). This raises the question: in instances where packing principles can describe observed crystal structures, does that necessarily imply that packing mechanisms are responsible?
For chemically bonded spherical particles, where, for example, electrostatic forces between oppositely charged colloids or ligand–ligand attraction between functionalized nanoparticles may dominate, packing arguments seem plausible due to the tendency toward close-packed structures. However, when attractive interparticle forces are weak and particles are nonspherical, entropy arising from thermal motion can dominate and invalidate packing rules (17–25). Nevertheless, there are examples in both situations where packing rules seem to explain self-assembled structures. Does that imply that the crystal formed via a packing mechanism? Or is it simply the case that packing rules are useful to rationalize the structure retrospectively, as is the case for molecular packing rules in ordered surfactant systems?
Statistical thermodynamics tells us that free energy minimization dictates equilibrium structures. In the case of hard particles, free energy minimization is achieved by structures that self-assemble to maximize entropy, except in the limit of very high pressures, where they maximize density (24, 26–31). It is these maximum density (or infinite pressure) structures that are invoked when packings are discussed. It is also this limiting case that offers an explanation of why systems of atoms, molecules, or nanoparticles might order through packing.
We can answer our questions by comparing for a given system the self-assembly density, (the lowest density at which spontaneous self-assembly is observed), with the “packing onset density,” (the lowest density at which the system exhibits packing behavior). We argue that packing behavior can occur in a finite pressure system if it follows the same asymptotic, infinite pressure behavior as idealized, mathematical packing. Therefore, the question of “when does matter pack?” reduces to searching for this asymptotic behavior. We test for the existence of this asymptotic behavior using generalized Maxwell relations derived in the alchemical ensemble first introduced in ref. 32. These generalized Maxwell relations are similar to the usual ones, but defined here in shape space, they can be used to define the packing onset density. One of these generalized relations directly relates the density of ordered structures to the “alchemical potential” , defined as the change in the alchemical free energy in response to a change in particle shape:
| [1] |
Here, denotes density, represents the alchemical (here, shape) variable, is pressure, is the total number of particles, and is temperature responsible for the thermal motion of the particles. The right-hand side of this equation can be computed analytically for systems at the limit of infinite pressure (i.e., densely packed systems), while the left-hand side can be computed via simulations in the isobaric alchemical ensemble (32). We define as the lowest density that satisfies this generalized Maxwell relation when the right-hand side is calculated at infinite pressure. To express this mathematically, we define
| [2] |
and note that there must exist some , such that for all . The packing density .
If we find for some system that , then this indicates that the onset of order is consistent with the existence of a global, dense packing mechanism. Conversely, if , this indicates that systems spontaneously order before they pack, and the mechanism that drives the order is not packing. However, in this case, it is possible that systems could be quenched to in a disordered state (33) and then, subsequently order by packing. To check for the existence of this possibility, we can compare with random close packing densities . Random close packing has been defined in ref. 34 as the density at which the metastable branch in the equation of state corresponding to a disordered system diverges (i.e., the maximum density at which it is possible for the system to be found in a disordered state). If , then we conclude that a given system cannot be ordered by a packing mechanism, as a system found at a density above must already be ordered. We will show below that, in all systems that we study, , indicating that not only is the spontaneous order not driven by packing but also, that the systems cannot be ordered by packing.
We also pose the following related question. When can packing arguments be used for the inverse problem of predicting the thermodynamically optimal particle shape for a particular structure? In other words, when—if ever—is the space-filling shape of a target crystal structure thermodynamically optimal for self-assembling that crystal?
Approach
To understand whether packing is driving self-assembly or fundamental to particle design, we study the most likely systems for this to be the case: idealized, perfectly hard, convex shapes. We consider three common structures [face-centered cubic (FCC), simple cubic (SC), and body-centered cubic (BCC)] and their corresponding space-filling (Voronoi) shapes (rhombic dodecahedron, cube, and truncated octahedron) shown in Fig. 1 B–D. It is well-known that, for each of these shapes, the corresponding structure is the only thermodynamic equilibrium assembly and the densest packing (at by definition) (17, 18, 27, 35, 36). However, we show that, in each case, the onset of packing behavior occurs at a higher density than , and therefore, the observed structures cannot be ordering via a packing mechanism. Moreover, we show that the space-filling shape for all three structures is never thermodynamically optimal, except at . From these two findings, we argue that there is only a correlation, not a causal relationship, between the observed thermodynamically assembled structures and those rationalized by packing arguments.
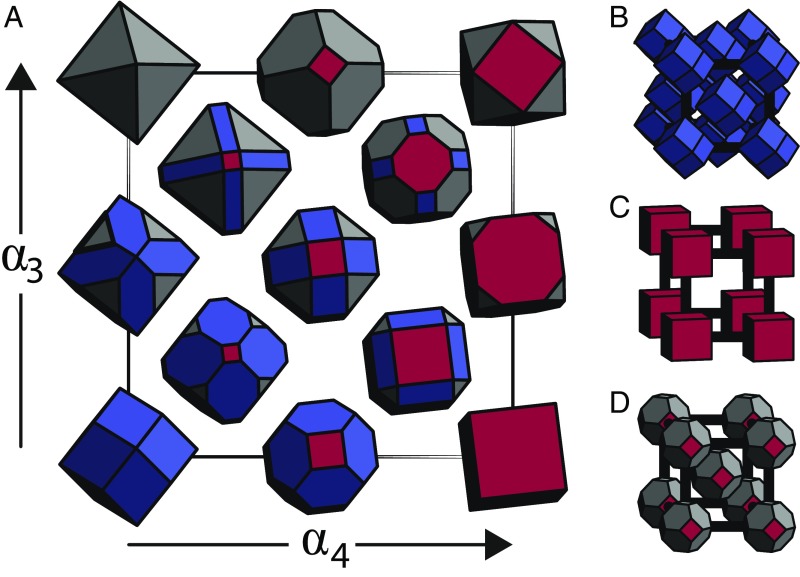
Fig. 1.
Shape family and structures. We rely on a previously defined parameterization (A), which continuously maps two values, and , to convex polyhedra. This parameterization, here known as the family, contains the space-filling shapes for (B) FCC, (C) SC, and (D) BCC.
Hard particle Monte Carlo (HPMC) simulations (37) of the self-assembly of FCC, SC, and BCC crystals were carried out for a family of spheric triangle group invariant particle shapes, (Fig. 1A), which includes each crystal’s space-filling particle, as shown in Fig. 1 B–D, but also, importantly, sets of truncated versions of those shapes that are nearby in shape space. This shape family maps two values, and , to convex polyhedra, with . The space-filling shapes for FCC, SC, and BCC are defined at (rhombic dodecahedron), (cube), and (Archimedean truncated octahedron), respectively.
To compute the packing onset density, we used analytical constructions of putative densest packings reported in ref. 38 for the entire shape family, giving as a function of , to evaluate the second term in Eq. 2 in the infinite pressure limit. We evaluated the first term in Eq. 2 at finite pressure using NPT HPMC simulations at varying pressures. From this, we estimated the lower limit of . We also performed simulations in the NVT ensemble to find the thermodynamically optimal shape for FCC, SC, and BCC as a function of density. Additional details and derivations for the parameterization of the shape family, extended ensembles, free energy calculations, and the simulations conducted can be found in Materials and Methods and SI Materials and Methods.
Results and Discussion
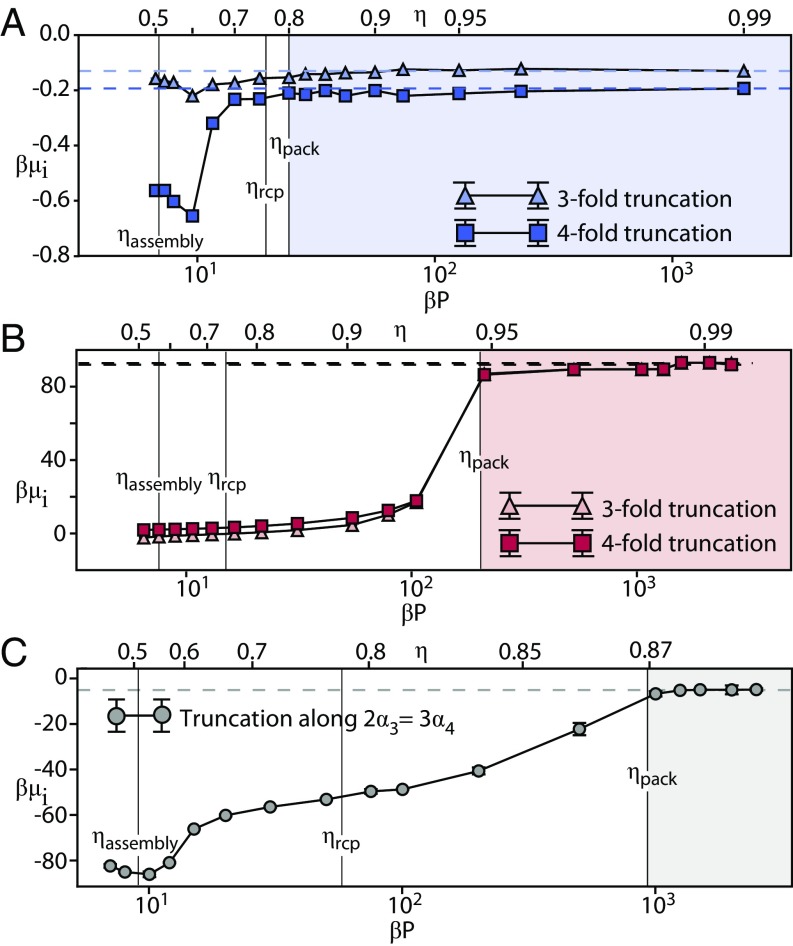
The computed alchemical potential as a function of pressure is plotted in Fig. 2 for FCC (Fig. 2A), SC (Fig. 2B), and BCC (Fig. 2C). Particle shape is fixed to that of the space-filling particle in each case. Asymptotic behavior extracted from analytical results reported in ref. 38 reveals that, in all three cases, asymptotes have zero slope in the limit of infinite pressure and thus, as , indicated with a horizontal line in each panel in Fig. 2. We distinguish the onset of packing behavior in Fig. 2 at 0.80, 0.95, and 0.87 for FCC, SC, and BCC, respectively, as the densities that correspond to the lowest pressures for which . In Fig. 2, results represent the first term in Eq. 2, and dashed lines represent the second term, adapted from analytical results reported in ref. 38. We also indicate both the assembly and random close packing densities for FCC, SC, and BCC: 0.5–0.55 (18, 39) and , , and , respectively. We estimated upper limits on using a procedure established in ref. 34. The procedure defined in ref. 34 determines an upper bound for from the divergence of the pressure on the metastable branch of the equation of state. The density at which this divergence occurs indicates the maximum density at which a system can be found in a disordered state, and it indicates the maximum density to which a system of hard particles can be quenched without order. To estimate upper bounds for , we use generalized equations of state for anisotropic hard particles reported in ref. 40 and identify the densities at which the equations of state diverge for each particle shape of interest. In every system, . Our results indicate that none of the systems investigated here order via a packing mechanism that occurs throughout space; rather, they indicate only that systems can self-assemble into the same structures that correspond to packings. Note that this does not rule out the possibility that systems could order by packing layer by layer through sedimentation, but that mechanism would be fundamentally different from spontaneously packing globally throughout space.
Fig. 2.
Onset of asymptotic packing behavior in (A) FCC, (B) SC, and (C) BCC. We use the generalized Maxwell relation in Eq. 1 to extract the onset of asymptotic packing behavior for (A) FCC, (B) SC, and (C) BCC with respect to their space-filing particles. The shaded region in each panel denotes the density–pressure regime where the system is found to be “packing” (i.e., where structure formation is driven by packing principles). By comparison, is much higher than either or shown for all three systems. For space-filling particles within FCC, SC, and BCC, 0.5–0.55 (18, 39) and 0.76, 0.74, and 0.78, respectively, calculated using methods from refs. 34 and 40.
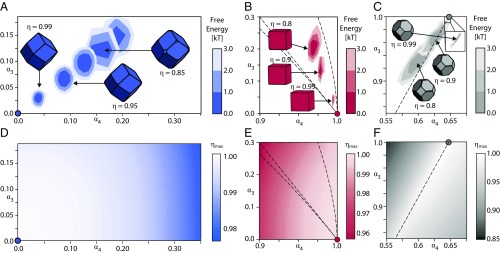
Moreover, results in Fig. 3 A–C indicate that packing cannot predict ideal particle shapes for self-assembly, because the perfect space-filling shape is never thermodynamically preferred away from . Contours plotted in Fig. 3 A–C indicate the per-particle free energy cost of modifying the shape of all colloidal particles while maintaining a fixed target structure. Even at , there is a tiny difference in shape that, in each case, produces a nontrivial difference in free energy (up to ) between identical crystals composed of the thermodynamically optimal shape and those composed of the space-filling shape. However, we do find that features in the global dense packing landscape do generally correlate with features found in the optimal particle shapes as seen by comparing the optimal shape (Fig. 3 A–C) with the corresponding densest packing landscape from ref. 38 (re-created in Fig. 3 D–F). Thus, while densest packing arguments do not predict the optimal shape for self-assembly, the densest packing landscape may provide qualitative guidance in determining optimal particle shape.
Fig. 3.
Contour maps of free energy for in (A) FCC, (B) SC, and (C) BCC. The perfect space-filling (Voronoi) shape, indicated by a filled circle in each panel, is different from any of the optimal shapes determined from simulation, even up to densities of . (D–F) The densest packing surface reported in ref. 38 in the regions closest to the space-filling shapes for (D) FCC, (E) SC, and (F) BCC. The dashed lines in B, C, E, and F denote discontinuities in the derivative of the dense filling surface.
Conclusions
Although packing arguments are often used successfully in nanoparticle and colloidal assembly, they often fail to explain experimental and computational observations. Our findings show that the use of packing arguments to rationalize observed structures or design particles to achieve target structures may not be well-founded, even when the observed structure is the same as that one would get from packing. Because one would expect packing principles—if they do hold—to hold for hard particles, our finding raises the question: is the apparent success of Pauling’s packing principles for atomic systems also a spurious correlation? It could also be that the imperfect hardness of atoms and molecules makes them more amenable to dense packing as a mechanism. This counterintuitive possibility would beg for additional understanding, as the initial reasons for applying packing arguments were based on the existence of steep, sterically repulsive interaction potentials that are nearly hard. Combining the approach for studying sphere packings developed in ref. 41 with the generalized Maxwell relation Eq. 1 could give additional insight into the behavior of putative sphere packings more generally. Indeed, for spherical nanoparticles, recent work analyzing experiments reported in ref. 12 has shown that the microscopic details of the particle organization are driven by a complex form of packing involving ligand topology (42–44). In addition, in providing thermodynamic formulations with which to investigate the packing of hard shapes, we offer alternative approaches to the ubiquitous but notoriously difficult set of general packing problems (45).
Our results combined with those reported in ref. 46 indicate that, in every case that has so far been investigated, there is not a single instance in which a space filling shape is thermodynamically optimal for the self-assembly of its corresponding target structure, at least for hard colloidal particles, as entropic contributions cannot be ignored. Small, stabilizing entropic contributions one might have guessed to be irrelevant can arise from nearly infinitesimal shape modifications, such as small truncations of vertices or edges of polyhedral nanoparticles. This means the space-filling shape is never thermodynamically optimal for self-assembling its corresponding structure, at least for hard colloidal particles. Our observations suggest that heroic efforts to synthesize perfectly shaped, space-filling particles to achieve the corresponding target structure are unnecessary and that the entropy gained from slight imperfections may actually facilitate assembly.
Materials and Methods
Here, we present a brief overview of the methods used to generate the data given in the text. Additional details and derivations can be found in SI Materials and Methods.
Shape Parameterization.
Spheric triangle group families are generated by the intersection of sets of symmetric planes (38). They are parameterized by parameters between zero and one, where encodes the inverse distance of the ith-fold symmetric planes from the particle center. Any parameter can be more readily understood as the truncation of an ith-fold axis of symmetry for the particle shape.
The shape family studied here is generated by intersections of planes perpendicular to the directions of the four-, two-, and threefold axes of rotational symmetry for a rhombic dodecahedron, shown in Fig. 1A as red, blue, and gray, respectively, and it is, therefore, named the 423 family of polyhedra (); is parameterized by three values (, and ) in the manner described above. Planes perpendicular to the twofold direction remain fixed, as does , and therefore, discussion is restricted to and . We restrict our exploration to a shape space with restricted point group symmetry due to (i) geometric reasoning about shape features that lead to optimal thermodynamic behavior and (ii) crystal growth processes that determine particle symmetries in nanoscale and synthesis protocols (47–49).
Simulation Methods.
We simulate our shapes in the alchemical ensemble using the digital alchemy (DA) framework (32). DA is a statistical mechanics simulation technique that uses thermodynamic ensembles extended into alchemical (here, particle shape) space by one or more dimensions, allowing fluctuations in the alchemical space or corresponding conjugate alchemical potential(s). This extended (“alchemical”) ensemble has the partition function (32)
| [3] |
where labels microstates; is the Hamiltonian; indicates the alchemical parameters describing model-specific particle shape attributes (detailed above); indicates thermodynamically conjugate alchemical potentials; is the number of particles; is a structural design criterion that initially keeps the system in an FCC, SC, or BCC crystal structure; and is the strength of the coupling to .
We used DA through the simulation method alchemical hard particle Monte Carlo (Alch–HPMC) (32). In Alch–HPMC simulations, is held constant, and particle position and orientation moves are accepted with standard acceptance criteria (50). Unbiased shape moves (hereafter, ) are performed, such that all particles in the system change simultaneously from a shape described by alchemical parameter to a shape described by , with probability
| [4] |
where is the potential energy and is the anisotropic particle moment of inertia tensor. Details are in SI Materials and Methods and ref. 32. For the hard particle systems studied here, the potential energy (and ) vanishes for all valid, nonoverlapping particle configurations, so that for a microstate in which any particles overlap.
We used DA and Alch–HPMC in two ways: (i) we computed the expectation value as a function of packing fraction in the ensemble, and (ii) we performed Alch–HPMC within the ensemble, obtained by Legendre transforming the ensemble twice, to calculate the alchemical potential . All simulations were run with systems of 500 or more particles. SI Materials and Methods has numerical details and state points for and simulations.
In i, we initialized independent simulations with distinct shapes, taking to be the potential energy function of an Einstein crystal for the target structure (FCC, SC, or BCC at some density). We maintained nonzero during initialization only to ensure that the system did not transition out of the target structure. All data were collected on equilibrated systems with ; results were validated by directly computing the free energy (51) for selected state points in simulations.
In ii, simulations were used to evaluate alchemical potentials for space-filling shapes using the thermodynamic relation
| [5] |
Our Alch–HPMC algorithm recorded the acceptance ratio for small trial moves from the space-filling shape without performing such moves. We evaluated Eq. 5 numerically using the Bennett acceptance ratio method (52), which is described as it applies to the alchemical potential in ref. 32 and uses a finite differencing method published in ref. 53.
In this ensemble, we derive a Maxwell relation between alchemical potential and packing fraction :
| [6] |
We used this expression to relate the high-pressure asymptotic behavior of the alchemical potential to dense packing surfaces that have been analytically computed in the literature (38).
Specifically, we consider systems to exhibit packing behavior when the slope of the alchemical potential approaches the infinite pressure asymptotic limit of the dense packing surface given by Eq. 1. Relevant data (38) have been re-created in SI Materials and Methods according to our variable notation.
All simulations were performed with an HPMC (37) extension to HOOMD-Blue (54, 55), which we further extended to allow Alch–HPMC moves. Runs were partially performed on Extreme Science and Engineering Discovery Environment computing resources (56). The data management for this publication was supported by the signac data management framework (57, 58). Details on statistical analyses can be found in SI Materials and Methods.
Supplementary Material
Acknowledgments
We thank J. Dshemuchadse, C. X. Du, Y. Geng, and E. Harper for helpful conversations and A. Travesset for helpful correspondence. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant ACI-1053575 and XSEDE Award DMR 140129. R.K.C. acknowledges support from the University of Michigan Rackham Merit Fellowship program and National Science Foundation Division of Materials Research Award DMR 1120923. P.M.D. acknowledges support from National Science Foundation Emerging Frontiers in Research and Innovation Award EFRI-1240264. This material is based on work supported (in part) by US Army Research Office Grant W911NF-10-1-0518. This work was partially supported by a Simons Investigator Award (to S.C.G.) from the Simons Foundation.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720139115/-/DCSupplemental.
References
- 1.Hales TC. A proof of the Kepler Conjecture. Ann Math. 2005;162:1065–1185. [Google Scholar]
- 2.Pauling L. The principles determining the structure of complex ionic crystals. J Am Chem Soc. 1929;51:1010–1026. [Google Scholar]
- 3.Bischoff S, Kobbelt L. Ellipsoid decomposition of 3D models. In: Werner B, editor. Proceedings of the First International Symposium on 3D Data Processing Visualization and Transmission. IEEE Computer Society; Los Alamitos, CA: 2002. pp. 480–488. [Google Scholar]
- 4.Cremer T, Cremer C. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet. 2001;2:292–301. doi: 10.1038/35066075. [DOI] [PubMed] [Google Scholar]
- 5.Marenduzzo D, Micheletti C, Orlandini E. Biopolymer organization upon confinement. J Phys Condens Matter. 2010;22:283102. doi: 10.1088/0953-8984/22/28/283102. [DOI] [PubMed] [Google Scholar]
- 6.Cines DB, et al. Clot contraction: Compression of erythrocytes into tightly packed polyhedra and redistribution of platelets and fibrin. Blood. 2014;123:1596–1603. doi: 10.1182/blood-2013-08-523860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ball P. Shapes: Nature’s Patterns: A Tapestry in Three Parts. Oxford Univ Press; Oxford: 2011. [Google Scholar]
- 8.Hales TC. Historical overview of the Kepler Conjecture. Discrete Comput Geom. 2006;36:5–20. [Google Scholar]
- 9.Frank FC, Kasper JS. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles. Acta Crystallogr. 1958;11:184–190. [Google Scholar]
- 10.Frank FC, Kasper JS. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures. Acta Crystallogr. 1959;12:483–499. [Google Scholar]
- 11.Israelachvili JN, Mitchell DJ, Ninham BW. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J Chem Soc Faraday Trans. 1976;2:1525. [Google Scholar]
- 12.Boles MA, Talapin DV. Self-assembly of tetrahedral CdSe nanocrystals: Effective “patchiness” via anisotropic steric interaction. J Am Chem Soc. 2014;136:5868–5871. doi: 10.1021/ja501596z. [DOI] [PubMed] [Google Scholar]
- 13.Cho K-S, Talapin DV, Gaschler W, Murray CB. Designing PbSe nanowires and nanorings through oriented attachment of nanoparticles. J Am Chem Soc. 2005;127:7140–7147. doi: 10.1021/ja050107s. [DOI] [PubMed] [Google Scholar]
- 14.Shevchenko EV, Talapin DV, Kotov NA, O’Brien S, Murray CB. Structural diversity in binary nanoparticle superlattices. Nature. 2006;439:55–59. doi: 10.1038/nature04414. [DOI] [PubMed] [Google Scholar]
- 15.Jones MR, et al. DNA-nanoparticle superlattices formed from anisotropic building blocks. Nat Mater. 2010;9:913–917. doi: 10.1038/nmat2870. [DOI] [PubMed] [Google Scholar]
- 16.Macfarlane RJ, et al. Establishing the design rules for DNA-mediated programmable colloidal crystallization. Angew Chem Int Ed. 2010;49:4589–4592. doi: 10.1002/anie.201000633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Damasceno PF, Engel M, Glotzer SC. Predictive self-assembly of polyhedra into complex structures. Science. 2012;337:453–457. doi: 10.1126/science.1220869. [DOI] [PubMed] [Google Scholar]
- 18.Smallenburg F, Filion L, Marechal M, Dijkstra M. Vacancy-stabilized crystalline order in hard cubes. Proc Natl Acad Sci USA. 2012;109:17886–17890. doi: 10.1073/pnas.1211784109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Evers WH, et al. Entropy-driven formation of binary semiconductor-nanocrystal superlattices. Nano Lett. 2010;10:4235–4241. doi: 10.1021/nl102705p. [DOI] [PubMed] [Google Scholar]
- 20.Graaf J, Roij Rv, Dijkstra M. Dense Regular packings of Irregular Nonconvex particles. Phys Rev Lett. 2011;107:155501. doi: 10.1103/PhysRevLett.107.155501. [DOI] [PubMed] [Google Scholar]
- 21.Rossi L, et al. Shape-sensitive crystallization in colloidal superball fluids. Proc Natl Acad Sci USA. 2015;112:5286–5290. doi: 10.1073/pnas.1415467112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Avendaño C, Escobedo FA. Packing, entropic patchiness, and self-assembly of non-convex colloidal particles: A simulation perspective. Curr Opin Colloid Interface Sci. 2017;30:62–69. [Google Scholar]
- 23.Avendaño C, Escobedo FA. Phase behavior of rounded hard-squares. Soft Matter. 2012;8:4675. [Google Scholar]
- 24.Escobedo FA. Engineering entropy in soft matter: The bad, the ugly and the good. Soft Matter. 2014;10:8388–8400. doi: 10.1039/c4sm01646g. [DOI] [PubMed] [Google Scholar]
- 25.Odriozola G, Jiménez-Ángeles F, Lozada-Cassou M. Entropy driven key-lock assembly. J Chem Phys. 2008;129:111101. doi: 10.1063/1.2981795. [DOI] [PubMed] [Google Scholar]
- 26.Anders G, Klotsa D, Ahmed NK, Engel M, Glotzer SC. Understanding shape entropy through local dense packing. Proc Natl Acad Sci USA. 2014;11:E4812–E4821. doi: 10.1073/pnas.1418159111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Anders G, Ahmed NK, Smith R, Engel M, Glotzer SC. Entropically patchy particles: Engineering valence through shape entropy. ACS Nano. 2014;8:931–940. doi: 10.1021/nn4057353. [DOI] [PubMed] [Google Scholar]
- 28.Frenkel D. Entropy-driven phase transitions. Physica A Stat Mech Appl. 1999;263:26–38. [Google Scholar]
- 29.Barry E, Dogic Z. Entropy driven self-assembly of nonamphiphilic colloidal membranes. Proc Natl Acad Sci USA. 2010;107:10348–10353. doi: 10.1073/pnas.1000406107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Manoharan VN. Colloidal matter: Packing, geometry, and entropy. Science. 2015;349:1253751–1253751. doi: 10.1126/science.1253751. [DOI] [PubMed] [Google Scholar]
- 31.Frenkel D. Order through entropy. Nat Mater. 2014;14:9–12. doi: 10.1038/nmat4178. [DOI] [PubMed] [Google Scholar]
- 32.Anders G, Klotsa D, Karas AS, Dodd PM, Glotzer SC. Digital alchemy for materials design: Colloids and beyond. ACS Nano. 2015;9:9542–9553. doi: 10.1021/acsnano.5b04181. [DOI] [PubMed] [Google Scholar]
- 33.Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science. 2000;287:627–631. doi: 10.1126/science.287.5453.627. [DOI] [PubMed] [Google Scholar]
- 34.Kamien RD, Liu AJ. Why is random close packing reproducible? Phys Rev Lett. 2007;99:155501. doi: 10.1103/PhysRevLett.99.155501. [DOI] [PubMed] [Google Scholar]
- 35.Ni R, Gantapara AP, Graaf J, Roij Rv, Dijkstra M. Phase diagram of colloidal hard superballs: From cubes via spheres to octahedra. Soft Matter. 2012;8:8826. [Google Scholar]
- 36.Gantapara AP, Graaf Jd, Roij Rv, Dijkstra M. Phase diagram and structural diversity of a family of truncated cubes: Degenerate close-packed structures and vacancy-rich states. Phys Rev Lett. 2013;111:015501. doi: 10.1103/PhysRevLett.111.015501. [DOI] [PubMed] [Google Scholar]
- 37.Anderson JA, Irrgang ME, Glotzer SC. Scalable metropolis Monte Carlo for simulation of hard shapes. Computer Phys Commun. 2016;204:21–30. [Google Scholar]
- 38.Chen ER, Klotsa D, Engel M, Damasceno PF, Glotzer SC. Complexity in surfaces of densest packings for families of polyhedra. Phys Rev X. 2014;4:11024. [Google Scholar]
- 39.Agarwal U, Escobedo FA. Mesophase behaviour of polyhedral particles. Nat Mater. 2011;10:230–235. doi: 10.1038/nmat2959. [DOI] [PubMed] [Google Scholar]
- 40.Song Y, Mason EA. Equation of state for a fluid of hard convex bodies in any number of dimensions. Phys Rev A. 1990;41:3121–3124. doi: 10.1103/physreva.41.3121. [DOI] [PubMed] [Google Scholar]
- 41.Kallus Y. The 3-ball is a local pessimum for packing. Adv Math. 2014;264:355–370. [Google Scholar]
- 42.Travesset A. Topological structure prediction in binary nanoparticle superlattices. Soft Matter. 2017;13:147–157. doi: 10.1039/c6sm00713a. [DOI] [PubMed] [Google Scholar]
- 43.Travesset A. Soft skyrmions, spontaneous valence and selection rules in nanoparticle superlattices. ACS Nano. 2017;11:5375–5382. doi: 10.1021/acsnano.7b02219. [DOI] [PubMed] [Google Scholar]
- 44.Waltmann C, Horst N, Travesset A. Capping ligand vortices as “atomic orbitals” in nanocrystal self-assembly. ACS Nano. 2017;11:11273–11282. doi: 10.1021/acsnano.7b05694. [DOI] [PubMed] [Google Scholar]
- 45.Lagarias JC, Zong C. Mysteries in packing regular tetrahedra. Not Am Math Soc. 2012;59:1392. [Google Scholar]
- 46.Geng Y, Anders G, Dodd PM, Dshemuchadse J, Glotzer SC. 2017. Engineering entropy for the inverse design of colloidal crystals from hard shapes. arXiv:1712.02471.
- 47.Sun Y, Xia Y. Shape-controlled synthesis of gold and Silver nanoparticles. Science. 2002;298:2176–2179. doi: 10.1126/science.1077229. [DOI] [PubMed] [Google Scholar]
- 48.Sau TK, Rogach AL. Nonspherical noble metal nanoparticles: Colloid-chemical synthesis and morphology control. Adv Mater. 2010;22:1781–1804. doi: 10.1002/adma.200901271. [DOI] [PubMed] [Google Scholar]
- 49.Xia Y, Xiong Y, Lim B, Skrabalak SE. Shape-controlled synthesis of metal nanocrystals: Simple chemistry meets complex physics? Angew Chem Int Ed. 2009;48:60–103. doi: 10.1002/anie.200802248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications. Elsevier; Amsterdam: 2002. [Google Scholar]
- 51.Frenkel D, Anthony JC. Ladd. New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres. J Chem Phys. 1984;81:3188–3193. [Google Scholar]
- 52.Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. J Comp Phys. 1976;22:245–268. [Google Scholar]
- 53.Fornberg B. Generation of finite difference formulas on arbitrarily spaced grids. Mathematics Comput. 1988;51:699–699. [Google Scholar]
- 54.Anderson JA, Lorenz CD, Travesset A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J Comput Phys. 2008;227:5342–5359. [Google Scholar]
- 55.Anderson JA, Glotzer SC. 2013. The development and expansion of HOOMD-blue through six years of GPU proliferation. arXiv:1308.5587.
- 56.Towns J, et al. XSEDE: Accelerating scientific discovery. Comput Sci Eng. 2014;16:62–74. [Google Scholar]
- 57.Adorf CS, Dodd PM, Glotzer SC. 2016. Signac - a simple data management framework. arXiv:1611.03543.
- 58.Adorf CS, Dodd PM. 2016. csadorf/signac: v0.7.0. Available at . . Accessed January 4, 2017. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.