Abstract
Electrocaloric (EC) refrigeration, an EC effect based technology has been accepted as an auspicious way in the development of next generation refrigeration due to high efficiency and compact size. Here, we report the results of our experimental investigations on electrocaloric response and electrical energy storage properties in lead-free nanocrystalline (1 − x)K0.5Na0.5NbO3-xLiSbO3 (KNN-xLS) ceramics in the range of 0.015 ≤ x ≤ 0.06 by the indirect EC measurements. Doping of LiSbO3 has lowered both the transitions (TC and TO–T) of KNN to the room temperature side effectively. A maximal value of EC temperature change, ΔT = 3.33 K was obtained for the composition with x = 0.03 at 345 K under an external electric field of 40 kV/cm. The higher value of EC responsivity, ζ = 8.32 × 10−7 K.m/V is found with COP of 8.14 and recoverable energy storage of 0.128 J/cm3 with 46% efficiency for the composition of x = 0.03. Our investigations show that this material is a very promising candidate for electrocaloric refrigeration and energy storage near room temperature.
Introduction
An enormous amount of global energy uses for refrigeration, processing plants and air-conditioners are mainly based on vapor compression technology based on a century ago developed mechanical compressor. Due to bulk sizes, complexity, non-capability of scaling down for modern technologies such as for electronic chips, mobile devices, etc, the traditional technology is not very effective and also the coolant are non-environmental friendly1–3. In terms of the cooling capacity the coefficient of performance (COP), stated as the heat extracted from the system in each unit of the electrical energy consumed is low for existing technology.
The alternative technology for eliminating the compressor, vapor refrigerant coolant and with the high COP, is the solid state based refrigeration technology. An active research in material science is for the search of caloric materials for applying in proposed prototype solid-state cooling devices which works on the electrocaloric effect4–6. The electrocaloric effect (ECE) is the adiabatic change entropy/temperature induced by the change in polarization due to a sudden operation of the electric field in ferroelectric materials7–9. Ferroelectric materials exhibit spontaneous polarization and when it comes under the operation of an external electric field, the electric dipoles change the orientation from disorder to order state. The entropy correlated with the polarization decreases. Since a conclusive entropy of the system is constant, to compensate the changes in the material system the lattice entropy increases which results in the increment of temperature (ECE). Polar nano-domains are randomly oriented in the ferroelectrics, multiple possible orientation leads to the enhanced ECE10 and also it is higher at the phase transition due to opposite dipoles in a unit cell. In terms of energy barrier, at critical point the energy barrier reduced which fall in between different phases, since more than one polar phase exists at this point and the entropy increased which enhance ECE.
Among all nanostructures, thin film can produce high ECE, but the electrocaloric strength (|ΔT|/|ΔE|) which is the main factor to decide the strength over applied field reduces, in bulk ceramics it is higher and more promiseable structure11–14. The colossal electric fields are the reason for high ECE in thin films that can be applied till the breakdown field, the cooling effect and specific density are low. The cooling strength of bulk ceramics are of high value but the observed ECE is sufficiently low for practical purposes in commercial refrigeration technologies and the reason behind is the low dielectric strength. So, the search for achieving high polarization ceramics with high dielectric strengths in the broad temperature range around room temperature is one of the most emerging fields of condensed matter and material science. The EC refrigeration based on ECE has shown significant potential for developing the next generation cooling technology due to high efficiency, easy miniaturisation and low cost for the replacement of traditional vapor compression technology15–17.
However, the giant ECE have been observed for lead-based material which is again hazardous and carcinogenic. In order to overcome this problem lead-free material like (Na0.5Ba0.5)TiO318,19, BaTiO320–23, (K0.5Na0.5)NbO39,13,24, Ba0.65Sr0.35TiO325,26 ferroelectric-based compounds are the better candidates. There had been a various report on the mentioned materials, but achieved EC temperature change (ΔT) is very less. It has been simulated for high polarization change, which is the key factor for ECE; associated with K0.5Na0.5NbO3 (KNN) based ceramics27 but experimentally there is no report for high positive ECE value so far. It is a ferroelectric material with the perovskite structure which exhibits temperature-dependent spontaneous polarization and possess giant ECE and also the best candidate for solid-state cooling28,29. In the present work, we have synthesized lead-free (1-x)K0.5Na0.5NbO3-xLiSbO3 (KNN-xLS) nanocrystalline ceramics with 0.015 ≤ x ≤ 0.06 and obtained the highest ECE value and EC responsivity experimentally by an indirect method based on Maxwell’s approach.
Results
Phase and microstructure
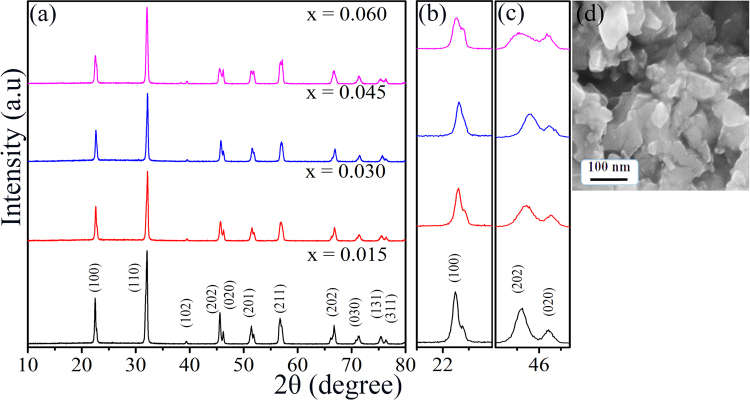
The purity and crystallinity of the as-prepared KNN-xLS powder samples were investigated by powder X-ray diffraction (XRD) measurements. Figure 1 shows room temperature XRD patterns from KNN-xLS powder samples, with x = 0.015, 0.03, 0.045 and 0.06, respectively. The crystal structure of KNN is an orthorhombic perovskite structure which is very different from the ilmenite structure of LiSbO330. All samples show the perovskite structure and we have not observed any extra or secondary peaks in XRD patterns, indicating that a homogeneous solid solution has formed by diffusing of Li+ and Sb5+ into the (K0.5Na0.5)NbO3 lattices, where Li+ goes to (Na0.5K0.5)+ sites and Sb5+ occupies the Nb5+ sites. Figure 1b,c show enlarged XRD patterns of (100) and (202/020) peak, respectively. For x ≤ 0.04, the diffraction peaks in Fig. 1 can be indexed to the orthorhombic structure (space group: Bmm2) of KNN with lattice constants of a = 5.69 Å, b = 3.97 Å, c = 5.72 Å and α = β = γ = 90°, which are in good agreement with literature results [i.e. JCPDS-ICDD 2001, Number 71-2171]. The orthorhombic structure is characterized by splitting of (020)/(202) peaks in the 2θ range of 44°–47°. The ceramic has an orthorhombic perovskite structure for x ≤ 0.04 which demonstrate the nonprimitive cell, increasing in the concentration of LiSbO3 leads to appear the tetragonal phase (primitive) and increases continuously for KNN-xLS. For x = 0.06, the orthorhombic and tetragonal phases coexist also reported by Lin et al.31. As can be seen in XRD patterns, the diffraction peaks show continuous shifts to higher 2θ values with increasing x due to lesser ionic radii of Li+ and Sb5+ than of the (Na0.5K0.5)+ and Nb5+.
Figure 1.
The room temperature XRD patterns of KNN-xLS powder samples (a) 2θ range 10°–80°, (b) enlarge view of (100) peak, (c) enlarge view of (202) and (020) peaks, and (d) FE-SEM micrograph of KNN-0.03LS ceramic.
The XRD data was used to calculate the average crystallite size using scherrer’s relation, d = 0.9λ/β cos θ 32, where d is the average crystallite size, β is the full width at half maxima (FWHM) value corrected with instrument broadening and λ is the wavelength of Cu-Kα radiation taken to be 1.54 Å. The calculated crystallite size for KNN-xLS are found to be 35, 41, 53 and 40 nm for x = 0.015, 0.03, 0.045 and 0.06 respectively for (110) peak confirming the nanocrystalline nature of the samples. Figure 1d shows the field emission scanning electron microscope (FE-SEM) micrograph of KNN-0.03LS ceramics. The observed grain size is in the 30–80 nm range, which matches with the obtained size from XRD. The grains are diffused in each other due to surface diffusion and coalescence while high sintering temperature. It also points to the high density of the sample as we have observed in the calculation of density which reflects in the high dielectric constant with high polarization.
Dielectric study
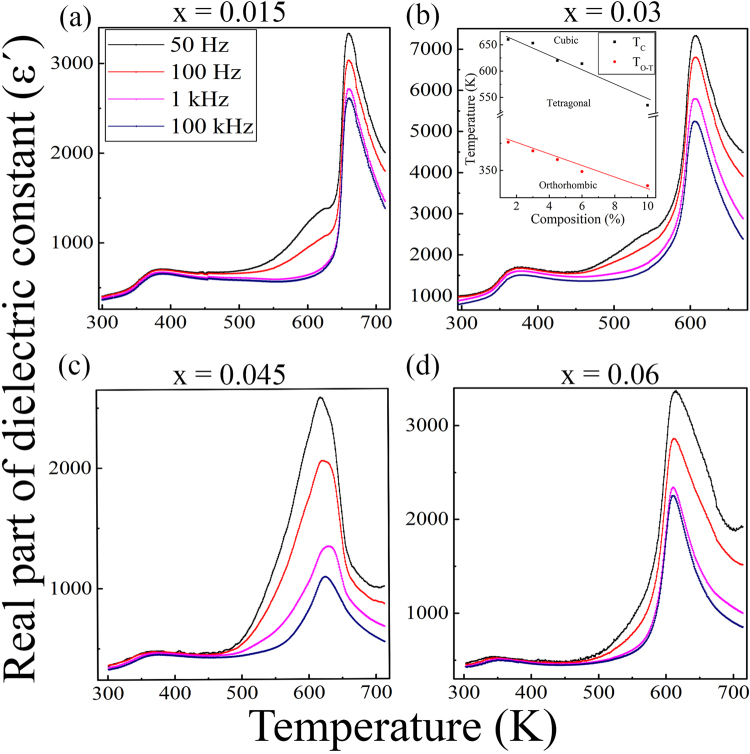
The variation of real part of dielectric permittivity (ε′) with temperature for different frequencies depicted in Fig. 2a–d for KNN-xLS nanocrystalline ceramics with x = 0.015, 0.03, 0.045 and 0.06, respectively. The ε′ was measured for sintered sample in the heating run conditions without any aging process. For pure KNN, the transition from orthorhombic ferroelectric to tetragonal ferroelectric phase (TO–T) occur at 463 K and tetragonal ferroelectric to cubic paraelectric phase (TC) at 670 K33. The addition of LiSbO3, shifts TC and TO–T to lower temperature side with retaining the ferroelectric behavior as shown in the inset of Fig. 2b. The TC decreases rapidly with increasing LiSbO3 than the TO–T. KNN-xLS have ABO3 structure, Li+ partially substituted to A site ions (K0.5Na0.5)+ and Sb5+ to the B site ion Nb5+. As it can be noticed the partial substitution of Li+ at A-site ions (K0.5Na0.5)+ become a cause of TC to increase whereas TO–T to decrease34. Whereas partial submission of Sb5+ at B-site ions Nb5+ decrease both TC and TO–T fastly35, conclusively the temperature falling rates are different for both TC and TO–T. The permittivity of KNN-xLS shows the normal ferroelectrics behavior, rather than the relaxor and the character of dependence of dielectric permittivity on frequency resembles the contribution from the increasing electrical conductivity upon increasing of temperature. The observed value of ε′ is high for x = 0.03 which is also depicted in the calculation of ECE, a high ECE has been achieved compare to other compositions.
Figure 2.
Temperature dependent real part of dielectric constant (ε′) of KNN-xLS ceramics for (a) x = 0.015, (b) x = 0.03, (c) x = 0.045, and (d) x = 0.06 in the temperature range of 300 K–714 K for frequency 50 Hz to 100 kHz. The inset of (b) shows the variation of both transitions TC and TO–T with composition for KNN-xLS ceramics.
ECE study
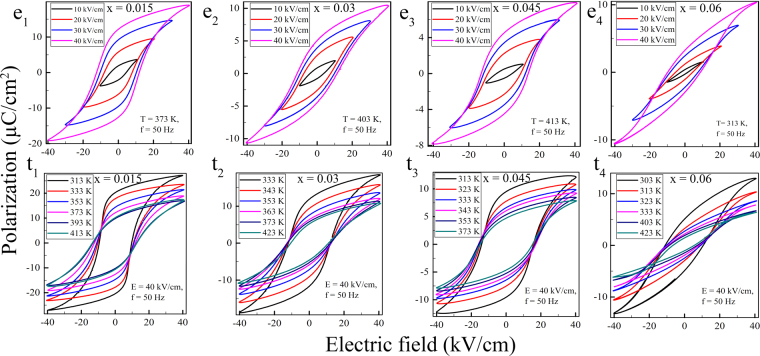
For calculating the electrocaloric effect of KNN-xLS, the polarization - electric field (P-E) hysteresis loops at 50 Hz were recorded for x = 0.015, 0.03, 0.045 and 0.06 at different temperatures with increment of 10 K and for maximum electric field 40 kV/cm The P-E hysteresis loops have shown in Fig. 3 (ei: i ⊂ ) for a different field from 10 kV/cm to 40 kV/cm at fixed operating temperature and Fig. 3 (ti: i ⊂ ) represents the P-E behavior at a fixed field of 40 kV/cm for varying temperatures.
Figure 3.
Variation of polarization with electric field at fixed temperature (ei: i ⊂ ) and with temperature at a fixed field (ti: i ⊂ ) for KNN-xLS (x = 0.015, 0.03, 0.045, and 0.06) nanocrystalline ceramics.
The variation of saturation polarization (P), isothermal entropy change (ΔS) and adiabatic temperature change (ΔT) with operating temperature for different electric field are shown in Fig. 4a–d for x = 0.015, 0.03, 0.045 and 0.06 respectively. P vs T data is fitted with 4th order polynomial, which is also accepted by a number of reports in order to apply Maxwell’s thermodynamic approach to calculate the ECE1,12. The key factor to calculate ECE is dP/dT, that can be found by the first order differentiation of P vs T curve. The electrocaloric effect (adiabatic temperature change, ΔT) have estimated by indirect approach based on Maxwell’s relation (∂P/∂T)E = (∂S/∂E)T, the isothermal entropy (ΔS) and the adiabatic temperature change (ΔT) at applied electric field E are given by11,12.
| 1 |
| 2 |
where E1, E2 denote the initial and final electric field, ρ is the bulk density, CP is the specific heat capacity, P is the saturation polarization. E1 is taken to be zero and E2 is the maximum field. Bulk densities for KNN-xLS; x = 0.015, 0.03, 0.045, 0.06 are 4.22, 4.38, 4.40, 4.39 g/cm3 respectively. The specific heat capacity has calculated to be 0.55 J/g.K at 345 K for KNN-0.03LS using differential scanning calorimeter (DSC) measurements and was used for other composition23,36. The maximum ΔS and ΔT are found to be 8.03 J/kg.K and 3.33 K at 345 K for 40 kV/cm using eqs 1 and 2 for KNN-0.03LS. The maximum ECE achieved for 40 kV/cm and higher field was not tried due to the breakdown field which also estimate and limits the dielectric strength. The obtained highest peak corresponding to ECE occurs around the first order phase transition (TO–T) as obtained by the dielectric permittivity measurement shown in Fig. 2b, the peak corresponds to the depolarization state of the sample37. Among x = 0.015, 0.03, 0.045, 0.06 composition, the calculated ECE increases from x = 0.015 to x = 0.03 then gets a low value for x = 0.045 and rise again for x = 0.06 shown in the Table 1. Electrocaloric responsivity (ΔT/ΔE), is the factor to define the variation of the adiabatic temperature change over change in applied field2, here E1 is taken to be zero and E2 is the applied field. The maximum calculated ΔT/ΔE for KNN-0.03LS is 8.32 × 10−7 K.m/V, the trend of variation in ΔT/ΔE follows the same as for the ECE listed in the Table 1.
Figure 4.
The change in polarization, entropy and electrocaloric temperature as a function of operating temperature for different external electric fields for KNN-xLS nanocrystalline ceramics (a) x = 0.015, (b) x = 0.03, (c) x = 0.045, and (d) x = 0.06.
Table 1.
Comparison of EC response for different bulk ceramics.
| Composition | ΔT(K) | E (kV/cm) | T (K) | ΔT/ΔE (×10−7 K.m/V) | refs |
|---|---|---|---|---|---|
| SrBi2(Nb0.2Ta0.8)2O9 | 0.19 | 60 | 333 | 43 | |
| Ba(Zr0.029Ti0.823)Sn0.075O3 | 0.19 | 8.7 | 303 | 2.2 | 44 |
| (Ba0.95Ca0.05) (Zr0.1Ti0.9)O3 | 0.205 | 8 | 368 | 2.56 | 22 |
| (Ba0.8Ca0.2) (Zr0.08Ti0.92)O3 | 0.22 | 7.95 | 377 | 2.7 | 45 |
| (Bi0.5Na0.5)0.94Ba0.06TiO3 4% | 0.25 | 40 | 375 | 17 | |
| 1 wt% Li doped (Ba0.85Ca0.15) (Zr0.1Ti0.9)O3 | 0.26 | 20 | 353 | 1.64 | 16 |
| (Ba0.8Ca0.2) (Zr0.04Ti0.96)O3 | 0.27 | 7.95 | 386 | 3.4 | 45 |
| 0.9(K0.5Na0.5)NbO3-0.1Sr(Sc0.5Nb0.5)O3* | 0.28 | 25 | 357 | 0.27 | 9 |
| (Ba0.8Ca0.2)1−xLa2x/3TiO3, x = 0.05 | 0.30 | 25 | 250–400 | 1.2 | 46 |
| B0.91Ca0.09Zr0.14Ti0.86O3 | 0.30 | 20 | 333 | 1.5 | 11 |
| Ba(Zr0.2Ti0.8)O3 | 0.325 | 30 | 310 | 21 | |
| 0.9(K0.5Na0.5)NbO3-0.1SrTiO3* | 0.43 | 40 | 330 | 0.7 | 42 |
| [(Bi1/2Na1/2)0.94Ba0.06]1−1.5xLaxTiO3, x = 0.03 | 0.44 | 42 | 363 | 15 | |
| 0.5 mol.% La -doped 0.88Pb(Mg1/3Nb2/3)O3-0.12PbTiO3 | 0.44 | 40 | 313 | 47 | |
| (Ba0.835Ca0.165) (Zr0.09Ti0.91)O3 | 0.46 | 12 | 404 | 3.8 | 48 |
| Ba0.65Sr0.35TiO3 | 0.49 | 50 | 303 | 1 | 25 |
| 0.96(K0.48Na0.52) (Nb0.95Sb0.05)O3-0.04Bi0.5(Na0.82K0.18)0.5ZrO3* | 0.51 | 40 | 350 | 1.3 | 24 |
| Ba0.94Sr0.06Ti0.9Sn0.1O3 | 0.55 | 20 | 342 | 2.75 | 49 |
| BaTi0.885Sn0.105O3 | 0.61 | 20 | 303 | 3.5 | 50 |
| (Pb0.88Sr0.88) (Nb0.08(Zr0.53Ti0.47)0.42)O3 | 0.65 | 15 | 453 | 4.3 | 51 |
| 0.9(0.75Pb(Mg1/3Nb2/3)O3-0.25PbTiO3)-0.1PbSnO3 | 0.66 | 30 | 373 | 2.20 | 52 |
| (1-x)Ba(Hf0.2Ti0.8)O3-x(Ba0.7Ca0.3)TiO3, x = 30 | 0.68 | 30 | 340 | 2.27 | 53 |
| Na1/2(Bi0.98Gd0.02)1/2TiO3 | 0.75 | 90 | 370 | 0.8 | 18 |
| BaCe0.12Ti0.88O3 | 0.8 | 24 | 251 | 23 | |
| BaTiO3 | 0.9 | 24 | 395 | 23 | |
| Ba0.85Ca0.15Ti0.94Hf0.06O3 | 1.03 | 35 | 406 | 54 | |
| 0.75(Na0.5Bi0.5)TiO3-0.25SrTiO3 | 1.64 | 50 | 333 | 3.3 | 19 |
| (Ba0.9Ca0.1) (Zr0.05Ti0.95)O3, | 1.64 | 70 | 403 | 2.3 | 55 |
| ([Bi1/2(Na0.84K0.16)1/2]0.96Sr0.04) (Ti0.975Nb0.025)O3 | 1.85 | 50 | 305 | 3.7 | 56 |
| 0.85K0.5Na0.5NbO3-0.15SrTiO3* | 1.9 | 159 | 340 | 13 | |
| Ba0.65Sr0.35TiO3 | 2.1 | 90 | 303 | 2.3 | 26 |
| P0.89La0.11(Zr0.7Ti0.3)0.9725O3 | 2.21 | 70 | 423 | 3.2 | 2 |
| Pb0.99Nb0.02[(Zr0.57Sn0.43)0.92Ti0.08]0.98O3 | 2.5 | 90 | 361 | 57 | |
| 0.985(K0.5Na0.5)NbO3-0.015LiSbO3* | 2.37 | 40 | 358 | 5.9 | this work |
| 0.97(K0.5Na0.5)NbO3-0.03LiSbO3* | 3.33 | 40 | 345 | 8.32 | this work |
| 0.955(K0.5Na0.5)NbO3-0.045LiSbO3* | 0.25 | 40 | 390 | 0.63 | this work |
| 0.94(K0.5Na0.5)NbO3-0.06LiSbO3* | 0.76 | 40 | 393 | 1.9 | this work |
(*KNN-based ceramics).
For ferroelectric ceramics, the electrical energy storage density and the efficiency can be obtained from P-E loops by the eqs 3, 4 and 5 38.
| 3 |
| 4 |
| 5 |
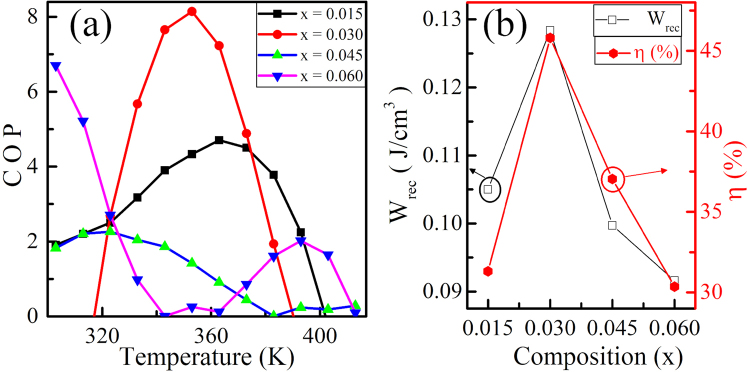
where E is the applied field, P is the polarization, Wrec is the recoverable energy, Wtotal is total energy and η is the efficiency. Figure 5 shows the variation of Wrec, η for all the value of x in KNN-xLS. The calculated maximum Wrec is 0.128 J/cm3 for KNN-0.03LS and efficiency (η) is 46% which is higher than various other lead - free ceramics. The coefficient of performance (COP), a factor to evaluate the cooling performance can be calculated as COP = |Q|/Wtotal, Where Q is T.ΔS; a ratio of extracted heat and the input work. The maximum COP, 8.14 at 353 K obtained for KNN-0.03LS shown in Fig. 5a and it is larger than for the other compositions.
Figure 5.
Variation of (a) COP with temperature (b) Wrec and η (%) with composition for KNN-xLS (x = 0.015, 0.03, 0.045, and 0.06) nanocrystalline ceramics.
Discussion
The recorded P-E loops at each temperature and the field are not slim, which is also an evident for non-relaxor behavior that is in connection with the variation of dielectric permittivity with temperature and it also represent the coarse grain microstructure for the material39. The size of the grain impacts the breakdown strength (BDS) over the applied field, which is described by E G−a, where E is the breakdown field, G is the grain size and ‘a’ is a constant40. It states that smaller grain increases the BDS which further results in high P and high ECE along with good energy storage capacity41. The net achieved polarization is induced by poling and the symmetry occurs in loops because of lacking of pining defect dipoles, increasing in space charge polarization is the reason for the change in shape of the P-E loops for compositions shown in Fig. 3(e1 to e4). At the lower field, the P-E loop is not in the saturated state and rising the field makes the P-E loop saturated, which resembles the higher energy density state and the increasing dielectric strength of the material. The saturated P-E hysteresis loop is due to the coexistence of both orthorhombic and tetragonal phases near the transition temperature. As rising in the temperature, the polarization decreases for all the compositions which indicates vanishing the dipole arrangement due to thermal agitation.
For the ECE measurement, the Maxwell relation has been used which is widely accepted with the 4th order polynomial fitted P vs T curve2. The calculated maximum ECE found for the case of KNN-0.03LS with the reason for having high real part of the dielectric constant which implies the high mobility of domains. Whereas for the x = 0.015, 0.045, 0.06 it is less than the 0.03 which is also depicted in the plot for real part of the dielectric permittivity shown in Fig. 2. This behavior of ECE is in relation with the obtained dielectric constant corresponding to their compositions concludes that ceramics with high dielectric constant exhibits ΔT more. As listed in the Table 1, KNN-0.03LS composition has large ECE value among all lead-free nanocrystalline ceramics reported so far in any mode of measurements.
Even if for the case of thin/thick films, the ECE obtained to be more, but the electrocaloric responsivity (ΔT/ΔE) is less than for the bulk due to thin film needs high field for ECE. Thin films have high breakdown field strength i.e. higher the sustainability whereas bulk ceramics have less breakdown strength due to some extrinsic factors (voids, interfaces, defects, etc). KNN-0.03LS also shows a high coefficient of performances (COP) among other lead-free ceramics, it shows the high refrigeration capacity for the material. The recoverable energy storage capacity and efficiency is higher among many other lead-free ceramics.
In summary, The electrocaloric effect of (1 − x)K0.5Na0.5NbO3-xLiSbO3 nanocrystalline ceramics with x = 0.015, 0.03, 0.045 and 0.06 are evaluated using Maxwell’s thermodynamic relation. The microstructures and dielectric permittivity of the sample were studied and discussed in relation with ECE. The remarkable electrocaloric efficiency (ΔT/ΔE), COP have been observed with the effective change of the temperature. The calculated maximum ECE peak has found near phase transition temperatures. It was found to be with high energy storage capacity and COP. Conclusively KNN-0.03LS become the more potential candidate for refrigeration as micro cooler and in energy storage applications, etc.
Methods
Preparation of samples
A conventional solid-state route had been followed in the synthesis of (1-x)K0.5Na0.5NbO3-xLiSbO3 samples9,42. The high purity (99%) starting precursors K2CO3 (Hi-Media), Na2CO3 (Hi-Media), Nb2O5 (Hi-Media), C2H3LiO2.2H2O (Sigma) and C6H9O6Sb (Hi-Media) were used. The stoichiometric, homogenized mixture of precursors were grinded using mortar and pestle (agate) for 8 h till to achieving the uniform small size of the mixture. The dried mixed precursor powder was calcined at 1153 K for 5 h. The calcined powder was uniaxially pressed (~125 kN) into the disk form of 10 mm diameter with 1 mm thickness using steel die after mixing with 5 wt% polyvinyl alcohol solution prepared in water and compacts were sintered further for 1343–1383 K for 4 h in ample oxygen using the double crucible method to suppress the volatile nature of alkali oxides.
Characterization
X-ray diffraction (XRD) data of sintered powder was obtained using a X-ray diffractometer (Rigaku mini Flex 600, Japan: λ = 1.54 Å) with Cu-Kα radiation. The surface morphology has been observed by field-emission scanning electron microscopy (FE-SEM, LYRA3-TESCAN). The density of the samples were measured using the Archimedes method with di-ionized water. The dielectric permittivity measurements have performed for the frequency 50 Hz–1 MHz in the temperature range of 303 K–773 K by an impedance analyzer (E4990A, Keysight Technologies) at 0.50 V osc voltage and zero bias voltage. Furthermore, the Polarization-electric field (P-E) characterization was carried out using a P-E Loop Tracer (Marine India). For the electric measurements, both the surfaces of the pallet was layered by a uniform thin silver paste and dried at 773 K for 25 minutes. The specific heat capacity (Cp) was calculated using a differential scanning calorimeter (Mettler Toledo DSC-3).
Acknowledgements
We acknowledge School of Physical Sciences and AIRF, JNU, New Delhi for extending the characterization facilities. S. Singh acknowledge the financial supports from SERB (EEQ/2016/000256), DST (PURSE-II) and UGC (Project #33, UPE-II), Govt. of India. R. Kumar acknowledges the award of the junior research fellowship of UGC. S Singh thanks to Jawaharlal Nehru University, New Delhi, India for providing funds for publication charges of this article.
Author Contributions
R. Kumar has conceived/conducted the experiment under the supervision of S. Singh. R. Kumar and S. Singh have analyzed the results and finalized the manuscript. All authors reviewed the manuscript.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Mischenko AS, Zhang Q, Scott JF, Whatmore RW, Mathur ND. Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3. Sci. 2006;311:1270–1271. doi: 10.1126/science.1123811. [DOI] [PubMed] [Google Scholar]
- 2.Lu B, et al. Large Electrocaloric Effect in Relaxor Ferroelectric and Antiferroelectric Lanthanum Doped Lead Zirconate Titanate Ceramics. Sci. Reports. 2017;7:45335. doi: 10.1038/srep45335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moya X, Kar-Narayan S, Mathur ND. Caloric materials near ferroic phase transitions. Nat. materials. 2014;13:439–450. doi: 10.1038/nmat3951. [DOI] [PubMed] [Google Scholar]
- 4.Neese B, et al. Large electrocaloric effect in ferroelectric polymers near room temperature. Science (New York, NY) 2008;321:821–823. doi: 10.1126/science.1159655. [DOI] [PubMed] [Google Scholar]
- 5.Li B, et al. Effect of surface tension on electrocaloric effects in the ferroelectric nanomaterial with vortex domain structures. J. Appl. Phys. 2013;114:044301. doi: 10.1063/1.4813508. [DOI] [Google Scholar]
- 6.Tušek J, et al. A regenerative elastocaloric heat pump. Nature Energy. 2016;1:16134. doi: 10.1038/nenergy.2016.134. [DOI] [Google Scholar]
- 7.Kar-Narayan S, et al. Direct electrocaloric measurements of a multilayer capacitor using scanning thermal microscopy and infra-red imaging. Appl. Phys. Lett. 2013;102:032903. doi: 10.1063/1.4788924. [DOI] [Google Scholar]
- 8.Moya X, et al. Giant electrocaloric strength in single-crystal BaTiO3. Adv. Mater. 2013;25:1360–1365. doi: 10.1002/adma.201203823. [DOI] [PubMed] [Google Scholar]
- 9.Kumar R, Singh S. Enhanced electrocaloric effect in lead-free 0.9(K0.5Na0.5)NbO3-0.1Sr(Sc0.5Nb0.5)O3 ferroelectric nanocrystalline ceramics. J. Alloy. Compd. 2017;723:589–594. doi: 10.1016/j.jallcom.2017.06.252. [DOI] [Google Scholar]
- 10.Pirc R, Kutnjak Z, Blinc R, Zhang QM. Electrocaloric effect in relaxor ferroelectrics. J. Appl. Phys. 2011;110:074113. doi: 10.1063/1.3650906. [DOI] [Google Scholar]
- 11.Bai Y, Han X, Ding K, Qiao LJL-J. Combined effects of diffuse phase transition and microstructure on the electrocaloric effect in Ba1-xSrxTiO3 ceramics. Applied Physics Letters. 2013;103:162902. doi: 10.1063/1.4853915. [DOI] [Google Scholar]
- 12.Li J, et al. Large room-temperature electrocaloric effect in lead-free BaHfxTi1−xO3 ceramics under low electric field. Acta Mater. 2016;115:58–67. doi: 10.1016/j.actamat.2016.05.044. [DOI] [Google Scholar]
- 13.Koruza J, et al. Large electrocaloric effect in lead-free K0.5Na0.5NbO3-SrTiO3 ceramics. Appl. Phys. Lett. 2015;106:202905. doi: 10.1063/1.4921744. [DOI] [Google Scholar]
- 14.Asbani B, et al. Dielectric permittivity enhancement and large electrocaloric effect in the lead free (Ba0.8Ca0.2)1-xLa2x/3TiO3 ferroelectric ceramics. J. Alloys Compd. 2018;730:501–508. doi: 10.1016/j.jallcom.2017.09.301. [DOI] [Google Scholar]
- 15.Li L, et al. Electrocaloric effect in la-doped bnt-6bt relaxor ferroelectric ceramics. Ceram. Int. 2018;44:343–350. doi: 10.1016/j.ceramint.2017.09.179. [DOI] [Google Scholar]
- 16.Shi J, et al. Large Electrocaloric Effect in Lead-Free (Ba0.85Ca0.15) (Zr0.1Ti0.9)O3 Ceramics Prepared via Citrate Route. Materials. 2017;10:1093. doi: 10.3390/ma10091093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Srikanth KS, Patel S, Vaish R. Enhanced electrocaloric effect in glass-added 0.94Bi0.5Na0.5TiO3-0.06BaTiO3 ceramics. J. Aust. Ceram. Soc. 2017;53:523. doi: 10.1007/s41779-017-0063-5. [DOI] [Google Scholar]
- 18.Zannen M, et al. Electrocaloric effect and energy storage in lead free Gd0.02Na0.5Bi0.48TiO3 ceramic. Solid State Sci. 2017;66:31–37. doi: 10.1016/j.solidstatesciences.2017.02.007. [DOI] [Google Scholar]
- 19.Cao WP, et al. Large electrocaloric response and high energy-storage properties over a broad temperature range in lead-free NBT-ST ceramics. J. Eur. Ceram. Soc. 2016;36:593–600. doi: 10.1016/j.jeurceramsoc.2015.10.019. [DOI] [Google Scholar]
- 20.Bai Yang, et al. Electrocaloric Refrigeration Cycles with Large Cooling Capacity in Barium Titanate Ceramics Near Room Temperature. Energy Technol. 2017;5:703–707. doi: 10.1002/ente.201600456. [DOI] [Google Scholar]
- 21.Weyland F, Eisele T, Steiner S. Long term stability of electrocaloric response in barium zirconate titanate. J. Eur. Ceram. Soc. 2017;38:551–556. doi: 10.1016/j.jeurceramsoc.2017.09.018. [DOI] [Google Scholar]
- 22.Kaddoussi H, et al. Sequence of structural transitions and electrocaloric properties in (Ba1-xCax) (Zr0.1Ti0.9)O3 ceramics. J. Alloys Compd. 2017;713:164–179. doi: 10.1016/j.jallcom.2017.04.148. [DOI] [Google Scholar]
- 23.Srikanth KS, Vaish R. Enhanced electrocaloric, pyroelectric and energy storage performance of BaCexTi1-xO3 ceramics. J. Eur. Ceram. Soc. 2017;37:3927–3933. doi: 10.1016/j.jeurceramsoc.2017.04.058. [DOI] [Google Scholar]
- 24.Wang XX, et al. Enhanced electrocaloric effect near polymorphic phase boundary in lead-free potassium sodium niobate ceramics. Appl. Phys. Lett. 2017;110:63904. doi: 10.1063/1.4976026. [DOI] [Google Scholar]
- 25.Ge P, et al. Energy storage properties and electrocaloric effect of Ba0.65Sr0.35TiO3 ceramics near room temperature. J. Mater. Sci. Mater. Electron. 2017;29:1075–1081. doi: 10.1007/s10854-017-8008-x. [DOI] [Google Scholar]
- 26.Liu XQ, Chen TT, Wu YJ, Chen XM. Enhanced electrocaloric effects in spark plasma-sintered Ba0.65Sr0.35TiO3-based ceramics at room temperature. J. Am. Ceram. Soc. 2013;96:1021–1023. doi: 10.1111/jace.12219. [DOI] [Google Scholar]
- 27.Barr JA, Beckman SP. Electrocaloric response of KNbO3 from a first-principles effective Hamiltonian. Mater. Sci. Eng. B: Solid-State Mater. Adv. Technol. 2015;196:40–43. doi: 10.1016/j.mseb.2015.02.004. [DOI] [Google Scholar]
- 28.Fatuzzo E, Kiess H, Nitsche R. Theoretical efficiency of pyroelectric power converters. J. Appl. Phys. 1966;37:510–516. doi: 10.1063/1.1708205. [DOI] [Google Scholar]
- 29.Liu M, Wang J. Giant electrocaloric effect in ferroelectric nanotubes near room temperature. Sci. reports. 2015;5:7728. doi: 10.1038/srep07728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kumada N. Preparation and Crystal Structure of a New Lithium Bismuth Oxide: LiBiO3. J. Solid State Chem. 1996;126:121–126. doi: 10.1006/jssc.1996.0319. [DOI] [Google Scholar]
- 31.Lin D, Kwok KW, Lam KH, Chan HLW. Structure and electrical properties of K0.5Na0.5NbO3−LiSbO3 lead-free piezoelectric ceramics. J. Appl. Phys. 2007;101:074111. doi: 10.1063/1.2715486. [DOI] [Google Scholar]
- 32.Holzwarth U, Gibson N. The Scherrer equation versus the’Debye-Scherrer equation’. Nat. Nanotechnol. 2011;6:534. doi: 10.1038/nnano.2011.145. [DOI] [PubMed] [Google Scholar]
- 33.Qu B, Du H, Yang Z. Lead Free Relaxor Ferroelectric Ceramics with High Optical Transparency and Energy Storage Ability. J. Mater. Chem. C. 2016;4:1795–1803. doi: 10.1039/C5TC04005A. [DOI] [Google Scholar]
- 34.Feng G, Zhenqi D, Le Y, Lihong C, Changsheng T. Phase transitional behavior and piezoelectric properties of BiYbO3-Pb(Ti0.5Zr0.5)O3-LiNbO3 ceramics. Ceram. Int. 2009;35:2885–2890. doi: 10.1016/j.ceramint.2009.03.045. [DOI] [Google Scholar]
- 35.Matsubara M, Kikuta K, Hirano S. Piezoelectric properties of (k0.5na0.5) (nb1−xtax)o3-k5.4cu ta10o29 ceramics. J. Appl. Phys. 2005;97:114105. doi: 10.1063/1.1926396. [DOI] [Google Scholar]
- 36.Patel S, Sharma P, Vaish R. Enhanced electrocaloric effect in Ba0.85Ca0.15Zr0.1Ti0.9−xSnxO3 ferroelectric ceramics. Phase Transitions. 2016;89:1062–1073. doi: 10.1080/01411594.2016.1144752. [DOI] [Google Scholar]
- 37.Sebald G, et al. Electrocaloric properties of high dielectric constant ferroelectric ceramics. J. Eur. Ceram. Soc. 2007;27:4021–4024. doi: 10.1016/j.jeurceramsoc.2007.02.088. [DOI] [Google Scholar]
- 38.Hao X. A review on the dielectric materials for high energy-storage application. J. Adv. Dielectr. 2013;03:1330001. doi: 10.1142/S2010135X13300016. [DOI] [Google Scholar]
- 39.Jin L, Li F, Zhang S. Decoding the fingerprint of ferroelectric loops: Comprehension of the material properties and structures. J. Am. Ceram. Soc. 2014;97:1–27. doi: 10.1111/jace.12773. [DOI] [Google Scholar]
- 40.Zhou M, et al. High energy storage properties of (Ni1/3Nb2/3)4+ complex-ion modified (Ba0.85Ca0.15) (Zr0.10Ti0.90)O3 ceramics. Mater. Res. Bull. 2018;98:166–172. doi: 10.1016/j.materresbull.2017.10.005. [DOI] [Google Scholar]
- 41.Patel S, Vaish R. Effect of sintering temperature and dwell time on electrocaloric properties of Ba0.85Ca0.075Sr0.075Ti0.90Zr0.10O3 ceramics. Phase Transitions. 2016;90:465–474. doi: 10.1080/01411594.2016.1219910. [DOI] [Google Scholar]
- 42.Gupta A, Kumar R, Singh S. Coexistence of negative and positive electrocaloric effect in lead-free 0.9(K0.5Na0.5)NbO3-0.1SrTiO3 nanocrystalline ceramics. Scripta Mater. 2018;143:5–9. doi: 10.1016/j.scriptamat.2017.08.045. [DOI] [Google Scholar]
- 43.Axelsson A-K, Le Goupil F, Valant M, Alford NM. Electrocaloric effect in lead-free Aurivillius relaxor ferroelectric ceramics. Acta Mater. 2017;124:120–126. doi: 10.1016/j.actamat.2016.11.001. [DOI] [Google Scholar]
- 44.Kaddoussi H, Lahmar YGA, Dellis BAJL. Ferroelectric phase changes and electrocaloric effects. J. Mater. Sci. 2016;51:3454–3462. doi: 10.1007/s10853-015-9663-z. [DOI] [Google Scholar]
- 45.Asbani B, et al. Electrocaloric effect in Ba0.2Ca0.8Ti0.95Ge0.05O3 determined by a new pyroelectric method. EPL. 2015;111:57008. doi: 10.1209/0295-5075/111/57008. [DOI] [Google Scholar]
- 46.Asbani B, et al. Dielectric permittivity enhancement and large electrocaloric effect in the lead free (Ba0.8Ca0.2)1-xLa2x/3TiO3 ferroelectric ceramics. J. Alloy. Compd. 2018;730:501–508. doi: 10.1016/j.jallcom.2017.09.301. [DOI] [Google Scholar]
- 47.Chen G, et al. Large electrocaloric effect in La-doped 0.88Pb(Mg1/3Nb2/3)O3-0.12PbTiO3 relaxor ferroelectric ceramics. J. Alloy. Compd. 2017;727:785–791. doi: 10.1016/j.jallcom.2017.08.204. [DOI] [Google Scholar]
- 48.Singh G, et al. Electro-caloric effect in 0.45BaZr0.2Ti0.8O3-0.55Ba0.7Ca0.3TiO3 single crystal. Appl. Phys. Lett. 2013;102:082902. doi: 10.1063/1.4793213. [DOI] [Google Scholar]
- 49.Qi S, et al. Electrocaloric effect in Pb-free Sr-doped BaTi0.9Sn0.1O3 ceramics. Mater. Res. Bull. 2017;91:31–35. doi: 10.1016/j.materresbull.2017.03.026. [DOI] [Google Scholar]
- 50.Luo Z, et al. Enhanced electrocaloric effect in lead-free BaTi1- xSnxO3 ceramics near room temperature. Appl. Phys. Lett. 2014;105:102904. doi: 10.1063/1.4895615. [DOI] [Google Scholar]
- 51.Chen C, et al. Coexistence of negative and positive electrocaloric effect in Sr and Nb co-doped Pb(Zr,Ti)O3 ferroelectric ceramics. Mater. Lett. 2017;189:303–306. doi: 10.1016/j.matlet.2016.11.006. [DOI] [Google Scholar]
- 52.Kriaa I, Maalej A, Khemakhem H. Electrocaloric Study Effect in the Relaxor Ferroelectric Ceramic 0.9(0.75PMN-0.25PT)-0.1PS. J. Electron. Mater. 2017;46:2529–2532. doi: 10.1007/s11664-017-5336-9. [DOI] [Google Scholar]
- 53.Wu P, et al. Direct and indirect measurement of electrocaloric effect in lead-free (100-x)Ba(Hf0.2Ti0.8)O3-x(Ba0.7Ca0.3)TiO3 ceramics near multi-phase boundary. J. Alloy. Compd. 2017;725:275–282. doi: 10.1016/j.jallcom.2017.07.103. [DOI] [Google Scholar]
- 54.Wang F, et al. Multicaloric effects in PbZr0.2Ti0.8O3 thin films with 90 degree domain structure. EPL. 2017;118:17005. doi: 10.1209/0295-5075/118/17005. [DOI] [Google Scholar]
- 55.Nie Xin, Yan Shiguang. and Guo, Shaobo and Cao, Fei and Yao, Chunhua and Mao, Chaoliang and Dong, Xianlin and Wang, G. The influence of phase transition on electrocaloric effect in lead-free (Ba0. 9Ca0. 1) (Ti1-xZrx) O3 ceramics. J. Am. Ceram. Soc. 2017;100:5202–5210. doi: 10.1111/jace.15040. [DOI] [Google Scholar]
- 56.Fan Zhongming, Liu Xiaoming, Tan X. Large electrocaloric responses in [Bi1/2(Na,K)1/2]TiO3 -based ceramics with giant electro-strains. J. Am. Ceram. Soc. 2017;100:2088–2097. doi: 10.1111/jace.14777. [DOI] [Google Scholar]
- 57.Xu Z, Fan Z, Liu X, Tan X. Impact of phase transition sequence on the electrocaloric effect in Pb(Nb,Zr,Sn,Ti)O3 ceramics. Appl. Phys. Lett. 2017;110:082901. doi: 10.1063/1.4976827. [DOI] [Google Scholar]