Identifying mechanisms of stance control: a single stimulus multiple output model-fit approach

Abstract

Background

Posture control models are instrumental to interpret experimental data and test hypotheses. However, as models have increased in complexity to include multi-segmental dynamics, discrepancy has arisen amongst researchers regarding the accuracy and limitations of identifying neural control parameters using a single stimulus.

New Method

The current study examines this topic using simulations with a parameterized model-fit approach. We first determine if the model-fit approach can identify parameters in the theoretical situation with no noise. Then, we measure variability and bias of parameter estimates when realistic noise is included. We also address how the accuracy is influenced by the frequency bandwidth of the stimulus, signal-to-noise of the data, and fitting procedures.

Results

We found perfect identification of parameters in the theoretical model without noise. With realistic noise, bias errors were 4.4% and 7.6% for fits that included frequencies 0.02–1.2 Hz and 0.02–0.4 Hz, respectively. Fits between 0.02–1.2 Hz also had the lowest variability in parameter estimates compared to other bandwidths. Parameters with the lowest variability tended to have the largest influence on body sways. Results also demonstrated the importance of closely examining model fits because of limitations in fitting algorithms.

Comparison with Existing Method

The single-input model-fit approach may be a simpler and more practical method for identifying neural control mechanisms compared to a multi-stimulus alternative.

Conclusions

This study provides timely theoretical and practical considerations applicable to the design and analysis of experiments contributing to the identification of mechanisms underlying stance control of a multi-segment body.

INTRODUCTION

Many studies have sought to understand the control of upright stance in humans by measuring body motion in various experimental conditions. However, interpretations of experimental results are often uncertain because of the complex interactions among the subsystems contributing to balance control. The subsystems contributing to the closed loop (feedback) control of stance include multi-segmental dynamics, muscle/tendon physiology, and sensorimotor processes (sensory integration and sensory-to-motor transformations represented by ‘neural controller’ properties). Feedback control models have been used to define the interactions among these subsystems and, thus, to provide a quantitative basis for interpreting how the various subsystems influence body sway characteristics. These feedback models are typically validated by determining the extent to which the models are able to account for results from experiments where body sway is evoked by an external stimulus (such as a moving stance surface or visual field, or applied forces) (Peterka 2002; Bingham et al. 2011; Oie et al. 2002; Kim et al. 2009; Kiemel et al. 2008; Goodworth & Peterka 2012; Engelhart et al. 2015; Boonstra et al. 2013; Maurer et al. 2006; Mergner 2010; Alexandrov et al. 2005) because an external stimulus is needed to accurately identify control parameters in a closed loop feedback control system (Fitzpatrick et al. 1996; van der Kooij 2005). Although several studies have successfully characterized sensorimotor processes using a single stimulus and simplified single-segment inverted pendulum model of the body (Peterka 2002; Oie et al. 2002; Bingham et al. 2011; Cenciarini & Peterka 2006), more insight into sensorimotor control of individual body segments is possible by representing the body’s multi-segment dynamics.

A few studies have interpreted multi-segment body dynamics using a two-segment model with a single external stimulus (Alexandrov et al. 2005; Park et al. 2004; Kim et al. 2009; Goodworth & Peterka 2012 & 2014; Kiemel et al. 2008). However, the validity of this “single-input multi-output” approach is not clear (Fig.1A). One research group claimed that, “when estimating the dynamics in a multivariate system, multiple perturbations need to be applied” (Boonstra et al. 2013) and “two independent disturbances must be applied that continuously challenge the balance control system” (Engelhart et al. 2015). The implication is that studies using a single external stimulus to characterize multi-segmental dynamics obtained results of questionable validity. In both studies quoted above, the research group used a model structure shown in Figure 1B to control a two-segment body in model simulations and showed major errors in calculating frequency response functions (FRFs) that represent the neural controller characteristics when a single stimulus was used. The calculation of neural controller FRFs from stimulus response data provides a “non-parametric” identification of the neural controller characteristics. To avoid errors in these FRF calculations, the authors offered an elegant alternative approach where two separate stimuli are applied to the lower and upper body. But is this complexity necessary?

Figure 1.

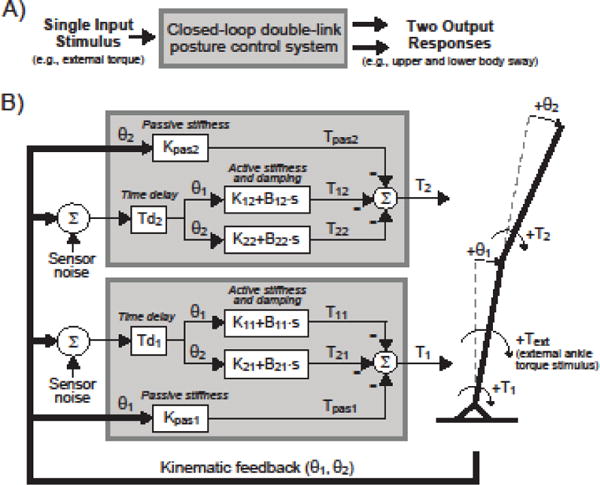
A) Schematic of a single-input multi-output system for closed loop posture control. B) Block diagram of the model used in the present study where a single external torque stimulus (T_ext) applied about the ankle joint evokes upper body sway (θ₂) and lower body sway (θ₁). Control is provided by generating corrective joint torques about the ankle (T₁) and hip (T₂) as a function of θ₁ and θ₂ scaled by stiffness and damping factors with time delay (for active control) and stiffness factors with no time delay (for passive control). Sensor noise is added to the kinematic feedback that contributes to active control to give simulation results with realistic sway variability. Note that the block diagram does not show torque components due to gravity and interactive torques due to body segment accelerations.

An alternative is to use “parametric” identification where the neural controllers are represented by a chosen model structure and the parameter values are estimated by model-fit procedures that adjust parameter values to best account for experimental stimulus-response data. We know of no a priori reason to believe that a parametric identification approach would not be able to obtain accurate estimates of neural controller parameters. A single stimulus evokes sway responses in multiple body segments and has the potential to provide a rich stimulus-response data set for a parametric identification procedure. However, even when the body is represented by only two segments, there is a proliferation of control parameters with potential redundancies in their influence and potential interactions among the parameters that may limit the ability of a model-fit procedure to obtain an accurate characterization of neural controller properties. An interaction between accurate parameter estimation and stimulus characteristics is also expected. For example, when an FRF is measured over a limited bandwidth, the small number of FRF data points may not be sufficient for a fit procedure to accurately identify the large number of model parameters. That is, many different combinations of parameters could potentially reproduce the available FRF data resulting in an inaccurate characterization of the neural controller properties.

The question about what system identification procedures are necessary or sufficient is of increasing importance as researchers seek to identify the mechanisms that contribute to balance control under realistic conditions that involve multi-segmental body motions. If there is a fundamental limitation in using a single stimulus to identify control characteristics of a multi-segment system, then future studies must factor this limitation into their experimental design prior to data collection. But developing an experimental system to deliver multiple stimuli across body segments may not be feasible for many research questions or clinical applications. In addition, if it is not possible to accurately identify neural controller parameters in a multi-segment system using a single stimulus, then the validity of numerous studies are in question. For example, Kim et al. (2009) used a single surface translation stimulus to perturb balance in the sagittal plane and identified neural controller parameters of a two-segment body in both healthy controls and subjects with Parkinson’s disease. Goodworth & Peterka (2012, 2014) used a single stimulus consisting of continuous surface tilts to perturb balance in the frontal plane and modeled the body as a multi-segment system to identify changes in neural processes across stance width. Therefore, the validity and limitations of the single stimulus approach has important implications for past and future studies.

The goal of the current study is to investigate the accuracy of a model-fit approach to identify neural controller parameters in a two-segment inverted pendulum body when a single stimulus is used (Fig. 1B). This approach differs from Engelhart et al. (2015) and Boonstra et al. (2013), who used a dual-stimulus paradigm (uncorrelated forces applied to the lower and upper body) and closed-loop system identification methods to calculate non-parametric representations of neural controller dynamics (i.e., FRFs) that characterize how lower body and upper body sway influences components of joint torques that contribute to the total compensatory lower body torque (T₁) and upper body torque (T₂) applied at the ankle joint and hip joint, respectively. This contrasts with our model-fit approach that uses a single stimulus (torque applied about the ankle joint) to evoke lower and upper body sway. The single-stimulus system identification method adjusts neural controller parameters of a parameterized model (Fig. 1B) to obtain optimal fits of model-predicted FRFs to FRFs obtained from experiments (or simulated experiments in the current study) that evoke upper and lower body sway across a range of frequencies. We first determine if this model fit approach can identify parameters in the theoretical situation where no sensor noise is present. Then, we measure variability and bias of parameter estimates when realistic noise is included in the model. We also address questions pertinent to research design. Specifically, how is the accuracy of parameter identification in the model-fit approach influenced by the frequency bandwidth of the stimulus, stimulus amplitude, and fitting procedures? This study provides timely theoretical and practical considerations applicable to the design and analysis of experiments contributing to the identification of mechanisms underlying stance control of a multi-segment body.

METHODS

Model description

Figure 1B shows the balance control model. This model is the same form as Engelhart et al. (2015, 2016) and Boonstra et al. (2013). A single external torque about the ankle joint evokes both lower body (LB) sway (θ₁) and upper body (UB) sway (θ₂). θ₁ is the angle between the lower body and upright; θ₂ is the angle between the upper body and lower body. The two-segment system is stabilized through corrective torque generated about the ankle and hip joints via active (time delayed) and passive (non-timed delayed) feedback control. Corrective torque is based on the scaling of body sway position, referred to as stiffness (either active or passive), and scaling of body sway velocity, referred to as damping.

For active control, neural controllers generate corrective torque as a function of θ₁ and θ₂ angular positions and velocities. There are 4 neural controllers and each generates a component of active ankle or hip torque by a sensory-to-motor transformation that scales body sway position (active stiffness factors, K_ii’s) and velocity (active damping factors, B_ii’s). Specifically, θ₁ position and velocity are scaled by K₁₁ and B₁₁, respectively, to generate a component of ankle joint torque, T₁₁. θ₁ position and velocity are also scaled by K₁₂ and B₁₂ to generate a component of hip torque, T₁₂. Similarly, θ₂ and θ₂ velocity are scaled by K₂₂ and B₂₂ to generate a component of hip torque, T₂₂, and are scaled by K₂₁ and B₂₁ to generate a component of ankle torque, T₂₁. Active ankle and hip torques are time delayed by Td₁ and Td₂. The time delays associated with active torque generation represents the time required for sensory transduction, neural signal transmission, sensorimotor processing, and muscle activation.

Passive mechanical muscle and tendon properties were represented by passive stiffness scale factors with no time delay (Engelhart 2016). θ₁ is scaled by K_pas1 and θ₂ is scaled by K_pas2 to generate passive components of ankle and hip torque, respectively. Passive parameters represent the intrinsic stiffness in the musculoskeletal system. Other models have also included passive damping (Engelhart et al. 2015; Boonstra et al. 2013; Goodworth and Peterka 2012, 2014), but only passive stiffness was included to simplify analyses and duplicate Engelhart et al. (2016). The value of K_pas1 is approximately 23% of mgh, where mgh is equal to the product of whole body mass, gravitational acceleration, and center of mass height above ankle joint. mgh is the minimum stiffness required to offset gravity and previous studies suggest passive stiffness around the ankle joint to be anywhere from 10% of mgh (Peterka 2002) to 90% (Loram & Lakie 2002) during perturbed and spontaneous sway, respectively.

The two-segment inverted pendulum mechanical model was developed following Koozekanani et al. (1980). Equations of motion were linearized about upright, identical to previous studies (e.g., Goodworth and Peterka 2012, Kiemel et al. 2008, Engelhart et al. 2015; Boonstra et al. 2013). Mass, center of mass height, moment of inertia, and neural controller parameters for each segment were based on data from Figure 5 in Engelhart (2016), but some neural controller parameters were modified slightly to those shown in Table 1 because system dynamics with the original parameters exhibited resonance behavior indicating that the system was close to instability. The parameters associated with body dimensions shown in Table 1 were held constant in all analyses. The remaining parameters in Table 1 (K’s, B’s, and time delays) represent the “true” control parameter values of the system.

Table I.

Parameters	“True” Values
K11 (Nm/rad)	891.07
B11 (Nm/(rad/s))	151.48
K21 (Nm/rad)	286.42
B21 (Nm/(rad/s))	19.09
Kpas1 (Nm/rad)	152.76
Td1 (ms)	90
K22 (Nm/rad)	175.03
B22 (Nm/(rad/s))	28.00
K12 (Nm/rad)	251.41
B12 (Nm/(rad/s))	50.70
Kpas2 (Nm/rad)	19.09
Td2 (ms)	80
m1, m2 (kg)	20.7, 48
J1, J2 (kg m2)	0.955, 2.73
h1, h2 (m)	0.521, 0.301
L1 (m)	0.826

Note: m1 and m2 are mass of lower body (LB) and upper body (UB) segments, respectively. h1 and h2 are center of mass height above the ankle and hip, respectively. J1 and J2 are moments of inertia about center of mass for LB and UB segments, respectively. L1 is the length of the LB segment. For comparison, Engelhart et al. (2015) reports inertia values about inferior end of segments. Control parameters are similar to those reported in Boonstra et al. (2013) and Engelhart et al. (2015).

Theoretical model equation without noise

We first addressed the question, “can a single input stimulus be used to accurately identify neural controller parameters in a two-segment inverted pendulum without any sensor noise present?” Equations of motion for the feedback control system shown in Fig. 1B and parameters in Table 1 were used to calculate two “true” FRFs that characterize the dynamic properties of the ankle and hip joint angles, respectively, evoked by the external torque stimulus (T_ext) applied to the ankle joint (see Appendix). Each FRF is represented by a set of complex numbers (real and imaginary values) that vary across a wide range of frequencies that correspond to frequency components of the ankle torque stimulus. The complex values can be expressed as gain and phase values that vary as a function of stimulus frequency, with gain values indicating the ratio of ankle or hip joint amplitude to the amplitude of the external torque stimulus and phase indicating the relative timing to joint angles relative to the torque stimulus (a negative phase value indicates the joint angle lags behind the torque stimulus). These FRFs are denoted “true” FRFs because they are based on the true parameters that we were attempting to identify.

A second set of “fit” FRFs were calculated by a fitting procedure that assumed that body mass, moment of inertia, and center of mass height information from Table 1 were known, but that all active and passive neural control parameters and time delays were not known but were estimated using a fitting procedure. These 12 neural controller parameters were estimated from fits to “true” FRFs that minimized the mean-square-error (MSE) cost function:

$$J_{\mathit{true}}=\frac{1}{2n}{\displaystyle \sum _{i=1}^n|{\mathit{FRFerror}}_{1i}{|}^2+|{\mathit{FRFerror}}_{2i}{|}^2}$$

where,

$${\mathit{FRFerror}}_{1i}=\frac{{\mathit{trueFRF}}_{1i}-{\mathit{fitFRF}}_{1i}}{\left|{\mathit{trueFRF}}_{1i}\right|}$$

$${\mathit{FRFerror}}_{2i}=\frac{{\mathit{trueFRF}}_{2i}-{\mathit{fitFRF}}_{2i}}{\left|{\mathit{trueFRF}}_{2i}\right|}$$

Subscripts ‘1’ and ‘2’ refer to the FRF that relates T_ext to θ₁ and T_ext to θ₂, respectively. The J_true cost function was calculated across a wide bandwidth of n=28 distinct frequencies that were approximately equally spaced on a logarithmic frequency scale from 0.023 – 8.0 Hz. The cost function normalization by the absolute value of the “trueFRF” allowed all frequency points to equally contribute to the cost function despite variation of FRF amplitude across frequency.

The minimization of the cost function was performed using a constrained nonlinear optimization routine, “fmincon” in Matlab software (2013a), Optimization Toolbox (The Mathworks, Natick, MA, USA). Within the “fmincon” routine, we specified the “interior-point” algorithm and a resolution of 10⁻¹⁶. The upper bounds on gains were set to 2 times the “true” neural controller and passive stiffness parameters (Table 1) and the lower bounds were set to zero. The upper and lower bounds on time delays were equal to the “true” parameter ±30 ms.

The fmincon routine requires that initial guesses be provided for each free parameter. However, results are not guaranteed to identify parameters that correspond to the global minimum of the cost function. A strategy to increase the likelihood that a global minimum is identified is to perform the fit multiple times using different initial guesses (Goodworth & Peterka 2012, 2014). To investigate how many fit procedures are necessary to achieve a high likelihood of finding a global minimum, we performed 500 iterations of the fmincon routine with different initial guesses that were randomly selected between the upper and lower bounds of each parameter according to a uniform distribution.

The accuracy of the fit results was assessed by computing a percentage error between true and fit values of neural controller parameters (i.e., 100 × |true parameter – fit parameter| / true parameter). Accuracy was also assessed by comparing FRFs that represent the dynamic characteristics of neural control. Specifically, the neural control in Fig. 1B can be represented by 4 neural controller Laplace transfer function equations:

$$T_{12}(s)/{\theta }_1(s)=(K_{12}+B_{12}s)e^{-T{d}_{2}s}$$

$$T_{22}(s)/{\theta }_2(s)=(K_{22}+B_{22}s)e^{-T{d}_{2}s}+K_{\mathit{Pas}2}$$

$$T_{11}(s)/{\theta }_1(s)=(K_{11}+B_{11}s)e^{-T{d}_{1}s}+K_{\mathit{Pas}1}$$

$$T_{21}(s)/{\theta }_2(s)=(K_{21}+B_{21}s)e^{-T{d}_{1}s}$$

where s is the Laplace variable. Substitution of $s=2\pi f\cdot \sqrt{-1}$ allows for calculation of 4 neural controller FRFs at the n=28 frequency points. Then the MSE between neural controller true FRFs (trueNC) and fit FRFs (fitNC) can be compared buy calculating:

$$J_{NC}=\frac{1}{4\cdot n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^4|{\mathit{NCerror}}_{i,k}{|}^2}}$$

$${\mathit{NCerror}}_{i,k}=\frac{\mathit{trueN}{C}_{i,k}-\mathit{fitN}{C}_{i,k}}{\left|\mathit{trueN}{C}_{i,k}\right|}$$

where k represents each of the 4 neural controllers at the n frequency points used in the comparison.

Simulations with sensor noise

To include noise in the model, we initially ran simulations of sway responses to an external ankle torque stimulus, T_ext, in the time domain and used these data to calculate FRFs relating T_ext to θ₁ and T_ext to θ₂. However, we observed that there were small errors between FRFs derived from simulations with no noise compared to those calculated from equations (Fig. 2D). These errors persisted across the different numerical solvers and with high sampling rates (10,000Hz). Although these simulation errors were small in magnitude, their effect on model fitting was noticeable because the fit error calculation includes a normalization by the magnitude of the FRF which amplified the effect of the small errors particularly at higher frequencies where the FRF magnitude becomes very small.

Figure 2.

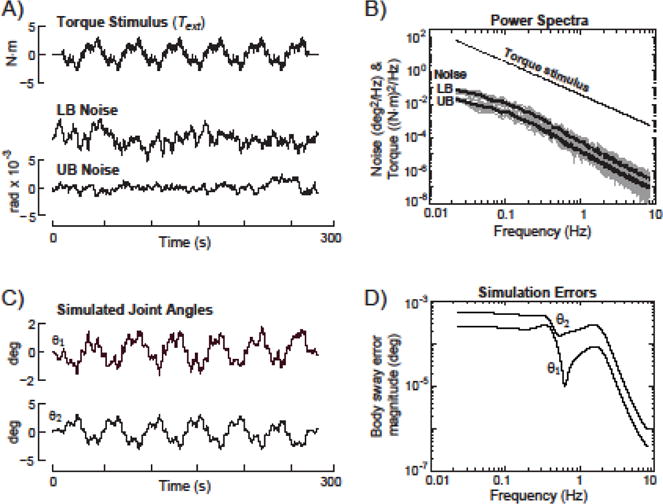
A) Time series of external torque stimulus and sensor noise across 6 repeated cycles. Noise was added as pink noise that was further low pass filtered to mimic spontaneous sway RMS and power spectra in previous studies. B) Power spectra of noise and torque stimulus (T_ext =3 N^.m peak amplitude). C) Illustration of realistic simulated lower body (θ₁) and upper body (θ₂) sway evoked by T_ext when the simulation included sensory noise. Because there were small systematic errors in sway responses obtained from T_ext simulations (sway angle errors shown in D) an alternative method was used to add noise to the frequency response functions (see Methods).

In order to avoid biases in parameter estimates due to simulation errors, we combined results from the theoretical model equations with results from simulations of body sways evoked by sensory noise alone. To do this, an ideal T_ext stimulus spectrum was calculated based on a pseudorandom stimulus used in previous studies (Goodworth & Peterka, 2009, 2012). Ideal body sway response spectra were given by the product (theoretical FRFs) × (ideal stimulus spectrum). Then, simulated noise-evoked body sways were analyzed to calculate noise spectra. Finally, the noise-corrupted FRFs were calculated by (ideal body sway spectra + noise spectra)/(ideal T_ext stimulus spectrum). All spectra for the various calculations are represented by complex numbers. Further details of this process are provided below.

Time domain noise simulations were run in Matlab Simulink (Simulink version 8.1) using a 200 Hz sampling rate and the 5^th order Dormand-Prince solver. Sensor noise signals (separate and independent) were added to θ₁ and θ₂ in the active torque feedback loops to represent uncertainty inherent in internal estimates of segmental body sway derived from multi-sensory processing and integration. Similar to existing studies (Boonstra et al. 2013; van der Kooij and Peterka 2011), sensor noise signals were modeled as pink noise (1/f power spectra) that was created by scaling a white noise signal (Zhivomirov 2013). The pink noise was further low-pass filtered (1^st order filter with a cut off of 0.15 Hz) to better approximate the power spectrum of body sway variability across frequencies reported previously (Fig. 5 in van der Kooij and Peterka 2011). The power spectral density of the noise signals added to θ₁ and θ₁ was 4×10⁻⁴ and 7×10⁻⁵ deg²/Hz at 0.5 Hz, respectively. Zero meaned root-mean-squared body sway evoked by these noise inputs were ~0.11 deg and ~0.08 deg for θ₁ and θ₁, similar to values reported for quiet stance (Goodworth & Peterka 2010; Peterka 2002).

The pink noise signals used in simulations had durations of 262.32 s which represents a time period equal to 6 cycles of the assumed ideal pseudorandom T_ext applied about the ankle joint (43.72 s/cycle). The ideal T_ext waveform had a power spectrum with spectral components declining in amplitude in proportion to the inverse square of frequency over the frequency range of 0.023 to 16.7 Hz. The T_ext waveform was scaled to have either a 3 N^.m or 5 N^.m peak-to-peak amplitude and a Fourier transform was used to calculate ideal stimulus spectra. Multiplication of these ideal stimulus spectra by the theoretical FRFs gave the ideal sway response spectra.

The sway responses to the noise signals were processed to calculate average noise spectra by dividing the simulated sway data into 43.72-s segments, calculating individual Fourier spectra of the final 5 segments (ignoring the first segment to avoid transients), and averaging these 5 spectra. Figure 2B shows the power spectrum of the ideal torque stimulus and examples of LB and UB sway power spectra calculated from noise simulations. Figure 2A shows the ideal T_ext stimulus and examples of LB and UB sway evoked by noise-only simulations. For illustrative purposes, Fig. 2C shows examples of LB and UB sway generated from simulations that simultaneously presented noise and T_ext. Although the small simulation errors (Fig. 2D) prevented using these simulation results to calculate FRFs, the time series in Fig, 2C demonstrate realistic levels of variability expected in experimental data.

The average noise spectra were added to the ideal sway response spectra and divided by the ideal stimulus spectra to yield the final noise-corrupted FRFs that we refer to as “sim” FRFs. To reduce FRF variability due to the noise, the “sim” FRF analysis included averaging of adjacent frequency points (Otnes and Enochson 1972). Generally, a larger number of points were averaged together with increasing frequency so that the final set of “sim” FRFs contained frequencies that were approximately equally spaced on a logarithmic frequency scale. However, to avoid distortions caused by averaging across rapidly changing FRF values in mid-frequency regions, no averaging was performed for frequencies 0.435–0.526 Hz. Final smoothed FRFs included 28 frequency points at 0.023, 0.069, 0.114, 0.183, 0.229, 0.275, 0.320, 0.366, 0.412, 0.435, 0.480, 0.526, 0.549, 0.640, 0.801, 1.00, 1.28, 1.62, 2.01, 2.45, 3.04, 3.77, 4.60, 5.38, 5.92, 6.40, 7.09, 8.00 Hz.

Corresponding to the analysis of the theoretical model without noise, a “fit” FRF was calculated using equations of motion with known mass, moment of inertia, and center of mass height parameters from Table 1, and estimates of neural controller, passive stiffness, and time delay parameters obtained by minimizing the MSE of the normalized difference between the “fit” FRF and “sim” FRF:

$$J_{\mathit{sim}}=\frac{1}{2n}{\displaystyle \sum _{i=1}^n|\mathit{simError}{\theta }_{1i}{|}^2+|\mathit{simError}{\theta }_{2i}{|}^2}$$

where

$$\mathit{simError}{\theta }_{1i}=\frac{\mathit{simFR}{F}_{1i}-{\mathit{fitFRF}}_{1i}}{\left|\mathit{simFR}{F}_{1i}\right|}$$

$$\mathit{simError}{\theta }_{2i}=\frac{\mathit{simFR}{F}_{2i}-{\mathit{fitFRF}}_{2i}}{\left|\mathit{simFR}{F}_{2i}\right|}$$

and n is the number of frequency points included in the fit, with a maximum of 28 possible points. We varied n to understand the upper range of frequencies, Fmax, most important for accurate system identification. The influence of reduced bandwidth on parameter estimates was investigated by using fewer frequency points with the normalization by n permitting comparison of MSE values that used a different number of frequency points. The fmincon optimization function used to minimize this cost function was the same as described above for the theoretical model with no noise.

Fifty separate simulations and analyses were performed using different realizations of the noise signals for each simulation (i.e., a different noise input was used for each simulation by randomly selecting a different noise seed in the random signal generator). Parameters reported from fits to the “sim” FRFs were represented as means and standard deviations across the 50 noise realizations.

Sensitivity

To determine the sensitivity of each model parameter on the resulting external torque to sway angle FRFs, we varied each parameter individually by ±10%, and then calculated the J_true MSE between the original “true” FRFs and the FRFs with the parameter value varied by ±10%. Because each parameter can impact a specific range of frequencies more than other frequencies, sensitivity results were reported across low, mid, and high frequencies.

RESULTS

Importance of multiple initial guesses and examination of model fits

In both the theoretical model with no noise and the simulated model with sensor noise, we found that multiple randomized initial parameter guesses in the fitting routine were required to reach optimal fits (i.e., to avoid local minimums in the cost function). Each data point in Figure 3A represents the MSE (J_true error) from model fits to T_ext to θ₁ and θ₂ FRFs, and corresponding MSE (J_NC error) of neural controller FRFs identified for the theoretical model with no noise and FRF data bandwidth of 0.023 to 8.0 Hz. This spread of the J_true error values along the horizontal axis clearly shows that minimization of the J_true cost function does not always converge to the very small MSE of model fits that would be expected for a global minimum from fits to FRFs with no noise. Thus, in the two-segment model, the initial guesses for parameter values have a large influence in fitting accuracy. Similar results were found when using different algorithms (interior-point vs. trust-region-reflective) in the fmincon function.

Figure 3.

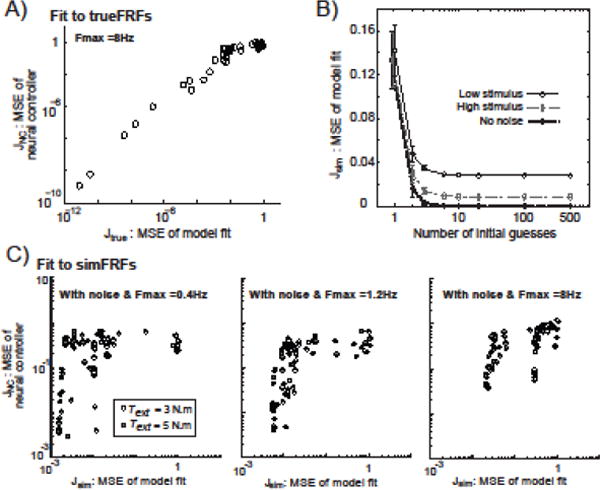
Influence of different initial parameter guesses on fitting results. In A), there was a nearly linear relationship (on a logarithmic scale) between mean-square-error (MSE) values representing the quality of fit to T_ext to θ₁ and T_ext to θ₂ frequency response functions (FRFs) (horizontal-axis; J_true MSE values for the theoretic no noise model) and the accuracy of estimated neural controller FRFs (vertical-axis; J_NC MSE values). In B), the number of initial parameter guesses required to obtain minimum J_sim MSE was consistent across the three different simulated signal-to-noise ratio conditions where Fmax was set to 1.2 Hz. In C), the relation between J_NC and J_sim MSEs from simulation results with different signal-to-noise conditions and different Fmax ranges.

Data points in Fig. 3A extended from the upper right (high errors in fitting T_ext to θ₁ and θ₂ FRFs and high errors in estimates of neural controller FRFs) to the lower left (low fitting errors and neural controller FRFs). This result implies that lower J_true MSE of model fits of T_ext to θ₁ and θ₂ FRFs were associated with more accurate identification of neural controllers. Therefore, the J_true MSE equation used in the current study can provide a suitable means to obtain estimates of neural controllers if sufficient numbers of initial guesses are used to provide confidence that the fit routine is identifying a global minimum. However, accurate identification of neural controller properties also was influenced by noise and the bandwidth of the frequencies included in the fit to the T_ext to θ₁ and θ₂ FRFs. The relationship between J_sim MSE of model fits to the J_NC accuracy of neural controller estimates became weaker when signal-to-noise decreased (i.e., in simulations using lower amplitude T_ext) or FRF uncertainty increased by including both noise and high frequency points in the “sim” FRF (Fig. 3C).

Because the above results demonstrate the need for multiple initial parameter guesses to obtain a global minimum in the cost function, it is of interest to know how many initial guesses were needed to reach a likely global minimum and whether the quality of the T_ext to θ₁ and θ₂ FRFs influences the number of initial parameter guesses needed to achieve adequate fits. Reduced FRF quality was created by adding sensor noise to joint angles in simulations and also by reducing the stimulus amplitude (from T_ext=5 N^.m to 3 N^.m) in simulations in order to increase the relative influence of sensor noise. From results of 20 simulations using different realizations of sensory noise (different noise inputs), T_ext to θ₁ and θ₂ FRFs were calculated, and 500 fits to each of the 20 sets of FRFs were performed. To estimate the J_sim MSE when “x” initial guesses were used, we randomly sampled “x” MSE values from the pool of 500 fits for each of the noise seeds and took the minimum MSE from this sample. This random sampling from the pool of 500 fits was repeated 500 times for each “x” number of initial guesses, and we calculated the mean and SD of the minimum MSEs. Figure 3B shows these mean and SD averaged across the 20 simulations. For the no noise condition, a similar procedure was used but only included five pools of 500 fits because each pool of MSEs showed only small variations since the “sim” FRFs did not change across the five pools.

Each line in Fig. 3B represents different stimulus amplitude-to-noise ratios. The bottom curve (lowest MSE) has no noise while the top curve (highest MSE) has the lowest stimulus amplitude relative to noise. We found that asymptotic levels of MSE in each curve, which are likely global minimums, were reached with about 20 different initial random parameter guesses and this finding was consistent across the no-noise condition and the two different noise conditions. However, it is important to note that these apparent global or near global minimums do not always yield a set of parameters that represent a quality or even a stable fit (Fig. 3C right plot). When Fmax was set to 8Hz and noise was present, it was not unusual for the fmincon function to converge to J_sim MSE minimums whose identified parameters corresponded to a balance control system that was unstable. The likelihood of obtaining results consistent with a stable system and with parameters close to their true values could often be dramatically improved with minor adjustments to the parameter identification routine, such as changing the lower bounds on initial parameter selections or excluding the highest frequency point, which tended to have large uncertainty. These findings highlight the various ways fitting routines can estimate a set of parameters that are not adequate to describe the system and emphasize the need to test for system stability with the identified parameters.

Parameters estimates from fits to theoretical FRFs without noise

In the model without noise, fits to the external torque to joint angle FRFs using FRF data up to 8 Hz were fit essentially perfectly. Parameters were based on the minimum normalized MSE (J_true error) of 50 initial guesses (which was on the order of 10⁻¹¹, Fig. 3A). These fits accurately identified the 12 neural controller parameters and the neural controller FRFs calculated from these identified parameters were similarly very accurate when compared to the true neural controller FRF (Fig. 4B). The average error across parameter estimates was about 0.008%. The parameter with highest error was the passive stiffness parameter K_pas2, but this error was still very small overall at 0.039%.

Figure 4.

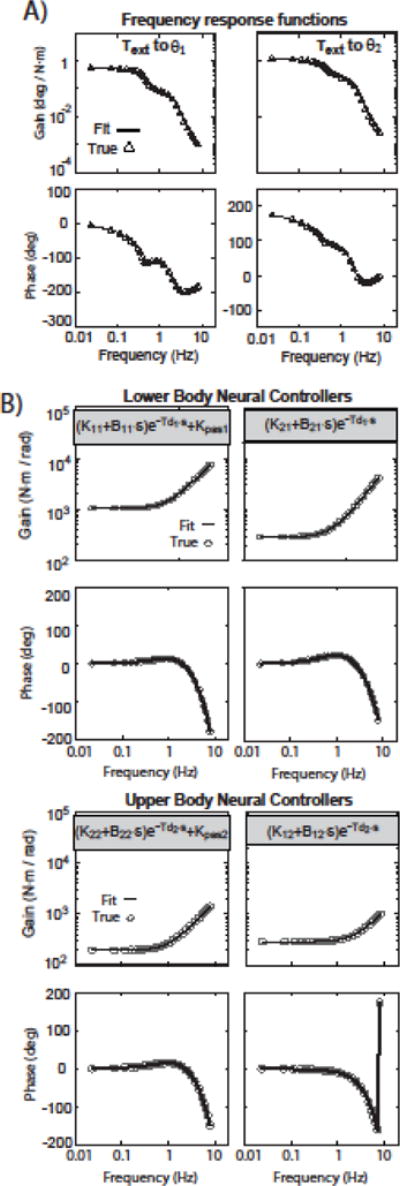
Results from the theoretical model without noise show essentially perfect fits to external torque to joint angle frequency response functions (FRFs) in A) resulting in identified parameters that give essentially perfect estimates of neural controller FRFs in B).

Parameters estimates with sensor noise

Figure 5 shows parameter estimates (mean and SD averaged across simulation results using 50 different realizations of noise, and for each noise realization, using parameters associated with the lowest J_sim MSE across 50 different random initial parameter guesses). The leftmost bar in each plot shows the “true” value, followed by 2 sets of fits to “sim” FRFs at Fmax=0.41 Hz, 1.2 Hz, and 8 Hz. In each set, the 2 parameter estimates are from “sim” FRFs obtained with high torque (T_ext=5 N^.m) and low torque (T_ext=3 N^.m) with noise.

Figure 5.

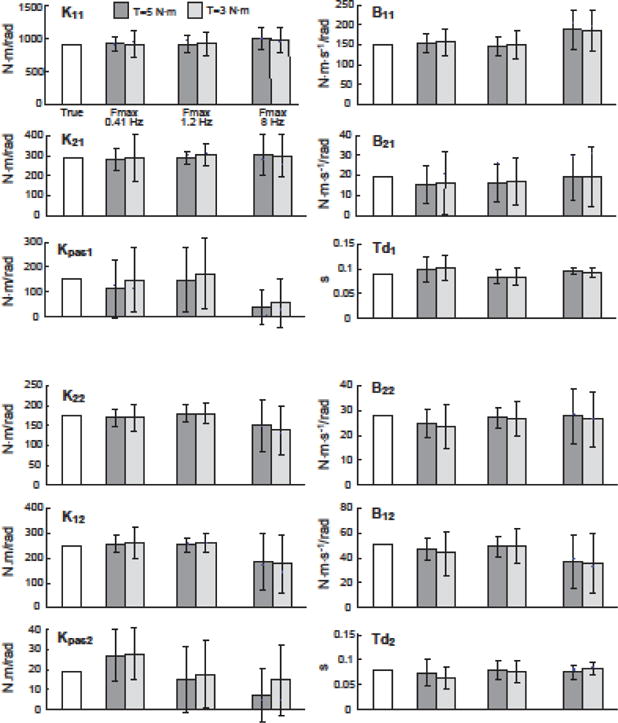
True parameter values and estimated parameter values from fits to simulated FRFs with sensor noise with varying bandwidths of FRF data from 0.023 Hz to Fmax. Bars show average ±1 SD values across 50 different realizations of sensory noise.

Relatively large deviations from the true values and high variability are evident in the K_pas1 and K_pas2 estimates shown in Fig. 5. Most likely these poor estimates were due to the functional redundancy between K_pas1 and K₁₁ and between K_pas2 and K₂₂. Specifically, the functional difference between these active (K₁₁, K₂₂) and passive (K_pas1, K_pas2) parameters is the time delay associated with the active parameter. Often, if the passive parameter was over estimated, then the active parameter was underestimated, and visa-versa, thus demonstrating an interaction among active and passive stiffness, and a limited ability of the fitting procedure to distinguish between them. Figure 6 shows the parameter estimates (mean and SD) of these combined stiffness parameters (i.e., K_pas1+ K₁₁ and K_pas2 + K₂₂). Bias errors and variability in individual parameters and in combined stiffness parameters are described below.

Figure 6.

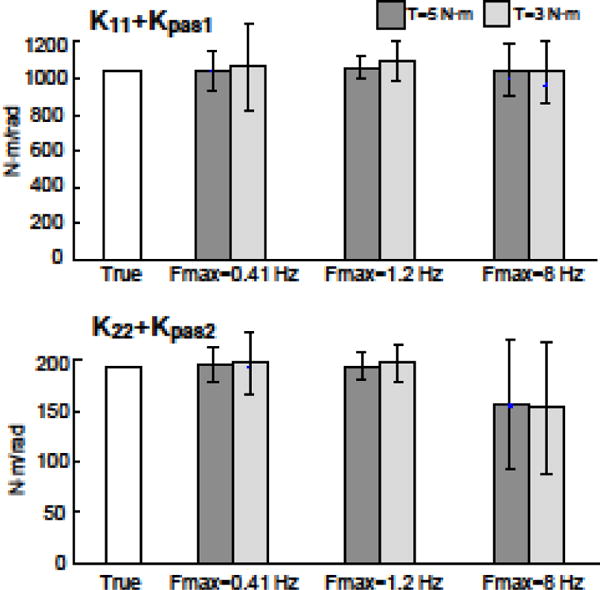
Estimated parameter values and SD across 50 different realizations of sensory noise for the combined active and passive parameters (K_pas1 + K₁₁ and K_pas2 + K₂₂) for the same conditions described in Figure 6.

BIAS ERRORS

Bias errors were calculated as the absolute value of the difference between the true parameter value and the average fit parameter normalized by the true value, and expressed as a percentage. The average fit parameter was calculated using values obtained from 50 noise realizations. Table II is a summary of bias errors for the three different ranges of Fmax and Figure 7A displays these values graphically for Fmax=1.2 Hz. Relatively low bias errors in parameters were obtained with model fits to data with Fmax=0.41 and 1.2 Hz. Average parameter errors were 11.6% and 5.8% for 0.41 Hz and 1.2 Hz, respectively. One might expect that including the widest bandwidth of FRF data in the fits would result in the lowest average bias errors. However, the opposite was true with fits using data up to 8 Hz, where these fits were associated with the least accurate parameters (average of 20% error). Fits to 8 Hz were apparently influenced by the low body sway relative to noise at higher frequencies, producing high FRF variability, and often yielding parameters that were not compatible with an stable system.

Table II.

Parameters	Bias Percentage Error
	Fmax=0.4 Hz	Fmax=1.2 Hz	Fmax=8 Hz
K11	2.9	2.6	11.2
B11	2.5	2.2	23.4
K21	14.7	4.1	5.8
B21	1.8	14.9	1.3
Kpas1	17.4	9.8	69.0
Td1	10.8	7.0	3.9
K22	3.2	2.8	17.6
B22	14.0	4.1	3.2
K12	44.4	2.1	27.6
B12	2.9	2.7	28.8
Kpas2	9.4	14.1	42.7
Td2	14.6	2.6	3.8
K11 + Kpas1	1.2	2.8	0.5
K22 + Kpas2	1.5	1.1	20.1

Note: Bias percentage errors are defined as 100 × absolute value of the difference between the mean fit parameter and true parameter divided by the true parameter. The mean fit parameter was the average parameter value estimated across simulation results that used 50 different noise realizations (i.e., 50 different random inputs). For each random input, 50 different initial guesses in parameters were used and parameters associated with the lower MSE (J_sim) were selected. Percentages are expressed as averages across the T_ext=3 N^.m and T_ext=5 N m conditions.

Figure 7.

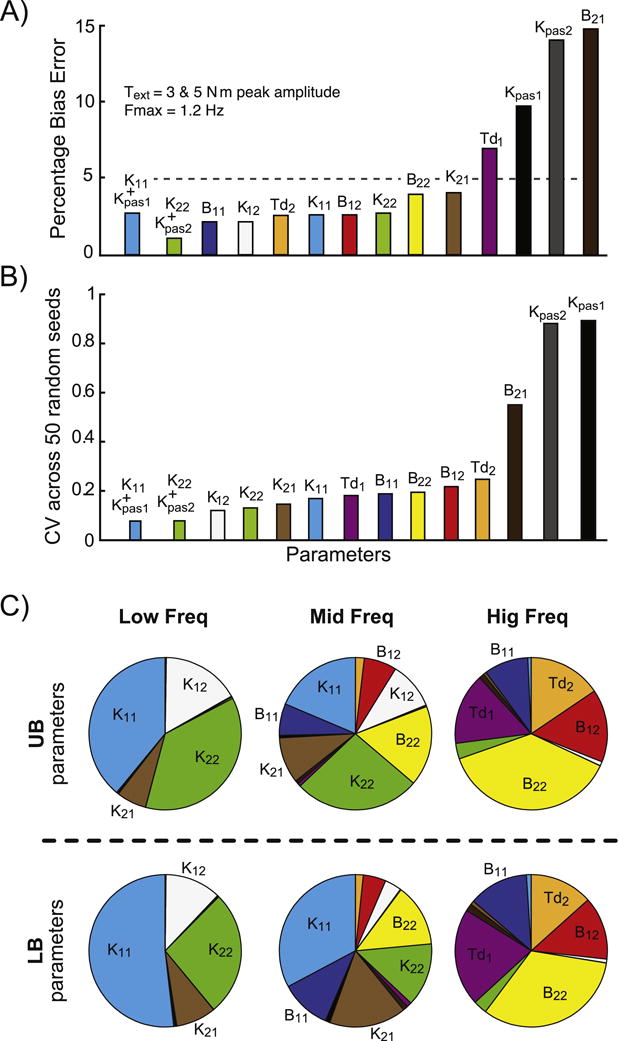
A) Bias percentage errors in parameters when the fitting routine included frequencies from 0.023 to 1.2Hz. Errors shown are an average of results from simulations with an external torque (T_ext) amplitude of 3 and 5 N^.m. B) Coefficient of variation across the 50 different realizations of sensory noise for the same fitting and torque conditions shown in A). In C), the sensitivity pie chart displays the relative impact of each parameter (when modified by ±10%) on the upper body and lower body frequency response functions (FRFs) at low (0.023–0.3 Hz), mid (0.43–2.5 Hz), and high (3.2–8.0 Hz) frequency bands.

Across all Fmax conditions, passive stiffness parameters exhibited large bias errors and variability across different noise seeds (Fig. 7A,B; right side columns). The limited ability of the fitting procedure to accurately distinguish between active and passive stiffness parameters is likely responsible for the large bias errors in passive stiffness estimates. Consistent with there being an interaction between active and passive stiffness parameters, when these parameters were combined to represent their net effect, the average bias errors across the combined stiffness parameters and across results from T_ext=3 and 5 N^.m simulations were low at 1.3%, and 1.9% for Fmax=0.4 Hz and 1.2 Hz., respectively (see Table II). Using the combined parameters, the overall average bias errors across all parameters was 7.6% and 4.4% for Fmax=0.4 Hz and 1.2 Hz, respectively. For fits to 8 Hz, the combined parameter bias error was 11.8%. Finally, we found that T_ext amplitude did not have a systematic effect on bias errors.

VARIABILITY

Each error bar in Fig. 5 represents parameter variability as the standard deviation in parameter estimates across results from the 50 simulations using different realizations of sensory noise. The lowest variability in parameter estimates was obtained with Fmax=1.2 Hz where the average parameter variability was 10% lower compared to Fmax=0.41 Hz (averaged across all parameters and external torque amplitudes). When analyzed with combined active and passive stiffness, fits with Fmax=1.2 Hz had an average parameter variability 41% lower than fits with Fmax=0.41 Hz. The higher variability in parameters with the Fmax=0.41 Hz bandwidth was consistent with our finding that fits at Fmax=0.41 Hz sometimes inaccurately estimated dynamics at frequencies higher than those included in the fits. Comparing Fmax=1.2 Hz to 8 Hz, time delays and passive parameters had lower variability in fits to 8Hz while all other parameters had lower variability in fits to 1.2 Hz.

Variability decreased with larger external torque amplitudes. Average variability across parameters with the high external torque (T_ext=5 N m) was 38%, 21%, and 9.4% lower than the low torque (T_ext=3 N^.m) for Fmax=0.41 Hz, 1.2 Hz, and 8 Hz, respectively. Similar to the bias results, the variability of the combined stiffness (i.e., K_pas1+ K₁₁ and K_pas2 + K₂₂) was typically lower than individual parameters (Fig. 6).

To determine which parameters were most (and least) accurately estimated in the presence of noise, the coefficient of variation (CV) was calculated across all parameters. Figure 7B shows CV values averaged across the two external torque conditions for Fmax=1.2 Hz. The three individual parameters with the lowest CV’s were K₁₂, K₂₂ and K₂₁, and the three with the highest CV’s were B₂₁, K_pas1 and K_pas2. When the passive and active stiffness parameters were combined (K_pas1+ K₁₁ and K_pas2 + K₂₂) their CV’s that were about half of K₁₁ and K₂₂, and were lower than any individual parameter.

Sensitivity analysis

The influence of each parameter on sway behavior evoked by the external ankle joint torque stimulus is summarized by the sensitivity analysis shown in Fig. 7C. Results show a complex interaction between parameters and their influence over different frequency ranges of the FRFs. Each parameter influenced T_ext to θ₁ and θ₂ FRFs over a range of frequencies but typically not across the full frequency range and each parameter influenced certain frequency regions much more than others. For example, both time delay parameters (Td₁, purple, and Td₂, orange) had a large influence across high frequencies but essentially no influence over lower frequencies. In general stiffness parameters had their largest influence at lower frequencies, damping parameters at higher frequencies, with both stiffness and damping parameters influencing mid-frequencies.

The individual parameters with low CV values (< 0.2; Fig. 7B) were among the parameters with the largest influence on FRFs (Fig. 7C). The three individual parameters with the largest CV values (K_pas1, K_pas2 and B₂₁; Fig. 7B, bars on the right side) had the smallest influence on FRFs (Fig. 7C).

Similarly, the three parameters with the lowest influence on FRFs (K_pas1, K_pas2 and B₂₁) also had the largest bias errors (Fig. 7A). We also found a relation between bias errors in stiffness and damping parameters and their influences across frequency. Specifically, stiffness parameters with low CV (K₁₂, K₂₂, K₂₁, and K₁₁) had the most impact on low and mid frequencies; while damping parameters (B₂₂, B₁₂, B₁₁, B₂₁) had larger CV and the most impact on mid and high frequencies. Passive stiffness parameters were the obvious exception to this trend as they had a very small overall influence on body sway compared to other parameters. In general, parameters with bias errors over 5% either had very small influences on body sway or had their largest impact across higher frequencies (above 3.2 Hz).

DISCUSSION

The main finding in this study is that a single external stimulus with a sufficiently rich frequency distribution can be used to identify neural controller parameters that stabilize a two-segment inverted pendulum body by fitting a parameterized model to experimentally determined FRFs that characterize the dynamic behavior of body segment motion evoked by an external stimulus. However, several qualifications need to be made. First, when using fitting methods that adjust model parameters to optimally match model-predicted FRFs to experimental FRFs, it was necessary to use at least 20 different initial guesses in parameters to increase the probability of obtaining a likely global minimum and thus accurate parameter estimates. Second, even with many different initial guesses, it is important to evaluate each model fit for accuracy and stability because these are not guaranteed. Third, when realistic noise was included, it was not generally possible to distinguish between passive and certain active stiffness parameters due to redundancy in their influence on body sway. Fourth, although bias errors in parameter estimates were typically less than 5% with Fmax=0.41 Hz or 1.2 Hz, less accurate and/or more variable parameter estimates occurred when FRF values were more uncertain (noise) or when too few frequencies points were included in the FRFs (increased variability fitting data with Fmax=0.41 Hz). Finally, it is important to note that each model parameter influenced both UB and LB sway, but the sensitivity to parameter changes was greater in some frequency regions than in others. Generally, parameters with the greatest overall influence on body sway were the same parameters that were estimated the most accurately when noise was included in the model (low bias and CV) and parameters with the least influence on body sway had the greatest variability in parameter estimation (higher bias and CV). Practically, the above findings point to the need for appropriate interpretation of modeling in light of the trade-offs in modeling human posture control, which is highlighted throughout the following sections.

Alternative approaches to identify multi-segment posture control

One approach to identify multi-segment posture control mechanisms includes the use of two independent external stimuli applied simultaneously to different body segments to obtain a nonparametric identification of neural controller characteristics (Boonstra et al. 2015; Engelhart et al. 2015). In these previous studies, the neural controllers were not estimated from a model fit. Instead, neural controller FRFs were identified by relating the total LB and UB torque (which could be obtained via inverse dynamics calculations) to the LB and UB sway using methods appropriate for closed loop feedback control systems. The advantage of this dual stimulus method is that neural controller dynamics are represented by FRFs and thus do not depend on an explicit model of the neural controller properties. The disadvantage is that two independent stimuli applied to different body segments are required, which may not always be feasible. Significant errors were found if the calculation of neural controller FRFs were attempted from data obtained in experiments using only one stimulus. The reason for the errors is apparent when one considers that total corrective ankle torque (T₁ in Fig. 1) cannot distinguish between T₁₁ and T₂₁ (i.e., ankle torque generated as a function of LB motion versus ankle torque generated as a function of UB motion). Similarly, total corrective hip torque (T₂ in Fig. 1) cannot distinguish between T₂₂ and T₁₂ (i.e., hip torque generated as a function of UB motion versus hip torque generated as a function of LB motion). We agree with these authors that it is not possible to accurately calculate the neural controller FRFs by relating total torque to joint angle motion with a single stimulus.

An alternative approach offered in our current study is to use a parameterized model where parameters are obtained from fits to FRFs relating a single external torque to UB and LB sway. This method provides a simpler experimental approach because it only requires one stimulus and does not require inverse dynamics calculations that could introduce errors in joint torque calculations. A single stimulus paradigm could have wider application due to simplified equipment requirements. Our results also clarify that statements made in previous publications (Boonstra et al. 2015; Engelhart et al. 2015), stating that it is not possible to identify neural controllers using a single stimulus, apply specifically to non-parametric identification of neural controller properties, but not to a parameterized model-fit identification schemelend more confidence to results from existing studies that used similar parameter identification methods. However, there are trade offs in using a parameterized model-fit identification scheme in that it explicitly assumes a model structure (i.e., stiffness and damping parameters organized in a specific manner). The non-parametric neural controller FRFs provided by the dual stimulus paradigm would be valuable in cases where the true neural control system deviated considerably from the assumed structure in a parameterized model (Perreault et al. 2000).

Effect of noise in sway data

Our results also showed lower confidence (larger variance) in parameter estimates when noise relative to stimulus amplitude was higher. However, uncertainty in parameter estimates was not uniform across parameters. Our sensitivity analysis indicated that parameters with the largest variability in estimates (highest CV) and bias errors had the least influence on body sway. In general, the most influential parameters (especially below 3.2 Hz) were estimated with high accuracy.

In our simulations, we selected noise amplitudes that represented realistic levels of an individual subject’s variability in posture sway and found the best parameter estimates with fits to FRFs with an Fmax of 1.2 Hz (considering both low bias and variability). In comparison to results where Fmax was 0.41 Hz, the increased bias and variability with limited bandwidth data is not surprising because, with inclusion of only a small range of frequencies, different combinations of parameters could potentially account for the FRF data but these combinations would not necessarily represent the true system. By the same logic that wider bandwidth is better, we expected results from fits to FRFs with Fmax=8 Hz to show further improvements. However, this was not the case due to the low body sway relative to noise at higher frequencies that increased errors with fits to 8Hz.

The inclusion of low signal to noise data points at the higher frequencies compromised estimates of both stiffness and damping parameters, even though stiffness parameters had a larger impact on low and mid frequencies. Thus, in a dynamic feedback system, inclusion of poor quality data points do not just impact a limited set of parameters but can negatively affect the accuracy of many parameter estimates. Experimental data also can be compromised at higher frequencies for multiple reasons. Specifically, researchers may not be able to accurately measure what are typically very low amplitude body motions that occur at higher frequencies of body sway. Higher frequency perturbations are more likely to produce body deformations due to compliant tissue properties such that the applied stimulus differs, in difficult to measure ways, from the desired stimulus. Additionally, higher frequency stimuli can produce deviations from the assumed rigid body segment motions (e.g., flexible spinal column motion). In a parameterized model-based identification, failing to account for these effects and others (head on trunk motion, arm motion) would be expected to add bias to parameter estimates. In the current study, we found that a frequency range of 0.02–0.4 Hz and 0.02–1.2 Hz (which may be reasonable for many researchers) provided fairly low bias errors across nearly all parameters (assuming active and passive stiffness parameters were combined). Parameters that impacted body sway below 3.2 Hz were estimated particularly well.

Parameter estimation considerations

Findings in our study have practical implications for researchers using models to interpret experimental results. Any individual application of the fit routine to the FRF data of the two-segment balance control system frequently did not produce an adequate fit to the experimental FRFs. This finding differs from our experience with modeling single-link pendulum dynamics, where cost function minimization typically converges to what is likely to be a global minimum value with a single set of reasonable initial guesses for balance control parameters (Cenciarini & Peterka 2006; Peterka 2002). Although the two-segment body and its accompanying control scheme are not exceptionally complex, it appears that there are many local minimums in the cost function to which optimization algorithms can converge leading to poor quality fits to the FRFs and associated biased parameter estimates. We were mostly able to overcome this limitation by using repeated and randomized (within a range) initial selections in parameters and then choosing final parameter estimates that correspond to the lowest cost function value. Future improvements in software and optimization routines may solve this problem. Also, we note that the optimization routine we used allows a researcher to define upper and lower bounds of parameters. When estimating unknown parameters with experimental data, it is important to consider if the parameter converged to an upper or lower bound. If so, one may consider widening bounds, provided that the widen bounds do not degrade interpretation (i.e., result in non-physiological values). In the present study, we chose somewhat large ranges in lower and upper bounds (0 to 2 times true values of parameters), but we found improvements in fits to 1.2 Hz and 8 Hz data when the lower bounds were set to 0.5 of true values. In practice, if one has a priori knowledge of reasonable parameter values based on previous studies and/or physiological data, then the lower and upper bounds could be selected more conservatively than the 0 to 2 times nominal values. Our previous experimental-modeling studies showed that the mean parameter estimates based on fits to individual subjects were similar to the parameter estimates based on mean experimental data (exhibiting lower noise than an individual subject’s data) in a homogeneous population (Goodworth & Peterka 2009, 2012). Thus, in a homogenous population parameters estimated from mean subject experimental data may provide a starting point for understanding reasonable upper and lower limits on model fits to individual subject data.

Another method used to increase accuracy of parameter estimation was to average FRFs across specific frequencies, with more averaging with increasing frequency. This averaging had the effect of lowering the influence of noise at any individual frequency and was necessary to obtain quality fits, but too much averaging could distort FRFs. In fact, to minimize distortions, it was necessary to not average across 0.435–0.526 Hz where FRFs changed rapidly across frequency. By comparison, fits performed with averaging across these frequencies had higher bias errors (likely due to distortion of FRFs) but had lower variance in FRFs across the 50 noise realizations.

An additional outcome of our study was to demonstrate the limitations of parameter identification in systems where there is functional redundancy in control parameters. Specifically, we concluded that our method was not capable of consistently distinguishing between active and passive stiffness factors although the sum of these factors could be accurately identified. In building a model of a particular biological system, first principles may lead to inclusion of multiple control mechanisms. These mechanisms may actually exist and may influence behavior, but a given identification scheme may not be capable of accurately characterizing each of their contributions, leading to inaccurate reports of their properties. The modeling, simulation, and system identification methods we demonstrated can be used more generally to determine whether individual components of control mechanisms can be accurately identified using a particular analysis. To reduce redundancy, many models have adopted either a simple biomechanical scheme (single link) or a simplified control scheme (e.g., exclusion of time delays (Park et al. 2004) or other redundant parameters (Goodworth & Peterka 2012)). The trade-off is that interpretations of model parameters must reflect these simplifications. For example, torque generated from a model that does not distinguish active from passive stiffness must be understood as the net contribution of both.

Finally, we note that identification of model parameters by the methods discussed does not guarantee that the model actually defines a stable system even when it appears that the model fit has identified parameters associated with a likely global minimum. Therefore, stability should be verified using stimulations.

In summary, feedback modeling can provide a unique window into neural mechanisms, test hypotheses, and guide experiments. However, there are numerous factors that influence the accuracy of parameter identification and several trade-offs that must be considered when developing models and interpreting model results. In practice, this type of feedback control modeling of neural systems is an iterative process where model accuracy, parameter redundancy, and meaningfulness and plausibility of the model structure all factor into consideration of the objective and subjective value of a particular model (Robinson 1973).

Highlights.

• Posture control models are used to identify neural mechanisms and test hypotheses

• It is unclear if parameters in a two-segment model can be found with one stimulus

• We found neural parameters can be identified with reasonable accuracy

• Noise, stimulus amplitude and frequency, and fitting algorithm influence accuracy

• Use of a single-stimulus is a viable alternative to multi-stimuli approaches

ABBREVIATIONS

LB

lower body

UB

upper body

θ₁

LB joint angle

θ₂

UB joint angle

T_ext

external torque applied to ankle joint

NC

neural controller

K

stiffness parameters

B

damping parameters

Td

time delays

sim

simulation

MSE

mean square error

CV

coefficient of variation

FRF

frequency response function

Fmax

maximum frequency used in fitting routine.

Appendix

Equations of motion for lower and upper body dynamics were calculated following Koozekanani et al. (1980), by developing free body diagrams (D’Alembert’s principle) of the two segments in an earth-fixed Cartesian coordinate system. The UB and LB equations are:

$${\theta }_{2s}(J_2{s}^2-A_{2}g)+{\theta }_1{C}_1{s}^2=-{\theta }_1(K_{12}+B_{12}s)e^{-T{d}_{2}s}-{\theta }_2(K_{22}+B_{22}s)e^{-T{d}_{2}s}-{\theta }_2{K}_{\mathit{Pas}2}$$

$${\theta }_1(J_1{s}^2-A_{1}g)+{\theta }_{2s}(C_2{s}^2-A_{2}g)=T_{\mathit{ext}}-{\theta }_2(K_{21}+B_{21}s)e^{-T{d}_{1}s}-{\theta }_1(K_{11}+B_{11}s)e^{-T{d}_{1}s}-{\theta }_1{K}_{\mathit{Pas}1}$$

where s is the Laplace variable. The left sides of the equations are associated with inter-segmental body dynamics and torques due to gravity, and the right sides are associated with corrective torques from neural controllers. The external torque stimulus, T_ext, is added as an individual term in the lower body equation. Note that θ_2s is the upper body segment angle (i.e., tilt with respect to gravity) while θ₁ and θ₂ are LB and UB joint angles, respectively, and g is gravity acceleration. In this linearized model, C₁, C₂, J₁, and J₂ are inertia-related terms; while A₁ and A₂ are terms related to segment position with respect to gravity. In the current study, C₁ =11.93 kg.m, C₂=19.01 kg.m, A₂ = 14.45 kg.m, and A₁ = 50.42 kg.m, J₁ = 51.26 kg.m² and J₂ = 7.08 kg.m². The equations can be expressed equivalently in an alternative form (Kiemel et al. 2008).