Gold Nanoparticles as Absolute Nanothermometers

Abstract

Nanothermometry is a challenging field that can open the door to intriguing questions ranging from biology and medicine to material sciences. Gold nanorods are excellent candidates to act as nanoprobes because they are reasonably bright emitters upon excitation with a monochromatic source. Gold nanoparticles are commonly used in photothermal therapy as efficient transducers of electromagnetic radiation into heat. In this work we use the spectrum of the anti-Stokes emission from gold nanorods irradiated in resonance to measure the absolute temperature of the nanoparticles and their surrounding medium without the need for a previous calibration. We show a 4 K accuracy in the determination of the temperature of the medium with spectral measurements of 180 s integration time. This procedure can be easily implemented in any microscope capable of acquiring emission spectra, and it is not limited to any specific shape of nanoparticles.

Most physical, chemical, and biological processes depend on temperature. Together with the miniaturization of devices and the advent of nanotechnology, the need for measuring temperature with high spatial accuracy started to emerge. Notably in biology^1,2 and medicine³ measuring and controlling temperature at a subcellular scale are the challenges that must be overcome to achieve better understanding and control of new therapies such as photothermal tumor ablation⁴ or controlled drug delivery.^5,6

Nanometer-size probes with distinctive spectral features are ideal candidates for temperature measurements since they provide high spatial accuracy while far-field optics allow a noncontact readout. Some of the proposed strategies include structures that undergo a conformational change upon an increase in temperature,⁷ thus inducing variations in fluorescence intensity of a dye molecule embedded in them.

Also cleverly designed lanthanide-based fluorescent probes in which the ratio of particular emission peaks depends on temperature provide a high accuracy and can be used as nanothermometers⁸ even in biological samples.⁹ Photobleaching is often an important limitation of these approaches. Recently, surface enhanced Raman spectroscopy (SERS) allowed to measure spectral changes induced by temperature down to single molecules,¹⁰ but a careful calibration of the measurements is crucial.

Gold nanoparticles continue to receive a fair amount of attention because of their unique optical properties.¹¹ The collective oscillation of conduction electrons, also known as surface plasmon, shows a resonance in the visible to near-infrared wavelengths. This resonance can be tuned by changing the shape of the particles¹² and is responsible for a large absorption and scattering cross section at the resonance wavelength. These cross sections can be calculated by solving the Maxwell equations numerically employing different computer packages,¹³⁻¹⁵ providing a good agreement between calculations and what is experimentally achievable.

Thanks to their high absorption and scattering cross section (several times higher than their geometrical cross section), it is relatively simple to detect nanoparticles in a dark-field scattering configuration¹⁶ or via photothermal imaging.^17,18 Alternatively, detecting gold nanoparticles through their luminescence¹⁹ is also possible; their low quantum yield,²⁰⁻²³ around 10^–6, is compensated by the enhanced cross section at the surface plasmon resonance (SPR). The luminescence signal is stable over time; gold nanoparticles do not blink nor bleach and therefore are useful labeling agents for processes that require extended periods of observation.²⁴

Different metallic nano-objects are being introduced as agents for photothermal therapy^5,25 or drug delivery.²⁶ One of the advantages of gold nanoparticles is the possibility of tuning their resonance to the near-infrared range, where the penetration of light into tissues can be of several centimeters.^{3−5,25,27,28} Moreover, the particles can be used not only for treatment, but also for imaging.^5,29 In the case of photothermal therapy, nanoparticles are used as heat sources^4,27 to locally increase the temperature in order to induce the death of specific cells in a tissue.^5,25 However, the temperatures reached³⁰ can only be estimated from models²⁹ or from an ad-hoc calibration. Therefore, a method to simultaneously increase and monitor the local temperature will be of great interest in a broad range of fields.

Luminescence of metallic nanoparticles has been the subject of extensive study in recent years. Since the first observation of luminescence from bulk gold,³¹ different groups have tried to quantitatively describe the observed properties,³²⁻³⁶ such as the quantum yield^20−23,37 and the emission spectrum.³⁸ In particular, gold nanorods present two distinct resonance energies, namely, the transverse and the longitudinal plasmon resonances. These particles can therefore be excited efficiently at one of those energies; the transverse resonance corresponds to a wavelength of about 530 nm and will give rise to a broad luminescence emission with a peak at the longitudinal plasmon energy. Conversely, it is possible to excite the particles with a wavelength matching the longitudinal plasmon resonance. In this case, the excitation benefits from an enhanced absorption cross section, but the emission that overlaps the plasmon resonance will be mostly blocked by the filters needed to prevent direct excitation light from reaching the detectors.

In this work, we call “photoluminescence” any secondary light emission³⁹ at energies different from the excitation laser energy, ℏω_L. After absorption (we do not specify whether the absorption is real or virtual) of an excitation photon, the excited electronic state^31,37 may interact and exchange energy with the phonon bath or, in the case of metals, with the bath of thermally excited charge carriers around the Fermi level. After a number of interactions, the excited electronic state will re-emit a photon, which can possess a lower or higher energy than that of the excitation photon.⁴⁰⁻⁴² For a nonresonant excitation, the probability of more than one interaction is negligible, and the main contribution to secondary emission is Raman scattering.³⁴ This is the case, for example, of insulators excited well below their electronic absorption edge. For resonant excitation, a relatively long-lived excited state is prepared. It will have enough time to interact repeatedly with thermal baths, particularly with phonons. This is the case of organic dye molecules or semiconductors in which relaxed fluorescence is observed. We also note that fluorescence always presents hot bands on the anti-Stokes side of the excitation laser. In most fluorescence detection schemes, however, these hot bands are ignored, but they are far from negligible in heavily doped samples.⁴³

Metal nanoparticles fall between those two extremes because the excited electronic state, an electron–hole pair, relaxes very rapidly by interacting with other charge carriers and with phonons. The photoluminescence lifetimes are on the order of tens of femtoseconds,⁴⁴ and therefore, there is not enough time to obtain a fully relaxed luminescence. In other words, the photoluminescence is always “hot”. It is worth noting that Raman scattering, corresponding to the lowest order of interaction with baths, will be an important contribution to photoluminescence.^34,36 However, second and higher orders may also contribute significantly. Because all these processes obey a Boltzmann-type relationship between anti-Stokes and Stokes emission, they cannot be easily distinguished from each other on the basis of their temperature dependence.

The anti-Stokes emission is highly sensitive to temperature, and thus, it can be used for thermometry.⁴⁵ In this Letter, we present a simple procedure to extract the absolute temperature from the anti-Stokes photoluminescence spectrum of individual gold nanorods without the need of any previous temperature calibration. We show that we can determine the particle temperature in situ with an accuracy of 6% by recording a single anti-Stokes spectrum (with an acquisition time of 3 min). Moreover, by performing this measurement at different excitation powers we can obtain the temperature of the surrounding medium with an accuracy better than 2%.

Phenomenological Model for the Luminescence Emission

In a nutshell, we consider the luminescence emission as radiative recombination of electron–hole pairs created by the decay of the plasmon, after their interaction with thermal baths. Before the recombination, carriers may interact with the baths one or more times, leading to secondary light emission with an energy different from the initial internal energy of the pair. The anti-Stokes spectral contribution arises from interactions that increase the energy of the pair, whereas the Stokes emission corresponds to a decrease in energy. The emission process will be enhanced by the surface plasmon; therefore, the luminescence spectrum will be modulated with the plasmon shape. A schematic representation of these ideas is shown in the Supporting Information.

Exciting a gold nanorod with a monochromatic beam at its resonance frequency, ω_SPR, generates a collective oscillation of the gas of conduction electrons, also called a plasmon. The plasmon decays by forming a pair of hot electron and hole with an internal energy equal to the exciting photon energy,⁴⁶⁻⁴⁸ i.e., E_e–h = ℏω_L, where ω_L is the laser frequency.

This hot electron–hole pair has a small probability of recombining radiatively, i.e., of re-emitting its high electronic energy as a photoluminescence photon. If the electron and hole have interacted only with static surfaces or defects, their energies will be the same. Therefore, the emitted photon will have the same energy as the incoming photon and will not contribute to the measured photoluminescence. It will be blocked by the notch filter used to remove the exciting laser from detection. If, however, the electron and hole have interacted with a phonon or a thermally excited electron or hole, they may have lost or acquired energy. In both cases the energy available upon recombination cannot much exceed ℏω_L + k_BT, where k_B represents Boltzmann’s constant and T the absolute temperature.

Radiative recombination gives rise to emission spectrally and spatially distributed throughout the particle over a broad frequency band with an exponential cutoff at ℏω_L + k_BT. The weak recombination emission can be greatly enhanced by the surface plasmon resonance, acting as an antenna. With this model, the following predictions can be made. First, the emission spectrum must follow the plasmon spectrum if the excitation laser is well above the plasmon resonance as shown in Figure 1, green line. If the excitation falls within the plasmon resonance, the spectrum is expected to follow the plasmon spectrum multiplied by a Bose–Einstein statistics factor arising from phonon population (here, we assume that the coupling to the phonons dominates the process, while refs (34) and (36) assume that carrier–carrier interactions dominate). Thus, under our assumption, the emission should be proportional to the phonon occupation number n̅ for anti-Stokes and n̅ + 1 for Stokes processes, with

1

where ℏΩ is the phonon energy. If carrier–carrier interactions dominate, the occupation number would obey Fermi statistics, i.e., .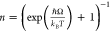

Figure 1.

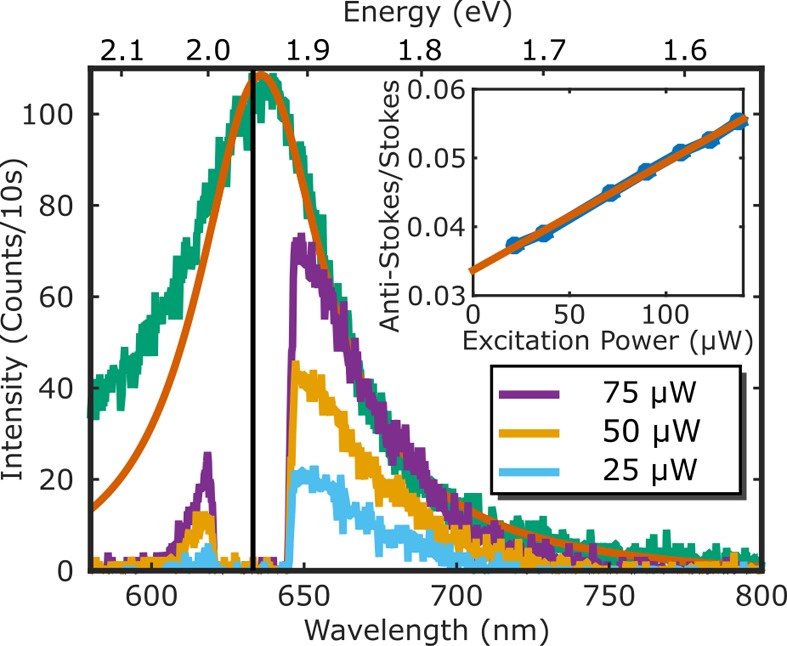
Luminescence emission spectra of a single gold nanorod. The green curve is the measured luminescence emission under 532 nm excitation, and the red curve shows the extracted I_SPR(ω) from this spectra. The other curves are the emission of the same particle under 633 nm irradiation at three different powers indicated in the legend. The inset shows the anti-Stokes-to-Stokes ratio as a function of the excitation power, overlapped with a linear fit in red. The dip centered on the laser wavelength is caused by the notch filter used to prevent the excitation laser from reaching the detectors. For these spectra, the acquisition time was 10 s.

With this model, we can also predict that the emission should be polarized. For the strong longitudinal plasmon of gold nanorods, this polarization coincides with the longitudinal axis of the particle.⁴⁹ Moreover, the lifetime should be determined by the lifetime of hot electrons and holes and should be significantly shorter than the thermalization time of the carriers. Indeed, a few interactions would suffice to reduce the carriers’ energy significantly, and therefore, the electron and hole would not have the energy required to produce an optical photon. One important assumption for this model is that the emission spectrum of radiative recombination is much broader than the plasmon. Therefore, excitation just above the plasmon resonance should excite the electron–hole pairs with nearly the same efficiency as well above the plasmon resonance.^23,36

Application to Nanothermometry

According to the model just described, the anti-Stokes emission spectrum follows the form

2

where I(ω) is the emitted intensity, ω is the angular frequency of the photons, ω_L is the frequency of the exciting laser, and I_SPR(ω) is the surface plasmon resonance spectrum. The only remaining free parameter is the temperature T (and a normalization constant not included in eq 2).

The procedure we propose to obtain the absolute temperature T of gold nanorods from the anti-Stokes luminescence emission without the need of any previous temperature calibration involves the following steps:

• 1.
  Obtain the surface plasmon resonance spectrum of the particle. This is usually expressed as a Lorentzian function,¹¹ i.e.,

  

  where ω is the photon energy frequency, ω_SPR is the resonance frequency, and Γ is the width of the surface plasmon resonance. In our case, we detect the spectrum of photoluminescence excited at 532 nm to extract ω_SPR and Γ, with the procedure explained in the Supporting Information.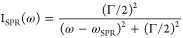
• 2.Excite near the longitudinal plasmonic resonance and detect the blue-shifted anti-Stokes emission spectra. For this we employed a 633 nm laser as a source.
• 3.Fit the high-energy part of the spectrum using eq 2 with T as the only free parameter.

We emphasize that we cannot simply use the anti-Stokes to Stokes intensity ratio to obtain the temperature of the particle, as is commonly done with Raman lines of molecules,^50,51 due to the presence of the strong plasmonic enhancement of the emission that must be considered in addition to the Boltzmann factor.

Experimental Methods

All the measurements in this work were performed with a home-built confocal microscope equipped with a spectrometer (Acton 500i) in the emission path. We focused our lasers to a diffraction-limited spot using a 60×, NA 1.4 oil immersion objective (Olympus) or a 60×, NA 0.9 air objective (Olympus) and collected the emitted photons through the same objective. This provided high excitation and collection efficiency. We employed a 532 nm (CNI) laser for characterizing the nanorods’ plasmon and a 633 nm HeNe (Thorlabs) to excite the nanorods in resonance. The intensity of the laser was controlled via an acousto-optic modulator. We provide a scheme of the setup and more details in the Supporting Information.

Wet-chemically synthesized nanorods⁵² with average dimensions of 25 nm × 50 nm and a plasmon resonance around 630 nm were spin-coated onto clean coverslips, controlling the superficial concentration to separate individual nanorods within the diffraction-limited spot.¹¹ The characterization of the gold nanorods sample with transmission electron microscopy (TEM) and the ensemble extinction spectrum are presented in the Supporting Information.

The samples were mounted in a flow cell that allowed us to increase the temperature of the medium up to 60 °C and to monitor it through a Pt100 resistance thermometer placed 1 mm away from the observation area. To compensate for the drift of the setup while increasing the temperature, we developed a computer program to continuously track a reference particle. The same program was responsible for recording the temperature and triggering the spectrometer. In this way, complete data sets were acquired at different temperatures, with excitation at 532 and 633 nm, at different laser intensities. A spectrum with 532 nm laser excitation was taken after every cycle to ensure that the particle under study had not reshaped due to high excitation power.

When recording anti-Stokes spectra to extract the temperature of the particles using the high NA objective, six accumulations of each spectrum were recorded with an exposure time of 10 s (total time of 60s). When we used the low NA objective the exposure time was increase to 30s in each exposition (total time 180s). This not only allowed us to lower the noise of the measurement because of a longer exposure time, but also allowed us to remove bright pixels generated by cosmic rays. Having several accumulations is also useful to monitor changes in the intensity of the spectra during the acquisition itself. These changes can be due to a drift of the setup while measuring or to reshaping of the particle. If the reshaping was confirmed by comparing the spectra acquired with the 532 nm laser,⁵³ the measurements where rejected. If the changes in the observed emission spectra were due to drift of the setup, the particular data set was not taken into account. For the purposes of this work, the excitation intensity is crucial for characterizing the method; if the particle is not in focus, it would result in an overestimation of the excitation power.

Results

The proposed model for the anti-Stokes emission requires the plasmon spectrum (I_SPR(ω) in eq 2) in order to fit the emission at shorter wavelengths and extract the particle temperature. It has been shown that both scattering and luminescence spectra roughly overlap over a broad range of wavelengths.²² Therefore, exciting gold nanorods with 532 nm allows us to record the longitudinal plasmon spectra, as shown in the green solid curve of Figure 1. It has to be recalled that the luminescence spectrum is not a perfect Lorentzian since there is a broadband contribution also observed in bulk gold.³¹ The procedure to extract the SPR profile from such a measurement is explained in the Supporting Information. We show in Figure 1 the extracted surface plasmon profile in the red solid curve.

The other curves in Figure 1 show the luminescence emission of the same nanorod with irradiation at 633 nm at different powers, ranging from 25 to 75 μW at the back aperture of the objective. The vertical black line shows the wavelength of the laser. The Stokes part of the spectrum at longer wavelengths than the excitation shows the same shape as the plasmon emission observed under 532 nm excitation, apart from a normalization factor. From the figure, it can readily be seen that the shape of the anti-Stokes emission, at shorter wavelengths than excitation, is exponential-like and does not follow the Lorentzian shape of the Stokes emission. The dip between Stokes and anti-Stokes is caused by the notch filter that prevents direct excitation light from reaching the detectors.

The inset of Figure 1 shows the anti-Stokes-to-Stokes ratio of the integrated luminescence for different laser excitation intensities. It is possible to see that even though the photoluminescence process is linear, the anti-Stokes intensity increases slightly more rapidly than the Stokes emission. We already exploited this phenomenon to image gold nanorods in high-background conditions.⁴³ For more information on the power dependence of both the anti-Stokes and Stokes luminescence, please refer to the Supporting Information.

To further characterize the anti-Stokes emission in gold nanorods, we measured the emission for 105 nanorods with different plasmon resonances under the same 633 nm excitation and calculated the ratio of integrated anti-Stokes to Stokes emissions. Figure 2 shows the experimental ratios as blue circles versus the surface plasmon resonance (SPR) of the particle. The vertical black line marks the laser wavelength. The particles measured had resonances between 600 and 690 nm; the ones showing the maximum ratio of anti-Stokes to Stokes are those with a resonance to the blue of the laser. For these particles, the longitudinal plasmon is enhancing preferably the anti-Stokes emission. For particles with a resonance at the laser wavelength, the anti-Stokes and the Stokes emission have similar enhancement and show a ratio close to 10%.

Figure 2.

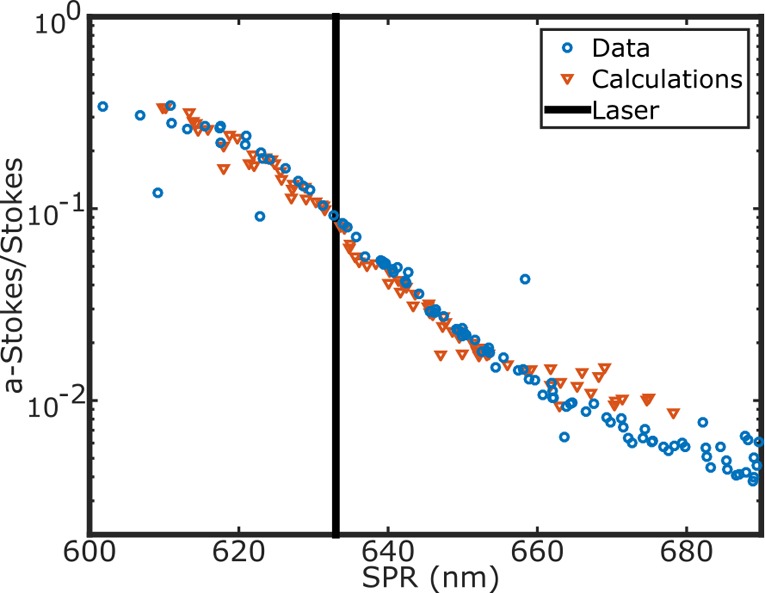
Characterization of anti-Stokes emission for different surface plasmon resonance. Ratio of the anti-Stokes to Stokes emission under 633 nm excitation as a function of the resonance wavelength of the particle. The blue circles are experimental results (105 different nanorods), while the red triangles are the results of numerical simulations with eq 1 (82 nanorods with different aspect ratio). There is a very good agreement between experiment and calculations. Particles with a resonance to the blue of the laser (indicated by the vertical black line) have an increased anti-Stokes emission.

Figure 2 also shows as red triangles the results of numerical calculations showing an excellent overlap between the measured and the calculated data. To obtain these results, we numerically calculated the absorption cross section of 82 particles with the ADDA package¹⁴ using a fixed width and different lengths to achieve different SPR wavelengths. Each calculated absorption spectrum was fitted by a Lorentzian and used as I_SPR(ω) in eq 2. Assuming a diffraction-limited laser spot and using the calculated absorption cross section, we calculated the temperature of the particle. This value was used in eq 2 to compute the anti-Stokes emission spectrum. The Stokes emission was set proportional to the excitation power with a shape given by the calculated absorption spectrum. Since both anti-Stokes and Stokes emissions are proportional to the excitation power, this term cancels out when computing the ratio. The laser power therefore only enters into the equation when calculating the temperature of the particles. It is remarkable that the agreement between data and calculations was achieved without free parameters, solely taking into account the transmission spectra of the filters.

We then use our protocol to extract the temperature of an individual nanorod. The anti-Stokes spectra shown in Figure 3 were recorded at four different excitation intensities, while the full lines are the fits using our model from eq 2; again, there is an excellent agreement between data and model. For every anti-Stokes measurement we have also acquired the full plasmon spectrum exciting with a 532 nm laser before and after the temperature extraction, to verify that the particle did not reshape while being excited at resonance.

Figure 3.

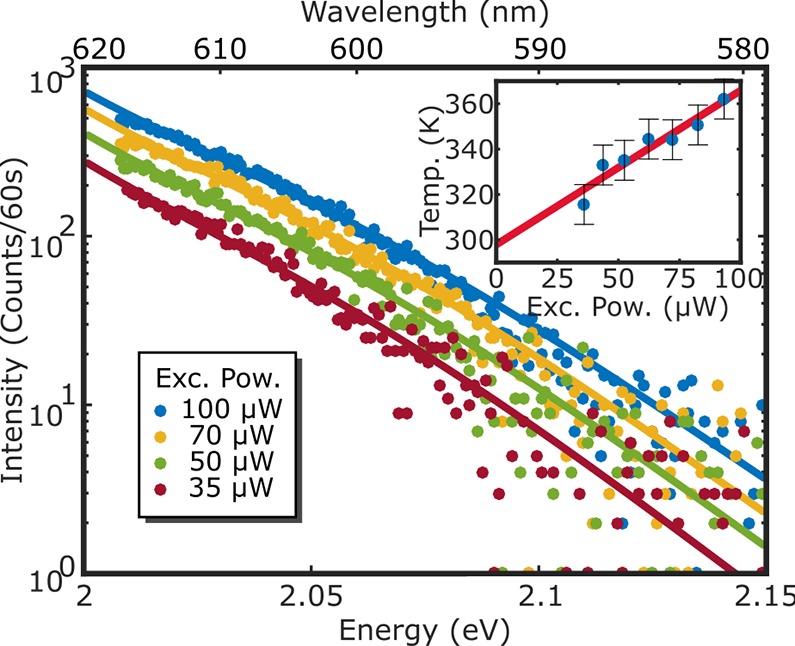
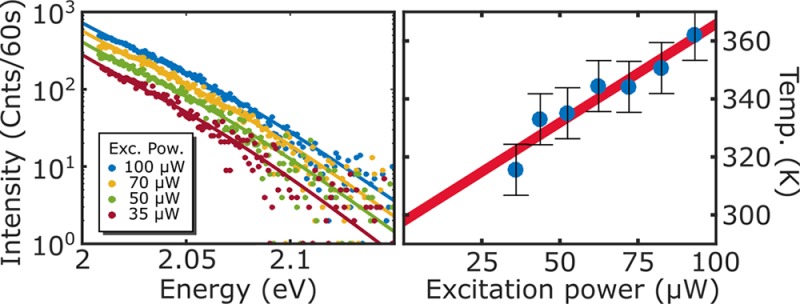
Anti-Stokes emission of a single nanorod at different irradiation powers. We used the model from eq 2 to fit the experimental data. There is an excellent agreement between data and model. The inset shows the extracted temperature at each power (blue dots) and a linear extrapolation of the data to 0 μW excitation power. The value obtained for room temperature was 293 K, while the measured value was 296 K.

The inset in Figure 3 shows the temperatures resulting from the fits at different irradiation intensities (blue dots). Note that the absolute temperatures of the particle at each excitation power were calculated without any calibration. As expected, the temperature of the nanorod varied linearly with excitation intensity or equivalently with the absorbed energy. Thus, this method provides an in situ way to measure the temperature reached by nanoparticles when they are excited with resonant monochromatic light. Additionally, from these data sets it is also possible to calculate the temperature at 0 μW excitation power, i.e., room temperature, by extrapolating the results with a linear fit. The value we obtained in this case is 293 ± 6 K, while room temperature was 296 K, a 2% accuracy.

The accuracy of the obtained temperature depends on the signal-to-noise ratio of the anti-Stokes spectra and on the accurate modeling of the photoluminescence. The first step in the protocol is the determination of the surface plasmon spectral profile, I_SPR(ω) in eq 2. In this Letter, we obtained this term by fitting an exponential background plus a Lorentzian to the spectra obtained at 532 nm excitation. We note that this choice was made for experimental convenience in our setup, but other options to obtain the SPR profile are suited for the procedure as well. The error bars in the inset of Figure 3 and in the following figures are the result of the estimated variance in the fit parameters for the anti-Stokes spectra using eq 2, step 3 in our protocol. More details about the error determination for the final temperature extracted are given in the Supporting Information.

As expected from the model, the anti-Stokes emission depends not only on the particle’s intrinsic properties but also on the temperature of the surrounding medium.⁵⁴ In order to further test this point, we changed the temperature of the sample in a controlled manner and recorded the luminescence emitted by a single nanorod.

For this set of experiments, we employed an air objective (60×, NA 0.9, Olympus) to avoid the presence of a heat sink directly in contact with the observed area. We employed longer exposure times to compensate for the lower excitation efficiency. At each temperature, six spectra (with 30 s integration time each) were acquired at different 633 nm excitation powers and also a spectrum of the plasmon before and after each measurement in order to monitor any possible reshaping of the particles during the experiment.

Figure 4 shows the extracted temperature of a particle at varying excitation powers and at different water temperatures. The blue squares are the results of the measurement at 60 °C, while the green crosses are measured at 40 °C and the yellow circles at 20 °C. The full lines are fits with the same slope for the three sets of data. Using these fits we can extrapolate the temperature value at zero excitation power to obtain the water temperature in each case. The values obtained with the extrapolation to 0 μW excitation power were 296 ± 4, 315 ± 4, and 339 ± 4 K for water temperatures of 293, 313, and 333 K, respectively. The inset plot in Figure 4 presents these points and a red solid line with the expected curve if both temperatures are identical. The dashed line shows a fit of the data that evidence a small systematic offset of 3.8 K. This represents an inaccuracy of 1.2%, which is a good result for a calibration-free method.

Figure 4.

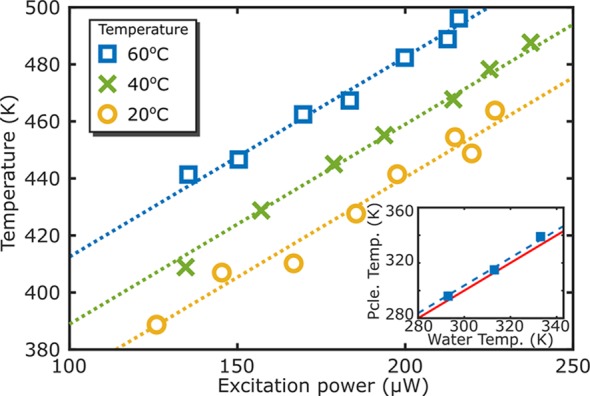
Calibration-free temperature measurement. Extracted temperatures from the anti-Stokes-luminescence emission of an individual nanorod at different excitation powers and at different sample temperatures. The dashed lines are fits with the same slope for the three temperatures. The squares in the inset plot show the local temperature of the sample obtained by extrapolating the temperature at zero excitation power as a function of the water temperature. The red line represents the expected curve if both temperatures are identical (equal). The dashed blue line is a fit to the data points with unit slope that shows a systematic offset of 3.8 K, a 1.2% difference.

Figure 4 clearly shows that the extracted temperature varies with the temperature of the surrounding medium. More strikingly, the method does not require any previous calibration nor adjustment. Notably, the presented calibration-free procedure would allow us to perform the same measurements in any other setup and could act as a reference for calibration of other nanothermometers.

Being able to control and monitor temperature at the nanoscale is of utmost importance in different fields ranging from photothermal therapy⁵ to nanofabrication.⁵⁵ In this work, we have shown a simple procedure that allows us to measure the temperature of single gold nanorods irradiated by a monochromatic continuous laser and without any previous calibration. The level of accuracy of the temperature measurement depends on several factors, but for a single nanorod, it can be estimated to be better than 6% with an integration time of 1 min without any previous calibration.

The model employed for describing the anti-Stokes emission takes into account the surface plasmon resonance of the particles under study, which is responsible for enhancing the emission, as well the electron–hole pair interaction with the thermal baths. Particles with a resonance to the red of the excitation wavelength would be more reliable in the temperature extraction procedure but would also exhibit a lower emission toward shorter wavelengths. The trade-off between both effects and the possibility to fully characterize the plasmon resonance will determine the specific particles that are better suited for each application.

A possible improvement of this technique would be the use of nanostructures with a narrow shape distribution such as gold bipyramids.⁵⁶ Such structures would be ideal candidates for temperature extraction since they present negligible size dispersion, and thus, their plasmon can be measured in bulk or determined from theory, avoiding the need of a second excitation source.

The proposed method does not require any temperature calibration since the only free parameter of the model is the absolute temperature of the nanoparticle under study. Moreover, the recording of the anti-Stokes spectrum is readily achievable in any confocal microscope with a coupled spectrometer. A 6 K accuracy may suffice for several applications; it is important to point out that this value can be improved in different ways: by carefully selecting the particles that show the most favorable plasmon resonance; by determining the plasmon resonance through white-light scattering, reducing the uncertainty in the fit; and by increasing the exposure times to increase the signal-to-noise ratio. A cheaper alternative would have two detectors and band-pass filters to detect the anti-Stokes and the Stokes emission independently. However, this approach would require a temperature calibration.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b04145.

• Anti-Stokes emission from gold nanorods, determination of the surface plasmon resonance energy, experimental setup, gold nanorods sample characterization, luminescence power dependence, determination of the error in the temperature extraction, gold nanorod temperature numerical calculations (PDF)

The authors declare no competing financial interest.