Dipole-like electrostatic asymmetry of gold nanorods

Seemingly symmetric nanoscale cylinders have hidden asymmetry of charge distribution.

Abstract

The symmetry of metallic nanocolloids, typically envisaged as simple geometrical shapes, is rarely questioned. However, the symmetry considerations are so essential for understanding their electronic structure, optical properties, and biological effects that it is important to reexamine these foundational assumptions for nanocolloids. Gold nanorods (AuNRs) are generally presumed to have nearly perfect geometry of a cylinder and therefore are centrosymmetric. We show that AuNRs, in fact, have a built-in electrostatic potential gradient on their surface and behave as noncentrosymmetric particles. The electrostatic potential gradient of 0.11 to 0.07 V/nm along the long axes of nanorods is observed by off-axis electron holography. Kelvin probe microscopy, secondary electron imaging, energy-filtered transmission electron microscopy, and plasmon mapping reveal that the axial asymmetry is associated with a consistently unequal number of cetyltrimethylammonium bromide moieties capping the two ends of the AuNRs. Electrostatic field maps simulated for the AuNR surface reproduce the holography images. The dipole-like surface potential gradient explains previously puzzling discrepancies in nonlinear optical effects originating from the noncentrosymmetric nature of AuNRs. Similar considerations of symmetry breaking are applicable to other nanoscale structures for which the property-governing symmetry of the organic shell may differ from the apparent symmetry of inorganic core observed in standard electron microscopy images.

INTRODUCTION

Symmetry assignments of colloidal particles are foundational for theoretical and experimental studies in numerous fields of science (1–3). Their multicomponent nature and multiscale dynamics make symmetry assignment to nanoscale colloids a difficult task; therefore, they are often simplified to simple geometrical shapes. It has largely been assumed that the geometry of the metal core obtained from transmission electron microscopy (TEM) is representative of the symmetry of the nanoscale metal particle as a whole. For example, gold nanorods (AuNRs) generally demonstrate nearly perfect cylinder–like centrosymmetric shapes in TEM images. Hence, their plasmon oscillations have been interpreted in terms of the electromagnetic modes confined in a perfect cylinder or prolate spheroid (4, 5). It is remarkable to notice that there are also multiple experimental observations that are difficult to explain in the same framework.

Plasmon mapping using different techniques, including electron energy-loss spectroscopy (EELS) (6–8), cathodoluminescence (9), and near-field microscopy (10), have consistently recorded curious asymmetry in NRs. For example, Rossouw et al. (8) reported plasmon modes to be displaced by (17 ± 3) nm, with respect to the center of nearly perfect silver NRs. Some of these observations were attributed to unspecified effects of the local environments around the NRs. However, calculations reveal that even a close topographical or chemical neighbor cannot produce the considerable mode shifts observed in experimental data of previous studies (fig. S1). Furthermore, the quantitative assessment of the catalytic reactivity of AuNRs was reported to have a distinct gradient along the longitudinal axis (11). This gradient of catalytic activity could not also be rationalized as effects of the local environment, because they would be averaged in the dispersed state and over the large number of nanowires and NRs.

Other phenomena that are difficult to explain under assumption of perfect centrosymmetric shapes of nanocolloids, are nonlinear optical (NLO) responses from NRs and nanoparticles (NPs). The second harmonic generation (SHG), third harmonic generation, and nonlinear (multiphoton) photoluminescence (NPL) of metal NPs have been extensively studied over the past decade (10, 12–21). However, a consistent description of NLO emission in metal nanostructures has not yet been attained. For instance, the strong SHG signal observed in the small seemingly centrosymmetric particles cannot be rationalized by conventional NLO processes because it should be forbidden in this system (12, 16). These phenomena have been attributed to surface defects, the asymmetry of metal-media interface, and retardation (16–19, 22). A recent observation of NPL from Au nanostructures, being dependent on NP shapes (20), contradicts the conventional interpretation of NPL as an electron-hole recombination located at different energy states in the metal (10, 23). Because the shape of nanoscale metals should have little effect on the energy of solid-state electronic levels and recombination rates, additional factors are necessary to explain this dependence. These considerations prompted us to investigate whether NRs are de facto centrosymmetric.

RESULTS

An unequal density of surface ligands due to the difference in their affinity to {111} facets compared to other major facets of gold NPs, such as different dense of cetyltrimethylammonium bromide (CTAB) on the sides and ends of NRs, is well known (24–28). Recent studies of NR geometries at atomic resolution (26, 29) also reported that the facet compositions may not necessarily be a simple, but rather a complex, combination of these facets due to the rounded shape and “bridging” face between the cylindrical body and the ends. These models still retain the central symmetry of the nanocolloids. We hypothesized that the different surface area of {111} and {110} facets at the two ends of the NRs (Fig. 1A) and/or the different packing density of the surface ligands may cause loss of the central symmetry. Because CTAB moieties carry charges, this model must lead to noncentrosymmetric electrostatic potential on the outer surface of the AuNRs (Fig. 1B, case 2).

Fig. 1. Schematic description of possible electrostatic potential in AuNRs.

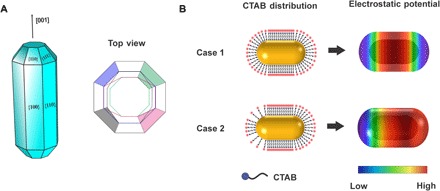
(A) Typical morphology and surface facets of AuNR grown with CTAB surfactant. The top view shows possible complexity of facets composing ends of AuNR. The colored areas present possible variation of {111} facet area. (B) Expected electrostatic potential at outer surface of CTAB with equal (case 1) and unequal (case 2) capping for two ends.

Asymmetric electrostatic potential of AuNRs

The nanometer-resolution off-axis electron holography (EH) enables direct imaging of the electrostatic potential around a nanoscale object (30). The potential can be determined by evaluating the phase shift, ϕ(x), of an electron wave that has passed through the sample, relative to the wave that has traveled through a vacuum

$$\mathrm{\varphi }(\mathit{x})={\mathit{C}}_{\mathrm{E}}{\displaystyle \int }\mathit{V}(\mathit{x},\mathit{z})\mathit{d}\mathit{z}‐\frac{\mathit{e}}{\mathrm{\hslash }}{\displaystyle \iint }\mathit{B}\perp (\mathit{x},\mathit{z})\mathit{d}\mathit{x}\mathit{d}\mathit{z}$$ (1)

where z is the incident beam direction, x is a direction in the plane of the sample, V is the electrostatic potential, B⊥ is the component of the magnetic induction perpendicular to both x and z, and C_E is the interaction constant depending on the acceleration voltage of the electron microscope (31). For a nonmagnetic material, such as gold, the second term of Eq. 1 is zero, and only the first term contributes. Therefore, the magnitude of ϕ(x) is proportional to the integral of the electrostatic potential along a straight-line path through the specimen. The phase shift map, reconstructed from the electron hologram, shows that standard NRs stabilized by CTAB is asymmetric (Fig. 2, A and B). The ϕ(x) along the long axis of the NR is linearly fitted with a slope of 0.02 rad/nm in the range of the cylinder body. We took EH images of more than 50 NRs, including different aspect ratios (from 3 to 6) in high- and low-magnification imaging conditions. Their ϕ(x) values, displaying distinct gradients along the long axis, which corresponds to electrostatic potential gradient of 0.11 to 0.07 V/nm, are consistent across multiple areas on the microscopy grid, separately prepared samples, and imaging conditions. Contrastingly, ϕ(x) values observed for NRs that lack a CTAB layer are symmetrical with no slope (Fig. 2, C and D).

Fig. 2. Electrostatic properties of individual AuNRs.

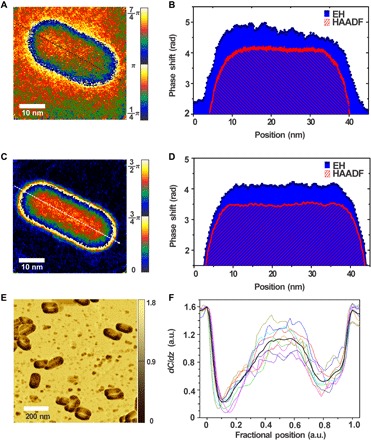
Phase map (A and C) and profiles (B and D) along the longitudinal axis of the AuNRs supported by silicon grids with (A and B) and without (C and D) CTAB coating. Blue and red curves are extracted from their phase shift maps by EH and HAADF images, respectively. (E) Capacitance gradient (dC/dZ) image and (F) line profiles of individual (dashed) particles and average curve (solid, black) along long axis, obtained by Kelvin probe microscopy. a.u., atomic unit.

The electrostatic potential at a given position, V(x,z), is a combination of the mean inner potential, V_MIP, and the potential from charge accumulation, V_CP (x,z), of the sample material. V_MIP is the volume-averaged potential due to incomplete screening of atomic cores and is defined as 1/Ω${\displaystyle \int }\mathit{V}(\overrightarrow{\mathit{r}}){\mathit{d}}^3\mathit{r}$ (31), where $\mathit{V}(\overrightarrow{\mathit{r}})$ is the total electric potential at point $\overrightarrow{\mathit{r}}$ due to all the charges in the solid, Ω is the volume of the solid, and the integral is over the entire crystal volume. Thus, the phase shift ϕ(x) gradient observed in hologram should be originated either from the thickness δ(x) or charge potential (V_CP) variation of the specimen. If our hypothesis is valid, then the observed electrostatic asymmetry is not originated from δ(x) variation of their cylinder body but rather from V_CP variation. To determine the origin of this asymmetry, we have thoroughly evaluated the potential sources for this slope.

One potential cause of ϕ(x) variability along the long axis of the AuNR is the variation of the gold core diameter, ε. To elucidate this possible source of asymmetry, high-angle annular dark-field (HAADF) scanning TEM (STEM) images were taken on the same AuNR (fig. S2, A and B). Because the intensity of HAADF signal is proportional to ε, that is, I_HAADF ∝ ε∙Z^α, where Z is the atomic number and α ≈ 1.6 to 2.0, the HAADF signal can be considered as ε profile and be simply converted to ϕ(x) by using two constants, V_MIP of gold and C_E of a 200-kV electron beam (e-beam) (V_MIP = 30 V, C_E = 0.00729 rad/V∙nm) (32). Because the HAADF intensity profile shows no variability along the long NR axis, the estimated phase shift profile from the gold core is symmetric (Fig. 2B, red). Similarly, direct visualization of the organic layer using secondary electron imaging and energy-filtered TEM (EF-TEM) shows no evidence of CTAB patchiness variation on the long sides of the NRs (Fig. 3) that could be potentially another source of thickness variation of the NRs from carbon layer, which is also expected to have minor effect on EH images due to its relatively smaller V_MIP to gold.

Fig. 3. Noncentrosymmetric distribution of CTAB on AuNR.

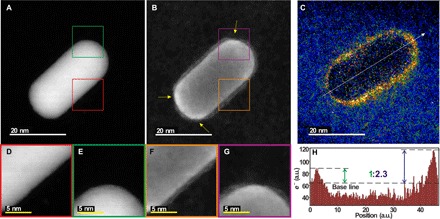
(A, D, and E) STEM-HAADF and (B, F, and G) SEM images for a same gold NR. (D to G) Atomic resolution images of the side (D and F) and end (E and G) sections of the AuNR. (C) Carbon element map and (H) carbon profile along the white arrow obtained by EF-TEM.

The question arises now whether the asymmetry of the charge trapped in the facet defects or edges rather than CTAB causes the loss of the central symmetry. Another possible artifact of similar nature—e-beam–induced charging (30)—should also be considered. One needs to remove CTAB to test it. The complete removal of CTAB from dispersed AuNRs without losing colloidal stability is difficult (33, 34). Therefore, we went a different route and prepared a solid-state sample of AuNRs in a polymer matrix using layer-by-layer (LBL) assembly. During LBL deposition, the rarefied layers of AuNRs anchored to the substrate by the previous polyelectrolyte stratum are exposed to solution of poly(sodium 4-styrene sulfonate) (PSS). The negatively charged polyelectrolyte draws away and strips positively charged CTAB from the surface of the NRs (fig. S3). The removal is complete because PSS is present in the vast excess. The annular electrostatic potentials disappeared from the holography image of AuNRs in the LBL matrix (Fig. 2C), and the EH line profile of the phase shift (Fig. 2D, blue) is now flat. Consequently, the ϕ(x) profile in Fig. 2B reflects the actual potential gradient specific to charge accumulation in the CTAB-AuNR electronic system, V_CP (x,z), due to positive charge of CTAB layer.

Asymmetric capacitance gradient of AuNRs

Electrostatic fields around nanostructures can also be investigated by Kelvin probe microscopy (Fig. 2, E and F), which allows one to visualize the capacitance gradient, dC/dz, related to ϕ(x) gradient with subnanometer resolution. The presence of the longitudinal gradient ϕ(x) can be independently confirmed by this technique. The dC/dz contrast relates to the dielectric permittivity (ε_r) being higher at locations with increasing permittivity (35). The contributions from several interfaces and materials, such as CTAB and gold, are manifested in dC/dz maps. The dC/dz map vividly shows the difference between the sides and ends of a NR (Fig. 2E), which should be attributed to different CTAB density on the sides and ends (25–27). Consistent and large differences in dC/dz values between the two ends (that is, for two dips in Fig. 2F) are observed indicating electrostatic asymmetry of the NR ends. For statistical analysis of their differences, we performed a paired P test for depths of the two dips for nine individual AuNRs. The difference is statistically considered extramurally significant based on the test result (fig. S2D, P = 0.0002). The dC/dZ profiles roughly matched the ϕ(x) of the charge potential [V_CP (x,z)] component, which can be extracted from the observed EH and HAADF profiles (fig. S2C).

Noncentrosymmetric distribution of CTAB on AuNR

Being guided by the data described above, we acquired the direct evidence about unequal distribution of CTAB ligands on AuNRs using high resolution electron microscopy. Aberration-corrected STEM with a secondary electron detector enables atomic-scale visualization of the CTAB layer. By comparing HAADF and scanning electron microscopy (SEM) images of the same NR, one can see that the CTAB coverage on the two caps is different (Fig. 3, A and B). Elemental mapping of carbon in the organic layer around the gold core by EF-TEM (Fig. 3C) enabled a quantitative analysis of CTAB density difference between two ends. Quantification of EF-TEM with the signal using a supporting carbon grid as the baseline showed that the NR has about 2.3 times more CTAB on one end than the other (Fig. 3H).

Comparison of experimental results and simulations

The quantitative assessment of the unequal density of CTAB layer at the termini of AuNRs (Fig. 3, C and H) enabled modeling of the asymmetrically charged NRs (Fig. 4A). With an average surface charge density of the CTAB layer obtained via electrophoretic mobility measurement, electrical properties of NRs are computed by solving the stationary domain form of Maxwell’s equations via finite element methods.

Fig. 4. Computational analysis of electrostatic properties for AuNRs.

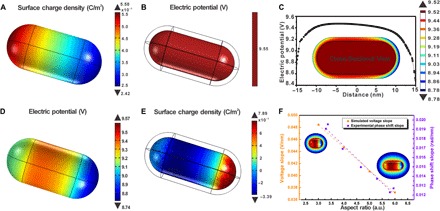
(A) Surface charge density of the CTAB layer. (B and D) Electric potential on the surface of gold and CTAB layer, respectively. (C) Electric potential line plot in the CTAB layer and cross-sectional view of electric potential of CTAB-AuNR. (E) Surface charge density on surface of gold. (F) Voltage (orange) and phase shift (violet) slope of AuNRs with various aspect ratios obtained by computation and experimental EH data, respectively. Both values are linearly fitted as dashed lines with R² value of 0.999 (orange) and 0.971 (violet).

The surface and cross-sectional potential of the CTAB layer (Fig. 4, C and D) exhibits a spatial variation due to the asymmetric fixed surface charge on the CTAB layer (Fig. 4A). The profile of the calculated potential at the interface layer along the cylindrical body of the NRs (Fig. 4C) has a distinctive slope that matches the gradient ϕ(x) observed above (Fig. 2B). The estimated voltage slope from their phase shift slope of 0.02 rad/nm shown in Fig. 2B can be estimated to 0.11 V/nm. This experimental electric field strength value is about doubled the value of the calculated voltage slope shown in CTAB layer (0.049 V/nm). Considering the fact that the hologram represents integrated potential through the short axis of AuNR, the observed and calculated results are accurately matched to each other.

Consequently, the asymmetric potential in an organic shell must lead a distinct surface charge polarization on gold surface to compensate the potential gradient (Fig. 4E). The maximum and minimum surface charge density on gold was calculated to be 7.9 × 10⁻³ and −3.4 × 10⁻³ C/m². By integral of the surface charge density of the gold core, the apparent “dipole” moment along the longitudinal axis direction is calculated to be 2.4 × 10⁻²⁵ C·m, which corresponds to 7.2 × 10⁴ D. However, note that the NR dipole is fundamentally different from molecular dipoles. Unlike the latter, there is no potential gradient in the metal core of the AuNRs due to the high polarizability of the metal, and all potential drops occur at the interfaces.

To test the validity of this model, we calculated the charge asymmetry of NRs with different aspect ratios and compared to the EH results. With a decrease in NR aspect ratio, the gradient of the potential linearly increased, although its absolute potential difference became smaller. The computed results matched the observed ϕ(x) data (Fig. 4F).

Plasmon mapping

To better understand the asymmetry observed during previous plasmon mapping (6–8), the electron energy loss was mapped in the energy window of 1.8 to 2.2 eV, which is associated with the longitudinal plasmon mode of AuNRs (fig. S4D). An EELS image also consistently showed asymmetry with brighter peaks on caps with smaller amounts of CTAB. As a control, we removed a part of the CTAB on the terminus with the denser surface ligand coating by focusing the e-beam for 5 min (fig. S4, C and E). A distinct change in the EELS map, with plasmon intensity becoming symmetrical, was observed (fig. S4F). To quantify the degree of EELS asymmetry, we obtained the ratio between the two bright poles by integrating the intensity of 20 spectra from an area around the caps (fig. S4G). The ratio change after e-beam treatment is turned to be statistically significant (P = 0.015). These results indicate that the electrostatic asymmetry should be taken into consideration when interpreting EELS of metal NPs.

NLO activity

As we discussed earlier, conventionally, a second-order NLO response is forbidden in materials of which a geometrical and material system retains centrosymmetry. However, the existence of the static dipole moments on the AuNRs shown here can lead to breakages of inversion symmetry for the electrical system, which may rationalize the strong SHG signal observed in the small seemingly centrosymmetric particles. To evaluate the population of AuNRs having optical asymmetry, we have prepared the dipolar AuNRs sitting on the cover glass in aqueous solution and took their images in SHG and fluorescence (FL) mode simultaneously (Fig. 5, A and B). SHG of the dipolar AuNRs was exceptionally strong when they were excited at their longitudinal resonance, 850 nm; individual particles were vividly observable and a signal-to-noise ratio in SHG images was better than that in FL images (fig. S5), which is valuable for biomedical SHG imaging, where often the resolving small particle tracking is hampered by auto-FL or penetration depth. The FL image can be used as a good reference where individual AuNRs are located, thus enabling a statistical analysis of the population of AuNRs having optical asymmetry. The dominance of noncentrosymmetric AuNRs can be appreciated from the histogram describing the relative intensity of the SHG to FL for each individual NR. Although the SHG intensity varies, among 119 of AuNRs identified with its FL, 113 of AuNRs were found to exhibit SHG, which indicates that 95% of AuNRs lack central symmetry.

Fig. 5. Asymmetrical optical properties of AuNRs.

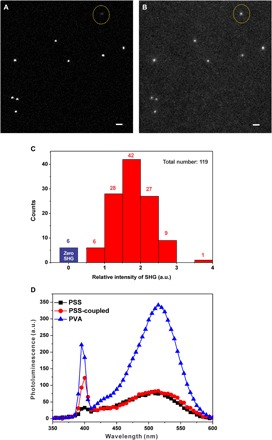
(A and B) Comparison of simultaneously obtained SHG and FL images of AuNRs. Max intensity projection of same z stacks of SHG (A) and FL (B) with same gray scale. The scale bars represent 1 μm. (C) Histogram of relative intensity of SHG compared to FL from 119 of individual AuNRs. Note that blue-colored bar represents the AuNRs having zero intensity. (D) NPL from AuNRs embedded in PSS (black, decoupled; red, coupled) and PVA (blue) matrix.

To investigate the NLO properties in the context of electrostatic asymmetry of AuNRs, we prepared optically transparent films containing AuNRs with and without electrostatic asymmetry. In both cases, care was taken to avoid formation of NP pairs and other assemblies that could lead to transient asymmetry of coupled plasmons. The film containing asymmetrical AuNRs was made by drop casting AuNR dispersions in uncharged poly(vinylalcohol) (PVA). The conserved CTAB layer on the AuNRs within this film was confirmed by x-ray photoelectron spectroscopy (fig. S3B). The average distance between AuNRs in these films was 300 nm; these gaps exceeding the dimension of AuNRs by three times are sufficient to decouple transient oscillating electrical dipoles. Another type of film containing symmetric AuNRs was made using LBL with negatively charged PSS polyelectrolyte, as described above (Fig. 2C and fig. S3A). In this case, films with both optically coupled and decoupled AuNRs were prepared by varying the distance between subsequent AuNR layers using spacer layers (fig. S6).

NLO properties of these samples were evaluated using high-intensity 800-nm 100-fs pulses, which are resonant with the longitudinal plasmon of the AuNRs. The two main NLO effects, SHG and NPL, can be seen for AuNRs imbedded in a PVA matrix at 400 and 530 nm, respectively (Fig. 5D, blue). By contrast, the AuNRs imbedded in PSS with a poly(acrylic acid) (PAA)/poly(diallyldimethylammonium chloride) (PDDA) spacer show weak or no SHG intensity at 400 nm and strong suppression of NPL (Fig. 5D, black).

The second-order NLO response in centrosymmetric particles has been attributed to either surface or retardation effects (19). The observed suppression of the SHG signal in PSS/AuNR films cannot be explained with these effects. Instead, SHG in these systems should be, at least in part, attributed to the second-order nonlinear susceptibilities χ² arising from the breaking of inversion symmetry of AuNRs by the longitudinal electrostatic polarization. The electrostatic asymmetry also can be one of the overlooked factors influencing NPL, giving us a fresh look for previously puzzling NPL behavior (20, 36). The even plasmon mode and optical asymmetry can be mediated by this built-in electrostatic field in AuNRs (15, 37). We found that removal of CTAB results in strong suppression of NPL (Fig. 5D).

Some contribution to SHG may come from hybridized plasmon modes of multiparticle noncentrosymmetric assemblies, although individual AuNRs are centrosymmetric. These expectations were confirmed in the closely spaced LBL films that produce these assemblies (Fig. 5D, red). Notably, the SHG peak by assemblies is enhanced, whereas NPL remains the same. This suggests that SHG and NPL can be “tuned” independently when we take AuNR asymmetry into consideration.

DISCUSSION

AuNRs are electrostatically noncentrosymmetric despite the appearance of the nearly perfect central symmetry in TEM images. Although the electrostatic potential in the metal body remains flat (Fig. 4B), the consistently uneven distribution of CTAB between the two ends leads to the gradient of the electrostatic potential at their surface, and therefore, the surface of gold is highly and unequally polarized on the two ends (Fig. 4E). This origin of the asymmetry is consistent with the normal distribution of relative SHG intensity in fig. S5B, reflecting, among other factors, variability of the CTAB on the two ends of the NR. The reason for end asymmetry of the AuNRs is likely to be associated with the dynamics of NR growth (33, 34). In any case, the structural inequality between the two ends is not an aberration characteristic of singular NRs but a property-determining feature characteristic of their ensembles, as demonstrated by the strong NLO activity. The unexpected lack of inversion symmetry of the AuNRs can be extended to other nanocolloids carrying surface ligands, in addition to the asymmetries originating from crystallography (38, 39) and truncations (40). The intrinsic electrostatic field gradient was also observed in semiconductor nanostructures (41, 42). However, the estimated surface polarization of AuNRs has a higher polarity than same-size wurtzite-phase zinc oxide NRs by five times (41). The presence of surface charge asymmetry should be explored in relation to optical properties (43, 44), electrical properties (45, 46), and agglomeration behaviors (47, 48). For example, the electrostatic asymmetry of AuNRs and potentially other nanostructures emerging from this study shows a new pathway to explain and, therefore, control NLO properties. Besides NLO, the lack of central symmetry is expected to play a role in, and be further exploited through, self-organization phenomena, including dissipative systems (3), chiral nanostructures (49), and catalysis (11).

MATERIALS AND METHODS

Synthesis of AuNRs

AuNRs were prepared using a slightly modified method developed by C. J. Murphy (50). Briefly, an aqueous solution of HAuCl₄ (0.25 ml, 0.01 M) was added to the CTAB stock solution (9.75 ml, 0.1 M). After gentle mixing, a freshly prepared ice-cold NaBH₄ solution (0.6 ml, 0.01 M) was added with vigorous stirring. A brown seed solution was obtained after 2 min, and the seed solution was aged for 2 hours. AuNRs were grown by injecting HAuCl₄ (0.4 ml, 0.01 M), various amounts of AgNO₃ (20 to 100 μl, 0.01 M), ascorbic acid (48 μl, 0.1 M), and seed solution (9.6 μl) to the CTAB stock solution (8 ml, 0.1 M) in sequence. The solutions were gently mixed after each addition. The final mixture solution was kept without disturbance for 24 hours to ensure full growth of AuNRs. Note that all reactions and aging were performed at a temperature of 30°C. The samples were purified by centrifugation (12,000 rpm for 10 min) three times and redispersed in water.

Electron microscopy analysis

All electron microscopic investigations were carried out using a JEOL ARM 200CF apparatus equipped with a cold field-emission gun and double spherical-aberration correctors at the Brookhaven National Laboratory.

Sample preparation

Unmodified AuNR (CTAB-AuNR) samples were prepared by typical drop casting methods. The redispersed corresponding solution after synthesis was purified two times more with a 100-kDa centrifugal device (4000 rpm for 10 min) to remove excess CTAB in solution and drop-casted 5 μl of solution on thin carbon and pure silicon grids, respectively. LBL CTAB-AuNR samples were prepared with PSS using previously described LBL technique (51). Bilayer ultrathin composite films composed of PSS and purified CTAB-AuNRs were fabricated on carbon and pure silicon grids, respectively. Note that EH, STEM-HADDF, and EELS analysis were conducted with silicon grid samples, whereas SEM and EF-TEM imaging were performed on the carbon grid samples to improve image resolution.

Off-axis EH

Holograms of AuNRs on the pure ultrathin (5 nm) silicon grid were acquired using the JEOL ARM 200CF, as described above, operated at 200 kV equipped with a biprism. Phase images were reconstructed using custom Gatan DigitalMicrograph scripts written by M. R. McCartney, Arizona State University (source code is available on request). The phase profiles presented in Fig. 2 (B and D) were calculated in Gatan DigitalMicrograph using the line profile tool.

STEM HAADF

The same silicon grid samples were used in STEM HAADF imaging as for EH imaging. All STEM measurements were performed with 200-kV electrons, and collection angles for HAADF detectors ranged from 68 to 280 mrad.

High-resolution SEM

A nanometer-resolution SEM image was acquired by using a secondary electron detector in high-resolution STEM. For better resolution images, which show the CTAB layer around the AuNRs, the samples on ultrathin carbon grids were used for analysis.

Energy-filtered TEM

For quantitative analysis of the variation of the CTAB layer around the AuNRs, we obtained EF-TEM images for individual AuNRs. The investigations were performed using the three-window method (52–54); background subtraction was achieved by using two images recorded by selecting two energy windows immediately before (pre-edge 1 and pre-edge 2) the plasmon energy and one image by selecting an energy window immediately after (post) the ionization edge. Because the pre- and post-edge images were acquired sequentially, the background subtraction algorithm accounted for specimen drift that occurred during the collection process.

Kelvin probe microscopy

Electrostatic fields around nanostructures were investigated by atomic force microscopy with a scanning probe microscope NEXT (NT-MDT) and conducting Pt-coated Si probes of NSG30/Pt type (NT-MDT). The AuNR solution was purified two times more as described previously in the Sample preparation section and drop-casted on a highly oriented pyrolytic graphite substrate. The map of capacitance gradient, dC/dz, of NRs was achieved in a single-pass technique using the probe response at second harmonic of 3-kHz frequency, at which probe-sample electrostatic force was stimulated (35).

Computational analysis

Calculations of electrostatic properties of AuNRs were performed using COMSOL Multiphysics. To account for the polarizability of a conductive particle with fixed surface charge, we treated gold as dielectrics with relative dielectric constants of 12,000, much greater than that of the surrounding CTAB layer. The COMSOL simulations were carried out with the boundary conditions that electric potential on the gold surface is constant (Fig. 4B) and the electrostatic potential, V, inside the AuNRs should obey the Laplace equation (∇²V = 0).

Estimation of average surface charge distribution onCTAB-AuNRs

By combining the experimental information obtained by EF-TEM and a ζ-potential analyzer, one can estimate the surface charge distribution from CTAB. We assumed that AuNRs were prolate spheroids (principle radii a and c, with c > a) and calculated their average charge density with their regulated geometrical factor, g(R), from their electrophoretic mobility experimentally obtained using a Malvern Zetasizer instrument.

The measured ζ-potential and mobility of AuNRs were 36.3 mV and 2.847 × 10⁻⁸ m²/Vs, respectively. The relationship between effective mobility (μ_eff) and surface charge density (σ), regulated with geometrical factor g(R), can be described as such (55)

$$\begin{array}{c}{\mathrm{\mu }}_{\text{eff}}=(2\mathit{a}\mathrm{\alpha }/3\mathrm{\eta })*\mathit{g}(\mathit{R}),\mathit{g}(\mathit{R})\\ =1/4{\mathit{R}}^2\cdot (\mathit{R}\sqrt{1‐{\mathit{R}}^2}+{\text{sin}}^{-1}(\mathit{R})) \text{ln}\left(\frac{1+\mathit{R}}{1-\mathit{R}}\right)\end{array}$$ (2)

where R is the ellipticity of the modeled AuNR $(\sqrt{1-{\mathit{a}}^2/{\mathit{c}}^2})$ and η is the media viscosity. By implementing the measured mobility of 2.847 × 10⁻⁸ m²/Vs for the batch of AuNRs, the mean surface charge density was determined to be 0.004 C/m². Because carbon concentration has a linear relationship with EF-TEM intensity, we could obtain information about the relative coverage of CTAB on the AuNRs; one end of a AuNR has 2.3 times more CTAB than the other (Fig. 3H). We applied a linear charge distribution for the NR model [67234 x(m) + 0.004 C/m²], retaining average charge density with 1:2.3 charge/charge ratio between the two ends observed in EF-TEM taken into consideration (Fig. 4A).

Electrostatics simulations

The structure, size, and electrostatic boundary conditions of CTAB-AuNRs were assigned on the basis of experimental findings. The AuNR and its CTAB layer were modeled as a cylinder (width, 17 nm; length, 30 nm), end-capped with hemispheres (diameter, 17 nm), and as an additional surface layer (thickness, 4 nm), respectively. Under static conditions, the electric potential V was defined by the equation E = −∇V. By combining this equation with the constitutive relationship between the electric displacement D and the electric field E, D = ε₀ε_r E, it is possible to represent Gauss’ law [∇(εE)= ρ] as a variant of Poisson’s equation: ρ = −(ε₀ε_r∇V).

EELS imaging of AuNRs before/after e-beam scrubbing

A light e-beam shower (3 min) was applied to the sample to prevent hydrocarbon growth during collection of the EELS spectrum; this treatment may slightly reduce the overall CTAB density on AuNRs but did not remove its asymmetry. An EELS spectrum was obtained for every 1 nm × 1 nm point in the STEM image, and signal intensities for 1.8- to 2.2-eV energy window were extracted to map the longitudinal plasmon mode of the AuNR. After taking the first plasmon map, SEM images of each particle were taken to find the end bearing excess CTAB. The e-beam was focused on the end with excess CTAB to homogenize the CTAB distribution. This step resulted in a decrease of the overall density of CTAB but a larger amount at the focused area (fig. S4, B and C).

SHG and FL imaging of AuNRs

AuNRs for SHG and FL imaging had a diameter of 40 nm and a length of 150 nm; these AuNRs were purchased from Nanopartz.inc. Ten microliters of AuNR solution was dropped on glass slide and stayed as flipped for 15 min to stabilize NRs sitting on the cover glass. Sequential images in SHG and FL mode were taken by using 850-nm pulsed multiphoton and 405-nm ultraviolet laser sources with a confocal laser scanning microscope Leica TCS SP8. From the sets of images obtained in two different modes, relative SHG intensities of individual AuNRs were calculated by dividing the integrated SHG with the integrated FL using particle analysis tool of ImageJ.

Sample preparation of charge-asymmetric and symmetric AuNR composite LBL films

To realize a random directionality, sufficient optical density (OD), and controlled interparticle spacing of AuNRs in the sample, we prepared AuNR composite films on quartz slides by two different methods. To prepare asymmetric AuNR samples as a polymer matrix, we chose an uncharged polymer, PVA, which has been proven to have almost negligible affinity to the surface of gold. The detailed information of their affinity to a gold surface is followed in the ligand exchange experiment section below. The symmetric AuNR samples were prepared by the LBL method using PSS with/without spacers of PAA and PDDA. PVA/AuNR film samples (asymmetric AuNRs) were prepared by drop casting 1 OD of AuNR colloids redispersed in PVA (7.5 weight %) onto quartz slides (56). To prepare LBL AuNR films (symmetric AuNRs), 1-mm-thick quartz slides were treated with piranha solution, precoated with one PAA/PDDA layer, and finished with one PSS layer. For both coupled and decoupled LBL samples, two bilayers of AuNR/PSS layer were deposited first. For a coupled LBL sample, five more bilayers of AuNR/PSS were simply added for the coupled AuNR film (fig. S6E). However, for the decoupled LBL samples, three bilayers of PAA/PDDA were added as spacers between every two bilayers of AuNR/PSS. The PDDA and PSS layers were put to make a positive and negative charge before adding spacers or bilayers of AuNR/PSS, respectively. The six bilayers of AuNR/PSS were deposited in total. Reference films were made for each film with only polymer or polyelectrolyte components of the corresponding samples. For example, 0.5 mM pure CTAB solution was used for the AuNR deposition step.

Measurements of NLO properties of AuNR/PSS LBL and AuNR/PVA films

The excitation source was a Ti/sapphire mode-locked laser, which delivered femtosecond pulses with a repetition rate of 76 MHz at 800 nm. The excitation power was controlled by a programmable attenuator to study the intensity dependence. The beam was focused into the AuNR film on quartz slides, which contained AuNRs with a diameter of 25 nm and length of 102 nm and resonant at 808 nm. Light scattered at 90° from the excitation beam was filtered through a monochromator and detected using photon counting. The optical signal was collected by a side lens, sent to a spectrometer, and then detected by a single-photon counting photomultiplier to study the spectral features. The gated photon counting technique was applied.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/2/e1700682/DC1

Supplementary Materials

Supplementary Methods

Supplementary Discussion

fig. S1. Computations of plasmon modes of silver nanowire (NW) with and without a neighbor particle.

fig. S2. HAADF images of AuNRs and analysis of capacitance gradient (dC/dz) profiles obtained by Kelvin probe microscopy.

fig. S3. Ligand exchange of CTAB on AuNRs with PSS and PVA.

fig. S4. e-beam ablation for selective removal of CTAB on single AuNRs and their plasmon mapping.

fig. S5. Intensity of individual AuNRs in SHG- and FL-mode imaging.

fig. S6. LBL-assembled AuNR/PSS films.

fig. S7. Computation of plasmon modes of AuNRs with and without centrosymmetrical gold core geometry.