A hierarchical modeling approach for assessing the safety of exposure to complex antiretroviral drug regimens during pregnancy

Abstract

Combination antiretroviral regimens have achieved tremendous success in reducing perinatal HIV transmission, and have become standard of care in pregnant women with HIV. However, the large variety of combination antiretroviral regimens utilized in practice raises the question of whether some of these highly potent drugs pose other risks to the pregnancy or infant. While HIV-infected pregnant women are almost always exposed to multiple antiretrovirals concurrently, standard safety screening strategies typically consider each individual antiretroviral separately, which fails to account for potential confounding due to simultaneous exposure to other antiretrovirals. In this paper, we evaluate a hierarchical modeling approach which groups antiretrovirals by drug class to screen for the safety of antiretrovirals taken during pregnancy, while still providing individual antiretroviral drug effect estimates. In simulation studies, we observed that the hierarchical approach may be advantageous as compared to considering each antiretroviral drug separately or simultaneously evaluating all antiretrovirals in a fixed effect model, particularly when there is prior evidence suggesting drugs from the same class behave similarly on the outcome. The characteristics of the hierarchical approach are illustrated in an application evaluating risk of preterm birth using a study including over 2000 pregnancies representing over 100 antiretroviral combinations, each involving up to three drug classes.

1 Introduction

The use of combination antiretroviral (ARV) therapy during pregnancy has been a public health success, reducing the risk of perinatal human immunodeficiency virus (HIV) transmission to less than 2%.^1,2 Despite widespread use of ARVs during pregnancy, there is a dearth of adequate and well-controlled human studies evaluating the safety of ARVs in pregnancy, leading to a need to monitor potential adverse effects that these highly potent drugs may have on the pregnancy or infant.³ Given the large number of available and effective ARVs, identification of individual ARVs with increased risks is critical, so that pregnant women can be advised to take ARVs with the safest profile.

The difficulty in assessing the safety of ARVs during pregnancy is due in part to the large number of different drugs available, yielding hundreds of possible combinations of ARV drugs that women can be exposed to during pregnancy. When prior research findings are suggestive or in settings with limited variability in regimens, a comparative effectiveness strategy may be used to compare two regimens against each other.⁴ However, such approaches may not be useful for general safety screening across many ARVs or regimens. In most cases, safety screening for a larger number of ARV drugs has been conducted by considering one drug at a time as part of a screening strategy. That is, studies have either restricted analysis to a single drug or drug class, or analyzed exposure to one drug or drug class at a time, and repeated the analysis for each drug and/or drug class.^5–14 Such analyses fail to adjust for exposure to other ARV drugs, and thus could be confounded by other ARV use. On the other hand, with so many different ARV exposures, it can become prohibitive to include all exposures at once in the statistical models ordinarily used.

As an alternative to these conventional approaches, hierarchical modeling has been advocated to address the multiple-exposure issues inherent to many epidemiologic investigations.^15–17 It has been used in areas such as nutrition, occupational health, and genetics.^15,17–26 Hierarchical models have also previously been used in evaluating outcomes among HIV-infected adults, but have not been utilized in the context of addressing safety of ARV use during pregnancy.^27–29

In this paper, we investigate a hierarchical model safety screening approach that includes first-stage effects for each drug class (nucleoside reverse transcriptase inhibitors (NRTI), non-nucleoside reverse transcriptase inhibitors (NNRTI), and protease inhibitors (PIs)), and second-stage effects for individual drugs. In essence, this model assumes that the effect of each drug is the summation of the (fixed) effect of its drug class and a residual effect specific to the individual drug. The effect for drugs less commonly used will be pulled toward the “mean” effect averaged over other, more common drugs from its same drug class. We would thus expect the hierarchical modeling method to perform well when drugs from the same drug class do indeed have similar effects on the outcome of interest.

The assumption of a similar effect for drugs within the same drug class can be justified by the fact that each class of ARV medications has a different mechanism of action. NRTIs are analogs of naturally occurring deoxynucleotides and terminate DNA chain formation.^30,31 NNRTIs bind to the HIV reverse transcriptase enzyme and cause a structural change that impairs further DNA synthesis.^30,32 PIs prevent the processing of viral proteins into their functional form, such that release of active virus particles is inhibited.^30,33 As a result of their mechanism of action, PIs as a class have been linked to increased rates of dyslipidemia in both children and adults with HIV infection,^34,35 and have also been associated with increased rates of preterm birth,^36,37 particularly when taken by HIV-infected women early in pregnancy.³⁸ In contrast, NRTIs have been linked to potential mitochondrial dysfunction and lactic acidosis based on evidence from both animal and human studies.³⁹ While their common mechanism of action supports an assumption that drugs within a class would behave similarly, and some studies have documented similar rates of outcomes,⁴⁰ there are also specific individual drugs which may confer increased or decreased risk as compared to others within the same class.^1,41,42 For example, the drug efavirenz (EFV) has been more commonly associated with psychiatric adverse effects than other drugs within the NNRTI class.⁴²

Given a plausible biological justification, the hierarchical modeling approach thus seems appealing. However, while a limited number of prior applications have utilized this approach, there is little information on how well this method will perform under various possible scenarios reflecting ARV drug effects. For example, this approach may not perform well when drugs from the same class do not behave similarly. Furthermore, previous research studies utilizing this approach considered multiple continuous exposures with considerably more variability than observed within our context.^18,19 Thus, examination of whether the hierarchical modeling approach is advantageous within the context of multiple binary exposures with many zero counts is warranted. Given the lack of prior knowledge regarding expected effects in these types of screening studies, we sought to quantify how much is gained by using the hierarchical model when the drug class assumption is correct, and also how much is lost by using the hierarchical model when the drug class assumption contradicts the true underlying data mechanism.

In Section 2, we detail the three screening approaches to be compared, and consider the analytical bias of the separate models approach and the hierarchical approach. In Section 3, we present a simulation study conducted to compare the conventional approaches and the hierarchical modeling approach under various true exposure-outcome scenarios in the context of screening the safety of ARV exposures during pregnancy. In Section 4, we illustrate the hierarchical modeling approach using data from the Surveillance Monitoring of ART Toxicities (SMARTT) study within the Pediatric HIV/AIDS Cohort Network Study (PHACS). In Section 5, we conclude with a discussion of the relative merits and limitations of the hierarchical approach for safety screening, and avenues of further research.

2 Methods

2.1 Models

We consider the setting of an observational cohort study with N participants for whom we have information on ARV exposures during pregnancy and perinatal outcome data. We let y be an N by 1 outcome vector, indicating a perinatal or infant outcome. We let X be an N by m matrix of zeroes and ones indicating the exposure history (no/yes) during pregnancy of each participant to m individual ARVs under investigation, and we let X_j be the N by 1 subvector of X indicating the exposure history for the jth ARV (j=1,2,… m). Lastly, we let 1_N be an N by 1 vector of ones and W be an N by q matrix of q potential confounding variables. Let g(·) denote the link function for a generalized linear model. In particular, we investigate the identity link (g(E(y))=E(y)) for continuous outcomes and the logit link (g(E(y)) = logit{E(y)}) for binary outcomes.

The standard, separate regression models approach involves running m models, where each model includes one ARV drug

$$g\left(\mathit{E}(\mathit{y}\mid X_j,\mathit{W})\right)={\alpha }^S{1}_N+{\mathit{X}}_{\mathit{j}}{\beta }_j^{\ast }+\mathit{W}{\mathit{\gamma }}_{\mathit{j}}^{\ast },j=1,2,\dots ,m$$ (1)

In equation (1), α^S represents the mean outcome (under the identity link) or the log odds of the outcome (under the logit link) among those unexposed to the jth ARV and for which all covariates in W equal zero. The ${\beta }_j^{\ast }$ represents the mean difference in outcome (under the identity link) or the difference in log odds of the outcome (under the logit link) between women exposed and unexposed to the jth ARV after adjusting for the covariates in W. The ${\mathit{\gamma }}_{\mathit{j}}^{\ast }$ is a vector indicating the mean differences in outcome (under the identity link) or the differences in log odds of the outcome (under the logit link) for a one unit increase in the covariates, when adjusting for the jth ARV.

The full fixed effect regression model involves running one model with all m ARVs included at once

$$g(\mathit{E}(\mathit{y}\mid \mathit{X},\mathit{W}))={\alpha }^F{1}_N+\mathit{X}{\mathit{\beta }}^{\mathit{F}}+\mathit{W}{\mathit{\gamma }}^{\mathit{F}}$$ (2)

In equation (2), α^F represents the mean outcome (under the identity link) or the log odds of the outcome (under the logit link) among those unexposed to all m ARVs and for which all covariates in W equal zero. The β^F vector represents the mean differences (or differences in log odds) in outcome under the identity link (or logit link) between women exposed and unexposed to each ARV after adjusting for the other m−1 ARVs and the covariates in W. The γ^F is a vector indicating the mean differences in outcome (under the identity link) or the differences in log odds of the outcome (under the logit link) for a one unit increase in the covariates, when adjusting for all m ARVs.

The hierarchical model adds a prior distribution to the β^F coefficients in equation (2), such that

$$\begin{gathered} {\mathit{\beta }}^{\mathit{H}}=\mathit{Z}\mathit{\pi }+\mathit{\delta } \\ \mathit{\delta }~N_m(0,{\tau }^2{\mathit{I}}_{\mathit{m}}) \end{gathered}$$ (3)

So, β^H ~ N_m(Zπ, τ²I_m), where Z is an m by p matrix indicating drug-class membership when the m individual drugs under investigation are from p different drug classes, and π is a p by 1 vector of the p fixed, drug class-specific mean effects. For example, with m=14 drugs from p=3 drug classes, Z may look like

$$\begin{array}{ll}\begin{array}{l}\hfill \\ \text{Abacavir}(\text{ABC})\hfill \\ \text{Emtricitabine}(\text{FTC})\hfill \\ \text{Tenofovir}(\text{TDF})\hfill \\ \text{Zidovudine}(\text{ZDV})\hfill \\ \text{Lamivudine}(\text{3TC})\hfill \\ \text{Efavirenz}(\text{EFV})\hfill \\ \text{Etravirine}(\text{ETR})\hfill \\ \text{Nevirapine}(\text{NVP})\hfill \\ \text{Rilpivirine}(\text{RPV})\hfill \\ \text{Atazanavir}(\text{ATV})\hfill \\ \text{Darunavir}(\text{DRV})\hfill \\ \text{Fosamprenavir}(\text{FPV})\hfill \\ \text{Ritonavir-boosted}\text{lopinavir}(\text{LPV}/\mathrm{r})\hfill \\ \text{Nelfinavir}(\text{NFV})\hfill \end{array}\hfill & \left[\begin{array}{lll}\text{NRTI}\hfill & \text{NNRTI}\hfill & \hfill \text{PI}\\ 1\hfill & 0\hfill & \hfill 0\\ 1\hfill & 0\hfill & \hfill 0\\ 1\hfill & 0\hfill & \hfill 0\\ 1\hfill & 0\hfill & \hfill 0\\ 1\hfill & 0\hfill & \hfill 0\\ 0\hfill & 1\hfill & \hfill 0\\ 0\hfill & 1\hfill & \hfill 0\\ 0\hfill & 1\hfill & \hfill 0\\ 0\hfill & 1\hfill & \hfill 0\\ 0\hfill & 0\hfill & \hfill 1\\ 0\hfill & 0\hfill & \hfill 1\\ 0\hfill & 0\hfill & \hfill 1\\ 0\hfill & 0\hfill & \hfill 1\\ 0\hfill & 0\hfill & \hfill 1\end{array}\right]\hfill \end{array}$$

δ is an m by 1 vector of residual effects for each individual drug, and the elements of δ are assumed to be independent normal random variables with mean 0 and variance τ². The hierarchical model thus becomes

$$\begin{gathered} g(\mathit{E}(\mathit{y}\mid \mathit{X},\mathit{Z},\mathit{W},\mathit{\delta }))=\alpha +\mathit{X}(\mathit{Z}\mathit{\pi }+\mathit{\delta })+\mathit{W}\mathit{\gamma }=\alpha 1_N+\mathit{XZ}\mathit{\pi }+\mathit{X}\mathit{\delta }+\mathit{X}\mathit{\gamma } \\ \mathit{\delta }~N_m(0,{\tau }^2{\mathit{I}}_{\mathit{m}}) \end{gathered}$$ (4)

From the formulation in equation (4), we can see that XZ is an N by p matrix indicating the number of drugs from each drug class that each participant was exposed to during pregnancy. The elements in π represent the effect on the outcome of each additional drug from a particular drug class that a woman is exposed to during pregnancy, conditional on the individual drugs taken and covariates in W. The elements of δ are the residual effects on the outcome for a particular drug above and beyond the effects attributed to its drug class. The α parameter represents the mean outcome (under the identity link) or the log odds of the outcome (under the logit link) among those unexposed to all m ARVs and for which all covariates in W equal zero; and γ is a vector of the covariate effects conditional on exposure to drug classes and individual drugs.

The variance of the random effects (τ²) controls the degree of shrinkage of the β^H’s to their drug class mean. Smaller values of τ² will result in more shrinkage to the drug class mean, with the hierarchical model reducing to a model with just fixed effects for drug class when τ² = 0. Larger values of τ² correspond to less shrinkage to the drug class mean, and the hierarchical model becomes equivalent to the ordinary full regression model when τ² = ∞.

2.2 Brief bias considerations under the linear model

As mentioned earlier, we would expect the hierarchical modeling method to perform well when drugs from the same drug class have similar effects on the outcome of interest. However, often there is little prior knowledge regarding the effects of ARV exposures on reproductive and perinatal outcomes, and the relative advantages of the hierarchical approach when only a subset of ARV drugs have an effect require evaluation. Suppose the true underlying data-generating mechanism is that only one drug, X₁, has an effect on a continuous outcome Y in the following form

$$y_i={\alpha }^{\ast }+X_1{\beta }_1^{\ast }+{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }^2)$$

Under the separate models approach, the maximum likelihood estimate (MLE) for ${\beta }_1^{\ast }$ will be unbiased and consistent when fitting drug 1, i.e. the correct model. However, MLE estimates for the ${\beta }_j^{\ast }$ from the other m−1 models will be biased due to uncontrolled confounding by X₁. In particular, it can be shown that the expected value of ${\widehat{\beta }}_j^{\ast }$ has the form

$$E\left[{\widehat{\beta }}_j^{\ast }\right]={\xi }_{1j}{\beta }_1^{\ast },j=2,3,\dots ,m$$

where ξ_1j is the difference in probability of receiving drug X₁ between women exposed and unexposed to drug X_j, i.e.

$$E\left[X_1\mid X_j\right]=P\left(X_1=1\mid X_j\right)={\xi }_{0j}+{\xi }_{1j}{X}_j,j=2,3,\dots ,m$$

Thus, the MLE estimators from a separate models approach will be biased for the true null effect ( ${\beta }_j^{\ast }=0$). As the magnitude of the effect of X₁ on $Y({\beta }_1^{\ast })$ increases, and as the correlation between exposure to drug X₁ and drug X_j (ξ_1j) increases, the bias in ${\widehat{\beta }}_j^{\ast }$ also increases. Furthermore, increasing the sample size only exacerbates the problem, as the separate models approach will show increasing certainty (smaller standard errors) around an incorrect effect estimate in m−1 of the models.

Often researchers adjust for potential confounders between the drug exposures and the outcome. However, the confounded effect estimate of X_j will remain unless the model controls for all covariates W^*that determine prescribing patterns by physicians such that ${\xi }_{1j}^{\ast }=0$ under $E\left[X_1\mid X_j,{\mathit{W}}^{\ast }\right]=P\left(X_1=1\mid X_j\right)={\xi }_{0j}^{\ast }+{\xi }_{1j}^{\ast }{X}_j+{\mathit{W}}^{\ast }\mathit{\theta }$. Given the differences in prescribing patterns across hospitals and physicians, it seems unlikely one could fully account for W^*.

Under the hierarchical modeling approach, the estimated drug-specific effects are also biased, but the bias decreases as the sample size increases. Greenland noted that β̂^H = BZπ̂+(I-B)β̂^F, where B=(V^* + τ²I_m)⁻¹ V^*, and V* is the covariance matrix of β̂^F.^16,20 For a given τ², as V*→0 with increasing sample size, β̂^F is given more weight and β̂^H is a consistent estimator for the true parameters of all m drugs. That is, as N→∞, ${\widehat{\beta }}_1^H\to {\beta }_1^{\ast }$ and ${\widehat{\beta }}_j^H\to 0$ for j=2,3,…m. Asymptotic properties, however, may not be reasonable approximations for estimators at the sample sizes commonly utilized for studies assessing ARV exposures and reproductive outcomes. In this paper, we will consider the bias under both methods at realistic sample sizes to assess finite-sample properties and further consider the bias under a binary outcome with generalized linear models.

3 Simulation study

A simulation study was performed to investigate the operating characteristics of the three different approaches under various outcome scenarios. The first approach involved separate univariate regression models for each drug (equation (1)); the second approach was the full ordinary regression model with all drugs included at once (equation (2)); and the third approach was the hierarchical model (equation (4)). We used a semi-Bayes approach for fitting the hierarchical model by specifying a priori the variance in the random effects (τ²), as advocated in prior studies using this approach.^{16,19,28,29,43} An empirical Bayes approach (estimating τ² from the data) was also considered, but τ² was consistently estimated to be zero, which reduces the model to having only fixed effects for drug class and is not helpful in making drug-specific conclusions. We considered a binary outcome (preterm birth) and a continuous outcome (Bayley-III score of the infant at 12 months). For each outcome, we considered various true exposure-outcome relationships, including no true effects, a subtle effect of all drugs within one drug class, a moderate effect of only one individual drug, and moderate effects of two drugs from the same class, but in opposite directions. Table 1 provides the specific models under which data were simulated for each scenario.

Table 1.

A summary of the true exposure-outcome relationship scenarios considered in the simulation studies.

Scenario	Binary outcome: Preterm birth (<37 weeks gestational age at delivery)a	Continuous outcome: Standardized Bayley-III score of infant at 12 months
(i) No effects	P(Y1)=0.12	E(Y2)=0
(ii) A class of drugs has a subtle effect	P(Y1)=0.12+0.04*PI (ORPI=1.40)	E(Y2)=0–0.3*PI
(iii) One ARV drug has a moderate effect
(a) more common ARV drug (>15% exposure)	P(Y1)=0.12+0.09*LPV/r (ORLPV/r=1.95)	E(Y2)=0–0.5*LPV/r
(b) less common ARV drug (5–15% exposure)	P(Y1)=0.12+0.09*ABC (ORABC=1.95)	E(Y2)=0–0.5*ABC
(c) rarely used ARV drug (<5% exposure)	P(Y1)=0.12+0.09*EFV (OREFV=1.95)	E(Y2)=0–0.5*EFV
(iv) Two drugs from the same drug class have moderate effects, but in opposite directions	P(Y1)=0.12+0.09* LPV/r – 0.05*DRV (ORLPV/r=1.95, ORDRV=0.55)	E(Y2)=0–0.5*LPV/r + 0.5*DRV

ABC: abacavir; DRV: darunavir; E: expected value; EFV: efavirenz; LPV/r: ritonavir-boosted lopinavir; OR_ABC: odds ratio comparing ABC-exposed to ABC-unexposed; OR_DRV: odds ratio comparing DRV-exposed to DRV-unexposed: OR_EFV: odds ratio comparing EFV-exposed to EFV-unexposed; OR_LPV/r: odds ratio comparing LPV/r-exposed to LPV/r-unexposed; OR_PI: odds ratio comparing PI-exposed to PI-unexposed; P: probability; PI: protease inhibitor; Y₁: preterm birth; Y₂: standardized Bayley-III cognitive score.

^aThe corresponding logistic models are: (i) logit(P(Y₁))= −1.9924; (ii) logit(P(Y₁))=−1.9924)0.3365*PI; (iii) logit(P(Y₁))=−1.9924)0.6678*X_j (where X_j indicates LPV/r, ABC, or EFV); and (iv) logit(P(Y₁))=−1.9924)0.6678*LPV/r – 0.5978*DRV. Note that LPV/r and DRV are mutually exclusive (women are never exposed to both drugs simultaneously).

A number of statistical properties were evaluated, including the percent of models that converged (for the binary outcome), the percent of false discoveries, the power to detect true effects, the bias in estimated effects for each exposure, the standard error in estimated effects for each exposure, and the observed coverage of 95% confidence intervals (CIs) for the effect for each exposure.

SAS 9.4 (SAS Institute Inc., Cary, North Carolina) was used for all simulations and applied data analysis. The SAS-provided GLIMMIX macro (http://support.sas.com/techsup/notes/v8/25/030.html) was used to implement the hierarchical modeling method for the binary outcome.¹⁹ Note that the GLIMMIX procedure does not yield estimates of the covariances between fixed and random effects, and thus cannot be used for this approach. The MIXED procedure was used to implement the hierarchical modeling method for the continuous outcome (programs are available by request to the author).

3.1 Exposure assignment

We used data from the SMARTT study to inform the ARV exposure distributions within the simulation study. The SMARTT study is a large cohort study with data on HIV-uninfected children born to HIV-infected women since 1995 to the present. Patterns in ARV use during pregnancy have changed dramatically over these years, but HIV-infected women typically receive a combination regimen during pregnancy consisting of a two-NRTI backbone plus either a PI or an NNRTI.⁴⁴ We are specifically interested in monitoring the safety of current combination regimens, and thus used the observed distribution of regimens reported in SMARTT between 2010 and 2015 to inform the exposure distribution. In particular, regimens were assigned via a multinomial distribution with 107 categories (for the 107 different observed regimens over this time period), with each category having the same probability (ranging between 0.0008 and 0.2264) as observed in the SMARTT cohort. Exposures to 14 individual drugs and three drug classes were then derived from the assigned regimen. Specifically, five NRTIs, four NNRTIs, and five PIs were included in the simulation analysis, as shown in the Z matrix in Section 2.1.

3.2 Outcome assignment

We acknowledge that it is improbable the hierarchical model being fit reflects the true underlying outcome mechanism. Rather, our interest lies in whether a hierarchical model can be a useful screening approach despite violations to its underlying assumptions. Consequently, outcomes were assigned randomly via the Bernoulli distribution (for preterm birth) or the standard Normal distribution (for standardized Bayley-III score) under simple models based on exposure and outcome scenario (see Table 1). Three thousand simulated datasets were created in this way. The main simulations were conducted with a sample size of 1000. Additional simulations were conducted with sample sizes of 500, 3000, and 5000.

For the binary outcome, the hierarchical model was fit specifying a τ² value of 0.125, which corresponds to 95% of the residual effects of a particular ARV drug (above and beyond the effects of its drug class) lying between odds ratios (OR) of ½ and $2([e^{-1.96/\sqrt{8}},e^{1.96/\sqrt{8}}])$. We also considered τ² values of 0.36 and 0.64, which are equivalent to allowing residual effects to fall within an expanded 10-fold and 25-fold range, respectively, but simulation results presented for the binary outcome are for τ² =0.125.¹⁶ For the continuous outcome, the hierarchical model was fit specifying a τ² value of 0.26, corresponding to 95% of the residual effects of a particular drug falling within one standard deviation. Additional analyses considered values of 1.04 and 2.34, equivalent to allowing residual effects to fall within two and three standard deviations, respectively.

3.3 Simulation results

For the binary outcome, convergence of the model was a sizeable problem with the full model but a minimal issue with the hierarchical model. At a sample size of 1000, all of the hierarchical models converged under each outcome scenario, whereas the full logistic model failed to converge in 14–22% of simulations, depending on the outcome scenario. With N=500, the full model failed to converge in over 75% of the simulations, while the hierarchical model failed to converge in 0.1% of simulations. The separate model approach converged for all 13 models over 95% of the time; however, results for rare exposures were sometimes nonsensical, with standard errors exceeding 500. For instance, the simple logistic model failed to yield interpretable results for EFV in up to 24% of the simulations at N=1000 and in up to 40% of the simulations at N=500.

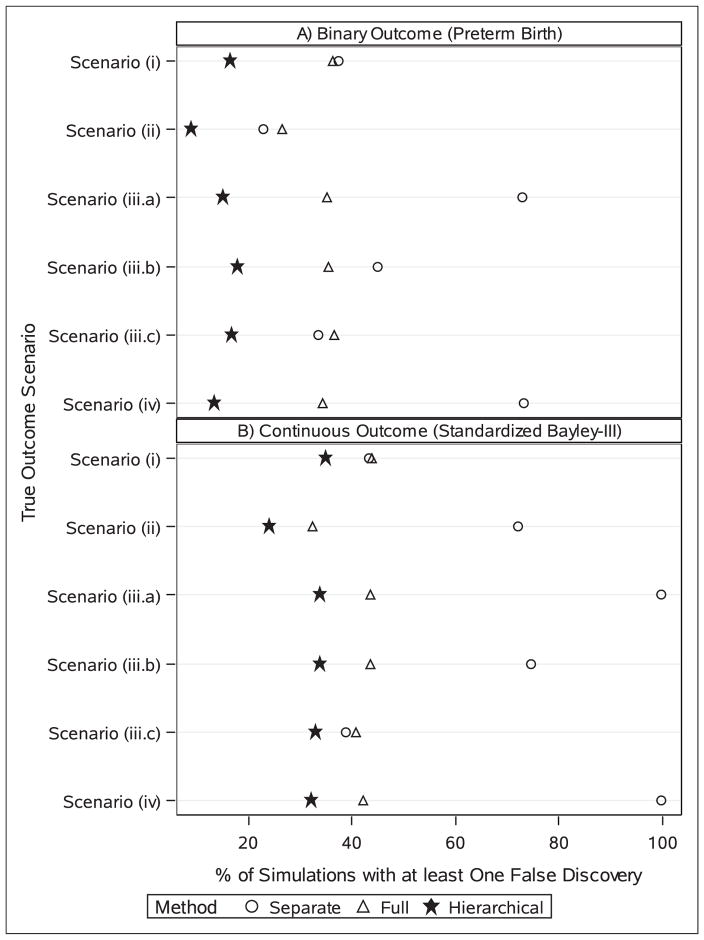
The hierarchical model outperformed both the full model and the separate model approaches in terms of false discoveries, regardless of outcome type and outcome scenario (Figure 1). With a binary outcome, the hierarchical model had no false discoveries over 80% of the time. The full model had no false discoveries for 64% (under scenario (i)) to 74% (under scenario (ii)) of simulations. The separate model approach had false discovery rates comparable to the full model approach under scenarios (i) and (ii), but did quite poorly under scenarios (iii.a) and (iv). Notably, under the latter two scenarios, the standard approach had at least one false discovery in over 70% of the simulations, and four or more false discoveries (of twelve truly null effects) in 40% of simulations under scenario (iv).

Figure 1.

The percent of simulations with at least one false discovery at a sample size of 1000 under three statistical approaches and six different true outcome-exposure relationships, by outcome type (a) binary; or (b) continuous. Each scenario considers 14 different antiretroviral drugs. Scenario (i) specifies no true effects; scenario (ii) specifies a subtle effect of all drugs from the protease inhibitors drug class; scenario (iii.a) involves a modest effect of one drug with more common exposure; scenario (iii.b) involves a modest effect of one drug with less common exposure; scenario (iii.c) involves a modest effect of one drug with rare exposure; scenario (iv) involves modest effects in opposite directions of two drugs from the protease inhibitor drug class. Results based on 3000 simulations.

For the continuous outcome, false discovery rates were consistently higher than observed for the binary outcome, though the hierarchical model maintained noticeably lower rates than the other two methods (Figure 1). Under scenarios (iii.a) and (iv), the separate models method identified one or more false discoveries in over 99% of the simulations, and four or more false discoveries in over 90% of the simulations.

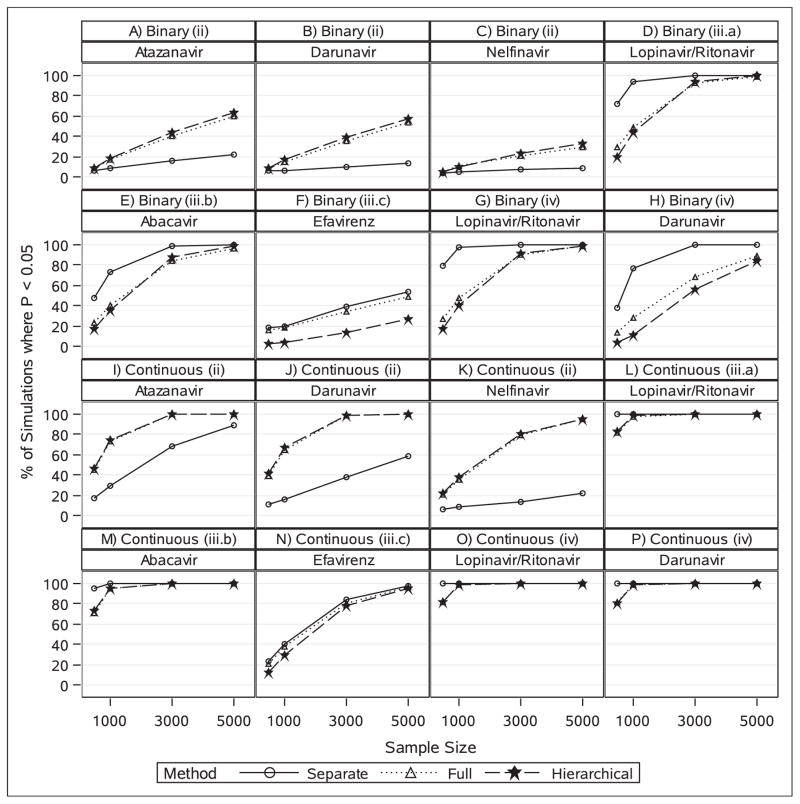
Detection of true effects is irrelevant to scenario (i). With N=1000, the true effects of the five PIs under a common drug class assumption (scenario (ii)) were detected most often by the hierarchical model for both outcome types (Figure 2). This result was to be expected because the hierarchical model assumes drugs from the same class behave similarly, which corresponds to the true underlying data mechanism in this scenario. For the remaining scenarios, detection of true effects differed depending on outcome type. With a binary outcome, the hierarchical model performed similarly to the full fixed effect model but substantially worse than the separate models method in detecting the true effects of the ARVs in scenarios (iii.a), (iii.b), (iii.c), and (iv). This result also was to be expected given that the hierarchical model assumes similar effects for drugs from the same class, which is not correct in scenarios (iii) and (iv). Interestingly, however, under the continuous outcome, all three methods detected the true effects of the ARVs almost 100% of the time in scenarios (iii.a), (iii.b), and (iv). Under scenario (iii.c), the separate models method detected the true effect of EFV more often than the other two methods, though the differences were not as large as under the binary outcome (Figure 2).

Figure 2.

The power to detect true effects of antiretroviral (ARV) exposures on preterm birth and standardized Bayley-III score as a function of sample size under three statistical approaches and six different true outcome-exposure relationships. Results are based on 3000 simulations. Each panel reflects the power to detect the true effect of an ARV drug under a specific scenario as outlined in Table 1. (a), (b), (c) Atazanavir (ATV, 26.1% exposed), darunavir (DRV, 14.2% exposed), and nelfinavir (NFV, 4.7% exposed), respectively; under scenario (ii) where all protease inhibitors have a subtle effect on preterm birth. (d), (e), and (f) Ritonavir-boosted lopinavir (LPV/r, 28.6% exposed), abacavir (ABC, 12.4% exposed), efavirenz (EFV, 1.2% exposed), respectively; under scenarios (iii.a), (iii.b), and (iii.c), respectively, where only one ARV has a modest effect on preterm birth. (g) and (h) Ritonavir-boosted lopinavir (LPV/r) and darunavir (DRV), respectively; under scenario (iv) where two protease inhibitors have modest effects in opposite directions on preterm birth. (i), (j), (k), Atazanavir (ATV), darunavir (DRV), and nelfinavir (NFV), respectively; under scenario (ii) where all protease inhibitors have a subtle effect on standardized Bayley-III score. (l), (m), and (n) Ritonavir-boosted lopinavir (LPV/r), abacavir (ABC), efavirenz (EFV), respectively; under scenarios (iii.a), (iii.b), and (iii.c), respectively, where only one ARV has a modest effect on standardized Bayley-III score. (o) and (p) Ritonavir-boosted lopinavir (LPV/r) and darunavir (DRV), respectively; under scenario (iv) where two protease inhibitors have modest effects in opposite directions on standardized Bayley-III score.

The additional simulations showed that as the sample size increases, the hierarchical model continued to detect the true effects of the PIs under scenario (ii) considerably more often than the separate models method, while also continuing to minimize the number of false discoveries. With the continuous outcome, all three methods detected the true effects of the ARVs equally under the other scenarios by N=3000 (Figure 2). With a binary outcome, the hierarchical model detected the true effects about as well as the other methods at N=5000 for scenarios (iii.a), (iii.b), and (iv), but failed to detect the true effect of EFV as often as the other methods under scenario (iii.c) even for N=5000 (Figure 2).

Simulation results under scenario (iv) for the bias and standard errors (SE) in estimated coefficients and coverage of 95% CIs among the three approaches are presented in Table 2 for the binary outcome and Table 3 for the continuous outcome. Scenario (iv) represents the “worst-case” type scenario for the hierarchical model since the prior being fit (assuming drugs from the same class behave similarly) contradicts the true underlying exposure-outcome relationship. Still, some patterns in these results remain consistent across scenarios (see Supplemental Tables 1 to 10). First, SEs were consistently largest under the full model. For rare exposures (<5% exposed), the SEs were smallest under the hierarchical model, but for the more common exposures (>15% exposed), they were smallest under the separate models method. Second, the bias in estimated coefficients tended to be minimized under the hierarchical model, the main exception being for when an uncommon drug was the only drug with a true effect (e.g. abacavir (ABC) in scenario (iii.b) and EFV in scenario (iii.c)). Third, the nominal coverage rates of the 95% CIs were quite poor for some of the ARVs under the separate models method. The poor coverage rates tended to be for more common drugs that had relatively high bias (due to uncontrolled confounding by other ARV exposures) and relatively small SEs. For example, under scenario (iv), the 95% CI for zidovudine (ZDV) captured its true effect (null) in only 59% of the simulations for the binary outcome (Table 2) and in only 1% of the simulations for the continuous outcome (Table 3).

Table 2.

Bias, efficiency, and coverage of 95% confidence intervals across statistical approaches for the binary outcome under scenario (iv) (two drugs from the same drug class have opposite effects on preterm birth; DRV has a protective effect and LPV/r has a detrimental effect).

% Exposed	Drug	Mean bias in log odds			Mean SE of log odds			Coverage of 95% CI
		Separatea	Fullb	Hierarchical	Separatea	Fullb	Hierarchical	Separatea	Fullb	Hierarchical
<5%	EFV	0.042	0.237	−0.008	0.862	0.914	0.516	0.98	0.96	0.99
	ETR	−0.287	0.055	−0.035	0.788	0.827	0.492	0.99	0.97	0.99
	NVP	−0.231	−0.062	−0.026	0.669	0.728	0.474	0.98	0.97	0.97
	FPV	−0.101	0.040	0.067	0.792	0.852	0.445	0.98	0.97	0.99
	NFV	−0.268	−0.050	0.021	0.493	0.591	0.402	0.97	0.96	0.98
5–15%	ABC	−0.187	−0.017	−0.040	0.297	0.424	0.297	0.93	0.95	0.97
	RPV	−0.248	−0.039	−0.003	0.436	0.523	0.423	0.96	0.96	0.96
	DRV	−0.306	−0.035	0.296	0.357	0.446	0.350	0.92	0.94	0.89
>15%	3TC	0.369	0.072	0.049	0.185	0.713	0.339	0.49	0.95	1.00
	FTC	−0.357	−0.017	−0.002	0.186	0.919	0.345	0.53	0.97	0.99
	TDF	−0.356	0.116	−0.002	0.185	0.928	0.342	0.52	0.96	0.99
	ZDV	0.386	0.022	0.060	0.184	0.474	0.297	0.44	0.94	0.98
	ATV	−0.234	0.011	0.048	0.219	0.358	0.319	0.84	0.95	0.96
	LPV/r	0.093	0.031	−0.118	0.189	0.363	0.312	0.92	0.95	0.94

ABC: abacavir; ATV: atazanavir; CI: confidence interval; DRV: darunavir; EFV: efavirenz; ETR: etravirine; FPV: fosamprenavir; FTC: emtricitabine; LPV/r: ritonavir-boosted lopinavir; NFV: nelfinavir; NVP: nevirapine; RPV: rilpivirine; SE: standard error; TDF: tenofovir; ZDV: zidovudine; 3TC: lamivudine.

^a21.8% of the EFV models, 13.9% of the ETR models, 13.5% of the FPV models, 0.3% of the NFV models, 5.0% of the NVP models, and 0.1% of the RPV models did not converge or yielded unreasonable SEs. Results presented exclude these models.

^b18.8% of the full models did not converge. Results presented exclude these models.

Note: Results are from 3000 simulations each with sample size 1000.

Table 3.

Bias, efficiency, and coverage of 95% confidence intervals across statistical approaches for the continuous outcome under scenario (iv) (two drugs from the same drug class have opposite effects on Bayley-III score; DRV has a protective effect and LPV/r has a detrimental effect).

% Exposed	Drug	Mean bias in difference			Mean SE of difference			Coverage of 95% CI
		Separate	Full	Hierarchical	Separate	Full	Hierarchical	Separate	Full	Hierarchical
<5%	EFV	0.081	0.007	0.004	0.313	0.314	0.280	0.95	0.95	0.96
	ETR	0.254	0.002	0.006	0.250	0.248	0.231	0.83	0.95	0.96
	NVP	0.073	−0.002	0.001	0.214	0.221	0.210	0.94	0.94	0.95
	FPV	0.042	−0.007	−0.008	0.269	0.273	0.249	0.95	0.95	0.96
	NFV	0.081	−0.006	0.001	0.157	0.182	0.176	0.93	0.95	0.96
5–15%	ABC	0.098	−0.003	0.005	0.101	0.140	0.132	0.84	0.96	0.97
	RPV	0.087	−0.005	−0.006	0.141	0.161	0.157	0.91	0.95	0.96
	DRV	0.168	−0.000	−0.013	0.093	0.123	0.121	0.56	0.95	0.95
>15%	3TC	−0.265	0.002	−0.003	0.066	0.224	0.201	0.02	0.96	0.97
	FTC	0.251	0.003	0.005	0.066	0.309	0.244	0.03	0.95	0.98
	TDF	0.250	−0.003	−0.001	0.066	0.310	0.243	0.03	0.94	0.98
	ZDV	−0.284	0.001	−0.002	0.066	0.154	0.143	0.01	0.95	0.97
	ATV	0.102	0.001	−0.001	0.076	0.114	0.112	0.73	0.95	0.95
	LPV/r	−0.100	−0.003	0.010	0.071	0.123	0.120	0.71	0.95	0.95

ABC: abacavir; ATV: atazanavir; CI: confidence interval; DRV: darunavir; EFV: efavirenz; ETR: etravirine; FPV: fosamprenavir; FTC: emtricitabine; LPV/r: ritonavir-boosted lopinavir; NFV: nelfinavir; NVP: nevirapine; RPV: rilpivirine; SE: standard error; TDF: tenofovir; ZDV: zidovudine; 3TC: lamivudine.

Note: Results are from 3000 simulations each with sample size 1000.

Additional simulations were conducted to assess how results may vary for binary outcomes that are much rarer or much more common than the moderate baseline prevalence (0.12) considered in the main simulations. In particular, baseline prevalences of 0.25 and 0.05 were considered. Although power increased for the more common outcome and decreased for the less common outcome, the relative differences across the three approaches remained similar to results from the main simulations and thus results are not shown here.

4 Illustrative example

We applied the hierarchical modeling approach to evaluate ARV use and preterm birth in the SMARTT cohort. The SMARTT study has been approved by the research ethics committee at Harvard T.H. Chan School of Public Health and all research sites, and study participants provided written informed consent. The SMARTT cohort has enrolled over 3000 HIV-infected pregnant women from 22 sites around the United States, as described elsewhere.⁹ Consistent with prior analyses, we controlled for birth cohort (1995–2004, 2005–2009, 2010–2012, and 2013–2015), annual income<$20,000, and black race.⁹

Our analysis included 2660 singleton pregnancies with ARV exposures and preterm birth outcomes available. The majority of women (71%) received only one ARV regimen during their pregnancy. For this analysis, we classified the maternal ARV regimen as that taken for the longest duration during pregnancy, and considered a woman exposed to a particular drug if that drug was included in her most common regimen. We assessed 18 individual drugs, including seven NRTIs, four NNRTIs, and seven PIs.

Table 4 presents ORs and 95% CIs from the hierarchical model under three different values of τ² and from the full logistic model (equivalent to the hierarchical model at τ² = ∞). Consistent with results from the simulation study, as τ² increased, the CIs tended to widen, with the CIs widest under the full logistic model. The shrinkage effect of the hierarchical model can be observed for rarely used ARVs, for which estimated ORs in the hierarchical model are further from their estimated ORs under the full model (i.e. they are being pulled more toward their drug class mean effect), whereas the estimated ORs for common drugs were more similar. For example, the estimated OR for the least common PI (indinavir (IDV)) was 1.24 (95% CI: 0.66, 2.31) in the hierarchical model with τ² = 0.125 and 1.51 (95% CI: 0.61, 3.73) in the full model. In comparison, the estimated ORs from those models for the most common PI (ritonavir-boosted lopinavir (LPV/r)) were 1.51 (95% CI: 1.10, 2.06) and 1.50 (95% CI: 1.08, 2.09), respectively. In addition, as τ² increases, the estimated ORs from the hierarchical model get closer to the estimated ORs from the full model. For example, for IDV, the estimated ORs are 1.24 (95% CI: 0.66, 2.31), 1.34 (95% CI: 0.62, 2.89), and 1.39 (95% CI: 0.61, 3.17) under τ² values of 0.125, 0.36, and 0.64, respectively.

Table 4.

Odds ratios (OR) and 95% confidence intervals (CI) for individual antiretroviral drug exposures and preterm birth from the Surveillance Monitoring for ART Toxicities Study cohort of 2668 singleton pregnancies between 1995 and 2015.

Drug Class	Drug	% Exposed	Hierarchical model						Full logistic model
			τ2 = 0.125		τ2 = 0.36		τ2 = 0.64		(τ2 = ∞)
			OR	95% CI	OR	95% CI	OR	95% CI	OR	95% CI
NRTI	ABC	16.2	0.96	0.71, 1.30	0.98	0.71, 1.35	0.98	0.71, 1.37	0.99	0.71, 1.38
	DDI	1.9	0.79	0.46, 1.38	0.79	0.41, 1.53	0.79	0.39, 1.60	0.80	0.37, 1.72
	D4T	2.6	0.74	0.44, 1.25	0.69	0.37, 1.28	0.67	0.35, 1.28	0.63	0.31, 1.28
	FTC	26.8	0.75	0.47, 1.19	0.74	0.43, 1.29	0.74	0.41, 1.34	0.74	0.39, 1.43
	TDF	29.3	0.79	0.52, 1.19	0.81	0.50, 1.31	0.82	0.49, 1.36	0.83	0.47, 1.47
	ZDV	63.1	0.67	0.48, 0.95	0.64	0.44, 0.94	0.63	0.42, 0.93	0.61	0.40, 0.92
	3TC	64.6	0.83	0.57, 1.19	0.85	0.56, 1.29	0.86	0.55, 1.33	0.88	0.55, 1.41
NNRTI	EFV	0.9	0.98	0.47, 2.01	0.83	0.34, 2.05	0.76	0.28, 2.02	0.58	0.17, 2.03
	ETR	0.8	1.58	0.77, 3.23	2.04	0.88, 4.77	2.32	0.94, 5.68	3.01	1.13, 7.98
	NVP	6.4	1.09	0.70, 1.70	1.07	0.68, 1.71	1.07	0.67, 1.71	1.05	0.65, 1.71
	RPV	2.3	1.08	0.58, 2.00	1.02	0.51, 2.04	0.99	0.48, 2.04	0.93	0.42, 2.04
PI	ATV	15.3	0.84	0.58, 1.24	0.80	0.53, 1.19	0.78	0.52, 1.17	0.75	0.49, 1.14
	DRV	6.3	0.88	0.56, 1.38	0.81	0.50, 1.31	0.78	0.47, 1.28	0.72	0.42, 1.22
	FPV	2.1	0.88	0.49, 1.59	0.76	0.38, 1.54	0.71	0.33, 1.50	0.61	0.26, 1.45
	IDV	1.2	1.24	0.66, 2.31	1.34	0.62, 2.89	1.39	0.61, 3.17	1.51	0.61, 3.73
	LPV/r	26.8	1.51	1.10, 2.06	1.52	1.10, 2.10	1.52	1.09, 2.10	1.50	1.08, 2.09
	NFV	16.3	0.95	0.67, 1.35	0.94	0.65, 1.36	0.94	0.65, 1.36	0.93	0.63, 1.36
	SQV	2.1	1.71	1.01, 2.89	2.01	1.12, 3.60	2.12	1.17, 3.86	2.31	1.25, 4.27

ABC: abacavir; ATV: atazanavir; CI: confidence interval; DDI: didanosine; DRV: darunavir; D4T: stavudine; EFV: efavirenz; ETR: etravirine; FPV: fosamprenavir; FTC: emtricitabine; IDV: indinavir; LPV/r: ritonavir-boosted lopinavir; NFV: nelfinavir; NNRTI: non-nucleoside reverse transcriptase inhibitor; NRTI: nucleoside reverse transcriptase inhibitor; NVP: nevirapine; OR: odds ratio; PI: protease inhibitor; RPV: rilpivirine; SE: standard error; SQV: saquinavir; TDF: tenofovir; ZDV: zidovudine; 3TC: lamivudine.

Results from the hierarchical model with τ² = 0.125 suggest that further studies should focus on the possible detrimental associations between saquinavir (SQV) and LPV/r and preterm birth (Table 4), as both these drugs have relatively high estimated ORs (>1.5) with fairly little variability around the estimates (95% CIs: 1.01, 2.89 and 1.10, 2.06, respectively). The estimated OR for etravirine (ETR) is also relatively high (OR=1.58), but with just 8% of women exposed to ETR in pregnancy, there is much more variability around that estimate (95% CI: 0.77, 3.23), suggesting follow-up on ETR would take lower priority than follow-up on SQV and LPV/r.

5 Discussion

We evaluated how a hierarchical modeling approach to screening ARV use in pregnancy would operate in practice under various conditions. In theory, a hierarchical model offers a compromise between evaluating individual ARV drugs one at a time (which is the current method of choice for assessing the safety of ARV exposures in pregnancy) and fitting a full fixed effect model. It has the benefit of adjusting for other ARV exposures like the full model, but has less convergence problems, smaller standard errors, and more stable estimates than a full fixed effect model approach. However, the hierarchical model groups ARVs from the same drug class together, when there is often little prior knowledge regarding possible effects and the underlying biological mechanisms that ARVs have on perinatal and infant outcomes. If drugs from the same class have disparate effects on an outcome, adopting a hierarchical model approach for ARV safety screening could potentially undermine the screening approach.

In this study, we compared the performance of three different approaches under six different underlying true exposure-outcome relationships. Our results suggest that the hierarchical model that groups ARVs by drug class is almost always advantageous with a large enough sample (e.g. 5000). It minimizes the number of false negatives under each scenario as compared to both the full and separate models; it is able to detect the true effects substantially better than the separate models method and as well as or slightly better than the full model method when drugs from the same class behave similarly; and is still able to detect true effects similarly to the other methods even when drugs from the same class have opposite effects, except in the case of a binary outcome with a rare exposure.

In reality, however, these types of safety screening studies usually have smaller sample sizes, and the implications of the simulation study for use of the hierarchical model in smaller samples are less straightforward. If we wish to optimize the detection of true effects regardless of the expense in false discovery, then determining which approach to employ may involve taking into account the strength of one’s prior belief regarding effects of drugs from the same class, the sample size, and the outcome type (binary or continuous). However, perhaps one of the surprising results from the simulations was just how high the false discovery rate can be when evaluating ARV drugs individually, with four or more false discoveries (among 12 drugs) over 90% of the time, and abysmal nominal coverage rates of 95% CIs for some drugs in certain scenarios. Its poor performance in these areas is largely due to biased effect estimates from uncontrolled confounding by other ARV exposures. Power considerations in such settings become irrelevant when there are numerous false signals detected, and as a result evaluating ARVs individually may not allow identification of safety signals to appropriately focus future studies (see Supplemental Figures 1 and 2).

We present the hierarchical modeling approach as a screening approach, where little prior knowledge is available regarding possible exposure-outcome relationships. However, if there is evidence of differing effects for drugs belonging to the same class, then the full model may be suggested as a first choice for model fit. Particularly for rare drugs and a binary outcome, the full model has more power to detect the true effects if drugs from the same class do not have similar effects on the outcome; the full model also exhibits less bias in the effect estimates for the drugs with the true effects and better nominal coverage rates for the 95% CIs for the drugs with true effects. Thus, presuming the model converges, the full model has advantages over the hierarchical model when drugs from the same class do not behave similarly on an outcome. Nonetheless, if the full model does not converge, the hierarchical model specified with a large variance for the random effects (τ²) to allow larger residual effects for individual drugs is an appropriate alternative.

Our simulations and applied data analysis considered drugs from three drug classes (NRTIs, NNRTIs, and PIs). The number of drug classes has expanded in recent years, and as new drugs from new drug classes are made available (e.g. fusion inhibitors, entry inhibitors), some drugs may be the only drug of their drug class. For these drugs, the advantages of the hierarchical model are limited. Drugs unique to their class could still be included in a hierarchical model as fixed effects, but they would not be able to “borrow” information from other drugs in their class. Alternatively, Wang et al.²⁸ grouped rare drugs unique to their class together in an “other” category. The drug class effect for this “other” group does not have any clinical meaning, but it may still improve the reliability of the estimates for those rare drugs. In particular, based on our simulation results, it may be an advantageous option so long as drugs in the “other” group do not have opposite effects.

We did not consider any interactions between ARVs in this study. Further research is needed to characterize how the hierarchical model performs when interactions are present.

This study highlights the shortcomings – in particular, the inherent bias – of the separate models approach that is currently used to screen the safety of ARVs used during pregnancy. A hierarchical modeling approach can be a superior alternative to the current method, particularly when considering a binary outcome in large samples (N>3000), a continuous outcome in moderate or large samples (N>500), and/or when there is prior evidence suggesting drugs from the same class behave similarly on the outcome of interest.