Engineered bio-inspired coating for passive flow control

Significance

Flow separation on moving bodies has a negative effect on energy efficiency. Reducing recirculating regions is key in the design of energy-efficient systems. Efficient design decreases fuel consumption and pollutant emissions, including the systems’ carbon footprint. The engineered bio-inspired coating presented here aims to contribute in that direction. The relative ease of manufacturing and installation and its cost effectiveness, as well as its functionality under both wet and dry conditions, make it a versatile solution of potentially high impact in a broad range of applications, including transportation, wind power, and underwater vehicles.

Abstract

Flow separation and vortex shedding are some of the most common phenomena experienced by bluff bodies under relative motion with the surrounding medium. They often result in a recirculation bubble in regions with adverse pressure gradient, which typically reduces efficiency in vehicles and increases loading on structures. Here, the ability of an engineered coating to manipulate the large-scale recirculation region was tested in a separated flow at moderate momentum thickness Reynolds number, $R{e}_{\theta }=\mathrm{1,200}$. We show that the coating, composed of uniformly distributed cylindrical pillars with diverging tips, successfully reduces the size of, and shifts downstream, the separation bubble. Despite the so-called roughness parameter, $k^{+}\approx 1$, falling within the hydrodynamic smooth regime, the coating is able to modulate the large-scale recirculating motion. Remarkably, this modulation does not induce noticeable changes in the near-wall turbulence levels. Supported with experimental data and theoretical arguments based on the averaged equations of motion, we suggest that the inherent mechanism responsible for the bubble modulation is essentially unsteady suction and blowing controlled by the increasing cross-section of the tips. The coating can be easily fabricated and installed and works under dry and wet conditions, increasing its potential impact on a diverse range of applications.

During the past few decades, considerable effort has been placed on controlling flow separation (1–4). This phenomenon is usually responsible for increased vibration and drag on bluff bodies as well as higher energy consumption in vehicles. The drag experienced by a body under subsonic motion mostly embodies viscous and pressure (form) effects. The former is a result of friction induced by the near-wall fluid, and the latter is a result of pressure imbalance around the surface of the body. The separation phenomenon is well exemplified in the canonic case of flow around a foil at a sufficiently high angle of attack. There, the adverse pressure gradient (APG) in the suction side leads to flow deceleration and eventually flow detachment. The direct consequence of this process is a change of the aerodynamic force components, namely lift and drag.

Surface roughness plays a significant role in the turbulence dynamics near the wall and, in particular, in the separation regions (5–8). Evidence suggests that randomly distributed roughness, e.g., sand grain roughness, may move the separation point against the flow direction in the case of foils (9, 10); this shift results in drag increase and lift decrease. Experiments by Song and Eaton (11) showed an upstream shift of the separation point in a channel expansion with rough walls. However, various studies have shown that triggering transition to turbulence may reduce separation (12). These findings have motivated the use of flow control strategies such as vortex generators (13) and synthetic jets (3) to effectively delay flow separation. Unfortunately, these methods increase the production of turbulent kinetic energy (TKE), which, in turn, increases viscous losses and thus energy dissipation near the wall region. This viscous loss suggests that the control of flow separation without turbulence penalty is an ideal way to control form drag.

Recent efforts have focused on passive control via bio-inspired surfaces. The morphology of some natural organisms such as the lotus leaf and shark skin suggests that this daunting task might be achieved through textured coatings. Synthetic microscale structures similar to those found in the lotus leaf have been effective in reducing viscous drag by creating a slip velocity with trapped air between the wall and the water flow (14). The surface, however, eventually wets, losing functionality over time (15). Denticles found on the skin of sharks have also shown drag-reducing properties (16–18). While not completely understood, these structures appear to inhibit the formation and evolution of near-wall coherent motions (19). However, the physical mechanism responsible for this phenomenon is still under debate.

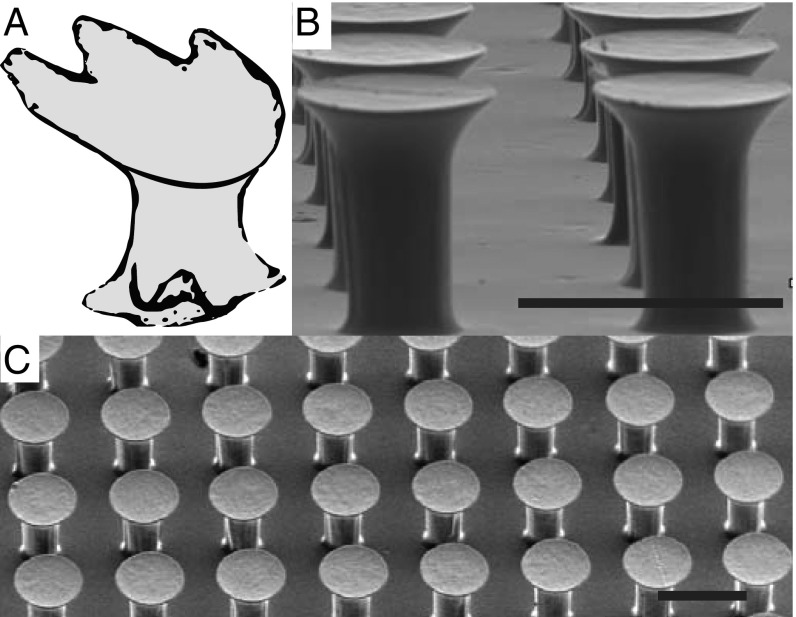
A feature of shark denticles, illustrated in Fig. 1, is the asymmetric geometry. The pillars used here (Fig. 1 B and C) are axisymmetric but take other elements of the denticles, including divergence and height (17). They are packed in a Cartesian layout and feature a “spatula” shape with stalk and tip diameters of $40\mathrm{\mu }\text{m}$ and $75\mathrm{\mu }\text{m}$, respectively, a height of $85\mathrm{\mu }\text{m}$ (defined here as the roughness height, $k$), and a center-to-center distance between pillars of $120\mathrm{\mu }\text{m}$. Another key difference is that the pillars do not include the channel-like indentations that denticles have on their top surfaces. Note that the pillars are arranged in a square packing with aligned rows and columns, but naturally occurring denticles overlap and are randomly aligned. Synthetic denticles have been successfully tested in Cartesian arrays without overlap (17). The main objective of this work is to demonstrate that this unique, engineered microsurface is capable of mitigating flow separation. The pillars’ simple manufacturing and cost-effective fabrication process may lead to a large impact in a wide range of energy applications.

Fig. 1.

(A) Shark denticle shows a divergent shape with an asymmetry in the wall-normal and streamwise directions. Adapted with permission from ref. 17. (B and C) Microscopy images of the micropillar arrays presented in this study, which have a similar asymmetric shape. (Scale bars: $100\mathrm{\mu }\text{m}$.) The height and tip diameter of each element are $85\mathrm{\mu }\text{m}$ and $75\mathrm{\mu }\text{m}$, whereas the stalk diameter is $40\mathrm{\mu }\text{m}$. The center-to-center distance between the pillars is $120\mathrm{\mu }\text{m}$.

Despite some success fabricating shark-inspired synthetic surfaces (17), such fabrication methods rely on 3D printing, making it difficult to replicate denticles in their original size. Wen et al. (17) scaled the structures by a factor of 12.4 to satisfactorily replicate geometric features. Furthermore, since every denticle must be 3D printed, this method may be slow and expensive. The method presented here instead relies on a series of etching and casting steps. While the initial step includes a complicated process consisting of deep reactive ion etching (20–22), the subsequent steps allow for replication of the desired surface using simple casting methods. Once a mold is made, it can be used almost indefinitely. This reusability allows for reproduction and scale-up of these engineered microsurfaces in a cost-effective manner, using a variety of materials capable of satisfying application-specific requirements. Furthermore, the structures can be casted directly on the surface to be coated, thus simplifying the installation process.

Results and Discussion

Measurements were performed in a refractive-index–matching (RIM) facility at University of Illinois at Urbana–Champaign with a diverging cross-section (Fig. 1C) at ${\text{Re}}_{\theta }\approx \mathrm{1,200}$. The RIM allowed measurement of the velocity very near the wall, down to $y^{+}\approx 3.6$ for the selected interrogation window. The flow field and turbulence statistics were compared with a smooth counterpart. The uncertainty of the velocity measurement, calculated using the method used by Waldman and Breuer (23), is 0.5% of $U_{\mathrm{\infty }}$. Details of the experiments are provided in Materials and Methods.

The resulting velocity fields reveal significant differences between the flows over the smooth and coated walls. Instantaneous velocity contours with superimposed mean streamlines (Fig. 2 A and B) illustrate a large region with reverse flow in the smooth case. In contrast, the divergent pillars induce a smaller separation bubble. Further, the reverse flow (blue) region is considerably smaller in the coated case. The reduced flow separation is confirmed by the mean streamwise velocity contours, which are shown superimposed for both cases in Fig. 3A. The contours for the smooth case (solid lines) recover farther away from the wall, and the reverse flow (black contour) is considerably larger over the smooth surface. The area with reverse flow is reduced by $\approx 60\%$ in the presence of the microscale coating. Our data also reveal a downstream shift in the separation point of ∼$0.4{\delta }_0$, where ${\delta }_0$ is the boundary layer thickness at the inlet of the expansion. The effect of the coating is also observed in the mean vertical velocity field. When the flow is attached, this velocity component should remain negative in this particular configuration. However, as observed in Fig. 2 D and E, a higher upward velocity (red outlined level) occurs in the smooth case, which is characteristic evidence that the boundary layer has detached from the wall; i.e., it is separated.

Fig. 2.

(A and B) Instantaneous normalized streamwise velocity $u/U_{\mathrm{\infty }}$ for (A) smooth and (B) coated cases. The smooth case has significantly more reverse flow (dark blue), which is associated with separated flow. (C and D) Contours of the mean vertical velocity $⟨V⟩/U_{\mathrm{\infty }}$ for the smooth and coated cases, respectively. The red level with black outline represents the area with flow moving away from the wall (upward velocity), which is linked to separation.

Fig. 3.

(A) Superimposed contour lines for the normalized mean streamwise velocity $⟨U⟩/U_{\mathrm{\infty }}$. Solid lines, smooth; dashed lines, coated. The smooth case shows an ∼60% larger area with negative flow (black level). (B and C) Velocity profiles for $⟨U⟩/U_{\mathrm{\infty }}$ and $⟨V⟩/U_{\mathrm{\infty }}$, respectively. Smooth, $\mathrm{\square }$; coated, •. B, Inset shows the region near the wall for $⟨U⟩/U_{\mathrm{\infty }}$, where a larger negative portion in the smooth case can be observed. Error bars represent SE (=$u_{rms}/\sqrt{N}$, where $N$ is the number of samples); for $U$ the error bars (not shown) are smaller than the symbol size.

Despite lift and drag measurements not being performed for the current study, previous wind-tunnel experiments carried out by our team (Supporting Information) on a coated S809 airfoil show a 25–40% increase in the lift coefficient at angles between $8^{\circ }$ and ${16}^{\circ }$ (Fig. S2). These results provide complementary evidence of the functionality of the pillars in reducing flow separation. This apparent functionality (lift coefficient increase) in wind-tunnel experiments implies that the coating also works in air. This supports our hypothesis that the mechanism by which the surface coating reduces flow separation does not rely on hydrophobicity.

The differences between the two cases are highlighted in the selected mean velocity profiles at $x/{\delta }_0=18.5$ (Fig. 3 B and C); they are consistent with reduced blockage from a smaller recirculation bubble. The streamwise velocity in the coated case is higher near the wall ($\approx 10\%$ of the local average) than in the baseline. The effect of the coating is most noticeable from the wall up to $y/\delta \approx 0.6$. Fig. 3A, Inset shows a closer view near the wall, where the area with negative velocity, i.e., below the dashed line, is larger over the smooth surface. The difference between the vertical velocity profiles at the same location is even larger, reaching almost 50% increase in the coated case around $y/\delta \approx 0.3$. It is also worth noting that the vertical velocity does not recover completely at the edge of the boundary layer. This effect is due to the separation bubble preventing the flow from moving downward along the wall.

When adding texture to a wall, there is a risk of increasing the production of turbulent kinetic energy, which is related to viscous losses (24). Our data show differences in the TKE production between the two cases that are within the measurement uncertainty (Fig. S3), suggesting that the pillars have minor effect on the turbulence production. This result is expected for “hydrodynamically smooth” walls (25).

While the results from the APG experiments show that the separation bubble is reduced and displaced downstream, the physical mechanism responsible for these phenomena is not evident from the data. To shed light on this mechanism, we carried out additional high-resolution experiments over a flat plate coated with the same engineered diverging pillars at ${\text{Re}}_{\theta }\approx \mathrm{3,600}$ (details given in Materials and Methods). For these measurements, the interrogation window was placed as close as $y^{+}\approx 1$. This setup was chosen to avoid the unsteadiness of the separation bubble in the APG flow. It should be noted that given the thickness of the laser sheet ($\approx 1$ mm), we inherently probe the flow over several rows of pillars, which creates an averaging effect in the transverse direction. The vertical velocity profile (Fig. 4A) for the coated case shows a downward (negative) flow near the wall. We believe this downward flow is due to a misalignment between the pillar rows and the bulk flow, creating a localized spanwise flow. The mechanism by which the pillars reduce flow separation can be gleaned from Fig. 4B. The pillars generate oscillations in the inner layer, which are reflected as a large peak in the wall-normal component of the Reynolds stresses near the edge of the pillar canopy. Complementary insight is illustrated in Fig. 4C. The pillars reduce the cross-sectional area, accelerating the fluid passing between them along the streamwise direction (red area). This acceleration decreases the pressure and generates suction. Additionally, pillars create a stagnation point (blue area) by blocking some of the fluid. This increases the pressure and pushes fluid up, inducing fluid ejection.

Fig. 4.

(A) Wall-normal velocity profile over smooth and coated flat plates at $x=\mathrm{2,100}\hspace{0.17em}\text{mm}$. The coated case shows a negative velocity in the vicinity of the wall, which is a result of suction between the pillars. (B) Profile of wall-normal Reynolds stress. The velocity fluctuation shows a marked increase in the area adjacent to the pillar canopy edge, which suggests that oscillations are induced by the pillars in the flow in the interface of the pillar canopy. (C) Schematic illustrating the physical mechanism by which the micropillars modify the flow in the area near the flow. Areas of low and high pressure create high- and low-velocity areas, respectively. They also create ejection and suction events (thick, black arrows), which increase the wall-normal velocity fluctuations. The schematic also shows three distinct regions that arise in the flow: an inertia-dominated region, a viscous-dominated region, and an interface region between these two layers.

Instead of the typical nonslip condition in canonical smooth walls, at the top of the pillars ($y=k$), the fluid velocity is not zero between the pillars. Instead, an “interlayer” is created above the pillars (Fig. 4C). In this layer a connection exists between the boundary layer (flow above the pillars) and the inner flow (i.e., within the canopy). Recalling the boundary layer momentum equation in the wall-normal direction (24),

$$\frac{1}{\rho }\frac{\partial ⟨P⟩}{\partial y}=\frac{\partial ⟨v^2⟩}{\partial y}+\frac{\partial ⟨v^{″2}⟩}{\partial y},$$ [1]

it is clear that $⟨v^2⟩$ and $⟨P⟩$ are directly related; here $⟨\cdot ⟩$ represents the time-averaging operator and $⟨v^{″2}⟩$ is a dispersive stress arising from the spatial averaging in the $x$ (streamwise) and $z$ (spanwise) directions (cf. refs. 26–28). Integrating Eq. 1 from the top of the diverging pillars to a point $y$ above the surface, it follows that

$$(⟨P_{oi}⟩-⟨P⟩)/\rho =⟨v^2⟩-⟨v_{oi}^2⟩+⟨v^{″2}⟩-⟨v_{oi}^{″2}⟩,$$ [2]

where $⟨P_{oi}⟩$ is the static pressure at the edge of the canopy; that is, $y_{oi}=k=85\mathrm{\mu }\text{m}$. Note that for the case of the smooth surface $⟨v_{oi}^2⟩=0$, but in the coated case $⟨v_{oi}^2⟩\ne 0$, as seen in the lower portion of Fig. 4B.

The flow regime is significantly different within the micropillar layer, however. It has a ${\text{Re}}_k\lesssim 1$, based on the geometry and the estimated friction velocity; thus, it is viscous dominated and governed by pressure gradient, i.e., Stokes flow. Eq. 1 can be used accordingly, recognizing that the gradient of the wall-normal Reynolds stress approaches zero. Therefore, $⟨P_w⟩\approx ⟨P_{oi}⟩$ within the pillar canopy, and the changes in the wall-normal Reynolds stress are proportional to the pressure difference between the static pressure at the wall, $⟨P_w⟩$, and the local pressure across the boundary layer. Consequently, it follows that

$$⟨v_{oi}^2⟩=⟨v^2⟩+⟨v^{″2}⟩-⟨v_{oi}^{″2}⟩-(⟨P_w⟩-⟨P⟩)/\rho .$$ [3]

This relation implies that the changes observed in the inner region for $⟨v^2⟩$ are likely due to suction and blowing events between the diverging pillars and along the high-momentum flow region. Despite the fact that these changes exist mainly below the buffer layer, significant variations are observed in the outer layer, where the bubble resides. Consequently, this microscale surface passively modulates the small scales of the flow in the wall region, which in turn affects the large scales in the outer flow. Given the size of the pillars, this result is surprising, but it is consistent with the findings by Bocanegra Evans et al. (29), who observed the propagation of the pressure perturbation over 35 times the pillar height.

The pressure modulation generated by the pillars can be described as small-scale weak jetting events that may reenergize the boundary layer and delay separation; however, the pillars passively induce small-scale perturbations over the entire surface. In the case of the divergent pillars, the contraction in the cross-sectional area is greater, amplifying the flow acceleration between the pillars. The regions of ejections and suctions are increased in the viscous sublayer. For the smooth case, this increase occurs in the buffer layer, suggesting evidence of an interlayer above the pillars—consistent with Eq. 3. While our results give evidence for the proposed mechanism, further work is needed to understand how the size and layout of the pillars affect the recirculation bubble, as well as how the scales of the micropillar geometry interact with the characteristic scales of the boundary layer, e.g., $\delta$, $u_{\tau }$.

The combined results from both experiments indicate that it is through pressure changes at the interlayer, between viscous-dominated flow within the canopy and the inertia-dominated flow above the pillars, that the large scales of the flow are affected. Thus, the wall-normal Reynolds stress at the interface, $⟨v_{oi}^2⟩$, modulates the flow between the diverging pillars (suction and blowing) by interacting with the pressure difference, $⟨P_w⟩-⟨P⟩$, across the roughness interlayer. It must be stressed that the diameter of the pillar is the largest at the interlayer between the roughness canopy and the boundary layer, and therefore its effect is largest precisely in this region of the flow.

Conclusions and Outlook

We have tested the flow control properties of an engineered bio-inspired surface coating. Our results confirm the functionality of the coating, which mitigated flow separation without a noticeable increase in the production of the turbulent kinetic energy. The microscale surface coating shifts the separation point downstream and significantly reduces the area of negative flow. The coating can be manufactured and installed with relative ease and is cost-effective in comparison with other solutions manufactured using 3D printing. The physical mechanism by which the coating works does not rely on (super)hydrophobicity. Instead, it relies on the generation of distributed wall-normal perturbations, giving it the versatility to work in liquid and gas media. These results have important implications in flow control, with applications in both power generation, e.g., wind turbines, and energy-efficient transport vehicles. These capabilities considerably increase the potential impact of the engineered coating.

While our results demonstrate the functionality and describe the working mechanism of the micropillars, it is necessary to test the surface coating under other flow conditions and different geometric configurations, e.g., spacing and height. Adapting the micropillar coating to a diverse array of applications will maximize the impact of this engineered surface on energy and transport systems.

Materials and Methods

The experiments were performed in a RIM flume of 112.5 $\times$ 112.5 mm² test section at the University of Illinois (laboratory of L.P.C.). The working fluid was a sodium iodide solution (63% by weight) with a kinematic viscosity $\nu =1.1\times {10}^{-6}{\text{m}}^2/\text{s}$ and a density $\rho =\mathrm{1,800}$ kg/m³. The minimum reflection from the wall allowed measurements within the viscous sublayer ($y^{+}\approx 3.6$). Details of the facility can be found in Blois et al. (30) and Hamed et al. (31), and details of the RIM technique are in Bai and Katz (32). The facility was adapted with a diverging wall (Fig. 5) to induce adverse pressure gradient and flow separation. The experiments were performed at a Reynolds number ${\text{Re}}_H=U_o{H}_{1/2}/\nu =\mathrm{4,600}$ (or in terms of the momentum thickness, $R{e}_{\theta }\approx 560$) measured right upstream of the expansion ($x=0$), where $U_o=0.225$ m/s is the centerline velocity and $H_{1/2}=H/2$. The boundary layer thickness at the inlet ${\delta }_0=16.2\text{mm}$, and the normalized roughness height $k^{+}\simeq 1$ is estimated with $c_f=0.026/{\text{Re}}_x^{1/7}$. The inlet velocity profile for both cases differed by $\le 1\%$ (Fig. S4). In the field of view shown in Fig. 2, $\delta \approx 27.5\text{mm}$ and ${\text{Re}}_{\theta }\approx \mathrm{1,200}$.

Fig. 5.

Schematics of the APG test section of a wind-turbine section. In these experiments, the boundary layer develops in an approach channel of height $H=45$ mm and length $L=\mathrm{1,250}$ mm. The origin of the coordinate system ($x=0$, $y=0$) is set at the bottom wall of the channel at the beginning of the expansion. The micropillar coating (shaded area) was applied from $x=-50\text{mm}$, and the S835 section is $370\text{mm}$ long.

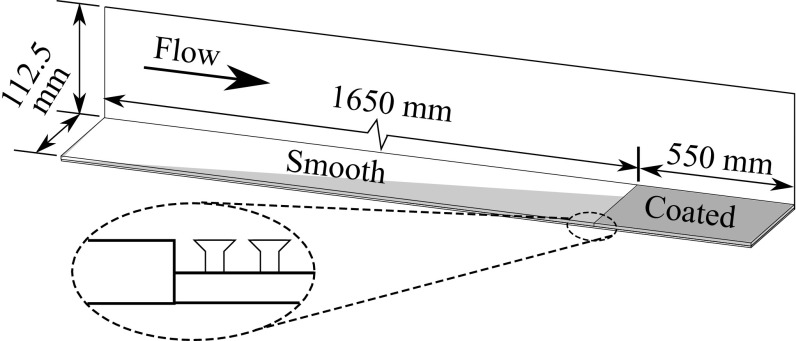
Flat-plate [zero pressure gradient (ZPG)], high-resolution experiments were carried out in the RIM flume described above to assess the changes in the velocity field near the wall. For this set of experiments, the cross-section ($112.5\text{mm}\times 112.5\text{mm}$) was unobstructed. As illustrated in Fig. 6, the bottom wall was coated over a 550-mm span past a 1,650-mm smooth development region. The height of the coated plate was adjusted to minimize disturbances. Furthermore, to reduce misalignment effects, the flow was probed 500 mm into the coated section. The mean free stream velocity $U_{\mathrm{\infty }}=0.8\text{m/s}$, equivalent to a momentum-based Reynolds number $R{e}_{\theta }=\mathrm{3,600}$. For these experiments, the field of view was considerably smaller than in the APG experiments, allowing us to resolve the viscous sublayer, down to a $y^{+}\approx 1$.

Fig. 6.

Schematics of the ZPG test section. The boundary layer develops over a smooth region of 1,650 mm followed by a coated plate of 550 mm length ($R_{\theta }\approx \mathrm{3,600}$), using the same diverging pillar geometry (shape, size, and spacing) as in the APG experiments. Careful alignment of the plates was performed by using $20-\mathrm{\mu }\text{m}$ shims.

Particle Image Velocimetry.

Planar (two-dimension, two-component) particle image velocimetry (PIV) was used to measure the velocity field in a vertical plane at the axis of the diverging flume. An 11-MP camera ($\mathrm{2,700}\times \mathrm{4,000}\hspace{0.17em}{\text{pixels}}^2$) and a pulsed, dual-head Nd:YAG laser were used for image capture. The APG experiments had a resolution of $46\mathrm{\mu }\text{m/pixel}$, resulting in a field of view of ∼$182\times 123{\text{mm}}^2$. Each experimental run consisted of 4,000 PIV realizations. The data processing was performed with a final interrogation window of $16\times 16{\text{pixels}}^2$ with 50% overlap, resulting in a vector separation $\mathrm{\Delta }x=\mathrm{\Delta }y=365\mathrm{\mu }\text{m}$.

The ZPG experiments used the same imaging system described above, but with higher resolution and a different processing algorithm. The optical field of view for these experiments was $26\text{mm}\times 17.4\text{mm}$. A PIV plus PTV (particle tracking velocimetry) processing (LaVision) was used to obtain the velocity field. The algorithm performed two PIV passes, $32\times 32$ pixels and $16\times 16$ pixels, with a final PTV pass. The mean velocity field was calculated from 2,000 samples with a vector separation of $6.5\mathrm{\mu }\text{m}$.

Fiber Fabrication.

The microscale coating was fabricated using a well-established method composed of photolithography, micromolding, and dip-transfer printing (20, 21, 33). In this method, a master template of cylindrical fibers is first fabricated using photolithography from photoresist (SU-8 2100; MicroChem). A shape-complementary mold, which features the negative of cylindrical fibers, is manufactured by casting the cylindrical master with silicone rubber (Mold Max 27T; Smooth-On). The complementary mold is then cast with polyurethane (ST 3180; BJB Enterprises) to manufacture cylindrical fibers, which are an exact replica of the master fibers. The second step of the fabrication forms the divergent tip, a feature similar to the shark denticle. The polyurethane cylindrical fibers are placed onto a very thin film of liquid polyurethane, formed by spin coating the liquid polyurethane on a polystyrene substrate, using a spinner (WS-650 MS; Laurell Technologies). When the cylindrical fibers are removed from the thin liquid film, they retain some of the liquid polymer on the tip of each individual fiber. Immediately after this step, the fiber array is placed onto a low–surface-energy dipping surface, a polypropylene substrate, allowing the liquid polymer to spread and morph into the desired shape. The pillars with divergent tips are then obtained by removing the fibers from the dipping surface after the liquid polymer on the tips of the fibers cures. This step creates the master template for the fiber array. A complementary mold is fabricated by casting the fibers with silicone rubber. This mold is then cast with a rigid polyurethane (Crystal Clear 200; Smooth-On) on an acrylic backing to obtain the diverging pillar arrays used in this study.