Surface structure evolution in a homologous series of ionic liquids

Significance

This high-resolution X-ray study resolves the liquid–air interface structure for a long homologous series of room temperature ionic liquids (RTILs). RTILs are intensely studied for many potential “green” applications and for their intriguingly complex and rare combination of intermolecular interactions. Varying their cation’s alkyl chain length provides, therefore, an opportunity to tune the main interaction from mostly long-range electrostatic to mostly short-range van der Waals. This variation is found here to drive the interface structure from simple, to layered, to liquid crystalline. The quantitative results obtained constitute an accurate yardstick for testing simulations and theory, impact the bulk–surface structure relations in general, and provide currently scarce data for many RTIL applications, like batteries and supercapacitors.

Abstract

Interfaces of room temperature ionic liquids (RTILs) are important for both applications and basic science and are therefore intensely studied. However, the evolution of their interface structure with the cation’s alkyl chain length $n$ from Coulomb to van der Waals interaction domination has not yet been studied for even a single broad homologous RTIL series. We present here such a study of the liquid–air interface for $n=2\text{to}\hspace{0.17em}22$, using angstrom-resolution X-ray methods. For $n\mathbf{<}6$, a typical “simple liquid” monotonic surface-normal electron density profile ${\rho }_e(z)$ is obtained, like those of water and organic solvents. For $n\mathbf{>}6$, increasingly more pronounced nanoscale self-segregation of the molecules’ charged moieties and apolar chains yields surface layering with alternating regions of headgroups and chains. The layering decays into the bulk over a few, to a few tens, of nanometers. The layering periods and decay lengths, their linear $n$ dependence, and slopes are discussed within two models, one with partial-chain interdigitation and the other with liquid-like chains. No surface-parallel long-range order is found within the surface layer. For $n=22$, a different surface phase is observed above melting. Our results also impact general liquid-phase issues like supramolecular self-aggregation and bulk–surface structure relations.

Formally, room-temperature ionic liquids (RTILs) are molten organic salts, which remain liquid to below 100 °C (1). This deceptively simple description covers an incredibly broad, complex, and intriguing novel class of liquids that has attracted an intense, and ever-growing, research activity since the 1990s (2, 3). RTILs consist of organic or inorganic anions and organic cations comprising charged headgroups attached to one or more alkyl moieties. This composition gives rise to a rich array of intermolecular and intramolecular interactions, seldom coexisting in a single material: Coulomb, dipolar, $\pi -\pi$, solvophobic, van der Waals (vdW), and hydrogen bonding (2, 3). These interactions were shown in simulations, (4, 5) and recently experimentally (2, 3, 6), to lead to the self-assembly of local nanostructure within the bulk, previously considered to be a homogeneous, locally isotropic, and unstructured simple liquid. While segregating the charged from the apolar moieties, the nanostructuring nevertheless leaves the corresponding bulk correlations liquid-like (LL) and short-ranged (2, 3, 6–9). RTILs are, therefore, an intriguing borderline case between molecularly ordered long-range-correlated solids and nanoscale-uniform, isotropic, short-range-ordered, simple liquids. Their study impacts therefore not only RTILs but liquids in general. RTILs’ bulk has been extensively studied by wide-angle X-ray scattering and small-angle X-ray scattering (SAXS) (2, 3, 7, 8), which probe directly the bulk’s molecular-scale structure, by other related measurements (7–9), and by simulations (10–12). All support strongly the existence of segregated domains of charged headgroups and apolar alkyl chains, organized, on a mesoscopic scale, as bilayers, clusters, hydrogen-bound networks, micelles, bicontinuous phases, etc. (2, 11, 13–15). Boundary-induced transitions among these, and spontaneous dynamical structural rearrangements, were also suggested (16). The flat topology of the liquid–air interface should render the segregation surface-normal and planar, yielding a stack of alternating headgroup and alkyl-chain regions, as indeed found at RTIL–air (17) and RTIL–solid (18) interfaces.

Being experimentally challenging, the structure of RTIL interfaces, and, in particular, the structure’s evolution when varying the balance among the various molecular interactions, has been much less studied than their bulk counterparts. While a detailed review is outside the scope of this manuscript (see refs. 2 and 3 for recent excellent overviews), most published RTIL–air interface studies address Coulomb-dominated RTILs with relatively short alkyl moieties. High-resolution X-ray studies of RTIL interfaces are particularly scarce. The structure of the RTIL–air interface, the subject of the present study, has been previously measured by angstrom-resolution X-ray methods only for a few short-chain ($n\le 4$) RTILs (19–23), one pair of $n=6,8$ RTILs (24), and a single RTIL with $n=18$ (17). For $n\lesssim 4$, only weak layering of one to two layers was found, or none at all. The RTILs with $n=6,8$ show the start of a more pronounced layering, and the single long ($n=18$) RTIL measured exhibits a distinct surface layering penetrating tens of nanometers into the liquid. Importantly, among all of the RTILs studied previously, not more than two belong to the same homologous series, and even those are of close lengths: $n=2,3$ (23) and $n=6,8$ (24). The full body of RTIL–air surfaces studied to date by X-ray methods does reveal a variation in the level and characteristics of the near-surface structure. Nevertheless, since only two different-length RTILs were studied within any single homologous series, one cannot confidently elucidate which changes within this body are due to chain length variation, and which are due to different sizes, conformations, and interactions of the many different ionic species used. Thus, the evolution of the RTIL–air interface structure as the main interactions change gradually from mixed Coulomb–vdW to vdW dominance by varying the chain length, and that only, has not been hitherto determined by high-resolution X-ray methods for even a single long homologous RTIL series. Related issues were, however, addressed by simulations (10–12), and macroscopic (9, 25, 26) and compositional (27–31) methods. Thus, a quantitative determination of the structure’s characteristics (layering periodicity and decay length) for a broad $n$ range in a single RTIL series, as done here, should also provide an important yardstick for testing theoretical and simulation studies. Finally, the interface structure of RTILs is of great importance not only to basic science but also to the many applications involving interfaces: supercapacitors, solar cells, batteries, metal extraction from wastes, chemical reactions and catalysis, and more (28, 32–34). Elucidation of the RTIL–air interface’s influence and its variation with $n$ should provide insights also for other interfaces, including the RTIL–solid one, involved in the above applications.

Here, we present a systematic angstrom-resolution synchrotron X-ray reflectivity (XR) study of the liquid–air interface structure of a homologous RTIL series, [C_nmim]⁺[NTf₂]⁻, with alkyl lengths $n=2\text{to}22$. A series of surface phases are found: For small $n$, a monotonic surface-normal electron density profile (EDP) is observed, akin to that of simple liquids like water and organic solvents. As $n$ increases, first a single high-density surface-segregated monolayer appears. For still-larger $n$, a nonmonotonic layered EDP develops, decaying into the bulk over a length scale which increases with $n$. For $n=22$, we observe a new surface phase above melting. The periodicities and decay lengths of the layering are determined, and their evolution with $n$ is characterized and discussed. The interfacial molecular ordering reflected in the EDP and its relation to the bulk’s nanoscale local structure are also discussed, along with the broader impact of these results on liquids in general.

Results

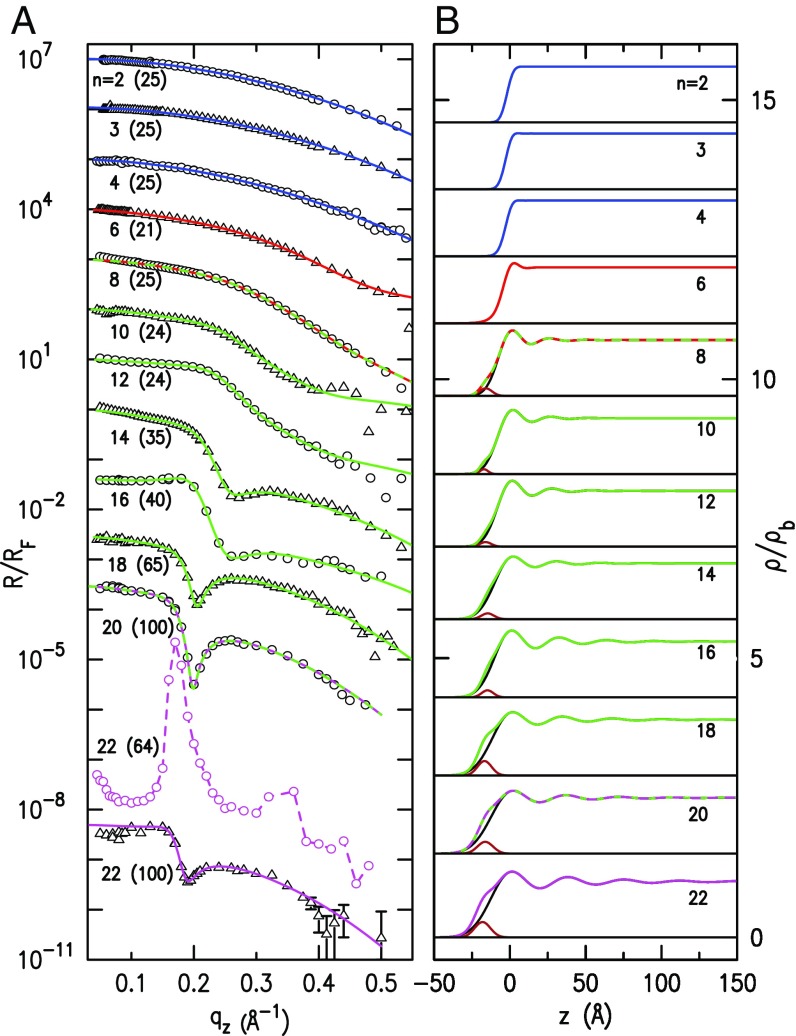
The measured, Fresnel-normalized XR curves, $R/R_F$, are plotted in Fig. 1A (symbols) versus the surface-normal scattering vector $q_z=(4\pi /\lambda )\sin (\alpha )$, where $\alpha$ is the grazing angle of incidence of the X-rays on the surface, and $R_F$ is the XR of an ideally abrupt and smooth surface (35).

Fig. 1.

(A) Fresnel-normalized measured (symbols) and model-fitted (lines) XR curves of the liquid–air interface of the RTILs studied at temperatures given in parentheses (in degrees Celsius). Note the higher temperatures for $n\ge 14$ which melt above RT (see Supporting Information for melting temperatures). Curves are shifted for clarity from each other by a decade for $n\ge 14$, and by multiplication by $4\times {10}^{-2}$ ($n=16$), $3\times {10}^{-3}$ ($n=18$), $3\times {10}^{-4}$ ($n=20$), and $3\times {10}^{-7}\text{and}\mathrm{\hspace{0.25em}5}\times {10}^{-9}$ ($n=22$). The different colors indicate different surface phases. Curves in two colors denote transitions between surface phases. Note the lower-temperature surface phase of $n=22$, tentatively identified as a liquid-crystal surface phase. (B) The EDPs (normalized to the bulk electron density) obtained from the model fits in A. The brown Gaussian represents the density enrichment at the air side of the surface. EDPs are shifted from each other for clarity, with black horizontal lines denoting $\rho /{\rho }_b=0$ for each. See Results for discussion.

Eye inspection reveals, for $n=2\text{to}\hspace{0.17em}4$, smoothly decreasing, unmodulated, $R/R_F$ curves typical of simple liquids, indicative of a ${\rho }_e(z)$ which varies monotonically from zero to the bulk’s electron density ${\rho }_b$ over a width dominated by thermally excited capillary waves (35–37). Changes in $R/R_F$ start appearing for our RTILs at $n=6\text{to}8$ with a steeper fall-off at high $q_z$, similar to the XR curves of the short-chain studies discussed in the Introduction (19–23): the $n=\mathrm{6,8}$ trialkyl-ammonium-based RTILs (24), and the $n=4$ RTILs with ${\text{BF}}_4^{-}$, ${\text{PF}}_6^{-}$, and halide anions, all of which are significantly less bulky than the ${\text{NTf}}_2^{-}$ used here. We note, in passing, that varying the cations, the dominant and largest of the two ion constituents of an RTIL molecule, would likely induce larger variations in the surface structure, including the threshold for layering. However, since systematic studies of the influence of cation symmetry and architecture on nanostructuring are still scarce even for the RTILs’ bulk (3, 8), and since the variety of available cations is significantly broader than that of the anions (2), elucidating general trends in the cation dependence of layering is not possible at this time.

At $n=10\text{to}\hspace{0.17em}12$, our RTILs exhibit a plateau at small $q_z$, which becomes, by $n=14$, a fully developed modulation with a well-defined dip, apparent in all higher-$n$ curves. A new surface phase, manifested by two peaks, is observed for $n=22$ above bulk melting. However, as the lowest curve in Fig. 1A shows, the typical $R/R_F$ shape of $n=16\text{to}\hspace{0.17em}20$ is recovered also for $n=22$ at high temperatures. The new phase of $n=22$ is tentatively identified as the surface equivalent of the bulk liquid-crystal phase reported recently for this compound (38, 39). Indeed, the $q_z$ positions of the two peaks of $n=22$ in Fig. 1A are close to those of the (001) and (002) powder reflexes of $n=22$’s bulk crystalline phase (38). Our peaks do not originate, however, from a 3D powder lying on the liquid surface, since they are confined to the $q_z$ axis rather than being cuts through powder rings, and their broad widths imply a short crystalline coherence length. Moreover, the bulk liquid-crystal phase (38) appears only upon cooling below the RTIL’s melting temperature, $T_m$. The present surface phase seems to exist over a significant temperature range (≲25°C) above $T_m$. The structure and evolution with temperature and $n$ of this surface phase deserve a detailed study.

Our grazing incidence X-ray diffraction (GID) measurements for all $n$ for surface-parallel scattering vectors 0.4 Å⁻¹$\le q_{\parallel }\le 1.9$ Å⁻¹ found no sharp peaks that would indicate long-range surface-parallel order akin to that detected in a different RTIL, [C₄mim][PF₆], near its $T_m$ (40). However, since we focused on the structure’s $n$ dependence, we have not measured detailed temperature-dependent grazing incidence SAXS (GISAXS) near $T_m$, where such surface-parallel order was reported to occur.

For quantitatively analyzing the measured XR curves, we used the distorted crystal model (DCM), developed for liquid mercury interfaces (41) and successfully used for liquid metals and alloys (35), and ionic liquids (17, 18, 24, 42). This model describes ${\rho }_e(z)$ by a series of equally spaced ($d$) Gaussians of increasing widths, yielding ${\rho }_e(z)$ modulations of amplitudes decreasing with $z$ and eventually merging smoothly with the constant average density of the bulk, ${\rho }_b$. The rate of amplitude decay is controlled by the width parameter $\overline{\sigma }$. To account for a possible density enhancement of the air side of the surface over the DCM contribution (17, 19), we also included a Gaussian of amplitude ${\rho }_a$. The model has the advantage of tuning ${\rho }_e(z)$ from a simple-liquid-like monotonic EDP for $d\lesssim \overline{\sigma }$ to that of a decaying-layered one for $d>\overline{\sigma }$. This property is particularly valuable here as it allows us to use the same consistent model to describe the structure despite the significant shape variations with $n$ of $R/R_F$ and ${\rho }_e(z)$, as discussed above. For further details of the model and the fits, see Supporting Information.

The fits, Fig. 1A (lines), reproduce well the measured $R/R_F$ curves (symbols) for all $n$ and over the full measured $q_z$ range. The corresponding EDPs in Fig. 1B show the evolution from a monotonic ${\rho }_e(z)$ for $n=2\text{to}\hspace{0.17em}4$, through a single higher-density surface-adsorbed layer for $n=6$, to a layered structure for $n\ge 8$. This accounts for the transition found in the range $n=6\pm 2$ in the surface composition and in several macroscopic surface properties (27, 43). For example, Rutherford backscattering spectroscopy (31) reveals a surface chain orientation change at $n\approx 4$, the surface tension $\gamma (n)$ shows a slope change from negative for $n<6$ to near zero at $n\ge 8$ (44, 45), and the surface enthalpy (25) exhibits a minimum at $n=6$. As discussed below, bulk SAXS reveals the emergence of a prepeak at $n\approx 6$, indicative of the start of bulk nanostructuring at this $n$ (13). The ${\rho }_e(z)$ modulation period $d$ is observed in Fig. 1B to increase with $n$. The additional Gaussian’s height also increases with $n$, although more moderately. A careful inspection of Fig. 1B also suggests that the EDP modulations’ decay length, $\xi$, increases with increasing $n$ faster than does $d$. These eye estimates are confirmed by the fit-derived parameter values plotted in Figs. 2 and 3 and discussed in the following paragraphs.

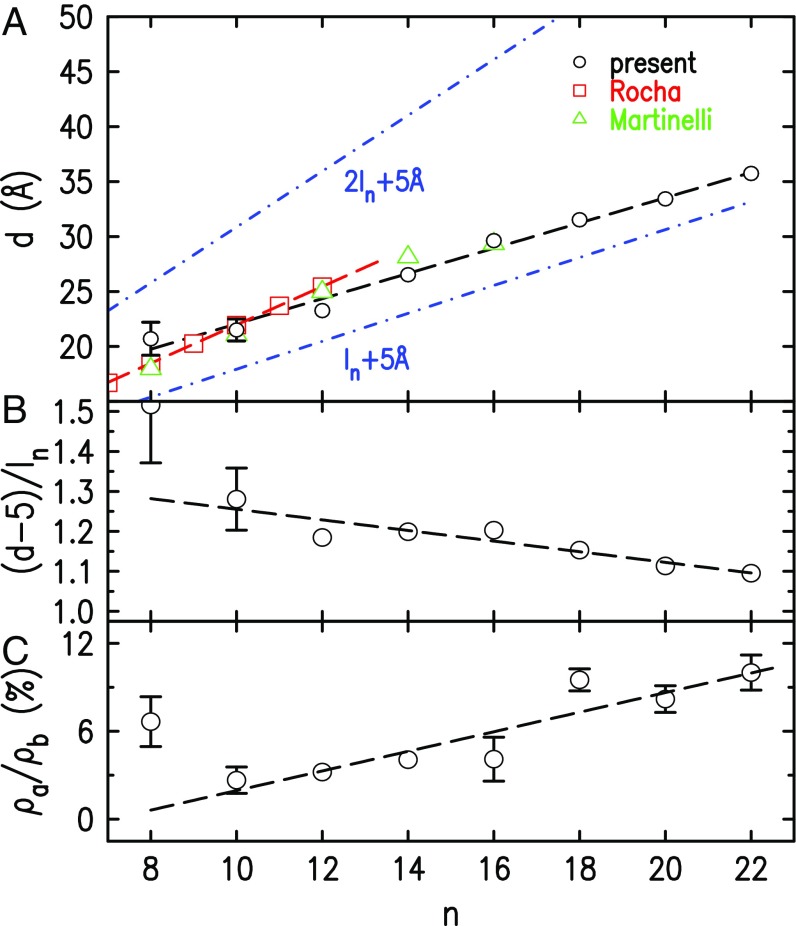
Fig. 2.

Variation with alkyl chain length, $n$, of (A) fit-derived (symbols) surface layering periodicity, $d$, compared with bulk values by Rocha et al. (8) and Martinelli et al. (7), (B) $d$ (less 5-Å headgroup size) normalized by the cation’s extended chain length $l_n$, and (C) surface density enrichment of the air side of the surface normalized to the bulk density, ${\rho }_a/{\rho }_b$. The dashed lines in B and C are linear fits, intended to highlight a general decreasing (B) or increasing (C) trend. The dash–dot lines in A are the calculated extended alkane lengths, $l_n$, and 2$l_n$, with 5-Å headgroup size added. For discussion, see Results and Discussion.

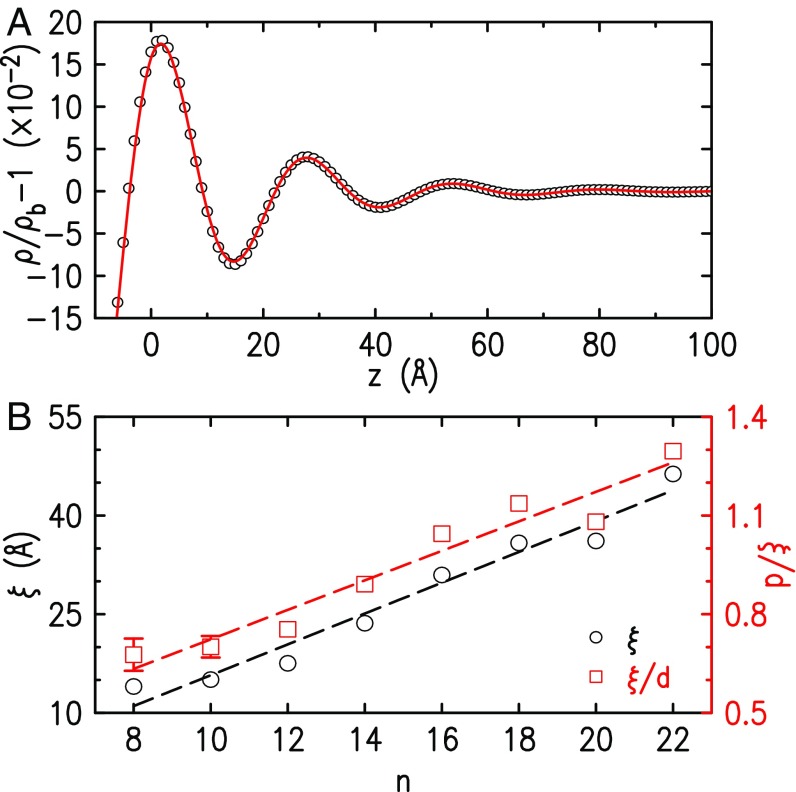
Fig. 3.

(A) The XR-derived EDP of $n=12$ (symbols), and fit (line) by a decaying cosine. (B) The EDP-fit-derived decay lengths, without ($\xi$, black) and with ($\xi /d$, red) normalization to the layering period $d$, for varying chain length $n$. Linear fits (dashed lines) are also shown.

The layer spacing $d$ in Fig. 2A increases linearly with $n$ from $\sim 20$ Å ($n=8$) to $\sim 35$ Å ($n=22$). All values obtained for $d$ are larger than the calculated extended lengths of the cations’ alkyl tails (46, 47), $l_n=1.27\times (n-1)+1.5$ Å, even with the $\sim 5$-Å headgroup size (38, 48) subtracted (Fig. 2B). Also, they are all significantly smaller than $2l_n+5$ Å. Thus, the $d$ values are too large to correspond to molecular monolayers even if comprising surface-normal-aligned, extended alkyl chains, and too small to correspond to bilayers with fully extended chains. They are, however, consistent with the two models used in the literature to account for the structure of the segregated alkyl chains’ domains in the bulk: a bilayer consisting of flexible, partly interdigitated, and/or tilted chains (6–8) and a layer comprising LL chains (49–51). We further discuss these points and the two models in Discussion.

The density enrichment of the surface’s air side, normalized to the bulk density, ${\rho }_a/{\rho }_b$ (Eq. S2), is plotted in Fig. 2C. For $n\le 6$, the $R/R_F$ fits did not require the additional Gaussian, indicating enrichment below our resolution. The excess density may be due to molecules crowding into the topmost molecular layer, or an enhanced number of chains on the air side, a possibility suggested by the $n$-increasing trend. This could occur if the balance of an equal number of down- and up-pointing chains in a subsurface cation layer is offset for the topmost cation layer by the presence of the surface, causing more chains to point up into the air than down into the first alkyl slab. A qualitative support, in trend and magnitude, for this interpretation is provided by reactive ion scattering measurements (29).

To quantify trends in ${\rho }_e(z)$ of Fig. 1B, they were fitted by an exponentially decaying oscillatory function, ${\rho }_e(z)={\rho }_b+A\exp (-z/\xi )\cos [(2\pi /\widehat{d})(z+z_0)]$, yielding excellent agreement; see the example in Fig. 3A. The decay length $\xi$, and the layer-spacing-normalized $\xi /d$, are plotted in Fig. 3B. The increase in $\xi /d$ from $\sim 0.7$ at $n=8$ to $\sim 1.3$ at $n=22$ reflects an increase in the number of layers and a concomitant reduction of the surface entropy, demonstrating the $n$-increasing dominance of the chain-segregating vdW interaction. This conclusion agrees with the conclusion of bulk RTIL vaporization enthalpy studies (43, 52, 53), where the increase in the enthalpy with $n$ is fully due to the increase in the vdW contribution. The Coulomb contribution remains constant, or even decreases slightly, rendering the vdW contribution at large $n$ twice or more larger than the Coulomb one (52–54). Simulation-based cohesive energy calculations (55) also support these results. The lower $\xi /d=0.8$, and hence the reduced surface order, found for the liquid–air interfacial layering of [C₁₈mim][FAP] (17), compared with our [C₁₈mim][NTf₂]’s $\xi /d\approx 1.1$, can be assigned to the bulkier [FAP]⁻ anion. Indeed, molecular dynamics simulations (56) found the [FAP]⁻ anion to disrupt interfacial order significantly more than smaller, quasi-linear anions like our [NTf₂]⁻.

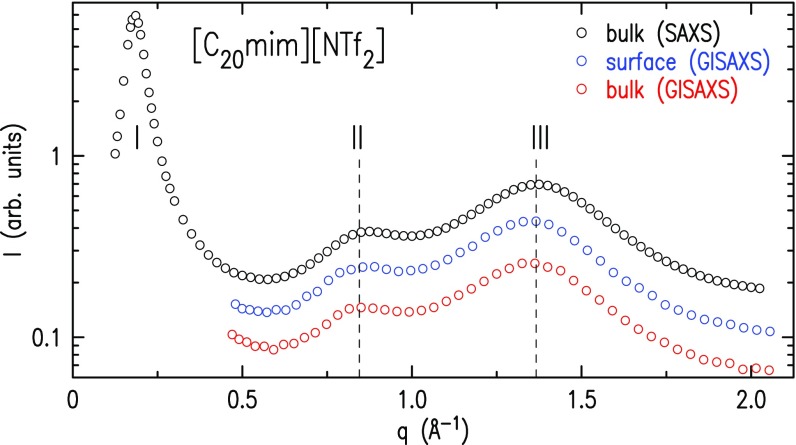
For further insight, the bulk and surface X-ray scattering are compared in Fig. 4. The signature of the RTILs’ supramolecular bulk nanostructure in transmission-mode SAXS is peaks I and II, appearing at scattering vectors $q$ smaller than that of the main liquid peak III. Only peak III is observed in a SAXS pattern of a nanoscale-uniform simple liquid (13). Peak I is assigned to the nanoscale segregation of the alkyl chains, thus separating the headgroups longitudinally by the $n$-increasing lengths shown as $\mathrm{\square }$ and $\mathrm{△}$ in Fig. 2A. As discussed above, these lengths agree well with the surface-layering periods $d$ ($○$). The other peaks arise from headgroup–headgroup (II) and intramolecular and chain–chain (III) correlations. Both include contributions from additional correlations (57), with those to II being more minor and those to III being more substantial (13).

Fig. 4.

The bulk X-ray scattering patterns for $n=20$ in the transmission (SAXS) (black) and grazing incidence (GISAXS) (red) modes are in excellent agreement with each other and with the pattern measured for the surface layers (blue). The agreement supports the same structural motif at the bulk and the surface. The two lowest-$q$ peaks, I and II, are the signatures of nanostructure due to alkyl chain segregation. Peak III is the usual liquid ring peak, the only one observed in this $q$ range for simple, nanoscale-uniform liquids. For a discussion, see Results.

Fig. 4 also shows reflection-mode GISAXS measurements (see Supporting Information) of the same RTIL, with the beam impinging on the interface at an angle $\alpha$ above (red) or below (blue) the critical angle for total external reflection, ${\alpha }_c={0.057}^{\circ }$ (35). For $\alpha >{\alpha }_c$, the X-rays penetrate to a macroscopic depth $z$ below the surface, thus sampling the bulk. The resultant GISAXS pattern (red symbols) is identical to the transmission-mode SAXS pattern (black symbols), as the figure demonstrates. For $\alpha <{\alpha }_c$, the X-rays penetrate to $\sim 70$ Å only (35) (see Supporting Information), and thus sample predominantly the layered surface region. The close match of the GISAXS pattern for this case (blue symbols) with those of the bulk in both scattering geometries (black and red symbols) clearly demonstrates that the lateral structure of the surface layers matches closely that of the nanostructured bulk. Further, the bulk’s low-$q$ SAXS peak I discernibly appears first for $n\approx 5\text{to}6$ (8, 57), in good agreement with the emergence of surface layering at $n=6\pm 2$, observed here. This $n$ seems therefore to be the minimum required for a vdW interaction strong enough to drive the segregation of the polar and apolar moieties into separate domains.

Discussion

Chain Packing in the Apolar Layer.

The XR results (see Results) resolve the surface-normal structure of our RTILs as alternating layers of polar headgroups and apolar alkyl chains. GISAXS measurements can, in principle, determine surface-parallel structure (35). In practice, however, the broad, overlapping, GISAXS peaks in Fig. 4 cannot support the type of atomic resolution structure determination provided by crystallographic methods for crystalline RTILs (38, 58–62). Still, the excellent correspondence between the surface GISAXS and the bulk SAXS patterns in Fig. 4 suggests that the lateral surface structure and, specifically, the chain packing in the alkyl layer are very similar to those of the nanosegregated bulk domains. The two literature models (6–8, 49–51) for this packing are shown as cartoons in Fig. 5: Fig. 5A, comprising flexible, kinked, partly overlapping interdigitated chains (IC), and Fig. 5B where the alkyl layer is LL and has a uniform density close to that of bulk liquid alkanes. We now discuss these in more detail.

Fig. 5.

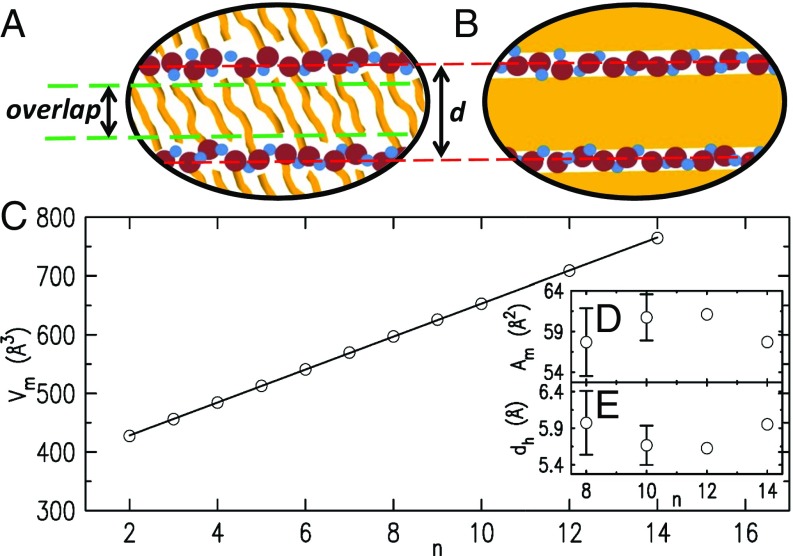
(A and B) Cartoons of the alkyl slab structure for (A) the IC model, comprising flexible ICs, and (B) the LL model, comprising a LL alkyl layer. Brown and blue circles, yellow flexible rods, and yellow areas represent, respectively, cation headgroups, anions, alkyl chains, and LL alkyl domains. (C–E) The density-based analysis. (C) The RTILs’ molecular volumes $V_m$ (symbols) as calculated from the RTILs’ mass densities ${\rho }_m$, and their linear fit (line). Note the excellent agreement for all $n$. (D) Calculated molecular areas $A_m$. (E) Calculated headgroup heights $d_h$. For discussion, see text.

The IC model, proposed originally for alcohols (63, 64) and adopted in numerous RTIL studies (6–8, 17, 49, 60, 65), proceeds from the RTILs’ crystalline bulk structure of alternating polar and alkyl planar layers, with the latter comprising fully extended, rigid, close-packed interdigitated chains (ICs) (3, 38, 58, 60, 62). The resultant long-range positional order yields a rich diffraction pattern allowing a full atomic resolution crystallographic refinement (38, 62). Melting reduces this long-range order to a short-range one, broadening the diffraction peaks and rendering them highly overlapping (6, 7). However, the longitudinal packing of alternating polar and alkyl layers is preserved, as shown by the persistence of the corresponding (001) crystal peak, albeit broadened, as peak I in Fig. 4. The close $q$ positions of these crystalline and liquid peaks (6, 62, 66, 67) suggest that no major reordering of the molecules occurs. This conclusion is supported by studies showing that, in alkanes (46, 68), the persistence length of the chain’s trans segments is still five methylenes long many tens of degrees above melting (46, 68). Thus, while melting clearly destroys the fully extended, rigid, all-trans conformation of the chains by introducing gauche defects, the interdigitation motif may largely survive in the RTILs’ liquid phase as well, similar to that found in molten alcohols (63, 64). The facts that the layer spacing $d$ for all $n\ge 8$ is intermediate between $l_n+5$ Å and $2l_n+5$ Å, that, in the bulk, it increases with $n$ by more than the projected C–C bond length, 1.27 Å/CH₂, but by less than $2\times 1.27$ Å/CH₂ (6, 7), and that it decreases with increasing temperature despite the overall volume expansion (17, 39) are taken, in this approach, as support for chain interdigitation.

The LL model originated in biological membranes (69), and has been used for RTILs (49–51) and organic photovoltaic thin films (70). It uses the measured (71) mass densities, ${\rho }_m$, available for [C_nmim][NTf₂] of $2\le n\le 14$, the molecular weights, $MW$, and Avogadro’s number, $N_A$, to calculate the molecular volumes $V_m=MW/({\rho }_m{N}_A)$. As shown in Fig. 5C, $V_m$ exhibits a perfect linear $n$ dependence over the full $n$ range, the slope of which is the volume per CH₂ moiety, $V_{C{H}_2}^{RTIL}$. Liquid alkanes (46) also exhibit a linear $n$ dependence for the alkanes’ molecular volumes, yielding $V_{C{H}_2}^{Alkane}$ as the slope, and $V_{C{H}_3}^{Alkane}$ as half the intercept when plotted against ($n-2$). $V_{C{H}_2}^{RTIL}$ and $V_{C{H}_3}^{Alkane}$ allow calculating the RTILs’ headgroup volume $V_{head}^{RTIL}=V_m-[(n-1)\times V_{C{H}_2}^{RTIL}$+$V_{C{H}_3}^{Alkane}]$. This simple analysis (49–51) yields two important results. First, the obtained $V_{C{H}_2}^{RTIL}=28.09\pm 0.05$ ų is about 4% higher than $V_{C{H}_2}^{Alkane}=27.01\pm 0.05$ ų. This near-coincidence supports the conclusion that the bulk alkyl domains, and the surface alkyl layers, consist of a uniform liquid similar to molten alkanes. Second, $n$-independence of the obtained $V_{head}^{RTIL}=344.3\pm 0.6$ ų, as expected, further supports the LL model. Also, the surface-bulk similarity discussed above yields the area per molecule at the surface, $A_m=2\times V_m/d$, for $n=8\text{to}14$ where experimental values are available for both bulk $V_m$ and surface $d$. The average of the $A_m$ values (Fig. 5D), $A_m=59.3\pm 1.6$ Ų, is threefold larger than the $\sim 20$ Ų of closely packed fully extended alkyl chains (72). This accounts, within the LL model, for the observed $\text{d}d/\text{d}n=1.14$ Å/CH₂, a value even lower than the 1.27 Å/CH₂ slope of the $l_n$ line in Fig. 2A. The common $A_m$ of the headgroup and chain yields also the headgroup’s height $d_h=(d/2)\times (V_{head}^{RTIL}/V_m)$ (Fig. 5E). The average $d_h=5.75\pm 0.16$ Å agrees with, although it is slightly larger than, the $\sim 5$ Å literature value (38, 48), further supporting the LL model.

Our results are consistent with both models, albeit with caveats. The IC model lacks an unambiguous signature in the X-ray and neutron scattering studies uniquely assignable to chain interdigitation. The LL model infers a particular, nanoscale-uniform, alkyl slab structure from macroscopic mass densities, while many different nanoscale-modulated structures may average to the same macroscopic ${\rho }_m$. We note, however, that the models are not necessarily contradictory, as long as the average density of the interdigitated model remains close to that of the alkanes’ bulk density. Further study is clearly required.

Evolution Trends.

As Fig. 2A shows, the $d$ values start between the $2l_n+5$ Å and the $l_n+5$ Å lines at $n=8$ but increasingly approach the $l_n+5$ Å line with increasing $n$. Within the IC model with fully extended, layer-normal chains, a $2l_n+5$ Å layer spacing implies a bilayer structure with zero chain overlap, while an $l_n+5$ Å spacing implies a monolayer with full chain overlap. The overlap, in this case, is $p_n=2l_n-(d-5)$. Taking the derivative of this expression and using the observed $\text{d}d/\text{d}n=1.14$ Å/CH₂ and the canonical $\text{d}{l}_n/\text{d}n=1.27$ Å/CH₂ yields an overlap which increases by $\text{d}{p}_n/\text{d}n=1.4$ Å/CH₂, slightly more than a single methyl, upon a unity increase of $n$. In practice, however, the chains in the IC model are not extended, but kinked, and have (unknown) effective lengths ${\widehat{l}}_n<l_n$. Necessarily, therefore, $\text{d}{p}_n/\text{d}n<1.4$ Å/CH₂, although a quantitative estimate must await the availability of ${\widehat{l}}_n$ values. We note, however, that the increase of the overlap with $n$ is energetically favorable, since it increases adjacent chains contacts and thus their vdW interaction.

Another important trend is reflected in the linear $\xi$ fit in Fig. 3B. The fit yields a slope $\text{d}\xi /\text{d}n=2.35\pm 0.19$ Å/CH₂. This value agrees within error with 2 $\times$ 1.27 Å/CH₂, the combined lengths of the two methylenes added to the alkyl layer upon increasing $n$ by unity. The $\text{d}\xi /\text{d}n$ parallels therefore the expected increase in the vdW interaction due to the added methylenes, implying that the layering range is determined by that interaction, with negligible contribution from interactions between the polar headgroups’ layers. This, in turn, suggests that the anomalously negative thermal expansion coefficients found for the surface $d$ of [C₁₈mim][FAP] (17), and for the bulk $d_I$ of $n=18$ and $n=22$ (39), originate in the alkyl layer, not in the interaction between the polar headgroups’ layers. Finally, we also note that, since $d$ increases with $n$ with a much smaller slope than $\xi$, $\xi /d$ still increases, reaching values of $\gtrsim 1$ for $n\ge 18$.

Bulk–Surface Order Relations.

The RTIL–air surface structure resolved here impacts also the important question of the correspondence between bulk and surface structure in liquids in general. For the small, symmetric, and monoatomic molecules of liquid metals, the layered surface structure found was demonstrated to be dominated by bulk correlations, exhibiting identical spacings and order decay lengths (35, 41). Simulations predict that this may be an intrinsic general property of all simple liquids below $\sim 10\text{to}\hspace{0.17em}20$% of their critical temperature, provided that they remain liquid (73, 74). Indeed, medium-size, roughly spherical organic molecules were found to exhibit surface layering with characteristics following their bulk correlations (75, 76). In contrast, for larger, asymmetric, molecules, surface-induced effects may dominate over the intrinsic bulk correlations and yield a surface ordering significantly different from the bulk’s. Examples are liquid crystals, exhibiting smectic surface phases on isotropic or nematic bulk (77, 78), and surface freezing of alkanes, and related molecules, where a crystalline monolayer or bilayer forms at the liquid melt’s surface (47). In particular, the elongated shape and combination of mainly polar and vdW interactions of liquid crystals are very similar to those of the RTILs, although they lack the RTILs’ ionic composition. Despite this similarity, which should yield in RTILs a surface phase different from the bulk, as occurs in liquid crystals, our $n\le 20$ RTILs exhibit a surface phase that practically coincides with that of the bulk (2, 3, 6–8). Intriguingly, however, for $n=22$, we find a transition to the behavior observed for long, asymmetric, molecules, namely, a distinct surface phase different from the bulk. This transition is clearly driven by the increasing dominance of the vdW interaction upon chain length increase. Both the new surface phase of $n=22$, tentatively identified as a liquid crystal, and the transition in the relation of the bulk and surface structures clearly call for further study.

Summary and Conclusions

We present here a first systematic study of the evolution of the liquid–air interface structure with increasing cation chain length for a broad homologous series of RTILs, [C_nmim]⁺[NTf₂]⁻, $n=4\text{to}\hspace{0.17em}22$. The angstrom-resolution X-ray measurements reveal, in detail, the progress of the EDP from a simple-liquid-like one for $n<6$, through a layered one for $8<n<20$, to a liquid-crystal surface phase for $n=22$ which reverts to a “conventional” layered surface phase at high temperatures. The layered phase consists of alternating charged and apolar surface-parallel slabs, the former comprising cation headgroups and anions, and the latter comprising alkyl chains. The layer spacing $d$ was found to be larger than the extended length of the cation’s alkyl chain but smaller than twice that length. This implies a bilayer-like packing of molecules within the layer. The $d$ exhibits a good quantitative agreement with the correlation distance of the bulk’s nanoscale structure, obtained from the bulk SAXS prepeak I positions (7). The surface layer spacing $d$ increases linearly with $n$, with a slope of 1.14 Å/CH₂, which is smaller than the 1.27 Å/CH₂ projected length of a C–C bond.

The lateral chain packing within the alkyl slab is discussed here within two models. The first, based on a close correspondence of the surface structure with the SAXS-determined nanostructure of the bulk (6–8, 17, 49, 60, 65), suggests the alkyl slab to consist of flexible, kinked, partially overlapping, interdigitated chains. The second, using macroscopic mass densities (49, 70), shows that the mass densities of the alkyl slab and bulk liquid alkane are within $\sim 4$% of each other, and thus suggests the alkyl slab to be liquid-like. Our results are consistent with both, indicating need for further studies.

We also discuss the trends in the derived quantities, showing, within the IC model, an increase in the chain overlap with increasing $n$, as well as a full domination of the layering decay length by the vdW interaction within the apolar layers. Also discussed are the broader implications of our results for the bulk–surface structure relations in our RTILs and in liquids in general.

Future X-ray measurements of the temperature evolution (24) of the surface structure of the present homologous RTIL series may shed more light on the issues discussed here, in particular the chain packing in the apolar domains. As found for [C₁₈mim][FAP] (17), we expect that $d$ for [C_nmim][NTf₂] contracts with increasing temperature at a similar $n$. However, the temperature slope should be stronger, and $\xi /d$ versus T should decrease more slowly, since here the vdW interaction seems more dominant than for [C₁₈mim][FAP]. This anomalous contraction should be, however, of a limited $n$ range. For large $n$, the limit in the IC model will be set by the achievement of a full IC overlap, above which normal thermal expansion should be recovered. For small $n$, the increasing dominance of the headgroups’ electrostatic interaction should also dominate the expansion. We speculate therefore that the slopes of $d$ versus T should be found to be maximally negative for some $n_c$ of order 18 to 20, and become increasingly less negative, and eventually positive, as $n$ deviates up, or down, from this $n_c$. Whether or not these speculations will be validated by experiment, the thermal behavior should provide important clues for the structure and underlying interactions of the surface layering.

The application of the present X-ray methods to the surfaces of binary mixtures of different-$n$ members of our homologous RTIL series should also be illuminating, particularly in comparison with the growing body of bulk (79, 80) and surface (81) studies on RTIL mixtures. Tuning the chain length difference in mixtures could drive the system from homogeneity to phase separation, induce different bulk and surface phases, and nucleate surface phases having no bulk counterparts, as found in other systems (82, 83). Finally, quantitative theoretical studies elucidating, for example, the roles of the various interactions and molecular conformations in the surface structure and its $n$ evolution, and other related issues, are also much desired.

Materials and Methods

Samples and Cell.

The homologous RTIL series 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([C_nmim]⁺[NTf₂]⁻) was synthesized by Iolitec, with purities of $>98$% ($>95$% for $n=20$ and $n=22$), and water contents of $<70$ ppm. All liquid samples ($n<14$) were dried in a vacuum oven at 70 °C to 80 °C for periods of 8 h to 24 h before use.

Samples were contained in a shallow machined PCTFE tray 45 mm long and $\sim 1$ mm deep, placed in a hermetically sealed, temperature-controlled (to ≤0.05°C) cell allowing measurements at temperatures of 0 °C to 150 °C. Possible beam damage was monitored by comparing repeated scans at the same position with that at a fresh spot. To minimize possible water vapor adsorption at the sample’s surface, particularly for the small-$n$, less-hydrophobic RTILs, hermetic cell sealing was used. Repeated measurements over a long time scale did not show changes attributable to adsorbed water layer buildup at the surface. No evidence for water adsorption was found upon comparing measurements done under sealed air-filled cell and under dry helium flow. The measurements presented here were done at RT, or, for higher-melting RTILs ($n\ge 14$), on melts above RT (see Supporting Information for melting temperatures). The measurement temperatures are listed in Fig. 1A.

X-Ray Measurements.

The surface-normal and surface-parallel structures were measured by XR and GISAXS, respectively. The liquid–surface diffractometers (84–86) high-energy microdiffraction (HEMD) at ID15A and ID10 [European Synchrotron Radiation Facility (ESRF)], liquid interfaces scattering apparatus (LISA) [P08, PETRA III; Deutsches Elektronen-Synchrotron (DESY)], and 9ID [advanced photon source (APS)] were used, with X-ray wavelengths $\lambda =0.1771$, 0.5586, 0.4958, and 0.9202 Å, respectively. The surface-normal EDP ${\rho }_e(z)$ is extracted from the measured XR curves by fits of a mathematical model to the measured data (35, 87). Transmission-mode SAXS from the bulk was carried out at ID15B (ESRF) for $n=20$; see Supporting Information for details.

Note Added in Proof.

A study of the liquid crystalline surface phase of [C₂₂mim][NTf₂] has now been published by Mars et al. (88).