Abrupt change of the superconducting gap structure at the nematic critical point in FeSe_1−xS_x

Significance

Electronic nematicity that spontaneously breaks the rotational symmetry of the underlying crystal lattice has been a growing issue in high-temperature superconductivity of iron pnictides/chalcogenides and cuprates. FeSe_{1 − x}S_x, in which the nematicity can be tuned by isoelectronic sulfur substitution, offers a fascinating opportunity to clarify the direct relationship between the nematicity and superconductivity. Here, we discover a dramatic change in the superconducting gap structure at the critical concentration of sulfur where the nematicity disappears, i.e., nematic critical point. Our observation provides direct evidence that the orbital-dependent nature of the critical nematic fluctuations has a strong impact on the superconducting pairing interaction.

Abstract

The emergence of the nematic electronic state that breaks rotational symmetry is one of the most fascinating properties of the iron-based superconductors, and has relevance to cuprates as well. FeSe has a unique ground state in which superconductivity coexists with a nematic order without long-range magnetic ordering, providing a significant opportunity to investigate the role of nematicity in the superconducting pairing interaction. Here, to reveal how the superconducting gap evolves with nematicity, we measure the thermal conductivity and specific heat of FeSe_{1 − x}S_x, in which the nematicity is suppressed by isoelectronic sulfur substitution and a nematic critical point (NCP) appears at $x_c\approx 0.17$. We find that, in the whole nematic regime ($0\le x\le 0.17$), the field dependence of two quantities consistently shows two-gap behavior; one gap is small but highly anisotropic with deep minima or line nodes, and the other is larger and more isotropic. In stark contrast, in the tetragonal regime ($x=0.20$), the larger gap becomes strongly anisotropic, demonstrating an abrupt change in the superconducting gap structure at the NCP. Near the NCP, charge fluctuations of $d_{xz}$ and $d_{yz}$ orbitals are enhanced equally in the tetragonal side, whereas they develop differently in the orthorhombic side. Our observation therefore directly implies that the orbital-dependent nature of the nematic fluctuations has a strong impact on the superconducting gap structure and hence on the pairing interaction.

Spin fluctuations are widely discussed as a primary driving force of various unconventional superconductors, whereas, in iron-based superconductors, spin and orbital degrees of freedoms are closely intertwined because of the multiple $d$-orbital characters at the Fermi level (1, 2). In most iron-based superconductors, tetragonal–orthorhombic structural (nematic) and magnetic transition lines follow closely each other. These orders have been suggested to play crucial roles in superconductivity, and thus strong spin and/or orbital fluctuations have been proposed to mediate the pairing (3–5). However, despite tremendous efforts in the past years, elucidating the exact pairing mechanism still remains a great challenge.

The iron chalcogenide superconductor FeSe (6), comprised only an Fe-Se layer, offers a novel platform to investigate the pairing mechanism of iron-based superconductors, because it displays several remarkable properties. The superconducting transition temperature of $T_c\approx 9$ K dramatically increases up to 38 K by the application of hydrostatic pressure (7). The superconductivity at ambient pressure coexists with a nematic order, whose properties are distinctly different from the other iron-based superconductors. The nematic transition occurs at $T_s\approx 90$ K, which is accompanied by the energy splitting of the Fe $d$ orbits (8–13). Although $T_s$ is comparable to other iron-based superconductors, no sizable low-energy spin fluctuations are observed above $T_s$ and no long-range magnetic order occurs below $T_s$ at ambient pressure (14–17). These results have raised questions regarding the spin fluctuation scenario envisaged in other iron-based superconductors. Although there is an argument that the magnetic fluctuation mechanism is still applicable (18–20), an alternative scenario where fluctuations stemming from orbital degree of freedom play a primary role has aroused great interest (16, 17, 21–23).

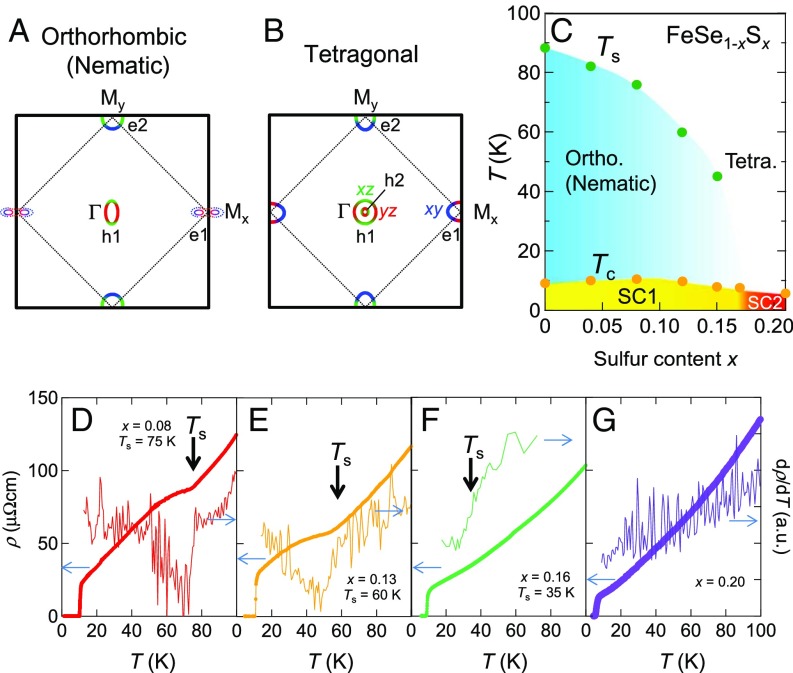
As shown in Fig. 1A, the Fermi surface in the nematic phase consists of an elliptical hole pocket at the Brillouin zone center (h1), elongated along the $\mathrm{\Gamma }$–$M_y$ line, and compensated electron pockets near the zone boundary (e1 and e2) (23). It has been reported that the e1 pocket is divided into two Dirac-like electrons in the presence of large orbital splitting (24–26), although the detailed structure of the Fermi surface is still controversial (8–13, 27, 28). The size of all of the pockets is extremely small, occupying only 1 to 3% of the whole Brillouin zone (29–31). Since the superconducting gap structure is intimately related to the pairing interaction, its elucidation is crucially important. The superconducting gap of FeSe has been reported to be highly anisotropic with deep minima or line nodes (31–33).

Fig. 1.

(A and B) Schematic illustrations of the Fermi surface in the nematic and the tetragonal phases (23). Green, red, and blue areas represent the Fermi surface regimes dominated by $d_{xz}$, $d_{yz}$, and $d_{xy}$ orbital characters, respectively. (C) $T$–$x$ phase diagram of FeSe_{1 − x}S_x. (D–G) Temperature dependence of resistivity (thick lines) and its temperature derivative (thin lines) for single crystals of FeSe_{1 − x}S_x for (D) $x=0.08$, (E) x = 0.13, (F) x = 0.16, and (G) x = 0.20. Thick arrows indicate the nematic transition temperatures.

The large anisotropy of the superconducting gap in FeSe is highly unusual because it directly implies that the pairing interaction strongly depends on the position of a tiny Fermi surface. However, the relationship between the nematicity and pairing interaction remains largely elusive. To tackle this key issue, it is of primary importance to clarify how the nematicity affects the superconducting gap structure. Isoelectronic sulfur substitution in FeSe provides the most suitable route to study this issue. In the series of FeSe_{1 − x}S_x, the density of states at the Fermi level (or bandwidth) can be tuned significantly through chemical pressure, leading to a change of the electron correlation effect (34–38). Indeed, with increasing x, the nematic transition temperature is suppressed without inducing long-range magnetic order, and the system can be tuned to a nonmagnetic tetragonal regime (39), whose band structure is shown in Fig. 1B (23). The $T$ - $x$ phase diagram of FeSe_{1 − x}S_x is depicted in Fig. 1C. The elastoresistance measurements reveal that, as x is increased in the nematic regime, the nematic fluctuations are strongly enhanced with x. and, near $x_c\approx 0.17$, where $T_s$ is suppressed to zero, the nematic susceptibility diverges toward absolute zero, indicating a nematic critical point (NCP) (39). In the nematic regime, the energy splitting of $d$ orbitals is suppressed with $x$ and elliptical h1 pocket becomes more circular while keeping its volume nearly constant (36). FeSe_{1 − x}S_x, therefore, offers a fascinating opportunity to investigate the role of nematic fluctuation on superconductivity. Here we report the superconducting gap structure of FeSe_{1 − x}S_x in a wide $x$ range from the nematic to tetragonal regime, which is determined by the thermal conductivity $\kappa$ and specific heat $C$.

Results and Discussion

Fig. 1 D–G depicts the $T$ dependences of the resistivity $\rho$ and $d\rho /dT$ for $x=0.08$, 0.13, 0.16, and 0.20, respectively. The nematic transition temperatures determined by the jump of $d\rho /dT$ are $T_s\approx 75$, 60, and 35 K for $x=0.08$, 0.13, and 0.16, respectively. These values are consistent with the previous report (39). At $x=0.20$, no anomaly is observed in $d\rho /dT$, indicating that the system is in the tetragonal regime. $T_c$ and upper critical field $H_{c2}$ for $x=0.20$ are rapidly suppressed from those in the nematic regime.

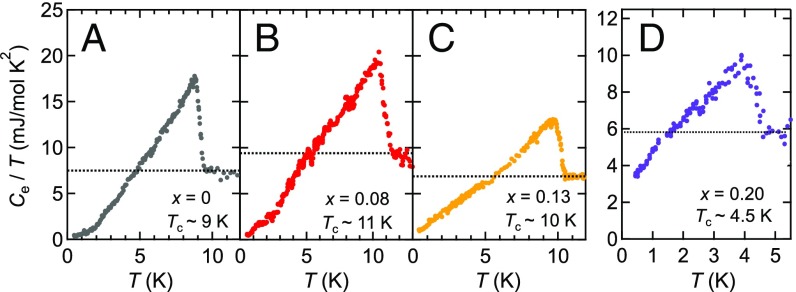
Fig. 2 shows the $T$ dependences of the electronic component of specific heat divided by temperature, $C_e/T$, for $x=0$, 0.08, 0.13, and 0.20, respectively. We obtained $C_e$ by subtracting the change of $C_n$(${\mu }_{0}H=14$ T) in the normal state from the value at $T_c$, $C_e=C(T)-\mathrm{\Delta }{C}_n$, and $\mathrm{\Delta }{C}_n=C_n(T)-\gamma T_c$. For $x=0$, 0.08, 0.13, and 0.20, the values of ${\mu }_0{H}_{c2}$ are ∼16, 20, 18, and 3 T, respectively. Since ${\mu }_0{H}_{c2}(T)$ in the nematic regime exceeds the maximum field of our experimental setup, 14 T, at low temperatures, $C_n(T)$ below $T_c(14\text{T})$ is estimated by extrapolating a curve obtained by the fitting of $C$ above $T_c$ with $C_n(T)=\gamma T+\beta T^3+A_5{T}^5$. At $T_c$, $C_e/T$ exhibits a sharp jump for all $x$, showing good homogeneity of S substitution. The Sommerfeld coefficient $\gamma$ is 7 mJ/mol$\cdot$K² to 9 mJ/mol⋅K² for all crystals in the nematic regime, suggesting that the electron correlation is little influenced by S substitution. The ratio of specific heat jump and normal state-specific heat, $\mathrm{\Delta }{C}_e/\gamma T_c$ = 1.5 for $x=0$, is larger than the Bardeen–Cooper–Schrieffer (BCS) value of 1.43, while, for 0.08, 0.13, and 0.2, $\mathrm{\Delta }{C}_e/\gamma T_c=1.3$, 1.1, and 0.82, respectively, are smaller than the BCS value. This may be due to the multigap nature of the superconductivity. For $x=0.20$ in the tetragonal regime, $T_c$ determined by $C_e/T$ is slightly lower than that determined by zero resistivity. $C_e/T$ below $T_c$ shows a concave-downward curvature, which also supports the multigap superconductivity.

Fig. 2.

The electronic component of the specific heat divided by temperature, $C_e/T$, vs. $T$ in FeSe_{1 − x}S_x for (A) $x=0$, (B) x = 0.08, (C) x = 0.13, and (D) x = 0.20. Dotted horizontal lines indicate the normal state values of $C_e/T$.

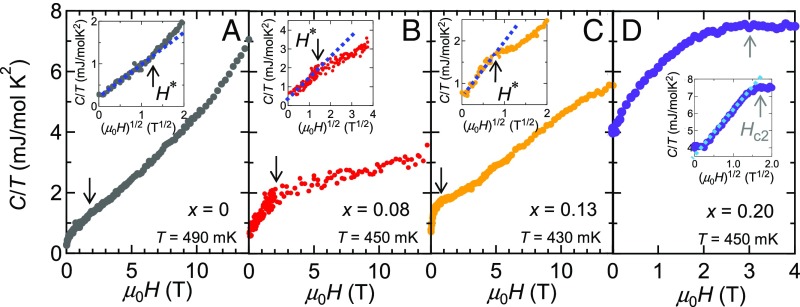
Fig. 3 shows the $H$ dependences of $C/T$ at around 450 mK for $x=0$, 0.08, 0.13, and 0.20, respectively. In conventional fully gapped superconductors, $C(H)/T$ increases linearly with $H$ due to the induced quasiparticles inside vortex cores. In stark contrast, as shown in Fig. 3, Insets, $C(H)/T$ increases with $\sqrt{H}$ for all $x$ at low fields. In superconductors with a highly anisotropic gap, the Doppler shift of the delocalized quasiparticle spectrum induces remarkable field dependence of density of states with $\sqrt{H}$ dependence for line node. For $x=0$, 0.08, and 0.13 in the nematic regime, $C(H)/T$ deviates from the $\sqrt{H}$ dependence at $H^{\ast }$, shown by arrows. For $x=0.08$ and 0.13, $C(H)/T$ exhibits a kink at $H^{\ast }$. Above $H^{\ast }$, $C(H)/T$ increases slowly as $C(H)/T\propto H^{\alpha }$ with $\alpha \gtrsim$ 1. The slight upward curvature of $C(H)/T$ above $H^{\ast }$ for $x=0$ and 0.13 is attributed to the Pauli paramagnetic effect on the superconductivity (40). The initial steep increase of $C(H)/T$ below $H^{\ast }$ indicates that a substantial portion of the quasiparticles is already restored at a magnetic field far below $H_{c2}$. The slope change at $H^{\ast }$ provides evidence for multigap superconductivity; $H^{\ast }$ is interpreted as a virtual upper critical field that determines the $H$ dependence of the smaller gap. The $\sqrt{H}$ behavior below $H^{\ast }$ indicates the presence of a Fermi pocket, whose superconducting gap is small and highly anisotropic with line node or deep minima. Moreover, $H^{\alpha }$ dependences with $\alpha \gtrsim 1$ above $H^{\ast }$ indicate the presence of another Fermi pocket, whose gap is much larger and isotropic.

Fig. 3.

Magnetic field dependence of $C/T$ for (A) $x=0$, (B) 0.08, (C) 0.13, and (D) 0.20. Insets show the same data plotted as a function of $\sqrt{{\mu }_{0}H}$. $H\text{*}$ represents a magnetic field at which $C/T$ deviates from $\sqrt{H}$ dependence. The black arrows in the main panels indicate $H\text{*}$. The gray arrow in D indicates upper critical field.

For $x=0.20$ in the tetragonal regime, $\sqrt{H}$ behavior is observed in the whole $H$ regime below $H_{c2}$, which is determined by the resistivity. As shown in Figs. 2D and 3D, large $C/T$ at $H=0$ indicates that a substantial number of quasiparticles are excited even at $T/T_c\approx 0.1$. Since entropy balance imposes ${\int }_0^{T_c}\{(C_e/T)-C_n/T_c)\}dT=0$, $C_e/T$ for $x=0.20$ is expected to decrease rapidly with decreasing $T$ below 0.4 K. Therefore, the remaining $C/T$ arises from the Fermi pockets with extremely small superconducting gaps. The $H$ dependence of $C(H)/T$ for $x=0.20$ suggests the presence of Fermi pocket(s) with very small gap and other pocket(s), whose gap is larger and highly anisotropic. These results lead us to conclude that the gap structure in the tetragonal regime is essentially different from that in the nematic regime.

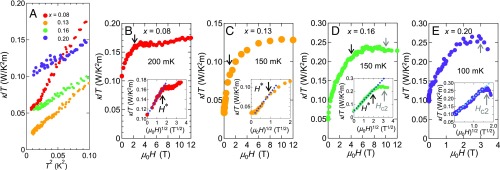
The thermal conductivity provides additional pivotal information on the superconducting gap structure, because the heat transport detects only the delocalized quasiparticles, insensitive to the localized quasiparticles. Fig. 4A depicts $\kappa /T$ plotted as a function of $T^2$ in zero field. At low temperature, $\kappa /T$ is well fitted by $\kappa /T={\kappa }_0/T+b{T}^2$, where $b$ is a constant. We confirmed that the ratio of ${\kappa }_0/T$ and the electrical conductivity ${\sigma }_0$ at $T\to 0$ above ${\mu }_0{H}_{c2}$ is $({\kappa }_0/T)/{\sigma }_0=(1.04\pm 0.02)L_0$ for $x=0.16$ and 0.20, where $L_0={\pi }^2/3(k_B/e)$ is the Lorenz number, indicating that the Wiedemann–Franz law holds. At zero field, the presence of a residual value in $\kappa /T$ at $T\to 0$, ${\kappa }_{00}/T$, indicates the presence of normal fluid, which can be attributed to the presence of line nodes in the gap function. Finite ${\kappa }_{00}/T$ is clearly resolved in $x=0.08$, 0.16, and 0.20, indicating the presence of line node. On the other hand, ${\kappa }_{00}/T$ for $x=0.13$ is much smaller or vanishes at $T\to 0$.

Fig. 4.

(A) Temperature dependence of thermal conductivity divided by $T$, $\kappa /T$, plotted as a function of $T^2$ in zero field. Magnetic field dependence of $\kappa (H)/T$ for (B) $x=$ 0.08, (C) x = 0.13, (D) x = 0.16, and (E) x = 0.20. The gray arrows indicate $H_{c2}$. Insets show $\kappa /T$ plotted as a function of $\sqrt{{\mu }_{0}H}$. $H\text{*}$ represents a magnetic field at which $\kappa (H)/T$ deviates from the $\sqrt{H}$ dependence. The black arrows in the main panels indicate $H\text{*}$.

Fig. 4 B–E depicts the $H$ dependences of $\kappa (H)/T$ for $x=0.08$, 0.13, 0.16, and 0.20. Similar to $C(H)/T$, the application of small magnetic fields causes a steep increase of $\kappa (H)/T$ for all $x$; as shown in Fig. 4 B–E, Insets, $\kappa (H)/T$ increases with $\sqrt{H}$ at low fields. Similarly to the specific heat, the $\sqrt{H}$ dependence of $\kappa (H)/T$ appears as a result of Doppler shift of quasiparticle spectra in the presence of line nodes. For $x=0.08$, 0.16, and 0.20, $\kappa (H)/T$ increases immediately when the magnetic field is applied. [We note that the lower critical field $H_{c1}$ is much smaller than the field scale of interest (34).] This $H$ dependence, along with the presence of finite ${\kappa }_{00}/T$, indicates the presence of line nodes. For $x=0.13$, on the other hand, $\kappa /T(H)$ is insensitive to $H$ at very low fields even above $H_{c1}$, suggesting that, although the gap function has a deep minimum at certain directions, it is finite, i.e., no nodes. This is consistent with very small or absent ${\kappa }_{00}/T$. As shown in Fig. 4 B–D, Insets, $\kappa (H)/T$ deviates from the $\sqrt{H}$ dependence above $H^{\ast }$ for $x=0.08$, 0.13, and 0.16. The values of $H^{\ast }$ for $x=0.08$ and 0.13 are close to the ones observed in $C(H)/T$ in Fig. 3 B and C. Above $H^{\ast }$, $\kappa (H)/T$ shows much weaker $H$ dependence than below $H^{\ast }$. In particular, $\kappa (H)/T$ is nearly $H$-independent for $x=0.08$ and 0.16. Since thermal conductivity is insensitive to localized quasiparticles inside vortices, $\kappa (H)/T$ in fully gapped superconductors is independent of $H$ except in the vicinity of $H_{c2}$. Thus the observed initial steep increase with $\sqrt{H}$ dependence, followed by much weaker $H$ dependence of $\kappa (H)/T$, provides evidence for the multigap superconductivity, in which a small gap has line nodes or deep minima and a large gap is nearly isotropic (41). This is consistent with the conclusion drawn from the specific heat. For $x=0.20$, $\kappa /T$ increases with $\sqrt{H}$ nearly up to $H_{c2}$, which is again consistent with the specific heat.

Next, we compare our results with other experimental observations. It has been reported by angle-resolved photoemission spectroscopy (ARPES) and quasiparticle interference (QPI) for $x<0.07$ that the superconducting gap of the h1 pocket is highly anisotropic, with deep minima or nodes (42, 43). Therefore, it is natural to assume that the observed $\sqrt{H}$ dependences of $C(H)/T$ and $\kappa (H)/T$ at low fields for $x<0.08$ come from the anisotropic gap of the h1 pocket. In our experiments for a wider $x$ range, this initial $\sqrt{H}$ dependence persists in the whole nematic regime. These observations suggest that the superconducting gap in the h1 pocket is always highly anisotropic in the whole nematic regime. The gap structure of the electron pockets has been less clear. In fact, no gap has been observed on the electron pockets in ARPES measurements (42). In the QPI measurements, anisotropic gap is inferred for the e1 pocket, but the gap structure of e2 pocket has not been resolved (43). However, the fact that $H^{\ast }$ is much smaller than $H_{c2}$ implies that the gap of the e2 pocket is larger than that of the h1 pocket. Moreover, $H$ dependences of $C/T$ and $\kappa /T$ above $H^{\ast }$ suggest that the gap of the e2 pocket is much more isotropic than that of the h1 pocket. It should be stressed that the line nodes in the h1 pocket are accidental, not symmetry-protected, because, as directly revealed by the scanning tunneling microscopy measurements, the nodes are lifted near the twin boundaries (44). Moreover, the presence of line nodes has been reported by thermal conductivity measurements on some crystals for $x=0$ (31), while a small but finite gap has been observed in different crystals (33), which may be attributed to the difference in the amount of impurities and twin boundaries.

Since the elliptical h1 pocket becomes more circular with increasing $x$, the highly anisotropic gap in the h1 pocket in the whole nematic regime implies that the anisotropic pairing interaction is little influenced by the elliptical distortion of the h1 pocket. This immediately excludes the possibility of the intraband pairing, in which the superconductivity is mediated by fluctuations with very small momentum. This is because, in such a case, the gap anisotropy should be sensitive to the shape of the Fermi surface. As displayed by the green area in the h1 pocket in Fig. 1A, the gap node/minimum locates at the area dominated by $d_{xz}$ orbital character for $x=0$ and 0.07 (42, 43) To explain such a highly anisotropic gap in a tiny Fermi pocket, a pairing interaction which is strongly orbital dependent has been proposed (26, 45). In this scenario, the gap minimum/node appears as a result of the strong nesting properties of $d_{yz}$ orbit area, shown by red in Fig. 1A, between the h1 and e1 pockets. Since the pairing interaction is dominated by $d_{yz}$ orbital, the gap minimum/node can appear in the area with $d_{xz}$ orbital character in the h1 pocket. In fact, strong nesting properties between $d_{yz}$ orbitals has been discussed in BaFe₂As₂ with stripe-type magnetic order.

Although the detailed superconducting gap structure in the tetragonal regime requires further investigation, the present results reveal a dramatic change in the gap function across the NCP (Fig. 1C, SC1 and SC2). Near the NCP, charge fluctuations of $d_{xz}$ and $d_{yz}$ orbitals are enhanced equally in the tetragonal side. On the other hand, they develop differently in the orthorhombic side. Thus, the nature of the nematic charge fluctuations drastically changes at the NCP. In the tetragonal phase ($x>x_c$), strong charge fluctuations of $d_{xz}$ and $d_{yz}$ orbitals develop near $x=x_c$, due to the Aslamazov–Larkin vertex correction (22, 23). In the orthorhombic phase ($x<x_c$), the orbital splitting $\mathrm{\Delta }E=E_{yz}-E_{xz}$ increases rapidly in proportion to ${(x_c-x)}^{1/2}$, by which the ferro-nematic fluctuations are suppressed. At the same time, the emergence of $\mathrm{\Delta }E$ causes a large imbalance of charge fluctuations between $d_{xz}$ and $d_{yz}$ orbitals, reflecting the improvement of the $d_{yz}$ orbital nesting condition with $\mathrm{\Delta }E>0$ (26). Such a change in the orbital fluctuations gives rise to the abrupt change of the superconducting gap structure at $x=x_c$, which may also be relevant to the change of $T_c$ at $x_c$. The present results therefore strongly indicate that the orbital selectivity of the nematic fluctuations plays an essential role for the superconductivity of FeSe. Intriguingly, a nodal superconducting state has also been reported in tetragonal FeS (46, 47). We also note that a possible $d_{x^2-y^2}$ pairing is proposed based on spin fluctuation theory (48). Pinning down the position of nodes and effect of orbital fluctuations in this end material would provide further clues to elucidate the pairing mechanism in iron-based superconductors.

In summary, the thermal conductivity and specific heat measurements on FeSe_{1 − x}S_x in a wide $x$ range provide bulk evidence for the presence of deep minima or line nodes in the superconducting gap function in both the whole nematic and tetragonal regimes. Moreover, the multigap nature of the superconductivity is commonly observed in both regimes. These results imply that the pairing interaction is significantly anisotropic in both the nematic and tetragonal regimes. We find that the gap structure dramatically changes when crossing the NCP. This demonstrates that the orbital-dependent nature of the nematic fluctuations has a strong impact on the superconducting pairing interaction, which should provide a clue to understanding a pairing mechanism of highly unusual superconductivity in FeSe.

Materials and Methods

Single crystals of FeSe_{1 − x}S_x ($x=0$, 0.08, 0.13, 0.16, and 0.20) were grown by chemical vapor transport technique (39, 49). Observation of quantum oscillations, even in the heavily substituted sample with $x=0.2$ (50), the nearly 100% Meissner signal, and the sharp jump in specific heat all demonstrate the high quality of the samples. Specific heat was measured for $x=0$, 0.08, 0.13, and 0.20 by the quasi-adiabatic method in ³He cryostat. The thermal conductivity was measured on crystals with the same $x$ values by the standard steady-state method by applying the thermal current in the 2D plane in a dilution refrigerator. In addition to these crystals, we measured $\kappa$ for $x=0.16$ in the vicinity of NCP. Since the physical properties of the crystals near NCP are sensitive to the inhomogeneous distribution of sulfur, we carefully selected a tiny crystal with a sharp superconducting transition. For both $C$ and $\kappa$ measurements, we applied a magnetic field perpendicular to the 2D plane (H $\parallel c$).