Significance
Optical tweezers enable scientists to follow the dynamics of molecular motors at high resolution. The ability to discern a motor’s discrete steps reveals important insights on its operation. Some motors operate at the scale of angstroms, rendering the observation of their steps extremely challenging. In some cases, such small steps have been observed sporadically; however, the full molecular trajectories of steps and intervals between steps remain elusive due to instrumental noise. Here, we eliminate the main source of noise of most high-resolution dual-trap optical tweezers and developed both a single-molecule assay and a self-learning algorithm to uncover the full trajectories of such a motor: RNA polymerase. Using this method, a whole new set of experiments becomes possible.
Keywords: optical tweezers, transcription, single molecule, step-finding
Abstract
In recent years, highly stable optical tweezers systems have enabled the characterization of the dynamics of molecular motors at very high resolution. However, the motion of many motors with angstrom-scale dynamics cannot be consistently resolved due to poor signal-to-noise ratio. Using an acousto-optic deflector to generate a “time-shared” dual-optical trap, we decreased low-frequency noise by more than one order of magnitude compared with conventional dual-trap optical tweezers. Using this instrument, we implemented a protocol that synthesizes single base-pair trajectories, which are used to test a Large State Space Hidden Markov Model algorithm to recover their individual steps. We then used this algorithm on real transcription data obtained in the same instrument to fully uncover the molecular trajectories of Escherichia coli RNA polymerase. We applied this procedure to reveal the effect of pyrophosphate on the distribution of dwell times between consecutive polymerase steps.
Proteins involved in a wide array of cellular functions are able to convert chemical energy into mechanical motion, thus functioning as molecular motors (1). A comprehensive description of the dynamics of such motors requires following their position with sufficient spatiotemporal resolution to determine their molecular trajectory. The trajectories of all motors described to date consist of alternating stationary periods (known as “dwells”) and translocation events (known as “bursts”). From these trajectories, we can extract fundamental parameters of a motor’s dynamic operation, such as the distribution of its step sizes and dwell times; these parameters, in turn, provide crucial insight into the mechanochemical coupling underlying the motor’s operation. For motors, such as dynein, that take steps with variable sizes (2), characterization of the molecular trajectory reveals how the motor adapts its step size to the conditions under which it operates (external load, ATP concentration, crowded environment, etc.). Conversely, knowledge of the dwell time distribution can, for example, shed light on the coordination mechanism in multisubunit motors (3–8).
Optical trapping can be used to characterize molecular motor dynamics with high precision over biologically relevant times, distances, and forces. The molecular trajectories of motors that take relatively large steps (such as kinesin, which takes 8-nm steps on microtubules) are now regularly accessed in many laboratories. However, the ability to reliably and routinely resolve the molecular trajectories (including all steps and interstep dwell times) of many nucleic acid-associated motors (e.g., DNA and RNA polymerases, helicases, dsDNA translocases, etc.), whose steps are on the order of 1 bp (∼3.4 Å), continues to elude biophysicists. While base-pair stepping by RNA polymerase and helicases have been previously observed with optical tweezers occasionally and over short distances and timescales (9, 10), sufficiently low levels of instrumentation noise even in the most sophisticated instruments are short-lived (typically lasting on the order of tens of seconds) and infrequent enough that upwards of 90% of the data have to be ignored and discarded (9). Thus, extraction of molecular trajectories with base-pair resolution in a reliable and consistent way has not been possible until now.
Here, we compare the resolution of split-path and time-shared optical tweezers instruments under identical conditions. We show that the ability to robustly extract trajectories with single base-pair resolution is limited by low-frequency noise present in the split-path design but not in the time-shared design. We introduce a protocol to experimentally synthesize trajectories simulating single base-pair stepping by a molecular motor. The synthesized data are used to evaluate the fitness of the tether and to test the performance of a Large State Space Hidden Markov Model (LSS-HMM) algorithm in extracting the corresponding molecular trajectories. Finally, we use this same algorithm to extract the full molecular trajectories (steps and dwells) of Escherichia coli RNA polymerase from transcription traces obtained in the time-shared instrument and to characterize the effect of pyrophosphate (PPi) on the distribution of dwell times between steps of the enzyme.
Theory
The fluctuations of a microscopic bead held in a harmonic trap of stiffness are described by its power spectrum. According to the fluctuation-dissipation theorem, the random, uncorrelated forces due to the collisions of surrounding molecules (at a temperature ) give rise to a Lorentzian power spectrum for the position of the bead (in the strongly overdamped regime) (11),
| [1] |
Here, is the drag coefficient, the Boltzmann constant, and the corner frequency, beyond which the system begins to lag behind an external driving stimulus (typically in the kilohertz range for optical traps). Eq. 1 describes how the noise is distributed over frequencies: the spectrum of fluctuations is approximately flat (white noise) at frequencies and decreases as for .
For a measurement at a bandwidth , the mean quadratic displacement of the trapped bead, , can be computed by integrating the power spectrum of the trajectory over frequencies ranging from zero to ,
| [2] |
which yields in the limit of small bandwidth
| [3] |
and in the limit of large bandwidth
| [4] |
The latter result is known as the equipartition theorem.
Ultimately, the quantity that determines whether a displacement of the bead (due, for example, to the displacement of a molecular motor) can be distinguished from all other fluctuation sources is the signal-to-noise ratio ()—that is, the ratio of this extension change to the root-mean-square displacement of the bead, .
Replacing the mean-square displacements obtained in the limits of low and high bandwidths, the signal-to-noise integrated to bandwidth is
| [5] |
and
| [6] |
where is the change in tether tension due to the bead displacement.
Thus, in principle, even very small displacements can be observed with a signal-to-noise ratio greater than one simply by decreasing the bandwidth to well below the corner frequency, provided that the instrument is Brownian noise-limited and that the bandwidth does not compromise the temporal resolution of the experiment. As discussed below, the first of these conditions is rarely fulfilled.
Split-Path Dual-Trap Configuration
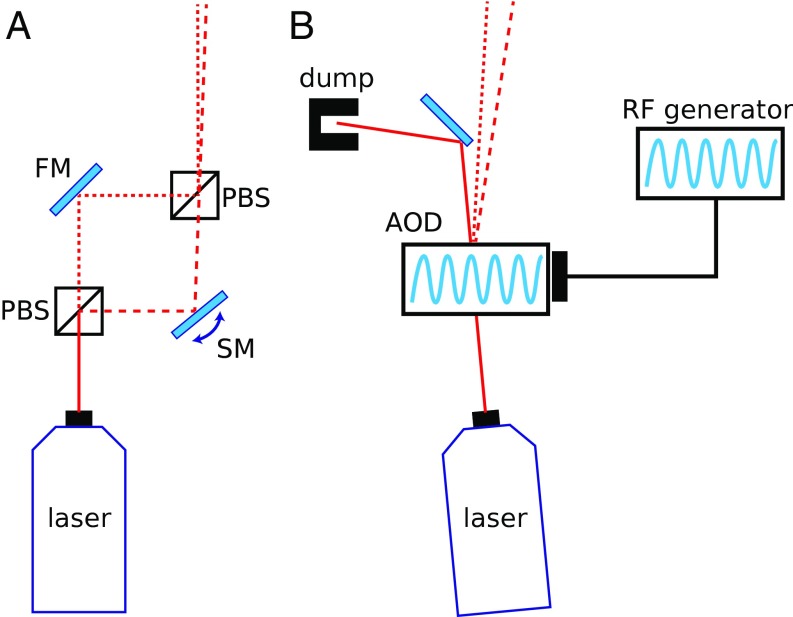
A common assay to record the position of a motor as a function of time is to optically trap a bead that is linked to the motor’s substrate (e.g., a microtubule, a DNA template, etc.), while the motor itself is directly or indirectly attached to another bead held in a second trap (12–14). In this dual-trap assay, the progress of the motor along its track is reported by the distance between the beads (differential detection scheme) (14). Any correlated motion of the two traps does not change the distance between the beads and is thus automatically removed when calculating the trap-to-trap distance. Only anticorrelated motion can contribute to the measured signal (14). In the most common dual-trap configuration, known as the split-path geometry, the two traps are generated by splitting the polarized light of a laser source into two beams that travel through different paths until they are recombined slightly shifted in angle relative to one another and finally sent through the back focal plane of a focusing objective (Fig. 1A).
Fig. 1.
Simplified diagrams of the optical setups. (A) The split-path setup splits the laser light into two orthogonally polarized beams to steer independently one trap (FM, fixed mirror; PBS, polarizing beamsplitter; SM, steerable mirror). (B) Time-sharing the traps with an AOD eliminates the need for the split paths.
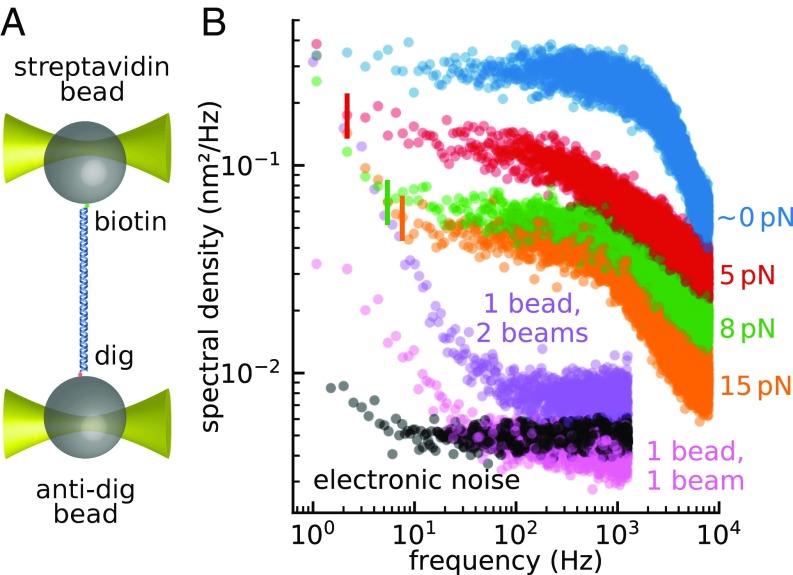
The noise in a split-path dual-trap instrument can be determined by tethering a DNA molecule between two beads held in the traps (Fig. 2A) and by monitoring their net differential displacement over time under applied tensions. The total noise to infinite bandwidth is the sum of correlated and anticorrelated contributions; moreover, its value only depends on the temperature and the combined stiffness of the tether and the traps (Eq. 4). As the tension is increased, the tether stiffens (due to the nonlinear mechanical properties of the DNA) and the beads’ motions become increasingly correlated. Consequently, the anticorrelated component (which is the only one measured in differential detection) must necessarily decrease, both because the total noise decreases and because a larger fraction of it goes in the correlated component (Fig. 2B) (15).
Fig. 2.
Measurement of the noise in a split-path instrument. (A) Two 1-µm beads were tethered by 1 kb DNA, using biotin–streptavidin linkage on one bead and digoxigenin–antidigoxigenin on the other. The beads were trapped using a split-path dual trap. (B) Power spectra of the differential signal were recorded while the tether was held under various tensions: ∼0 pN (blue), 5 pN (red), 8 pN (green), and 15 pN (orange). The vertical lines indicate the frequencies below which a non-Lorentzian component emerges from the Brownian floor. The purple curve shows the power spectrum of the differential signal from a single bead trapped with both trapping beams. The single-bead measurement measures relative drift between the two optical traps as well as contributions from bead-related artifacts (pink) and electronic noise (black).
Note, however, that as the anticorrelated noise is suppressed, a non-Lorentzian noise source becomes apparent at lower frequencies. Because this noise is independent of force, the frequency at which it emerges over the Brownian floor becomes larger as force increases (see vertical lines in Fig. 2B). Although the power spectrum of fluctuations of a bead in a single trap is almost white below the corner frequency (Fig. 3B, blue curve) (16), the power spectra of two tethered beads in all dual traps display this low-frequency noise component (9, 16–19), also known as pink noise. Eq. 5 indicates that resolving single base-pair stepping by RNA polymerase requires using a bandwidth as low as a few hertz (although the exact value depends on the signal-to-noise ratio required for detection, which depends itself on the algorithm used); at this bandwidth, the low-frequency noise, rather than Brownian noise, becomes the resolution-limiting factor.
Fig. 3.
Measurement of the noise of a bead trapped by two colocalized beams in a split-path instrument. (A) A strong and a weak trap were formed in a split-path instrument and were focused onto the same bead. The recorded displacement signal in the two traps shows that the vast majority of the noise occurs in the weak trap signal, suggesting that the anticorrelated signal arises because the two traps are physically drifting relative to each other. (B) The power spectrum of the weak trap signal measured in A exhibits low-frequency pink noise comparable to the one measured on the tethered construct (Fig. 2), whereas no pink noise component is observable in the power spectrum of the strong trap signal. Similarly as in A, this suggests that the increased low-frequency noise in the differential signal is due to relative trap drift.
Several sources for this low-frequency noise have been proposed, including optical turbulence in the split paths, trap positional instability, bead asymmetry, and tether dynamics (9, 17). Indeed, this noise can be reduced—but not eliminated—by replacing air with helium in the optical path or by shortening the length of the split paths (9, 17). However, the origin of the residual noise remains unknown. Here, we establish that a major contributor to the low-frequency noise is the time-dependent change (physical drift) of the trap positions relative to one another.
To characterize the positional stability of the traps in our split-path instrument, we focused both traps onto a single 1 μm-diameter microsphere and monitored the differential signal (). In this dual-beam, single-bead experiment, the differential signal only reports the relative trap displacements at the focal plane (Fig. 2B, purple curve). Note that the low-frequency noise remains present even without a tethered molecule or without any protein coating on the microspheres. Thus, neither tether attachment dynamics nor excess molecules bound to the beads can fully account for the 1/ noise. Notice that the electronic noise floor (Fig. 2B, black curve) is well below the single-bead noise.
In these single-bead experiments, the single trap formed by precisely overlaying the two orthogonally polarized trapping beams emerging from the split path is equivalent to a single beam polarized at 45°. Strikingly, however, when a single 45° polarized beam is focused to trap the bead, the low-frequency noise is reduced significantly (Fig. 2B, pink curve) compared with the same measurement using the beam-steering path (Fig. 2B, purple curve). Finally, focusing a weak and a strong trap onto the same bead and measuring the fluctuations in both channels shows that nearly all of the measured drift occurs in the weaker trap, demonstrating that the anticorrelated signal arises because the two traps physically drift relative to each other (Fig. 3) (drift is mainly encoded into the weak trap since the bead tends to follow the stronger trap). Thus, we conclude that the positional instability of the two traps originates within the beam-steering path of the optical trap and is the main source of the low-frequency noise.
The remaining low-frequency noise above the electronic floor (Fig. 2B, compare pink and black curves) could originate from asymmetry or optical anisotropy of the beads. However, this errant displacement signal (pink curve) contributes an insignificant amount of noise compared with the single bead measurement when the instrument includes the beam-steering path (purple curve).
What causes the positional instability of the traps in the split-path design? Since the positions of the traps depend directly on the angles at which the beams enter the back focal plane of the objective lens, the relative positional stability of the traps is determined by the relative angular stability of the respective beams. To move one trap relative to the other in the split-path design, the orthogonally polarized beams are steered immediately after they are separated and before they are recombined (Fig. 1A) (9, 16–19). The optical components in each path exclusively interact with one of the beams and thus can introduce angular drift between them. Therefore, an alternative way of steering the traps that does not require the light path to be branched can overcome this limitation.
Time-Shared Dual-Trap Configuration
A single beam can be used to form two traps, if its direction is switched at a high rate by an acousto-optic deflector (AOD) (13, 20–25). Two beads, linked by a DNA tether, can be trapped in this system, whose corner frequency is, as before, , where is the total stiffness of the DNA and one of the traps (as only one trap is on at any time). This corner frequency (typically in the kilohertz range) determines the rate above which the AOD must switch the beam direction to keep the beads stationary.
This time-sharing scheme eliminates the need to split the light into two different paths (Fig. 1B) while maintaining the ability to individually steer each trap by controlling the amplitude of the deflection through the AOD. In this scheme, the beams forming each trap never encounter different optical components, and any mechanical drift of these components can only result in a correlated motion of the two traps that is automatically cancelled when calculating the distance between the beads in the traps, (Materials and Methods).
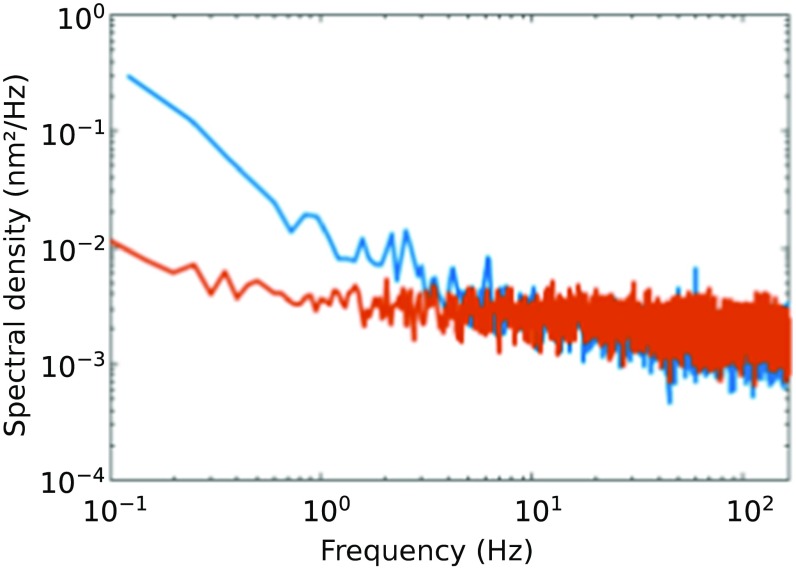
We compared the steady-state stability of a split-path dual-trap and a time-shared dual-trap (both custom-built) under identical conditions, as follows. We linked two polystyrene beads of 1 μm diameter with a 3.5-kb dsDNA by means of streptavidin/biotin and digoxigenin/antidigoxigenin conjugations and held the tether for 5 min under 5 pN of tension. The power spectrum of the differential signal in the time-shared instrument reveals a low-frequency noise more than one order of magnitude smaller than that of the split-path instrument at 0.1 Hz (Fig. 4). A similar conclusion was arrived at using an alternative split-path instrument. This result supports the idea that the relative drift of the split beams is responsible for the low-frequency noise.
Fig. 4.
Power spectra of a split-path (blue) and a time-shared (red) instrument obtained monitoring the extension of a 3.5-kb DNA tether held at 5 pN of tension. 1/f noise dominates at low frequencies, especially in the split-path instrument. Only the portion of the spectra below the corner frequency (f < fc) is shown.
LSS-HMM Algorithm
Most motors take steps of a single, constant size. For such motors, stepping motion may be resolved even if the signal-to-noise ratio is locally smaller than 1. For example, if a motor sometimes takes steps that are sufficiently slow, the step size distribution can be estimated from such slow regions and then be used to elucidate the stepping motion over regions of faster displacement.
Specifically, we adapted the LSS-HMM fitter (26–28), which models the measured trace as arising from a random process, as follows. At any time, the molecular motor is assumed to occupy an unknown position (the “hidden state”), discretized to a small “state size” chosen to be much smaller than the expected step size of the motor—we set it to 0.025 nm (less than 0.1 bp). The position measured by the optical tweezers is modeled as the sum of the actual position of the motor and of a Gaussian error with an unknown but fixed variance . Between each time point, the motor moves by a random amount (zero if the motor is not moving); the size of this displacement (the “step size”) is drawn from an unknown but fixed distribution, .
The procedure to find both the step-size distribution and the noise variance that maximizes the likelihood of observing the trace that was actually measured is called the Baum–Welch algorithm. However, due to the large number of states in the model, a specific optimization (introduced by Felzenzswalb et al.), must be used (26). Unlike most other popular approaches to step-finding (29, 30), the LSS-HMM algorithm learns the distribution of step sizes from the data and can therefore avoid taking large jumps upon encountering an outlier in the trace, all without manual intervention.
Experimental Synthesis of Stepping Trajectories
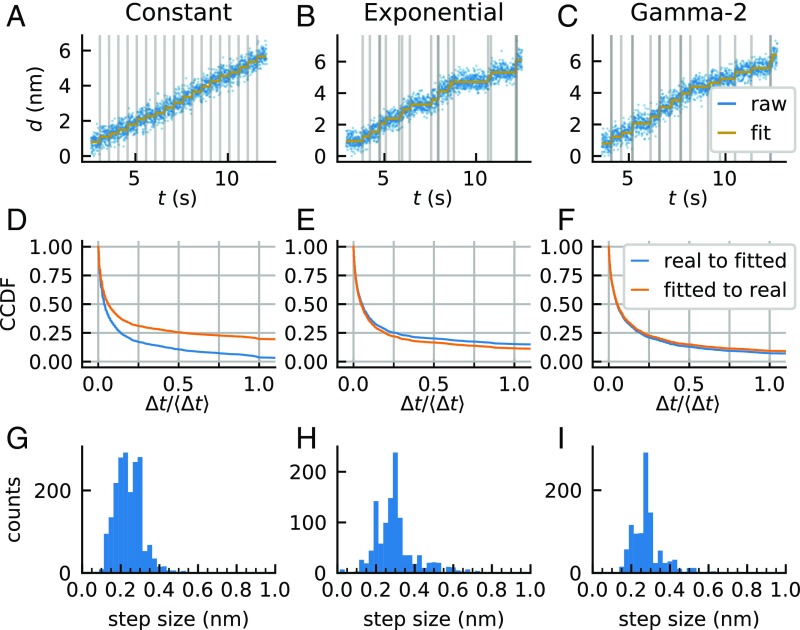
To characterize the resolution capabilities of the time-shared dual-trap, we implemented a procedure using a tethered molecule to experimentally synthesize the molecular trajectories of a motor taking single base-pair steps according to a prespecified dwell time distribution (Fig. 5). We call this procedure “STEPS,” for Stepping Trajectories by ExPerimental Synthesis.
Fig. 5.
Collection and analysis of STEPS data. (A–C) Traps holding tethered beads were displaced away from each other by 0.34 nm at times separated by (A) constant, (B) exponentially distributed, or (C) gamma-2 distributed dwells, in each case with a mean dwell time of Δt = 0.5 s (blue, differential signal at 200 Hz; gray vertical lines, times of actual trap motion), and fitted by VSS-HMM without knowledge of the step size or the stepping times (gold, result of the fit). Good agreement between fitted times and actual trap motion can be observed. (D–F) Blue, complementary cumulative distributions of the time intervals between each real step and the closest fitted step, with the constraint that two real steps may not be associated with the same fitted step. Orange, complementary cumulative distributions of the time intervals between each fitted step and the closest real step, with the constraint that two fitted steps may not be associated with the same real step. The time axis is in units of mean dwell time (〈Δt〉 = 0.5 s). (D) Constant, (E) exponentially distributed, and (F) gamma-2 distributed dwells (SI Materials and Methods, Quantification of the Accuracy of the Fit for STEPS Data). (G–I) Step size distribution in the three cases. (G) Constant, (H) exponentially distributed, and (I) gamma-2 distributed dwells.
To fully reproduce the noise characteristics present in transcription elongation, the STEPS procedure was performed using a stalled elongation complex tethered via a DNA handle to a 1 µm-diameter bead (held in one trap), while the distal end of the DNA template was tethered to another 1-µm bead (in the second trap), yielding a 3.5-kb tether kept under 15 pN of tension. In this geometry, polymerase translocation would cause a corresponding change in bead-to-bead distance. To simulate this motion, we moved one trap toward the other in twenty 0.34-nm (∼1 bp) increments according to various time interval protocols (dwells): constant dwells (Fig. 5A), exponentially distributed dwells (Fig. 5B), and dwells drawn from a gamma distribution with shape parameter 2 (“gamma-2,” Fig. 5C). The second and third cases simulate a molecular motor translocating with one and two rate-limiting steps, respectively.
We used the sum of the displacements of the two beads from their respective traps as the analyzed signal. Because the stiffness of the tether is ∼17 times greater than the joint stiffness of the two traps, ∼94% of the trap displacement is transduced into this total displacement signal, which should thus exhibit steps of ∼0.32 nm (SI Discussion).
Recorded STEPS traces were fitted using the LSS-HMM algorithm, without prior knowledge of the actual step size and trap motion times (see Materials and Methods). In general, at least 70% of the scored steps occurred within 100 ms (i.e., 20% of the mean dwell time) of a real step, and likewise, for at least 70% of the real steps, a step was scored no more than 100 ms away. The only exception is the case of steps separated by a constant dwell time, in which 70% of the scored steps are within 165 ms of their matched real step (Fig. 5 D–F). On the other hand, the step size distributions are relatively broad in all cases (in mean ± SD, constant stepping: 0.24 ± 0.25 nm; exponential: 0.30 ± 0.25 nm; and gamma-2: 0.27 ± 0.25 nm) (Fig. 5 G–I). Thus, interestingly, step times can be correctly obtained even though the step sizes are recovered with limited accuracy (SI Discussion). We note, however, that the width of the step size distribution is not broad in absolute terms compared with step size distributions seen for other motors—it only appears so here because the step size is small compared with the magnitude of the noise.
Full Experimental Trajectories of RNA Polymerase
Analysis of STEPS data allowed us to establish that the time-shared dual-trap instrument used in combination with the LSS-HHM algorithm can score single base-pair steps from synthesized data in an accurate and robust manner. We could now take up the challenge of extracting the full molecular trajectories of individual elongating E. coli RNA polymerase molecules, with base pair resolution and over long distances.
Tethered, stalled elongation complexes were prepared and trapped as described above. Once a stalled elongation complex passed the test of the STEPS protocol, we then delivered 10 μM NTP and recorded the tether extension under a mean tension of 15 pN applied in a direction that assisted forward translocation (Fig. 6A). In this geometry, translocation by the polymerase causes the tension to decrease; whenever the tension dropped below 14 pN, the traps were displaced to restore a tension of 16 pN (“semipassive” mode). At the low NTP concentration of 10 µM, the pause-free transcription velocity is three times slower than the rate used in the STEPS procedure (0.62 bp/s vs. 2 bp/s), and single steps can be resolved. We discarded any trace where the total change in tether extension was less than 5 nm or where extraneous noise was visually obvious (e.g., Fig. S1). All other traces, amounting to 14,625 s of activity covering a distance of 1,589 nm, were taken into account for further analysis.
Fig. 6.
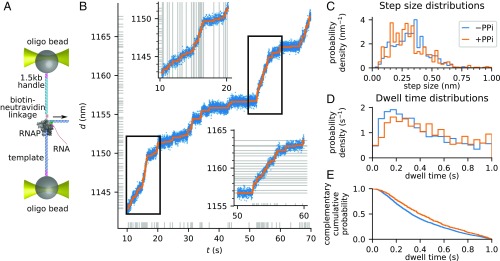
Observation of full molecular trajectories of RNA polymerase at single base-pair resolution. (A) Experimental geometry used to record transcription activity under assisting force, on a time-shared instrument. Details of the construct are presented in Full Experimental Trajectories of RNA Polymerase and SI Materials and Methods, Measurements of STEPS and Transcription Traces. (B) A sample transcription trace, covering 70 bp (blue, raw data) in 1 min, and the fitted molecular trajectory (orange). Horizontal gray ticks indicate the positions of the dwells between two steps. Vertical gray ticks indicate the times of the scored steps. Insets are zooms into the regions marked by black rectangles. Horizontal gray ticks or lines in Insets mark the position of each fitted step, showing that they are separated by ∼0.33 nm. Vertical gray ticks or lines indicate the times of the scored steps. (C) The distribution of fitted step sizes in the absence of PPi (−PPi, blue) is peaked at 0.32 ± 0.15 nm, corresponding to the expected size of 1 bp. The distribution of fitted step sizes in the presence of 100 µM PPi (+PPi, orange) is peaked at 0.30 ± 0.15 nm, corresponding to the expected size of 1 bp. (D) The distributions of dwell times in the absence and presence of PPi are nonexponential but peaked around Δt ∼ 0.2 s. (E) Comparison of the complementary cumulative dwell time distributions in the absence (blue) and presence (orange) of PPi shows that PPi slows down processive elongation by 20%.
The LSS-HMM algorithm failed to converge on a fraction of the traces. Such traces were recursively split into smaller segments until they could be successfully fit, except for segments shorter than 5 s or 10 bp, which were discarded (see Materials and Methods). The data successfully fitted by LSS-HMM amounted to steps from 30 different molecules, corresponding to 6,344 s of activity covering 1,198 nm. Despite the lack of prior assumption on the step size, the histogram of observed step sizes peaks at 0.32 ± 0.15 nm (Fig. 6C), which compares favorably with the expected step size of 0.33 nm at 15 pN as predicted by the worm-like chain equation (15). We were able to recover the single base-pair trajectory with high accuracy in segments as long as 70 bp (Fig. 6B).
Finally, we tested the effect of PPi on the dynamics of RNA polymerase at the base-pair scale. In the presence of PPi, RNA polymerase can catalyze the pyrophosphorolysis of the nascent RNA chain (31). Under intermediate concentrations of PPi, transcription elongation thus occurs at a reduced rate (32). We collected transcription traces in the presence of 100 µM PPi. From 6,730 s of activity, covering a distance of 470 nm, we successfully fitted, using the same procedure as above, steps over 1,509 s of activity, with a step size of (0.30 ± 0.15) nm (Fig. 6C).
Visual inspection of the traces did not reveal significant long-lived pausing events due to the binding of PPi. On the other hand, comparison of the dwell time distributions of the transcribing enzyme in the absence and presence of PPi (Fig. 6 D and E) showed that the enzyme slows down due to a 20% lengthening of the median dwell periods during processive elongation, from 0.33 s to 0.40 s (Mann–Whitney test, P < 10–4). The dwell time distributions were nonexponential in either case but peaked around Δt ≈ 0.2 s.
Conclusions
Optical tweezers is a powerful method to investigate the dynamics of molecular motors. These dynamics are encoded in the interspersed dwells and steps of the molecular trajectories of a motor. The partitioning between these phases and its dependence on various external conditions provide important information about the motor mechanism. However, extracting the full molecular trajectories of motors such as RNA and DNA polymerases, helicases, and other translocases with step sizes of one base pair has been challenging. The spatial resolution of optical tweezers can be improved by increasing the tension applied on the tether (if the motor can remain active under such tension), by shortening or stiffening the handles (33), or by using smaller beads (14). However, most optical tweezer instruments display a noise component that greatly limits their resolution in the frequency range where motor dynamics are monitored. We identified a source of low-frequency noise in the split paths of the most common dual-trap configuration. By using a time-shared scheme, we eliminated path splitting and decreased low-frequency noise more than 10-fold. We also implemented a protocol (STEPS) that allows us to directly check the quality of a tether in real time, before the addition of nucleotide triphosphates, and test the performance of the LSS-HMM step-finding algorithm. Altogether, these improvements permitted us to fully uncover the molecular trajectories of E. coli RNA polymerase at single base-pair resolution in a robust and consistent manner. We have demonstrated the power of this approach by measuring the effect of PPi on the dwell time distribution of actively elongating polymerases.
The ability to resolve single base-pair stepping and the interspersed dwells in a reliable manner and over large distances in optical tweezers opens the possibility to study the subnanometer activity of many molecular motors. For instance, the effect of mutations or antibiotics on the molecular trajectories of RNA polymerase can now be resolved in terms of the phases of the motor’s cycle. Similarly, the ability to precisely follow the enzyme dynamics upon each nucleotide incorporation will make it possible to investigate how the template sequence controls transcription elongation and characterize the dynamics of other important processes such as transcription proofreading (34–36), termination (37–39), or transcription through the nucleosome (40–42) with unprecedented detail.
Materials and Methods
A detailed description of the experimental procedures including instrument setup, sample preparation, data acquisition, and data analysis is included in SI Materials and Methods.
Supplementary Material
Acknowledgments
We dedicate this manuscript to the memory of Ignacio Tinoco Jr. We thank Matthew J. Comstock and Charles Wickersham for advice and help in setting up the time-shared trap and the members of the C.B. laboratory for helpful discussions. This work was supported by Howard Hughes Medical Institute (C.B.), NIH Grants R01GM032543 (to C.B.) and R01GM071552 (to C.B.), and the US Department of Energy Office of Basic Energy Sciences Nanomachine Program under Contract DE-AC02-05CH11231 (to C.B.).
Footnotes
Conflict of interest statement: C.B. and D.J.K. are collaborating on a forthcoming book.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1719906115/-/DCSupplemental.
References
- 1.Schliwa M. Molecular motors. In: Ganten D, Ruckpaul K, editors. Encyclopedic Reference of Genomics and Proteomics in Molecular Medicine. Springer; Berlin: 2006. pp. 1160–1174. [Google Scholar]
- 2.Mallik R, Carter BC, Lex SA, King SJ, Gross SP. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- 3.Svoboda K, Mitra PP, Block SM. Fluctuation analysis of motor protein movement and single enzyme kinetics. Proc Natl Acad Sci USA. 1994;91:11782–11786. doi: 10.1073/pnas.91.25.11782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chemla YR, Moffitt JR, Bustamante C. Exact solutions for kinetic models of macromolecular dynamics. J Phys Chem B. 2008;112:6025–6044. doi: 10.1021/jp076153r. [DOI] [PubMed] [Google Scholar]
- 5.Asbury CL, Fehr AN, Block SM. Kinesin moves by an asymmetric hand-over-hand mechanism. Science. 2003;302:2130–2134. doi: 10.1126/science.1092985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chistol G, et al. High degree of coordination and division of labor among subunits in a homomeric ring ATPase. Cell. 2012;151:1017–1028. doi: 10.1016/j.cell.2012.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cordova JC, et al. Stochastic but highly coordinated protein unfolding and translocation by the ClpXP proteolytic machine. Cell. 2014;158:647–658. doi: 10.1016/j.cell.2014.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sen M, et al. The ClpXP protease unfolds substrates using a constant rate of pulling but different gears. Cell. 2013;155:636–646. doi: 10.1016/j.cell.2013.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Abbondanzieri EA, Greenleaf WJ, Shaevitz JW, Landick R, Block SM. Direct observation of base-pair stepping by RNA polymerase. Nature. 2005;438:460–465. doi: 10.1038/nature04268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cheng W, Arunajadai SG, Moffitt JR, Tinoco I, Jr, Bustamante C. Single-base pair unwinding and asynchronous RNA release by the hepatitis C virus NS3 helicase. Science. 2011;333:1746–1749. doi: 10.1126/science.1206023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Callen HB, Welton TA. Irreversibility and generalized noise. Phys Rev. 1951;83:34–40. [Google Scholar]
- 12.Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: Piconewton forces and nanometre steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 13.Visscher K, Gross SP, Block SM. Construction of multiple-beam optical traps with nanometer-resolution position sensing. IEEE J Sel Top Quantum Electron. 1996;2:1066–1076. [Google Scholar]
- 14.Moffitt JR, Chemla YR, Izhaky D, Bustamante C. Differential detection of dual traps improves the spatial resolution of optical tweezers. Proc Natl Acad Sci USA. 2006;103:9006–9011. doi: 10.1073/pnas.0603342103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 16.Neuman KC, Block SM. Optical trapping. Rev Sci Instrum. 2004;75:2787–2809. doi: 10.1063/1.1785844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bustamante C, Chemla YR, Moffitt JR. High-resolution dual-trap optical tweezers with differential detection: Managing environmental noise. Cold Spring Harb Protoc. 2009;2009:pdb.ip72. doi: 10.1101/pdb.ip72. [DOI] [PubMed] [Google Scholar]
- 18.Mahamdeh M, Schäffer E. Optical tweezers with millikelvin precision of temperature-controlled objectives and base-pair resolution. Opt Express. 2009;17:17190–17199. doi: 10.1364/OE.17.017190. [DOI] [PubMed] [Google Scholar]
- 19.Carter AR, Seol Y, Perkins TT. Precision surface-coupled optical-trapping assay with one-basepair resolution. Biophys J. 2009;96:2926–2934. doi: 10.1016/j.bpj.2008.12.3933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brau RR, Tarsa PB, Ferrer JM, Lee P, Lang MJ. Interlaced optical force-fluorescence measurements for single molecule biophysics. Biophys J. 2006;91:1069–1077. doi: 10.1529/biophysj.106.082602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sasaki K, Koshioka M, Misawa H, Kitamura N, Masuhara H. Pattern formation and flow control of fine particles by laser-scanning micromanipulation. Opt Lett. 1991;16:1463–1465. doi: 10.1364/ol.16.001463. [DOI] [PubMed] [Google Scholar]
- 22.Mio C, Gong T, Terray A, Marr D. Design of a scanning laser optical trap for multiparticle manipulation. Rev Sci Instrum. 2000;71:2196–2200. [Google Scholar]
- 23.Nambiar R, Meiners J-C. Fast position measurements with scanning line optical tweezers. Opt Lett. 2002;27:836–838. doi: 10.1364/ol.27.000836. [DOI] [PubMed] [Google Scholar]
- 24.Valentine MT, et al. Precision steering of an optical trap by electro-optic deflection. Opt Lett. 2008;33:599–601. doi: 10.1364/ol.33.000599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Comstock MJ, Ha T, Chemla YR. Ultrahigh-resolution optical trap with single-fluorophore sensitivity. Nat Methods. 2011;8:335–340. doi: 10.1038/nmeth.1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Felzenszwalb PF, Huttenlocher DP, Kleinberg JM. Fast algorithms for large-state-space HMMs with applications to web usage analysis. In: Thrun S, Saul LK, Schölkopf B, editors. Advances in Neural Information Processing Systems 16. MIT Press; Cambridge, MA: 2004. pp. 409–416. [Google Scholar]
- 27.Müllner FE, Syed S, Selvin PR, Sigworth FJ. Improved hidden Markov models for molecular motors, part 1: Basic theory. Biophys J. 2010;99:3684–3695. doi: 10.1016/j.bpj.2010.09.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Syed S, Müllner FE, Selvin PR, Sigworth FJ. Improved hidden Markov models for molecular motors, part 2: Extensions and application to experimental data. Biophys J. 2010;99:3696–3703. doi: 10.1016/j.bpj.2010.09.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kerssemakers JW, et al. Assembly dynamics of microtubules at molecular resolution. Nature. 2006;442:709–712. doi: 10.1038/nature04928. [DOI] [PubMed] [Google Scholar]
- 30.Kalafut B, Visscher K. An objective, model-independent method for detection of non-uniform steps in noisy signals. Comput Phys Commun. 2008;179:716–723. [Google Scholar]
- 31.Rozovskaya TA, Chenchik AA, Beabealashvilli RSh. Processive pyrophosphorolysis of RNA by Escherichia coli RNA polymerase. FEBS Lett. 1982;137:100–104. doi: 10.1016/0014-5793(82)80323-2. [DOI] [PubMed] [Google Scholar]
- 32.Wang MD, et al. Force and velocity measured for single molecules of RNA polymerase. Science. 1998;282:902–907. doi: 10.1126/science.282.5390.902. [DOI] [PubMed] [Google Scholar]
- 33.Kilchherr F, et al. Single-molecule dissection of stacking forces in DNA. Science. 2016;353:aaf5508. doi: 10.1126/science.aaf5508. [DOI] [PubMed] [Google Scholar]
- 34.Komissarova N, Kashlev M. RNA polymerase switches between inactivated and activated states by translocating back and forth along the DNA and the RNA. J Biol Chem. 1997;272:15329–15338. doi: 10.1074/jbc.272.24.15329. [DOI] [PubMed] [Google Scholar]
- 35.Shaevitz JW, Abbondanzieri EA, Landick R, Block SM. Backtracking by single RNA polymerase molecules observed at near-base-pair resolution. Nature. 2003;426:684–687. doi: 10.1038/nature02191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nudler E. RNA polymerase backtracking in gene regulation and genome instability. Cell. 2012;149:1438–1445. doi: 10.1016/j.cell.2012.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Epshtein V, Dutta D, Wade J, Nudler E. An allosteric mechanism of Rho-dependent transcription termination. Nature. 2010;463:245–249. doi: 10.1038/nature08669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Larson MH, Greenleaf WJ, Landick R, Block SM. Applied force reveals mechanistic and energetic details of transcription termination. Cell. 2008;132:971–982. doi: 10.1016/j.cell.2008.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Koslover DJ, Fazal FM, Mooney RA, Landick R, Block SM. Binding and translocation of termination factor rho studied at the single-molecule level. J Mol Biol. 2012;423:664–676. doi: 10.1016/j.jmb.2012.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kireeva ML, et al. Nucleosome remodeling induced by RNA polymerase II: Loss of the H2A/H2B dimer during transcription. Mol Cell. 2002;9:541–552. doi: 10.1016/s1097-2765(02)00472-0. [DOI] [PubMed] [Google Scholar]
- 41.Bintu L, et al. The elongation rate of RNA polymerase determines the fate of transcribed nucleosomes. Nat Struct Mol Biol. 2011;18:1394–1399. doi: 10.1038/nsmb.2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Teves SS, Weber CM, Henikoff S. Transcribing through the nucleosome. Trends Biochem Sci. 2014;39:577–586. doi: 10.1016/j.tibs.2014.10.004. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.