SUMMARY
Instrumental variables are widely used for estimating causal effects in the presence of
unmeasured confounding. The discrete instrumental variable model has testable implications
for the law of the observed data. However, current assessments of instrumental validity
are typically based solely on subject-matter arguments rather than these testable
implications, partly due to a lack of formal statistical tests with known properties. In
this paper, we develop simple procedures for testing the binary instrumental variable
model. Our methods are based on existing techniques for comparing two treatments, such as
the 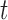 -test and the Gail–Simon test. We illustrate
the importance of testing the instrumental variable model by evaluating the exogeneity of
college proximity using the National Longitudinal Survey of Young Men.
-test and the Gail–Simon test. We illustrate
the importance of testing the instrumental variable model by evaluating the exogeneity of
college proximity using the National Longitudinal Survey of Young Men.
Keywords: Binary response, Gail–Simon test, Instrumental variable, Qualitative interaction, t-test, Two-by-two table
1. INTRODUCTION
The instrumental variable method has been widely used for estimating causal effects in the
presence of unmeasured confounders. A variable 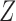 is called an instrumental
variable if: (a) it is independent of unmeasured confounders
is called an instrumental
variable if: (a) it is independent of unmeasured confounders 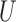 ; (b) it
does not have a direct effect on the outcome
; (b) it
does not have a direct effect on the outcome 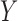 ; (c) it has a nonzero
average causal effect on the treatment
; (c) it has a nonzero
average causal effect on the treatment 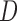 (Angrist et al., 1996). In many applications, assumption (a) is reasonable
only after controlling for observed covariates
(Angrist et al., 1996). In many applications, assumption (a) is reasonable
only after controlling for observed covariates 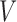 (Baiocchi et al., 2014). The resulting model is called the conditional
instrumental variable model. Figure 1 gives a directed
acyclic graphical model representation (Pearl, 2009)
of the conditional instrumental variable model, in which the faithfulness (Spirtes et al., 2000) of the edge
(Baiocchi et al., 2014). The resulting model is called the conditional
instrumental variable model. Figure 1 gives a directed
acyclic graphical model representation (Pearl, 2009)
of the conditional instrumental variable model, in which the faithfulness (Spirtes et al., 2000) of the edge
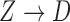 is assumed.
is assumed.
Fig. 1.
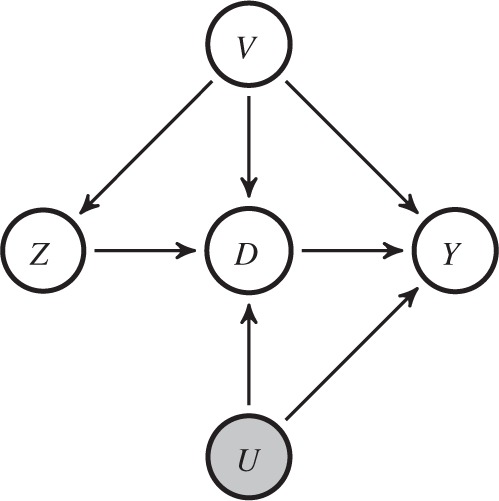
Directed acyclic graph representing an instrumental variable model. The variables
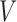 ,
, 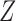 ,
,
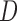 and
and 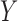 are
observed;
are
observed; 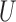 is unobserved.
is unobserved.
Unlike the assumption of no unmeasured confounders between 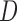 and
and
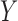 , the instrumental variable model with
discrete observables
, the instrumental variable model with
discrete observables 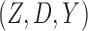 imposes nontrivial constraints on the
observed-data distribution. In particular, Balke & Pearl
(1997) and Bonet (2001) give the following
necessary and sufficient condition for an observed-data distribution
imposes nontrivial constraints on the
observed-data distribution. In particular, Balke & Pearl
(1997) and Bonet (2001) give the following
necessary and sufficient condition for an observed-data distribution
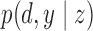 to be compatible with an
unconditional binary instrumental variable model where
to be compatible with an
unconditional binary instrumental variable model where  ,
,
 and
and  take
values
take
values 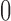 and
and 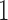 :
:
| (1) |
Here the unconditional instrumental variable model refers to the model with an empty
control variable set 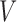 . In particular, if the potential instrument
. In particular, if the potential instrument
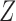 is randomized so that assumption (a) holds,
then violation of each inequality in (1)
corresponds to a nonzero average controlled direct effect of
is randomized so that assumption (a) holds,
then violation of each inequality in (1)
corresponds to a nonzero average controlled direct effect of 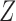 on
on
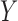 , which violates assumption (b) (Cai et al., 2008; Richardson et al., 2011). Although assumption (c) imposes on the observables the
constraint
, which violates assumption (b) (Cai et al., 2008; Richardson et al., 2011). Although assumption (c) imposes on the observables the
constraint
| (2) |
it is in general not possible to reject (2) with a statistical test. Hence hereafter we do not discuss constraint (2). Similarly, the testable implications of a conditional binary instrumental variable model are given by
| (3) |
where 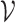 contains all possible values for
contains all possible values for
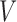 . In practice, the inequalities (1) can be used to partially test the binary
unconditional instrumental variable model. Likewise, (3) can be used to test the binary conditional instrumental variable
model. In contrast, it is impossible to empirically falsify the assumption of no unmeasured
confounders between
. In practice, the inequalities (1) can be used to partially test the binary
unconditional instrumental variable model. Likewise, (3) can be used to test the binary conditional instrumental variable
model. In contrast, it is impossible to empirically falsify the assumption of no unmeasured
confounders between 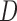 and
and 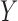 as in an
observational study without an instrument.
as in an
observational study without an instrument.
Although there have been many discussions of estimation of causal effects under the binary
instrumental variable model (Vansteelandt et al.,
2011; Clarke & Windmeijer, 2012), less
attention has been paid to testing its validity. Prior to our work, Ramsahai & Lauritzen (2011) considered testing an unconditional
binary instrumental variable model using a likelihood ratio test. Their approach involves
solving a constrained optimization problem and cannot be used to test the conditional binary
instrumental variable model as described by Fig. 1.
Furthermore, their approach tests the four inequalities in (1) jointly. Hence, without modification, it can only be used to
falsify the binary instrumental variable model, but cannot identify which specific average
controlled direct effect of 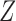 on
on 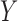 must be
positive or negative. In related work, Kang et al.
(2013) provided a falsification test for the instrumental variable assumptions
given knowledge of a subpopulation where the edge
must be
positive or negative. In related work, Kang et al.
(2013) provided a falsification test for the instrumental variable assumptions
given knowledge of a subpopulation where the edge 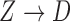 is absent.
In this paper we develop a novel perspective on falsification of the binary instrumental
variable model. Specifically, we show that testing (1) or (3) is
equivalent to testing for a nonpositive effect of the instrument
is absent.
In this paper we develop a novel perspective on falsification of the binary instrumental
variable model. Specifically, we show that testing (1) or (3) is
equivalent to testing for a nonpositive effect of the instrument 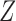 on a
constructed variable.
on a
constructed variable.
2. TESTS FOR THE UNCONDITIONAL BINARY INSTRUMENTAL VARIABLE MODEL
To fix ideas, we first consider testing the instrumental variable inequality
| (4) |
Equation (4) can be rewritten as
Define a new variable
where 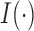 is the indicator function. It then follows that
is the indicator function. It then follows that
Testing (4) is therefore equivalent to the testing problem
| (5) |
which is simply one-sided testing for a  table.
table.
In general, we have four inequalities of the form (4) with a binary instrumental variable model, so multiplicity
adjustment is needed. Suppose for now that we have one-sided tests 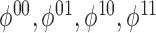 such
that the size of
such
that the size of 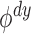 goes to zero asymptotically in the
interior of the null space defined by
goes to zero asymptotically in the
interior of the null space defined by 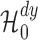 .
Furthermore, assume that the rejection region of
.
Furthermore, assume that the rejection region of 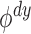 has no
intersection with the null space defined by
has no
intersection with the null space defined by 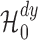 (Perlman & Wu, 1999). To get a
level-
(Perlman & Wu, 1999). To get a
level-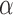 test for (1), a naive Bonferroni correction would
require that each
test for (1), a naive Bonferroni correction would
require that each 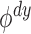 have size less than or equal to
have size less than or equal to
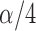 for testing
for testing
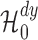 . However, the left-hand
sides of the four inequalities in (1)
sum to 2, and hence at most two of them can simultaneously hold with equality. Based on
this, we now show that it suffices to control the level of each test
. However, the left-hand
sides of the four inequalities in (1)
sum to 2, and hence at most two of them can simultaneously hold with equality. Based on
this, we now show that it suffices to control the level of each test
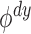 at
at 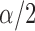 .
.
Specifically, let 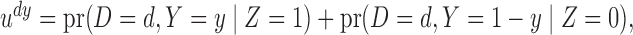 and let
and let 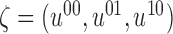 . The null
space defined by (1) can be represented
by an octahedron
. The null
space defined by (1) can be represented
by an octahedron 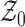 in the simplex
in the simplex
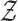 , where
, where 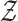 is defined as
is defined as
Figure 2 gives a graphical depiction of
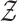 and
and  . Each of the four blue-shaded
facets corresponds to one inequality in (1) holding with equality. Six points, shown in red, have two inequalities in
(1) holding with equality. The
interior of the null space
. Each of the four blue-shaded
facets corresponds to one inequality in (1) holding with equality. Six points, shown in red, have two inequalities in
(1) holding with equality. The
interior of the null space 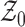 corresponds to cases where none
of the four inequalities in (1) holds
with equality.
corresponds to cases where none
of the four inequalities in (1) holds
with equality.
Fig. 2.
Representation of the simplex  and the
null space
and the
null space 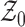 . The edges of the simplex
. The edges of the simplex
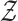 are represented by thick
black lines, and the null space
are represented by thick
black lines, and the null space 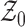 is the
octahedron whose vertices are shown in red; four of the eight surfaces are shaded
blue.
is the
octahedron whose vertices are shown in red; four of the eight surfaces are shaded
blue.
We are now ready to present our multiplicity adjustment procedure. The proof of Theorem 1 is given in the Appendix.
THEOREM 1.
Propose a testing procedure as follows: reject (1) if for
and
at least one of
is rejected by
at level
. Under the null hypotheses (1):
(i) if two inequalities in (1) hold with equality at the true value
, then the proposed test has size
;
(ii) if only one of the inequalities in (1) holds with equality at the true value
, then asymptotically the proposed test has size
;
(iii) if none of the inequalities in (1) holds with equality at the true value
, then asymptotically the proposed test has size
.
In particular, the proposed test always has asymptotic size no greater than
.
We now turn to the choice of 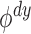 . Over the past century, there has
been much discussion on testing association in
. Over the past century, there has
been much discussion on testing association in 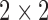 tables, including
size and power comparisons for different test statistics and methods of computing the
tables, including
size and power comparisons for different test statistics and methods of computing the
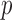 -value; see Lydersen et al. (2009) for a review. When the sample size is large, asymptotic
tests such as those based on the
-value; see Lydersen et al. (2009) for a review. When the sample size is large, asymptotic
tests such as those based on the 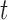 -statistic are popular
among researchers. However, under independent and identically distributed sampling they may
not preserve the test size with small samples, in which case unconditional exact tests such
as the Fisher–Boschloo test are recommended.
-statistic are popular
among researchers. However, under independent and identically distributed sampling they may
not preserve the test size with small samples, in which case unconditional exact tests such
as the Fisher–Boschloo test are recommended.
Remark 1.
The computation time for unconditional tests can be excessive when the sample size is moderate or large, in which case it may be desirable to use the procedure of Berger & Boos (1994) to reduce computation time. The proposed test still has asymptotic size no greater than
provided
, where
is the confidence level for the nuisance parameter.
Remark 2.
The Wald test for the
table corresponding to (5) coincides with the Wald test for (4), where
and
are estimated via maximum likelihood. However, our introduction of
builds the connection between testing unconditional instrumental inequalities and testing
tables, and hence motivates many more approaches to testing the unconditional instrumental inequalities.
We now discuss the interpretation of results from our testing procedure. As noted by Cai et al. (2008) and Richardson et al. (2011), under the randomization assumption, the average
controlled direct effect of 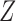 on
on 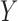 ,
,
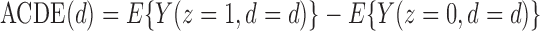 ,
satisfies
,
satisfies
| (6) |
It follows that violation of each inequality in (1) corresponds to a nonzero average controlled direct effect of
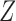 on
on 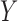 . Our testing procedure is
therefore interpretable in the sense that if we reject the binary instrumental variable
model, we would also know which average controlled direct effect is positive or negative.
For example, suppose we reject the null that
. Our testing procedure is
therefore interpretable in the sense that if we reject the binary instrumental variable
model, we would also know which average controlled direct effect is positive or negative.
For example, suppose we reject the null that 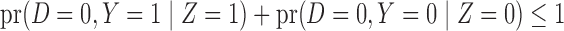 ,
then from (6) we would also conclude
that
,
then from (6) we would also conclude
that  is positive.
is positive.
3. TESTS FOR THE CONDITIONAL BINARY INSTRUMENTAL VARIABLE MODEL
Suppose now we wish to test the instrumental variable inequality that
| (7) |
Using the same arguments as in § 2, we can rewrite the testing problem of (7) as
| (8) |
where 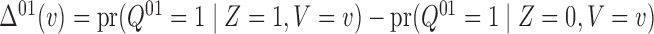 and a subscript c denotes conditional.
and a subscript c denotes conditional.
The testing problem (8) concerns the
null hypothesis that a particular treatment is at least as good as the other treatment in
all subsets of units, which has been studied extensively. For example, with
 discrete, the Gail–Simon test for qualitative
interaction can be used to test hypotheses of the form (8) with a slight modification (Gail
& Simon, 1985 p. 364). Chang et al.
(2015) considered the problem with a general
discrete, the Gail–Simon test for qualitative
interaction can be used to test hypotheses of the form (8) with a slight modification (Gail
& Simon, 1985 p. 364). Chang et al.
(2015) considered the problem with a general 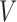 based on
based on
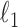 -type functionals of uniformly
consistent nonparametric kernel estimators of
-type functionals of uniformly
consistent nonparametric kernel estimators of 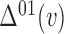 . These tests
make no assumptions on the functional form of
. These tests
make no assumptions on the functional form of 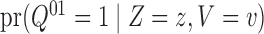 , which is
particularly appealing as
, which is
particularly appealing as 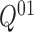 is not directly interpretable.
is not directly interpretable.
As we have four hypotheses of the form (7), a multiplicity adjustment is warranted. However, unlike the case with
unconditional instrumental variable models, the four inequalities in (3) can be violated simultaneously, as each
of them concerns multiple covariate values. In other words, no result analogous to Theorem 1
holds unless 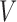 takes only one value. Instead, a naive
Bonferroni correction may be used to account for multiple comparisons so that to get an
overall level-
takes only one value. Instead, a naive
Bonferroni correction may be used to account for multiple comparisons so that to get an
overall level-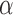 test, hypotheses of the form (7) are tested at level
test, hypotheses of the form (7) are tested at level
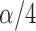 .
.
Remark 3.
When
is discrete, one can alternatively apply Theorem 1 to test, for each
, the hypotheses
(9) and then use a Bonferroni correction to account for multiple testing due to levels of
. In this way, each hypothesis in (9) is tested at level
, where
is the number of possible levels for
. Since tests of the forms (7) and (9) are different, neither approach generally dominates the other.
Remark 4.
The Gail–Simon test examines the hypotheses (3) for all possible values of
simultaneously. Alternatively, it may be tempting to test (3) for different levels of
and claim that
is a valid instrument within the subset of the population for which the hypotheses (3) are not rejected. Failure to violate an instrumental variable inequality, however, does not prove that
is an instrument. This will ultimately rest on whether, based on subject-matter knowledge, we believe that we have measured enough covariates
to control confounding, as well as subject-matter arguments for the absence of direct effects of
on
.
Consequently, one should avoid using the test (3) as a way to restrict the range of
, unless a substantive argument could be made that
is an instrument for one range of
but not for another.
4. THE CAUSAL EFFECT OF EDUCATION ON EARNINGS
We illustrate the use of the proposed tests by examining the instrumental variable model assumed by Okui et al. (2012). The goal of their analysis was to estimate the causal effect of education on earnings. To account for unobserved preferences for education levels, Okui et al. (2012) followed Card (1995) and used presence of a nearby four-year college as an instrument. The validity of this approach relies on the assumptions that college proximity affects earnings only through education and, conditional on adjusted potential confounders, college proximity is independent of underlying factors that also affect earnings. These assumptions, however, are hardly watertight. In fact, as pointed out by Card (1995), living near a college may influence earnings through higher elementary and secondary school quality, and it may also be associated with higher motivation to achieve labour market success.
To investigate the possible exogeneity of college proximity, we use the dataset provided by
Okui et al. (2012), which contains 3010
observations from the National Longitudinal Survey of Young Men. Following Tan (2006), we consider education after high school as
the treatment 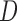 . The outcome wage is dichotomized at its
median. For illustrative purposes, we consider three instrumental variable models with
nested sets of covariates: (I) experience only; (II) experience and race; (III) experience,
race and region of residence. The third set was also considered previously by Okui et al. (2012). We use the Gail–Simon test with
Bonferroni correction to examine the testable implications of these instrumental variable
models.
. The outcome wage is dichotomized at its
median. For illustrative purposes, we consider three instrumental variable models with
nested sets of covariates: (I) experience only; (II) experience and race; (III) experience,
race and region of residence. The third set was also considered previously by Okui et al. (2012). We use the Gail–Simon test with
Bonferroni correction to examine the testable implications of these instrumental variable
models.
Table 1 summarizes the test results. The model
conditional only on experience is rejected by the proposed test. The
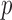 -value from the test on
-value from the test on
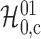 is significant
at the 0
is significant
at the 0 05 level, and the
05 level, and the
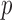 -value from the test on
-value from the test on
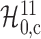 is also
borderline significant. These show that either college proximity has positive {direct}
effects on earnings in some subgroups, or after adjusting for experience college proximity
is still correlated with unmeasured confounders such as underlying motivation for labour
market success. The proposed test fails to reject the instrumental variable model of Okui et al. (2012). However, as we discussed in Remark 4,
with large sample sizes, failure to violate the instrumental variable inequalities shows
that an instrumental variable model is compatible with the observed data, but does not
validate such a model. Specifically, if one believes that the sample size is sufficiently
large, then the results in Table 1 show that the instrumental variable model of Okui et al. (2012) is compatible with the observed data.
One should use their model if one also believes that college proximity affects earnings only
through education, and that there is no unmeasured confounding after adjusting for
experience, race and region of residence. In contrast, one should not trust the instrumental
variable model conditional only on experience, regardless of one’s prior substantive
belief.
is also
borderline significant. These show that either college proximity has positive {direct}
effects on earnings in some subgroups, or after adjusting for experience college proximity
is still correlated with unmeasured confounders such as underlying motivation for labour
market success. The proposed test fails to reject the instrumental variable model of Okui et al. (2012). However, as we discussed in Remark 4,
with large sample sizes, failure to violate the instrumental variable inequalities shows
that an instrumental variable model is compatible with the observed data, but does not
validate such a model. Specifically, if one believes that the sample size is sufficiently
large, then the results in Table 1 show that the instrumental variable model of Okui et al. (2012) is compatible with the observed data.
One should use their model if one also believes that college proximity affects earnings only
through education, and that there is no unmeasured confounding after adjusting for
experience, race and region of residence. In contrast, one should not trust the instrumental
variable model conditional only on experience, regardless of one’s prior substantive
belief.
Table 1.
The 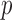 -values and numbers of subgroups
obtained from partial tests for the binary instrumental variable models using
college proximity as an instrument for education after high school
-values and numbers of subgroups
obtained from partial tests for the binary instrumental variable models using
college proximity as an instrument for education after high school
Covariate set 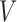
|
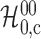
|
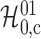
|
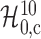
|
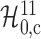
|
Number of subgroups |
|---|---|---|---|---|---|
| (I) | 1 000 000 |
0 010 010 |
1 000 000 |
0 034 034 |
24 |
| (II) | 1 000 000 |
0 132 132 |
1 000 000 |
0 143 143 |
47 |
| (III) | 1 000 000 |
1 000 000 |
1 000 000 |
1 000 000 |
819 |
5. DISCUSSION
Although instrumental variable methods are widely used to identify causal effects in the presence of unmeasured confounding, their assumptions have mainly been assessed based on subject-matter arguments rather than statistical evidence. However, there are controversies about the validity of many instruments, especially if they are not randomized; for example, see Rosenzweig & Wolpin (2000) for a discussion on using natural experiments as instruments. Therefore, it should be routine to check the instrumental variable model against the observed data; see also Didelez et al. (2010). In this paper, we introduce a simple method for testing the binary instrumental variable model.
Our approach can be extended to test discrete instrumental variable models with binary outcomes. According to Pearl (1995), testable implications in this case include
| (10) |
where
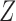 takes values in
takes values in 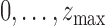 and
and
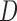 takes values in
takes values in 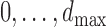 . With slight
modifications of the multiplicity adjustments, the techniques introduced in this paper can
be used to test the inequalities (10);
see the Appendix for details. In general, there are other observed-data constraints implied
by the discrete instrumental variable model (Bonet,
2001), the testing of which is an interesting topic for future research.
. With slight
modifications of the multiplicity adjustments, the techniques introduced in this paper can
be used to test the inequalities (10);
see the Appendix for details. In general, there are other observed-data constraints implied
by the discrete instrumental variable model (Bonet,
2001), the testing of which is an interesting topic for future research.
Monotonicity is also often assumed in instrumental variable analysis. See Huber & Mellace (2015) for a joint test of the unconditional instrumental variable model and the monotonicity assumption. A future research problem would be to extend the proposed method to test the binary instrumental variable model under monotonicity.
Although we have focused primarily on testing the binary instrumental variable model, as we
explain in § 2, with randomized experiments our
proposed tests can be directly applied to identify the sign of the average controlled direct
effects 
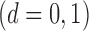 .
These average controlled direct effects quantify the extent to which the randomized
treatment
.
These average controlled direct effects quantify the extent to which the randomized
treatment 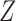 affects the outcome
affects the outcome
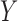 not through the mediator
not through the mediator
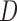 , and are important for explaining causal
mechanisms.
, and are important for explaining causal
mechanisms.
ACKNOWLEDGEMENT
We thank Chengchun Shi for helpful comments. This research was supported by the U.S. National Institutes of Health and Office of Naval Research. This work was initiated when the first author was a graduate student at the University of Washington.
Appendix
Proof of Theorem 1
The second and third claims in Theorem 1 follow directly from the assumption that the
size of 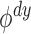 goes to zero asymptotically in
the interior of the null space defined by
goes to zero asymptotically in
the interior of the null space defined by 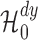 . We
now consider the case where two inequalities in (1) hold with equality at the true value
. We
now consider the case where two inequalities in (1) hold with equality at the true value 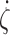 . Without loss of generality, we
assume
. Without loss of generality, we
assume 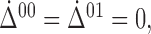 where the dot denotes the true value. As
where the dot denotes the true value. As 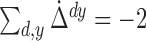 and
and
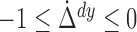
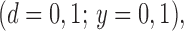 we immediately get that for
we immediately get that for
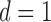 and
and 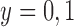 ,
,
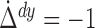 } and hence
} and hence
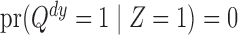 and
and
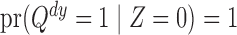 . As a
result, for
. As a
result, for 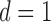 and
and 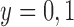 {one cannot reject
{one cannot reject 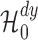 , with probability 1}. On
the other hand, as at most one of
, with probability 1}. On
the other hand, as at most one of 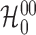 and
and
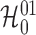 can be violated
empirically, they cannot be rejected simultaneously given our assumptions on
can be violated
empirically, they cannot be rejected simultaneously given our assumptions on
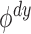 . The probability of rejecting at
least one of
. The probability of rejecting at
least one of 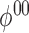 and
and 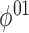 therefore equals
therefore equals
 in this case.
in this case.
Multiplicity adjustment with the discrete instrumental variable model
The constraints in (10) can be written as
| (A1) |
There are 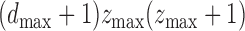 inequalities in (A1), the left-hand sides of which sum to
inequalities in (A1), the left-hand sides of which sum to 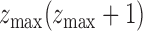 . Hence at
most
. Hence at
most 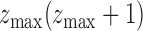 of them
can hold with equality simultaneously. Similar to Theorem 1, the proposed testing
procedure for the unconditional discrete instrumental variable model proceeds as follows:
reject (A1) if for
of them
can hold with equality simultaneously. Similar to Theorem 1, the proposed testing
procedure for the unconditional discrete instrumental variable model proceeds as follows:
reject (A1) if for 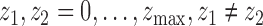 and
and 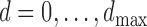 , at least one of
the hypotheses in (A1), denoted as
, at least one of
the hypotheses in (A1), denoted as 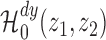 , is rejected by
the corresponding
, is rejected by
the corresponding 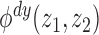 at level
at level
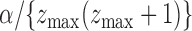 .
For the conditional discrete instrumental variable model, the Bonferroni correction is
appropriate; see also Remark 3.
.
For the conditional discrete instrumental variable model, the Bonferroni correction is
appropriate; see also Remark 3.
References
- Angrist J. D. Imbens G. W. & Rubin D. B. (1996). Identification of causal effects using instrumental variables. J. Am. Statist. Assoc. 91, 444–55. [Google Scholar]
- Baiocchi M. Cheng J. & Small D. S. (2014). Instrumental variable methods for causal inference. Statist. Med. 33, 2297–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balke A. & Pearl J. (1997). Bounds on treatment effects from studies with imperfect compliance. J. Am. Statist. Assoc. 92, 1171–6. [Google Scholar]
-
Berger R. L. & Boos D.
D. (1994).
 values maximized over a confidence set
for the nuisance parameter. J. Am. Statist.
Assoc. 89,
1012–6. [Google Scholar]
values maximized over a confidence set
for the nuisance parameter. J. Am. Statist.
Assoc. 89,
1012–6. [Google Scholar] - Bonet B. (2001). Instrumentality tests revisited. In Proc. 17th Conf. Uncert. Artif. Intel., Breese J. & Koller D. eds. San Francisco, California: Morgan Kaufmann Publishers, pp. 48–55. [Google Scholar]
- Cai Z. Kuroki M. Pearl J. & Tian J. (2008). Bounds on direct effects in the presence of confounded intermediate variables. Biometrics 64, 695–701. [DOI] [PubMed] [Google Scholar]
- Card D. (1995). Using geographic variation in college proximity to estimate the return to schooling. In Aspects of Labour Market Behaviour: Essays in Honour of John Vanderkamp, Christofides L. N. Swidinsky R. & Grant E. K. eds. Toronto: University of Toronto Press, pp. 201–22. [Google Scholar]
- Chang M. Lee S. & Whang Y.-J. (2015). Nonparametric tests of conditional treatment effects with an application to single-sex schooling on academic achievements. Economet. J. 18, 307–46. [Google Scholar]
- Clarke P. S. & Windmeijer F. (2012). Instrumental variable estimators for binary outcomes. J. Am. Statist. Assoc. 107, 1638–52. [Google Scholar]
- Didelez V. Meng S. & Sheehan N. A. (2010). Assumptions of IV methods for observational epidemiology. Statist. Sci. 25, 22–40. [Google Scholar]
- Gail M. & Simon R. (1985). Testing for qualitative interactions between treatment effects and patient subsets. Biometrics 41, 361–72. [PubMed] [Google Scholar]
- Huber M. & Mellace G. (2015). Testing instrument validity for LATE identification based on inequality moment constraints. Rev. Econ. Statist. 97, 398–411. [Google Scholar]
- Kang H. Kreuels B. Adjei O. Krumkamp R. May J. & Small D. S. (2013). The causal effect of malaria on stunting: A Mendelian randomization and matching approach. Int. J. Epidemiol. 42, 1390–8. [DOI] [PubMed] [Google Scholar]
-
Lydersen S. Fagerland M. W. &
Laake P.
(2009). Recommended tests for association in
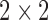 tables. Statist. Med. 28,
1159–75. [DOI] [PubMed] [Google Scholar]
tables. Statist. Med. 28,
1159–75. [DOI] [PubMed] [Google Scholar] - Okui R. Small D. S. Tan Z. & Robins J. M. (2012). Doubly robust instrumental variable regression. Statist. Sinica 22, 173–205. [Google Scholar]
- Pearl J. (1995). Causal inference from indirect experiments. Artif. Intel. Med. 7, 561–82. [DOI] [PubMed] [Google Scholar]
- Pearl J. (2009). Causality. Cambridge: Cambridge University Press. [Google Scholar]
- Perlman M. D. & Wu L. (1999). The emperor’s new tests. Statist. Sci. 14, 355–69. [Google Scholar]
- Ramsahai R. & Lauritzen S. (2011). Likelihood analysis of the binary instrumental variable model. Biometrika 98, 987–94. [Google Scholar]
- Richardson T. S. Evans R. J. & Robins J. M. (2011). Transparent parameterizations of models for potential outcomes. Bayesian Statist. 9, 569–610. [Google Scholar]
- Rosenzweig M. R. & Wolpin K. I. (2000). Natural “natural experiments” in economics. J. Econ. Lit. 38, 827–74. [Google Scholar]
- Spirtes P. Glymour C. N. & Scheines R. (2000). Causation, Prediction, and Search. Cambridge, Massachusetts: MIT Press. [Google Scholar]
- Tan Z. (2006). Regression and weighting methods for causal inference using instrumental variables. J. Am. Statist. Assoc. 101, 1607–18. [Google Scholar]
- Vansteelandt S. Bowden J. Babanezhad M. & Goetghebeur E. (2011). On instrumental variables estimation of causal odds ratios. Statist. Sci. 26, 403–22. [Google Scholar]


